JVLA - Basic and Advanced Imaging in CASA
- Topical guide, part 2 of 2
- This CASA guide is designed for CASA 4.5.2
Overview
This CASA guide will cover data calibration and advanced imaging. Topics in this guide include several CLEAN algorithms, Multi-Scale (MS) deconvolution on regular images, Multi Scale-Multi Frequency Synthesis (MS-MFS), imaging in widefield mode, which will make use of w and aw-projection algorithms, imaging outlier fields, and spectral indices. We will also briefly cover image weights, tapering, small scale bias, primary beam corrections, and modifying image headers.
JVLA - Importing and Initial Flagging in CASA:Part 1 of the guide covered the importing of the dataset, time-averaging, and data flagging, including shadow, zero-clipping, tfcrop, rflag, quacking, and online flagging.
We will be utilizing data taken with the Karl G. Jansky, Very Large Array, of a supernova remnant G055.7+3.4.. The data were taken on August 23, 2010, in the first D-configuration for which the new wide-band capabilities of the WIDAR (Wideband Interferometric Digital ARchitecture) correlator were available. The 8-hour-long observation includes all available 1 GHz of bandwidth in L-band, from 1-2 GHz in frequency.
The guide will reference the CASA cookbook which can be downloaded here.
Obtaining the Data
We will be utilizing the time-averaged and flagged data from part 1. If you'd like to skip the first part of the tutorial and delve into part 2, you can acquire the measurement set for this tutorial here.
Start and confirm your version of CASA
Start CASA by typing casa on a terminal command line. If you have not used CASA before, some helpful tips are available on the Getting Started in CASA page.
This guide has been written for CASA release 4.5.2. Please confirm your version before proceeding by checking the message in the command line interface window or the CASA logger after startup.
Calibrating Data
Now that we are satisfied with the RFI excision, we will move on to the calibration stage.
Flux Density Scale
Since we will be using 3C147 as the source of the absolute flux scale for this observation, we must first run setjy to set the appropriate model amplitudes for this source.
If the flux calibrator is spatially resolved, it is necessary to include a model image as well. Although 3C147 is not resolved at L-band in D configuration, we include the model image here for completeness.
First, we use the listmodimages parameter to find the model image path:
# In CASA
setjy(vis='SNR_G55_10s.ms', listmodels=True)
This lists any images in the current working directory as well as images in CASA's repository. In this second list, we see that there is "3C147_L.im", which is appropriate for our flux calibrator and band, and that it is in the directory "/home/casa/packages/RHEL6/release/casa-release-4.4.0/data/nrao/VLA/CalModels ". We can optionally give the full path of the model image, but setjy should now be able to locate it by name alone:
# In CASA
setjy(vis='SNR_G55_10s.ms', field='0542*', scalebychan=True, model='3C147_L.im')
- scalebychan=True: scales the model flux density value for each channel.
Note: The task setjy uses the Perley-Butler 2010 standard by default. Periodically, the flux density scale at the VLA is revised, updated, or expanded. The most recent standard is Perley-Butler 2013, and can be used by explicitly setting standard='Perley-Butler 2013' in the task. See help setjy for more details.
Ionospheric TEC Corrections
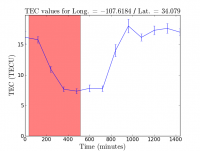
Low frequency observations (4 through S Bands) are affected by the ionosphere conditions. A delay can be introduced into the signal path, which is proportional to the Total Electron Content (TEC) along the line of sight, and is inversely proportional to the square of the frequency. We can apply a correction by utilizing GPS measurements taken at two different frequencies from the International GPS Services (IGS) website. We will utilize the gencal task with paramter caltype set to 'tecim'. This should generate a plot of TEC vs Time for the VLA site, for the day of the observation.
# In CASA
tec_image, tec_rms_image = tec_maps.create(vis='SNR_G55_10s.ms',doplot=True)
gencal(vis='SNR_G55_10s.ms',caltable='SNR_G55_10s.tecim',caltype='tecim',infile=tec_image)
The resulting images can be inspected with the CASA viewer task. As we can see, there was a lot of ionospheric activity on this particular day, therefore applying this correction can result in a better image quality for low-band observing.
Delay and Bandpass Calibration
We will follow a similar procedure as the one outlined in part 1, when we created the preliminary bandpass calibration table SN_G55_10s.initPh. This time, we will use the actual designated bandpass calibration source 0542+498=3C147. Although the phase calibration source used previously (J1925+2106) has the advantage of having been observed throughout the run, it has an unknown spectrum which could introduce amplitude slopes to each spectral window. In addition, we will calibrate the residual antenna-based delays (for further information on this topic, please see this tutorial: [[1]].)
As before, we first generate a phase-only gain calibration table that will be used to help smooth-out the phases before running bandpass itself:
# In CASA
gaincal(vis='SNR_G55_10s.ms', field = '2',
caltable='SNR_G55_10s.initPh.2',
spw='*:45~49', solint='int', refant='ea24',
minblperant=3, minsnr=3.0, calmode='p',
gaintable=['SNR_G55_10s.pos', 'SNR_G55_10s.tecim'])
Again, you will notice a few messages that read "Insufficient unflagged antennas to proceed with this solve."
We can now solve for the residual antenna-based delays that can be seen in plots of the phase vs. frequency for the calibrator sources in plotms. This uses the gaintype='K' option in gaincal. This setting will solve for a simple antenna-based delay, via a Fast-Fourier Transform (FFT) of the spectra, on baselines to the reference antenna.
Note that this is not a "global fringe-fitting" solution for delays, but instead does a baseline-based delay solution to all baselines to the refant, treating these as antenna-based delays. In most cases with high-enough S/N to get baseline-based delay solutions this will suffice. We use our bright bandpass calibrator, 3C147, to calibrate the delays:
# In CASA
gaincal(vis='SNR_G55_10s.ms', field='2',
caltable='SNR_G55_10s.K0',
solint='inf', refant='ea24',
gaintype='K', combine='scan', minsnr=3,
gaintable=['SNR_G55_10s.pos', 'SNR_G55_10s.tecim', 'SNR_G55_10s.initPh.2'])
We pre-apply our initial phase table, and produce a new K-type caltable for input to bandpass calibration. We can plot the delays, in nanoseconds, as a function of antenna index (you will get one for each sub-band and polarization):
# In CASA
plotcal(caltable='SNR_G55_10s.K0', xaxis='antenna', yaxis='delay')
The delays range from around -3 to 5 nanoseconds, which is good. Anything over 10ns would be cause for concern.
Now let's solve for the bandpass using the previous tables:
# In CASA
bandpass(vis='SNR_G55_10s.ms', caltable='SNR_G55_10s.bPass',
field='2', solint='inf', combine='scan',
refant='ea24', minblperant=3, minsnr=10.0,
gaintable=['SNR_G55_10s.pos', 'SNR_G55_10s.tecim', 'SNR_G55_10s.initPh.2','SNR_G55_10s.K0'],
interp=['', 'nearest', 'nearest'], solnorm=False)
- solint='inf', combine='scan': again, the solution interval of 'inf' will automatically break-up the data by scans; this requests that the solution intervals be combined over scans, so that we will get one solution per antenna. Note that you must set solnorm=False here or later on you will find some offsets between spws due to the way in which amplitude scaling adjusts weights internally during solving.
Note that since we have flagged-out the vast majority of the RFI-affected data, there are many fewer failed solutions. Again, we can plot the calculated bandpasses to check that they look reasonable:
# In CASA
plotcal(caltable='SNR_G55_10s.bPass', xaxis='freq', yaxis='amp',
iteration='antenna', subplot=331)
#
plotcal(caltable='SNR_G55_10s.bPass', xaxis='freq', yaxis='phase',
iteration='antenna', subplot=331)
Don't let the apparently odd-looking phases for ea24 fool you -- check the scale! Remember, this is our reference antenna.
Gain calibration
Next, we will calculate the per-antenna gain solutions. We will now use the intent parameter. Since this is low-frequency data, we do not expect substantial variations over short timescales, so we calculate one solution per scan (using solint='inf'):
# In CASA
gaincal(vis='SNR_G55_10s.ms', caltable='SNR_G55_10s.phaseAmp',
intent='*PHASE*,*AMPLI*', solint='inf', refant='ea24', minblperant=3,
minsnr=10.0, gaintable=['SNR_G55_10s.pos', 'SNR_G55_10s.tecim', 'SNR_G55_10s.K0','SNR_G55_10s.bPass'])
- solint='inf': We request one solution per scan.
- intent = '*PHASE*,*AMPLI*': This is part of our selection parameters. It will limit our search to sources in our measurement set with CALIBRATE_PHASE and CALIBRATE_AMPLI intents. Note that these intents are initially set by the Primary Investigator (PI) or person initially creating their observation within the Observation Preparation Tool (OPT). Your observations intents may differ, so it may be a good idea to double-check your calibrator intents with listobs. We could just as easily have used field='0,2' to choose our calibrators. We merely present the intents parameter to show a different way of selecting data.
Plot these solutions as a function of amplitude and phase versus time for the phase calibrator (field 0), iterating over each antenna:
# In CASA
plotcal(caltable='SNR_G55_10s.phaseAmp', xaxis='time', yaxis='amp',
field = '0', iteration='antenna')
plotcal(caltable='SNR_G55_10s.phaseAmp', xaxis='time', yaxis='phase',
field = '0', plotsymbol='-', iteration='antenna')
Flux Scaling the Gain Solutions
Now that we have a complete set of gain solutions, we must scale the phase calibrator's absolute flux correctly, using 3C147 as our reference source. To do this, we run fluxscale on the gain table we just created, which will write a new, flux-corrected gain table (SNR_G55_10s.phaseAmp.fScale):
# In CASA
myFlux = fluxscale(vis='SNR_G55_10s.ms', caltable='SNR_G55_10s.phaseAmp',
fluxtable='SNR_G55_10s.phaseAmp.fScale', reference='2', incremental=False)
Note that the myFlux Python dictionary will contain information about the scaled fluxes and fitted spectrum. The logger will display information about the flux density it has deduced for J1925+2106:
2016-03-16 21:16:00 INFO fluxscale Found reference field(s): 0542+498=3C147 2016-03-16 21:16:00 INFO fluxscale Found transfer field(s): J1925+2106 2016-03-16 21:16:01 INFO fluxscale Flux density for J1925+2106 in SpW=0 (freq=1.319e+09 Hz) is: 1.50509 +/- 0.0283309 (SNR = 53.1254, N = 40) 2016-03-16 21:16:01 INFO fluxscale Flux density for J1925+2106 in SpW=1 (freq=1.447e+09 Hz) is: 1.56106 +/- 0.0252717 (SNR = 61.7711, N = 40) 2016-03-16 21:16:01 INFO fluxscale Flux density for J1925+2106 in SpW=2 (freq=1.711e+09 Hz) is: 1.71527 +/- 0.0249139 (SNR = 68.8477, N = 40) 2016-03-16 21:16:01 INFO fluxscale Flux density for J1925+2106 in SpW=3 (freq=1.839e+09 Hz) is: 1.7623 +/- 0.0265479 (SNR = 66.382, N = 40) 2016-03-16 21:16:01 INFO fluxscale Fitted spectrum for J1925+2106 with fitorder=1: Flux density = 1.63244 +/- 0.00551612 (freq=1.56544 GHz) spidx=0.495241 +/- 0.0264202
The flux density listed in the VLA Calibrator Manual for J1925+2106 (known then as J1925+211 for J2000 epoch) is around the same magnitude at L-Band:
1925+211 J2000 A 19h25m59.605370s 21d06'26.162180" Aug01 1923+210 B1950 A 19h23m49.792400s 21d00'23.305000" ----------------------------------------------------- BAND A B C D FLUX(Jy) UVMIN(kL) UVMAX(kL) ===================================================== 20cm L P S S S 1.30 visplot 6cm C P P S S 1.5 3.7cm X P P P P 1.00 visplot 2cm U P P P P 1.8 1.3cm K S S S S 0.90 visplot 0.7cm Q S S S S 1.0
This is a good indication that our calibration up to this point is reasonable. We will now apply these calibration tables to our data, and begin our imaging.
Applying calibration
Finally, we must apply the calibration to our data. To do this, we run applycal in two stages: the first is to self-calibrate our calibration sources; the second, to apply calibration to the supernova remnant. These must be done separately, since we want to use "nearest" interpolation for the self-calibration and "linear" (this is the default, so we can omit requesting the interpolation) for the application to the science target:
# In CASA
applycal(vis='SNR_G55_10s.ms', intent='*PHASE*,*AMPLI*',
gaintable=['SNR_G55_10s.pos', 'SNR_G55_10s.tecim', 'SNR_G55_10s.K0',
'SNR_G55_10s.bPass', 'SNR_G55_10s.phaseAmp.fScale'],
calwt=False, interp=['','nearest','nearest','nearest'])
applycal(vis='SNR_G55_10s.ms', intent='*TARGET*',
gaintable=['SNR_G55_10s.pos', 'SNR_G55_10s.tecim', 'SNR_G55_10s.K0',
'SNR_G55_10s.bPass', 'SNR_G55_10s.phaseAmp.fScale'], calwt=False)
Plotting calibrated data
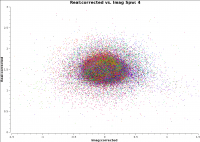
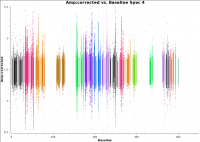
To check that everything has truly proceeded as well as we would like, this is a good time to look at the calibrated data in plotms. A very useful way to check the quality of the calibration, is to plot the corrected real vs. imaginary portions of the visibilities of our calibrators.
For a point source at the phase center, the plot should look like scatter around zero for the imaginary axis (zero phase), and scatter around the flux density value (amplitude) of the source, in the real axis. The corrected amplitude vs. baseline, which should be a flat line of points for a point source, will reveal any lingering antenna-based problems. For a resolved source, it may be more instructive to plot corrected amplitude vs. UV-distance.
# In CASA
plotms(vis='SNR_G55_10s.ms', field='0', xaxis='imag', yaxis='real',
xdatacolumn='corrected', ydatacolumn='corrected', coloraxis='antenna1',
avgchannel='10', avgtime='30', correlation='RR,LL', iteraxis='spw',
plotrange=[-1.5,1.5,0,2.8])
#
plotms(vis='SNR_G55_10s.ms', field='0', xaxis='baseline', yaxis='amp',
xdatacolumn='corrected', ydatacolumn='corrected', coloraxis='antenna1',
avgchannel='10', avgtime='30', correlation='RR,LL', iteraxis='spw',
plotrange=[0,450,0.5,2.5])
#
plotms(vis='SNR_G55_10s.ms', field='2', xaxis='imag', yaxis='real',
xdatacolumn='corrected', ydatacolumn='corrected', coloraxis='antenna1',
avgchannel='10', avgtime='30', correlation='RR,LL', iteraxis='spw',
plotrange=[-5,5,18,28])
#
plotms(vis='SNR_G55_10s.ms', field='2', xaxis='baseline', yaxis='amp',
xdatacolumn='corrected', ydatacolumn='corrected', coloraxis='antenna1',
avgchannel='10', avgtime='30', correlation='RR,LL', iteraxis='spw',
plotrange=[0,450,18,28])
Splitting out data for G55.7+3.4
Now that we are satisfied with the calibration, we will create a new MS which contains only the corrected data for G55.7+3.4 using the task split2. The split task is used to make a new data set that is a subset of an existing data set. The Split2 task provides the functionality of split, but is based on the mstransform framework underneath, which is more versatile. For more on split2, see the CASA Cookbook, section 4.7.4.1. Starting with CASA version 4.6, the split2 task will be renamed split, and replace the current split task.
Splitting out just the target we want to image will substantially reduce the size of the MS, and will speed up the imaging process. We can also drop the polarization products since they have not been calibrated and will not be used for imaging.
# In CASA
split2(vis='SNR_G55_10s.ms', field='1', keepflags=False,
outputvis='SNR_G55_10s.calib.ms', datacolumn='corrected',
correlation = 'RR,LL')
Imaging
The CLEAN Algorithm
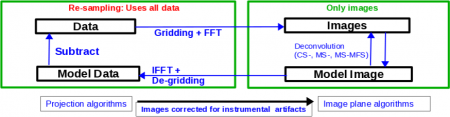
The CLEAN algorithm, developed by J. Högbom (1974) enabled the synthesis of complex objects, even if they have relatively poor Fourier uv-plane coverage. Poor coverage occurs with partial earth rotation synthesis, or with arrays composed of few antennas. The "dirty" image is formed by a simple Fourier inversions of the sampled visibility data, with each point on the sky being represented by a suitably scaled and centered PSF (Point Spread Function, sometimes called the dirty beam). This algorithm attempts to interpolate from the measured (u,v) points across gaps in the (u,v) coverage. It, in short, provides solutions to the convolution equation by representing radio sources by a number of point sources in an empty field.
The brightest points are found by performing a cross-correlation between the dirty image, and the PSF. The brightest parts are subtracted (minor-cycle), and the process is repeated again for the next brighter sources (major-cycle). A large part of the work in CLEAN involves shifting and scaling the dirty beam.
The clean algorithm works well with points sources, as well as most extended objects. Where it can fall short is in speed, as convergence can be slow for extended objects, or for images containing several bright point sources. A solution to deconvolve these images would be the MEM (Maximum Entropy Method) algorithm, which has faster performance, although we can improve the CLEAN algorithm by employing other means, some of which will be mentioned below.
1. Högbom Algorithm
This algorithm will initially find the strength and position of a peak in a dirty image, subtract it from the dirty image, record this position and maginitude, and repeat for further peaks. The remainder of the dirty image is known as the residuals.
The accumulated point sources, now residing in a model, is convolved with an idealized CLEAN beam (usually a Gaussian fitted to the central lobe of the dirty beam), creating a CLEAN image. As the final step, the residuals of the dirty image are then added to the CLEAN image.
2. Clark Algorithm
Clark (1980), developed a FFT-based CLEAN algorithm, which more efficiently shifts and scales the dirty beam by approximating the position and strength of components using a small patch of the dirty beam. This algorithm is the default within the clean task, which involves major and minor cycles.
The algorithm will first select a beam patch, which will include the highest exterior sidelobes. Points are then selected from the dirty image, which are up to a fraction of the image peak, and are greater than the highest exterior sidelobe of the beam. It will then conduct a list-based Högbom CLEAN, creating a model and convolution with an idealized CLEAN beam. This process is the minor cycle.
The major cycle involves transforming the point source model via a FFT (Fast-Fourier Transform), mutiplying this by the weight sampling function (more on this below), and transformed back. This is then subtracted from the dirty image, creating your CLEAN image. The process is then repeated with subsequent minor cycles.
3. Cotton-Schwab Algorithm
This is the default imager mode (csclean), and is a variant of the Clark algorith in which the major cycle involves the subtraction of CLEAN components of ungridded visibility data. This allows the removal of gridding errors, as well as noise. One advantage is its ability to image and clean many seperate fields simultaneously. Fields are cleaned independently in the minor cycle, and components from all fields cleaned together in the major cycles.
This algorithm is faster than the Clark algorithm, except when dealing with a large number of visibility samples, due to the re-gridding process it undergoes. It is most useful in cleaning sensitive high-resolution images at lower frequencies where a number of confusing sources are within the primary beam.
For more details on imaging and deconvolution, you can refer to the Astronomical Society of the Pacific Conference Series book entitled Synthesis Imaging in Radio Astronomy II. The chapter on Deconvolution may prove helpful.
Weights and Tapering
When imaging data, a map is created associating the visibilities with the image. The sampling function, which is a function of the visibilities, is modified by a weight function. [math]\displaystyle{ S(u,v) \to S(u,v)W(u,v) }[/math].
This process can be considered a convolution. The convolution map, is the weights by which each visiblity is multiplied by before gridding is undertaken. Due to the fact that each VLA antenna performs slightly differently, different weights should be applied to each antenna. Therefore, the weight column in the data table reflects how much weight each corrected data sample should receive.
For a brief intro to the different clean algorithms, as well as other deconvolution and imaging information, please see the website kept by Urvashi R.V. here.
The following are a few of the more used forms of weighting, which can be used within the clean task. Each one has their own benefits and drawbacks.
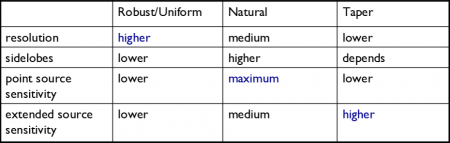
1. Natural: The weight function can be described as [math]\displaystyle{ W(u,v) = 1/ \sigma^2 }[/math], where [math]\displaystyle{ \sigma^2 }[/math] is the noise variance. Natural weighting will maximize point source sensitivity, and provide the lowest rms noise within an image, as well as the highest signal-to-noise. It will also generaly give more weight to short baselines, thus angular resolutions can be degraded. This form of weighting is the default within the clean task.
2. Uniform: The weight function can be described as [math]\displaystyle{ W(u,v) = W(u,v) / W_k }[/math], where [math]\displaystyle{ W_k }[/math] represents the local density of (u,v) points, otherwise known as the gridded weights. This form of weighting will increase the influence of data with lower weight, filling the (u,v) plane more uniformly, thereby reducing sidelobe levels in the field-of-view, but increasing the rms image noise. More weight is given to long baselines, therefore increasing angular resolution. Point source sensitivity is degraded due to the downweighting of some data.
3. Briggs: A flexible weighting scheme, that is a variant of uniform, and avoids giving too much weight to (u,v) points with a low natural weight. Weight function can be described as [math]\displaystyle{ W(u,v) = 1/ \sqrt{1+S_N^2/S_{thresh}^2} }[/math], where [math]\displaystyle{ S_N }[/math] is the natural weight of the cell, [math]\displaystyle{ S_{thresh} }[/math] is a threshold. A high threshold will go to a natural weight, where as a low threshold will go to a uniform weight. This form of weighting also has adjustable parameters. The robust parameter will give variation between resolution and maximum point source sensitivity. It's value can range from -2.0 (close to uniform weight) to 2.0 (close to natural weight). By default, the parameter is set to 0.0, which gives a good trade-off.
I. Tapering: In conjunction with weighting, we can include the uvtaper parameter within clean, which will control the radial weighting of visibilities, in the uv-plane. This in effect, reduces the visibilities, with weights decreasing as a function of uv-radius. The tapering will apodize, or filter/change the shape of the weight function (which is itself a Gaussian), which can be expressed as:
[math]\displaystyle{ W(u,v) = e^{-(u^2+v^2)/t^2} }[/math], where t is the adjustable tapering parameter. This process can smooth the image plane, give more weight to short baselines, but in turn degrade angular resolution. Due to the downweight of some data, point source sensitivity can be degraded. If your observation was sampled by short baselines, tapering may improve sensitivity to extended structures.
Primary and Synthesized Beam
The primary beam of the VLA antennas can be taken to be a Gaussian with FWHM equal to [math]\displaystyle{ 90*\lambda_{cm} }[/math] or [math]\displaystyle{ 45/ \nu_{GHz} }[/math]. Taking our observed frequency to be the middle of the band, 1.5GHz, our primary beam will be around 30 arcmin. Note that if your science goal is to image a source, or field of view that is significantly larger than the FWHM of the VLA primary beam, then creating a mosaic from a number of pointings would be best. For a tutorial on mosaicing, see the 3C391 tutorial.
Since our observation was taken in D-configuration, we can check the Observational Status Summary's section on VLA resolution to find that the synthesized beam will be around 46 arcsec. We want to oversample the synthesized beam by a factor of around five, so we will use a cell size of 8 arcsec.
Since this field contains bright point sources significantly outside the primary beam, we will create images that are 170 arcminutes on a side, or almost 6x the size of the primary beam. This is ideal for showcasing both the problems inherent in such wide-band, wide-field imaging, as well as some of the solutions currently available in CASA to deal with these issues.
First, it's worth considering why we are even interested in sources which are far outside the primary beam. This is mainly due to the fact that the EVLA, with its wide bandwidth capabilities, is quite sensitive even far from phase center -- for example, at our observing frequencies in L-band, the primary beam gain is as much as 10% around 1 degree away. That means that any imaging errors for these far-away sources will have a significant impact on the image rms at phase center. The error due to a source at distance R can be parametrized as:
[math]\displaystyle{ \Delta(S) = S(R) \times PB(R) \times PSF(R) }[/math]
So, for R = 1 degree, source flux S(R) = 1 Jy, [math]\displaystyle{ \Delta(S) }[/math] = 1 mJy − 100 [math]\displaystyle{ {\mu} }[/math]Jy. Clearly, this will be a source of significant error.
Multi-Scale Clean
Since G55.7+3.4 is an extended source with many spatial scales, the most basic (yet still reasonable) imaging procedure is to use clean with multiple scales. MS-CLEAN is an extension of the classical CLEAN algorithm for handling extended sources. It works by assuming the sky is composed of emission at different spatial scales and works on them simultaneously, thereby creating a linear combination of images at different spatials scales. For a more detailed description of Multi Scale CLEAN, see the paper by J.T. Cornwell entitled [http://arxiv.org/abs/0806.2228 Multi-Scale CLEAN deconvolution of radio synthesis images].
It can also be possible to utilize tclean, (t for test) which is a refactored version of clean, with a better interface, and provides more possible combinations of algorithms. It also allows for process computing parallelization of the imaging and deconvolution. Eventually, tclean will replace the current clean task, but for now, we will stick with the original clean, as tclean is merely experimental at the moment.
As is suggested, we will use a set of scales (which are expressed in units of the requested pixel, or cell, size) which are representative of the scales that are present in the data, including a zero-scale for point sources.
Note that interrupting clean by Ctrl+C may corrupt your visibilities -- you may be better off choosing to let clean finish. We are currently implementing a command that will nicely exit to prevent this from happening, but for the moment try to avoid Ctrl+C.
# In CASA
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.MultiScale',
imsize=1280, cell='8arcsec', multiscale=[0,6,10,30,60], smallscale=0.9,
interactive=False, niter=1000, pbcor=True, weighting='briggs', uvtaper='
stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.MultiScale',
imsize=1280, cell='8arcsec', multiscale=[0,6,10,30,60],
interactive=False, niter=1000, weighting='briggs',
stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')
viewer('SN_G55_10s.MultiScale.image')
- imagename='SN_G55_10s.MultiScale': the root filename used for the various clean outputs. These include the final image (<imagename>.image), the relative sky sensitivity over the field (<imagename>.flux), the point-spread function (also known as the dirty beam; <imagename>.psf), the clean components (<imagename>.model), and the residual image (<imagename>.residual).
- imsize=1280: the image size in number of pixels. Note that entering a single value results in a square image with sides of this value.
- cell='8arcsec': the size of one pixel; again, entering a single value will result in a square pixel size.
- multiscale=[0,6,10,30,60]: a set of scales on which to clean. A good rule of thumb when using multiscale is [0, 2xbeam, 5xbeam] (where beam is the synthesized beam) and larger scales up to the maximum scale the interferometer can image. Since these are in units of the pixel size, our chosen values will be multiplied by the requested cell size. Thus, we are requesting scales of 0 (a point source), 48, 80, 240, and 480 arcseconds. Note that 16 arcminutes (960 arcseconds) roughly corresponds to the size of G55.7+3.4.
- smallscale=0.9: This parameter is known as the small scale bias, and helps with faint extended structure, by balancing the weight given to smaller structures which tend to be brighter, but have less flux density. Increasing this value gives more weight to smaller scales. A value of 1.0 weighs the largest scale to zero, and a value of less than 0.2 weighs all scales nearly equally. The default value is 0.6.
- interactive=False: we will let clean use the entire field for placing model components. Alternatively, you could try using interactive=True, and create regions to constrain where components will be placed. However, this is a very complex field, and creating a region for every bit of diffuse emission as well as each point source can quickly become tedious. For a tutorial that covers more of an interactive clean, please see IRC+10216 tutorial.
- niter=1000: this controls the number of iterations clean will do in the minor cycle.
- pbcor=True: We can correct for the relative sky sensitivity while running clean. This will help in creating a near circularly symmetric beam, which may be better able to image extended sources, over long observations. setting this to true, forces the raw image to be rescaled by dividing by the noise and primary beam correction image (<imagename>.flux). Note that this can also be done via the immath task if pbcor=False.
- weighting='briggs': use Briggs weighting with a robustness parameter of 0 (halfway between uniform and natural weighting).
- usescratch=F: do not write the model visibilities to the model data column (only needed for self-calibration)
- imagermode='csclean': use the Cotton-Schwab clean algorithm
- stokes='I': since we have not done any polarization calibration, we only create a total-intensity image.
- threshold='0.1mJy': threshold at which the cleaning process will halt; i.e. no clean components with a flux less than this value will be created. This is meant to avoid cleaning what is actually noise (and creating an image with an artificially low rms). It is advisable to set this equal to the expected rms, which can be estimated using the EVLA exposure calculator. However, in our case, this is a bit difficult to do, since we have lost a hard-to-estimate amount of bandwidth due to flagging, and there is also some residual RFI present. Therefore, we choose 0.1 mJy as a relatively conservative limit.
This is the fastest of the imaging techniques described here, but it's easy to see that there are artifacts in the resulting image. Note that you may have to play with the image color map to get a better view of the image details. This can be done by clicking on Data Display Options (wrench icon on top right corner), and choosing "rainbow 3" under basic settings. We can use the viewer to explore the point sources near the edge of the field by zooming in on them. Some have prominent arcs, as well as spots in a six-pointed pattern surrounding them. Note that you may need to play with the brightness/contrast of the image to see more detail, or change the color map under data display options.
Next we will explore some more advanced imaging techniques to mitigate these artifacts.
Multi-Scale, Wide-Field Clean (w-projection)
The next clean algorithm we will employ is w-projection, which is a wide-field imaging technique that takes into account the non-coplanarity of the baselines as a function of distance from the phase center. For wide-field imaging, the sky curvature and non-coplanar baselines results in a non-zero w-term. The w-term introduced by the sky and array curvature introduces a phase term that will limit the dynamic range of the resulting image. Applying 2-D imaging to such data will result in artifacts around sources away from the phase center, as we saw in running MS-CLEAN. Note that this affects mostly the lower frequency bands, especially for the more extended configurations, due to the field of view decreasing with higher frequencies.
The w-term can be corrected by faceting (describe the sky curvature by many smaller planes) in either the image or uv-plane, or by employing w-projection. A combination of the two can also be employed within clean by setting the parameter gridmode='widefield'. If w-projection is employed, it will be done for each facet. Note that w-projections is an order of magnitude faster than the faceting algorithm, but will require more memory.
For more details on w-projection, as well as the algorithm itself, see "The Noncoplanar Baselines Effect in Radio Interferometry: The W-Projection Algorithm". Also, the chapter on Imaging with Non-Coplanar Arrays may be helpful.
# In CASA
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.ms.wProj',
gridmode='widefield', imsize=1280, cell='8arcsec',
wprojplanes=128, multiscale=[0,6,10,30,60],
interactive=False, niter=1000, weighting='briggs',
stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')
viewer('SNR_G55_10s.ms.wProj.image')
- gridmode='widefield': Use the w-projection algorithm.
- wprojplanes=128: The number of w-projection planes to use for deconvolution; 128 is the minimum recommended number.
This will take slightly longer than the previous imaging round; however, the resulting image has noticeably fewer artifacts. In particular, compare the same outlier source in the Multi-Scale w-projected image with the Multi-Scale-only image: note that the swept-back arcs have disappeared. There are still some obvious imaging artifacts remaining, though.
Multi-Scale, Multi-Frequency Synthesis
Another consequence of simultaneously imaging the wide fractional bandwidths available with the EVLA is that the primary beam has substantial frequency-dependent variation over the observing band. If this is not accounted for, it will lead to imaging artifacts and compromise the achievable image rms.
If sources which are being imaged have intrinsically flat spectra, this will not be a problem. However, most astronomical objects are not flat-spectrum sources, and without any estimation of the intrinsic spectral properties, the fact that the primary beam is twice as large at 2 than at 1 GHz will have substantial consequences.
Note that the dimentions of the (u,v) plane are measured in wavelengths, and therefore observing at several frequencies, a baseline can sample several ellipses in the (u,v) plane, each with different sizes. We can therefore fill in the gaps in the single frequency (u,v) coverage, hence Multi-Frequency Synthesis (MFS). Also when observing in low-frequencies, it may prove beneficial to observe in small time-chunks, which are spread out in time. This will allow the coverage of more spatial-frequencies, allowing us to employ this algorithm more efficiently.
The Multi-Scale Multi-Frequency-Synthesis (MS-MFS) algorithm provides the ability to simultaneously image and fit for the intrinsic source spectrum. The spectrum is approximated using a polynomial in frequency, with the degree of the polynomial as a user-controlled parameter. A least-squares approach is used, along with the standard clean-type iterations. Using this method of imaging will dramatically improve our (u,v) coverage, hence improving image fidelity.
For a more detailed explanation of the MS-MFS deconvolution algorithm, please see the paper by Urvashi Rau and Tim J. Cornwell entitled A multi-scale multi-frequency deconvolution algorithm for synthesis imaging in radio interferometry
# In CASA
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.ms.MFS',
imsize=1280, cell='8arcsec', mode='mfs', nterms=2,
multiscale=[0,6,10,30,60],
interactive=False, niter=1000, weighting='briggs',
stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')
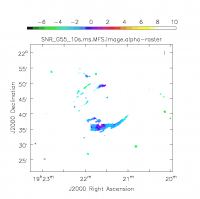
viewer('SNR_G55_10s.ms.MFS.image.tt0')
viewer('SNR_G55_10s.ms.MFS.image.alpha')
- nterms=2:the number of Taylor terms to be used to model the frequency dependence of the sky emission. Note that the speed of the algorithm will depend on the value used here (more terms will be slower); of course, the image fidelity will improve with a larger number of terms (assuming the sources are sufficiently bright to be modeled more completely).
This will take much longer than the two previous methods, so it would probably be a good time to have coffee or chat about EVLA data reduction with your neighbor at this point.
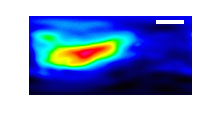
When clean is done <imagename>.image.tt0 will contain a total intensity image, where tt0 is a suffix to indicate the Taylor term; <imagename>.image.alpha will contain an image of the spectral index in regions where there is sufficient signal-to-noise. Having this spectral index image can help convey information about the emission mechanism involved within the supernova remnant. It can also give information on the optical depth of the source. I've included a color widget on the top of the plot to give an idea of the spectral index variation.
For more information on the multi-frequency synthesis mode and its outputs, see section 5.2.5.1 in the CASA cookbook.
Inspect the brighter point sources in the field near the supernova remnant. You will notice that some of the artifacts which had been symmetric around the sources themselves are now gone; however, since we did not use W-Projection this time, there are still strong features related to the non-coplanar baseline effects still apparent for sources further away.
Multi-Scale, Multi-Frequency, Widefield Clean
Finally, we will combine the W-Projection and MS-MFS algorithms to simultaneously account for both of the effects. Be forewarned -- these imaging runs will take a while, and it's best to start them running and then move on to other things.
First, we will image the autoflagged data. Using the same parameters for the individual-algorithm images above, but combined into a single clean run, we have:
# In CASA
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.ms.MFS.wProj',
gridmode='widefield', imsize=1280, cell='8arcsec', mode='mfs',
nterms=2, wprojplanes=128, multiscale=[0,6,10,30,60],
interactive=False, niter=1000, weighting='briggs',
stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')
viewer('SNR_G55_10s.ms.MFS.wProj.image.tt0')
viewer('SNR_G55_10s.ms.MFS.wProj.image.alpha')
Again, looking at the same outlier source, we can see that the major sources of error have been removed, although there are still some residual artifacts. One possible source of error is the time-dependent variation of the primary beam; another is the fact that we have only used nterms=2, which may not be sufficient to model the spectra of some of the point sources.
Ultimately, it isn't too surprising that there was still some RFI present in our auto-flagged data, since we were able to see this with plotms. It's also possible that the auto-flagging overflagged some portions of the data, also leading to a reduction in the achievable image rms.
Imaging with tclean
The tclean task will eventually be replacing clean as the default when imaging, so it would be a good idea to familiarize ourselves with the parameters, which differ from clean. Let us now create the same MS-MFS, w-projection image, via tclean:
# In CASA
tclean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.tclean.MS.MFS.wProj', imsize=1280,
cell='8arcsec', specmode='mfs', gridder='wproject', wprojplanes=128,
deconvolver='multiscale', scales=[0,6,10,30,60], interactive=False, niter=1000,
weighting='briggs', stokes='I', threshold='0.1mJy', nterms=2)
We can now specify w-projection within the gridder parameter (gridmode in clean), and mfs within the specmode parameter (mode in clean). In addition, you will notice the tclean process runs faster than clean. tclean also has a parallel parameter, which will run major cycles in parallel. This option is set to False by default, as it requires MPI (Message Passing Interface) to be enabled on your system for tclean to run. See chapter 10 in the CASA Cookbook.
Image Information
This portions will cover topics on image headers, and frequency reference frames.
Frequency Reference Frame
The velocity within your image is calculated based on your choice of frame, velocity definition, and spectral line rest frequency. The initial frequency reference frame is initially given by the telescope, however, it can be transformed to several other frames, including:
- LSRK - Local Standard of Rest Kinematic. Conventional LSR based on average velocity of stars in the solar neighborhood.
- LSRD - Local Standard of Rest Dynamic. Velocity with respect to a frame in circular motion about the galactic center.
- BARY - Barycentric. Referenced to JPL ephemeris DE403. Slightly different and more accurate than heliocentric.
- GEO - Geocentric. Referenced to the Earth's center. This will just remove the observatory motion.
- TOPO - Topocentric. Fixed observing frequency and constantly changing velocity.
- GALACTO - Galactocentric. Referenced to the dynamical center of the galaxy.
- LGROUP - Local Group. Referenced to the mean motion of Local Group of Galaxies.
- CMB - Cosmic Microwave Background dipole. Based on COBE measurements of dipole anisotropy.
Image Header
The image header holds meta data associated with your CASA image. The task imhead will display this data within the casalog. We will first run imhead with mode='summary':
# In CASA
imhead(imagename='SNR_G55_10s.ms.MFS.wProj.image.tt0', mode='summary')
- mode='summary': gives general information about the image, including the object name, sky coordinates, image units, the telescope the data was taken with, and more.
For further information about the image, let's now run it with mode='list':
# In CASA
imhead(imagename='SNR_G55_10s.ms.MFS.wProj.image.tt0', mode='list')
- mode='list': gives more detailed information, including beam major/minor axes, beam primary angle, and the location of the max/min intensity, and lots more.
We will now want to change our image header units from Jy/beam to Kelvin. To do this, we will run the task with mode='put':
# In CASA
imhead(imagename='SNR_G55_10s.ms.MFS.wProj.image.tt0', mode='put', hdkey='bunit', hdvalue='K')
Let's also change the direction reference frame from J2000 to Galactic:
# In CASA
imhead(imagename='SNR_G55_10s.ms.MFS.wProj.image.tt0', mode='put', hdkey='equinox', hdvalue='GALACTIC')
-- original: ??
--modifications: Lorant Sjouwerman (4.4.0, 2015/07/07)
--modifications: Jose Salcido (4.5.2, 2016/02/24)
Last checked on CASA Version 4.5.2