EVLA 3-bit Tutorial G192: Difference between revisions

From CASA Guides
Jump to navigationJump to search
← Older editNewer edit →
Knyland (talk | contribs)
93 edits
Jott (talk | contribs)
operators
5,026 edits
No edit summary
Line 1: Line 1:
This is an Advanced EVLA data reduction tutorial that calibrates and images a 6-cm wide-band continuum dataset.
This is an advanced Jansky VLA data reduction tutorial that calibrates and images a 3-bit dataset.
 
<b>This CASA Guide is for CASA version 4.2.0.</b>


<b>This casaguide is for Version 4.2.0 of CASA.</b>
== Overview ==
== Overview ==


This article describes the calibration and imaging of a single-pointing 6-cm EVLA wideband continuum dataset of the galaxy NGC2967 (UGC5180) which was the location of the supernova candidate SN2010FZ. No supernova was detected in this observation, but the galactic continuum emission from this face-on spiral is nicely imaged. The data were taken in with 1024 MHz of bandwidth in each of two widely spaced basebands (each comprised of 8 128-MHz spectral windows), spanning 4.5 to 7.5 GHz.  We will use wideband imaging techniques in this tutorial.
This article describes the calibration and imaging of the protostar G192.16-3.84. The data were taken in Ka-band using the VLA's 3-bit samplers and widely-spaced basebands centered at 29 and 36.5 GHz.  Each baseband has over 4 GHz of bandwidth comprised of 32 128-MHz spectral windows.  In this tutorial, we will examine, flag, and calibrate the data, including the corrections for the requantizer gains (which are necessary for 3-bit data calibration and harmless on 8-bit data).  We will then image and analyze the calibrated data, using wideband imaging techniques.


This is a more advanced tutorial, and if you are a relative novice (and <em>particularly</em> for EVLA continuum calibration and imaging), it is <em>strongly</em> recommended that you start with the [[EVLA Continuum Tutorial 3C391]] (at least read it through) before tackling this dataset.  We will not include basic information on CASA processing in this tutorial.
This is a more advanced tutorial, so if you are a relative novice, it is <em>strongly</em> recommended that you start with the [[EVLA Continuum Tutorial 3C391]] (at least read it through) before proceeding with this tutorial.


From the [http://casaguides.nrao.edu MainPage] of this guide you can find helpful information:
In addition, on the [http://casaguides.nrao.edu MainPage] of the CASA Guides you can find these helpful pages:
* [[What is CASA?]]
* [[What is CASA?]]
* [[Getting Started in CASA]]
* [[Getting Started in CASA]]
Line 15: Line 16:
* [[AIPS-to-CASA Cheat Sheet]]
* [[AIPS-to-CASA Cheat Sheet]]


In this tutorial we will be invoking the tasks as function calls.  You can cut and paste these to your casapy session. We also recommend that you copy all the commands you use, with any relevant commentary, to a text file.  This is good practice when tackling large datasets.  If you wish, you can use the [http://casaguides.nrao.edu/index.php?title=Extracting_scripts_from_these_tutorials Script Extractor] to create a file with the tutorial commands, which can subsequently be edited as desired.
In this tutorial we will be invoking the tasks as function calls.  You can cut and paste these to your casapy session. We also recommend that you copy all the commands you use, with any relevant commentary, to a text file.  This is ''very'' good practice when tackling large datasets.  If you wish, you can use the [http://casaguides.nrao.edu/index.php?title=Extracting_scripts_from_these_tutorials Script Extractor] to create a file with the tutorial commands, which can subsequently be edited and annotated as desired.


Occasionally we will be setting Python variables (e.g. as lists for flags) outside the function call so make sure you
Occasionally we will be setting Python variables (e.g., as lists for flags) outside the function call so make sure you set those before running the task command.  Note that when you call a CASA task as a function, any task parameters that are not set in the function call will be used with their default values.  This means they will ''not'' use values you set in any previous calls or outside the call. See [[Getting_Started_in_CASA#Task_Execution]] for more on calling tasks and setting parameters in the scripting interface.
set those before running the task command.  Note that when you call a CASA task as a function the task parameters you
do not set in the function call (assuming there is at least one) will be set to their defaults, and will not use values
you set in previous calls or outside the call. See [[Getting_Started_in_CASA#Task_Execution]] for more  
on calling tasks and setting parameters in the scripting interface.


NOTE: If you find that the figures on the right margin of the browser window overlap the text too much and make reading difficult,
NOTE: If you find that the figures on the right margin of the browser window overlap the text too much and make reading difficult, you can adjust the width of the browser window.
go ahead and widen the browser window.


== Obtaining the Data ==
== Obtaining the Data ==


The data for this tutorial were taken with the EVLA under program AS1015 as the scheduling block (SB) <tt>AS1015_sb1658169_1.55388.89474846065</tt>, and was run on 2010-07-11 from 21:28 to 22:28 UT (size 37.74GB).   
The data for this tutorial were taken with the VLA during its commissioning phase.  They comprise the scheduling block (SB) <tt>TVER0004.sb14459364.eb14492359.56295.26287841435</tt>, which was run on 2013-01-03 from 6:18 to 7:47 UT (its raw size is 57.04 GB).   


The data can be directly downloaded from [http://casa.nrao.edu/Data/EVLA/SN2010FZ/SN2010FZ_10s.ms.tar.gz http://casa.nrao.edu/Data/EVLA/SN2010FZ/SN2010FZ_10s.ms.tar.gz] (dataset size: 2.9 GB). For example, in you Linux terminal:
The data can be downloaded directly from [http://casa.nrao.edu/Data/EVLA/G192/G192_6s.ms.tar.gz http://casa.nrao.edu/Data/EVLA/G192/G192_6s.ms.tar.gz] (dataset size: 18 GB)
 
Your first step will be to unzip and untar the file in a terminal (before you start CASA):


<source lang="bash">
<source lang="bash">
wget http://casa.nrao.edu/Data/EVLA/SN2010FZ/SN2010FZ_10s.ms.tar.gz
tar -xzvf G192_6s.ms.tar.gz  
</source>
</source>


Your first step will be to unzip and untar the file in a terminal, before you start CASA:
If you are brave enough, you can also get the data directly from the VLA archive. Go to the [https://archive.nrao.edu/archive/advquery.jsp NRAO Science Data Archive], and search for "TVER0004.sb14459364" in the Archive File ID field.  Then select the dataset and choose a time-averaging value of 6 seconds. (Although the data were taken in A-configuration, we will not be imaging outside of the center of the field, so we aren't too worried about time-average smearing and will take advantage of averaging to reduce the dataset size.)  Also select the "Create tar file" option.


<source lang="bash">
In addition, only the fields used for analysis and observation are included in the downloadable file.  This can be accomplished using the {{split}} task in CASA:
tar -xzvf SN2010FZ_10s.ms.tar.gz
<source lang="python">
# In CASA
split('TVER0004.sb14459364.eb14492359.56295.26287841435.ms', outputvis='G192_6s.ms', \
      datacolumn='all', field='3,6,7,10', keepflags=False, spw='2~65')
</source>
</source>


If you are brave enough, you can also get the data straight from the EVLA archive. Go to the [https://archive.nrao.edu/archive/advquery.jsp NRAO Science Data Archive], and search for project **AS1015**. Then select the <tt>AS1015_sb1658169_1.55388.89474846065</tt> dataset and choose to apply the online flags  (check box "Apply flags generated during observing") and time-averaging of 10 seconds. (The data were taken in D-configuration [max baselines 1km], so one can safely average to 3s or even 10s to reduce dataset size.) Also select the tar option. This will create a file equivalent to what is used at the workshop.
(If you're downloading from the archive and feeling ambitious, you could also select only the scans with fields 3, 6, 7, and 10 in the "Select scans for MS or AIPS FITS" box.) This will create a file equivalent to what is used at the start of this tutorial.
 
Finally, you will need to modify some information in the SOURCE and FIELD tables of the measurement set (this has already been done for you in the file available for download, but must be done by hand if obtaining from the archive).  Follow [http://casaguides.nrao.edu/index.php?title=Modifying_SOURCE_and_FIELD_tables the instructions here] to make these changes.


== Starting CASA ==
== Starting CASA ==


{{CaltechCASAStartup}}
To start CASA, type:
 
<source lang="bash">
casapy
</source>
 
This will run a script to initialize CASA, setting paths appropriately. It will also start writing to a file called ipython-<unique-stamp>.log, which will contain a record of all the text you enter at the CASA prompt, as well as casapy-<unique-stamp>.log, which will contain all the messages that are printed to the CASA logger window.  It is recommended that you keep your log files in tact - you may need them to remind you of the last step you completed in your data reduction!  (It is also a good idea to include your log files when submitting a help desk ticket).
 
Once CASA has started, a logger window will appear.  Note that you can rescale this window or change the font size as desired (the latter is under "View").


== Examining the MS ==
== Examining the Measurement Set (MS) ==


We use {{listobs}} to summarize our MS:
We use {{listobs}} to summarize our MS:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
listobs('SN2010FZ_10s.ms')
listobs('G192_6s.ms', listfile='G192_listobs.txt')
</source>
</source>


In the logger you should see:
This will write the output to a file called <tt>G192_listobs.txt</tt>, which we can print to the terminal using the <tt>cat</tt> command:
 
<source lang="python">
# In CASA
cat G192_listobs.txt
</source>


<pre>
<pre>
##########################################
##### Begin Task: listobs            #####
================================================================================
================================================================================
           MeasurementSet Name:  SN2010FZ_10s.ms      MS Version 2
           MeasurementSet Name:  /lustre/knyland/casa_guides/protostar/G192_6s.ms      MS Version 2
================================================================================
================================================================================
   Observer: Dr. Alicia M. Soderberg     Project: T.B.D.  
   Observer: Dr. Debra Shepherd     Project: uid://evla/pdb/7303457  
Observation: EVLA
Observation: EVLA
Data records: 1570726       Total integration time = 3359 seconds
Data records: 10061248       Total integration time = 4557 seconds
   Observed from  11-Jul-2010/21:30:44.0  to  11-Jul-2010/22:26:43.0 (UTC)
   Observed from  03-Jan-2013/06:31:51.0  to  03-Jan-2013/07:47:48.0 (UTC)


   ObservationID = 0        ArrayID = 0
   ObservationID = 0        ArrayID = 0
  Date        Timerange (UTC)          Scan  FldId FieldName          nRows  Int(s)  SpwIds      ScanIntent
  Date        Timerange (UTC)          Scan  FldId FieldName            nRows    SpwIds  Average Interval(s)    ScanIntent
  11-Jul-2010/21:30:44.0 - 21:30:52.0    2      0 J0925+0019          404    6.43    [0, 1]                      CALIBRATE_PHASE#UNSPECIFIED
  03-Jan-2013/06:31:48.0 - 06:36:42.0    6      0 3C147                  1019200  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35,
   ID  Name                SpwId RestFreq(MHz)  SysVel(km/s)  
   ID  Name                SpwId RestFreq(MHz)  SysVel(km/s)  
   0    J0925+0019          0    -              -             
   0    3C147              0    -              -             
   0    J0925+0019          1    -              -             
   0    3C147              1    -              -             
   0    J0925+0019          2    -              -             
   0    3C147              2    -              -             
   0    J0925+0019          3    -              -             
   0    3C147              3    -              -             
   0    J0925+0019          4    -              -             
   0    3C147              4    -              -             
   0    J0925+0019          5    -              -             
   0    3C147              5    -              -             
   0    J0925+0019          6    -              -             
   0    3C147              6    -              -             
   0    J0925+0019          7    -              -             
   0    3C147              7    -              -             
   0    J0925+0019          8    -              -             
   0    3C147              8    -              -             
   0    J0925+0019          9    -              -             
   0    3C147              9    -              -             
   0    J0925+0019          10    -              -             
   0    3C147              10    -              -             
   0    J0925+0019          11    -              -             
   0    3C147              11    -              -             
   0    J0925+0019          12    -              -             
   0    3C147              12    -              -             
   0    J0925+0019          13    -              -             
   0    3C147              13    -              -             
   0    J0925+0019          14    -              -             
   0    3C147              14    -              -             
   0    J0925+0019          15    -              -             
   0    3C147              15    -              -             
   0    J0925+0019          16    -              -             
   0    3C147              16    -              -             
   0    J0925+0019          17    -              -             
   0    3C147              17    -              -             
   1   SN2010FZ            2    -              -             
   0    3C147              18   -              -             
   1   SN2010FZ            3    -              -             
   0    3C147              19   -              -             
   1   SN2010FZ            4    -              -             
   0    3C147              20   -              -             
   1   SN2010FZ            5    -              -             
   0    3C147              21   -              -             
   1   SN2010FZ            6    -              -             
   0    3C147              22   -              -             
   1   SN2010FZ            7    -              -             
   0    3C147              23   -              -             
   1   SN2010FZ            8    -              -             
   0    3C147              24   -              -             
   1   SN2010FZ            9    -              -             
   0    3C147              25   -              -             
   1   SN2010FZ            10   -              -             
   0   3C147              26   -              -             
   1   SN2010FZ            11   -              -             
   0   3C147              27   -              -             
   1   SN2010FZ            12   -              -             
   0   3C147              28   -              -             
   1   SN2010FZ            13   -              -             
   0   3C147              29   -              -             
   1   SN2010FZ            14   -              -             
   0   3C147              30   -              -             
   1   SN2010FZ            15   -              -             
   0   3C147              31   -              -             
   1   SN2010FZ            16   -              -             
   0   3C147              32   -              -             
   1   SN2010FZ            17   -              -             
   0   3C147              33   -              -             
   2   3C286               2    -              -             
   0   3C147               34    -              -             
   2   3C286               3    -              -             
   0   3C147               35    -              -             
   2   3C286               4    -              -             
   0   3C147               36    -              -             
   2   3C286               5    -              -             
   0   3C147               37    -              -             
   2   3C286               6    -              -             
   0   3C147               38    -              -             
   2   3C286               7    -              -             
   0   3C147               39    -              -             
   2   3C286               8    -              -             
   0   3C147               40    -              -             
   2   3C286               9    -              -             
   0   3C147               41    -              -             
   2   3C286               10   -              -             
   0   3C147               42   -              -             
   2   3C286               11   -              -             
   0   3C147               43   -              -             
   2   3C286               12   -              -             
   0   3C147               44   -              -             
   2   3C286               13   -              -             
   0   3C147               45   -              -             
   2   3C286               14   -              -             
   0   3C147               46   -              -             
   2   3C286               15   -              -             
   0   3C147               47   -              -             
   2   3C286               16   -              -             
   0   3C147               48   -              -             
   2   3C286               17   -              -             
   0   3C147               49   -              -             
Antennas: 27:
   0    3C147              50   -              -           
   ID  Name  Station  Diam.   Long.        Lat.       
   0    3C147              51    -              -           
   0    ea01  W09      25.0 m  -107.37.25.2  +33.53.51.0 
  0   3C147              52    -              -          
   1   ea02  E02      25.0 m  -107.37.04.4  +33.54.01.1 
   0   3C147              53    -              -          
   2   ea03  E09      25.0 m  -107.36.45.1  +33.53.53.6 
   0   3C147              54    -              -          
   3   ea04  W01      25.0 m  -107.37.05.9  +33.54.00.5 
   0   3C147              55    -              -           
   4   ea05  W08      25.0 m  -107.37.21.6  +33.53.53.0 
  0   3C147              56    -              -          
   5   ea06  N06      25.0 m  -107.37.06.9  +33.54.10.3 
   0   3C147              57    -              -          
   6   ea08  N01      25.0 m  -107.37.06.0  +33.54.01.8 
   0   3C147              58    -              -          
   7   ea09  E06      25.0 m  -107.36.55.6  +33.53.57.7 
   0   3C147              59    -              -          
   8   ea10  N03      25.0 m   -107.37.06.3  +33.54.04.8 
   0    3C147              60   -              -           
   9   ea11  E04      25.0 m  -107.37.00.8  +33.53.59.7 
  0   3C147              61    -              -          
   10  ea12  E08      25.0 m  -107.36.48.9  +33.53.55.1 
   0   3C147              62    -              -           
   11  ea13  N07      25.0 m  -107.37.07.2  +33.54.12.9 
  0   3C147              63    -              -           
   12  ea14  E05      25.0 m   -107.36.58.4  +33.53.58.8 
   1    gcal-J0603+174      0    -              -           
   13  ea15  W06      25.0 m   -107.37.15.6  +33.53.56.4 
   1   gcal-J0603+174      1    -              -           
   14  ea16  W02      25.0 m  -107.37.07.5  +33.54.00.9 
  1    gcal-J0603+174      2    -              -           
   15  ea17  W07      25.0 m  -107.37.18.4  +33.53.54.8 
   1    gcal-J0603+174      3    -              -           
   16  ea18  N09      25.0 m  -107.37.07.8  +33.54.19.0 
  1    gcal-J0603+174      4    -              -           
   17  ea19  W04      25.0 m  -107.37.10.8  +33.53.59.1
   1    gcal-J0603+174      5    -              -           
   18  ea20  N05      25.0 m  -107.37.06.7  +33.54.08.0 
   1    gcal-J0603+174      6    -              -           
   19  ea21  E01      25.0 m  -107.37.05.7  +33.53.59.2 
   1    gcal-J0603+174      7    -              -           
   20  ea22  N04      25.0 m   -107.37.06.5  +33.54.06.1 
   1    gcal-J0603+174      8    -              -           
   21  ea23  E07      25.0 m  -107.36.52.4  +33.53.56.5 
   1    gcal-J0603+174      9    -              -           
   22  ea24  W05      25.0 m  -107.37.13.0  +33.53.57.8 
   1    gcal-J0603+174      10    -              -           
   23  ea25  N02      25.0 m  -107.37.06.2  +33.54.03.5 
   1    gcal-J0603+174      11    -              -           
   24  ea26  W03      25.0 m  -107.37.08.9  +33.54.00.1 
   1    gcal-J0603+174      12    -              -           
   25  ea27  E03      25.0 m  -107.37.02.8  +33.54.00.5 
   1    gcal-J0603+174      13    -              -           
  26  ea28  N08      25.0 m  -107.37.07.5 +33.54.15.8 
  1   gcal-J0603+174      14    -              -           
 
   1    gcal-J0603+174      15    -              -           
##### End Task: listobs              #####
  1    gcal-J0603+174      16    -              -           
##########################################
   1    gcal-J0603+174      17    -              -           
   1    gcal-J0603+174      18    -              -           
   1    gcal-J0603+174      19    -              -           
   1    gcal-J0603+174      20    -              -           
   1    gcal-J0603+174      21    -              -           
   1    gcal-J0603+174      22    -              -           
   1    gcal-J0603+174      23    -              -           
   1    gcal-J0603+174      24    -              -           
  1    gcal-J0603+174      25   -              -           
   1    gcal-J0603+174      26    -              -           
  1    gcal-J0603+174      27    -              -           
  1    gcal-J0603+174      28    -              -           
  1    gcal-J0603+174      29    -              -           
  1    gcal-J0603+174      30    -              -           
  1    gcal-J0603+174      31    -              -           
  1    gcal-J0603+174      32    -              -           
  1    gcal-J0603+174      33    -              -           
  1    gcal-J0603+174      34    -              -           
  1    gcal-J0603+174      35    -              -           
  1    gcal-J0603+174      36    -              -           
  1    gcal-J0603+174      37    -              -           
  1    gcal-J0603+174      38    -              -           
  1    gcal-J0603+174      39    -              -           
  1    gcal-J0603+174      40    -              -           
  1    gcal-J0603+174      41    -              -           
  1    gcal-J0603+174      42    -              -           
  1    gcal-J0603+174      43    -              -           
  1    gcal-J0603+174      44    -              -           
  1    gcal-J0603+174      45    -              -           
  1    gcal-J0603+174      46    -              -           
  1    gcal-J0603+174      47    -              -           
  1    gcal-J0603+174      48    -              -           
  1    gcal-J0603+174      49    -              -           
  1    gcal-J0603+174      50    -              -           
  1    gcal-J0603+174      51    -              -           
  1    gcal-J0603+174      52    -              -           
  1    gcal-J0603+174      53    -              -           
  1    gcal-J0603+174      54    -              -           
  1    gcal-J0603+174      55    -              -           
  1    gcal-J0603+174      56    -              -           
  1    gcal-J0603+174      57    -              -           
  1    gcal-J0603+174      58    -              -           
  1    gcal-J0603+174      59    -              -           
  1    gcal-J0603+174      60    -              -           
  1    gcal-J0603+174      61    -              -           
  1    gcal-J0603+174      62    -              -           
  1    gcal-J0603+174      63    -              -           
  2    G192.16-3.84        0    -              -           
  2    G192.16-3.84        1    -              -           
  2    G192.16-3.84        2    -              -           
  2    G192.16-3.84        3    -              -           
  2    G192.16-3.84        4    -              -           
  2    G192.16-3.84        5    -              -           
  2    G192.16-3.84        6    -              -           
  2    G192.16-3.84        7    -              -           
  2    G192.16-3.84        8    -              -           
  2    G192.16-3.84        9    -              -           
  2    G192.16-3.84        10    -              -           
  2    G192.16-3.84        11    -              -           
  2    G192.16-3.84        12    -              -           
  2    G192.16-3.84        13    -              -           
  2    G192.16-3.84        14    -              -           
  2    G192.16-3.84        15    -              -           
  2    G192.16-3.84        16    -              -           
  2    G192.16-3.84        17    -              -           
  2    G192.16-3.84        18    -              -           
  2    G192.16-3.84        19    -              -           
  2    G192.16-3.84        20    -              -           
  2    G192.16-3.84        21    -              -           
  2    G192.16-3.84        22    -              -           
  2    G192.16-3.84        23    -              -           
  2    G192.16-3.84        24    -              -           
  2    G192.16-3.84        25    -              -           
  2    G192.16-3.84        26    -              -           
  2    G192.16-3.84        27    -              -           
  2    G192.16-3.84        28    -              -           
  2    G192.16-3.84        29    -              -           
  2    G192.16-3.84        30    -              -           
  2    G192.16-3.84        31    -              -           
  2    G192.16-3.84        32    -              -           
  2    G192.16-3.84        33    -              -           
  2    G192.16-3.84        34    -              -           
  2    G192.16-3.84        35    -              -           
  2    G192.16-3.84        36    -              -           
  2    G192.16-3.84        37    -              -           
  2    G192.16-3.84        38    -              -           
  2    G192.16-3.84        39    -              -           
  2    G192.16-3.84        40    -              -           
  2    G192.16-3.84        41    -              -           
  2    G192.16-3.84        42    -              -           
  2    G192.16-3.84        43    -              -           
  2    G192.16-3.84        44    -              -           
  2    G192.16-3.84        45    -              -           
  2    G192.16-3.84        46    -              -           
  2    G192.16-3.84        47    -              -           
  2    G192.16-3.84        48    -              -           
  2    G192.16-3.84        49    -              -           
  2    G192.16-3.84        50    -              -           
  2    G192.16-3.84        51    -              -           
  2    G192.16-3.84        52    -              -           
  2    G192.16-3.84        53    -              -           
  2    G192.16-3.84        54    -              -           
  2    G192.16-3.84        55    -              -           
  2    G192.16-3.84        56    -              -           
  2    G192.16-3.84        57    -              -           
  2    G192.16-3.84        58    -              -           
  2    G192.16-3.84        59    -              -           
  2    G192.16-3.84        60    -              -           
  2    G192.16-3.84        61    -              -           
  2    G192.16-3.84        62    -              -           
  2    G192.16-3.84        63    -              -           
  3    3c84-J0319+413      0    -              -           
  3    3c84-J0319+413      1    -              -           
  3    3c84-J0319+413      2    -              -           
  3    3c84-J0319+413      3    -              -           
  3    3c84-J0319+413      4    -              -           
  3    3c84-J0319+413      5    -              -           
  3    3c84-J0319+413      6    -              -           
  3    3c84-J0319+413      7    -              -           
  3    3c84-J0319+413      8    -              -           
  3    3c84-J0319+413      9    -              -           
  3    3c84-J0319+413      10    -              -           
  3    3c84-J0319+413      11    -              -           
  3    3c84-J0319+413      12    -              -           
  3    3c84-J0319+413      13    -              -           
  3    3c84-J0319+413      14    -              -           
  3    3c84-J0319+413      15    -              -           
  3    3c84-J0319+413      16    -              -           
  3    3c84-J0319+413      17    -              -           
  3    3c84-J0319+413      18    -              -           
  3    3c84-J0319+413      19    -              -           
  3    3c84-J0319+413      20    -              -           
  3    3c84-J0319+413      21    -              -           
  3    3c84-J0319+413      22    -              -           
  3    3c84-J0319+413      23    -              -           
  3    3c84-J0319+413      24    -              -           
  3    3c84-J0319+413      25    -              -           
  3    3c84-J0319+413      26    -              -           
  3    3c84-J0319+413      27    -              -           
  3    3c84-J0319+413      28    -              -           
  3    3c84-J0319+413      29    -              -           
  3    3c84-J0319+413      30    -              -           
  3    3c84-J0319+413      31    -              -           
  3    3c84-J0319+413      32    -              -           
  3    3c84-J0319+413      33    -              -           
  3    3c84-J0319+413      34    -              -           
  3    3c84-J0319+413      35    -              -           
  3    3c84-J0319+413      36    -              -           
  3    3c84-J0319+413      37    -              -           
  3    3c84-J0319+413      38    -              -           
  3    3c84-J0319+413      39    -              -           
  3    3c84-J0319+413      40    -              -           
  3    3c84-J0319+413      41    -              -           
  3    3c84-J0319+413      42    -              -           
  3    3c84-J0319+413      43    -              -           
  3    3c84-J0319+413      44    -              -           
  3    3c84-J0319+413      45    -              -           
  3    3c84-J0319+413      46    -              -           
  3    3c84-J0319+413      47    -              -           
  3    3c84-J0319+413      48    -              -           
  3    3c84-J0319+413      49    -              -           
  3    3c84-J0319+413      50    -              -           
  3    3c84-J0319+413      51    -              -           
  3    3c84-J0319+413      52    -              -           
  3    3c84-J0319+413      53    -              -           
  3    3c84-J0319+413      54    -              -           
  3    3c84-J0319+413      55    -              -           
  3    3c84-J0319+413      56    -              -           
  3    3c84-J0319+413      57    -              -           
  3    3c84-J0319+413      58    -              -           
  3    3c84-J0319+413      59    -              -           
  3    3c84-J0319+413      60    -              -           
  3    3c84-J0319+413      61    -              -           
  3    3c84-J0319+413      62    -              -           
  3    3c84-J0319+413      63    -              -           
Antennas: 26:
  ID  Name  Station  Diam.    Long.        Lat.                Offset from array center (m)                ITRF Geocentric coordinates (m)       
                                                                    East        North    Elevation              x              y              z
  0    ea01  N48      25.0 m  -107.37.38.1  +33.59.06.2      -855.2759    9405.9595      -25.9351 -1600374.885000 -5036704.201000  3562667.881900
  1    ea02  N56      25.0 m  -107.37.47.9  +34.00.38.4      -1105.2071    12254.3069      -34.2426 -1600128.383400 -5035104.146500  3565024.672100
  2    ea03  N16      25.0 m  -107.37.10.9  +33.54.48.0      -155.8511    1426.6436      -9.3827 -1601061.956000 -5041175.880700  3556058.037600
  3    ea05  W08      25.0 m  -107.37.21.6  +33.53.53.0      -432.1184    -272.1472      -1.5070 -1601614.092200 -5042001.650900  3554652.508900
  4    ea06  N32      25.0 m  -107.37.22.0  +33.56.33.6      -441.7237    4689.9748      -16.9332 -1600781.042100 -5039347.435200  3558761.533000
  5    ea07  E40      25.0 m  -107.32.35.4  +33.52.16.9      6908.8279    -3240.7316      39.0057 -1595124.924100 -5045829.461500  3552210.685200
  6    ea09  E24      25.0 m  -107.35.13.4  +33.53.18.1      2858.1754    -1349.1257      13.7290 -1598663.097500 -5043581.389700  3553767.027800
  7    ea10  E32      25.0 m  -107.34.01.5  +33.52.50.3      4701.6588    -2209.7063      25.2191 -1597053.120700 -5044604.691600  3553059.009300
  8    ea11  W56      25.0 m  -107.44.26.7  +33.49.54.6    -11333.2153    -7637.6824      15.3542 -1613255.404300 -5042613.085000  3548545.901400
  9    ea12  E08      25.0 m  -107.36.48.9  +33.53.55.1        407.8285    -206.0065      -3.2272 -1600801.926000 -5042219.366500  3554706.448200
  10  ea13  W24      25.0 m  -107.38.49.0  +33.53.04.0      -2673.3434    -1784.5870      10.4960 -1604008.742800 -5042135.827600  3553403.728800
  11  ea14  W16      25.0 m  -107.37.57.4  +33.53.33.0      -1348.7083    -890.6269        1.3068 -1602592.853600 -5042055.005300  3554140.703900
  12  ea15  W72      25.0 m  -107.48.24.0  +33.47.41.2    -17419.4730  -11760.2869      14.9578 -1619757.314900 -5042937.673700  3545120.385300
  13  ea16  N08      25.0 m  -107.37.07.5  +33.54.15.8        -68.9252      433.1901      -5.0683 -1601147.956700 -5041733.824100  3555235.952500
  14  ea17  E48      25.0 m  -107.30.56.1  +33.51.38.4      9456.5938    -4431.6366      37.9317 -1592894.088800 -5047229.121000  3551221.221100
  15  ea18  E72      25.0 m  -107.24.42.3  +33.49.18.0      19041.8754    -8769.2059        4.7234 -1584460.867200 -5052385.599300  3547599.997600
  16  ea19  W64      25.0 m  -107.46.20.1  +33.48.50.9    -14240.7600    -9606.2738      17.1055 -1616361.584300 -5042770.519200  3546911.442800
  17  ea20  N72      25.0 m  -107.38.10.5  +34.04.12.2      -1685.6775    18861.8403      -43.4734 -1599557.932000 -5031396.371000  3570494.760600
  18  ea21  E64      25.0 m  -107.27.00.1  +33.50.06.7      15507.6045    -7263.7280      67.1961 -1587600.190400 -5050575.873800  3548885.396600
  19  ea22  N24      25.0 m  -107.37.16.1  +33.55.37.7      -290.3745    2961.8582      -12.2374 -1600930.087700 -5040316.398500  3557330.387000
  20  ea23  N64      25.0 m  -107.37.58.7  +34.02.20.5      -1382.3750    15410.1463      -40.6373 -1599855.675100 -5033332.371000  3567636.622500
  21  ea24  W40      25.0 m  -107.41.13.5  +33.51.43.1      -6377.9740    -4286.7919        8.2191 -1607962.456900 -5042338.214500  3551324.943600
  22  ea25  W48      25.0 m  -107.42.44.3  +33.50.52.1      -8707.9407    -5861.7854      15.5265 -1610451.925400 -5042471.123100  3550021.056800
  23  ea26  W32      25.0 m  -107.39.54.8  +33.52.27.2      -4359.4561    -2923.1223      11.7579 -1605808.647100 -5042230.071500  3552459.203400
  24  ea27  E16      25.0 m  -107.36.09.8  +33.53.40.0      1410.0316    -673.4696      -0.7909 -1599926.110000 -5042772.967300  3554319.791200
  25  ea28  N40      25.0 m  -107.37.29.5  +33.57.44.4      -633.6167    6878.5984      -20.7748 -1600592.764000 -5038121.352000 3560574.847300
</pre>
</pre>


This task displays a lot of information about the MS. We can see that the observation was performed with the EVLA, for a total integration of 3359 seconds (1 hour).  The number of data records (1570726) is equal to the number of baselines (N_antenna * [N_antenna - 1] / 2) X the number of integrations (observing time / time-average binning) X the number of spectral windows.   For this observation, this is roughly 351 baselines (27X26/2) X 360 integrations (3600s total/10s avg) X 16 spectral windows = 2021760.  Note that this is high by ~30%; this is because the archive already flagged bad data, and there are some scans which only have two (rather than 16) spectral windows present.  Extra exercise: examine the MS using {{browsetable}} to see what a data record looks like (equivalent to a row, as displayed by this task).
This task displays a lot of information about the MS. We can see that the observation was performed with the EVLA over an integration time of 4557 seconds (1.3 hours).  The number of data records (10,061,248) is approximately equal to the number of baselines (N_antenna * [N_antenna - 1] / 2) X the number of integrations (observing time / time-average binning) X the number of spectral windows. For this observation, this is roughly 325 baselines (26X25/2) X 760 integrations (4557s total/6s avg) X 64 spectral windows = 15,808,000.  Note that this is high by ~50%; this is because the "total time" reported is simply (start time) - (end time) of the MS, which includes periods of slewing, flagged data, and scans that were excluded from the final MS.  Extra exercise: examine the MS using {{browsetable}} to see what a data record looks like (equivalent to a row, as displayed by this task).


The most useful parts of the {{listobs}} output are the scan, field, and spectral window listings.   
The most useful parts of the {{listobs}} output are the scan, field, and spectral window listings.  From the spectral window information, we can see that there are a total of 64 (0 through 63) spectral windows in this dataset, each with 128 channels, and that they are all at Ka-band (which spans 26.5 - 40.0 GHz).   


From the spectral window information, we can see that there were a total of 18 (0 through 17) spectral windows in this dataset.  The first two of these (0 and 1) were only used to help set up the correlator. 
The field listing shows four sources:


Looking at the scan listing, we can see that the first four scans which are present used only these spectral windows. These are referred to as "dummy scans". We will not be using these, since they often contain bad data.
* 3C147 (Field ID 0), the flux calibration source;
* J0603+174 (1), used for calibrating the complex gains;
* G192.16-3.84 (2), the science target; and
* 3c84 (3), used for calibrating the spectral bandpass.


The C-band data of interest is contained in scans 6-44 and spectral windows 2 to 17.  Careful examination shows that scan 8 is missing but from the time ranges that the data has been merged into scan 7.  This sort of correlator back-end data-capture issue was occasionally seen during 2010.  Hopefully, it will not affect our data, but we should keep an eye out for problems with scan 7.
Note the rapid switching between G192 and J0603: this will help us accurately calculate and transfer the gain phase solutions for these high-frequency data.  Note that the original MS also included reference pointing calibration scans at X-band, but since the pointing solutions were already applied during observing, we did not retain these scans (in the interest of limiting dataset size).


The field listing shows three sources:
== Flagging the MS ==


* J0925+0019 (also referred to by its field ID, 0), which will serve as a calibrator for the visibility phases,
[[Image:PlotG192_flagcmd_4.1.png|200px|thumb|right|online flags plotted from flagcmd]]
* SN2010FZ (1), our science target field, and
* 3C286 (2), which will serve as a calibrator for the visibility amplitudes, i.e., it is assumed to have a precisely known flux density; as well as the spectral bandpass.


== Flagging the MS ==
The online flags, which are a record of known bad data produced by the VLA online system, were applied by the archive when it generated the MS.  However, it's good to have a sense of what was deleted in this process.  A record of the flags is stored in a table in the MS called <tt>FLAG_CMD</tt>.  (In fact, the information for this table is actually a subdirectory within the MS; you can see this by listing the contents of <tt>G192_6s.ms</tt>.)


The online flags, which are a record of known bad data produced by the EVLA online system, have already been applied by the archive as it generated the MS.  However, it's good to have a sense of what was deleted in this process.  A record of the flags is also stored in a separate table in the MS, called <tt>FLAG_CMD</tt>.  (In fact, the information for this table is actually a subdirectory within the MS; you can see this by listing the contents of <tt>SN2010FZ_10s.ms</tt>.)
You can examine the commands stored in the <tt>FLAG_CMD</tt> table using {{flagcmd}}:
 
[[Image:PlotSN2010FZ_flagcmd_3.4.png|200px|thumb|right|online flags plotted from flagcmd]]
You can examine the commands stored in the <tt>FLAG_CMD</tt> table using {{flagcmd}}.
<source lang="python">
<source lang="python">
# In CASA
# In CASA
flagcmd(vis='SN2010FZ_10s.ms',inpmode='table',action='list')
flagcmd(vis='G192_6s.ms', inpmode='table', action='list', \
        useapplied=True)
</source>
</source>
These will go to the logger or terminal (they appear to go to the terminal now in 4.2).
* <tt>useapplied=True</tt>: tells the task to list flags that have already been applied to the MS (which includes all online flags; otherwise, they would be ignored)
 
The flag information will be printed to the terminal (all 2870 rows). The majority of the flags are "ANTENNA_NOT_ON_SOURCE" -- most of these were generated as a result of the slewing required for the fast switching between G192 and the phase calibrator.


You can also plot the commands stored in the <tt>FLAG_CMD</tt> table:
You can also plot the commands stored in the <tt>FLAG_CMD</tt> table:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
myrows = range(285)
myrows = range(2868)
flagcmd(vis='SN2010FZ_10s.ms',inpmode='table',action='plot',tablerows=myrows)
flagcmd(vis='G192_6s.ms', inpmode='table', action='plot', \
        useapplied=True, tablerows=myrows)
</source>
</source>


Note that we are only plotting the first 285 rows -- this is because the last few are from flagging zeros in the data (caused by correlator errors) and data which have been flagged due to [http://evlaguides.nrao.edu/index.php?title=Observational_Status_Summary#Shadowing_and_Cross-Talk antenna shadowing]. Note that you can not do the <tt>tablerows</tt> selection and plot those too, you will just get lines at the bottom marked as "All" antennas for these flags.
Note that for demonstration purposes, we have chosen to only plot the first 2868 rows.  The last two rows are from flagging zeros in the data (caused by correlator errors) and data which have been flagged due to [http://evlaguides.nrao.edu/index.php?title=Observational_Status_Summary#Shadowing_and_Cross-Talk antenna shadowing]. (Since the data were taken in the most widely spaced A-configuration, little if any data were likely affected by shadowing.)  If you prefer you can omit the <tt>tablerows</tt> selection parameter and plot the last two rows as well -- you will just get lines at the bottom marked as "All" antennas for these flags.


This will bring up a <tt>matplotlib</tt> plotter.  You can have it plot to a PNG file instead:
By default, this will bring up a <tt>matplotlib</tt> plotter.  You can have it plot to a PNG file instead:


<source lang="python">
<source lang="python">
# In CASA
# In CASA
flagcmd(vis='SN2010FZ_10s.ms', inpmode='table', action='plot', tablerows=myrows,  
flagcmd(vis='G192_6s.ms', inpmode='table', action='plot', tablerows=myrows,  
         plotfile='PlotSN2010FZ_flagcmd_4.2.png')
         useapplied=True, plotfile='PlotG192_flagcmd_4.1.png')
</source>
</source>


The flags as plotted in the figure to the above right look normal.   
The flags as plotted in the figure to the above right look normal.  They are color-coded by REASON, and you see the ANTENNA_NOT_ON_SOURCE flags between scans, some FOCUS_ERROR flags here and there, and the occasional SUBREFLECTOR_ERROR flag also between scans (most likely after the receiver band changes that are necessary for reference pointing; when the subreflectors rotate to pick up the new feed on the ring, some are slower than others).  You want to be wary of long blocks of unexpected flags, which might be false alarms and cause you to flag too much data.  In that case, look at the data itself in {{plotms}} (see below for examples) to decide whether or not to apply all flags. (Note: for the dataset in this tutorial, we have already deleted all the flagged data to reduce the file size, so you won't be able to inspect the flagged data within the MS.  To do so, you will need to download the original dataset from the  [https://archive.nrao.edu/archive/advquery.jsp NRAO Science Data Archive].)
They are color-coded by REASON, and you see ANTENNA_NOT_ON_SOURCE flags between scans, and the occasional SUBREFLECTOR_ERROR flag also between scans (most likely after band changes when the subreflector rotates to  
pick up the new feed on the ring, some are slower than others).  What you watch for here are long blocks of unexpected flags, which might be false alarms and cause you to flag too much data.  In that case, look at the data itself in {{plotms}} (see below for examples) to decide whether or not to apply all flags.


[[Image:plotSN2010FZ_plotants.png|200px|thumb|right|plotants plotter]]
[[Image:plotG192_plotants.png|200px|thumb|right|plotants plotter]]
To plot up the antenna positions in the array:
To plot up the antenna positions in the array:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotants('SN2010FZ_10s.ms')
plotants('G192_6s.ms')
</source>
</source>


Line 288: Line 563:
</source>
</source>


Now we examine the MS looking for bad data to flag. We will use {{plotms}} to bring up an interactive GUI that will display 2-D Y vs.X style line plots. <b>NOTE: We do not recommend using the editing/flagging features of plotms.</b>  It is very easy to mess up your data this way.  Also, to improve speed we will be restricting the scope of plotting so most box/flag operations would not get rid of all the bad data.   
Now we examine the MS looking for bad data to flag. We will use {{plotms}} to bring up an interactive GUI that will display 2-D Y vs. X style line plots. <b>NOTE: We do not recommend using the editing/flagging features of {{plotms}}.</b>  It is very easy to mess up your data this way.  Also, to improve speed we will be restricting the scope of plotting, so most box/flag operations would not get rid of all the bad data -- although they would ''appear'' to delete it, which is misleading.   


We will instead use plotms to identify bad data and then use flagcmd to flag it.  This will also allow full scripting of the flagging, which is ultimately the best way to keep track of what's been deleted.  Given the large dataset sizes now being generated, reproducibility is extremely important.  Imaging spending a day flagging your data, then a disk error corrupts the MS.  It's imperative that you have an automated way to regenerate your work. This is also why we encourage you to keep a running file with all the commands you use on a dataset.
We will instead use {{plotms}} to identify bad data and then use {{flagcmd}} to flag it.  This will also allow full scripting of the flagging, which is ultimately the best way to keep track of what's been deleted.  Given the large dataset sizes now being generated, reproducibility is extremely important.  Imagine spending a day flagging your data, then a disk error corrupts the MS: it's imperative that you have an automated way to regenerate your work! This is also why we also encourage you to keep a running file with all the commands you use to process a dataset.


NOTE: If you need an introduction to {{plotms}}, see:
NOTE: If you need an introduction to {{plotms}}, see:
Line 297: Line 572:
* [[What's the difference between Antenna1 and Antenna2? Axis definitions in plotms]]
* [[What's the difference between Antenna1 and Antenna2? Axis definitions in plotms]]


WARNING: The '''Flag''' [[Image:FlagThoseData.png]] button on the plotms GUI is close to other buttons you will be using, in particular the one that gets rid of boxes you have drawn.  Be careful and don't hit the '''Flag''' button by mistake!
WARNING: The '''Flag''' [[Image:FlagThoseData.png]] button on the plotms GUI is close to other buttons you will be using, in particular the one that deletes boxes you have drawn [[Image:DeleteBox.png]].  Be careful you don't hit the '''Flag''' button by mistake!


As we found above, the useful spectral windows are 2-17. To get an idea of the data layout, plot a single baseline (ea01&ea02) and channel (31, for all spectral windows) versus time:
To get an idea of the data layout, plot a single baseline (ea02&ea05), channel (31, for all spectral windows), and polarization (RR) versus time.  Note that limiting the selected data with appropriate filters is extremely helpful when plotting large datasets:
 
[[Image:screenshotPlotG192_plotms_ant02-05_4.1.png|200px|thumb|right|plotms of ea02&ea05 amp vs time]]
[[Image:screenshotPlotSN2010FZ_plotms_ants1_4.0.png|200px|thumb|right|plotms ea01&ea02 amp vs time]]
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotms(vis='SN2010FZ_10s.ms',field='',spw='2~17:31~31', \
plotms(vis='G192_6s.ms', field='', spw='*:31~31', \
       antenna='ea01&ea02',correlation='RR,LL',xaxis='time',yaxis='amp')
       antenna='ea02&ea05', xaxis='time', yaxis='amp', \
      correlation='rr', coloraxis='field')
</source>
</source>


Here, we can see the alternating phase calibration and science target scans, as well as the (brighter) flux calibrator at the end of the observation.  Feel free to play with ways to view, or color the data: for example, go to the "Display" left-hand tab, and choose "Colorize by: Field".  You can also change the size of the plotted points, if they are too small to see easily, by setting "Unflagged Points Symbol" to "Custom" and increasing the number of pixels under "Style".
Here, we can see the alternating phase calibration and science target scans, as well as the (brighter) bandpass calibrator at the end of the observation.  Feel free to play with ways to view.  For example, you can change the size of the plotted points, if they are too small to see easily, by setting "Unflagged Points Symbol" to "Custom" and increasing the number of pixels under "Style."  You can also experiment with data averaging, plotting different correlations (if you're not doing polarization calibration, you can ignore the "cross-hand" correlations RL and LR and focus on "parallel-hand" correlations RR and LL), changing the plotted axes, altering the colorization scheme (try colorizing by baseline, correlation, field, etc.).
 
[[Image:screenshotPlotG192_plotms_baseline_4.1.png|200px|thumb|right|plotms baseline amplitudes for field 3]]


[[Image:screenshotPlotSN2010FZ_plotms_ants2_4.0.png|200px|thumb|right|plotms ea01 for field 2 showing amp versus ANTENNA2]]
Look for bad antennas by picking the bandpass calibrator and plotting baselines.  We color the points by "antenna1" to see which antennas might be troublesome:
Look for bad antennas by picking the last field and plotting baselines versus antenna <tt>ea01</tt>:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotms(vis='SN2010FZ_10s.ms',field='2',spw='2~17:31~31', \
plotms(vis='G192_6s.ms', field='3', spw='*:31~31', \
       antenna='ea01',correlation='RR,LL',xaxis='antenna2',yaxis='amp')
       antenna='', xaxis='baseline',\
      yaxis='amp', coloraxis='antenna1')
</source>
</source>


You should be able to see that antenna 11 (= ea13) is bad (very low amplitude, it has no C-band receiver!) and that some of the spectral windows on 15 and 23 (ea17, ea25) are also on the low side.  Boxing with the '''Mark Regions''' [[Image:MarkRegionsButton.png]] tool and using the '''Locate''' [[File:casaplotms-locate-tool.png]] tool will show in the logger that spw 10-17 are suspect for these antennas. (Note: you may also leave these in for now if you like; if this were truly a first pass through the data it is unlikely that they would be caught.  Since this is a tutorial, and there is limited time for a second pass through the data, it's probably best to trust us and delete them now.)
You should be able to see that three of the antennas have lower amplitudes than the rest.  Boxing with the '''Mark Regions''' [[File:MarkRegionsButton.png]] tool and using the '''Locate''' [[File:casaplotms-locate-tool.png]] tool will show in the logger that these are antennas ea01, ea10 and ea19; indeed, checking the [https://archive.nrao.edu/archive/ArchiveRouter?OBS_LOGS=EVLA,TVER0004,56295.000000,56296.000000 Operator Log] for this observation shows that these antennas have collimation offsets and that the data have been corrupted.  We will delete these antennas.
 
[[Image:plotG192_plotms_field3_ea05_ea13.png|200px|thumb|right|plotms field 3 ea05 and ea13 amp vs frequency]]


[[Image:plotSN2010FZ_plotms_ea02.png|200px|thumb|right|plotms field 2 ea02 amp vs frequency]]
Now look at the raw spectral bandpasses of baselines to ea05.  It is in the inner core of the array and a prospective reference antenna. Since we plan to flag them, we will exclude antennas ea01, ea10, and ea19 using negation (represented by "!") in the selection, and iterate by antenna:
Now look at the bandpass for ea02 - it is in the inner core and a prospective reference antenna. Exclude ea13 using negation (represented by "!") in the selection:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotms(vis='SN2010FZ_10s.ms',field='2',spw='2~17', \
plotms(vis='G192_6s.ms', field='3', \
       antenna='ea02;!ea13',correlation='RR,LL',xaxis='frequency',yaxis='amp')
      antenna='ea05;!ea01;!ea10;!ea19', \
       xaxis='frequency', yaxis='amp',  
      coloraxis='corr', iteraxis='antenna')
</source>
</source>
There is clearly less data for spw 11, and use of Locate shows spw 11 data only for ea02,ea03,04,08,09,11,12. We will later delete this incomplete spw.  Note also the very strong RFI spike at 6614 MHz (spw 10 ch 63) with clear ringing contaminating both spw 10 and 11. There is also a tremendous roll-off in spw 10.  We will drop these spectral window when we process the data.


[[Image:plotSN2010FZ_plotms_ea02ea20.png|200px|thumb|right|plotms ea02 iteration with baseline stopped at ea02&ea20 showing phase vs frequency]]
As you iterate through baselines with ea05, you'll notice that the plot for ea05&ea13 shows that ea13's RCP (correlation = "RR") is weak, as noted in the log file as well.  We will flag this antenna over all correlations, since current restrictions do not allow for single-polarization data to be imaged if it's part of a full-polarization dataset. 
We can also step through the baselines to our antenna using iteraxis:
 
Also, note that spectral windows 16 through 31 (the upper baseband) for antenna ea18 look very suspicious.  We need to keep an eye on these data.
 
For antenna ea24, there appear to be some issues with spectral windows 47 and 48, and the RCP of spw 40 also looks problematic, so we'll flag this as well.
 
[[Image:plotG192_plotms_field3_ea05_ea18.png|200px|thumb|right|plotms field 3 ea05 and ea18 phase vs frequency]]
 
Now plot the phases, iterating through baselines to ea05:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotms(vis='SN2010FZ_10s.ms',field='2',spw='2~17',antenna='ea02;!ea13', \
plotms(vis='G192_6s.ms', field='3', \
       correlation='RR,LL',xaxis='frequency',yaxis='amp',iteraxis='baseline')
      antenna='ea05;!ea01;!ea10;!ea13;!ea19', \
       xaxis='frequency', yaxis='phase', \
      coloraxis='spw', iteraxis='antenna')
</source>
</source>
and use the '''Next Iteration''' [[Image:NextIterationButton.png]] button to step through the baselines.
 
This will make it easier to isolate the bad antennas. Now plot the phases, iterating through baselines to ea02:
Notice the rapidly winding phases with frequency due to residual instrumental delays (we will calibrate the instrumental delays and smooth-out the phases later). Most span a turn or less over each 128-MHz subband, but there are some outliers.  Step through to ea18.  You will see that there are large jumps between spectral windows for spw 16-31 (see plot on the right). This reinforces our suspicion that something is wrong with these data on ea18 and we will flag them as well.
 
To carry out the flagging, we again use {{flagcmd}} in the mode where it takes a list of command strings:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotms(vis='SN2010FZ_10s.ms',field='2',spw='2~17',antenna='ea02;!ea13', \
flaglist = ['antenna="ea01,ea10,ea19,ea13"',
      correlation='RR,LL',xaxis='frequency',yaxis='phase',iteraxis='baseline')
            'antenna="ea24" spw="40,47~48"',
            'antenna="ea18" spw="16~31"']
flagcmd(vis='G192_6s.ms', inpmode='list', inpfile=flaglist, \
        action='apply', flagbackup=True)
</source>
</source>
You see the slopes due to residual delays. Mostly a turn or less over a 128MHz subband, but there are some outliers.
These commands will carry out the flags and add a record of them to the FLAG_CMD table (where they will be marked as applied).  Before applying the flags, a backup version of the flags will be stored as <tt>flagcmd_1</tt>, in case you would like to restore the MS to the state it was in prior to your new flags (this can be done using {{flagmanager}} with mode = "restore" and, in this case, versionname = "flagcmd_1").
Step through to ea20.  You see that there is a very large delay in RR (via locate) for
the first baseband (spw 0~7).  We will delete this (will also delete LL so there are no orphan polarization products, which would be ignored by {{clean}} in the imaging stage).
Note ea17 and ea25 baselines drop close to zero in the middle of upper baseband (e.g. plot 'ea17&ea25') so we will delete these.


To carry out flagging, we again use {{flagcmd}} in the mode where it takes a list of command strings:
Plot the data again, now that is has been flagged (this time, we'll look at amplitude vs. frequency):
<source lang="python">
<source lang="python">
# In CASA
# In CASA
flaglist = ['antenna="ea13"',
plotms(vis='G192_6s.ms', field='3', antenna='ea05', \
            'antenna="ea17" spw="10~17"',
      xaxis='frequency', yaxis='amp')
            'antenna="ea25" spw="10~17"',
            'antenna="ea20" spw="2~9"']
flagcmd(vis='SN2010FZ_10s.ms',inpmode='list',inpfile=flaglist,action='apply',flagbackup=True)
</source>
</source>
These commands will be carried out as well as being added to the FLAG_CMD table (marked as applied).


Plot the data again, now that is has been flagged:
[[Image:plotG192_plotms_ea02fld3.png|200px|thumb|right|plotms field 3 ea05 amp vs frequency]]
 
Now let's look at our phase calibrator -- it is weaker, and we can see some RFI:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotms(vis='SN2010FZ_10s.ms',field='',spw='5:30~33',avgchannel='64', \
plotms(vis='G192_6s.ms', field='1', antenna='ea05', coloraxis = 'spw',\
       antenna='ea01&ea02',correlation='RR,LL',xaxis='time',yaxis='amp')
       correlation = 'RR,LL', xaxis='frequency', yaxis='amp', scan='10,20,30,40,50,60')
plotms(vis='SN2010FZ_10s.ms',field='2',spw='2~17',antenna='ea02', \
      correlation='RR,LL',xaxis='frequency',yaxis='amp',scan='7~43')
</source>
</source>
Note that we've chosen a subset of scans to limit the amount of data being plotted.  This will give us a sense of whether there is serious RFI (or other issues) present in the data, but will obviously not display everything.  Later on, when we plot the calibrated data, we will need to again inspect for possible bad data (and we will flag and recalibrate).


[[Image:plotSN2010FZ_plotms_ea02fld0.png|200px|thumb|right|plotms field 0 ea02 amp vs frequency]]
Use the Zoom button [[File:ZoomButton.png]], Mark Regions [[File:MarkRegionsButton.png]], and Locate [[File:Casaplotms-locate-tool.png]] to identify the frequency/channels of the RFI. In particular, we note the following:
Now our phase calibrator - it is weaker, and we now start to really see the RFI:
* 27.228 GHz (spw 33 ch 124)
<source lang="python">
* 27.707 GHz (spw 37 ch 91)
# In CASA
* 27.81-27.811 GHz (spw 38 ch 66-67)
plotms(vis='SN2010FZ_10s.ms',field='0',spw='2~17',antenna='ea02', \
* 27.819-27.821 GHz (spw 38 ch 75-77)
      correlation='RR,LL',xaxis='frequency',yaxis='amp',scan='7~43')
* 28.894 GHz (spw 46 ch 126)
</source>
* 28.976 GHz (spw 48 ch 0)
Use the Zoom feature, Mark rectangles and use Locate to identify the frequency/channel of RFI. In particular, we note in our analysis:
* 29.684-20.685 GHz (spw 53 ch 68-69)
* 6614MHz (spw 10 ch 63) super strong
* 30.976 GHz (spw 63 ch 80) very strong
* 6772-6778MHz (spw 12 ch 14-17)
* 35.782 GHz (spw 10 ch 26)
* 7260-7264MHz (spw 16 ch 2-4)
* 36.523 GHz (spw 15 ch 127)
* 7314-7340MHz (spw 16 ch 29-42)
* 37.946 GHz (spw 27 ch 62)
* 7402-7418MHz (spw 17 ch 9-17)
* 37.948 GHz (spw 27 ch 64)
* 7458-7466MHz (spw 17 ch 37-41)
* 7488MHz (spw 17 ch 52)


If you plot all antennas and avoid the band edges you see spw 16 and 17 are pretty wiped out:
Flag these channels:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotms(vis='SN2010FZ_10s.ms',field='0',spw='2~17:4~59',antenna='', \
flaglist = ['spw="33:124,37:91,38:66~67;75~77,46:126,48:0"', \
      correlation='RR,LL',xaxis='frequency',yaxis='amp',scan='7~43')
            'spw="53:68~69,63:80,10:26,15:127,27:62,27:64"']
flagcmd(vis='G192_6s.ms', inpmode='list', inpfile=flaglist, \
        action='apply', flagbackup=True)
</source>
</source>
When this is finished, it's useful to have a look at the flagged data.  To reload the plotms window after taking the new flags into account, check the "force reload" box on the lower left of the plotms GUI and click on "Plot."  (As a shortcut, you can also hold down the "Shift" key while clicking on the "Plot" button to force-reload a plot.)


For now we will not flag these spectral windows, but note the bad channels, which we will mask out when creating continuum calibration tables and images.
Finally, split off the good data, without retaining the flagged data.  This will allow us to work on the data without having to start completely over (if we mess something up badly), as well as let us do simpler data selections (since the data size will be a bit smaller).
 
Finally, split off the good scans and spw, this will allow us to work on the data without having to start completely over (if we mess something up badly) as well as letting us do simpler data selections.  Note that we do not include spw 10, because of the bad RFI, or spw 11, because of the many missing antennas.


<source lang="python">
<source lang="python">
# In CASA
# In CASA
# Remove any existing split data, otherwise split will not happen
# Remove any existing split data, otherwise split will not happen
os.system('rm -rf SN2010FZ_flagged10s.ms')
os.system('rm -rf G192_flagged_6s.ms')
split(vis='SN2010FZ_10s.ms',outputvis='SN2010FZ_flagged10s.ms',datacolumn='data',spw='2~9,12~17',scan='7~43')
split(vis='G192_6s.ms', outputvis='G192_flagged_6s.ms', \
      datacolumn='data', keepflags=False)
</source>
</source>
* keepflags=False: again, to limit the size of the MS, we do not propagate flagged data to the split-off MS.


You now have a MS called <tt>SN2010FZ_flagged10s.ms</tt> in your working area.  This should be 2.8GB in size, which you can see while still at the CASA command prompt by typing:
You now have a MS called <tt>G192_flagged_6s.ms</tt> in your working area.  This should be 16GB in size, which you can determine at the CASA command prompt by typing:


<source lang="python">
<source lang="python">
# In CASA
# In CASA
os.system('du -sh SN2010FZ_flagged10s.ms')
os.system('du -sh G192_flagged_6s.ms')
</source>
</source>


Note that the built-in <tt>system</tt> function allows one to execute UNIX shell commands within a CASA session.  (Some, like <tt>ls</tt>, don't need this extra wrapper, but most are not automatically understood.)
Note that the built-in <tt>system</tt> function allows one to execute UNIX shell commands within a CASA session.  (Some, like <tt>ls</tt>, don't need this extra wrapper, but most are not automatically understood.)


[[Image:PlotSN2010FZ_plotms_datastream_zoomed.png|200px|thumb|right|plotms antenna2 vs. time "datastream" plot, zoomed in on last scan]]
[[Image:PlotG192_plotms_datastream.png|200px|thumb|right|plotms antenna2 vs. time "datastream" plot]]
At this point it is useful to plot a "datastream" view of the dataset to show what antennas are present at what time. You can do this using
At this point it is useful to plot a "datastream" view of the MS to show which antennas are present at different times. You can do this using:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotms(vis='SN2010FZ_flagged10s.ms',field='',correlation='RR,LL',
plotms(vis='G192_flagged_6s.ms', xaxis='time', yaxis='antenna2', \
       timerange='',antenna='',spw='0:31',
       symbolshape = 'circle', plotrange=[-1,-1,0,26], coloraxis='field')
      xaxis='time',yaxis='antenna2',
      plotrange=[-1,-1,0,26],coloraxis='field')
</source>
</source>
This shows the times where data is present on baselines TO a given Antenna2 (which means there is no line for ea01 which is antenna 0). You can pick up ea01 (and drop ea28) by setting <tt>yaxis='antenna1'</tt>. To the right we show this plot, having zoomed in on the last scan on 3C286. You see here that some antennas are present in this scan earlier than others (e.g. ea02 comes in one 10s integration later than ea04).
This shows the times where data is present on baselines '''to''' a given antenna (controlled by setting yaxis="Antenna2").  Note that this means there is no "line" plotted for ea01 (antenna 0). You can pick-up ea01 (and drop ea28) by setting <tt>yaxis='antenna1'</tt>. To the right we show this plot. You can see that, for the most part, all antennas are present for the entire observation.  One exception to this is antenna ea16, which comes in a little late on the first scan of G192.


== Calibration ==
== Calibration ==


Summarize the split flagged MS:
Before proceeding with calibration, we will summarize the split flagged MS:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
listobs('SN2010FZ_flagged10s.ms')
listobs('G192_flagged_6s.ms', listfile='G192_flagged_listobs.txt')
</source>
</source>
In the logger we see:
<pre>
##########################################
##### Begin Task: listobs            #####


================================================================================
As before, inspection of the listobs output text file shows that there are now 6,958,621 data records present, and 22 antennas remaining in the MS.
          MeasurementSet Name:  SN2010FZ_flagged10s.ms      MS Version 2
================================================================================
  Observer: Dr. Alicia M. Soderberg    Project: T.B.D. 
Observation: EVLA
Data records: 1375038      Total integration time = 3042 seconds
  Observed from  11-Jul-2010/21:36:01.0  to  11-Jul-2010/22:26:43.0 (UTC)
 
  ObservationID = 0        ArrayID = 0
  Date        Timerange (UTC)          Scan  FldId FieldName          nRows  Int(s)  SpwIds      ScanIntent
  11-Jul-2010/21:36:01.0 - 21:38:20.5    7      0 J0925+0019          73710  9.93    [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]CALIBRATE_PHASE#UNSPECIFIED
              21:38:44.0 - 21:39:51.0    9      1 SN2010FZ            39312  9.16    [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              21:40:01.0 - 21:41:20.5    10      1 SN2010FZ            44226  9.89    [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              21:41:30.0 - 21:42:50.0    11      1 SN2010FZ            44226  10      [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              21:43:00.0 - 21:44:20.0    12      1 SN2010FZ            44226  10      [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              21:44:30.0 - 21:45:50.0    13      1 SN2010FZ            44226  10      [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              21:46:00.0 - 21:47:19.5    14      1 SN2010FZ            44226  9.89    [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              21:47:29.0 - 21:47:49.0    15      1 SN2010FZ            14742  9.67    [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              21:48:12.0 - 21:49:18.5    16      0 J0925+0019          39312  9        [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]CALIBRATE_PHASE#UNSPECIFIED
              21:49:42.0 - 21:50:49.0    17      1 SN2010FZ            39312  9.17    [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              21:50:59.0 - 21:52:19.0    18      1 SN2010FZ            44226  10      [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              21:52:29.0 - 21:53:48.5    19      1 SN2010FZ            44226  9.89    [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              21:53:58.0 - 21:55:18.0    20      1 SN2010FZ            44226  10      [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              21:55:28.0 - 21:56:48.0    21      1 SN2010FZ            44226  10      [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              21:56:58.0 - 21:58:18.0    22      1 SN2010FZ            44226  10      [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              21:58:28.0 - 21:58:47.5    23      1 SN2010FZ            14742  9.67    [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              21:59:10.5 - 22:00:17.0    24      0 J0925+0019          39312  8.99    [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]CALIBRATE_PHASE#UNSPECIFIED
              22:00:39.5 - 22:01:47.0    25      1 SN2010FZ            39312  9.18    [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              22:01:57.0 - 22:03:17.0    26      1 SN2010FZ            44226  10      [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              22:03:27.0 - 22:04:47.0    27      1 SN2010FZ            44226  10      [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              22:04:57.0 - 22:06:16.5    28      1 SN2010FZ            44226  9.89    [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              22:06:26.0 - 22:07:46.0    29      1 SN2010FZ            44226  10      [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              22:07:56.0 - 22:09:16.0    30      1 SN2010FZ            44226  10      [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              22:09:26.0 - 22:09:45.5    31      1 SN2010FZ            14742  9.67    [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              22:10:08.0 - 22:11:15.5    32      0 J0925+0019          39312  9.13    [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]CALIBRATE_PHASE#UNSPECIFIED
              22:11:38.0 - 22:12:45.5    33      1 SN2010FZ            39312  9.19    [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              22:12:55.0 - 22:14:15.0    34      1 SN2010FZ            44226  10      [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              22:14:25.0 - 22:15:45.0    35      1 SN2010FZ            44226  10      [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              22:15:55.0 - 22:17:15.0    36      1 SN2010FZ            44226  10      [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              22:17:25.0 - 22:18:44.5    37      1 SN2010FZ            44226  9.89    [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              22:18:54.0 - 22:20:14.0    38      1 SN2010FZ            44226  10      [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              22:20:24.0 - 22:20:43.5    39      1 SN2010FZ            14742  9.67    [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]OBSERVE_TARGET#UNSPECIFIED
              22:21:06.0 - 22:22:13.5    40      0 J0925+0019          38584  9.15    [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]CALIBRATE_PHASE#UNSPECIFIED
              22:25:13.0 - 22:25:13.0    42      2 3C286              924    2.88    [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]CALIBRATE_BANDPASS#UNSPECIFIED,CALIBRATE_AMPLI#UNSPECIFIED
              22:25:23.0 - 22:26:43.0    43      2 3C286              43148  9.6      [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]CALIBRATE_BANDPASS#UNSPECIFIED,CALIBRATE_AMPLI#UNSPECIFIED
          (nVis = Total number of time/baseline visibilities per scan)
Fields: 3
  ID  Code Name                RA              Decl          Epoch  SrcId nVis 
  0    D    J0925+0019          09:25:07.81503 +00.19.13.9334 J2000  0    230230
  1    NONE SN2010FZ            09:42:04.77000 +00.19.51.0000 J2000  1    1100736
  2    K    3C286              13:31:08.28798 +30.30.32.9589 J2000  2    44072 
  (nVis = Total number of time/baseline visibilities per field)
Spectral Windows:  (14 unique spectral windows and 1 unique polarization setups)
  SpwID  #Chans Frame Ch1(MHz)    ChanWid(kHz)  TotBW(kHz)  Corrs         
  0          64 TOPO  4488        2000          128000      RR  RL  LR  LL 
  1          64 TOPO  4616        2000          128000      RR  RL  LR  LL 
  2          64 TOPO  4744        2000          128000      RR  RL  LR  LL 
  3          64 TOPO  4872        2000          128000      RR  RL  LR  LL 
  4          64 TOPO  5000        2000          128000      RR  RL  LR  LL 
  5          64 TOPO  5128        2000          128000      RR  RL  LR  LL 
  6          64 TOPO  5256        2000          128000      RR  RL  LR  LL 
  7          64 TOPO  5384        2000          128000      RR  RL  LR  LL 
  8          64 TOPO  6744        2000          128000      RR  RL  LR  LL 
  9          64 TOPO  6872        2000          128000      RR  RL  LR  LL 
  10        64 TOPO  7000        2000          128000      RR  RL  LR  LL 
  11        64 TOPO  7128        2000          128000      RR  RL  LR  LL 
  12        64 TOPO  7256        2000          128000      RR  RL  LR  LL 
  13        64 TOPO  7384        2000          128000      RR  RL  LR  LL 
<snip>
</pre>
Note that the spectral windows are re-numbered to 0 through 13.


=== Setting the flux density scale ===
=== Setting the flux density scale ===


It is now time to begin calibrating the data. The general data reduction strategy is to derive a series of scaling factors or corrections from the calibrators, which are then collectively applied to the science data.   
It is now time to begin calibration! The general data reduction strategy is to derive a series of scaling factors or corrections from the calibrators, which, in addition to <i>a priori</i> calibration information, are collectively applied to the science target.  For <em>much</em> more discussion of the philosophy, strategy, and implementation of calibration of synthesis data within CASA, see [http://casa.nrao.edu/docs/UserMan/UserManch4.html#x195-1920004 Synthesis Calibration] in the CASA Cookbook and User Reference Manual .
For <em>much</em> more discussion of the philosophy, strategy, and implementation of calibration of synthesis data within CASA, see [http://casa.nrao.edu/docs/UserMan/UserManch4.html#x195-1920004 Synthesis Calibration] in the CASA Cookbook and User Reference Manual .


Before calibrating, we insert a model for flux calibration source 3C286 into the MS.  In order to do this, we first have to locate the model image on our system with {{setjy}}, which we will also use to set the flux density scale.  The {{setjy}} task (in release 3.3.0 and later) has an option to list possible model images it knows about:
The first step is to insert a model for our flux calibrator source (3C147) into the MS in order to set the flux density scale for bootstrapping to other sources.  In order to do this, we first have to locate the model image on our system with {{setjy}}.  The {{setjy}} task has an option to list available model images:


<source lang="python">
<source lang="python">
# In CASA
# In CASA
setjy(vis='SN2010FZ_flagged10s.ms', listmodels=True)
setjy(vis='G192_flagged_6s.ms', listmodels=True)
</source>
</source>
which sends output to your terminal (but not the logger). For example, on an NRAO workstation:
which sends output to your terminal (but not the logger). For example, on an NRAO workstation, we obtain the following:
<pre>
<pre>
No candidate modimages matching '*.im* *.mod*' found in .
No candidate modimages matching '*.im* *.mod*' found in .


Candidate modimages (*) in /usr/lib64/casapy/release/4.2.0/data/nrao/VLA/CalModels:
Candidate modimages (*) in /home/casa/packages/RHEL5/prerelease/casapy-42.0.prerelease-10-1-64b/data/nrao/VLA/CalModels:
3C138_A.im  3C138_S.im  3C147_K.im 3C147_X.im  3C286_Q.im 3C48_C.im  3C48_U.im
3C138_A.im  3C138_L.im 3C138_U.im  3C147_C.im 3C147_Q.im  3C147_X.im 3C286_K.im  3C286_S.im 3C48_A.im  3C48_L.im  3C48_U.im
3C138_C.im  3C138_U.im  3C147_L.im 3C286_A.im  3C286_S.im 3C48_K.im  3C48_X.im
3C138_C.im  3C138_Q.im 3C138_X.im  3C147_K.im 3C147_S.im  3C286_A.im 3C286_L.im  3C286_U.im 3C48_C.im  3C48_Q.im  3C48_X.im
3C138_K.im  3C138_X.im 3C147_Q.im  3C286_C.im  3C286_U.im 3C48_L.im  README
3C138_K.im  3C138_S.im 3C147_A.im  3C147_L.im 3C147_U.im  3C286_C.im 3C286_Q.im  3C286_X.im 3C48_K.im 3C48_S.im README
3C138_L.im  3C147_A.im 3C147_S.im  3C286_K.im 3C286_X.im  3C48_Q.im
3C138_Q.im  3C147_C.im 3C147_U.im  3C286_L.im 3C48_A.im   3C48_S.im
</pre>
</pre>
The relevant image for our purposes is <tt>3C286_C.im</tt>, in the directory <tt>/usr/lib64/casapy/release/data/nrao/VLA/CalModels</tt>.  Your system may show a different location (for example <tt>/home/casa/data/nrao/VLA/CalModels/</tt>, or <tt>/Applications/CASA.app/Contents/data/nrao/VLA/CalModels</tt> on a Mac).  Since it knows about this image, we only have to give the image name and not the entire path. Otherwise, you will need to give it the entire path.  We now run the task using this model:
 
The relevant image for our purposes is <tt>3C147_A.im</tt>, in the directory <tt>/home/casa/packages/RHEL5/prerelease/casapy-42.0.prerelease-10-1-64b/data/nrao/VLA/CalModels/</tt>.  Your system may show a different location (for example <tt>/home/casa/data/nrao/VLA/CalModels/</tt>, or <tt>/Applications/CASA.app/Contents/data/nrao/VLA/CalModels</tt> on a Mac).  Since CASA knows about this image, we only have to give the image name and not the entire path. Note that outside of the NRAO, you may need to provide setjy with the entire path along with the model image name (this depends on your platform and installation location).   
 
We can now run the {{setjy}} task using the appropriate model:


<source lang="python">
<source lang="python">
# In CASA
# In CASA
mysetjy = setjy(vis='SN2010FZ_flagged10s.ms', field='2', scalebychan=True, model='3C286_C.im', usescratch=False)
setjy(vis='G192_flagged_6s.ms', field='0', scalebychan=True, \
      model='3C147_A.im')
</source>
</source>


[[Image:screenshotPlotG192_setjy_4.1.png|200px|thumb|right|plotms of model amp vs freq for 3C147]]
* <tt>scalebychan=True</tt>: will fill the model with per-channel values; otherwise, {{setjy}} would use a single value per spectral window.
* <tt>scalebychan=True</tt>: will fill the model with per-channel values; otherwise, {{setjy}} would use a single value per spectral window.
* <tt>usescratch=False</tt>: put the model in the header instead of creating scratch columns in the MS.  This will take up considerably less disk space.
* <tt>usescratch=False</tt>: put the model in the header instead of creating scratch columns in the MS.  This will take up considerably less disk space.


We have not specified a Flux Density Scale Standard and are thus using the default (<tt>standard='Perley-Butler 2010'</tt>) as that was current when these observations were taken. In particular, there is a more recent "Perley-Butler 2013" scale that most users will want to use! See <tt>help setjy</tt> for more details.
We can plot the model data using {{plotms}}:
<source lang="python">
# In CASA
plotms(vis='G192_flagged_6s.ms', field='0', antenna='ea02&ea05', \
      xaxis='freq', yaxis='amp', ydatacolumn='model')
</source>


Inspecting the logger report shows that 3C286 is about 7.7 Jy at lower end of the band to 5.7 Jy at the upper end.
Inspecting the logger report shows that 3C147 has a flux density of 1.40608 Jy at the lower end of the band (spw 63; ~31 GHz) and 1.2779 Jy at the upper end (spw 0; ~35 GHz).


Note: With release 4.2 {{setjy}} now returns a dictionary to Python, which we have captured in a variable. This can be used in scripts.
=== Deriving <i>a priori</i> calibrations ===


=== Deriving pre-determined calibrations: antenna position corrections, gain-elevation curves, and requantizer gains ===
Some calibration products are carried along throughout the calibration process and used as priors for subsequent calibration steps.  These include the antenna position corrections, gain-elevation curves, tropospheric opacity corrections, and requantizer gains.


Some calibration products are carried along throughout the calibration process and used as priors for subsequent calibration steps.  These include the antenna position corrections, gain-elevation curves, and requantizer gains.
==== Antenna position corrections ====


We use {{gencal}} to determine any antenna-position corrections that need to be applied to the data. This is based on a database of corrections with the time they were determined and when they were applied by the observing system, compared to the times in your observations.
We use {{gencal}} to determine any antenna-position corrections that need to be applied to the data. This is based on a database of corrections with the dates and times the corrections were determined and when they were included in the online observing system.
<source lang="python">
<source lang="python">
# In CASA
# In CASA
gencal('SN2010FZ_flagged10s.ms',caltable='calSN2010FZ.antpos',caltype='antpos',antenna='')
gencal('G192_flagged_6s.ms', caltable='calG192.antpos', \
      caltype='antpos', antenna='')
</source>
</source>
You should see in the logger:
You should see in the logger:
<pre style="background-color: #fffacd;">
<pre style="background-color: #fffacd;">
Determine antenna position offests from the baseline correction database
Determine antenna position offests from the baseline correction database
offsets for antenna ea01 :  0.00000   0.00300   0.00000
offsets for antenna ea05 :  0.00000 -0.00100   0.00090
offsets for antenna ea02 : -0.00080   0.00000  0.00000
offsets for antenna ea16 : -0.00310   0.00000  0.00100
offsets for antenna ea03 : -0.00280  0.00000  0.00000
</pre>
offsets for antenna ea05 :  0.00000  0.00280  0.00000
 
offsets for antenna ea06 : 0.00220  0.00100  0.00590
So this dataset does require antenna position corrections on ea05 & ea16.  If no corrections were necessary, the output from gencal would have appeared as follows:
offsets for antenna ea10 : 0.00080  0.00300  -0.00140
   
offsets for antenna ea11 : 0.00090  0.00000  0.00000
<pre style="background-color: #fffacd;">
offsets for antenna ea12 : -0.00280  0.00000  0.00000
No offsets found for this MS
offsets for antenna ea13 :  0.00000  -0.00080  0.00000
*** Warning *** No offsets found. No caltable created.
offsets for antenna ea17 : -0.00120  0.00000  0.00000
gencal::::casa An error occurred running task gencal.
offsets for antenna ea18 :  0.00040  -0.00080  0.00040
offsets for antenna ea22 : -0.00370  -0.00130  0.00000
offsets for antenna ea23 : -0.00140  0.00000  0.00000
offsets for antenna ea24 : -0.00150  0.00000  0.00000
offsets for antenna ea26 : -0.00190  0.00000  0.00210
offsets for antenna ea27 : 0.00000  0.00190  -0.00160
</pre>
</pre>
Note that there are significant position corrections for a number of the antennas.  
Although the "warning" makes it seem as if the task has failed, the message is normal and means there simply aren't any antenna corrections to apply.


In CASA 4.1, we now have the option to use {{gencal}} to create a calibration table containing the gain curves for the antennas. Although you can still use the <tt>gaincurve=True</tt> option in each task, we will make use of this new feature (note that the <tt>gaincurve=True</tt> will be phased out in future CASA releases):
==== Gain-elevation curves ====
 
We will use {{gencal}} to create calibration tables containing the gain curves and tropospheric opacity corrections for the antennas. Note that the <tt>gaincurve=True</tt> option that was previously available in calibration tasks (e.g., bandpass) is no longer available as of CASA 4.2.  The syntax for generating a gaincurve calibration table in gencal is as follows:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
gencal('SN2010FZ_flagged10s.ms',caltable='calSN2010FZ.gaincurve',caltype='gc')
gencal('G192_flagged_6s.ms', caltable='calG192.gaincurve', \
      caltype='gc')
</source>
</source>


Finally, we will use {{gencal}} to create a calibration table containing corrections for the requantizer gains.  Although this is only necessary for 3-bit data (and our SN2010FZ is 8-bit), we include it here for completeness.  It will not affect the calibration for our 8-bit data, but if one is following this CASA Guide as a template for 3-bit data, this step is needed to account for the small gain changes (~5-10%) that result from resetting the quantizer gains as the correlator changes to a new 3-bit configuration.
==== Tropospheric opacity corrections ====
 
[[Image:G192_plotWX.png|200px|thumb|right|plotweather output]]
 
The atmospheric opacity during the observations can be computed from a seasonal model and/or weather station information.  We will use the {{plotweather}} task to display the weather information and to calculate the zenith opacities for each spectral window.  After the zenith opacities are derived, {{gencal}} will recompute the correct elevation of the data automatically using <math>e^{(-\csc[el]\tau_z)}</math> and create the opacity-correction calibration table.
 
To start, we want to plot the opacity of the atmosphere at the time these observations was taken.  {{plotweather}} plots the weather conditions during the observations and calculates the atmospheric opacities based on these data, in combination with a seasonal model that contains long-term statistics at the VLA site. Using <tt>seasonal_weight=0.5</tt> (the default value) gives equal weights to the seasonal model and weather station data:
 
We will be running {{plotweather}} in a way that will assign the opacity list (one entry for each spectral window in ascending order) to the variable myTau:
 
<source lang="python">
<source lang="python">
# In CASA
# In CASA
gencal('SN2010FZ_flagged10s.ms',caltable='calSN2010FZ.requantizer',caltype='rq')
myTau = plotweather(vis='G192_flagged_6s.ms', doPlot=T)
</source>
</source>


Since we're running {{gencal}} on 3-bit data, it logs that it found "0 TIME/SPW switched power samples."
The logger should display:
<pre style="background-color: #fffacd;">
##########################################
##### Begin Task: plotweather        #####
plotweather(vis="G192_flagged_6s.ms",seasonal_weight=0.5,doPlot=True,plotName="")
2013-06-18 21:47:00 INFO plotweather SPW : Frequency (GHz) : Zenith opacity (nepers)
0  :  34.476  :  0.03
1  :  34.604  :  0.031
2  :  34.732  :  0.031
3  :  34.860  :  0.031
4  :  34.988  :  0.032
<snip>
61  :  30.640  :  0.024
62  :  30.768  :  0.024
63  :  30.896  :  0.024
wrote weather figure: G192_flagged_6s.ms.plotweather.png
##### End Task: plotweather          #####
##########################################
</pre>
 
In addition to assigning the myTau variable to the full list of opacities per spw, plotweather also creates a file <tt>G192_flagged_6s.ms.plotweather.png</tt> with the elevation of the sun, the wind speed and direction, the temperature, and precipitable water vapor (PWV) as functions of time over the course of the observation (view this file with your preferred image viewer like gthumb, xv, or Preview).
 
We can now create a calibration table to correct for the atmospheric opacity with {{gencal}} using the <tt>calmode='opac'</tt> parameter.  We could input the opacities directly, but it's easier to use the myTau variable with a little Python:
 
<source lang="python">
# In CASA
SPWs = []
for window in range(0,64):
    SPWs.append(str(window))
</source>
 
<source lang="python">
# In CASA
spwString = ','.join(SPWs)
gencal(vis='G192_flagged_6s.ms', caltable='calG192.opacity',
      caltype='opac', spw=spwString, parameter=myTau)
</source>
 
==== Requantizer gain corrections ====
 
Finally, we will use {{gencal}} to create a calibration table containing corrections for the requantizer gains.  Although this is only necessary for 3-bit data, such as our G192 dataset, it can be done for 8-bit datasets without any ill effects.  For 3-bit data, this step is needed to account for the small gain changes (~5-10%) that result from resetting the quantizer gains as the correlator changes to a new 3-bit configuration.  (Here is [https://science.nrao.edu/facilities/vla/docs/manuals/obsguide/modes/set-up/3bit/#dp more information on observing with the 3-bit system].)
<source lang="python">
# In CASA
gencal('G192_flagged_6s.ms', caltable='calG192.requantizer', \
      caltype='rq')
</source>


The caltables we have generated -- <tt>calSN2010FZ.antpos</tt>, <tt>calSN2010FZ.gaincurve</tt>, and <tt>calSN2010FZ.requantizer</tt> -- will need to be pre-applied in subsequent calibration steps.
The caltables we have generated (<tt>calG192.antpos</tt>, <tt>calG192.gaincurve</tt>, <tt>calG192.opacity</tt>, and <tt>calG192.requantizer</tt>) will need to be pre-applied in subsequent calibration steps.


=== Calibrating delays and bandpass ===
=== Calibrating delays and initial bandpass solutions ===


[[Image:plotSN2010FZ_plotcal_G0p1_4.0.png|200px|thumb|right|plotcal G0 phase ant 0~15]]
[[Image:plotG192_plotcal_G0p1_4.0.png|200px|thumb|right|plotcal G0 phase ant 0~15]]
[[Image:plotSN2010FZ_plotcal_G0p2_4.0.png|200px|thumb|right|plotcal G0 phase ant 16~26]]
[[Image:plotG192_plotcal_G0p2_4.0.png|200px|thumb|right|plotcal G0 phase ant 16~26]]


[[Image:plotSN2010FZ_plotcal_delays_4.2.png|200px|thumb|right|plotcal K0 delay vs. antenna]]
[[Image:plotG192_plotcal_delays.png|200px|thumb|right|plotcal K0 delay vs. antenna]]


[[Image:plotSN2010FZ_plotcal_B0a1_4.0.png|200px|thumb|right|plotcal B0 bandpass amp ant 0~15]]
[[Image:plotG192_plotcal_B0a1_4.0.png|200px|thumb|right|plotcal B0 bandpass amp ant ea06 spw 0-31]]
[[Image:plotSN2010FZ_plotcal_B0a2_4.0.png|200px|thumb|right|plotcal B0 bandpass amp ant 16~26]]
[[Image:plotG192_plotcal_B0a2_4.0.png|200px|thumb|right|plotcal B0 bandpass amp ant ea06 spw 32-63]]
[[Image:plotSN2010FZ_plotcal_B0p1_4.0.png|200px|thumb|right|plotcal B0 bandpass phase ant 0~15]]
[[Image:plotSN2010FZ_plotcal_B0p2_4.0.png|200px|thumb|right|plotcal B0 bandpass phase ant 16~26]]
[[Image:plotSN2010FZ_plotcal_B0ea14_4.0.png|200px|thumb|right|plotcal B0 amp and phase vs. freq for ea14]]


First, we do a phase-only calibration solution on a narrow range of channels in each spw on the bandpass/flux calibrator 3c286 to flatten them before solving for the bandpass. Note where we saw RFI in the higher spw and avoid those channels. The range 23~28 should work. Pick a refant near center - ea04 is a reasonable bet (see above):
First, we do a phase-only calibration solution on a narrow range of channels near the center of each spectral window on the bandpass calibrator 3C84 to flatten them with respect to time before solving for the bandpass. The range 60~68 should work. Pick a reference antenna near the center of the array -- ea05 is a reasonable choice (see above):
<source lang="python">
<source lang="python">
# In CASA
# In CASA
gaincal(vis='SN2010FZ_flagged10s.ms',caltable='calSN2010FZ.G0',field='2',spw='0~13:23~28', \
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G0', \
         gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve'],\
        field='3', spw='*:60~68', \
         gaintype='G',refant='ea04',calmode='p',solint='int',minsnr=3)  
         gaintable=['calG192.antpos','calG192.gaincurve', \
                  'calG192.requantizer','calG192.opacity'], \
         gaintype='G', refant='ea05', calmode='p', \
        solint='int', minsnr=3)
 
</source>
</source>


* <tt>refant='ea04'</tt> : try to use ea04 as the reference antenna
* <tt>refant='ea05'</tt> : Use ea05 as the reference antenna
* <tt>solint='int'</tt> : do a per-integration solve (every 10 seconds, since we've time-averaged the data)
* <tt>solint='int'</tt> : Do a per-integration solve (every 6 seconds, since we've time-averaged the data).
* <tt>minsnr=3</tt> : apply a minimum signal-to-noise cutoff.  Solutions with less than this value will be flagged
* <tt>minsnr=3</tt> : Apply a minimum signal-to-noise cutoff.  Solutions with less than this value will be flagged.
* <tt>gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve']</tt> : pre-apply the antpos and gaincurve caltables
* <tt>gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', 'calG192.opacity']</tt> : Pre-apply the antenna position corrections, gaincurve, opacity, and requantizer calibration tables.


Plot the phase solutions (using full phase range, -180 to 180, instead of autorange):
Plot the phase solutions (using full phase range, -180 to 180, instead of autorange):
Line 622: Line 894:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotcal(caltable='calSN2010FZ.G0',xaxis='time',yaxis='phase',iteration='antenna', \
plotcal(caltable='calG192.G0', xaxis='time', yaxis='phase', \
        plotrange=[-1,-1,-180,180])
        iteration='antenna', plotrange=[-1,-1,-180,180])
</source>
</source>


Step through the antenna-based solutions.  They look good (and fairly flat over the scans).
Step through the antenna-based solutions.  They look good (and fairly flat over the scans).


NOTE: When you are done plotting and want to use the caltable in another task, use the Quit button on the GUI to dismiss the plotter and free up the lock on the caltable. You should see a message in your terminal window saying "Resetting plotcal" which means you are good to go!
NOTE: When you are done plotting and want to use the calibration table in another task (e.g., for subsequent calibration or viewing with plotms), use the Quit button on the GUI to dismiss the plotter and free-up the lock on the calibration table. You should see a message in your terminal window saying "Resetting plotcal" which means you are good to go!


If you want to make single-page multipanel plots (like those shown to the right), particularly for a
If you want to make single-page, multipanel plots (like those shown to the right), particularly for a hardcopy (where it only shows the first page), you can do:
hardcopy (where it only shows the first page), you can do:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotcal(caltable='calSN2010FZ.G0',xaxis='time',yaxis='phase', \
plotcal(caltable='calG192.G0', xaxis='time', yaxis='phase', \
         antenna='0~10,12~15',subplot=531,iteration='antenna', \
         antenna='0~10,12~15', subplot=531, iteration='antenna', \
         plotrange=[-1,-1,-180,180],showgui=False,fontsize=6.0, \
         plotrange=[-1,-1,-180,180], fontsize=8.0, \
         figfile='plotSN2010FZ_plotcal_G0p1.png')
         markersize=3.0, figfile='plotG192_plotcal_G0p1.png')
plotcal(caltable='calSN2010FZ.G0',xaxis='time',yaxis='phase', \
plotcal(caltable='calG192.G0', xaxis='time', yaxis='phase', \
         antenna='16~26',subplot=531,iteration='antenna', \
         antenna='16~26', subplot=531, iteration='antenna', \
         plotrange=[-1,-1,-180,180],showgui=False,fontsize=6.0, \
         plotrange=[-1,-1,-180,180], fontsize=8.0, \
         figfile='plotSN2010FZ_plotcal_G0p2.png')
         markersize=3.0, figfile='plotG192_plotcal_G0p2.png')
</source>
</source>


We can now solve for the residual antenna-based delays that we saw in phase vs. frequency.
We can now solve for the residual delays that we saw in plotms when we plotted phase vs. frequency. This uses the <tt>gaintype='K'</tt> option in gaincal. Note that this currently does not do a "global fringe-fitting" solution for delays, but instead does a baseline-based delay solution for all baselines to the reference antenna, treating these as antenna-based delays.  In most cases with high-enough S/N to get baseline-based delay solutions, this will suffice. We avoid the edge channels of each spectral window by selecting channels 5~122:
This uses the gaintype='K' option in gaincal. Note that this currently does not do a "global fringe-fitting" solution for delays,
but instead does a baseline-based delay solution to all baselines to the refant, treating these
as antenna-based delays.  In most cases with high-enough S/N to get baseline-based delay solutions
this will suffice. We avoid the beginning of spw 0 due to the extreme roll-off (with loss of S/N) at the
starting edge.
 
<source lang="python">
<source lang="python">
# In CASA
# In CASA
gaincal(vis='SN2010FZ_flagged10s.ms',caltable='calSN2010FZ.K0',\
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.K0', \
         gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve','calSN2010FZ.G0'],\
         gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', \
         field='2',spw='0:8~59,1~13:4~59',gaintype='K', \
                  'calG192.opacity', 'calG192.G0'], \
         refant='ea04',combine='scan',solint='inf',minsnr=3)
         field='3', spw='*:5~122', gaintype='K', \
         refant='ea05', solint='inf', minsnr=3)
</source>
</source>
We pre-apply our initial phase table, and produce a new K-type caltable for input to bandpass calibration.
We can plot the delays, in nanoseconds, as a function of antenna index (you will get one for each subband and polarization):


Note that we have also pre-applied our initial phase table, calG192.G0.  We can plot the delays, in nanoseconds, as a function of antenna index (you will get one for each spw and polarization):
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotcal(caltable='calSN2010FZ.K0', xaxis='antenna', yaxis='delay')
plotcal(caltable='calG192.K0', xaxis='antenna', yaxis='delay')
</source>
</source>


The delays range from around -6 to 6 nanoseconds.
The delays range from around -5 to 4 nanoseconds.


Now solve for the bandpass using the previous tables:
Now we solve for the antenna bandpasses using the previous tables:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
bandpass(vis='SN2010FZ_flagged10s.ms',caltable='calSN2010FZ.B0', \
bandpass(vis='G192_flagged_6s.ms', caltable='calG192.B0', \
         gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve', \
         gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', \
                     'calSN2010FZ.G0','calSN2010FZ.K0'], \
                     'calG192.opacity', 'calG192.G0', 'calG192.K0'], \
         field='2',refant='ea04',solnorm=False, \
         field='3', refant='ea05', solnorm=False, \
         bandtype='B', combine='scan', solint='inf')
         bandtype='B', solint='inf')
</source>
</source>
'''WARNING''': You must set <tt>solnorm=False</tt> here or later on you will find some offsets
'''WARNING''': You must set <tt>solnorm=False</tt> here or later on you will find some offsets
between spw due to how amplitude scaling adjusts weights internally during solving.
among spws due to the way the amplitude scaling adjusts weights internally during solving.


You will see in the terminal some reports of solutions failing below our default S/N>3 cutoff:
[[Image:plotG192_plotcal_B0p1_4.0.png|200px|thumb|right|plotcal B0 bandpass phase ant ea06 spw 0-31]]
<pre>
[[Image:plotG192_plotcal_B0p2_4.0.png|200px|thumb|right|plotcal B0 bandpass phase ant ea06 spw 32-63]]
32 of 50 solutions flagged due to SNR < 3 in spw=0 (chan=1) at 2010/07/11/22:26:05.4
44 of 50 solutions flagged due to SNR < 3 in spw=0 (chan=0) at 2010/07/11/22:26:05.4
</pre>


These are in the first two edge channels of the first spw where the response is low, and not unexpected.
You will see in the terminal some reports of solutions failing due to "Insufficient unflagged antennas" -- note that these are for the channels we flagged earlier.
In the logger you will also see reports of reference antennas jumping in those channels, which can be
be safely ignored (we will drop those channels later anyway).


This is the first amplitude-scaling calibration that we do, so it is important to have used the <tt>calSN2010FZ.gaincurve</tt> caltable (or set <tt>gaincurve=True</tt>). If we were at higher frequency we would also have made an opacity caltable (or set <tt>opacity</tt>).
This is the first amplitude-scaling calibration that we do, so it is important to have used the <tt>calG192.gaincurve</tt> caltable (or set <tt>gaincurve=True</tt>) as well as the <tt>calG192.opacity</tt> caltable (or set <tt>opacity</tt> appropriately).


Now plot this, in amplitude then phase:
Plot the resulting bandpasses in amplitude and phase:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotcal(caltable='calSN2010FZ.B0',xaxis='freq',yaxis='amp',iteration='antenna')
plotcal(caltable='calG192.B0', xaxis='freq', yaxis='amp', \
        spw='0~31', iteration='antenna')
#
#
plotcal(caltable='calSN2010FZ.B0',xaxis='freq',yaxis='phase',iteration='antenna', \
plotcal(caltable='calG192.B0', xaxis='freq', yaxis='amp', \
        spw='32~63', iteration='antenna')
#
plotcal(caltable='calG192.B0', xaxis='freq', yaxis='phase', \
        iteration='antenna', spw='0~31', \
         plotrange=[-1,-1,-180,180])
         plotrange=[-1,-1,-180,180])
</source>
or to plot them all together
<source lang="python">
# In CASA
plotcal(caltable='calSN2010FZ.B0',xaxis='freq',yaxis='amp',
        antenna='0~10,12~15',subplot=531,iteration='antenna',
        fontsize=6.0, figfile='plotSN2010FZ_plotcal_B0a1_4.2.png')
plotcal(caltable='calSN2010FZ.B0',xaxis='freq',yaxis='amp',
        antenna='16~26',subplot=531,iteration='antenna',
        fontsize=6.0, figfile='plotSN2010FZ_plotcal_B0a2_4.2.png')
#
#
plotcal(caltable='calSN2010FZ.B0',xaxis='freq',yaxis='phase',
plotcal(caltable='calG192.B0', xaxis='freq', yaxis='phase', \
         antenna='0~10,12~15',subplot=531,iteration='antenna',
         iteration='antenna', spw='32~63', \
        plotrange=[-1,-1,-180,180],fontsize=6.0,
         plotrange=[-1,-1,-180,180])
        figfile='plotSN2010FZ_plotcal_B0p1_4.2.png')
plotcal(caltable='calSN2010FZ.B0',xaxis='freq',yaxis='phase',
        antenna='16~26',subplot=531,iteration='antenna',
         plotrange=[-1,-1,-180,180],fontsize=6.0,
        figfile='plotSN2010FZ_plotcal_B0p2_4.2.png')
</source>
</source>
(this can take a long time to plot).


In the bandpass phase you no longer see the residual antenna delays (just residual spw phase offsets from  
In the bandpass phases you no longer see the residual antenna delays (just residual spw phase offsets from the delay solution registration), but there are some band edge effects apparent.
the delay solution registration) but there are some band edge effects.
 
Note that some antennas have a little strange bandpasses at upper end of lower baseband in spw 5,6,7
=== Bootstrapping the bandpass calibrator spectrum ===
(e.g. ea14,ea16,ea17,ea25).
 
To plot amp and phase for a single antenna versus frequency (see plots at right):
Unfortunately, our flux density calibrator was not bright enough at Ka-band to use as the bandpass calibration source. Since there is no <i>a priori</i> spectral information for our chosen bandpass calibrator, 3C84, we need to bootstrap to find its spectral index, then recalibrate with this information in order to avoid folding the intrinsic spectral shape of 3C84 into our calibration.


First, we use the initial round of bandpass calibration to create gain solutions for the flux and bandpass calibrators:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotcal(caltable='calSN2010FZ.B0',xaxis='freq',yaxis='amp', \
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G1', field='0,3', \
         antenna='ea14',subplot=211)
         gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', \
plotcal(caltable='calSN2010FZ.B0',xaxis='freq',yaxis='phase', \
                  'calG192.opacity', 'calG192.K0', \
         antenna='ea14',subplot=212,plotrange=[-1,-1,-180,180])
                  'calG192.B0'], \
         gaintype='G', refant='ea05', calmode='ap', solint='30s', minsnr=3)
</source>
</source>


Because our flux density calibrator 3C286 is bright enough, we were able to use this as the bandpass calibrator.
Now let's have a look at the phase and amplitude solutions, iterating over antenna. We will look at the flux calibrator (3C147) and bandpass calibrator (3C84) individually since they're widely separated in time:
Since {{setjy}} put the correct spectrum for 3C286 into the MODEL_DATA column, our bandpass will reflect the
true bandpass of the instrument.  However, if for your observation you were unable to use a source of known spectrum
as the bandpass calibrator, then you would need to use the output of {{fluxscale}} later on to bootstrap a {{setjy}}
on your bandpass source using the derived spectral index information.
 
=== Final phase and amplitude calibration ===
 
[[Image:plotSN2010FZ_plotcal_G1intp1_4.0.png|200px|thumb|right|plotcal G1int per-int phase ant 0~15]]
[[Image:plotSN2010FZ_plotcal_G1intp2_4.0.png|200px|thumb|right|plotcal G1int per-int phase ant 16~26]]
 
[[Image:plotSN2010FZ_plotcal_G1intp_ea01_4.0.png|200px|thumb|right|plotcal G1int per-int phase ant 0~15]]
[[Image:plotSN2010FZ_plotcal_G1infp_ea01_4.0.png|200px|thumb|right|plotcal G1inf per-scan phase ant 0~15]]
 
Now calibrate phases using the full bandwidth.
First both our calibrators, one at a time - we could do them together, but in general you might need
to do different solution intervals for each, so we keep the runs separate to illustrate how to
do separate solutions and append them.
We exclude RFI channels here, and obtain one solution per integration (these are bright enough):
<source lang="python">
<source lang="python">
# In CASA
# In CASA
gaincal(vis='SN2010FZ_flagged10s.ms',caltable='calSN2010FZ.G1int', \
plotcal(caltable='calG192.G1', xaxis='time', yaxis='amp', \
        gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve',
         field='0', iteration='antenna')
                  'calSN2010FZ.K0','calSN2010FZ.B0'], \
         field='2',refant='ea04',solnorm=F, \
        spw='0:10~59,1~7:4~59,8:4~13;18~59,9~11:4~59,12:4~13;18~29;31~33;46~51;53~59,13:4~8;15~36;42~59', \
        solint='int',gaintype='G',calmode='p')
#
#
gaincal(vis='SN2010FZ_flagged10s.ms',caltable='calSN2010FZ.G1int', \
plotcal(caltable='calG192.G1', xaxis='time', yaxis='amp', \
         gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve',
         field='3', iteration='antenna')
                  'calSN2010FZ.K0','calSN2010FZ.B0'], \
#
         field='0',refant='ea04',solnorm=F, \
plotcal(caltable='calG192.G1', xaxis='time', yaxis='phase', \
         spw='0:10~59,1~7:4~59,8:4~13;18~59,9~11:4~59,12:4~13;18~29;31~33;46~51;53~59,13:4~8;15~36;42~59', \
        iteration='antenna', plotrange=[-1,-1,-180,180], \
         solint='int',gaintype='G',calmode='p',append=True)
         field='0')
#
plotcal(caltable='calG192.G1', xaxis='time', yaxis='phase', \
         iteration='antenna', plotrange=[-1,-1,-180,180], \
         field='3')
</source>
</source>
These will get applied when solving for amplitudes, and when calibrating the calibrators themselves.


The phases look reasonably connected:
The solutions all look reasonable and relatively constant with time. 
 
Now that we have gain solutions for the flux and bandpass calibrators, we can use {{fluxscale}} to scale the gain amplitudes of the bandpass calibrator:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotcal(caltable='calSN2010FZ.G1int',xaxis='time',yaxis='phase',iteration='antenna', \
flux1 = fluxscale(vis='G192_flagged_6s.ms', caltable='calG192.G1', \
        plotrange=[-1,-1,-180,180])
                  fluxtable='calG192.F1', reference='0', \
                  transfer='3', listfile='3C84.fluxinfo', fitorder=1)
</source>
</source>
* <tt>flux1 = fluxscale(...)</tt>: by providing a variable <tt>flux1</tt>, we allow {{fluxscale}} to use this for the output Python dictionary it returns with lots of information about the flux scaling.  You can inspect the output dictionary flux1 by typing "print flux1" at the CASA command line.
* <tt>fluxtable='calG192.F1'</tt>: this is the output scaled gain table.  Since we are only using this to find the spectral index of 3C84, we won't be using this table.
* <tt>listfile='3C84.fluxinfo'</tt>: an output file that contains the derived flux values and fit information.
* <tt>fitorder=1</tt>: only find a spectral index, ignoring curvature in the spectrum.
The last line in the file (and displayed in the logger) shows:
<pre style="background-color: #fffacd;">
# Fitted spectrum for 3c84-J0319+413 with fitorder=1: Flux density = 29.8756 +/- 0.0381051 (freq=32.4488 GHz) spidx=-0.598926 +/- 0.0105203
</pre>


To apply phase calibration to the target, we make a second table with one solution on our gain calibrator per scan:
[[Image:screenshotPlotG192_setjy_bp_4.1.png|200px|thumb|right|plotms of model amp vs freq for 3C84]]
[[Image:plotG192_3C84_fluxspec_4.2.png|200px|thumb|right|3C84 flux values returned by fluxscale]]
 
Using the information in the returned <tt>flux</tt> dictionary, we can plot the derived spectrum:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
gaincal(vis='SN2010FZ_flagged10s.ms',caltable='calSN2010FZ.G1inf',
freq = flux1['freq'] / 1e9
        gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve',
spw_list = range(0,64)
                  'calSN2010FZ.K0','calSN2010FZ.B0'], \
spw_str = []
        field='0',refant='ea04',solnorm=F, \
for i in spw_list:
        spw='0:10~59,1~7:4~59,8:4~13;18~59,9~11:4~59,12:4~13;18~29;31~33;46~51;53~59,13:4~8;15~36;42~59', \
  thisspw = str(i)
        solint='inf',gaintype='G',calmode='p')
  spw_str.append(thisspw)
 
bootstrapped_fluxes = []
for j in spw_str:
    thisflux = a[j]['fluxd'][0]
    bootstrapped_fluxes.append(thisflux)
 
pl.clf()
pl.plot(freq, bootstrapped_fluxes, 'bo')
pl.xlabel('Frequency (GHz)')
pl.ylabel('Flux Density (Jy)')
pl.title('3C84')
pl.show()
</source>
</source>
These scan phases will get interpolated by {{applycal}} onto our target. These look good also:
 
Note the bump around 37 GHz -- what is this?  We will not be able to account for it with the simple spectral index model, but still, ours is a good first approximation.
 
We can use the model from {{fluxscale}} to fill the MODEL column with 3C84's spectral information using {{setjy}}:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotcal(caltable='calSN2010FZ.G1inf',xaxis='time',yaxis='phase',iteration='antenna', \
setjy(vis='G192_flagged_6s.ms', field='3', scalebychan=True, \
        plotrange=[-1,-1,-180,180])
      fluxdensity=[29.8756, 0, 0, 0], spix=-0.598929, \
      reffreq='32.4488GHz')
</source>
</source>


Now solve for amplitudes on a per scan interval, after applying the per-integration phases.
Checking with plotms that the data have been appropriately filled:
Do these separately using <tt>gainfield</tt> so phases don't get
transferred across fields.  For field 2 (3C286) we use <tt>combine='scan'</tt> as there are two scans
on this source, with the first one having much less data (and will thus give a noisy solution on its own).
Note that {{gaincal}} uses linear interpolation of the previously determined phases by default, so
set this to "nearest" if you want to override this.
<source lang="python">
<source lang="python">
# In CASA
# In CASA
gaincal(vis='SN2010FZ_flagged10s.ms', caltable='calSN2010FZ.G2', \
plotms(vis='G192_flagged_6s.ms', field='3', antenna='ea05&ea02', \
        gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve',
      xaxis='freq', yaxis='amp', ydatacolumn='model')
                  'calSN2010FZ.K0','calSN2010FZ.B0','calSN2010FZ.G1int'], \
        gainfield=['','','2','2','2'], \
        interp=['','','nearest','nearest','nearest'], \
        field='2',refant='ea04',solnorm=F,
        spw='0:10~59,1~7:4~59,8:4~13;18~59,9~11:4~59,12:4~13;18~29;31~33;46~51;53~59,13:4~8;15~36;42~59', \
        solint='inf',combine='scan',gaintype='G',calmode='a')
#
gaincal(vis='SN2010FZ_flagged10s.ms', caltable='calSN2010FZ.G2', \
        gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve',
                  'calSN2010FZ.K0','calSN2010FZ.B0','calSN2010FZ.G1int'],\
        gainfield=['','','2','2','0'], \
        interp=['','','nearest','nearest','nearest'], \
        field='0',refant='ea04',solnorm=F, \
        spw='0:10~59,1~7:4~59,8:4~13;18~59,9~11:4~59,12:4~13;18~29;31~33;46~51;53~59,13:4~8;15~36;42~59', \
        solint='inf',gaintype='G',calmode='a',append=True)
</source>
</source>
This is the table we will apply to the data.


[[Image:plotSN2010FZ_plotcal_G2infa1_4.0.png|200px|thumb|right|plotcal G2 per-scan amp ant 0~15]]
[[Image:plotG192_plotcal_B0a1.b_4.1.png|200px|thumb|right|plotcal B0 bootstrapped bandpass amp ant ea06 spw 0-31]]
[[Image:plotSN2010FZ_plotcal_G2infa2_4.0.png|200px|thumb|right|plotcal G2 per-scan amp ant 16~26]]
[[Image:plotG192_plotcal_B0a2.b_4.1.png|200px|thumb|right|plotcal B0 bootstrapped bandpass amp ant ea06 spw 32-63]]
[[Image:plotG192_plotcal_B0p1.b_4.1.png|200px|thumb|right|plotcal B0 bootstrapped bandpass phase ant ea06 spw 0-31]]
[[Image:plotG192_plotcal_B0p2.b_4.1.png|200px|thumb|right|plotcal B0 bootstrapped bandpass phase ant ea06 spw 32-63]]  


We do a second version of the amplitude calibration, this time using <tt>combine='scan'</tt> on field 0. This is
Finally, we redo the previous calibration using this new model information. Although the commands are the same as what we issued earlier, keep in mind that the model values for the bandpass calibrator have changed, and therefore the results of these calibration calculations will differ:
to use for input to {{fluxscale}} in the next step.
<source lang="python">
<source lang="python">
# In CASA
# In CASA
gaincal(vis='SN2010FZ_flagged10s.ms', caltable='calSN2010FZ.G3', \
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G0.b', \
         gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve',
         field='3', spw='*:60~68', \
                  'calSN2010FZ.K0','calSN2010FZ.B0','calSN2010FZ.G1int'], \
         gaintable=['calG192.antpos', 'calG192.gaincurve', \
         gainfield=['','','2','2','2'], \
                  'calG192.requantizer', 'calG192.opacity'], \
        interp=['','','nearest','nearest','nearest'], \
         gaintype='G', refant='ea05', calmode='p', \
         field='2',refant='ea04',solnorm=F,
         solint='int', minsnr=3)  
        spw='0:10~59,1~7:4~59,8:4~13;18~59,9~11:4~59,12:4~13;18~29;31~33;46~51;53~59,13:4~8;15~36;42~59', \
         solint='inf',combine='scan',gaintype='G',calmode='a')
#
#
gaincal(vis='SN2010FZ_flagged10s.ms', caltable='calSN2010FZ.G3', \
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.K0.b', \
         gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve',
         gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', \
                  'calSN2010FZ.K0','calSN2010FZ.B0','calSN2010FZ.G1int'],\
                  'calG192.opacity', 'calG192.G0.b'], \
         gainfield=['','','2','2','0'], \
         field='3', spw='*:5~122', gaintype='K', \
        interp=['','','nearest','nearest','nearest'], \
        refant='ea05', solint='inf', minsnr=3)
        field='0',refant='ea04',solnorm=F, \
#
        spw='0:10~59,1~7:4~59,8:4~13;18~59,9~11:4~59,12:4~13;18~29;31~33;46~51;53~59,13:4~8;15~36;42~59', \
bandpass(vis='G192_flagged_6s.ms', caltable='calG192.B0.b', \
        solint='inf',combine='scan',gaintype='G',calmode='a',append=True)
        gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', \
                    'calG192.opacity', 'calG192.G0.b', 'calG192.K0.b'], \
        field='3', refant='ea05', solnorm=False, \
        bandtype='B', solint='inf')
</source>
</source>


Since the flux on the gain calibrator is not scaled to its correct flux (but to 1.0 Jy by default),
It's a good idea to inspect these solutions as well:
use {{fluxscale}} to transfer the amplitude gains from 3c286:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
myflux = fluxscale(vis='SN2010FZ_flagged10s.ms',caltable='calSN2010FZ.G3', \
plotcal(caltable='calG192.B0.b', xaxis='freq', yaxis='amp', \
                  fluxtable='calSN2010FZ.F3inc',reference='2',transfer='0',
        spw='0~31', iteration='antenna')
                  incremental=True)
#
plotcal(caltable='calG192.B0.b', xaxis='freq', yaxis='amp', \
        spw='32~63', iteration='antenna')
#
plotcal(caltable='calG192.B0.b', xaxis='freq', yaxis='phase', \
        iteration='antenna', spw='0~31', \
        plotrange=[-1,-1,-180,180])
#
plotcal(caltable='calG192.B0.b', xaxis='freq', yaxis='phase', \
        iteration='antenna', spw='32~63', \
        plotrange=[-1,-1,-180,180])
</source>
</source>
where we have captured the returned dictionary in the Python variable <tt>myflux</tt>. We have used the
<tt>incremental=True</tt> option (new to CASA 4.0) to make this table contain only the scale factors
per-antenna per-spw per-field needed to scale the data (rather than rescaling the input table). Thus, it
can be applied in addition to our <tt>G2</tt> table even though it was derived from the <tt>G3</tt> table.


The logger output gives:
They look virtually unchanged from the previous solutions, with the exception that the amplitude scaling is corrected for the spectrum of 3C84.  Now that we have the final version of our bandpass calibration, we can proceed to the full calibration of the dataset.
<pre>
Found reference field(s): 3C286
Found transfer field(s):  J0925+0019
Flux density for J0925+0019 in SpW=0 (freq=4.488e+09 Hz) is: 0.977483 +/- 0.00278572 (SNR = 350.891, N = 50)
Flux density for J0925+0019 in SpW=1 (freq=4.616e+09 Hz) is: 0.975972 +/- 0.00253876 (SNR = 384.429, N = 50)
Flux density for J0925+0019 in SpW=2 (freq=4.744e+09 Hz) is: 0.978538 +/- 0.00242824 (SNR = 402.982, N = 50)
Flux density for J0925+0019 in SpW=3 (freq=4.872e+09 Hz) is: 0.979278 +/- 0.00244155 (SNR = 401.088, N = 50)
Flux density for J0925+0019 in SpW=4 (freq=5e+09 Hz) is: 0.981804 +/- 0.00219239 (SNR = 447.823, N = 50)
Flux density for J0925+0019 in SpW=5 (freq=5.128e+09 Hz) is: 0.981478 +/- 0.00314805 (SNR = 311.773, N = 50)
Flux density for J0925+0019 in SpW=6 (freq=5.256e+09 Hz) is: 0.985493 +/- 0.00343534 (SNR = 286.869, N = 50)
Flux density for J0925+0019 in SpW=7 (freq=5.384e+09 Hz) is: 0.978491 +/- 0.00201807 (SNR = 484.865, N = 50)
Flux density for J0925+0019 in SpW=8 (freq=6.744e+09 Hz) is: 0.959005 +/- 0.00260159 (SNR = 368.623, N = 48)
Flux density for J0925+0019 in SpW=9 (freq=6.872e+09 Hz) is: 0.955123 +/- 0.00262785 (SNR = 363.462, N = 48)
Flux density for J0925+0019 in SpW=10 (freq=7e+09 Hz) is: 0.954202 +/- 0.00281227 (SNR = 339.3, N = 48)
Flux density for J0925+0019 in SpW=11 (freq=7.128e+09 Hz) is: 0.950797 +/- 0.00354085 (SNR = 268.522, N = 48)
Flux density for J0925+0019 in SpW=12 (freq=7.256e+09 Hz) is: 0.94732 +/- 0.00391511 (SNR = 241.965, N = 48)
Flux density for J0925+0019 in SpW=13 (freq=7.384e+09 Hz) is: 0.939356 +/- 0.00383532 (SNR = 244.922, N = 48)
Fitted spectrum for J0925+0019 with fitorder=1: Flux density = 0.968048 +/- 0.00159415 (freq=5.74863 GHz)
    spidx=-0.0721976 +/- 0.00943577
...
</pre>
You may see slightly different numbers on your machine (and will see more extensive output).  Note that "N" here is the number of antennas x the number of polarizations used for the calculations; in this case, there are 24 unflagged antennas and 2 polarizations. As of CASA 4.0, {{fluxscale}} now returns a fitted spectral index (and possibly curvature, e.g. if fitorder>1), which can be input to {{setjy}} if you want to use these derived fluxes for a model.  


As it so happens, the derived flux for J0925+0019 is about 1 Jy (you can plot up the raw amplitudes for fields 0,2 and convince yourself this is indeed true and not a bug). The spectrum rises a bit to peak in spw 6 then falls again. We will not use the fitted spectrum (setjy does not yet take fitorder>1) but will apply a incremental table in subsequent processing.
=== Final phase and amplitude calibration ===


== Applying the Calibration and Final Editing ==
[[Image:plotG192_plotcal_G1.int_4.1.png|200px|thumb|right|plotcal G1.int per-int phase ea06]]


Next we actually apply all our accumulated calibration tables. We apply these to the
[[Image:plotG192_plotcal_G1.inf_4.1.png|200px|thumb|right|plotcal G1.inf per-scan phase ea06]]
calibration fields individually using the appropriate gainfields and interpolation for each:
* For 3C286 (field 2) we did short-timescale phase solutions and a single scan amplitude, so use "linear" and "nearest" interpolation respectively.
* For the nearby gain calibrator (field 0) we did only scan-based phase and amplitude solutions so we use "nearest" interpolation
* For the target source we use field 0 to calibrate field 1, so use "linear" interpolation. This takes a few minutes.


[[Image:plotSN2010FZ_plotms_applied_fld2.png|200px|thumb|right|plotms of 3C286 with calibration applied]]
Now we will compute the calibrators' gain phases using the full bandwidth.  We will do the calibrators one at a time and append subsequent solutions, since we will use different solution intervals.  For 3C147 and 3C84, we obtain one solution per integration (these are bright enough); for the phase calibrator, J0603+174, we will use 12 second solution intervals:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
applycal(vis='SN2010FZ_flagged10s.ms',field='2', \
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G1.int', \
        gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve','calSN2010FZ.K0',
        gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', \
                    'calSN2010FZ.B0','calSN2010FZ.G1int','calSN2010FZ.G2'], \
                  'calG192.opacity', 'calG192.K0.b', 'calG192.B0.b'], \
        gainfield=['','','','','2','2'],
        field='0', refant='ea05', solnorm=F, \
        interp=['','','nearest','nearest','nearest','nearest'], \
        solint='int', gaintype='G', calmode='p')
        parang=False,calwt=False)
#
#
applycal(vis='SN2010FZ_flagged10s.ms',field='0', \
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G1.int', \
        gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve','calSN2010FZ.K0',
        gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', \
                    'calSN2010FZ.B0','calSN2010FZ.G1int','calSN2010FZ.G2',
                  'calG192.opacity', 'calG192.K0.b', 'calG192.B0.b'], \
                    'calSN2010FZ.F3inc'], \
        field='1', refant='ea05', solnorm=F, \
        gainfield=['','','','','0','0','0'],
        solint='12s', gaintype='G', calmode='p', append=True)
        interp=['','','nearest','nearest','nearest','nearest',''], \
        parang=False,calwt=False)
#
#
applycal(vis='SN2010FZ_flagged10s.ms',field='1', \
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G1.int', \
        gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve','calSN2010FZ.K0',
        gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', \
                    'calSN2010FZ.B0','calSN2010FZ.G1inf','calSN2010FZ.G2',
                  'calG192.opacity', 'calG192.K0.b', 'calG192.B0.b'], \
                    'calSN2010FZ.F3inc'], \
        field='3', refant='ea05', solnorm=F, \
        gainfield=['','','','','0','0','0'],
        solint='int', gaintype='G', calmode='p', append=True)
        interp=['','','nearest','nearest','linear','linear',''], \
        parang=False,calwt=False)
</source>
</source>
Because we used <tt>usesratch=False</tt> in {{setjy}}, the <tt>CORRECTED_DATA</tt> scratch column will be created the first time you run {{applycal}}. This will store the calibrated data.
These will get applied when solving for amplitudes (see the "G2" calibration tables below), and when calibrating the calibrators themselves (with the task {{applycal}}).


We can examine the corrected data on 3c286 using our RFI mask from above and avoiding band edges
The phases track nicely with time:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotms(vis='SN2010FZ_flagged10s.ms',field='2', \
plotcal(caltable='calG192.G1.int', xaxis='time', yaxis='phase', \
      spw='0:10~59,1~7:4~59,8:4~13;18~59,9~11:4~59,12:4~13;18~29;31~33;46~51;53~59,13:4~8;15~36;42~59', \
        iteration='antenna', plotrange=[-1,-1,-180,180])
      correlation='RR,LL',xaxis='frequency',yaxis='amp',ydatacolumn='corrected')
</source>
</source>


See figure above right.  There is clearly discrepant data visible spw 5 and 6, in particular for baseline ea17&ea25 (use the '''Mark Regions''' [[Image:MarkRegionsButton.png]] tool on some of it and then use the '''Locate''' [[File:casaplotms-locate-tool.png]] tool), which gives a really strange response.  You can plot just this baseline to be sure:
To apply phase calibration to the target, we will make a second table for the gain calibrator (J0603+174) with one solution per scan:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotms(vis='SN2010FZ_flagged10s.ms',field='2', \
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G1.inf', \
      spw='0:10~59,1~7:4~59,8:4~13;18~59,9~11:4~59,12:4~13;18~29;31~33;46~51;53~59,13:4~8;15~36;42~59', \
        gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', \
      antenna='ea17&ea25', \
                  'calG192.opacity', 'calG192.K0.b', 'calG192.B0.b'], \
      correlation='RR,LL',xaxis='frequency',yaxis='amp',ydatacolumn='corrected')
        field='1', refant='ea05', solnorm=F, \
        solint='inf', gaintype='G', calmode='p')
</source>
</source>


You can exclude this through antenna negation:
These phase gain solutions in calG192.G1.inf will be interpolated by {{applycal}} onto our target. These look good as well:
 
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotms(vis='SN2010FZ_flagged10s.ms',field='2', \
plotcal(caltable='calG192.G1.inf', xaxis='time', yaxis='phase', \
      spw='0:10~59,1~7:4~59,8:4~13;18~59,9~11:4~59,12:4~13;18~29;31~33;46~51;53~59,13:4~8;15~36;42~59', \
        iteration='antenna', plotrange=[-1,-1,-180,180])
      antenna='!ea17&ea25', \
      correlation='RR,LL',xaxis='frequency',yaxis='amp',ydatacolumn='corrected')
</source>
</source>


Then use '''Locate''' [[File:casaplotms-locate-tool.png]] for the other bad points, which seem to indicate spw 5,6,7 for ea14,ea16,ea17,ea25.
Now, let's solve for amplitudes on a per-scan interval, after applying the per-integration phases. Do these separately using <tt>gainfield</tt> so phases don't get transferred  across fields.  Note that {{gaincal}} uses linear interpolation of the previously determined phases by default.  This is generally fine; we will set the interpolation to "nearest" (in time).
Exclude these and replot:
 
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotms(vis='SN2010FZ_flagged10s.ms',field='2', \
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G2', \
      spw='0:10~59,1~7:4~59,8:4~13;18~59,9~11:4~59,12:4~13;18~29;31~33;46~51;53~59,13:4~8;15~36;42~59', \
        gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', \
      antenna='!ea14;!ea16;!ea17;!ea25', \
                  'calG192.opacity', 'calG192.K0.b', 'calG192.B0.b', 'calG192.G1.int'], \
      correlation='RR,LL',xaxis='frequency',yaxis='amp',ydatacolumn='corrected')
        gainfield=['', '', '', '', '3', '3', '0'], \
        interp=['', '', '', '', 'nearest', 'nearest', 'nearest'], \
        field='0', refant='ea05', solnorm=F, \
        solint='inf', gaintype='G', calmode='a')
 
#
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G2', \
        gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', \
                  'calG192.opacity', 'calG192.K0.b', 'calG192.B0.b', 'calG192.G1.int'], \
        gainfield=['', '', '', '', '3', '3', '1'], \
        interp=['', '', '', '', 'nearest', 'nearest', 'nearest'], \
        field='1', refant='ea05', solnorm=F, \
        solint='inf', gaintype='G', calmode='a', append=True)
#
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G2', \
        gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', \
                  'calG192.opacity', 'calG192.K0.b', 'calG192.B0.b', 'calG192.G1.int'], \
        gainfield=['', '', '', '', '3', '3', '3'], \
        interp=['', '', '', '', 'nearest', 'nearest', 'nearest'], \
        field='3', refant='ea05', solnorm=F, \
        solint='inf', gaintype='G', calmode='a', append=True)
#
</source>
</source>


[[Image:plotSN2010FZ_plotms_appliedflags_fld2.png|200px|thumb|right|plotms cal applied flagged fld2]]
[[Image:plotG192_plotcal_G2.inf_4.1.png|200px|thumb|right|plotcal G2 per-scan amp ant ea06]]
[[Image:plotSN2010FZ_plotms_appliedflags_fld2_phase.png|200px|thumb|right|plotms cal applied flagged fld2 phase]]
[[Image:plotSN2010FZ_plotms_appliedflags_fld0_amp.png|200px|thumb|right|plotms cal applied flagged fld0 amp]]
[[Image:plotSN2010FZ_plotms_appliedflags_fld0_phase.png|200px|thumb|right|plotms cal applied flagged fld0 phase]]
[[Image:plotSN2010FZ_plotms_appliedflags_fld0_amp_exc_4.0.png|200px|thumb|right|plotms cal applied flagged fld0 amp, with new spw selection]]
[[Image:plotSN2010FZ_plotms_appliedflags_fld0_ampavg_4.0.png|200px|thumb|right|plotms cal applied flagged fld0 amp averaged]]


This now looks clean except for the RFI in the upper subbands.
Let's have a look at the amplitudes:
 
Do flagging based on these:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
flaglist2 = ['antenna="ea14,ea16,ea17,ea25" spw="5~7"']
plotcal(caltable='calG192.G2', xaxis='time', yaxis='amp', \
flagcmd(vis='SN2010FZ_flagged10s.ms',inpmode='list',inpfile=flaglist2,action='apply')
        iteration='antenna')
</source>
</source>


Now replot the corrected data (you may have to force reload if you plotted same thing right before this):
We will apply this table (calG192.G2) to the data.
 
First, we need to use {{fluxscale}} to transfer the amplitude solutions from 3C147:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotms(vis='SN2010FZ_flagged10s.ms',field='2', \
flux2 = fluxscale(vis='G192_flagged_6s.ms', caltable='calG192.G2', \
      spw='0:10~59,1~7:4~59,8:4~13;18~59,9~11:4~59,12:4~13;18~29;31~33;46~51;53~59,13:4~8;15~36;42~59', \
                  fluxtable='calG192.F2', reference='0')
      correlation='RR,LL',xaxis='frequency',yaxis='amp',ydatacolumn='corrected')
</source>
</source>
where we have now captured the return dictionary in the Python object <tt>flux2</tt>.
The logger output gives:
<pre>
Found reference field(s): 3C147
Found transfer field(s):  gcal-J0603+174 3c84-J0319+413
Flux density for gcal-J0603+174 in SpW=0 is: 0.252043 +/- 0.00779693 (SNR = 32.3259, N = 44)
Flux density for gcal-J0603+174 in SpW=1 is: 0.250608 +/- 0.00785259 (SNR = 31.9141, N = 44)
Flux density for gcal-J0603+174 in SpW=2 is: 0.250149 +/- 0.00783195 (SNR = 31.9395, N = 44)
Flux density for gcal-J0603+174 in SpW=3 is: 0.249326 +/- 0.00870076 (SNR = 28.6556, N = 44)
Flux density for gcal-J0603+174 in SpW=4 is: 0.24779 +/- 0.00860759 (SNR = 28.7873, N = 44)
<snip>
Flux density for gcal-J0603+174 in SpW=60 is: 0.280642 +/- 0.00884987 (SNR = 31.7115, N = 44)
Flux density for gcal-J0603+174 in SpW=61 is: 0.279742 +/- 0.00874457 (SNR = 31.9904, N = 44)
Flux density for gcal-J0603+174 in SpW=62 is: 0.278071 +/- 0.00910153 (SNR = 30.5521, N = 44)
Flux density for gcal-J0603+174 in SpW=63 is: 0.277588 +/- 0.00955455 (SNR = 29.0529, N = 44)
Flux density for 3c84-J0319+413 in SpW=0 is: 1.01141 +/- 0.0316725 (SNR = 31.9333, N = 44)
Flux density for 3c84-J0319+413 in SpW=1 is: 0.994812 +/- 0.0326974 (SNR = 30.4248, N = 44)
Flux density for 3c84-J0319+413 in SpW=2 is: 1.00473 +/- 0.0314246 (SNR = 31.9729, N = 44)
Flux density for 3c84-J0319+413 in SpW=3 is: 1.0042 +/- 0.0325531 (SNR = 30.8479, N = 44)
<snip>
Flux density for 3c84-J0319+413 in SpW=60 is: 1.00232 +/- 0.0243617 (SNR = 41.1434, N = 44)
Flux density for 3c84-J0319+413 in SpW=61 is: 1.00589 +/- 0.0248197 (SNR = 40.5277, N = 44)
Flux density for 3c84-J0319+413 in SpW=62 is: 1.01762 +/- 0.0240088 (SNR = 42.3855, N = 44)
Flux density for 3c84-J0319+413 in SpW=63 is: 1.01145 +/- 0.0249814 (SNR = 40.488, N = 44)
Fitted spectrum for gcal-J0603+174 with fitorder=1: Flux density = 0.264382 +/- 0.000149793 (freq=32.4488 GHz) spidx=-0.834342 +/- 0.00458913
Fitted spectrum for 3c84-J0319+413 with fitorder=1: Flux density = 1.00101 +/- 0.00121263 (freq=32.4488 GHz) spidx=0.00866148 +/- 0.0100409
Storing result in calG192.F2
Writing solutions to table: calG192.F2
</pre>
You may see slightly different numbers on your machine.  Note that "N" here is the number of antennas x the number of polarizations used for the calculations.  In this case, there are 22 unflagged antennas and 2 polarizations.


Looks pretty good.
Also, note that the flux-scaled amplitudes for 3C84 are all almost exactly 1 Jy.  This is not because the actual flux of 3C84 is 1 Jy, of course.  Rather, remember that the spectrum and flux information is now included in the bandpass table.  When we apply the calibration, in the next section, you will see that 3C84's flux does indeed come out as expected.


Plot the phase:
== Applying the Calibration and Final Editing ==
 
Next we apply all our accumulated calibration tables to the flagged MS.  We apply these to the calibration fields individually, using the appropriate gainfields and interpolation for each:
* For 3C147 (field 0) we did per-integration phase solutions and a single scan amplitude, so use "linear" and "nearest" interpolation, respectively;
* for the nearby gain calibrator (field 1) we did 12-s phase and per-scan amplitude solutions, for which we will use "linear" and "nearest" interpolation, respectively;
* for G192 (field 2), we will calibrate with field 1, using the per-scan solutions and "linear" interpolation; and finally,
* for the bandpass calibrator 3C84 (field 3), we did per-integration phase solutions and a single scan amplitude, so use "linear" and "nearest" interpolation respectively.
 
[[Image:plotG192_plotms_applied_fld0.png|200px|thumb|right|3C147 with calibration applied]]
[[Image:plotG192_plotms_fld0_bybaseline.png|200px|thumb|right|3C147 with calibration applied, amp vs. baseline]]
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotms(vis='SN2010FZ_flagged10s.ms',field='2', \
applycal(vis='G192_flagged_6s.ms', field='0', \
      spw='0:10~59,1~7:4~59,8:4~13;18~59,9~11:4~59,12:4~13;18~29;31~33;46~51;53~59,13:4~8;15~36;42~59', \
        gaintable=['calG192.antpos', 'calG192.requantizer', 'calG192.gaincurve', \
      correlation='RR,LL',xaxis='frequency',yaxis='phase',ydatacolumn='corrected')
                    'calG192.opacity', 'calG192.K0.b', 'calG192.B0.b', \
                    'calG192.G1.int', 'calG192.G2'], \
        gainfield=['', '', '', '', '', '', '0', '0'],
        interp=['', '', '', '', 'nearest', 'nearest', 'linear', 'nearest'], calwt=False)
#
applycal(vis='G192_flagged_6s.ms', field='1', \
        gaintable=['calG192.antpos', 'calG192.requantizer', 'calG192.gaincurve', \
                    'calG192.opacity', 'calG192.K0.b', 'calG192.B0.b', \
                    'calG192.G1.int', 'calG192.F2'], \
        gainfield=['', '', '', '', '', '', '1', '1'],
        interp=['', '', '', '', 'nearest', 'nearest', 'linear', 'nearest'], calwt=False)
#
applycal(vis='G192_flagged_6s.ms', field='2', \
        gaintable=['calG192.antpos', 'calG192.requantizer', 'calG192.gaincurve', \
                    'calG192.opacity', 'calG192.K0.b', 'calG192.B0.b',\
                    'calG192.G1.inf', 'calG192.F2'], \
        gainfield=['', '', '', '', '', '', '1', '1'],
        interp=['', '', '', '', 'nearest', 'nearest', 'linear', 'linear'], calwt=False)
#
applycal(vis='G192_flagged_6s.ms', field='3', \
        gaintable=['calG192.antpos', 'calG192.requantizer', 'calG192.gaincurve', \
                    'calG192.opacity', 'calG192.K0.b', 'calG192.B0.b', \
                    'calG192.G1.int', 'calG192.F2'], \
        gainfield=['', '', '', '', '', '', '3', '3'],
        interp=['', '', '', '', 'nearest', 'nearest', 'linear', 'nearest'], calwt=False)
</source>
</source>
Note the characteristic "bowtie" pattern of the phases about the sub-band centers.
Because we used <tt>usesratch=False</tt> in {{setjy}}, the <tt>CORRECTED_DATA</tt> scratch column will be created the first time you run {{applycal}}. This will take a few minutes to write, increasing the size of the MS to 30 GB, and will store the calibrated data in the calibrated data column of the MS.
Here we can see the effect of the EVLA "delay clunking", where the delay steps through discrete values such that
the phase goes from -11deg to +11deg across the sub-band as the delay changes due to geometry.  This is D-configuration so the delays change slowly, it will change faster in wider configurations. As of Q3 2011 we have not enabled the corrections for this in the EVLA system so you will always have this remaining delay error in your data.  In principle, you could solve for delays on short timescales and take this out; in practice, this in not possible for your weaker science target source (where it would matter most for results).


Now let's plot the corrected data amplitude for the phase calibrator (field 0):
<source lang="python">
# In CASA
plotms(vis='SN2010FZ_flagged10s.ms',field='0', \
      spw='0:10~59,1~7:4~59,8:4~13;18~59,9~11:4~59,12:4~13;18~29;31~33;46~51;53~59,13:4~8;15~36;42~59', \
      correlation='RR,LL',xaxis='frequency',yaxis='amp',ydatacolumn='corrected')
</source>
You can see the bandpass filter roll-off increasing the noise at the baseband edges (about 8-16 channels worth). Also, we can see some RFI we missed:
* <6804 MHz spw  8 below ch 30 lots of bad stuff (a lot from ea18,ea22 but others too)
*  7168 MHz spw 11 ch 20
*  pretty much all of spw 12,13
The ch 20 ones are all harmonics of a notorious 128 MHz tone. NOTE: You can get the frequency of a RFI feature by looking at the logger report from using the '''Locate''' [[File:casaplotms-locate-tool.png]] tool.


We will not flag these, but exclude them in imaging (so that more advanced students can try flagging these in detail or using auto-flagging). A good channel selection string for imaging might be:
<pre style="background-color: #98FB98;">
IMPORTANT NOTES ON THE USE OF YOUR FLUXSCALE (F2) TABLE IN APPLYCAL:
 
* When we ran fluxscale and generated table calG192.F2 to transfer the amplitude solutions
from our flux calibrator, fluxscale was run with incremental = False by default.  This
means that the flux density scale correction factors derived from the primary flux calibrator
were applied to the gains of the secondary calibrators.  So, the information from calG192.G2
(which contains the amplitude solutions) is already accounted for in calG192.F2 and we will
NOT need to supply calG192.G2 to our list of calibration tables for our secondary
calibrators and science target fields (in this case, fields 1, 2, and 3 -- we do still need
our G2 table for field 0 though!).
 
* It is also possible to run fluxscale with incremental = True.  In this case, only the
scale correction factors are written out to the fluxtable, and calG192.G2 would need to be
included in the list of gaintables for ALL fields at the applycal stage.


<pre>
</pre>  
spw = '0:16~59,1~6:4~59,7:4~54,8:30~59,9~10:4~59,11:4~19;21~59'
</pre>


Without further flagging, it may be best to drop spw 12-13 for imaging (we will do so from now on).


Plot again (including this selection for spw 0-11):
Now we examine the corrected data for 3C147.  We will avoid spectral window edges and bin the data in time and frequency:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotms(vis='SN2010FZ_flagged10s.ms',field='0', \
plotms(vis='G192_flagged_6s.ms', field='0', \
       spw='0:16~59,1~6:4~59,7:4~54,8:30~59,9~10:4~59,11:4~19;21~59', \
       xaxis='frequency', yaxis='amp', \
       correlation='RR,LL',xaxis='frequency',yaxis='amp',ydatacolumn='corrected')
      ydatacolumn='corrected', spw='*:5~122', \
       averagedata=True, avgchannel='8', \
      avgtime='1000s', coloraxis='baseline')
</source>
</source>


Looks better.
In this plot (see figure above, right) there is some suspicious data in the frequency range of 38.15-38.26 GHz (spw 29).  We can plot around this frequency range with respect to time to see if it's isolated RFI or something we should flag from the whole dataset:
 
Now plot amplitudes for the corrected data averaged over baseline to see the source spectrum:


<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotms(vis='SN2010FZ_flagged10s.ms',field='0',
plotms(vis='G192_flagged_6s.ms', field='0', \
       spw='0:16~59,1~6:4~59,7:4~54,8:30~59,9~10:4~59,11:4~19;21~59,12:4~13;18~29;31~33;46~51;53~59,13:4~8;15~36;42~59',
       xaxis='time', yaxis='amp', \
       correlation='RR,LL',avgbaseline=True,avgtime='60000s',
       ydatacolumn='corrected', spw='29:5~122', \
       xaxis='frequency',yaxis='amp',ydatacolumn='corrected',
       averagedata=True, avgchannel='16', \
      customsymbol=True,symbolshape='circle',symbolsize=2)
      avgtime='', coloraxis='baseline')
</source>
</source>
The "custom" plotting parameters show how to control the symbol shape and size from the task.


The last two sub-bands spw 12-13 give reasonable values, with only a tiny offset from spw 8-11.
Indeed, something looks wrong for the time interval 6:35:00-6:36:40 for this spectral window.  Flag these data:
There are also strange amplitude excursions, particularly in the low end of the first baseband.  These must be coming
from one or more scans.  You can iterate over scan to see the strange amplitudes (mostly from scan 7):


<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotms(vis='SN2010FZ_flagged10s.ms',field='0',
flagdata(vis='G192_flagged_6s.ms', field='0', \
      spw='0:16~59,1~6:4~59,7:4~54,8:30~59,9~10:4~59,11:4~19;21~59,12:4~13;18~29;31~33;46~51;53~59,13:4~8;15~36;42~59',
        spw='29', timerange='6:35:00~6:36:40')
      correlation='RR,LL',avgbaseline=True,avgtime='600s',iteraxis='scan',
      xaxis='frequency',yaxis='amp',ydatacolumn='corrected',
      customsymbol=True,symbolshape='circle',symbolsize=2)
</source>
</source>


Also, there is an offset with the amplitudes for spw 6, perhaps due to the problem with baseline ea17&ea25 (which we flagged, but didn't recalibrate afterward) and likely affected the {{fluxscale}} solution. This is troubling enough that we will quickly go through a second round of calibration.
It's also instructive to plot the corrected amplitude as a function of baseline:
 
<source lang="python">
== A Quick Recalibration ==
# In CASA
 
plotms(vis='G192_flagged_6s.ms', field='0', \
We now go back and recalibrate the data.  We may as well flag scan 7 first, as well:
      xaxis='baseline', yaxis='amp', \
      ydatacolumn='corrected', spw='*:5~122', \
      averagedata=True, avgchannel='8', \
      avgtime='1000s', coloraxis='antenna1')
</source>
Looks good now!


Next, we examine the corrected data for the gain calibrator, J0603+174, again avoiding spectral window edges where we know the data will be noisy.  This time, we will bin the data even more in frequency, since the source is fainter:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
flagdata(vis='SN2010FZ_flagged10s.ms', scan='7')
plotms(vis='G192_flagged_6s.ms', field='1', \
#
      xaxis='frequency', yaxis='amp', \
# Clear the corrected data and model from header
      ydatacolumn='corrected', spw='*:5~122', \
clearcal('SN2010FZ_flagged10s.ms',addmodel=False)
      averagedata=True, avgchannel='32', \
#
      avgtime='6000s', coloraxis='baseline')
chanStr = '0:16~59,1~6:4~59,7:4~54,8:30~59,9~10:4~59,11:4~19;21~59'
#
mysetjy2 = setjy(vis='SN2010FZ_flagged10s.ms', field='2', scalebychan=True, modimage='3C286_C.im')
#
gaincal(vis='SN2010FZ_flagged10s.ms',caltable='calSN2010FZ.G0.2',field='2',spw='0~11:23~28',
        gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve'],
        gaintype='G',refant='ea04',calmode='p',solint='int',minsnr=3)
#
gaincal(vis='SN2010FZ_flagged10s.ms',caltable='calSN2010FZ.K0.2',
        gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve','calSN2010FZ.G0.2'],
        field='2', spw=chanStr, gaintype='K',
        refant='ea04', combine='scan', solint='inf', minsnr=3)
#
bandpass(vis='SN2010FZ_flagged10s.ms',caltable='calSN2010FZ.B0.2',
        gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve',
                    'calSN2010FZ.G0.2','calSN2010FZ.K0.2'],
        field='2',refant='ea04',solnorm=False,
        spw='0~11',
        bandtype='B', combine='scan', solint='inf')
#
gaincal(vis='SN2010FZ_flagged10s.ms',caltable='calSN2010FZ.G1.2int',
        gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve',
                  'calSN2010FZ.K0.2','calSN2010FZ.B0.2'],
        field='2',refant='ea04',solnorm=F,
        spw=chanStr,
        solint='int',gaintype='G',calmode='p')
#
gaincal(vis='SN2010FZ_flagged10s.ms',caltable='calSN2010FZ.G1.2int',
        gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve',
                  'calSN2010FZ.K0.2','calSN2010FZ.B0.2'],
        field='0',refant='ea04',solnorm=F,
        spw=chanStr,
        solint='int',gaintype='G',calmode='p',append=True)
#
gaincal(vis='SN2010FZ_flagged10s.ms',caltable='calSN2010FZ.G1.2inf',
        gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve',
                  'calSN2010FZ.K0.2','calSN2010FZ.B0.2'],
        field='0',refant='ea04',solnorm=F,
        spw=chanStr,
        solint='inf',gaintype='G',calmode='p')
#
gaincal(vis='SN2010FZ_flagged10s.ms', caltable='calSN2010FZ.G2.2',
        gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve',
                  'calSN2010FZ.K0.2','calSN2010FZ.B0.2','calSN2010FZ.G1.2int'],
        gainfield=['','','2','2','2'],
        interp=['','','nearest','nearest','nearest'],
        field='2',refant='ea04',solnorm=F,
        spw=chanStr,
        solint='inf',combine='scan',gaintype='G',calmode='a')
#
gaincal(vis='SN2010FZ_flagged10s.ms', caltable='calSN2010FZ.G2.2',
        gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve',
                  'calSN2010FZ.K0.2','calSN2010FZ.B0.2','calSN2010FZ.G1.2int'],
        gainfield=['','','2','2','0'],
        interp=['','','nearest','nearest','nearest'],
        field='0',refant='ea04',solnorm=F,
        spw=chanStr,
        solint='inf',gaintype='G',calmode='a',append=True)
#
gaincal(vis='SN2010FZ_flagged10s.ms', caltable='calSN2010FZ.G2.3',
        gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve',
                  'calSN2010FZ.K0.2','calSN2010FZ.B0.2','calSN2010FZ.G1.2int'],
        gainfield=['','','2','2','2'],
        interp=['','','nearest','nearest','nearest'],
        field='2',refant='ea04',solnorm=F,
        spw=chanStr,
        solint='inf',combine='scan',gaintype='G',calmode='a')
#
gaincal(vis='SN2010FZ_flagged10s.ms', caltable='calSN2010FZ.G2.3',
        gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve',
                  'calSN2010FZ.K0.2','calSN2010FZ.B0.2','calSN2010FZ.G1.2int'],
        gainfield=['','','2','2','0'],
        interp=['','','nearest','nearest','nearest'],
        field='0',refant='ea04',solnorm=F,
        spw=chanStr,
        solint='inf',combine='scan',gaintype='G',calmode='a',append=True)
#
myflux2 = fluxscale(vis='SN2010FZ_flagged10s.ms',caltable='calSN2010FZ.G2.3',
                    fluxtable='calSN2010FZ.F2.3inc',reference='2',transfer='0',
                    incremental=True)
#
applycal(vis='SN2010FZ_flagged10s.ms',field='2',spw='0~11',
        gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve','calSN2010FZ.K0.2',
                    'calSN2010FZ.B0.2','calSN2010FZ.G1.2int','calSN2010FZ.G2.2'],
        gainfield=['','','','','2','2'],
        interp=['','','nearest','nearest','linear','nearest'],
        parang=False,calwt=False)
#
applycal(vis='SN2010FZ_flagged10s.ms',field='0',spw='0~11',
        gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve','calSN2010FZ.K0.2',
                    'calSN2010FZ.B0.2','calSN2010FZ.G1.2int','calSN2010FZ.G2.2',
                    'calSN2010FZ.F2.3inc'],
        gainfield=['','','','','0','0','0'],
        interp=['','','nearest','nearest','nearest','nearest',''],
        parang=False,calwt=False)
#
applycal(vis='SN2010FZ_flagged10s.ms',field='1',spw='0~11',
        gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve','calSN2010FZ.K0.2',
                    'calSN2010FZ.B0.2','calSN2010FZ.G1.2inf','calSN2010FZ.G2.2',
                    'calSN2010FZ.F2.3inc'],
        gainfield=['','','','','0','0','0'],
        interp=['','','nearest','nearest','linear','linear',''],
        parang=False,calwt=False)
</source>
</source>


Note that we have set the variable <tt>chanStr</tt> for our channel selection; this makes the task commands shorter and easier to read.
This generally looks quite good.  Plot with respect to baseline as well:
 
The {{fluxscale}} output this time around is slightly different to the last:
<pre>
Found reference field(s): 3C286
Found transfer field(s): J0925+0019
Flux density for J0925+0019 in SpW=0 (freq=4.488e+09 Hz) is: 0.978946 +/- 0.00284837 (SNR = 343.686, N = 50)
Flux density for J0925+0019 in SpW=1 (freq=4.616e+09 Hz) is: 0.978634 +/- 0.00264066 (SNR = 370.602, N = 50)
Flux density for J0925+0019 in SpW=2 (freq=4.744e+09 Hz) is: 0.980438 +/- 0.00251668 (SNR = 389.575, N = 50)
Flux density for J0925+0019 in SpW=3 (freq=4.872e+09 Hz) is: 0.980116 +/- 0.00255481 (SNR = 383.636, N = 50)
Flux density for J0925+0019 in SpW=4 (freq=5e+09 Hz) is: 0.982175 +/- 0.00230804 (SNR = 425.545, N = 50)
Flux density for J0925+0019 in SpW=5 (freq=5.128e+09 Hz) is: 0.979574 +/- 0.00269688 (SNR = 363.225, N = 42)
Flux density for J0925+0019 in SpW=6 (freq=5.256e+09 Hz) is: 0.980193 +/- 0.00271312 (SNR = 361.279, N = 42)
Flux density for J0925+0019 in SpW=7 (freq=5.384e+09 Hz) is: 0.98102 +/- 0.00249166 (SNR = 393.721, N = 42)
Flux density for J0925+0019 in SpW=8 (freq=6.744e+09 Hz) is: 0.962693 +/- 0.00282815 (SNR = 340.397, N = 48)
Flux density for J0925+0019 in SpW=9 (freq=6.872e+09 Hz) is: 0.960313 +/- 0.00285418 (SNR = 336.459, N = 48)
Flux density for J0925+0019 in SpW=10 (freq=7e+09 Hz) is: 0.957056 +/- 0.00303716 (SNR = 315.116, N = 48)
Flux density for J0925+0019 in SpW=11 (freq=7.128e+09 Hz) is: 0.953964 +/- 0.00378326 (SNR = 252.154, N = 48)
Flux density for J0925+0019 in SpW=12 is:  INSUFFICIENT DATA
Flux density for J0925+0019 in SpW=13 is:  INSUFFICIENT DATA
Fitted spectrum for J0925+0019 with fitorder=1: Flux density = 0.973376 +/- 0.00118872 (freq=5.52174 GHz)
    spidx=-0.0573991 +/- 0.00778736201
</pre>
 
The source spectrum plot now looks somewhat better:
 
[[Image:plotSN2010FZ_plotms_reproc_fld0_ampavg_4.0.png|200px|thumb|right|plotms recalibrated applied flagged fld0 amp averaged]]
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotms(vis='SN2010FZ_flagged10s.ms',field='0', \
plotms(vis='G192_flagged_6s.ms', field='1', \
       spw='0:16~59,1~6:4~59,7:4~54,8:30~59,9~10:4~59,11:4~19;21~59', \
       xaxis='baseline', yaxis='amp', \
       correlation='RR,LL',avgbaseline=True,avgtime='60000s',
       ydatacolumn='corrected', spw='*:5~122', \
       xaxis='frequency',yaxis='amp',ydatacolumn='corrected',
       averagedata=True, avgchannel='32', \
      customsymbol=True,symbolshape='circle',symbolsize=2)
      avgtime='6000s', coloraxis='antenna1')
</source>
</source>
As you see in the figure to the right, there are still spectral window to window variations that deviate from a smooth spectrum. This is due to noise in the {{fluxscale}} median filter now used in CASA 4.0 (in this well-calibrated case, the old weighted means used by {{fluxscale}} in CASA3.4 behaved better). If we use {{plotcal}} to plot the solutions versus antenna
A few antennas look a little noisier, but nothing bad enough to flag for now.
 
Finally, we examine the corrected data for 3C84:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotcal(caltable='calSN2010FZ.G2.3',xaxis='antenna',yaxis='amp',field='0',
plotms(vis='G192_flagged_6s.ms', field='3', \
        subplot=211,plotrange=[-1,-1,0.9,1.1])
      xaxis='frequency', yaxis='amp', \
plotcal(caltable='calSN2010FZ.G2.3',xaxis='antenna',yaxis='amp',field='2',
      ydatacolumn='corrected', spw='*:5~122', \
        subplot=212,plotrange=[-1,-1,0.9,1.1],figfile='plotSN2010FZ_plotcal_G2.3_ampant.png')
      averagedata=True, avgchannel='8', \
      avgtime='1000s', coloraxis='baseline')
</source>
</source>
we see that there are variations that will enter into the medians. Some antennas are better behaved than others, for example ea12 (index 10) seems better than most.
In general, it looks good, though there is one rather suspicious baseline dropping below the rest of the data.  Box a few data points and use the "Locate" button to find that this is ea03&ea07.  Plotting the same baseline for 3C147, we see that it doesn't look the best there either, so we will flag this baseline:


[[Image:plotSN2010FZ_plotcal_G2.3_ampant.png|200px|thumb|right|plotcal of G2.3 table, showing variation of solutions per antenna]]
[[Image:screenshotPlotSN2010FZ_plotcal_fluxedit3_ea12.png|200px|thumb|right|plotcal of G2.3.ea12 table, marking all solutions but those for ea12 for flagging]]
[[Image:screenshotPlotSN2010FZ_plotms_recalibrated3_EA12_fld0_amp_4.0.png|200px|thumb|right|plotms for fld 0 after application of F2.3.ea12 table]]
Because we are applying an incremental correction for the flux scale, we have the latitude to change the caltable that goes into {{fluxscale}} to get a better result. For example, we can restrict the antennas that are used to derive the scale. Although there is not yet antenna selection in {{fluxscale}} itself, we can edit the caltable using {{plotcal}}. For example, make a copy of the G2.3 caltable and select only a single antenna:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
os.system('cp -rf calSN2010FZ.G2.3 calSN2010FZ.G2.3.ea12')
flagdata(vis='G192_flagged_6s.ms', antenna='ea03&ea07')
plotcal(caltable='calSN2010FZ.G2.3.ea12',xaxis='antenna',yaxis='amp')
</source>
</source>
In the plot to the right we show the GUI where we have boxed all but antenna ea12.
 
Now we carry on with the {{fluxscale}} and {{applycal}}:
Now, let's plot amplitude vs. baseline:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
myfluxEdit3 = fluxscale(vis='SN2010FZ_flagged10s.ms',caltable='calSN2010FZ.G2.3.ea12',
plotms(vis='G192_flagged_6s.ms', field='3', \
                        fluxtable='calSN2010FZ.F2.3.ea12',reference='2',transfer='0',
      xaxis='baseline', yaxis='amp', \
                        incremental=True)
      ydatacolumn='corrected', spw='*:5~122', \
#
      averagedata=True, avgchannel='8', \
applycal(vis='SN2010FZ_flagged10s.ms',field='0',spw='0~11',
      avgtime='1000s', coloraxis='antenna1')
        gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve','calSN2010FZ.K0.2',
                    'calSN2010FZ.B0.2','calSN2010FZ.G1.2int','calSN2010FZ.G2.2',
                    'calSN2010FZ.F2.3.ea12'],
        gainfield=['','','','','0','0','0'],
        interp=['','','nearest','nearest','nearest','nearest',''],
        parang=False,calwt=False)
#
applycal(vis='SN2010FZ_flagged10s.ms',field='1',spw='0~11',
        gaintable=['calSN2010FZ.antpos','calSN2010FZ.gaincurve','calSN2010FZ.K0.2',
                    'calSN2010FZ.B0.2','calSN2010FZ.G1.2inf','calSN2010FZ.G2.2',
                    'calSN2010FZ.F2.3.ea12'],
        gainfield=['','','','','0','0','0'],
        interp=['','','nearest','nearest','linear','linear',''],
        parang=False,calwt=False)
</source>
</source>
The results appear better:
Looks good!
 
* In theory, the calibrated data should yield, in a simple case of a point source in the center of the field, a physical source visibility amplitude (the source flux density) and zero phase.  Although in practice we never achieve such "perfection," it is very useful to gauge the "quality" of your calibrated data by plotting either amplitude vs. phase or real vs. imaginary in plotms for your calibrators.  This type of plot is intended as a diagnostic for calibrators only - unless your science targets are extremely bright, compact, and located directly at the phase center of the field, this type of plot will appear quite noisy and be of little use.  Note that you can plot the corrected data column (as shown below), or the corrected-model column (this will tend to reduce the scatter in the plots and remove the effects of any structure in the model itself).  Let's take a look:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotms(vis='SN2010FZ_flagged10s.ms',field='0', \
plotms(vis='G192_flagged_6s.ms', field='3', \
       spw='0:16~59,1~6:4~59,7:4~54,8:30~59,9~10:4~59,11:4~19;21~59', \
       xaxis='phase', yaxis='amp', \
       correlation='RR,LL',avgbaseline=True,avgtime='60000s',
       xdatacolumn='corrected', \
       xaxis='frequency',yaxis='amp',ydatacolumn='corrected',
      ydatacolumn='corrected', spw='*:5~122', \
      customsymbol=True,symbolshape='circle',symbolsize=2)
       averagedata=True, avgchannel='8', \
      avgtime='1000s', coloraxis='baseline')
</source>
</source>
Note that if you choose a different antenna than ea12 to use for this, you will get
For well-calibrated data, we expect a fairly small amount of scatter and compact distribution of the data. (Note: if you see arc or doughnut-like shapes in your dataset, try selecting the corrected-model column instead.)  Although we can see in the figures below that our calibration was not perfect, there is less than 2 degrees of phase scatter, and a plot of amplitude vs. frequency shows that this is mostly in the highest frequencies.  We will keep all of these data.
different results, usually worse. But this procedure illustrates how to use the
incremental solutions from {{fluxscale}} to your possible advantage.


We now return to examining our calibration.
== Recalibration ==
 
Since we flagged additional data, we will now go back and recalibrate:


We can also plot the corrected phase - looks good:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotms(vis='SN2010FZ_flagged10s.ms',field='0', \
# Clear the corrected data and model from header
      spw='0:16~59,1~6:4~59,7:4~54,8:30~59,9~10:4~59,11:4~19;21~59', \
clearcal('G192_flagged_6s.ms', addmodel=False)
      correlation='RR,LL',xaxis='frequency',yaxis='phase',ydatacolumn='corrected')
 
# Insert the flux density model for 3C147 into the MS
setjy(vis='G192_flagged_6s.ms', field='0', scalebychan=True, \
      model='3C147_A.im')
 
# Fill the MODEL column with 3C84's spectral information
setjy(vis='G192_flagged_6s.ms', field='3', scalebychan=True, \
      fluxdensity=[29.8756, 0, 0, 0], spix=-0.598929, \
      reffreq='32.4488GHz')
 
# Initial Phase Calibration
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G0.b.2', field='3', spw='*:60~68',\
        gaintable=['calG192.antpos', 'calG192.gaincurve', \
                  'calG192.requantizer', 'calG192.opacity'], \
        gaintype='G', refant='ea05', calmode='p', solint='int', minsnr=3)
 
# Delay Calibration
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.K0.b.2', \
        field='3', spw='*:5~122', gaintype='K', \
        gaintable=['calG192.antpos', 'calG192.gaincurve', \
                  'calG192.requantizer', 'calG192.opacity','calG192.G0.b.2'], \
        refant='ea05', solint='inf', minsnr=3)
 
# Bandpass Calibration
bandpass(vis='G192_flagged_6s.ms', caltable='calG192.B0.b.2', \
        field='3', refant='ea05', solnorm=False, \
        gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer',\
                  'calG192.opacity','calG192.G0.b.2', 'calG192.K0.b.2'], \
        bandtype='B', solint='inf')
 
# Phase Gain Calibration Solutions - Field 0
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G1.int.2', \
        field='0', refant='ea05', solnorm=F, \
        gaintable=['calG192.antpos', 'calG192.requantizer','calG192.gaincurve', \
                  'calG192.opacity', 'calG192.K0.b.2','calG192.B0.b.2'], \
        solint='int', gaintype='G', calmode='p')
 
# Phase Gain Calibration Solutions - Field 1
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G1.int.2', \
        field='1', refant='ea05', solnorm=F, \
        gaintable=['calG192.antpos', 'calG192.requantizer','calG192.gaincurve', \
                  'calG192.opacity', 'calG192.K0.b.2','calG192.B0.b.2'], \
        solint='12s', gaintype='G', calmode='p', append=True)
 
# Phase Gain Calibration Solutions - Field 3
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G1.int.2', \
        field='3', refant='ea05', solnorm=F, \
        gaintable=['calG192.antpos', 'calG192.requantizer','calG192.gaincurve', \
                  'calG192.opacity', 'calG192.K0.b.2','calG192.B0.b.2'], \
        solint='int', gaintype='G', calmode='p', append=True)
 
# Phase Gain Calibration Solutions - Field 1 - infinite solution interval
# (Note: we will apply this table to our science target at the applycal stage.)
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G1.inf.2', \
        field='1', refant='ea05', solnorm=F, \
        gaintable=['calG192.antpos', 'calG192.requantizer','calG192.gaincurve', \
                  'calG192.opacity', 'calG192.K0.b.2','calG192.B0.b.2'], \
        solint='inf', gaintype='G', calmode='p')
 
# Amplitude Calibration Solutions - Field 0
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G2.2', \
        field='0', refant='ea05', solnorm=F, \
        gaintable=['calG192.antpos', 'calG192.requantizer', 'calG192.gaincurve', \
                  'calG192.opacity', 'calG192.K0.b.2', \
                  'calG192.B0.b.2', 'calG192.G1.int.2'], \
        gainfield=['', '', '', '', '3', '3', '0'], \
        interp=['', '', '', '', 'nearest', 'nearest', 'nearest'], \
        solint='inf', gaintype='G', calmode='a')
 
# Amplitude Calibration Solutions - Field 1
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G2.2', \
        field='1', refant='ea05', solnorm=F, \
        gaintable=['calG192.antpos', 'calG192.requantizer', 'calG192.gaincurve', \
                  'calG192.opacity', 'calG192.K0.b.2', \
                  'calG192.B0.b.2', 'calG192.G1.int.2'], \
        gainfield=['', '', '', '', '3', '3', '1'], \
        interp=['', '', '', '', 'nearest', 'nearest', 'nearest'], \
        solint='inf', gaintype='G', calmode='a', append=True)
 
# Amplitude Calibration Solutions - Field 3
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G2.2', \
        field='3', refant='ea05', solnorm=F, \
        gaintable=['calG192.antpos', 'calG192.requantizer', 'calG192.gaincurve', \
                  'calG192.opacity', 'calG192.K0.b.2', \
                  'calG192.B0.b.2', 'calG192.G1.int.2'], \
        gainfield=['', '', '', '', '3', '3', '3'], \
        interp=['', '', '', '', 'nearest', 'nearest', 'nearest'], \
        solint='inf', gaintype='G', calmode='a', append=True)
 
# Flux Scale Calibration Table (to apply to secondary calibrators)
flux3 = fluxscale(vis='G192_flagged_6s.ms', caltable='calG192.G2.2', \
                  fluxtable='calG192.F2.2', reference='0')
 
# Apply Calibration Tables to Field 0 (Flux Calibrator)
applycal(vis='G192_flagged_6s.ms', field='0', \
        gaintable=['calG192.antpos', 'calG192.requantizer', 'calG192.gaincurve', 'calG192.opacity',\
                    'calG192.K0.b.2', 'calG192.B0.b.2', 'calG192.G1.int.2', 'calG192.G2.2'], \
        gainfield=['', '', '', '', '', '', '0', '0'], \
        interp=['', '', '', '', 'nearest', 'nearest', 'linear', 'nearest'], calwt=False)
 
# Apply Calibration Tables to Field 1 (Phase Calibrator)
applycal(vis='G192_flagged_6s.ms', field='1', \
        gaintable=['calG192.antpos', 'calG192.requantizer', 'calG192.gaincurve', 'calG192.opacity',\
                    'calG192.K0.b.2', 'calG192.B0.b.2', 'calG192.G1.int.2', 'calG192.F2.2'], \
        gainfield=['', '', '', '', '', '', '1', '1'], \
        interp=['', '', '', '', 'nearest', 'nearest', 'linear', 'nearest'], calwt=False)
 
# Apply Calibration Tables to Field 2 (Science Target)
applycal(vis='G192_flagged_6s.ms', field='2', \
        gaintable=['calG192.antpos', 'calG192.requantizer', 'calG192.gaincurve', 'calG192.opacity',\
                    'calG192.K0.b.2', 'calG192.B0.b.2', 'calG192.G1.inf.2', 'calG192.F2.2'], \
        gainfield=['', '', '', '', '', '', '1', '1'], \
        interp=['', '', '', '', 'nearest', 'nearest', 'linear', 'linear'], calwt=False)
 
# Apply Calibration Tables to Field 3 (Bandpass Calibrator)
applycal(vis='G192_flagged_6s.ms', field='3', \
        gaintable=['calG192.antpos', 'calG192.requantizer', 'calG192.gaincurve', 'calG192.opacity',\
                    'calG192.K0.b.2', 'calG192.B0.b.2', 'calG192.G1.int.2', 'calG192.F2.2'], \
        gainfield=['', '', '', '', '', '', '3', '3'], \
        interp=['', '', '', '', 'nearest', 'nearest', 'linear', 'nearest'], calwt=False)
</source>
</source>


We can average over baseline and each scan:
The recalibration will take a little while -- it was over 1.5 hours on our system -- so this is a good time to work on a different project or grab some lunch!
 
The {{fluxscale}} output this time around is slightly different:
<pre>
Found reference field(s): 3C147
Found transfer field(s):  gcal-J0603+174 3c84-J0319+413
Flux density for gcal-J0603+174 in SpW=0 is: 0.252049 +/- 0.00779748 (SNR = 32.3244, N = 44)
Flux density for gcal-J0603+174 in SpW=1 is: 0.250619 +/- 0.00784916 (SNR = 31.9294, N = 44)
Flux density for gcal-J0603+174 in SpW=2 is: 0.250149 +/- 0.00783732 (SNR = 31.9177, N = 44)
Flux density for gcal-J0603+174 in SpW=3 is: 0.249327 +/- 0.00869472 (SNR = 28.6757, N = 44)
Flux density for gcal-J0603+174 in SpW=4 is: 0.247794 +/- 0.00861206 (SNR = 28.7729, N = 44)
<snip>
Flux density for gcal-J0603+174 in SpW=60 is: 0.280654 +/- 0.00883115 (SNR = 31.78, N = 44)
Flux density for gcal-J0603+174 in SpW=61 is: 0.279748 +/- 0.00876293 (SNR = 31.924, N = 44)
Flux density for gcal-J0603+174 in SpW=62 is: 0.27807 +/- 0.00912204 (SNR = 30.4833, N = 44)
Flux density for gcal-J0603+174 in SpW=63 is: 0.277579 +/- 0.00954328 (SNR = 29.0863, N = 44)
Flux density for 3c84-J0319+413 in SpW=0 is: 1.01141 +/- 0.0316702 (SNR = 31.9356, N = 44)
Flux density for 3c84-J0319+413 in SpW=1 is: 0.994812 +/- 0.0326958 (SNR = 30.4262, N = 44)
Flux density for 3c84-J0319+413 in SpW=2 is: 1.00473 +/- 0.0314171 (SNR = 31.9805, N = 44)
Flux density for 3c84-J0319+413 in SpW=3 is: 1.00419 +/- 0.0325563 (SNR = 30.8449, N = 44)
Flux density for 3c84-J0319+413 in SpW=4 is: 1.00361 +/- 0.0333546 (SNR = 30.0893, N = 44)
<snip>
Flux density for 3c84-J0319+413 in SpW=60 is: 1.00232 +/- 0.0243542 (SNR = 41.156, N = 44)
Flux density for 3c84-J0319+413 in SpW=61 is: 1.00588 +/- 0.0248152 (SNR = 40.5347, N = 44)
Flux density for 3c84-J0319+413 in SpW=62 is: 1.01771 +/- 0.0239908 (SNR = 42.4207, N = 44)
Flux density for 3c84-J0319+413 in SpW=63 is: 1.01143 +/- 0.0249739 (SNR = 40.4996, N = 44)
Fitted spectrum for gcal-J0603+174 with fitorder=1: Flux density = 0.264388 +/- 0.000149708 (freq=32.4488 GHz) spidx=-0.834284 +/- 0.00458657
Fitted spectrum for 3c84-J0319+413 with fitorder=1: Flux density = 1.00109 +/- 0.00122518 (freq=32.4488 GHz) spidx=0.00940404 +/- 0.010148
</pre>
 
[[Image:plotG192_plotms_fld0_phaseamp.png|200px|thumb|right|3C147 with calibration applied, amp vs. phase]]
[[Image:plotG192_plotms_fld1_phaseamp.png|200px|thumb|right|J0603+174 with calibration applied, amp vs. phase]]
[[Image:plotG192_plotms_fld3_phaseamp.png|200px|thumb|right|3C84 with calibration applied, amp vs. phase]]
 
As always, it's a good idea to check the corrected data with {{plotms}}.  Plots of corrected amplitude vs. baseline:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotms(vis='SN2010FZ_flagged10s.ms',field='0', \
plotms(vis='G192_flagged_6s.ms', field='0', \
       spw='0:16~59,1~6:4~59,7:4~54,8:30~59,9~10:4~59,11:4~19;21~59', \
       xaxis='baseline', yaxis='amp', \
       correlation='RR,LL',avgbaseline=True,avgtime='600s',
      ydatacolumn='corrected', spw='*:5~122', \
       xaxis='frequency',yaxis='phase',ydatacolumn='corrected')
      averagedata=True, avgchannel='8', \
      avgtime='1000s', coloraxis='antenna1')
#
plotms(vis='G192_flagged_6s.ms', field='1', \
      xaxis='baseline', yaxis='amp', \
      ydatacolumn='corrected', spw='*:5~122', \
       averagedata=True, avgchannel='32', \
      avgtime='6000s', coloraxis='antenna1')
#
plotms(vis='G192_flagged_6s.ms', field='3', \
       xaxis='baseline', yaxis='amp', \
      ydatacolumn='corrected', spw='*:5~122', \
      averagedata=True, avgchannel='8', \
      avgtime='1000s', coloraxis='antenna1')
</source>
</source>
[[Image:plotSN2010FZ_plotms_appliedflags_fld0_phaseavg.png|200px|thumb|right|plotms cal applied flagged fld0 phase averaged]]
In this case, we can see the residual effect of the EVLA "delay clunking" described above, but it is reduced due to the averaging that we applied, but it is still there.
You can look at the target source field='1', but there are lots of data so you will need to do a lot of averaging.
For example:


And, finally, corrected amplitude vs. corrected phase:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotms(vis='SN2010FZ_flagged10s.ms',field='1',avgtime='300s', \
plotms(vis='G192_flagged_6s.ms', field='0', \
       spw='0:16~59,1~6:4~59,7:4~54,8:30~59,9~10:4~59,11:4~19;21~59', \
      xaxis='phase', yaxis='amp', \
       correlation='RR,LL',xaxis='frequency',yaxis='amp',ydatacolumn='corrected')
      xdatacolumn='corrected', \
       ydatacolumn='corrected', spw='*:5~122', \
      averagedata=True, avgchannel='8', \
      avgtime='1000s', coloraxis='baseline')
#
plotms(vis='G192_flagged_6s.ms', field='1', \
      xaxis='phase', yaxis='amp', \
      xdatacolumn='corrected', \
      ydatacolumn='corrected', spw='*:5~122', \
      averagedata=True, avgchannel='32', \
       avgtime='6000s', coloraxis='baseline')
#
plotms(vis='G192_flagged_6s.ms', field='3', \
      xaxis='phase', yaxis='amp', \
      xdatacolumn='corrected', \
      ydatacolumn='corrected', spw='*:5~122', \
      averagedata=True, avgchannel='8', \
      avgtime='1000s', coloraxis='baseline')
</source>
</source>


Alas, the upper baseband still has lots of low level RFI.
Everything looks good, and the recalibration made only minor adjustments since there wasn't very much additional flagged data.


Now split off the data for calibrators and target, to avoid later issues that can corrupt the MSs.  We don't keep spw 12-15, since they weren't included in the last round of calibration, and we don't plan to image them.
Now, split off the data for the calibrators and target field into separate MSs, so we can restore easily our calibrated dataset in case issues with data corruption arise.  Before running split each time, we will remove any existing split data with the same name.  Split will not automatically overwrite an existing MS. The inputs are:


<source lang="python">
<source lang="python">
# In CASA
# In CASA
# Remove any existing split data, otherwise split will not happen
os.system('rm -rf 3C147_split_6s.ms')
os.system('rm -rf SN2010FZ_split10s.ms')
split(vis='G192_flagged_6s.ms', outputvis='3C147_split_6s.ms', \
split(vis='SN2010FZ_flagged10s.ms',outputvis='SN2010FZ_split10s.ms', \
      datacolumn='corrected', field='0')
       datacolumn='corrected',field='1',spw='0~11')
#
os.system('rm -rf J0603_split_6s.ms')
split(vis='G192_flagged_6s.ms', outputvis='J0603_split_6s.ms', \
       datacolumn='corrected', field='1')
#
#
# Remove any existing split data, otherwise split will not happen
os.system('rm -rf G192_split_6s.ms')
os.system('rm -rf SN2010FZ_3c28610s.ms')
split(vis='G192_flagged_6s.ms', outputvis='G192_split_6s.ms', \
split(vis='SN2010FZ_flagged10s.ms',outputvis='SN2010FZ_3c28610s.ms', \
       datacolumn='corrected', field='2')
       datacolumn='corrected',field='2',spw='0~11')
#
#
# Remove any existing split data, otherwise split will not happen
os.system('rm -rf 3C84_split_6s.ms')
os.system('rm -rf SN2010FZ_J092510s.ms')
split(vis='G192_flagged_6s.ms', outputvis='3C84_split_6s.ms', \
split(vis='SN2010FZ_flagged10s.ms',outputvis='SN2010FZ_J092510s.ms', \
       datacolumn='corrected', field='3')
       datacolumn='corrected',field='0',spw='0~11')
</source>
</source>
We can now move on to imaging!


== Imaging ==
== Imaging ==


This is EVLA D-configuration data at C-band.  To determine the best parameters for imaging, it helps to start with the relevant information in the [http://evlaguides.nrao.edu/index.php?title=Observational_Status_Summary_-_Current Observational Status Summary]:
The G192 data were taken in the VLA's highest-resolution A-configuration at Ka-band.  To determine the best parameters for imaging, it helps to start with the relevant information in the [https://science.nrao.edu/facilities/vla/oss/oss Observational Status Summary]:


* Synthesized beam should be 12" at 6 GHz with primary beam field of view of 7.5 arcmin (450")
* The synthesized beam is expected to be ~0.059" at 33 GHz with a primary beam field-of-view of 1.4 arcmin (82").


Our data spans 4.5-7.5 GHz: this is a relatively large fractional bandwidth, resulting in substantial variation of the field of view over the entire frequency range.  FOV = 45 arcmin / Frequency (GHz), giving 10 arcmin at 4.5 GHz, and 6 arcmin at 7.5 GHz.  Likewise, the synthesized beam ranges from 16" at 4.5 GHz to 9.6" at 7.5 GHz.  We want to subsample the synthesized beam by a factor of 3-4, so will use a cellsize of 3".  To cover the full FOV (keeping it at the inner part of the image) at the lowest frequencies, we will want an image size of >400 pixels, or >20 arcmin.
Our data spans 27.0-38.4 GHz: this is a relatively very large fractional bandwidth (about 35%), resulting in substantial variation of the field of view over the entire frequency range.  The FOV = 45 arcmin / Frequency (GHz), giving 1.7 arcmin at 27 GHz and 1.2 arcmin at 38.4 GHz.  Likewise, the synthesized beam ranges from 0.072" at 27 GHz to 0.051" at 38.4 GHz.  We want to subsample the synthesized beam by a factor of 3-5, so we will use a cellsize of 0.015".  To cover the full FOV, we would want a minimum image size of 6800 pixels.  However, there isn't much outside the center of the field for G192 -- this is what gave us leeway to average to 6 seconds -- so, to save time, we will only image a 1280x1280 pixel field (19.2"x19.2").


We will also use the Briggs robust (with <tt>robust=0.5</tt>) weighting, which is a compromise between uniform and natural weighting,
We will also use the Briggs robust (with <tt>robust=0.5</tt>) weighting, which is a compromise between uniform and natural weighting.  Briggs weighting will produce an image with a reasonable resolution, but will allow us to still see larger scale structure.  Noise from sidelobes will also be reduced compared to Natural weighting.
and will give reasonable resolution but will allow us to still see larger scale structure.


Due to the numerology of [http://www.fftw.org/ FFTW's] (which {{clean}} uses under the hood for FFTs) optimal sizes,  
Due to the numerology of [http://www.fftw.org/ FFTW's] (which {{clean}} uses under the hood for FFTs) optimal sizes, <tt>imsize</tt> should be an even number with prime factors chosen from 2, 3, 5, and 7.  Since 1280 = (2^8)*5, it will give us optimal clean performance.  Note that {{clean}} will still run if imsize does not have prime factors 2, 3, 5, or 7 (it will just be a bit slower) but you should always choose an even number.
<tt>imsize</tt> should be composite number with two and only two prime factors chosen from
2, 3, and 5.  Taking into account the x1.2 padding that clean uses internally to the imsize
you give it (and 1.2 = 2*3/5), we choose 640 or 1280 as our imsize (640 = 2^7*5). Other
reasonable sets would be 405, 1215, etc. (405 = 3^4*5) or 432, 648, 1296 (these are 2^n*3^m*5).
In practice, if you give it non-optimal values for imsize, you may find that the transforms
take a bit longer, which is noticeable if you are doing interactive clean.


WARNING: By default, a single-field nterms=1 clean does NOT use Cotton-Schwab (CS) clean to break
For more information on using {{clean}}, in particular on using the interactive GUI, see [[EVLA_Continuum_Tutorial_3C391#Imaging]].  
into major cycles going back to data residuals, it just does cleaning in a bunch of minor
cycles in the image plane.  This can give much poorer imaging quality in cases with poor
uv coverage (snapshots) or in the case of complex emission structure (like ours) -- clean tends to
diverge in this case.  You should explicitly set <tt>imagermode='csclean'</tt> in your
call to clean.  Also, in our case the psf is very good using mfs, so by default it will not
take many major cycle breaks.  We use the <tt>cyclefactor</tt> parameter to control this, which
sets the break threshold to be cyclefactor times the max psf sidelobe level (outside the main
peak).  We start at <tt>cyclefactor=1.5</tt> in a single spw, and ratchet it up to 4.5 when we
clean all the spw.  This seems to work ok.  Rule of thumb is if it is gobbling up many hundreds of
clean iterations in the minor cycles early on, increase cyclefactor.  Conversely, if your psf is poor
but you source structure is simple, you can reduce cyclefactor (e.g. below 1) to stop it from taking
lots of extra major cycles.
 
For more information on using {{clean}}, in particular on using the interactive GUI, see
[[EVLA_Continuum_Tutorial_3C391#Imaging]]. WARNING: In CASA 4.0 the GUI interface for clean
and the viewer has changed slightly. Some of the screenshots shown below may differ slightly
from what you see.


NOTE: If you are pressed for time, then you might want to jump ahead to
NOTE: If you are pressed for time, then you might want to jump ahead to
[[EVLA_6-cm_Wideband_Tutorial_SN2010FZ_(Caltech)#Cleaning_the_lower_baseband_using_two_MFS_Taylor_terms]]
[http://casaguides.nrao.edu/index.php?title=EVLA_3-bit_Tutorial_G192#Cleaning_both_basebands_using_two_MFS_Taylor_terms cleaning both basebands], and while it is cleaning you can read the other Imaging descriptions.
and while it is cleaning you can read the other Imaging descriptions.


=== Cleaning a single spectral window ===
=== Cleaning a single spectral window ===


Let us start by interactively cleaning one of the lower baseband spw (spw 5 in this example).
Let us start by interactively cleaning one spectral window in the lower-frequency baseband (spw 48). (For Ka-band, the higher-numbered spectral-window baseband is actually the lower-frequency baseband.) 
NOTE: this first time will take a few minutes at start to create scratch columns
in the MS in case we want to do self-calibration later.


'''Note that interrupting {{clean}} by Ctrl+C may corrupt your visibilities -- you may be better off choosing to let {{clean}} finish.  We are currently implementing a command that will nicely exit to prevent this from happening, but for the moment try to avoid Ctrl+C.'''
'''Note that interrupting {{clean}} by Ctrl+C may corrupt your visibilities -- you may be better off choosing to let {{clean}} finish.  We are working on a way to prevent this from happening, but for the moment it's best to avoid Ctrl+C.'''


[[Image:viewSN2010FZ_spw5_clean640_4.0.png|200px|thumb|right|interactive clean spw5 640x640 after around 1000 iterations]]
[[Image:viewG192_spw48_1280.png|200px|thumb|right|viewer showing clean spw48 1280x1280 restored image]]
[[Image:viewSN2010FZ_spw5_clean1280.png|200px|thumb|right|2nd interactive clean spw5 1280x1280 before cleaning]]
[[Image:viewSN2010FZ_spw5_clean1280final_4.0.png|200px|thumb|right|viewer showing clean spw5 1280x1280 restored image]]


<source lang="python">
<source lang="python">
Line 1,379: Line 1,677:
# If you want to continue this from a previous clean run,  
# If you want to continue this from a previous clean run,  
# the rm -rf system command should be be skipped
# the rm -rf system command should be be skipped
os.system ('rm -rf imgSN2010FZ10s_spw5_clean640*')
os.system ('rm -rf imgG192_6s_spw48*')
clean(vis='SN2010FZ_split10s.ms',spw='5:4~59', \
clean(vis='G192_split_6s.ms', spw='48:5~122', \
       imagename='imgSN2010FZ10s_spw5_clean640', \
       imagename='imgG192_6s_spw48', \
       mode='mfs',nterms=1,niter=10000,gain=0.1,threshold='0.0mJy', \
       mode='mfs', nterms=1, niter=10000, \
       psfmode='clark',imsize=[640,640],cell=['3.0arcsec'],stokes='I', \
       imsize=[1280], cell=['0.015arcsec'], \
       imagermode='csclean', cyclefactor=1.5, \
       imagermode='csclean', cyclefactor=1.5, \
       weighting='briggs',robust=0.5,interactive=True)
       weighting='briggs', robust=0.5, \
      interactive=True)
</source>
</source>
* Click on the wrench icon [[File:ViewerWrench.png]] to bring up the Data Display Options and change the color scale to "Hot Metal 1" under "basic settings"
* Zoom in 4 times
* Draw a box the point-like source and double-click inside the box to set your clean box (or clean "mask")
Change the number of iterations on the upper left to 50. (Note: this number is independent from the niter clean parameter, which applies to cleaning in mode interactive = False and is used if you click the right-pointing arrow button on the upper right to continue cleaning non-interactively.)
* The curved arrow on the upper right should now be highlighted in green.  Click this green icon to clean the boxed source.
* Stop cleaning when the residuals look like the noise (this will probably happen after the first 50-100 iterations).
* To stop, click the red [[File:clean-stop.png]] button.


* Start carefully by boxing the bright source and setting iterations to 10 at first
When clean is finished, we can look at the restored image:
* Gradually add more boxes and increase the number of iterations
<source lang="python">
* Since this is not much more than a snapshot you see the six-fold sidelobe pattern
# In CASA
of the extended emission in the center of the map. This decreases as you clean
viewer('imgG192_6s_spw48.image')
out this emission.
</source>
* Stop cleaning when the residuals look like noise (and you cannot clearly see sources).
 
* To stop, click the red [[File:clean-stop.png]] button.
The restored image is shown above.
 
Check the rms of the residuals using the {{imstat}} task:
<source lang="python">
# In CASA
mystat = imstat('imgG192_6s_spw48.residual')
print 'Residual standard deviation = '+str(mystat['sigma'][0]) + ' Jy'
</source>
In this particular case, it's 136 uJy; yours may be slightly different.


The top figure to the right shows a zoom in on the end state of the clean, where
=== Cleaning the lower-frequency baseband ===
we have marked a number of boxes and cleaned them out.


Note that there are some strange sidelobe patterns in lower left, possibly
[[Image:viewG192_spw32-63_boxes.png|200px|thumb|right|clean boxes spw32-63]]
from a source outside the image area.  We can make a bigger image starting from
[[Image:viewG192_spw32-63.png|200px|thumb|right|clean spw32-63 restored image center]]
our current model:
Here we will image the entire lower-frequency baseband (spw 32-63).  Follow the same iterative procedure as before, and get the best residuals you can without "cleaning the noise".   


<source lang="python">
<source lang="python">
Line 1,408: Line 1,721:
# This assumes you want to start this clean from scratch
# This assumes you want to start this clean from scratch
# If you want to continue this from a previous clean run,  
# If you want to continue this from a previous clean run,  
# the rm -rf system command should be skipped
# the rm -rf system command should be be skipped
os.system ('rm -rf imgSN2010FZ10s_spw5_clean1280*')
os.system ('rm -rf imgG192_6s_spw32-63*')
clean(vis='SN2010FZ_split10s.ms',spw='5:4~59', \
clean(vis='G192_split_6s.ms', spw='32~63:5~122', \
       imagename='imgSN2010FZ10s_spw5_clean1280', \
       imagename='imgG192_6s_spw32-63', \
       mode='mfs',nterms=1,niter=10000,gain=0.1,threshold='0.0mJy', \
       mode='mfs', nterms=1, niter=10000, \
       psfmode='clark',imsize=[1280,1280],cell=['3.0arcsec'],stokes='I', \
       imsize=[1280], cell=['0.015arcsec'], \
       imagermode='csclean', cyclefactor=1.5, \
       imagermode='csclean', cyclefactor=1.5, \
      modelimage='imgSN2010FZ10s_spw5_clean640.model', \
       weighting='briggs', robust=0.5, \
       weighting='briggs',robust=0.5,interactive=True)
      interactive=True)
#
viewer('imgG192_6s_spw32-63.image')
mystat = imstat('imgG192_6s_spw32-63.residual')
print 'Residual standard deviation = '+str(mystat['sigma'][0]) + ' Jy'
</source>
</source>
* Because of the increased bandwidth, it is easier to see two fainter point sources.
* Be careful cleaning sources that lie near or on sidelobe peaks.
* Clean the central emission region first (50 iterations) to reduce the sidelobe level before adding any more components.  The screenshot above shows the interactive clean window after 50 iterations with the three clean boxes we created.


Sure enough, there is a bright source near the lower left (see middle panel at right).
For this run, the rms is 23 uJy.  To the right is a zoom-in on the center of the restored image.
Box it, clean it a bit, and look again.  There is a second source in the mid-left (track
it down by its sidelobes). Box this one, clean it a bit, and when satisfied stop.


You can use the CASA {{viewer}} to display the images that {{clean}} creates.  If you need more guidance
Finally, we will fit the central point source to determine its flux.  First, create a box region around the source in the viewer, and save it as <tt>G192.crtf</tt> (View -> Regions -> File; see the screenshot below right). Note that you can drag the Regions window out of the main Viewer window if it's taking up too much space.
on using the viewer, see the [http://casa.nrao.edu/CasaViewerDemo/casaViewerDemo.html CASA Viewer Demo] video
(note that this is for a much earlier version of the viewer, and the interface has changed since then).  


Bring up your restored image directly:
Use this region to fit the source flux:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
viewer('imgSN2010FZ10s_spw5_clean1280.image')
myfit = imfit('imgG192_6s_spw32-63.image', region='G192.crtf')
print 'Source flux = '+str(myfit['results']['component0']['flux']['value'][0])+'+/-'+str(myfit['results']['component0']['flux']['error'][0]) + ' Jy'
</source>
</source>


The restored image is shown in the bottom panel to the right.  I have chosen the Grayscale1 instead of default color
[[Image:viewG192_region.png|200px|thumb|right|saving CASA region for G192]]
map as I prefer "Grayscale" to false color "Rainbow" for assessing image quality.  Also, you can change the scaling of the image using the "scaling power cycles" slider under "basic settings".


Check the rms of the residuals using the {{imstat}} task:
The derived flux is 2.64 +/- 0.04 mJy.  Also, have a look at the logger output:
<source lang="python">
 
# In CASA
<pre>
mystat = imstat('imgSN2010FZ10s_spw5_clean1280.residual')
Image component size (convolved with beam) ---
print 'Residual standard deviation = '+str(mystat['sigma'][0])
      --- major axis FWHM:    80.01 +/- 0.98 marcsec
</source>
      --- minor axis FWHM:    71.51 +/- 1.01 marcsec
In this particular case, it's 31.8 uJy; yours will likely be slightly different.
      --- position angle: 63.2 +/- 2.2 deg
 
Clean beam size ---
      --- major axis FWHM: 0.06 arcsec
      --- minor axis FWHM: 0.06 arcsec
      --- position angle: 29.00 deg
Image component size (deconvolved from beam) ---
      --- major axis FWHM:    51.3 +/- 1.8 marcsec
      --- minor axis FWHM:    37.7 +/- 2.3 marcsec
      --- position angle: 78.5 +/- 6.3 deg
</pre>


=== Cleaning the lower baseband ===
The deconvolved size of around 51.3 x 37.7 milliarcseconds corresponds to a size of roughly 90 AU (assuming a distance of approximately 2 kpc).  Indeed, this is thought to be the accretion disk around the protostar!  (See [http://www.sciencemag.org/content/292/5521/1513.full?ijkey=y1tFwtUnFnXoc&keytype=ref&siteid=ci this article] for the initial report, using 43 GHz data, of the accretion disk around G192.)


[[Image:viewSN2010FZ_spw0to7_clean1280final.png|200px|thumb|right|clean spw0-7 restored image center]]
=== Cleaning the upper-frequency baseband ===
Now, image the entire lower baseband (spw 0-7).
Follow same iterative procedure as before, and get the best
residuals you can without "cleaning the noise". 


* Because of the bandwidth and frequency synthesis, the sidelobe pattern is different than before and it is much easier to see fainter emission.
[[Image:viewG192_spw0-31.png|200px|thumb|right|clean spw32-63 restored image center]]
* Be careful cleaning sources that lie near or on sidelobe splotches.
Now we will image the entire upper-frequency baseband (spw 0-31).  Follow the same iterative procedure as before, and get the best residuals you can without "cleaning the noise".
* Clean the central emission region way down first to reduce the sidelobe level before adding components in the sidelobe areas.


<source lang="python">
<source lang="python">
Line 1,461: Line 1,783:
# If you want to continue this from a previous clean run,  
# If you want to continue this from a previous clean run,  
# the rm -rf system command should be be skipped
# the rm -rf system command should be be skipped
os.system ('rm -rf imgSN2010FZ10s_spw0to7_clean1280*')
os.system ('rm -rf imgG192_6s_spw0-31*')
clean(vis='SN2010FZ_split10s.ms',spw='0:16~59,1~6:4~59,7:4~54', \
clean(vis='G192_split_6s.ms', spw='0~31:5~122', \
       imagename='imgSN2010FZ10s_spw0to7_clean1280', \
       imagename='imgG192_6s_spw0-31', \
       mode='mfs',nterms=1,niter=10000,gain=0.1,threshold='0.0mJy', \
       mode='mfs', nterms=1, niter=10000, \
       psfmode='clark',imsize=[1280,1280],cell=['3.0arcsec'],stokes='I', \
       imsize=[1280], cell=['0.015arcsec'], \
       imagermode='csclean', cyclefactor=1.5, \
       imagermode='csclean', cyclefactor=1.5, \
       weighting='briggs',robust=0.5,interactive=True)
       weighting='briggs', robust=0.5, \
      interactive=True)
#
#
mystat = imstat('imgSN2010FZ10s_spw0to7_clean1280.residual')
viewer('imgG192_6s_spw0-31.image')
print 'Residual standard deviation = '+str(mystat['sigma'][0])
mystat = imstat('imgG192_6s_spw0-31.residual')
print 'Residual standard deviation = '+str(mystat['sigma'][0]) + ' Jy'
myfit = imfit('imgG192_6s_spw0-31.image', region='G192.crtf')
print 'Source flux = '+str(myfit['results']['component0']['flux']['value'][0])+'+/-'+str(myfit['results']['component0']['flux']['error'][0]) + ' Jy'
</source>
</source>


For this run, the rms is 11.3 uJy (and there is clearly some structure left in the residual). To the right is a zoom-in on the center of the restored image.
For this run, the rms is 31 uJy, and the source flux is 3.07 +/- 0.06 mJy.  Again, {{imfit}} finds that the source is slights extended and provides a deconvolved size. To the right is a zoomed-in image of the center of the restored image.
 
=== Cleaning both basebands using two MFS Taylor terms ===


==== Cleaning the lower baseband using two MFS Taylor terms ====
From the individual images of the upper- and lower-frequency basebands, we can see that the source spectrum of G192 is relatively flat, with a spectral index of approximately
 
<math>
\alpha = \log(S_1 / S_2) / \log(\nu_1 / \nu_2)
</math>
<math>
= \log(3.07 / 2.64) / \log(36.5 / 29.0)
</math>
<math>
= 0.66,
</math>


The mfs nterms=2 option creates two "Taylor Term" images - an average intensity image (with suffix <tt>.image.tt0</tt>)
where the convention for the spectral index alpha is that  
and a spectral slope image (with suffix <tt>.image.tt1</tt>) which is intensity x alpha (where alpha is spectral index).
For convenience there is a spectral index image (with suffix <tt>.image.alpha</tt>).  These Taylor expansions are with respect to the "Reference Frequency" of the image (by default the center frequency of the spw selected, but can be specified using the <tt>reffreq</tt> parameter in {{clean}}). The convention for spectral index alpha is that


<math>
<math>
S \propto \nu^\alpha
S \propto \nu^\alpha.
</math>
</math>


so negative spectral indexes indicate a "steep" spectrum (falling with frequency).
Within a single baseband, neglecting to account for the spectral index will make little difference -- however, when we combine the two basebands, it is best to account for the spectral variation across the total band.  For this, we will set <tt>nterms=2</tt> in {{clean}}.


[[Image:viewSN2010FZ_spw0to7_mfs2clean.png|200px|thumb|right|clean spw0-7 mfs nterms=2 in progress]]
This option creates two "Taylor term" images -- an average intensity image (with suffix <tt>.image.tt0</tt>), and a spectral slope image (with suffix <tt>.image.tt1</tt>), which is intensity x alpha (where alpha is the spectral index).  For convenience, there is also a spectral index image (with suffix <tt>.image.alpha</tt>).  These Taylor expansions are with respect to the "reference frequency" of the image (by default the center frequency of the selected spectral window, but can be specified using the <tt>reffreq</tt> parameter in {{clean}}).
Let's try using multi-frequency synthesis with nterms=2 on the lower baseband.
 
The dirty beam will have lower sidelobes so we turn up <tt>cyclefactor</tt> for <tt>csclean</tt> a bit.  Note: if you're feeling a bit lazy, and trust your previous set of clean boxes, you can also set <tt>mask='imgSN2010FZ10s_spw0to7_clean1280.mask'</tt> to use these as a starting point:
We will clean the complete dataset using <tt>nterms=2</tt>.  Note: if you prefer, you can clean your image using interactive = False.  For non-interactive cleaning, make sure you define a clean mask with <tt>mask='imgG192_6s_spw0-31.mask'</tt> or <tt>mask='imgG192_6s_spw32-63.mask'</tt> to use these as a starting point rather than running an interactive clean session.  You can also draw a new region file from scratch in the Viewer, save the region as a .crtf file, and supply this file to the mask parameter in clean.  If you set interactive = False you should also modify the <tt>threshold</tt> and <tt>niter</tt> parameters to avoid over-cleaning (the threshold parameter should always be higher than the expected theoretical rms noise; for an estimation of the rms noise for this image see below).


<source lang="python">
<source lang="python">
Line 1,497: Line 1,833:
# If you want to continue this from a previous clean run,  
# If you want to continue this from a previous clean run,  
# the rm -rf system command should be be skipped
# the rm -rf system command should be be skipped
os.system ('rm -rf imgSN2010FZ10s_spw0to7_mfs2_clean1280*')
os.system ('rm -rf imgG192_6s_spw0-63_mfs2*')
clean(vis='SN2010FZ_split10s.ms',spw='0:16~59,1~6:4~59,7:4~54', \
clean(vis='G192_split_6s.ms', spw='0~63:5~122', \
       imagename='imgSN2010FZ10s_spw0to7_mfs2_clean1280', \
       imagename='imgG192_6s_spw0-63_mfs2', \
       mode='mfs',nterms=2,niter=10000,gain=0.1,threshold='0.0mJy', \
       mode='mfs', nterms=2, niter=10000, gain=0.1, \
      psfmode='clark',imsize=[1280,1280],cell=['3.0arcsec'],stokes='I', \
      threshold='0.0mJy', psfmode='clark', imsize=[1280], \
      imagermode='csclean', cyclefactor=4.5, \
      cell=['0.015arcsec'], \
       weighting='briggs',robust=0.5,interactive=True,mask=[])
       weighting='briggs', robust=0.5, interactive=True)
#
#
mystat = imstat('imgSN2010FZ10s_spw0to7_mfs2_clean1280.residual.tt0')
mystat = imstat('imgG192_6s_spw0-63_mfs2.residual.tt0') + ' Jy'
print 'Residual standard deviation = '+str(mystat['sigma'][0])
print 'Residual standard deviation = '+str(mystat['sigma'][0])
myfit = imfit('imgG192_6s_spw0-63_mfs2.image.tt0', region='G192.crtf') + ' Jy'
print 'Source flux = '+str(myfit['results']['component0']['flux']['value'][0])+'+/-'+str(myfit['results']['component0']['flux']['error'][0])
</source>
</source>


For this run, the rms is 10.5 uJy (somewhat better-looking than the nterms=1).
For this run, the rms is 19.7 uJy, and the peak of the emission from G192 is 1.8 mJy, and the integrated source flux is 2.86 +/- 0.04 mJy (as before, the source is found to be extended). You can use the {{viewer}} to load the average intensity image:
The top screenshot to the right shows an intermediate but early stage of cleaning where we are looking at
the central emission and cleaning it out slowly.
 
You can use the {{viewer}} to load the average intensity image:


<source lang="python">
<source lang="python">
# In CASA
# In CASA
viewer('imgSN2010FZ10s_spw0to7_mfs2_clean1280.image.tt0')
viewer('imgG192_6s_spw0-63_mfs2.image.tt0')
</source>
</source>


and then use the Open Data panel to load the spectral index image <tt>imgSN2010FZ10s_spw0to7_mfs2_clean1280.image.alpha</tt>
[[Image:viewG192_spw0-63_mfs2loadalpha.png|200px|thumb|right|clean spw0-63 mfs nterms=2 load alpha with LEL]]
which can then be blinked (optionally plotted side-by-side using the Panel Display Options panel to set 2 panels in the x direction). 


[[Image:viewSN2010FZ_spw0to7_mfs2loadalpha_4.0.png|200px|thumb|right|clean spw0-7 mfs nterms=2 load alpha with LEL]]
Since the spectral index image is very noisy in the lower-intensity regions, we will use {{immath}} task to filter the spectral index image explicitly, using a Lattice Expression Language (LEL) expression:
[[Image:viewSN2010FZ_spw0to7_mfs2panelalpha_4.0.png|200px|thumb|right|clean spw0-7 mfs nterms=2 tt0 and alpha (filtered at 0.1mJy in tt0)]]
 
Note there is a lot of noise in alpha in the low-intensity regions, and thus filtering the alpha image based on the values in the tt0 image is desirable. You can use the {{immath}} task to make this filtered alpha image explicitly, using a  
Lattice Expression Language (LEL) expression:  


<source lang="python">
<source lang="python">
# In CASA
# In CASA
immath(imagename=['imgSN2010FZ10s_spw0to7_mfs2_clean1280.image.alpha',  
immath(imagename=['imgG192_6s_spw0-63_mfs2.image.alpha',  
                   'imgSN2010FZ10s_spw0to7_mfs2_clean1280.image.tt0'],
                   'imgG192_6s_spw0-63_mfs2.image.tt0'],
       mode='evalexpr',
       mode='evalexpr',
       expr='IM0[IM1>1.0E-4]',
       expr='IM0[IM1>2.0E-4]',
       outfile='imgSN2010FZ10s_spw0to7_mfs2_clean1280.image.alpha.filtered')
       outfile='imgG192_6s_spw0-63_mfs2.image.alpha.filtered')
</source>
</source>


This will use 0.1 mJy (or 10 x the sigma we found) as the cutoff.
This will use 0.2 mJy (10 x the rms) as the cutoff. You can then view or manipulate the filtered alpha image as usual.
You can then view or manipulate the filtered alpha image as normal.
 
We can also use LEL to filter the alpha image on the intensity on-the-fly when we load this raster in the Open Data panel
by specifying a LEL string in the LEL box instead of selecting the image from the directory
listing.  The LEL string:


We can also use LEL to filter the alpha image on intensity on-the-fly when we load the raster via the Open Data panel, by specifying a LEL string in the LEL box instead of selecting the image from the directory listing.  The LEL string
<pre>
<pre>
'imgSN2010FZ10s_spw0to7_mfs2_clean1280.image.alpha'['imgSN2010FZ10s_spw0to7_mfs2_clean1280.image.tt0'>1.0E-04]
'imgG192_6s_spw0-63_mfs2.image.alpha'['imgG192_6s_spw0-63_mfs2.image.tt0'>2E-04]
</pre>
</pre>
will replicate what we did above.  The middle figure to the right shows the Open Data panel with our LEL string in it.  Just click the Raster button to load this.


will replicate what we did above. The middle figure to the right shows the Open Data panel
[[Image:viewG192_spw0-63_mfs2panelalpha.png|200px|thumb|right|clean spw0-63 mfs nterms=2 tt0 and alpha (filtered at 0.2 mJy in tt0)]]
with our LEL string in it. Just click the Raster button to load this.
[[Image:viewG192_spw0-63_mfs2panelalphaerr.png|200px|thumb|right|clean spw0-63 mfs nterms=2 alpha and alpha error (filtered at 0.2 mJy in tt0)]]


The lower panel to the right shows the intensity and LEL-filtered alpha images side-by-side in the viewer, zoomed
The lower panel to the right shows the intensity and LEL-filtered alpha images side-by-side in the viewer, zoomed in on the brightest source of emission.  Creating a box around this region and double-clicking reveals that the spectral index varies from around -0.33 to 1.4, with the pixels in the brightest portion of the image at around 0.8, similar to what we found by hand using the information from the single-baseband images.
in on the galaxy emission.  Mousing over the alpha shows spectral indexes ranging from -1 to +1 in the center, with
the brightest emission with alpha -0.7 in the knots in the disk.


=== Cleaning using both basebands combined ===
To get a sense of the probable errors for this spectral index information, we perform a similar filtering operation on the <tt>imgG192_6s_spw0-63_mfs2.image.alpha.error>/tt> image:
 
For the ultimate image, use the "clean" part of the upper baseband in addition
to the lower (use spw 0-11). We will use mfs with nterms=2 (if you try nterms=1
on this wide bandwidth you will get much poorer residuals). Because of the added
work and extra data involved, this will take much longer than our other runs of
clean.  Therefore, we will get a head start by doing a non-interactive clean using
the mask left from the previous clean (spw 0-7). We will insert a clean threshold
to limit runaway cleaning too far beneath the noise level.  
 
This will take a while, especially if there are other processes running on your machine (with nothing else running, expect ~30-40 minutes).


<source lang="python">
<source lang="python">
# In CASA
# In CASA
# Removing any previous cleaning information
immath(imagename=['imgG192_6s_spw0-63_mfs2.image.alpha.error',  
# This assumes you want to start this clean from scratch
                  'imgG192_6s_spw0-63_mfs2.image.tt0'],
# If you want to continue this from a previous clean run,
      mode='evalexpr',
# the rm -rf system command should be be skipped
      expr='IM0[IM1>2E-4]',
os.system ('rm -rf imgSN2010FZ10s_spw0to11_mfs2_clean1280*')
      outfile='imgG192_6s_spw0-63_mfs2.image.alpha.error.filtered')
clean(vis='SN2010FZ_split10s.ms', \
      spw='0:16~59,1~6:4~59,7:4~54,8:30~59,9~10:4~59,11:4~19;21~59', \
      imagename='imgSN2010FZ10s_spw0to11_mfs2_clean1280', \
      mode='mfs',nterms=2,niter=3000,gain=0.1,threshold='0.002mJy', \
      psfmode='clark',imsize=[1280,1280],cell=['3.0arcsec'],stokes='I', \
      imagermode='csclean', cyclefactor=4.5, \
      mask=['imgSN2010FZ10s_spw0to7_mfs2_clean1280.mask'], \
      weighting='briggs',robust=0.5,interactive=False)
#
mystat = imstat('imgSN2010FZ10s_spw0to11_mfs2_clean1280.residual.tt0')
print 'Residual standard deviation = '+str(mystat['sigma'][0])
</source>
</source>


For this particular run, the rms was 8.9 uJy (noticeably better than the lower baseband only results).
Now, we can load both the <tt>alpha</tt> and <tt>alpha.error</tt> images side-by-side in the viewer:
 
[[Image:viewSN2010FZ spw0to11_mfs2resid.png|200px|thumb|right|final residual and mask]]
 
Let us see if there is more to clean. Bring this up in interactive mode:
 
<source lang="python">
<source lang="python">
# In CASA
# In CASA
clean(vis='SN2010FZ_split10s.ms', \
viewer('imgG192_6s_spw0-63_mfs2.image.alpha.filtered')
      spw='0:16~59,1~6:4~59,7:4~54,8:30~59,9~10:4~59,11:4~19;21~59', \
      imagename='imgSN2010FZ10s_spw0to11_mfs2_clean1280', \
      mode='mfs',nterms=2,niter=3000,gain=0.1,threshold='0.001mJy', \
      psfmode='clark',imsize=[1280,1280],cell=['3.0arcsec'],stokes='I', \
      imagermode='csclean', cyclefactor=4.5, \
      mask='imgSN2010FZ10s_spw0to11_mfs2_clean1280.mask', \
      weighting='briggs',robust=0.5,interactive=True)
</source>
</source>


This should start cleaning from where our previous non-interactive clean left off.
As one might expect, the errors are higher outside the emission peak (see the screenshot on the right). However, it seems possible that the <tt>.error</tt> image is underestimating the true errors on the mfs-calculated spectral index, since the central brightest pixels only have errors of around 0.15, when we calculated an alpha of 0.66 (compared with the mfs-calculated alpha of 0.8). If we were planning to use the reported spectral index information for publication, we would need to go through a more thorough investigation of the actual error analysis and spectral index.
<b>Note for 4.2.0:</b> In this case we have specified <tt>mask='imgSN2010FZ10s_spw0to11_mfs2_clean1280.mask'</tt> explicitly due to a bug where it will not otherwise allow you to edit the mask interactively.
 
You might find a few more sources revealed in the outer parts of the image, and also more
emission around the galaxy disk in the center. Try drawing new boxes, perhaps extend the box
in the center, and do ~100-1000 more iterations. At the end, what is left should be dominated
by the error patterns from mis-calibration.  Only self-calibration will get rid of
these. Stop cleaning for now. See the figure to the right for the interactive display panel
showing final residuals and mask (changing the colormap to <tt>Greyscale 1</tt>).
 
Check the residual levels:
<source lang="python">
# In CASA
mystat = imstat('imgSN2010FZ10s_spw0to11_mfs2_clean1280.residual.tt0')
sigma = mystat['sigma'][0]
print 'Residual standard deviation = '+str(mystat['sigma'][0])
</source>
 
The final rms achieved here is 8.6 uJy; slightly better.


== Analyzing the image ==
== Analyzing the image ==


Let's see how close we got to expected noise and dynamic range:
From {{imstat}} on the final combined-baseband image, we got an image rms of 19.7 uJy.  A reasonable question to ask is what we would <i>expect</i> the image rms to be: one way to estimate this is to determine the effective on-source time, then input the appropriate parameters to the [https://science.nrao.edu/facilities/vla/proposing/evlaExpoCalc.jnlp VLA exposure calculator] to determine the expected rms.


<source lang="python">
<source lang="python">
# In CASA
# In CASA
mystat = imstat('imgSN2010FZ10s_spw0to11_mfs2_clean1280.image.tt0')
listobs('G192_split_6s.ms', listunfl=True)
peak = mystat['max'][0]
print 'Image max flux = '+str(mystat['max'][0])
#
mystat = imstat('imgSN2010FZ10s_spw0to11_mfs2_clean1280.model.tt0')
total = mystat['sum'][0]
print 'Model total flux = '+str(mystat['sum'][0])
#
snr = peak/sigma
print 'SN2010FZ peak S/N = '+str(snr)
#
snr = total/sigma
print 'SN2010FZ total S/N = '+str(snr)
</source>
</source>
The output gives:
<pre>
Residual standard deviation = 8.60710739215e-06
Image max flux = 0.00995589420199
Model total flux = 0.0371581438531
SN2010FZ peak S/N = 1156.70616717
SN2010FZ total S/N = 4317.14653485
</pre>


What do we expect? If we do {{listobs}} on this MS we see the scans:
This will show:
<pre>
<pre>
   Date        Timerange (UTC)          Scan  FldId FieldName           nRows   Int(s) 
ID   Code Name                RA              Decl           Epoch   SrcId     nRows   nUnflRows
  11-Jul-2010/21:38:44.0 - 21:39:51.0    9     0 SN2010FZ            33696  9.16   
0    NONE G192.16-3.84        05:58:13.540000 +16.31.58.30001 J2000  0       2931890  2901697.32
              21:40:01.0 - 21:41:20.5   10      0 SN2010FZ            37908  9.89   
              21:41:30.0 - 21:42:50.0    11      0 SN2010FZ            37908  10     
              21:43:00.0 - 21:44:20.0    12      0 SN2010FZ            37908  10     
              21:44:30.0 - 21:45:50.0    13     0 SN2010FZ            37908  10     
              21:46:00.0 - 21:47:19.5    14      0 SN2010FZ            37908  9.89   
              21:47:29.0 - 21:47:49.0    15      0 SN2010FZ            12636  9.67   
              21:49:42.0 - 21:50:49.0    17      0 SN2010FZ            33696  9.17   
              21:50:59.0 - 21:52:19.0    18      0 SN2010FZ            37908  10     
              21:52:29.0 - 21:53:48.5    19      0 SN2010FZ            37908  9.89   
              21:53:58.0 - 21:55:18.0    20      0 SN2010FZ            37908  10     
              21:55:28.0 - 21:56:48.0    21      0 SN2010FZ            37908  10     
              21:56:58.0 - 21:58:18.0    22      0 SN2010FZ            37908  10     
              21:58:28.0 - 21:58:47.5    23      0 SN2010FZ            12636  9.67   
              22:00:39.5 - 22:01:47.0    25      0 SN2010FZ            33696  9.18   
              22:01:57.0 - 22:03:17.0    26      0 SN2010FZ            37908  10     
              22:03:27.0 - 22:04:47.0    27      0 SN2010FZ            37908  10     
              22:04:57.0 - 22:06:16.5    28      0 SN2010FZ            37908  9.89   
              22:06:26.0 - 22:07:46.0    29      0 SN2010FZ            37908  10     
              22:07:56.0 - 22:09:16.0    30      0 SN2010FZ            37908  10     
              22:09:26.0 - 22:09:45.5    31     0 SN2010FZ            12636  9.67   
              22:11:38.0 - 22:12:45.5    33      0 SN2010FZ            33696  9.19   
              22:12:55.0 - 22:14:15.0    34      0 SN2010FZ            37908  10     
              22:14:25.0 - 22:15:45.0    35      0 SN2010FZ            37908  10     
              22:15:55.0 - 22:17:15.0    36      0 SN2010FZ            37908  10     
              22:17:25.0 - 22:18:44.5    37      0 SN2010FZ            37908  9.89   
              22:18:54.0 - 22:20:14.0    38      0 SN2010FZ            37908  10     
              22:20:24.0 - 22:20:43.5    39      0 SN2010FZ            12636  9.67   
          (nVis = Total number of time/baseline visibilities per scan)
</pre>
</pre>
(listing columns truncated) and we estimate about 37 minutes on target. We had about 25 antennas on average, and our spw selection picked out 610 channels (2 MHz each) for a total of 1220 MHz bandwidth. If we plug this
Note that the "nUnflRows," or number of unflagged rows, is 2901697.32.  Every row is a single baseline-integration-spw record, as you probably learned if you looked at the MS with {{browsetable}}.  So, to use this to calculate an "effective" exposure time for the VLA Exposure Calculator for 22 antennas (22*21/2 = 231 baselines), we find that time = 2901697.32 * 6 seconds / 231 baselines / 64 spectral windows = 1178 seconds = 19.6 minutes. Our effective bandwidth is 7552 MHz, taking into account the spectral window selection.  Using the median frequency of 32.7 GHz, the [https://science.nrao.edu/facilities/vla/proposing/evlaExpoCalc.jnlp VLA exposure calculator] reports that we should achieve an image rms of 13.5 uJy.  Although our actual rms is somewhat higher, this is not unexpected; we have not done any self-calibration, for example.
into the
[https://science.nrao.edu/facilities/evla/calibration-and-tools/exposure EVLA exposure calculator], at 5 GHz, we find that we expect a rms thermal noise level of 8.7 uJy, and at 7 GHz, 7.0 uJy.  So, our values are within the expected range (a bit higher than theoretical, but that's expected).


[[Image:plotSN2010FZ_viewerfinal.png|200px|thumb|right|final image]]
Next, we will do some rough analysis on the spectral index to determine an intensity-weighted mean spectral index for G192. The <tt>.image.tt1</tt> from our mfs is an intensity times alpha image (see the figure to the right). Let's filter this Taylor-term image by intensity as we did with the <tt>.alpha</tt> image:
Look at this in the viewer:
<source lang="python">
# In CASA
viewer('imgSN2010FZ10s_spw0to11_mfs2_clean1280.image.tt0')
</source>
Zoom in on the center (see figure to the right).
 
[[Image:viewSN2010FZ_spw0to11_mfs2tt1.png|200px|thumb|right|final tt1 image with box]]
In the previous section we demonstrated how to process and display the spectral index image. You can do
the same for this final image.  Here, we will do some rough analysis on the spectral index to determine
an intensity-weighted mean spectral index over the core region.
The <tt>.image.tt1</tt> from our mfs is an intensity times alpha image.  See the figure to the right.
Let's gate the Taylor-term images on intensity:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
# Removing any file output from previous runs, so immath will proceed
# Removing any file output from previous runs, so immath will proceed
os.system('rm -rf imgSN2010FZ10s_spw0to11_mfs2_clean1280.image.tt1.filtered')
os.system('rm -rf imgG192_6s_spw0-63_mfs2.image.tt1.filtered')
immath(imagename=['imgSN2010FZ10s_spw0to11_mfs2_clean1280.image.tt1',
immath(imagename=['imgG192_6s_spw0-63_mfs2.image.tt1',
                   'imgSN2010FZ10s_spw0to11_mfs2_clean1280.image.tt0'],
                   'imgG192_6s_spw0-63_mfs2.image.tt0'],
       mode='evalexpr',
       mode='evalexpr',
       expr='IM0[IM1>5.0E-5]',
       expr='IM0[IM1>2E-4]',
       outfile='imgSN2010FZ10s_spw0to11_mfs2_clean1280.image.tt1.filtered')
       outfile='imgG192_6s_spw0-63_mfs2.image.tt1.filtered')
#
#
# Removing any file output from previous runs, so immath will proceed
# Removing any file output from previous runs, so immath will proceed
os.system('rm -rf imgSN2010FZ10s_spw0to11_mfs2_clean1280.image.tt0.filtered')
os.system('rm -rf imgG192_6s_spw0-63_mfs2.image.tt0.filtered')
immath(imagename=['imgSN2010FZ10s_spw0to11_mfs2_clean1280.image.tt0'],
immath(imagename=['imgG192_6s_spw0-63_mfs2.image.tt0'],
       mode='evalexpr',
       mode='evalexpr',
       expr='IM0[IM0>5.0E-5]',
       expr='IM0[IM0>2E-4]',
       outfile='imgSN2010FZ10s_spw0to11_mfs2_clean1280.image.tt0.filtered')
       outfile='imgG192_6s_spw0-63_mfs2.image.tt0.filtered')
</source>
</source>


We can identify a box containing the central emission (see figure of tt1 in viewer) and note the corners.
We can use the same region we created for {{imstat}}. Let us compute the intensity-weighted spectral index over this region by averaging these masked images using {{imstat}} and computing the ratio:
(We could also use the region tools from the viewer, but that is for another exercise.)
Let us compute the intensity-weighted spectral index over this box by averaging
these masked images using {{imstat}} and computing the ratio:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
mystat = imstat('imgSN2010FZ10s_spw0to11_mfs2_clean1280.image.tt1.filtered',
mystat = imstat('imgG192_6s_spw0-63_mfs2.image.tt1.filtered',
                 box='503,533,756,762')
                 region='G192.crtf')
avgtt0alpha = mystat['mean'][0]
avgtt0alpha = mystat['mean'][0]
#
#
mystat = imstat('imgSN2010FZ10s_spw0to11_mfs2_clean1280.image.tt0.filtered',
mystat = imstat('imgG192_6s_spw0-63_mfs2.image.tt0.filtered',
                 box='503,533,756,762')
                 region='G192.crtf')
avgtt0 = mystat['mean'][0]
avgtt0 = mystat['mean'][0]
avgalpha = avgtt0alpha/avgtt0
avgalpha = avgtt0alpha / avgtt0
print 'SN2010FZ I-weighted Alpha = '+str(avgalpha)
print 'G192 intensity-weighted alpha = ' + str(avgalpha)
</source>
</source>
We get  
We get:
<pre>
<pre>
SN2010FZ I-weighted Alpha = -1.38157453384
G192 intensity-weighted alpha = 0.737300481129
</pre>
</pre>


The emission in this source is on the steep side. At this point we do not know how reliable this is or
This is pretty close to the value we found from the single-baseband images of alpha = 0.66, validating the results from mfs with <tt>nterms=2</tt>.
what we expect (though our calibrators come out with correct spectral indexes if we image them the
same way). But this illustrates a way to extract spectral information from our wideband mfs images.
 
== Comparing with the Optical/Infrared ==
 
As a final comparison, we turn to the Sloan Digital Sky Survey (SDSS) and a cutout image of our galaxy:
[[Image:NGC_2967_UGC_5180_IRAS_09394+0033_irg.jpg|400px|thumb|center|]]
from their [http://cosmo.nyu.edu/hogg/rc3/NGC_2967_UGC_5180_IRAS_09394+0033_irg.jpg RC3]
album (courtesy D.Hogg, M.Blanton, SDSS collaboration - see [[#Credits]]). This looks like a nice nearby
face-on spiral galaxy. How does our 6cm continuum emission line up with the optical?
 
Here is the EVLA 6cm image side by side with a i-band image from the Sloan Digital Sky Survey (SDSS) registered to our image:
 
[[Image:plotSN2010FZ viewerfinalandSDSS.png|600px|thumb|center|final and sdss image]]
 
You can also find this image, named <tt>NGC_2967_UGC_5180_IRAS_09394+0033-i.fits</tt>, on the web at <tt>http://casa.nrao.edu/Data/EVLA/SN2010FZ/NGC_2967_UGC_5180_IRAS_09394+0033-i.fits</tt> (at the CASA workshop, it's in <tt>/data/casa/evla/</tt> or a similar location that will be given to you in the instructions). Load it into your viewer, and blink against our 6cm image.
 
We can also plot one as a raster and the other overlaid as contours. You can load the SDSS image
from the viewer Load Data panel and fiddle with contours. Once you know contour levels, you can
also use the imview task to load a raster and contour image:
 
<source lang="python">
# In CASA
imview(raster={ 'file' : 'imgSN2010FZ10s_spw0to11_mfs2_clean1280.image.tt0'},
      contour = { 'file' : 'NGC_2967_UGC_5180_IRAS_09394+0033-i.fits',
                  'levels' : [0.2, 0.5, 1, 1.5, 3],
                  'base' : 0.0,
                  'unit' : 1.0 } )
</source>
 
The figure below shows the SDSS contours overlaid on our 6cm image (after fiddling with the
colormap shift/slope for the EVLA raster image).
 
[[Image:viewSN2010FZ_spw0to11_mfs2tt0plusSDSS.png|400px|thumb|center|6cm EVLA raster plus SDSS i-band contours]]
 
Likewise, we can plot the SDSS image as a raster and overlay EVLA 6cm contours:
 
<source lang="python">
# In CASA
imview(raster={ 'file' : 'NGC_2967_UGC_5180_IRAS_09394+0033-i.fits',
                'scaling' : -2.0,
                'range' : [0,10] },
      contour = { 'file' : 'imgSN2010FZ10s_spw0to11_mfs2_clean1280.image.tt0',
                  'levels' : [0.04, 0.08, 0.16, 0.32, 0.64, 1.28, 2.56],
                  'base' : 0.0,
                  'unit' : 0.001 },
      zoom = { 'blc' : [397,300],
                'trc' : [1567,1231] } )
</source>
 
This is shown in the figure below.  Is the compact 6cm emission in upper left associated with a
spiral arm?
 
[[Image:viewSN2010FZ_spw0to11_SDSSiplusEVLA6cm.png|400px|thumb|center|SDSS i-band raster plus EVLA 6cm contours]]


== What to do next: some exercises for the user ==
== What to do next: some exercises for the user ==
Line 1,806: Line 1,959:


# Use self-calibration to improve the data and re-clean to make a better image.  See [http://casaguides.nrao.edu/index.php?title=WorkshopSelfcal_(Caltech) this tutorial] for more information on self-calibration.
# Use self-calibration to improve the data and re-clean to make a better image.  See [http://casaguides.nrao.edu/index.php?title=WorkshopSelfcal_(Caltech) this tutorial] for more information on self-calibration.
# Use multi-scale clean by adding non-zero scales to the <tt>multiscale</tt> parameter.
# Investigate the data further to see if any more flagging is needed.
# Image the calibrators.  What sort of dynamic range can you get on them?  Is self-calibration needed (and if so what dynamic range do you get when you use it)?
# Image the calibrators.  What sort of dynamic range can you get on them?  Is self-calibration needed (and if so what dynamic range do you get when you use it)?
# Try the <tt>testautoflag</tt> task (in 3.3.0 and later) to automatically flag RFI from the upper sideband.  There is more information on running <tt>testautoflag</tt> in [http://casaguides.nrao.edu/index.php?title=EVLA_Wide-Band_Wide-Field_Imaging:_G55.7_3.4_(Caltech) this tutorial].
# Try the <tt>rflag</tt> algorithm in the flagdata task to automatically flag bad data based on the statistics of the data (though there is not much left, really).  There is more information on running the <tt>rflag</tt> algorithm in [http://casaguides.nrao.edu/index.php?title=EVLA_Wide-Band_Wide-Field_Imaging:_G55.7_3.4 this tutorial].


== Credits ==
== Credits ==
The EVLA data was taken by A. Soderberg et al. as part of project AS1015. See
[https://science.nrao.edu/enews/3.8/index.shtml#evlanoise NRAO eNews 3.8] (1-Sep-2010) for more on this result.


<blockquote><i>
<blockquote><i>
The Expanded Very Large Array (EVLA) is a partnership of the United States, Canada, and Mexico. The EVLA is funded in the United States by the National Science Foundation, in Canada by the National Research Council, and in Mexico by the Comisión Nacional de Investigación Científica y Tecnológica (CONICyT).
The Jansky Very Large Array (VLA) is a partnership of the United States, Canada, and Mexico. The VLA is funded in the United States by the National Science Foundation, in Canada by the National Research Council, and in Mexico by the Comisión Nacional de Investigación Científica y Tecnológica (CONICyT).
</i></blockquote>
</i></blockquote>


<blockquote><i>
<blockquote><i>
The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc.
The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc.
</i></blockquote>
SDSS image courtesy David Hogg & Michael Blanton, private communication.  Data comes from
SDSS DR7, see [http://adsabs.harvard.edu/abs/2009ApJS..182..543A Abazajian et. al 2009].
<blockquote><i>
Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the U.S. Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is [http://www.sdss.org/].
</i></blockquote>
<blockquote><i>
The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington.
</i></blockquote>
</i></blockquote>


{{Checked 4.2.0}}
{{Checked 4.2.0}}

Revision as of 19:59, 10 February 2014

This is an advanced Jansky VLA data reduction tutorial that calibrates and images a 3-bit dataset.

This CASA Guide is for CASA version 4.2.0.

Overview

This article describes the calibration and imaging of the protostar G192.16-3.84. The data were taken in Ka-band using the VLA's 3-bit samplers and widely-spaced basebands centered at 29 and 36.5 GHz. Each baseband has over 4 GHz of bandwidth comprised of 32 128-MHz spectral windows. In this tutorial, we will examine, flag, and calibrate the data, including the corrections for the requantizer gains (which are necessary for 3-bit data calibration and harmless on 8-bit data). We will then image and analyze the calibrated data, using wideband imaging techniques.

This is a more advanced tutorial, so if you are a relative novice, it is strongly recommended that you start with the EVLA Continuum Tutorial 3C391 (at least read it through) before proceeding with this tutorial.

In addition, on the MainPage of the CASA Guides you can find these helpful pages:

In this tutorial we will be invoking the tasks as function calls. You can cut and paste these to your casapy session. We also recommend that you copy all the commands you use, with any relevant commentary, to a text file. This is very good practice when tackling large datasets. If you wish, you can use the Script Extractor to create a file with the tutorial commands, which can subsequently be edited and annotated as desired.

Occasionally we will be setting Python variables (e.g., as lists for flags) outside the function call so make sure you set those before running the task command. Note that when you call a CASA task as a function, any task parameters that are not set in the function call will be used with their default values. This means they will not use values you set in any previous calls or outside the call. See Getting_Started_in_CASA#Task_Execution for more on calling tasks and setting parameters in the scripting interface.

NOTE: If you find that the figures on the right margin of the browser window overlap the text too much and make reading difficult, you can adjust the width of the browser window.

Obtaining the Data

The data for this tutorial were taken with the VLA during its commissioning phase. They comprise the scheduling block (SB) TVER0004.sb14459364.eb14492359.56295.26287841435, which was run on 2013-01-03 from 6:18 to 7:47 UT (its raw size is 57.04 GB).

The data can be downloaded directly from http://casa.nrao.edu/Data/EVLA/G192/G192_6s.ms.tar.gz (dataset size: 18 GB)

Your first step will be to unzip and untar the file in a terminal (before you start CASA): 

tar -xzvf G192_6s.ms.tar.gz

If you are brave enough, you can also get the data directly from the VLA archive. Go to the NRAO Science Data Archive, and search for "TVER0004.sb14459364" in the Archive File ID field. Then select the dataset and choose a time-averaging value of 6 seconds. (Although the data were taken in A-configuration, we will not be imaging outside of the center of the field, so we aren't too worried about time-average smearing and will take advantage of averaging to reduce the dataset size.) Also select the "Create tar file" option.

In addition, only the fields used for analysis and observation are included in the downloadable file. This can be accomplished using the split task in CASA: 

# In CASA
split('TVER0004.sb14459364.eb14492359.56295.26287841435.ms', outputvis='G192_6s.ms', \
      datacolumn='all', field='3,6,7,10', keepflags=False, spw='2~65')

(If you're downloading from the archive and feeling ambitious, you could also select only the scans with fields 3, 6, 7, and 10 in the "Select scans for MS or AIPS FITS" box.) This will create a file equivalent to what is used at the start of this tutorial.

Finally, you will need to modify some information in the SOURCE and FIELD tables of the measurement set (this has already been done for you in the file available for download, but must be done by hand if obtaining from the archive). Follow the instructions here to make these changes.

Starting CASA

To start CASA, type: 

casapy

This will run a script to initialize CASA, setting paths appropriately. It will also start writing to a file called ipython-<unique-stamp>.log, which will contain a record of all the text you enter at the CASA prompt, as well as casapy-<unique-stamp>.log, which will contain all the messages that are printed to the CASA logger window. It is recommended that you keep your log files in tact - you may need them to remind you of the last step you completed in your data reduction! (It is also a good idea to include your log files when submitting a help desk ticket).

Once CASA has started, a logger window will appear. Note that you can rescale this window or change the font size as desired (the latter is under "View").

Examining the Measurement Set (MS)

We use listobs to summarize our MS: 

# In CASA
listobs('G192_6s.ms', listfile='G192_listobs.txt')

This will write the output to a file called G192_listobs.txt, which we can print to the terminal using the cat command: 

# In CASA
cat G192_listobs.txt

================================================================================
           MeasurementSet Name:  /lustre/knyland/casa_guides/protostar/G192_6s.ms      MS Version 2
================================================================================
   Observer: Dr. Debra Shepherd     Project: uid://evla/pdb/7303457  
Observation: EVLA
Data records: 10061248       Total integration time = 4557 seconds
   Observed from   03-Jan-2013/06:31:51.0   to   03-Jan-2013/07:47:48.0 (UTC)

   ObservationID = 0         ArrayID = 0
  Date        Timerange (UTC)          Scan  FldId FieldName             nRows     SpwIds   Average Interval(s)    ScanIntent
  03-Jan-2013/06:31:48.0 - 06:36:42.0     6      0 3C147                  1019200  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 5.94, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [CALIBRATE_FLUX#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              06:46:15.0 - 06:46:54.0    10      1 gcal-J0603+174          145600  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57, 5.57] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              06:47:09.0 - 06:47:54.0    11      2 G192.16-3.84            163200  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65, 5.65] [OBSERVE_TARGET#UNSPECIFIED]
              06:48:06.0 - 06:48:39.0    12      1 gcal-J0603+174          124800  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              06:48:51.0 - 06:49:39.0    13      2 G192.16-3.84            166400  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [OBSERVE_TARGET#UNSPECIFIED]
              06:49:51.0 - 06:50:24.0    14      1 gcal-J0603+174          124800  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              06:50:36.0 - 06:51:24.0    15      2 G192.16-3.84            166400  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [OBSERVE_TARGET#UNSPECIFIED]
              06:51:36.0 - 06:52:09.0    16      1 gcal-J0603+174          124800  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              06:52:19.5 - 06:53:09.0    17      2 G192.16-3.84            166400  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [OBSERVE_TARGET#UNSPECIFIED]
              06:53:21.0 - 06:53:54.0    18      1 gcal-J0603+174          124800  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              06:54:06.0 - 06:54:54.0    19      2 G192.16-3.84            166400  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [OBSERVE_TARGET#UNSPECIFIED]
              06:55:06.0 - 06:55:39.0    20      1 gcal-J0603+174          124800  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              06:55:51.0 - 06:56:39.0    21      2 G192.16-3.84            166400  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [OBSERVE_TARGET#UNSPECIFIED]
              06:56:51.0 - 06:57:24.0    22      1 gcal-J0603+174          124800  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              06:57:36.0 - 06:58:24.0    23      2 G192.16-3.84            166400  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [OBSERVE_TARGET#UNSPECIFIED]
              06:58:36.0 - 06:59:12.0    24      1 gcal-J0603+174          124800  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              06:59:21.0 - 07:00:12.0    25      2 G192.16-3.84            187200  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67] [OBSERVE_TARGET#UNSPECIFIED]
              07:00:19.5 - 07:00:57.0    26      1 gcal-J0603+174          124800  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              07:01:06.0 - 07:01:57.0    27      2 G192.16-3.84            187200  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67] [OBSERVE_TARGET#UNSPECIFIED]
              07:02:03.0 - 07:02:42.0    28      1 gcal-J0603+174          125184  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99, 5.99] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              07:02:48.0 - 07:03:36.0    29      2 G192.16-3.84            166400  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [OBSERVE_TARGET#UNSPECIFIED]
              07:03:48.0 - 07:04:21.0    30      1 gcal-J0603+174          124800  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              07:04:33.0 - 07:05:21.0    31      2 G192.16-3.84            166400  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [OBSERVE_TARGET#UNSPECIFIED]
              07:05:33.0 - 07:06:06.0    32      1 gcal-J0603+174          124800  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              07:06:18.0 - 07:07:06.0    33      2 G192.16-3.84            166400  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [OBSERVE_TARGET#UNSPECIFIED]
              07:07:18.0 - 07:07:51.0    34      1 gcal-J0603+174          124800  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              07:08:03.0 - 07:08:51.0    35      2 G192.16-3.84            166400  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [OBSERVE_TARGET#UNSPECIFIED]
              07:09:03.0 - 07:09:36.0    36      1 gcal-J0603+174          124800  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              07:09:48.0 - 07:10:36.0    37      2 G192.16-3.84            166400  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [OBSERVE_TARGET#UNSPECIFIED]
              07:10:46.5 - 07:11:21.0    38      1 gcal-J0603+174          123200  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49, 5.49] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              07:11:33.0 - 07:12:21.0    39      2 G192.16-3.84            166400  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [OBSERVE_TARGET#UNSPECIFIED]
              07:12:33.0 - 07:13:06.0    40      1 gcal-J0603+174          124800  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              07:13:18.0 - 07:14:06.0    41      2 G192.16-3.84            166400  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [OBSERVE_TARGET#UNSPECIFIED]
              07:14:16.5 - 07:14:51.0    42      1 gcal-J0603+174          124800  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              07:15:01.5 - 07:15:51.0    43      2 G192.16-3.84            166400  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [OBSERVE_TARGET#UNSPECIFIED]
              07:16:03.0 - 07:16:36.0    44      1 gcal-J0603+174          124800  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              07:16:48.0 - 07:17:39.0    45      2 G192.16-3.84            187200  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67] [OBSERVE_TARGET#UNSPECIFIED]
              07:17:48.0 - 07:18:24.0    46      1 gcal-J0603+174          124800  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              07:18:33.0 - 07:19:24.0    47      2 G192.16-3.84            187200  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67, 5.67] [OBSERVE_TARGET#UNSPECIFIED]
              07:19:30.0 - 07:20:09.0    48      1 gcal-J0603+174          124864  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              07:20:18.0 - 07:21:06.0    49      2 G192.16-3.84            166400  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [OBSERVE_TARGET#UNSPECIFIED]
              07:21:15.0 - 07:21:48.0    50      1 gcal-J0603+174          124800  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              07:22:00.0 - 07:22:48.0    51      2 G192.16-3.84            166400  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [OBSERVE_TARGET#UNSPECIFIED]
              07:23:00.0 - 07:23:33.0    52      1 gcal-J0603+174          124800  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              07:23:45.0 - 07:24:33.0    53      2 G192.16-3.84            166400  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [OBSERVE_TARGET#UNSPECIFIED]
              07:24:45.0 - 07:25:18.0    54      1 gcal-J0603+174          124800  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              07:25:30.0 - 07:26:18.0    55      2 G192.16-3.84            166400  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [OBSERVE_TARGET#UNSPECIFIED]
              07:26:30.0 - 07:27:03.0    56      1 gcal-J0603+174          124800  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              07:27:15.0 - 07:28:03.0    57      2 G192.16-3.84            166400  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [OBSERVE_TARGET#UNSPECIFIED]
              07:28:15.0 - 07:28:48.0    58      1 gcal-J0603+174          124800  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              07:29:00.0 - 07:29:48.0    59      2 G192.16-3.84            166400  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [OBSERVE_TARGET#UNSPECIFIED]
              07:30:00.0 - 07:30:33.0    60      1 gcal-J0603+174          124800  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5] [CALIBRATE_AMPLI#UNSPECIFIED, CALIBRATE_PHASE#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
              07:40:27.0 - 07:47:51.0    64      3 3c84-J0319+413         1537600  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]  [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [CALIBRATE_BANDPASS#UNSPECIFIED, OBSERVE_TARGET#UNSPECIFIED]
           (nRows = Total number of rows per scan) 
Fields: 4
  ID   Code Name                RA               Decl           Epoch   SrcId      nRows
  0    E    3C147               05:42:36.137916 +49.51.07.23356 J2000   0        1019200
  1    D    gcal-J0603+174      06:03:09.130269 +17.42.16.81070 J2000   1        3264448
  2    NONE G192.16-3.84        05:58:13.540000 +16.31.58.30001 J2000   2        4240000
  3    F    3c84-J0319+413      03:19:48.160102 +41.30.42.10305 J2000   3        1537600
Spectral Windows:  (64 unique spectral windows and 1 unique polarization setups)
  SpwID  Name            #Chans   Frame   Ch0(MHz)  ChanWid(kHz)  TotBW(kHz) BBC Num  Corrs          
  0      EVLA_KA#A1C1#2     128   TOPO   34476.000      1000.000    128000.0      10  RR  LL
  1      EVLA_KA#A1C1#3     128   TOPO   34604.000      1000.000    128000.0      10  RR  LL
  2      EVLA_KA#A1C1#4     128   TOPO   34732.000      1000.000    128000.0      10  RR  LL
  3      EVLA_KA#A1C1#5     128   TOPO   34860.000      1000.000    128000.0      10  RR  LL
  4      EVLA_KA#A1C1#6     128   TOPO   34988.000      1000.000    128000.0      10  RR  LL
  5      EVLA_KA#A1C1#7     128   TOPO   35116.000      1000.000    128000.0      10  RR  LL
  6      EVLA_KA#A1C1#8     128   TOPO   35244.000      1000.000    128000.0      10  RR  LL
  7      EVLA_KA#A1C1#9     128   TOPO   35372.000      1000.000    128000.0      10  RR  LL
  8      EVLA_KA#A1C1#10    128   TOPO   35500.000      1000.000    128000.0      10  RR  LL
  9      EVLA_KA#A1C1#11    128   TOPO   35628.000      1000.000    128000.0      10  RR  LL
  10     EVLA_KA#A1C1#12    128   TOPO   35756.000      1000.000    128000.0      10  RR  LL
  11     EVLA_KA#A1C1#13    128   TOPO   35884.000      1000.000    128000.0      10  RR  LL
  12     EVLA_KA#A1C1#14    128   TOPO   36012.000      1000.000    128000.0      10  RR  LL
  13     EVLA_KA#A1C1#15    128   TOPO   36140.000      1000.000    128000.0      10  RR  LL
  14     EVLA_KA#A1C1#16    128   TOPO   36268.000      1000.000    128000.0      10  RR  LL
  15     EVLA_KA#A1C1#17    128   TOPO   36396.000      1000.000    128000.0      10  RR  LL
  16     EVLA_KA#A2C2#18    128   TOPO   36476.000      1000.000    128000.0      11  RR  LL
  17     EVLA_KA#A2C2#19    128   TOPO   36604.000      1000.000    128000.0      11  RR  LL
  18     EVLA_KA#A2C2#20    128   TOPO   36732.000      1000.000    128000.0      11  RR  LL
  19     EVLA_KA#A2C2#21    128   TOPO   36860.000      1000.000    128000.0      11  RR  LL
  20     EVLA_KA#A2C2#22    128   TOPO   36988.000      1000.000    128000.0      11  RR  LL
  21     EVLA_KA#A2C2#23    128   TOPO   37116.000      1000.000    128000.0      11  RR  LL
  22     EVLA_KA#A2C2#24    128   TOPO   37244.000      1000.000    128000.0      11  RR  LL
  23     EVLA_KA#A2C2#25    128   TOPO   37372.000      1000.000    128000.0      11  RR  LL
  24     EVLA_KA#A2C2#26    128   TOPO   37500.000      1000.000    128000.0      11  RR  LL
  25     EVLA_KA#A2C2#27    128   TOPO   37628.000      1000.000    128000.0      11  RR  LL
  26     EVLA_KA#A2C2#28    128   TOPO   37756.000      1000.000    128000.0      11  RR  LL
  27     EVLA_KA#A2C2#29    128   TOPO   37884.000      1000.000    128000.0      11  RR  LL
  28     EVLA_KA#A2C2#30    128   TOPO   38012.000      1000.000    128000.0      11  RR  LL
  29     EVLA_KA#A2C2#31    128   TOPO   38140.000      1000.000    128000.0      11  RR  LL
  30     EVLA_KA#A2C2#32    128   TOPO   38268.000      1000.000    128000.0      11  RR  LL
  31     EVLA_KA#A2C2#33    128   TOPO   38396.000      1000.000    128000.0      11  RR  LL
  32     EVLA_KA#B1D1#34    128   TOPO   26976.000      1000.000    128000.0      13  RR  LL
  33     EVLA_KA#B1D1#35    128   TOPO   27104.000      1000.000    128000.0      13  RR  LL
  34     EVLA_KA#B1D1#36    128   TOPO   27232.000      1000.000    128000.0      13  RR  LL
  35     EVLA_KA#B1D1#37    128   TOPO   27360.000      1000.000    128000.0      13  RR  LL
  36     EVLA_KA#B1D1#38    128   TOPO   27488.000      1000.000    128000.0      13  RR  LL
  37     EVLA_KA#B1D1#39    128   TOPO   27616.000      1000.000    128000.0      13  RR  LL
  38     EVLA_KA#B1D1#40    128   TOPO   27744.000      1000.000    128000.0      13  RR  LL
  39     EVLA_KA#B1D1#41    128   TOPO   27872.000      1000.000    128000.0      13  RR  LL
  40     EVLA_KA#B1D1#42    128   TOPO   28000.000      1000.000    128000.0      13  RR  LL
  41     EVLA_KA#B1D1#43    128   TOPO   28128.000      1000.000    128000.0      13  RR  LL
  42     EVLA_KA#B1D1#44    128   TOPO   28256.000      1000.000    128000.0      13  RR  LL
  43     EVLA_KA#B1D1#45    128   TOPO   28384.000      1000.000    128000.0      13  RR  LL
  44     EVLA_KA#B1D1#46    128   TOPO   28512.000      1000.000    128000.0      13  RR  LL
  45     EVLA_KA#B1D1#47    128   TOPO   28640.000      1000.000    128000.0      13  RR  LL
  46     EVLA_KA#B1D1#48    128   TOPO   28768.000      1000.000    128000.0      13  RR  LL
  47     EVLA_KA#B1D1#49    128   TOPO   28896.000      1000.000    128000.0      13  RR  LL
  48     EVLA_KA#B2D2#50    128   TOPO   28976.000      1000.000    128000.0      14  RR  LL
  49     EVLA_KA#B2D2#51    128   TOPO   29104.000      1000.000    128000.0      14  RR  LL
  50     EVLA_KA#B2D2#52    128   TOPO   29232.000      1000.000    128000.0      14  RR  LL
  51     EVLA_KA#B2D2#53    128   TOPO   29360.000      1000.000    128000.0      14  RR  LL
  52     EVLA_KA#B2D2#54    128   TOPO   29488.000      1000.000    128000.0      14  RR  LL
  53     EVLA_KA#B2D2#55    128   TOPO   29616.000      1000.000    128000.0      14  RR  LL
  54     EVLA_KA#B2D2#56    128   TOPO   29744.000      1000.000    128000.0      14  RR  LL
  55     EVLA_KA#B2D2#57    128   TOPO   29872.000      1000.000    128000.0      14  RR  LL
  56     EVLA_KA#B2D2#58    128   TOPO   30000.000      1000.000    128000.0      14  RR  LL
  57     EVLA_KA#B2D2#59    128   TOPO   30128.000      1000.000    128000.0      14  RR  LL
  58     EVLA_KA#B2D2#60    128   TOPO   30256.000      1000.000    128000.0      14  RR  LL
  59     EVLA_KA#B2D2#61    128   TOPO   30384.000      1000.000    128000.0      14  RR  LL
  60     EVLA_KA#B2D2#62    128   TOPO   30512.000      1000.000    128000.0      14  RR  LL
  61     EVLA_KA#B2D2#63    128   TOPO   30640.000      1000.000    128000.0      14  RR  LL
  62     EVLA_KA#B2D2#64    128   TOPO   30768.000      1000.000    128000.0      14  RR  LL
  63     EVLA_KA#B2D2#65    128   TOPO   30896.000      1000.000    128000.0      14  RR  LL
Sources: 256
  ID   Name                SpwId RestFreq(MHz)  SysVel(km/s) 
  0    3C147               0     -              -            
  0    3C147               1     -              -            
  0    3C147               2     -              -            
  0    3C147               3     -              -            
  0    3C147               4     -              -            
  0    3C147               5     -              -            
  0    3C147               6     -              -            
  0    3C147               7     -              -            
  0    3C147               8     -              -            
  0    3C147               9     -              -            
  0    3C147               10    -              -            
  0    3C147               11    -              -            
  0    3C147               12    -              -            
  0    3C147               13    -              -            
  0    3C147               14    -              -            
  0    3C147               15    -              -            
  0    3C147               16    -              -            
  0    3C147               17    -              -            
  0    3C147               18    -              -            
  0    3C147               19    -              -            
  0    3C147               20    -              -            
  0    3C147               21    -              -            
  0    3C147               22    -              -            
  0    3C147               23    -              -            
  0    3C147               24    -              -            
  0    3C147               25    -              -            
  0    3C147               26    -              -            
  0    3C147               27    -              -            
  0    3C147               28    -              -            
  0    3C147               29    -              -            
  0    3C147               30    -              -            
  0    3C147               31    -              -            
  0    3C147               32    -              -            
  0    3C147               33    -              -            
  0    3C147               34    -              -            
  0    3C147               35    -              -            
  0    3C147               36    -              -            
  0    3C147               37    -              -            
  0    3C147               38    -              -            
  0    3C147               39    -              -            
  0    3C147               40    -              -            
  0    3C147               41    -              -            
  0    3C147               42    -              -            
  0    3C147               43    -              -            
  0    3C147               44    -              -            
  0    3C147               45    -              -            
  0    3C147               46    -              -            
  0    3C147               47    -              -            
  0    3C147               48    -              -            
  0    3C147               49    -              -            
  0    3C147               50    -              -            
  0    3C147               51    -              -            
  0    3C147               52    -              -            
  0    3C147               53    -              -            
  0    3C147               54    -              -            
  0    3C147               55    -              -            
  0    3C147               56    -              -            
  0    3C147               57    -              -            
  0    3C147               58    -              -            
  0    3C147               59    -              -            
  0    3C147               60    -              -            
  0    3C147               61    -              -            
  0    3C147               62    -              -            
  0    3C147               63    -              -            
  1    gcal-J0603+174      0     -              -            
  1    gcal-J0603+174      1     -              -            
  1    gcal-J0603+174      2     -              -            
  1    gcal-J0603+174      3     -              -            
  1    gcal-J0603+174      4     -              -            
  1    gcal-J0603+174      5     -              -            
  1    gcal-J0603+174      6     -              -            
  1    gcal-J0603+174      7     -              -            
  1    gcal-J0603+174      8     -              -            
  1    gcal-J0603+174      9     -              -            
  1    gcal-J0603+174      10    -              -            
  1    gcal-J0603+174      11    -              -            
  1    gcal-J0603+174      12    -              -            
  1    gcal-J0603+174      13    -              -            
  1    gcal-J0603+174      14    -              -            
  1    gcal-J0603+174      15    -              -            
  1    gcal-J0603+174      16    -              -            
  1    gcal-J0603+174      17    -              -            
  1    gcal-J0603+174      18    -              -            
  1    gcal-J0603+174      19    -              -            
  1    gcal-J0603+174      20    -              -            
  1    gcal-J0603+174      21    -              -            
  1    gcal-J0603+174      22    -              -            
  1    gcal-J0603+174      23    -              -            
  1    gcal-J0603+174      24    -              -            
  1    gcal-J0603+174      25    -              -            
  1    gcal-J0603+174      26    -              -            
  1    gcal-J0603+174      27    -              -            
  1    gcal-J0603+174      28    -              -            
  1    gcal-J0603+174      29    -              -            
  1    gcal-J0603+174      30    -              -            
  1    gcal-J0603+174      31    -              -            
  1    gcal-J0603+174      32    -              -            
  1    gcal-J0603+174      33    -              -            
  1    gcal-J0603+174      34    -              -            
  1    gcal-J0603+174      35    -              -            
  1    gcal-J0603+174      36    -              -            
  1    gcal-J0603+174      37    -              -            
  1    gcal-J0603+174      38    -              -            
  1    gcal-J0603+174      39    -              -            
  1    gcal-J0603+174      40    -              -            
  1    gcal-J0603+174      41    -              -            
  1    gcal-J0603+174      42    -              -            
  1    gcal-J0603+174      43    -              -            
  1    gcal-J0603+174      44    -              -            
  1    gcal-J0603+174      45    -              -            
  1    gcal-J0603+174      46    -              -            
  1    gcal-J0603+174      47    -              -            
  1    gcal-J0603+174      48    -              -            
  1    gcal-J0603+174      49    -              -            
  1    gcal-J0603+174      50    -              -            
  1    gcal-J0603+174      51    -              -            
  1    gcal-J0603+174      52    -              -            
  1    gcal-J0603+174      53    -              -            
  1    gcal-J0603+174      54    -              -            
  1    gcal-J0603+174      55    -              -            
  1    gcal-J0603+174      56    -              -            
  1    gcal-J0603+174      57    -              -            
  1    gcal-J0603+174      58    -              -            
  1    gcal-J0603+174      59    -              -            
  1    gcal-J0603+174      60    -              -            
  1    gcal-J0603+174      61    -              -            
  1    gcal-J0603+174      62    -              -            
  1    gcal-J0603+174      63    -              -            
  2    G192.16-3.84        0     -              -            
  2    G192.16-3.84        1     -              -            
  2    G192.16-3.84        2     -              -            
  2    G192.16-3.84        3     -              -            
  2    G192.16-3.84        4     -              -            
  2    G192.16-3.84        5     -              -            
  2    G192.16-3.84        6     -              -            
  2    G192.16-3.84        7     -              -            
  2    G192.16-3.84        8     -              -            
  2    G192.16-3.84        9     -              -            
  2    G192.16-3.84        10    -              -            
  2    G192.16-3.84        11    -              -            
  2    G192.16-3.84        12    -              -            
  2    G192.16-3.84        13    -              -            
  2    G192.16-3.84        14    -              -            
  2    G192.16-3.84        15    -              -            
  2    G192.16-3.84        16    -              -            
  2    G192.16-3.84        17    -              -            
  2    G192.16-3.84        18    -              -            
  2    G192.16-3.84        19    -              -            
  2    G192.16-3.84        20    -              -            
  2    G192.16-3.84        21    -              -            
  2    G192.16-3.84        22    -              -            
  2    G192.16-3.84        23    -              -            
  2    G192.16-3.84        24    -              -            
  2    G192.16-3.84        25    -              -            
  2    G192.16-3.84        26    -              -            
  2    G192.16-3.84        27    -              -            
  2    G192.16-3.84        28    -              -            
  2    G192.16-3.84        29    -              -            
  2    G192.16-3.84        30    -              -            
  2    G192.16-3.84        31    -              -            
  2    G192.16-3.84        32    -              -            
  2    G192.16-3.84        33    -              -            
  2    G192.16-3.84        34    -              -            
  2    G192.16-3.84        35    -              -            
  2    G192.16-3.84        36    -              -            
  2    G192.16-3.84        37    -              -            
  2    G192.16-3.84        38    -              -            
  2    G192.16-3.84        39    -              -            
  2    G192.16-3.84        40    -              -            
  2    G192.16-3.84        41    -              -            
  2    G192.16-3.84        42    -              -            
  2    G192.16-3.84        43    -              -            
  2    G192.16-3.84        44    -              -            
  2    G192.16-3.84        45    -              -            
  2    G192.16-3.84        46    -              -            
  2    G192.16-3.84        47    -              -            
  2    G192.16-3.84        48    -              -            
  2    G192.16-3.84        49    -              -            
  2    G192.16-3.84        50    -              -            
  2    G192.16-3.84        51    -              -            
  2    G192.16-3.84        52    -              -            
  2    G192.16-3.84        53    -              -            
  2    G192.16-3.84        54    -              -            
  2    G192.16-3.84        55    -              -            
  2    G192.16-3.84        56    -              -            
  2    G192.16-3.84        57    -              -            
  2    G192.16-3.84        58    -              -            
  2    G192.16-3.84        59    -              -            
  2    G192.16-3.84        60    -              -            
  2    G192.16-3.84        61    -              -            
  2    G192.16-3.84        62    -              -            
  2    G192.16-3.84        63    -              -            
  3    3c84-J0319+413      0     -              -            
  3    3c84-J0319+413      1     -              -            
  3    3c84-J0319+413      2     -              -            
  3    3c84-J0319+413      3     -              -            
  3    3c84-J0319+413      4     -              -            
  3    3c84-J0319+413      5     -              -            
  3    3c84-J0319+413      6     -              -            
  3    3c84-J0319+413      7     -              -            
  3    3c84-J0319+413      8     -              -            
  3    3c84-J0319+413      9     -              -            
  3    3c84-J0319+413      10    -              -            
  3    3c84-J0319+413      11    -              -            
  3    3c84-J0319+413      12    -              -            
  3    3c84-J0319+413      13    -              -            
  3    3c84-J0319+413      14    -              -            
  3    3c84-J0319+413      15    -              -            
  3    3c84-J0319+413      16    -              -            
  3    3c84-J0319+413      17    -              -            
  3    3c84-J0319+413      18    -              -            
  3    3c84-J0319+413      19    -              -            
  3    3c84-J0319+413      20    -              -            
  3    3c84-J0319+413      21    -              -            
  3    3c84-J0319+413      22    -              -            
  3    3c84-J0319+413      23    -              -            
  3    3c84-J0319+413      24    -              -            
  3    3c84-J0319+413      25    -              -            
  3    3c84-J0319+413      26    -              -            
  3    3c84-J0319+413      27    -              -            
  3    3c84-J0319+413      28    -              -            
  3    3c84-J0319+413      29    -              -            
  3    3c84-J0319+413      30    -              -            
  3    3c84-J0319+413      31    -              -            
  3    3c84-J0319+413      32    -              -            
  3    3c84-J0319+413      33    -              -            
  3    3c84-J0319+413      34    -              -            
  3    3c84-J0319+413      35    -              -            
  3    3c84-J0319+413      36    -              -            
  3    3c84-J0319+413      37    -              -            
  3    3c84-J0319+413      38    -              -            
  3    3c84-J0319+413      39    -              -            
  3    3c84-J0319+413      40    -              -            
  3    3c84-J0319+413      41    -              -            
  3    3c84-J0319+413      42    -              -            
  3    3c84-J0319+413      43    -              -            
  3    3c84-J0319+413      44    -              -            
  3    3c84-J0319+413      45    -              -            
  3    3c84-J0319+413      46    -              -            
  3    3c84-J0319+413      47    -              -            
  3    3c84-J0319+413      48    -              -            
  3    3c84-J0319+413      49    -              -            
  3    3c84-J0319+413      50    -              -            
  3    3c84-J0319+413      51    -              -            
  3    3c84-J0319+413      52    -              -            
  3    3c84-J0319+413      53    -              -            
  3    3c84-J0319+413      54    -              -            
  3    3c84-J0319+413      55    -              -            
  3    3c84-J0319+413      56    -              -            
  3    3c84-J0319+413      57    -              -            
  3    3c84-J0319+413      58    -              -            
  3    3c84-J0319+413      59    -              -            
  3    3c84-J0319+413      60    -              -            
  3    3c84-J0319+413      61    -              -            
  3    3c84-J0319+413      62    -              -            
  3    3c84-J0319+413      63    -              -            
Antennas: 26:
  ID   Name  Station   Diam.    Long.         Lat.                Offset from array center (m)                ITRF Geocentric coordinates (m)        
                                                                     East         North     Elevation               x               y               z
  0    ea01  N48       25.0 m   -107.37.38.1  +33.59.06.2       -855.2759     9405.9595      -25.9351 -1600374.885000 -5036704.201000  3562667.881900
  1    ea02  N56       25.0 m   -107.37.47.9  +34.00.38.4      -1105.2071    12254.3069      -34.2426 -1600128.383400 -5035104.146500  3565024.672100
  2    ea03  N16       25.0 m   -107.37.10.9  +33.54.48.0       -155.8511     1426.6436       -9.3827 -1601061.956000 -5041175.880700  3556058.037600
  3    ea05  W08       25.0 m   -107.37.21.6  +33.53.53.0       -432.1184     -272.1472       -1.5070 -1601614.092200 -5042001.650900  3554652.508900
  4    ea06  N32       25.0 m   -107.37.22.0  +33.56.33.6       -441.7237     4689.9748      -16.9332 -1600781.042100 -5039347.435200  3558761.533000
  5    ea07  E40       25.0 m   -107.32.35.4  +33.52.16.9       6908.8279    -3240.7316       39.0057 -1595124.924100 -5045829.461500  3552210.685200
  6    ea09  E24       25.0 m   -107.35.13.4  +33.53.18.1       2858.1754    -1349.1257       13.7290 -1598663.097500 -5043581.389700  3553767.027800
  7    ea10  E32       25.0 m   -107.34.01.5  +33.52.50.3       4701.6588    -2209.7063       25.2191 -1597053.120700 -5044604.691600  3553059.009300
  8    ea11  W56       25.0 m   -107.44.26.7  +33.49.54.6     -11333.2153    -7637.6824       15.3542 -1613255.404300 -5042613.085000  3548545.901400
  9    ea12  E08       25.0 m   -107.36.48.9  +33.53.55.1        407.8285     -206.0065       -3.2272 -1600801.926000 -5042219.366500  3554706.448200
  10   ea13  W24       25.0 m   -107.38.49.0  +33.53.04.0      -2673.3434    -1784.5870       10.4960 -1604008.742800 -5042135.827600  3553403.728800
  11   ea14  W16       25.0 m   -107.37.57.4  +33.53.33.0      -1348.7083     -890.6269        1.3068 -1602592.853600 -5042055.005300  3554140.703900
  12   ea15  W72       25.0 m   -107.48.24.0  +33.47.41.2     -17419.4730   -11760.2869       14.9578 -1619757.314900 -5042937.673700  3545120.385300
  13   ea16  N08       25.0 m   -107.37.07.5  +33.54.15.8        -68.9252      433.1901       -5.0683 -1601147.956700 -5041733.824100  3555235.952500
  14   ea17  E48       25.0 m   -107.30.56.1  +33.51.38.4       9456.5938    -4431.6366       37.9317 -1592894.088800 -5047229.121000  3551221.221100
  15   ea18  E72       25.0 m   -107.24.42.3  +33.49.18.0      19041.8754    -8769.2059        4.7234 -1584460.867200 -5052385.599300  3547599.997600
  16   ea19  W64       25.0 m   -107.46.20.1  +33.48.50.9     -14240.7600    -9606.2738       17.1055 -1616361.584300 -5042770.519200  3546911.442800
  17   ea20  N72       25.0 m   -107.38.10.5  +34.04.12.2      -1685.6775    18861.8403      -43.4734 -1599557.932000 -5031396.371000  3570494.760600
  18   ea21  E64       25.0 m   -107.27.00.1  +33.50.06.7      15507.6045    -7263.7280       67.1961 -1587600.190400 -5050575.873800  3548885.396600
  19   ea22  N24       25.0 m   -107.37.16.1  +33.55.37.7       -290.3745     2961.8582      -12.2374 -1600930.087700 -5040316.398500  3557330.387000
  20   ea23  N64       25.0 m   -107.37.58.7  +34.02.20.5      -1382.3750    15410.1463      -40.6373 -1599855.675100 -5033332.371000  3567636.622500
  21   ea24  W40       25.0 m   -107.41.13.5  +33.51.43.1      -6377.9740    -4286.7919        8.2191 -1607962.456900 -5042338.214500  3551324.943600
  22   ea25  W48       25.0 m   -107.42.44.3  +33.50.52.1      -8707.9407    -5861.7854       15.5265 -1610451.925400 -5042471.123100  3550021.056800
  23   ea26  W32       25.0 m   -107.39.54.8  +33.52.27.2      -4359.4561    -2923.1223       11.7579 -1605808.647100 -5042230.071500  3552459.203400
  24   ea27  E16       25.0 m   -107.36.09.8  +33.53.40.0       1410.0316     -673.4696       -0.7909 -1599926.110000 -5042772.967300  3554319.791200
  25   ea28  N40       25.0 m   -107.37.29.5  +33.57.44.4       -633.6167     6878.5984      -20.7748 -1600592.764000 -5038121.352000  3560574.847300

This task displays a lot of information about the MS. We can see that the observation was performed with the EVLA over an integration time of 4557 seconds (1.3 hours). The number of data records (10,061,248) is approximately equal to the number of baselines (N_antenna * [N_antenna - 1] / 2) X the number of integrations (observing time / time-average binning) X the number of spectral windows. For this observation, this is roughly 325 baselines (26X25/2) X 760 integrations (4557s total/6s avg) X 64 spectral windows = 15,808,000. Note that this is high by ~50%; this is because the "total time" reported is simply (start time) - (end time) of the MS, which includes periods of slewing, flagged data, and scans that were excluded from the final MS. Extra exercise: examine the MS using browsetable to see what a data record looks like (equivalent to a row, as displayed by this task).

The most useful parts of the listobs output are the scan, field, and spectral window listings. From the spectral window information, we can see that there are a total of 64 (0 through 63) spectral windows in this dataset, each with 128 channels, and that they are all at Ka-band (which spans 26.5 - 40.0 GHz).

The field listing shows four sources:

  • 3C147 (Field ID 0), the flux calibration source;
  • J0603+174 (1), used for calibrating the complex gains;
  • G192.16-3.84 (2), the science target; and
  • 3c84 (3), used for calibrating the spectral bandpass.

Note the rapid switching between G192 and J0603: this will help us accurately calculate and transfer the gain phase solutions for these high-frequency data. Note that the original MS also included reference pointing calibration scans at X-band, but since the pointing solutions were already applied during observing, we did not retain these scans (in the interest of limiting dataset size).

Flagging the MS

online flags plotted from flagcmd

The online flags, which are a record of known bad data produced by the VLA online system, were applied by the archive when it generated the MS. However, it's good to have a sense of what was deleted in this process. A record of the flags is stored in a table in the MS called FLAG_CMD. (In fact, the information for this table is actually a subdirectory within the MS; you can see this by listing the contents of G192_6s.ms.)

You can examine the commands stored in the FLAG_CMD table using flagcmd: 

# In CASA
flagcmd(vis='G192_6s.ms', inpmode='table', action='list', \
        useapplied=True)
  • useapplied=True: tells the task to list flags that have already been applied to the MS (which includes all online flags; otherwise, they would be ignored)

The flag information will be printed to the terminal (all 2870 rows). The majority of the flags are "ANTENNA_NOT_ON_SOURCE" -- most of these were generated as a result of the slewing required for the fast switching between G192 and the phase calibrator.

You can also plot the commands stored in the FLAG_CMD table: 

# In CASA
myrows = range(2868)
flagcmd(vis='G192_6s.ms', inpmode='table', action='plot', \
        useapplied=True, tablerows=myrows)

Note that for demonstration purposes, we have chosen to only plot the first 2868 rows. The last two rows are from flagging zeros in the data (caused by correlator errors) and data which have been flagged due to antenna shadowing. (Since the data were taken in the most widely spaced A-configuration, little if any data were likely affected by shadowing.) If you prefer you can omit the tablerows selection parameter and plot the last two rows as well -- you will just get lines at the bottom marked as "All" antennas for these flags.

By default, this will bring up a matplotlib plotter. You can have it plot to a PNG file instead: 

# In CASA
flagcmd(vis='G192_6s.ms', inpmode='table', action='plot', tablerows=myrows, 
        useapplied=True, plotfile='PlotG192_flagcmd_4.1.png')

The flags as plotted in the figure to the above right look normal. They are color-coded by REASON, and you see the ANTENNA_NOT_ON_SOURCE flags between scans, some FOCUS_ERROR flags here and there, and the occasional SUBREFLECTOR_ERROR flag also between scans (most likely after the receiver band changes that are necessary for reference pointing; when the subreflectors rotate to pick up the new feed on the ring, some are slower than others). You want to be wary of long blocks of unexpected flags, which might be false alarms and cause you to flag too much data. In that case, look at the data itself in plotms (see below for examples) to decide whether or not to apply all flags. (Note: for the dataset in this tutorial, we have already deleted all the flagged data to reduce the file size, so you won't be able to inspect the flagged data within the MS. To do so, you will need to download the original dataset from the NRAO Science Data Archive.)

plotants plotter

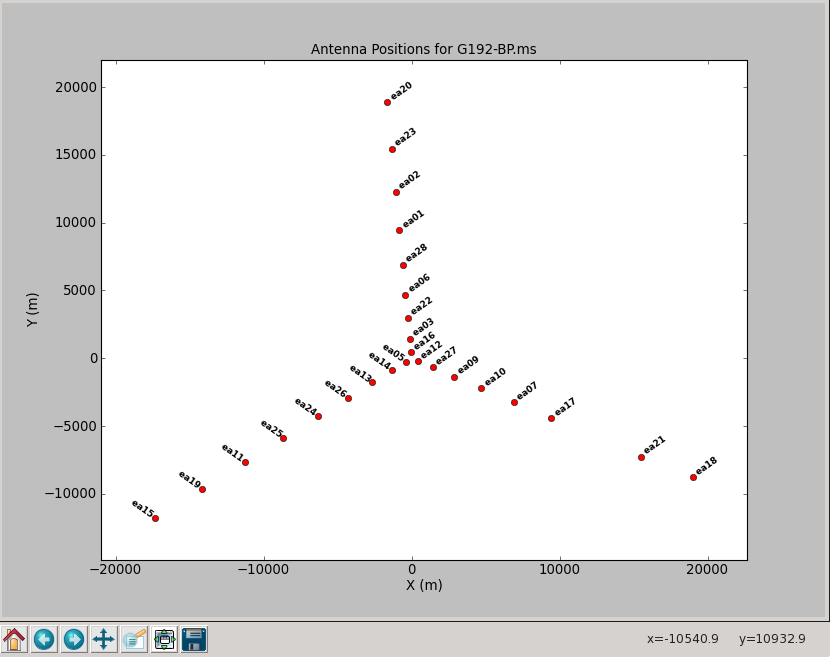
To plot up the antenna positions in the array: 

# In CASA
plotants('G192_6s.ms')

NOTE: if after this point (or any other) you get "table locks", which may occur erroneously and are sometimes triggered by plotting tasks, use clearstat to clear them: 

# In CASA
clearstat

Now we examine the MS looking for bad data to flag. We will use plotms to bring up an interactive GUI that will display 2-D Y vs. X style line plots. NOTE: We do not recommend using the editing/flagging features of plotms. It is very easy to mess up your data this way. Also, to improve speed we will be restricting the scope of plotting, so most box/flag operations would not get rid of all the bad data -- although they would appear to delete it, which is misleading.

We will instead use plotms to identify bad data and then use flagcmd to flag it. This will also allow full scripting of the flagging, which is ultimately the best way to keep track of what's been deleted. Given the large dataset sizes now being generated, reproducibility is extremely important. Imagine spending a day flagging your data, then a disk error corrupts the MS: it's imperative that you have an automated way to regenerate your work! This is also why we also encourage you to keep a running file with all the commands you use to process a dataset.

NOTE: If you need an introduction to plotms, see:

WARNING: The Flag button on the plotms GUI is close to other buttons you will be using, in particular the one that deletes boxes you have drawn . Be careful you don't hit the Flag button by mistake!

To get an idea of the data layout, plot a single baseline (ea02&ea05), channel (31, for all spectral windows), and polarization (RR) versus time. Note that limiting the selected data with appropriate filters is extremely helpful when plotting large datasets:

plotms of ea02&ea05 amp vs time
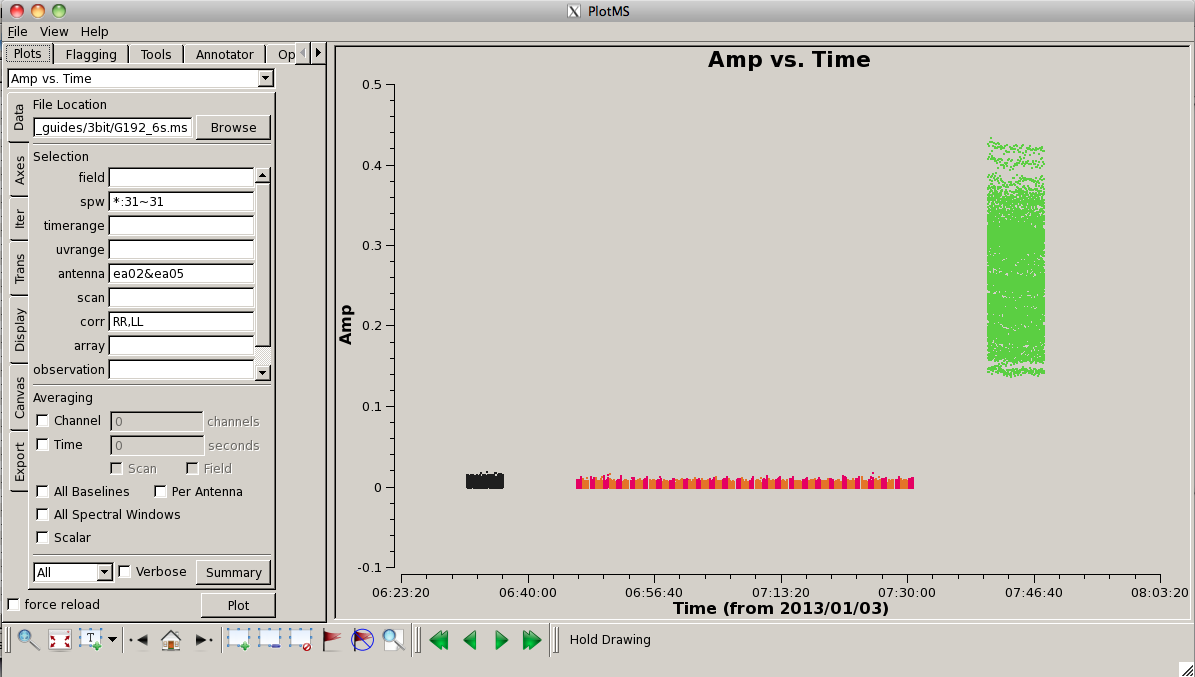
# In CASA
plotms(vis='G192_6s.ms', field='', spw='*:31~31', \
       antenna='ea02&ea05', xaxis='time', yaxis='amp', \
       correlation='rr', coloraxis='field')

Here, we can see the alternating phase calibration and science target scans, as well as the (brighter) bandpass calibrator at the end of the observation. Feel free to play with ways to view. For example, you can change the size of the plotted points, if they are too small to see easily, by setting "Unflagged Points Symbol" to "Custom" and increasing the number of pixels under "Style." You can also experiment with data averaging, plotting different correlations (if you're not doing polarization calibration, you can ignore the "cross-hand" correlations RL and LR and focus on "parallel-hand" correlations RR and LL), changing the plotted axes, altering the colorization scheme (try colorizing by baseline, correlation, field, etc.).

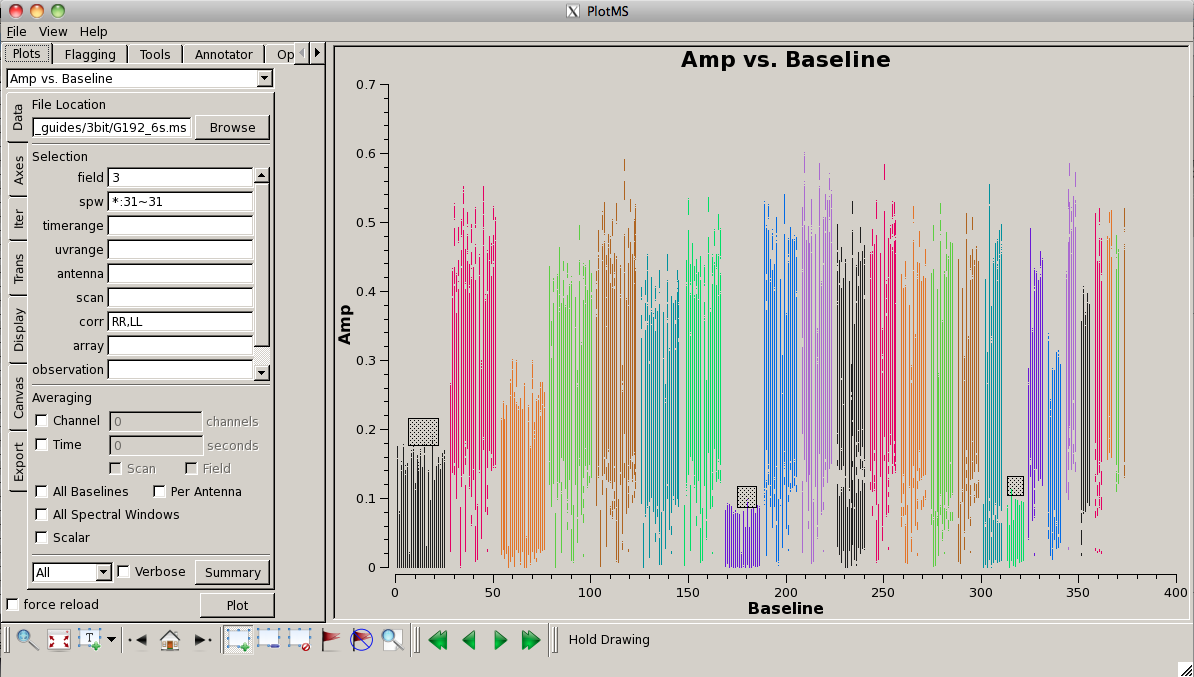
plotms baseline amplitudes for field 3

Look for bad antennas by picking the bandpass calibrator and plotting baselines. We color the points by "antenna1" to see which antennas might be troublesome: 

# In CASA
plotms(vis='G192_6s.ms', field='3', spw='*:31~31', \
       antenna='', xaxis='baseline',\
       yaxis='amp', coloraxis='antenna1')

You should be able to see that three of the antennas have lower amplitudes than the rest. Boxing with the Mark Regions tool and using the Locate tool will show in the logger that these are antennas ea01, ea10 and ea19; indeed, checking the Operator Log for this observation shows that these antennas have collimation offsets and that the data have been corrupted. We will delete these antennas.

plotms field 3 ea05 and ea13 amp vs frequency

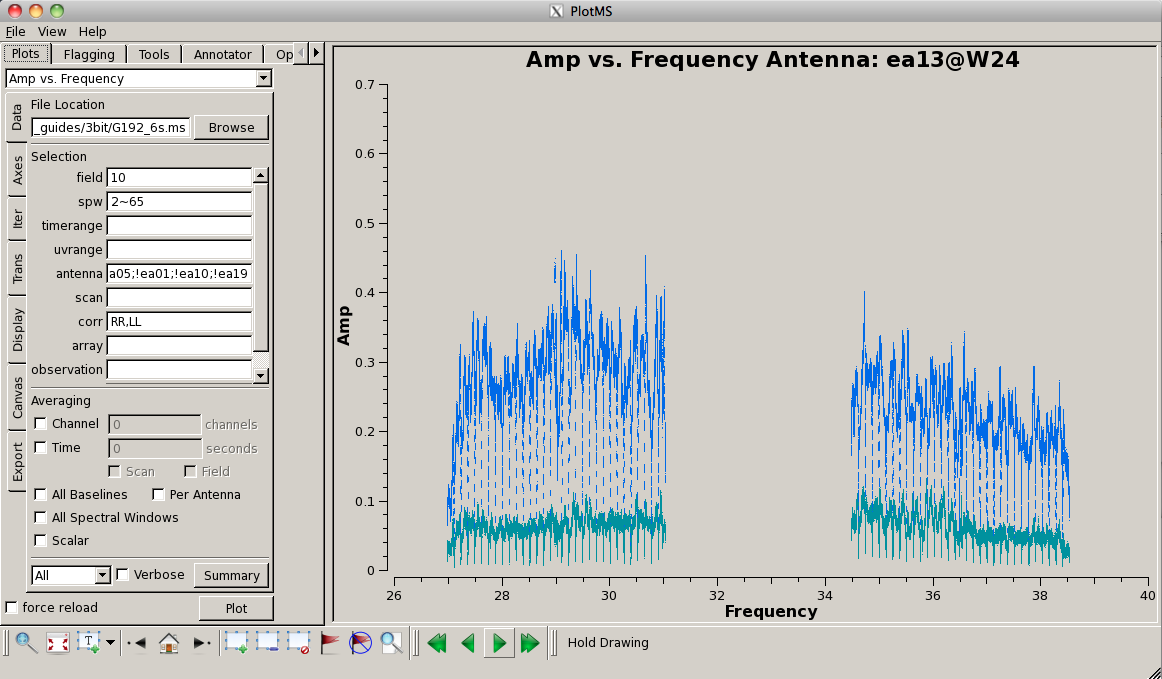
Now look at the raw spectral bandpasses of baselines to ea05. It is in the inner core of the array and a prospective reference antenna. Since we plan to flag them, we will exclude antennas ea01, ea10, and ea19 using negation (represented by "!") in the selection, and iterate by antenna: 

# In CASA
plotms(vis='G192_6s.ms', field='3', \
       antenna='ea05;!ea01;!ea10;!ea19', \
       xaxis='frequency', yaxis='amp', 
       coloraxis='corr', iteraxis='antenna')

As you iterate through baselines with ea05, you'll notice that the plot for ea05&ea13 shows that ea13's RCP (correlation = "RR") is weak, as noted in the log file as well. We will flag this antenna over all correlations, since current restrictions do not allow for single-polarization data to be imaged if it's part of a full-polarization dataset.

Also, note that spectral windows 16 through 31 (the upper baseband) for antenna ea18 look very suspicious. We need to keep an eye on these data.

For antenna ea24, there appear to be some issues with spectral windows 47 and 48, and the RCP of spw 40 also looks problematic, so we'll flag this as well.

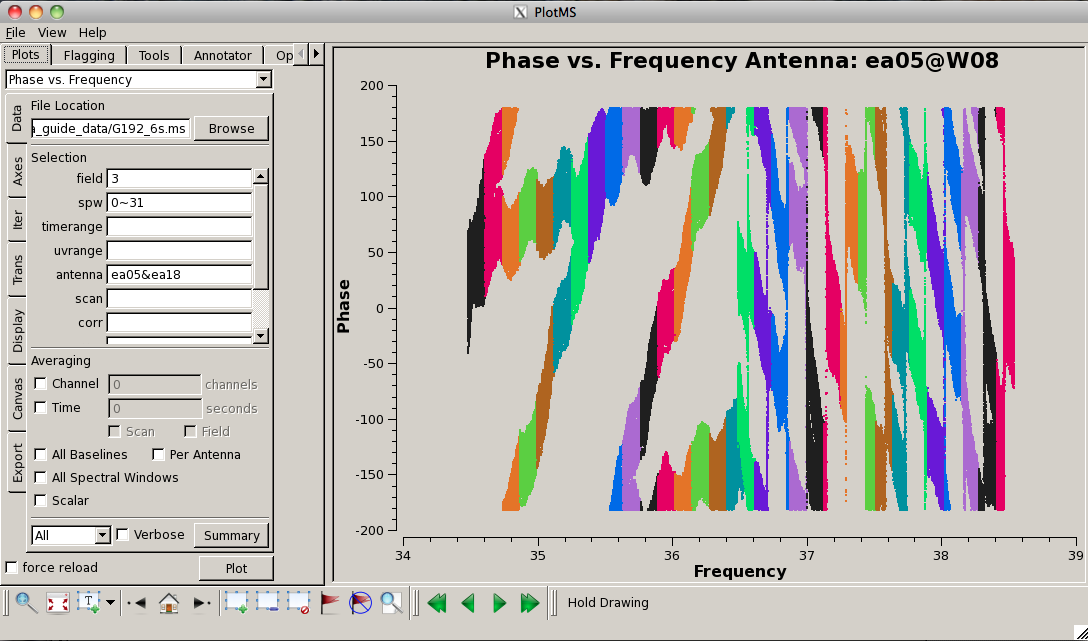
plotms field 3 ea05 and ea18 phase vs frequency

Now plot the phases, iterating through baselines to ea05: 

# In CASA
plotms(vis='G192_6s.ms', field='3', \
       antenna='ea05;!ea01;!ea10;!ea13;!ea19', \
       xaxis='frequency', yaxis='phase', \
       coloraxis='spw', iteraxis='antenna')

Notice the rapidly winding phases with frequency due to residual instrumental delays (we will calibrate the instrumental delays and smooth-out the phases later). Most span a turn or less over each 128-MHz subband, but there are some outliers. Step through to ea18. You will see that there are large jumps between spectral windows for spw 16-31 (see plot on the right). This reinforces our suspicion that something is wrong with these data on ea18 and we will flag them as well.

To carry out the flagging, we again use flagcmd in the mode where it takes a list of command strings: 

# In CASA
flaglist = ['antenna="ea01,ea10,ea19,ea13"',
            'antenna="ea24" spw="40,47~48"',
            'antenna="ea18" spw="16~31"']
flagcmd(vis='G192_6s.ms', inpmode='list', inpfile=flaglist, \
        action='apply', flagbackup=True)

These commands will carry out the flags and add a record of them to the FLAG_CMD table (where they will be marked as applied). Before applying the flags, a backup version of the flags will be stored as flagcmd_1, in case you would like to restore the MS to the state it was in prior to your new flags (this can be done using flagmanager with mode = "restore" and, in this case, versionname = "flagcmd_1").

Plot the data again, now that is has been flagged (this time, we'll look at amplitude vs. frequency): 

# In CASA
plotms(vis='G192_6s.ms', field='3', antenna='ea05', \
       xaxis='frequency', yaxis='amp')
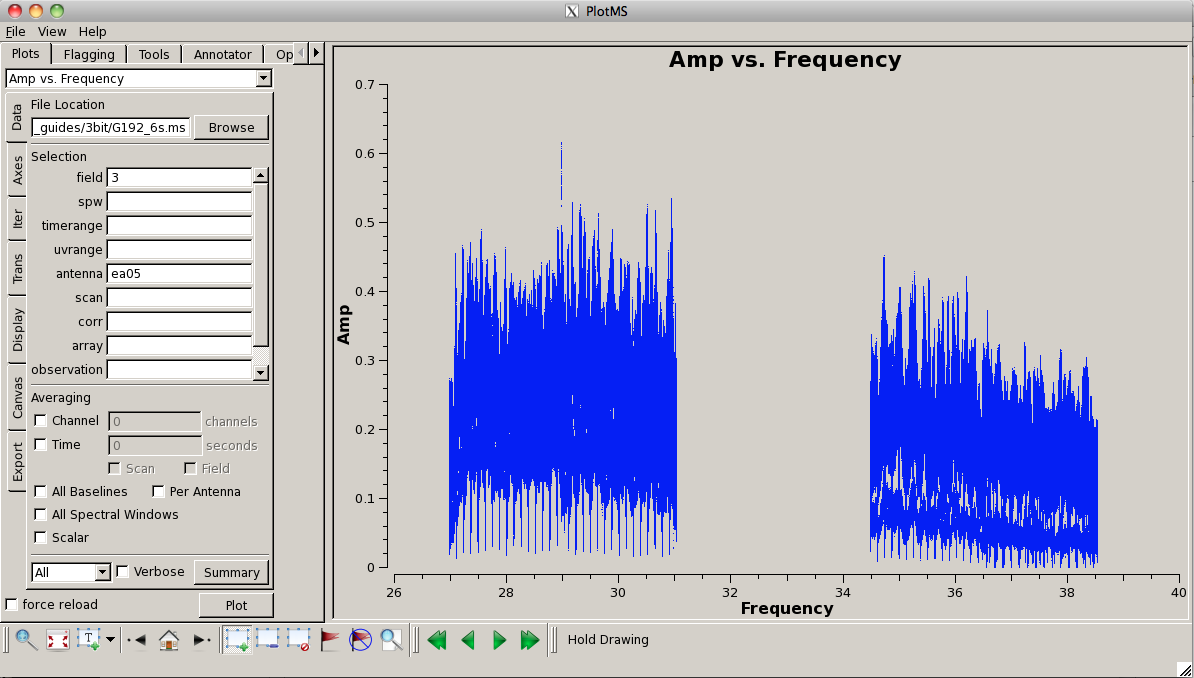
plotms field 3 ea05 amp vs frequency

Now let's look at our phase calibrator -- it is weaker, and we can see some RFI: 

# In CASA
plotms(vis='G192_6s.ms', field='1', antenna='ea05', coloraxis = 'spw',\
       correlation = 'RR,LL', xaxis='frequency', yaxis='amp', scan='10,20,30,40,50,60')

Note that we've chosen a subset of scans to limit the amount of data being plotted. This will give us a sense of whether there is serious RFI (or other issues) present in the data, but will obviously not display everything. Later on, when we plot the calibrated data, we will need to again inspect for possible bad data (and we will flag and recalibrate).

Use the Zoom button , Mark Regions , and Locate to identify the frequency/channels of the RFI. In particular, we note the following:

  • 27.228 GHz (spw 33 ch 124)
  • 27.707 GHz (spw 37 ch 91)
  • 27.81-27.811 GHz (spw 38 ch 66-67)
  • 27.819-27.821 GHz (spw 38 ch 75-77)
  • 28.894 GHz (spw 46 ch 126)
  • 28.976 GHz (spw 48 ch 0)
  • 29.684-20.685 GHz (spw 53 ch 68-69)
  • 30.976 GHz (spw 63 ch 80) very strong
  • 35.782 GHz (spw 10 ch 26)
  • 36.523 GHz (spw 15 ch 127)
  • 37.946 GHz (spw 27 ch 62)
  • 37.948 GHz (spw 27 ch 64)

Flag these channels: 

# In CASA
flaglist = ['spw="33:124,37:91,38:66~67;75~77,46:126,48:0"', \
            'spw="53:68~69,63:80,10:26,15:127,27:62,27:64"']
flagcmd(vis='G192_6s.ms', inpmode='list', inpfile=flaglist, \
        action='apply', flagbackup=True)

When this is finished, it's useful to have a look at the flagged data. To reload the plotms window after taking the new flags into account, check the "force reload" box on the lower left of the plotms GUI and click on "Plot." (As a shortcut, you can also hold down the "Shift" key while clicking on the "Plot" button to force-reload a plot.)

Finally, split off the good data, without retaining the flagged data. This will allow us to work on the data without having to start completely over (if we mess something up badly), as well as let us do simpler data selections (since the data size will be a bit smaller). 

# In CASA
# Remove any existing split data, otherwise split will not happen
os.system('rm -rf G192_flagged_6s.ms')
split(vis='G192_6s.ms', outputvis='G192_flagged_6s.ms', \
      datacolumn='data', keepflags=False)
  • keepflags=False: again, to limit the size of the MS, we do not propagate flagged data to the split-off MS.

You now have a MS called G192_flagged_6s.ms in your working area. This should be 16GB in size, which you can determine at the CASA command prompt by typing: 

# In CASA
os.system('du -sh G192_flagged_6s.ms')

Note that the built-in system function allows one to execute UNIX shell commands within a CASA session. (Some, like ls, don't need this extra wrapper, but most are not automatically understood.)

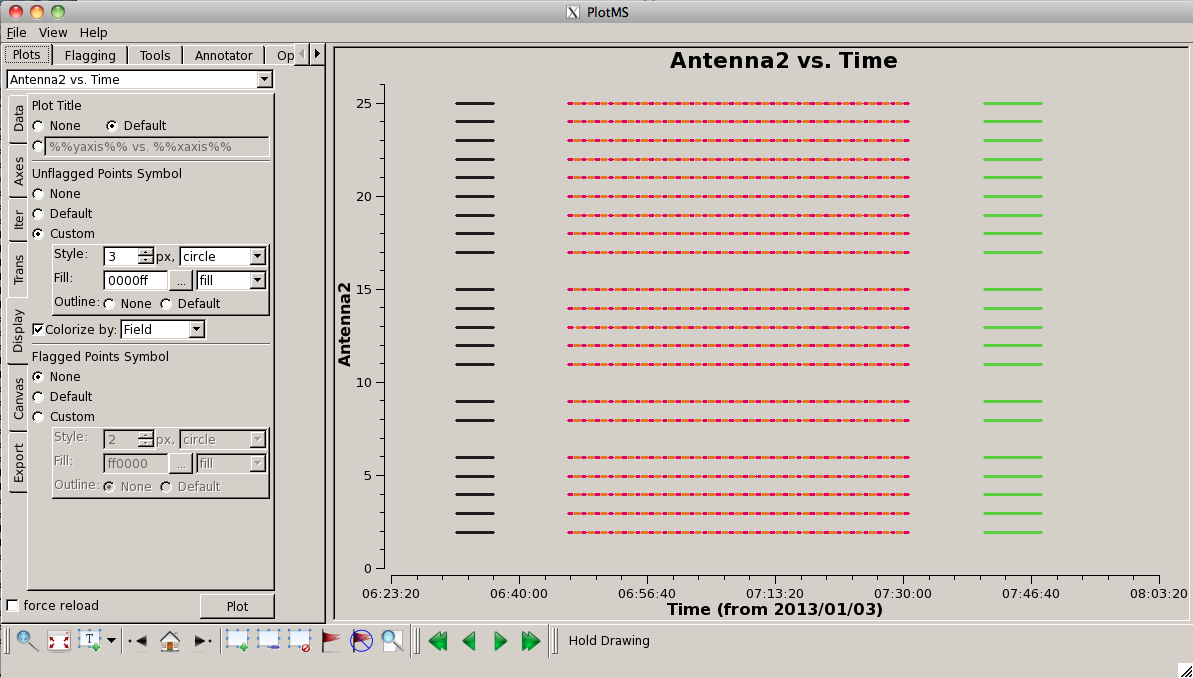
plotms antenna2 vs. time "datastream" plot

At this point it is useful to plot a "datastream" view of the MS to show which antennas are present at different times. You can do this using: 

# In CASA
plotms(vis='G192_flagged_6s.ms', xaxis='time', yaxis='antenna2', \
       symbolshape = 'circle', plotrange=[-1,-1,0,26], coloraxis='field')

This shows the times where data is present on baselines to a given antenna (controlled by setting yaxis="Antenna2"). Note that this means there is no "line" plotted for ea01 (antenna 0). You can pick-up ea01 (and drop ea28) by setting yaxis='antenna1'. To the right we show this plot. You can see that, for the most part, all antennas are present for the entire observation. One exception to this is antenna ea16, which comes in a little late on the first scan of G192.

Calibration

Before proceeding with calibration, we will summarize the split flagged MS: 

# In CASA
listobs('G192_flagged_6s.ms', listfile='G192_flagged_listobs.txt')

As before, inspection of the listobs output text file shows that there are now 6,958,621 data records present, and 22 antennas remaining in the MS.

Setting the flux density scale

It is now time to begin calibration! The general data reduction strategy is to derive a series of scaling factors or corrections from the calibrators, which, in addition to a priori calibration information, are collectively applied to the science target. For much more discussion of the philosophy, strategy, and implementation of calibration of synthesis data within CASA, see Synthesis Calibration in the CASA Cookbook and User Reference Manual .

The first step is to insert a model for our flux calibrator source (3C147) into the MS in order to set the flux density scale for bootstrapping to other sources. In order to do this, we first have to locate the model image on our system with setjy. The setjy task has an option to list available model images: 

# In CASA
setjy(vis='G192_flagged_6s.ms', listmodels=True)

which sends output to your terminal (but not the logger). For example, on an NRAO workstation, we obtain the following: 

No candidate modimages matching '*.im* *.mod*' found in .

Candidate modimages (*) in /home/casa/packages/RHEL5/prerelease/casapy-42.0.prerelease-10-1-64b/data/nrao/VLA/CalModels:
3C138_A.im  3C138_L.im	3C138_U.im  3C147_C.im	3C147_Q.im  3C147_X.im	3C286_K.im  3C286_S.im	3C48_A.im  3C48_L.im  3C48_U.im
3C138_C.im  3C138_Q.im	3C138_X.im  3C147_K.im	3C147_S.im  3C286_A.im	3C286_L.im  3C286_U.im	3C48_C.im  3C48_Q.im  3C48_X.im
3C138_K.im  3C138_S.im	3C147_A.im  3C147_L.im	3C147_U.im  3C286_C.im	3C286_Q.im  3C286_X.im	3C48_K.im  3C48_S.im  README

The relevant image for our purposes is 3C147_A.im, in the directory /home/casa/packages/RHEL5/prerelease/casapy-42.0.prerelease-10-1-64b/data/nrao/VLA/CalModels/. Your system may show a different location (for example /home/casa/data/nrao/VLA/CalModels/, or /Applications/CASA.app/Contents/data/nrao/VLA/CalModels on a Mac). Since CASA knows about this image, we only have to give the image name and not the entire path. Note that outside of the NRAO, you may need to provide setjy with the entire path along with the model image name (this depends on your platform and installation location).

We can now run the setjy task using the appropriate model: 

# In CASA
setjy(vis='G192_flagged_6s.ms', field='0', scalebychan=True, \
      model='3C147_A.im')
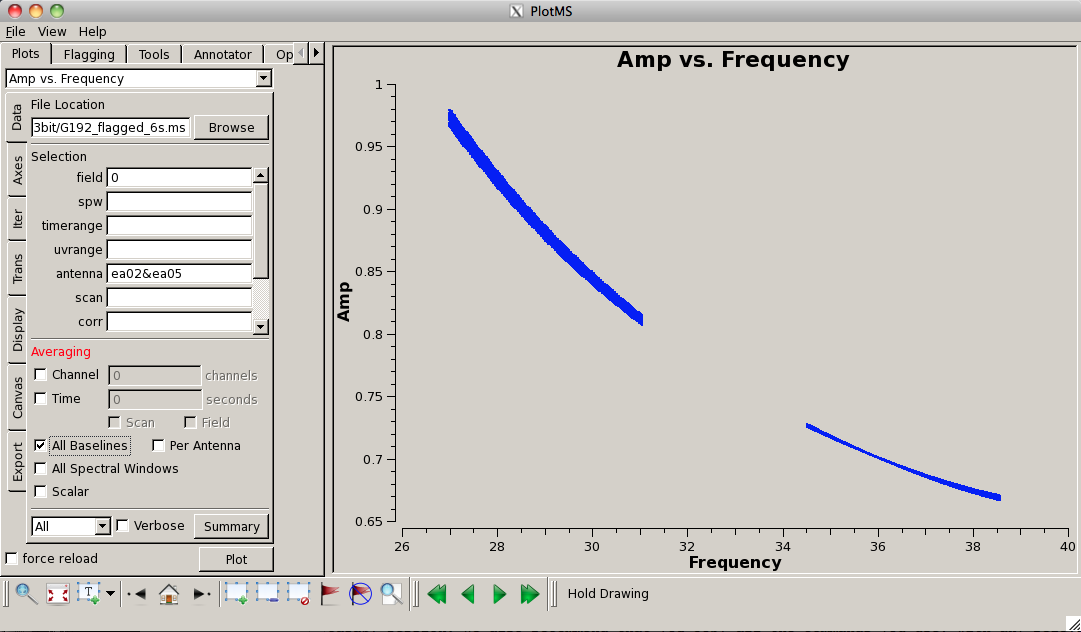
plotms of model amp vs freq for 3C147
  • scalebychan=True: will fill the model with per-channel values; otherwise, setjy would use a single value per spectral window.
  • usescratch=False: put the model in the header instead of creating scratch columns in the MS. This will take up considerably less disk space.

We can plot the model data using plotms: 

# In CASA
plotms(vis='G192_flagged_6s.ms', field='0', antenna='ea02&ea05', \
       xaxis='freq', yaxis='amp', ydatacolumn='model')

Inspecting the logger report shows that 3C147 has a flux density of 1.40608 Jy at the lower end of the band (spw 63; ~31 GHz) and 1.2779 Jy at the upper end (spw 0; ~35 GHz).

Deriving a priori calibrations

Some calibration products are carried along throughout the calibration process and used as priors for subsequent calibration steps. These include the antenna position corrections, gain-elevation curves, tropospheric opacity corrections, and requantizer gains.

Antenna position corrections

We use gencal to determine any antenna-position corrections that need to be applied to the data. This is based on a database of corrections with the dates and times the corrections were determined and when they were included in the online observing system. 

# In CASA
gencal('G192_flagged_6s.ms', caltable='calG192.antpos', \
       caltype='antpos', antenna='')

You should see in the logger: 

Determine antenna position offests from the baseline correction database
offsets for antenna ea05 :  0.00000  -0.00100   0.00090
offsets for antenna ea16 : -0.00310   0.00000   0.00100

So this dataset does require antenna position corrections on ea05 & ea16. If no corrections were necessary, the output from gencal would have appeared as follows: 

No offsets found for this MS
*** Warning *** No offsets found. No caltable created.
gencal::::casa	An error occurred running task gencal.

Although the "warning" makes it seem as if the task has failed, the message is normal and means there simply aren't any antenna corrections to apply.

Gain-elevation curves

We will use gencal to create calibration tables containing the gain curves and tropospheric opacity corrections for the antennas. Note that the gaincurve=True option that was previously available in calibration tasks (e.g., bandpass) is no longer available as of CASA 4.2. The syntax for generating a gaincurve calibration table in gencal is as follows: 

# In CASA
gencal('G192_flagged_6s.ms', caltable='calG192.gaincurve', \
       caltype='gc')

Tropospheric opacity corrections

plotweather output

The atmospheric opacity during the observations can be computed from a seasonal model and/or weather station information. We will use the plotweather task to display the weather information and to calculate the zenith opacities for each spectral window. After the zenith opacities are derived, gencal will recompute the correct elevation of the data automatically using [math]\displaystyle{ e^{(-\csc[el]\tau_z)} }[/math] and create the opacity-correction calibration table.

To start, we want to plot the opacity of the atmosphere at the time these observations was taken. plotweather plots the weather conditions during the observations and calculates the atmospheric opacities based on these data, in combination with a seasonal model that contains long-term statistics at the VLA site. Using seasonal_weight=0.5 (the default value) gives equal weights to the seasonal model and weather station data:

We will be running plotweather in a way that will assign the opacity list (one entry for each spectral window in ascending order) to the variable myTau: 

# In CASA
myTau = plotweather(vis='G192_flagged_6s.ms', doPlot=T)

The logger should display: 

##########################################
##### Begin Task: plotweather        #####
plotweather(vis="G192_flagged_6s.ms",seasonal_weight=0.5,doPlot=True,plotName="")
2013-06-18 21:47:00 INFO plotweather	SPW : Frequency (GHz) : Zenith opacity (nepers)
 0  :   34.476  :  0.03
 1  :   34.604  :  0.031
 2  :   34.732  :  0.031
 3  :   34.860  :  0.031
 4  :   34.988  :  0.032
<snip>
61  :   30.640  :  0.024
62  :   30.768  :  0.024
63  :   30.896  :  0.024
wrote weather figure: G192_flagged_6s.ms.plotweather.png
##### End Task: plotweather          #####
##########################################

In addition to assigning the myTau variable to the full list of opacities per spw, plotweather also creates a file G192_flagged_6s.ms.plotweather.png with the elevation of the sun, the wind speed and direction, the temperature, and precipitable water vapor (PWV) as functions of time over the course of the observation (view this file with your preferred image viewer like gthumb, xv, or Preview).

We can now create a calibration table to correct for the atmospheric opacity with gencal using the calmode='opac' parameter. We could input the opacities directly, but it's easier to use the myTau variable with a little Python: 

# In CASA
SPWs = []
for window in range(0,64):
    SPWs.append(str(window))

# In CASA
spwString = ','.join(SPWs)
gencal(vis='G192_flagged_6s.ms', caltable='calG192.opacity',
       caltype='opac', spw=spwString, parameter=myTau)

Requantizer gain corrections

Finally, we will use gencal to create a calibration table containing corrections for the requantizer gains. Although this is only necessary for 3-bit data, such as our G192 dataset, it can be done for 8-bit datasets without any ill effects. For 3-bit data, this step is needed to account for the small gain changes (~5-10%) that result from resetting the quantizer gains as the correlator changes to a new 3-bit configuration. (Here is more information on observing with the 3-bit system.) 

# In CASA
gencal('G192_flagged_6s.ms', caltable='calG192.requantizer', \
       caltype='rq')

The caltables we have generated (calG192.antpos, calG192.gaincurve, calG192.opacity, and calG192.requantizer) will need to be pre-applied in subsequent calibration steps.

Calibrating delays and initial bandpass solutions

plotcal G0 phase ant 0~15
plotcal G0 phase ant 16~26
plotcal K0 delay vs. antenna
plotcal B0 bandpass amp ant ea06 spw 0-31
plotcal B0 bandpass amp ant ea06 spw 32-63

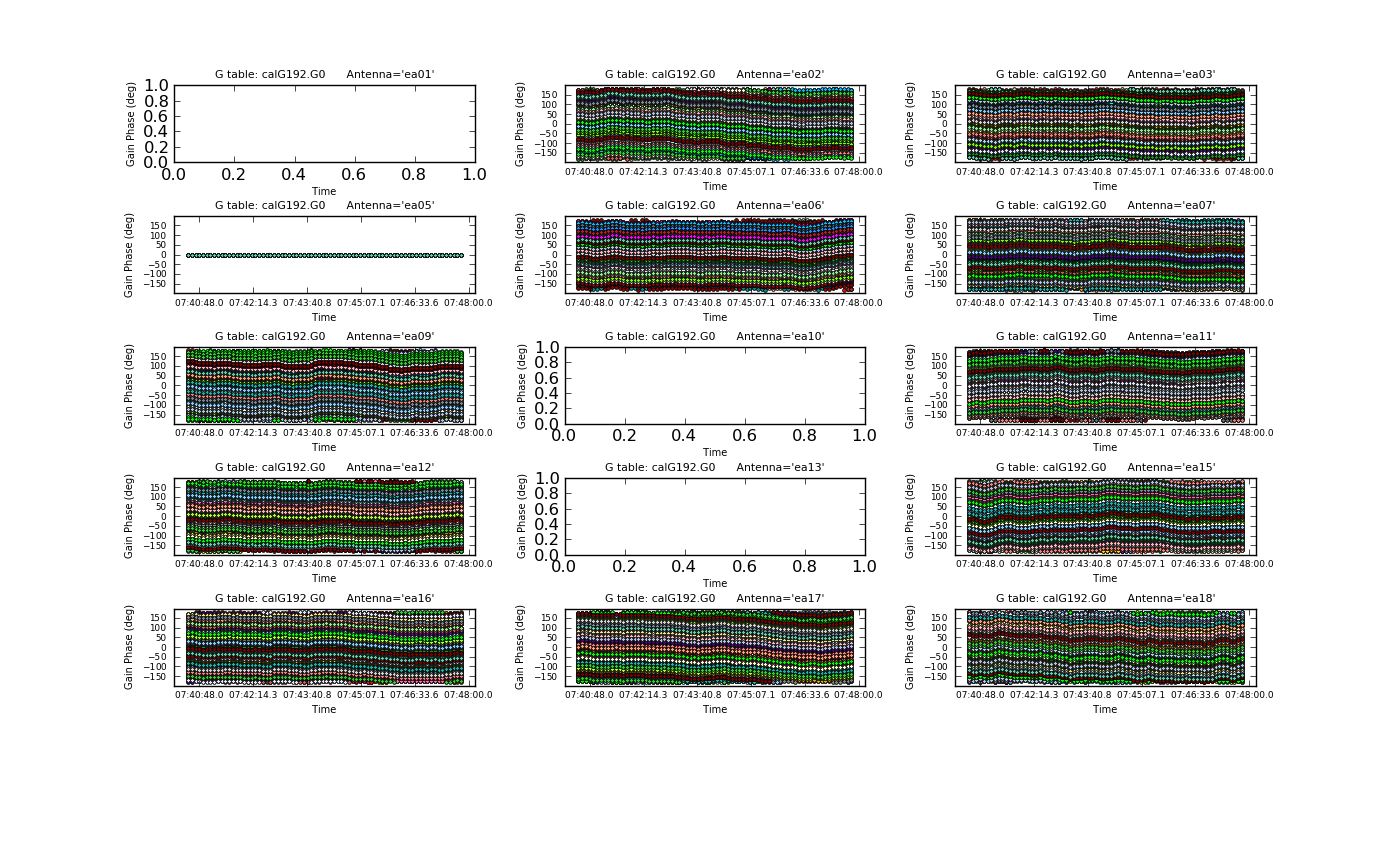
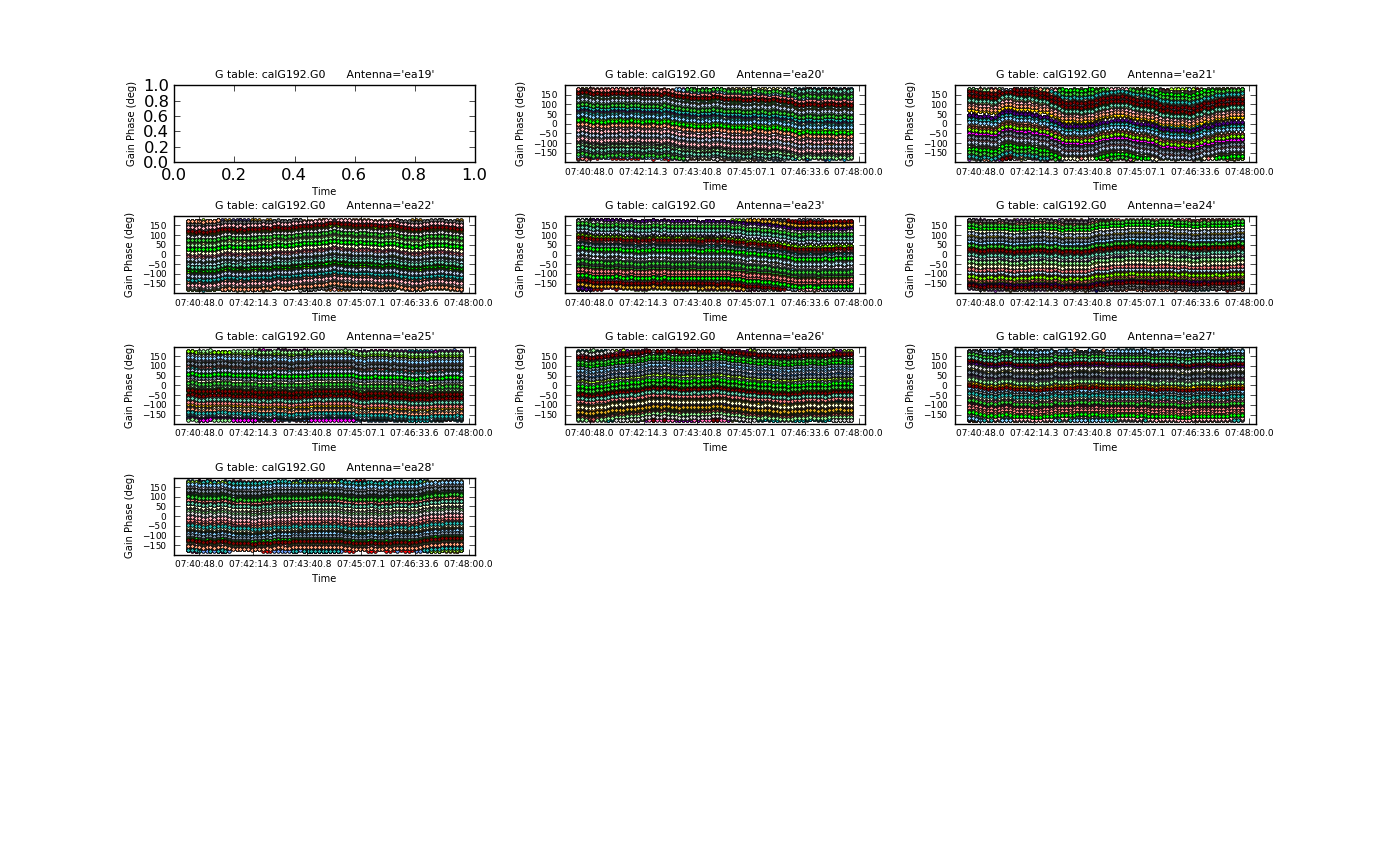
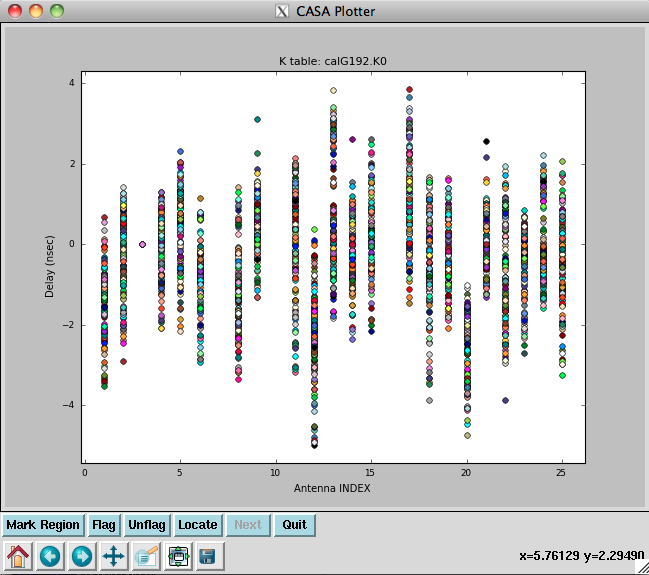
First, we do a phase-only calibration solution on a narrow range of channels near the center of each spectral window on the bandpass calibrator 3C84 to flatten them with respect to time before solving for the bandpass. The range 60~68 should work. Pick a reference antenna near the center of the array -- ea05 is a reasonable choice (see above): 

# In CASA
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G0', \
        field='3', spw='*:60~68', \
        gaintable=['calG192.antpos','calG192.gaincurve', \
                   'calG192.requantizer','calG192.opacity'], \
        gaintype='G', refant='ea05', calmode='p', \
        solint='int', minsnr=3)
  • refant='ea05' : Use ea05 as the reference antenna
  • solint='int' : Do a per-integration solve (every 6 seconds, since we've time-averaged the data).
  • minsnr=3 : Apply a minimum signal-to-noise cutoff. Solutions with less than this value will be flagged.
  • gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', 'calG192.opacity'] : Pre-apply the antenna position corrections, gaincurve, opacity, and requantizer calibration tables.

Plot the phase solutions (using full phase range, -180 to 180, instead of autorange): 

# In CASA
plotcal(caltable='calG192.G0', xaxis='time', yaxis='phase', \
        iteration='antenna', plotrange=[-1,-1,-180,180])

Step through the antenna-based solutions. They look good (and fairly flat over the scans).

NOTE: When you are done plotting and want to use the calibration table in another task (e.g., for subsequent calibration or viewing with plotms), use the Quit button on the GUI to dismiss the plotter and free-up the lock on the calibration table. You should see a message in your terminal window saying "Resetting plotcal" which means you are good to go!

If you want to make single-page, multipanel plots (like those shown to the right), particularly for a hardcopy (where it only shows the first page), you can do: 

# In CASA
plotcal(caltable='calG192.G0', xaxis='time', yaxis='phase', \
        antenna='0~10,12~15', subplot=531, iteration='antenna', \
        plotrange=[-1,-1,-180,180], fontsize=8.0, \
        markersize=3.0, figfile='plotG192_plotcal_G0p1.png')
plotcal(caltable='calG192.G0', xaxis='time', yaxis='phase', \
        antenna='16~26', subplot=531, iteration='antenna', \
        plotrange=[-1,-1,-180,180], fontsize=8.0, \
        markersize=3.0, figfile='plotG192_plotcal_G0p2.png')

We can now solve for the residual delays that we saw in plotms when we plotted phase vs. frequency. This uses the gaintype='K' option in gaincal. Note that this currently does not do a "global fringe-fitting" solution for delays, but instead does a baseline-based delay solution for all baselines to the reference antenna, treating these as antenna-based delays. In most cases with high-enough S/N to get baseline-based delay solutions, this will suffice. We avoid the edge channels of each spectral window by selecting channels 5~122: 

# In CASA
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.K0', \
        gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', \
                   'calG192.opacity', 'calG192.G0'], \
        field='3', spw='*:5~122', gaintype='K', \
        refant='ea05', solint='inf', minsnr=3)

Note that we have also pre-applied our initial phase table, calG192.G0. We can plot the delays, in nanoseconds, as a function of antenna index (you will get one for each spw and polarization): 

# In CASA
plotcal(caltable='calG192.K0', xaxis='antenna', yaxis='delay')

The delays range from around -5 to 4 nanoseconds.

Now we solve for the antenna bandpasses using the previous tables: 

# In CASA
bandpass(vis='G192_flagged_6s.ms', caltable='calG192.B0', \
         gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', \
                    'calG192.opacity', 'calG192.G0', 'calG192.K0'], \
         field='3', refant='ea05', solnorm=False, \
         bandtype='B', solint='inf')

WARNING: You must set solnorm=False here or later on you will find some offsets among spws due to the way the amplitude scaling adjusts weights internally during solving.

plotcal B0 bandpass phase ant ea06 spw 0-31
plotcal B0 bandpass phase ant ea06 spw 32-63

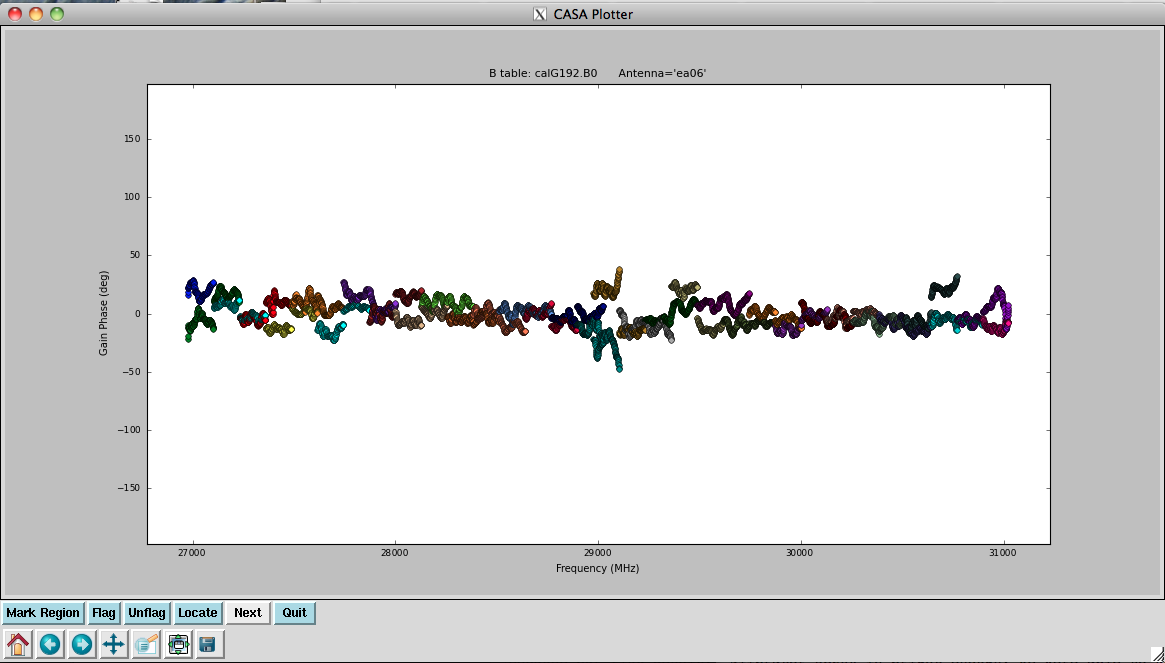
You will see in the terminal some reports of solutions failing due to "Insufficient unflagged antennas" -- note that these are for the channels we flagged earlier.

This is the first amplitude-scaling calibration that we do, so it is important to have used the calG192.gaincurve caltable (or set gaincurve=True) as well as the calG192.opacity caltable (or set opacity appropriately).

Plot the resulting bandpasses in amplitude and phase: 

# In CASA
plotcal(caltable='calG192.B0', xaxis='freq', yaxis='amp', \
        spw='0~31', iteration='antenna')
#
plotcal(caltable='calG192.B0', xaxis='freq', yaxis='amp', \
        spw='32~63', iteration='antenna')
#
plotcal(caltable='calG192.B0', xaxis='freq', yaxis='phase', \
        iteration='antenna', spw='0~31', \
        plotrange=[-1,-1,-180,180])
#
plotcal(caltable='calG192.B0', xaxis='freq', yaxis='phase', \
        iteration='antenna', spw='32~63', \
        plotrange=[-1,-1,-180,180])

In the bandpass phases you no longer see the residual antenna delays (just residual spw phase offsets from the delay solution registration), but there are some band edge effects apparent.

Bootstrapping the bandpass calibrator spectrum

Unfortunately, our flux density calibrator was not bright enough at Ka-band to use as the bandpass calibration source. Since there is no a priori spectral information for our chosen bandpass calibrator, 3C84, we need to bootstrap to find its spectral index, then recalibrate with this information in order to avoid folding the intrinsic spectral shape of 3C84 into our calibration.

First, we use the initial round of bandpass calibration to create gain solutions for the flux and bandpass calibrators: 

# In CASA
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G1', field='0,3', \
        gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', \
                   'calG192.opacity', 'calG192.K0', \
                   'calG192.B0'], \
        gaintype='G', refant='ea05', calmode='ap', solint='30s', minsnr=3)

Now let's have a look at the phase and amplitude solutions, iterating over antenna. We will look at the flux calibrator (3C147) and bandpass calibrator (3C84) individually since they're widely separated in time: 

# In CASA
plotcal(caltable='calG192.G1', xaxis='time', yaxis='amp', \
        field='0', iteration='antenna')
#
plotcal(caltable='calG192.G1', xaxis='time', yaxis='amp', \
        field='3', iteration='antenna')
#
plotcal(caltable='calG192.G1', xaxis='time', yaxis='phase', \
        iteration='antenna', plotrange=[-1,-1,-180,180], \
        field='0')
#
plotcal(caltable='calG192.G1', xaxis='time', yaxis='phase', \
        iteration='antenna', plotrange=[-1,-1,-180,180], \
        field='3')

The solutions all look reasonable and relatively constant with time.

Now that we have gain solutions for the flux and bandpass calibrators, we can use fluxscale to scale the gain amplitudes of the bandpass calibrator: 

# In CASA
flux1 = fluxscale(vis='G192_flagged_6s.ms', caltable='calG192.G1', \
                  fluxtable='calG192.F1', reference='0', \
                  transfer='3', listfile='3C84.fluxinfo', fitorder=1)
  • flux1 = fluxscale(...): by providing a variable flux1, we allow fluxscale to use this for the output Python dictionary it returns with lots of information about the flux scaling. You can inspect the output dictionary flux1 by typing "print flux1" at the CASA command line.
  • fluxtable='calG192.F1': this is the output scaled gain table. Since we are only using this to find the spectral index of 3C84, we won't be using this table.
  • listfile='3C84.fluxinfo': an output file that contains the derived flux values and fit information.
  • fitorder=1: only find a spectral index, ignoring curvature in the spectrum.

The last line in the file (and displayed in the logger) shows: 

# Fitted spectrum for 3c84-J0319+413 with fitorder=1: Flux density = 29.8756 +/- 0.0381051 (freq=32.4488 GHz) spidx=-0.598926 +/- 0.0105203
plotms of model amp vs freq for 3C84
3C84 flux values returned by fluxscale

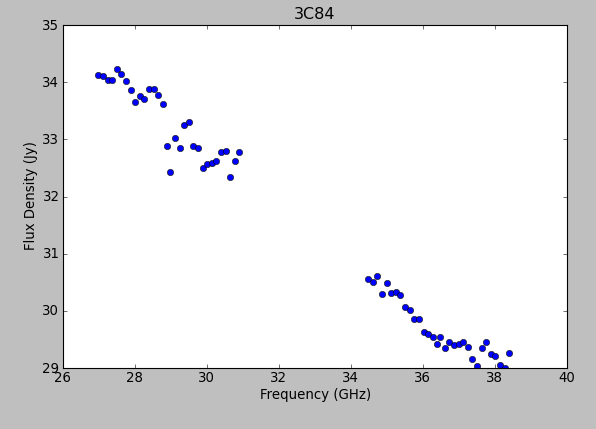
Using the information in the returned flux dictionary, we can plot the derived spectrum: 

# In CASA
freq = flux1['freq'] / 1e9
spw_list = range(0,64)
spw_str = []
for i in spw_list:
   thisspw = str(i)
   spw_str.append(thisspw)

bootstrapped_fluxes = []
for j in spw_str:
    thisflux = a[j]['fluxd'][0]
    bootstrapped_fluxes.append(thisflux)

pl.clf()
pl.plot(freq, bootstrapped_fluxes, 'bo')
pl.xlabel('Frequency (GHz)')
pl.ylabel('Flux Density (Jy)')
pl.title('3C84')
pl.show()

Note the bump around 37 GHz -- what is this? We will not be able to account for it with the simple spectral index model, but still, ours is a good first approximation.

We can use the model from fluxscale to fill the MODEL column with 3C84's spectral information using setjy: 

# In CASA
setjy(vis='G192_flagged_6s.ms', field='3', scalebychan=True, \
      fluxdensity=[29.8756, 0, 0, 0], spix=-0.598929, \
      reffreq='32.4488GHz')

Checking with plotms that the data have been appropriately filled: 

# In CASA
plotms(vis='G192_flagged_6s.ms', field='3', antenna='ea05&ea02', \
       xaxis='freq', yaxis='amp', ydatacolumn='model')
plotcal B0 bootstrapped bandpass amp ant ea06 spw 0-31
plotcal B0 bootstrapped bandpass amp ant ea06 spw 32-63
plotcal B0 bootstrapped bandpass phase ant ea06 spw 0-31
plotcal B0 bootstrapped bandpass phase ant ea06 spw 32-63

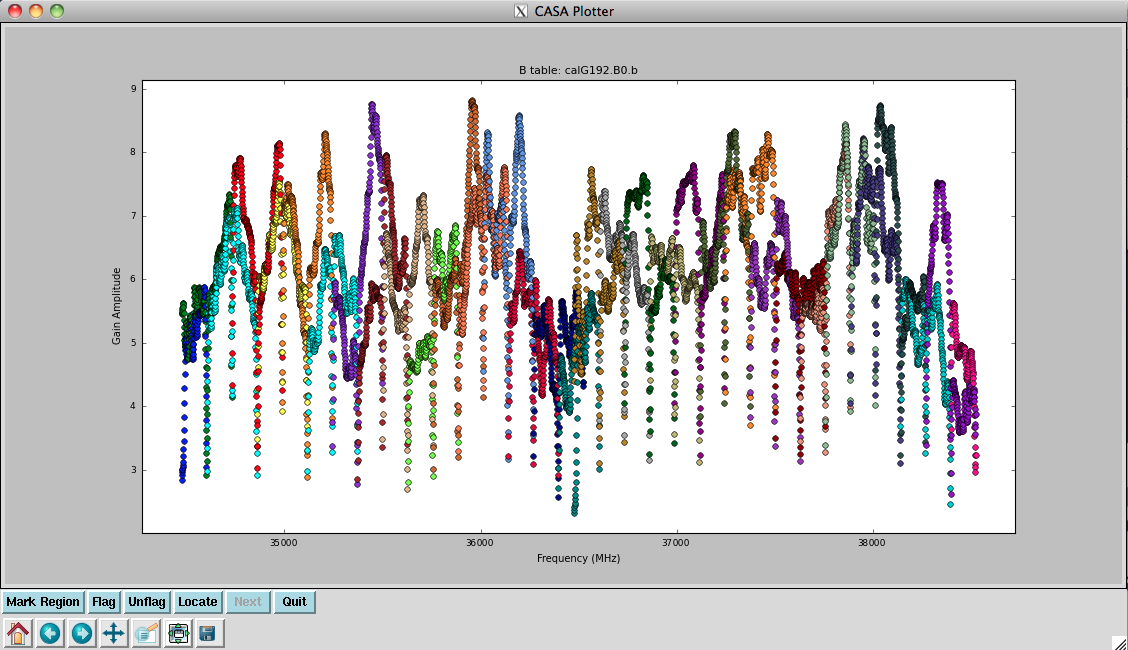
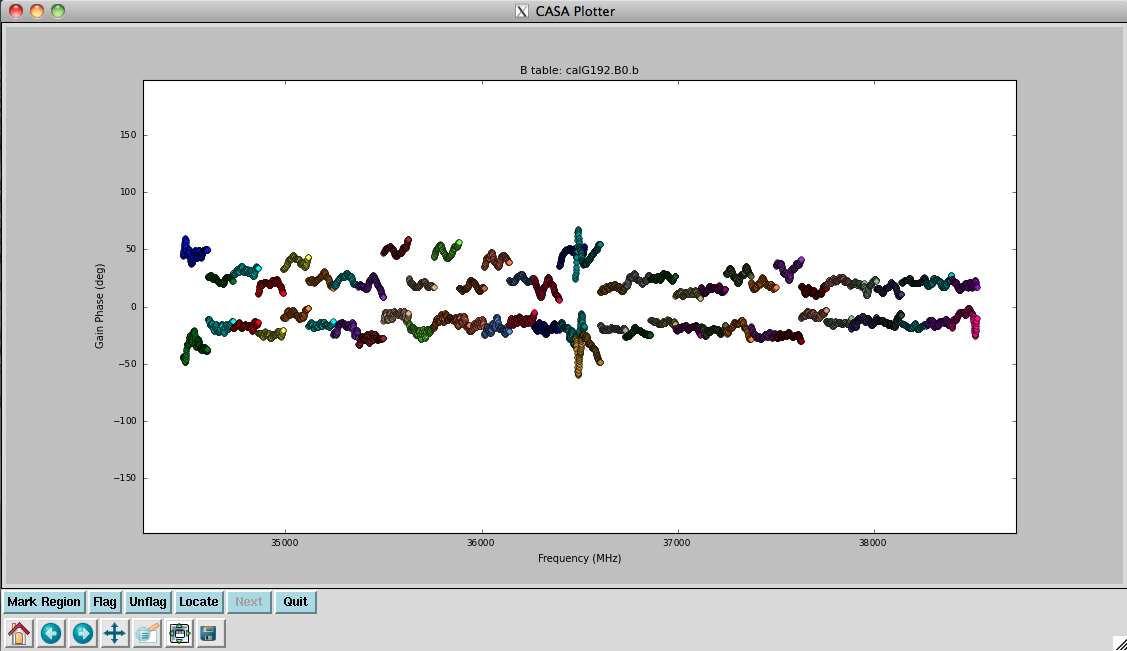
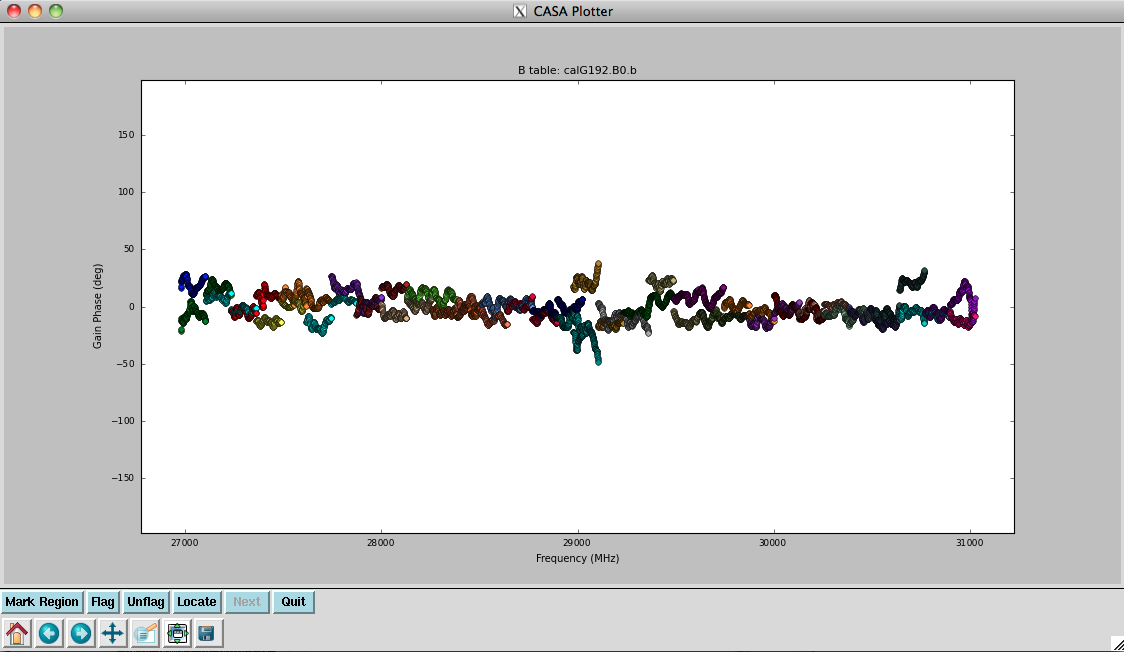
Finally, we redo the previous calibration using this new model information. Although the commands are the same as what we issued earlier, keep in mind that the model values for the bandpass calibrator have changed, and therefore the results of these calibration calculations will differ: 

# In CASA
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G0.b', \
        field='3', spw='*:60~68', \
        gaintable=['calG192.antpos', 'calG192.gaincurve', \
                   'calG192.requantizer', 'calG192.opacity'], \
        gaintype='G', refant='ea05', calmode='p', \
        solint='int', minsnr=3) 
#
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.K0.b', \
        gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', \
                  'calG192.opacity', 'calG192.G0.b'], \
        field='3', spw='*:5~122', gaintype='K', \
        refant='ea05', solint='inf', minsnr=3)
#
bandpass(vis='G192_flagged_6s.ms', caltable='calG192.B0.b', \
         gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', \
                    'calG192.opacity', 'calG192.G0.b', 'calG192.K0.b'], \
         field='3', refant='ea05', solnorm=False, \
         bandtype='B', solint='inf')

It's a good idea to inspect these solutions as well: 

# In CASA
plotcal(caltable='calG192.B0.b', xaxis='freq', yaxis='amp', \
        spw='0~31', iteration='antenna')
#
plotcal(caltable='calG192.B0.b', xaxis='freq', yaxis='amp', \
        spw='32~63', iteration='antenna')
#
plotcal(caltable='calG192.B0.b', xaxis='freq', yaxis='phase', \
        iteration='antenna', spw='0~31', \
        plotrange=[-1,-1,-180,180])
#
plotcal(caltable='calG192.B0.b', xaxis='freq', yaxis='phase', \
        iteration='antenna', spw='32~63', \
        plotrange=[-1,-1,-180,180])

They look virtually unchanged from the previous solutions, with the exception that the amplitude scaling is corrected for the spectrum of 3C84. Now that we have the final version of our bandpass calibration, we can proceed to the full calibration of the dataset.

Final phase and amplitude calibration

plotcal G1.int per-int phase ea06
plotcal G1.inf per-scan phase ea06

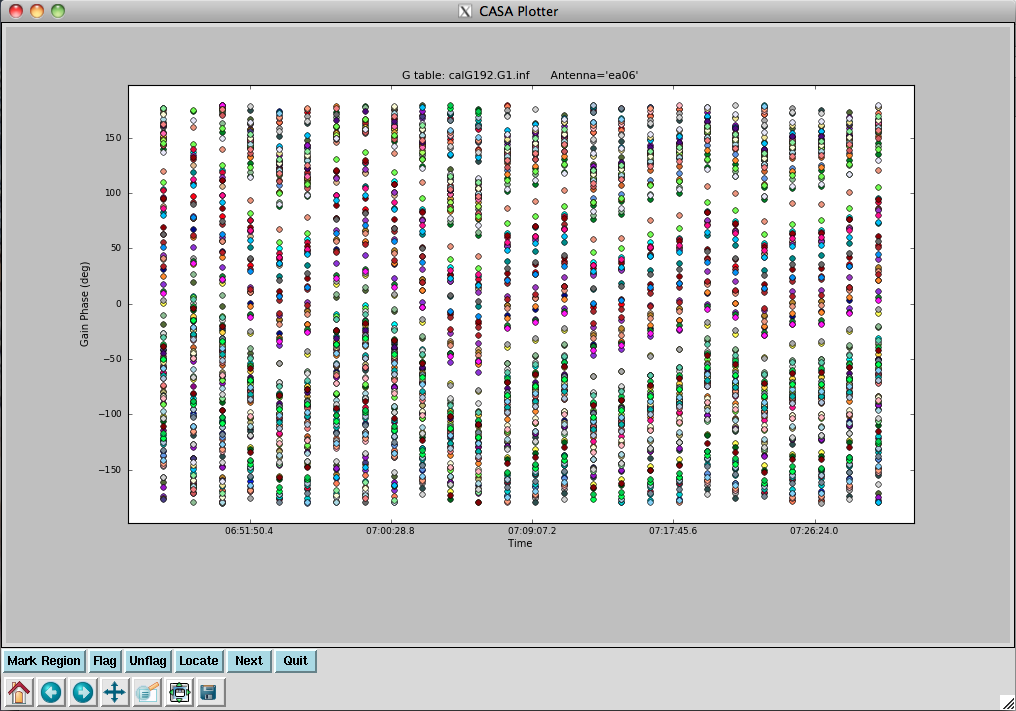
Now we will compute the calibrators' gain phases using the full bandwidth. We will do the calibrators one at a time and append subsequent solutions, since we will use different solution intervals. For 3C147 and 3C84, we obtain one solution per integration (these are bright enough); for the phase calibrator, J0603+174, we will use 12 second solution intervals: 

# In CASA
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G1.int', \
        gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', \
                   'calG192.opacity', 'calG192.K0.b', 'calG192.B0.b'], \
        field='0', refant='ea05', solnorm=F, \
        solint='int', gaintype='G', calmode='p')
#
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G1.int', \
        gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', \
                   'calG192.opacity', 'calG192.K0.b', 'calG192.B0.b'], \
        field='1', refant='ea05', solnorm=F, \
        solint='12s', gaintype='G', calmode='p', append=True)
#
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G1.int', \
        gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', \
                   'calG192.opacity', 'calG192.K0.b', 'calG192.B0.b'], \
        field='3', refant='ea05', solnorm=F, \
        solint='int', gaintype='G', calmode='p', append=True)

These will get applied when solving for amplitudes (see the "G2" calibration tables below), and when calibrating the calibrators themselves (with the task applycal).

The phases track nicely with time: 

# In CASA
plotcal(caltable='calG192.G1.int', xaxis='time', yaxis='phase', \
        iteration='antenna', plotrange=[-1,-1,-180,180])

To apply phase calibration to the target, we will make a second table for the gain calibrator (J0603+174) with one solution per scan: 

# In CASA
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G1.inf', \
        gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', \
                   'calG192.opacity', 'calG192.K0.b', 'calG192.B0.b'], \
        field='1', refant='ea05', solnorm=F, \
        solint='inf', gaintype='G', calmode='p')

These phase gain solutions in calG192.G1.inf will be interpolated by applycal onto our target. These look good as well: 

# In CASA
plotcal(caltable='calG192.G1.inf', xaxis='time', yaxis='phase', \
        iteration='antenna', plotrange=[-1,-1,-180,180])

Now, let's solve for amplitudes on a per-scan interval, after applying the per-integration phases. Do these separately using gainfield so phases don't get transferred across fields. Note that gaincal uses linear interpolation of the previously determined phases by default. This is generally fine; we will set the interpolation to "nearest" (in time). 

# In CASA
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G2', \
        gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', \
                   'calG192.opacity', 'calG192.K0.b', 'calG192.B0.b', 'calG192.G1.int'], \
        gainfield=['', '', '', '', '3', '3', '0'], \
        interp=['', '', '', '', 'nearest', 'nearest', 'nearest'], \
        field='0', refant='ea05', solnorm=F, \
        solint='inf', gaintype='G', calmode='a')

#
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G2', \
        gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', \
                   'calG192.opacity', 'calG192.K0.b', 'calG192.B0.b', 'calG192.G1.int'], \
        gainfield=['', '', '', '', '3', '3', '1'], \
        interp=['', '', '', '', 'nearest', 'nearest', 'nearest'], \
        field='1', refant='ea05', solnorm=F, \
        solint='inf', gaintype='G', calmode='a', append=True)
#
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G2', \
        gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer', \
                   'calG192.opacity', 'calG192.K0.b', 'calG192.B0.b', 'calG192.G1.int'], \
        gainfield=['', '', '', '', '3', '3', '3'], \
        interp=['', '', '', '', 'nearest', 'nearest', 'nearest'], \
        field='3', refant='ea05', solnorm=F, \
        solint='inf', gaintype='G', calmode='a', append=True)
#
plotcal G2 per-scan amp ant ea06

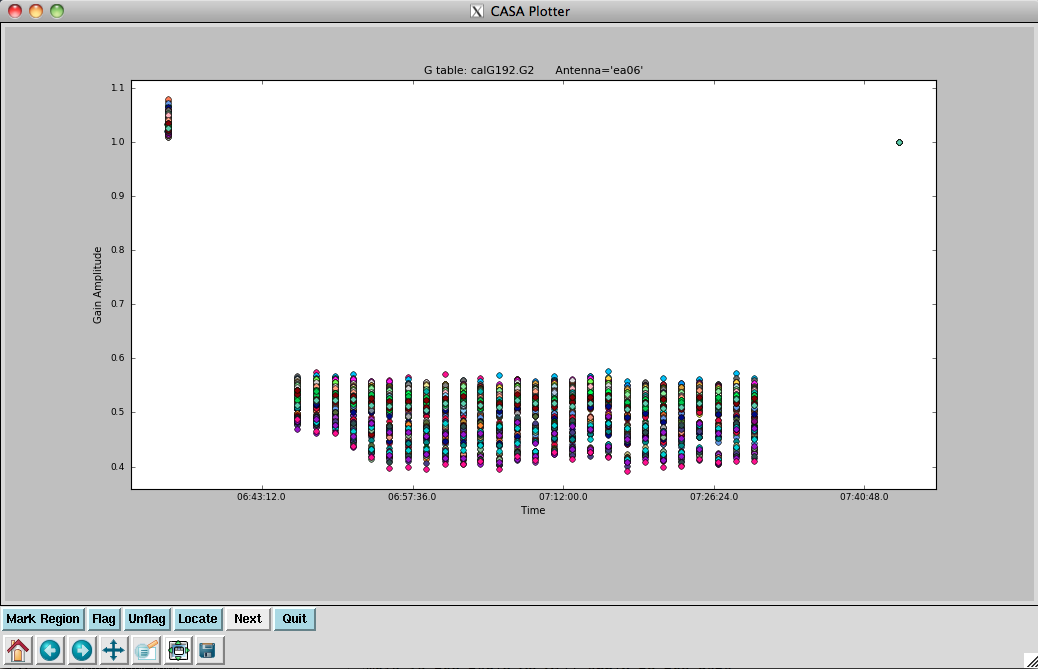
Let's have a look at the amplitudes: 

# In CASA
plotcal(caltable='calG192.G2', xaxis='time', yaxis='amp', \
        iteration='antenna')

We will apply this table (calG192.G2) to the data.

First, we need to use fluxscale to transfer the amplitude solutions from 3C147: 

# In CASA
flux2 = fluxscale(vis='G192_flagged_6s.ms', caltable='calG192.G2', \
                  fluxtable='calG192.F2', reference='0')

where we have now captured the return dictionary in the Python object flux2.

The logger output gives: 

Found reference field(s): 3C147
Found transfer field(s):  gcal-J0603+174 3c84-J0319+413
Flux density for gcal-J0603+174 in SpW=0 is: 0.252043 +/- 0.00779693 (SNR = 32.3259, N = 44)
Flux density for gcal-J0603+174 in SpW=1 is: 0.250608 +/- 0.00785259 (SNR = 31.9141, N = 44)
Flux density for gcal-J0603+174 in SpW=2 is: 0.250149 +/- 0.00783195 (SNR = 31.9395, N = 44)
Flux density for gcal-J0603+174 in SpW=3 is: 0.249326 +/- 0.00870076 (SNR = 28.6556, N = 44)
Flux density for gcal-J0603+174 in SpW=4 is: 0.24779 +/- 0.00860759 (SNR = 28.7873, N = 44)
<snip>
Flux density for gcal-J0603+174 in SpW=60 is: 0.280642 +/- 0.00884987 (SNR = 31.7115, N = 44)
Flux density for gcal-J0603+174 in SpW=61 is: 0.279742 +/- 0.00874457 (SNR = 31.9904, N = 44)
Flux density for gcal-J0603+174 in SpW=62 is: 0.278071 +/- 0.00910153 (SNR = 30.5521, N = 44)
Flux density for gcal-J0603+174 in SpW=63 is: 0.277588 +/- 0.00955455 (SNR = 29.0529, N = 44)
Flux density for 3c84-J0319+413 in SpW=0 is: 1.01141 +/- 0.0316725 (SNR = 31.9333, N = 44)
Flux density for 3c84-J0319+413 in SpW=1 is: 0.994812 +/- 0.0326974 (SNR = 30.4248, N = 44)
Flux density for 3c84-J0319+413 in SpW=2 is: 1.00473 +/- 0.0314246 (SNR = 31.9729, N = 44)
Flux density for 3c84-J0319+413 in SpW=3 is: 1.0042 +/- 0.0325531 (SNR = 30.8479, N = 44)
<snip>
Flux density for 3c84-J0319+413 in SpW=60 is: 1.00232 +/- 0.0243617 (SNR = 41.1434, N = 44)
Flux density for 3c84-J0319+413 in SpW=61 is: 1.00589 +/- 0.0248197 (SNR = 40.5277, N = 44)
Flux density for 3c84-J0319+413 in SpW=62 is: 1.01762 +/- 0.0240088 (SNR = 42.3855, N = 44)
Flux density for 3c84-J0319+413 in SpW=63 is: 1.01145 +/- 0.0249814 (SNR = 40.488, N = 44)
Fitted spectrum for gcal-J0603+174 with fitorder=1: Flux density = 0.264382 +/- 0.000149793 (freq=32.4488 GHz) spidx=-0.834342 +/- 0.00458913
Fitted spectrum for 3c84-J0319+413 with fitorder=1: Flux density = 1.00101 +/- 0.00121263 (freq=32.4488 GHz) spidx=0.00866148 +/- 0.0100409
Storing result in calG192.F2
Writing solutions to table: calG192.F2

You may see slightly different numbers on your machine. Note that "N" here is the number of antennas x the number of polarizations used for the calculations. In this case, there are 22 unflagged antennas and 2 polarizations.

Also, note that the flux-scaled amplitudes for 3C84 are all almost exactly 1 Jy. This is not because the actual flux of 3C84 is 1 Jy, of course. Rather, remember that the spectrum and flux information is now included in the bandpass table. When we apply the calibration, in the next section, you will see that 3C84's flux does indeed come out as expected.

Applying the Calibration and Final Editing

Next we apply all our accumulated calibration tables to the flagged MS. We apply these to the calibration fields individually, using the appropriate gainfields and interpolation for each:

  • For 3C147 (field 0) we did per-integration phase solutions and a single scan amplitude, so use "linear" and "nearest" interpolation, respectively;
  • for the nearby gain calibrator (field 1) we did 12-s phase and per-scan amplitude solutions, for which we will use "linear" and "nearest" interpolation, respectively;
  • for G192 (field 2), we will calibrate with field 1, using the per-scan solutions and "linear" interpolation; and finally,
  • for the bandpass calibrator 3C84 (field 3), we did per-integration phase solutions and a single scan amplitude, so use "linear" and "nearest" interpolation respectively.
3C147 with calibration applied
3C147 with calibration applied, amp vs. baseline
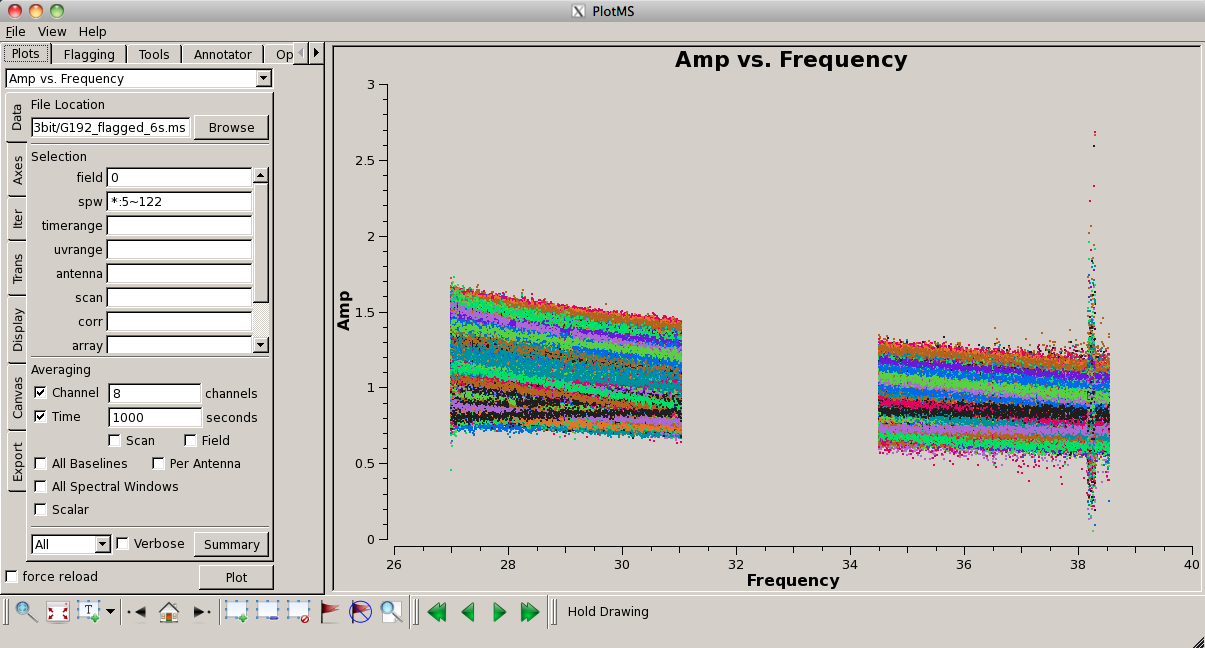
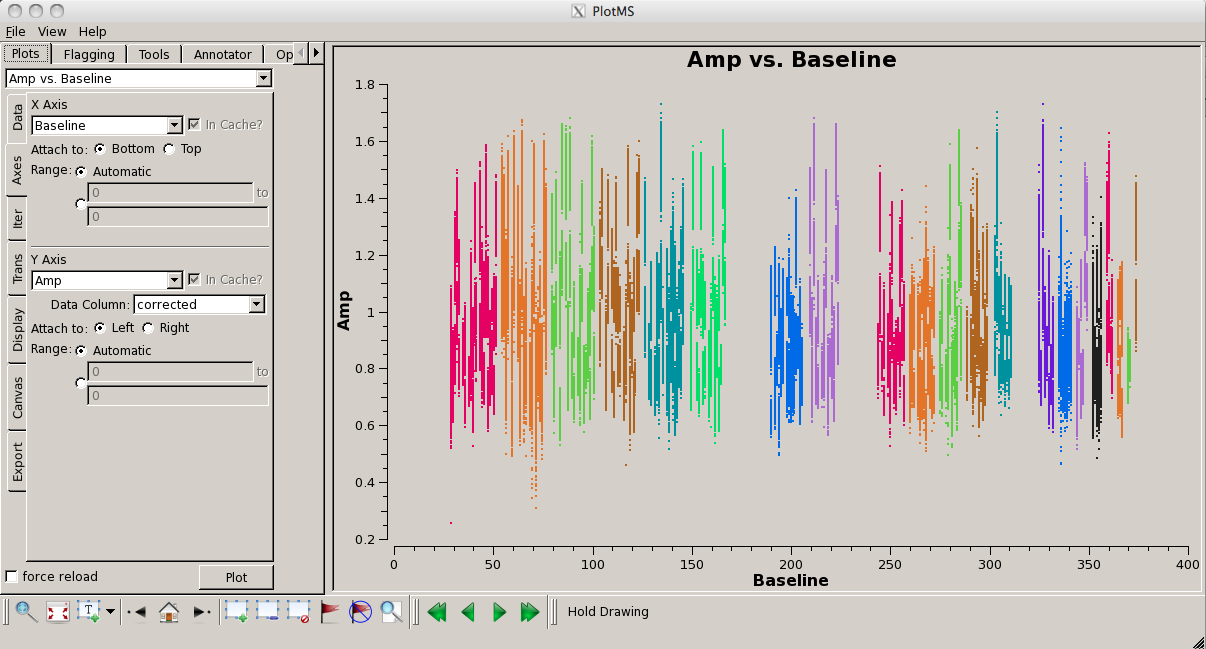
# In CASA
applycal(vis='G192_flagged_6s.ms', field='0', \
         gaintable=['calG192.antpos', 'calG192.requantizer', 'calG192.gaincurve', \
                    'calG192.opacity', 'calG192.K0.b', 'calG192.B0.b', \
                    'calG192.G1.int', 'calG192.G2'], \
         gainfield=['', '', '', '', '', '', '0', '0'],
         interp=['', '', '', '', 'nearest', 'nearest', 'linear', 'nearest'], calwt=False)
#
applycal(vis='G192_flagged_6s.ms', field='1', \
         gaintable=['calG192.antpos', 'calG192.requantizer', 'calG192.gaincurve', \
                    'calG192.opacity', 'calG192.K0.b', 'calG192.B0.b', \
                    'calG192.G1.int', 'calG192.F2'], \
         gainfield=['', '', '', '', '', '', '1', '1'],
         interp=['', '', '', '', 'nearest', 'nearest', 'linear', 'nearest'], calwt=False)
#
applycal(vis='G192_flagged_6s.ms', field='2', \
         gaintable=['calG192.antpos', 'calG192.requantizer', 'calG192.gaincurve', \
                    'calG192.opacity', 'calG192.K0.b', 'calG192.B0.b',\
                    'calG192.G1.inf', 'calG192.F2'], \
         gainfield=['', '', '', '', '', '', '1', '1'],
         interp=['', '', '', '', 'nearest', 'nearest', 'linear', 'linear'], calwt=False)
#
applycal(vis='G192_flagged_6s.ms', field='3', \
         gaintable=['calG192.antpos', 'calG192.requantizer', 'calG192.gaincurve', \
                    'calG192.opacity', 'calG192.K0.b', 'calG192.B0.b', \
                    'calG192.G1.int', 'calG192.F2'], \
         gainfield=['', '', '', '', '', '', '3', '3'],
         interp=['', '', '', '', 'nearest', 'nearest', 'linear', 'nearest'], calwt=False)

Because we used usesratch=False in setjy, the CORRECTED_DATA scratch column will be created the first time you run applycal. This will take a few minutes to write, increasing the size of the MS to 30 GB, and will store the calibrated data in the calibrated data column of the MS. 


IMPORTANT NOTES ON THE USE OF YOUR FLUXSCALE (F2) TABLE IN APPLYCAL:

* When we ran fluxscale and generated table calG192.F2 to transfer the amplitude solutions 
from our flux calibrator, fluxscale was run with incremental = False by default.  This 
means that the flux density scale correction factors derived from the primary flux calibrator 
were applied to the gains of the secondary calibrators.  So, the information from calG192.G2 
(which contains the amplitude solutions) is already accounted for in calG192.F2 and we will 
NOT need to supply calG192.G2 to our list of calibration tables for our secondary 
calibrators and science target fields (in this case, fields 1, 2, and 3 -- we do still need 
our G2 table for field 0 though!).

* It is also possible to run fluxscale with incremental = True.  In this case, only the 
scale correction factors are written out to the fluxtable, and calG192.G2 would need to be 
included in the list of gaintables for ALL fields at the applycal stage.


Now we examine the corrected data for 3C147. We will avoid spectral window edges and bin the data in time and frequency: 

# In CASA
plotms(vis='G192_flagged_6s.ms', field='0', \
       xaxis='frequency', yaxis='amp', \
       ydatacolumn='corrected', spw='*:5~122', \
       averagedata=True, avgchannel='8', \
       avgtime='1000s', coloraxis='baseline')

In this plot (see figure above, right) there is some suspicious data in the frequency range of 38.15-38.26 GHz (spw 29). We can plot around this frequency range with respect to time to see if it's isolated RFI or something we should flag from the whole dataset: 

# In CASA
plotms(vis='G192_flagged_6s.ms', field='0', \
       xaxis='time', yaxis='amp', \
       ydatacolumn='corrected', spw='29:5~122', \
       averagedata=True, avgchannel='16', \
       avgtime='', coloraxis='baseline')

Indeed, something looks wrong for the time interval 6:35:00-6:36:40 for this spectral window. Flag these data: 

# In CASA
flagdata(vis='G192_flagged_6s.ms', field='0', \
         spw='29', timerange='6:35:00~6:36:40')

It's also instructive to plot the corrected amplitude as a function of baseline: 

# In CASA
plotms(vis='G192_flagged_6s.ms', field='0', \
       xaxis='baseline', yaxis='amp', \
       ydatacolumn='corrected', spw='*:5~122', \
       averagedata=True, avgchannel='8', \
       avgtime='1000s', coloraxis='antenna1')

Looks good now!

Next, we examine the corrected data for the gain calibrator, J0603+174, again avoiding spectral window edges where we know the data will be noisy. This time, we will bin the data even more in frequency, since the source is fainter: 

# In CASA
plotms(vis='G192_flagged_6s.ms', field='1', \
       xaxis='frequency', yaxis='amp', \
       ydatacolumn='corrected', spw='*:5~122', \
       averagedata=True, avgchannel='32', \
       avgtime='6000s', coloraxis='baseline')

This generally looks quite good. Plot with respect to baseline as well: 

# In CASA
plotms(vis='G192_flagged_6s.ms', field='1', \
       xaxis='baseline', yaxis='amp', \
       ydatacolumn='corrected', spw='*:5~122', \
       averagedata=True, avgchannel='32', \
       avgtime='6000s', coloraxis='antenna1')

A few antennas look a little noisier, but nothing bad enough to flag for now.

Finally, we examine the corrected data for 3C84: 

# In CASA
plotms(vis='G192_flagged_6s.ms', field='3', \
       xaxis='frequency', yaxis='amp', \
       ydatacolumn='corrected', spw='*:5~122', \
       averagedata=True, avgchannel='8', \
       avgtime='1000s', coloraxis='baseline')

In general, it looks good, though there is one rather suspicious baseline dropping below the rest of the data. Box a few data points and use the "Locate" button to find that this is ea03&ea07. Plotting the same baseline for 3C147, we see that it doesn't look the best there either, so we will flag this baseline: 

# In CASA
flagdata(vis='G192_flagged_6s.ms', antenna='ea03&ea07')

Now, let's plot amplitude vs. baseline: 

# In CASA
plotms(vis='G192_flagged_6s.ms', field='3', \
       xaxis='baseline', yaxis='amp', \
       ydatacolumn='corrected', spw='*:5~122', \
       averagedata=True, avgchannel='8', \
       avgtime='1000s', coloraxis='antenna1')

Looks good!

  • In theory, the calibrated data should yield, in a simple case of a point source in the center of the field, a physical source visibility amplitude (the source flux density) and zero phase. Although in practice we never achieve such "perfection," it is very useful to gauge the "quality" of your calibrated data by plotting either amplitude vs. phase or real vs. imaginary in plotms for your calibrators. This type of plot is intended as a diagnostic for calibrators only - unless your science targets are extremely bright, compact, and located directly at the phase center of the field, this type of plot will appear quite noisy and be of little use. Note that you can plot the corrected data column (as shown below), or the corrected-model column (this will tend to reduce the scatter in the plots and remove the effects of any structure in the model itself). Let's take a look:
# In CASA
plotms(vis='G192_flagged_6s.ms', field='3', \
       xaxis='phase', yaxis='amp', \
       xdatacolumn='corrected', \
       ydatacolumn='corrected', spw='*:5~122', \
       averagedata=True, avgchannel='8', \
       avgtime='1000s', coloraxis='baseline')

For well-calibrated data, we expect a fairly small amount of scatter and compact distribution of the data. (Note: if you see arc or doughnut-like shapes in your dataset, try selecting the corrected-model column instead.) Although we can see in the figures below that our calibration was not perfect, there is less than 2 degrees of phase scatter, and a plot of amplitude vs. frequency shows that this is mostly in the highest frequencies. We will keep all of these data.

Recalibration

Since we flagged additional data, we will now go back and recalibrate: 

# In CASA
# Clear the corrected data and model from header
clearcal('G192_flagged_6s.ms', addmodel=False)

# Insert the flux density model for 3C147 into the MS
setjy(vis='G192_flagged_6s.ms', field='0', scalebychan=True, \
      model='3C147_A.im')

# Fill the MODEL column with 3C84's spectral information
setjy(vis='G192_flagged_6s.ms', field='3', scalebychan=True, \
      fluxdensity=[29.8756, 0, 0, 0], spix=-0.598929, \
      reffreq='32.4488GHz')

# Initial Phase Calibration
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G0.b.2', field='3', spw='*:60~68',\
        gaintable=['calG192.antpos', 'calG192.gaincurve', \
                  'calG192.requantizer', 'calG192.opacity'], \
        gaintype='G', refant='ea05', calmode='p', solint='int', minsnr=3) 

# Delay Calibration
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.K0.b.2', \
        field='3', spw='*:5~122', gaintype='K', \
        gaintable=['calG192.antpos', 'calG192.gaincurve', \
                  'calG192.requantizer', 'calG192.opacity','calG192.G0.b.2'], \
        refant='ea05', solint='inf', minsnr=3)

# Bandpass Calibration
bandpass(vis='G192_flagged_6s.ms', caltable='calG192.B0.b.2', \
         field='3', refant='ea05', solnorm=False, \
        gaintable=['calG192.antpos', 'calG192.gaincurve', 'calG192.requantizer',\
                   'calG192.opacity','calG192.G0.b.2', 'calG192.K0.b.2'], \
         bandtype='B', solint='inf')

# Phase Gain Calibration Solutions - Field 0
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G1.int.2', \
        field='0', refant='ea05', solnorm=F, \
        gaintable=['calG192.antpos', 'calG192.requantizer','calG192.gaincurve', \
                   'calG192.opacity', 'calG192.K0.b.2','calG192.B0.b.2'], \
        solint='int', gaintype='G', calmode='p')

# Phase Gain Calibration Solutions - Field 1
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G1.int.2', \
        field='1', refant='ea05', solnorm=F, \
        gaintable=['calG192.antpos', 'calG192.requantizer','calG192.gaincurve', \
                   'calG192.opacity', 'calG192.K0.b.2','calG192.B0.b.2'], \
        solint='12s', gaintype='G', calmode='p', append=True)

# Phase Gain Calibration Solutions - Field 3
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G1.int.2', \
        field='3', refant='ea05', solnorm=F, \
        gaintable=['calG192.antpos', 'calG192.requantizer','calG192.gaincurve', \
                   'calG192.opacity', 'calG192.K0.b.2','calG192.B0.b.2'], \
        solint='int', gaintype='G', calmode='p', append=True)

# Phase Gain Calibration Solutions - Field 1 - infinite solution interval 
# (Note: we will apply this table to our science target at the applycal stage.)
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G1.inf.2', \
        field='1', refant='ea05', solnorm=F, \
        gaintable=['calG192.antpos', 'calG192.requantizer','calG192.gaincurve', \
                   'calG192.opacity', 'calG192.K0.b.2','calG192.B0.b.2'], \
        solint='inf', gaintype='G', calmode='p')

# Amplitude Calibration Solutions - Field 0
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G2.2', \
        field='0', refant='ea05', solnorm=F, \
        gaintable=['calG192.antpos', 'calG192.requantizer', 'calG192.gaincurve', \
                   'calG192.opacity', 'calG192.K0.b.2', \
                   'calG192.B0.b.2', 'calG192.G1.int.2'], \
        gainfield=['', '', '', '', '3', '3', '0'], \
        interp=['', '', '', '', 'nearest', 'nearest', 'nearest'], \
        solint='inf', gaintype='G', calmode='a')

# Amplitude Calibration Solutions - Field 1
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G2.2', \
        field='1', refant='ea05', solnorm=F, \
        gaintable=['calG192.antpos', 'calG192.requantizer', 'calG192.gaincurve', \
                   'calG192.opacity', 'calG192.K0.b.2', \
                   'calG192.B0.b.2', 'calG192.G1.int.2'], \
        gainfield=['', '', '', '', '3', '3', '1'], \
        interp=['', '', '', '', 'nearest', 'nearest', 'nearest'], \
        solint='inf', gaintype='G', calmode='a', append=True)

# Amplitude Calibration Solutions - Field 3
gaincal(vis='G192_flagged_6s.ms', caltable='calG192.G2.2', \
        field='3', refant='ea05', solnorm=F, \
        gaintable=['calG192.antpos', 'calG192.requantizer', 'calG192.gaincurve', \
                   'calG192.opacity', 'calG192.K0.b.2', \
                   'calG192.B0.b.2', 'calG192.G1.int.2'], \
        gainfield=['', '', '', '', '3', '3', '3'], \
        interp=['', '', '', '', 'nearest', 'nearest', 'nearest'], \
        solint='inf', gaintype='G', calmode='a', append=True)

# Flux Scale Calibration Table (to apply to secondary calibrators)
flux3 = fluxscale(vis='G192_flagged_6s.ms', caltable='calG192.G2.2', \
                  fluxtable='calG192.F2.2', reference='0')

# Apply Calibration Tables to Field 0 (Flux Calibrator)
applycal(vis='G192_flagged_6s.ms', field='0', \
         gaintable=['calG192.antpos', 'calG192.requantizer', 'calG192.gaincurve', 'calG192.opacity',\
                    'calG192.K0.b.2', 'calG192.B0.b.2', 'calG192.G1.int.2', 'calG192.G2.2'], \
         gainfield=['', '', '', '', '', '', '0', '0'], \
         interp=['', '', '', '', 'nearest', 'nearest', 'linear', 'nearest'], calwt=False)

# Apply Calibration Tables to Field 1 (Phase Calibrator)
applycal(vis='G192_flagged_6s.ms', field='1', \
         gaintable=['calG192.antpos', 'calG192.requantizer', 'calG192.gaincurve', 'calG192.opacity',\
                    'calG192.K0.b.2', 'calG192.B0.b.2', 'calG192.G1.int.2', 'calG192.F2.2'], \
         gainfield=['', '', '', '', '', '', '1', '1'], \
         interp=['', '', '', '', 'nearest', 'nearest', 'linear', 'nearest'], calwt=False)

# Apply Calibration Tables to Field 2 (Science Target)
applycal(vis='G192_flagged_6s.ms', field='2', \
         gaintable=['calG192.antpos', 'calG192.requantizer', 'calG192.gaincurve', 'calG192.opacity',\
                    'calG192.K0.b.2', 'calG192.B0.b.2', 'calG192.G1.inf.2', 'calG192.F2.2'], \
         gainfield=['', '', '', '', '', '', '1', '1'], \
         interp=['', '', '', '', 'nearest', 'nearest', 'linear', 'linear'], calwt=False)

# Apply Calibration Tables to Field 3 (Bandpass Calibrator)
applycal(vis='G192_flagged_6s.ms', field='3', \
         gaintable=['calG192.antpos', 'calG192.requantizer', 'calG192.gaincurve', 'calG192.opacity',\
                    'calG192.K0.b.2', 'calG192.B0.b.2', 'calG192.G1.int.2', 'calG192.F2.2'], \
         gainfield=['', '', '', '', '', '', '3', '3'], \
         interp=['', '', '', '', 'nearest', 'nearest', 'linear', 'nearest'], calwt=False)

The recalibration will take a little while -- it was over 1.5 hours on our system -- so this is a good time to work on a different project or grab some lunch!

The fluxscale output this time around is slightly different: 

Found reference field(s): 3C147
Found transfer field(s):  gcal-J0603+174 3c84-J0319+413
Flux density for gcal-J0603+174 in SpW=0 is: 0.252049 +/- 0.00779748 (SNR = 32.3244, N = 44)
Flux density for gcal-J0603+174 in SpW=1 is: 0.250619 +/- 0.00784916 (SNR = 31.9294, N = 44)
Flux density for gcal-J0603+174 in SpW=2 is: 0.250149 +/- 0.00783732 (SNR = 31.9177, N = 44)
Flux density for gcal-J0603+174 in SpW=3 is: 0.249327 +/- 0.00869472 (SNR = 28.6757, N = 44)
Flux density for gcal-J0603+174 in SpW=4 is: 0.247794 +/- 0.00861206 (SNR = 28.7729, N = 44)
<snip>
Flux density for gcal-J0603+174 in SpW=60 is: 0.280654 +/- 0.00883115 (SNR = 31.78, N = 44)
Flux density for gcal-J0603+174 in SpW=61 is: 0.279748 +/- 0.00876293 (SNR = 31.924, N = 44)
Flux density for gcal-J0603+174 in SpW=62 is: 0.27807 +/- 0.00912204 (SNR = 30.4833, N = 44)
Flux density for gcal-J0603+174 in SpW=63 is: 0.277579 +/- 0.00954328 (SNR = 29.0863, N = 44)
Flux density for 3c84-J0319+413 in SpW=0 is: 1.01141 +/- 0.0316702 (SNR = 31.9356, N = 44)
Flux density for 3c84-J0319+413 in SpW=1 is: 0.994812 +/- 0.0326958 (SNR = 30.4262, N = 44)
Flux density for 3c84-J0319+413 in SpW=2 is: 1.00473 +/- 0.0314171 (SNR = 31.9805, N = 44)
Flux density for 3c84-J0319+413 in SpW=3 is: 1.00419 +/- 0.0325563 (SNR = 30.8449, N = 44)
Flux density for 3c84-J0319+413 in SpW=4 is: 1.00361 +/- 0.0333546 (SNR = 30.0893, N = 44)
<snip>
Flux density for 3c84-J0319+413 in SpW=60 is: 1.00232 +/- 0.0243542 (SNR = 41.156, N = 44)
Flux density for 3c84-J0319+413 in SpW=61 is: 1.00588 +/- 0.0248152 (SNR = 40.5347, N = 44)
Flux density for 3c84-J0319+413 in SpW=62 is: 1.01771 +/- 0.0239908 (SNR = 42.4207, N = 44)
Flux density for 3c84-J0319+413 in SpW=63 is: 1.01143 +/- 0.0249739 (SNR = 40.4996, N = 44)
Fitted spectrum for gcal-J0603+174 with fitorder=1: Flux density = 0.264388 +/- 0.000149708 (freq=32.4488 GHz) spidx=-0.834284 +/- 0.00458657
Fitted spectrum for 3c84-J0319+413 with fitorder=1: Flux density = 1.00109 +/- 0.00122518 (freq=32.4488 GHz) spidx=0.00940404 +/- 0.010148
3C147 with calibration applied, amp vs. phase
J0603+174 with calibration applied, amp vs. phase
3C84 with calibration applied, amp vs. phase

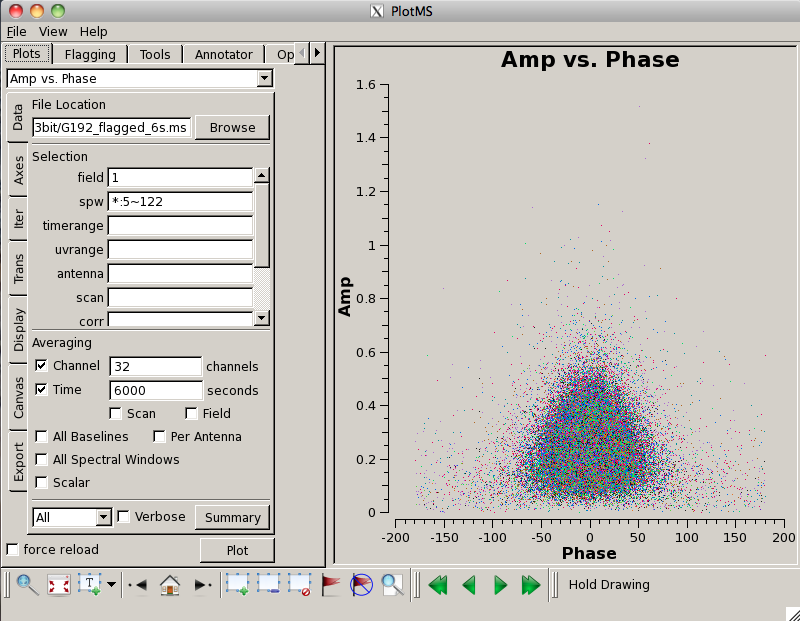
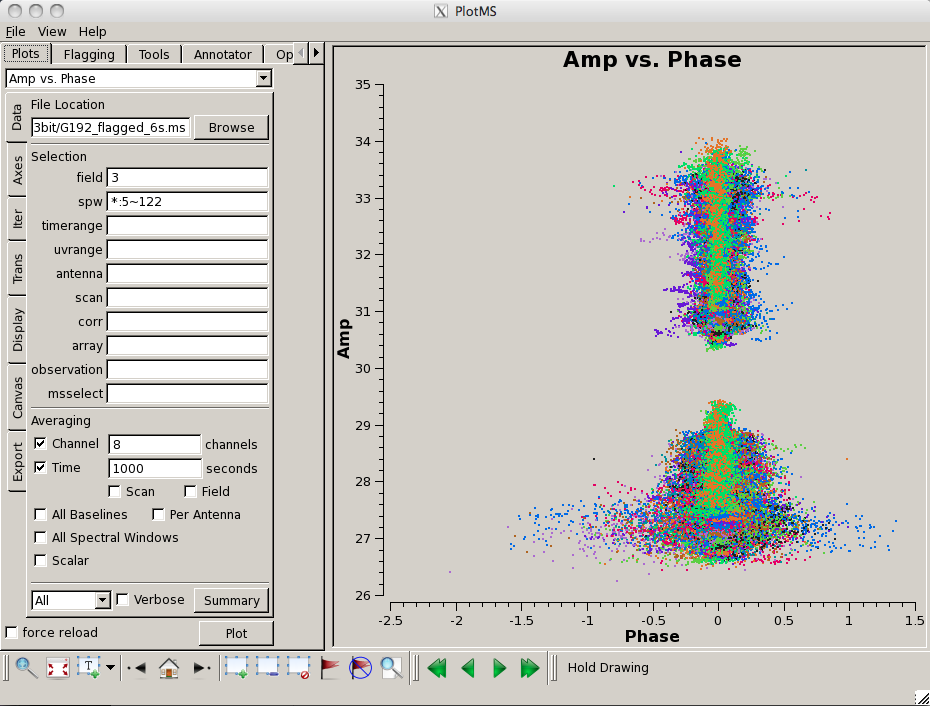
As always, it's a good idea to check the corrected data with plotms. Plots of corrected amplitude vs. baseline: 

# In CASA
plotms(vis='G192_flagged_6s.ms', field='0', \
       xaxis='baseline', yaxis='amp', \
       ydatacolumn='corrected', spw='*:5~122', \
       averagedata=True, avgchannel='8', \
       avgtime='1000s', coloraxis='antenna1')
#
plotms(vis='G192_flagged_6s.ms', field='1', \
       xaxis='baseline', yaxis='amp', \
       ydatacolumn='corrected', spw='*:5~122', \
       averagedata=True, avgchannel='32', \
       avgtime='6000s', coloraxis='antenna1')
#
plotms(vis='G192_flagged_6s.ms', field='3', \
       xaxis='baseline', yaxis='amp', \
       ydatacolumn='corrected', spw='*:5~122', \
       averagedata=True, avgchannel='8', \
       avgtime='1000s', coloraxis='antenna1')

And, finally, corrected amplitude vs. corrected phase: 

# In CASA
plotms(vis='G192_flagged_6s.ms', field='0', \
       xaxis='phase', yaxis='amp', \
       xdatacolumn='corrected', \
       ydatacolumn='corrected', spw='*:5~122', \
       averagedata=True, avgchannel='8', \
       avgtime='1000s', coloraxis='baseline')
#
plotms(vis='G192_flagged_6s.ms', field='1', \
       xaxis='phase', yaxis='amp', \
       xdatacolumn='corrected', \
       ydatacolumn='corrected', spw='*:5~122', \
       averagedata=True, avgchannel='32', \
       avgtime='6000s', coloraxis='baseline')
#
plotms(vis='G192_flagged_6s.ms', field='3', \
       xaxis='phase', yaxis='amp', \
       xdatacolumn='corrected', \
       ydatacolumn='corrected', spw='*:5~122', \
       averagedata=True, avgchannel='8', \
       avgtime='1000s', coloraxis='baseline')

Everything looks good, and the recalibration made only minor adjustments since there wasn't very much additional flagged data.

Now, split off the data for the calibrators and target field into separate MSs, so we can restore easily our calibrated dataset in case issues with data corruption arise. Before running split each time, we will remove any existing split data with the same name. Split will not automatically overwrite an existing MS. The inputs are: 

# In CASA
os.system('rm -rf 3C147_split_6s.ms')
split(vis='G192_flagged_6s.ms', outputvis='3C147_split_6s.ms', \
      datacolumn='corrected', field='0')
#
os.system('rm -rf J0603_split_6s.ms')
split(vis='G192_flagged_6s.ms', outputvis='J0603_split_6s.ms', \
      datacolumn='corrected', field='1')
#
os.system('rm -rf G192_split_6s.ms')
split(vis='G192_flagged_6s.ms', outputvis='G192_split_6s.ms', \
      datacolumn='corrected', field='2')
#
os.system('rm -rf 3C84_split_6s.ms')
split(vis='G192_flagged_6s.ms', outputvis='3C84_split_6s.ms', \
      datacolumn='corrected', field='3')

We can now move on to imaging!

Imaging

The G192 data were taken in the VLA's highest-resolution A-configuration at Ka-band. To determine the best parameters for imaging, it helps to start with the relevant information in the Observational Status Summary:

  • The synthesized beam is expected to be ~0.059" at 33 GHz with a primary beam field-of-view of 1.4 arcmin (82").

Our data spans 27.0-38.4 GHz: this is a relatively very large fractional bandwidth (about 35%), resulting in substantial variation of the field of view over the entire frequency range. The FOV = 45 arcmin / Frequency (GHz), giving 1.7 arcmin at 27 GHz and 1.2 arcmin at 38.4 GHz. Likewise, the synthesized beam ranges from 0.072" at 27 GHz to 0.051" at 38.4 GHz. We want to subsample the synthesized beam by a factor of 3-5, so we will use a cellsize of 0.015". To cover the full FOV, we would want a minimum image size of 6800 pixels. However, there isn't much outside the center of the field for G192 -- this is what gave us leeway to average to 6 seconds -- so, to save time, we will only image a 1280x1280 pixel field (19.2"x19.2").

We will also use the Briggs robust (with robust=0.5) weighting, which is a compromise between uniform and natural weighting. Briggs weighting will produce an image with a reasonable resolution, but will allow us to still see larger scale structure. Noise from sidelobes will also be reduced compared to Natural weighting.

Due to the numerology of FFTW's (which clean uses under the hood for FFTs) optimal sizes, imsize should be an even number with prime factors chosen from 2, 3, 5, and 7. Since 1280 = (2^8)*5, it will give us optimal clean performance. Note that clean will still run if imsize does not have prime factors 2, 3, 5, or 7 (it will just be a bit slower) but you should always choose an even number.

For more information on using clean, in particular on using the interactive GUI, see EVLA_Continuum_Tutorial_3C391#Imaging.

NOTE: If you are pressed for time, then you might want to jump ahead to cleaning both basebands, and while it is cleaning you can read the other Imaging descriptions.

Cleaning a single spectral window

Let us start by interactively cleaning one spectral window in the lower-frequency baseband (spw 48). (For Ka-band, the higher-numbered spectral-window baseband is actually the lower-frequency baseband.)

Note that interrupting clean by Ctrl+C may corrupt your visibilities -- you may be better off choosing to let clean finish. We are working on a way to prevent this from happening, but for the moment it's best to avoid Ctrl+C.

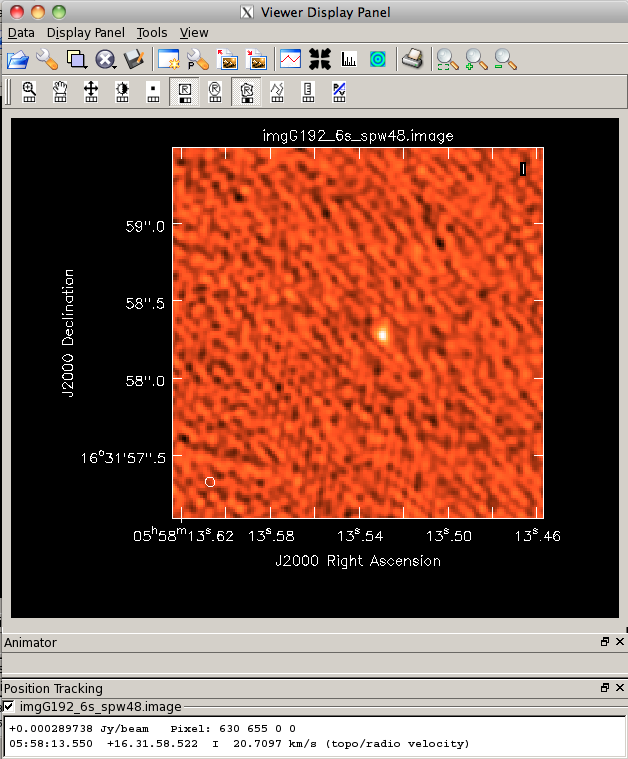
viewer showing clean spw48 1280x1280 restored image
# In CASA
# Removing any previous cleaning information
# This assumes you want to start this clean from scratch
# If you want to continue this from a previous clean run, 
# the rm -rf system command should be be skipped
os.system ('rm -rf imgG192_6s_spw48*')
clean(vis='G192_split_6s.ms', spw='48:5~122', \
      imagename='imgG192_6s_spw48', \
      mode='mfs', nterms=1, niter=10000, \
      imsize=[1280], cell=['0.015arcsec'], \
      imagermode='csclean', cyclefactor=1.5, \
      weighting='briggs', robust=0.5, \
      interactive=True)
  • Click on the wrench icon to bring up the Data Display Options and change the color scale to "Hot Metal 1" under "basic settings"
  • Zoom in 4 times
  • Draw a box the point-like source and double-click inside the box to set your clean box (or clean "mask")

Change the number of iterations on the upper left to 50. (Note: this number is independent from the niter clean parameter, which applies to cleaning in mode interactive = False and is used if you click the right-pointing arrow button on the upper right to continue cleaning non-interactively.)

  • The curved arrow on the upper right should now be highlighted in green. Click this green icon to clean the boxed source.
  • Stop cleaning when the residuals look like the noise (this will probably happen after the first 50-100 iterations).
  • To stop, click the red button.

When clean is finished, we can look at the restored image: 

# In CASA
viewer('imgG192_6s_spw48.image')

The restored image is shown above.

Check the rms of the residuals using the imstat task: 

# In CASA
mystat = imstat('imgG192_6s_spw48.residual')
print 'Residual standard deviation = '+str(mystat['sigma'][0]) + ' Jy'

In this particular case, it's 136 uJy; yours may be slightly different.

Cleaning the lower-frequency baseband

clean boxes spw32-63
clean spw32-63 restored image center

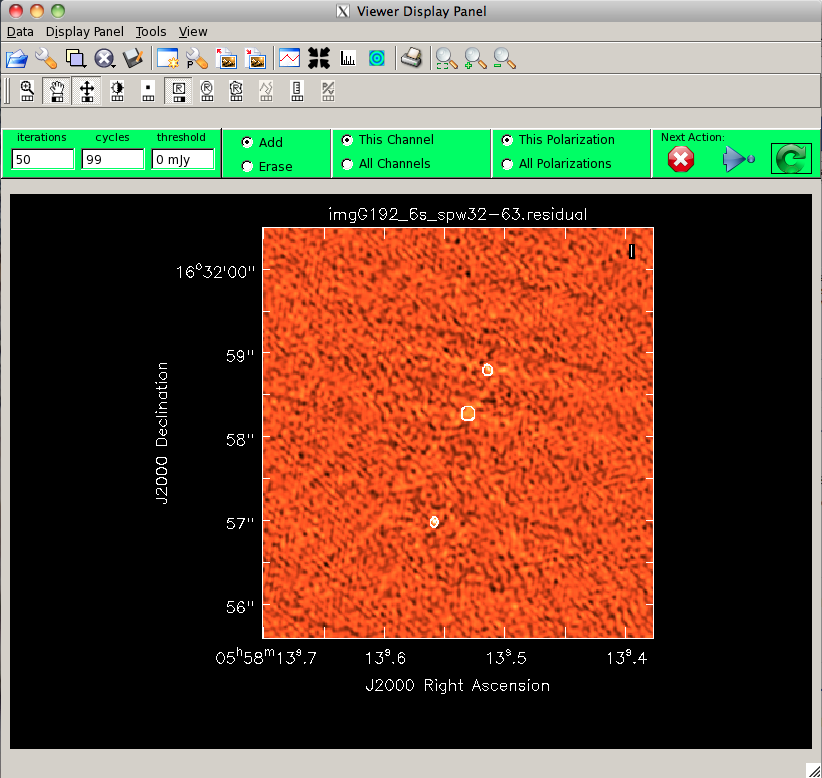
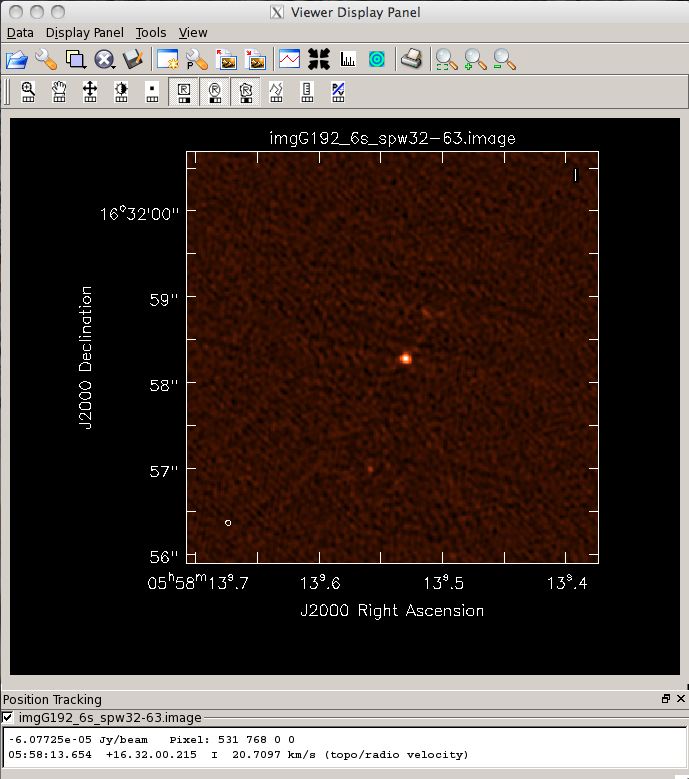
Here we will image the entire lower-frequency baseband (spw 32-63). Follow the same iterative procedure as before, and get the best residuals you can without "cleaning the noise". 

# In CASA
# Removing any previous cleaning information
# This assumes you want to start this clean from scratch
# If you want to continue this from a previous clean run, 
# the rm -rf system command should be be skipped
os.system ('rm -rf imgG192_6s_spw32-63*')
clean(vis='G192_split_6s.ms', spw='32~63:5~122', \
      imagename='imgG192_6s_spw32-63', \
      mode='mfs', nterms=1, niter=10000, \
      imsize=[1280], cell=['0.015arcsec'], \
      imagermode='csclean', cyclefactor=1.5, \
      weighting='briggs', robust=0.5, \
      interactive=True)
#
viewer('imgG192_6s_spw32-63.image')
mystat = imstat('imgG192_6s_spw32-63.residual')
print 'Residual standard deviation = '+str(mystat['sigma'][0]) + ' Jy'
  • Because of the increased bandwidth, it is easier to see two fainter point sources.
  • Be careful cleaning sources that lie near or on sidelobe peaks.
  • Clean the central emission region first (50 iterations) to reduce the sidelobe level before adding any more components. The screenshot above shows the interactive clean window after 50 iterations with the three clean boxes we created.

For this run, the rms is 23 uJy. To the right is a zoom-in on the center of the restored image.

Finally, we will fit the central point source to determine its flux. First, create a box region around the source in the viewer, and save it as G192.crtf (View -> Regions -> File; see the screenshot below right). Note that you can drag the Regions window out of the main Viewer window if it's taking up too much space.

Use this region to fit the source flux: 

# In CASA
myfit = imfit('imgG192_6s_spw32-63.image', region='G192.crtf')
print 'Source flux = '+str(myfit['results']['component0']['flux']['value'][0])+'+/-'+str(myfit['results']['component0']['flux']['error'][0]) + ' Jy'
saving CASA region for G192

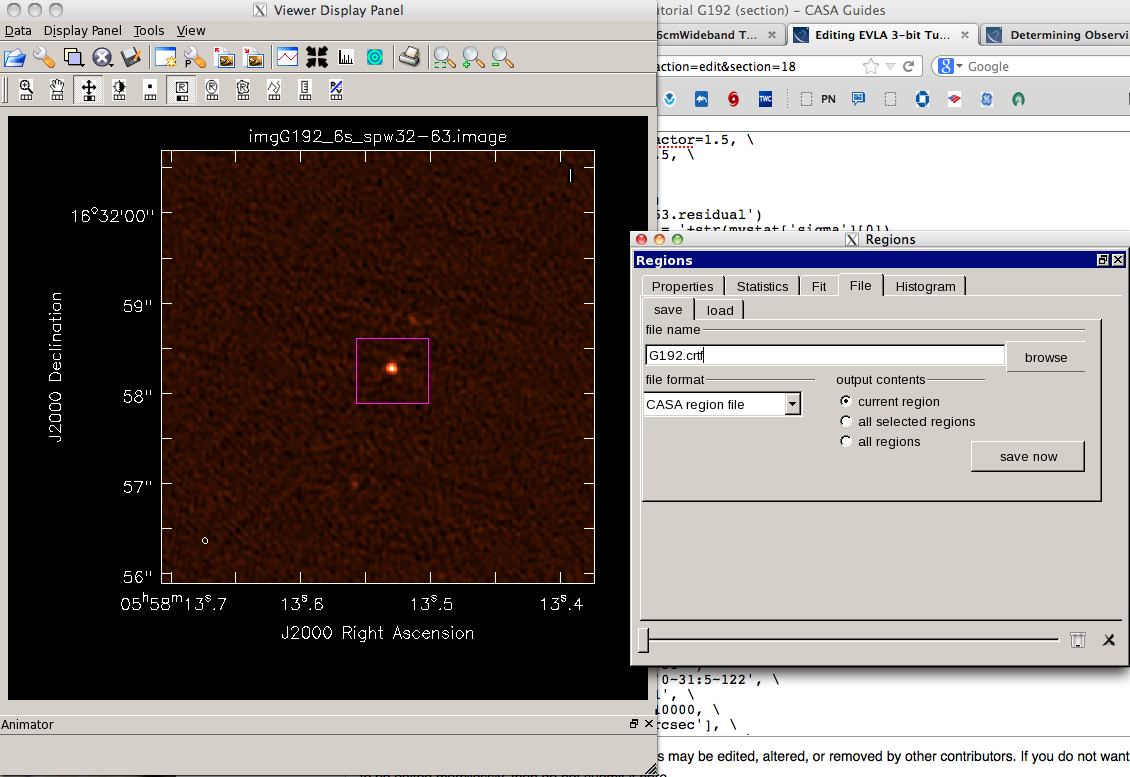
The derived flux is 2.64 +/- 0.04 mJy. Also, have a look at the logger output: 

Image component size (convolved with beam) ---
       --- major axis FWHM:     80.01 +/- 0.98 marcsec
       --- minor axis FWHM:     71.51 +/- 1.01 marcsec
       --- position angle: 63.2 +/- 2.2 deg
   
Clean beam size ---
       --- major axis FWHM: 0.06 arcsec
       --- minor axis FWHM: 0.06 arcsec
       --- position angle: 29.00 deg
Image component size (deconvolved from beam) ---
       --- major axis FWHM:     51.3 +/- 1.8 marcsec
       --- minor axis FWHM:     37.7 +/- 2.3 marcsec
       --- position angle: 78.5 +/- 6.3 deg

The deconvolved size of around 51.3 x 37.7 milliarcseconds corresponds to a size of roughly 90 AU (assuming a distance of approximately 2 kpc). Indeed, this is thought to be the accretion disk around the protostar! (See this article for the initial report, using 43 GHz data, of the accretion disk around G192.)

Cleaning the upper-frequency baseband

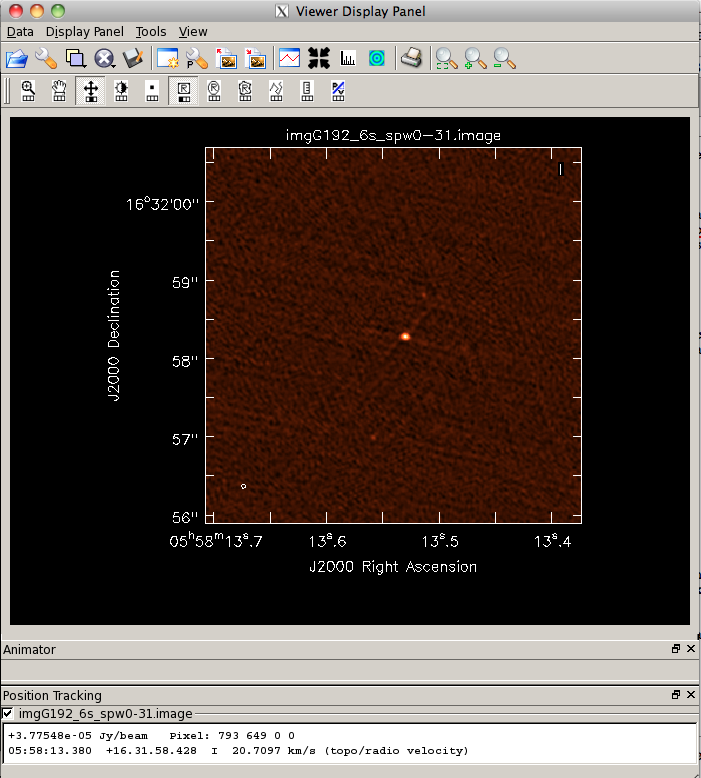
clean spw32-63 restored image center

Now we will image the entire upper-frequency baseband (spw 0-31). Follow the same iterative procedure as before, and get the best residuals you can without "cleaning the noise". 

# In CASA
# Removing any previous cleaning information
# This assumes you want to start this clean from scratch
# If you want to continue this from a previous clean run, 
# the rm -rf system command should be be skipped
os.system ('rm -rf imgG192_6s_spw0-31*')
clean(vis='G192_split_6s.ms', spw='0~31:5~122', \
      imagename='imgG192_6s_spw0-31', \
      mode='mfs', nterms=1, niter=10000, \
      imsize=[1280], cell=['0.015arcsec'], \
      imagermode='csclean', cyclefactor=1.5, \
      weighting='briggs', robust=0.5, \
      interactive=True)
#
viewer('imgG192_6s_spw0-31.image')
mystat = imstat('imgG192_6s_spw0-31.residual')
print 'Residual standard deviation = '+str(mystat['sigma'][0]) + ' Jy'
myfit = imfit('imgG192_6s_spw0-31.image', region='G192.crtf')
print 'Source flux = '+str(myfit['results']['component0']['flux']['value'][0])+'+/-'+str(myfit['results']['component0']['flux']['error'][0]) + ' Jy'

For this run, the rms is 31 uJy, and the source flux is 3.07 +/- 0.06 mJy. Again, imfit finds that the source is slights extended and provides a deconvolved size. To the right is a zoomed-in image of the center of the restored image.

Cleaning both basebands using two MFS Taylor terms

From the individual images of the upper- and lower-frequency basebands, we can see that the source spectrum of G192 is relatively flat, with a spectral index of approximately

[math]\displaystyle{ \alpha = \log(S_1 / S_2) / \log(\nu_1 / \nu_2) }[/math] [math]\displaystyle{ = \log(3.07 / 2.64) / \log(36.5 / 29.0) }[/math] [math]\displaystyle{ = 0.66, }[/math]

where the convention for the spectral index alpha is that

[math]\displaystyle{ S \propto \nu^\alpha. }[/math]

Within a single baseband, neglecting to account for the spectral index will make little difference -- however, when we combine the two basebands, it is best to account for the spectral variation across the total band. For this, we will set nterms=2 in clean.

This option creates two "Taylor term" images -- an average intensity image (with suffix .image.tt0), and a spectral slope image (with suffix .image.tt1), which is intensity x alpha (where alpha is the spectral index). For convenience, there is also a spectral index image (with suffix .image.alpha). These Taylor expansions are with respect to the "reference frequency" of the image (by default the center frequency of the selected spectral window, but can be specified using the reffreq parameter in clean).

We will clean the complete dataset using nterms=2. Note: if you prefer, you can clean your image using interactive = False. For non-interactive cleaning, make sure you define a clean mask with mask='imgG192_6s_spw0-31.mask' or mask='imgG192_6s_spw32-63.mask' to use these as a starting point rather than running an interactive clean session. You can also draw a new region file from scratch in the Viewer, save the region as a .crtf file, and supply this file to the mask parameter in clean. If you set interactive = False you should also modify the threshold and niter parameters to avoid over-cleaning (the threshold parameter should always be higher than the expected theoretical rms noise; for an estimation of the rms noise for this image see below). 

# In CASA
# Removing any previous cleaning information
# This assumes you want to start this clean from scratch
# If you want to continue this from a previous clean run, 
# the rm -rf system command should be be skipped
os.system ('rm -rf imgG192_6s_spw0-63_mfs2*')
clean(vis='G192_split_6s.ms', spw='0~63:5~122', \
      imagename='imgG192_6s_spw0-63_mfs2', \
      mode='mfs', nterms=2, niter=10000, gain=0.1, \
      threshold='0.0mJy', psfmode='clark', imsize=[1280], \
      cell=['0.015arcsec'], \
      weighting='briggs', robust=0.5, interactive=True)
#
mystat = imstat('imgG192_6s_spw0-63_mfs2.residual.tt0') + ' Jy'
print 'Residual standard deviation = '+str(mystat['sigma'][0])
myfit = imfit('imgG192_6s_spw0-63_mfs2.image.tt0', region='G192.crtf') + ' Jy'
print 'Source flux = '+str(myfit['results']['component0']['flux']['value'][0])+'+/-'+str(myfit['results']['component0']['flux']['error'][0])

For this run, the rms is 19.7 uJy, and the peak of the emission from G192 is 1.8 mJy, and the integrated source flux is 2.86 +/- 0.04 mJy (as before, the source is found to be extended). You can use the viewer to load the average intensity image: 

# In CASA
viewer('imgG192_6s_spw0-63_mfs2.image.tt0')
clean spw0-63 mfs nterms=2 load alpha with LEL

Since the spectral index image is very noisy in the lower-intensity regions, we will use immath task to filter the spectral index image explicitly, using a Lattice Expression Language (LEL) expression: 

# In CASA
immath(imagename=['imgG192_6s_spw0-63_mfs2.image.alpha', 
                  'imgG192_6s_spw0-63_mfs2.image.tt0'],
       mode='evalexpr',
       expr='IM0[IM1>2.0E-4]',
       outfile='imgG192_6s_spw0-63_mfs2.image.alpha.filtered')

This will use 0.2 mJy (10 x the rms) as the cutoff. You can then view or manipulate the filtered alpha image as usual.

We can also use LEL to filter the alpha image on intensity on-the-fly when we load the raster via the Open Data panel, by specifying a LEL string in the LEL box instead of selecting the image from the directory listing. The LEL string 

'imgG192_6s_spw0-63_mfs2.image.alpha'['imgG192_6s_spw0-63_mfs2.image.tt0'>2E-04]

will replicate what we did above. The middle figure to the right shows the Open Data panel with our LEL string in it. Just click the Raster button to load this.

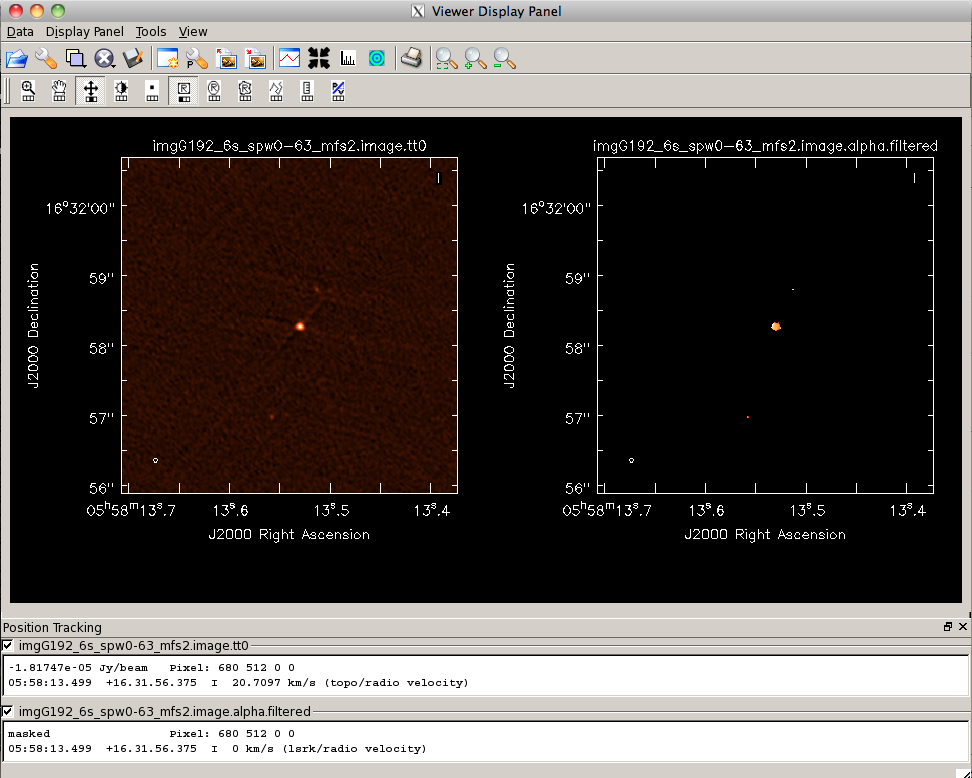
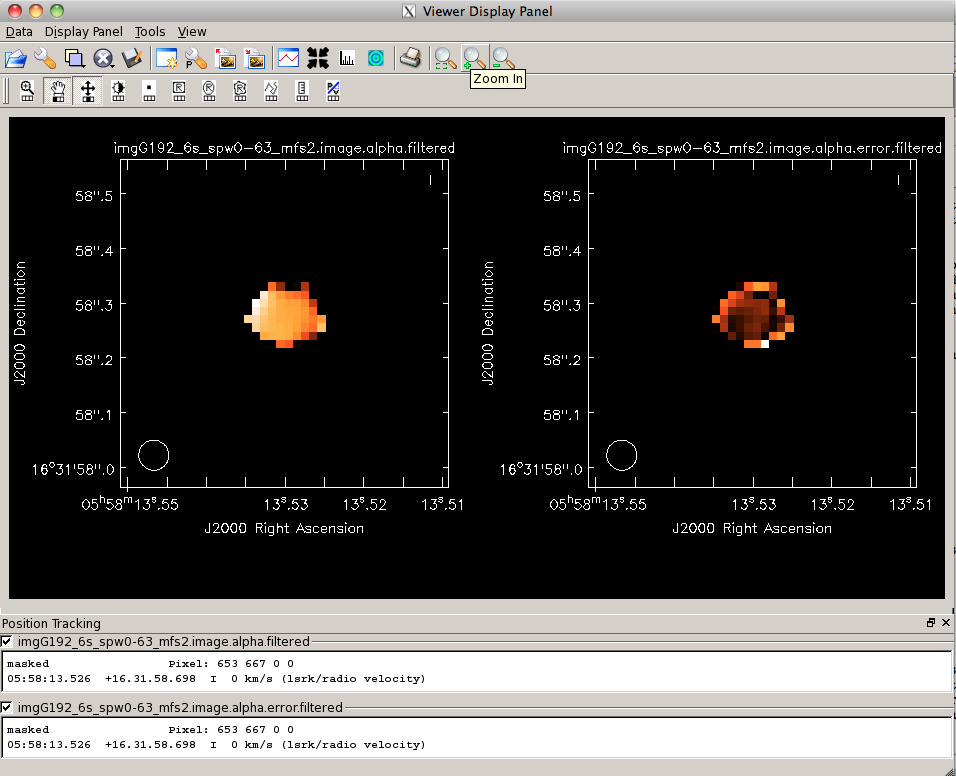
clean spw0-63 mfs nterms=2 tt0 and alpha (filtered at 0.2 mJy in tt0)
clean spw0-63 mfs nterms=2 alpha and alpha error (filtered at 0.2 mJy in tt0)

The lower panel to the right shows the intensity and LEL-filtered alpha images side-by-side in the viewer, zoomed in on the brightest source of emission. Creating a box around this region and double-clicking reveals that the spectral index varies from around -0.33 to 1.4, with the pixels in the brightest portion of the image at around 0.8, similar to what we found by hand using the information from the single-baseband images.

To get a sense of the probable errors for this spectral index information, we perform a similar filtering operation on the imgG192_6s_spw0-63_mfs2.image.alpha.error>/tt> image: 

# In CASA
immath(imagename=['imgG192_6s_spw0-63_mfs2.image.alpha.error', 
                  'imgG192_6s_spw0-63_mfs2.image.tt0'],
       mode='evalexpr',
       expr='IM0[IM1>2E-4]',
       outfile='imgG192_6s_spw0-63_mfs2.image.alpha.error.filtered')

Now, we can load both the alpha and alpha.error images side-by-side in the viewer: 

# In CASA
viewer('imgG192_6s_spw0-63_mfs2.image.alpha.filtered')

As one might expect, the errors are higher outside the emission peak (see the screenshot on the right). However, it seems possible that the .error image is underestimating the true errors on the mfs-calculated spectral index, since the central brightest pixels only have errors of around 0.15, when we calculated an alpha of 0.66 (compared with the mfs-calculated alpha of 0.8). If we were planning to use the reported spectral index information for publication, we would need to go through a more thorough investigation of the actual error analysis and spectral index.

Analyzing the image

From imstat on the final combined-baseband image, we got an image rms of 19.7 uJy. A reasonable question to ask is what we would expect the image rms to be: one way to estimate this is to determine the effective on-source time, then input the appropriate parameters to the VLA exposure calculator to determine the expected rms. 

# In CASA
listobs('G192_split_6s.ms', listunfl=True)

This will show: 

ID   Code Name                RA               Decl           Epoch   SrcId      nRows    nUnflRows
0    NONE G192.16-3.84        05:58:13.540000 +16.31.58.30001 J2000   0        2931890   2901697.32

Note that the "nUnflRows," or number of unflagged rows, is 2901697.32. Every row is a single baseline-integration-spw record, as you probably learned if you looked at the MS with browsetable. So, to use this to calculate an "effective" exposure time for the VLA Exposure Calculator for 22 antennas (22*21/2 = 231 baselines), we find that time = 2901697.32 * 6 seconds / 231 baselines / 64 spectral windows = 1178 seconds = 19.6 minutes. Our effective bandwidth is 7552 MHz, taking into account the spectral window selection. Using the median frequency of 32.7 GHz, the VLA exposure calculator reports that we should achieve an image rms of 13.5 uJy. Although our actual rms is somewhat higher, this is not unexpected; we have not done any self-calibration, for example.

Next, we will do some rough analysis on the spectral index to determine an intensity-weighted mean spectral index for G192. The .image.tt1 from our mfs is an intensity times alpha image (see the figure to the right). Let's filter this Taylor-term image by intensity as we did with the .alpha image: 

# In CASA
# Removing any file output from previous runs, so immath will proceed
os.system('rm -rf imgG192_6s_spw0-63_mfs2.image.tt1.filtered')
immath(imagename=['imgG192_6s_spw0-63_mfs2.image.tt1',
                  'imgG192_6s_spw0-63_mfs2.image.tt0'],
       mode='evalexpr',
       expr='IM0[IM1>2E-4]',
       outfile='imgG192_6s_spw0-63_mfs2.image.tt1.filtered')
#
# Removing any file output from previous runs, so immath will proceed
os.system('rm -rf imgG192_6s_spw0-63_mfs2.image.tt0.filtered')
immath(imagename=['imgG192_6s_spw0-63_mfs2.image.tt0'],
       mode='evalexpr',
       expr='IM0[IM0>2E-4]',
       outfile='imgG192_6s_spw0-63_mfs2.image.tt0.filtered')

We can use the same region we created for imstat. Let us compute the intensity-weighted spectral index over this region by averaging these masked images using imstat and computing the ratio: 

# In CASA
mystat = imstat('imgG192_6s_spw0-63_mfs2.image.tt1.filtered',
                region='G192.crtf')
avgtt0alpha = mystat['mean'][0]
#
mystat = imstat('imgG192_6s_spw0-63_mfs2.image.tt0.filtered',
                region='G192.crtf')
avgtt0 = mystat['mean'][0]
avgalpha = avgtt0alpha / avgtt0
print 'G192 intensity-weighted alpha = ' + str(avgalpha)

We get: 

G192 intensity-weighted alpha = 0.737300481129

This is pretty close to the value we found from the single-baseband images of alpha = 0.66, validating the results from mfs with nterms=2.

What to do next: some exercises for the user

Here are a number of things you can try after completing this tutorial:

  1. Use self-calibration to improve the data and re-clean to make a better image. See this tutorial for more information on self-calibration.
  2. Investigate the data further to see if any more flagging is needed.
  3. Image the calibrators. What sort of dynamic range can you get on them? Is self-calibration needed (and if so what dynamic range do you get when you use it)?
  4. Try the rflag algorithm in the flagdata task to automatically flag bad data based on the statistics of the data (though there is not much left, really). There is more information on running the rflag algorithm in this tutorial.

Credits

The Jansky Very Large Array (VLA) is a partnership of the United States, Canada, and Mexico. The VLA is funded in the United States by the National Science Foundation, in Canada by the National Research Council, and in Mexico by the Comisión Nacional de Investigación Científica y Tecnológica (CONICyT).

The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc.

Last checked on CASA Version 4.2.0.

Retrieved from "https://casaguides.nrao.edu/index.php?title=EVLA_3-bit_Tutorial_G192&oldid=15620"