VLA Self-calibration Tutorial-CASA5.7.0: Difference between revisions
| Line 145: | Line 145: | ||
'''Wide-field effects''': Large images may require additional consideration due to non-coplanar baselines (the W-term). In CASA, this is usually addressed by turning on the W-project algorithm. [https://casa.nrao.edu/casadocs/casa-5.4.1/synthesis-imaging/wide-field-imaging-full-primary-beam See this link to CASAdocs for a more detailed discussion.] | '''Wide-field effects''': Large images may require additional consideration due to non-coplanar baselines (the W-term). In CASA, this is usually addressed by turning on the W-project algorithm. [https://casa.nrao.edu/casadocs/casa-5.4.1/synthesis-imaging/wide-field-imaging-full-primary-beam See this link to CASAdocs for a more detailed discussion.] | ||
We can estimate whether our image requires W-projection by calculating the recommended number of W-planes using this formula taken from the | We can estimate whether our image requires W-projection by calculating the recommended number of W-planes using this formula taken from page 392 of the NRAO 'white book', | ||
<math> | <math> | ||
| Line 160: | Line 160: | ||
which gives a W_max of 5680 wavelengths. From the listobs output above, we | which gives a W_max of 5680 wavelengths. From the listobs output above, we see that the highest frequency channel is 6.512 GHz which corresponds to a wavelength of | ||
Revision as of 20:22, 3 December 2019
This page is currently under construction.
Introduction
This CASA guide describes the basics of the self-calibration process and in particular how to choose parameters to achieve the best result. Even after the initial calibration of the dataset using the amplitude calibrator and the phase calibrator, there are likely to be residual phase and/or amplitude errors in the data. Self-calibration is the process of using an existing model, usually constructed from imaging the data itself, to reduce the remaining phase and amplitude errors in your image.
The dataset that will be used for this CASA tutorial is an observation of a massive galaxy cluster at z~1 which was taken with the goal to determine the morphology of the radio sources within the cluster.
Data for this Tutorial
Obtaining the Data
The original observation has been calibrated using the VLA CASA Pipeline. It can be downloaded from the archive by searching for the following SDM name: 17B-197.sb34290063.eb34589992.58039.86119096065.
We will instruct the archive to apply the calibration solutions derived by the original pipeline execution. Therefore, the measurement set (MS) we will be downloading will contain both the raw (uncalibrated) visibilities and the calibrated visibilities, which will appear in the 'DATA' and 'CORRECTED_DATA' columns of the MS, respectively.
The raw data alone is 11.4 GB, and this will grow to 20.5 GB after applying the calibration.
As an alternative to requesting these data from the archive you may instead download the calibrated MS directly here:
-- link to data download --
A smaller data set is also available (see Section Splitting the Target Visibilities)
Observation Details
First, we will start CASA in the directory containing the data and then collect some basic information about the observation. The task listobs can be used to display the individual scans comprising the observation, the frequency setup, source list, and antenna locations.
# in CASA
listobs(vis='17B-197.sb34290063.eb34589992.58039.86119096065.ms')
A portion of the listobs output appears below:
================================================================================
MeasurementSet Name: 17B-197.sb34290063.eb34589992.58039.86119096065.ms MS Version 2
================================================================================
Observer: Prof. Anthony H. Gonzalez Project: uid://evla/pdb/34052589
Observation: EVLA
Data records: 5290272 Total elapsed time = 2853 seconds
Observed from 13-Oct-2017/20:40:09.0 to 13-Oct-2017/21:27:42.0 (UTC)
ObservationID = 0 ArrayID = 0
Date Timerange (UTC) Scan FldId FieldName nRows SpwIds Average Interval(s) ScanIntent
13-Oct-2017/20:40:09.0 - 20:45:03.0 1 0 J1549+5038 550368 [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15] [3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3] [SYSTEM_CONFIGURATION#UNSPECIFIED]
20:45:06.0 - 20:50:03.0 2 0 J1549+5038 555984 [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15] [3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3] [CALIBRATE_AMPLI#UNSPECIFIED,CALIBRATE_PHASE#UNSPECIFIED]
20:50:06.0 - 20:59:27.0 3 1 MOO_1506+5136 1050192 [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15] [3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3] [OBSERVE_TARGET#UNSPECIFIED]
20:59:30.0 - 21:00:51.0 4 0 J1549+5038 151632 [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15] [3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3] [CALIBRATE_AMPLI#UNSPECIFIED,CALIBRATE_PHASE#UNSPECIFIED]
21:00:54.0 - 21:10:15.0 5 1 MOO_1506+5136 1050192 [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15] [3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3] [OBSERVE_TARGET#UNSPECIFIED]
21:10:18.0 - 21:11:39.0 6 0 J1549+5038 151632 [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15] [3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3] [CALIBRATE_AMPLI#UNSPECIFIED,CALIBRATE_PHASE#UNSPECIFIED]
21:11:42.0 - 21:21:03.0 7 1 MOO_1506+5136 1050192 [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15] [3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3] [OBSERVE_TARGET#UNSPECIFIED]
21:21:06.0 - 21:22:27.0 8 0 J1549+5038 151632 [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15] [3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3] [CALIBRATE_AMPLI#UNSPECIFIED,CALIBRATE_PHASE#UNSPECIFIED]
21:22:30.0 - 21:27:03.0 9 2 3C286 511056 [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15] [3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3] [CALIBRATE_BANDPASS#UNSPECIFIED,CALIBRATE_FLUX#UNSPECIFIED]
21:27:06.0 - 21:27:42.0 10 2 3C286 67392 [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15] [3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3] [CALIBRATE_BANDPASS#UNSPECIFIED,CALIBRATE_FLUX#UNSPECIFIED]
(nRows = Total number of rows per scan)
Fields: 3
ID Code Name RA Decl Epoch SrcId nRows
0 NONE J1549+5038 15:49:17.468534 +50.38.05.78820 J2000 0 1561248
1 NONE MOO_1506+5136 15:06:20.353700 +51.36.53.63460 J2000 1 3150576
2 NONE 3C286 13:31:08.287984 +30.30.32.95886 J2000 2 578448
Spectral Windows: (16 unique spectral windows and 1 unique polarization setups)
SpwID Name #Chans Frame Ch0(MHz) ChanWid(kHz) TotBW(kHz) CtrFreq(MHz) BBC Num Corrs
0 EVLA_C#A0C0#0 64 TOPO 4488.000 2000.000 128000.0 4551.0000 12 RR RL LR LL
1 EVLA_C#A0C0#1 64 TOPO 4616.000 2000.000 128000.0 4679.0000 12 RR RL LR LL
2 EVLA_C#A0C0#2 64 TOPO 4744.000 2000.000 128000.0 4807.0000 12 RR RL LR LL
3 EVLA_C#A0C0#3 64 TOPO 4872.000 2000.000 128000.0 4935.0000 12 RR RL LR LL
4 EVLA_C#A0C0#4 64 TOPO 5000.000 2000.000 128000.0 5063.0000 12 RR RL LR LL
5 EVLA_C#A0C0#5 64 TOPO 5128.000 2000.000 128000.0 5191.0000 12 RR RL LR LL
6 EVLA_C#A0C0#6 64 TOPO 5256.000 2000.000 128000.0 5319.0000 12 RR RL LR LL
7 EVLA_C#A0C0#7 64 TOPO 5384.000 2000.000 128000.0 5447.0000 12 RR RL LR LL
8 EVLA_C#B0D0#8 64 TOPO 5488.000 2000.000 128000.0 5551.0000 15 RR RL LR LL
9 EVLA_C#B0D0#9 64 TOPO 5616.000 2000.000 128000.0 5679.0000 15 RR RL LR LL
10 EVLA_C#B0D0#10 64 TOPO 5744.000 2000.000 128000.0 5807.0000 15 RR RL LR LL
11 EVLA_C#B0D0#11 64 TOPO 5872.000 2000.000 128000.0 5935.0000 15 RR RL LR LL
12 EVLA_C#B0D0#12 64 TOPO 6000.000 2000.000 128000.0 6063.0000 15 RR RL LR LL
13 EVLA_C#B0D0#13 64 TOPO 6128.000 2000.000 128000.0 6191.0000 15 RR RL LR LL
14 EVLA_C#B0D0#14 64 TOPO 6256.000 2000.000 128000.0 6319.0000 15 RR RL LR LL
15 EVLA_C#B0D0#15 64 TOPO 6384.000 2000.000 128000.0 6447.0000 15 RR RL LR LL
Initial Inspection
Since we have obtained the calibrated visibilites for the calibrator fields, we can now take this opportunity to investigate at high signal-to-noise the magnitude and timescale of the phase fluctuations we will be trying to correct for with selfcal.
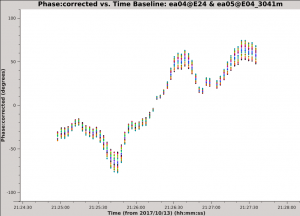
Looking at the output of listobs we see that there is a long scan on the amplitude calibrator, 3C 286 (field ID 2). We will plot the calibrated phase vs. time on a single baseline:
# in CASA
plotms(vis='17B-197.sb34290063.eb34589992.58039.86119096065.ms', xaxis='time', yaxis='phase', ydatacolumn='corrected', field='2', antenna='ea05', correlation='RR,LL', avgchannel='64', iteraxis='baseline', coloraxis='spw')
- vis='17B-197.sb34290063.eb34589992.58039.86119096065.ms' : To plot visibilities from the pipeline calibrated MS.
- xaxis='time', yaxis='phase' : To set time as the x-axis and phase as the y-axis of the plot.
- ydatacolumn='corrected' : To plot the calibrated data (from the CORRECTED_DATA column).
- field='2' : To select visibilities from field ID 2, i.e., the amplitude calibrator 3C 286.
- antenna='ea05', iteraxis='baseline' : To view a single baseline at a time.
- correlation='RR,LL' : To plot both parallel-hand correlation products.
- avgchannel='64' : To average all channels in each SPW to increase signal-to-noise. Since the bandpass solutions have been applied to these data the channels will average coherently.
- coloraxis='spw' : To plot each SPW as a different color, which will make it easier to distinguish them.
Use the 'Next Iteration' button of the plotms GUI to cycle through additional baselines. You should see plots that look similar to the example image of the ea04-ea05 baseline. The plotted data have a mean of zero phase because the pipeline calibration solutions have already been applied. The phase is seen to vary with time over a large range (in some cases more than +/- 100 degrees) and the variations appear to be smooth over time scales of a few integrations. All of the spectral windows and both correlations follow the same trend with time. Additionally, the magnitude of the phase variations is larger for the higher frequency spectral windows, a pattern that is consistent with a change in atmospheric density.
Optional extra steps: Create and inspect similar plots using scan 2 of the phase calibrator field (J1549+5038). Repeat for baselines to other antennas.
Splitting the Target Visibilities
It is essential that we split the calibrated visibilities for the target we want to self-calibrate, meaning that the visibilities of the target source get copied from the CORRECTED_DATA column of the pipeline calibrated MS to the DATA column of a new measurement set. CASA calibration tasks always operate by comparing the visibilities in the DATA column to the source model, where the source model is given by either the MODEL_DATA column, a model image or component list, or the default model of a 1 Jy point source at the phase center. In the same way that the calibration pipeline used the raw visibilities in the DATA column to solve for calibration tables and then created the CORRECTED_DATA column by dividing the DATA column by these tables, self-calibration will work by comparing the pipeline calibrated visibilities (in the DATA column of the split MS) to a model, solving for self-calibration tables, and then creating a new CORRECTED_DATA column by applying the self-calibration tables.
# in CASA
split(vis='17B-197.sb34290063.eb34589992.58039.86119096065.ms',datacolumn='corrected',field='1', correlation='RR,LL', outputvis='obj.ms')
- vis='17B-197.sb34290063.eb34589992.58039.86119096065.ms' : The input visibilities for split. Here, these are the visibilities produced by the pipeline.
- datacolumn='corrected' : To copy the calibrated visibilities from the input MS.
- field='1' : The field ID of the target we want to self-calibrate.
- correlation='RR,LL' : To select only the parallel hand correlations. This will make the output data set smaller by about a factor of two.
- outputvis='obj.ms' : The name of the new measurement set that split will create.
-- The output MS can be can be directly downloaded here: obj.ms (3.4 GB) --
Initial Imaging
Prior to solving for self-calibration solutions we need to make an initial model of the target field. We will generate this model by deconvolving the target field using the task tclean. But before doing so, there are several imaging considerations that we should address prior to making this model (discussed below):
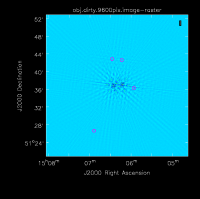
Image field-of-view: Ideally, we want our self-calibration model to include all of the sources present in the data (e.g., sources near the edge of the primary beam or in the first sidelobe). This is typically achieved by making an image large enough to encompass all of the apparent sources, or by making a smaller image of the target plus one or more outlier fields. We will start with a large dirty image of the entire primary beam (PB) in order to better understand the sources in the galaxy cluster plus any background sources that will need to be cleaned. A rule of thumb for the VLA is that the FWHM of the PB in arcminutes is approximately 45 * (1 GHz / nu). For our C-band observations, the VLA primary beam is ~8' FWHM. In order to image the entire PB and the first sidelobe we need an image field of view that is a few times larger. We will choose a 24' field-of-view for our initial image.
Image cell size: The observations were taken in C-band in the B-configuration, which gives a resolution of 1.2". We want at least 5 image pixels across the resolution of 1.2", therefore we require a cell size of 0.24"/pixel or smaller.
Image pixel size: We can convert our desired field-of-view to pixels using the cell size: 24 arcmin * (60 arcsec / 1 arcmin) * (1 pixel / 0.24 arcsec) = 6000 pixels. However, when making large images, CASA will run faster if we choose an image size that is optimized for the FFT algorithm. The recommendation is to choose an image size that can be expressed as 5*2^n*3^m. This is so that after CASA applies an internal padding factor of 1.2, the images being used in the FFTs can be broken down into small 2x2 and 3x3 matrices. So we will choose an optimized image size of 6480 (n=4,m=4) for this image.
Wide-field effects: Large images may require additional consideration due to non-coplanar baselines (the W-term). In CASA, this is usually addressed by turning on the W-project algorithm. See this link to CASAdocs for a more detailed discussion.
We can estimate whether our image requires W-projection by calculating the recommended number of W-planes using this formula taken from page 392 of the NRAO 'white book',
[math]\displaystyle{ N_{wprojplanes} = 0.5 \times \left ( \frac{W_{max}}{\lambda} \right ) \times \left ( \frac{I_{FOV}}{1\, \mathrm{radian}} \right ) }[/math]
where W_max is the range of extreme w-values in the data set, lambda is the shorted wavelength being imaged and I_FOV is the image field-of-view. We can calculate W_max with the following lines of code:
# in CASA
ms.open('obj.ms')
ms.range('w')
ms.close()
which gives a W_max of 5680 wavelengths. From the listobs output above, we see that the highest frequency channel is 6.512 GHz which corresponds to a wavelength of
# in CASA
tclean(vis='obj.ms',imagename='obj.dirty.6480pix',imsize=6480, cell='0.24arcsec', pblimit=-0.1 )
- cell='0.24arcsec': The size of an image pixel (see above).
- imsize=6480: The number of pixels across one side of the (square) image.
- pblimit=-0.1: We set this to a small negative number to turn off the PB mask.
Wide-band imaging: Our images will combine data from all spectral windows, spanning a frequency range of about 4.5-6.5 GHz (a fractional bandwidth of about 36%). Each source's amplitude may vary substantially over this frequency range, due to either the source's intrinsic spectral variation and/or the frequency dependence of the VLA's primary beam. To mitigate these errors during deconvolution we will use deconvolver='mtmfs' and nterms=2 . For further discussion, see the CASA documentation for wide-band imaging and the VLA Imaging CASAguide.
Imaging weights: Briggs not natural.
Now, we can make a preliminary clean image before rounds of self-calibration to use as a reference. This image will provide the starting model that is required by the calibration routines, and it will showcase why we need self-calibration for these data.
# in CASA
tclean(vis='obj.ms',imagename='obj.prelim_clean.3am',imsize=750,cell='0.24arcsec',weighting='briggs',deconvolver='mtmfs',niter=1000,interactive=True)
- cell='0.24arcsec': The observations were taken in C-band in configuration B which gives a resolution of 1.2". Thus to 5 elements across the resolution of 1.2", we require a cell size of 0.24"/pixel.
- imsize=750: For the science, we are only interested in the sources within ~1.5' of the cluster center. From the dirty image we also know that there are not any particularly problematic outliers in the field nearby, thus we create a 3' image. Thus to get an image of the entire PB, we use an imsize of 750 pixels.
- deconvolver='mtmfs': Josh:I believe you recommended this to be based on the width of the band of observations with respect to the observing frequency -- I don't remember the qualitative guidelines for center_frequency/total_bandwidth. This corrects for the spectral slope when wideband width -- in this case 1.87GHz.
- niter=1000: Set a relatively large number of iterations as a starting point.
- interactive=True: So we can interactively place the mask.
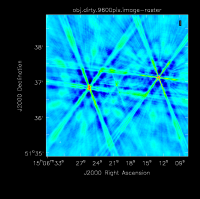
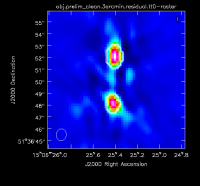
For this preliminary clean, we place circles around each of the strong sources in turn:
- The rightmost source (Figure 2A) -- continue forward and let it clean by pressing the green circle arrow
- The leftmost double-lobed source (Figure 2B)
- The middle source (Figure 2C)
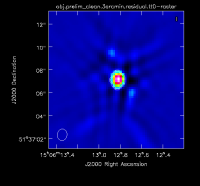
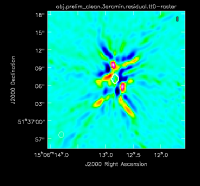
At this point, there is no more emission that is believably real and we stop cleaning (a total of about 225 iterations)(see Figure 2D for an example of the artifacts that are not believable). The final cleaned image without the help of self-cal (Figure 3) shows a lot of artifacts and demonstrates a need for self-calibration (Josh: more details about why need self-cal? or why should we think self-cal would help?).
File:Prelim clean 3.png Figure 2C: The mask for the middle. |
Self-Calibration Process Outline
What is self-calibration (self-cal)? Self-calibration is the process of using an existing model, often constructed from imaging the data itself, to reduce the remaining phase and amplitude errors in your image. First you create a model using the data itself (using tclean), then iteratively improve this model with further rounds of self-cal (using Template:Gaincall to compare the model to the data and applycal to create a corrected data column).
A few typical cases in which self-cal will help improve the image (Josh: any other ideas?):
- Extensive sidelobes/artifacts from the source of interest or outliers
Each "round" of self-calibration follows a general procedure:
- Conservatively clean target and save the model. Using interactive clean, only include the pixels that you are absolutely certain are real emission as this will be the basis of the model for calibration.
- Use gaincal with a particular solution interval to calculate a table of solutions.
- Check the solutions using plotcal.
- Determine if the solutions should be applied (or if it is time to stop). Is there structure to the solutions?
- Use applycal to apply the table of solutions to the data.
- Use split to make the calibrated data with the applied solutions, the new data (the starting point for the next round of self-cal).
- Start the next round of self-cal.
This guide will cover:
- How to do the self-calibration process in general.
- How to determine optimal selfcal parameters (e.g. solution interval).
- When to stop self-cal.
First Round of Self-Calibration
For this first round of self-cal, we will explore various parameters in order to settle on the optimal parameters. First, we make a conservative clean, meaning that we include in the mask only the pixels that we are absolutely convinced that is real emission.
Preliminary Clean
# in CASA
tclean(vis='obj.ms',imagename='obj.sc_init',imsize=750,cell='0.24arcsec',weighting='briggs',deconvolver='mtmfs',niter=500,savemodel='modelcolumn',interactive=True)
We keep the same parameters as before, but reduce the number of iterations and include savemodel='modelcolumn' which is crucial. By including savemodel, we ensure that the model is explicitly saved to the model column.
Show an example of the masks we used and say approximately how many iterations. It looks like we did just the left source and the middle source. Do you perhaps know why we didn't include the right source at all in the mask? This is perplexing to me as that is the main source that we would want to model I would think.
Check that the model saved?
Choose a Solution Interval
Next, we investigate which solution interval (solint) is optimal for this particular dataset. We will do this by generating and viewing the corrections calculated over several solution intervals (namely on the order of the integration time, 15 seconds, and 45 seconds) using gaincal.
# in CASA
gaincal(vis='obj.ms',caltable='sc1_tb_int',solint='int',refant='ea24',calmode='p',gaintype='T')
- caltable='sc1_tb_int':'Name the calibration tables something intuitive to distinguish each one. In this case, sc1 for self-calibration round 1, tb for table, and int for a solution interval of the integration time.
- solint='int': For this first calibration table, we choose the solutions to be calculated on the level of the integration time (3 seconds in this case) in order to get a sense of the structure and durations of the variations.
- refant='ea24': Choose a reference antenna that is near the center of the array but not the exact center (Josh: I think that is why we chose this one?). In order to view what antennas are near the center use plotants.
- calmode='p': Start with phase only calibration as that is where the most gain is to be had (there is a way more technical way to say that).
- gaintype='T': It is often a good idea to combine the polarizations to understand the overall data.
To view these solutions, we use plotcal.
# in CASA
plotcal(caltable='sc1_tb_int.gain',xaxis='time',yaxis='phase',iteration='antenna',subplot=321)
- xaxis='time' & yaxis='phase': View the phase variations over time with respect to antenna 24.
- iteration='antenna': View the corrections for each antenna.
- subplot=321: It can be helpful to view multiple plots at once, as we will be scrolling through the solutions for each antenna. In this case, 3 rows and two columns.
Show examples of a few of these. gaincal calculates the gains for each antenna/spwid are determined from the ratio of the data column (raw data), divided by the model column, for the specified data selection.(Josh: a bit more about technically what we are looking at and how they affect the data? -- these are the variations in phase between pairs of antennas which can cause the artifacts?) Each color represents a different spectral window. There is definitely structure we want to correct for. We use this solint = int to get a sense of on what time scale the variations occur and the amplitude of the variations. Use the zoom in feature to zoom in on these variations and estimate what the time interval of these variations are. The solint of int shows the variations, but we postulate that a 15 second or 45 second interval would catch these overall variations better.
# in CASA
gaincal(vis='obj.ms',caltable='sc1_tb_15s',solint='15s',refant='ea24',calmode='p',gaintype='T')
gaincal(vis='obj.ms',caltable='sc1_tb_45s',solint='45s',refant='ea24',calmode='p',gaintype='T')
Images of both of these. Comparing the two, we see that they both encapsulate the structure of the variations, however solint=15s encapsulates the variations the best. Thus we choose to apply sc1_tb_15s.gain. Note the amplitude of these variations in sc1_tb_15s.gain; they are typically up to 40 degrees and -60 yo -80 degrees.
Apply Calibration
# in CASA
applycal(vis='obj.ms',gaintable='sc1_tb_15s.gain')
Other potential intervals that could be useful to use are 5 seconds and 60 seconds. Additionally, if the plotcal reveals no structure in these intervals, you can combine the spws together and apply a combined solution by setting combine='spw' (you will have to set spwmap=[0 x number of spectral windows] in apply cal in order to tell CASA to apply the combined solution to all of the spectral windows -- in this case spwmap = [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0])
Our goal is to create a better model of the source using the data itself to create a better image. The process with calculating corrections and applying them has (if done correctly) reduced the errors allowing us to make a better image and create a better model. applycal applies the solutions to the (raw) MS DATA column and writes the calibrated data into the CORRECTED_DATA column, thus for determining the next order/level of corrections during the next round of calibration we need to make the corrected data column the data column.
# in CASA
split(vis='obj.ms',outputvis='sc1_obj.ms')
Second Round of Self-Calibration
We will go through the same process again: image, gaincal, applycal, and image. This time the image we create at first will be an indication if the solutions we applied made a difference.
# in CASA
tclean(vis='obj.ms',imagename='obj.sc1',imsize=750,cell='0.24arcsec',weighting='briggs',deconvolver='mtmfs',niter=500,savemodel='modelcolumn',interactive=True)
Larger mask.
# in CASA
gaincal(vis='obj.ms',caltable='sc2_tb_15s',solint='15s',refant='ea24',calmode='p',gaintype='T')
- solint='15s': Since we found a good interval of 15 seconds previously, we move forward with 15s.
Josh: do we want to suggest/show other solution intervals? Do we want to comment on using various intervals -- when is it useful to do several rounds with one interval versus several rounds with each a different solint?
View the solutions.
# in CASA
plotcal(caltable='sc1_tb_int.gain',xaxis='time',yaxis='phase',iteration='antenna',subplot=321)
We can see our corrections made a difference. In particular notice the amplitude of the phase variations, instead of +_60-80 degress they are fractions of a degree. This indicates that we have corrected for a majority of the variations.
When to stop: (looking at amplitude of corrections, image has improved/dynamical range)
Notes about amplitude corrections (?) (mode='ap' or 'a').
When self-cal helped, but didn't improve the image enough: (suggestions for other things to do)