VLA Continuum Tutorial 3C391-CASA6.2.0: Difference between revisions
No edit summary |
Tag: Undo |
||
| (34 intermediate revisions by 6 users not shown) | |||
| Line 8: | Line 8: | ||
The observations were taken with a full-polarization correlator setup and include a polarization calibrator. For the purposes of this tutorial, we will focus on the continuum (Stokes I) calibration and imaging. (See the CASAguide on radio galaxy 3C75 for an introduction to polarization calibration.) | The observations were taken with a full-polarization correlator setup and include a polarization calibrator. For the purposes of this tutorial, we will focus on the continuum (Stokes I) calibration and imaging. (See the CASAguide on radio galaxy 3C75 for an introduction to polarization calibration.) | ||
== How to Use This CASA Guide == | |||
There are a number of possible ways to run CASA, described in more detail in [[Getting Started in CASA]]. In brief, there are at least three different ways to use CASA: | |||
* Interactively examining task inputs. In this mode, one types '''taskname''' to load the task, '''inp''' to examine the inputs, and '''go''' once those inputs have been set to your satisfaction. Allowed inputs are shown in blue and bad inputs are colored red. The input parameters themselves are changed one by one, e.g., ''selectdata=True''. Screenshots of the inputs to various tasks used in the data reduction below are provided, to illustrate which parameters need to be set. More detailed help can be obtained on any task by typing '''help ''taskname'''''. Once a task is run, the set of inputs are stored and can be retrieved via '''tget ''taskname'''''; subsequent runs will overwrite the previous '''tget''' file. | |||
* Pseudo-interactively via task function calls. In this case, all of the desired inputs to a task are provided at once on the CASA command line. This tutorial is made up of such calls, which were developed by looking at the inputs for each task and deciding what needed to be changed from default values. For task function calls, only parameters that you want to be different from their defaults need to be set. | |||
* Non-interactively via a script. A series of task function calls can be combined together into a script, and run from within CASA via '''execfile('scriptname.py')'''. This and other CASA Tutorial Guides have been designed to be extracted into a script via the script extractor by using the method described at the [[Extracting_scripts_from_these_tutorials]] page. Should you use the script generated by the script extractor for this CASA Guide, be aware that it will require some small amount of interaction related to the plotting, occasionally suggesting that you close the graphics window and hitting return in the terminal to proceed. It is in fact unnecessary to close the graphics windows (it is suggested that you do so purely to keep your desktop uncluttered). | |||
If you are a relative novice or just new to CASA, it is strongly recommended to work through this tutorial by cutting and pasting the task function calls provided below after you have read all the associated explanations. Work at your own pace, look at the inputs to the tasks to see what other options exist, and read the help files. Later, when you are more comfortable, you might try to extract the script, modify it for your purposes, and begin to reduce other data. | |||
== Obtaining the Data == | == Obtaining the Data == | ||
| Line 31: | Line 43: | ||
tar xzvf 3c391_ctm_mosaic_10s_spw0.ms.tgz | tar xzvf 3c391_ctm_mosaic_10s_spw0.ms.tgz | ||
</pre> | </pre> | ||
== The Observation == | == The Observation == | ||
| Line 70: | Line 70: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
listobs(vis='3c391_ctm_mosaic_10s_spw0.ms') | obs_dict = listobs(vis='3c391_ctm_mosaic_10s_spw0.ms') | ||
</source> | </source> | ||
A Python dictionary containing some of the observation's fundamental information is created in the variable ''obs_dict'' and the [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.information.listobs.html listobs] output will show up in the CASA logger window: | |||
<pre style="background-color: #fffacd;"> | <pre style="background-color: #fffacd;"> | ||
| Line 257: | Line 257: | ||
</pre> | </pre> | ||
Notice in this listobs, the first scans are the fields that will be used for calibration before scanning the target fields we want to observe. Note that the antenna IDs (which are numbered sequentially up to the total number of antennas in the array; 0 through 25 in this instance) do not correspond to the actual antenna names (ea01 through ea28; these numbers correspond to those painted on the side of the dishes). The antennas can be referenced using either convention; ''antenna='22' '' would correspond to | Notice in this listobs, the first scans are the fields that will be used for calibration before scanning the target fields we want to observe. Note that the antenna IDs (which are numbered sequentially up to the total number of antennas in the array; 0 through 25 in this instance) do not correspond to the actual antenna names (ea01 through ea28; these numbers correspond to those painted on the side of the dishes). The antennas can be referenced using either convention; ''antenna='22' '' would correspond to ea23, whereas ''antenna='ea22' '' would correspond to ea22. Note that the antenna numbers in the observer log correspond to the actual antenna names, i.e., the 'ea??' numbers given in listobs. | ||
Also, note the portion listing the spectral windows (in this example only one, spw='0'): | |||
<pre style="background-color: #fffacd;"> | |||
Spectral Windows: (1 unique spectral windows and 1 unique polarization setups) | |||
SpwID Name #Chans Frame Ch0(MHz) ChanWid(kHz) TotBW(kHz) CtrFreq(MHz) Corrs | |||
0 Subband:0 64 TOPO 4536.000 2000.000 128000.0 4599.0000 RR RL LR LL | |||
</pre> | |||
In the calibration steps below we will define spw and channel range. Since this C-band instrument configuration uses Full polarization, the spw has 64 channels that are 2.0MHz wide. | |||
Both to get a sense of the array, as well as identify an antenna for later use in calibration, use the task [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.visualization.plotants.html plotants] (see Figure 1). In general, for calibration purposes, one would like to select an antenna that is close to the center of the array (and that is not listed in the operator's log as having had problems!). | Both to get a sense of the array, as well as identify an antenna for later use in calibration, use the task [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.visualization.plotants.html plotants] (see Figure 1). In general, for calibration purposes, one would like to select an antenna that is close to the center of the array (and that is not listed in the operator's log as having had problems!). | ||
| Line 489: | Line 500: | ||
This command will show all available calibrator models: | This command will show all available calibrator models: | ||
<pre style="background-color: #fffacd;"> | <pre style="background-color: #fffacd;"> | ||
3C123_P.im 3C138_P.im 3C147_A.im 3C147_Q.im 3C286_A.im 3C286_Q.im 3C380_P.im 3C48_P.im README | |||
3C138_A.im 3C138_Q.im 3C147_C.im 3C147_S.im 3C286_C.im 3C286_S.im 3C48_A.im 3C48_Q.im | |||
3C138_C.im 3C138_S.im 3C147_K.im 3C147_U.im 3C286_K.im 3C286_U.im 3C48_C.im 3C48_S.im | |||
3C138_K.im 3C138_U.im 3C147_L.im 3C147_X.im 3C286_L.im 3C286_X.im 3C48_K.im 3C48_U.im | |||
3C138_L.im 3C138_X.im 3C147_P.im 3C196_P.im 3C286_P.im 3C295_P.im 3C48_L.im 3C48_X.im | |||
</pre> | </pre> | ||
Since any image could be a potential calibrator model, [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.setjy.html setjy] will list all ''*.im'' and ''*.mod'' images in the working directory. In addition, it will list all models that are provided by NRAO with the CASA package, and they will be picked by their names. We will be using the C-band VLA standard model for 3C286 which is aptly named '3C286_C.im': | Since any image could be a potential calibrator model, [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.setjy.html setjy] will list all ''*.im'' and ''*.mod'' images in the working directory. In addition, it will list all models that are provided by NRAO with the CASA package, and they will be picked by their names. We will be using the C-band VLA standard model for 3C286 which is aptly named '3C286_C.im': | ||
| Line 557: | Line 565: | ||
* ''gaintable=['3c391_ctm_mosaic_10s_spw0.antpos'] '': Having produced antenna position corrections (as we did above with [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.calibration.gencal.html gencal]), they should now be applied. | * ''gaintable=['3c391_ctm_mosaic_10s_spw0.antpos'] '': Having produced antenna position corrections (as we did above with [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.calibration.gencal.html gencal]), they should now be applied. | ||
To really see what is going on, we use [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.visualization.plotms.html plotms] to inspect the solutions from [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.calibration.gaincal.html gaincal] for a single antenna at a time, iterating through each antenna in sequence by clicking on the Next button ( | To really see what is going on, we use [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.visualization.plotms.html plotms] to inspect the solutions from [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.calibration.gaincal.html gaincal] for a single antenna at a time, iterating through each antenna in sequence by clicking on the Next button (right pointing single green arrow) on the GUI to advance the displayed antenna. | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
| Line 566: | Line 574: | ||
* ''vis='3c391_ctm_mosaic_10s_spw0.G0all' '': the calibration table to examine solutions | * ''vis='3c391_ctm_mosaic_10s_spw0.G0all' '': the calibration table to examine solutions | ||
* ''xaxis='time' '': plotting phase solutions vs time | * ''xaxis='time' '': plotting phase solutions vs time | ||
* ''yaxis=phase '': plotting phase solutions vs time | * ''yaxis='phase' '': plotting phase solutions vs time | ||
* ''coloraxis=corr '': colorize by polarization (black=R, pink=L; coloring choice is automatic in plotms) | * ''coloraxis=corr '': colorize by polarization (black=R, pink=L; coloring choice is automatic in plotms) | ||
* '' | * ''iteraxis='antenna' '': iterating the plot across each antenna | ||
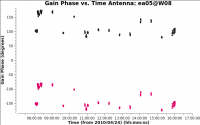
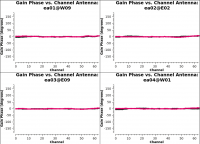
[[Image:plotms-3C286-G0all-phase-ea05_CASA5.4.0.png|200px|thumb|right|Figure 5: Initial gain phases colorized by polarization, stepped through to show ea05]]<pre style="background-color: lightgrey;”> | [[Image:plotms-3C286-G0all-phase-ea05_CASA5.4.0.png|200px|thumb|right|Figure 5: Initial gain phases colorized by polarization, stepped through to show ea05]]<pre style="background-color: lightgrey;”> | ||
| Line 620: | Line 628: | ||
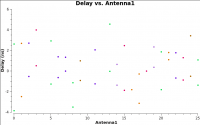
[[Image:Plotms_3c391-K0-delay_CASA5.4.0.png|200px|thumb|right|Figure 6: delay solutions]] | [[Image:Plotms_3c391-K0-delay_CASA5.4.0.png|200px|thumb|right|Figure 6: delay solutions]] | ||
We can plot these solutions (in nanoseconds) as a function of antenna: | We can plot these solutions (in nanoseconds) as a function of antenna (Figure 6): | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
| Line 631: | Line 639: | ||
This step solves for the complex bandpass, <math>B_i</math>. | This step solves for the complex bandpass, <math>B_i</math>. | ||
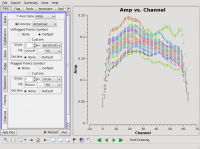
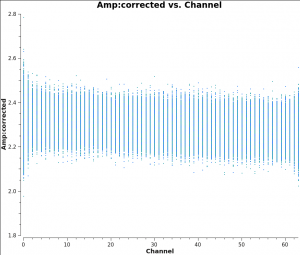
[[Image:Plotms-3C286-RRbandpass2.png|200px|thumb|right|Figure 7: bandpass illustration]] | [[Image:Plotms-3C286-RRbandpass2.png|200px|thumb|right|Figure 7: bandpass illustration]] | ||
All data with the VLA are taken in spectral line mode, even if the science that one is conducting is continuum, and therefore requires a bandpass solution to account for gain variations with frequency. Solving for the bandpass won't hurt for continuum data, and, for moderate or high dynamic range image, it is essential. To motivate the need for solving for the bandpass, consider Figure 7. It shows the right circularly polarized data (RR correlation) for the source J1331+3030, which will serve as the bandpass calibrator. The data are color coded by spectral window, as earlier plots from [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.visualization.plotms.html plotms] indicated that the visibility data are nearly constant with baseline length. Ideally, the visibility data would be constant as a function of frequency as well. The variations with frequency are a reflection of the (slightly) different antenna bandpasses. (''Exercise for the reader, reproduce Figure 7 using [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.visualization.plotms.html plotms].'') <font color="CDCDCD"> (x-axis is Channel, y-axis is Amp (data column), field=0, antenna=ea01, correlation=RR, channel range is -10--70, amp range is 0--0.25, colorized by antenna2)</font> | All data with the VLA are taken in spectral line mode, even if the science that one is conducting is continuum, and therefore requires a bandpass solution to account for gain variations with frequency. Solving for the bandpass won't hurt for continuum data, and, for moderate or high dynamic range image, it is essential. To motivate the need for solving for the bandpass, consider Figure 7. It shows the right circularly polarized data (RR correlation) for the source J1331+3030, which will serve as the bandpass calibrator. The data are color coded by spectral window, as earlier plots from [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.visualization.plotms.html plotms] indicated that the visibility data are nearly constant with baseline length. Ideally, the visibility data would be constant as a function of frequency as well. The variations with frequency are a reflection of the (slightly) different antenna bandpasses. (''Exercise for the reader, reproduce Figure 7 using [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.visualization.plotms.html plotms].'')<!-- <font color="CDCDCD"> (x-axis is Channel, y-axis is Amp (data column), field=0, antenna=ea01, correlation=RR, channel range is -10--70, amp range is 0--0.25, colorized by antenna2)</font>--> | ||
Now form the bandpass, using the phase solutions just derived. | Now form the bandpass, using the phase solutions just derived. | ||
| Line 649: | Line 657: | ||
* ''gaintable=['3c391_ctm_mosaic_10s_spw0.antpos', '3c391_ctm_mosaic_10s_spw0.G0', '3c391_ctm_mosaic_10s_spw0.K0'] '': Apply antenna positions, phase solutions, and delays before computing bandpass. | * ''gaintable=['3c391_ctm_mosaic_10s_spw0.antpos', '3c391_ctm_mosaic_10s_spw0.G0', '3c391_ctm_mosaic_10s_spw0.K0'] '': Apply antenna positions, phase solutions, and delays before computing bandpass. | ||
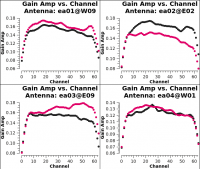
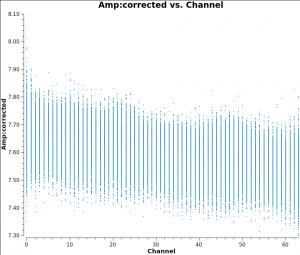
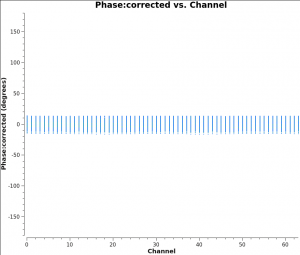
Once again, one can use [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.visualization.plotms.html plotms] to display the bandpass solutions. Note that in the inputs below, the amplitudes are being displayed as a function of frequency channel. The parameters ''gridrows=2'' and ''gridcols=2'' are used to display multiple plots per page (2 plots per page in the y direction and 2 in the x direction). The first command below shows the amplitude solutions (one per polarization) and the second command below shows the phase solutions (one per each polarization). Parameter ''iteration='antenna' '' is used to step through separate plots for each antenna. | Once again, one can use [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.visualization.plotms.html plotms] to display the bandpass solutions. Note that in the inputs below, the amplitudes are being displayed as a function of frequency channel. The parameters ''gridrows=2'' and ''gridcols=2'' are used to display multiple plots per page (2 plots per page in the y direction and 2 in the x direction). The first command below shows the amplitude solutions (one per polarization) (Figure 8A) and the second command below shows the phase solutions (one per each polarization). Parameter ''iteration='antenna' '' is used to step through separate plots for each antenna. | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
| Line 660: | Line 668: | ||
iteraxis='antenna',gridrows=2,gridcols=2) | iteraxis='antenna',gridrows=2,gridcols=2) | ||
</source> | </source> | ||
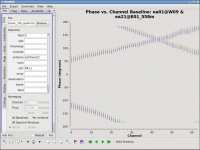
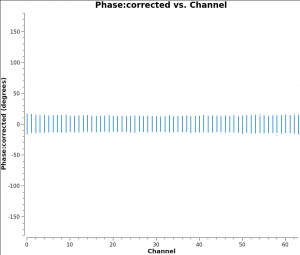
As expected, the bandpass phases are relatively flat (see Figure 8B) | As expected, the bandpass phases are relatively flat (see Figure 8B) with the slopes (Figure 3C) removed by the delay calibration. Residual phase excursions are on the order of a few degrees. | ||
{| | {| | ||
| Line 1,029: | Line 1,037: | ||
correlation='L',coloraxis='baseline') | correlation='L',coloraxis='baseline') | ||
</source> | </source> | ||
You can see in Figures | You can see in Figures 11A and 11B that the amplitude gain factors are now similar across sources, compared to the raw factors in the G1 table. | ||
{| | {| | ||
| [[Image:plotms_3c391-fluxscale1-amp-R-CASA5.5.0.png|200px|thumb|left|Figure | | [[Image:plotms_3c391-fluxscale1-amp-R-CASA5.5.0.png|200px|thumb|left|Figure 11A: post-fluxscale amp solutions, R pol]] | ||
| [[Image:plotms_3c391-fluxscale1-amp-L-CASA5.5.0.png|200px|thumb|center|Figure | | [[Image:plotms_3c391-fluxscale1-amp-L-CASA5.5.0.png|200px|thumb|center|Figure 11B: post-fluxscale amp solutions, L pol]] | ||
|} | |} | ||
| Line 1,090: | Line 1,098: | ||
We should now have fully-calibrated visibilities in the CORRECTED_DATA column of the measurement set, and it is worthwhile pausing to inspect them to ensure that the calibration did what we expected it to. We make some standard plots (see Figures | We should now have fully-calibrated visibilities in the CORRECTED_DATA column of the measurement set, and it is worthwhile pausing to inspect them to ensure that the calibration did what we expected it to. We make some standard plots (see Figures 12A through 12D): | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
| Line 1,115: | Line 1,123: | ||
plotfile='plotms_3c391-fld1-corrected-phase.png') | plotfile='plotms_3c391-fld1-corrected-phase.png') | ||
</source> | </source> | ||
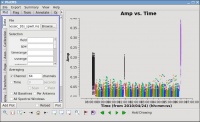
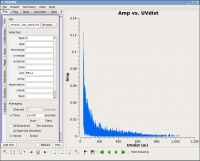
Inspecting the data at this stage may well show up previously-unnoticed bad data. Plotting the '''corrected''' amplitude against UV distance or against time is a good way to find such issues. If you find bad data, you can remove them via interactive flagging in [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.visualization.plotms.html plotms] or via manual flagging in [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.flagging.flagdata.html flagdata] once you have identified the offending antennas/baselines/channels/times. When you are happy that all data (particularly on your target source) look good, you may proceed. Images | Inspecting the data at this stage may well show up previously-unnoticed bad data. Plotting the '''corrected''' amplitude against UV distance or against time is a good way to find such issues. If you find bad data, you can remove them via interactive flagging in [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.visualization.plotms.html plotms] or via manual flagging in [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.flagging.flagdata.html flagdata] once you have identified the offending antennas/baselines/channels/times. When you are happy that all data (particularly on your target source) look good, you may proceed. Images 12A through 12D show that there is no sign of bad data remaining. | ||
{| | {| | ||
| [[Image:plotms_3c391-fld0-corrected-amp_5.5.0.png|thumb|Figure | | [[Image:plotms_3c391-fld0-corrected-amp_5.5.0.png|thumb|Figure 12A: amp vs channel for 3C286 RR,LL]] | ||
| [[Image:plotms_3c391-fld0-corrected-phase_5.5.0.png|thumb|Figure | | [[Image:plotms_3c391-fld0-corrected-phase_5.5.0.png|thumb|Figure 12B: phase vs channel for 3C286 RR,LL]] | ||
| [[Image:plotms_3c391-fld1-corrected-amp_5.5.0.png|thumb|Figure | | [[Image:plotms_3c391-fld1-corrected-amp_5.5.0.png|thumb|Figure 12C: amp vs channel for J1822-0938 RR,LL]] | ||
| [[Image:plotms_3c391-fld1-corrected-phase_5.5.0.png|thumb|Figure | | [[Image:plotms_3c391-fld1-corrected-phase_5.5.0.png|thumb|Figure 12D: phase vs channel for J1822-0938 RR,LL]] | ||
|} | |} | ||
| Line 1,157: | Line 1,165: | ||
== Imaging parameters == | == Imaging parameters == | ||
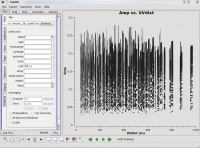
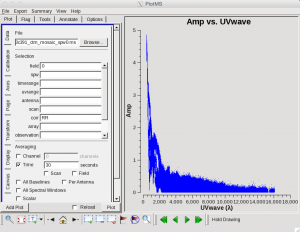
[[Image:plotms_3c391-mosaic0-uvwave.png|thumb|Figure | [[Image:plotms_3c391-mosaic0-uvwave.png|thumb|Figure 13: ''plotms'' plot showing Amplitude vs UV Distance in wavelengths for 3C391 at 4600 MHz]] | ||
It is important to have an idea of what values to use for the image pixel (cell) size and the overall size of the image. Setting the appropriate pixel size for imaging depends upon basic optics aspects of interferometry. Using [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.visualization.plotms.html plotms] to look at the newly-calibrated, target-only data set: | It is important to have an idea of what values to use for the image pixel (cell) size and the overall size of the image. Setting the appropriate pixel size for imaging depends upon basic optics aspects of interferometry. Using [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.visualization.plotms.html plotms] to look at the newly-calibrated, target-only data set: | ||
| Line 1,166: | Line 1,174: | ||
plotfile='plotms_3c391-mosaic0-uvwave.png',overwrite=True) | plotfile='plotms_3c391-mosaic0-uvwave.png',overwrite=True) | ||
</source> | </source> | ||
You should obtain a plot similar to Figure | You should obtain a plot similar to Figure 13 with the calibrated visibility amplitude as a function of <math>u</math>-<math>v</math> distance. Note that while 'uvdist' and 'uvwave' are in essence the same, they differ in units and by respect values. The difference is that 'uvdist' is measured in physical units, i.e., meters (as the antenna separation is in meters), whereas 'uvwave' is measured in units of wavelengths at the specific frequency. | ||
The maximum baseline is about 16,000 wavelengths, i.e., a smallest angular scale of 12 arcseconds (<math>\lambda/D=1/16000</math>). The most effective cleaning occurs with at least 4-5 pixels across the synthesized beam. For the resolution element of 12 arcseconds, a cell size of 2.5 arcseconds will give just under 5 pixels per beam. | The maximum baseline is about 16,000 wavelengths, i.e., a smallest angular scale of 12 arcseconds (<math>\lambda/D=1/16000</math>). The most effective cleaning occurs with at least 4-5 pixels across the synthesized beam. For the resolution element of 12 arcseconds, a cell size of 2.5 arcseconds will give just under 5 pixels per beam. | ||
The supernova remnant itself is known to have a diameter of order 9 arcminutes, corresponding to about 216 pixels for the chosen cell size. The mosaic was set up with 7 fields, 1 centered on the remnant with 6 flanking fields; the spacing of the fields was chosen based on the size of the antenna primary beam. With the choice of ''gridder='mosaic' ''(our main mosaicking algorithm), we will image an area somewhat larger than the size of the supernova remnant in order to have a bit of padding around the outside. Although CASA has the feature that its Fourier transform engine (FFTW) does ''not'' require a strict power of 2 for the number of linear pixels in a given image axis, it is somewhat more efficient if the number of pixels on a side is a composite number divisible by ''any pair'' of 2 and 3 and/or 5. Because [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean] internally applies a padding of 1.2 (= | The supernova remnant itself is known to have a diameter of order 9 arcminutes, corresponding to about 216 pixels for the chosen cell size. The mosaic was set up with 7 fields, 1 centered on the remnant with 6 flanking fields; the spacing of the fields was chosen based on the size of the antenna primary beam. With the choice of ''gridder='mosaic' ''(our main mosaicking algorithm), we will image an area somewhat larger than the size of the supernova remnant in order to have a bit of padding around the outside. Although CASA has the feature that its Fourier transform engine (FFTW) does ''not'' require a strict power of 2 for the number of linear pixels in a given image axis, it is somewhat more efficient if the number of pixels on a side is a composite number divisible by ''any pair'' of 2 and 3 and/or 5. Because [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean] internally applies a padding of 1.2 (= 3 x 2/5), we will use an image size of 480, which is 2<sup>5</sup> × 3 × 5 (so 480 × 1.2 = 576 = 2<sup>6</sup> × 3<sup>2</sup>). We therefore set ''imsize=[480,480]'' and our mosaic fits comfortably inside the image. | ||
== Multi-scale Mosaic Clean == | == Multi-scale Mosaic Clean == | ||
| Line 1,194: | Line 1,202: | ||
Task [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean] is powerful with many inputs and a certain amount of experimentation likely is required. | Task [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean] is powerful with many inputs and a certain amount of experimentation likely is required. | ||
[[Image:3c391-tclean-interactive-start_CASA5.4.0.jpeg|thumb|Figure | [[Image:3c391-tclean-interactive-start_CASA5.4.0.jpeg|thumb|Figure 14: Interactive clean at the beginning, having selected polygon region and ready to double-click inside to set the mask.]] | ||
* ''vis='3c391_ctm_mosaic_spw0.ms' '': this split MS contains our 7-pt mosaic fields, now indexed as 0-6. Field 0 is the central field of the mosaic (you can use [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.information.listobs.html listobs] to verify this). | * ''vis='3c391_ctm_mosaic_spw0.ms' '': this split MS contains our 7-pt mosaic fields, now indexed as 0-6. Field 0 is the central field of the mosaic (you can use [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.information.listobs.html listobs] to verify this). | ||
* ''imagename='3c391_ctm_spw0_multiscale' '': the output image names will all start with this (e.g., 3c391_ctm_spw0_multiscale.image, 3c391_ctm_spw0_multiscale.rms, etc.) | * ''imagename='3c391_ctm_spw0_multiscale' '': the output image names will all start with this (e.g., 3c391_ctm_spw0_multiscale.image, 3c391_ctm_spw0_multiscale.rms, etc.) | ||
| Line 1,208: | Line 1,216: | ||
* ''savemodel='modelcolumn' '': We recommend here the use of a physical MODEL_DATA scratch column for complicated gridders such as 'mosaic' (unlike the calibration steps, above). This will save some time, as it can be faster in the case of complicated gridding to read data from disk instead of doing all of the computations on-the-fly. However, this has the unfortunate side effect of increasing the size of the ms on disk. | * ''savemodel='modelcolumn' '': We recommend here the use of a physical MODEL_DATA scratch column for complicated gridders such as 'mosaic' (unlike the calibration steps, above). This will save some time, as it can be faster in the case of complicated gridding to read data from disk instead of doing all of the computations on-the-fly. However, this has the unfortunate side effect of increasing the size of the ms on disk. | ||
[[Image:3c391-tclean-multiscale-500iters_CASA5.4.0.jpeg|thumb|Figure | [[Image:3c391-tclean-multiscale-500iters_CASA5.4.0.jpeg|thumb|Figure 15: After the first 500 iterations of multi-scale clean]] | ||
As mentioned above, we can guide the clean process by allowing it to find clean components only within a user-specified region. When [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean] runs in interactive mode, a '''[https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.visualization.viewer.html viewer]''' window will pop up as shown in Figure | As mentioned above, we can guide the clean process by allowing it to find clean components only within a user-specified region. When [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean] runs in interactive mode, a '''[https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.visualization.viewer.html viewer]''' window will pop up as shown in Figure 14. To get a more detailed view of the central regions containing the emission, zoom in by first left clicking on the zoom button (leftmost button in third row) and tracing out a rectangle with the left mouse button and double-clicking inside the zoom box you just made. Play with the color scale to bring out the emission better, by holding down the middle mouse button and moving it around. To create a clean box (a region within which components may be found), hold down the right mouse button and trace out a rectangle around the source, then double-click inside that rectangle to set it as a box. Note that the clean box must turn white for it to be registered; if the box is not white, it has not been set! Alternatively, you can trace out a more custom shape to better enclose the irregular outline of the supernova remnant. To do that, right-click on the closed polygonal icon. Then trace out a shape by right-clicking where you want the corners of that shape. Once you have come full circle, the shape will be traced out in green, with small squares at the corners. Double-click inside this region and the green outline will turn white. You have now set the clean region. If you have made a mistake with your clean box, click on the Erase button, trace out a rectangle around your erroneous region, and double-click inside that rectangle. You can also set multiple clean regions. | ||
At any stage in the cleaning, you can adjust the number of iterations that [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean] will do before returning to the GUI. By default this is set to 100 (see the iterations field in mid-upper left of panel). You probably want to set this to a high number for this mosaic due to the complicated structure, values from 1000 to 5000 later on seem to work. Note that this will override the ''niter'' that was set when you started the clean task. [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean] will keep going until it reaches threshold or runs out of cycles (the cycles field to the right of the iterations). | At any stage in the cleaning, you can adjust the number of iterations that [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean] will do before returning to the GUI. By default this is set to 100 (see the iterations field in mid-upper left of panel). You probably want to set this to a high number for this mosaic due to the complicated structure, values from 1000 to 5000 later on seem to work. Note that this will override the ''niter'' that was set when you started the clean task. [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean] will keep going until it reaches threshold or runs out of cycles (the cycles field to the right of the iterations). | ||
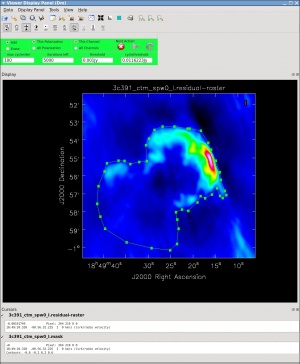
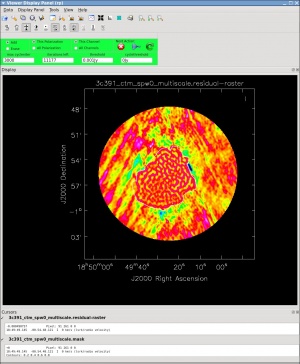
[[Image:3c391-tclean-residuals_CASA5.4.0.jpeg|thumb|Figure | [[Image:3c391-tclean-residuals_CASA5.4.0.jpeg|thumb|Figure 16: Interactive residuals after about 14000 iterations of multi-scale clean]] | ||
When you are happy with the clean regions, press the green circular arrow button on the far right to continue deconvolution. After completing a cycle, a revised image will come up. As the brightest points are removed from the image (cleaned off), fainter emission may show up. You can adjust the clean boxes each cycle, to enclose all real emission. After many cycles, when only noise is left, you can hit the red-and-white stop-sign icon to stop cleaning. Figure | When you are happy with the clean regions, press the green circular arrow button on the far right to continue deconvolution. After completing a cycle, a revised image will come up. As the brightest points are removed from the image (cleaned off), fainter emission may show up. You can adjust the clean boxes each cycle, to enclose all real emission. After many cycles, when only noise is left, you can hit the red-and-white stop-sign icon to stop cleaning. Figure 15 shows the interactive viewer panel later in the process, after cleaning 500 iterations. We have used the polygon tool to add to the clean region, drawing around emission that shows up in the residual image outside of the original clean region. After about 14000 iterations (Figure 16) the residuals were looking good (similar noise level inside and outside of the clean region). As mentioned above, restarting [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean] with different ''multiscale=[...]'' choices can help also. | ||
Task [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean] will make several output files, all named with the prefix given as ''imagename''. These include: | Task [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean] will make several output files, all named with the prefix given as ''imagename''. These include: | ||
| Line 1,226: | Line 1,234: | ||
* ''.sumwt'': a single pixel image containing sum of weights per plane | * ''.sumwt'': a single pixel image containing sum of weights per plane | ||
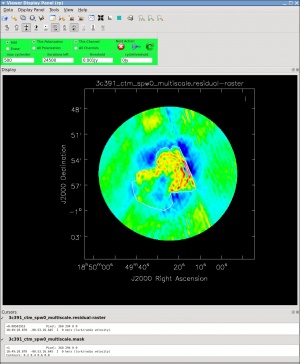
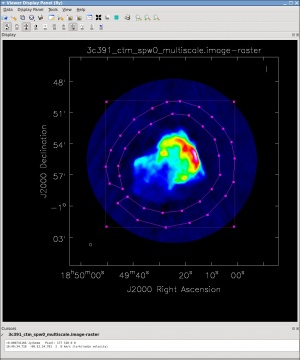
[[Image:3c391-viewer-multiscale-final_CASA5.4.0.jpeg|thumb|Figure | [[Image:3c391-viewer-multiscale-final_CASA5.4.0.jpeg|thumb|Figure 17: Viewer panel of final restored image (using HotMetal1 colormap and Scaling Power Cycles = -1)]] | ||
After the imaging and deconvolution process has finished, you can use the '''[https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.visualization.viewer.html viewer]''' to look at your image. | After the imaging and deconvolution process has finished, you can use the '''[https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.visualization.viewer.html viewer]''' to look at your image. | ||
| Line 1,233: | Line 1,241: | ||
viewer('3c391_ctm_spw0_multiscale.image') | viewer('3c391_ctm_spw0_multiscale.image') | ||
</source> | </source> | ||
You can adjust the color scale and zoom in to a selected region by assigning mouse buttons to the icons immediately above the image (hover over the icons to get a description of what they do). Also, using the wrench panel to change Display Options will be helpful here. We chose the Hot Metal 1 colormap and set the Scaling Power Cycles to -1 to better emphasize the faint emission and compare to the noise (Figure | You can adjust the color scale and zoom in to a selected region by assigning mouse buttons to the icons immediately above the image (hover over the icons to get a description of what they do). Also, using the wrench panel to change Display Options will be helpful here. We chose the Hot Metal 1 colormap and set the Scaling Power Cycles to -1 to better emphasize the faint emission and compare to the noise (Figure 17). | ||
The [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean] task naturally operates in a flat noise image, i.e., an image where the effective weighting across the mosaic field of view is set so that the noise is constant. This is so that the clean threshold has a uniform meaning for the stopping criterion and that the image fed into the minor cycles has uniform noise levels. However, this means that the image does not take into account the primary beam fall-off in the edges and interstices of the mosaic. We could have set parameter ''pbcor=True'' in [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean], but it is useful to see the flat-noise image and residuals to evaluate the quality of the clean image. Therefore, we use [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.impbcor.html impbcor] to divide the ''.image'' by the ''.pb'' image to produce a primary beam corrected restored image: | The [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean] task naturally operates in a flat noise image, i.e., an image where the effective weighting across the mosaic field of view is set so that the noise is constant. This is so that the clean threshold has a uniform meaning for the stopping criterion and that the image fed into the minor cycles has uniform noise levels. However, this means that the image does not take into account the primary beam fall-off in the edges and interstices of the mosaic. We could have set parameter ''pbcor=True'' in [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean], but it is useful to see the flat-noise image and residuals to evaluate the quality of the clean image. Therefore, we use [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.impbcor.html impbcor] to divide the ''.image'' by the ''.pb'' image to produce a primary beam corrected restored image: | ||
| Line 1,248: | Line 1,256: | ||
The three most basic analyses are to determine the peak brightness, the flux density, and the image noise level. These are useful measures of how well the imaging efforts are in approaching the thermal noise limit or in reproducing what is already known about a source. Additional discussion of image analysis and manipulation, including the combination of multiple images, mathematical operations on images, and much more can be found in the [https://casadocs.readthedocs.io/en/v6.2.0/notebooks/image_analysis.html Image Analysis] section of the CASA documentation. | The three most basic analyses are to determine the peak brightness, the flux density, and the image noise level. These are useful measures of how well the imaging efforts are in approaching the thermal noise limit or in reproducing what is already known about a source. Additional discussion of image analysis and manipulation, including the combination of multiple images, mathematical operations on images, and much more can be found in the [https://casadocs.readthedocs.io/en/v6.2.0/notebooks/image_analysis.html Image Analysis] section of the CASA documentation. | ||
The most straightforward statistic is the peak brightness, which is determined by | The most straightforward statistic is the peak brightness, which is determined by [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.information.imstat.html imstat]. | ||
<source lang="python"> | <source lang="python"> | ||
mystat = imstat(imagename='3c391_ctm_spw0_multiscale.pbcorimage') | mystat = imstat(imagename='3c391_ctm_spw0_multiscale.pbcorimage') | ||
| Line 1,287: | Line 1,295: | ||
and so the peak flux density is 0.157 Jy/beam. | and so the peak flux density is 0.157 Jy/beam. | ||
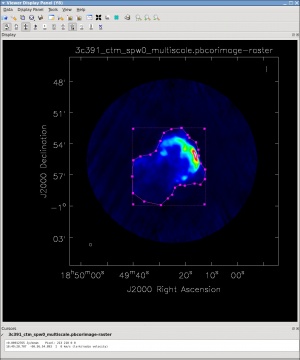
[[Image:3c391-viewer-final-polygon_CASA5.4.0.jpeg|thumb|right|Figure | [[Image:3c391-viewer-final-polygon_CASA5.4.0.jpeg|thumb|right|Figure 18: viewer polygon region drawing for on-source statistics]] | ||
[[Image:3c391-viewer-polygon-forrms_CASA5.4.0.jpeg|thumb|right|Figure | [[Image:3c391-viewer-polygon-forrms_CASA5.4.0.jpeg|thumb|right|Figure 19: viewer polygon region for off-source statistics (with Scaling Power Cycles = -1)]] | ||
The other two statistics require slightly more care. The flux density of a source is determined by integrating its brightness or intensity over some solid angle, i.e., | The other two statistics require slightly more care. The flux density of a source is determined by integrating its brightness or intensity over some solid angle, i.e., | ||
| Line 1,295: | Line 1,303: | ||
</center> | </center> | ||
where <math>I</math> is the intensity (measured in units of Jy/beam), <math>\Omega</math> is the solid angle of the source (e.g., number of synthesized beams), and <math>S</math> is the flux density (measured in units of Jy). In general, if the noise is well-behaved in the image, when averaged over a reasonable solid angle, the noise contribution should approach 0 Jy. If that is the case, then the flux density of the source is also reported by | where <math>I</math> is the intensity (measured in units of Jy/beam), <math>\Omega</math> is the solid angle of the source (e.g., number of synthesized beams), and <math>S</math> is the flux density (measured in units of Jy). In general, if the noise is well-behaved in the image, when averaged over a reasonable solid angle, the noise contribution should approach 0 Jy. If that is the case, then the flux density of the source is also reported by [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.information.imstat.html imstat]. However, there are many cases for which a noise contribution of 0 Jy may not be a safe assumption. If the source is in a complicated region (e.g., a star formation region, the Galactic center, near the edge of a galaxy), a better estimate of the source's flux density will be obtained by limiting carefully the solid angle over which the integration is performed. | ||
Open '''[https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.visualization.viewer.html viewer]''' and use it to display the corrected image (Figure | Open '''[https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.visualization.viewer.html viewer]''' and use it to display the corrected image (Figure 18). For this analysis, it is better to use the version of the viewer that is run from the OS command line rather than the CASA command line. You can open this from inside CASA using '!': | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
!casaviewer '3c391_ctm_spw0_multiscale.pbcorimage' & | !casaviewer '3c391_ctm_spw0_multiscale.pbcorimage' & | ||
</source> | </source> | ||
One can choose the function assigned to each mouse button; after zooming into the desired view, assign polygon region to a desired mouse button (e.g., left button) by selecting the polygon tool [[File:Polygon_btn.png]] to create the polygonal region as shown in Figure | One can choose the function assigned to each mouse button; after zooming into the desired view, assign polygon region to a desired mouse button (e.g., left button) by selecting the polygon tool [[File:Polygon_btn.png]] to create the polygonal region as shown in Figure 18 with the desired mouse button. | ||
Using the mouse button just assigned to polygon region, outline the supernova remnant. | Using the mouse button just assigned to the polygon region, outline the supernova remnant. Start drawing vertices by clicking on points in the image in succession, when you draw the final vertex then double-click to connect and close the region. When your mouse is inside the region, a bounding box will appear with the vertices shown as draggable solid squares. If you want to adjust the vertices you can do so. | ||
If you find you don't like your region you can dismiss it with with ESC key or using the remove region "X" button in lower right of the panel. You can also employ the region panel to save a region you have created for later use. | If you find you don't like your region you can dismiss it with with ESC key or using the remove region "X" button in the lower right of the panel. You can also employ the region panel to save a region you have created for later use. | ||
Double click inside of that region (using the same mouse button used to make the region), and the statistics will be reported. This will include the flux density value within the region selected. | Double click inside of that region (using the same mouse button used to make the region), and the statistics will be reported. This will include the flux density value within the region selected. | ||
| Line 1,329: | Line 1,337: | ||
!casaviewer '3c391_ctm_spw0_multiscale.image' & | !casaviewer '3c391_ctm_spw0_multiscale.image' & | ||
</source> | </source> | ||
and to ''exclude'' the source's emission to the extent possible as shown in Figure | and to ''exclude'' the source's emission to the extent possible as shown in Figure 19, as the source's emission will bias the estimated noise level high. Likewise, one should avoid the clean bowl around the source emission. One can repeat the procedure above, defining a polygonal region, then double clicking inside it to determine the statistics. For example, from the region selection shown to the right for off-source statistics: | ||
<pre style="background-color: #E0FFFF;"> | <pre style="background-color: #E0FFFF;"> | ||
---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- | ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- | ||
| Line 1,369: | Line 1,377: | ||
where <math>G_i</math> is the complex gain for the <math>i^{\mathrm{th}}</math> antenna and <math>V_{ij}</math> is the true visibility. For an array of <math>N</math> antennas, at any given instant, there are <math>N(N-1)/2</math> visibility data, but only <math>N</math> gain factors. For an array with a reasonable number of antennas, <math>N</math> >~ 8, solutions to this set of coupled equations converge quickly. | where <math>G_i</math> is the complex gain for the <math>i^{\mathrm{th}}</math> antenna and <math>V_{ij}</math> is the true visibility. For an array of <math>N</math> antennas, at any given instant, there are <math>N(N-1)/2</math> visibility data, but only <math>N</math> gain factors. For an array with a reasonable number of antennas, <math>N</math> >~ 8, solutions to this set of coupled equations converge quickly. | ||
There is a small amount of discussion in the old CASA Reference Manual on | For a more detailed introduction to self-calibration, see our [https://casaguides.nrao.edu/index.php/Karl_G._Jansky_VLA_Tutorials#Self-calibration_of_VLA_Data VLA Self-calibration Tutorial]. There is also a small amount of discussion in the old CASA Reference Manual on | ||
[http://casa.nrao.edu/docs/cookbook/casa_cookbook006.html#sec355 self calibration] (see Section 5.11), | [http://casa.nrao.edu/docs/cookbook/casa_cookbook006.html#sec355 self calibration] (see Section 5.11), and we have lectures on [https://science.nrao.edu/facilities/alma/naasc-workshops/nrao-cd-stsci/cde_selfcal.pdf Self-calibration] given at NRAO community days. In self-calibrating data, it is useful to keep in mind the structure of a Measurement Set: there are three columns of interest for an MS: the DATA column, the MODEL column, and the CORRECTED_DATA column. In normal usage, as part of the initial split, the CORRECTED_DATA column is set equal to the DATA column. The self-calibration procedure is then: | ||
* Produce an image ([https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean]) using the CORRECTED_DATA column. | * Produce an image ([https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean]) using the CORRECTED_DATA column. | ||
| Line 1,412: | Line 1,420: | ||
</source> | </source> | ||
The ''CORRECTED_DATA'' column of the MS now contains the self-calibrated visibilities, they will now be used by [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean]. The | The ''CORRECTED_DATA'' column of the MS now contains the self-calibrated visibilities, they will now be used by [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean]. The | ||
[https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.calibration.gaincal.html gaincal] step will report a number of solutions with insufficient SNR. By default, with parameter ''applymode='calflag', '' data with no good solutions will be flagged by [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.calibration.applycal.html applycal]; in this case you will see it report the flagged fraction increasing to about 45%. This may or may not be a good thing. You can control the action of [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.calibration.applycal.html applycal] in this regard by changing the value of parameter ''applymode''. The setting ''applymode='calflagstrict' ''will be even more stringent about flagging things without valid calibration, while ''applymode='calonly' ''will calibrate those with solutions while passing through data | [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.calibration.gaincal.html gaincal] step will report a number of solutions with insufficient SNR. By default, with parameter ''applymode='calflag', '' data with no good solutions will be flagged by [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.calibration.applycal.html applycal]; in this case you will see it report the flagged fraction increasing to about 45%. This may or may not be a good thing. You can control the action of [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.calibration.applycal.html applycal] in this regard by changing the value of parameter ''applymode''. The setting ''applymode='calflagstrict' ''will be even more stringent about flagging things without valid calibration, while ''applymode='calonly' ''will calibrate those with solutions while passing through without changing the data. You can see ahead of time what applycal will do by running with ''applymode='trial' ''which will do the reporting but nothing else. | ||
{| style="background:#98FB98" | {| style="background:#98FB98" | ||
| Line 1,445: | Line 1,453: | ||
| '''Questions for the Advanced Student:''' | | '''Questions for the Advanced Student:''' | ||
* Is this better than the original multiscale image? By how much? | * Is this better than the original multiscale image? By how much? | ||
* Can you make a difference image (between the original and selfcal1 images) using | * Can you make a difference image (between the original and selfcal1 images) using [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.analysis.immath.html immath]? | ||
* How big were the phase changes made by the calibration? Were there specific antennas with larger errors? | * How big were the phase changes made by the calibration? Were there specific antennas with larger errors? | ||
|- | |- | ||
| Line 1,468: | Line 1,476: | ||
* In initial rounds of self-calibration, consider solution intervals longer than the nominal sampling time (parameter ''solint'' in [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.calibration.gaincal.html gaincal]) and/or lower signal-to-noise ratio thresholds (parameter ''minsnr'' in [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.calibration.gaincal.html gaincal]). Depending upon the frequency and configuration and fidelity of the model image, it can be quite reasonable to start with ''solint='30s' ''or'' solint='60s' ''and/or ''minsnr=3 (''or even lower). One might also want to consider specifying a uvrange, if, for example, the field has structure on large scales (small <math>u</math>-<math>v</math>) that is not well represented by the current image. | * In initial rounds of self-calibration, consider solution intervals longer than the nominal sampling time (parameter ''solint'' in [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.calibration.gaincal.html gaincal]) and/or lower signal-to-noise ratio thresholds (parameter ''minsnr'' in [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.calibration.gaincal.html gaincal]). Depending upon the frequency and configuration and fidelity of the model image, it can be quite reasonable to start with ''solint='30s' ''or'' solint='60s' ''and/or ''minsnr=3 (''or even lower). One might also want to consider specifying a uvrange, if, for example, the field has structure on large scales (small <math>u</math>-<math>v</math>) that is not well represented by the current image. | ||
* The task [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.calibration.applycal.html applycal] will flag data with no good calibration solutions. During the initial self-calibration steps, this flagging may be excessive. If so, one can restore the flags to the state right before running applycal by using the task '''[https:// | * The task [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.calibration.applycal.html applycal] will flag data with no good calibration solutions. During the initial self-calibration steps, this flagging may be excessive. If so, one can restore the flags to the state right before running applycal by using the task '''[https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.flagging.flagmanager.html flagmanager]'''. | ||
* You can track the agreement between the DATA, CORRECTED_DATA, and MODEL in [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.visualization.plotms.html plotms]. The options in the Axes tab allows one to select which column is to be plotted. If the MODEL agrees well with the CORRECTED_DATA, one can use shorter solint and/or higher minsnr values. | * You can track the agreement between the DATA, CORRECTED_DATA, and MODEL in [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.visualization.plotms.html plotms]. The options in the Axes tab allows one to select which column is to be plotted. If the MODEL agrees well with the CORRECTED_DATA, one can use shorter solint and/or higher minsnr values. | ||
Latest revision as of 11:29, 14 February 2023
This CASA Guide is for Version 6.2.0 of CASA. If you are using a later version of CASA and this is the most recent available guide, then you should be able to use most, if not all, of this tutorial.
Overview
This CASA guide describes the calibration and imaging of a multiple-pointing continuum data set taken with the Karl G. Jansky Very Large Array (VLA) of the supernova remnant 3C 391. The data were taken in early science shared-risk observing mode, with 128 MHz of bandwidth in each of two widely spaced spectral windows, centered at 4.6 and 7.5 GHz.
The observations were taken with a full-polarization correlator setup and include a polarization calibrator. For the purposes of this tutorial, we will focus on the continuum (Stokes I) calibration and imaging. (See the CASAguide on radio galaxy 3C75 for an introduction to polarization calibration.)
How to Use This CASA Guide
There are a number of possible ways to run CASA, described in more detail in Getting Started in CASA. In brief, there are at least three different ways to use CASA:
- Interactively examining task inputs. In this mode, one types taskname to load the task, inp to examine the inputs, and go once those inputs have been set to your satisfaction. Allowed inputs are shown in blue and bad inputs are colored red. The input parameters themselves are changed one by one, e.g., selectdata=True. Screenshots of the inputs to various tasks used in the data reduction below are provided, to illustrate which parameters need to be set. More detailed help can be obtained on any task by typing help taskname. Once a task is run, the set of inputs are stored and can be retrieved via tget taskname; subsequent runs will overwrite the previous tget file.
- Pseudo-interactively via task function calls. In this case, all of the desired inputs to a task are provided at once on the CASA command line. This tutorial is made up of such calls, which were developed by looking at the inputs for each task and deciding what needed to be changed from default values. For task function calls, only parameters that you want to be different from their defaults need to be set.
- Non-interactively via a script. A series of task function calls can be combined together into a script, and run from within CASA via execfile('scriptname.py'). This and other CASA Tutorial Guides have been designed to be extracted into a script via the script extractor by using the method described at the Extracting_scripts_from_these_tutorials page. Should you use the script generated by the script extractor for this CASA Guide, be aware that it will require some small amount of interaction related to the plotting, occasionally suggesting that you close the graphics window and hitting return in the terminal to proceed. It is in fact unnecessary to close the graphics windows (it is suggested that you do so purely to keep your desktop uncluttered).
If you are a relative novice or just new to CASA, it is strongly recommended to work through this tutorial by cutting and pasting the task function calls provided below after you have read all the associated explanations. Work at your own pace, look at the inputs to the tasks to see what other options exist, and read the help files. Later, when you are more comfortable, you might try to extract the script, modify it for your purposes, and begin to reduce other data.
Obtaining the Data
For the purposes of this tutorial we have created a starting data set, upon which several initial processing steps have already been conducted. You may obtain the data set from here: http://casa.nrao.edu/Data/EVLA/3C391/3c391_ctm_mosaic_10s_spw0.ms.tgz (dataset size: 3.1GB).
If you wish to start from the very beginning, you may download the dataset from the NRAO Archive: TDEM0001_sb1218006_1.55310.33439732639
We are providing this starting data set, rather than the true initial data set for at least two reasons. First, many of these initial processing steps can be rather time consuming (> 1 hr). Second, while necessary, many of these steps are not fundamental to the calibration and imaging process, which is the focus of this tutorial. For completeness, however, here are the steps that were taken from the initial data set to produce the starting data set.
- The initial Science Data Model (SDM) file was converted into a measurement set.
- Basic data flagging was applied, to account for shadowing of the antennas. These data are from the D configuration, in which antennas are particularly susceptible to being blocked (shadowed) by other antennas in the array, depending upon the elevation of the source.
- The data were averaged from the initial 1-second correlator sample time to 10-second samples. In the D configuration, the fringe rate is relatively slow and time-average smearing is less of a concern.
- The data were acquired with two subbands (spectral windows) around 4.6 and 7.5 GHz. Because of disk space concerns on some machines, the focus will be on only one of the two spectral windows.
All of these steps can be done directly from the NRAO Archive's Download page, by selecting CASA MS as the download format (it's a good idea to also check the Create MS or SDM tar file box), checking the Apply flags generated during observing box, and setting Time Averaging to 10s.
Once the download is complete, unzip and unpack the file (within a working directory, where you will later run CASA):
# In a terminal, inside your working directory: tar xzvf 3c391_ctm_mosaic_10s_spw0.ms.tgz
The Observation
Before starting the calibration process, we want to get some basic information about the data set. To examine the observing conditions during the observing run, and to find out any known problems with the data, download the observer log. Simply fill in the known observing date (in our case 2010-Apr-24) as both the Start and Stop date, and click on the Show Logs button. The relevant log is labeled with the project code, TDEM0001, and can be downloaded as a PDF file. From this, we find the following:
Information from observing log: There is no C-band receivers on ea13 Antenna ea06 is out of the array Antenna ea15 has some corrupted data Antennas ea10, ea12, ea22 do not have good baseline positions Gusty winds, mixed clouds, API rms up to 11.5.
Before beginning our data reduction, we must start CASA. If you have not used CASA before, some helpful tips are available on the Getting Started in CASA page.
Once you have CASA up and running in the directory containing the data, then start your data reduction by getting some basic information about the data. The task listobs can be used to get a listing of the individual scans (set amounts of time devoted to specific targets) comprising the observation, the frequency setup, source list, and antenna locations. One will note that there are ten sources observed. Here the various sources are introduced briefly, with more detail contained in the sections below in which they are used.
- J1331+3030 = 3C 286, which will later serve as a calibrator for the visibility amplitudes, i.e., it is assumed to have a precisely known flux density; will also serve as the (spectral) bandpass calibrator;
- J1822-0938, which will serve as a calibrator for the visibility phases;
- J0319+4130 = 3C 84, which was used as a polarization calibrator; and
- 3C391 C1--C7, which are 7 fields centered on and surrounding the supernova remnant.
This observation was set up as a 7-pointing mosaic because the supernova remnant is so large that it essentially fills the primary beam.
To run listobs:
# In CASA
obs_dict = listobs(vis='3c391_ctm_mosaic_10s_spw0.ms')
A Python dictionary containing some of the observation's fundamental information is created in the variable obs_dict and the listobs output will show up in the CASA logger window:
##########################################
##### Begin Task: listobs #####
listobs(vis="3c391_ctm_mosaic_10s_spw0.ms",selectdata=True,spw="",field="",antenna="",
uvrange="",timerange="",correlation="",scan="",intent="",
feed="",array="",observation="",verbose=True,listfile="",
listunfl=False,cachesize=50,overwrite=False)
================================================================================
MeasurementSet Name: 3c391_ctm_mosaic_10s_spw0.ms MS Version 2
================================================================================
Observer: Dr. James Miller-Jones Project: T.B.D.
Observation: EVLA
Data records: 845379 Total integration time = 28681.5 seconds
Observed from 24-Apr-2010/08:02:10.0 to 24-Apr-2010/16:00:11.5 (UTC)
ObservationID = 0 ArrayID = 0
Date Timerange (UTC) Scan FldId FieldName nRows SpwIds Average Interval(s) ScanIntent
24-Apr-2010/08:02:10.0 - 08:02:30.0 1 0 J1331+3030 650 [0] [10]
08:02:20.0 - 08:09:30.0 2 0 J1331+3030 13975 [0] [10]
08:09:20.0 - 08:16:28.0 3 0 J1331+3030 13975 [0] [10]
08:19:38.0 - 08:24:26.5 4 1 J1822-0938 7035 [0] [10]
08:24:48.0 - 08:29:48.0 5 2 3C391 C1 7590 [0] [10]
08:29:38.0 - 08:34:48.0 6 3 3C391 C2 7821 [0] [10]
08:34:38.0 - 08:39:48.0 7 4 3C391 C3 7821 [0] [10]
08:39:38.0 - 08:44:48.0 8 5 3C391 C4 7821 [0] [10]
08:44:38.0 - 08:49:48.0 9 6 3C391 C5 7843 [0] [10]
08:49:38.0 - 08:54:48.0 10 7 3C391 C6 7843 [0] [10]
08:54:38.0 - 08:59:43.5 11 8 3C391 C7 7843 [0] [10]
09:00:03.0 - 09:01:31.0 12 1 J1822-0938 2925 [0] [10]
09:01:52.0 - 09:06:52.0 13 2 3C391 C1 7941 [0] [10]
09:06:42.0 - 09:11:52.0 14 3 3C391 C2 9801 [0] [10]
09:11:42.0 - 09:16:52.0 15 4 3C391 C3 10075 [0] [10]
09:16:42.0 - 09:21:52.0 16 5 3C391 C4 10050 [0] [10]
09:21:42.0 - 09:26:52.0 17 6 3C391 C5 10075 [0] [10]
09:26:42.0 - 09:31:52.0 18 7 3C391 C6 10075 [0] [10]
09:31:42.0 - 09:36:47.5 19 8 3C391 C7 10075 [0] [10]
09:37:07.0 - 09:38:35.0 20 1 J1822-0938 2900 [0] [10]
09:38:57.0 - 09:43:57.0 21 2 3C391 C1 9700 [0] [10]
09:43:47.0 - 09:48:57.0 22 3 3C391 C2 10050 [0] [10]
09:48:47.0 - 09:53:57.0 23 4 3C391 C3 10075 [0] [10]
09:53:47.0 - 09:58:57.0 24 5 3C391 C4 10075 [0] [10]
09:58:47.0 - 10:03:57.0 25 6 3C391 C5 10075 [0] [10]
10:03:47.0 - 10:08:57.0 26 7 3C391 C6 10075 [0] [10]
10:08:47.0 - 10:13:47.0 27 8 3C391 C7 9750 [0] [10]
10:14:12.0 - 10:15:39.5 28 1 J1822-0938 2925 [0] [10]
10:16:01.0 - 10:21:01.0 29 2 3C391 C1 9000 [0] [10]
10:20:51.0 - 10:26:01.0 30 3 3C391 C2 10050 [0] [10]
10:25:51.0 - 10:31:01.0 31 4 3C391 C3 10075 [0] [10]
10:30:51.0 - 10:36:01.0 32 5 3C391 C4 10075 [0] [10]
10:35:51.0 - 10:41:01.0 33 6 3C391 C5 10075 [0] [10]
10:40:51.0 - 10:46:01.0 34 7 3C391 C6 10075 [0] [10]
10:45:51.0 - 10:50:51.0 35 8 3C391 C7 9750 [0] [10]
10:51:15.0 - 10:52:42.5 36 1 J1822-0938 2925 [0] [10]
10:55:14.0 - 10:57:42.0 37 0 J1331+3030 3364 [0] [10]
11:00:13.0 - 11:02:41.0 38 1 J1822-0938 3883 [0] [10]
11:03:03.0 - 11:08:03.0 39 2 3C391 C1 9750 [0] [10]
11:07:53.0 - 11:12:53.0 40 3 3C391 C2 9725 [0] [10]
11:12:43.0 - 11:17:43.0 41 4 3C391 C3 9750 [0] [10]
11:17:33.0 - 11:22:33.0 42 5 3C391 C4 9750 [0] [10]
11:22:23.0 - 11:27:23.0 43 6 3C391 C5 9750 [0] [10]
11:27:13.0 - 11:32:13.0 44 7 3C391 C6 9750 [0] [10]
11:32:03.0 - 11:36:53.0 45 8 3C391 C7 9425 [0] [10]
11:37:21.0 - 11:38:47.0 46 1 J1822-0938 2700 [0] [10]
11:39:11.0 - 11:44:11.0 47 2 3C391 C1 9750 [0] [10]
11:44:01.0 - 11:49:01.0 48 3 3C391 C2 9700 [0] [10]
11:48:51.0 - 11:53:41.0 49 4 3C391 C3 8355 [0] [10]
11:53:41.0 - 11:58:31.0 50 5 3C391 C4 9425 [0] [10]
11:58:21.0 - 12:03:21.0 51 6 3C391 C5 9725 [0] [10]
12:03:11.0 - 12:08:11.0 52 7 3C391 C6 9701 [0] [10]
12:08:01.0 - 12:12:59.0 53 8 3C391 C7 9725 [0] [10]
12:13:29.0 - 12:14:48.0 54 1 J1822-0938 2600 [0] [10]
12:15:18.0 - 12:20:08.0 55 2 3C391 C1 9425 [0] [10]
12:19:58.0 - 12:24:58.0 56 3 3C391 C2 9750 [0] [10]
12:24:48.0 - 12:29:48.0 57 4 3C391 C3 9750 [0] [10]
12:29:38.0 - 12:34:38.0 58 5 3C391 C4 9725 [0] [10]
12:34:28.0 - 12:39:28.0 59 6 3C391 C5 9725 [0] [10]
12:39:18.0 - 12:44:18.0 60 7 3C391 C6 9750 [0] [10]
12:44:08.0 - 12:49:04.5 61 8 3C391 C7 9750 [0] [10]
12:49:35.0 - 12:50:53.0 62 1 J1822-0938 2600 [0] [10]
12:51:24.0 - 12:56:14.0 63 2 3C391 C1 9425 [0] [10]
12:56:04.0 - 13:01:04.0 64 3 3C391 C2 9000 [0] [10]
13:00:54.0 - 13:05:54.0 65 4 3C391 C3 9750 [0] [10]
13:05:44.0 - 13:10:44.0 66 5 3C391 C4 9750 [0] [10]
13:10:34.0 - 13:15:34.0 67 6 3C391 C5 9725 [0] [10]
13:15:24.0 - 13:20:24.0 68 7 3C391 C6 9750 [0] [10]
13:20:14.0 - 13:25:10.0 69 8 3C391 C7 9000 [0] [10]
13:25:40.0 - 13:26:57.5 70 1 J1822-0938 2600 [0] [10]
13:27:28.0 - 13:32:18.0 71 2 3C391 C1 9425 [0] [10]
13:32:08.0 - 13:37:08.0 72 3 3C391 C2 9750 [0] [10]
13:36:58.0 - 13:41:58.0 73 4 3C391 C3 9750 [0] [10]
13:41:48.0 - 13:46:48.0 74 5 3C391 C4 9750 [0] [10]
13:46:38.0 - 13:51:38.0 75 6 3C391 C5 9725 [0] [10]
13:51:28.0 - 13:56:28.0 76 7 3C391 C6 9750 [0] [10]
13:56:18.0 - 14:01:14.0 77 8 3C391 C7 9750 [0] [10]
14:01:44.0 - 14:03:01.5 78 1 J1822-0938 2024 [0] [10]
14:03:33.0 - 14:08:23.0 79 2 3C391 C1 8900 [0] [10]
14:08:13.0 - 14:13:13.0 80 3 3C391 C2 9750 [0] [10]
14:13:03.0 - 14:18:03.0 81 4 3C391 C3 9750 [0] [10]
14:17:53.0 - 14:22:53.0 82 5 3C391 C4 9350 [0] [10]
14:22:43.0 - 14:27:43.0 83 6 3C391 C5 9000 [0] [10]
14:27:33.0 - 14:32:33.0 84 7 3C391 C6 8595 [0] [10]
14:32:23.0 - 14:37:18.5 85 8 3C391 C7 7590 [0] [10]
14:37:48.0 - 14:39:05.5 86 1 J1822-0938 1848 [0] [10]
14:39:36.0 - 14:44:26.0 87 2 3C391 C1 7337 [0] [10]
14:44:16.0 - 14:49:16.0 88 3 3C391 C2 7568 [0] [10]
14:49:06.0 - 14:54:06.0 89 4 3C391 C3 7590 [0] [10]
14:53:56.0 - 14:58:56.0 90 5 3C391 C4 7527 [0] [10]
14:58:46.0 - 15:03:46.0 91 6 3C391 C5 7568 [0] [10]
15:03:36.0 - 15:08:36.0 92 7 3C391 C6 7590 [0] [10]
15:08:26.0 - 15:13:22.0 93 8 3C391 C7 7590 [0] [10]
15:13:51.0 - 15:15:09.0 94 1 J1822-0938 1680 [0] [10]
15:15:40.0 - 15:20:30.0 95 2 3C391 C1 7337 [0] [10]
15:20:20.0 - 15:25:20.0 96 3 3C391 C2 7568 [0] [10]
15:25:10.0 - 15:30:10.0 97 4 3C391 C3 7590 [0] [10]
15:30:00.0 - 15:35:00.0 98 5 3C391 C4 7564 [0] [10]
15:34:50.0 - 15:39:50.0 99 6 3C391 C5 7260 [0] [10]
15:39:40.0 - 15:44:40.0 100 7 3C391 C6 6930 [0] [10]
15:44:30.0 - 15:49:26.0 101 8 3C391 C7 6930 [0] [10]
15:49:55.0 - 15:51:13.5 102 1 J1822-0938 1088 [0] [10]
15:54:52.0 - 16:00:11.5 103 9 J0319+4130 8768 [0] [10]
(nRows = Total number of rows per scan)
Fields: 10
ID Code Name RA Decl Epoch SrcId nRows
0 N J1331+3030 13:31:08.287984 +30.30.32.95886 J2000 0 31964
1 J J1822-0938 18:22:28.704200 -09.38.56.83501 J2000 1 39733
2 NONE 3C391 C1 18:49:24.244000 -00.55.40.58001 J2000 2 105580
3 NONE 3C391 C2 18:49:29.149001 -00.57.48.00001 J2000 3 110533
4 NONE 3C391 C3 18:49:19.339000 -00.57.48.00001 J2000 4 110331
5 NONE 3C391 C4 18:49:14.434001 -00.55.40.58001 J2000 5 110862
6 NONE 3C391 C5 18:49:19.339000 -00.53.33.16000 J2000 6 110546
7 NONE 3C391 C6 18:49:29.149001 -00.53.33.16000 J2000 7 109884
8 NONE 3C391 C7 18:49:34.054000 -00.55.40.58001 J2000 8 107178
9 Z J0319+4130 03:19:48.160102 +41.30.42.10305 J2000 9 8768
Spectral Windows: (1 unique spectral windows and 1 unique polarization setups)
SpwID Name #Chans Frame Ch0(MHz) ChanWid(kHz) TotBW(kHz) CtrFreq(MHz) Corrs
0 Subband:0 64 TOPO 4536.000 2000.000 128000.0 4599.0000 RR RL LR LL
Sources: 10
ID Name SpwId RestFreq(MHz) SysVel(km/s)
0 J1331+3030 0 - -
1 J1822-0938 0 - -
2 3C391 C1 0 - -
3 3C391 C2 0 - -
4 3C391 C3 0 - -
5 3C391 C4 0 - -
6 3C391 C5 0 - -
7 3C391 C6 0 - -
8 3C391 C7 0 - -
9 J0319+4130 0 - -
Antennas: 26:
ID Name Station Diam. Long. Lat. Offset from array center (m) ITRF Geocentric coordinates (m)
East North Elevation x y z
0 ea01 W09 25.0 m -107.37.25.2 +33.53.51.0 -521.9407 -332.7782 -1.1977 -1601710.017000 -5042006.928200 3554602.355600
1 ea02 E02 25.0 m -107.37.04.4 +33.54.01.1 9.8247 -20.4292 -2.7808 -1601150.059500 -5042000.619800 3554860.729400
2 ea03 E09 25.0 m -107.36.45.1 +33.53.53.6 506.0591 -251.8666 -3.5832 -1600715.948000 -5042273.187000 3554668.184500
3 ea04 W01 25.0 m -107.37.05.9 +33.54.00.5 -27.3562 -41.3030 -2.7418 -1601189.030140 -5042000.493300 3554843.425700
4 ea05 W08 25.0 m -107.37.21.6 +33.53.53.0 -432.1158 -272.1493 -1.5032 -1601614.091000 -5042001.655700 3554652.509300
5 ea07 N06 25.0 m -107.37.06.9 +33.54.10.3 -54.0667 263.8720 -4.2292 -1601162.593200 -5041829.000000 3555095.890500
6 ea08 N01 25.0 m -107.37.06.0 +33.54.01.8 -30.8810 -1.4664 -2.8597 -1601185.634945 -5041978.156586 3554876.424700
7 ea09 E06 25.0 m -107.36.55.6 +33.53.57.7 236.9058 -126.3369 -2.4443 -1600951.588000 -5042125.911000 3554773.012300
8 ea11 E04 25.0 m -107.37.00.8 +33.53.59.7 102.8046 -63.7684 -2.6412 -1601068.791200 -5042051.910200 3554824.835300
9 ea12 E08 25.0 m -107.36.48.9 +33.53.55.1 407.8394 -206.0057 -3.2252 -1600801.916000 -5042219.371000 3554706.449900
10 ea13 N07 25.0 m -107.37.07.2 +33.54.12.9 -61.1040 344.2335 -4.6144 -1601155.635800 -5041783.843000 3555162.374100
11 ea14 E05 25.0 m -107.36.58.4 +33.53.58.8 164.9788 -92.8032 -2.5268 -1601014.462000 -5042086.252000 3554800.799800
12 ea15 W06 25.0 m -107.37.15.6 +33.53.56.4 -275.8288 -166.7451 -2.0590 -1601447.198000 -5041992.502500 3554739.687600
13 ea16 W02 25.0 m -107.37.07.5 +33.54.00.9 -67.9687 -26.5614 -2.7175 -1601225.255200 -5041980.383590 3554855.675000
14 ea17 W07 25.0 m -107.37.18.4 +33.53.54.8 -349.9866 -216.7507 -1.7978 -1601526.386100 -5041996.840100 3554698.327400
15 ea18 N09 25.0 m -107.37.07.8 +33.54.19.0 -77.4352 530.6274 -5.5867 -1601139.485500 -5041679.036000 3555316.532800
16 ea19 W04 25.0 m -107.37.10.8 +33.53.59.1 -152.8599 -83.8054 -2.4614 -1601315.893000 -5041985.320170 3554808.304600
17 ea20 N05 25.0 m -107.37.06.7 +33.54.08.0 -47.8454 192.6015 -3.8723 -1601168.786100 -5041869.054000 3555036.936000
18 ea21 E01 25.0 m -107.37.05.7 +33.53.59.2 -23.8638 -81.1510 -2.5851 -1601192.467800 -5042022.856800 3554810.438800
19 ea22 N04 25.0 m -107.37.06.5 +33.54.06.1 -42.5986 132.8623 -3.5431 -1601173.953700 -5041902.660400 3554987.536500
20 ea23 E07 25.0 m -107.36.52.4 +33.53.56.5 318.0523 -164.1848 -2.6960 -1600880.570000 -5042170.388000 3554741.457400
21 ea24 W05 25.0 m -107.37.13.0 +33.53.57.8 -210.0944 -122.3885 -2.2581 -1601377.008000 -5041988.665500 3554776.393400
22 ea25 N02 25.0 m -107.37.06.2 +33.54.03.5 -35.6245 53.1806 -3.1345 -1601180.861480 -5041947.453400 3554921.628700
23 ea26 W03 25.0 m -107.37.08.9 +33.54.00.1 -105.3429 -51.7191 -2.6054 -1601265.151700 -5041982.533050 3554834.856300
24 ea27 E03 25.0 m -107.37.02.8 +33.54.00.5 50.6647 -39.4832 -2.7249 -1601114.365500 -5042023.153700 3554844.945600
25 ea28 N08 25.0 m -107.37.07.5 +33.54.15.8 -68.9057 433.1889 -5.0602 -1601147.940400 -5041733.837000 3555235.956000
##### End Task: listobs #####
##########################################
Notice in this listobs, the first scans are the fields that will be used for calibration before scanning the target fields we want to observe. Note that the antenna IDs (which are numbered sequentially up to the total number of antennas in the array; 0 through 25 in this instance) do not correspond to the actual antenna names (ea01 through ea28; these numbers correspond to those painted on the side of the dishes). The antennas can be referenced using either convention; antenna='22' would correspond to ea23, whereas antenna='ea22' would correspond to ea22. Note that the antenna numbers in the observer log correspond to the actual antenna names, i.e., the 'ea??' numbers given in listobs.
Also, note the portion listing the spectral windows (in this example only one, spw='0'):
Spectral Windows: (1 unique spectral windows and 1 unique polarization setups) SpwID Name #Chans Frame Ch0(MHz) ChanWid(kHz) TotBW(kHz) CtrFreq(MHz) Corrs 0 Subband:0 64 TOPO 4536.000 2000.000 128000.0 4599.0000 RR RL LR LL
In the calibration steps below we will define spw and channel range. Since this C-band instrument configuration uses Full polarization, the spw has 64 channels that are 2.0MHz wide.
Both to get a sense of the array, as well as identify an antenna for later use in calibration, use the task plotants (see Figure 1). In general, for calibration purposes, one would like to select an antenna that is close to the center of the array (and that is not listed in the operator's log as having had problems!).
# In CASA
plotants(vis='3c391_ctm_mosaic_10s_spw0.ms',figfile='plotants_3c391_antenna_layout.png')
clearstat() # This removes the table lock generated by plotants in script mode
Examining and Editing the Data
It is always a good idea to examine the data before jumping straight into calibration. Moreover, from the observer's log, we already know that one antenna will need to be flagged because it does not have a C-band receiver. Start by flagging data known to be bad, then examine the data.
In the scheduling block configuration, it is common to insert a setup scan as the first scan. From the listobs output above, one may have noticed that the first scan is less than 1 minute long. This first scan can safely be flagged.
# In CASA
flagdata(vis='3c391_ctm_mosaic_10s_spw0.ms', flagbackup=True, mode='manual', scan='1')
- flagbackup=True : A comment is warranted on the setting of flagbackup. If set to True, flagdata will save a copy of the existing set of flags before entering any new flags. The setting of flagbackup is therefore a matter of some taste. You could choose not to save any flags or only save major flags, or you could save every flag. flagbackup=True is the default.
- mode='manual' : Specific data are going to be selected to be edited.
- scan='1' : is chosen to select only the first scan. Note that scan expects an entry in the form of a string (scan=1 would generate an error).
If satisfied with the inputs, run this task. The initial display in the logger will include
########################################## ##### Begin Task: flagdata ##### . . . . Backup original flags before applying new flags Table type is Measurement Set Creating new backup flag file called flagdata_1 Table type is Measurement Set Manual mode is active Initializing the agents autocorr is 0 There are 1 valid agents in list Running the agentflagger tool ------------------------------------------------------------------------------------ Chunk = 1 [progress: 100%], Observation = 0, Array = 0, Scan = 1, Field = 0 (J1331+3030), Spw = 0, Channels = 64, Corrs = [ RR RL LR LL ], Total Rows = 650 => Data flagged so far 100% ==================================================================================== => Percentage of data flagged in table selection: 100% => Writing flags to the MS . . ##### End Task: flagdata ##### ##########################################
which indicates that, among other things, the flags that existed in the data set prior to this run will be saved to another file called flagdata_1. Should you ever desire to revert to the data prior to this run, the task flagmanager could be used. Also note that the values of all the task parameters (explicit or hidden) are given at the start of the task listing.
From the observer's log, we know that antenna ea13 does not have a C-band receiver and antenna ea15 had some corrupted data, so they should be flagged as well. The parameters are similar as before.
# In CASA
flagdata(vis='3c391_ctm_mosaic_10s_spw0.ms', flagbackup=True, mode='manual', antenna='ea13,ea15')
- antenna='ea13,ea15' : Once again, this parameter requires a string input. Remember that antenna='ea13' and 'antenna='13' are not the same antenna. (See the discussion after our call to listobs above.)
Finally, it is common for the array to require a small amount of time to settle down at the start of a scan. Consequently, it has become standard practice to flag the initial samples from the start of each scan. This is known as 'quack' flagging.
# In CASA
flagdata(vis='3c391_ctm_mosaic_10s_spw0.ms', mode='quack', quackinterval=10.0, quackmode='beg')
- mode='quack' : Quack is another mode in which the same edit will be applied to all scans for all baselines.
- quackmode='beg' : In this case, data from the start of each scan will be flagged. Other options include flagging data at the end of the scan.
- quackinterval=10 : In this data set, the sampling time is 10 seconds, so this choice flags the first sample from all scans on all baselines.
Having now done some basic editing of the data, based in part on a priori information, it is time to look at the data to determine if there are any other obvious problems. One task to examine the data themselves is plotms.
# In CASA
clearstat() # This removes any existing table locks generated by flagdata
plotms(vis='3c391_ctm_mosaic_10s_spw0.ms', selectdata=True, correlation='RR,LL', averagedata=True, avgchannel='64', coloraxis='field')
- selectdata=True : One can choose to plot only selected subsets of the data.
- correlation='RR,LL' : Plot only the left- and right-handed polarization correlation products. The cross-terms ('RL' and 'LR') will be close to zero for non-polarized sources.
- averagedata=True: One can choose to average data points before plotting them.
- avgchannel='64' : With this plot, we are mainly interested in the fields vs time. Averaging over all 64 channels in the spectral window makes the plotting faster.
- coloraxis='field' : Color-code the plotting symbols by field name/number.
The default x- and y-axis parameters are 'time' and 'amp', so the above call to plotms produces an amplitude vs time plot of the data for a selected subset of the data (if desired) and with data averaging (if desired). Many other values have also been left to defaults, but it is possible to select them from within the plotms GUI.
Task plotms allows one to select and view the data in many ways. Figure 2 shows the result of running plotms with the field selection discussed above. You can quickly see that the last source observed (J0319+4130, a polarization calibrator, shown in purple) is the brightest source in this observation. The next brightest is the first source observed (J1331+3030, a.k.a. 3C286, shown in black), which was also observed about a third of the way through the scheduling block. The complex gain calibrator (J1822-0938, shown in magenta) is slightly brighter than the target fields. Even though each of the target scans is on the same source (3C391), the observation is done as a mosaic of 7 fields (see the listobs output above). Each of the 7 3C391 fields is given its own field number/name identification, so each is shown as its own color. The spread of amplitudes in each field is partly due to the difference in gain on each antenna and baseline. Data calibration will take care of much of that scatter.
Across the top of the left panel are a set of tabs labeled Plot, Flag, Tools, Annotate, and Options. In the default view, the Plot tab is visible, and there are a number of tabs running down the side of the left hand panel, including Data, Calibration, Axes, Page, Transform, Display, and Canvas. These allow you to make changes to the plotting selection without having to re-launch plotms. Even if was started with xaxis=' ' (defaulting to 'time'), you can choose a different X-axis by selecting the Axes tab, then using the dropdown menu to switch to (for example) xaxis='Frequency' (although to get something sensible when plotting with frequency, channel averaging must be turned off).
You should spend several minutes displaying the data in various formats. You can save the version of the plotms plot as a graphics file by using the menu bar in the plotms GUI to select the Export... option under the Export menu.
As another example of using plotms for a quick look at your data, select the Data tab and specify field 0 (source J1331+3030, a.k.a. 3C 286) to display data associated with the amplitude calibrator, then select the Axes tab and change the X-axis to be UVdist (baseline length in meters). Remove the channel averaging (Data tab), and plot the data using the Plot button at the bottom of the plotms GUI. The result should be similar to Figure 3A. Again, the scatter is normal at this pre-calibration stage. The important observation is that the amplitude distribution is relatively constant as a function of UV distance or baseline length (i.e., [math]\displaystyle{ \sqrt{u^2+v^2} }[/math] ). A relatively constant visibility amplitude as a function of baseline length means that the source is very nearly a point source. (The Fourier transform of a point source, i.e. a delta function, is a constant function.)
By contrast, if you make a similar plot for field 8 (one of the 3C 391 fields), the result is a visibility function that falls rapidly with increasing baseline length. Figure 3B shows this example, including time averaging of '1e6' seconds (any large number that encompasses more than a full scan will do). Such a visibility function indicates a highly resolved source. The baseline length at which the visibility function falls to some fiducial value (e.g., 1/2 of its peak value) gives a rough estimate of the angular scale of the source. (Angular scale [in radians] ~ 1/baseline [in wavelengths]. To plot baseline length in wavelengths rather than meters, select UVwave as the X-axis parameter.)
A final example is shown in Figure 3C. In this example, we have elected to show phase as a function of (frequency) channel for a single baseline (antenna='ea01&ea21' ) on the bandpass calibrator. If you choose to iterate by baseline (e.g., antenna='ea01' and iteraxis='baseline' ), you can see similar phase-frequency variations on all baselines, but with different slopes. These linear variations are 'delays' that need to be calibrated for, below. We have chosen to colorize by scan; it's clear that the slopes are steady over time. The two different lines for each baseline correspond to the 'RR' and 'LL' polarization correlations.
At this stage in the data reduction process, the general data editing and examination strategy is to focus on the calibrators. The reduction strategy is to determine various corrections from the calibrators, then apply these correction factors to the science data. The 3C 286 data look relatively clean in that there are no wildly egregious data (e.g., amplitudes that are 100,000x larger than the rest of the data). You may notice that there are antenna-to-antenna variations (under the Display tab select Colorize by Antenna1). These antenna-to-antenna variations are acceptable, this variation is taken care of by the calibration process.
One final useful plot we will make is a datastream plot of the antenna2 in a baseline for the data versus ea01, using spw 0 and channel 31. This shows, assuming that ea01 is in the entire observation, when various antennas drop out.
# In CASA
plotms(vis='3c391_ctm_mosaic_10s_spw0.ms',field='',correlation='RR,LL',
timerange='',antenna='ea01',spw='0:31',
xaxis='time',yaxis='antenna2',
plotrange=[-1,-1,0,26],coloraxis='field')
From this display (see Figure 4), you see immediately that the flagging we did earlier of antennas 10 and 12 (ea13 and ea15) has taken affect. For the remaining antennas, you see that 1, 6, and 13 (ea02, ea08, and ea16) are missing some blocks toward the beginning and also toward the end of the run. Antenna 3 (ea04) is missing the last scan and antenna 23 (ea26) is missing scans near the end. None of these antennas should be chosen as the reference antenna during the calibration process, below.
Calibrating the Data
It is now time to begin calibrating the data. The general data reduction strategy is to derive a series of scaling factors or corrections from the calibrators, which are then collectively applied to the science data. For more discussion of the philosophy, strategy, and implementation of calibration of synthesis data within CASA, see Synthesis Calibration in the CASA documentation.
Recall that the observed visibility [math]\displaystyle{ V^{\prime} }[/math] between two antennas [math]\displaystyle{ (i,j) }[/math] is related to the true visibility [math]\displaystyle{ V }[/math] by:
[math]\displaystyle{ V^{\prime}_{i,j}(u,v,f) = b_{ij}(t)\,[B_i(f,t) B^{*}_j(f,t)]\,g_i(t) g_j(t)\,V_{i,j}(u,v,f)\,e^{i [\theta_i(t) - \theta_j(t)]} }[/math]
Here, for generality, we show the visibility as a function of frequency [math]\displaystyle{ f }[/math] and spatial wave numbers [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math]. The other terms are:
- [math]\displaystyle{ g_i }[/math] and [math]\displaystyle{ \theta_i }[/math] are the amplitude and phase portions of what is commonly termed the complex gain. They are shown separately here because they are usually determined separately. For completeness, these are shown as a function of time [math]\displaystyle{ t }[/math] to indicate that they can change with temperature, atmospheric conditions, etc.
- [math]\displaystyle{ B_i }[/math] is the complex bandpass, the instrumental response as a function of frequency [math]\displaystyle{ f }[/math]. As shown here, the bandpass may also vary as a function of time.
- [math]\displaystyle{ b(t) }[/math] is the often-neglected baseline term. It can be important to include for the highest dynamic range images or shortly after a configuration change at the VLA, when antenna positions may not be known well.
Strictly, the equation above is a simplification of a more general measurement equation formalism, but it is a useful simplification in many cases.
A priori Antenna Position Corrections
Given the VLA is composed of 27 individual antennas, it is necessary to know their exact positions in order to correctly correlate (match and combine) each signal. Observations are sometimes made before some antenna positions are known exactly, as they can be corrected if the positions are known later. As mentioned in the observing log above, antennas ea10, ea12, and ea22 do not have good baseline positions. Antenna ea10 was not in the array, but, for the other two antennas, any improved baseline positions need to be incorporated. The importance of this step is that the visibility function is a function of [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math]. If the baseline positions are incorrect, then [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math] will be calculated incorrectly and there will be errors in the image. These corrections could also be determined later by a baseline-based calibration incorporating the [math]\displaystyle{ b_{ij} }[/math] term from the equation above, but since they are known a priori it makes sense to incorporate them now.
NRAO monitors the positions of the VLA antennas on a regular basis. The corrections are then placed into an NRAO database. If updated positions were entered into the database AFTER your observation date, the corrections to the newly measured positions can still be applied during your data reduction process in this step. Any updated positions that were entered into the database BEFORE your observations will already be accounted for in your data.
The calculations are inserted via gencal which allows automated lookup of the corrections. To see how to calculate corrections manually, go to the VLA Baseline Corrections site.
# In CASA
gencal(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic_10s_spw0.antpos',caltype='antpos')
In the logger you can see the corrections reported:
##########################################
##### Begin Task: gencal #####
gencal(vis="3c391_ctm_mosaic_10s_spw0.ms",caltable="3c391_ctm_mosaic_10s_spw0.antpos",caltype="antpos",infile="",spw="",
antenna="",pol="",parameter=[],uniform=True)
Opening MS: 3c391_ctm_mosaic_10s_spw0.ms for calibration.
Initializing nominal selection to the whole MS.
Determine antenna position offests from the baseline correction database
offsets for antenna ea01 : 0.00000 0.00300 0.00000
offsets for antenna ea02 : -0.00080 0.00000 0.00000
offsets for antenna ea03 : -0.00280 0.00000 0.00000
offsets for antenna ea05 : 0.00000 0.00280 0.00000
offsets for antenna ea11 : 0.00090 0.00000 0.00000
offsets for antenna ea12 : -0.01000 0.00450 -0.00170
offsets for antenna ea13 : 0.00000 -0.00080 0.00000
offsets for antenna ea17 : -0.00120 0.00000 0.00000
offsets for antenna ea18 : 0.00040 -0.00080 0.00040
offsets for antenna ea22 : -0.02570 0.00270 -0.01900
offsets for antenna ea23 : -0.00140 0.00000 0.00000
offsets for antenna ea24 : -0.00150 0.00000 0.00000
offsets for antenna ea26 : -0.00190 0.00000 0.00210
offsets for antenna ea27 : 0.00000 0.00190 -0.00160
Beginning specifycal-----------------------
Creating KAntPos Jones table from specified parameters.
Writing solutions to table: 3c391_ctm_mosaic_10s_spw0.antpos
##### End Task: gencal #####
##########################################
This particular set of observations was taken 24 April 2010, so the corrections shown above are for antennas that were moved BEFORE that date, but whose updated positions were not placed into the online database until later. Most likely, the antenna positions were re-measured after 24 April. You can verify this by looking at the online database for the first part of 2010:
; 2010 BASELINE CORRECTIONS IN METERS
;ANT
;MOVED OBSDATE Put_In_ MC(IAT) ANT PAD Bx By Bz
;
JAN27 FEB12 FEB21 01:57 11 E04 0.0000 0.0000 0.0000
JAN27 FEB12 FEB21 01:57 26 W03 -0.0170 0.0204 0.0041
MAR24 MAR25 MAR26 18:28 17 W07 -0.0061 -0.0069 -0.0055
APR21 MAY02 MAY04 23:25 12 E08 -0.0072 0.0045 -0.0017
MAR09 MAY02 MAY04 23:25 22 N04 -0.0220 0.0040 -0.0190
JUN08 JUN20 JUN22 03:00 10 N03 0.0046 -0.0196 0.0090
JUL17 JUL18 21:44 1 W09 0.0000 0.0030 0.0000
JUL17 JUL18 21:44 2 E02 -0.0008 0.0000 0.0000
JUL17 JUL18 21:44 3 E09 -0.0028 0.0000 0.0000
JUL17 JUL18 21:44 5 W08 0.0000 0.0028 0.0000
JUL01 JUL17 JUL18 21:44 6 N06 0.0022 0.0010 0.0059
JUL17 JUL18 21:44 10 N03 0.0008 0.0030 -0.0014
JUL17 JUL18 21:44 11 E04 0.0009 0.0000 0.0000
JUL17 JUL18 21:44 12 E08 -0.0028 0.0000 0.0000
JUL17 JUL18 21:44 13 N07 0.0000 -0.0008 0.0000
JUL17 JUL18 21:44 17 W07 -0.0012 0.0000 0.0000
JUL17 JUL18 21:44 18 N09 0.0004 -0.0008 0.0004
JUL17 JUL18 21:44 22 N04 -0.0037 -0.0013 0.0000
JUL17 JUL18 21:44 23 E07 -0.0014 0.0000 0.0000
JUL17 JUL18 21:44 24 W05 -0.0015 0.0000 0.0000
JUL17 JUL18 21:44 26 W03 -0.0019 0.0000 0.0021
JUL17 JUL18 21:44 27 E03 0.0000 0.0019 -0.0016
Initial Flux Density Scaling
The next step is to provide a flux density value for the amplitude calibrator J1331+3030 (a.k.a. 3C 286). Later, for the final step in determining the calibration solutions, we will use the calibrated gains of the two calibrator sources to transfer the flux density scaling to the secondary gain calibrator (J1822-0938).
For the pre-upgrade VLA, the ultimate flux density scale at most frequencies was set long ago by observations of 3C 295. The flux scaling was then transferred to a small number of primary flux density calibrators, including 3C 286. For the upgraded Karl G. Jansky VLA, the flux density scale at most frequencies is determined from WMAP observations of the planet Mars, which, in turn, was transferred to a small number of primary flux density calibrators. The procedure is to assume that the flux density of a primary calibrator source is known and, by comparison with the observed data for that calibrator, determine the [math]\displaystyle{ g_i }[/math] values (the antenna gains).
To start, let's find the available calibrator models with setjy and setting the parameter listmodels=True:
# In CASA
setjy(vis='3c391_ctm_mosaic_10s_spw0.ms', listmodels=True)
This command will show all available calibrator models:
3C123_P.im 3C138_P.im 3C147_A.im 3C147_Q.im 3C286_A.im 3C286_Q.im 3C380_P.im 3C48_P.im README 3C138_A.im 3C138_Q.im 3C147_C.im 3C147_S.im 3C286_C.im 3C286_S.im 3C48_A.im 3C48_Q.im 3C138_C.im 3C138_S.im 3C147_K.im 3C147_U.im 3C286_K.im 3C286_U.im 3C48_C.im 3C48_S.im 3C138_K.im 3C138_U.im 3C147_L.im 3C147_X.im 3C286_L.im 3C286_X.im 3C48_K.im 3C48_U.im 3C138_L.im 3C138_X.im 3C147_P.im 3C196_P.im 3C286_P.im 3C295_P.im 3C48_L.im 3C48_X.im
Since any image could be a potential calibrator model, setjy will list all *.im and *.mod images in the working directory. In addition, it will list all models that are provided by NRAO with the CASA package, and they will be picked by their names. We will be using the C-band VLA standard model for 3C286 which is aptly named '3C286_C.im':
# In CASA
setjy(vis='3c391_ctm_mosaic_10s_spw0.ms',field='J1331+3030',standard='Perley-Butler 2017',
model='3C286_C.im',usescratch=False,scalebychan=True,spw='')
- field='J1331+3030' : if the flux density calibrator is not specified then all sources will be assumed to have the same flux density.
- standard='Perley-Butler 2017' : The flux density scale at the VLA is periodically revised, updated, or expanded. The specified value represents the most recent determination of the flux density scale by R. Perley and B. Butler in 2017, ApJS, 230, 7 (now the default); older scales can also be specified, and might be important if, for example, one was attempting to conduct a careful comparison with a previously published result.
- model='3C286_C.im' : From plotms above, it can be estimated that 3C 286 is roughly a point source at this observation's frequency. Depending upon the frequency and configuration, the source may be slightly resolved. Fiducial model images have been determined from a painstaking set of observations, and, if one is available, it should be used to compensate for slight resolution effects (any deviation of the calibrator from a point source model). In this case, spectral window 0 (at 4.536 GHz) is in the C-band, so we use the C-band model image.
- usescratch=False : To save disk space, we will NOT force the writing of the model visibilities to the MODEL_DATA scratch column. For usescratch=False, CASA saves the model information and calculates the individual model visibilities on-the-fly when needed for calibration and for plotms.
- scalebychan=True : In order to take account for the intrinsic spectral index of our flux density calibrator 3C286 when we use it as our bandpass calibrator, we let setjy determine a flux density value per channel rather than one value for the entire spectral window.
- spw=' ' : The original data contained two spectral windows. Having split off spectral window 0, it is not necessary to specify spw. Had the spectral window 0 not been split off, we might wish to specify the spectral window because, in this observation, the spectral windows were sufficiently separated that two different model images for 3C 286 would be appropriate; 3C286_C.im at 4.6 GHz and 3C286_X.im at 7.5 GHz. This would require two separate runs of setjy, one for each spectral window. If the spectral windows were much closer together, it might be possible to calibrate both using the same model.
In this case, a model image of a primary flux density calibrator exists. However, for some kinds of polarization calibration or in extreme situations (e.g., there are problems with the scan on the flux density calibrator), it can be useful (or necessary) to set the flux density of the source explicitly.
The most important output from setjy should look similar to the following:
Selected 31964 out of 845379 rows. J1331+3030 (fld ind 0) spw 0 [I=7.6686, Q=0, U=0, V=0] Jy @ 4.536e+09Hz, (Perley-Butler 2017) Scaling spw(s) [0]'s model image by channel to I = 7.66964, 7.5989, 7.53174 Jy @(4.535e+09, 4.601e+09, 4.665e+09)Hz ...
As set, the flux density scale is being calculated only for spectral window 0 (spw='0' ), as it is the only one in the dataset. The flux density in each Stokes plane (IQUV) for the reference channel 0 is reported, followed by the I flux density in each of the channels to be used for scaling the data. This value is determined from an analytical formula for the spectrum of the source as a function of frequency; this value must be determined so that the flux density in the image can be scaled to it, as it is unlikely that the observation was taken at exactly the same frequency as the model image. Also, setjy will clear any previous calibration model that fits the selection. In this case, no such previous model data was found.
Note that setjy also returns a python dictionary (CASA record) containing the reference flux density used. In our case, you will find the return value in the CASA command line window:
{'0': {'0': {'fluxd': array([ 7.6685524, 0. , 0. , 0. ])},
'fieldName': 'J1331+3030'},
'format': "{field Id: {spw Id: {fluxd: [I,Q,U,V] in Jy}, 'fieldName':field name }}"}
If desired, this can be captured by calling the task by setting it to a variable, e.g. myset = setjy(...).
Initial Phase Calibration
Before solving for the bandpass, we will do an initial phase calibration. The reason for this step is to average over the (typically small) variations of phase with time in the bandpass, before solving for the bandpass solution itself. Depending upon frequency and configuration, there could be significant gain variations between different scans of the bandpass calibrator, particularly if the scans happen at much different elevations. One can solve for an initial set of antenna-based gains, which will later be discarded, in order to moderate the effects of variations from integration to integration and from scan to scan on the bandpass calibrator. While amplitude variations with time will have little effect on the bandpass solutions, it is important to solve for phase variations with time to prevent de-correlation when vector averaging the data for computing the final bandpass solution.
We use the CASA task gaincal to solve for phase versus time for the central channels on our three calibrators:
# In CASA
gaincal(vis='3c391_ctm_mosaic_10s_spw0.ms', caltable='3c391_ctm_mosaic_10s_spw0.G0all',
field='0,1,9', refant='ea21', spw='0:27~36',
gaintype='G',calmode='p', solint='int',
minsnr=5, gaintable=['3c391_ctm_mosaic_10s_spw0.antpos'])
- caltable='3c391_ctm_mosaic_10s_spw0.G0all' : The gain solutions will be stored in this external table.
- field='0,1,9' : Specify the calibrators. Although the bandpass solution will be based only on the bandpass calibrator, We will use this opportunity to inspect solutions for ALL calibrators in order to potentially identify any bad data.
- refant='ea21' : Earlier, by looking at the output from plotants, a reference antenna near the center of the array was noted. Here is the first time that choice is used, as the antenna closest to the center without being shadowed is generally used as the reference antenna. Strictly, all of the gain corrections derived will be relative to this reference antenna.
- spw='0:27~36' : Choose a subset of the channels from which to determine the gain corrections. These should be near the center of the band, and there should be enough channels chosen so that a reasonable signal-to-noise ratio can be obtained; the central 10% of the channels is a good guideline. Particularly at lower frequencies where RFI can manifest itself, one should choose RFI-free frequency channels; the VLA Observing Guide RFI page lists the known RFI frequencies for each band. Also note that, even though these data have only a single spectral window, the syntax requires specifying the spectral window ('0') in order to specify specific channels ('27~36' in this example).
- gaintype='G' : Compute the complex gain solutions, one per antenna per spw per polarization per solution interval. Note that gaintype='G' assumes the V stokes is zero if not told otherwise, so for the case where the calibrator has significant circular polarization, a model incorporating polarization must be used (this can be set with setjy). For the current dataset we know that the calibrator has negligible circular polarization so the V polarization does not need to be set.
- calmode='p' : Solve for only the phase portion of the gain.
- solint='int' : To track the phases, a short solution interval is chosen. (int refers to a single integration time or 10 seconds for this case)
- minsnr=5 : Restrict the solutions to be at relatively high signal-to-noise ratios, although this parameter may need to be varied depending upon the source and frequency.
- gaintable=['3c391_ctm_mosaic_10s_spw0.antpos'] : Having produced antenna position corrections (as we did above with gencal), they should now be applied.
To really see what is going on, we use plotms to inspect the solutions from gaincal for a single antenna at a time, iterating through each antenna in sequence by clicking on the Next button (right pointing single green arrow) on the GUI to advance the displayed antenna.
# In CASA
plotms(vis='3c391_ctm_mosaic_10s_spw0.G0all',xaxis='time',yaxis='phase',
coloraxis='corr',iteraxis='antenna',plotrange=[-1,-1,-180,180])
- vis='3c391_ctm_mosaic_10s_spw0.G0all' : the calibration table to examine solutions
- xaxis='time' : plotting phase solutions vs time
- yaxis='phase' : plotting phase solutions vs time
- coloraxis=corr : colorize by polarization (black=R, pink=L; coloring choice is automatic in plotms)
- iteraxis='antenna' : iterating the plot across each antenna
Note: plotms was originally designed to plot visibility data, while the task plotcal (no longer maintained as of CASA version 5.4.0) was used for plotting calibration tables. Plotms has now taken over the functionality of plotcal. However, some of the input parameter names (e.g., "vis" instead of "caltable") still reflect the original design for plotms. Examples of using plotcal to examine calibration tables can be found in the earlier versions of this and other CASAguide tutorials.
Antennas that have been flagged will show a blank plot, as there are no solutions for these antennas. For most antennas, we see a fairly smooth variation with time, so we expect to be able to calibrate the data nicely. However, when you get to ea05, note that there are phase jumps where the phase appears to be oscillating between two states. Stepping through to that antenna reveals Figure 5.
Antennas other than ea05 look OK. We will not be able to transfer calibration for antenna ea05 so we flag it from the data:
# In CASA
flagdata(vis='3c391_ctm_mosaic_10s_spw0.ms',
flagbackup=True, mode='manual', antenna='ea05')
For the following bandpass solution we need only solve for our bandpass calibrator, and we will do so now after flagging. The following call to gaincal is similar to the one above, but selects only the bandpass calibrator (using the field parameter). This is the calibration table we will use when solving for the bandpass solution, below.
# In CASA
gaincal(vis='3c391_ctm_mosaic_10s_spw0.ms', caltable='3c391_ctm_mosaic_10s_spw0.G0',
field='J1331+3030', refant='ea21', spw='0:27~36', calmode='p', solint='int',
minsnr=5, gaintable=['3c391_ctm_mosaic_10s_spw0.antpos'])
You can inspect this with plotms as we did above. For example, plot (with colorization by polarization) for the first block of 3C286 data only:
# In CASA
plotms(vis='3c391_ctm_mosaic_10s_spw0.G0',
xaxis='time',yaxis='phase',coloraxis='corr',field='J1331+3030',iteraxis='antenna',
plotrange=[-1,-1,-180,180],timerange='08:02:00~08:17:00')
Delay Calibration
The first stage of bandpass calibration involves solving for the antenna-based delays which put a phase ramp versus frequency channel in each spectral window (Figure 3C). The K gain type in gaincal solves for the relative delays of each antenna relative to the reference antenna (parameter refant), so be sure you pick one that is there for this entire scan and good. This is not a full global delay, but gives one value per spw per polarization.
# In CASA
gaincal(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic_10s_spw0.K0',
field='J1331+3030',refant='ea21',spw='0:5~58',gaintype='K',
solint='inf',combine='scan',minsnr=5,
gaintable=['3c391_ctm_mosaic_10s_spw0.antpos',
'3c391_ctm_mosaic_10s_spw0.G0'])
- field='J1331+3030' : For the bandpass calibrator
- refant='ea21' : Delays will be relative to this antenna, make sure it is there!
- spw='0:5~58' : Widest possible frequency range in the spw, avoiding edge channels because they have lower sensitivity
- gaintype='K' : Compute K (i.e., delay) solutions, one per antenna per spw per polarization per solution interval
- solint='inf ',combine='scan' : Only need one solution averaged over all times and scans. solint='inf ' sets the solution interval to 'infinite' but respects scan boundaries; combine='scan' combines data across scan boundaries
- minsnr=5 : Restrict the solutions to be at relatively high signal-to-noise ratios, although this parameter may need to be varied depending upon the source and frequency.
- gaintable=['3c391_ctm_mosaic_10s_spw0.antpos','3c391_ctm_mosaic_10s_spw0.G0'] : Use the antpos and G0 tables that were created earlier
We can plot these solutions (in nanoseconds) as a function of antenna (Figure 6):
# In CASA
plotms(vis='3c391_ctm_mosaic_10s_spw0.K0',xaxis='antenna1',yaxis='delay',coloraxis='baseline')
These are within about 4 nanoseconds, as expected for the early science observations with the newly upgraded VLA.
Bandpass Calibration
This step solves for the complex bandpass, [math]\displaystyle{ B_i }[/math].
All data with the VLA are taken in spectral line mode, even if the science that one is conducting is continuum, and therefore requires a bandpass solution to account for gain variations with frequency. Solving for the bandpass won't hurt for continuum data, and, for moderate or high dynamic range image, it is essential. To motivate the need for solving for the bandpass, consider Figure 7. It shows the right circularly polarized data (RR correlation) for the source J1331+3030, which will serve as the bandpass calibrator. The data are color coded by spectral window, as earlier plots from plotms indicated that the visibility data are nearly constant with baseline length. Ideally, the visibility data would be constant as a function of frequency as well. The variations with frequency are a reflection of the (slightly) different antenna bandpasses. (Exercise for the reader, reproduce Figure 7 using plotms.)
Now form the bandpass, using the phase solutions just derived.
# In CASA
bandpass(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic_10s_spw0.B0',
field='J1331+3030',spw='',refant='ea21',combine='scan',
solint='inf',bandtype='B',
gaintable=['3c391_ctm_mosaic_10s_spw0.antpos',
'3c391_ctm_mosaic_10s_spw0.G0',
'3c391_ctm_mosaic_10s_spw0.K0'])
- caltable='3c391_ctm_mosaic_10s_spw0.B0' : Specify where to store the bandpass corrections.
- solint='inf ', combine='scan' : This observation contains multiple scans on the bandpass calibrator, J1331+3030. Because these are continuum observations, it is probably acceptable to combine all the scans and compute one bandpass correction per antenna, which is achieved by the combination of 'solint='inf ' and combine='scan' . The value inf means infinite, which means to combine solutions for all times, but to respect scan boundaries. combine='scan' additionally averages over all scans. Had combine=' ' then there would have been a bandpass correction derived for each scan (which might be desirable for very high dynamic range spectral line observations).
- bandtype='B' : The bandpass solution will be derived on a channel-by-channel basis. There is an alternate option of parameter bandtype='BPOLY' that will fit an nth order polynomial to the bandpass.
- gaintable=['3c391_ctm_mosaic_10s_spw0.antpos', '3c391_ctm_mosaic_10s_spw0.G0', '3c391_ctm_mosaic_10s_spw0.K0'] : Apply antenna positions, phase solutions, and delays before computing bandpass.
Once again, one can use plotms to display the bandpass solutions. Note that in the inputs below, the amplitudes are being displayed as a function of frequency channel. The parameters gridrows=2 and gridcols=2 are used to display multiple plots per page (2 plots per page in the y direction and 2 in the x direction). The first command below shows the amplitude solutions (one per polarization) (Figure 8A) and the second command below shows the phase solutions (one per each polarization). Parameter iteration='antenna' is used to step through separate plots for each antenna.
# In CASA
plotms(vis='3c391_ctm_mosaic_10s_spw0.B0',field='J1331+3030',
xaxis='chan',yaxis='amp',coloraxis='corr',
iteraxis='antenna',gridrows=2,gridcols=2)
plotms(vis='3c391_ctm_mosaic_10s_spw0.B0',field='J1331+3030',
xaxis='chan',yaxis='phase',coloraxis='corr',plotrange=[-1,-1,-180,180],
iteraxis='antenna',gridrows=2,gridcols=2)
As expected, the bandpass phases are relatively flat (see Figure 8B) with the slopes (Figure 3C) removed by the delay calibration. Residual phase excursions are on the order of a few degrees.
Gain Calibration
The next step is to derive corrections for the complex antenna gains, [math]\displaystyle{ g_i }[/math] and [math]\displaystyle{ \theta_i }[/math]. As discussed above, the absolute magnitude of the gain amplitudes ([math]\displaystyle{ g_i }[/math]) are determined by reference to a standard flux density calibrator. In order to determine the appropriate complex gains for the target source, and to minimize differences through the atmosphere (neutral and/or ionized) between the lines of sight to the phase calibrator and the target source, you want to observe a so-called phase calibrator that is much closer to the target. If we establish the relative gain amplitudes and phases for different antennas using the phase calibrator, we can later determine the absolute flux density scale by comparing the gain amplitudes, [math]\displaystyle{ g_i }[/math], derived for 3C 286 with those derived for the phase calibrator. This will eventually be done using the task fluxscale. Since there is no such thing as absolute phase, we determine a zero phase by selecting a reference antenna for which the gain phase is defined to be zero.
In principle, one could determine the complex antenna gains for all sources with a single invocation of gaincal; for clarity here, two separate invocations will be used.
In the first step, we derive the appropriate complex gains [math]\displaystyle{ g_i }[/math] and [math]\displaystyle{ \theta_i }[/math] for the flux density calibrator 3C 286.
# In CASA
gaincal(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic_10s_spw0.G1',
field='J1331+3030',spw='0:5~58',
solint='inf',refant='ea21',gaintype='G',calmode='ap',solnorm=False,
gaintable=['3c391_ctm_mosaic_10s_spw0.antpos',
'3c391_ctm_mosaic_10s_spw0.K0',
'3c391_ctm_mosaic_10s_spw0.B0'],
interp=['','','nearest'])
- caltable='3c391_ctm_mosaic_10s_spw0.G1' : Produce a new calibration table containing these gain solutions. In order to make the bookkeeping easier, a '1' is appended to the file name to distinguish it from the earlier set of gain solutions, which are effectively being thrown away.
- spw='0:5~58' : From the inspection of the bandpass, one can determine the range of edge channels that are affected by the bandpass filter rolloff. Because the amplitude is dropping rapidly in these channels, one does not want to include them in the solution.
- field='J1331+3030' : in this first of the two invocations of gaincal, we are finding gain solutions for calibrator source J1331+3030 (3C 286).
- gaintype='G' : with this option, we will determine complex antenna gain solutions separately for each polarization and each spectral window
- calmode='ap', solnorm=False: The objective is to relate the measured data values to the (assumed known) flux density of 3C 286, thus the solution is both amplitude and phase ('ap') and the solutions should not be normalized to unity amplitude.
- solint='inf ' : Produce a solution for each scan. Phase coherence for these observations is good.
- gaintable=['3c391_ctm_mosaic_10s_spw0.antpos', '3c391_ctm_mosaic_10s_spw0.K0', '3c391_ctm_mosaic_10s_spw0.B0'] : Use the antenna position corrections, delays, and bandpass solutions determined earlier before solving for the gain amplitudes.
- interp=[' ',' ','nearest']: the temporal interpolation to use for each gaintable. When there is no attribute included, it will default to 'linear' although it is not recommended to leave all the attributes blank. When there are multiple bandpass solutions, it can be especially important to use 'nearest' for the bandpass table, as linear would allow extrapolation beyond the sampled times. (As there is only one bandpass solution for this Guide, specifying 'nearest' is not strictly necessary as 'linear' and 'nearest' result in the same behavior in the case of a single time solution. We include the specification for demonstration purposes.)
In the second step, the appropriate complex gains for a direction on the sky close to the target source will be determined from the phase calibrator J1822-0938.
# In CASA
gaincal(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic_10s_spw0.G1',
field='J1822-0938',
spw='0:5~58',solint='inf',refant='ea21',gaintype='G',calmode='ap',
gaintable=['3c391_ctm_mosaic_10s_spw0.antpos',
'3c391_ctm_mosaic_10s_spw0.K0',
'3c391_ctm_mosaic_10s_spw0.B0'],
append=True)
- caltable='3c391_ctm_mosaic_10s_spw0.G1', append=True: In the previous invocation of gaincal, append was set to False. Here, the gain solutions from the phase calibrator are going to be appended to the existing set from 3C 286 and thus stored in a single table. In following steps, all of these gain solutions will then be used together to derive a set of complex gains that are applied to the science data for the target source.
If one checks the gain phase solutions using plotms, one should see smooth solutions for each antenna as a function of time (see Figures 9A--9B).
# In CASA
plotms(vis='3c391_ctm_mosaic_10s_spw0.G1',xaxis='time',yaxis='phase',
gridrows=1,gridcols=2,iteraxis='corr',coloraxis='baseline',
plotrange=[-1,-1,-180,180],plotfile='plotms_3c391-G1-phase.png')
plotms(vis='3c391_ctm_mosaic_10s_spw0.G1',xaxis='time',yaxis='amp',
gridrows=1,gridcols=2,iteraxis='corr',coloraxis='baseline',
plotfile='plotms_3c391-G1-amp.png')
The lower gain solution values (near 1.0) correspond to the two scans of 3C 286, while the higher gain solution values (near 1.5) correspond to the scans of the phase calibrator, J1822-0938. At this stage in the calibration, we have not yet solved for the flux density scaling. In order for the amplitude of 3C 286 in the data to match the amplitude of its model (which we set above with setjy), little scaling of the solution is required (value = 1.0). J1822-0938 is fainter than 3C 286, leading to a higher solution value. The ratio of amplitude solutions between the two sources will be used in a later calibration step (fluxscale) to determine the actual flux density of J1822-0938.
This is also a good time to check that our chosen reference antenna (ea21) has good phase stability (i.e., the phase difference between the right and left polarizations is stable with time). To do this, we plot the complex polarization ratio by selecting correlation=' / ' :
# In CASA
plotms(vis='3c391_ctm_mosaic_10s_spw0.G1', xaxis='time', yaxis='phase',
correlation='/', coloraxis='baseline', plotrange=[-1,-1,-180,180])
As can be seen in Figure 10, there is a bit of drift (a few degrees here and there), but no phase jumps. This means that ea21 is, indeed, a good choice for reference antenna.
Scaling the Amplitude Gains
While we know the flux density of our primary calibrator (J1331+3030[math]\displaystyle{ \equiv }[/math]3C 286), the model assumed for the secondary calibrator (J1822-0938) was a point source of 1 Jy located at the phase center. While the secondary calibrator was chosen to be a point source (at least, over some limited range of uv-distance; see the VLA calibrator manual for any u-v restrictions on your calibrator of choice at the observing frequency), its absolute flux density is unknown. Being point-like, secondary calibrators typically vary on timescales of months to years, in some cases by up to 50--100%.
We use the primary (flux) calibrator to determine the system response to a source of known flux density and assume that the mean gain amplitudes for the primary calibrator are the same as those for the secondary calibrator. This allows us to find the true flux density of the secondary calibrator. To do this, we use the task fluxscale, which produces a new calibration table containing properly-scaled amplitude gains for the secondary calibrator.
# In CASA
myscale = fluxscale(vis='3c391_ctm_mosaic_10s_spw0.ms',
caltable='3c391_ctm_mosaic_10s_spw0.G1',
fluxtable='3c391_ctm_mosaic_10s_spw0.fluxscale1',
reference='J1331+3030',
transfer=['J1822-0938'],
incremental=False)
- myscale = fluxscale(...) : fluxscale returns a dictionary of results, which we capture in the variable myscale
- caltable='3c391_ctm_mosaic_10s_spw0.G1' : We provide fluxscale with the calibration table containing the amplitude gain solutions derived earlier.
- fluxtable='3c391_ctm_mosaic_10s_spw0.fluxscale1' : We specify the name of the new output table to be written, which will contain the properly-scaled amplitude gains.
- reference='J1331+3030' : We specify the source with the known flux density.
- transfer=['J1822-0938']: We specify the source whose amplitude gains are to be rescaled; if there were multiple secondary calibrators to be used, this parameter value would need to be a python list.
- incremental=False: Make a new output fluxtable replacing caltable with rescaled transfer gains. If parameter incremental=True then the new table would be used in addition to caltable in subsequent applications.
Task fluxscale will print to the CASA logger the derived flux densities of all calibrator sources specified with the transfer parameter. These are also captured in the return variable from the task. You should examine the output to ensure that it looks sensible. If the data set has more than one spectral window, depending upon where they are spaced and the spectrum of the source, it is possible to find quite different flux densities and spectral indexes for the secondary calibrators. Example output would be
CASA <99>: myscale['1']
Out[99]:
{'0': {'fluxd': array([ 2.29600096, 0. , 0. , 0. ]),
'fluxdErr': array([ 0.00692024, 0. , 0. , 0. ]),
'numSol': array([ 46., 0., 0., 0.])},
'fieldName': 'J1822-0938',
'fitFluxd': 0.0,
'fitFluxdErr': 0.0,
'fitRefFreq': 0.0,
'spidx': array([ 0., 0., 0.]),
'spidxerr': array([ 0., 0., 0.])}
The index '1' above refers to the field number. You can also find the flux density values in the CASA logger:
... Found reference field(s): J1331+3030 Found transfer field(s): J1822-0938 Flux density for J1822-0938 in SpW=0 (freq=4.599e+09 Hz) is: 2.296 +/- 0.00692024 (SNR = 331.781, N = 46) Storing result in 3c391_ctm_mosaic_10s_spw0.fluxscale1 ...
Again, the VLA calibrator manual may be used to check whether the derived flux densities look sensible. Wildly different flux densities or flux densities with very high error bars should be treated with suspicion; in such cases you will have to figure out whether something has gone wrong.
We plot the rescaled amplitudes from this table:
# In CASA
plotms(vis='3c391_ctm_mosaic_10s_spw0.fluxscale1',xaxis='time',yaxis='amp',
correlation='R',coloraxis='baseline')
plotms(vis='3c391_ctm_mosaic_10s_spw0.fluxscale1',xaxis='time',yaxis='amp',
correlation='L',coloraxis='baseline')
You can see in Figures 11A and 11B that the amplitude gain factors are now similar across sources, compared to the raw factors in the G1 table.
Applying the Calibration
Now that we have derived all the calibration solutions, we need to apply them to the actual data, using the task applycal. The measurement set DATA column contains the original data. To apply the calibration we have derived, we specify the appropriate calibration tables, which are then applied to the DATA column, with the results being written in the CORRECTED_DATA column. If the dataset does not already have a CORRECTED_DATA scratch column, then one will be created in the first applycal run.
First, we apply the calibration to each individual calibrator, using the gain solutions derived on that calibrator alone to compute the CORRECTED_DATA. To do this, we iterate over the different calibrators, in each case specifying the source to be calibrated (using the field parameter). The relevant function calls are given below.
# In CASA
applycal(vis='3c391_ctm_mosaic_10s_spw0.ms',
field='J1331+3030',
gaintable=['3c391_ctm_mosaic_10s_spw0.antpos',
'3c391_ctm_mosaic_10s_spw0.fluxscale1',
'3c391_ctm_mosaic_10s_spw0.K0',
'3c391_ctm_mosaic_10s_spw0.B0'],
gainfield=['','J1331+3030','',''],
interp=['','nearest','',''],
calwt=False)
applycal(vis='3c391_ctm_mosaic_10s_spw0.ms',
field='J1822-0938',
gaintable=['3c391_ctm_mosaic_10s_spw0.antpos',
'3c391_ctm_mosaic_10s_spw0.fluxscale1',
'3c391_ctm_mosaic_10s_spw0.K0',
'3c391_ctm_mosaic_10s_spw0.B0'],
gainfield=['','J1822-0938','',''],
interp=['','nearest','',''],
calwt=False)
- gaintable : We provide a Python list of the calibration tables to be applied. This list must contain the antenna position corrections (.antpos), the properly-scaled gain calibration for the amplitudes and phases (.fluxscale1) which were just made using fluxscale, the parallel-hand delays (.K0), and the bandpass solutions (.B0).
- gainfield, interp : To ensure that we use the correct gain amplitudes and phases for a given calibrator (those derived on that same calibrator), we must specify for each calibrator source the particular subset of gain solutions to be applied. This requires use of the gainfield and interp parameters; these are both Python lists, and for the list item corresponding to the calibration table made by fluxscale, we set gainfield to the field name corresponding to that calibrator, and the desired interpolation type (interp) to nearest.
- calwt=False : Using calwt=True (calibrating the weights) is dependent on having truly representative weights in the data and currently the VLA data does not do this, though ALMA does. For the VLA, we are not yet using system calibration data to compute real (1/Jy2) weights, thus trying to calibrate them during the applycal stage can produce nonsensical results. In particular, experience has shown that calibrating the weights will lead to problems especially in the self-calibration steps. We will instead set the weights before imaging using the statwt task (further details below).
Finally, we apply the calibration to the target fields in the mosaic, linearly interpolating the gain solutions from the secondary calibrator, J1822-0938. In this case however, we want to apply the amplitude and phase gains derived from the secondary calibrator, J1822-0938, since that is close to the target source on the sky and we assume that the gains applicable to the target source are very similar to those derived in the direction of the secondary calibrator. Of course, this is not strictly true, since the gains on J1822-0938 were derived at a different time and in a different position on the sky from the target. However, assuming that the calibrator was sufficiently close to the target, and the weather was sufficiently well-behaved, then this is a reasonable approximation and should get us a sufficiently good calibration that we can later use self-calibration to correct for the small inaccuracies thus introduced.
The procedure for applying the calibration to the target source is very similar to what we just did for the calibrator sources.
# In CASA
applycal(vis='3c391_ctm_mosaic_10s_spw0.ms',
field='2~8',
gaintable=['3c391_ctm_mosaic_10s_spw0.antpos',
'3c391_ctm_mosaic_10s_spw0.fluxscale1',
'3c391_ctm_mosaic_10s_spw0.K0',
'3c391_ctm_mosaic_10s_spw0.B0'],
gainfield=['','J1822-0938','',''],
interp=['','linear','',''],
calwt=False)
- field : We can calibrate all seven target fields at once by setting field='2~8' .
- gainfield : In this case, we wish to use the gains derived on the secondary calibrator, for the reasons explained in the previous paragraph.
- interp : This time, we linearly interpolate between adjacent calibrator scans, to compute the appropriate gains for the intervening observations of the target.
We should now have fully-calibrated visibilities in the CORRECTED_DATA column of the measurement set, and it is worthwhile pausing to inspect them to ensure that the calibration did what we expected it to. We make some standard plots (see Figures 12A through 12D):
# In CASA
plotms(vis='3c391_ctm_mosaic_10s_spw0.ms',field='0',correlation='RR,LL',
antenna='',avgtime='60',xaxis='channel',yaxis='amp',
ydatacolumn='corrected',coloraxis='corr',
plotfile='plotms_3c391-fld0-corrected-amp.png')
plotms(vis='3c391_ctm_mosaic_10s_spw0.ms',field='0',correlation='RR,LL',
antenna='',avgtime='60',xaxis='channel',yaxis='phase',
ydatacolumn='corrected',coloraxis='corr',
plotrange=[-1,-1,-180,180],
plotfile='plotms_3c391-fld0-corrected-phase.png')
plotms(vis='3c391_ctm_mosaic_10s_spw0.ms',field='1',correlation='RR,LL',
antenna='',avgtime='60',xaxis='channel',yaxis='amp',
ydatacolumn='corrected',coloraxis='corr',
plotfile='plotms_3c391-fld1-corrected-amp.png')
plotms(vis='3c391_ctm_mosaic_10s_spw0.ms',field='1',correlation='RR,LL',
antenna='',avgtime='60',xaxis='channel',yaxis='phase',
ydatacolumn='corrected',coloraxis='corr',
plotrange=[-1,-1,-180,180],
plotfile='plotms_3c391-fld1-corrected-phase.png')
Inspecting the data at this stage may well show up previously-unnoticed bad data. Plotting the corrected amplitude against UV distance or against time is a good way to find such issues. If you find bad data, you can remove them via interactive flagging in plotms or via manual flagging in flagdata once you have identified the offending antennas/baselines/channels/times. When you are happy that all data (particularly on your target source) look good, you may proceed. Images 12A through 12D show that there is no sign of bad data remaining.
Now that the calibration has been applied to the target data we can split off the science targets, creating a new, calibrated measurement set containing all the target fields.
# In CASA
split(vis='3c391_ctm_mosaic_10s_spw0.ms',outputvis='3c391_ctm_mosaic_spw0.ms',
datacolumn='corrected',field='2~8',correlation='RR,LL')
- outputvis : We give the name of the new measurement set to be written, which will contain the calibrated data on the science targets.
- datacolumn : We use the CORRECTED_DATA column, containing the calibrated data which we just wrote using applycal.
- field : We wish to put all the mosaic pointings into a single measurement set, for imaging and joint deconvolution.
- correlation : For the purposes of this tutorial, we have calibrated only the parallel polarization correlations.
Prior to imaging, it is a good idea to run the statwt task to correct the data weights (weight and sigma columns) in the measurement set. Running statwt will remove the effects of relative noise scatter that may have been introduced from flagging uneven bits in the visibility data between the channels and times. We will run this task here on the newly calibrated and split-out data set before moving on to imaging.
# In CASA
statwt(vis='3c391_ctm_mosaic_spw0.ms',datacolumn='data')
Imaging
Now that we have split off the target data into a separate measurement set with all the calibration applied, it's time to make an image. Recall that the visibility data and the sky brightness distribution (a.k.a. image) are Fourier transform pairs.
[math]\displaystyle{ I(l,m) = \int V(u,v) e^{[2\pi i(ul + vm)]} dudv }[/math]
The [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math] coordinates are the baselines measured in units of the observing wavelength, while the [math]\displaystyle{ l }[/math] and [math]\displaystyle{ m }[/math] coordinates are the direction cosines on the sky. For generality, the sky coordinates are written in terms of direction cosines, but for most VLA (and ALMA) observations they can be related simply to the right ascension ([math]\displaystyle{ l }[/math]) and declination ([math]\displaystyle{ m }[/math]). Also recall that this equation is valid only if the [math]\displaystyle{ w }[/math] coordinate of the baselines can be neglected. This assumption is almost always true at high frequencies and smaller VLA configurations (such as the 4.6 GHz D-configuration observations here). The [math]\displaystyle{ w }[/math] coordinate cannot be neglected at lower frequencies and larger configurations (e.g., 0.33 GHz, A-configuration observations). This expression also neglects other factors, such as the shape of the primary beam. For more information on imaging, see the Synthesis Imaging section of the CASA documentation.
CASA has a task tclean which both Fourier transforms the data and deconvolves the resulting image. For the purposes of this tutorial, we will make a mosaic clean image in Stokes I. We will use a multi-scale cleaning algorithm because the supernova remnant contains both diffuse, extended structure on large spatial scales and finer filamentary structure on smaller scales. This approach will do a better job of modeling the image than the classic clean delta function. For broader examples of many tclean options, please see the Topical Guide for Imaging VLA Data.
Imaging parameters
It is important to have an idea of what values to use for the image pixel (cell) size and the overall size of the image. Setting the appropriate pixel size for imaging depends upon basic optics aspects of interferometry. Using plotms to look at the newly-calibrated, target-only data set:
# In CASA
plotms(vis='3c391_ctm_mosaic_spw0.ms',xaxis='uvwave',yaxis='amp',
ydatacolumn='data', field='0',avgtime='30',correlation='RR',
plotfile='plotms_3c391-mosaic0-uvwave.png',overwrite=True)
You should obtain a plot similar to Figure 13 with the calibrated visibility amplitude as a function of [math]\displaystyle{ u }[/math]-[math]\displaystyle{ v }[/math] distance. Note that while 'uvdist' and 'uvwave' are in essence the same, they differ in units and by respect values. The difference is that 'uvdist' is measured in physical units, i.e., meters (as the antenna separation is in meters), whereas 'uvwave' is measured in units of wavelengths at the specific frequency.
The maximum baseline is about 16,000 wavelengths, i.e., a smallest angular scale of 12 arcseconds ([math]\displaystyle{ \lambda/D=1/16000 }[/math]). The most effective cleaning occurs with at least 4-5 pixels across the synthesized beam. For the resolution element of 12 arcseconds, a cell size of 2.5 arcseconds will give just under 5 pixels per beam.
The supernova remnant itself is known to have a diameter of order 9 arcminutes, corresponding to about 216 pixels for the chosen cell size. The mosaic was set up with 7 fields, 1 centered on the remnant with 6 flanking fields; the spacing of the fields was chosen based on the size of the antenna primary beam. With the choice of gridder='mosaic' (our main mosaicking algorithm), we will image an area somewhat larger than the size of the supernova remnant in order to have a bit of padding around the outside. Although CASA has the feature that its Fourier transform engine (FFTW) does not require a strict power of 2 for the number of linear pixels in a given image axis, it is somewhat more efficient if the number of pixels on a side is a composite number divisible by any pair of 2 and 3 and/or 5. Because tclean internally applies a padding of 1.2 (= 3 x 2/5), we will use an image size of 480, which is 25 × 3 × 5 (so 480 × 1.2 = 576 = 26 × 32). We therefore set imsize=[480,480] and our mosaic fits comfortably inside the image.
Multi-scale Mosaic Clean
In this tutorial, we will run the cleaning task interactively so that we can set and modify the mask:
# In CASA
tclean(vis='3c391_ctm_mosaic_spw0.ms',imagename='3c391_ctm_spw0_multiscale',
field='',spw='',
specmode='mfs',
niter=20000,
gain=0.1, threshold='1.0mJy',
gridder='mosaic',
deconvolver='multiscale',
scales=[0, 5, 15, 45], smallscalebias=0.9,
interactive=True,
imsize=[480,480], cell=['2.5arcsec','2.5arcsec'],
stokes='I',
weighting='briggs',robust=0.5,
pbcor=False,
savemodel='modelcolumn')
Task tclean is powerful with many inputs and a certain amount of experimentation likely is required.
- vis='3c391_ctm_mosaic_spw0.ms' : this split MS contains our 7-pt mosaic fields, now indexed as 0-6. Field 0 is the central field of the mosaic (you can use listobs to verify this).
- imagename='3c391_ctm_spw0_multiscale' : the output image names will all start with this (e.g., 3c391_ctm_spw0_multiscale.image, 3c391_ctm_spw0_multiscale.rms, etc.)
- specmode='mfs' : Use multi-frequency synthesis imaging. The fractional bandwidth of these data is non-zero (128 MHz at a central frequency of 4.6 GHz). Recall that the [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math] coordinates are defined as the baseline coordinates, measured in wavelengths. Thus, slight changes in the frequency from channel to channel result in slight changes in [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math]. There is an accompanying improvement in [math]\displaystyle{ u }[/math]-[math]\displaystyle{ v }[/math] coverage if the visibility data from the multiple spectral channels are gridded separately onto the [math]\displaystyle{ u }[/math]-[math]\displaystyle{ v }[/math] plane, as opposed to treating all spectral channels as having the same frequency.
- niter=20000,gain=0.1,threshold='1.0mJy' : Recall that the gain is the amount by which a clean component is subtracted during the cleaning process. Parameters niter and threshold are (coupled) means of determining when to stop the cleaning process, with niter specifying to find and subtract that many clean components while threshold specifies a minimum flux density threshold a clean component can have before tclean stops. See also interactive below. Imaging is an iterative process, and to set the threshold and number of iterations, it is usually wise to clean interactively in the first instance, stopping when spurious emission from sidelobes (arising from gain errors) dominates the residual emission in the field. Here, we have used our experience in interactive mode to set a threshold level based on the rms noise in the resulting image. The number of iterations should then be set high enough to reach this threshold, although this can take many hours if the user does all 20000 iterations.
- gridder='mosaic' : The data consist of a 7-pointing mosaic, since the supernova remnant fills almost the full primary beam at 4.6 GHz. A mosaic combines the data from all of the fields, with imaging and deconvolution being done jointly on all 7 fields. A mosaic both helps compensate for the shape of the primary beam and reduces the amount of large (angular) scale structure that is resolved out by the interferometer.
- interactive=True : Very often, particularly when one is exploring how a source appears for the first time, it can be valuable to interact with the cleaning process. If True, interactive causes a viewer window to appear. One can then set clean regions, restricting where tclean searches for clean components, as well as monitor the cleaning process. A standard procedure is to set a large value for niter, and stop the cleaning when it visually appears to be approaching the noise level. This procedure also allows one to change the cleaning region, in cases when low-level intensity becomes visible as the cleaning process proceeds.
- imsize=[480,480],cell=['2.5arcsec'] : See the discussion above regarding the setting of the image size and cell size. If only one number is specified, the same value is used in both x and y directions (square image and/or pixel shape).
- stokes='I' : A single image will be made for total intensity I.
- deconvolver='multiscale', scales=[0, 5, 15, 45], smallscalebias=0.9 : The settings for multiscale are in units of pixels, with 0 pixels equivalent to the traditional delta-function clean. The scales here are chosen to provide delta functions and then three logarithmically scaled sizes to fit to the data. The first scale (5 pixels) is chosen to be comparable to the size of the synthesized beam. The smallscalebias attempts to balance the weight given to larger scales, which often have more flux density, and the smaller scales, which often are brighter. Considerable experimentation is likely to be necessary; one of the authors of this document found that it was useful to clean several rounds with this setting, change to multiscale=[] and remove much of the smaller scale structure, then return to this setting.
- weighting='briggs',robust=0.5 : 3C391 has diffuse, extended emission that is (at least partially) resolved out by the interferometer owing to a lack of short spacings. A naturally-weighted image would show large-scale patchiness in the noise. In order to suppress this effect, Briggs weighting is used (intermediate between natural and uniform weighting), with a default robust factor of 0.5 (which corresponds to something between natural and uniform weighting).
- pbcor=False : by default pbcor=False and a flat-noise image is produced. We can do the primary beam correction later (see below).
- savemodel='modelcolumn' : We recommend here the use of a physical MODEL_DATA scratch column for complicated gridders such as 'mosaic' (unlike the calibration steps, above). This will save some time, as it can be faster in the case of complicated gridding to read data from disk instead of doing all of the computations on-the-fly. However, this has the unfortunate side effect of increasing the size of the ms on disk.
As mentioned above, we can guide the clean process by allowing it to find clean components only within a user-specified region. When tclean runs in interactive mode, a viewer window will pop up as shown in Figure 14. To get a more detailed view of the central regions containing the emission, zoom in by first left clicking on the zoom button (leftmost button in third row) and tracing out a rectangle with the left mouse button and double-clicking inside the zoom box you just made. Play with the color scale to bring out the emission better, by holding down the middle mouse button and moving it around. To create a clean box (a region within which components may be found), hold down the right mouse button and trace out a rectangle around the source, then double-click inside that rectangle to set it as a box. Note that the clean box must turn white for it to be registered; if the box is not white, it has not been set! Alternatively, you can trace out a more custom shape to better enclose the irregular outline of the supernova remnant. To do that, right-click on the closed polygonal icon. Then trace out a shape by right-clicking where you want the corners of that shape. Once you have come full circle, the shape will be traced out in green, with small squares at the corners. Double-click inside this region and the green outline will turn white. You have now set the clean region. If you have made a mistake with your clean box, click on the Erase button, trace out a rectangle around your erroneous region, and double-click inside that rectangle. You can also set multiple clean regions.
At any stage in the cleaning, you can adjust the number of iterations that tclean will do before returning to the GUI. By default this is set to 100 (see the iterations field in mid-upper left of panel). You probably want to set this to a high number for this mosaic due to the complicated structure, values from 1000 to 5000 later on seem to work. Note that this will override the niter that was set when you started the clean task. tclean will keep going until it reaches threshold or runs out of cycles (the cycles field to the right of the iterations).
When you are happy with the clean regions, press the green circular arrow button on the far right to continue deconvolution. After completing a cycle, a revised image will come up. As the brightest points are removed from the image (cleaned off), fainter emission may show up. You can adjust the clean boxes each cycle, to enclose all real emission. After many cycles, when only noise is left, you can hit the red-and-white stop-sign icon to stop cleaning. Figure 15 shows the interactive viewer panel later in the process, after cleaning 500 iterations. We have used the polygon tool to add to the clean region, drawing around emission that shows up in the residual image outside of the original clean region. After about 14000 iterations (Figure 16) the residuals were looking good (similar noise level inside and outside of the clean region). As mentioned above, restarting tclean with different multiscale=[...] choices can help also.
Task tclean will make several output files, all named with the prefix given as imagename. These include:
- .image: final restored image, with the clean components convolved with a restoring beam and added to the remaining residuals at the end of the imaging process
- .pb: effective response of the telescope (the primary beam)
- .mask: areas where tclean has been allowed to search for emission
- .model: sum of all the clean components, which also has been stored as the MODEL_DATA column in the measurement set
- .psf: dirty beam, which is being deconvolved from the true sky brightness during the clean process
- .residual: what is left at the end of the deconvolution process; this is useful to diagnose whether or not to clean more deeply
- .weight: image of un-normalized sum of PB-square (for mosaics)
- .sumwt: a single pixel image containing sum of weights per plane
After the imaging and deconvolution process has finished, you can use the viewer to look at your image.
# In CASA
viewer('3c391_ctm_spw0_multiscale.image')
You can adjust the color scale and zoom in to a selected region by assigning mouse buttons to the icons immediately above the image (hover over the icons to get a description of what they do). Also, using the wrench panel to change Display Options will be helpful here. We chose the Hot Metal 1 colormap and set the Scaling Power Cycles to -1 to better emphasize the faint emission and compare to the noise (Figure 17).
The tclean task naturally operates in a flat noise image, i.e., an image where the effective weighting across the mosaic field of view is set so that the noise is constant. This is so that the clean threshold has a uniform meaning for the stopping criterion and that the image fed into the minor cycles has uniform noise levels. However, this means that the image does not take into account the primary beam fall-off in the edges and interstices of the mosaic. We could have set parameter pbcor=True in tclean, but it is useful to see the flat-noise image and residuals to evaluate the quality of the clean image. Therefore, we use impbcor to divide the .image by the .pb image to produce a primary beam corrected restored image:
# In CASA
impbcor(imagename='3c391_ctm_spw0_multiscale.image',pbimage='3c391_ctm_spw0_multiscale.pb',
outfile='3c391_ctm_spw0_multiscale.pbcorimage')
You can open this in the viewer and see that it has indeed raised the noise (and signal) at the edges of the mosaic.
Image Analysis
The three most basic analyses are to determine the peak brightness, the flux density, and the image noise level. These are useful measures of how well the imaging efforts are in approaching the thermal noise limit or in reproducing what is already known about a source. Additional discussion of image analysis and manipulation, including the combination of multiple images, mathematical operations on images, and much more can be found in the Image Analysis section of the CASA documentation.
The most straightforward statistic is the peak brightness, which is determined by imstat.
mystat = imstat(imagename='3c391_ctm_spw0_multiscale.pbcorimage')
This task returns a Python dictionary which we capture in the variable mystat.
The dictionary contains the values which you can extract for further use. For example, for a particular instance of the previous clean, we found:
CASA <4>: mystat
Out[4]:
{'blc': array([0, 0, 0, 0], dtype=int32),
'blcf': '18:50:04.251, -01.05.40.567, I, 4.59835e+09Hz',
'flux': array([ 9.78121725]),
'max': array([ 0.15670438]),
'maxpos': array([288, 256, 0, 0], dtype=int32),
'maxposf': '18:49:16.243, -00.55.00.579, I, 4.59835e+09Hz',
'mean': array([ 0.00387879]),
'medabsdevmed': array([ 0.00120803]),
'median': array([ 0.00038406]),
'min': array([-0.00684072]),
'minpos': array([237, 414, 0, 0], dtype=int32),
'minposf': '18:49:24.744, -00.48.25.580, I, 4.59835e+09Hz',
'npts': array([ 116013.]),
'q1': array([-0.00064426]),
'q3': array([ 0.00203547]),
'quartile': array([ 0.00267972]),
'rms': array([ 0.01261286]),
'sigma': array([ 0.01200169]),
'sum': array([ 449.99001048]),
'sumsq': array([ 18.45584197]),
'trc': array([479, 479, 0, 0], dtype=int32),
'trcf': '18:48:44.407, -00.45.43.065, I, 4.59835e+09Hz'}
CASA <5>: mystat['max'][0]
Out[5]: 0.156704381108284
and so the peak flux density is 0.157 Jy/beam.
The other two statistics require slightly more care. The flux density of a source is determined by integrating its brightness or intensity over some solid angle, i.e.,
[math]\displaystyle{ S = \int d\Omega I }[/math]
where [math]\displaystyle{ I }[/math] is the intensity (measured in units of Jy/beam), [math]\displaystyle{ \Omega }[/math] is the solid angle of the source (e.g., number of synthesized beams), and [math]\displaystyle{ S }[/math] is the flux density (measured in units of Jy). In general, if the noise is well-behaved in the image, when averaged over a reasonable solid angle, the noise contribution should approach 0 Jy. If that is the case, then the flux density of the source is also reported by imstat. However, there are many cases for which a noise contribution of 0 Jy may not be a safe assumption. If the source is in a complicated region (e.g., a star formation region, the Galactic center, near the edge of a galaxy), a better estimate of the source's flux density will be obtained by limiting carefully the solid angle over which the integration is performed.
Open viewer and use it to display the corrected image (Figure 18). For this analysis, it is better to use the version of the viewer that is run from the OS command line rather than the CASA command line. You can open this from inside CASA using '!':
# In CASA
!casaviewer '3c391_ctm_spw0_multiscale.pbcorimage' &
One can choose the function assigned to each mouse button; after zooming into the desired view, assign polygon region to a desired mouse button (e.g., left button) by selecting the polygon tool ![]() to create the polygonal region as shown in Figure 18 with the desired mouse button.
to create the polygonal region as shown in Figure 18 with the desired mouse button.
Using the mouse button just assigned to the polygon region, outline the supernova remnant. Start drawing vertices by clicking on points in the image in succession, when you draw the final vertex then double-click to connect and close the region. When your mouse is inside the region, a bounding box will appear with the vertices shown as draggable solid squares. If you want to adjust the vertices you can do so.
If you find you don't like your region you can dismiss it with with ESC key or using the remove region "X" button in the lower right of the panel. You can also employ the region panel to save a region you have created for later use.
Double click inside of that region (using the same mouse button used to make the region), and the statistics will be reported. This will include the flux density value within the region selected.
---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ----
(3c391_ctm_spw0_multiscale.pbcorimage)
Stokes Velocity Frame Doppler Frequency
I 0km/s LSRK RADIO 4.59835e+09
BrightnessUnit BeamArea Npts Sum FluxDensity
Jy/beam 46.0055 18836 4.318515e+02 9.386948e+00
Mean Rms Std dev Minimum Maximum
2.292692e-02 3.106691e-02 2.096504e-02 -1.934644e-03 1.567044e-01
region count
1
---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ----
In our example we find a total Flux density of 9.4 Jy. Note that the numbers you get may be slightly different depending on how deeply you cleaned.
By contrast, for the rms noise level, one can load the original (un-pbcor) image:
# In CASA
!casaviewer '3c391_ctm_spw0_multiscale.image' &
and to exclude the source's emission to the extent possible as shown in Figure 19, as the source's emission will bias the estimated noise level high. Likewise, one should avoid the clean bowl around the source emission. One can repeat the procedure above, defining a polygonal region, then double clicking inside it to determine the statistics. For example, from the region selection shown to the right for off-source statistics:
---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ----
(3c391_ctm_spw0_multiscale.image)
Stokes Velocity Frame Doppler Frequency
I 0km/s LSRK RADIO 4.59835e+09
BrightnessUnit BeamArea Npts Sum FluxDensity
Jy/beam 46.0055 23833 -1.520854e+00 -3.305808e-02
Mean Rms Std dev Minimum Maximum
-6.381295e-05 5.174784e-04 5.135396e-04 -2.055434e-03 1.800399e-03
region count
1
---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ----
Thus the Stokes I rms is 0.5 mJy. It will be useful later on to have the flat-noise and pb-corrected images available separately along with the statistics.
Self-Calibration
Even after the initial calibration using the amplitude calibrator and the phase calibrator, there are likely to be residual phase and/or amplitude errors in the data. Self-calibration is the process of using an existing model, often constructed from imaging the data itself, provided that sufficient visibility data have been obtained. This is essentially always the case with data: the system of equations is wildly over-constrained for the number of unknowns.
More specifically, the observed visibility data on the [math]\displaystyle{ i }[/math]-[math]\displaystyle{ j }[/math] baseline can be modeled as
[math]\displaystyle{ V'_{ij} = G_i G^*_j V_{ij} }[/math]
where [math]\displaystyle{ G_i }[/math] is the complex gain for the [math]\displaystyle{ i^{\mathrm{th}} }[/math] antenna and [math]\displaystyle{ V_{ij} }[/math] is the true visibility. For an array of [math]\displaystyle{ N }[/math] antennas, at any given instant, there are [math]\displaystyle{ N(N-1)/2 }[/math] visibility data, but only [math]\displaystyle{ N }[/math] gain factors. For an array with a reasonable number of antennas, [math]\displaystyle{ N }[/math] >~ 8, solutions to this set of coupled equations converge quickly.
For a more detailed introduction to self-calibration, see our VLA Self-calibration Tutorial. There is also a small amount of discussion in the old CASA Reference Manual on self calibration (see Section 5.11), and we have lectures on Self-calibration given at NRAO community days. In self-calibrating data, it is useful to keep in mind the structure of a Measurement Set: there are three columns of interest for an MS: the DATA column, the MODEL column, and the CORRECTED_DATA column. In normal usage, as part of the initial split, the CORRECTED_DATA column is set equal to the DATA column. The self-calibration procedure is then:
- Produce an image (tclean) using the CORRECTED_DATA column.
- Derive a series of gain corrections (gaincal) by comparing the DATA columns and the Fourier transform of the image, which is stored in the MODEL column. These corrections are stored in an external table.
- Apply these corrections (applycal) to the DATA column, to form a new CORRECTED_DATA column, overwriting the previous contents of CORRECTED_DATA.
The following example begins with the standard data set, 3c391_ctm_mosaic_spw0.ms (resulting from the steps above). From this we will make an I-only multiscale image (3c391_ctm_spw0_I.image) -- and in particular the model (3c391_ctm_spw0_I.model) -- to generate a series of gain corrections that will be stored in 3C391_ctm_mosaic_spw0.selfcal1. These gain corrections are then applied to the data to form a set of self-calibrated data, and a new image is then formed (3c391_ctm_spw0_IQUV_selfcal1.image). We first use delmod on the MS to get rid of the previous model.
#In CASA
delmod('3c391_ctm_mosaic_spw0.ms')
tclean(vis='3c391_ctm_mosaic_spw0.ms',imagename='3c391_ctm_spw0_ms_I',
field='',spw='',
specmode='mfs',
niter=500,
gain=0.1,threshold='1mJy',
gridder='mosaic',
deconvolver='multiscale',
scales=[0, 5, 15, 45],smallscalebias=0.9,
interactive=True,
imsize=[480,480],cell=['2.5arcsec','2.5arcsec'],
stokes='I',
weighting='briggs',robust=0.5,
pbcor=False,
savemodel='modelcolumn')
You should not clean very deeply. You want to be sure to capture as much of the source total flux density as possible, but not include low-level questionable features or sub-structure (ripples) that might be due to calibration or clean artifacts.
After you are happy with the image:
#In CASA
gaincal(vis='3c391_ctm_mosaic_spw0.ms',caltable='3c391_ctm_mosaic_spw0.selfcal1',
field='',spw='',selectdata=False,
solint='30s',refant='ea21',minblperant=4,minsnr=3,
gaintype='G',calmode='p')
applycal(vis='3c391_ctm_mosaic_spw0.ms',
field='',spw='',selectdata=False,
gaintable= ['3c391_ctm_mosaic_spw0.selfcal1'],gainfield=[''],interp=['nearest'],
calwt=[False],applymode='calflag')
The CORRECTED_DATA column of the MS now contains the self-calibrated visibilities, they will now be used by tclean. The gaincal step will report a number of solutions with insufficient SNR. By default, with parameter applymode='calflag', data with no good solutions will be flagged by applycal; in this case you will see it report the flagged fraction increasing to about 45%. This may or may not be a good thing. You can control the action of applycal in this regard by changing the value of parameter applymode. The setting applymode='calflagstrict' will be even more stringent about flagging things without valid calibration, while applymode='calonly' will calibrate those with solutions while passing through without changing the data. You can see ahead of time what applycal will do by running with applymode='trial' which will do the reporting but nothing else.
Questions for the Advanced Student:
|
To see what this selfcal has done, do a deep clean:
#In CASA
tclean(vis='3c391_ctm_mosaic_spw0.ms',imagename='3c391_ctm_spw0_multiscale_selfcal1',
field='',spw='',
specmode='mfs',
niter=20000,
gain=0.1,threshold='1mJy',
gridder='mosaic',
deconvolver='multiscale',
scales=[0, 5, 15, 45],smallscalebias=0.9,
interactive=True,
imsize=[480,480],cell=['2.5arcsec','2.5arcsec'],
stokes='I',
weighting='briggs',robust=0.5,
pbcor=False,
savemodel='modelcolumn')
Questions for the Advanced Student:
|
Commonly, this self-cal procedure is applied multiple times. The number of iterations is determined by a combination of the data quality and number of antennas in the array, the structure of the source, the extent to which the original self-calibration assumptions are valid, and the user's patience. With reference to the original self-calibration equation above, if the observed visibility data cannot be modeled well by this equation, no amount of self-calibration will help. A not-uncommon limitation for moderately high dynamic range imaging is that there may be baseline-based factors that modify the true visibility. If the corruptions to the true visibility cannot be modeled as antenna-based, as they are above, self-calibration won't help.
Self-calibration requires experimentation. Do not be afraid to dump an image, or even a set of gain corrections, change something and try again. Having said that, here are several general comments or guidelines:
- Bookkeeping is important! Suppose one conducts 9 iterations of self-calibration. Will it be possible to remember one month later (or maybe even one week later!) which set of gain corrections and images are which? In the example above, the descriptor 'selfcal1' is attached to various files to help keep straight which is what. Successive iterations of self-cal could then be 'selfcal2' , 'selfcal3' , etc.
- Care is required in the setting of imagename. If one has an image that already exists, CASA will continue cleaning it (if it can), which is almost certainly not what one wants during self-calibration. Rather one wants a unique imagename for each pass of self-calibration.
- A common metric for self-calibration is whether the image dynamic range (= max/rms) has improved. An improvement of 10% is quite acceptable.
- Be careful when making images and setting clean regions or masks. Self-calibration assumes that the model is perfect. If one cleans a noise bump, self-calibration will quite happily try to adjust the gains so that the CORRECTED_DATA describe a source at the location of the noise bump. It is far better to exclude some feature of a source or a weak source from initial cleaning and conduct another round of self-calibration than to create an artificial source. If a real source is excluded from initial cleaning, it will continue to be present in subsequent iterations of self-calibration; if it's not a real source, one probably isn't interested in it anyway.
- Start self-calibration with phase-only solutions (parameter calmode='p' in gaincal). As discussed in the High Dynamic Range Imaging lecture, a phase error of 20 deg is as bad as an amplitude error of 10%.
- In initial rounds of self-calibration, consider solution intervals longer than the nominal sampling time (parameter solint in gaincal) and/or lower signal-to-noise ratio thresholds (parameter minsnr in gaincal). Depending upon the frequency and configuration and fidelity of the model image, it can be quite reasonable to start with solint='30s' or solint='60s' and/or minsnr=3 (or even lower). One might also want to consider specifying a uvrange, if, for example, the field has structure on large scales (small [math]\displaystyle{ u }[/math]-[math]\displaystyle{ v }[/math]) that is not well represented by the current image.
- The task applycal will flag data with no good calibration solutions. During the initial self-calibration steps, this flagging may be excessive. If so, one can restore the flags to the state right before running applycal by using the task flagmanager.
- You can track the agreement between the DATA, CORRECTED_DATA, and MODEL in plotms. The options in the Axes tab allows one to select which column is to be plotted. If the MODEL agrees well with the CORRECTED_DATA, one can use shorter solint and/or higher minsnr values.
- You should consider examining the solutions from gaincal by using plotms in order to assure that the corrections are sensible. Smoothly varying phases are good, jumps are usually not. (However, because the phases are plotted ±180 degrees, there can be apparent jumps if the phases are very near +180 deg or −180 deg.)
- In the case of a mosaic, such as here, one should also verify that the solutions are of equal quality for all of the fields.
On Your Own: 3C391 second frequency and G93.3+6.9
Now that you have run through spw 0 of 3C391, you are ready to strike off on your own with other datasets. We have provided two options here, described below. The first option is simplest as it is the same object using a different spectral window; for a more rewarding challenge try the L-band dataset on G93.3+6.9.
You can find the data in the CASA repository. Both datasets -- 3C391 spw 1 (at 7.5 GHz) and Supernova Remnant G93.3+6.9 at L-band -- are contained in this tarball.
1. 3C391 spw 1 (at 7.5 GHz)
This is the second spectral window split off from the 3C391 dataset. You can process this as you did the first time, but beware of RFI in this band. You will have to avoid it through channel ranges and/or edit it out. Once you have processed this data, you can combine the two calibrated MSs in tclean to make a deeper MFS image (this might be tricky).
2. Supernova Remnant G93.3+6.9 at L-band
This is data taken at L-band of an entirely different Supernova Remnant, centered near 1400 MHz. You should be able to process this data in a very similar manner to the C-band data on 3C391. Note that we are not telling you what you will see in the image ahead of time. Here are some data reduction hints to help you along:
- There is strong RFI in this spectral window of the original 2 spw dataset. You will need to find it (e.g., using plotms) and avoid it in imaging. You can also flag those channels using flagdata, but this is not necessary. Note that there is a single baseline that shows very strong interference, see if you can find it. You can flag it using the baseline syntax in flagdata (e.g., parameter antenna='ea0x&ea0y' ).
- We have not edited out bad or dead antennas for you (unlike in 3C391). You will need to find these using plotms and then flagdata them. One helpful plotms trick is to set parameter antenna='ea01' and pick a few channels (like spw='0:30~33' ) and a single scan (e.g., scan='2~3' ) and plot the amp versus Antenna2 on the X-axis. You should see the bad antennas (the low ones). As a check set antenna='ea02' and repeat. Is it the same?
- In spite of RFI, the antenna-based calibration is remarkably resilient to moderate-to-low RFI contamination (which tends to be baseline-based). So rather than flagging channels with RFI, you might try going ahead with calibration and seeing if the solutions make sense. We were able to calibrate this data without flagging channels (only getting the bad baseline noted above).
- There is no observation of a flux calibrator like J1331+3030. You need to use setjy to set the Stokes I flux of the gain calibrator. We use the approximate flux density of 5.8 Jy for J2038+5119.
- The L-band field of view is much larger than at C-band. From the VLA Observational Status Summary (OSS) the resolution should be around 46" in D-config. Use a cellsize of 15" or smaller. What is the primary beam of the VLA at 1.4MHz? How big should you make your image?
- As you clean you will see faint sources all over the field; welcome to L-band imaging. This supernova remnant has lots of structure - try both standard and multi-scale clean.
Questions about this tutorial? Please contact the NRAO Helpdesk.
Last checked on CASA Version 6.2.0.