Simulating ngVLA Data-CASA5.4.1
tbd simobserve
The following tutorial shows how to simulate next generation very large array (ngVLA) data. The ngVLA is composed of different subarrays that are part of the current reference design. The configuration files are found in "ngVLA Configuration Tools" and can be used for simulations and calculations that investigate the scientific capabilities of the ngVLA. A configuration (.cfg) file contains the information of the name of the observatory, the coordinate system which in this case is in WCS, the x, y, z antenna positions, antenna diameters in meters and the pad names of each antenna.
CASA has two simulation tools available: the simobserve task and the sm toolkit. With these methods we can generate measurement sets, add thermal noise and predict model visibilities, from which one can explore the ngVLA’s imaging capabilities. The simobserve task is very user friendly but it is important to be aware that at the moment it has several limitations for making simulations for observatories other than ALMA and EVLA. For this reason, our suggested method for making simulations is using the sm toolkit which provides a great deal of flexibility in the use of parameters even for observatories unknown by CASA.
In this tutorial we show how to properly estimate the scaling factor needed to add thermal noise to the visibilities and we present three examples for making the simulations: (i) simobserve using a model image, (ii) simobserve using a component list, and (iii) sm toolkit simulation. For more information about component lists see
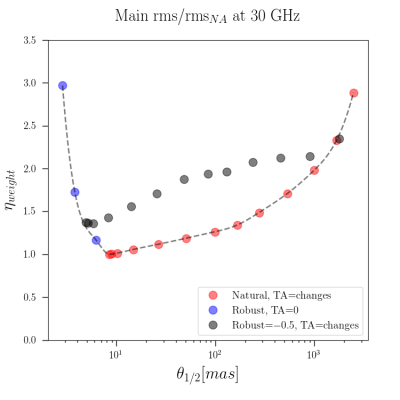
"this CASA guide". The model image use in this guide can be found here [add link]. All our examples are at 93 GHz, single channel, 4h of total observation, and 60 s integration time (in order to make the files small) with added thermal noise and no deconvolution. In this guide we will make a measurement set using the Main ngVLA subarray which is composed of 214 18 m antennas and that extends over a maximum baseline of 1005.4 km. The configuration file that we will use through this tutorial is called ngvla-main-revC.cfg and it is found "here". For the imaging we will use a robust value of R=-0.5 which will help to mitigate the broad skirt of the natural psf of these ngVLA subarray (see ngVLA memo #55) and a uv-taper of 5 mas.
Estimating the scaling parameter for adding thermal noise
Simobserve's parameter to corrupt the simulated data is called thermalnoise and for interferometric data the allowed values are 'tsys-atm', 'tsys-manual' or False (see more in "this CASA guide"). The option 'tsys-atm' is applicable predominantly to ALMA since it uses gain corrections, atmospheric corrections, etc for that observatory. If using the 'tsys-manual' many parameters are neccesary in order to construct the atmospheric model. Therefore, to have more flexibility and control we recommend to corrupt the simulated data using the sm toolkit, specifically the "sm.setnoise" function which in addition of 'tsys-atm' and 'tsys-manual' it also allows the option of 'simplenoise'. As the name indicates, 'simplenoise' calculate random Gaussian numbers and adds to the visibilities this noise uniformly to each antenna of the same diameter. In order to estimate the scaling factor for the 'simplenoise' parameter in sm.setnoise we use the following procedure:
The point source rms noise in a Stokes I image is (see "setnoise function")
[math]\displaystyle{ \sim \frac{\sigma}{\sqrt{ n_{pol} n_{baselines} n_{integrations} }} }[/math] (1)
where [math]\displaystyle{ \sigma }[/math] is the simplenoise parameter in sm.setnoise and corresponds to the noise in amplitude per visibility, [math]\displaystyle{ n_{pol} }[/math] are the number of polarizations in the measurement set (typically 2), and [math]\displaystyle{ n_{integrations} }[/math] are the number of correlator integration times in the measurement set (~ track time / int. time). For this example, the track time is 4 h and the integration time is 60 s, thus [math]\displaystyle{ n_{integrations}=240 }[/math]. The number of baselines [math]\displaystyle{ n_{baselines} }[/math] is estimated by [math]\displaystyle{ N(N-1)/2 }[/math] where N is the number of antennas in the array. In this case, N=214 thus [math]\displaystyle{ n_{baselines}= 22791 }[/math].
If we know the rms that we want for our resulting image, we can solve for [math]\displaystyle{ \sigma }[/math] which is the scaling parameter of the simplenoise parameter in sm.setnoise. Then,
# In CASA
sm.setnoise(mode=’simplenoise’, simplenoise=sigma)
and your resulting image will have a rms ~ point source noise.
If instead you want to calculate the expected rms noise for an ngVLA image we suggest the below procedure. Following is an example for a simulation at 93 GHz and 4h integration:
(i) Calculate the expected naturally weighted point source sensitivity in a ngVLA performance table. The "ngVLA memo #55 " in Appendix D have key performance metrics for 6 subarrays including the Main interferometric array of the ngVLA where we can find the noise performance values as a function of frequency. For our example, we find in the ngVLA memo #5 Table 10 that the naturally weighted rms at 93 GHz for 1 hour is 0.83 uJy/beam.
(ii) Scale that number to the desired integration time, in this case [math]\displaystyle{ t_{int}= }[/math]4h. Therefore, [math]\displaystyle{ 0.83/\sqrt{(t_{int}/1\,hour)} = 0.415 }[/math] uJy/beam.
(iii) Use the taperability curve for the ngVLA Main interferometric array shown in Fig 1. (this corresponds to Fig. 9 of the ngVLA memo #55) to find the inefficiency factor. This taperability curve is at 30 GHz therefore we need to scale the resolution with frequency (see ngVLA memo #55 Appendix A). Our frequency is 93 GHz and the expected resolution at that frequency is [math]\displaystyle{ \theta_{1/2\,at\,\nu}= }[/math] 5 mas, therefore the resolution at 30 GHz is [math]\displaystyle{ \theta_{1/2\,at\,30GHz} = \theta_{1/2\,at\,\nu} \times (\nu/30\,\text{GHz})=15.5 }[/math] mas. From For a robust value of R=-0.5 from Fig. 1 we see that that corresponds to [math]\displaystyle{ \eta_{weight}\sim 1.6 }[/math].
(iv) Multiply the naturally weighted point source rms noise and the inefficiency factor to get the desired image noise, this is 0.415*1.6 = 0.66 uJy.
(v) Use the desired image noise into the above equation 1 to solve for the simplenoise parameter [math]\displaystyle{ \sigma }[/math]
%In what cases do we need to look at the performance table? if we select a rms for our resulting image how do we know for how long do we need to run the observation for?
%% The track time in seconds is given in the header under 'Total elapsed time' and the int. time in seconds for each spectral window is provided under 'Average Interval'. The number of baselines [math]\displaystyle{ n_{baselines} }[/math] is estimated by [math]\displaystyle{ N(N-1)/2 }[/math] where N is the number of antennas in the array. You can verify that the number of integrations is correct comparing the 'Data records' reported in listobs which should be equal to [math]\displaystyle{ n_{integrations} * n_{baselines} }[/math].
Simobserve using a model image
Simobserve using a component list
sm toolkit using either a model image or a component list
# In CASA
## Using the configuration file obtained from the ngVLA's website
conf_file = 'ngvla-main-revC.cfg'
## Make an ASCII file with the configuration file i.e., change the extension from .cfg to .tab
tabname = 'antenna_positions_'+conf_file.split('.cfg')[0]+'.tab'
## The resulting file is called 'antenna_positions_ngvla-main-revC.tab'
## Create a CASA table from an ASCII table using the table utilities (tb) tool
tb.fromascii(tabname, conf_file, firstline=3, sep=' ',
columnnames=['X','Y','Z','DIAM','NAME'], datatypes=['D','D','D','D','A'])
xx=[]; yy=[]; zz=[];
xx = tb.getcol('X') ## antenna positions
yy = tb.getcol('Y')
zz = tb.getcol('Z')
diam = tb.getcol('DIAM') ## diameter of the antennas
anames = tb.getcol('NAME') ## name of each antenna
tb.close()
##############################################################
## Setting the observation framework making the resources,
## similar to what we would do in the OPT when setting up
## our observations.
##############################################################
## Simulate measurement set using the simulation utilities sm tool
ms_name = ’ngVLA_214_ant_1s.ms’ ## Name of your measurement set
sm.open( ms_name )
## Get the position of the ngVLA using the measures utilities (me)
pos_ngVLA = me.observatory(’ngvla’)
## set the antenna configuration using the sm tool using the positions,
## diameter and names of the antennas as read from the configuration file
sm.setconfig(telescopename = ’ngvla’, x = xx, y = yy, z = zz,
dishdiameter = diam, mount = ’alt-az’,
antname = list(anames),padname = list(anames),
coordsystem = ’global’, referencelocation = pos_ngVLA)
## set the spectral windows, in this case is a single channel
## simulation with a channel resolution of 1 MHz and bandwidth of 1 MHz
sm.setspwindow(spwname = ’Band4’, freq = ’93GHz’, deltafreq = ’1MHz’,
freqresolution = ’1MHz’, nchannels = 1, stokes = ’RR RL LR LL’)
## set feed parameters for the antennas
sm.setfeed(’perfect R L’)
## set the field of observation that we are going to simulate
## (where the telescope is pointing), in this example we are using
## a Dec of +24deg
sm.setfield(sourcename=’My source’,
sourcedirection=[’J2000’,’00h0m0.0’,’+24.0.0.000’])
## set the limit of the observation for the antennas
sm.setlimits(shadowlimit=0.001, elevationlimit=’8.0deg’)
## weight to assign autocorrelation
sm.setauto(autocorrwt=0.0)
## integration time or how often the array writes one visibility
integrationtime = ’1s’
sm.settimes(integrationtime = integrationtime, usehourangle = True,
referencetime = me.epoch(’utc’, ’today’))
## setting the observation time, which for our example is 4 h
starttime = ’-2h’
stoptime = ’2h’
sm.observe(’My source’, ’Band4’, starttime = starttime, stoptime = stoptime)
Now we are going to write a scan of a source using the resource made above. Set the model either using a .fits model or a component list. After that we can predict the visibilities using sm.predict tool function. If using a component list follow the steps below:
# In CASA
## Position of the source that we are observing. In this case the source is in the same location where the telescope is pointing
direction = me.direction(rf = 'J2000', v0= qa.unit('00h0m0.0'), v1=qa.unit('+24.0.0.000'))
## component list cl to make a model centered at the direction given above, and with a source of flux=3.2 Jy
cl.addcomponent(dir = direction, flux = 3.2, freq = '93GHz')
## name of the component list model
cl.rename(filename='my_component.cl')
## close the component list
cl.done()
## predicts the visibility of the source
sm.predict( complist = 'my_component.cl')
However, if you want to use a model image instead please follow the steps below:
# In CASA
## To export the .fits file to .image
importfits( fitsimage = 'my_model.fits', imagename = 'my_model.image')
## To predict the model visibilities
sm.predict( imagename = 'my_model.image')
Note: the model image should have units of Jy/pixel and not Jy/beam which in that case will be the restored image.
Finally, in order to add thermal noise we do the following:
# In CASA
## Adding noise with ’simplenoise’
## set the noise level
sm.setnoise(mode=’simplenoise’, simplenoise=’1Jy’)
## adds the noise: calculate random Gaussian numbers and add to visibilities
sm.corrupt()
sm.close()
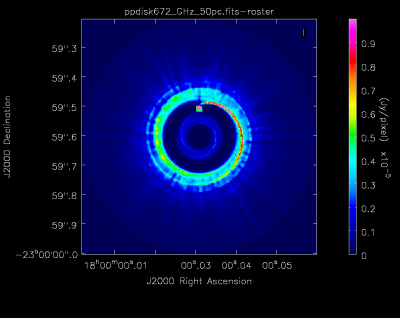
We will use the same image as the ALMA tutorial "Protoplanetary Disk Simulation". Follow this link to obtain the protoplanetary disk model image. Model images are in units of Jy/pixel. Other simulation options, e.g. using component lists, or how to use the toolkit are explained in the Simulations in CASA section of the CASAguides.
Fig. 1 shows the model that we will use for this simulation tutorial.
The ALMA version of the tutorial describes CASA tools to derive the center of the image. We will use their results and specify direction='J2000 18h00m00.031s -22d59m59.6s' for all of our simulations. The image center can also be determined with the CASA viewer. Given that the VLA primary beams at the VLA frequencies are much larger than the image, the precise pointing direction center is less important.
We will mostly use the simobserve and simanalyze tasks similar to the ALMA tutorials (in we will follow the ALMA plotted image sequence). The ALMA model, however, has a specified frequency of 672GHz and we will adapt it to work for VLA frequencies.
Note that simobserve has a few limitations. E.g. it cannot simulate different spectral windows. If this is desired, each spw needs to be simulated separately, followed by a concatenation (concat) of all simulated MeasurementSets. In addition, simobserve has no option to add pointing errors to the simulated data. All VLA configurations and the VLA receiver temperatures are, however, accessible in simobserve.
Q-band, 128MHz bandwidth, noiseless image, 1h integration time, A-configuration, no deconvolution
Let's start with a simulation at 44GHz (Q-band), with a bandwidth of 128MHz, the largest possible bandwidth of a spectral window at the VLA. We will simulate observations with the VLA A-configuration as it provides the resolution that is needed for the disk to be well resolved. To start with, we do not add any noise to the data:
# In CASA
simobserve(project='psimvla1',
skymodel='ppdisk672_GHz_50pc.fits',
inbright='3e-5Jy/pixel',
incenter='44GHz',
inwidth='128MHz' ,
setpointings=True,
integration='2s',
direction='J2000 18h00m00.031s -22d59m59.6s',
mapsize= '0.78arcsec',
obsmode='int',
antennalist='vla.a.cfg',
hourangle='transit',
totaltime='3600s',
thermalnoise='',
graphics='both',
overwrite=True)
project: The name of our project is psimvla1. All data will be stored in a directory that is created using the project name.
skymodel: The input model image in Jy/pixel units. We overwrite the fits header to assume that the model is valid for 44GHz with the incenter parameter and the bandwidth to 128MHz with inwidth. We also adjust the peak to a lower [math]\displaystyle{ 3\times10^{-5} }[/math]Jy/pixel value with the inbright parameter, as expected at the lower frequency.
setpointings: allows simobserve to derive the pointing positions by its own algorithm. Given that the primary beam at Q-band is about 1 arcminutes (see the VLA observational status summary (OSS)), and the size of the model is less than an arcsecond, a single pointing will be adequate.
integration: To avoid time smearing, we follow the guidance for data rates in the VLA OSS and assume 2s integration time per visibility.
direction: the center of the map. For a single pointing this is equivalent to the pointing center.
obsmode: int is used for interferometric data such as VLA observations.
antennalist: the VLA configuration antenna position file. The files are available in CASA via 'vla.x.cfg' where 'x' is the name of the array configuration. Here 'vla.a.cfg' is the VLA A configuration (the python command os.getenv("CASAPATH").split()[0]+"/data/alma/simmos/" shows the directory that contains all array configurations that are packaged in CASA)
hourangle: is used to simulate observations at a specific hour angle. We use 'transit' for culmination.
totaltime: This is the time on source.
thermalnoise: We leave this parameter empty for this noise-less simulation.
graphics: 'both' will show graphics on the screen and save them as png files in the project directory.
overwrite: True will overwrite previous results; be careful when running multiple setups as the files may have different names and only the files with the same names will be overwritten.
The output of the simulation is shown in Figs. 2 and 3. The first image is the sky coverage which shows clearly that the primary beam exceeds the size of the model image by far. The other outputs are explained in the caption of Fig. 3.
Last checked on CASA Version 5.4.1.