M51 at z = 0.1 and z = 0.3 (CASA 4.0)
↵ Simulating Observations in CASA
- This guide is applicable to CASA version 4.0. For older versions of CASA see M51 at z = 0.1 and z = 0.3 (CASA 3.4).
- To create a script of the Python code on this page see Extracting scripts from these tutorials.
- Notice that this page uses global Python variables (e.g. fluxScale), not to be confused with task inputs (e.g. inbright).
Overview
This tutorial presents a simulation of ALMA observations of the well-known galaxy M51 in the CO 1-0 transition. This galaxy is located relatively nearby (luminosity distance = 9 Mpc), but, in this simulation, we will model how it would appear at redshift z = 0.1 (luminosity distance = 460 Mpc).
The goal of this tutorial is to provide a complete run-through of a relatively simple simulation. The simulation will include effects of (u, v) sampling of a 50-antenna ALMA, the primary beam of the ALMA, and thermal noise. Neither calibration overheads nor errors are included, and so this simulation should be viewed as optimistic. The CASA task simobserve will generate simulated visibility measurements from an input model. The task simanalyze will image the visibilities and generate diagnostic plots.
For this tutorial, we'll use the BIMA SONG (Helfer et al. 2003) observations of M51 as the basis for the model. Grab the file NGC5194.bima12m.cm.fits.gz and uncompress it in a working directory.
# in bash (or other unix shell)
gunzip NGC5194.bima.12m.cm.fits.gz
Initializing the Data and Tasks
Task simobserve takes an input model in the form of a CASA image. So, we begin by converting the BIMA SONG FITS cube into a CASA image using task importfits. Here we invoke importfits as a function, where the task inputs are set as function input parameters. For convenience, we store the name of the resulting image into the Python variable cubeName. The task will produce the new image (which is actually a directory) in the current working directory.
# in CASA
cubeName = 'm51-song.image'
# If m51-song.image exists, it needs to be removed for importfits to work as set
os.system('rm -rf '+cubeName)
importfits(fitsimage='NGC5194.bima12m.cm.fits', imagename=cubeName)
We initialize the simulation tasks by setting their parameters to the default values. We then make the new CASA image the input model to simobserve by setting parameter skymodel.
# in CASA
default("simobserve")
default("simanalyze")
skymodel = cubeName
Noise in the Input Model
The input model is actually an observation and, as such, certainly contains noise. We're OK as long as the noise in the model falls below the expected thermal noise of the ALMA observation. Here's a quick, back-of-the-envelope calculation.
The noise on the BIMA SONG channels measures roughly 0.1 Jy/beam, which scales to 0.04 mJy/beam at z = 0.1 (to within factors of powers of 1+z for cosmology and root-small-integer for the to-be-degraded beam; see below). For comparison, the expected thermal noise of the ALMA observation is 0.1 mJy / beam (using the ALMA Sensitivity Calculator, assuming 8 hrs integration, and, to match roughly the BIMA SONG observation, a 4 MHz channel width), a factor of 2.5 greater than the anticipated contribution of noise from the model. Added in quadrature, the noise components total 0.108 mJy, and so we can expect that the input model noise degrades the simulation noise by about 8%.
Cosmology Calculations
Next we'll set up some python globals to handle the scaling of the model coordinates and flux densities appropriate for new redshift. We'll primarily need the angular size and luminosity distances for a given cosmology. To keep things simple, we'll use Ned Wright's CosmoCalc (2006) with the default cosmology; redshifts were collected from NED.
# in CASA
# Distinguish between z_lsrk, which sets the observed frequency for scaling,
# and z_cmb, which is needed to get cosmological distances.
z_old_cmb = 0.002122 # CMB-referenced z for cosmological distances from NED
z_old_lsrk = 0.001544 # from NED
z_new = 0.1
#
# angular size distances from CosmoCalc
da_old = 9.0
da_new = 375.9
#
# luminosity distances from CosmoCalc
dl_old = 8.937
dl_new = 454.8
We will use the convention where old refers to M51 as observed at its proper redshift, and new refers to the new, higher redshift for our model.
Preparing the Model
The next step is to scale the M51 data cube into a model cube appropriate for simobserve. First, we establish the file naming convention by setting the task parameter project. Thinking ahead, we might want to rerun this simulation for other redshifts. So, to make this easy we will include the redshift in the project name: we'll write 0.1 as p1 (or "point one") and assign it to Python variable suffix. Then we'll use suffix to define project.
# in CASA
suffix = "-p1"
project = "M51-AtZ" + suffix
Flux Density Scaling
Our goal in this step is to set the inbright parameter of simobserve, which will scale the data cube appropriately for its new luminosity distance. The task wants models in units of Jy / pixel, but the BIMA SONG cube has units of Jy / beam. We'll use the task imhead to get the BIMA SONG clean beam dimensions and we'll use the qa tool to convert the dimensions from radians to arcseconds.
# in CASA
# Get the major and minor axes of the model clean beam
bmaj = imhead(imagename=cubeName,mode='get',hdkey='beammajor')
bmin = imhead(imagename=cubeName,mode='get',hdkey='beamminor')
# Convert radians to 1-arcsecond pixels using the qa tool
bmaj = qa.convert(bmaj,'arcsec')['value']
bmin = qa.convert(bmin,'arcsec')['value']
# Gaussian beam conversion = beams / pixel
toJyPerPix = 1.0 / (1.1331 * bmaj * bmin)
Next, scale the flux for the new luminosity distance. Make the approximation that each pixel is a point source, and use the inverse square law to scale. We then set inbright to the newly scaled peak flux.
# in CASA
# Correct flux density for luminosity distance
fluxScale = (dl_old/dl_new)**2 * (1.0 + z_new) / (1.0 + z_old_cmb)
# Current peak flux (Jy / pixel)
peak = imstat(cubeName)['max'][0] * toJyPerPix
# Desired peak flux (using Python formatting convention)
inbright = "%fJy/pixel" % (peak*fluxScale)
Notice that there is an additional (1+z) correction because we are scaling flux densities rather than bolometric fluxes.
Angular Size Scaling
The sky coordinates axes of the model need to be adjusted (1) to place M51 in the southern hemisphere and (2) to correct for the new angular size distance. These tasks can be accomplished by the simobserve parameters indirection (to change the location of M51 on the sky) and incell (to change the angular scale of an input pixel). To perform task (1), we'll just flip the sign of the declination using imhead. We'll use the qa tool to convert radians to sexagesimal units.
# in CASA
# For clarity, build up "indirection" string one term at a time.
indirection = "J2000 " # Epoch
# RA
crval1 = imhead(imagename=cubeName,mode='get',hdkey='crval1')['value']
indirection += qa.formxxx(str(crval1)+'rad',format='hms') + " "
# Dec * -1
crval2 = imhead(imagename=cubeName,mode='get',hdkey='crval2')['value']
indirection += qa.formxxx('%frad' % (-1*float(crval2)),format='dms')
Next, adjust the pixel scale for the new angular size distance. To perform this adjustment, we'll use imhead with mode = "get" to read in the original pixel scale, then use the simobserve input parameter incell to designate the new pixel size.
# in CASA
# Scale pixel size: imhead returns radians; convert to arcsec
cdelt2 = imhead(imagename=cubeName,mode='get',hdkey='cdelt2')['value']
oldCell = cdelt2 * 206265
# Scale for new angular size distance
newCell = oldCell * da_old / da_new
# Format the new pixel size for input to simobserve
incell = "%farcsec" % (newCell)
Adjusting the Frequency Axis
Changing the frequency axis of the model header is just a straightforward (1+z) correction. simobserve adjusts the channelwidth using the inwidth parameter and the observing frequency using incenter.
Notice that the absolute value of the BIMA SONG channel width is used. The noise calculation in simobserve needs positive channel widths, but the input cube is ordered in increasing velocity rather than increasing frequency. We could transpose the cube; on the other hand, the only penalty of changing the sign is that the sense of rotation will be flipped. Since this simulation is a simple detection experiment, the rotation sense is irrelevant, and so we'll take the easy way out.
# in CASA
# Move freq to z_new
oldFreq = imhead(imagename=cubeName,mode='get',hdkey='crval3')['value']
newFreq = oldFreq * (1.0 + z_old_lsrk) / (1.0 + z_new)
nchan = imstat("NGC5194.bima12m.cm.fits")['trc'][2]
# Adjust frequency channelwidth for new z
oldDnu = imhead(imagename=cubeName,mode='get',hdkey='cdelt3')['value']
newDnu = abs((1.0+z_old_lsrk) /(1.0+z_new)*oldDnu) # make channel widths positive
inwidth = "%fHz" % newDnu
# Specify the observing frequency at the center of the observing band:
incenter = "%fHz" % (newFreq + 0.5*nchan*newDnu)
Map Size and Mosaicking
The original BIMA SONG image is about 480 arcseconds across; scale this image size to the new redshift and assign to parameter mapsize. We will also use this value later.
# in CASA
imSize = 480.0 * (da_old / da_new) # arcseconds
mapsize = "%farcsec" % imSize
For relatively high redshifts, there should be no need to mosaic the observations. We'll nevertheless allow for mosaicking in case we want to repeat the simulation for lower redshift. simobserve needs the spacing between pointings in the mosaic; we'll require pointings spaced by half of the primary beam. The ALMA primary beam is 17 arcseconds at 300 GHz.
# in CASA
primaryBeam = 17.0 * (300e9 / newFreq) # arcseconds
pointingspacing = "%farcsec" % (primaryBeam / 2.0)
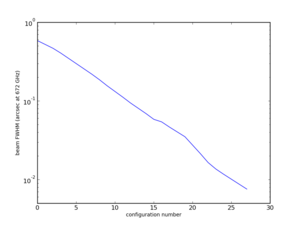
Array Configuration
We want to set antennalist such that simobserve will decide on an appropriate ALMA configuration based on the desired beam size. Thus, we first must estimate the desired output "clean" beam size. We don't want the new beam to be so large so that we cannot resolve a rotation curve, but we also don't want it to be so small that we effectively resolve out the BIMA SONG data. The BIMA SONG beam was 5 arcsec, and so as a reasonable guess we'll adopt the equivalent of a 15" beam at its true distance (3 times coarser than the BIMA SONG beam) and then scale appropriately to z = 0.1.
Looking ahead to imaging our simulated data, it's important to sample the beam at least 3 times for stable deconvolution. We'll sample the beam by 4 times, rounded off to the nearest milliacsecond.
# in CASA
beamNew = 15.0 * (da_old / da_new)
pixelSize = round(beamNew * 1000.0 / 4.0) / 1000.0
Now, to guard against undersampling the beam as a result of rounding error, reset the desired beam to 4 times the pixel size.
# in CASA
beamNew = 4.0 * pixelSize
Now we can set parameter antennalist using the beam size (but see Aside: Antenna Configurations below).
# in CASA
antennalist = "alma;%farcsec" % beamNew
Integration and Total Time
We will set the integration time to 100 seconds and the total integration time to 8 hours. For a real observation, 10 seconds will be a more appropriate integration time. However, we can decrease the simulation CPU time by increasing the integration interval (See Etime study for details). Whenever simulating a new data set, we recommend beginning with a large integration time for initial testing and then lowering the integration time to generate a more realistic measurement set.
# in CASA
integration = '100s'
# 8 hours of total integration
totaltime = '28800s'
Noise
We will add thermal noise to the simulated data by setting parameter thermalnoise to tsys-atm. We keep the default values of precipitable water vapor (1 mm) and ambient temperature (269 K).
# in CASA
thermalnoise="tsys-atm"
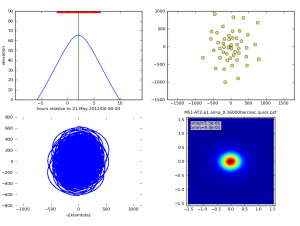
simobserve Execution
Finally, we set graphics to "both" to send plots to the screen and disk; we set verbose to True to print additional information to the logger and terminal; and we set overwrite to True to overwrite existing files in the project subdirectory. Now we are ready to run simobserve.
# in CASA
graphics="both"
verbose = True
overwrite = True
simobserve()
Aside: Antenna Configurations
In this tutorial the selection of the ALMA antenna configuration is automated to produce a decent cube of M51 as viewed at z = 0.1, but, for other simulations (or this one, for that matter), it will be worth playing with the configurations, or perhaps evaluating the possibility of detections in CSV or early science. CASA comes with stock antenna configurations in the directory $CASAPATH/data/alma/simmos/. Use the Python os module to resolve the CASA path. For example:
# In CASA
os.getenv('CASAPATH').split(' ')[0] + '/data/alma/simmos/'
CASA <99>: ls /usr/lib64/casapy/stable/data/alma/simmos/ aca_cycle1.cfg alma.out05.cfg alma.out21.cfg pdbi-c.cfg aca.i.cfg alma.out06.cfg alma.out22.cfg pdbi-d.cfg aca.ns.cfg alma.out07.cfg alma.out23.cfg sma.compact.cfg aca.tp.cfg alma.out08.cfg alma.out24.cfg sma.compact.n.cfg alma.cycle0.compact.cfg alma.out09.cfg alma.out25.cfg sma.extended.cfg alma.cycle0.extended.cfg alma.out10.cfg alma.out26.cfg sma.subcompact.cfg alma_cycle1_1.cfg alma.out11.cfg alma.out27.cfg sma.vextended.cfg alma_cycle1_2.cfg alma.out12.cfg alma.out28.cfg vla.a.cfg alma_cycle1_3.cfg alma.out13.cfg carma.a.cfg vla.b.cfg alma_cycle1_4.cfg alma.out14.cfg carma.b.cfg vla.bna.cfg alma_cycle1_5.cfg alma.out15.cfg carma.c.cfg vla.c.cfg alma_cycle1_6.cfg alma.out16.cfg carma.d.cfg vla.cnb.cfg alma.out01.cfg alma.out17.cfg carma.e.cfg vla.d.cfg alma.out02.cfg alma.out18.cfg meerkat.cfg vla.dnc.cfg alma.out03.cfg alma.out19.cfg pdbi-a.cfg WSRT.cfg alma.out04.cfg alma.out20.cfg pdbi-b.cfg
Note that when setting the antennalist parameter, it is not necessary to provide the full path. simobserve will search the standard CASA directory and your current working automatically.
The version of CASA 3.4 contains 36 array configurations for ALMA, as well as configuration files for ACA, EVLA, SMA, and other interferometers.
simobserve Output
Outputs from simobserve will be written to a directory specified by the project parameter, in this case M51-AtZ-p1. simobserve will generate these files:
| Filename | Description |
|---|---|
| M51-AtZ-p1.alma_0.360000arcsec.ms | Model measurement set sans noise |
| M51-AtZ-p1.alma_0.360000arcsec.noisy.ms | Model measurement set with thermal noise |
| M51-AtZ-p1.alma_0.360000arcsec.quick.psf | CASA image of the point spread function |
| M51-AtZ-p1.alma_0.360000arcsec.skymodel | CASA image of the input sky model rescaled according to the skymodel sub-parameters |
| M51-AtZ-p1.alma_0.360000arcsec.skymodel.flat | flattened CASA image of the input sky model rescaled |
| M51-AtZ-p1.alma_0.360000arcsec.skymodel.png | flattened PNG image of the input sky model rescaled and overlaid with the mosaic pattern specified by the setpointings sub-parameters |
| M51-AtZ-p1.alma_0.360000arcsec.observe.png | 2x2 PNG summary plot showing: source elevation vs. time, antenna position, uv coverage, and the point spread function |
| M51-AtZ-p1.alma_0.360000arcsec.ptg.txt | ASCII text listing of mosaic pointings |
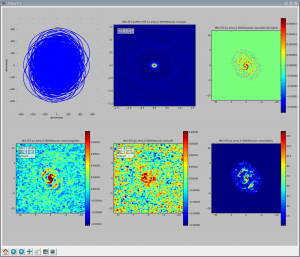
simanalyze Execution
After running simobserve and producing a simulated measurement set, the task simanalyze will quickly and easily image the simulated data and produce diagnostic plots and images. (Remember that simanalyze is a convenience task. You can also use other CASA tasks, like clean, directly on the simulated data.)
To setup the simanalyze parameters we will keep the values of project and verbose that we set for simobserve. We set vis to image the noisy measurement set by concatenating project, antennalist with ";" replaced by "_", and ".noisy.ms". We set modelimage = cubeName so simanalyze will use the model image when cleaning the simulated data. We then set the clean threshold to 1 mJy.
# in CASA
modelimage = cubeName
vis = project +'.'+ antennalist.replace(';','_') +'.noisy.ms'
threshold = "1.0mJy"
We now set cell to the pixel size calculated above.
cell = "%farcsec" % pixelSize
Now we have both the image size and pixel size in arcseconds, but the simanalyze parameter imsize wants the ratio: the number of pixels along the RA or Dec axis. To keep the image from becoming too small, set the minimum image size to be 256 pixels.
# in CASA
imSizePix = int(round(imSize / pixelSize))
if imSizePix < 256: imSizePix = 256
imsize = [imSizePix,imSizePix]
Now we are ready to execute the task.
simanalyze()
simanalyze Output
The simanalyze output files will appear in the CASA plotter and in subdirectory M51-AtZ-p1.
| Filename | Description |
|---|---|
| M51-AtZ-p1.alma_0.360000arcsec.noisy.image | CLEAN-deconvolved cube of M51-AtZ-p1.alma_0.360000arcsec.noisy.ms |
| M51-AtZ-p1.alma_0.360000arcsec.noisy.residual | Residual image after cleaning |
| M51-AtZ-p1.alma_0.360000arcsec.skymodel.flat.regrid | Input model image regridded to match the output image |
| M51-AtZ-p1.alma_0.360000arcsec.skymodel.flat.regrid.conv | Input model image regridded to match the output image and convolved with the output clean beam |
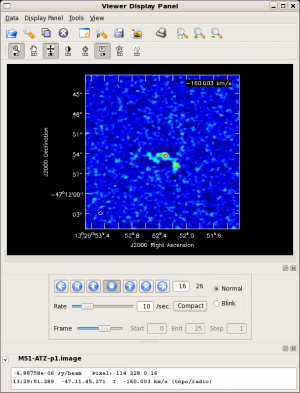
Additional (or fewer) outputs can be produced by simanalyze by setting the analyze subparameters. The image at the right can be displayed by running the task viewer and loading the appropriate image file, e.g. viewer(infile = 'M51-AtZ-p1/M51-AtZ-p1.image', channel = 16).
The rest frequency will have been lost in the simulation, and it's worth restoring to the header.
# in CASA
imhead(imagename="M51-AtZ-p1/M51-AtZ-p1.alma_0.360000arcsec.noisy.image",
mode="put", hdkey="restfreq", hdvalue="115.27120180GHz")
The simulated data cube can be analyzed just like any other CASA image -- examples are given in the CARMA tutorial and the VLA 21cm tutorial.
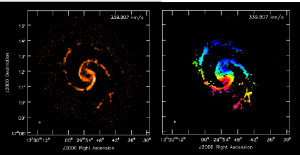
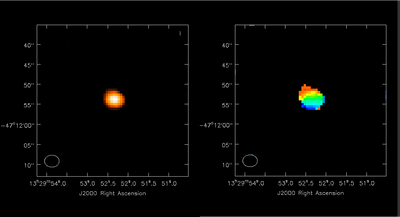
Moment Maps
Use immoments to calculate the integrated intensity and velocity field maps from the simulated cube. The excludepix option applies a 3σ cut.
# Must remove this file before immoments is run, if this has been run previously in the directory
os.system('rm -rf M51-AtZ-p1/M51-AtZ-p1.alma_0.360000arcsec.noisy.moments.*')
immoments(imagename='M51-AtZ-p1/M51-AtZ-p1.alma_0.360000arcsec.noisy.image',
moments=[0,1],axis='spectral', excludepix=[-100,0.0006],
outfile='M51-AtZ-p1/M51-AtZ-p1.alma_0.360000arcsec.noisy.moments')
The results are shown at right.
You can view these results by running the task viewer, then selecting the moments maps found in the directory M51-AtZ-p1.
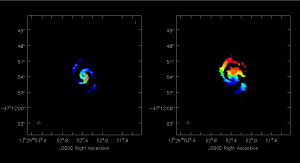
Pushing M51 out to z = 0.3
We'll leave as an exercise for the reader the tuning of this simulation to push M51 all the way out to z = 0.3 (luminosity distance = 1540 Mpc). simobserve produces a reasonable detection in 8 hrs integration, but you'll need to consider more carefully the antenna configuration needed to produce the requisite sensitivity. To conclude, here are the moment maps for the z = 0.3 simulation.
↵ Simulating Observations in CASA
Last checked on CASA Version 4.0.0.