M51 at z = 0.1
This article is under construction. Watch this space!
Overview
This tutorial presents a simulation of ALMA observations of the well-known galaxy M51 in the CO 1-0 transition. This galaxy is located relatively nearby (luminosity distance = 9 Mpc), but, in this simulation, we will model how it would appear at redshift z = 0.1 (luminosity distance = 460 Mpc).
The goal of this tutorial is to provide a complete run-through of a relatively simple simulation. Included in this simulation are the effects of (u, v) sampling of a 50-antenna ALMA, the primary beam of the ALMA, and thermal noise. Neither calibration overheads nor errors are included, and so this simulation should be viewed as optimistic.
For this tutorial, we'll use the BIMA SONG (Helfer et al. 2003) observations of M51 as the basis for the model. Grab the file NGC5194.bima12m.cm.fits.gz and uncompress it in a working directory.
# in bash (or other unix shell)
gunzip NGC5194.bima.12m.cm.fits.gz
Load these data into CASA. For later convenience, we'll store the name of the resulting measurement set into the python global cubeName.
cubeName = 'm51-song'
importfits(fitsimage='NGC5194.bima12m.cm.fits', imagename=cubeName)
Noise in the Input Model
The input model is actually an observation and, as such, certainly contains noise. We're OK as long as the noise in the model falls below the expected thermal noise of the ALMA observation.
The noise on the BIMA SONG channels measures roughly 0.1 Jy, which scales to 0.04 mJy at z = 0.1 (to within factors of powers of 1+z for cosmology and root-small-integer for the degraded beam; see below). For comparison, the expected thermal noise of the ALMA observation (using the ALMA Sensitivity Calculator and assuming a 4 MHz channel width) is 0.1 mJy, a factor of 2.5 greater than the anticipated contribution of noise from the model. Added in quadrature, the noise components total 0.108 mJy, and so we can expect that the input model noise degrades the simulation noise by about 8%.
Cosmology Calculations
Next we'll set up some python globals to handle the scaling of the model coordinates and flux densities appropriate for new redshift. We'll primarily need the angular size and luminosity distances for a given cosmology. To keep things simple, we'll use Ned Wright's CosmoCalc with the default cosmology; redshifts were collected from NED.
#z's
# Distinguish between z_lsrk, which sets the observed frequency for scaling, from z_cmb,
# which is needed to get cosmological distances.
z_old_cmb = 0.002122 # CMB-referenced z for cosmological distances from NED
z_old_lsrk = 0.001544 # from NED
z_new = 0.1
# angular size distances from CosmoCalc
da_old = 9.0
da_new = 375.9
# luminosity distances from CosmoCalc
dl_old = 8.937
dl_new = 454.8
The convention is "old" refers to M51 as observed at its proper redshift, and "new" refers to the new, higher redshift for our model.
Preparing the Model
The next step is to scale the M51 data cube into a model cube appropriate for simdata. First, we'll set up some globals to establish some file naming conventions.
suffix = "-p1" # z = 0.1, or point-1; useful to distinguish from repeated simulations at different z's
cubeOut = 'm51-atz' + suffix + '.im' # name for the model image (input to simdata)
Flux Density Scaling
Simdata wants models in units of Jy / pixel, but the BIMA SONG cube is in units of Jy / beam. That's an easy conversion.
# BIMA SONG beam -- could use imhead mode = 'get' to automate this step
bmaj = 5.82
bmin = 5.08 # note: BIMA SONG pixels = 1 arcsec, so this is the fwhm in pixels, too
toJyPerPix = 1.0 / (1.1331 * bmaj * bmin) # gaussian beam conversion = beams / pixel
Next, scale the flux for the new luminosity distance. Make the approximation that each pixel is a point source, and use the inverse square law to scale.
# correct flux density for luminosity distance
fluxScale = (dl_old/dl_new)**2 * (1.0 + z_new) / (1.0 + z_old_cmb)
Notice that there is an additional (1+z) correction because we are scaling flux densities rather than bolometric fluxes. Now we can use immath to perform the scaling. Immath needs an string expression to describe the scaling.
fluxExpression = "(IM0 * %f * %f)" % (toJyPerPix, fluxScale)
Here, fluxExpression is just a python string that will feed into immath, IM0 symbolically represents the input image (the BIMA SONG cube), and we use python formatting conventions to transfer the Jy/pix and flux scaling conversions into the expression string.
Now, generate the model cubeOut = m51-atz-p1.im.
immath(imagename=cubeName, outfile=cubeOut, mode='evalexpr',
expr=fluxExpression) # now in Jy / pixel at new redshift
Just for bookkeeping's sake, we'll change the brightness unit in the header of the model image.
# adjust brightness units
hdval = 'Jy/pixel'
dummy = imhead(imagename=cubeOut, mode = 'put', hdkey='BUNIT',
hdvalue=hdval)
Angular Size Scaling
The sky coordinates axes of the model need to be adjusted (1) to place M51 in the southern hemisphere and (2) to correct for the new angular size distance. To accomplish (1), we'll just flip the sign of the declination using imhead.
# move to southern hemisphere
hdval = imhead(imagename=cubeName, mode = 'get', hdkey='CRVAL2')
hdval['value'] = -1.0 * float(hdval['value'])
dummy = imhead(imagename=cubeOut, mode = 'put', hdkey='CRVAL2',
hdvalue=hdval)
The global variable "dummy" is just a throwaway to store the status of the imhead operation.
Next, adjust the pixel scale for the new angular size distance. To accomplish this adjustment, we'll use imhead with mode = "get" to read in the original pixel scale, and mode="put" to store the new pixel scale in the model header.
# x-pixel
hdval = imhead(imagename=cubeName, mode = 'get', hdkey='CDELT1')
# correct for new angular size distance
hdval['value'] = (da_old / da_new)*float(hdval['value'])
dummy = imhead(imagename=cubeOut, mode = 'put', hdkey='CDELT1',
hdvalue=hdval)
# y-pixel
hdval = imhead(imagename=cubeName, mode = 'get', hdkey='CDELT2')
# correct for new angular size distance
hdval['value'] = (da_old / da_new)*float(hdval['value'])
dummy = imhead(imagename=cubeOut, mode = 'put', hdkey='CDELT2',
hdvalue=hdval)
Adjusting the Frequency Axis
Changing the frequency axis of the model header is just a straightforward (1+z) correction.
# move to z_new
hdval = imhead(imagename=cubeName, mode = 'get', hdkey='CRVAL3')
hdval['value'] = (1.0 + z_old_lsrk) / (1.0 + z_new) * float(hdval['value'])
dummy = imhead(imagename=cubeOut, mode = 'put', hdkey='CRVAL3',
hdvalue=hdval)
The frequency axis pixel scale also needs to be corrected by (1+z), but there's a slight problem. Simdata needs to read the channel width from the header to estimate the thermal noise of the simulated observation. Unfortunately, simdata currently (CASA 3.0.0) accepts only positive channel widths from the header for the purposes of calculating thermal noise, but the BIMA SONG data have a negative channel width, because the data are organized in increasing velocity = decreasing frequency. One solution would be to rearrange the model cube in increasing frequency order, but, to keep things simple, we'll just change the sign of the frequency axis and accept the small error introduced into the frequency scaling and the flip of the orientation of the kinematic line of nodes.
# frequency pixel
hdval = imhead(imagename=cubeName, mode = 'get', hdkey='CDELT3')
# (1+z) correction for dnu
# abs added to debug --- simdata cannot handle -dnu properly
hdval['value'] = abs((1.0+z_old_lsrk) /(1.0+z_new)*float(hdval['value']) )
# store the new channel width
dummy = imhead(imagename=cubeOut, mode = 'put', hdkey='CDELT3',
hdvalue=hdval)
Simdata
The CASA task simdata will monolithically simulate an ALMA observation, produce measurement sets with and without thermal noise, and finally produce an CLEANed image cube based on the simulated observation.
Imaging parameters (e.g., synthesized beam, primary beam) will scale with frequency, and so it's handy to have a reference frequency stored in a python global. The reference frequency in the BIMA SONG header is 115.141 GHz, which is adjusted to z = 0.1.
# need to estimate frequency for beam / config calculation
thisFreq0 = 1.15141e2 # GHz
thisFreq1 = thisFreq0 * (1.0 + z_old_lsrk) / (1.0 + z_new)
The original BIMA SONG image is about 480 arcseconds across; scale this image size to the new redshift.
# estimate final image size
imSize = 480.0 * (da_old / da_new) # in arcseconds
For relatively high redshifts, there should be no need to mosaic the observations. We'll nevertheless allow for mosaicking in case we want to repeat the simulation for lower redshift. Simdata needs the spacing between pointings in the mosaic; we'll require pointings spaced by half of the primary beam.
# mosaicking info
primaryBeam = 17.0 * (300. / thisFreq1) # in arcseconds; ALMA primary beam = 17 arcsec at 300 GHz
pointingSpacing = primaryBeam / 2.0 # in arcseconds
mosaicSize = "%farcsec" % imSize # how big to make the mosaic
We also need to estimate the desired synthesized beam size. We don't want the new beam to be so large so that we cannot resolve a rotation curve, but we also don't want it to be so small that we effectively resolve out the BIMA SONG data. The BIMA SONG beam was 5 arcsec, and so as a reasonable guess we'll adopt the equivalent of a 15" beam (3 times coarser than the BIMA SONG beam), scaled appropriately to z = 0.1.
# Estimate desired beam size. BIMA SONG has 5": use 15" projected to new redshift
beamNew = 15.0 * (da_old / da_new)
We want pixels that sample the beam at least 3 times for stable deconvolution; we'll use 4 times sampling, rounded off to the nearest milliarcsec.
pixelSize = round(beamNew * 1000.0/ 4.0) / 1000.0
Now we know the image size in arcseconds and the pixel size in arcseconds, but simdata wants the number of pixels along the RA or Dec axis.
imSizePix = int(round(imSize / pixelSize))
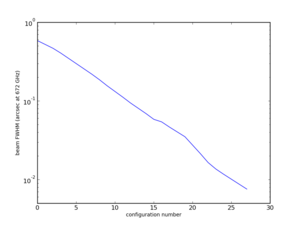
Finally, we need to know which ALMA configuration number, ranging from 1-28, to use to achieve the desired resolution. (See the figure at right and the discussion in Antenna List.) The configuration number can be approximated by
[math]\displaystyle{ {\rm Config} = {\rm floor}(-13.72 \log_{10}\left({\rm Beam}(^{\prime\prime}) \times \nu / 672{\rm\ GHz} + 0.145\right)). }[/math]
Here's how to express the calculation in python and store the outcome as the name of the matching antenna configuration file.
# estimate ALMA config number -- very crude!
config = floor(-13.72 * (log10(beamNew * thisFreq1 / 672.) + 0.145))
if config < 1: config = 1
if config > 28: config = 28
configFile = 'alma.out%02i.cfg' % config
Turns out that this algorithm selects antenna configuration 15 (although that is buried in the python string configFile).
Now we have enough information to run simdata, and hopefully some of the python global variables that were defined above will start to make sense.
modelimage = cubeOut
integration = '10s' # watch out for memory limits here; 10s is usually safe for large mosaics
# set up the antenna configuration
repodir=os.getenv("CASAPATH").split(' ')[0]+"/data/alma/simmos/"
antennalist=repodir+configFile # defined above
project = "M51-ATZ" + suffix
# The date doesn't really matter: simdata will find the optimum observing time for any given date
refdate="2010/04/27/14:30:00"
totaltime="28800s" # 8 hour integration on source
checkinputs = "yes"
inbright = 'unchanged'
# Just use the model image coords
ignorecoord=F
startfreq = ''
chanwidth = ''
# the pointing center is hardwired in this example
direction = "J2000 13h29m52.349 -47d11m53.795"
pointingspacing = "%farcsec" % pointingSpacing
mosaicsize = [mosaicSize, mosaicSize] # single pointing
scanlength=1
cell = "%farcsec" % pixelSize
imsize = [imSizePix,imSizePix]
# clean parameters
niter = 500
threshold = "1.0mJy"
psfmode = "clark"
weighting = "natural"
stokes = 'I'
# Add thermal noise: assume default 1mm H2O
noise_thermal = True
noise_mode = 'tsys-atm'
user_pwv = 1.0
t_ground = 269.0
verbose = True
async = False
fidelity = True
display = False
saveinputs("simdata", project + ".simdata.saved")
simdata()
Take a Break
If you have got this far, you've earned it. Simdata will be running for a while, and coffee sure sounds good right now.
Results
Here is an inventory of some of the simdata products.
| Filename | Description |
|---|---|
| M51-ATZ-p1.ms | Model measurement set sans noise |
| M51-ATZ-p1.noisy.ms | Model measurement set with noise |
| M51-ATZ-p1.clean.image | CLEAN-deconvolved cube of M51-ATZ-p1.noisy.ms |
And there are plenty of other auxiliary files.
The rest frequency will have been lost in the simulation, and it's worth restoring.
imhead(imagename="M51-ATZ-p1.clean.image", mode="put", hdkey="restfreq", hdvalue="115.27120180GHz")
The simulated data cube can be analyzed just like any other CASA image -- examples are given in the CARMA tutorial and the VLA 21cm tutorial.
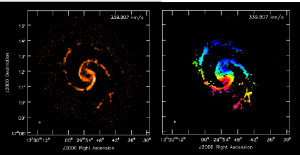
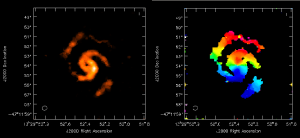
Moment Maps
Use immoments to calculate the integrated intensity and velocity field maps from the simulated cube. The excludepix option applies a 3σ cut.
immoments(imagename='M51-ATZ-p1.clean.image',moments=[0,1],axis='spectral',
excludepix=[-100,0.0006],outfile='M51-ATZ-p1.moments')
The results are shown at right.
--Jack Gallimore 15:55, 30 April 2010 (UTC)