EVLA high frequency spectral line tutorial - IRC+10216 - imaging
This tutorial picks up where EVLA high frequency spectral line tutorial - IRC+10216 - calibration leaves off.
Image the Spectral Line Data
The continuum-subtracted spectral line data is contained in IRC10216_spls.ms. Use plotms to plot the lines.
plotms(vis='IRC10216_spls.ms', xaxis='channel', yaxis='amp',
avgtime='1e8', avgscan=T, coloraxis='spw')
Now it is time to image the visibility data using clean. For illustration, we will clean channel 22 of the SiS line.
# In CASA
clean(vis='IRC10216_spls.ms', imagename='ch22', spw='1:22~22',
mode='channel', nchan=1, start='', width=1, niter=100000,
gain=0.1, threshold='3.0mJy', psfmode='clark', imagermode='csclean',
interactive=T, npercycle=100, imsize=300, cell=['0.4arcsec', '0.4arcsec'],
stokes='I', weighting='briggs', robust=0.5)
After running the above command, make a region in the CASA viewer. Double-click inside the region and clean by clicking the green circular arrow. After each cycle, click the green circular arrow again if the flux inside the region is brighter than the flux peaks outside the region. When you are finished cleaning, click the red 'STOP' button.
Open the resulting image using the viewer.
# In CASA
viewer("ch22.image")
In the viewer, make a region and click inside it to get statistics about the portion of the image in the region.
Image the Continuum data
Below the use of mode='mfs' will make a single multi-frequency synthesis image out of the specified spw/channels. Again you should make an interactive clean mask. Since no threshold is set, you will need to stop cleaning when the residual looks noise like using the red x "Next Action" button (it will be done when the viewer comes back the second time). The continuum for IRC10216 is very weak but interesting -- it is essentially tracing the photosphere of the AGB star.
# In CASA
clean(vis='IRC10216.cont',imagename='IRC10216.36GHzcont',
mode='mfs',imagermode='csclean',
imsize=300,cell=['0.4arcsec'],spw='0~1:5~59',
weighting='briggs',robust=0.5,
interactive=T)
Now look at the result in the viewer if you like
# In CASA
viewer
Image Analysis and Viewing
Next make integrated intensity maps (moment 0) and intensity-weighted velocity maps (moment 1). For HC3N, we also produce a velocity dispersion, peak flux, and median map. All are derived with immoments. To do this, we'll want to know what channels the line emission starts and ends on, and also the rms noise in a single channel. So first lets open the viewer:
# In CASA
viewer
Then use the Viewer tape deck to see which channels have significant line emission. For HC3N, the line channel range in the cube is 16 to 45, and it is the same for SiS.
Then use the tape deck to go to a line free channel, select the box region tool and make a box. When you double click in the box, the image statistics for the channel you are on will print to the terminal. Move the box around a bit to see what the variation in rms noise is. You should get something like 2 mJy. Note that the rms is much worse in channels with strong emission because of the low dynamic range of these data. If you want the box tool to go away (i.e. if you want to make a new one), hit the escape key.
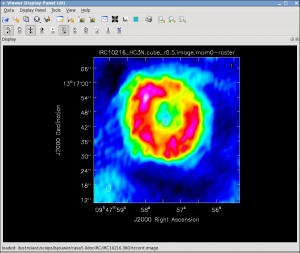
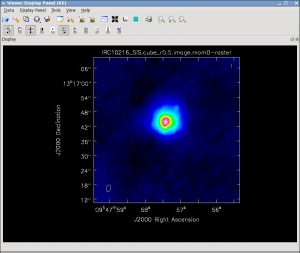
Now lets make the moment 0 and moment 1 maps. For moment zero, it's best to limit the calculation to image channels with significant signal in them, but not to apply a flux cutoff, as this will bias the derived integrated intensities upward.
# In CASA
immoments(imagename='IRC10216_HC3N.cube_r0.5.image',moments=[0],
axis='spectral',
chans='16~45',
outfile='IRC10216_HC3N.cube_r0.5.image.mom0')
# In CASA
immoments(imagename='IRC10216_SiS.cube_r0.5.image',moments=[0],
axis='spectral',
chans='16~45',
outfile='IRC10216_SiS.cube_r0.5.image.mom0')
For moment 1, it is essential to apply a conservative flux cutoff to limit the calculation to high signal-to-noise areas. Here we use about 5sigma.
# In CASA
immoments(imagename='IRC10216_HC3N.cube_r0.5.image',moments=[1],
axis='spectral',
chans='16~46',excludepix=[-100,0.01],
outfile='IRC10216_HC3N.cube_r0.5.image.mom1')
# In CASA
immoments(imagename='IRC10216_SiS.cube_r0.5.image',moments=[1],
axis='spectral',
chans='16~45',excludepix=[-100,0.01],
outfile='IRC10216_SiS.cube_r0.5.image.mom1')
and finally we will do velocity dispersion, peak flux, and median map in a single step for HC3N. immoments can perform these steps even though the latter two are not 'moments' in a mathematical sense. Check the help file to find out the options. Peak flux and median are produced with the moment parameter set to 8 and 3:
# In CASA
immoments(imagename='IRC10216_HC3N.cube_r0.5.image',moments=[2,8,3],
axis='spectral',
chans='16~46',excludepix=[-100,0.01],
outfile='IRC10216_HC3N.cube_r0.5.image.extramoms')
will create the files IRC10216_HC3N.cube_r0.5.image.extramoms.weighted_dispersion_coord, IRC10216_HC3N.cube_r0.5.image.extramoms.median, and IRC10216_HC3N.cube_r0.5.image.extramoms.maximum.
Now use the viewer to further explore the images you've made.
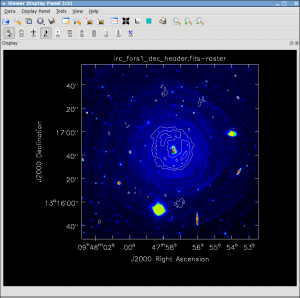
For fun you can download the VLT V-band image at http://casa.nrao.edu/Data/EVLA/IRC10216/irc_fors1_dec_header.fits kindly provided by Izan Leão and overlay the moment images and 36 GHz continuum. More information about the dust properties can be found in the Leão et al. (2006) paper http://adsabs.harvard.edu/abs/2006A%26A...455..187L
The creation of position velocity cuts from the viewer is currently being developed and hopefully available soon in CASA. If you are interested in a work-around, you may have a look at the pV casaguide. Masking the data cube to extract the emission is described here.
Spectrum Fitting
Frequently, one would like to fit Gaussians or polynomials to the spectral line in the data cube. This can be done with CASA's specfit task. specfit can fit those functions to an average spectrum define by some bounding box, or, alternatively, for each pixel. In the following, we will do both.
Fitting an average spectrum
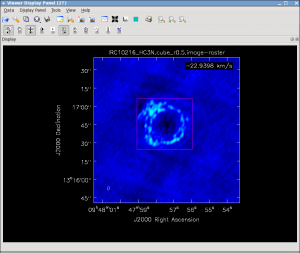
First, we want to inspect the spectrum. Load the image into the viewer (here: the HC3N image cube), select "spectral profile" from the Tools menu and open a region with the mouse button that is assigned to the rectangular "R" region in the tool bar. Best to do this at a plane that shows the entire extent of the source. The average spectrum will be displayed in a separate panel.
To fit this profile in specfit, we need a region file outlining the 2-D region that is averaged (the green box in the viewer screenshot).
In the following we use the new CASA region format (CASA 3.3 and higher) that is described here. Following the guidelines on that page, we create a file named specfit.rgn that describes a box with its [[x1,y1],[x2,y2]] corners in J2000 RA DEC coordinates.
#CRTFv0 box[[09:47:59.2, 13.16.24], [09:47:55.8, 13.17.09]]
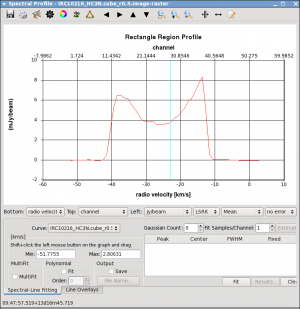
We will fit 2 Gaussians to the two peaks of the spectrum (the scientific merit is debatable). A file with initial values for the fit can be provided via the estimates parameter - see specfit for details. Here we will let CASA figure out the start values by itself:
# In CASA
specfit(imagename='IRC10216_HC3N.cube_r0.5.image', region='specfit.rgn', multifit=F,
estimates='', ngauss=2)
delivers the output below (or something similar depending on the details of flagging etc.):
Fit centered at:
RA : 09:47:57.49
Dec : 13.16.46.46
Stokes : I
Pixel : [146.002, 164.499, 0.000, *]
Attempted : YES
Converged : YES
Iterations : 25
Results for component 0:
Type : GAUSSIAN
Peak : 5.66 +/- 0.41 mJy/beam
Center : -16.21 +/- 0.33 km/s
40.53 +/- 0.32 pixel
FWHM : 8.38 +/- 0.80 km/s
8.14 +/- 0.78 pixel
Results for component 1:
Type : GAUSSIAN
Peak : 4.55 +/- 0.32 mJy/beam
Center : -33.40 +/- 0.54 km/s
23.84 +/- 0.52 pixel
FWHM : 14.5 +/- 1.4 km/s
14.0 +/- 1.4 pixel
which seems to have caught the two peaks pretty well.
Spectral Fitting pixel by pixel
specfit can also fit Gaussians to every spectrum in each single spatial pixel. The following command will do this within the spectfit.rgn region defined above:
# In CASA
specfit(imagename='IRC10216_HC3N.cube_r0.5.image', region='specfit.rgn', ngauss=2,
multifit=T, amp='fit.amp.image', center='fitcenter.image', fwhm='fitfwhm.image')
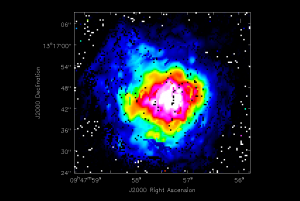
In this example, specfit will produce three images per Gaussian, images that map the best fit values of the Gauss peaks (amplitudes), velocity centers, and full widths at half maximum. For the first Gaussian, the image to the right displays the amplitude image fit.amp.image_0.
Self-Calibration
The many different aspects of self-calibration could fill several casaguides. Here we describe a simple process for this particular relatively low S/N data (low S/N per channel at least).
While running clean above, the model column for each channel will have been filled with the clean model (if you made a Fourier transform of this model, you would see an image of the clean components).
We chose to do the self cal on the spw=1 SiS line data because it has the strongest emission in a single channel and is a bit more compact than the HC3N data. We will run gaincal specifying the channel in the uv-data that has the brightest peak in the image (use the viewer to figure out which channel this is for spw=1), note down what the peak flux is. Since we started the image with a channel range we need to account for the fact that the image channel numbers do not map exactly to the uv-data channel numbers (they are off by 5 so that channel 13 in the image is roughly channel 19 in the uv-data).
The next thing we need to understand is the S/N of the data. In particular, to self-cal, you need enough signal on a single baseline over the course of your chosen solint to get a S/N of about 3. Above we calculated an average rms noise of about 2 mJy/beam/channel for the whole timerange (about 95 minutes on source time) and all antennas (16). We can use our knowledge of the radiometer equation (see EVLA Sensitivity) where rms scales as 1/sqrt(time * #baselines), and the number of baselines= N(N-1)/2 and N=# of antennas. So the rms noise on one baseline, one 10 second integration is given by:
[math]\displaystyle{ {\rm RMS(baseline)} = {\rm 2\ mJy\ beam^{-1}\ channel^{-1}} \sqrt{ \frac{95\times 60\ {\rm sec}}{10\ {\rm sec}}\times\frac{16\times 15}{2\times 1}} }[/math]
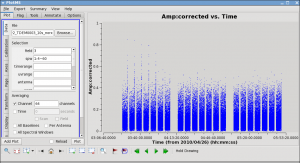
The 95 minutes of on-source time can be estimated from a plot like:
# In CASA
plotms(vis='day2_TDEM0003_10s_norx',field='3',ydatacolumn='corrected',
xaxis='time',yaxis='amp',correlation='RR,LL',
avgchannel='64',spw='1:4~60',antenna='')
This analysis suggests that the rms noise on one baseline, one 10 second integration is about 525 mJy. In contrast the peak flux density in the strongest SiS channel is only about 200 mJy (you can check using the viewer). Because the emission is fairly compact, most baselines will see about this peak flux, this is why we chose the more compact of the two possible lines. This peak flux density tells us that we need to use a solint large enough so that the rms noise is not worse than about 1/3 of 200 mJy. Thus, a solint of 10 minutes is about the shortest we can use and be reasonably confident of the solutions.
Now we run gaincal with the solint we have determined. Note that because our desired solint is more than the scan time, we need to include combine='scan'.
# In CASA
gaincal(vis='IRC10216.contsub',caltable='pcal_ch19one_10min',
spw='1:19~19',calmode='p',solint='10min',combine='scan',
refant='ea02',minsnr=3.0)
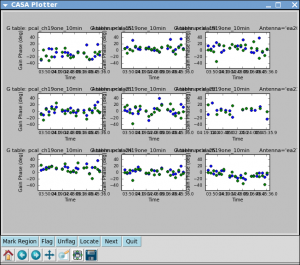
Now let's look at the solutions:
# In CASA
plotcal(caltable='pcal_ch19one_10min',xaxis='time',yaxis='phase',
iteration='antenna',subplot=331,plotrange=[0,0,-50,50])
For some antennas you can see clear global trends away from zero: ea08, ea21,ea24 are examples, and you can also see some smaller variations with time.
Now let's explore whether applying this solution actually improves matters. To do this we need to run applycal to apply the solutions to the line dataset, both spw. We need to use spwmap to tell it that the solutions derived for spw=1 should be applied to both spw=0 and spw=1. Again it's important to set calwt=F here.
# In CASA
applycal(vis='IRC10216.contsub',field='',spw='0,1',
gaintable=['pcal_ch19one_10min'],spwmap=[[1,1]],calwt=F)
Note: in this example we ran the self-cal steps on the full uv continuum subtracted spectral line data set. For a more complex iterative self-calibration proceedure, you may find it easier to split off the channel/spw you want to experiment on with split, and then do all the imaging (clean) and gaincal steps with it. The gaincal tables created on the single channel can still be applied with applycal to the multi-channel/spw dataset. If you do this though, keep in mind that once split, the single-channel data will have its spw id reset to 0 (you can check with listobs), no matter what spw it came from. Thus in order to applycal with it you would need spwmap=[[0,0]].
To save time we can use the clean mask we made before and run in a non-interactive mode. You can use a mask over again as long as the number of channels in the clean call haven't changed. You can change cell or imsize and it will still do the right thing.
# In CASA
clean(vis='IRC10216.contsub',imagename='IRC10216_HC3N.cube_r0.5.pselfcal',
imagermode='csclean',
imsize=300,cell=['0.4arcsec'],spw='0:5~58',
mode='velocity',interpolation='linear',
restfreq='36.39232GHz',outframe='LSRK',
weighting='briggs',robust=0.5,
mask='IRC10216_HC3N.cube_r0.5.mask',
interactive=F,threshold='3.0mJy',niter=100000)
# In CASA
clean(vis='IRC10216.contsub',imagename='IRC10216_SiS.cube_r0.5.pselfcal',
imagermode='csclean',calready=T,
imsize=300,cell=['0.4arcsec'],spw='1:5~58',
mode='velocity',interpolation='linear',
restfreq='36.30963GHz',outframe='LSRK',
weighting='briggs',robust=0.5,
mask='IRC10216_SiS.cube_r0.5.mask',
interactive=F,threshold='3.0mJy',niter=100000)
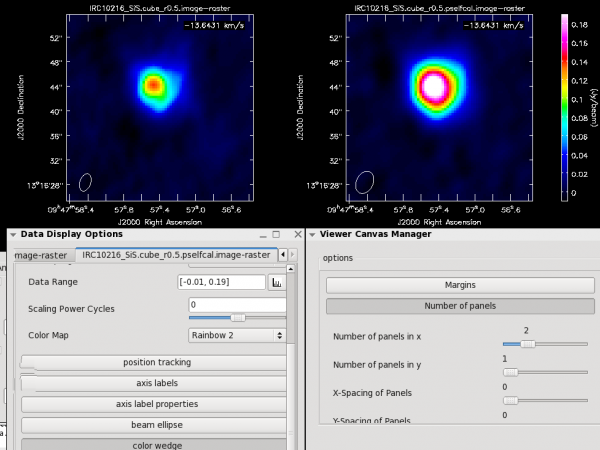
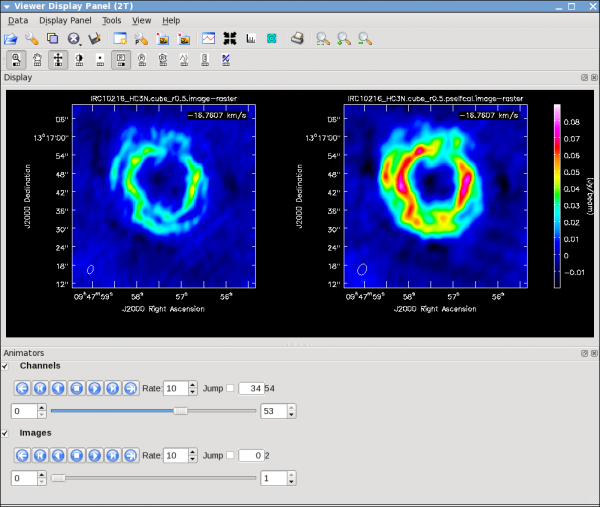
Now investigate the original and self-cal'ed images in the viewer. You will find that even this single self-cal step significantly improves the images. Try opening both versions of the SiS image cubes. Then select a bright channel from the tape deck like channel 37, then use the "wrench" and "pwrench" guis to make a plot like below setting the same image range for both cubes, and two panels in x, then to see both images of that channel side-by-side click the blink toggle (see image below for more tips on setup.)
Repeat for HC3N:
Now you can redo the moment images if you like with the improved cubes, be sure to change the output file names.
--Crystal Brogan --additions:Juergen Ott
Last checked on CASA Version 3.3.0.