DataWeightsAndCombination
This page is currently under construction.
Principles of Data Weighting
When combining data with disparate properties it is very important that the relative weights of each visibility be in the correct proportion to the other data according to the radiometer equation. Formally, the visibility weights should be proportional to 1/sigma2 where sigma is the variance or rms noise of a given visibility.
Assuming that the 7m and 12m antennas have similar aperture and quantization efficiencies (a reasonable assumption since they were designed this way), the rms noise in a single channel for a single visibility is:
[math]\displaystyle{ \sigma_{ij}=\frac{2k}{A_{eff}} }[/math] [math]\displaystyle{ \sqrt{\frac{T_{sys,i} T_{sys,j}}{\Delta\nu_{ch} t_{ij}}}, }[/math]
where k is Boltzmann's constant, Aeff is the effective antenna area, Tsys,i is the system temperature for antenna i, Δνch is the channel width, and tij is the integration time per visibility.
Weights in CASA
A memo describing weights in CASA, in particular the significant changes that were made with CASA 4.2.2, can be found at http://casa.nrao.edu/Memos/CASA-data-weights.pdf
To summarize the situation specifically as applied to ALMA data reduction delivered to PIs:
- CASA 4.2.1 and earlier: Weights were only scaled by 1/[(Tsys(i) * Tsys(j)] using calwt=True at the applycal stage for Tsys table.
- CASA 4.2.2 and later: Upon import data weights are scaled by 2ΔνchΔtij and also scaled by 1/[(Tsys(i) * Tsys(j)] using calwt=True at the applycal stage for Tsys table. Additionally:
- For data calibrated by the 4.2.2 CASA Pipeline the weights are further modified by [(gain(i))2 * (gain(j))2] when the amplitude gain table is applied using calwt=True. Thus, these weights are correct.
- For data manually calibrated in CASA 4.2.2, unfortunately calwt=False was still used to apply the antenna gain table, thus, these data have weights that are not correct in a relative sense when compared to other data, especially of different antenna size by the factor [(gain(i))2 * (gain(j))2].
- CASA 4.3: Data calibrated in either the pipeline or manually will have correct weights.
Concat with 1/sigma2 scaling of Weights
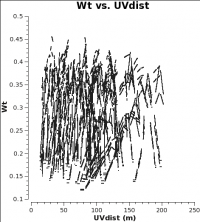
<figure id="7m_WT.png">
</figure>
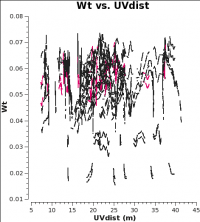
<figure id="12m_WT.png">
</figure>
When combining data with disparate properties it is very important that the relative weights of each visibility be in the correct proportion to the other data according to the radiometer equation. Formally, the visibility weights should be proportional to 1/sigma**2 where sigma is the variance or rms noise of a given visibility.
In CASA 4.2.1 and earlier, the data weights are 1 upon import, later in the standard calibration procedure, applycal scales the weights by 1/[(Tsys(i) * Tsys(j)] if calwt=True for the Tsys table applycal. As an example, we plot the weights of 7m and 12m data imported in CASA 4.2.1. No averaging can be turned on when plotting the weights.
# In CASA
os.system('rm -rf 7m_WT.png 12m_WT.png')
plotms(vis='m100_12m_CO.ms',yaxis='wt',xaxis='uvdist',spw='0~2:200',
coloraxis='spw',plotfile='12m_WT.png')
#
plotms(vis='m100_7m_CO.ms',yaxis='wt',xaxis='uvdist',spw='0~2:200',
coloraxis='spw',plotfile='7m_WT.png')
As you can see from these plots, the weights are quite similar at this stage because the data were taken under similar weather conditions and hence Tsys. Additionally, for these data calwt=False was used to apply the antenna-based amplitude gains (see next section).
Assuming that the 7m and 12m antennas have similar apperture and quantization efficiencies (a reasonable assumption since they were designed this way), the rms noise in a single channel for a single visibility is:
[math]\displaystyle{ \sigma_{ij}=\frac{2k}{A_{eff}} }[/math] [math]\displaystyle{ \sqrt{\frac{T_{sys,i} T_{sys,j}}{\Delta\nu_{ch} t_{ij}}} }[/math]
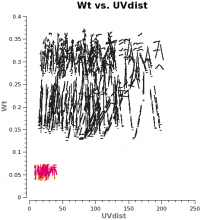
<figure id="Intcombo_0.193_WT.png">
</figure>
Where k is Boltzmann's constant, Aeff is the effective antenna area, Tsys,i is the system temperature for antenna i, Δνch is the channel width, and tij is the integration time per visibility.
The two key things that are different between the 7m and 12m-array data are that the effective dish Areas are different by (7/12)2 and the integration times are different by sqrt(10.1/6.05). Since dish area is in the numerator of the radiometer equation and integration time per visibility is in the denominator, and assuming WT propto 1/sigma2, the 7m weight should be scaled by: (7./12.)4 x (10.1/6.05) = 0.193 to account for the difference in telescope size and integration time per visibility.
# In CASA
# Concat and scale weights
os.system('rm -rf M100_Intcombo_0.193.ms')
concat(vis=['m100_12m_CO.ms','m100_7m_CO.ms'],
concatvis='M100_Intcombo_0.193.ms',
visweightscale=[1,0.193])
Now plot the concatenated weights to verify they are as expected.
# In CASA
os.system('rm -rf Intcombo_0.193_WT.png')
plotms(vis='M100_Intcombo_0.193.ms',yaxis='wt',xaxis='uvdist',spw='0~2:200',
coloraxis='spw',plotfile='Intcombo_0.193_WT.png')
Applycal with calwt=True for Amplitude Gain
If applycal=True for any calibration table that contains amplitude gains, the weights will be scaled by (G_i*G_j)2 (where i and j gains correspond to antennas i and j). Since the amplitude gains are directly proportional to the individual antenna sensitivities, scaling the weights by the amplitude gains will take into account antenna size differences, and also downweight antennas with comparatively low gain.
Because it had not been thoroughly tested, the standard procedure for applying amplitude tables *pre-*CASA 4.2.2 was to set calwt=False for the amplitude gain table. However, the ALMA pipeline is using calwt=True as this alleviates the need to apply additional weight scaling due to differences in antenna size when combining data.
In summary if CASA 4.2.2 is used to import the data AND calwt=True is used to apply the amplitude calibration, no additional weighting should be required to combine 7m+12m ALMA data.