DataWeightsAndCombination: Difference between revisions
| Line 69: | Line 69: | ||
====Option 1: Re-calibrate your data in CASA 4.2.2 or later==== | ====Option 1: Re-calibrate your data in CASA 4.2.2 or later==== | ||
:<span style="color:#B22222"> & | :<span style="color:#B22222"> ⇒ This option is easiest to implement for Case 2B (Data observed in Cycle 2 manually calibrated in 4.2.2 with calwt=False for amplitude/flux gain table. </span> | ||
Importing your data in 4.2.2 (or later) will automatically adjust the weights by 2Δν<sub>ch</sub>Δt<sub>ij</sub>. The Tsys application should already be correct in your scripts. Be sure however, to change calwt=True for the amplitude table applycal. | Importing your data in 4.2.2 (or later) will automatically adjust the weights by 2Δν<sub>ch</sub>Δt<sub>ij</sub>. The Tsys application should already be correct in your scripts. Be sure however, to change calwt=True for the amplitude table applycal. | ||
| Line 84: | Line 84: | ||
::'''Caveat 3:''' Scripts from earlier than 4.2.1 are likely to have commands that make them incompatible to run directly in later versions of CASA. It may be difficult for a non-expert to update the script to current syntax. | ::'''Caveat 3:''' Scripts from earlier than 4.2.1 are likely to have commands that make them incompatible to run directly in later versions of CASA. It may be difficult for a non-expert to update the script to current syntax. | ||
====Option 2: Run the task statwt on your calibrated science target data==== | ====Option 2: Make an approximate overall correction:==== | ||
Since all ALMA data reduced in CASA should already have 1/Tsys<sup>2</sup> weighting, other factors that need inclusion if there are differences in | |||
====Option 3: Run the task statwt on your calibrated science target data==== | |||
This task attempts to assess the sensitivity per visibility and adjust the weights accordingly. It is very commonly used for JVLA data (including their pipeline). | This task attempts to assess the sensitivity per visibility and adjust the weights accordingly. It is very commonly used for JVLA data (including their pipeline). | ||
::'''Caveat 1:''' One must limit the calculation to line-free channels. For complex line projects this can be painful, however, typically the line-free channels are already known from the continuum subtraction, and can be reused here. However, it is best run statwt before continuum subtraction. | ::'''Caveat 1:''' One must limit the calculation to line-free channels. For complex line projects this can be painful, however, typically the line-free channels are already known from the continuum subtraction, and can be reused here. However, it is best run statwt before continuum subtraction. | ||
== Example of Correcting Weights from CASA 4.2.1 Calibrated Data Using Option 3== | == Example of Correcting Weights from CASA 4.2.1 Calibrated Data Using Option 3== | ||
Revision as of 13:24, 21 July 2015
This page is currently under construction.
Principles of Data Weighting
For optimal imaging performance it is critical that in a relative sense each visibility in the data have the correct weight -- that is, data with better sensitivity have more weight than data with less sensitivity. Formally, the visibility weights should be equal to 1/σij2 where σij is the variance or rms noise of a given visibility.
[math]\displaystyle{ \sigma_{ij}=\frac{2k}{\eta_{q}\eta_{c}A_{eff}} }[/math] [math]\displaystyle{ \sqrt{\frac{T_{sys,i} T_{sys,j}}{\Delta\nu_{ch} t_{ij}}}, }[/math]
where:
k is Boltzmann's constant.
Aeff is the effective antenna area which is equal to the aperture efficiency x the geometric area of the antenna. The aperture efficiency depends on the rms antenna surface accuracy and the geometric area on the antenna dish radius2.
ηq and ηc are the quantization and correlator efficiencies, respectively. These have values near 1 and will be ignored for the purposes of this casaguide, but see the ALMA Technical Handbook for more information.
Tsys,i is the system temperature for antenna i, and Tsys,j is the system temperature for antenna j
Δνch is the channel width.
tij is the integration time per visibility.
Note, when this equation is extended to a whole dataset rather than a single visibility, Tsys,iTsys,j is replaced by the average Tsys2 and the factors sqrt[N(N-1)] and np are included in the denominator, where N is the number of antennas and np is the number of polarizations (1 for single pol and 2 for dual pol data).
In order to correctly combine and image data that have different Tsys, Δνch, tij, or antenna size it is essential to use visibility weights proportional to 1/σij2. The remainder of this guide deals with ensuring that the individual visibility weights are correct in your ALMA data.
Additionally, when combining data from different antenna configurations, one will get optimal overall sensitivity to all spatial scales by matching the surface brightness sensitivity at each uv-distance. This can only be achieved by having time-on-source per configuration in the right proportion. This topic is covered in ALMA Memo http://library.nrao.edu/public/memos/alma/memo598.pdf and informs the relative amount that ALMA observes 7m-array data versus 12m-array data, and compact versus extended 12m-array configurations. However, since telescope time is expensive, one typically does not actually observe in the optimal proportion, in that case one will not fully realize the expected "impact" of adding the less sensitive config data. In that case, one may chose to "upweight" the less sensitive config explicitly by changing its data weights, above and beyond 1/σij2. However, it should be noted that there are no free lunches, and such a change will come at the expense of overall image sensitivity though it may very well be the optimal choice for your science case. Finding the optimal up-weighting is usually a matter of experimentation, but can easily be explored using the visweightscale parameter in concat. As a general rule of thumb extra up-weighting by more than a factor of 2-3 is not recommended. Before messing with this however, its always best to start with data that simply has the correct 1/σij2 weights.
Weights in CASA
A memo describing weights in CASA, in particular the significant changes that were made with CASA 4.2.2, can be found at http://casa.nrao.edu/Memos/CASA-data-weights.pdf
To summarize the situation specifically as applied to ALMA data reduction in the ALMA archive and delivered to PIs:
- 1) CASA 4.2.1 and earlier: Weights were only scaled by 1/[(Tsys(i) * Tsys(j)] using calwt=True at the applycal stage for Tsys table. Assuming that (i) there aren't any unflagged antennas with significantly low gain due to for example pointing errors, or hardware problems, and (ii) all the antennas have similar surface errors -- usually good assumptions for ALMA data, data calibrated this way are to good approximation internally consistent and can produce good imaging results, but should not be combined with other data that have different Δνch, tij, or antenna size without further modification. An example of what you can do in this situation is given in XX.
- 2) CASA 4.2.2 and later: Upon import data weights are scaled by 2ΔνchΔtij and also scaled by 1/[(Tsys(i) * Tsys(j)] using calwt=True at the applycal stage for Tsys table. Additionally:
- (A) For data calibrated by the 4.2.2 CASA Pipeline the weights are further modified by [gain(i)2 * gain(j)2] when the amplitude gain table is applied using calwt=True. Since the amplitude gains are directly proportional to the effective Antenna area, scaling the weights by the amplitude gains will take into account antenna size differences, and also down-weight antennas with comparatively low gain. Thus, these weights are completely correct.
- (B) For data manually calibrated in CASA 4.2.2, unfortunately calwt=False was still used to apply the antenna gain table, thus, these data have weights that are not correct in a relative sense when compared to other data with different antenna size by the factor [gain(i)2 * gain(j)2].
- 3) CASA 4.3 and later: Data calibrated in either the pipeline or manually will have completely correct weights. An example of this situation is demonstrated in https://casaguides.nrao.edu/index.php/M100_Band3_Combine_4.3
How Do I Know the Situation For My Data?
- Data taken in Cycle 0 and Cycle 1 were reduced in 4.2.1 or earlier versions and correspond to Situation 1 above. ACA 7m-array data were first offered in Cycle 1. If you want to combine 12m-array and 7m-array data from Cycle 1 is very likely you need to correct weights before imaging.
- The situation for Cycle 2 is more confused (this includes actual Cycle 2 projects and carry-over projects or parts of projects from Cycle 1).
- Key dates:
- Start Cycle 2: June 1, 2014
- CASA 4.2.2 release date: Sept. 4, 2014
- Pipeline release date: Oct. 20, 2014
- How to distinguish between pipeline and manual data reduction.
- In your data delivery, the README file should say but there were some oversights on this front.
- A sure way to tell: look in the directory called script for a particular member_ouss. If you see a file with PPR*.xml, the data was calibrated by the pipeline. Otherwise it was done manually.
What Are the Options for Adjusting the Weights for Older Reductions?
If the data weights are not correct in the data you want to combine there are three options to correct the situation. These different methods carry different levels of pain/complexity depending on your situation. For example, for data manually calibrated in 4.2.2, Option 1 is pretty easy, but harder for older data/ versions of CASA. The situation can also be extra confusing if your data fall into multiple categories above. For example, it is not uncommon that in Cycle 2 the 12m-array data could be pipeline calibrated, but the 7m-array data done manually.
Option 1: Re-calibrate your data in CASA 4.2.2 or later
- ⇒ This option is easiest to implement for Case 2B (Data observed in Cycle 2 manually calibrated in 4.2.2 with calwt=False for amplitude/flux gain table.
Importing your data in 4.2.2 (or later) will automatically adjust the weights by 2ΔνchΔtij. The Tsys application should already be correct in your scripts. Be sure however, to change calwt=True for the amplitude table applycal.
- Caveat 1: You must have the raw ALMA ASDM to correctly start over, unless you are in the CASA 4.2.2 manual calibration case. In that case you can simply change calwt=True for the amplitude table applycal and re-run.
- Caveat 2: Most (all except early Cycle 0) ALMA manual calibration scripts have within them the CASA version used to create the script. For example, if your manual calibration script says the following, using any other version than 4.3.1 will give an error:
if re.search('^4.3.1', casadef.casa_version) == None:
sys.exit('ERROR: PLEASE USE THE SAME VERSION OF CASA THAT YOU USED FOR GENERATING THE SCRIPT: 4.3.1')
- You must change the version number to match the version you want to use or the script will not run.
- Caveat 3: Scripts from earlier than 4.2.1 are likely to have commands that make them incompatible to run directly in later versions of CASA. It may be difficult for a non-expert to update the script to current syntax.
Option 2: Make an approximate overall correction:
Since all ALMA data reduced in CASA should already have 1/Tsys2 weighting, other factors that need inclusion if there are differences in
Option 3: Run the task statwt on your calibrated science target data
This task attempts to assess the sensitivity per visibility and adjust the weights accordingly. It is very commonly used for JVLA data (including their pipeline).
- Caveat 1: One must limit the calculation to line-free channels. For complex line projects this can be painful, however, typically the line-free channels are already known from the continuum subtraction, and can be reused here. However, it is best run statwt before continuum subtraction.
Example of Correcting Weights from CASA 4.2.1 Calibrated Data Using Option 3
<figure id="12m_WT.png">
</figure>
<figure id="7m_WT_old.png">
</figure>
Below we show what could have been done to correct the M100 SV data if it was reduced in CASA 4.2.1 (rather than 4.3 as demonstrated in https://casaguides.nrao.edu/index.php?title=M100_Band3_Combine_4.3).
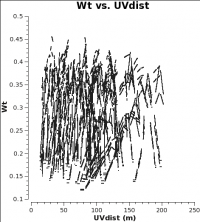
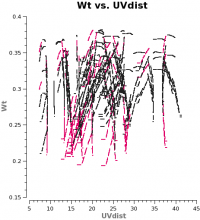
In CASA 4.2.1 and earlier, the data weights are 1 upon import, later in the standard calibration procedure, applycal scales the weights by 1/[(Tsys(i) * Tsys(j)] if calwt=True for the Tsys table applycal. As an example, we plot the weights of 7m and 12m data imported in CASA 4.2.1. No averaging can be turned on when plotting the weights.
# In CASA
os.system('rm -rf 7m_WT.png 12m_WT.png')
plotms(vis='m100_12m_CO.ms',yaxis='wt',xaxis='uvdist',spw='0~2:200',
coloraxis='spw',plotfile='12m_WT.png')
#
plotms(vis='m100_7m_CO.ms',yaxis='wt',xaxis='uvdist',spw='0~2:200',
coloraxis='spw',plotfile='7m_WT.png')
As you can see from these plots, the weights are quite similar at this stage because the data were taken under similar weather conditions and hence Tsys, and this is the only thing the weights have been scaled by so far.
Recall that the rms noise in a single channel for a single visibility is:
[math]\displaystyle{ \sigma_{ij}=\frac{2k}{A_{eff}} }[/math] [math]\displaystyle{ \sqrt{\frac{T_{sys,i} T_{sys,j}}{\Delta\nu_{ch} t_{ij}}} }[/math]
<figure id="Intcombo_0.193_WT.png">
</figure>
Beyond the obvious difference in the antenna dish sizes, looking at the listobs output for these two datasets, we see that the same channel width was used but that the integration time per visibility is 10.1 sec for the 7m-array and 6.05 sec for the 12m-array. Since dish area is in the numerator of the radiometer equation and integration time per visibility is in the denominator, and assuming WT propto 1/sigma2, the 7m weight should be scaled by: (7./12.)4 x (10.1/6.05) = 0.193 to account for the difference in telescope size and integration time per visibility.
An easy way to perform this overall scaling is using the visweightscale parameter in concat.
# In CASA
# Concat and scale weights
os.system('rm -rf M100_Intcombo_0.193.ms')
concat(vis=['m100_12m_CO.ms','m100_7m_CO.ms'],
concatvis='M100_Intcombo_0.193.ms',
visweightscale=[1,0.193])
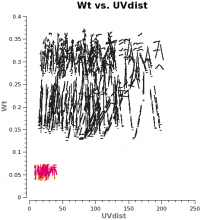
Now plot the concatenated weights to verify they are as expected.
# In CASA
os.system('rm -rf Intcombo_0.193_WT.png')
plotms(vis='M100_Intcombo_0.193.ms',yaxis='wt',xaxis='uvdist',spw='0~2:200',
coloraxis='spw',plotfile='Intcombo_0.193_WT.png')
These combined data with correct relative weights are now ready for imaging.