DataWeightsAndCombination: Difference between revisions
| Line 19: | Line 19: | ||
</math> | </math> | ||
where k is Boltzmann's constant, A<sub>eff</sub> is the effective antenna area, T<sub>sys,i</sub> is the system temperature for antenna i, Δν<sub>ch</sub> is the channel width, and t<sub>ij</sub> is the integration time per visibility. | where k is Boltzmann's constant, A<sub>eff</sub> is the effective antenna area and depends on the surface errors and antenna size, T<sub>sys,i</sub> is the system temperature for antenna i, Δν<sub>ch</sub> is the channel width, and t<sub>ij</sub> is the integration time per visibility. | ||
'''Thus, in order to combine data that have different T<sub>sys, Δν<sub>ch</sub>, t<sub>ij</sub>, or antenna size it is essential to use the correct data weights.''' | '''Thus, in order to combine data that have different T<sub>sys, Δν<sub>ch</sub>, t<sub>ij</sub>, or antenna size it is essential to use the correct data weights.''' | ||
Revision as of 11:48, 16 July 2015
This page is currently under construction.
Principles of Data Weighting
When combining data with disparate properties it is very important that the relative weights of each visibility be in the correct proportion to the other data according to the radiometer equation. Formally, the visibility weights should be proportional to 1/sigma2 where sigma is the variance or rms noise of a given visibility.
Assuming that the 7m and 12m antennas have similar aperture and quantization efficiencies (a reasonable assumption since they were designed this way), the rms noise in a single channel for a single visibility is:
[math]\displaystyle{ \sigma_{ij}=\frac{2k}{A_{eff}} }[/math] [math]\displaystyle{ \sqrt{\frac{T_{sys,i} T_{sys,j}}{\Delta\nu_{ch} t_{ij}}}, }[/math]
where k is Boltzmann's constant, Aeff is the effective antenna area and depends on the surface errors and antenna size, Tsys,i is the system temperature for antenna i, Δνch is the channel width, and tij is the integration time per visibility.
Thus, in order to combine data that have different Tsys, Δνch, tij, or antenna size it is essential to use the correct data weights.
Weights in CASA
A memo describing weights in CASA, in particular the significant changes that were made with CASA 4.2.2, can be found at http://casa.nrao.edu/Memos/CASA-data-weights.pdf
To summarize the situation specifically as applied to ALMA data reduction delivered to PIs:
- CASA 4.2.1 and earlier: Weights were only scaled by 1/[(Tsys(i) * Tsys(j)] using calwt=True at the applycal stage for Tsys table. Assuming that (1) there aren't any antennas with significant pointing errors (which causes low gain), (2) all the antennas have similar surface errors, and (3) antennas with very low gain have already been flagged -- usually good assumptions for ALMA data, data calibrated this way are (nearly) internally consistent and can produce good imaging results, but should not be combined with other data that have different Δνch, tij, or antenna size without further modification. An example of what you can do in this situation is given in XX.
- CASA 4.2.2 and later: Upon import data weights are scaled by 2ΔνchΔtij and also scaled by 1/[(Tsys(i) * Tsys(j)] using calwt=True at the applycal stage for Tsys table. Additionally:
- For data calibrated by the 4.2.2 CASA Pipeline the weights are further modified by [gain(i)2 * gain(j)2] when the amplitude gain table is applied using calwt=True. Since the amplitude gains are directly proportional to the individual antenna sensitivities, scaling the weights by the amplitude gains will take into account antenna size differences, and also down-weight antennas with comparatively low gain. Thus, these weights are completely correct.
- For data manually calibrated in CASA 4.2.2, unfortunately calwt=False was still used to apply the antenna gain table, thus, these data have weights that are not correct in a relative sense when compared to other data with different antenna size by the factor [gain(i)2 * gain(j)2].
- CASA 4.3 and later: Data calibrated in either the pipeline or manually will have completely correct weights. An example of this situation is demonstrated in https://casaguides.nrao.edu/index.php/M100_Band3_Combine_4.3
How Do I Know the Situation For My Data?
What Are the Options for Adjusting the Weights for Older Reductions?
Example of Correcting Weights from CASA 4.2.1 Data
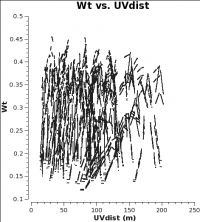
<figure id="7m_WT.png">
</figure>
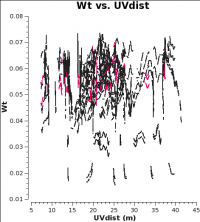
<figure id="12m_WT.png">
</figure>
In CASA 4.2.1 and earlier, the data weights are 1 upon import, later in the standard calibration procedure, applycal scales the weights by 1/[(Tsys(i) * Tsys(j)] if calwt=True for the Tsys table applycal. As an example, we plot the weights of 7m and 12m data imported in CASA 4.2.1. No averaging can be turned on when plotting the weights.
# In CASA
os.system('rm -rf 7m_WT.png 12m_WT.png')
plotms(vis='m100_12m_CO.ms',yaxis='wt',xaxis='uvdist',spw='0~2:200',
coloraxis='spw',plotfile='12m_WT.png')
#
plotms(vis='m100_7m_CO.ms',yaxis='wt',xaxis='uvdist',spw='0~2:200',
coloraxis='spw',plotfile='7m_WT.png')
As you can see from these plots, the weights are quite similar at this stage because the data were taken under similar weather conditions and hence Tsys. Additionally, for these data calwt=False was used to apply the antenna-based amplitude gains (see next section).
Assuming that the 7m and 12m antennas have similar apperture and quantization efficiencies (a reasonable assumption since they were designed this way), the rms noise in a single channel for a single visibility is:
[math]\displaystyle{ \sigma_{ij}=\frac{2k}{A_{eff}} }[/math] [math]\displaystyle{ \sqrt{\frac{T_{sys,i} T_{sys,j}}{\Delta\nu_{ch} t_{ij}}} }[/math]
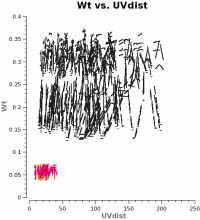
<figure id="Intcombo_0.193_WT.png">
</figure>
Where k is Boltzmann's constant, Aeff is the effective antenna area, Tsys,i is the system temperature for antenna i, Δνch is the channel width, and tij is the integration time per visibility.
The two key things that are different between the 7m and 12m-array data are that the effective dish Areas are different by (7/12)2 and the integration times are different by sqrt(10.1/6.05). Since dish area is in the numerator of the radiometer equation and integration time per visibility is in the denominator, and assuming WT propto 1/sigma2, the 7m weight should be scaled by: (7./12.)4 x (10.1/6.05) = 0.193 to account for the difference in telescope size and integration time per visibility.
# In CASA
# Concat and scale weights
os.system('rm -rf M100_Intcombo_0.193.ms')
concat(vis=['m100_12m_CO.ms','m100_7m_CO.ms'],
concatvis='M100_Intcombo_0.193.ms',
visweightscale=[1,0.193])
Now plot the concatenated weights to verify they are as expected.
# In CASA
os.system('rm -rf Intcombo_0.193_WT.png')
plotms(vis='M100_Intcombo_0.193.ms',yaxis='wt',xaxis='uvdist',spw='0~2:200',
coloraxis='spw',plotfile='Intcombo_0.193_WT.png')