EVLA Wide-Band Wide-Field Imaging: G55.7 3.4-CASA3.4-updated
- This CASA Guide is designed for CASA v3.4. If you are using an older version of CASA please see the same guide for CASA v3.3.
Overview
This CASA Guide describes the imaging of the supernova remnant G55.7+3.4.. The data were taken on August 23, 2010, in the first D-configuration for which the new wide-band capabilities of the WIDAR correlator were available. The 8-hour-long observation includes all available 1 GHz of bandwidth in L-band, from 1-2 GHz in frequency.
Obtaining the data
A copy of the data can be downloaded here: http://casa.nrao.edu/Data/EVLA/G55/G55.7+3.4_10s.ms.tar.gz
Note that this dataset is rather large: ~14GB
As a start, unzip and untar the data:
tar -xzvf G55.7+3.4_10s.ms.tar.gz
This will take a minute, but once it's complete, you will have a directory called G55.7+3.4_10s.ms which is the data. Online flags have been applied (which delete known bad data), some uninteresting scans removed, and the data time-averaged to 10 seconds. (The data were taken in D-configuration, where maximum baselines are 1 km, so one can safely average to 3s or even 10s to reduce data set size.) This is equivalent to what you would download from the archive if you requested time-averaging, scans 16~313, and online flag application.
You can also find the dataset in the NRAO archive. Note that it is 170 GB in raw form.
Averaging to 10 seconds and the removal of some scans which are not used in this tutorial reduces the size of the data set to around 14 GB; the addition of columns for model and corrected data (known as "scratch columns") inflates it to 43 GB, which is the size of the MS we will be using here.
Start and confirm your version of CASA
Start CASA by typing casapy on the command line. If you have not used CASA before, some helpful tips are available on the Getting Started in CASA page.
This guide has been written for CASA release 3.4.0. Please confirm your version before proceeding. Here's a little Python code that will do the check for you (note that you can also see the version number when CASA starts up; it's the first line that's printed):
# In CASA
version = casalog.version()
print "You are using " + version
if (int(version.split()[4][1:-1]) < 19915):
print "\033[91m YOUR VERSION OF CASA IS TOO OLD FOR THIS GUIDE."
print "\033[91m PLEASE UPDATE IT BEFORE PROCEEDING."
else:
print "Your version of CASA is appropriate for this guide."
Preliminary data evaluation
As a first step, use listobs to have a look at the MS:
# In CASA
listobs('G55.7+3.4_10s.ms')
Note that throughout this tutorial, we will run tasks using the task(parameter=value) syntax. When called in this manner, all parameters not explicitly set will use their default values.
The logger output will look like this:
##########################################
##### Begin Task: listobs #####
================================================================================
MeasurementSet Name: /scr2/casa/evla_G55/G55.7+3.4_10s.ms MS Version 2
================================================================================
Observer: Dr. Sanjay Sanjay Bhatnagar Project: T.B.D.
Observation: EVLA
Data records: 7343848 Total integration time = 26691.5 seconds
Observed from 23-Aug-2010/01:00:25.0 to 23-Aug-2010/08:25:16.5 (UTC)
ObservationID = 0 ArrayID = 0
Date Timerange (UTC) Scan FldId FieldName nRows Int(s) SpwIds ScanIntent
23-Aug-2010/01:00:25.0 - 01:01:00.5 16 1 J1925+2106 8008 7.79 [0, 1, 2, 3, 4, 5, 6, 7] CALIBRATE_PHASE.UNSPECIFIED
01:01:10.0 - 01:02:30.0 17 1 J1925+2106 25272 10 [0, 1, 2, 3, 4, 5, 6, 7] CALIBRATE_PHASE.UNSPECIFIED
01:02:40.0 - 01:04:00.0 18 1 J1925+2106 25272 10 [0, 1, 2, 3, 4, 5, 6, 7] CALIBRATE_PHASE.UNSPECIFIED
01:04:10.0 - 01:05:29.5 19 1 J1925+2106 25272 9.89 [0, 1, 2, 3, 4, 5, 6, 7] CALIBRATE_PHASE.UNSPECIFIED
01:05:39.0 - 01:06:59.0 20 1 J1925+2106 25272 9.89 [0, 1, 2, 3, 4, 5, 6, 7] CALIBRATE_PHASE.UNSPECIFIED
01:07:12.0 - 01:08:29.0 21 2 G55.7+3.4 25064 9.33 [0, 1, 2, 3, 4, 5, 6, 7] OBSERVE_TARGET.UNSPECIFIED
01:08:39.0 - 01:09:59.0 22 2 G55.7+3.4 25272 10 [0, 1, 2, 3, 4, 5, 6, 7] OBSERVE_TARGET.UNSPECIFIED
01:10:09.0 - 01:11:29.0 23 2 G55.7+3.4 25272 10 [0, 1, 2, 3, 4, 5, 6, 7] OBSERVE_TARGET.UNSPECIFIED
01:11:39.0 - 01:12:58.5 24 2 G55.7+3.4 25272 9.89 [0, 1, 2, 3, 4, 5, 6, 7] OBSERVE_TARGET.UNSPECIFIED
01:13:08.0 - 01:14:28.0 25 2 G55.7+3.4 25272 10 [0, 1, 2, 3, 4, 5, 6, 7] OBSERVE_TARGET.UNSPECIFIED
01:14:38.0 - 01:15:58.0 26 2 G55.7+3.4 25272 10 [0, 1, 2, 3, 4, 5, 6, 7] OBSERVE_TARGET.UNSPECIFIED
01:16:08.0 - 01:17:28.0 27 2 G55.7+3.4 25272 10 [0, 1, 2, 3, 4, 5, 6, 7] OBSERVE_TARGET.UNSPECIFIED
01:17:38.0 - 01:18:57.5 28 2 G55.7+3.4 25272 9.89 [0, 1, 2, 3, 4, 5, 6, 7] OBSERVE_TARGET.UNSPECIFIED
01:19:07.0 - 01:20:27.0 29 2 G55.7+3.4 25272 10 [0, 1, 2, 3, 4, 5, 6, 7] OBSERVE_TARGET.UNSPECIFIED
01:20:37.0 - 01:21:57.0 30 2 G55.7+3.4 25272 10 [0, 1, 2, 3, 4, 5, 6, 7] OBSERVE_TARGET.UNSPECIFIED
<snip>
08:04:31.0 - 08:05:50.5 300 2 G55.7+3.4 25272 9.89 [0, 1, 2, 3, 4, 5, 6, 7] OBSERVE_TARGET.UNSPECIFIED
08:06:00.0 - 08:07:20.0 301 2 G55.7+3.4 25272 10 [0, 1, 2, 3, 4, 5, 6, 7] OBSERVE_TARGET.UNSPECIFIED
08:07:30.0 - 08:08:50.0 302 2 G55.7+3.4 25272 10 [0, 1, 2, 3, 4, 5, 6, 7] OBSERVE_TARGET.UNSPECIFIED
08:09:00.0 - 08:10:20.0 303 2 G55.7+3.4 25272 10 [0, 1, 2, 3, 4, 5, 6, 7] OBSERVE_TARGET.UNSPECIFIED
08:10:30.0 - 08:11:49.5 304 2 G55.7+3.4 25272 9.89 [0, 1, 2, 3, 4, 5, 6, 7] OBSERVE_TARGET.UNSPECIFIED
08:11:59.0 - 08:13:19.0 305 2 G55.7+3.4 25272 10 [0, 1, 2, 3, 4, 5, 6, 7] OBSERVE_TARGET.UNSPECIFIED
08:13:29.0 - 08:14:48.5 306 2 G55.7+3.4 25272 9.89 [0, 1, 2, 3, 4, 5, 6, 7] OBSERVE_TARGET.UNSPECIFIED
08:17:50.5 - 08:17:50.5 308 3 0542+498=3C147 80 4 [0, 1, 2, 3, 4, 5, 6, 7] CALIBRATE_AMPLI.UNSPECIFIED,UNSPECIFIED.UNSPECIFIED,CALIBRATE_BANDPASS.UNSPECIFIED
08:17:59.0 - 08:19:18.5 309 3 0542+498=3C147 17152 9.36 [0, 1, 2, 3, 4, 5, 6, 7] CALIBRATE_AMPLI.UNSPECIFIED,UNSPECIFIED.UNSPECIFIED,CALIBRATE_BANDPASS.UNSPECIFIED
08:19:28.0 - 08:20:48.0 310 3 0542+498=3C147 18216 10 [0, 1, 2, 3, 4, 5, 6, 7] CALIBRATE_AMPLI.UNSPECIFIED,UNSPECIFIED.UNSPECIFIED,CALIBRATE_BANDPASS.UNSPECIFIED
08:20:58.0 - 08:22:18.0 311 3 0542+498=3C147 18216 10 [0, 1, 2, 3, 4, 5, 6, 7] CALIBRATE_AMPLI.UNSPECIFIED,UNSPECIFIED.UNSPECIFIED,CALIBRATE_BANDPASS.UNSPECIFIED
08:22:28.0 - 08:23:47.5 312 3 0542+498=3C147 18216 9.89 [0, 1, 2, 3, 4, 5, 6, 7] CALIBRATE_AMPLI.UNSPECIFIED,UNSPECIFIED.UNSPECIFIED,CALIBRATE_BANDPASS.UNSPECIFIED
08:23:57.0 - 08:25:16.5 313 3 0542+498=3C147 18216 9.89 [0, 1, 2, 3, 4, 5, 6, 7] CALIBRATE_AMPLI.UNSPECIFIED,UNSPECIFIED.UNSPECIFIED,CALIBRATE_BANDPASS.UNSPECIFIED
(nVis = Total number of time/baseline visibilities per scan)
Fields: 3
ID Code Name RA Decl Epoch SrcId nVis
1 D J1925+2106 19:25:59.60537 +21.06.26.1622 J2000 1 1004816
2 NONE G55.7+3.4 19:21:40.00000 +21.45.00.0000 J2000 2 6248936
3 N 0542+498=3C147 05:42:36.13792 +49.51.07.2336 J2000 3 90096
(nVis = Total number of time/baseline visibilities per field)
Spectral Windows: (8 unique spectral windows and 1 unique polarization setups)
SpwID #Chans Frame Ch1(MHz) ChanWid(kHz) TotBW(kHz) Corrs
0 64 TOPO 1000 2000 128000 RR RL LR LL
1 64 TOPO 1128 2000 128000 RR RL LR LL
2 64 TOPO 1256 2000 128000 RR RL LR LL
3 64 TOPO 1384 2000 128000 RR RL LR LL
4 64 TOPO 1520 2000 128000 RR RL LR LL
5 64 TOPO 1648 2000 128000 RR RL LR LL
6 64 TOPO 1776 2000 128000 RR RL LR LL
7 64 TOPO 1904 2000 128000 RR RL LR LL
Sources: 24
ID Name SpwId RestFreq(MHz) SysVel(km/s)
1 J1925+2106 0 - -
1 J1925+2106 1 - -
1 J1925+2106 2 - -
1 J1925+2106 3 - -
1 J1925+2106 4 - -
1 J1925+2106 5 - -
1 J1925+2106 6 - -
1 J1925+2106 7 - -
2 G55.7+3.4 0 - -
2 G55.7+3.4 1 - -
2 G55.7+3.4 2 - -
2 G55.7+3.4 3 - -
2 G55.7+3.4 4 - -
2 G55.7+3.4 5 - -
2 G55.7+3.4 6 - -
2 G55.7+3.4 7 - -
3 0542+498=3C147 0 - -
3 0542+498=3C147 1 - -
3 0542+498=3C147 2 - -
3 0542+498=3C147 3 - -
3 0542+498=3C147 4 - -
3 0542+498=3C147 5 - -
3 0542+498=3C147 6 - -
3 0542+498=3C147 7 - -
Antennas: 27:
ID Name Station Diam. Long. Lat.
0 ea01 W09 25.0 m -107.37.25.2 +33.53.51.0
1 ea02 E02 25.0 m -107.37.04.4 +33.54.01.1
2 ea03 E09 25.0 m -107.36.45.1 +33.53.53.6
3 ea04 W01 25.0 m -107.37.05.9 +33.54.00.5
4 ea05 W08 25.0 m -107.37.21.6 +33.53.53.0
5 ea06 N06 25.0 m -107.37.06.9 +33.54.10.3
6 ea07 E05 25.0 m -107.36.58.4 +33.53.58.8
7 ea08 N01 25.0 m -107.37.06.0 +33.54.01.8
8 ea09 E06 25.0 m -107.36.55.6 +33.53.57.7
9 ea10 N03 25.0 m -107.37.06.3 +33.54.04.8
10 ea11 E04 25.0 m -107.37.00.8 +33.53.59.7
11 ea12 E08 25.0 m -107.36.48.9 +33.53.55.1
12 ea13 N07 25.0 m -107.37.07.2 +33.54.12.9
13 ea15 W06 25.0 m -107.37.15.6 +33.53.56.4
14 ea16 W02 25.0 m -107.37.07.5 +33.54.00.9
15 ea17 W07 25.0 m -107.37.18.4 +33.53.54.8
16 ea18 N09 25.0 m -107.37.07.8 +33.54.19.0
17 ea19 W04 25.0 m -107.37.10.8 +33.53.59.1
18 ea20 N05 25.0 m -107.37.06.7 +33.54.08.0
19 ea21 E01 25.0 m -107.37.05.7 +33.53.59.2
20 ea22 N04 25.0 m -107.37.06.5 +33.54.06.1
21 ea23 E07 25.0 m -107.36.52.4 +33.53.56.5
22 ea24 W05 25.0 m -107.37.13.0 +33.53.57.8
23 ea25 N02 25.0 m -107.37.06.2 +33.54.03.5
24 ea26 W03 25.0 m -107.37.08.9 +33.54.00.1
25 ea27 E03 25.0 m -107.37.02.8 +33.54.00.5
26 ea28 N08 25.0 m -107.37.07.5 +33.54.15.8
##### End Task: listobs #####
##########################################
We can see that there are three sources in this observation:
- J1925+2106, field ID 1: the phase calibrator;
- G55.7+3.4, field ID 2: the supernova remnant;
- 0542+498=3C147, field ID 3: the flux and bandpass calibrator.
We can also see that these sources have associated "scan intents", which indicate their function in the observation, and may be selected on using CASA tasks. In particular,
- CALIBRATE_PHASE indicates that this is a scan to be used for gain calibration;
- OBSERVE_TARGET indicates that this is the science target;
- CALIBRATE_AMPLI indicates that this is to be used for flux calibration; and
- CALIBRATE_BANDPASS indicates that these scans are to be used for bandpass calibration.
Note that 3C147 is to be used for both flux and bandpass calibration.
We can see the antenna configuration for this observation using plotants:
# In CASA
plotants('G55.7+3.4_10s.ms')
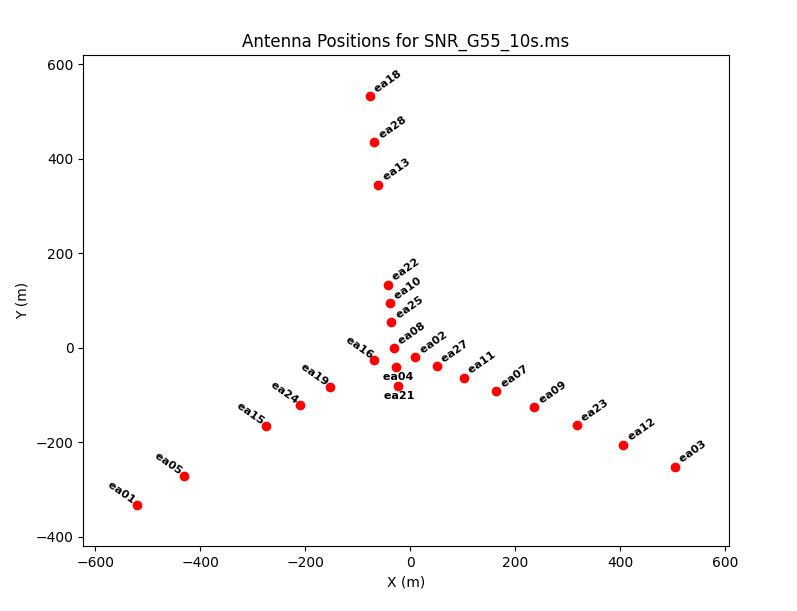
This shows that antennas ea01, ea18, and ea03 were on the extreme ends of the west, north, and east arms, respectively. The antenna position diagram is particularly useful in determining if a co-located set of antennas is affected, which can help with flagging.
We may also inspect the raw data using plotms. To start with, let's look at a subset of scans on the supernova remnant:
# In CASA
plotms(vis='G55.7+3.4_10s.ms', scan='30,75,120,165,190,235,303',
antenna='ea24', xaxis='freq', yaxis='amp', coloraxis='spw',
iteraxis='scan', correlation='rr,ll')
The coloraxis parameter indicates that a different color will be assigned to each spectral window, and the iteraxis parameter tells plotms to display a new plot for each scan. We have chosen only one antenna (ea24) and just the right and left circular polarizations (without the cross-hand terms) to reduce the amount of data in the selection, One can flip through these plots using the green arrows located at the bottom of the plotting gui: the double-left arrow will display the very first plot in the set, the single left arrow will go back one plot, and the right arrows have similar behavior for moving forward in the set.
Flipping through the scans, it's clear that there is significant time- and frequency-variable RFI present in this observation. Since this is L-band data taken in the most compact EVLA configuration ("D"), this comes as no surprise. However, it also poses one of the greatest challenges for obtaining a good image.
In particular, we can see that two spectral windows (SPWs) are quite badly affected. To determine which these are, click in the "Mark Regions" tool at the bottom of the gui (the open box with a green "plus" sign), and use the mouse to select a few of the highest-amplitude points in each of these SPWs. Click on the "Locate" button (magnifying glass), and information associated with the selected points will be displayed in the logger window:
Frequency in [1.23 1.25833] or [1.58167 1.62833], Amp in [23.0201 25.6823] or [59.5078 62.6398]: Scan=30 Field=G55.7+3.4[2] Time=2010/08/23/01:20:57.0 BL=ea03&ea24[2&22] Spw=1 Chan=59 Freq=1.246 Corr=RR X=1.246 Y=23.032 (73964/11/748) Scan=30 Field=G55.7+3.4[2] Time=2010/08/23/01:20:57.0 BL=ea12&ea24[11&22] Spw=1 Chan=59 Freq=1.246 Corr=RR X=1.246 Y=23.5243 (76268/11/3052) Scan=30 Field=G55.7+3.4[2] Time=2010/08/23/01:21:07.0 BL=ea03&ea24[2&22] Spw=1 Chan=59 Freq=1.246 Corr=RR X=1.246 Y=23.6116 (80620/12/748) Scan=30 Field=G55.7+3.4[2] Time=2010/08/23/01:21:07.0 BL=ea12&ea24[11&22] Spw=1 Chan=59 Freq=1.246 Corr=RR X=1.246 Y=23.4432 (82924/12/3052) Scan=30 Field=G55.7+3.4[2] Time=2010/08/23/01:21:17.0 BL=ea03&ea24[2&22] Spw=1 Chan=59 Freq=1.246 Corr=RR X=1.246 Y=23.1712 (87276/13/748) Scan=30 Field=G55.7+3.4[2] Time=2010/08/23/01:21:37.0 BL=ea03&ea24[2&22] Spw=1 Chan=59 Freq=1.246 Corr=LR X=1.246 Y=23.2663 (100590/15/750) Scan=30 Field=G55.7+3.4[2] Time=2010/08/23/01:21:47.0 BL=ea03&ea24[2&22] Spw=1 Chan=59 Freq=1.246 Corr=LR X=1.246 Y=23.4466 (107246/16/750) Scan=30 Field=G55.7+3.4[2] Time=2010/08/23/01:21:57.0 BL=ea03&ea24[2&22] Spw=1 Chan=59 Freq=1.246 Corr=RR X=1.246 Y=23.7536 (113900/17/748) Scan=30 Field=G55.7+3.4[2] Time=2010/08/23/01:21:07.0 BL=ea12&ea24[11&22] Spw=4 Chan=41 Freq=1.602 Corr=RR X=1.602 Y=61.9097 (262564/39/2980) Scan=30 Field=G55.7+3.4[2] Time=2010/08/23/01:21:17.0 BL=ea12&ea24[11&22] Spw=4 Chan=41 Freq=1.602 Corr=RR X=1.602 Y=61.1769 (269220/40/2980) Scan=30 Field=G55.7+3.4[2] Time=2010/08/23/01:21:27.0 BL=ea12&ea24[11&22] Spw=4 Chan=41 Freq=1.602 Corr=RR X=1.602 Y=60.1834 (275876/41/2980) Found 11 points (11 unflagged) among 479232 in 0.04s.
We can see that SPWs 1 and 4 are among the worst affected by RFI. At this point, feel free to play around a bit more with plotms; you might try experimenting with different axes for iteration (under the "Iter" left-hand tab), different data selection parameters (under "Data"), different axes ("Axes"), or different averaging techniques (under "Data").
A priori calibration and flagging
Before we proceed with further processing, we should check the observation log to see if there were any issues noted during the run that need to be addressed. The observing log file is linked to the archive web page for this observation (at far right; under "logs etc."). Looking at the log, we can see that antenna ea07 may need a position correction, and antennas ea06, ea17, ea20, and ea26 did not have L-band receivers installed at the time and should be flagged.
Antenna position correction
Correcting the position of an antenna is done with the task gencal. This is important, because the observed visibilities are a function of [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math]. If an antenna's position is incorrect, then [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math] will be calculated incorrectly, and there will be errors in any image derived from the data.
Any corrections can be ascertained from the EVLA/VLA Baseline Corrections site. For future reference, be sure to read to the bottom of that document to see how to calculate the additive corrections. Fortunately, the current case is simple as there is only a single correction for antenna ea07.
To find the necessary x, y, and z-offsets to perform the position correction, first select the year "2010" for the EVLA baseline corrections. From the log, we know that the observation was performed on 23 August 2010; looking at the position table, we can see that antenna ea07 was moved on 5 August, but that the updated position was not included in the online system's database until 15 September. Therefore, we need to record the x, y, and z-position information for this antenna and input it into gencal to create a position-correction calibration table:
# In CASA
gencal(vis='G55.7+3.4_10s.ms', caltable='G55.7+3.4_10s.pos',
caltype='antpos', antenna='ea07',
parameter=[0.0087, 0.0137, 0.0000])
We will carry this table throughout the calibration to account for the revised antenna position for ea07.
Gain curve and opacity correction
A decision has been made here to ignore both the corrections for atmospheric opacity and for the elevation-dependent telescope gain throughout this tutorial (opacity=[], gaincurve=False in tasks such as gaincal, bandpass, and applycal). These effects are very small (less than or about 1%) across the frequency range of this observation (1-2 GHz).
Flagging non-operational antennas
In addition to updating the position for antenna ea07, we have to flag antennas ea06, ea17, ea20, and ea26, since these did not have working L-band receivers at the time of observation. We do this with the task flagdata:
# In CASA
flagdata(vis='G55.7+3.4_10s.ms', mode='manualflag',
antenna='ea06,ea17,ea20,ea26')
Note that the first thing flagdata does is create a backup flag file, in this case named "manualflag_1". This flag file contains a copy of the flags present in the MS prior to the requested flagging operation, and can be found inside the <MS_name>.flagversions directory, along with any other backed up flag files. Since these flag files take up a fair amount of space (in this particular case, 230 MB), we won't me making them every time we run flagdata -- the automatic flag backup can be turned off by setting flagbackup=False. However, it's good to keep a record of the names of the backup files and the associated processing step, in case you wish to restore a previous version of the flags.
Flagging shadowed antennas and zero-amplitude data
Since this is the most compact EVLA configuration, there may be instances where one antenna blocks, or "shadows" another. Therefore, we will run flagdata to remove these data:
# In CASA
flagdata(vis='G55.7+3.4_10s.ms', mode='shadow',
flagbackup=False)
In this particular observation, there appears not to be any data affected by shadowing, as can be seen in the logger report.
In addition, there may be times during which the correlator writes out pure zero-valued data. In order to remove this bad data, we run flagdata to clip against the data values:
# In CASA
flagdata(vis='G55.7+3.4_10s.ms', mode='manualflag',
clipminmax=[0.0, 1E-10], flagbackup=False,
clipoutside=False, clipcolumn='DATA',
clipexpr=['ABS RR','ABS LL','ABS RL','ABS LR'])
- clipminmax=[0.0, 1E-10]: this is the clip range to be used. Since we cannot give it [0.0, 0.0], the second value is extremely low to pick up only zero-valued data.
- clipoutside=False: tells flagdata which data to flag; in this case; we wish to flag inside the specified data range.
- clipcolumn='DATA': the column on which to flag.
- clipexpr=['ABS RR','ABS LL','ABS RL','ABS LR']: flag any correlation which is zero-valued.
Inspecting the logger output which is generated by flagdata shows that there is a very small quantity of zero-valued data present in this MS.
Note that the archive will automatically flag shadowed antennas as well as zero-valued data, if you request that online flags are applied.
Automatic RFI excision
Now, we move on to one of the most difficult parts of L-band, D-configuration data processing: excising the RFI. For the original reduction of this MS, flagging was done by hand and took several weeks. The resulting data are offered as an option for the imaging stage of this tutorial (because careful by-hand flagging does yield a better image); however, it's not practical to undertake this endeavor for the present workshop.
Therefore, we will demonstrate the use of the automatic RFI excision task, testautoflag, currently available in CASA. It should be noted that this task is under development, and we expect changes and improvements to be made at a rapid pace over the course of the next year or so.
Hanning-smoothing data
Prior to flagging any data which is affect by strong RFI, one should Hanning-smooth over channel to remove Gibbs ringing. This is done with the task hanningsmooth, which can either write a new, Hanning-smoothed MS or directly operate on the requested column of the input MS. To conserve space, we will request the latter. Note that if you wish to make your own "before" and "after" plots, you should make the first prior to running hanningsmooth, since you will be overwriting the non-Hanning-smoothed data in the process -- and this is not reversible.
# In CASA
os.system('rm amp_v_freq.beforeHanning.png')
plotms(vis='G55.7+3.4_10s.ms', scan='30', antenna='ea24', spw='0~2',
xaxis='freq', yaxis='amp', coloraxis='spw',
correlation='rr,ll', plotrange=[1.0,1.27,-0.3,2.5],
plotfile='amp_v_freq.beforeHanning.png')
hanningsmooth(vis='G55.7+3.4_10s.ms', datacolumn='data')
os.system('rm amp_v_freq.afterHanning.png')
plotms(vis='G55.7+3.4_10s.ms', scan='30', antenna='ea24', spw='0~3',
xaxis='freq', yaxis='amp', coloraxis='spw',
correlation='rr,ll', plotrange=[1.0,1.27,-0.3,2.5],
plotfile='amp_v_freq.afterHanning.png')
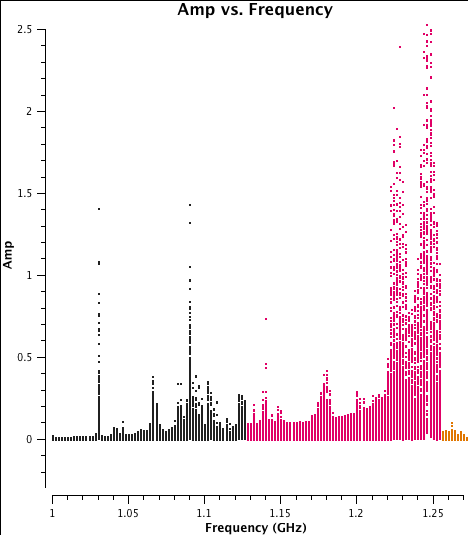
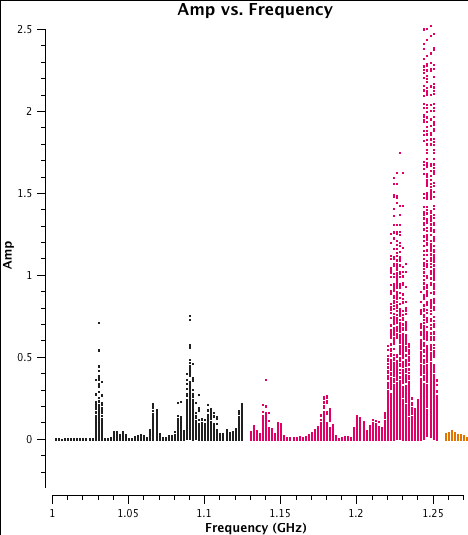
Task hanningsmooth will take a few minutes to run. Note that the 2nd plotms command above contains a trivial change in the spw selection (trivial because the 4th spw is outside of the specified plotrange). This forces plotms to reload the plot since by default, plotms will not redraw a plot if the input parameters are unchanged. In this case, since the data column was changed between calls to plotms a redraw is necessary. When using the GUI, you can simply check "force reload" in the bottom left corner of the side bar before clicking "Plot".
We can compare the Hanning-smoothed data with the raw data by plotting a subset of data to show the result of Hanning-smoothing (see plots to the left and right). As you can see, the smoothing has spread the single-channel RFI into three channels, but has also removed the effects of some of the worst RFI from a number of channels. Overall, this will improve our ability to flag RFI from the data and retain as much good data as possible.
Clearcal
We want to create the MODEL_DATA and CORRECTED_DATA (also known as the "scratch") columns, which we will do using clearcal:
# In CASA
clearcal(vis='G55.7+3.4_10s.ms')
This will also take a few minutes to run, since it will be writing approximately 22 GB back to disk.
Using phase calibration source for preliminary bandpass calibration
In order to get the best possible result from the automatic RFI excision, we will first apply bandpass calibration to the MS. Since the RFI is time-variable, using the phase calibration source to make an average bandpass over the entire observation will mitigate the amount of RFI present in the calculated bandpass. (For the final calibration, we will use the designated bandpass source 3C147; however, since this object was only observed in the last set of scans, it doesn't sample the time variability and would not provide a good average bandpass.)
Since there are likely to be gain variations over the course of the observation, we will run gaincal to solve for an initial set of antenna-based phases over a narrow range of channels. These will be used to create the bandpass solutions. While amplitude variations will have little effect on the bandpass solutions, it is important to solve for these phase variations with sufficient time resolution to prevent decorrelation when vector averaging the data in computing the bandpass solutions.
In order to choose a narrow range of channels for each spectral window which are relatively RFI-free over the course of the observation, we can look at the data with plotms. Note that it's important to only solve for phase using a narrow channel range, since an antenna-specific delay will cause the phase to vary with respect to frequency over the spectral window, perhaps by a substantial amount.
# In CASA
plotms(vis='G55.7+3.4_10s.ms', scan='30,75,120,165,190,235,303',
antenna='ea24', xaxis='channel', yaxis='amp', iteraxis='spw',
yselfscale=True, correlation='rr,ll')
- yselfscale=True: sets the y-scaling to be for the currently displayed spectral window, since some spectral windows have much worse RFI and will skew the scale for others.
Looking at these plots, we can choose appropriate channel ranges for each SPW:
SPW 0: 10-13 SPW 1: 30-33 SPW 2: 32-35 SPW 3: 30-33 SPW 4: 35-38 SPW 5: 30-33 SPW 6: 30-33 SPW 7: 46-49
Using these channel ranges, we run gaincal to perform phase-only solutions over the course of the observation:
# In CASA
gaincal(vis='G55.7+3.4_10s.ms', caltable='G55.7+3.4_10s.initPh',
intent='CALIBRATE_PHASE*', solint='int',
spw='0:10~13,1;3;5~6:30~33,2:32~35,4:35~38,7:46~49',
refant='ea24', minblperant=3,
minsnr=3.0, calmode='p', gaintable='G55.7+3.4_10s.pos')
- caltable='G55.7+3.4_10s.initPh': this is the output calibration table that will be written.
- intent='CALIBRATE_PHASE*': this is the way we have chosen to select data. Alternatively, we could have used "field='J1925+2106'", since this is the only source with the CALIBRATE_PHASE* scan intent. Note the use of the wildcard character "*" at the end of the string; this accounts for the fact that all the intents end with ".UNSPECIFIED". We could just as well have used "*PHASE*".
- solint='int': we request a solution for each 10-second integration.
- spw='0:10~13,1;3;5~6:30~33,2:32~35,4:35~38,7:46~49': note the syntax of this selection: a ":" is used to separate the SPW from channel selection, ";" is used to separate within this selection, and "~" is used to indicate an inclusive range.
- refant='ea24': we have chosen ea24 as the reference antenna after inspecting the antenna position diagram (see above). It is relatively close to, but not directly in, the center of the array, which could be important in D-configuration, since you don't want the reference antenna to have a high probability of being shadowed by nearby antennas.
- minblperant=3: the minimum number of baselines which must be present to attempt a phase solution.
- minsnr=3.0: the minimum signal-to-noise a solution must have to be considered acceptable. Note that solutions which fail this test will cause these data to be flagged downstream of this calibration step.
- calmode='p': perform phase-only solutions.
- gaintable='G55.7+3.4_10s.pos': use the antenna position correction for ea07 that we created earlier.
Note that a number of solutions do not pass the requirements of the minimum 3 baselines (generating the terminal message "Insufficient unflagged antennas to proceed with this solve.") or minimum signal-to-noise ratio (outputting "n of x solutions rejected due to SNR < 3 ..."). A particularly large number of solutions are rejected in SPW 4, where the RFI is most severe.
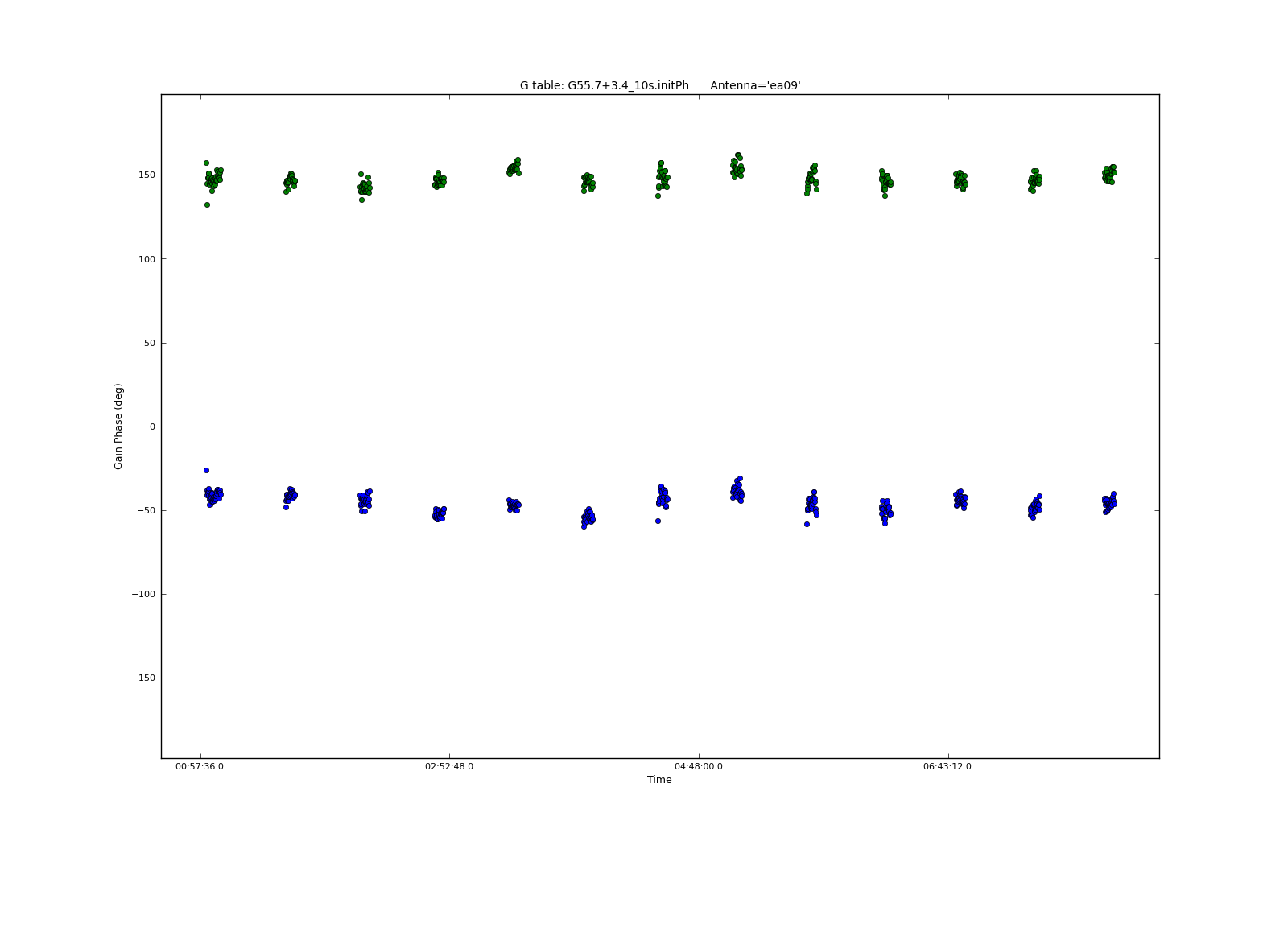
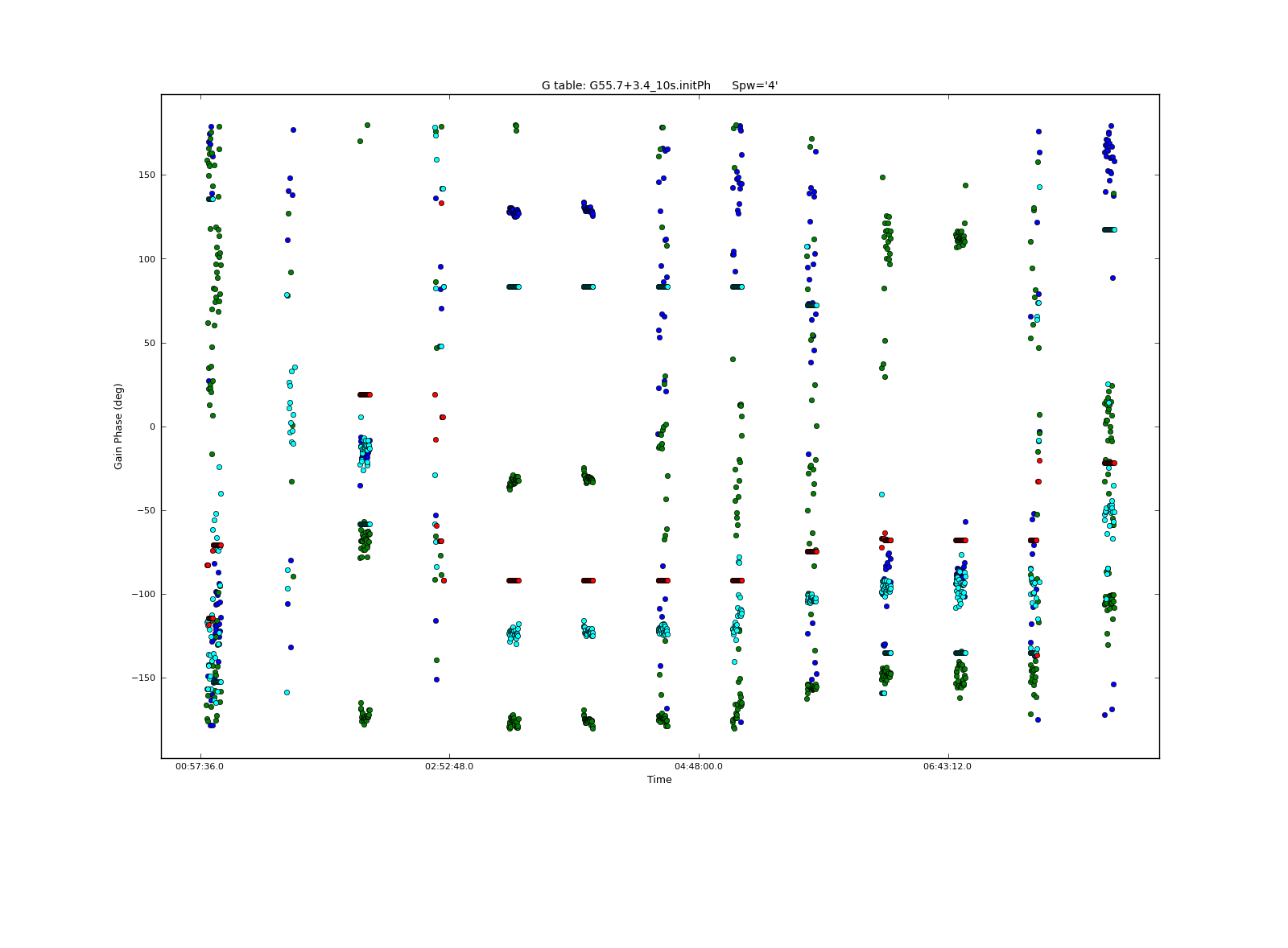
We can inspect the resulting calibration table with plotcal:
# In CASA
plotcal(caltable='G55.7+3.4_10s.initPh', xaxis='time', yaxis='phase',
iteration='antenna', spw='0', plotrange=[-1,-1,-180,180])
This iterates over antenna for a single spectral window; we can see that the phase does not change much over the course of the observation for SPW 0. We may also iterate over spectral window for a subset of antennas:
# In CASA
plotcal(caltable='G55.7+3.4_10s.initPh', xaxis='time', yaxis='phase',
iteration='spw', antenna='ea01,ea05,ea24', plotrange=[-1,-1,-180,180])
Clearly, the phases are affected by RFI in some places, especially in SPW 4.
Using this phase information, we create time-averaged bandpass solutions for the phase calibration source:
# In CASA
bandpass(vis='G55.7+3.4_10s.ms', caltable='G55.7+3.4_10s.initBP',
intent='CALIBRATE_PHASE*', solint='inf',
combine='scan', refant='ea24', minblperant=3, minsnr=10.0,
gaintable=['G55.7+3.4_10s.pos', 'G55.7+3.4_10s.initPh'],
interp=['', 'nearest'], solnorm=False)
- solint='inf', combine='scan': the solution interval of 'inf' will automatically break by scans; this requests that the solution intervals be combined over scans, so that we will get one solution per antenna.
- gaintable=['G55.7+3.4_10s.pos', 'G55.7+3.4_10s.initPh']: we will pre-apply both the corrected antenna position as well as the initial phase solutions.
- interp=['', 'nearest']: by default, gaincal will use linear interpolation for pre-applied calibration. However, we want the nearest phase solution to be used for a given time.
Again, we can see that a number of solutions have been rejected by our choices of minblperant and minsnr.
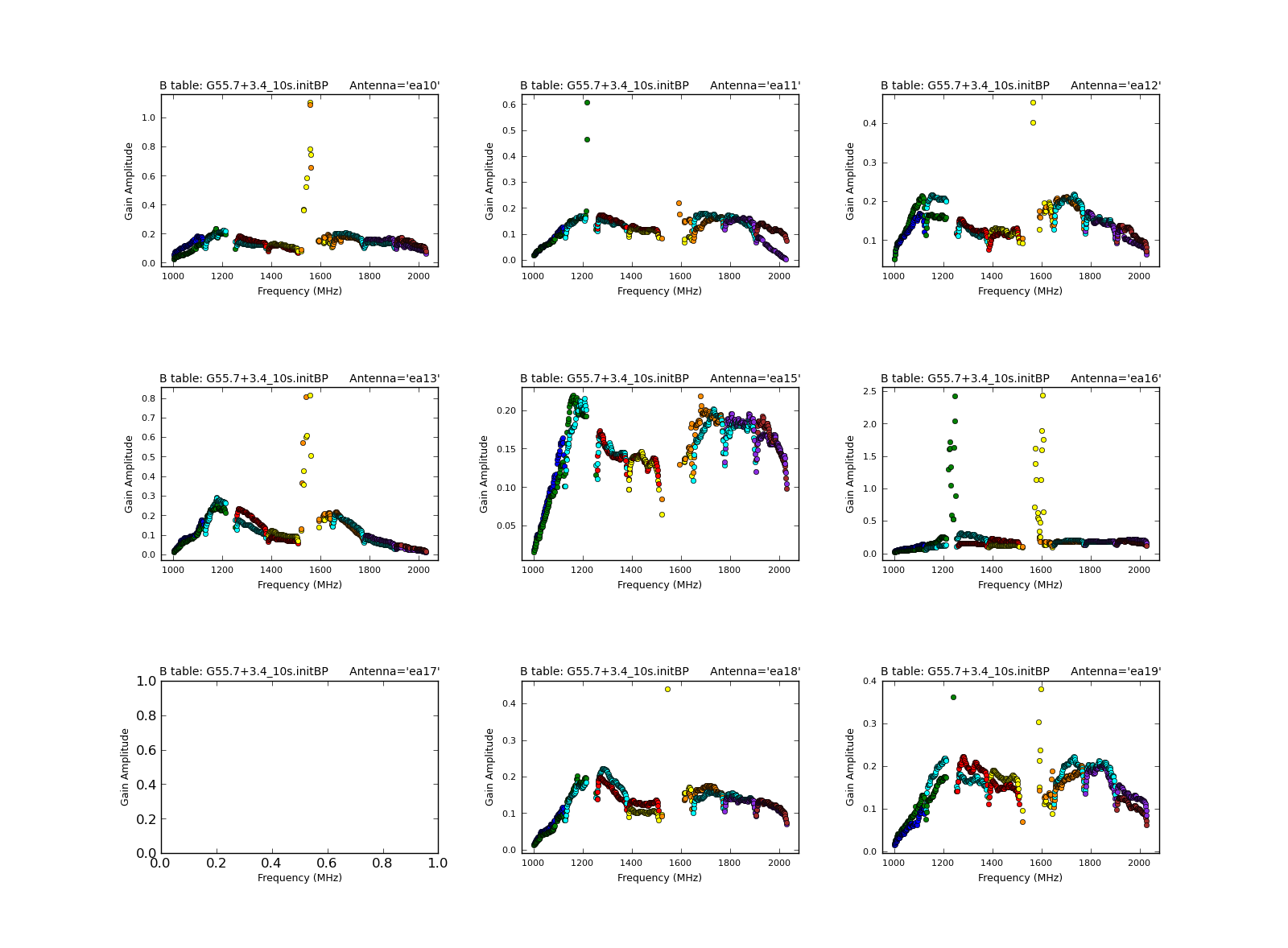
We may plot the bandpasses with plotcal; first looking at the amplitudes:
# In CASA
plotcal(caltable='G55.7+3.4_10s.initBP', xaxis='freq', yaxis='amp',
iteration='antenna', subplot=331)
- subplot=331: displays 3x3 plots per screen
Also, we can look at the phase solutions:
# In CASA
plotcal(caltable='G55.7+3.4_10s.initBP', xaxis='freq', yaxis='phase',
iteration='antenna', subplot=331)
We can see that SPW 4 is virtually wiped out by RFI; furthermore, there are channels in SPW 1 that are consistently badly affected. Prior to running testautoflag, we will flag these manually. In addition, we will flag the first 9 channels in SPW 0, since this is affected by an issue which causes the noise to be substantially higher:
# In CASA
flagdata(vis='G55.7+3.4_10s.ms', mode='manualflag', spw='0:0~8,1:41~63,4')
Note that this has created a backup flag file called "manualflag_2". Now we apply the antenna position correction and this bandpass calibration to the data:
# In CASA
applycal(vis='G55.7+3.4_10s.ms',
gaintable=['G55.7+3.4_10s.pos', 'G55.7+3.4_10s.initBP'],
calwt=False)
This operation will flag data that correspond to flagged solutions, so applycal makes a backup version of the flags prior to operating on the data -- in this case, it's called "before_applycal_1". Note that running applycal might take a little while, likely around 10 minutes.
To see the corrected data, we can plot the data as we did before, choosing "ydatacolumn='corrected'" this time:
# In CASA
plotms(vis='G55.7+3.4_10s.ms', scan='30,75,120,165,190,235,303',
antenna='ea24', xaxis='freq', yaxis='amp', coloraxis='spw',
iteraxis='scan', ydatacolumn='corrected')
Note that some of the worst RFI is no longer there; also note that the amplitude scale has changed, since the bandpass solutions include amplitude scaling.
Running testautoflag
Now that we have bandpass-corrected data with some of the worst RFI flagged out, we will run testautoflag. Note that there are many parameters which may be modified:
# In CASA
default testautoflag
inp
---------> inp(testautoflag)
# testautoflag :: Task for automatic identification and flagging of RFI
vis = '' # Name of measurement set
field = '' # Field names or field index numbers: ''==>all, field='0~2,3C286'
spw = '' # spectral-window/frequency/channel
selectdata = False # Other data selection parameters (antenna, timerange etc)
datacolumn = 'data' # Data column on which to operate (data,corrected,model,residual)
ntime = 100 # Time-range (seconds) to use for each chunk
corrs = [] # list of ones/zeros to choose correlations (e.g. [1,0,0,1]). Default(all)
tfcrop = True # Automatic identification and flagging of narrow-band RFI
timecutoff = 4.0 # Flagging thresholds in units of deviation from the fit
freqcutoff = 3.0 # Flagging thresholds in units of deviation from the fit
timefit = 'line' # Fitting function for the time direction (poly/line)
freqfit = 'poly' # Fitting function for the frequency direction (poly/line)
maxnpieces = 7 # Number of pieces in the polynomial-fits (for 'freqfit' or 'timefit' = 'poly')
flagdimension = 'freqtime' # Dimensions along which to calculate fits (freq/time/freqtime/timefreq)
usewindowstats = 'none' # Calculate additional flags using sliding window statistics (none,sum,std,both)
halfwin = 1 # Half-width of sliding window to use with 'usewindowstats' (1,2,3).
extendflags = True # Extend flags in various ways
extendpols = False # If any correlation is flagged, flag all correlations
growtime = 50.0 # Flag all 'ntime' integrations if more than X% of the timerange is flagged (0-100)
growfreq = 50.0 # Flag all selected channels if more than X% of the frequency range is flagged(0-100)
growaround = True # Flag data based on surrounding flags
flagneartime = False # Flag one timestep before and after a flagged one (True/False)
flagnearfreq = False # Flag one channel before and after a flagged one (True/False)
datadisplay = False # Display data and flags at runtime
plotsummary = False # Parse the flag counts and show some plots at the end (True/False)
usepreflags = True # Use flags already present in the MS
preflagzeros = True # Flag visibilities with values equal to 0.0
writeflags = False # Write Flags to the MS
async = False # If true the taskname must be started using testautoflag(...)
Additional information on the algorithm used in this task ("TFCrop"), as well as some heuristics and more examples, can be found on this webpage.
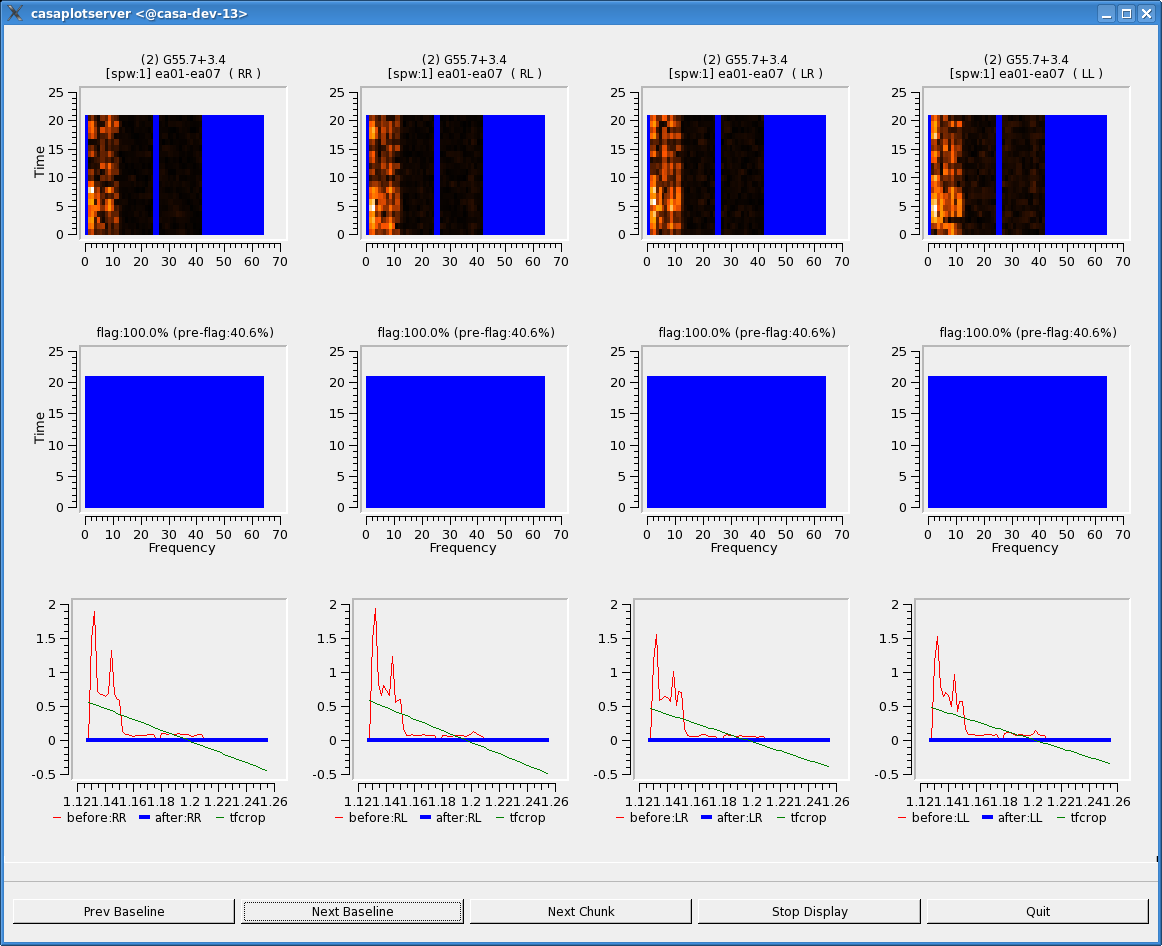
Following are a set of testautoflag commands which have been found to work reasonably well with these data. Please take some time to play with the parameters and the plotting capabilities. Since these runs set "datadisplay=True" and "writeflags=False", the flags are displayed but not actually written to the MS. This allows one to try different sets of parameters before actually applying the flags to the data.
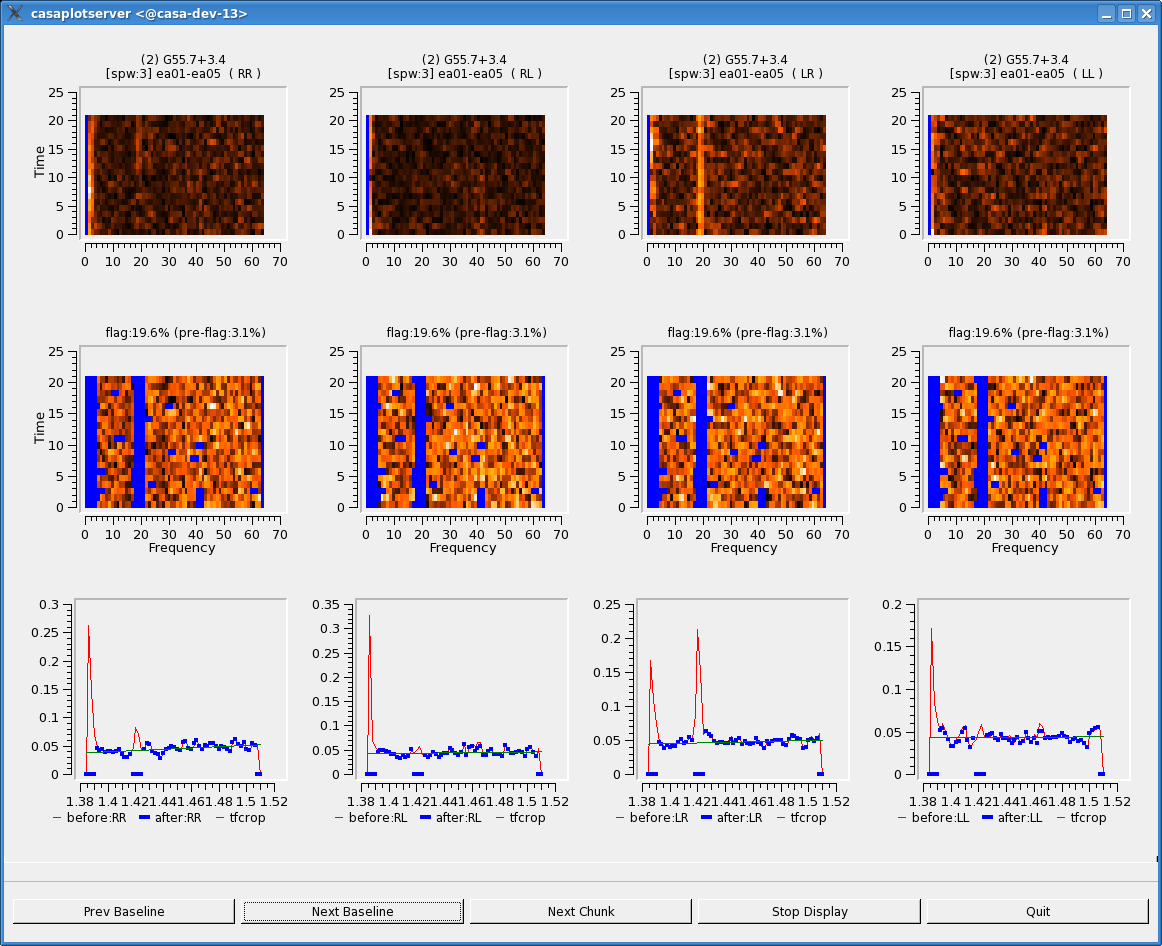
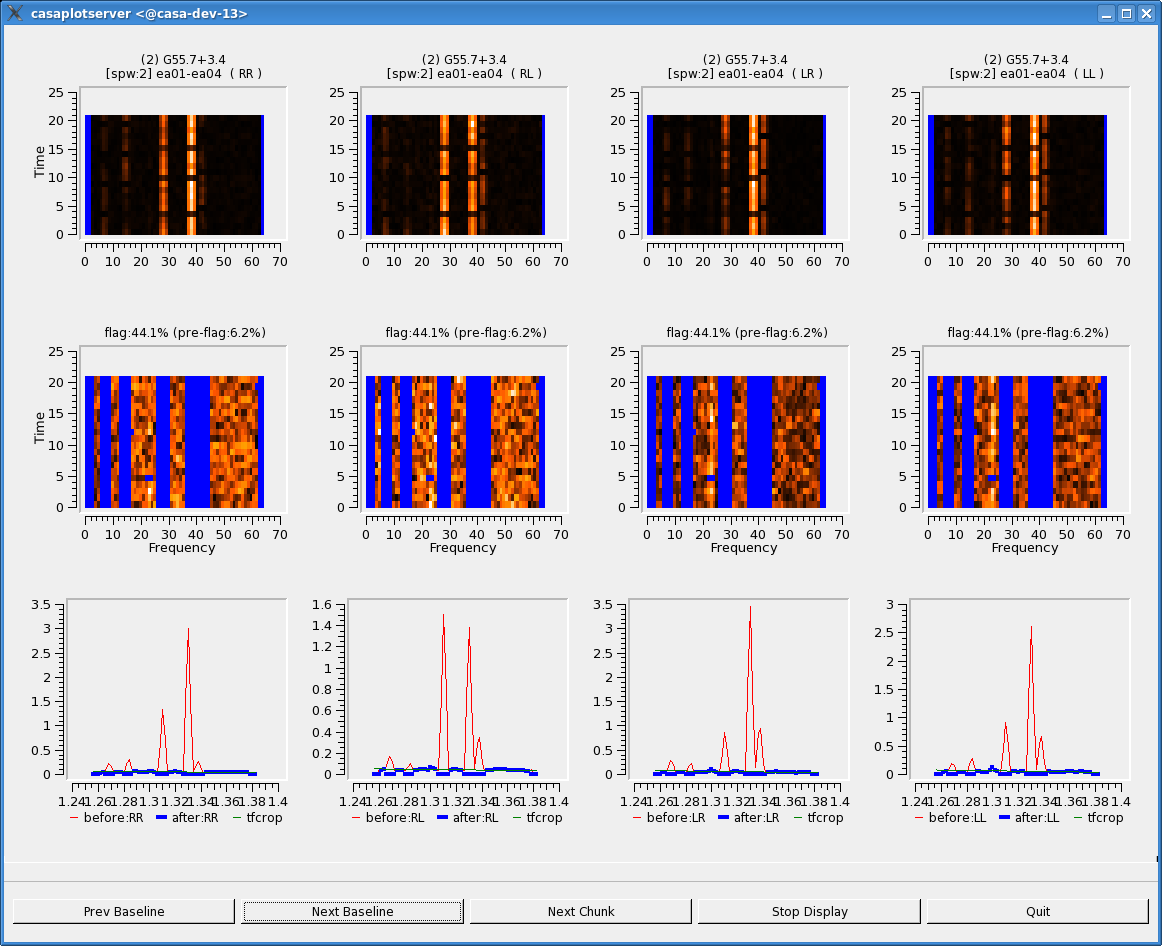
Some representative plots are also displayed. Each column displays an individual polarization product; since we're using all four, from left to right are RR, RL, LR, and LL. The first row shows the data with current flags applied, and the second includes the flags generated by testautoflag. The x-axis is channel number (the spectral window ID is displayed in the top title) and the y-axis of the first two rows is all integrations included in a time "chunk", set by the ntime parameter. These are the data considered by the testautoflag algorithm during its fitting and flagging process, and changes in ntime will have some (relatively small) affect on what data are flagged. The third row displays a histogram of the spectrum over this chunk (in red), as well as the fit determined by testautoflag (in green), and the post-flagged data (blue points).
Each plot page displays data for a single baseline and time chunk. The buttons at the bottom allow one to step through baselines (backward as well as forward) as well as time; "Stop Display" will continue the flagging operation without the GUI, and "Quit" aborts the run.
Looking at the plots for our data, we can see that testautoflag works quite well with narrow-band RFI but struggles with wide-band RFI or spectral windows where many channels have already been flagged.
# In CASA
testautoflag(vis='G55.7+3.4_10s.ms', field='2', spw='0',
datacolumn='corrected', freqfit='line',
timefit='poly', maxnpieces=1, ntime=200,
datadisplay=True, timecutoff=4, freqcutoff=2.7,
extendpols=True, preflagzeros=False, flagnearfreq=True)
- datacolumn='corrected': we wish to operate on the bandpass-corrected data, since we will be using the 'line' option for frequency fitting (which will fit a straight line rather than a bandpass-approximating polynomial).
- freqfit='line': since there is RFI present which is broad in frequency, using a polynomial (freqfit='poly') on the raw data will not work well here -- it will simply fit the RFI as if it were part of the bandpass. Therefore, we are using bandpass-corrected data and a line for the fitting process.
- timefit='poly': sets the time-domain portion of the fitting to use a polynomial (default is 'line'). Feel free to play with this parameter; your mileage may vary.
- maxnpieces=1: the TFCrop algorithm performs a robust fit to the data using up to 5 iterations, each of which uses a third-order polynomial for each "piece" of data.
# In CASA
testautoflag(vis='G55.7+3.4_10s.ms', field='2', spw='1',
datacolumn='corrected', freqfit='line',
timefit='poly', maxnpieces=1, ntime=200,
datadisplay=True, timecutoff=4, freqcutoff=2.7,
extendpols=True, preflagzeros=False, flagnearfreq=True)
testautoflag(vis='G55.7+3.4_10s.ms', field='2', spw='2',
datacolumn='corrected', freqfit='line',
timefit='poly', maxnpieces=1, ntime=200,
datadisplay=True, timecutoff=4, freqcutoff=2.8,
extendpols=True, preflagzeros=False, flagnearfreq=True)
testautoflag(vis='G55.7+3.4_10s.ms', field='2', spw='3',
datacolumn='corrected', freqfit='line',
timefit='poly', maxnpieces=1, ntime=200,
datadisplay=True, timecutoff=4, freqcutoff=3,
extendpols=True, preflagzeros=False, flagnearfreq=True)
testautoflag(vis='G55.7+3.4_10s.ms', field='2', spw='5',
datacolumn='corrected', freqfit='line',
timefit='poly', maxnpieces=1, ntime=200,
datadisplay=True, timecutoff=4, freqcutoff=3,
extendpols=True, preflagzeros=False, flagnearfreq=True)
testautoflag(vis='G55.7+3.4_10s.ms', field='2', spw='6',
datacolumn='corrected', freqfit='line',
timefit='poly', maxnpieces=1, ntime=200,
datadisplay=True, timecutoff=4, freqcutoff=3.5,
extendpols=True, preflagzeros=False, flagnearfreq=True)
testautoflag(vis='G55.7+3.4_10s.ms', field='2', spw='7',
datacolumn='corrected', freqfit='line',
timefit='poly', maxnpieces=1, ntime=200,
datadisplay=True, timecutoff=4, freqcutoff=3,
extendpols=True, preflagzeros=False, flagnearfreq=True)
Once you are happy (or as much so as possible), run testautoflag with "writeflags=True" to write the flags to the data. Note that we are now flagging all sources, and the spectral windows have been grouped according to the "freqcutoff" parameter, which is the only parameter that has changed in this example. Of course, the amount of time one may spend investigating the data and trying different parameters could be vast. It's important to keep in mind that the reason we're using automatic flagging in the first place is to minimize the amount of time a human must spend worrying about RFI excision.
# In CASA
testautoflag(vis='G55.7+3.4_10s.ms', spw='0~1',
datacolumn='corrected', freqfit='line',
timefit='poly', maxnpieces=1, ntime=200,
writeflags=True, timecutoff=4, freqcutoff=2.7,
extendpols=True, preflagzeros=False, flagnearfreq=True)
#
testautoflag(vis='G55.7+3.4_10s.ms', spw='2',
datacolumn='corrected', freqfit='line',
timefit='poly', maxnpieces=1, ntime=200,
writeflags=True, timecutoff=4, freqcutoff=2.8,
extendpols=True, preflagzeros=False, flagnearfreq=True)
#
testautoflag(vis='G55.7+3.4_10s.ms', spw='3,5,7',
datacolumn='corrected', freqfit='line',
timefit='poly', maxnpieces=1, ntime=200,
writeflags=True, timecutoff=4, freqcutoff=3,
extendpols=True, preflagzeros=False, flagnearfreq=True)
#
testautoflag(vis='G55.7+3.4_10s.ms', spw='6',
datacolumn='corrected', freqfit='line',
timefit='poly', maxnpieces=1, ntime=200,
writeflags=True, timecutoff=4, freqcutoff=3.5,
extendpols=True, preflagzeros=False, flagnearfreq=True)
Running testautoflag will take some time (likely around 10 minutes), as the task must pass through all of the data. As it runs, the logger will display the fraction of data flagged in each "chunk", as well as summaries at the end. From this set of runs (the output has been rearranged to make it easier to read):
Summary of Flag Counts Field[1]:J1925+2106 Spw[0]:1000.00MHz-1126.00MHz --> Flagged 78.29%. Field[2]:G55.7+3.4 Spw[0]:1000.00MHz-1126.00MHz --> Flagged 83.91%. Field[3]:0542+498=3C147 Spw[0]:1000.00MHz-1126.00MHz --> Flagged 51.10%. Field[1]:J1925+2106 Spw[1]:1128.00MHz-1254.00MHz --> Flagged 99.49%. Field[2]:G55.7+3.4 Spw[1]:1128.00MHz-1254.00MHz --> Flagged 99.48%. Field[3]:0542+498=3C147 Spw[1]:1128.00MHz-1254.00MHz --> Flagged 87.58%. Field[1]:J1925+2106 Spw[2]:1256.00MHz-1382.00MHz --> Flagged 58.28%. Field[2]:G55.7+3.4 Spw[2]:1256.00MHz-1382.00MHz --> Flagged 60.99%. Field[3]:0542+498=3C147 Spw[2]:1256.00MHz-1382.00MHz --> Flagged 49.12%. Field[1]:J1925+2106 Spw[3]:1384.00MHz-1510.00MHz --> Flagged 35.99%. Field[2]:G55.7+3.4 Spw[3]:1384.00MHz-1510.00MHz --> Flagged 37.49%. Field[3]:0542+498=3C147 Spw[3]:1384.00MHz-1510.00MHz --> Flagged 33.37%. Field[1]:J1925+2106 Spw[5]:1648.00MHz-1774.00MHz --> Flagged 45.38%. Field[2]:G55.7+3.4 Spw[5]:1648.00MHz-1774.00MHz --> Flagged 47.03%. Field[3]:0542+498=3C147 Spw[5]:1648.00MHz-1774.00MHz --> Flagged 37.64%. Field[1]:J1925+2106 Spw[6]:1776.00MHz-1902.00MHz --> Flagged 33.12%. Field[2]:G55.7+3.4 Spw[6]:1776.00MHz-1902.00MHz --> Flagged 34.13%. Field[3]:0542+498=3C147 Spw[6]:1776.00MHz-1902.00MHz --> Flagged 30.61%. Field[1]:J1925+2106 Spw[7]:1904.00MHz-2030.00MHz --> Flagged 61.48%. Field[2]:G55.7+3.4 Spw[7]:1904.00MHz-2030.00MHz --> Flagged 63.38%. Field[3]:0542+498=3C147 Spw[7]:1904.00MHz-2030.00MHz --> Flagged 63.76%.
The vast majority of spectral windows 0 and 1 have been flagged, so we will make the executive decision at this point to completely flag these data:
# In CASA
flagdata(vis='G55.7+3.4_10s.ms', mode='manualflag', spw='0~1')
Evaluating results & further manual flagging
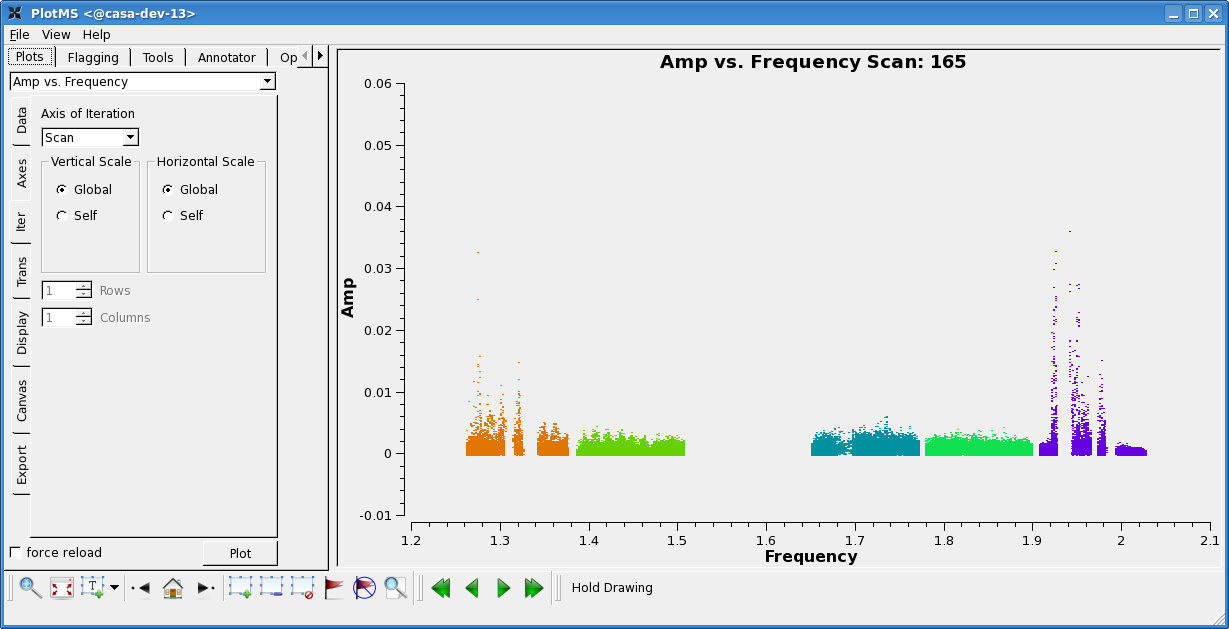
Now that the automatic RFI excision is complete, have a look at the data with plotms and evaluate the results. Note: since this is the same plotms command as we gave above, you might need to use Shift+Plot (or check "force reload") to see the data with the new flags applied.
# In CASA
plotms(vis='G55.7+3.4_10s.ms', scan='30,75,120,165,190,235,303',
antenna='ea24', xaxis='freq', yaxis='amp', iteraxis='scan',
correlation='rr,ll', spw='2~3,5~7', coloraxis='spw')
Looking at these plots, it's clear that SPW 7 is still dominated by RFI in most cases. Manually flag these data:
# In CASA
flagdata(vis='G55.7+3.4_10s.ms', mode='manualflag', spw='7')
Another instructive way to view the data is by baseline and uv-distance. Note that we're plotting all baselines in these plots, rather than just baselines to ea24 as before.
# In CASA
plotms(vis='G55.7+3.4_10s.ms', scan='30,75,120,165,190,235,303',
xaxis='baseline', yaxis='amp', iteraxis='spw',
correlation='rr,ll', spw='2~3,5~6', coloraxis='antenna1')
The baseline between ea01 and ea05 should be flagged (we specify an explicit spectral window selection here; this will help flagdata run more quickly):
# In CASA
flagdata(vis='G55.7+3.4_10s.ms', mode='manualflag', antenna='ea01&ea05',
spw='2~3,5~6')
# In CASA
plotms(vis='G55.7+3.4_10s.ms', scan='30,75,120,165,190,235,303',
xaxis='uvdist', yaxis='amp', iteraxis='spw',
correlation='rr,ll', spw='2~3,5~6', coloraxis='antenna1')
This reveals a few more spectral-window-specific baselines that should be flagged. This time, we'll use the flagcmd task to input a list of flagging commands:
# In CASA
flagList = ["mode='manualflag' spw='5' antenna='ea02&ea09;ea16&ea19;ea08&ea16;ea02&ea16;ea08&ea22'", \
"mode='manualflag' spw='2' antenna='ea03&ea15;ea12&ea19;ea19&ea23;ea09&ea16;ea03&ea19;ea07&ea16;ea11&ea16'", \
"mode='manualflag' spw='2' uvrange='0~100'"]
#
flagcmd(vis='G55.7+3.4_10s.ms', inpmode='cmd', command=flagList)
One final plot of the flagged data using plotms -- this time, we'll use a slightly different set of scans to be sure we haven't missed any serious RFI:
# In CASA
plotms(vis='G55.7+3.4_10s.ms', scan='22,48,80,100,130,150,174,200,242,267,306',
xaxis='freq', yaxis='amp', iteraxis='scan',
correlation='rr,ll', spw='2~3,5~6', coloraxis='spw')
Clearly, there is still some residual RFI left here and there -- however, for the purposes of this tutorial, we will accept the current state of the flags and move on. Feel free to hunt and excise some more, if desired.
Calibrating data
Now that we are (mostly) happy with the RFI excision, we will move on to the calibration stage.
Setting the flux density scale
Since we will be using 3C147 as the source of the absolute flux scale for this observation, we must first run setjy to set the appropriate model amplitudes for this source.
If the flux calibrator is spatially resolved, it is necessary to include a model image as well. Although 3C147 is not resolved at L-band in D configuration, we include the model image here for completeness.
First, we use the listmodimages parameter to find the model image path:
# In CASA
setjy(vis='G55.7+3.4_10s.ms', listmodels=True)
This lists any images in the current working directory as well as images in CASA's repository. In this second list, we see that there is "3C147_L.im", which is appropriate for our flux calibrator and band, and that it is in the directory "/usr/lib64/casapy/release/nrao/VLA/CalModels". We can optionally give the full path of the model image, but setjy should now be able to locate it by name alone:
# In CASA
setjy(vis='G55.7+3.4_10s.ms', field='0542*', scalebychan=True,
spw='2~3,5~6', modimage='3C147_L.im')
- scalebychan=True: scales the model flux density value for each channel. By default, only one value per spectral window is calculated.
Bandpass calibration
We will follow the same procedure outlined above for calculating the antenna bandpasses, except that this time, we will use the actual designated bandpass calibration source, 3C147. Although the phase calibration source has the advantage of having been observed throughout the run, it has an unknown spectrum which could introduce amplitude slopes to each spectral window.
# In CASA
gaincal(vis='G55.7+3.4_10s.ms', intent='*BANDPASS*',
caltable='G55.7+3.4_10s.initPh.2',
spw='3;5~6:30~33,2:32~35',
solint='int', refant='ea24',
minblperant=3, minsnr=3.0, calmode='p',
gaintable='G55.7+3.4_10s.pos')
#
bandpass(vis='G55.7+3.4_10s.ms', caltable='G55.7+3.4_10s.bPass',
intent='*BANDPASS*', solint='inf', spw='2~3,5~6',
combine='scan', refant='ea24', minblperant=3, minsnr=10.0,
gaintable=['G55.7+3.4_10s.pos','G55.7+3.4_10s.initPh.2'],
interp=['', 'nearest'], solnorm=False)
- solint='inf', combine='scan': again, the solution interval of 'inf' will automatically break by scans; this requests that the solution intervals be combined over scans, so that we will get one solution per antenna.
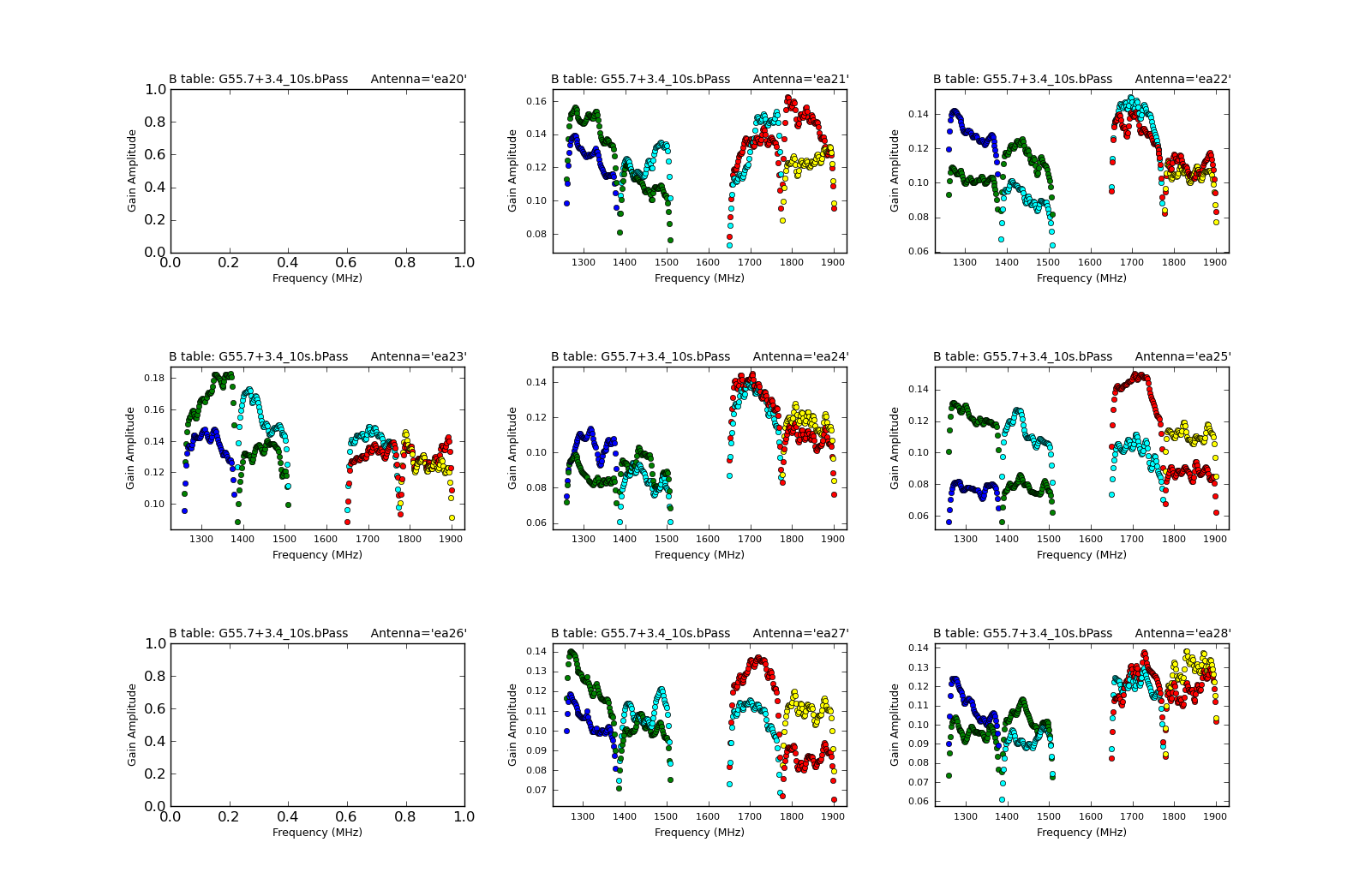
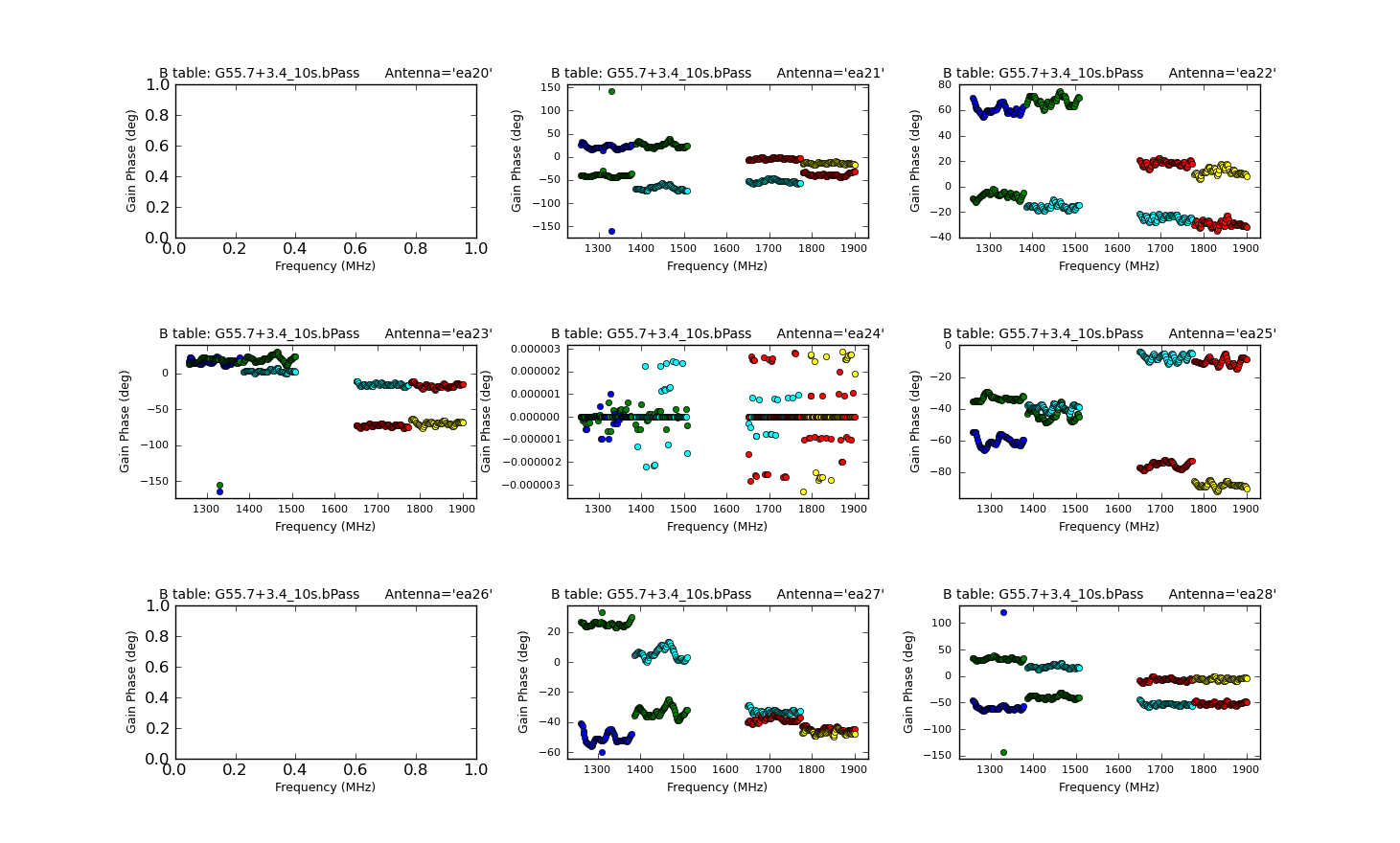
Note that since we have flagged out the vast majority of the RFI-affected data, there are many fewer failed solutions. Again, we can plot the calculated bandpasses to check that they look reasonable:
# In CASA
plotcal(caltable='G55.7+3.4_10s.bPass', xaxis='freq', yaxis='amp',
iteration='antenna', subplot=331)
#
plotcal(caltable='G55.7+3.4_10s.bPass', xaxis='freq', yaxis='phase',
iteration='antenna', subplot=331)
Don't let the apparently odd-looking phases for ea24 fool you -- check the scale! Remember, this is our reference antenna.
Gain calibration
Next, we will calculate the per-antenna gain solutions. Since this is low-frequency data, we do not expect substantial variations over short timescales, so we calculate one solution per scan (using "solint='inf'"):
# In CASA
gaincal(vis='G55.7+3.4_10s.ms', caltable='G55.7+3.4_10s.phaseAmp',
intent='*PHASE*,*AMPLI*',
spw='2~3,5~6', solint='inf', refant='ea24', minblperant=3,
minsnr=10.0, gaintable=['G55.7+3.4_10s.pos','G55.7+3.4_10s.bPass'])
- solint='inf': we request one solution per scan.
Plot these solutions as a function of time, iterating over antenna:
# In CASA
plotcal(caltable='G55.7+3.4_10s.phaseAmp', xaxis='time', yaxis='amp',
iteration='antenna')
plotcal(caltable='G55.7+3.4_10s.phaseAmp', xaxis='time', yaxis='phase',
iteration='antenna')
Flux scaling the gain solutions
Now that we have a complete set of gain solutions, we must scale the phase calibrator's absolute flux correctly, using 3C147 as our reference source. To do this, we run fluxscale on the gain table we just created, which will write a new, flux-corrected gain table:
# In CASA
fluxscale(vis='G55.7+3.4_10s.ms', caltable='G55.7+3.4_10s.phaseAmp',
fluxtable='G55.7+3.4_10s.phaseAmp.fScale', reference='3')
The logger will display information about the flux density it has deduced for J1925+2106:
Found reference field(s): 0542+498=3C147 Found transfer field(s): J1925+2106 Flux density for J1925+2106 in SpW=0 is: INSUFFICIENT DATA Flux density for J1925+2106 in SpW=1 is: INSUFFICIENT DATA Flux density for J1925+2106 in SpW=2 is: 1.45706 +/- 0.0276287 (SNR = 52.7371, N= 40) Flux density for J1925+2106 in SpW=3 is: 1.53199 +/- 0.0252889 (SNR = 60.5794, N= 40) Flux density for J1925+2106 in SpW=4 is: INSUFFICIENT DATA Flux density for J1925+2106 in SpW=5 is: 1.70974 +/- 0.0250203 (SNR = 68.3342, N= 40) Flux density for J1925+2106 in SpW=6 is: 1.76682 +/- 0.0266609 (SNR = 66.27, N= 40) Flux density for J1925+2106 in SpW=7 is: INSUFFICIENT DATA
The flux density listed in the VLA Calibrator Manual for this source is around the same magnitude:
1925+211 J2000 A 19h25m59.605370s 21d06'26.162180" Aug01 1923+210 B1950 A 19h23m49.792400s 21d00'23.305000" ----------------------------------------------------- BAND A B C D FLUX(Jy) UVMIN(kL) UVMAX(kL) ===================================================== 20cm L P S S S 1.30 visplot
So we should be satisfied that our calibration up to this point is reasonable.
Applying calibration
Finally, we must apply the calibration to our data. To do this, we run applycal in two stages: the first is to self-calibrate our calibration sources; the second, to apply calibration to the supernova remnant. These must be done separately, since we want to use "nearest" interpolation for the self-calibration and "linear" for the application to the science target:
# In CASA
applycal(vis='G55.7+3.4_10s.ms', spw='2~3,5~6', intent='*TARGET*',
gaintable=['G55.7+3.4_10s.pos','G55.7+3.4_10s.bPass', \
'G55.7+3.4_10s.phaseAmp.fScale'], calwt=False)
#
applycal(vis='G55.7+3.4_10s.ms', spw='2~3,5~6', intent='*PHASE*,*AMPLI*',
gaintable=['G55.7+3.4_10s.pos','G55.7+3.4_10s.bPass', \
'G55.7+3.4_10s.phaseAmp.fScale'],
calwt=False, interp=['','nearest','nearest'])
Plotting calibrated data
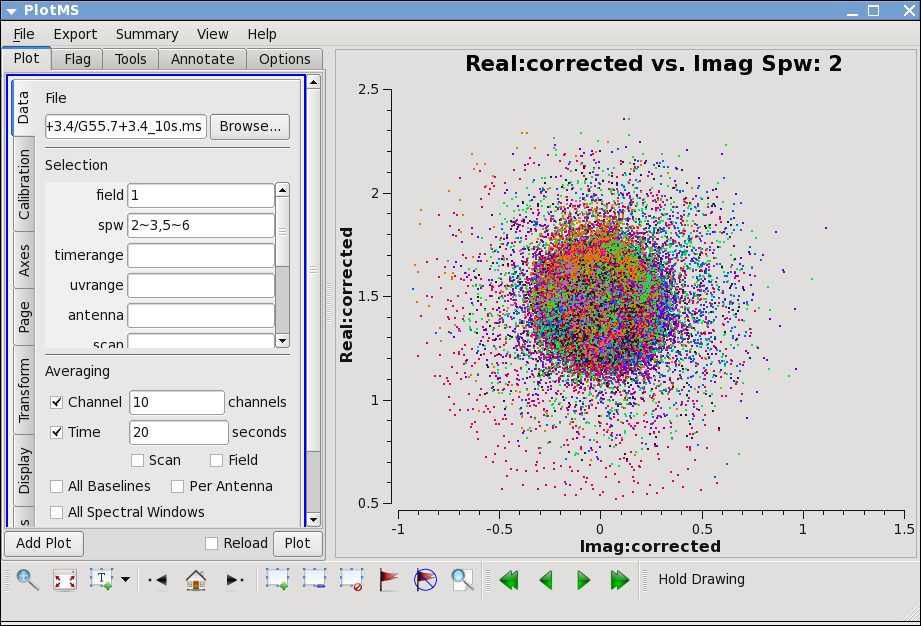
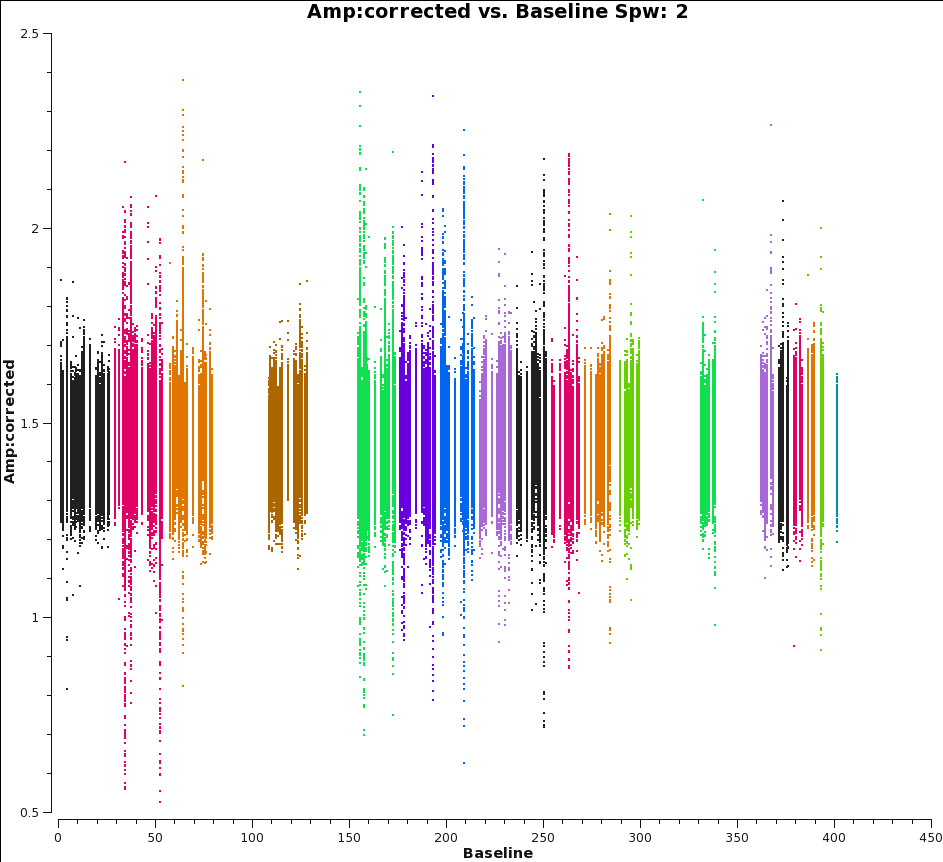
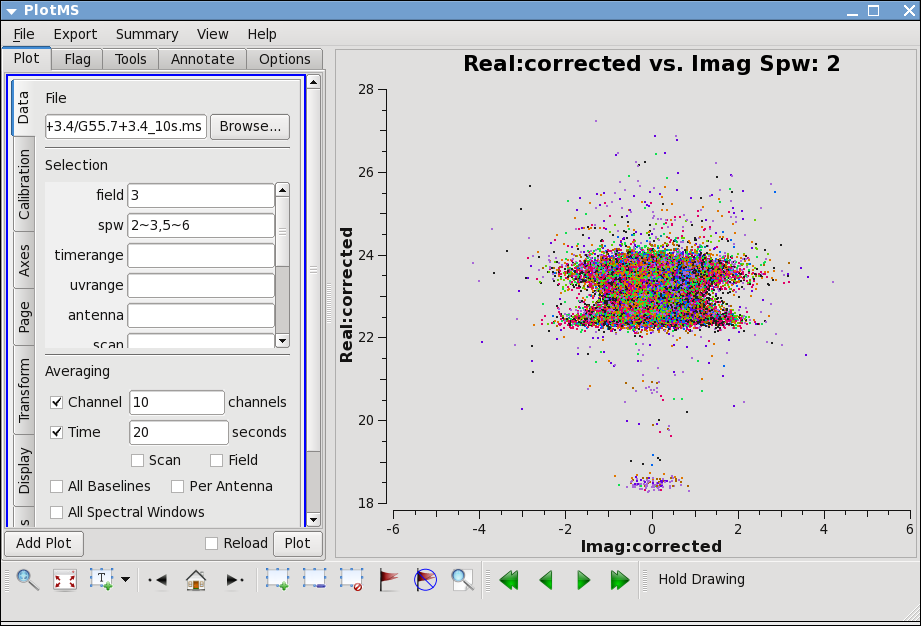
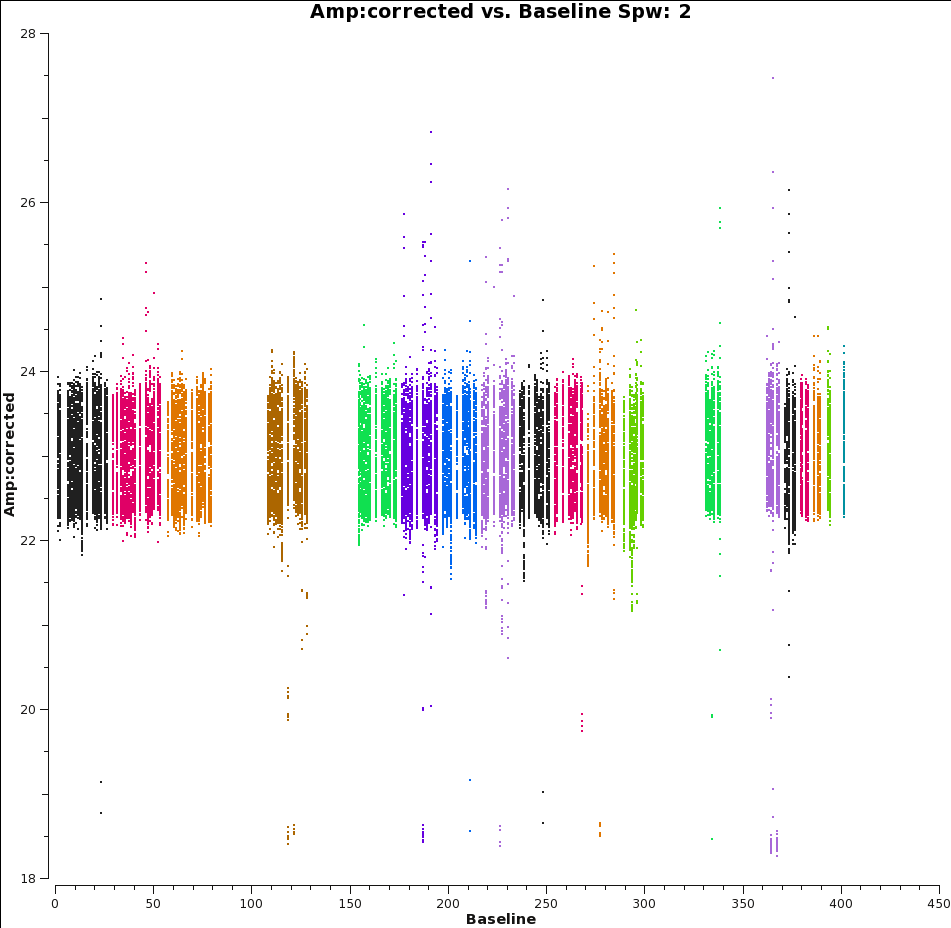
To check that everything has truly proceeded as well as we would like, this is a good time to look at the calibrated data in plotms. A very useful way to check the goodness of calibration is to plot the corrected amplitude vs. corrected phase (which should look like a tight ball for a point source, and will have organized structure if the source is resolved), and corrected amplitude vs. baseline, which should be a flat line of points for a point source, and will reveal any lingering antenna-based problems. For a resolved source, it may be more instructive to plot corrected amplitude vs. uv-distance.
# In CASA
plotms(vis='G55.7+3.4_10s.ms', field='1', xaxis='phase', yaxis='amp',
xdatacolumn='corrected', ydatacolumn='corrected', coloraxis='antenna1',
avgchannel='10', avgtime='20', correlation='rr,ll', iteraxis='spw',
spw='2~3,5~6')
#
plotms(vis='G55.7+3.4_10s.ms', field='1', xaxis='baseline', yaxis='amp',
xdatacolumn='corrected', ydatacolumn='corrected', coloraxis='antenna1',
avgchannel='10', avgtime='20', correlation='rr,ll', iteraxis='spw',
spw='2~3,5~6')
#
plotms(vis='G55.7+3.4_10s.ms', field='3', xaxis='phase', yaxis='amp',
xdatacolumn='corrected', ydatacolumn='corrected', coloraxis='antenna1',
avgchannel='10', avgtime='20', correlation='rr,ll', iteraxis='spw',
spw='2~3,5~6')
#
plotms(vis='G55.7+3.4_10s.ms', field='3', xaxis='baseline', yaxis='amp',
xdatacolumn='corrected', ydatacolumn='corrected', coloraxis='antenna1',
avgchannel='10', avgtime='20', correlation='rr,ll', iteraxis='spw',
spw='2~3,5~6')
Splitting out data for G55.7+3.4
Now that we are satisfied with the calibration, we will create a new MS which contains only the corrected data for G55.7+3.4 using the task split. This will substantially reduce the size of the MS, and will speed up the imaging process. We can also drop the polarization products since they have not been calibrated and will not be used for imaging.
# In CASA
split(vis='G55.7+3.4_10s.ms', field='2', keepflags=False,
outputvis='G55.7+3.4.calib.ms', datacolumn='corrected',
spw='2~3,5~6', correlation = 'rr,ll')
Imaging
At this point, one may image either the resulting MS from the flagging and calibration steps above, or the MS that was flagged by hand and calibrated. The latter is available as "G55.7+3.4.byHandFlag.ms". (For internal, pre-workshop testers: the data can be found at /lustre/sbhatnag/Tests/ThursdayLectures/G55.7+3.4_10s_Calib.ms.) For this tutorial, we will use the MS that has been produced using testautoflag and the minimal amount of manual flagging described here, with the exception of the final clean step, where we will run identical commands on both sets of data and compare the results.
The size of the primary beam is 45 arcmin divided by the observed frequency in GHz, or around 30 arcmin. Since the observation was taken in D-configuration, we can check the Observational Status Summary to find that the synthesized beam will be around 44 arcsec. We want to oversample the synthesized beam by a factor of around five, so we will use a cell size of 8 arcsec.
Since this field contains bright point sources significantly outside the primary beam, we will create images that are 170 arcminutes on a side, or almost 6 x the size of the primary beam. This is ideal for showcasing both the problems inherent in such wide-band, wide-field imaging, as well as some of the solutions currently available in CASA to deal with these issues.
First, it's worth considering why we are even interested in sources which are far outside the primary beam. This is mainly due to the fact that the EVLA, with its wide bandwidth capabilities, is quite sensitive even far from phase center -- for example, at our observing frequencies in L-band, the primary beam gain is as much as 10% around 1 degree away. That means that any imaging errors for these far-away sources will have a significant impact on the image rms at phase center. The error due to a source at distance R can be parametrized as:
[math]\displaystyle{ \Delta(S) = S(R) \times PB(R) \times PSF(R) }[/math]
So, for R = 1 degree, source flux S(R) = 1 Jy, [math]\displaystyle{ \Delta(S) }[/math] = 1 mJy − 100 [math]\displaystyle{ {\mu} }[/math]Jy. Clearly, this will be a source of significant error.
Multi-scale clean
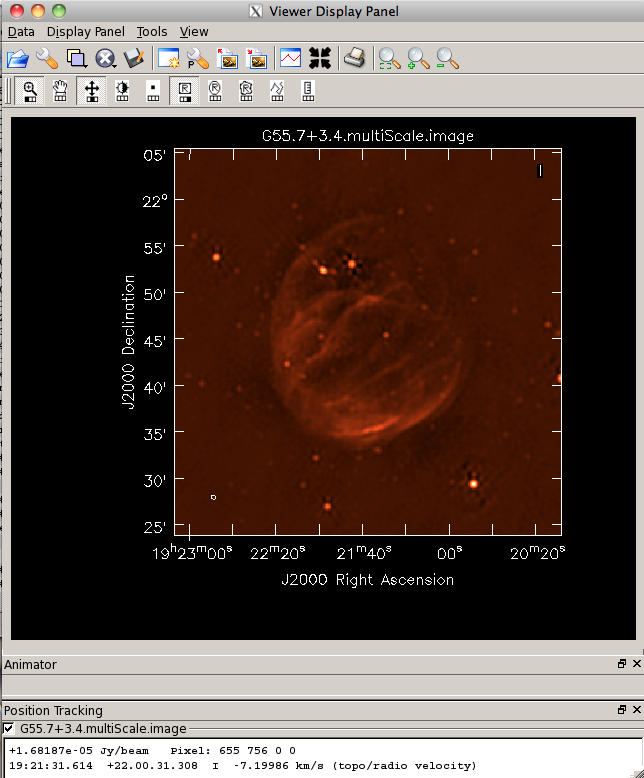
Since G55.7+3.4 is an extended source with many spatial scales, the most basic (yet still reasonable) imaging procedure is to use clean with multiple scales. As is suggested, we will use a set of scales (which are expressed in units of the requested pixel, or cell, size) which are representative of the scales that are present in the data, including a zero-scale for point sources.
Note that interrupting clean by Ctrl+C may corrupt your visibilities -- you may be better off choosing to let clean finish. We are currently implementing a command that will nicely exit to prevent this from happening, but for the moment try to avoid Ctrl+C.
# In CASA
clean(vis='G55.7+3.4.calib.ms', imagename='G55.7+3.4.multiScale',
imsize=1280, cell='8arcsec', multiscale=[0,6,10,30,60],
interactive=False, niter=1000, weighting='briggs',
stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')
viewer('G55.7+3.4.multiScale.image')
- imagename='G55.7+3.4.multiScale': the root filename used for the various clean outputs. These include the final image (<imagename>.image), the relative sky sensitivity over the field (<imagename>.flux), the point-spread function (also known as the dirty beam; <imagename>.psf), the clean components (<imagename>.model), and the residual image (<imagename>.residual).
- imsize=1280: the image size in number of pixels. Note that entering a single value results in a square image with sides of this value.
- cell='8arcsec': the size of one pixel; again, entering a single value will result in a square pixel size.
- multiscale=[0,6,10,30,60,120]: a set of scales on which to clean. Since these are in units of the pixel size, we are requesting scales of 0 (a point source), 48, 80, 240, 480, and 960 arcseconds. The large scale, equal to 16 arcminutes, roughly corresponds to the size of G55.7+3.4.
- interactive=False: we will let clean use the entire field for placing model components. Alternatively, you could try using interactive=True, and create regions to constrain where components will be placed. However, this is a very complex field, and creating a region for every bit of diffuse emission as well as each point source can quickly become tedious.
- niter=1000: this controls the number of iterations clean will do in the minor cycle.
- weighting='briggs': use Briggs weighting with a robustness parameter of 0 (halfway between uniform and natural weighting).
- calready=F: do not write the model visibilities to the model data column (only needed for self-calibration)
- imagermode='csclean': use the Cotton-Schwab clean algorithm
- stokes='I': since we have not done any polarization calibration, we only create a total-intensity image.
- threshold='0.1mJy': threshold at which the cleaning process will halt; i.e. no clean components with a flux less than this value will be created. This is meant to avoid cleaning what is actually noise (and creating an image with an artificially low rms). It is advisable to set this equal to the expected rms, which can be estimated using the EVLA exposure calculator. However, in our case, this is a bit difficult to do, since we have lost a hard-to-estimate amount of bandwidth due to flagging, and there is also some residual RFI present. Therefore, we choose 0.1 mJy as a relatively conservative limit.
This is the fastest of the imaging techniques described here (it will probably take less than ten minutes to complete), but it's easy to see that there are artifacts in the resulting image. For example, use the viewer to explore the point sources near the edge of the field. Some have prominent arcs, as well as spots in a six-pointed pattern surrounding them. Next we will explore some more advanced imaging techniques to mitigate these artifacts.
Multi-scale, wide-field clean
The next clean algorithm we will employ is W-projection, which is a wide-field imaging technique that takes into account the non-coplanarity of the baselines as a function of distance from the phase center. For more details on the motivation for this correction, as well as the algorithm itself, see "The Noncoplanar Baselines Effect in Radio Interferometry: The W-Projection Algorithm".
# In CASA
clean(vis='G55.7+3.4.calib.ms', imagename='G55.7+3.4.MS.wProj',
gridmode='widefield', imsize=1280, cell='8arcsec',
wprojplanes=128, multiscale=[0,6,10,30,60],
interactive=False, niter=1000, weighting='briggs',
stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')
viewer('G55.7+3.4.MS.wProj.image')
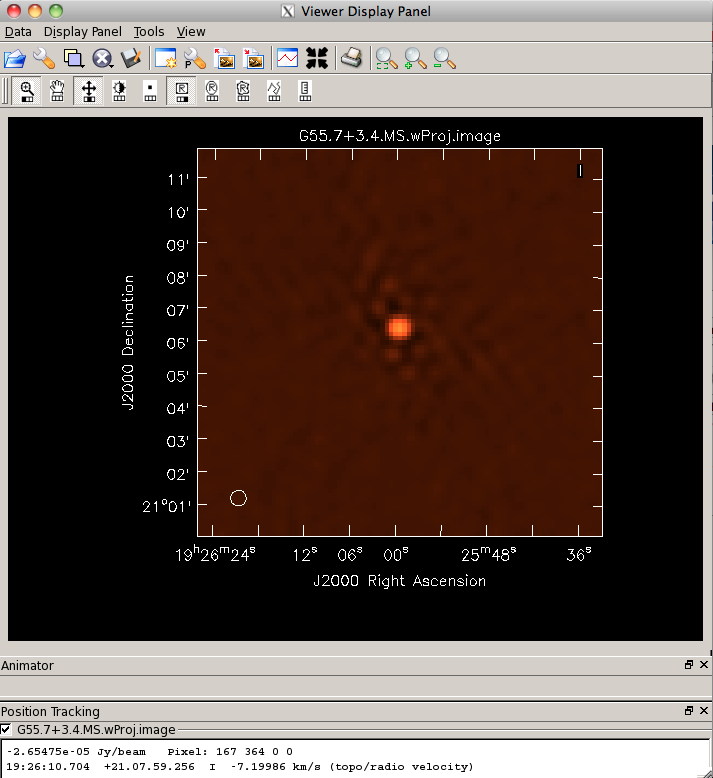
- gridmode='widefield': use the W-projection algorithm.
- wprojplanes=128: the number of W-projection planes to use for deconvolution; 128 is the minimum recommended number.
This will take longer than the previous imaging round (likely around 15 minutes); however, the resulting image has noticeably fewer artifacts. In particular, compare the same outlier source in the W-projected image with the multi-scale-only image: note that the swept-back arcs have disappeared. There are still some obvious imaging artifacts remaining, though.
Multi-scale, multi-frequency synthesis
Another consequence of simultaneously imaging the wide fractional bandwidths available with the EVLA is that the primary beam has substantial frequency-dependent variation over the observing band. If this is not accounted for, it will lead to imaging artifacts and compromise the achievable image rms.
If sources which are being imaged have intrinsically flat spectra, this will not be a problem. However, most astronomical objects are not flat-spectrum sources, and without any estimation of the intrinsic spectral properties, the fact that the primary beam is twice as large at 2 than at 1 GHz will have substantial consequences.
The Multi-Scale Multi-Frequency-Synthesis (MS-MFS) algorithm provides the ability to simultaneously image and fit for the intrinsic source spectrum. The spectrum is approximated using a polynomial in frequency, with the degree of the polynomial as a user-controlled parameter.
# In CASA
clean(vis='G55.7+3.4.calib.ms', imagename='G55.7+3.4.MS.MFS',
imsize=1280, cell='8arcsec', mode='mfs', nterms=2,
multiscale=[0,6,10,30,60],
interactive=False, niter=1000, weighting='briggs',
stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')
viewer('G55.7+3.4.MS.MFS.image.tt0')
viewer('G55.7+3.4.MS.MFS.image.alpha')
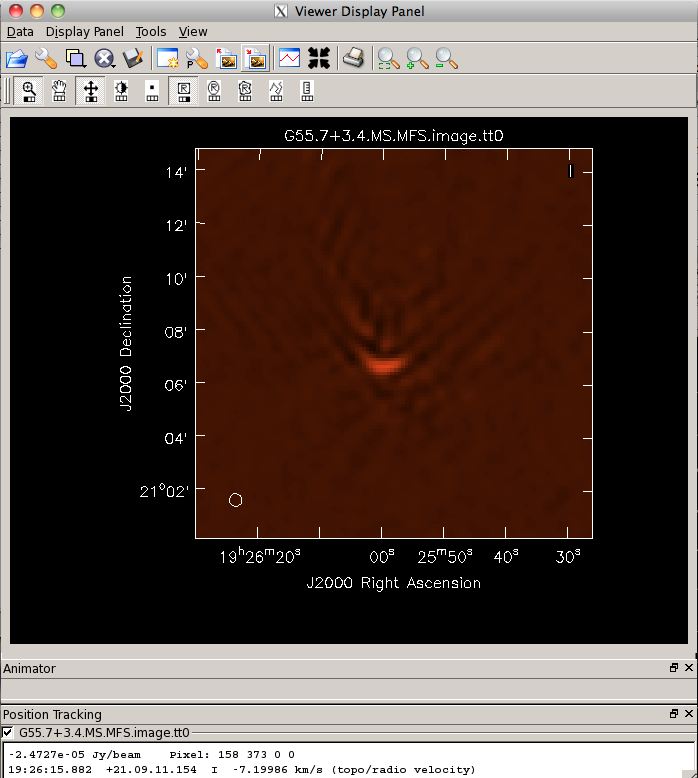
- nterms=2:the number of Taylor terms to be used to model the frequency dependence of the sky emission. Note that the speed of the algorithm will depend on the value used here (more terms will be slower); of course, the image fidelity will improve with a larger number of terms (assuming the sources are sufficiently bright to be modeled more completely).
This will take a little while (likely around 30 minutes), so it would probably be a good time to have coffee or chat about EVLA data reduction with your neighbor at this point.
When clean is done <imagename>.image.tt0 will contain a total intensity image; <imagename>.image.alpha will contain an image of the spectral index in regions where there is sufficient signal-to-noise. For more information on the multi-frequency synthesis mode and its outputs, see the CASA cookbook. Inspect the brighter point sources in the field. You will notice that some of the artifacts which had been symmetric around the sources themselves are now gone; however, since we did not use W-projection this time, there are still strong features related to the non-coplanar baseline effects still apparent.
Multi-scale, multi-frequency, wide-field clean
Finally, we will combine the W-projection and MS-MFS algorithms to simultaneously account for both of the effects. Be forewarned -- these imaging runs will take a while, and it's best to start them running and then move on to other things. In testing, both of these runs (on the auto- and by-hand-flagged data) took around an hour.
First, we will image the autoflagged data. Using the same parameters for the individual-algorithm images above, but combined into a single clean run, we have:
# In CASA
clean(vis='G55.7+3.4.calib.ms', imagename='G55.7+3.4.MS.MFS.wProj',
gridmode='widefield', imsize=1280, cell='8arcsec', mode='mfs',
nterms=2, wprojplanes=128, multiscale=[0,6,10,30,60],
interactive=False, niter=1000, weighting='briggs',
stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')
viewer('G55.7+3.4.MS.MFS.wProj.image.tt0')
viewer('G55.7+3.4.MS.MFS.wProj.image.alpha')
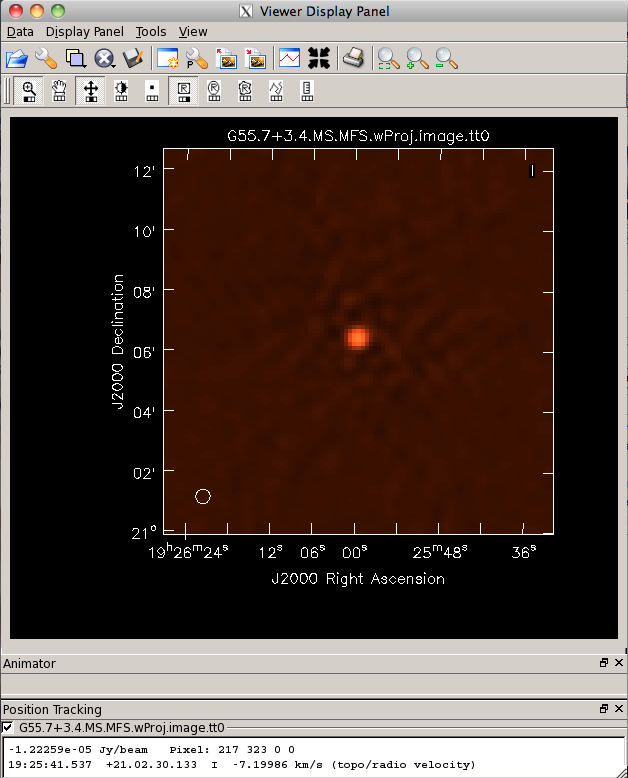
Again, looking at the same outlier source, we can see that the major sources of error have been removed, although there are still some residual artifacts. One possible source of error is the time-dependent variation of the primary beam; another is the fact that we have only used nterms=2, which may not be sufficient to model the spectra of some of the point sources.
Finally, imaging the data which were flagged by hand (these can be found in the same directory as the unflagged data), and using the same parameters as before (again, this will probably take around an hour):
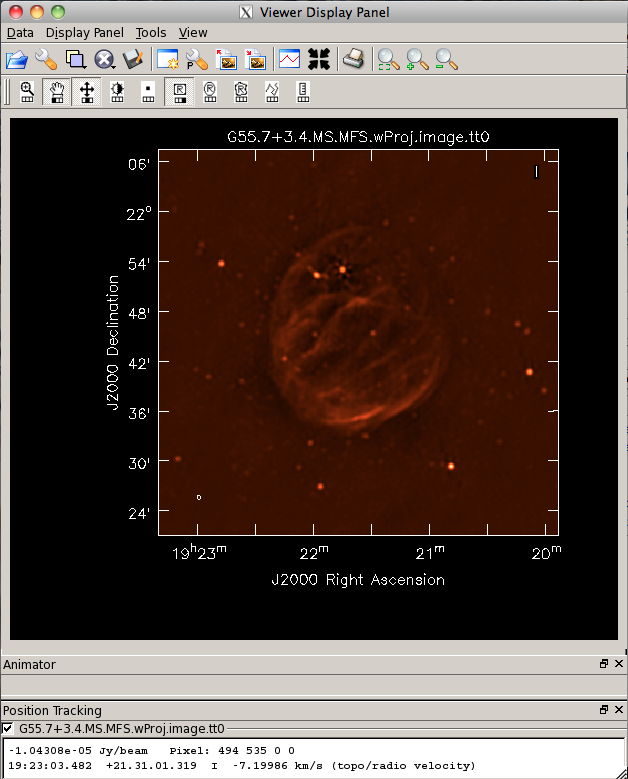
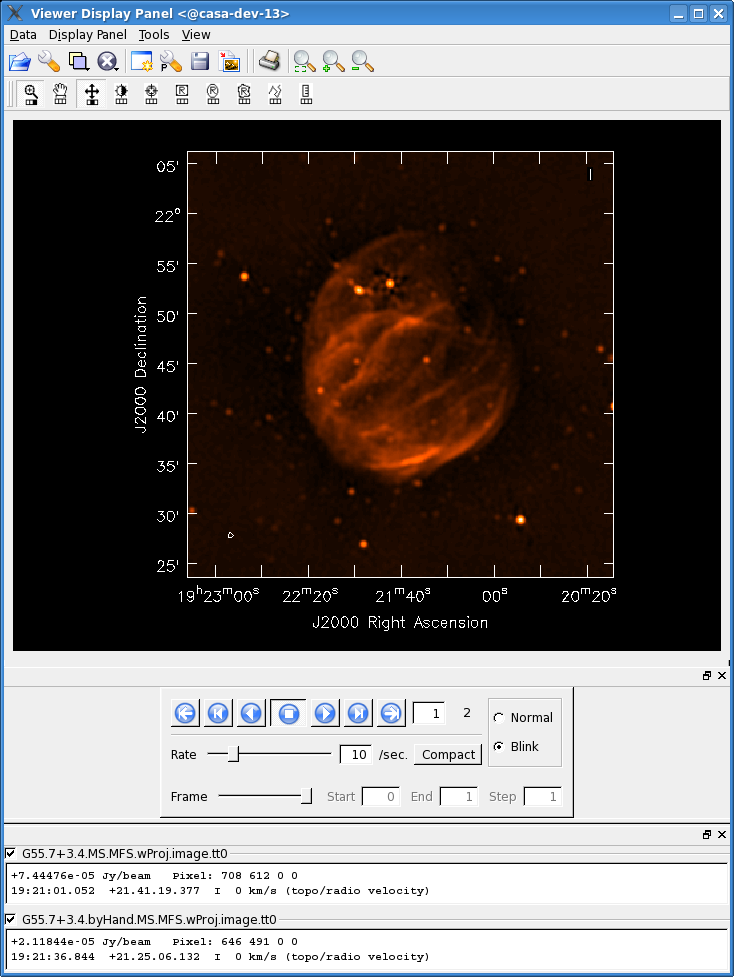
# In CASA
clean(vis='G55.7+3.4.byHandFlag.ms',
imagename='G55.7+3.4.byHand.MS.MFS.wProj',
gridmode='widefield', imsize=1280, cell='8arcsec', mode='mfs',
nterms=2, wprojplanes=128, multiscale=[0,6,10,30,60],
interactive=False, niter=1000, weighting='briggs',
stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')
viewer('G55.7+3.4.byHand.MS.MFS.wProj.image.tt0')
viewer('G55.7+3.4.byHand.MS.MFS.wProj.image.alpha')
Comparing the images using the two different data sets, we can see that there is still a substantial improvement in image fidelity using the by-hand-flagged data. This isn't too surprising, since our plotms displays showed that there was still some RFI present, and it's also possible that the auto-flagging overflagged some portions of the data, also leading to a reduction in the achievable image rms.