EVLA Continuum Tutorial 3C391
Overview
This article describes the calibration and imaging of a multiple-pointing EVLA continuum dataset on the supernova remnant 3C 391. The data were taken in OSRO1 mode, with 128 MHz of bandwidth in each of two widely spaced spectral windows, centered at 4.6 and 7.5 GHz, and were set up for full polarization calibration. To generate the full data reduction script described here, use the script extractor. As an alternative to the function calls as provided by the script extractor, all tasks may be run interactively by typing default taskname to load the task, inp to examine the inputs, and go once those inputs have been set to your satisfaction. Allowed inputs are shown in blue, and bad inputs are colored red. If you prefer this more interactive CASA experience, screenshots of the inputs to the different tasks used in the data reduction are provided, to illustrate which parameters need to be set. The attentive reader will see that all non-default inputs to the tasks correspond exactly to the parameters set in the function calls derived from the script extractor.
Should you use the script generated by the script extractor, be aware that it will require some small amount of interaction, occasionally suggesting that you close the graphics window and hitting return in the terminal to proceed. It is in fact unnecessary to close the graphics windows (it is suggested that you do so purely to keep your desktop uncluttered), and in one case (that of plotms), you must leave the graphics window open, as the GUI cannot be reopened without first exiting from CASA.
Obtaining the Data
For the purposes of this tutorial, we have created a "starting" data set, upon which several initial processing steps have already been conducted. This data set may already be present on the machine that you are using; if not, obtain it from the CASA data archive.
We are providing this "starting" data set, rather than the "true" initial data set for (at least) two reasons. First, many of these initial processing steps can be rather time consuming (> 1 hr), and the time for the data reduction tutorial is limited. Second, while necessary, many of these steps are not fundamental to the calibration and imaging process, upon which we want to focus today. For completeness, however, here are the steps that were taken from the initial data set to produce the "starting" data set:
- The data loaded into CASA, converting the initial Science Data Model (SDM) file into a measurement set.
- Basic data flagging was applied, to account for "shadowing" of the antennas. These data are from the D configuration, and antennas can block or "shadow" other antennas in the array, depending upon the elevation of the source.
- The data were averaged to 10-second samples, from the initial 1-second correlator sample time. In the D configuration, the fringe rate is relatively slow and time-average smearing is less of a concern.
- The data were acquired with two spectral windows (around 4.6 and 7.5 GHz). Because of disk space concerns on some machines, the focus will be on only one of the two spectral windows.
We emphasize that, were this a real science observation, all of these steps would need to be run. Detailed instructions on obtaining the data from the archive and creating this "starting" data set may be found in the Obtaining EVLA Data: 3C 391 Example tutorial.
Examining the Data
Before starting the calibration process, we want to get some basic information about the data set. To examine the observing conditions during the observing run, and to find out any known problems with the data, download the observer log. Simply fill in the known observing date (in our case 2010-Apr-24) as both the Start and Stop date, and click on the "Show Logs" button. The relevant log is labeled with the project code, TDEM0001, and can be downloaded as a PDF file. From this, we find the following:
Information from observing log: There is no C-band receivers on ea13 Antenna ea06 is out of the array Antenna ea12 is newly back Antenna ea15 has some corrupted data Antennas ea10, ea12, ea22 do not have good baseline positions Gusty winds, mixed clouds, API rms up to 11.5.
To get a listing of the individual scans comprising the observation, the frequency setup, source list, and antenna locations, use the task listobs.
# In CASA
listobs(vis='3c391_ctm_mosaic_10s_spw0.ms',verbose=T)
listobs should now produce the following output in the casa logger:
INFO listobs::::casa ########################################## INFO listobs::::casa ##### Begin Task: listobs ##### INFO listobs::::casa INFO listobs::ms::summary ================================================================================ INFO listobs::ms::summary+ MeasurementSet Name: /export/home/hamal/jmiller/TDEM0001_sb1218006/3c391_mosaic_fullres.ms MS Version 2 INFO listobs::ms::summary+ ================================================================================ INFO listobs::ms::summary+ Observer: Dr. James Miller-Jones Project: T.B.D. INFO listobs::ms::summary+ Observation: EVLA INFO listobs::ms::summary Data records: 18666050 Total integration time = 28716 seconds INFO listobs::ms::summary+ Observed from 24-Apr-2010/08:01:34.5 to 24-Apr-2010/16:00:10.5 (UTC) INFO listobs::ms::summary INFO listobs::ms::summary+ ObservationID = 0 ArrayID = 0 INFO listobs::ms::summary+ Date Timerange (UTC) Scan FldId FieldName nVis Int(s) SpwIds INFO listobs::ms::summary+ 24-Apr-2010/08:01:34.5 - 08:02:28.5 1 0 J1331+3030 35750 1 [0, 1] INFO listobs::ms::summary+ 08:02:29.5 - 08:09:27.5 2 0 J1331+3030 272350 1 [0, 1] INFO listobs::ms::summary+ 08:09:28.5 - 08:16:26.5 3 0 J1331+3030 272350 1 [0, 1] INFO listobs::ms::summary+ 08:16:27.5 - 08:24:25.5 4 1 J1822-0938 311350 1 [0, 1] INFO listobs::ms::summary+ 08:24:26.5 - 08:29:44.5 5 2 3C391 C1 207350 1 [0, 1] INFO listobs::ms::summary+ 08:29:45.5 - 08:34:43.5 6 3 3C391 C2 194350 1 [0, 1] INFO listobs::ms::summary+ 08:34:44.5 - 08:39:42.5 7 4 3C391 C3 194350 1 [0, 1] INFO listobs::ms::summary+ 08:39:43.5 - 08:44:41.5 8 5 3C391 C4 194350 1 [0, 1] INFO listobs::ms::summary+ 08:44:42.5 - 08:49:40.5 9 6 3C391 C5 194350 1 [0, 1] INFO listobs::ms::summary+ 08:49:41.5 - 08:54:40.5 10 7 3C391 C6 195000 1 [0, 1] INFO listobs::ms::summary+ 08:54:41.5 - 08:59:39.5 11 8 3C391 C7 194350 1 [0, 1] INFO listobs::ms::summary+ 08:59:40.5 - 09:01:29.5 12 1 J1822-0938 71500 1 [0, 1] INFO listobs::ms::summary+ 09:01:30.5 - 09:06:48.5 13 2 3C391 C1 207350 1 [0, 1] INFO listobs::ms::summary+ 09:06:49.5 - 09:11:47.5 14 3 3C391 C2 194350 1 [0, 1] INFO listobs::ms::summary+ 09:11:48.5 - 09:16:46.5 15 4 3C391 C3 194350 1 [0, 1] INFO listobs::ms::summary+ 09:16:47.5 - 09:21:45.5 16 5 3C391 C4 194350 1 [0, 1] INFO listobs::ms::summary+ 09:21:46.5 - 09:26:44.5 17 6 3C391 C5 194350 1 [0, 1] INFO listobs::ms::summary+ 09:26:45.5 - 09:31:44.5 18 7 3C391 C6 195000 1 [0, 1] INFO listobs::ms::summary+ 09:31:45.5 - 09:36:43.5 19 8 3C391 C7 194350 1 [0, 1] INFO listobs::ms::summary+ 09:36:44.5 - 09:38:32.5 20 1 J1822-0938 70850 1 [0, 1] INFO listobs::ms::summary+ 09:38:33.5 - 09:43:52.5 21 2 3C391 C1 208000 1 [0, 1] INFO listobs::ms::summary+ 09:43:53.5 - 09:48:51.5 22 3 3C391 C2 194350 1 [0, 1] INFO listobs::ms::summary+ 09:48:52.5 - 09:53:50.5 23 4 3C391 C3 194350 1 [0, 1] INFO listobs::ms::summary+ 09:53:51.5 - 09:58:49.5 24 5 3C391 C4 194350 1 [0, 1] INFO listobs::ms::summary+ 09:58:50.5 - 10:03:48.5 25 6 3C391 C5 194350 1 [0, 1] INFO listobs::ms::summary+ 10:03:49.5 - 10:08:47.5 26 7 3C391 C6 194350 1 [0, 1] INFO listobs::ms::summary+ 10:08:48.5 - 10:13:47.5 27 8 3C391 C7 195000 1 [0, 1] INFO listobs::ms::summary+ 10:13:48.5 - 10:15:36.5 28 1 J1822-0938 70850 1 [0, 1] INFO listobs::ms::summary+ 10:15:37.5 - 10:20:55.5 29 2 3C391 C1 207350 1 [0, 1] INFO listobs::ms::summary+ 10:20:56.5 - 10:25:55.5 30 3 3C391 C2 195000 1 [0, 1] INFO listobs::ms::summary+ 10:25:56.5 - 10:30:54.5 31 4 3C391 C3 194350 1 [0, 1] INFO listobs::ms::summary+ 10:30:55.5 - 10:35:53.5 32 5 3C391 C4 194350 1 [0, 1] INFO listobs::ms::summary+ 10:35:54.5 - 10:40:52.5 33 6 3C391 C5 194350 1 [0, 1] INFO listobs::ms::summary+ 10:40:53.5 - 10:45:51.5 34 7 3C391 C6 194350 1 [0, 1] INFO listobs::ms::summary+ 10:45:52.5 - 10:50:51.5 35 8 3C391 C7 195000 1 [0, 1] INFO listobs::ms::summary+ 10:50:52.5 - 10:52:40.5 36 1 J1822-0938 70850 1 [0, 1] INFO listobs::ms::summary+ 10:52:41.5 - 10:57:39.5 37 0 J1331+3030 194350 1 [0, 1] INFO listobs::ms::summary+ 10:57:40.5 - 11:02:39.5 38 1 J1822-0938 195000 1 [0, 1] INFO listobs::ms::summary+ 11:02:40.5 - 11:07:58.5 39 2 3C391 C1 207350 1 [0, 1] INFO listobs::ms::summary+ 11:07:59.5 - 11:12:47.5 40 3 3C391 C2 187850 1 [0, 1] INFO listobs::ms::summary+ 11:12:48.5 - 11:17:36.5 41 4 3C391 C3 187850 1 [0, 1] INFO listobs::ms::summary+ 11:17:37.5 - 11:22:25.5 42 5 3C391 C4 187850 1 [0, 1] INFO listobs::ms::summary+ 11:22:26.5 - 11:27:15.5 43 6 3C391 C5 188500 1 [0, 1] INFO listobs::ms::summary+ 11:27:16.5 - 11:32:04.5 44 7 3C391 C6 187850 1 [0, 1] INFO listobs::ms::summary+ 11:32:05.5 - 11:36:53.5 45 8 3C391 C7 187850 1 [0, 1] INFO listobs::ms::summary+ 11:36:54.5 - 11:38:43.5 46 1 J1822-0938 71500 1 [0, 1] INFO listobs::ms::summary+ 11:38:44.5 - 11:44:02.5 47 2 3C391 C1 207350 1 [0, 1] INFO listobs::ms::summary+ 11:44:03.5 - 11:48:51.5 48 3 3C391 C2 187850 1 [0, 1] INFO listobs::ms::summary+ 11:48:52.5 - 11:53:40.5 49 4 3C391 C3 187850 1 [0, 1] INFO listobs::ms::summary+ 11:53:41.5 - 11:58:29.5 50 5 3C391 C4 187850 1 [0, 1] INFO listobs::ms::summary+ 11:58:30.5 - 12:03:19.5 51 6 3C391 C5 188500 1 [0, 1] INFO listobs::ms::summary+ 12:03:20.5 - 12:08:08.5 52 7 3C391 C6 187850 1 [0, 1] INFO listobs::ms::summary+ 12:08:09.5 - 12:12:57.5 53 8 3C391 C7 187850 1 [0, 1] INFO listobs::ms::summary+ 12:12:58.5 - 12:14:47.5 54 1 J1822-0938 71500 1 [0, 1] INFO listobs::ms::summary+ 12:14:48.5 - 12:20:06.5 55 2 3C391 C1 207350 1 [0, 1] INFO listobs::ms::summary+ 12:20:07.5 - 12:24:55.5 56 3 3C391 C2 187850 1 [0, 1] INFO listobs::ms::summary+ 12:24:56.5 - 12:29:44.5 57 4 3C391 C3 187850 1 [0, 1] INFO listobs::ms::summary+ 12:29:45.5 - 12:34:34.5 58 5 3C391 C4 188500 1 [0, 1] INFO listobs::ms::summary+ 12:34:35.5 - 12:39:23.5 59 6 3C391 C5 187850 1 [0, 1] INFO listobs::ms::summary+ 12:39:24.5 - 12:44:12.5 60 7 3C391 C6 187850 1 [0, 1] INFO listobs::ms::summary+ 12:44:13.5 - 12:49:01.5 61 8 3C391 C7 187850 1 [0, 1] INFO listobs::ms::summary+ 12:49:02.5 - 12:50:51.5 62 1 J1822-0938 71500 1 [0, 1] INFO listobs::ms::summary+ 12:50:52.5 - 12:56:10.5 63 2 3C391 C1 207350 1 [0, 1] INFO listobs::ms::summary+ 12:56:11.5 - 13:00:59.5 64 3 3C391 C2 187850 1 [0, 1] INFO listobs::ms::summary+ 13:01:00.5 - 13:05:48.5 65 4 3C391 C3 187850 1 [0, 1] INFO listobs::ms::summary+ 13:05:49.5 - 13:10:38.5 66 5 3C391 C4 188500 1 [0, 1] INFO listobs::ms::summary+ 13:10:39.5 - 13:15:27.5 67 6 3C391 C5 187850 1 [0, 1] INFO listobs::ms::summary+ 13:15:28.5 - 13:20:16.5 68 7 3C391 C6 187850 1 [0, 1] INFO listobs::ms::summary+ 13:20:17.5 - 13:25:05.5 69 8 3C391 C7 187850 1 [0, 1] INFO listobs::ms::summary+ 13:25:06.5 - 13:26:55.5 70 1 J1822-0938 71500 1 [0, 1] INFO listobs::ms::summary+ 13:26:56.5 - 13:32:14.5 71 2 3C391 C1 207350 1 [0, 1] INFO listobs::ms::summary+ 13:32:15.5 - 13:37:03.5 72 3 3C391 C2 187850 1 [0, 1] INFO listobs::ms::summary+ 13:37:04.5 - 13:41:52.5 73 4 3C391 C3 187850 1 [0, 1] INFO listobs::ms::summary+ 13:41:53.5 - 13:46:42.5 74 5 3C391 C4 188500 1 [0, 1] INFO listobs::ms::summary+ 13:46:43.5 - 13:51:31.5 75 6 3C391 C5 187850 1 [0, 1] INFO listobs::ms::summary+ 13:51:32.5 - 13:56:20.5 76 7 3C391 C6 187850 1 [0, 1] INFO listobs::ms::summary+ 13:56:21.5 - 14:01:09.5 77 8 3C391 C7 187850 1 [0, 1] INFO listobs::ms::summary+ 14:01:10.5 - 14:02:59.5 78 1 J1822-0938 71500 1 [0, 1] INFO listobs::ms::summary+ 14:03:00.5 - 14:08:18.5 79 2 3C391 C1 207350 1 [0, 1] INFO listobs::ms::summary+ 14:08:19.5 - 14:13:07.5 80 3 3C391 C2 187850 1 [0, 1] INFO listobs::ms::summary+ 14:13:08.5 - 14:17:57.5 81 4 3C391 C3 188500 1 [0, 1] INFO listobs::ms::summary+ 14:17:58.5 - 14:22:46.5 82 5 3C391 C4 187850 1 [0, 1] INFO listobs::ms::summary+ 14:22:47.5 - 14:27:35.5 83 6 3C391 C5 187850 1 [0, 1] INFO listobs::ms::summary+ 14:27:36.5 - 14:32:24.5 84 7 3C391 C6 187850 1 [0, 1] INFO listobs::ms::summary+ 14:32:25.5 - 14:37:13.5 85 8 3C391 C7 187850 1 [0, 1] INFO listobs::ms::summary+ 14:37:14.5 - 14:39:03.5 86 1 J1822-0938 71500 1 [0, 1] INFO listobs::ms::summary+ 14:39:04.5 - 14:44:22.5 87 2 3C391 C1 207350 1 [0, 1] INFO listobs::ms::summary+ 14:44:23.5 - 14:49:11.5 88 3 3C391 C2 187850 1 [0, 1] INFO listobs::ms::summary+ 14:49:12.5 - 14:54:01.5 89 4 3C391 C3 188500 1 [0, 1] INFO listobs::ms::summary+ 14:54:02.5 - 14:58:50.5 90 5 3C391 C4 187850 1 [0, 1] INFO listobs::ms::summary+ 14:58:51.5 - 15:03:39.5 91 6 3C391 C5 187850 1 [0, 1] INFO listobs::ms::summary+ 15:03:40.5 - 15:08:28.5 92 7 3C391 C6 187850 1 [0, 1] INFO listobs::ms::summary+ 15:08:29.5 - 15:13:17.5 93 8 3C391 C7 187850 1 [0, 1] INFO listobs::ms::summary+ 15:13:18.5 - 15:15:07.5 94 1 J1822-0938 71500 1 [0, 1] INFO listobs::ms::summary+ 15:15:08.5 - 15:20:26.5 95 2 3C391 C1 207350 1 [0, 1] INFO listobs::ms::summary+ 15:20:27.5 - 15:25:15.5 96 3 3C391 C2 187850 1 [0, 1] INFO listobs::ms::summary+ 15:25:16.5 - 15:30:05.5 97 4 3C391 C3 188500 1 [0, 1] INFO listobs::ms::summary+ 15:30:06.5 - 15:34:54.5 98 5 3C391 C4 187850 1 [0, 1] INFO listobs::ms::summary+ 15:34:55.5 - 15:39:43.5 99 6 3C391 C5 187850 1 [0, 1] INFO listobs::ms::summary+ 15:39:44.5 - 15:44:32.5 100 7 3C391 C6 187850 1 [0, 1] INFO listobs::ms::summary+ 15:44:33.5 - 15:49:22.5 101 8 3C391 C7 188500 1 [0, 1] INFO listobs::ms::summary+ 15:49:23.5 - 15:51:11.5 102 1 J1822-0938 70850 1 [0, 1] INFO listobs::ms::summary+ 15:51:12.5 - 16:00:10.5 103 9 J0319+4130 350350 1 [0, 1] INFO listobs::ms::summary (nVis = Total number of time/baseline visibilities per scan) INFO listobs::ms::summary Fields: 10 INFO listobs::ms::summary+ ID Code Name RA Decl Epoch SrcId nVis INFO listobs::ms::summary+ 0 N J1331+3030 13:31:08.2880 +30.30.32.9589 J2000 0 774800 INFO listobs::ms::summary+ 1 J J1822-0938 18:22:28.7042 -09.38.56.8350 J2000 1 1361750 INFO listobs::ms::summary+ 2 NONE 3C391 C1 18:49:24.2440 -00.55.40.5800 J2000 2 2488850 INFO listobs::ms::summary+ 3 NONE 3C391 C2 18:49:29.1490 -00.57.48.0000 J2000 3 2280850 INFO listobs::ms::summary+ 4 NONE 3C391 C3 18:49:19.3390 -00.57.48.0000 J2000 4 2282150 INFO listobs::ms::summary+ 5 NONE 3C391 C4 18:49:14.4340 -00.55.40.5800 J2000 5 2282150 INFO listobs::ms::summary+ 6 NONE 3C391 C5 18:49:19.3390 -00.53.33.1600 J2000 6 2281500 INFO listobs::ms::summary+ 7 NONE 3C391 C6 18:49:29.1490 -00.53.33.1600 J2000 7 2281500 INFO listobs::ms::summary+ 8 NONE 3C391 C7 18:49:34.0540 -00.55.40.5800 J2000 8 2282150 INFO listobs::ms::summary+ 9 Z J0319+4130 03:19:48.1601 +41.30.42.1030 J2000 9 350350 INFO listobs::ms::summary+ (nVis = Total number of time/baseline visibilities per field) INFO listobs::ms::summary Spectral Windows: (2 unique spectral windows and 1 unique polarization setups) INFO listobs::ms::summary+ SpwID #Chans Frame Ch1(MHz) ChanWid(kHz)TotBW(kHz) Ref(MHz) Corrs INFO listobs::ms::summary+ 0 64 TOPO 4536 2000 128000 4536 RR RL LR LL INFO listobs::ms::summary+ 1 64 TOPO 7436 2000 128000 7436 RR RL LR LL INFO listobs::ms::summary Sources: 20 INFO listobs::ms::summary+ ID Name SpwId RestFreq(MHz) SysVel(km/s) INFO listobs::ms::summary+ 0 J1331+3030 0 - - INFO listobs::ms::summary+ 0 J1331+3030 1 - - INFO listobs::ms::summary+ 1 J1822-0938 0 - - INFO listobs::ms::summary+ 1 J1822-0938 1 - - INFO listobs::ms::summary+ 2 3C391 C1 0 - - INFO listobs::ms::summary+ 2 3C391 C1 1 - - INFO listobs::ms::summary+ 3 3C391 C2 0 - - INFO listobs::ms::summary+ 3 3C391 C2 1 - - INFO listobs::ms::summary+ 4 3C391 C3 0 - - INFO listobs::ms::summary+ 4 3C391 C3 1 - - INFO listobs::ms::summary+ 5 3C391 C4 0 - - INFO listobs::ms::summary+ 5 3C391 C4 1 - - INFO listobs::ms::summary+ 6 3C391 C5 0 - - INFO listobs::ms::summary+ 6 3C391 C5 1 - - INFO listobs::ms::summary+ 7 3C391 C6 0 - - INFO listobs::ms::summary+ 7 3C391 C6 1 - - INFO listobs::ms::summary+ 8 3C391 C7 0 - - INFO listobs::ms::summary+ 8 3C391 C7 1 - - INFO listobs::ms::summary+ 9 J0319+4130 0 - - INFO listobs::ms::summary+ 9 J0319+4130 1 - - INFO listobs::ms::summary Antennas: 26: INFO listobs::ms::summary+ ID Name Station Diam. Long. Lat. INFO listobs::ms::summary+ 0 ea01 W09 25.0 m -107.37.25.2 +33.53.51.0 INFO listobs::ms::summary+ 1 ea02 E02 25.0 m -107.37.04.4 +33.54.01.1 INFO listobs::ms::summary+ 2 ea03 E09 25.0 m -107.36.45.1 +33.53.53.6 INFO listobs::ms::summary+ 3 ea04 W01 25.0 m -107.37.05.9 +33.54.00.5 INFO listobs::ms::summary+ 4 ea05 W08 25.0 m -107.37.21.6 +33.53.53.0 INFO listobs::ms::summary+ 5 ea07 N06 25.0 m -107.37.06.9 +33.54.10.3 INFO listobs::ms::summary+ 6 ea08 N01 25.0 m -107.37.06.0 +33.54.01.8 INFO listobs::ms::summary+ 7 ea09 E06 25.0 m -107.36.55.6 +33.53.57.7 INFO listobs::ms::summary+ 8 ea11 E04 25.0 m -107.37.00.8 +33.53.59.7 INFO listobs::ms::summary+ 9 ea12 E08 25.0 m -107.36.48.9 +33.53.55.1 INFO listobs::ms::summary+ 10 ea13 N07 25.0 m -107.37.07.2 +33.54.12.9 INFO listobs::ms::summary+ 11 ea14 E05 25.0 m -107.36.58.4 +33.53.58.8 INFO listobs::ms::summary+ 12 ea15 W06 25.0 m -107.37.15.6 +33.53.56.4 INFO listobs::ms::summary+ 13 ea16 W02 25.0 m -107.37.07.5 +33.54.00.9 INFO listobs::ms::summary+ 14 ea17 W07 25.0 m -107.37.18.4 +33.53.54.8 INFO listobs::ms::summary+ 15 ea18 N09 25.0 m -107.37.07.8 +33.54.19.0 INFO listobs::ms::summary+ 16 ea19 W04 25.0 m -107.37.10.8 +33.53.59.1 INFO listobs::ms::summary+ 17 ea20 N05 25.0 m -107.37.06.7 +33.54.08.0 INFO listobs::ms::summary+ 18 ea21 E01 25.0 m -107.37.05.7 +33.53.59.2 INFO listobs::ms::summary+ 19 ea22 N04 25.0 m -107.37.06.5 +33.54.06.1 INFO listobs::ms::summary+ 20 ea23 E07 25.0 m -107.36.52.4 +33.53.56.5 INFO listobs::ms::summary+ 21 ea24 W05 25.0 m -107.37.13.0 +33.53.57.8 INFO listobs::ms::summary+ 22 ea25 N02 25.0 m -107.37.06.2 +33.54.03.5 INFO listobs::ms::summary+ 23 ea26 W03 25.0 m -107.37.08.9 +33.54.00.1 INFO listobs::ms::summary+ 24 ea27 E03 25.0 m -107.37.02.8 +33.54.00.5 INFO listobs::ms::summary+ 25 ea28 N08 25.0 m -107.37.07.5 +33.54.15.8 INFO listobs::::casa INFO listobs::::casa ##### End Task: listobs ##### INFO listobs::::casa ##########################################
Both to get a sense of the array, as well as identify an antenna for later use in calibration, use the task plotants. In general, for calibration purposes, one would like to select an antenna that is close to the center of the array (and that is not listed in the operator's log as having had problems!).
# In CASA
pl.ion() # This is a temporary fix to allow the GUI to come up; should be fixed soon
plotants(vis='3c391_ctm_mosaic_10s_spw0.ms',figfile='3c391_ctm_mosaic_antenna_layout.png')
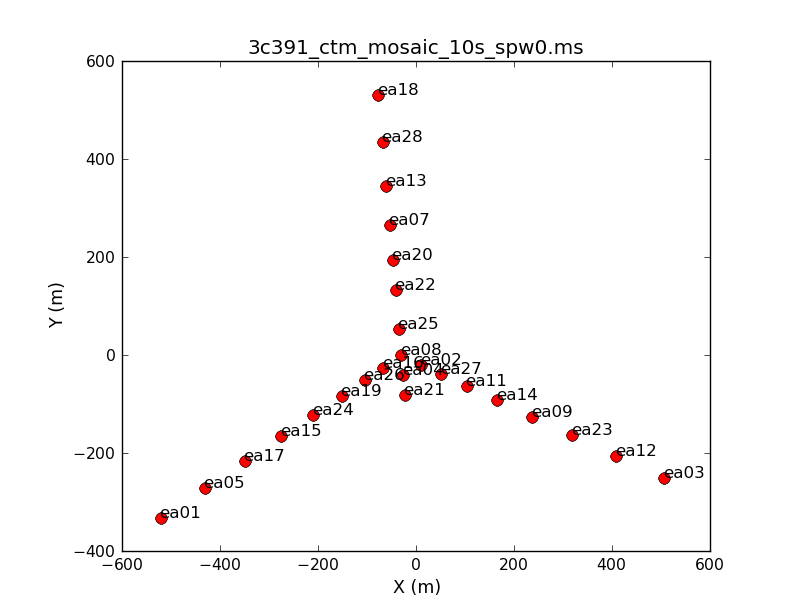
Examining and Editing the Data
It is always a good idea, particularly with a new system like the EVLA, to examine the data. Moreover, from the observer's log, we already know that one antenna will need to be flagged because it does not have a C-band receiver. Start by flagging data known to be bad, then examine the data.
In its current operation, it is common to insert a dummy scan as the first scan. (From the listobs output above, one may have noticed that the first scan is less than 1 minute long.) This first scan can safely be deleted.
# In CASA
flagdata(vis='3c391_ctm_mosaic_10s_spw0.ms',flagbackup=T,mode='manualflag',selectdata=T,scan='1')
- flagbackup=T : A comment is warranted on the setting of flagbackup (here set to T or True). If set to True, flagdata will save a copy of the existing set of flags before entering any new flags. The setting of flagbackup is therefore a matter of some taste. One could choose not to save any flags or only save "major" flags, or one could save every flag. (One of the authors of this document was glad that flagbackup was set to True as he recently ran flagdata with a typo in one of the entries.)
- mode='manualflag' : Specific data are going to be selected to be edited.
- selectdata=T : In order to select the specific data to be flagged, selectdata has to be set to True. Once selectdata is set to True, then the various data selection options become visible (use help flagdata to see the possible options). In this case, scan='1' is chosen to select only the first scan. Note that scan expects an entry in the form of a string. (scan=1 would generate an error.)
If satisfied with the inputs, run this task. The initial display in the logger will include
########################################## ##### Begin Task: flagdata ##### flagdata::::casa attached MS [...] Saving current flags to manualflag_2 before applying new flags Creating new backup flag file called manualflag_2
which indicates that, among other things, the flags that existed in the data set prior to this run will be saved to another file called manualflag_2. Should one ever desire to revert to the data prior to this run, the task flagmanager could be used.
From the observer's log, we know that antenna 13 does not have a C band receiver, so it should be flagged as well. The parameters are similar as before.
# In CASA
flagdata(vis='3c391_ctm_mosaic_10s_spw0.ms',flagbackup=T,mode='manualflag',selectdata=T,antenna='ea13')
- antenna='ea13' : Once again, this parameter requires a string input. Also note that antenna='ea13' and 'antenna='13' are not the same antenna. (Check the output from listobs above.)
Finally, it is common for the array to require a small amount of time to "settle down" at the start of a scan. Consequently, it has become standard practice to edit out the initial samples from the start of each scan.
# In CASA
flagdata(vis='3c391_ctm_mosaic_10s_spw0.ms',mode='quack',quackinterval=10.0,quackmode='beg')
- mode='quack' : Quack is another mode in which the same edit will be applied to all scans for all baselines.
- quackmode='beg' : In this case, data from the start of each scan will be flagged. Other options include flagging data at the end of the scan.
- quackinterval=10 : In this data set, the sampling time is 10 seconds, so this choice flags the first sample from all scans on all baselines.
Having now done some basic editing of the data, based in part on a priori information, it is time to look at the data to determine if there are any other obvious problems. One task to examine the data themselves is plotms.
# In CASA
plotms(vis='3c391_ctm_mosaic_10s_spw0.ms',xaxis='',yaxis='',averagedata=False,transform=False,extendflag=False,
plotfile='',selectdata=True,field='0')
- xaxis=' ', yaxis=' ' : One can choose the axes of the plot, i.e., the way of visualizing the data, by using the GUI display once the task is executed.
- averagedata=F : It is possible to average the data in time, frequency, etc.
- transform=F : It is possible to change the velocity reference frame of the data.
- extendflag=F : It is possible to "extend" a flag, i.e., flag data surrounding bad data. For example, one might want to flag spectral channels surrounding a bad spectral channel or one might want to flag cross-polarization data if one flags the parallel polarization data.
- plotfile=' ' : It is possible to produce a hard copy (e.g., for a paper, report, or Web site) by specifying a file.
- selectdata=T : One can choose to plot only subsets of the data.
- field='0': The entire dataset is rather large, and different sources have very different amplitudes, so it is advisable to start by loading a subset of the data. One can later loop through the different fields (i.e. sources) and spectral windows using the GUI interface.
In this case, many other values have been left to defaults as it is also possible to select them from within the plotms GUI. Review the inputs, then run the task.
plotms should produce a GUI, with the default view being to show the visibility amplitude as a function of time.
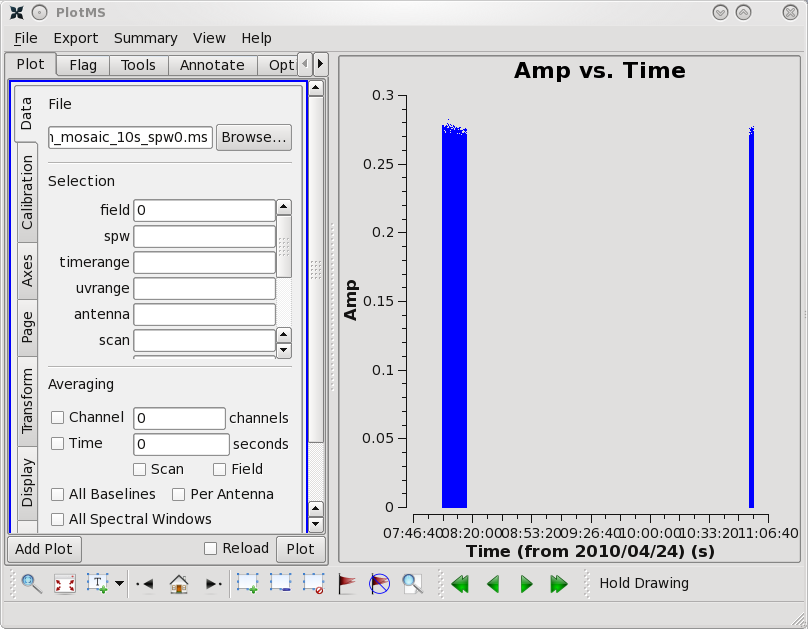
plotms allows one to select and view the data in many ways. Across the top of the left panel are a set of tabs labeled 'Plots', 'Flagging', 'Tools', 'Annotator', and 'Options'. If one selects the 'Flagging' tab, the option is to 'Extend flags'. Thus, even though plotms was started with extendflag=F, if one decides that it does make sense to extend the flags, one can still do so here.
In the default view, the 'Plots' tab is visible, and there are a number of tabs running down the side of the left hand panel, including 'Data', 'Axes', 'Trans', 'Cache', 'Display', 'Canvas', and 'Export'. Once again, one can make changes on the fly. Thus, supposing that one wants to save a hard copy, even if plotms was started with plotfile=' ', one can select 'Export' and enter a file name in which to save a copy of a plot.
One should spend several minutes displaying the data in various formats. For instance, one could select the 'Data' tab and specify field 0 (source J1331+3030, a.k.a. 3C 286) to display data associated with the amplitude calibrator, then select the 'Axes' tab and change the x axis to be UVDist, and plot the data. The result should be that of the first thumbnail image shown below. The amplitude distribution is relatively constant as a function of u-v distance or baseline length (i.e., [math]\displaystyle{ \sqrt{u^2+v^2} }[/math]). From the various lectures, one should recognize that a relatively constant visibility amplitude as a function of baseline length means that the source is very nearly a point source. (The Fourier transform of a constant is a delta function, a.k.a. a point source.)
By contrast, if one selects field 3 (one of the 3C 391 fields) in the 'Data' tab and plots these data, one sees a visibility function that falls rapidly with increasing baseline length. Such a visibility function indicates a highly resolved source. By noting the baseline length at which the visibility function falls to some fiducial value (e.g., 1/2 of its peak value), one can obtain a rough estimate of the angular scale of the source. (From the lectures, angular scale [in radians] ~ 1/baseline [in wavelengths].)
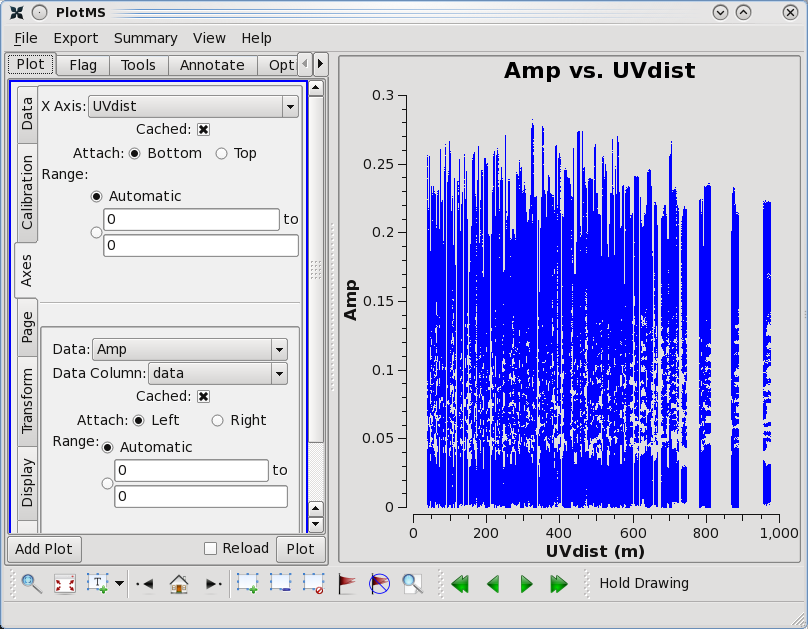
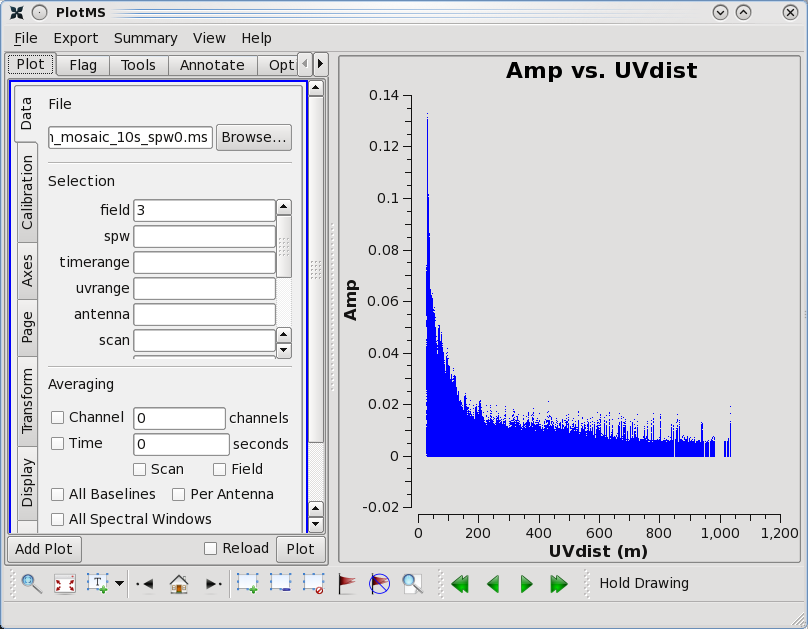
As a general data editing and examination strategy, at this stage in the data reduction process, one wants to focus on the calibrators. The data reduction strategy is to determine various corrections from the calibrators, then apply these correction factors to the science data. The 3C 286 data look relatively clean. There are no wildly egregious data (e.g., amplitudes that are 100,000x larger than the rest of the data). One may notice that there are antenna-to-antenna variations (under the 'Display' tab, select 'Colorize by Antenna1'). These antenna-to-antenna variations are acceptable, that's what calibration will help determine.
Do not close the plotms GUI after running plotms, or you will need to exit casapy and restart if at any point you wish to run plotms again, otherwise the GUI will not come up a second time.
Calibrating the Data
It is now time to begin calibrating the data. The general data reduction strategy is to derive a series of scaling factors or corrections from the calibrators, which are then collectively applied to the science data. For much more discussion of the philosophy, strategy, and implementation of calibration of synthesis data within CASA, see Synthesis Calibration in the CASA Reference Manual.
Recall that the observed visibility [math]\displaystyle{ V^{\prime} }[/math] between two antennas [math]\displaystyle{ (i,j) }[/math] is related to the "true" visibility [math]\displaystyle{ V }[/math] by
[math]\displaystyle{ V^{\prime}_{i,j}(u,v,f) = b_{ij}(t)\,[B_i(f,t) B^{*}_j(f,t)]\,g_i(t) g_j(t)\,V_{i,j}(u,v,f)\,e^{i [\theta_i(t) - \theta_j(t)]} }[/math]
Here, for generality, we show the visibility as a function of frequency [math]\displaystyle{ f }[/math] and spatial wavenumbers [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math]. The other terms are
- [math]\displaystyle{ g_i }[/math] and [math]\displaystyle{ \theta_i }[/math] are the amplitude and phase portions of what is commonly termed the complex gain. They are shown separately here because they are usually determined separately. For completeness, these are shown as a function of time t to indicate that they can change with temperature, atmospheric conditions, etc.
- [math]\displaystyle{ B_i }[/math] is the complex bandpass. This is clearly a function of frequency [math]\displaystyle{ f }[/math], but, for completeness, it is also shown as a function of time.
- [math]\displaystyle{ b(t) }[/math] is the often-neglected baseline term. It shall be neglected here as well, though it can be important to include for the highest dynamic range images or shortly after a configuration change at the [E]VLA, when antenna positions may not be known well.
Strictly, the equation above is a simplification of a more general measurement equation formalism, but it is a useful simplification in many cases.
For safety or sanity, one can begin by "clearing the calibration." In CASA, the data structure is that the observed data are stored in a DATA column, estimates of the data (e.g., a priori models for the calibrators, and those derived from the self-calibration process to be done later) are stored in the MODEL_DATA column, and the calibrated data are stored in the CORRECTED_DATA column. The task clearcal initializes the MODEL_DATA and CORRECTED_DATA and sets up some scratch data columns as well. For a pristine data set, straight from the Archive, clearcal probably should not be required; clearcal could be quite important if one decides later that a horrible mistake has been made in the calibration process and one wishes to start over. If you have started with the 10s-averaged dataset suggested at the top of this tutorial, this step has already been done for you, so may be omitted.
# In CASA
clearcal(vis='3c391_ctm_mosaic_10s_spw0.ms',field='',spw='')
All parameters are set to blank so that the initialization occurs for all sources and spectral windows.
The first step is to provide a flux density value for the amplitude calibrator J1331+3030 (a.k.a. 3C 286). For the VLA, the ultimate flux density scale at most frequencies was set by 3C 295, which was then transferred to a small number of "primary flux density calibrators," including 3C 286. For the EVLA, at the time of this writing, the flux density scale at most frequencies will be determined from WMAP observations of the planet Mars, in turn then transferred to a small number of primary flux density calibrators. Thus, the procedure is to assume that the flux density of a primary calibrator source is known and, by comparison with the observed data for that calibrator, determine the [math]\displaystyle{ g_i }[/math] values.
# In CASA
setjy(vis='3c391_ctm_mosaic_10s_spw0.ms',field='J1331+3030',
modimage='/home/casa/data/nrao/VLA/CalModels/3C286_C.im',standard='Perley-Taylor 99',
fluxdensity=-1)
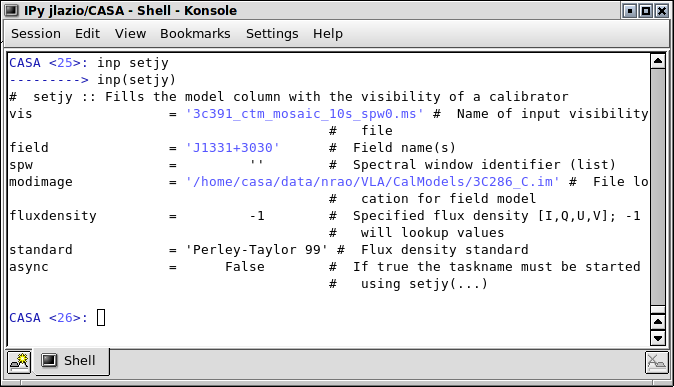
- field='J1331+3030' : Clearly one has to specify what the flux density calibrator is, otherwise all sources will be assumed to have the same flux density.
- modimage='/home/casa/data/nrao/VLA/CalModels/3C286_C.im' : Although above, from plotms, it was estimated that 3C 286 is roughly a point source, depending upon the frequency and configuration, the source may be slightly resolved. Fiducial model images have been determined from a painstaking set of observations, and, if one is available, it should be used to compensate for slight resolution effects. In this case, spectral window 0 (at 4.536 GHz) is in the C band, so the C-band model image is used.
- standard='Perley-Taylor 99' : Periodically, the flux density scale at the VLA was revised, updated, or expanded. The specified value represents the most recent determination of the flux density scale (by R. Perley and G. Taylor in 1999); older scales can also be specified, and might be important if, for example, one was attempting to conduct a careful comparison with a previously published result.
- fluxdensity=-1 : It is possible to specify (i.e., force) the flux density of the source to be a particular value.
- spw='0' : The original data contained two spectral windows. Having split off spectral window 0, it is not necessary to specify spw, but it will not hurt to do so. Had the spectral window 0 not been split off, as has been done here, it would be necessary to specify the spectral window because, in this observation, the spectral windows were sufficiently separated that the spectrum of 3C 286 means that the same flux density for the calibrator source cannot be assumed for both. If the spectral windows were much closer together, it might be possible to calibrate both with the same flux density value.
In this case, a model image of a primary flux density calibrator exists. However, for some kinds of polarization calibration or in extreme situations (e.g., there are problems with the scan on the flux density calibrator), it can be useful or required to set the flux density of the source explicitly.
The output from setjy should look similar to the following.
INFO taskmanager::::casa ##### async task launch: setjy ######################## INFO setjy::imager::setjy() J1331+3030 spwid= 0 [I=7.747, Q=0, U=0, V=0] Jy, (Perley-Taylor 99) INFO setjy::imager::setjy() Using model image /home/casa/data/nrao/VLA/CalModels/3C286_C.im INFO setjy::imager::setjy() The model image's reference pixel is 0.00302169 arcsec from J1331+3030's phase center. INFO setjy::imager::setjy() Scaling model image to I=7.74664 Jy for visibility prediction. INFO setjy::imager::data selection Selecting data
As set, the flux density scale is being set only for spectral window 0 (spw='0' ). The flux density at the center of the spectral window is reported. This value is determined from an analytical formula for the spectrum of the source as a function of frequency; this value must be determined so that the flux density in the image can be scaled to it, as it is unlikely that the observation was taken at exactly the same frequency as the model image.
Bandpass Calibration
In this step one solves for the complex bandpass, [math]\displaystyle{ B_i }[/math].
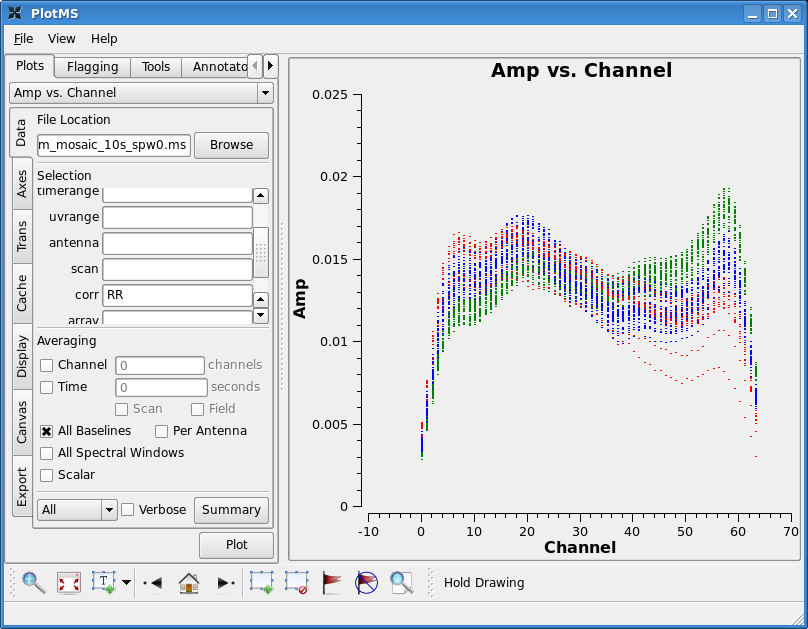
For the VLA, in its old continuum modes, this step could be skipped. With the EVLA, all data are spectral line, even if the science that one is conducting is continuum. Solving for the bandpass won't hurt for continuum data, and, for moderate or high dynamic range image, it is essential. To motivate the need for solving for the bandpass, consider the image to the left. It shows the right circularly polarized data (RR polarization) for the source J1331+3030, which will serve as the bandpass calibrator. The data are color coded by scan, and they are averaged over all baselines, as earlier plots from plotms indicated that the visibility data are nearly constant with baseline length. Ideally, the visibility data would be constant as a function of frequency, with the same amplitude on all baselines. The variations with frequency are a reflection of the (slightly) different antenna bandpasses. (Exercise for the reader, reproduce this plot using plotms.)
Depending upon frequency and configuration, there could be gain variations between the different scans of the bandpass calibrator, particularly if the scans happen at much different elevations. One can solve for an initial set of antenna-based gains, which will later be discarded, in order to moderate the effects of gain variations from scan to scan on the bandpass calibrator.
# In CASA
gaincal(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic.gcal0',field='J1331+3030',
refant='ea21',spw='0:27~36',calmode='p',solint='int',minsnr=5,solnorm=T)
- caltable='3c391_ctm_mosaic.gcal0' : The gain solutions will be stored in an external table.
- field='J1331+3030' : Specify the bandpass calibrator. In this case, the bandpass calibrator and the amplitude calibrator happen to be the same source, but it is not always so.
- refant='ea21' : Earlier, by looking at the output from plotants, a reference antenna near the center of the array was noted. Here is the first time that that choice will be used. Strictly, all of the gain corrections derived will be relative to this reference antenna.
- spw='0:27~36': One wants to choose a subset of the channels from which to determine the gain corrections. These should be near the center of the band, and there should be enough channels chosen so that a reasonable signal-to-noise ratio can be obtained. (See the output of plotms above.) Particularly at lower frequencies where RFI can manifest itself, one should choose RFI-free frequency channels. Also note that, even though these data have only a single spectral window, the syntax requires specifying the spectral window in order to specify the spectral channels.
- calmode='p' : Solve for only the phase portion of the gain.
- solint='int' : One wants to be able to track the phases, so a short solution interval is chosen. (A single integration time or 10 seconds for this case)
- minsnr=5 : One probably wants to restrict the solutions to be at relatively high signal-to-noise ratios, although this parameter may need to be varied depending upon the source and frequency.
- solnorm=T : Strictly, for a phase-only solution, the amplitudes should be normalized by zero. This setting enforces that.
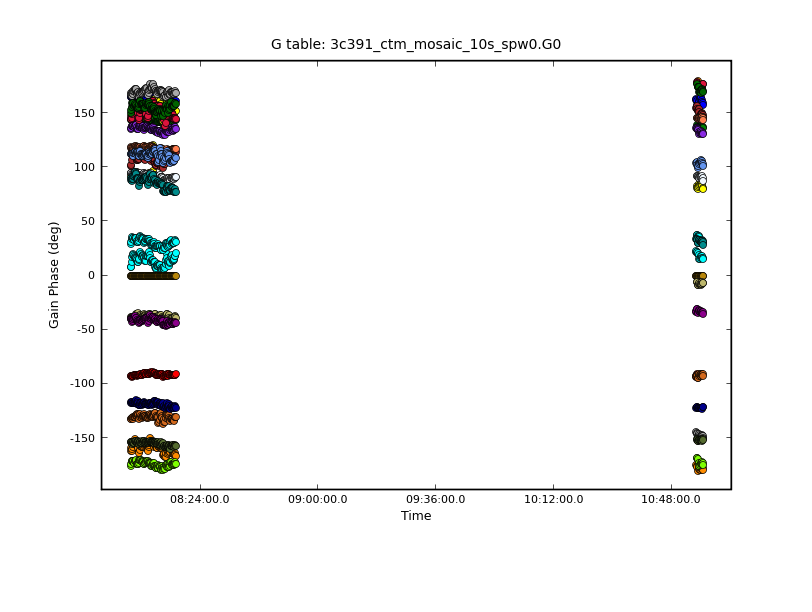
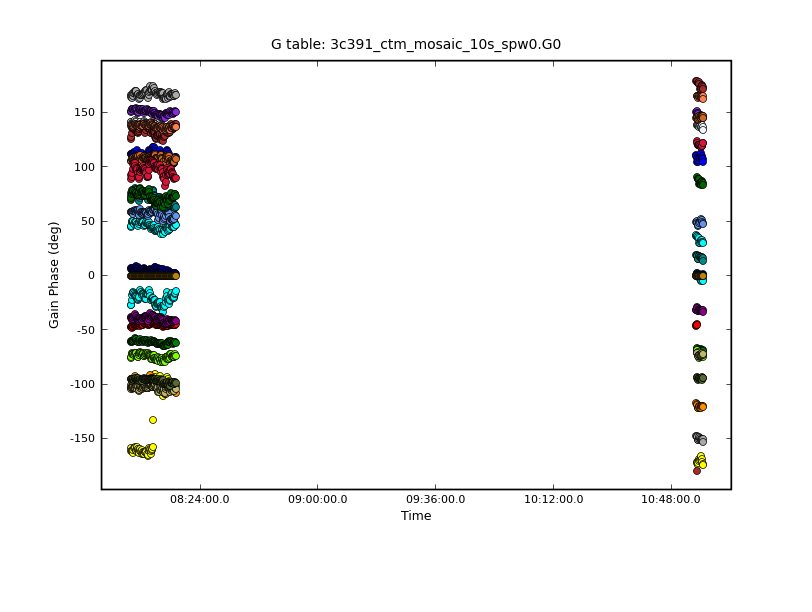
One can now examine the phase solutions using plotcal. The inputs shown below plot the phase portion of the gain solutions as a function of time for the calibrator for R and L polarization separately.
# In CASA
plotcal(caltable='3c391_ctm_mosaic.gcal0',xaxis='time',yaxis='phase',poln='R',field='J1331+3030',spw='',
figfile='plotcal-3C286-G0-phase-R.png')
# In CASA
plotcal(caltable='3c391_ctm_mosaic.gcal0',xaxis='time',yaxis='phase',poln='L',field='J1331+3030',spw='',
figfile='plotcal-3C286-G0-phase-L.png')
Inspection of the resulting plots (shown below, exercise for the reader, reproduce these plots) shows that the phase is relatively stable within a scan, but does vary from scan to scan. If plotcal is run interactively, with the GUI, one can select sub-regions within the plot and zoom into them to look at the phase in more detail.
Now form the bandpass itself, using the phase solutions just derived.
# In CASA
bandpass(vis='3c391_ctm_mosaic_10s_spw0.ms',gaintable='3c391_ctm_mosaic.gcal0',caltable='3c391_ctm_mosaic.bcal0',
field='J1331+3030',spw='',refant='ea21',solnorm=True,combine='scan',solint='inf',bandtype='B')
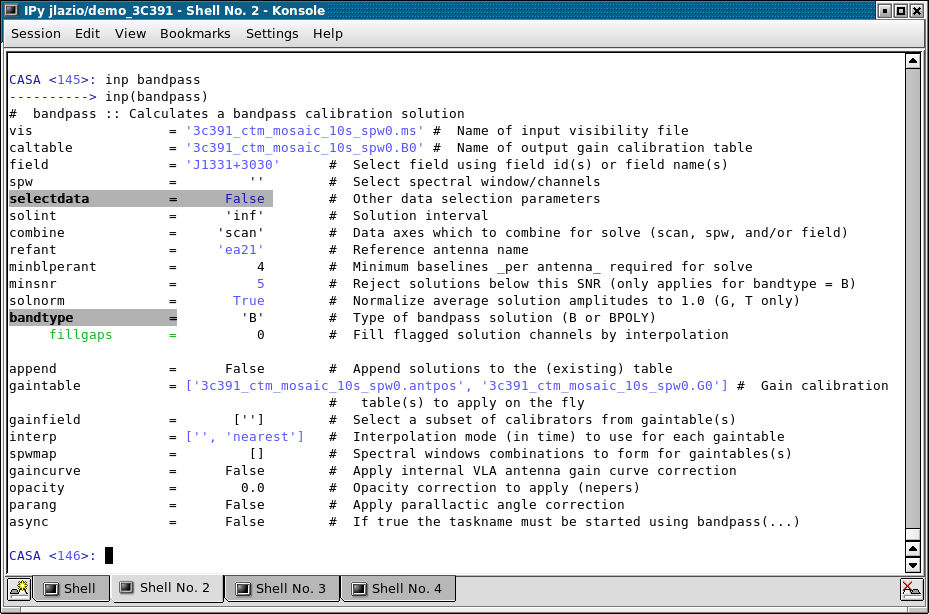
- gaintable='3c391_ctm_mosaic.gcal0' : This gaintable contains the phase solutions just derived. By having a non-blank value for gaintable, bandpass will apply the solutions contained within it before deriving the bandpass corrections themselves.
- caltable='3c391_ctm_mosaic.bcal0' : Specify where to store the bandpass corrections.
- solnorm=T : Make sure that the amplitudes of the bandpass corrections are normalized to unity.
- solint='inf' and combine='scan' : This observation contains multiple scans on the bandpass calibrator, J1331+3030. Because these are continuum observations, it is probably acceptable to combine all the scans and compute one bandpass correction per antenna, which is achieved by the combination of solint='inf' and combine='scan'. Had combine=' ', then there would have been a bandpass correction derived per scan, which might be necessary for the highest dynamic range spectral line observations.
- bandtype='B' : The bandpass solution will be derived on a channel-by-channel basis. There is an alternate, somewhat experimental option of bandtype='BPOLY' that will attempt to fit an n-th order polynomial to the bandpass.
Once again, one can use plotcal to display the bandpass solutions. Note that in the plotcal inputs below, the amplitudes are being displayed as a function of frequency channel and, for compactness, subplot=221 is used to display multiple plots per page. One could use yaxis='phase' to view the phases as well. We use iteration='antenna' to step through separate plots for each antenna.
# In CASA
plotcal(caltable= '3c391_ctm_mosaic.bcal0',poln='R',xaxis='chan',yaxis='amp',field= 'J1331+3030',subplot=221,
iteration='antenna',figfile='plotcal-3C286-B0-R.png')
plotcal(caltable= '3c391_ctm_mosaic.bcal0',poln='L',xaxis='chan',yaxis='amp',field= 'J1331+3030',subplot=221,
iteration='antenna',figfile='plotcal-3C286-B0-L.png')
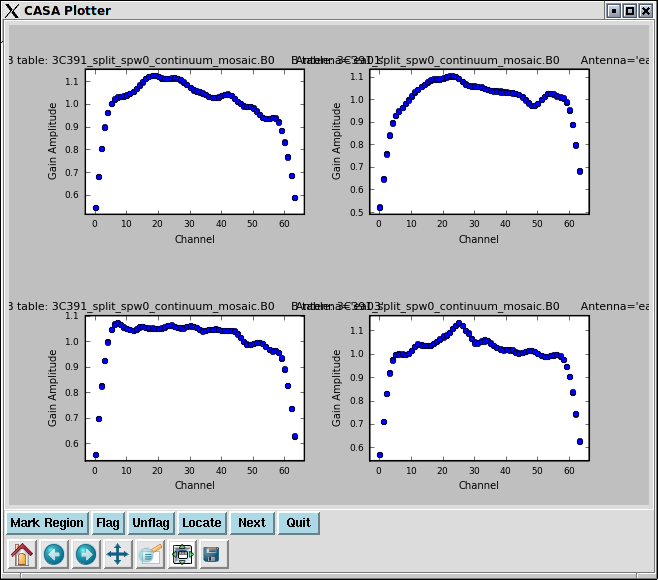
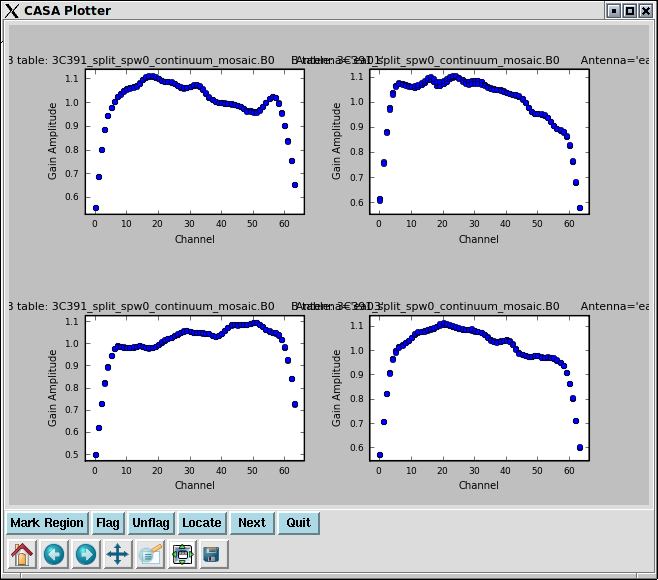
Gain Calibration
The next step is to derive corrections for the complex antenna gains, [math]\displaystyle{ g_i }[/math] and [math]\displaystyle{ \theta_i }[/math]. As discussed in the lectures and above, the gain amplitudes [math]\displaystyle{ g_i }[/math] are determined by reference to a standard flux density calibrator. In order to determine the gain phases [math]\displaystyle{ \theta_i }[/math], one wants to observe a phase calibrator that is much closer to the target source, in order to minimize differences through the atmosphere (neutral and/or ionized) between the lines of sight to the phase calibrator and the target source. In principle, one could determine the complex antenna gains with a single invocation of gaincal; for clarity here, two separate invocations will be used.
In the first step, the gain amplitudes [math]\displaystyle{ g_i }[/math] will be determined from the flux density calibrator 3C 286.
# In CASA
gaincal(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic.gcal1',field='J1331+3030',spw='0:5~58',
refant='ea21',gaintype='G',gaintable='3c391_ctm_mosaic.bcal0',calmode='ap',solint='inf')
- caltable='3c391_ctm_mosaic.gcal1' : Produce a new calibration table containing these gain solutions. In order to make the bookkeeping easier, a '1' is appended to the file name to distinguish it from the earlier set of gain solutions, which are effectively being "thrown away."
- spw='0:5~58' : From the inspection of the bandpass, one can determine the range of edge channels that are affected by the bandpass filter rolloff. Because the amplitude is dropping rapidly in these channels, one does not want to include them in the solution.
- gaintype='G' and calmode='ap' : Solve for the complex antenna gains.
- solint='inf' : Produce a solution for each scan.
- gaintable='3c391_ctm_mosaic.bcal0' : Use the bandpass solutions determined earlier to correct for the bandpass shape before solving for the gain amplitudes.
After reviewing the inputs to gaincal and running it, one could use plotcal to plot the solutions. While a useful sanity check, the plots themselves will be rather sparse as only a single gain amplitude is being determined for each antenna for each scan.
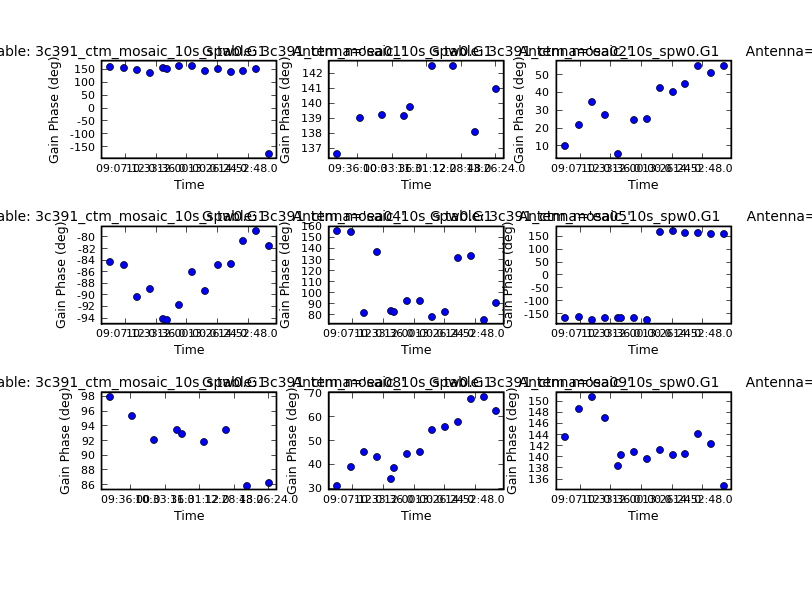
In the second step, the gain amplitudes [math]\displaystyle{ \theta_i }[/math] will be determined from the phase calibrators J1822-0938 and J0319+4130.
# In CASA
gaincal(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic.gcal1',field='J1822-0938,J0319+4130',
spw='0:5~58',refant='ea21',gaintype='G',gaintable='3c391_ctm_mosaic.bcal0',calmode='ap',
solint='inf',append=True)
- caltable='3c391_ctm_mosaic.gcal1' and append=True : In all previous invocations of gaincal, append has been set to False. Here, the gain solutions from the phase calibrators are going to be appended to the existing set from 3C 286. In following steps, all of these gain solutions will then be used together to derive a set of complex gains that are applied to the science data for the target source.
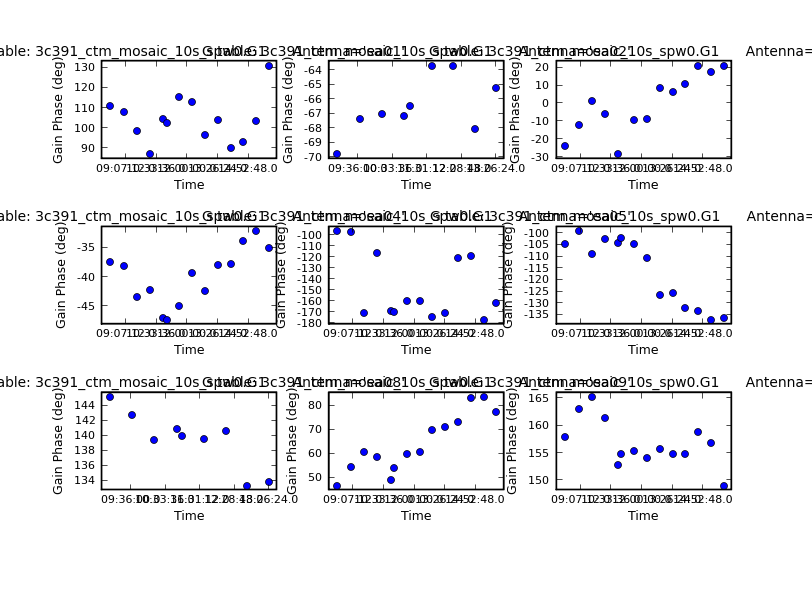
If one checks the gain phase solutions using plotcal, one should see several solutions for each antenna as a function of time. In order to track the phases, the phase calibrator is typically observed much more frequently during the course of an observation than is the flux density calibrator. In the examples shown below, note that one of the panels is blank, which corresponds to antenna 13, the one flagged earlier in the process.
Polarization Calibration
[If time is running short, skip this step and proceed to [Applying the Calibration].]
Having set the complex gains, we now need to do the polarization calibration. This should be done prior to running fluxscale, since it has to run using the un-rescaled gains in the MODEL_DATA column of the measurement set. Polarization calibration is done in two steps. First, we solve for the instrumental polarization (the frequency-dependent leakage terms, or 'D-terms'), using either an unpolarized source or a source which has sufficiently good parallactic angle coverage. Second, we solve for the polarization position angle using a source with a known polarization position angle (3C 286 is recommended here).
Our initial run of setjy only set the total intensity of our flux calibrator source, 3C 286. This source is known to have a fractional polarization of 11.2% at C-band, and a polarization position angle of 66 degrees. In order to calibrate the position angle, we need to set the appropriate values for Stokes Q and U. Examining our casapy.log file to find the output of setjy, we find that the total intensity was set to 7.74664 Jy in spw0. We therefore use python to find the polarized flux, P, and the values of Stokes Q and U.
# In CASA
i0=7.74664 # Stokes I value for spw 0
p0=0.112*i0 # Fractional polarization=11.2%
q0=p0*cos(66*pi/180) # Stokes Q for spw 0
u0=p0*sin(66*pi/180) # Stokes U for spw 0
We now set the values of Stokes Q and U for 3C 286, using setjy as we did before.
# In CASA
setjy(vis='3c391_ctm_mosaic_10s_spw0.ms',field='J1331+3030',modimage='',spw='0',fluxdensity=[i0,q0,u0,0])
- modimage=' ' : A model image is not used here.
Note that the Stokes V flux value is set to zero, corresponding to no circular polarization.
Solving for the Leakage Terms
The task we will use to do all the polarization calibration is polcal. In this data set, we observed the unpolarized calibrator J0319+4130 (a.k.a. 3C 84) in order to solve for the instrumental polarization. polcal uses the Stokes IQU values in the MODEL_DATA column (Q and U being zero for our unpolarized calibrator) to derive the leakage solutions. The final function call is:
# In CASA
polcal(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic.pcal0',field='J0319+4130',
spw='',refant=refant,poltype='Df',
gaintable=['3c391_ctm_mosaic.gcal1', '3c391_ctm_mosaic.bcal0'],
gainfield=['J0319+4130', 'J1331+3030'])
- caltable='3c391_ctm_mosaic.pcal0' : polcal will create a new calibration table containing the leakage solutions, which we specify with the caltable argument.
- field='J0319+4130' : We use the unpolarized source J0319+4130 (a.k.a. 3C 84) to solve for the leakages.
- poltype='Df' : We will solve for the leakages (D) on a per-channel basis (f). Had we have been solving for the leakages using a calibrator with unknown polarization but with good parallactic angle coverage, we would simultaneously have needed to solve for the source polarization (poltype='Df+QU' ).
- gaintable=['3c391_ctm_mosaic.gcal1', '3c391_ctm_mosaic.bcal0'] : We apply our existing gain and bandpass tables on-the-fly by specifying them in a Python list.
- gainfield=['J0319+4130','J1331+3030'] : Use only the specified sources from 3c391_ctm_mosaic.gcal1 and 3c391_ctm_mosaic.bcal0, respectively, when applying these previous gain and bandpass corrections.
After polcal has finished running, you are strongly advised to examine the solutions with plotcal, to ensure that everything looks good.
# In CASA
plotcal(caltable='3c391_ctm_mosaic.pcal0',xaxis='chan',yaxis='amp',spw='',field='',iteration='antenna')
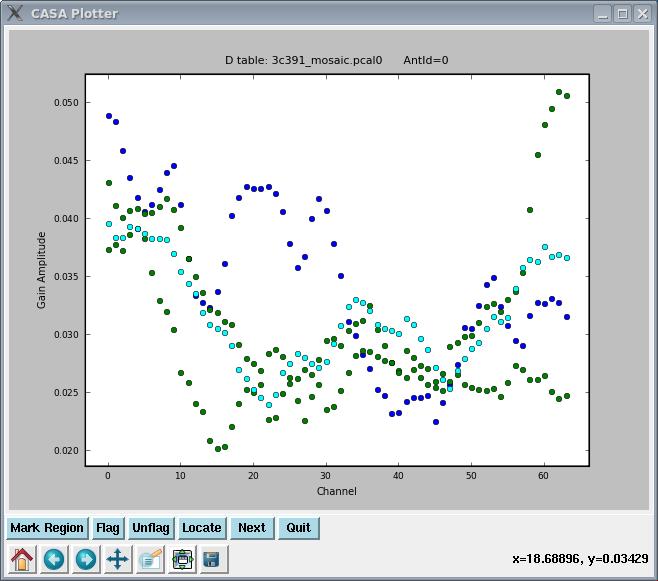
This will produce plots similar to that shown at right. As ever, you can cycle through the antennas by clicking the "Next" button. You should see leakages of between 5 and 15% in most cases.
Solving for the R-L polarization angle
Having calibrated the instrumental polarization, the total polarization is now correct, but we still need to calibrate the R-L phase, to get an accurate polarization position angle. We use the same task, polcal, but this time set poltype='Xf' , which specifies a frequency-dependent (f) position angle (X) calibration, using the source J1331+3030 (aka 3C 286), whose position angle we know, having set this earlier using setjy. Note that we must correct for the leakages before determining the R-L phase, which we do by adding the calibration table made in the previous step (3c391_ctm_mosaic.pcal0) to the gain tables which are applied on-the-fly.
# In CASA
polcal(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic.xcal0',poltype='Xf',
gaintable=['3c391_ctm_mosaic.gcal1', '3c391_ctm_mosaic.bcal0', '3c391_ctm_mosaic.pcal0'],
field='J1331+3030',refant='ea21')
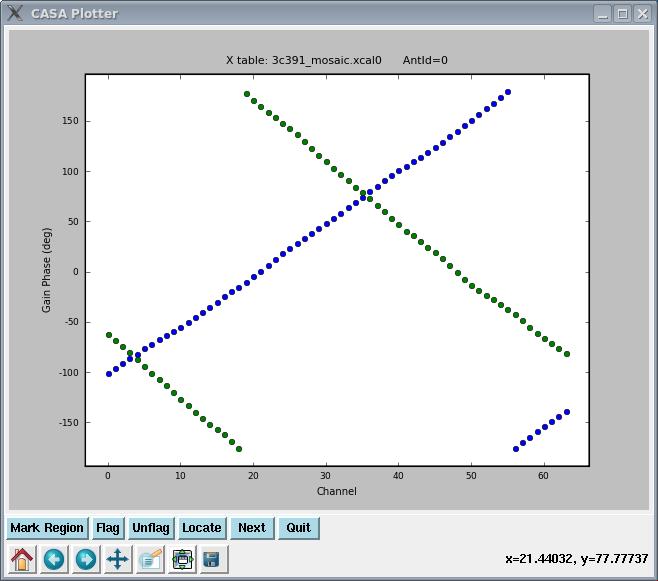
Again, it is strongly suggested that you check the calibration worked properly, by plotting up the newly-generated calibration table using plotcal. The results are shown at right. You will notice that when iterating, the calibration appears to be identical for all antennas.
# In CASA
plotcal(caltable='3c391_ctm_mosaic.xcal0',xaxis='chan',yaxis='phase',iteration='antenna')
At this point, your dataset contains all the necessary polarization calibration, which will shortly be applied to the data.
Applying the Calibration
While we know the flux density of our primary calibrator (in our case, J1331+3030[math]\displaystyle{ \equiv }[/math]3C 286), the model assumed for the secondary calibrator (here, J1822-0938) was a point source of 1 Jy located at the phase center. While the secondary calibrator was chosen to be a point source (at least, over some limited range of uv-distance; see the VLA calibrator manual for any u-v restrictions on your calibrator of choice at the observing frequency), its absolute flux density is unknown. Being pointlike, secondary calibrators typically vary on timescales of months to years, in some cases by up to 50--100%. A nice Java Applet is available to track the flux density history of various calibrators over time. Play around with it to see how much some of the calibrators from the manual can vary, and over what sorts of timescales.
We use the primary calibrator (the 'flux calibrator') to determine the system response to a source of known flux density, and assume that the mean gain amplitudes for the primary calibrator are the same as those for the secondary calibrator. This then allows us to find the true flux density of the secondary calibrator. To do this, we use the task fluxscale, which produces a new calibration table containing properly-scaled amplitude gains for the secondary calibrator.
# In CASA
fluxscale(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic.gcal1',fluxtable='3c391_ctm_mosaic.fluxscale1',
reference='J1331+3030',transfer='J1822-0938,J0319+4130',append=True)
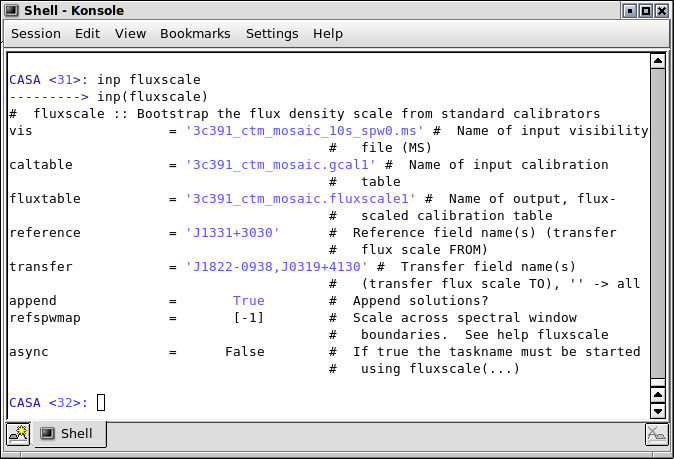
- caltable='3c391_ctm_mosaic.gcal1' : We provide fluxscale with the calibration table containing the amplitude gain solutions derived earlier
- fluxtable='3c391_ctm_mosaic.fluxscale1' : We specify the name of the new output table to be written, which will contain the properly-scaled amplitude gains.
- reference='J1331+3030' : We specify the source with the known flux density.
- transfer='J1822-0938,J0319+4130' : We specify the sources whose amplitude gains are to be rescaled.
fluxscale will print to the CASA logger the derived flux densities of all calibrator sources specified with the transfer argument. You should examine the output to ensure that it looks sensible. If one's data set has more than 1 spectral window, depending upon where they are spaced and the spectrum of the source, it is quite possible to find (quite) different flux densities at the different frequencies for the secondary calibrators. Example output for this data set would be
INFO fluxscale::::casa ########################################## INFO fluxscale::::casa ##### Begin Task: fluxscale ##### INFO fluxscale::::casa INFO fluxscale::calibrater::open Opening MS: 3c391_mosaic_10s.ms for calibration. INFO fluxscale::Calibrater:: Initializing nominal selection to the whole MS. INFO fluxscale::calibrater::fluxscale Beginning fluxscale--(MSSelection version)------- INFO fluxscale:::: Found reference field(s): J1331+3030 INFO fluxscale:::: Found transfer field(s): J1822-0938 J0319+4130 INFO fluxscale:::: Flux density for J1822-0938 in SpW=0 is: 2.32824 +/- 0.00706023 (SNR = 329.768, nAnt= 25) INFO fluxscale:::: Flux density for J0319+4130 in SpW=0 is: 13.7643 +/- 0.0348429 (SNR = 395.04, nAnt= 25) INFO fluxscale::Calibrater::fluxscale Appending result to 3c391_mosaic.fluxscale1 INFO fluxscale:::: Appending solutions to table: 3c391_mosaic.fluxscale1 INFO fluxscale::::casa INFO fluxscale::::casa ##### End Task: fluxscale #####
The VLA calibrator manual can be used to check whether the derived flux densities look sensible. Wildly different flux densities or flux densities with very high error bars should be treated with suspicion; in such cases you will have to figure out whether something has gone wrong.
Now that we have derived all the calibration solutions, we need to apply them to the actual data, using the task applycal. The measurement set contains three data columns; DATA, MODEL_DATA, and CORRECTED_DATA. The DATA column contains the original data. The MODEL_DATA column contains whatever model we used for the calibration; for J1331+3030, this is what we specified in setjy, and for all other sources, this was set to a point source of 1 Jy at the phase center when the scratch columns were originally created using clearcal. To apply the calibration we have so painstakingly derived, we specify the appropriate calibration tables, which are then applied to the DATA column, with the results being written in the CORRECTED_DATA column.
First, we apply the calibration to each individual calibrator, using the gain solutions derived on that calibrator alone to compute the CORRECTED_DATA. To do this, we iterate over the different calibrators, in each case specifying the source to be calibrated (using the field parameter).
# In CASA
applycal(vis='3c391_ctm_mosaic_10s_spw0.ms',
gaintable=['3c391_ctm_mosaic.fluxscale1','3c391_ctm_mosaic.bcal0','3c391_ctm_mosaic.pcal0','3c391_ctm_mosaic.xcal0'],
parang=True,field='J1331+3030',gainfield=['J1331+3030','','',''],interp=['nearest','','',''])
applycal(vis='3c391_ctm_mosaic_10s_spw0.ms',
gaintable=['3c391_ctm_mosaic.fluxscale1','3c391_ctm_mosaic.bcal0','3c391_ctm_mosaic.pcal0','3c391_ctm_mosaic.xcal0'],
parang=True,field='J0319+4130',gainfield=['J0319+4130','','',''],interp=['nearest','','',''])
applycal(vis='3c391_ctm_mosaic_10s_spw0.ms',
gaintable=['3c391_ctm_mosaic.fluxscale1','3c391_ctm_mosaic.bcal0','3c391_ctm_mosaic.pcal0','3c391_ctm_mosaic.xcal0'],
parang=True,field='J1822-0938',gainfield=['J1822-0938','','',''],interp=['nearest','','',''])
- gaintable : We provide a Python list of the calibration tables to be applied. This must contain our properly-scaled gain calibration for the amplitudes and phases (in 3c391_ctm_mosaic.fluxscale1) which we just made using fluxscale, our bandpass solutions (in 3c391_ctm_mosaic.bcal0), our leakage calibration (in 3c391_ctm_mosaic.pcal0) and the R-L phase corrections (in 3c391_ctm_mosaic.xcal0). While the latter three tables were derived using a particular calibrator source, the table containing the gain solutions for amplitude and phase was derived separately for each individual calibrator.
- gainfield, interp : To ensure that we use the correct gain amplitudes and phases for a given calibrator (those derived on that same calibrator), then for each calibrator source, we need to specify the particular subset of gain solutions to be applied. This requires use of the gainfield and interp arguments; these are both Python lists, and for the list item corresponding to the calibration table made by fluxscale, we set gainfield to the field name corresponding to that calibrator, and the desired interpolation type (interp) to nearest.
- parang : Since we have performed polarization calibration, we must set parang=True, or we will discard all that hard work we did earlier.
Finally, we apply the calibration to the target fields in the mosaic, linearly interpolating the gain solutions from the secondary calibrator, J1822-0938. In this case however, we want to apply the amplitude and phase gains derived from the secondary calibrator, J1822-0938, since that is close to the target source on the sky, and we assume that the gains applicable to the target source are very similar to those derived in the direction of the secondary calibrator. Of course, this is not strictly true, since the gains on J1822-0938 were derived at a different time and in a different position on the sky from the target. However, assuming that the calibrator was sufficiently close to the target, and the weather was sufficiently well-behaved, then this is a reasonable approximation, and should get us a sufficiently good calibration that we can later use self-calibration to correct for the small inaccuracies thus introduced.
The procedure for applying the calibration to the target source is very similar to what we just did for the calibrator sources.
# In CASA
applycal(vis='3c391_ctm_mosaic_10s_spw0.ms',
field='2~8',
gaintable=['3c391_ctm_mosaic.fluxscale1','3c391_ctm_mosaic.bcal0','3c391_ctm_mosaic.pcal0','3c391_ctm_mosaic.xcal0'],
gainfield=['J1822-0938','','',''],
interp=['linear','','',''],
parang=True)
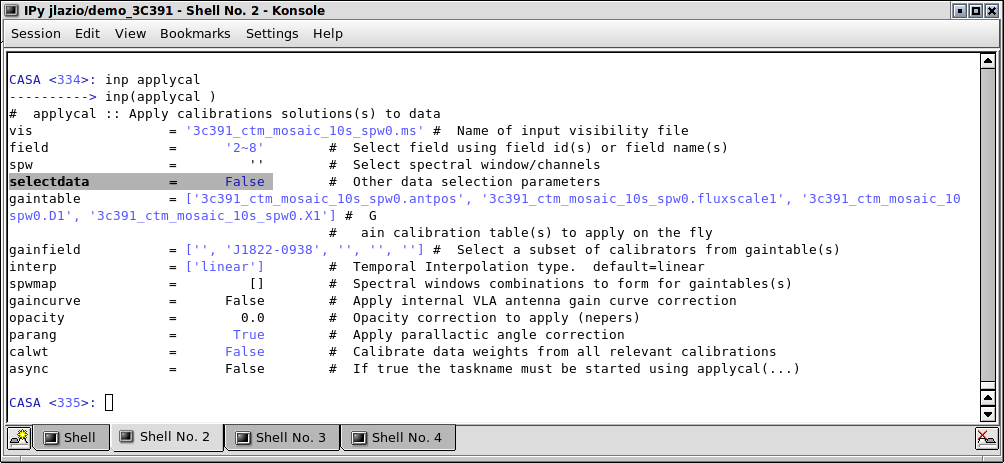
- field : We can calibrate all seven target fields at once by setting field='2~8' .
- gainfield : In this case, we wish to use the gains derived on the secondary calibrator, for the reasons explained in the previous paragraph.
- interp : This time, we linearly interpolate between adjacent calibrator scans, to compute the appropriate gains for the intervening observations of the target.
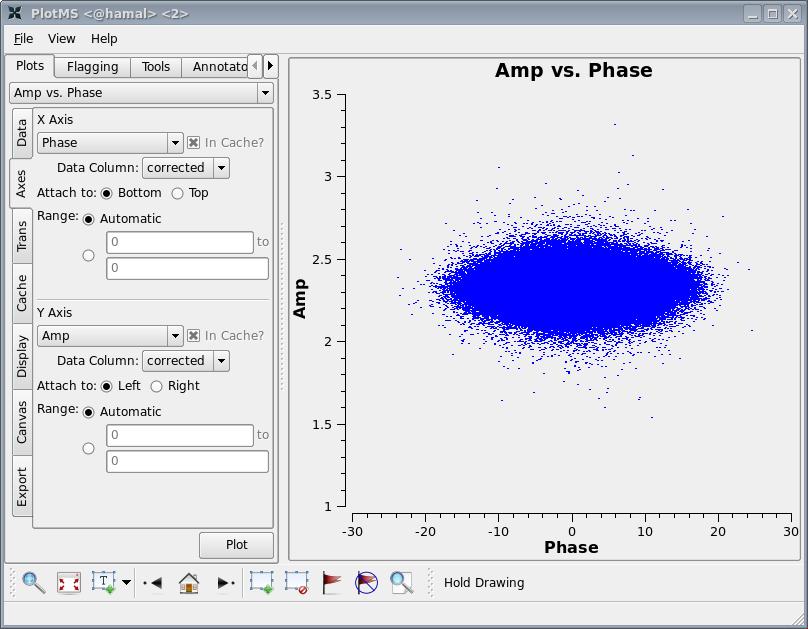
We should now have fully-calibrated visibilities in the CORRECTED_DATA column of the measurement set, and it is worthwhile pausing to inspect them, to ensure that the calibration did what we expected it to. A nice way of doing this is to use plotms to plot the amplitude and phase of the CORRECTED_DATA column against one another. This should show a nice ball of visibilities centered at zero phase (with some scatter) and the amplitude found for that source in fluxscale. An example is shown at right.
Once the calibration has been applied to the target data, we can split off the science targets, creating a new, calibrated measurement set containing all the target fields.
# In CASA
split(vis='3c391_ctm_mosaic_10s_spw0.ms',outputvis='3c391_ctm_mosaic_spw0.ms',
datacolumn='corrected',field='2~8')
- outputvis : We give the name of the new measurement set to be written, which will contain the calibrated data on the science targets.
- datacolumn : We use the CORRECTED_DATA column, containing the calibrated data which we just wrote using applycal.
- field : We wish to put all the mosaic pointings into a single measurement set, for imaging and joint deconvolution.
Imaging
Now that we have split off the target data into a separate measurement set with all the calibration applied, it's time to make an image. Recall from the lectures that the visibility data and the sky brightness distribution (a.k.a. image) are Fourier transform pairs
[math]\displaystyle{ I(l,m) = \int V(u,v) e^{[2\pi i(ul + vm)]} dudv }[/math]
The [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math] coordinates are the baselines, measured in units of the observing wavelength while the [math]\displaystyle{ l }[/math] and [math]\displaystyle{ m }[/math] coordinates are the direction cosines on the sky. For generality, the sky coordinates are written in terms of direction cosines, but for most EVLA (and ALMA) observations they can be related simply to the right ascension ([math]\displaystyle{ l }[/math]) and declination ([math]\displaystyle{ m }[/math]). Also recall from the lectures that this equation is valid only if the [math]\displaystyle{ w }[/math] coordinate of the baselines can be neglected. This assumption is almost always true at high frequencies and smaller EVLA configurations (such as the 4.6 GHz, D-configuration observations here); the [math]\displaystyle{ w }[/math] coordinate cannot be neglected at lower frequencies and larger configurations (e.g., 0.33 GHz, A-configuration observations). This expression also neglects other factors, such as the shape of the primary beam. For more information on imaging, see [Synthesis Imaging] within the CASA Reference Manual.
CASA has a single task, clean which both Fourier transforms the data and deconvolves the resulting image.
A command line call to image and deconvolve the dataset would be:
# In CASA
clean(vis='3c391_ctm_mosaic_spw0.ms',imagename='3c391_ctm_spw0_IQUV',
field='',spw='',
mode='mfs',
niter=5000,
gain=0.1, threshold='0.0mJy',
psfmode='clarkstokes',
imagermode='mosaic', ftmachine='mosaic',
multiscale=[0, 6, 18, 54], smallscalebias=0.9,
interactive=True,
imsize=[576,576], cell=['2.5arcsec','2.5arcsec'],
stokes='IQUV',
weighting='briggs',robust=0.0,
calready=True)
clean is a powerful task, with many inputs, and a certain amount of experimentation may be (likely is) required.
- mode='mfs' : Use multi-frequency synthesis imaging. The fractional bandwidth of these data is non-zero (128 MHz at a central frequency of 4.6 GHz). Recall that the u and v coordinates are defined as the baseline coordinates, measured in wavelengths. Thus, slight changes in the frequency from channel to channel result in slight changes in u and v. There is a concomitant improvement in u-v coverage if the visibility data from the multiple spectral channels are gridded separately onto the u-v plane, as opposed to treating all spectral channels as having the same frequency.
- niter=5000,gain=0.1,threshold='0.0mJy' : Recall that the CLEAN gain is the amount by which a CLEAN component is subtracted during the CLEANing process. niter and threshold are (coupled) means of determining when to stop the CLEANing process, with niter specifying to find and subtract that many CLEAN components while threshold specifies a minimum flux density threshold a CLEAN component can have before CLEAN stops. See also interactive below.
- interactive=T : Very often, particularly when one is exploring how a source appears for the first time, it can be valuable to interact with the CLEANing process. If True, interactive causes a viewer window to appear. One can then set CLEAN regions, restricting where CLEAN searches for CLEAN components, as well as monitor the CLEANing process. A standard procedure is to set a large value for niter, and stop the CLEANing when it visually appears to be approaching the noise level. This procedure also allows one to change the CLEANing region, in cases when low-level intensity becomes visible as the CLEANing process proceeds. See also [Interactive Cleaning].
- imsize=[576,576], cell=['2.5arcsec','2.5arcsec'] : See the discussion below regarding the setting of the image size and cell size.
- stokes='IQUV' and psfmode='clarkstokes' : Separate images will be made in all four polarizations (total intensity I, linear polarizations Q and U, and circular polarization V), and, with psfmode='clarkstokes', the Clark CLEAN algorithm will deconvolve each Stokes plane separately thereby making the polarization image more independent of the total intensity.
- weighting='briggs',robust=0.0 : 3C 391 has diffuse, extended emission that is (at least partially) resolved out by the interferometer owing to a lack of short spacings. A naturally-weighted image would show large-scale patchiness in the noise. In order to suppress this effect, Briggs weighting is used (intermediate between natural and uniform weighting), with a default robust factor of 0.
- imagermode='mosaic', ftmachine='mosaic' : The data consist of a 7-pointing mosaic, since the supernova remnant fills almost the full primary beam at 4.6 GHz. A mosaic combines the data from all of the fields, with imaging and deconvolution being done jointly on all 7 fields. A mosaic both helps compensate for the shape of the primary beam and reduces the amount of large (angular) scale structure that is resolved out by the interferometer.
- multiscale=[0, 6, 18, 54], smallscalebias=0.9 : A multi-scale CLEANing algorithm is used because the supernova remnant contains both diffuse, extended structure on large spatial scales and finer filamentary structure on smaller scales. The settings for multiscale are in units of pixels, with 0 pixels equivalent to the traditional delta-function CLEAN. The scales here are chosen to provide delta functions and then three logarithmically scaled sizes to fit to the data. The first scale (6 pixels) is chosen to be comparable to the size of the beam. The smallscalebias attempts to balance the weight given to larger scales, which often have more flux density, and the smaller scales, which often are brighter. Considerable experimentation is likely to be necessary; one of the authors of this document found that it was useful to CLEAN several rounds with this setting, change multiscale to be multiscale=[] and remove much of the smaller scale structure, then return to this setting.
We need to select the appropriate pixel size to use. Using plotms to look at the newly-calibrated, target-only data set:
# In CASA
plotms(vis='3c391_ctm_mosaic_spw0.ms',xaxis='uvdist_l',yaxis='amp')
we select the axes tab on the left hand side, and select UVDist_L as the x-axis.
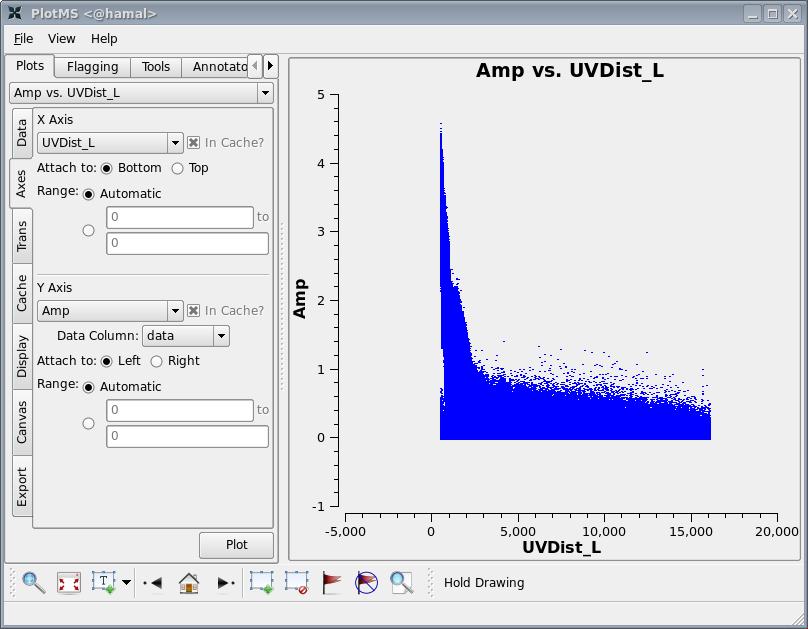
This gives the plot shown at right.
The maximum baseline shown corresponds to about 16,000 wavelengths, i.e. an angular scale of 12 arcseconds ([math]\displaystyle{ \lambda/D=1/16000 }[/math]). Since we wish to have a number of pixels across a resolution element, we then select a pixel size of 2.5 arcseconds in both co-ordinates by setting cell=['2.5arcsec','2.5arcsec']. The supernova remnant is known to have a diameter of order 9 arcmin, which corresponds to about 216 pixels. To prevent image artifacts arising from aliasing, we wish to keep the emission region to roughly the inner quarter of the image. The Fourier transform is most efficient if the number of pixels on a side is a composite number divisible by 2 and 3 and/or 5. We choose 576, which is [math]\displaystyle{ 2^6\times3^2 }[/math], and is close to [math]\displaystyle{ 2\times216 }[/math]. We therefore set imsize=[576,576].
clean will make several output files, all named with the prefix given as imagename. These include:
- .image - the final restored image, with the clean components convolved with a restoring beam and added to the remaining residuals at the end of the imaging process
- .flux - the effective response of the telescope (the primary beam)
- .flux.pbcoverage - the effective response of the full mosaic image
- .mask - the areas where you have permitted imager to find clean components
- .model - the sum of all the clean components, which has been stored as the model_data column in the measurement set
- .psf - the dirty beam, which is being deconvolved from the true sky brightness during the clean process
- .residual - what is left at the end of the deconvolution process; this is useful to diagnose whether or not to clean more deeply
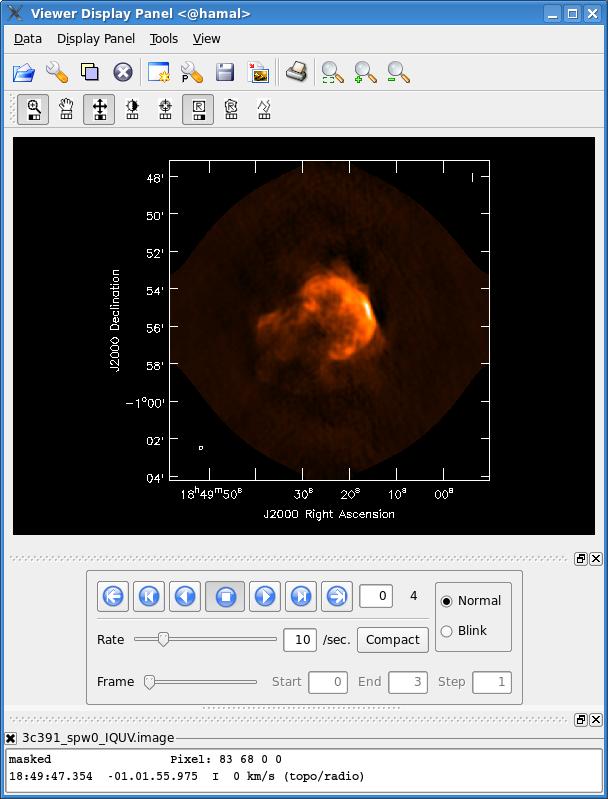
After the imaging and deconvolution process has finished, you can use the viewer to look at your image.
# In CASA
viewer('3c391_ctm_spw0_IQUV.image')
This will bring up a viewer window containing the image, which should look similar to that shown at right. The tape deck buttons that you see under the image can be used to step through the different Stokes parameters (I,Q,U,V). You can adjust the color scale and zoom in to a selected region by assigning mouse buttons to the icons immediately above the image (hover over the icons to get a description of what they do).
Note that the image is cut off in a circular fashion at the edges, corresponding to the default minimum primary beam response within clean of 0.2.
The example above illustrates multi-scale CLEAN. Not all sources or fields will require multi-scale CLEAN; for reference, here is the same data set, but without multi-scale CLEANing.
# In CASA
clean(vis='3c391_ctm_mosaic_spw0.ms',imagename='3c391_ctm_spw0_no_multiscale_IQUV',
field='',spw='',
mode='mfs',
niter=5000,
gain=0.1, threshold='0.0mJy',
psfmode='clarkstokes',
imagermode='mosaic', ftmachine='mosaic',
interactive=True,
imsize=[576,576], cell=['2.5arcsec','2.5arcsec'],
stokes='IQUV',
weighting='briggs',robust=0.0,
calready=True)
Next Steps
There are a variety of additional analyses that could be done, including extracting the statistics of the images just produced, continuing with the polarization imaging, and self-calibration of the data. Examples of these topics are included in EVLA Advanced Topics 3C391.
If one is reading this as part of the Day 1 Summer School Tutorial, and there is time, one could consider beginning one of these advanced topics.