Etime study

Naturally, one would run a simulation with a short integration time (~3s-10s) to calculate visibilities at complete uv coverage and density. However, corrupting with thermal noise is (currently - we're working on it) quite slow, and such a simulation can take hours to run. We suggest that you increase the integration time by up to an order of magnitude - if you have a long track with ALMA, the uv coverage will still be quite realistic, and the simulation will run an order of magnitude faster.

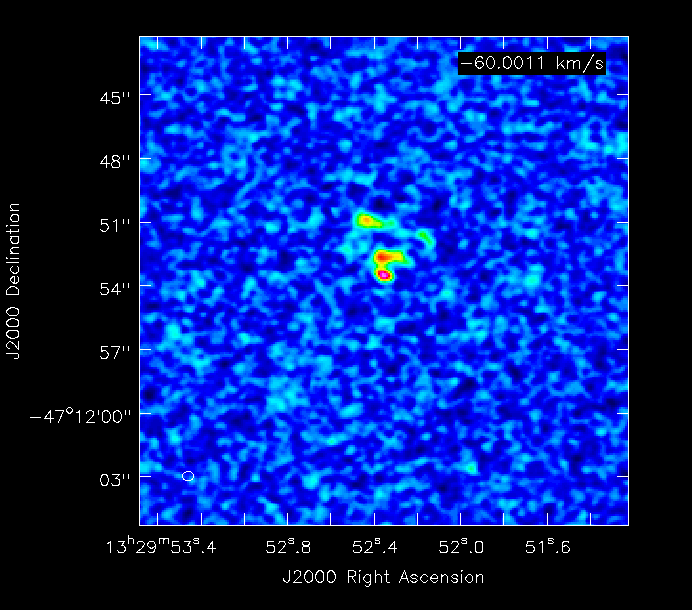
Here is an example of the M51 simulation (8hr track) with 10, 15, 30, 120, and 240s integration times, and the correspondingly decreasing number of time samples in the Measurement Set:

etime	uv	ch6 image
10s	(indistinguishable from 30s)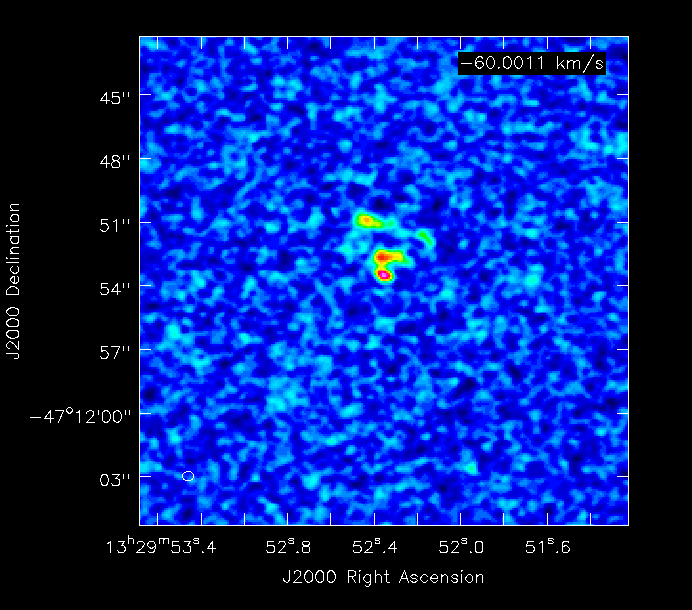
15s	(indistinguishable from 30s)
30s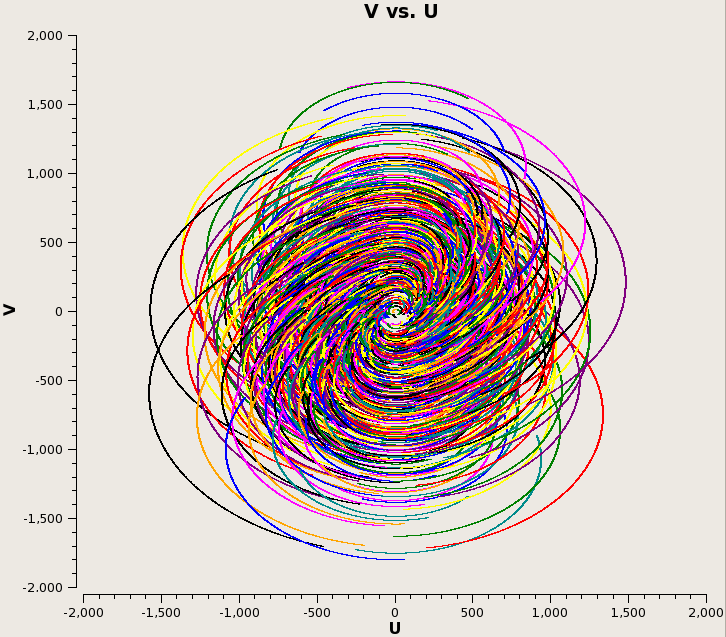
120s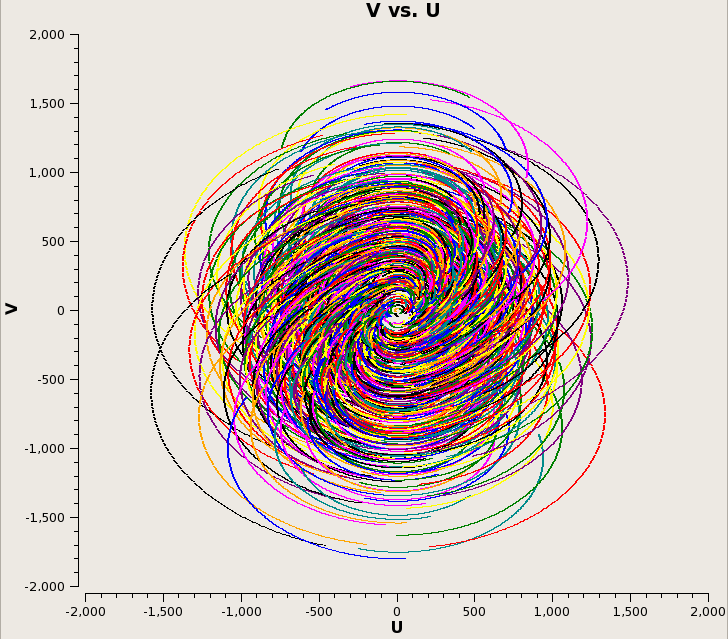
240s

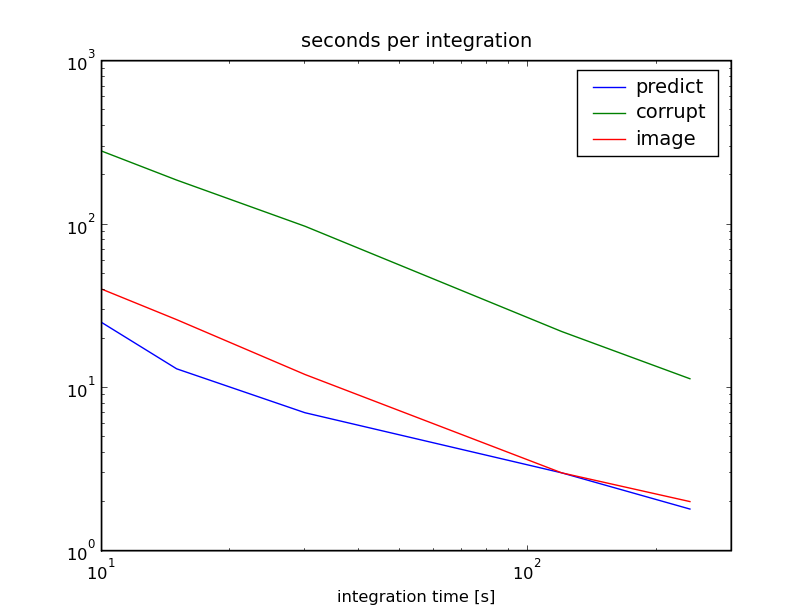
The uv coverage is slightly less filled at 240s integration, but the runtime is >20x faster: Plot of runtime as a function of integration time, and plot of runtime as a function of integration time divided by the number of samples (8hr/integration time). Each plot is split into the time required to predict visibilities, corrupt the data, and then re-image the corrupted visibilities:

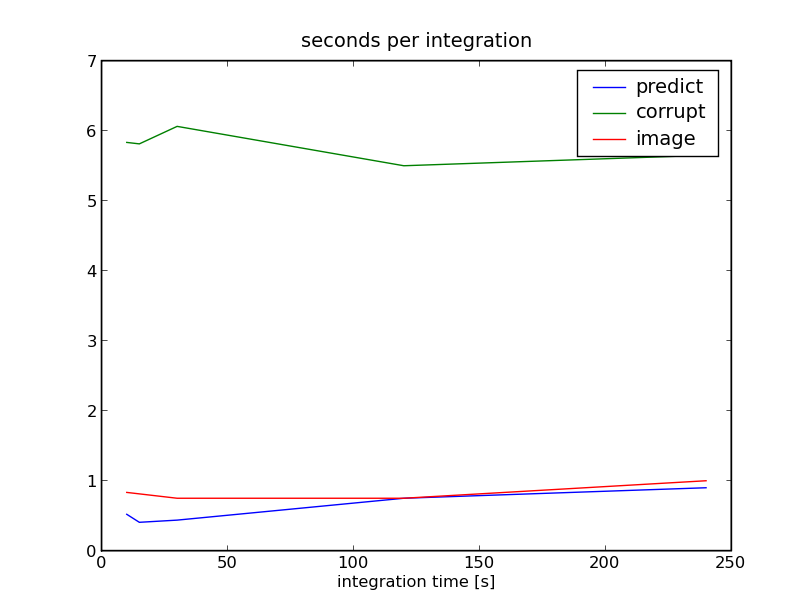
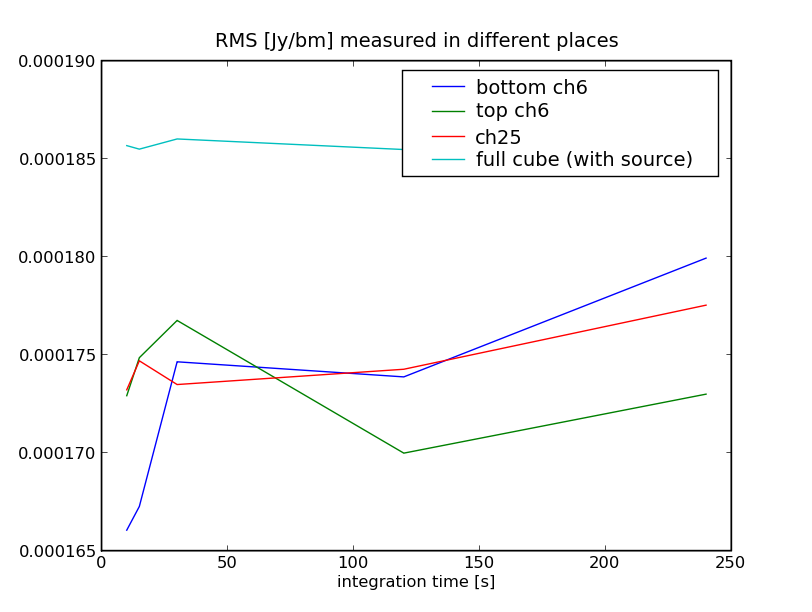
Naturally, what is of interest is if the images are quantitatively the same, and they are: This is the rms measured in several places: