CARMA spectral line mosaic M99 3.1
Overview
This tutorial describes the data reduction for CO (1-0) data observed toward the galaxy M99 (NGC 4254) using CARMA. These data were kindly provided by the CARMA STING team and should not be used for scientific purposes. More information about STING and these data in particular can be found in Rahman et al. (2010) and CARMA STING webpage.
In this tutorial we follow common CARMA practice to utilize a wide band (500 MHz) spectral window to calibrate narrow band (6 MHz) spectral windows in order to achieve better signal-to-noise.
The tutorial below assumes that you have followed the initial miriad data reduction and export to fits steps described at Importing_Data_from_MIRIAD.
A tar file of the resulting fits files can be downloaded from http://casa.nrao.edu/Data/CARMA/M99/M99_CARMA.fits.tar
After downloading, unpack the data in the directory you will be working in with
tar -xvf M99_CARMA.fits.tar
this will create a directory called fits.
Import fits files
Below we show an example of creating a python dictionary and using "for" loops in python to run importuvfits multiple times, and then use the output as the input to the concat task.
myfiles = []
for i in range(4,7):
msfile = "c0104I"+str(i)+".ms"
importuvfits(fitsfile="fits/c0104I."+str(i)+".fits",
vis=msfile)
myfiles.append(msfile)
concat(vis=myfiles,concatvis='c0104I',timesort=True)
listobs(vis='c0104I')
Look at the logger output. Notice that the CARMA data comes into CASA with antenna names that are numbers and that CASA also creates an antenna id number for each antenna (it also creates id numbers for fields and spw). Both the antenna name and id can be used to identify an antenna, which is very confusing if both are numbers -- but not the same number. The python commands below will append the antenna names with CA to more easily distinguish them from their ids. ALMA will already have antenna names that are strings, as does the EVLA. This step is only needed for data that comes into CASA via importuvfits.
tb.open("c0104I/ANTENNA",nomodify=False)
namelist=tb.getcol("NAME").tolist()
for i in range(len(namelist)):
name = 'CA'+namelist[i]
print ' Changing '+namelist[i]+' to '+name
namelist[i]=name
tb.putcol("NAME",namelist)
tb.close()
listobs(vis='c0104I')
Fields: 22
ID Code Name RA Decl Epoch nVis
0 MARS 09:15:50.0585 +17.21.03.8918 J2000 9450
1 3C273 12:29:06.7000 +02.03.08.5980 J2000 60480
2 NGC4254 12:18:47.8090 +14.24.13.9342 J2000 24570
3 NGC4254 12:18:49.6000 +14.24.13.9342 J2000 24570
4 NGC4254 12:18:51.3910 +14.24.13.9342 J2000 24570
5 NGC4254 12:18:52.2865 +14.24.36.4672 J2000 24570
6 NGC4254 12:18:50.4955 +14.24.36.4672 J2000 24570
7 NGC4254 12:18:48.7045 +14.24.36.4672 J2000 24570
8 NGC4254 12:18:46.9135 +14.24.36.4672 J2000 24570
9 NGC4254 12:18:46.0179 +14.24.59.0000 J2000 24570
10 NGC4254 12:18:47.8090 +14.24.59.0000 J2000 24570
11 NGC4254 12:18:49.6000 +14.24.59.0000 J2000 24570
12 NGC4254 12:18:51.3910 +14.24.59.0000 J2000 24570
13 NGC4254 12:18:53.1821 +14.24.59.0000 J2000 24570
14 NGC4254 12:18:52.2865 +14.25.21.5328 J2000 24570
15 NGC4254 12:18:50.4955 +14.25.21.5328 J2000 24570
16 NGC4254 12:18:48.7045 +14.25.21.5328 J2000 24570
17 NGC4254 12:18:46.9135 +14.25.21.5328 J2000 22680
18 NGC4254 12:18:47.8090 +14.25.44.0658 J2000 22680
19 NGC4254 12:18:49.6000 +14.25.44.0658 J2000 22680
20 NGC4254 12:18:51.3910 +14.25.44.0658 J2000 22680
21 3C274 12:30:49.4230 +12.23.28.0440 J2000 45360
(nVis = Total number of time/baseline visibilities per field)
Spectral Windows: (3 unique spectral windows and 1 unique polarization setups)
SpwID Chans Frame Ch1(MHz) ChanWid(kHz)TotBW(kHz) Ref(MHz) Corrs
0 15 LSRK 113978.067 31250 468750 113978.067 RR
1 63 LSRK 114289.671 976.5625 61523.4375 114289.671 RR
2 63 LSRK 114341.036 976.5625 61523.4375 114341.036 RR
The SOURCE table is empty: see the FIELD table
Antennas: 15:
ID Name Station Diam. Long. Lat.
0 CA1 ANT1 10.4 m -116.45.01.0 +37.13.43.4
1 CA2 ANT2 10.4 m -116.59.48.3 +37.52.00.3
2 CA3 ANT3 10.4 m -120.06.43.6 +37.35.02.8
3 CA4 ANT4 10.4 m -119.38.33.8 +38.26.22.2
4 CA5 ANT5 10.4 m -119.13.25.0 +35.03.23.4
5 CA6 ANT6 10.4 m -119.06.39.2 +38.54.24.4
6 CA7 ANT7 6.1 m -119.30.34.9 +36.58.55.6
7 CA8 ANT8 6.1 m -118.08.34.0 +37.16.45.8
8 CA9 ANT9 6.1 m -118.46.59.9 +36.48.41.4
9 CA10 ANT10 6.1 m -118.29.04.6 +36.03.45.6
10 CA11 ANT11 6.1 m -118.48.40.9 +37.15.57.8
11 CA12 ANT12 6.1 m -119.33.27.5 +36.06.46.1
12 CA13 ANT13 6.1 m -118.31.43.5 +37.05.19.4
13 CA14 ANT14 6.1 m -118.13.18.7 +36.50.34.6
14 CA15 ANT15 6.1 m -117.23.50.2 +36.25.48.2
Observing Strategy: Bandpass, Gain, and Flux calibrator: 3c273 field id=1 Secondary Gain Calibrator 3C274 field id=21 Extra flux calibrator Mars field id=0 The target mosaic is in field ids 2~20 There is one wideband channel (spw=0) and two narrow band channels (spw=1,2)
Initial Inspection and Flagging
First, flag edge channels:
flagdata(vis='c0104I',mode='manualflag',selectdata=True,spw='0:0~1;13~14')
flagdata(vis='c0104I',mode='manualflag',selectdata=True,spw='1~2:0~1;61~62')
Let's look at the wide band channel on all sources:
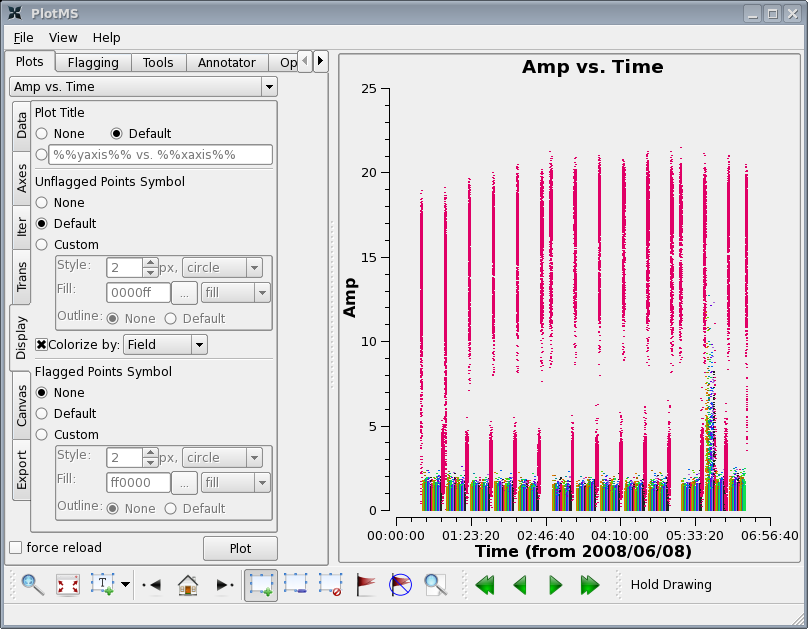
plotms(vis='c0104I',xaxis='time',yaxis='amp',field='1~21', spw='0',
avgchannel='15')
Click "Display" tab in the plotms GUI and select "Colorize by: Field", then click the plot button.
There are a few things to notice:
First there is some very noticeably bad target data near the end of the observation. Use the zoom button to zoom in on the bad timerange and then click the Mark Region icon and put a box over a modest number of the offending high points, and then press the Locate button.
Information about the located points will display to the terminal (not the Log Messages window). This will tell you that the offending telescope is antenna name=CA13 (id=12) and that the field-ids are 2~11. Looking at the plot the bad time range is 05:43:00~05:54:00.
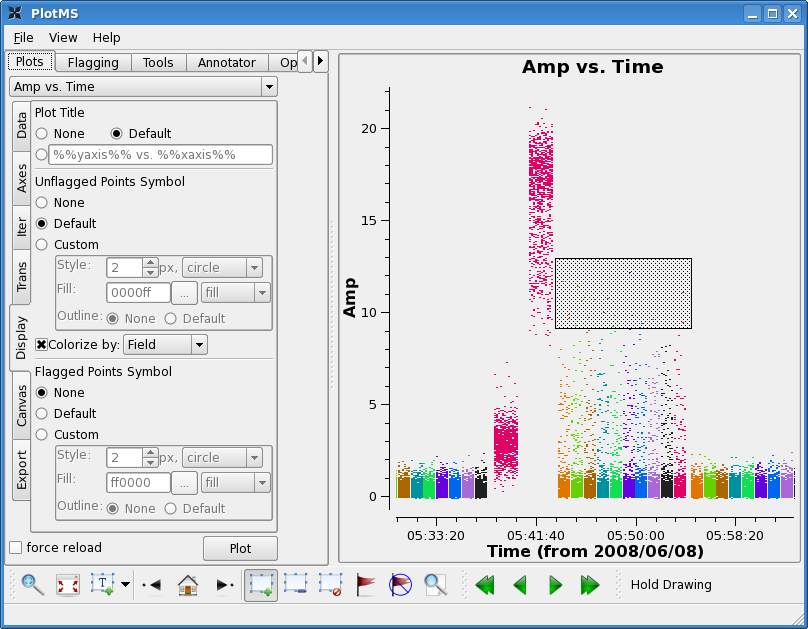
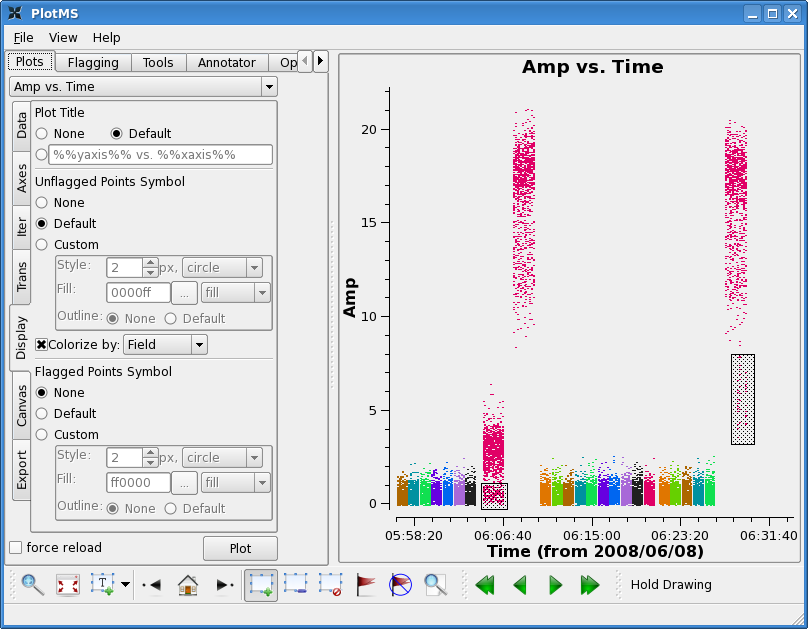
Click the "Clear Regions" button, and then the "house" button to unzoom.
Next note that the first two scans on 3c273 and the last scan on
3c273 show some low points. Also the last scan on 3c274 shows low
points. Again use zoom, mark, and locate to see if you can see a
pattern.
The first two scans on 3c273 don't show a particular pattern -- no particular antenna or individual time range appears to be responsible. This is usually a good indication that it cannot be calibrated out. Also note that it is unlikely that the target data in between is good, though this is not obvious because the target is weak. However, 3c274 does look ok, before the second 3c273 scan. Unfortunately, there is no way to calibrate the first target scans even if they are good, with no calibrator scan to precede them. For now we will flag 3c273 scans and the target in that timerange.
As for the last scans, there is a pattern: problems with the last scan on 3c273 appears to be caused by antenna CA7 (in scan 272) and problems with the last scan on 3c274 appears to be related to antenna CA8 (scan 255).
Looking at the lowest points on all the 3c273 scans, baseline CA2-CA8 appears low, we will also wait to see if this calibrates out.
We will flag the narrow band channels wherever we see problems in wideband. You can either make separate plotting commands, or combine as below. To demonstrate different possibilities we use timerange to identify some data, and scan number others.
flagdata(vis='c0104I',spw='0~2',
antenna=['CA13','','CA7','CA8'],
field=['2~11','1~20','1','21'],
scan=['','','272','255'],
timerange=['05:43:00~05:54:00','00:25:00~00:55:00','',''])
Note that each of these flagging commands could have been written out separately, but combining them into one command will run much faster than the combined time of multiple calls as the data only have to be searched once.
Set the Absolute Flux Scale
Often for millimeter observations, the absolute flux scale is determined by observing a planet and using a model of its flux as a function of baseline length (most planets are not point sources at mm frequencies using typical arrays). This is because the flux of planets change in a mostly predictable way (depending primarily on distance at any given time) than quasars. CASA does not yet have this functionality (we expect it for the next release). The flux of 3c273 is inserted from CARMA flux monitoring (which used the Mars observation to derive the 3c273 flux).
setjy(vis='c0104I', field='3C273',fluxdensity=[17.8,0.,0.,0.], spw='0~2')
Calibrate the Wideband Bandpass
Lets start by looking at the bandpass calibrator's phase as a function of channel for the wideband data.
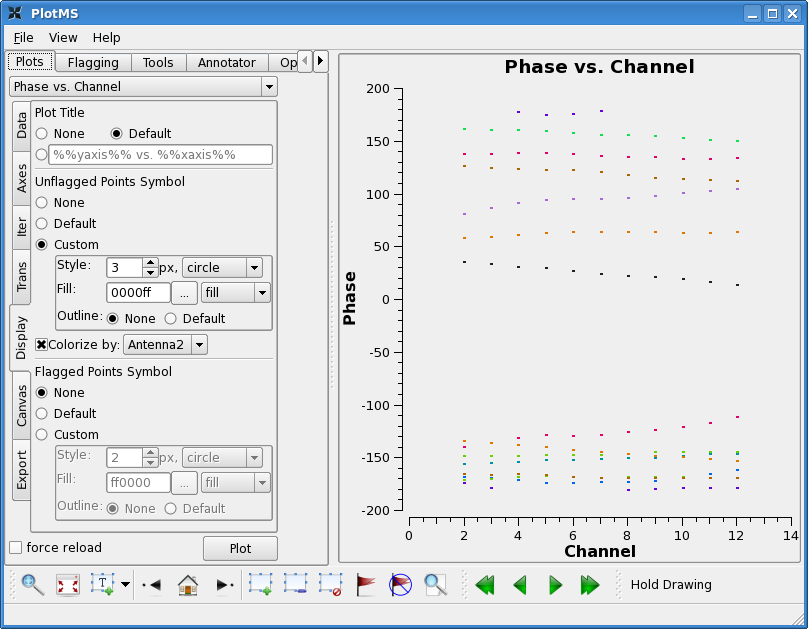
plotms(vis='c0104I',xaxis='channel',yaxis='phase',
field='1',spw='0',antenna='CA1',
avgtime='1e8',avgscan=T)
Select colorize by antenna2, and select "custom" for unflagged points, and then raise the style to 3 and you will see that the phase does not change a great deal on individual baselines over the wide band channel (spw=0). This means that averaging over some channels will not introduce significant closure errors. Check other antennas if you like.
Now look at the phase as a function of time. With avgtime a large number, but no avgscan=T, this command will show the average phase per scan. Since the cache changes, the colorize option changes too. You will have to select these again as above.
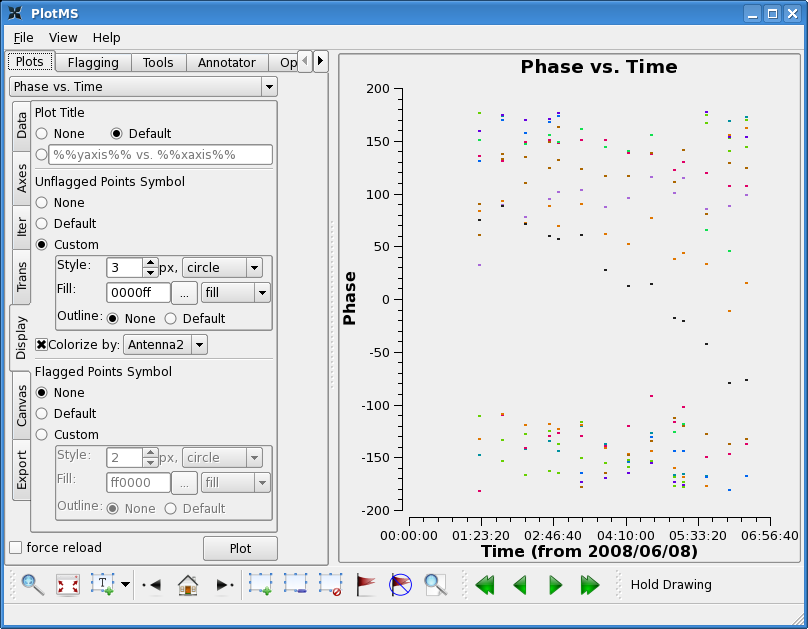
plotms(vis='c0104I',xaxis='time',yaxis='phase',
field='1',spw='0',
antenna='CA1',
avgchannel='15',avgtime='1e8')
Here you see significant variation with time. This is not surprising as the bandpass calibrator was observed over a fairly long period of time (~6 hours). In this case, it is important to calibrate the phase before solving for the bandpass. We choose a fairly narrow channel range since the bandpass phase as a function of frequency has not been taken out yet (though for these data it is quite well behaved).
gaincal(vis='c0104I',caltable='c0104I.bpphase_widecal',
field='1',spw='0:5~9',
refant='CA9',calmode='p',solint='inf',minsnr=2.0)
The use of solint='inf' here without setting combine will get one solution per scan.
Look at the solutions
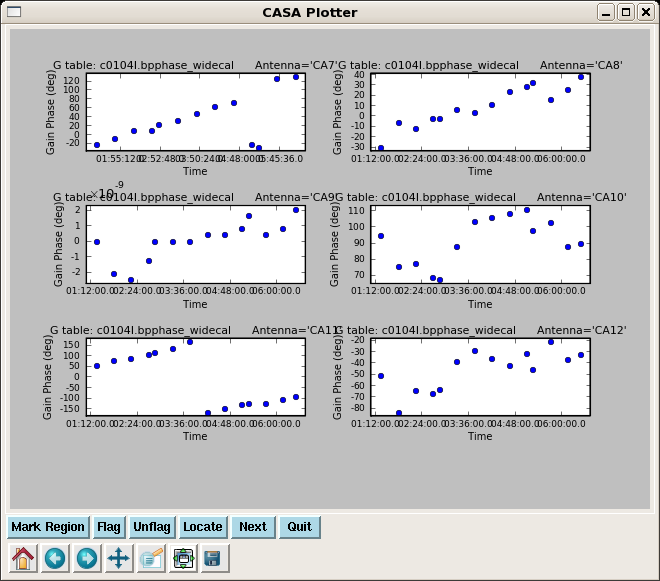
plotcal(caltable='c0104I.bpphase_widecal',
xaxis='time',yaxis='phase',
iteration='antenna',subplot=321)
Note the phase drift is > 100 degrees on some antennas -- this is why it would not have been appropriate to vector average these data into one bp solution before taking out the phase. Use the "Next" button to page through all antennas.
Having done a preliminary phase solution we can now combine all the 3C273 scans into one bandpass solution. Note the default combine parameter is different for bandpass : combine='scan'.
bandpass(vis='c0104I',caltable='c0104I.bp_widecal',
interp='',field='1',spw='0',
bandtype='B',solint='inf',
refant='CA9',solnorm=F,
gaintable=['c0104I.bpphase_widecal'],
spwmap=[[]])
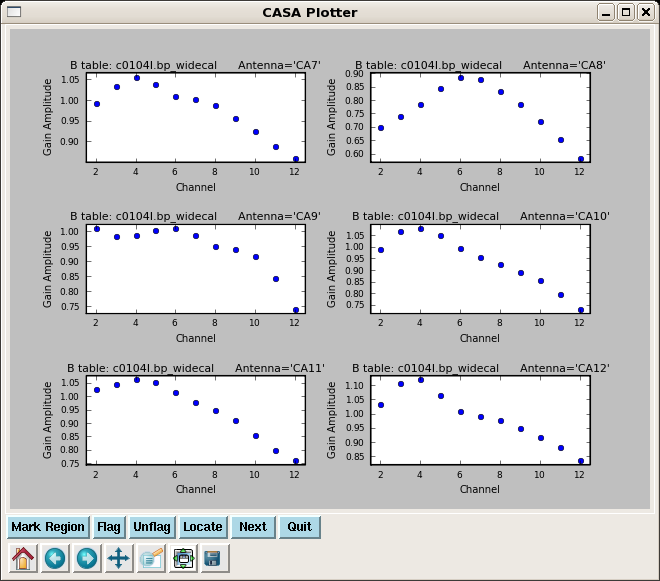
plotcal(caltable='c0104I.bp_widecal',xaxis='chan',yaxis='amp',
iteration='antenna',subplot=321)
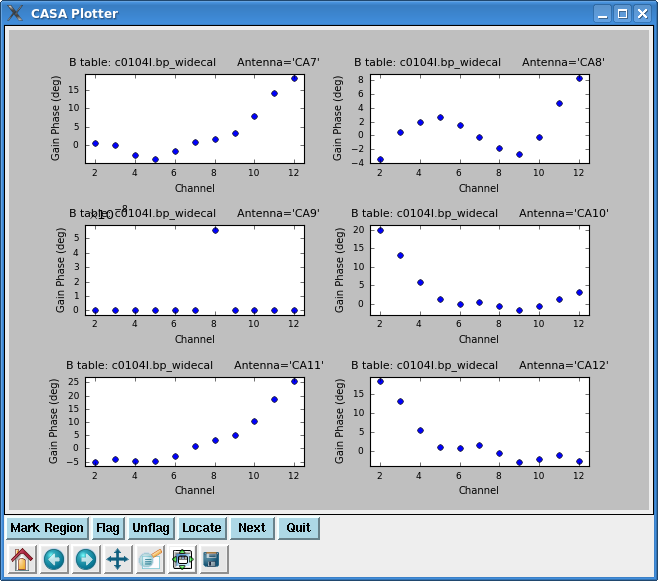
plotcal(caltable='c0104I.bp_widecal',xaxis='chan',yaxis='phase',
iteration='antenna',subplot=321)
Calibrate the Wideband Gains
Now resolve for phase and also amplitude while applying the bandpass solutions, for both calibrators 3c273 and 3c274. We will not use the first gain solution again.
gaincal(vis='c0104I',caltable='c0104I.phase_widecal',
field='1,21',spw='0',
refant='CA9',calmode='p',solint='int',minsnr=2.0,
gaintable=['c0104I.bp_widecal'],
spwmap=[[]])
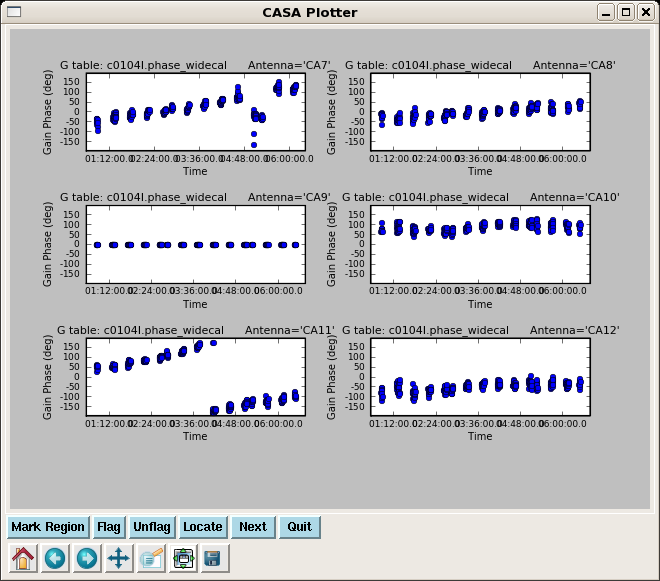
plotcal(caltable='c0104I.phase_widecal',xaxis='time',yaxis='phase',
iteration='antenna',subplot=321,plotrange=[0,0,-180,180])
Note the significant phase variation within a single scan. If we used an average phase in the next step to derive the amplitude solutions, it would decorrelate the subsequent amplitude corrections.
gaincal(vis='c0104I',caltable='c0104I.amp_inf_widecal',
field='1,21',spw='0',
refant='CA9',calmode='ap',solint='inf',minsnr=2.0,
gaintable=['c0104I.bp_widecal','c0104I.phase_widecal'],
spwmap=[[]])
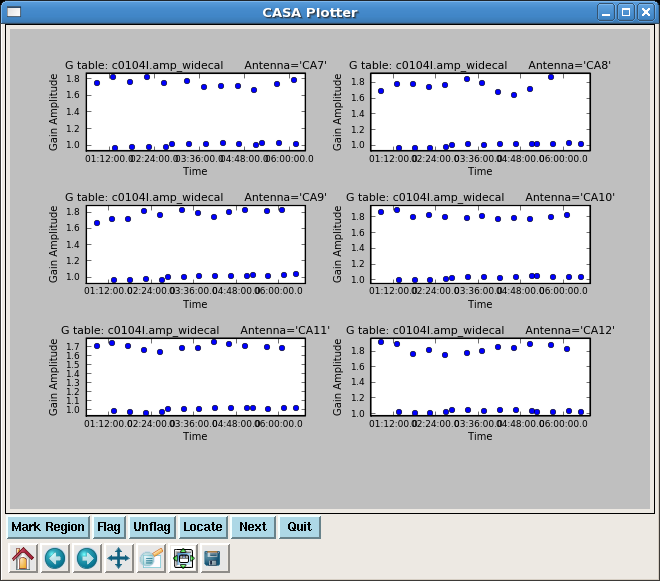
plotcal(caltable='c0104I.amp__inf_widecal',xaxis='time',yaxis='amp',
iteration='antenna',subplot=321)
Note the different gains for 3c273 scans and 3c274 scans, this just reflects that the two calibrators have different strengths.
Next plot the phase from the amplitude solutions -- this will be the residual phase after taking out the integration-time based solutions. This gives a good idea of the residual phase noise. If this is more than a few degrees, the cause should be investigated. Note that the scatter for 3c274 is larger than 3c273 -- this reflects that 3c274 is significantly weaker and thus has lower S/N.
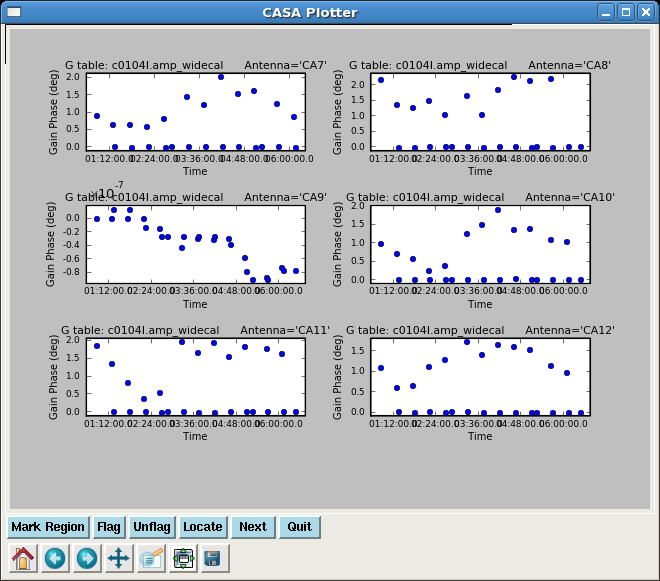
plotcal(caltable='c0104I.amp_inf_widecal',xaxis='time',yaxis='phase',
iteration='antenna',subplot=321)
Here we re-run the phase only calibration but now getting one solution per scan to apply later to the target. An alternative would be to smooth the integration time phase calibration table, but this is a bit simpler.
gaincal(vis='c0104I',caltable='c0104I.phase_inf_widecal',
field='1,21',spw='0',
refant='CA9',calmode='p',solint='inf',minsnr=2.0,
gaintable=['c0104I.bp_widecal'],
spwmap=[[]])
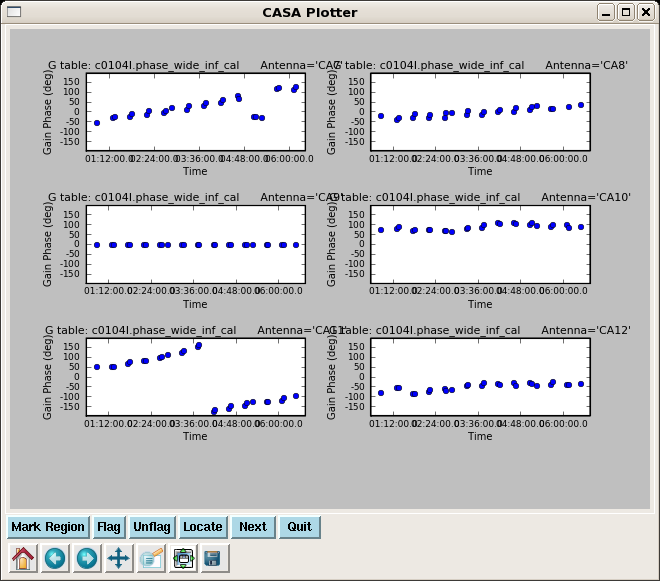
plotcal(caltable='c0104I.phase_inf_widecal',xaxis='time',yaxis='phase',
iteration='antenna',subplot=321,plotrange=[0,0,-180,180])
This is a very important plot to look at carefully as these are the phase solutions that will be applied to the target. Note that the phases for 3c273 and 3c274 are very similar, but not exactly the same. Unfortunately we can not color by field here to make it easier to see.
Calibrate the Narrow Band Bandpasses
Solve for narrow band bandpasses, applying wideband phase and amplitude corrections. Because there are 3 spw in the data, you must set a placeholder for all three in spwmap, even though we are only solving for 2 of them.
bandpass(vis='c0104I',caltable='c0104I.bp_narrowcal',
interp='',field='1',spw='1,2',
bandtype='B',solint='inf',
refant='CA9',solnorm=F,
gaintable=['c0104I.phase_widecal','c0104I.amp_inf_widecal'],
spwmap=[[0,0,0],[0,0,0]])
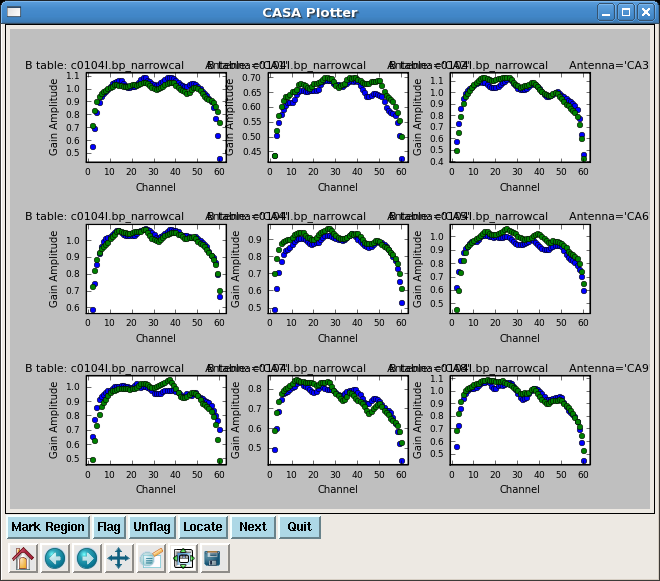
plotcal(caltable='c0104I.bp_narrowcal',xaxis='chan',yaxis='amp',
iteration='antenna',subplot=331)
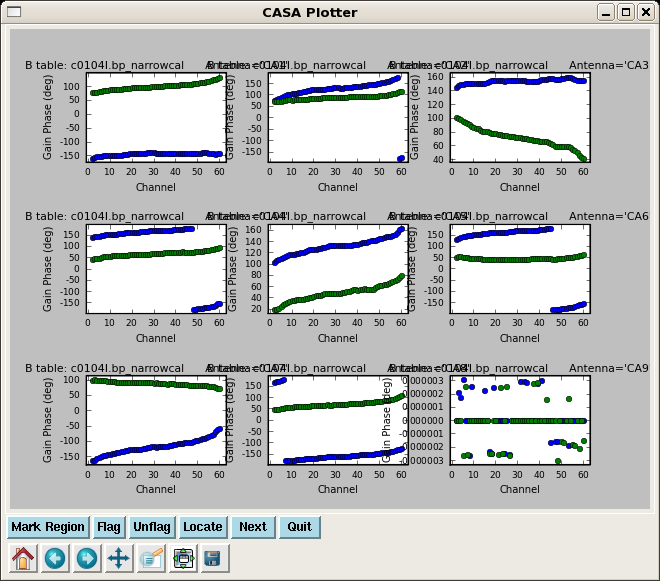
plotcal(caltable='c0104I.bp_narrowcal',xaxis='chan',yaxis='phase',
iteration='antenna',subplot=331)
Calibrate Absolute Flux
fluxscale(vis='c0104I',caltable='c0104I.amp_inf_widecal',
fluxtable='c0104I.fluxcal',reference='1')
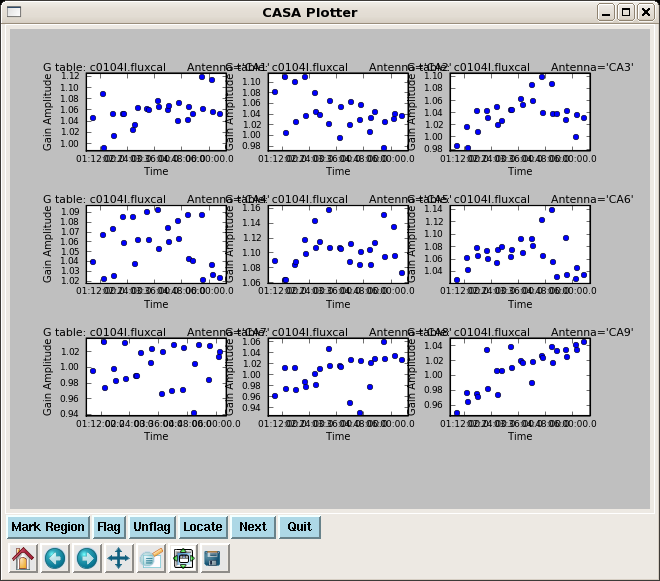
Flux density for 3C274 in SpW=0 is: 3.11626 +/- 0.0146614 (SNR = 212.549, nAnt= 15)
Check that the flux table looks as expected: the amplitude table scaled by correct flux.
plotcal(caltable='c0104I.fluxcal',xaxis='time',yaxis='amp',
iteration='antenna',subplot=331)
Applycal and Inspect
We run applycal separately for the wide and narrow band data so we can apply the appropriate bandpass tables.
applycal(vis='c0104I',field='1',spw='0',
gaintable=['c0104I.bp_widecal','c0104I.phase_widecal','c0104I.fluxcal'],
spwmap=[[],[],[]],gainfield=['1','1','1'])
applycal(vis='c0104I',field='1',spw='1,2',
gaintable=['c0104I.bp_narrowcal','c0104I.phase_widecal','c0104I.fluxcal'],
spwmap=[[],[0,0,0],[0,0,0]],gainfield=['1','1','1'])
applycal(vis='c0104I',field='21',spw='0',
gaintable=['c0104I.bp_widecal','c0104I.phase_widecal','c0104I.fluxcal'],
spwmap=[[],[],[]],gainfield=['1','21','21'])
applycal(vis='c0104I',field='21',spw='1,2',
gaintable=['c0104I.bp_narrowcal','c0104I.phase_widecal','c0104I.fluxcal'],
spwmap=[[],[0,0,0],[0,0,0]],gainfield=['1','21','21'])
For the target we will use both gain calibrators, so which ever is closest in time will be applied to the target.
applycal(vis='c0104I',field='2~20',spw='0',
gaintable=['c0104I.bp_widecal','c0104I.phase_wide_inf_cal','c0104I.fluxcal'],
spwmap=[[],[],[]],gainfield=['1','1,21','1,21'])
applycal(vis='c0104I',field='2~20',spw='1,2',
gaintable=['c0104I.bp_narrowcal','c0104I.phase_wide_inf_cal','c0104I.fluxcal'],
spwmap=[[],[0,0,0],[0,0,0]],gainfield=['1','1,21','1,21'])
plotms(vis='c0104I',xaxis='frequency',ydatacolumn='corrected',
field='1',avgtime='1e8')
plotms(vis='c0104I',xaxis='time',yaxis='amp',ydatacolumn='corrected',
field='1~21',spw='0',
avgchannel='15',avgtime='1e8')
Deconvolution and Imaging
plotms(vis='c0104I',xaxis='velocity',yaxis='amp',ydatacolumn='corrected',
field='2',spw='1~2',avgtime='1e8')
in plotms in the "trans" tab set the CO rest frequency (115271.2 MHz) in order to see the velocity range of the narrow band channels. Unfortunately the individual pointings are a bit too weak to see the UV vector averaged CO signal but you can at least see the observed velocity range.
Go to display tab and chose colorize by spw. Notice that the edge channels are a bit noisy -- especially a concern in the overlap region. We will exclude these below.
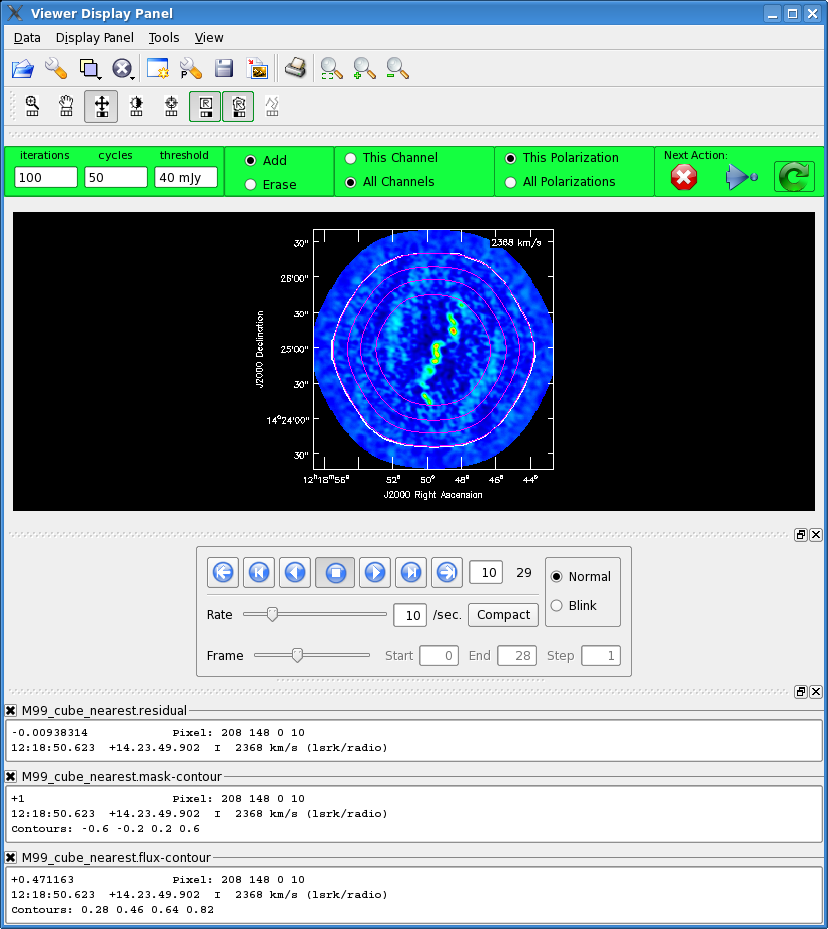
The clean call below, uses the interactive clean mode. This is important for complex extended emission as is seen in the CO(1-0) for M99. Below we provide a brief description of one easy way you might make a clean mask for this image. Of course making a clean mask for each channel individually would be better if you have the time and patience.
clean(vis='c0104I',imagename='M99_cube_nearest',spw='1~2:3~59',field='2~20',
phasecenter='11',
cell='0.9arcsec',imsize=450,
mode='velocity',start='2268km/s',width='10.0km/s',
interpolation='nearest',
imagermode='mosaic',cyclefactor=2,
restfreq='115.2712GHz',interactive=T,
mask='../M99_cube.mask',
minpb=0.1,pbcor=F,
niter=5000,threshold='40mJy')
When the interactive viewer pops up, click the "folder" icon in top left. From file gui select "M99_cube_nearest.flux" and then select "display as" contour. This will show the convolution of the primary beam coverage. Next click the "wrench" next to the file folder icon. This will open the "Data Display Options" gui. At the top, tab over until you see the "M99_cube_nearest.flux-contour" tab. Now change the line color to magenta (from foreground). Now click the zoom button in the Display panel and zoom in on the mosaic region. Chose "all channels" toggle and then chose the polygon tool from the top, and make a clean mask around the outermost contour (this happens to be the 0.2 contour level). Double click inside the polygon area, and you should see it turn white. If you now use the tape deck to move back and forth through the cube you can check that all the emission falls within the masked region. Once you are satisfied with the mask, go to the data drop down menu and close the "M99_cube_nearest.flux-contour" file. If you don't do this you will get a table lock and the final image will not be constructed. Then hit the blue arrow to continue cleaning with this mask until the threshold is reached. More clean masking tips and techniques are described in the EVLA_spectral_line_IRC10216 casaguide.
Image Analysis
First lets see what the rms noise level in a single channel is using the viewer.
viewer(infile='M99_cube_nearest.image')
Then use the tape deck to go to a line free channel, select the box region tool and make a box. When you double click in the box, the image statistics for the whole cube will print to the terminal and for that window to a pop up window. Move the box around a bit to see what the variation is. You should get something like 22 - 25 mJy. If you want the box tool to go away, hit the escape key.
Next make integrated intensity maps (moment 0) and integrated velocity maps (moment 1). to do this, we'll want to know what channels the line emission starts on. The first channel with significant emission is channel 1, while the last channel with significant emission is channel 23.
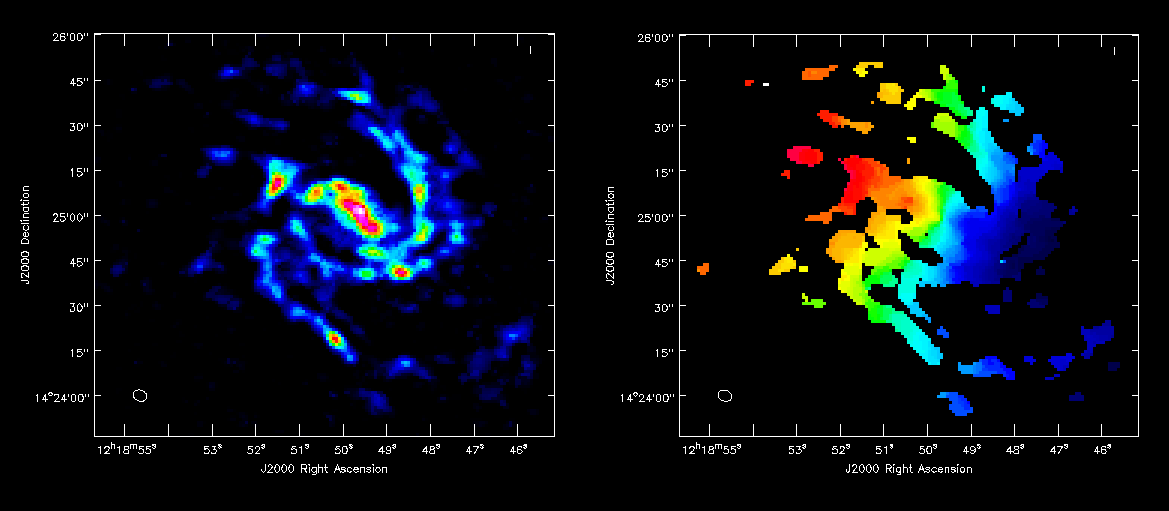
For moment zero, its best to limit the calculation to image channels with significant signal in them, but not to apply a flux cutoff, as this will bias the derived integrated intensities upward.
immoments(imagename='M99_cube_nearest.image',moments=[0],
axis='spectral',
chans='1~23',outfile='M99_cube.moment0')
For moment 1, it is essential to apply a conservative flux cutoff to limit the calculation to high signal-to-noise areas. Here we use about 5sigma.
immoments(imagename='M99_cube_nearest.image',moments=[1],
axis='spectral',
chans='1~23',excludepix=[-100,0.125],
outfile='M99_cube.moment1')
Next you can open the viwer by typing
viewer
You can open both moment maps as rasters and blink between them. You might also try opening the "p wrench tool" (Viewer Canvas Manager), go to "Number of panels" and up the number in x to 2. Then select blink in the Viewer display to see both images side by side. It will help to make your viewer window fairly wide.
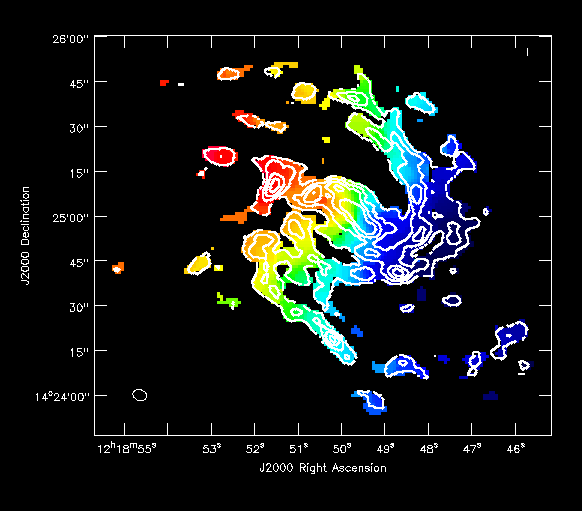
Also try opening the moment1 as a raster and moment0 as a contour map as in the example (I've played with the default contour levels in the "Data display options".
Last checked on CASA Version 3.0.2 (r11631).