VLA CASA Bandpass Slope-CASA6.4.1: Difference between revisions
No edit summary |
No edit summary |
||
| Line 15: | Line 15: | ||
This tutorial uses the default calibrator model distributed with this version. | This tutorial uses the default calibrator model distributed with this version. | ||
A different CASA version or update may include a different model than used here, | A different CASA version or update may include a different model than used here, | ||
in particular in the Ka-band (a.k.a. A-band), i.e., in the 28-40 GHz range. | in particular in the Ka-band (a.k.a. A-band), i.e., in the 28-40 GHz range. | ||
The plots and results will be different than in this guide in those cases. | The plots and results will be different than in this guide in those cases. | ||
</pre> | </pre> | ||
| Line 21: | Line 21: | ||
== Overview == | == Purpose Background and Method Overview == | ||
For the standard VLA flux density calibrators 3C138, 3C147, 3C286 and | For the standard VLA flux density calibrators 3C138, 3C147, 3C286 and | ||
| Line 36: | Line 36: | ||
Although the standard VLA flux density calibrators are usually still | Although the standard VLA flux density calibrators are usually still | ||
sufficiently bright enough for absolute flux density calibration even | sufficiently bright enough for absolute flux density calibration even | ||
at the higher frequency bands, a good bandpass determination — | at the higher frequency bands, a good delay and bandpass determination | ||
which is important for spectral line observations or measuring the | — which is important for spectral line observations or measuring | ||
spectral index of continuum sources — may require higher | the spectral index of continuum sources — may require higher | ||
signal-to-noise ratio bandpass solutions derived from either a long | signal-to-noise ratio bandpass solutions derived from either a long | ||
integration time or a very bright source (refer to the | integration time or a very bright source (refer to the | ||
| Line 47: | Line 47: | ||
these sources will be undetermined, and no ''a-priori'' flux density | these sources will be undetermined, and no ''a-priori'' flux density | ||
model is available. If not accounted for, using undetermined spectral | model is available. If not accounted for, using undetermined spectral | ||
behavior will introduce bias in the bandpass calibration. | behavior will introduce bias in the delay and bandpass calibration. | ||
Whereas there are different ways of doing this depending on the | Whereas there are different ways of doing this depending on the | ||
| Line 60: | Line 60: | ||
This tutorial describes how to determine the spectral characteristics | This tutorial describes how to determine the spectral characteristics | ||
for a point like (!) source and how to correct the bandpass | for a point like (!) source and how to correct the delay and bandpass | ||
for such an effect using alternative bandpass calibrator sources. For | solutions for such an effect using alternative bandpass calibrator | ||
that follow these four general steps (below) to obtain a | sources. For that follow these four general steps (below) to obtain a | ||
delay calibration as determined from a non-standard bandpass | delay and bandpass calibration as determined from a non-standard | ||
calibrator source, and avoid including the (higher) noise of the flux | bandpass calibrator source, and avoid including the (higher) noise of | ||
density calibrator in the bandpass: | the flux density calibrator in the bandpass: | ||
<pre style="background-color: #fffacd;"> | <pre style="background-color: #fffacd;"> | ||
A) After a phase-only self-calibration iteration, determine a good delay and bandpass | |||
calibration using the alternative bandpass calibrator. | calibration using the alternative bandpass calibrator. | ||
B) Use this first order delay and bandpass solution to calibrate the standard flux densty | |||
calibrator using the the non-standard bandpass calibrator source. This will bias the | calibrator using the the non-standard bandpass calibrator source. This will bias the | ||
standard flux density calibrator observations with the spectral features of the | standard flux density calibrator observations with the spectral features of the | ||
bandpass calibrator. | bandpass calibrator. | ||
C) Compare the newly self-calibrated and initial bandpass-corrected non-standard bandpass | |||
calibrator fluxes (as function of frequency) with the self-calibrated and initial | calibrator fluxes (as function of frequency) with the self-calibrated and initial | ||
bandpass-corrected standard flux density calibrator. Fitting these fluxes will yield | bandpass-corrected standard flux density calibrator. Fitting these fluxes will yield | ||
the spectral characteristics, including the spectral index of the bandpass calibrator. | the spectral characteristics, including the spectral index of the bandpass calibrator. | ||
D) With this spectral index model, determine a new, second order delay and bandpass | |||
calibration using the non-standard bandpass calibrator source. | calibration using the non-standard bandpass calibrator source. | ||
| Line 90: | Line 90: | ||
== Obtaining the Data and Starting CASA == | == Obtaining the (Tutorial-Modified) Data and Starting CASA == | ||
The data used in this guide are taken for a target field in Ka-band | The data used in this guide are taken for a target field in Ka-band | ||
| Line 116: | Line 116: | ||
<pre style="background-color:lightgrey;"> | <pre style="background-color:lightgrey;"> | ||
# in a terminal, outside of CASA: | # in a terminal, outside of CASA, prepare the measurement set: | ||
tar -xzf G192-BP.ms.tar.gz | tar -xzf G192-BP.ms.tar.gz | ||
</pre> | </pre> | ||
| Line 127: | Line 127: | ||
<pre style="background-color:lightgrey;"> | <pre style="background-color:lightgrey;"> | ||
# in a terminal, outside of CASA: | # OPTIONAL ! | ||
# in a terminal, outside of CASA, rename (shorten) the MS to a link: | |||
ln -s <path-to-data>/G192-BP.ms my-vis.ms | ln -s <path-to-data>/G192-BP.ms my-vis.ms | ||
</pre> | </pre> | ||
| Line 134: | Line 135: | ||
<pre style="background-color:lightgrey;"> | <pre style="background-color:lightgrey;"> | ||
# in a terminal, outside of CASA: | # in a terminal, outside of CASA, start the default package: | ||
casa | casa | ||
</pre> | </pre> | ||
| Line 143: | Line 144: | ||
<pre style="background-color:lightgrey;"> | <pre style="background-color:lightgrey;"> | ||
# in a terminal, outside of CASA: | # in a terminal, outside of CASA, start the specific package: | ||
casa -r 6.4.1-12-pipeline-2022.2.0.64 | casa -r 6.4.1-12-pipeline-2022.2.0.64 | ||
</pre> | </pre> | ||
| Line 164: | Line 165: | ||
remember). | remember). | ||
== Examining the Measurement Set (MS) == | == Examining the Measurement Set (MS) and Pre-Defining Variables == | ||
In order to proceed it is important to know the details of the | In order to proceed it is important to know the details of the | ||
observation as | observation as captured in the data set. Typical pieces of information | ||
to look for are the calibrator sources (with their intents), and | to look for are 1) the calibrator sources (with their intents), and 2) | ||
finding a reference antenna, next to the overal structure of the | finding a reference antenna, next to the overal structure of the | ||
frequency setup and sequence of observing scans (fields). Furthermore, | frequency setup and sequence of observing scans (fields). Furthermore, | ||
at this stage it is also useful to set the flux model for the standard | at this stage it is also useful to 3) set the flux model for the | ||
flux density calibrator, although that can be done at later stages | standard flux density calibrator, although that can be done at later | ||
too; it is done here to finish up the preparations before doing the | stages too; it is done here to finish up the preparations before doing | ||
actual bandpass calibration procedure. | the actual bandpass calibration procedure. | ||
From here on in this tutorial, the ''G192-BP.ms'' name in the | From here on in this tutorial, the ''G192-BP.ms'' name in the | ||
| Line 185: | Line 186: | ||
<pre style="background-color: #d8bfd8;"> | <pre style="background-color: #d8bfd8;"> | ||
# In CASA | # In CASA, define the data root and MS: | ||
visbase = 'G192-BP' (or whatever base name the data set or link to be used has, like "my-vis" above) | visbase = 'G192-BP' (or whatever base name the data set or link to be used has, like "my-vis" above) | ||
id_ms = visbase + '.ms' (this should match and find the measurement set created earlier) | id_ms = visbase + '.ms' (this should match and find the measurement set created earlier) | ||
</pre> | </pre> | ||
'''Frequency setup, calibrator intents, scan listing, etc''' | '''1) Frequency setup, calibrator intents, scan listing, etc''' | ||
Use [https://casadocs.readthedocs.io/en/v6.4.1/api/tt/casatasks.information.listobs.html listobs] to summarize the MS: | Use [https://casadocs.readthedocs.io/en/v6.4.1/api/tt/casatasks.information.listobs.html listobs] to summarize the MS: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA: | # In CASA, dump the MS listing in a file: | ||
listobs(vis=id_ms, listfile=visbase+'_list.txt'); | listobs(vis=id_ms, listfile=visbase+'_list.txt'); | ||
</source> | </source> | ||
| Line 209: | Line 210: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA, e.g. | # In CASA, view the file with the MS listing, e.g.: | ||
!emacs <visbase>_list.txt | !emacs <visbase>_list.txt | ||
</source> | </source> | ||
| Line 290: | Line 291: | ||
This redacted MS contains only scans on the flux density calibrator | This redacted MS contains only scans on the flux density calibrator | ||
3C147 (field 0) and the bandpass calibrator 3C84 (field 1). Both | 3C147 (field 0) and the bandpass calibrator 3C84 (field 1, here named | ||
fields have 64 spectral windows (spws); each spw consists of 128 dual | ''3c84-J0319+413''). Both fields have 64 spectral windows (spws); each | ||
(RR, LL) polarization 1 MHz wide channels, for a total bandwidth of | spw consists of 128 dual (RR, LL) polarization 1 MHz wide channels, | ||
128 MHz per spw. | for a total bandwidth of 128 MHz per spw. | ||
As the intents for these fields are clearly included in the scan | As the intents for these fields are clearly included in the scan | ||
| Line 299: | Line 300: | ||
convenience now introduce new variables to recall the general use of | convenience now introduce new variables to recall the general use of | ||
these intents without having to remember their details like field ID | these intents without having to remember their details like field ID | ||
numbers or name strings — variable names aren't | numbers or name strings — variable names aren't strings so | ||
therefore using them also avoids typing the quotes when filling in | therefore using them also avoids typing the quotes when filling in | ||
task parameters (as will be seen in most of the below): | task parameters (as will be seen in most of the below): | ||
<pre style="background-color: #d8bfd8;"> | <pre style="background-color: #d8bfd8;"> | ||
# In CASA | # In CASA, define field identifiers using standard variable names: | ||
id_flx = '3C147' (or '0' for using the field name or field ID respectively) | id_flx = '3C147' (or '0' for using the field name or field ID respectively) | ||
id_bp = '3c84-J0319+413' (or '1') | id_bp = '3c84-J0319+413' (or '1') | ||
| Line 310: | Line 311: | ||
'''Selecting a reference antenna form the array configuration''' | '''2) Selecting a reference antenna form the array configuration''' | ||
As a first step, a reference antenna for all phase calibrations needs | As a first step, a reference antenna for all phase calibrations needs | ||
| Line 321: | Line 322: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA, plot antenna locations: | ||
plotants(vis=id_ms) | plotants(vis=id_ms) | ||
</source> | </source> | ||
[[Image:plotG192_plotants.png|200px|thumb|right|Figure 2: Antenna locations plotted with plotants() task.]] | |||
Although the plot is a bit crowded (Figure 2), zooming in with the | Although the plot is a bit crowded (Figure 2), zooming in with the | ||
| Line 334: | Line 338: | ||
<pre style="background-color: #d8bfd8;"> | <pre style="background-color: #d8bfd8;"> | ||
# In CASA: | # In CASA, define the reference antenna identifier using a standard name: | ||
id_ref = 'ea05' (or '3' or 'W08' which are the antenna ID number or pad name for ea05) | id_ref = 'ea05' (or '3' or 'W08' which are the antenna ID number or pad name for ea05) | ||
</pre> | </pre> | ||
'''3) Setting the Model of the Flux Density Calibrator''' | |||
'''Setting the Model of the Flux Density Calibrator''' | |||
To start preparing for a flux comparison later (in step | To start preparing for a flux comparison later (in step C above), | ||
insert the spectral and angular models for the flux density | insert the spectral and angular models for the flux density | ||
calibrator, here 3C147 (field 0), with the | calibrator, here 3C147 (field 0), with the | ||
| Line 353: | Line 353: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA, insert the the flux density calibrator model in the MS model column: | ||
setjy(vis=id_ms, field=id_flx, scalebychan=True, | setjy(vis=id_ms, field=id_flx, scalebychan=True, | ||
standard='Perley-Butler 2017', model=id_flx+'_A.im'); | standard='Perley-Butler 2017', model=id_flx+'_A.im'); | ||
| Line 360: | Line 360: | ||
* <tt>scalebychan=True</tt>: If ''scalebychan=False'' [https://casadocs.readthedocs.io/en/v6.4.1/api/tt/casatasks.imaging.setjy.html setjy] would use a single value per spectral window. | * <tt>scalebychan=True</tt>: If ''scalebychan=False'' [https://casadocs.readthedocs.io/en/v6.4.1/api/tt/casatasks.imaging.setjy.html setjy] would use a single value per spectral window. | ||
[[Image:PlotG192_setjy.png|200px|thumb|right|Figure 1: plotms() output | [[Image:PlotG192_setjy.png|200px|thumb|right|Figure 1: plotms() output for model amplitudes as function of freqency for the flux density calibrator 3C147]] | ||
for model amplitudes as function of freqency for the flux density | |||
calibrator 3C147]] | |||
Inspecting the logger report shows that the flux density calibrator | Inspecting the logger report shows that the flux density calibrator | ||
| Line 373: | Line 371: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA, plot the model amplitude as function of frequency | ||
# for baselines to antenna ea03: | |||
plotms(vis=id_ms, field=id_flx, antenna='ea03', | plotms(vis=id_ms, field=id_flx, antenna='ea03', | ||
xaxis='freq', yaxis='amp', ydatacolumn='model',coloraxis='ant2') | xaxis='freq', yaxis='amp', ydatacolumn='model',coloraxis='ant2') | ||
| Line 383: | Line 382: | ||
function of frequency. | function of frequency. | ||
== | == A) Calibrating Initial Delays and Bandpass Solutions == | ||
Start this | Start this procedure with a phase-only, time-dependent | ||
solution for the bandpass calibrator, which should be easy for these | (self-)calibration solution for the bandpass calibrator, which should | ||
supposedly bright sources. Note that the calibration solutions are | be easy for these supposedly bright sources. Note that the calibration | ||
written to a calibration table, <tt>cal.ign</tt>, where 'ign' stands | solutions are written to a calibration table, <tt>cal.ign</tt>, where | ||
for per-integration gain. This table is not a variable but a | 'ign' stands for per-integration gain. This table is not a variable | ||
string/name so it needs to be quoted in the input parameter. Solutions | but a string/name so it needs to be quoted in the input | ||
for each integration will remove most of the (phase) decorrelation of | parameter. Solutions for each integration will remove most of the | ||
the signal. For best results, the phase variations will be derived | (phase) decorrelation of the signal allowing for the delay/bandpass | ||
from a narrow range of channels (say 60~68 here, out of the 128 | calibration to succeed. For best results, the phase variations will be | ||
available per spw) near the centers of each spw, narrow enough to not | derived from a narrow range of channels (say 60~68 here, out of the | ||
be affected by uncorrected delay (i.e., reduce possible decorrelation | 128 available per spw) near the centers of each spw, narrow enough to | ||
by excluding any large phase differences due to a phase slope over the | not be affected by uncorrected delay (i.e., reduce possible | ||
frequency range of the spw): | decorrelation by excluding any large phase differences due to a phase | ||
slope over the frequency range of the spw): | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA, do a phase-only self-calibration on the bandpass calibrator | ||
# (self-calibrating amplitudes is premature before determining a | |||
# preliminary bandpass calibration and will be done in a later step): | |||
gaincal(vis=id_ms, caltable='cal.ign', | gaincal(vis=id_ms, caltable='cal.ign', | ||
field=id_bp, spw='*:60~68', | field=id_bp, spw='*:60~68', | ||
| Line 413: | Line 415: | ||
Check that the phase solutions (using full phase range -180 to 180 | |||
of autorange): | instead of autorange) are smoothly varying, supposedly reflecting the | ||
changing phases due to atmospheric effects (i.e., for these high | |||
frequencies due to the troposphere): | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA, plot phase solutions as function of time, displaying one-for-one | ||
# a plot for baselines to each antena: | |||
plotms(vis='cal.ign', xaxis='time', yaxis='phase', | plotms(vis='cal.ign', xaxis='time', yaxis='phase', | ||
iteraxis='antenna', plotrange=[-1,-1,-180,180]) | iteraxis='antenna', plotrange=[-1,-1,-180,180]) | ||
| Line 439: | Line 444: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA, dump images of multi-panel plots for different antenna-ID ranges: | ||
plotms(vis='cal.ign', xaxis='time', yaxis='phase', | plotms(vis='cal.ign', xaxis='time', yaxis='phase', | ||
antenna='0~11', gridrows=3, gridcols=3, iteraxis='antenna', | antenna='0~11', gridrows=3, gridcols=3, iteraxis='antenna', | ||
| Line 485: | Line 490: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA, determine residual delays from the bandpass calibrator scans: | ||
gaincal(vis=id_ms, caltable='cal.dly', | gaincal(vis=id_ms, caltable='cal.dly', | ||
field=id_bp, spw='*:5~122', gaintype='K', | field=id_bp, spw='*:5~122', gaintype='K', | ||
| Line 492: | Line 497: | ||
</source> | </source> | ||
Note that | Note that this applies the initial phase table <tt>cal.ign</tt> | ||
to reduce decorrelation due to short-term phase fluctuations (as they | to reduce decorrelation due to short-term phase fluctuations (as they | ||
will be corrected by the solutions in ''cal.ign''). | will be corrected by the solutions in ''cal.ign''). | ||
| Line 502: | Line 507: | ||
calibration table via parameter ''append=True''. | calibration table via parameter ''append=True''. | ||
[[Image:plotG192_delays.png|200px|thumb|right|Figure 4: Antenna based | [[Image:plotG192_delays.png|200px|thumb|right|Figure 4: Antenna based delays after running gaincal().]] | ||
delays after running gaincal().]] | |||
Now plot the delays, in nanoseconds, as a function of antenna index | Now plot the delays, in nanoseconds, as a function of antenna index | ||
| Line 509: | Line 513: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA, display the delay solutions for each spw as function of antenna-ID: | ||
plotms(vis='cal.dly', xaxis='ant1', yaxis='delay', coloraxis='spw') | plotms(vis='cal.dly', xaxis='ant1', yaxis='delay', coloraxis='spw') | ||
</source> | </source> | ||
| Line 521: | Line 525: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA: | # In CASA, determine the bandpass from the bandpass calibrator scans: | ||
bandpass(vis=id_ms, caltable='cal.bp', | bandpass(vis=id_ms, caltable='cal.bp', | ||
gaintable=['cal.ign', 'cal.dly'], | gaintable=['cal.ign', 'cal.dly'], | ||
| Line 543: | Line 547: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA, display the bandpass solutions for amplitude and phase for | ||
# the different (2x 4GHz) spw ranges; first range, amplitude: | |||
plotms(vis='cal.bp', xaxis='freq', yaxis='amp', | plotms(vis='cal.bp', xaxis='freq', yaxis='amp', | ||
spw='0~31', iteraxis='antenna', coloraxis='spw') | spw='0~31', iteraxis='antenna', coloraxis='spw') | ||
# | # second range, amplitude: | ||
plotms(vis='cal.bp', xaxis='freq', yaxis='amp', | plotms(vis='cal.bp', xaxis='freq', yaxis='amp', | ||
spw='32~63', iteraxis='antenna', coloraxis='spw') | spw='32~63', iteraxis='antenna', coloraxis='spw') | ||
# | # first range, phase: | ||
plotms(vis='cal.bp', xaxis='freq', yaxis='phase', | plotms(vis='cal.bp', xaxis='freq', yaxis='phase', | ||
spw='0~31', iteraxis='antenna', coloraxis='spw', | spw='0~31', iteraxis='antenna', coloraxis='spw', | ||
plotrange=[-1,-1,-180,180]) | plotrange=[-1,-1,-180,180]) | ||
# | # second range, phase: | ||
plotms(vis='cal.bp', xaxis='freq', yaxis='phase', | plotms(vis='cal.bp', xaxis='freq', yaxis='phase', | ||
spw='32~63', iteraxis='antenna', coloraxis='spw', | spw='32~63', iteraxis='antenna', coloraxis='spw', | ||
| Line 569: | Line 574: | ||
|} | |} | ||
== | == B) Applying the Initial Bandpass Solutions to the Flux Density Calibrator == | ||
| Line 589: | Line 594: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA, phase-only self-calibrate the flux density and bandpass calibrators | ||
# using the obtained first-order bandpass calibration above: | |||
gaincal(vis=id_ms, caltable='cal.ign2pha', field=id_flx+','+id_bp, | gaincal(vis=id_ms, caltable='cal.ign2pha', field=id_flx+','+id_bp, | ||
gaintable=['cal.dly', 'cal.bp'], | gaintable=['cal.dly', 'cal.bp'], | ||
| Line 601: | Line 607: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA: | # In CASA, now self-calibrate the phase-corrected amplitudes as well: | ||
gaincal(vis=id_ms, caltable='cal.ign2', field=id_flx+','+id_bp, | gaincal(vis=id_ms, caltable='cal.ign2', field=id_flx+','+id_bp, | ||
gaintable=['cal.dly', 'cal.bp','cal.ign2pha'], | gaintable=['cal.dly', 'cal.bp','cal.ign2pha'], | ||
| Line 610: | Line 616: | ||
Let's have a look at the phase and amplitude solutions, iterating over antenna. We will look at the flux density calibrator (3C147, id_flx) and bandpass calibrator (3C84, id_bp) individually since they're widely separated in time: | Let's have a look at the phase and amplitude solutions, iterating over antenna. We will look at the flux density calibrator (3C147, id_flx) and bandpass calibrator (3C84, id_bp) individually since they're widely separated in time: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | ## In CASA | ||
plotcal(caltable='cal.ign2', xaxis='time', yaxis='amp', | plotcal(caltable='cal.ign2', xaxis='time', yaxis='amp', | ||
field=id_flx, iteration='antenna') | field=id_flx, iteration='antenna') | ||
# | ## | ||
plotcal(caltable='cal.ign2', xaxis='time', yaxis='amp', | plotcal(caltable='cal.ign2', xaxis='time', yaxis='amp', | ||
field=id_bp, iteration='antenna') | field=id_bp, iteration='antenna') | ||
# | ## | ||
plotcal(caltable='cal.ign2', xaxis='time', yaxis='phase', | plotcal(caltable='cal.ign2', xaxis='time', yaxis='phase', | ||
iteration='antenna', plotrange=[-1,-1,-180,180], | iteration='antenna', plotrange=[-1,-1,-180,180], | ||
field=id_flx) | field=id_flx) | ||
# | ## | ||
plotcal(caltable='cal.ign2', xaxis='time', yaxis='phase', | plotcal(caltable='cal.ign2', xaxis='time', yaxis='phase', | ||
iteration='antenna', plotrange=[-1,-1,-180,180], | iteration='antenna', plotrange=[-1,-1,-180,180], | ||
| Line 629: | Line 635: | ||
--> | --> | ||
== | == C) Bootstrapping the Bandpass Calibrator Field Spectrum == | ||
With gain solutions for the flux density and bandpass calibrators, now use [https://casadocs.readthedocs.io/en/v6.4.1/api/tt/casatasks.calibration.fluxscale.html fluxscale] to scale the gain amplitudes of the bandpass calibrator using those of the flux density calibrator. Store the solutions in <tt>cal.flx2</tt> and the model for the bandpass calibrator in <tt><visbase>+'_'+id_bp+'_fluxinfo.txt'</tt>: | With gain solutions for the flux density and bandpass calibrators, now use [https://casadocs.readthedocs.io/en/v6.4.1/api/tt/casatasks.calibration.fluxscale.html fluxscale] to scale the gain amplitudes of the bandpass calibrator using those of the flux density calibrator. Store the solutions in <tt>cal.flx2</tt> and the model for the bandpass calibrator in <tt><visbase>+'_'+id_bp+'_fluxinfo.txt'</tt>: | ||
| Line 635: | Line 641: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA, determine the bandpass calibrator fluxes as function of frequency by | ||
# using the fluxes set for the flux density calibrator with setjy earlier and | |||
# store the output dictionary with these values in the variable flux_bp: | |||
flux_bp = fluxscale(vis=id_ms, caltable='cal.ign2', | |||
fluxtable='cal.flx2', reference=id_flx, transfer=id_bp, | fluxtable='cal.flx2', reference=id_flx, transfer=id_bp, | ||
listfile=visbase+'_'+id_bp+'_fluxinfo.txt', fitorder=1) | listfile=visbase+'_'+id_bp+'_fluxinfo.txt', fitorder=1) | ||
</source> | </source> | ||
* <tt> | * <tt>flux_bp = fluxscale(...)</tt>: the Python dictionary returned by the [https://casadocs.readthedocs.io/en/v6.4.1/api/tt/casatasks.calibration.fluxscale.html fluxscale] task will be stored in the <tt>flux_bp</tt> variable. Inspect the dictionary flux_bp by typing "print flux_bp" at the CASA command line. Alternatively, when not interested in the dictionary type ''fluxscale(...);'' with a semicolon after the parentheses and not assigning it to a variable. This will prevent the dictionary to be printed in the terminal. Here however the dictionary is captured in flux_bp as it is going to be used below | ||
* <tt>fluxtable='cal.flx2'</tt>: this is the output scaled gain table. Since | * <tt>fluxtable='cal.flx2'</tt>: this is the output scaled gain table. Since this is only used to find the spectral index of the bandpass calibrator source field, this table is not used further. | ||
* <tt>listfile=visbase+'_'+id_bp+'_fluxinfo.txt'</tt>: an output file that contains the derived flux values and fit information. | * <tt>listfile=visbase+'_'+id_bp+'_fluxinfo.txt'</tt>: an output file that contains the derived flux values and fit information. | ||
* <tt>fitorder=1</tt>: only find a (linear) spectral index, ignoring curvature in the spectrum. | * <tt>fitorder=1</tt>: only find a (linear) spectral index, ignoring curvature in the spectrum. | ||
| Line 655: | Line 663: | ||
[[Image:PlotG192-3C84-fluxspec-4.5.png|200px|thumb|right|Figure 7: Bootstrapped 3C84 flux density spectrum.]] | [[Image:PlotG192-3C84-fluxspec-4.5.png|200px|thumb|right|Figure 7: Bootstrapped 3C84 flux density spectrum.]] | ||
Using the information in the returned <tt> | Using the information in the returned <tt>flux_bp</tt> dictionary, the derived spectrum can be plotted (Figure 7); for that the two loops below fill the parameter variables used in the plotting: | ||
<pre style="background-color: #AAffff;"> | |||
Note that the use of IPython in the command line requires the use of "%cpaste" to allow | |||
copy/pasting of loops, conditions, etc.. Press "Enter" (or "Return") after "--" at the | |||
end, this stops (or exits) the copy/paste prompt and will return you to the CASA prompt. | |||
</pre> | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA, use python code to plot the model spectrum of the bandpass calibrator: | ||
import matplotlib.pyplot as pl | |||
%cpaste | %cpaste | ||
# Press Enter or Return, then copy/paste the following: | # Press Enter or Return, then copy/paste the following: | ||
freq = | freq = flux_bp['freq'] / 1e9 | ||
spw_list = range(0,64) | spw_list = range(0,64) | ||
spw_str = [] | spw_str = [] | ||
| Line 670: | Line 684: | ||
thisspw = str(i) | thisspw = str(i) | ||
spw_str.append(thisspw) | spw_str.append(thisspw) | ||
bootstrapped_fluxes = [] | bootstrapped_fluxes = [] | ||
for j in spw_str: | for j in spw_str: | ||
thisflux = | thisflux = flux_bp['1'][j]['fluxd'][0] | ||
if thisflux ==None: | if thisflux ==None: | ||
continue | continue | ||
else: | else: | ||
bootstrapped_fluxes.append(thisflux) | bootstrapped_fluxes.append(thisflux) | ||
pl.clf() | pl.clf() | ||
pl.plot(freq, bootstrapped_fluxes, 'bo') | pl.plot(freq, bootstrapped_fluxes, 'bo') | ||
| Line 703: | Line 702: | ||
</source> | </source> | ||
The model from [https://casadocs.readthedocs.io/en/v6.4.1/api/tt/casatasks.calibration.fluxscale.html fluxscale] is used to fill the ''<tt>MODEL</tt>'' column with the banpass source's spectral information using [https://casadocs.readthedocs.io/en/v6./4.1api/tt/casatasks.imaging.setjy.html setjy]. With ''standard='fluxscale''', we can directly use the <tt>flux_bp</tt> Python dictionary as input via ''fluxdict'': | |||
[[Image:ScreenshotPlotG192-setjy-bp-4.5.png|200px|thumb|right|Figure 8: Model amplitude of 3C84 as a function of frequency.]] | [[Image:ScreenshotPlotG192-setjy-bp-4.5.png|200px|thumb|right|Figure 8: Model amplitude of 3C84 as a function of frequency.]] | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA, insert the spectral information for the bandpass calibrator field: | ||
setjy(vis=id_ms, field=id_bp, scalebychan=True, | setjy(vis=id_ms, field=id_bp, scalebychan=True, | ||
standard = 'fluxscale', fluxdict= | standard = 'fluxscale', fluxdict=flux_bp); | ||
</source> | </source> | ||
| Line 716: | Line 715: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA, display the spectral model of the bandpass calibrator field, in this | ||
# case for a specific baseline (which should be identical for all baselines | |||
# for a point-like source, otherwise it will depend on baseline length): | |||
plotms(vis=id_ms, field=id_bp, antenna='ea05&ea02', | plotms(vis=id_ms, field=id_bp, antenna='ea05&ea02', | ||
xaxis='freq', yaxis='amp', ydatacolumn='model') | xaxis='freq', yaxis='amp', ydatacolumn='model') | ||
</source> | </source> | ||
== | == D) Create a New Bandpass Using the Bandpass Calibrator Spectral Model == | ||
Next, | Next, redo the previous calibration using this new model information. Although the commands are the same as issued earlier, keep in mind that the model values for the bandpass calibrator have changed and, therefore, the results of these calibration calculations accordingly will differ if the specral index differs significanlty from zero: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA, redo a phase-only self-calibration on the bandpass calibrator: | ||
gaincal(vis=id_ms, caltable='cal.ign.redo', | gaincal(vis=id_ms, caltable='cal.ign.redo', | ||
field=id_bp, spw='*:60~68', | field=id_bp, spw='*:60~68', | ||
| Line 732: | Line 733: | ||
solint='int', minsnr=3) | solint='int', minsnr=3) | ||
# In CASA | # In CASA, re-determine residual delays from the bandpass calibrator scans: | ||
gaincal(vis=id_ms, caltable='cal.dly.redo', | gaincal(vis=id_ms, caltable='cal.dly.redo', | ||
gaintable=['cal.ign.redo'], | gaintable=['cal.ign.redo'], | ||
| Line 738: | Line 739: | ||
refant=id_ref, solint='inf', minsnr=3) | refant=id_ref, solint='inf', minsnr=3) | ||
# In CASA: | # In CASA, re-determine the bandpass from the bandpass calibrator scans: | ||
bandpass(vis=id_ms, caltable='cal.bp.redo', | bandpass(vis=id_ms, caltable='cal.bp.redo', | ||
gaintable=['cal.ign.redo', 'cal.dly.redo'], | gaintable=['cal.ign.redo', 'cal.dly.redo'], | ||
| Line 745: | Line 746: | ||
</source> | </source> | ||
Finally, | Finally, inspect these solutions (Figures 9a, 9b, 10a, and 10b; again note that antenna ea01 is fully flagged): | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA, display and check the bandpass solutions; first range, amplitude: | ||
plotms(vis='cal.bp.redo', xaxis='freq', yaxis='amp', | plotms(vis='cal.bp.redo', xaxis='freq', yaxis='amp', | ||
spw='0~31', iteraxis='antenna', coloraxis='spw') | spw='0~31', iteraxis='antenna', coloraxis='spw') | ||
# | # second range, amplitude: | ||
plotms(vis='cal.bp.redo', xaxis='freq', yaxis='amp', | plotms(vis='cal.bp.redo', xaxis='freq', yaxis='amp', | ||
spw='32~63', iteraxis='antenna', coloraxis='spw') | spw='32~63', iteraxis='antenna', coloraxis='spw') | ||
# | # first range, phase: | ||
plotms(vis='cal.bp.redo', xaxis='freq', yaxis='phase', | plotms(vis='cal.bp.redo', xaxis='freq', yaxis='phase', | ||
spw='0~31', iteraxis='antenna', coloraxis='spw', | spw='0~31', iteraxis='antenna', coloraxis='spw', | ||
plotrange=[-1,-1,-180,180]) | plotrange=[-1,-1,-180,180]) | ||
# | # second range, phase: | ||
plotms(vis='cal.bp.redo', xaxis='freq', yaxis='phase', | plotms(vis='cal.bp.redo', xaxis='freq', yaxis='phase', | ||
spw='32~63', iteraxis='antenna', coloraxis='spw', | spw='32~63', iteraxis='antenna', coloraxis='spw', | ||
| Line 774: | Line 775: | ||
|} | |} | ||
They look virtually unchanged from the previous solutions with the exception that the amplitude scaling is corrected for the spectrum of the bandpass calibrator. | They look virtually unchanged from the previous solutions with the exception that the amplitude scaling is corrected for the spectrum of the bandpass calibrator. These steps yielded the final version of the delay and bandpass calibration tables, '''cal.dly.redo''' and '''cal.bp.redo''', which now would be used for all subsequent calibration steps. | ||
{{Checked 6.4.1}} | {{Checked 6.4.1}} | ||
Revision as of 23:39, 18 January 2023
This CASA Guide is for CASA version 6.4.1
If new to CASA, or to VLA data reduction in CASA,
it is strongly recommended to start with the Getting Started in CASA guide, the IRC+10216 spectral line tutorial, or the VLA 3C391 Continuum Tutorial
before proceeding with this tutorial.
Also note that this guide is meant to be used with monolithic CASA and not pip-wheel, because the GUIs have not been validated.
This tutorial uses the default calibrator model distributed with this version. A different CASA version or update may include a different model than used here, in particular in the Ka-band (a.k.a. A-band), i.e., in the 28-40 GHz range. The plots and results will be different than in this guide in those cases.
Purpose Background and Method Overview
For the standard VLA flux density calibrators 3C138, 3C147, 3C286 and 3C48, the CASA distribution includes angular and spectral models that are referenced during calibration (but see the note in bright lime green at the top of this tutorial). The models account for the observational source characteristics, resulting in improved calibration solutions that therefore more accurately represent the instrumental and atmospheric corrections. These VLA standard calibrators, however, exhibit a negative spectral index (i.e., flux density decreasing with increasing frequency) and become relatively weak at high frequencies.
Although the standard VLA flux density calibrators are usually still sufficiently bright enough for absolute flux density calibration even at the higher frequency bands, a good delay and bandpass determination — which is important for spectral line observations or measuring the spectral index of continuum sources — may require higher signal-to-noise ratio bandpass solutions derived from either a long integration time or a very bright source (refer to the Spectral Line (Bandpass Setup) section within the Guide to Observing with the VLA). Generally, instead of a long integration on a fainter source, additional observations of non-standard, but bright bandpass calibrators are used. Unfortunately, the spectral characteristics of these sources will be undetermined, and no a-priori flux density model is available. If not accounted for, using undetermined spectral behavior will introduce bias in the delay and bandpass calibration.
Whereas there are different ways of doing this depending on the trade-off one chooses to make, here, instead of using a bandpass determined from the standard flux density calibrator that might be noisier and transferring this noise to the target source, a less noisy bandpass from a different source is applied. To avoid bias to an undesired and initially unknown spectral index of that source, one needs to determine and model its spectral behavior so that it can be taken out during the determination of the bandpass using this brighter (higher signal-to noise) source.
This tutorial describes how to determine the spectral characteristics for a point like (!) source and how to correct the delay and bandpass solutions for such an effect using alternative bandpass calibrator sources. For that follow these four general steps (below) to obtain a delay and bandpass calibration as determined from a non-standard bandpass calibrator source, and avoid including the (higher) noise of the flux density calibrator in the bandpass:
A) After a phase-only self-calibration iteration, determine a good delay and bandpass calibration using the alternative bandpass calibrator. B) Use this first order delay and bandpass solution to calibrate the standard flux densty calibrator using the the non-standard bandpass calibrator source. This will bias the standard flux density calibrator observations with the spectral features of the bandpass calibrator. C) Compare the newly self-calibrated and initial bandpass-corrected non-standard bandpass calibrator fluxes (as function of frequency) with the self-calibrated and initial bandpass-corrected standard flux density calibrator. Fitting these fluxes will yield the spectral characteristics, including the spectral index of the bandpass calibrator. D) With this spectral index model, determine a new, second order delay and bandpass calibration using the non-standard bandpass calibrator source. This method thus does not use the flux density calibrator for bandpass calibration; the flux density calibrator is only used for obtaining the model spectral behavior of the alternative bandpass calibrator.
These resulting delay and bandpass solution tables then can be applied to the rest of the (target) data.
Obtaining the (Tutorial-Modified) Data and Starting CASA
The data used in this guide are taken for a target field in Ka-band with four 2-GHz basebands paired to two chunks of 4 GHz contiguous frequency coverage centered at 29 and 36.5 GHz for a total of 8 GHz frequency coverage. That is, each baseband consists of a series of 16 consecutive 128-MHz subbands "attached" to another baseband for a total of 64 individual spectral windows.
As this tutorial only concerns bandpass calibration, all scans on fields other than the flux density and bandpass calibrator fields were removed from the measurement set (MS). All pre-calibration steps including flagging, antenna position offsets, requantizer gains, opacity corrections, and gain-elevation curves were applied. The original data (TVER0004.sb14459364.eb14492359.56295.26287841435) can be obtained through the NRAO archive and has a raw size of 57.04 GB.
The trimmed measurement set used here can be downloaded directly from http://casa.nrao.edu/Data/EVLA/G192/G192-BP.ms.tar.gz (dataset size: 3.4 GB).
The first step will be to uncompress and untar the file in a terminal (before starting CASA):
# in a terminal, outside of CASA, prepare the measurement set: tar -xzf G192-BP.ms.tar.gz
Then move to the working directory (if not the same as the location of the raw data) and optionally move/copy or link the data to a preferred shortcut name. This is particularly useful if the original observation name has it's full extent like TVER0004.sb14459364.eb14492359.56295.26287841435, for example:
# OPTIONAL ! # in a terminal, outside of CASA, rename (shorten) the MS to a link: ln -s <path-to-data>/G192-BP.ms my-vis.ms
To start CASA, type:
# in a terminal, outside of CASA, start the default package: casa
or better, to make sure to be running the CASA version for which this tutorial was designed (list the installed versions to choose from by typing casa -ls):
# in a terminal, outside of CASA, start the specific package: casa -r 6.4.1-12-pipeline-2022.2.0.64
This will initialize CASA and set the necessary paths appropriately. This will also create two files; one is ipython-<unique-timestamp>.log which contains a record of all the text entered at the CASA prompt, and another as casapy-<unique-timestamp>.log which will contain all the messages that are printed to the CASA logger window. It is recommended to keep these log files intact as a reminder of the steps completed in the data reduction. These log files may also be helpful when submitting a helpdesk ticket.
Once CASA has started, a logger window will appear. Note that this window can be rescaled and the font size can be changed as desired; see the options under the View menu. I personally like to remove clutter columns by moving the mouse to the logger window and press "Ctrl-N", "Ctrl-Y","Ctrl-E", (New Years Eve is one way to remember).
Examining the Measurement Set (MS) and Pre-Defining Variables
In order to proceed it is important to know the details of the observation as captured in the data set. Typical pieces of information to look for are 1) the calibrator sources (with their intents), and 2) finding a reference antenna, next to the overal structure of the frequency setup and sequence of observing scans (fields). Furthermore, at this stage it is also useful to 3) set the flux model for the standard flux density calibrator, although that can be done at later stages too; it is done here to finish up the preparations before doing the actual bandpass calibration procedure.
From here on in this tutorial, the G192-BP.ms name in the directory will be replaced by the variable value stored in id_ms (identify-the-MS). This makes the instructions below less dependent on the actual name of the data root so that if another measurement set name is used, only the definition here needs to be edited to the other file name. In order to do that first define these parameters as variables inside of CASA:
# In CASA, define the data root and MS: visbase = 'G192-BP' (or whatever base name the data set or link to be used has, like "my-vis" above) id_ms = visbase + '.ms' (this should match and find the measurement set created earlier)
1) Frequency setup, calibrator intents, scan listing, etc
Use listobs to summarize the MS:
# In CASA, dump the MS listing in a file:
listobs(vis=id_ms, listfile=visbase+'_list.txt');
- Note the use of a semicolon (i.e., ;) after the parentheses. This will prevent the return dictionary to be printed in the terminal.
This will write the listobs output of the input MS (stored as the variable id_ms) to a file called <visbase>_list.txt, which can be examined using various operating system tools in a terminal, or within CASA by using an explanation mark (!) before the command, such as cat, less, or more. Preferably use an editor and keep it on the desktop for frequent consultation with e.g. emacs, vi, or nedit:
# In CASA, view the file with the MS listing, e.g.:
!emacs <visbase>_list.txt
================================================================================
MeasurementSet Name: <path-to-data>/<visbase>.ms MS Version 2
================================================================================
Observer: Dr. Observer Project: uid://evla/pdb/7303457
Observation: EVLA
Data records: 1769355 Total elapsed time = 4563 seconds
Observed from 03-Jan-2013/06:31:48.0 to 03-Jan-2013/07:47:51.0 (UTC)
ObservationID = 0 ArrayID = 0
Date Timerange (UTC) Scan FldId FieldName nRows SpwIds Average Interval(s) ScanIntent
03-Jan-2013/06:31:48.0 - 06:36:42.0 6 0 3C147 704865 [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63] [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 5.94, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [CALIBRATE_FLUX#UNSPECIFIED,OBSERVE_TARGET#UNSPECIFIED]
07:40:27.0 - 07:47:51.0 64 1 3c84-J0319+413 1064490 [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63] [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [CALIBRATE_BANDPASS#UNSPECIFIED,OBSERVE_TARGET#UNSPECIFIED]
(nRows = Total number of rows per scan)
Fields: 2
ID Code Name RA Decl Epoch SrcId nRows
0 E 3C147 05:42:36.137916 +49.51.07.23356 J2000 0 704865
1 F 3c84-J0319+413 03:19:48.160102 +41.30.42.10305 J2000 1 1064490
Spectral Windows: (64 unique spectral windows and 1 unique polarization setups)
SpwID Name #Chans Frame Ch0(MHz) ChanWid(kHz) TotBW(kHz) CtrFreq(MHz) BBC Num Corrs
0 EVLA_KA#A1C1#2 128 TOPO 34476.000 1000.000 128000.0 34539.5000 10 RR LL
1 EVLA_KA#A1C1#3 128 TOPO 34604.000 1000.000 128000.0 34667.5000 10 RR LL
2 EVLA_KA#A1C1#4 128 TOPO 34732.000 1000.000 128000.0 34795.5000 10 RR LL
3 EVLA_KA#A1C1#5 128 TOPO 34860.000 1000.000 128000.0 34923.5000 10 RR LL
<snip>
13 EVLA_KA#A1C1#15 128 TOPO 36140.000 1000.000 128000.0 36203.5000 10 RR LL
14 EVLA_KA#A1C1#16 128 TOPO 36268.000 1000.000 128000.0 36331.5000 10 RR LL
15 EVLA_KA#A1C1#17 128 TOPO 36396.000 1000.000 128000.0 36459.5000 10 RR LL
16 EVLA_KA#A2C2#18 128 TOPO 36476.000 1000.000 128000.0 36539.5000 11 RR LL
17 EVLA_KA#A2C2#19 128 TOPO 36604.000 1000.000 128000.0 36667.5000 11 RR LL
18 EVLA_KA#A2C2#20 128 TOPO 36732.000 1000.000 128000.0 36795.5000 11 RR LL
<snip>
29 EVLA_KA#A2C2#31 128 TOPO 38140.000 1000.000 128000.0 38203.5000 11 RR LL
30 EVLA_KA#A2C2#32 128 TOPO 38268.000 1000.000 128000.0 38331.5000 11 RR LL
31 EVLA_KA#A2C2#33 128 TOPO 38396.000 1000.000 128000.0 38459.5000 11 RR LL
32 EVLA_KA#B1D1#34 128 TOPO 26976.000 1000.000 128000.0 27039.5000 13 RR LL
33 EVLA_KA#B1D1#35 128 TOPO 27104.000 1000.000 128000.0 27167.5000 13 RR LL
34 EVLA_KA#B1D1#36 128 TOPO 27232.000 1000.000 128000.0 27295.5000 13 RR LL
<snip>
45 EVLA_KA#B1D1#47 128 TOPO 28640.000 1000.000 128000.0 28703.5000 13 RR LL
46 EVLA_KA#B1D1#48 128 TOPO 28768.000 1000.000 128000.0 28831.5000 13 RR LL
47 EVLA_KA#B1D1#49 128 TOPO 28896.000 1000.000 128000.0 28959.5000 13 RR LL
48 EVLA_KA#B2D2#50 128 TOPO 28976.000 1000.000 128000.0 29039.5000 14 RR LL
49 EVLA_KA#B2D2#51 128 TOPO 29104.000 1000.000 128000.0 29167.5000 14 RR LL
50 EVLA_KA#B2D2#52 128 TOPO 29232.000 1000.000 128000.0 29295.5000 14 RR LL
<snip>
61 EVLA_KA#B2D2#63 128 TOPO 30640.000 1000.000 128000.0 30703.5000 14 RR LL
62 EVLA_KA#B2D2#64 128 TOPO 30768.000 1000.000 128000.0 30831.5000 14 RR LL
63 EVLA_KA#B2D2#65 128 TOPO 30896.000 1000.000 128000.0 30959.5000 14 RR LL
Sources: 128
ID Name SpwId RestFreq(MHz) SysVel(km/s)
0 3C147 0 - -
0 3C147 1 - -
0 3C147 2 - -
<snip>
0 3C147 61 - -
0 3C147 62 - -
0 3C147 63 - -
1 3c84-J0319+413 0 - -
1 3c84-J0319+413 1 - -
1 3c84-J0319+413 2 - -
<snip>
1 3c84-J0319+413 61 - -
1 3c84-J0319+413 62 - -
1 3c84-J0319+413 63 - -
<snip>
Antennas: 22:
ID Name Station Diam. Long. Lat. Offset from array center (m) ITRF Geocentric coordinates (m)
East North Elevation x y z
1 ea02 N56 25.0 m -107.37.47.9 +34.00.38.4 -1105.2071 12254.3069 -34.2426 -1600128.383400 -5035104.146500 3565024.672100
2 ea03 N16 25.0 m -107.37.10.9 +33.54.48.0 -155.8511 1426.6436 -9.3827 -1601061.956000 -5041175.880700 3556058.037600
3 ea05 W08 25.0 m -107.37.21.6 +33.53.53.0 -432.1184 -272.1472 -1.5070 -1601614.092200 -5042001.650900 3554652.508900
<snip>
This redacted MS contains only scans on the flux density calibrator 3C147 (field 0) and the bandpass calibrator 3C84 (field 1, here named 3c84-J0319+413). Both fields have 64 spectral windows (spws); each spw consists of 128 dual (RR, LL) polarization 1 MHz wide channels, for a total bandwidth of 128 MHz per spw.
As the intents for these fields are clearly included in the scan listing (CALIBRATE_FLUX and CALIBRATE_BANDPASS), for convenience now introduce new variables to recall the general use of these intents without having to remember their details like field ID numbers or name strings — variable names aren't strings so therefore using them also avoids typing the quotes when filling in task parameters (as will be seen in most of the below):
# In CASA, define field identifiers using standard variable names: id_flx = '3C147' (or '0' for using the field name or field ID respectively) id_bp = '3c84-J0319+413' (or '1')
2) Selecting a reference antenna form the array configuration
As a first step, a reference antenna for all phase calibrations needs to be specified. Since observations were performed with the VLA in the most extended A-configuration, it is desirable to use an antenna that is near the center of the array. Futhermore, it needs to have valid calibrator data on all baselines with the least amount of data flagged. The array can be mapped with plotants:
# In CASA, plot antenna locations:
plotants(vis=id_ms)
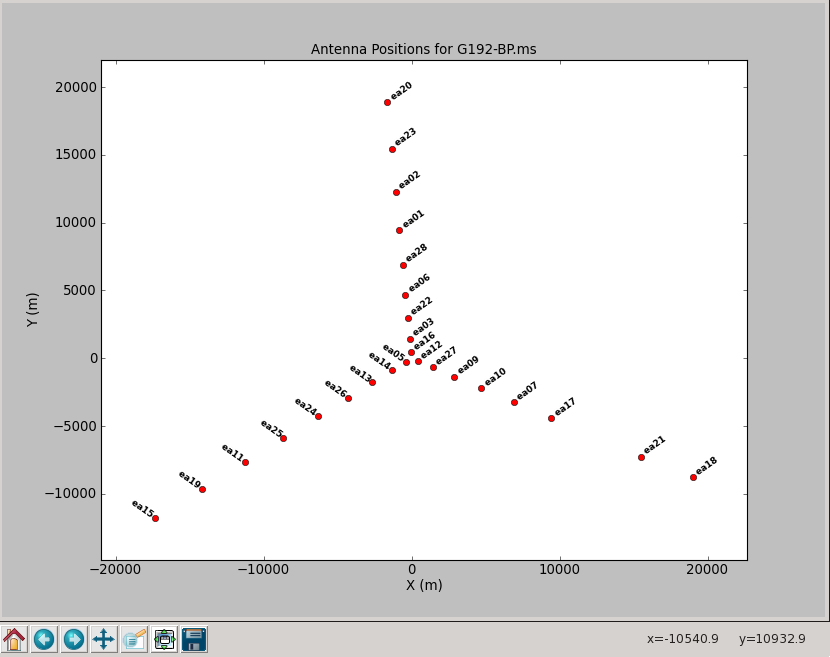
Although the plot is a bit crowded (Figure 2), zooming in with the
magnifying glass icon shows that antenna "ea05" is located close to
the center. Using the
flagdata task with mode='summary' it can be seen that "ea05" has
small number of flags. Therefore, this antenna can be used relatively
safely as the reference antenna; for convenience (and for people with
memory issues) introduce a variable name for it:
# In CASA, define the reference antenna identifier using a standard name: id_ref = 'ea05' (or '3' or 'W08' which are the antenna ID number or pad name for ea05)
3) Setting the Model of the Flux Density Calibrator
To start preparing for a flux comparison later (in step C above),
insert the spectral and angular models for the flux density
calibrator, here 3C147 (field 0), with the
setjy task. Use the 'Perley-Butler 2017' standard and 3C147_A.im for
Ka-band (which can be written as id_flx+'_A.im because here
fortunately id_flx and the model name agree):
# In CASA, insert the the flux density calibrator model in the MS model column:
setjy(vis=id_ms, field=id_flx, scalebychan=True,
standard='Perley-Butler 2017', model=id_flx+'_A.im');
- scalebychan=True: If scalebychan=False setjy would use a single value per spectral window.
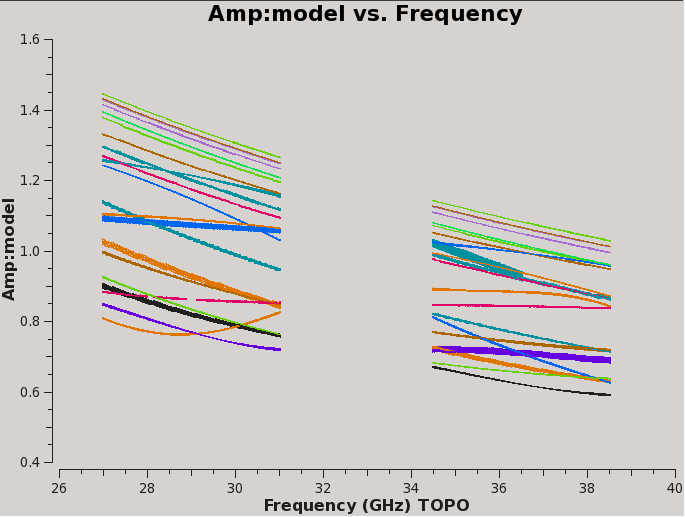
Inspecting the logger report shows that the flux density calibrator (3C147 here) has amplitudes ranging from about 1.0 to about 1.5 Jy across the spws. (Note the output sorting in increasing spw number, not in frequency.)
The model data can be plotted, e.g. for antenna 'ea03', using plotms (Figure 1):
# In CASA, plot the model amplitude as function of frequency
# for baselines to antenna ea03:
plotms(vis=id_ms, field=id_flx, antenna='ea03',
xaxis='freq', yaxis='amp', ydatacolumn='model',coloraxis='ant2')
This plot shows baselines to antenna "ea03". Since both a spectral and an angular model for this well resolved calibrator was provided, each baseline has a somewhat different amplitude and phase behavior as function of frequency.
A) Calibrating Initial Delays and Bandpass Solutions
Start this procedure with a phase-only, time-dependent (self-)calibration solution for the bandpass calibrator, which should be easy for these supposedly bright sources. Note that the calibration solutions are written to a calibration table, cal.ign, where 'ign' stands for per-integration gain. This table is not a variable but a string/name so it needs to be quoted in the input parameter. Solutions for each integration will remove most of the (phase) decorrelation of the signal allowing for the delay/bandpass calibration to succeed. For best results, the phase variations will be derived from a narrow range of channels (say 60~68 here, out of the 128 available per spw) near the centers of each spw, narrow enough to not be affected by uncorrected delay (i.e., reduce possible decorrelation by excluding any large phase differences due to a phase slope over the frequency range of the spw):
# In CASA, do a phase-only self-calibration on the bandpass calibrator
# (self-calibrating amplitudes is premature before determining a
# preliminary bandpass calibration and will be done in a later step):
gaincal(vis=id_ms, caltable='cal.ign',
field=id_bp, spw='*:60~68',
gaintype='G', refant=id_ref, calmode='p',
solint='int', minsnr=3)
- refant=id_ref : Use the variable identifying the reference antenna (ea05 here) as the reference antenna.
- solint='int' : Do a per-integration solve (every 6 seconds, which is the time-averaging applied to the data for this tutorial).
- minsnr=3 : Apply a minimum signal-to-noise cutoff of three. Solutions with less signal-to-noise than this value will be flagged.
- gaintable is not set here as earlier calibrations (to prepare for this tutorial have already been applied.
Check that the phase solutions (using full phase range -180 to 180
instead of autorange) are smoothly varying, supposedly reflecting the
changing phases due to atmospheric effects (i.e., for these high
frequencies due to the troposphere):
# In CASA, plot phase solutions as function of time, displaying one-for-one
# a plot for baselines to each antena:
plotms(vis='cal.ign', xaxis='time', yaxis='phase',
iteraxis='antenna', plotrange=[-1,-1,-180,180])
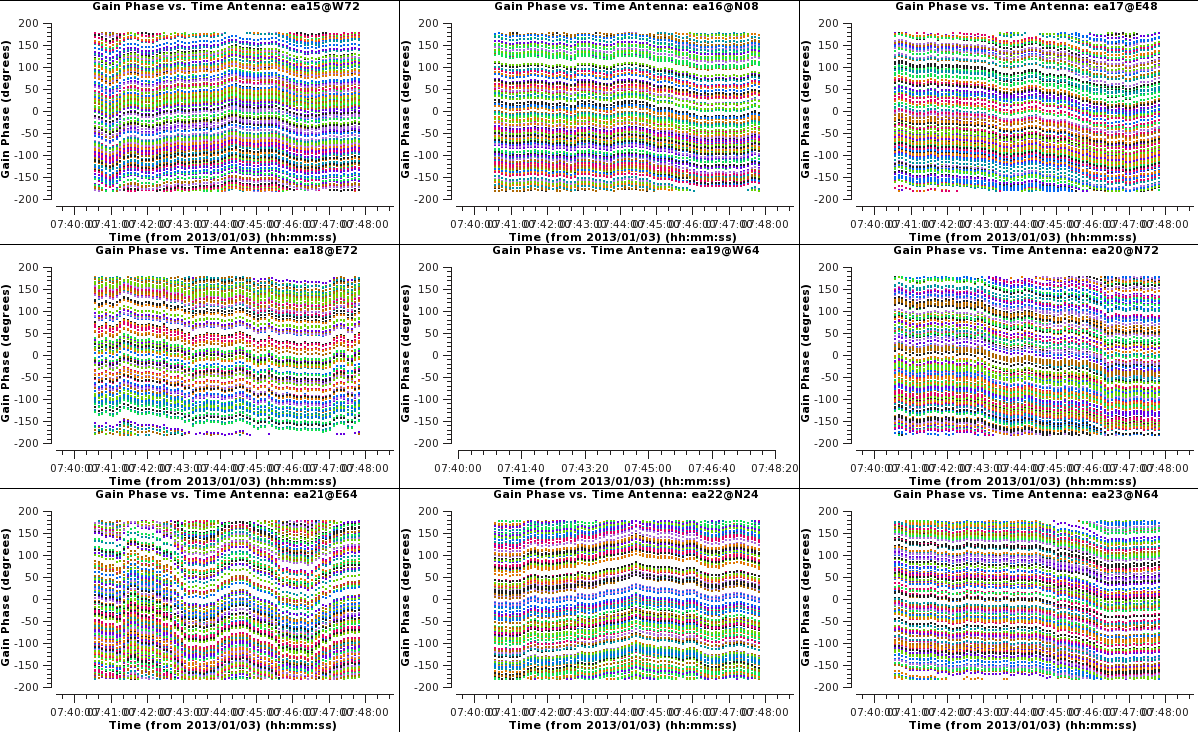
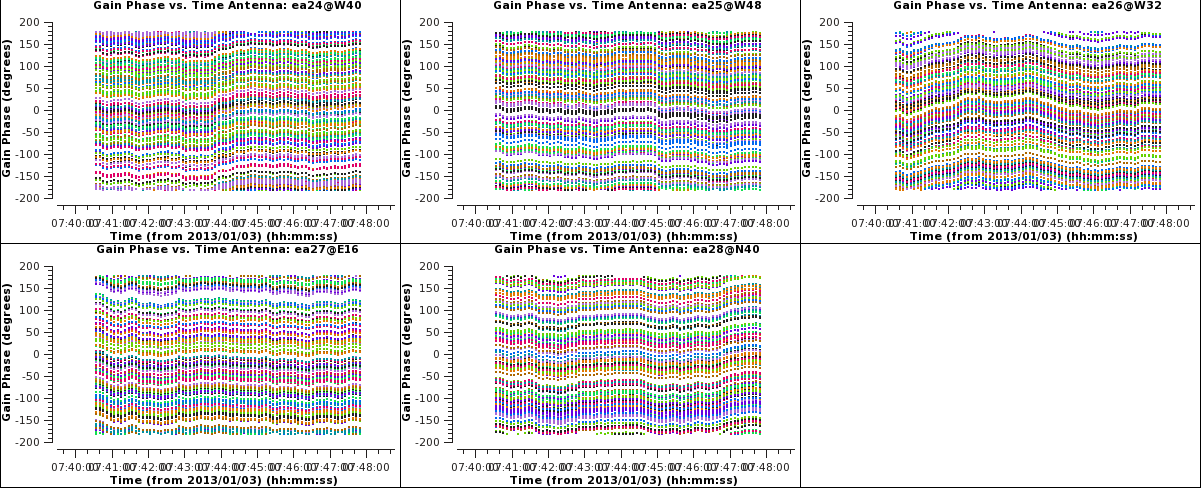
Note that antenna the first plot showing the results for ea01 is empty as ea01 previously was fully flagged, and so were ea10 and ea19. Click on the green arrows to pass through the plots for the other antennas. Also note that the reference antenna (ea05 here) has all phases equal to zero degrees, which they should be by definition for the reference antenna.
Multipanel plots of the phase solutions can be written to output files as well as to the screen display (Figures 3a, 3b, & 3c). The output files that are generated are PNG files and can be viewed at any occasion using CASA by executing an external viewer program, e.g., !xv <visbase>_cal.ign_p1*.png; or by running an image viewing application such as xv, Preview, Gimp, Photoshop, etc., external to CASA at the operating system level.
# In CASA, dump images of multi-panel plots for different antenna-ID ranges:
plotms(vis='cal.ign', xaxis='time', yaxis='phase',
antenna='0~11', gridrows=3, gridcols=3, iteraxis='antenna',
coloraxis='spw',
plotfile=visbase+'_cal.ign_p1.png', width=1300, height=800)
- width=1300 and height=800 specify the output PNG pixel dimensions.
Note that recently the name of the output file gets appended with the selection of the iteraxis and there unfortunately seems to be no possibility to switch that off; to get the file name as specified in the plotfile-parameter one would edit the file name using the operating system tools.
plotms(vis='cal.ign', xaxis='time', yaxis='phase',
antenna='12~20', gridrows=3, gridcols=3, iteraxis='antenna',
coloraxis='spw',
plotfile=visbase+'_cal.ign_p2.png', width=1300, height=800)
#
plotms(vis='cal.ign', xaxis='time', yaxis='phase',
antenna='21~26', gridrows=2, gridcols=3, iteraxis='antenna',
coloraxis='spw',
plotfile=visbase+'_cal.ign_p3.png', width=1300, height=800)
The next step is to solve for the residual delays using the parameter
gaintype='K' option in
gaincal and store the solutions in the cal.dly table. Note
that this currently does not do a global fringe-fitting solution for
delays. Instead it determines a baseline-based delay solution per spw
for all baselines to the reference antenna, treating these as
antenna-based delays. In most cases, with high enough S/N to get
baseline-based delay solutions, this will suffice. Avoid the edge
channels of each spectral window by de-selecting them (say select
channels 5~122 here, from the 128 available per spw):
# In CASA, determine residual delays from the bandpass calibrator scans:
gaincal(vis=id_ms, caltable='cal.dly',
field=id_bp, spw='*:5~122', gaintype='K',
gaintable=['cal.ign'],
refant=id_ref, solint='inf', minsnr=3)
Note that this applies the initial phase table cal.ign to reduce decorrelation due to short-term phase fluctuations (as they will be corrected by the solutions in cal.ign).
Alternatively, one can derive a delay across all spws of a baseband. If this is desired, use parameter combine='spw' in gaincal and run the task for each baseband separately. The solutions from the second and following runs can be appended to the same calibration table via parameter append=True.
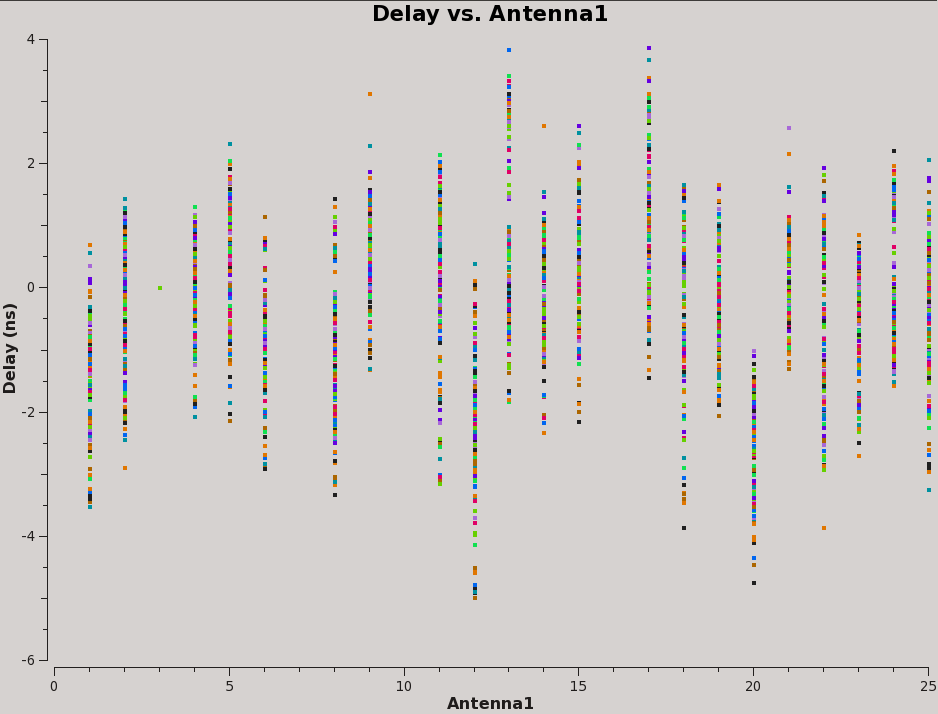
Now plot the delays, in nanoseconds, as a function of antenna index (you will get one for each spw and polarization):
# In CASA, display the delay solutions for each spw as function of antenna-ID:
plotms(vis='cal.dly', xaxis='ant1', yaxis='delay', coloraxis='spw')
The delays range from around -5 to 4 nanoseconds (Figure 4).
Now solve for the antenna bandpasses using the previously generated tables cal.ign and cal.dly correcting for possible decorrelation due to phase and delay inaccuracies, and store the solutions in cal.bp:
# In CASA, determine the bandpass from the bandpass calibrator scans:
bandpass(vis=id_ms, caltable='cal.bp',
gaintable=['cal.ign', 'cal.dly'],
field=id_bp, refant=id_ref, solnorm=False,
bandtype='B', solint='inf')
WARNING: Set solnorm=False here; otherwise there will be some offsets seen later between spws due to the way the amplitude scaling adjusts weights internally during solving.
Expect to see solutions failing due to "Insufficient unflagged
antennas" — these are for bad channels that have been
pre-flagged.
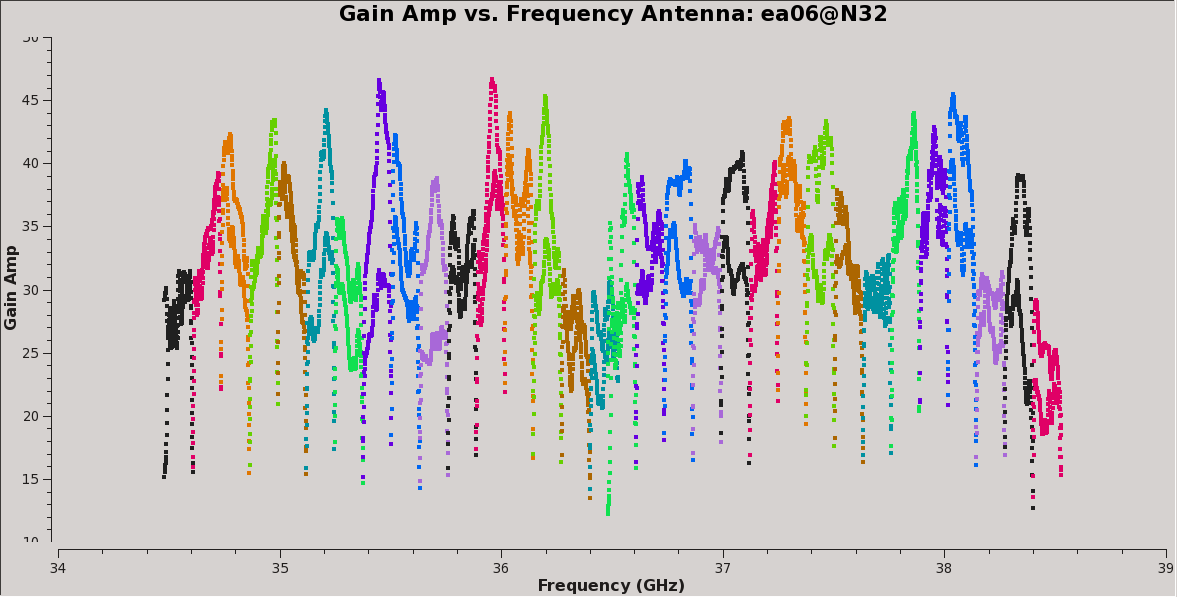
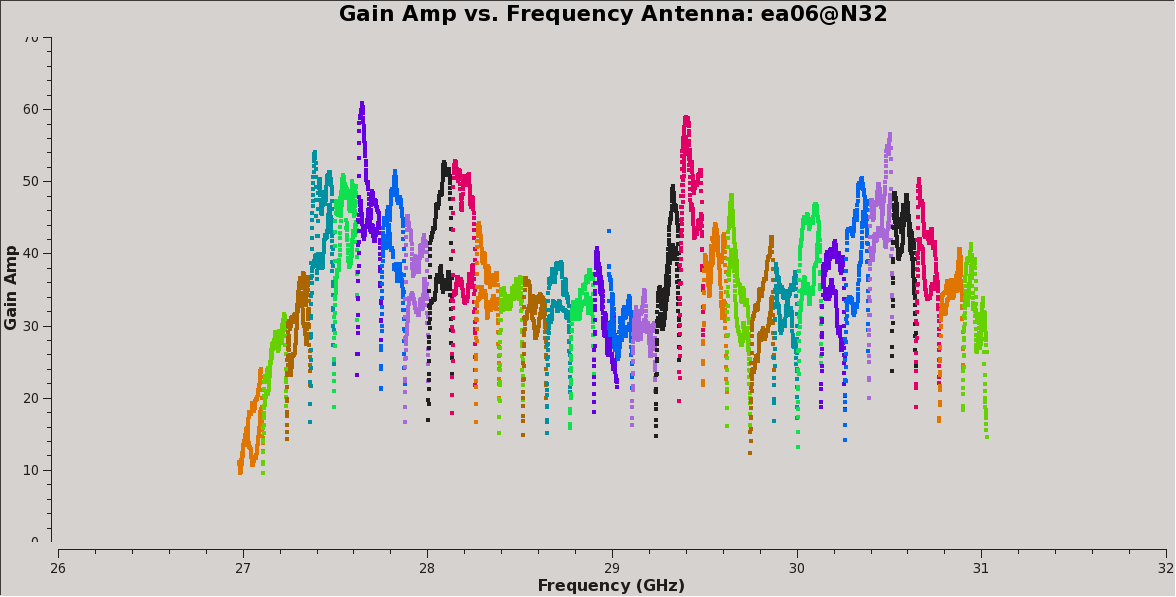
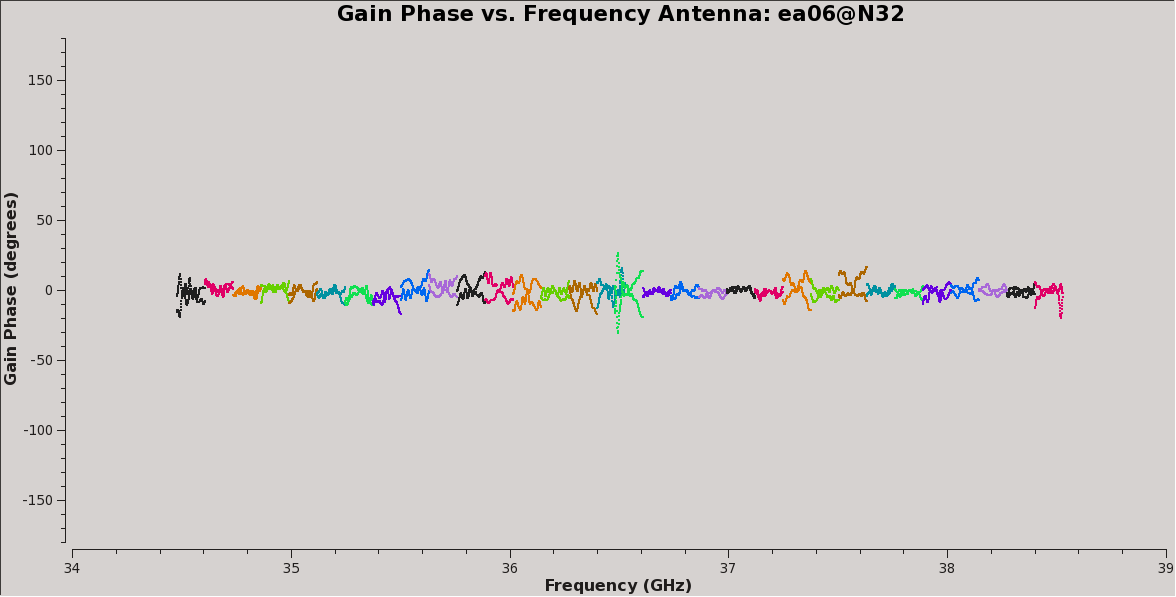
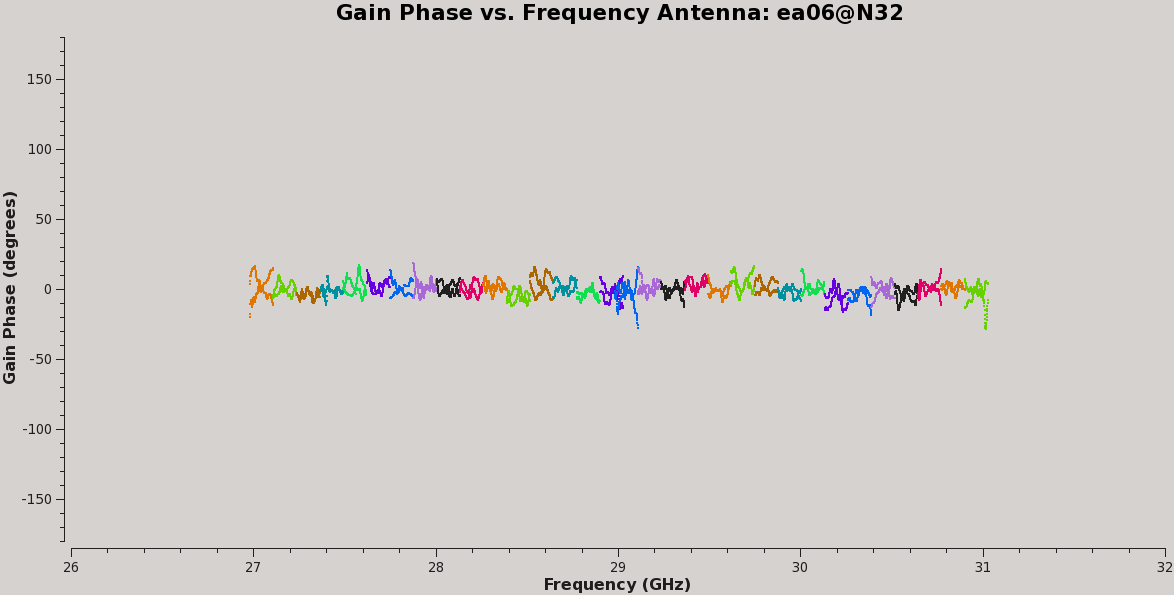
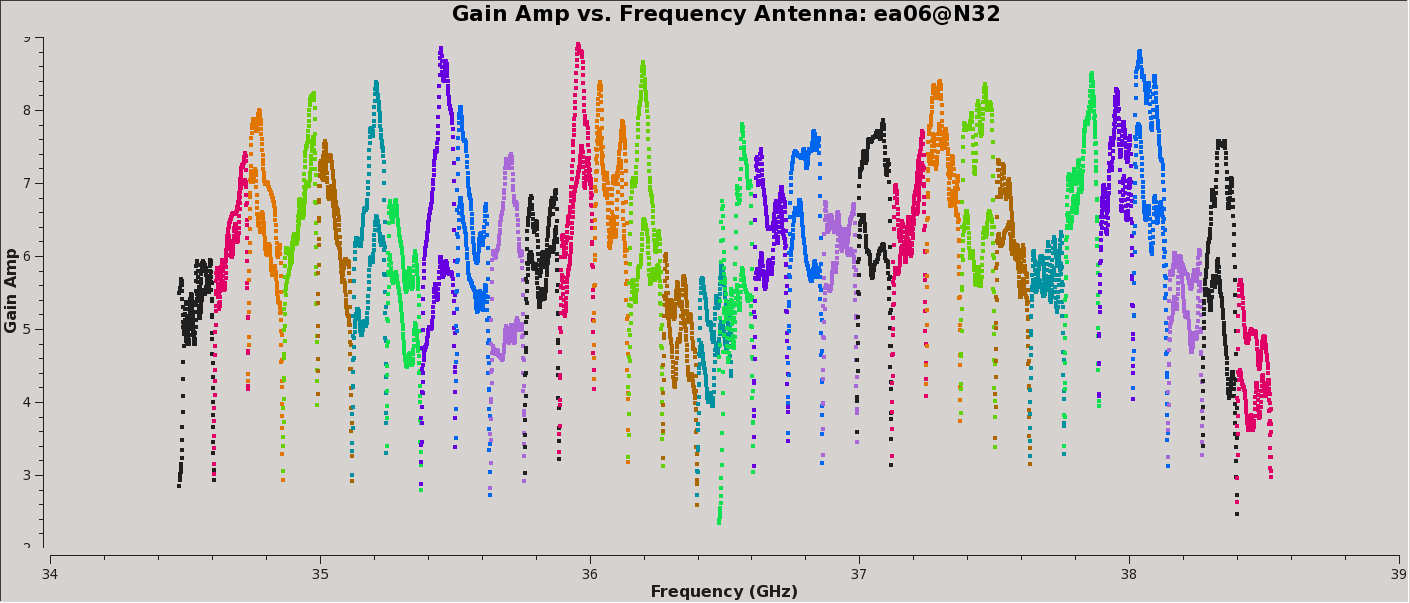
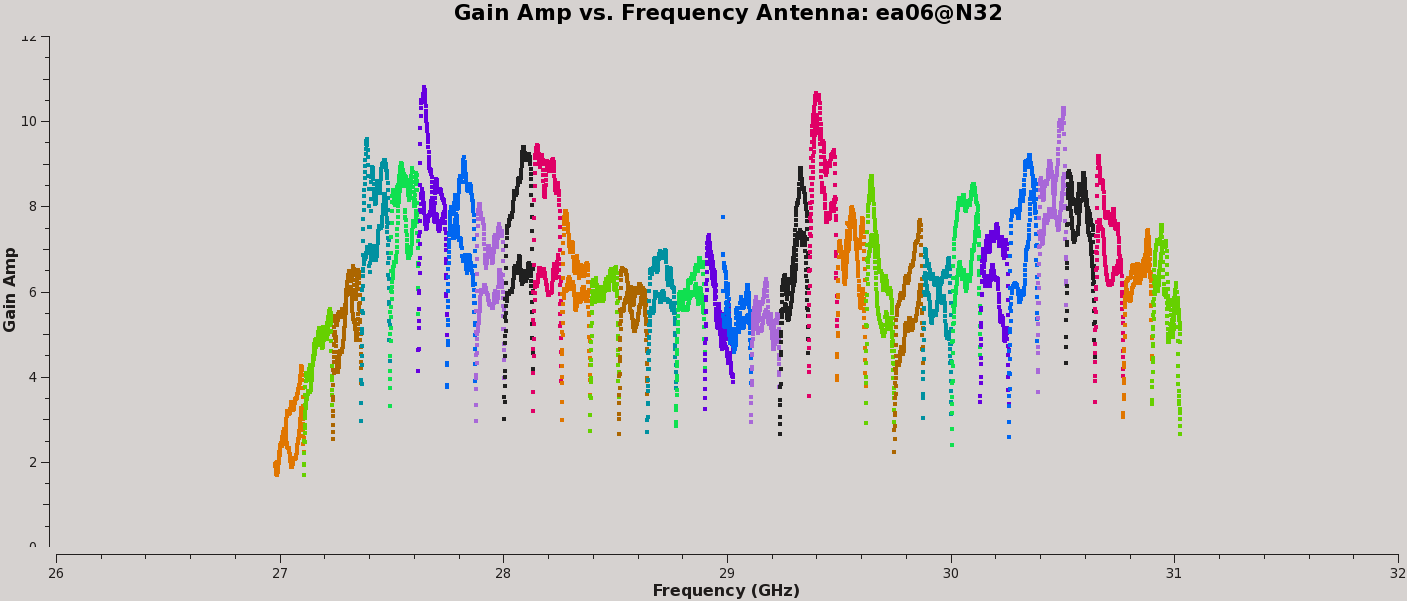
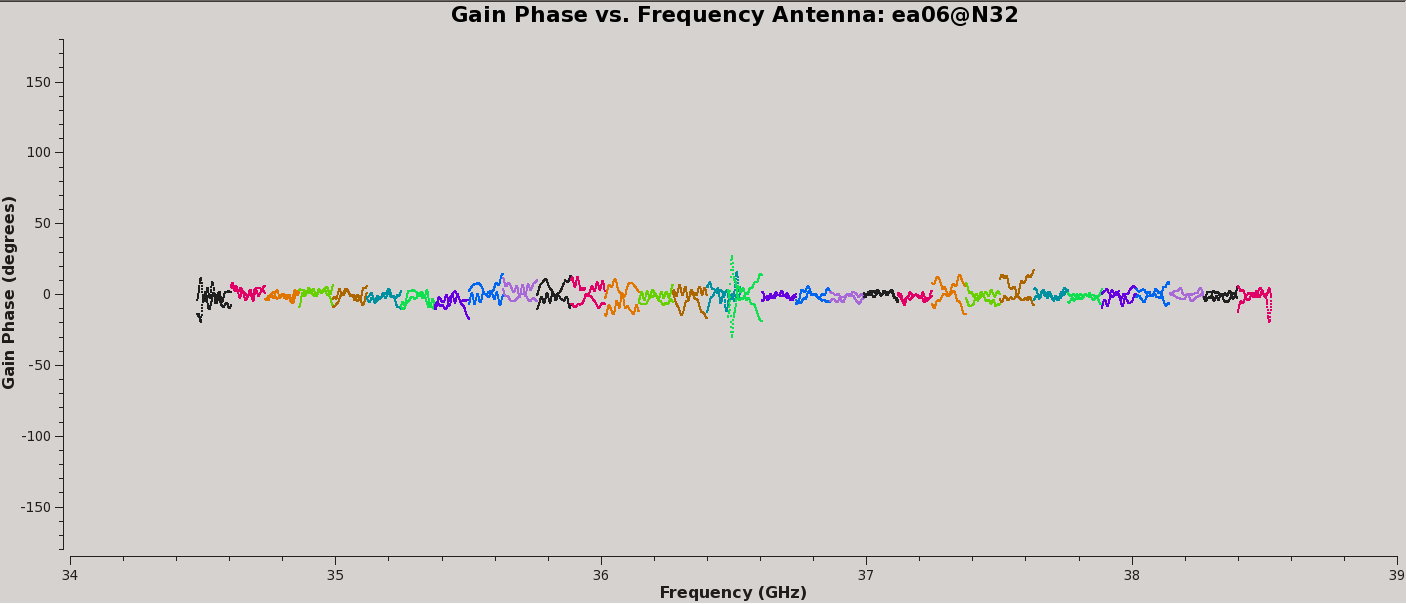
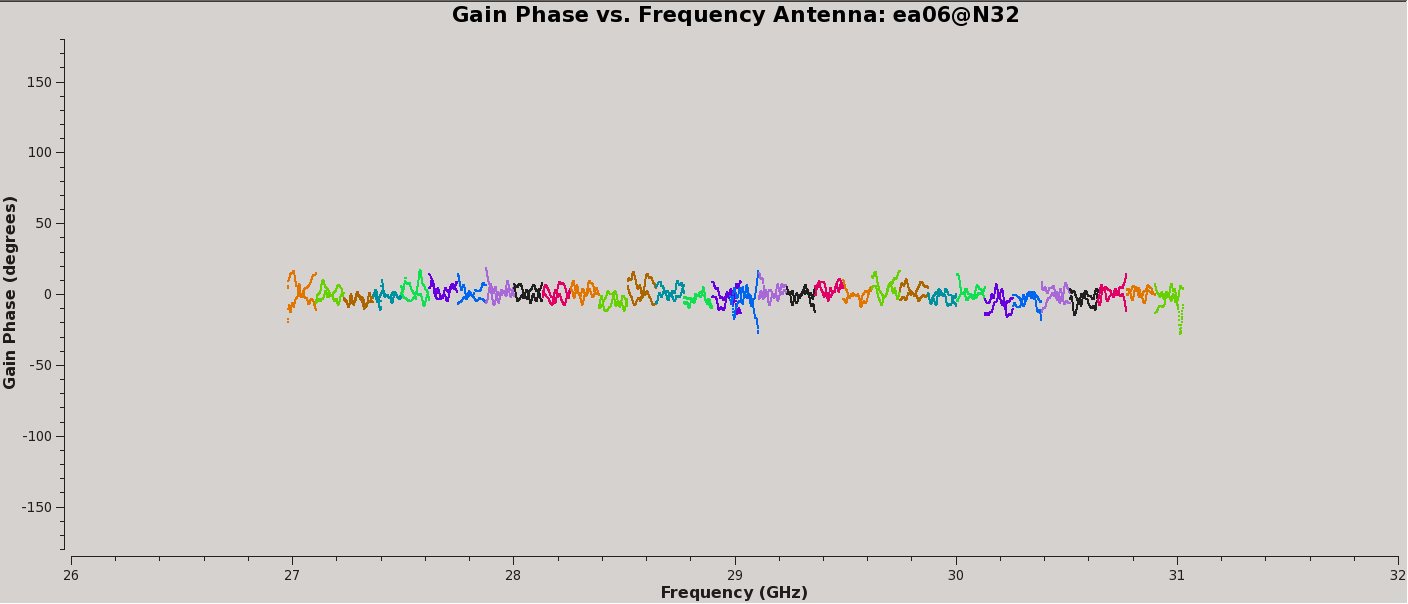
Plot the amplitude and phase soutions of this new bandpass. Note that the first panel with ea01 is empty as it is completely flagged. Proceed to ea06 to see the plots as shown in Figures 5a, 5b, 6a, and 6b:
# In CASA, display the bandpass solutions for amplitude and phase for
# the different (2x 4GHz) spw ranges; first range, amplitude:
plotms(vis='cal.bp', xaxis='freq', yaxis='amp',
spw='0~31', iteraxis='antenna', coloraxis='spw')
# second range, amplitude:
plotms(vis='cal.bp', xaxis='freq', yaxis='amp',
spw='32~63', iteraxis='antenna', coloraxis='spw')
# first range, phase:
plotms(vis='cal.bp', xaxis='freq', yaxis='phase',
spw='0~31', iteraxis='antenna', coloraxis='spw',
plotrange=[-1,-1,-180,180])
# second range, phase:
plotms(vis='cal.bp', xaxis='freq', yaxis='phase',
spw='32~63', iteraxis='antenna', coloraxis='spw',
plotrange=[-1,-1,-180,180])
B) Applying the Initial Bandpass Solutions to the Flux Density Calibrator
Since there is no a priori spectral information for the chosen bandpass calibrator (here 3C84), bootstrapping it is needed to determine its spectral index. This information is then used to recalibrate the bandpass in order to avoid folding the intrinsic spectral shape of the bandpass calibrator into the bandpass calibration.
First, repeat the phase-only calibration solution, this time for both the bandpass and the flux density calibrator (which need to be separated by a comma) and store the solutions in cal.ign2pha (use the 2pha to distinguish it as the second stage for phase-only). This will correct for short-term phase decorrelation of the signals. Similarly to avoid decorrelation due to a wide frequency range, use the narrow center channel range (which was channel 60~68) and apply the bandpass and delay calibration tables:
# In CASA, phase-only self-calibrate the flux density and bandpass calibrators
# using the obtained first-order bandpass calibration above:
gaincal(vis=id_ms, caltable='cal.ign2pha', field=id_flx+','+id_bp,
gaintable=['cal.dly', 'cal.bp'],
gaintype='G', refant=id_ref, calmode='p', solint='int', minsnr=3)
This again allows to calibrate both phase and gain for each scan, now corrected with the delay and bandpass of the bandpass. Store the solutions in cal.ign2 (use the 2 to distinguish it as the second stage gain calibration):
# In CASA, now self-calibrate the phase-corrected amplitudes as well:
gaincal(vis=id_ms, caltable='cal.ign2', field=id_flx+','+id_bp,
gaintable=['cal.dly', 'cal.bp','cal.ign2pha'],
gaintype='G', refant=id_ref, calmode='ap', solint='inf', minsnr=3)
C) Bootstrapping the Bandpass Calibrator Field Spectrum
With gain solutions for the flux density and bandpass calibrators, now use fluxscale to scale the gain amplitudes of the bandpass calibrator using those of the flux density calibrator. Store the solutions in cal.flx2 and the model for the bandpass calibrator in <visbase>+'_'+id_bp+'_fluxinfo.txt':
# In CASA, determine the bandpass calibrator fluxes as function of frequency by
# using the fluxes set for the flux density calibrator with setjy earlier and
# store the output dictionary with these values in the variable flux_bp:
flux_bp = fluxscale(vis=id_ms, caltable='cal.ign2',
fluxtable='cal.flx2', reference=id_flx, transfer=id_bp,
listfile=visbase+'_'+id_bp+'_fluxinfo.txt', fitorder=1)
- flux_bp = fluxscale(...): the Python dictionary returned by the fluxscale task will be stored in the flux_bp variable. Inspect the dictionary flux_bp by typing "print flux_bp" at the CASA command line. Alternatively, when not interested in the dictionary type fluxscale(...); with a semicolon after the parentheses and not assigning it to a variable. This will prevent the dictionary to be printed in the terminal. Here however the dictionary is captured in flux_bp as it is going to be used below
- fluxtable='cal.flx2': this is the output scaled gain table. Since this is only used to find the spectral index of the bandpass calibrator source field, this table is not used further.
- listfile=visbase+'_'+id_bp+'_fluxinfo.txt': an output file that contains the derived flux values and fit information.
- fitorder=1: only find a (linear) spectral index, ignoring curvature in the spectrum.
- reference=id_flx: the reference field from which the flux scaling is transferred (here: the flux density calibrator 3C147, field 0, assigned by id_flx)
- transfer=id_bp: the target field to which the flux scaling is transferred (here: the bandpass calibrator 3C84, field 1, assigned by id_bp)
The last line in the file (and displayed in the logger) shows:
Fitted spectrum for 3c84-J0319+413 with fitorder=1: Flux density = 29.0286 +/- 0.0308709 (freq=32.5128 GHz) spidx=-0.538803 +/- 0.00883078
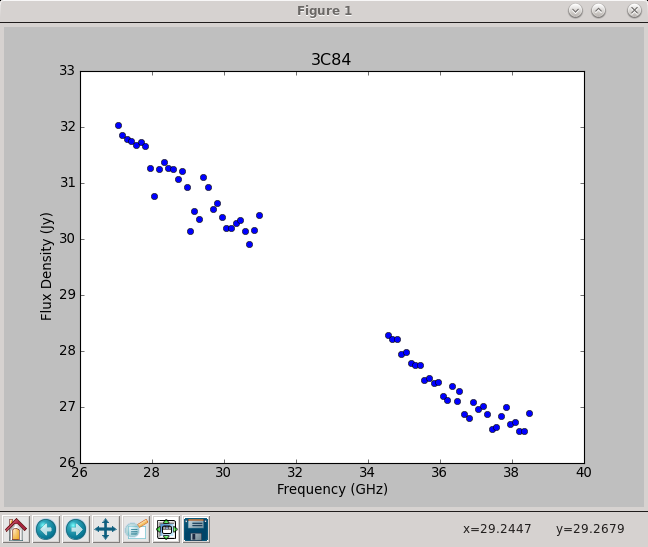
Using the information in the returned flux_bp dictionary, the derived spectrum can be plotted (Figure 7); for that the two loops below fill the parameter variables used in the plotting:
Note that the use of IPython in the command line requires the use of "%cpaste" to allow copy/pasting of loops, conditions, etc.. Press "Enter" (or "Return") after "--" at the end, this stops (or exits) the copy/paste prompt and will return you to the CASA prompt.
# In CASA, use python code to plot the model spectrum of the bandpass calibrator:
import matplotlib.pyplot as pl
%cpaste
# Press Enter or Return, then copy/paste the following:
freq = flux_bp['freq'] / 1e9
spw_list = range(0,64)
spw_str = []
for i in spw_list:
thisspw = str(i)
spw_str.append(thisspw)
bootstrapped_fluxes = []
for j in spw_str:
thisflux = flux_bp['1'][j]['fluxd'][0]
if thisflux ==None:
continue
else:
bootstrapped_fluxes.append(thisflux)
pl.clf()
pl.plot(freq, bootstrapped_fluxes, 'bo')
pl.xlabel('Frequency (GHz)')
pl.ylabel('Flux Density (Jy)')
pl.title(id_bp)
pl.show()
--
The model from fluxscale is used to fill the MODEL column with the banpass source's spectral information using setjy. With standard='fluxscale', we can directly use the flux_bp Python dictionary as input via fluxdict:
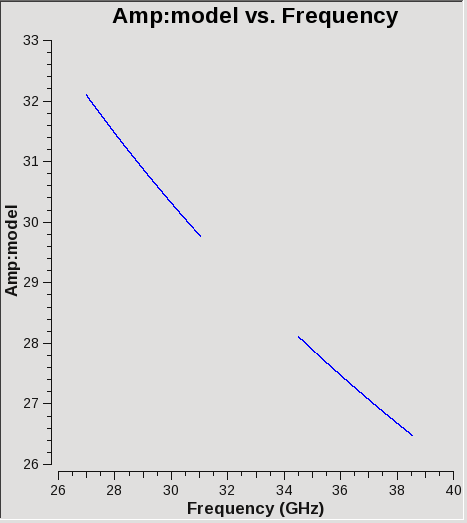
# In CASA, insert the spectral information for the bandpass calibrator field:
setjy(vis=id_ms, field=id_bp, scalebychan=True,
standard = 'fluxscale', fluxdict=flux_bp);
Check with plotms that the data have been appropriately filled (Figure 8):
# In CASA, display the spectral model of the bandpass calibrator field, in this
# case for a specific baseline (which should be identical for all baselines
# for a point-like source, otherwise it will depend on baseline length):
plotms(vis=id_ms, field=id_bp, antenna='ea05&ea02',
xaxis='freq', yaxis='amp', ydatacolumn='model')
D) Create a New Bandpass Using the Bandpass Calibrator Spectral Model
Next, redo the previous calibration using this new model information. Although the commands are the same as issued earlier, keep in mind that the model values for the bandpass calibrator have changed and, therefore, the results of these calibration calculations accordingly will differ if the specral index differs significanlty from zero:
# In CASA, redo a phase-only self-calibration on the bandpass calibrator:
gaincal(vis=id_ms, caltable='cal.ign.redo',
field=id_bp, spw='*:60~68',
gaintype='G', refant=id_ref, calmode='p',
solint='int', minsnr=3)
# In CASA, re-determine residual delays from the bandpass calibrator scans:
gaincal(vis=id_ms, caltable='cal.dly.redo',
gaintable=['cal.ign.redo'],
field=id_bp, spw='*:5~122', gaintype='K',
refant=id_ref, solint='inf', minsnr=3)
# In CASA, re-determine the bandpass from the bandpass calibrator scans:
bandpass(vis=id_ms, caltable='cal.bp.redo',
gaintable=['cal.ign.redo', 'cal.dly.redo'],
field=id_bp, refant=id_ref, solnorm=False,
bandtype='B', solint='inf')
Finally, inspect these solutions (Figures 9a, 9b, 10a, and 10b; again note that antenna ea01 is fully flagged):
# In CASA, display and check the bandpass solutions; first range, amplitude:
plotms(vis='cal.bp.redo', xaxis='freq', yaxis='amp',
spw='0~31', iteraxis='antenna', coloraxis='spw')
# second range, amplitude:
plotms(vis='cal.bp.redo', xaxis='freq', yaxis='amp',
spw='32~63', iteraxis='antenna', coloraxis='spw')
# first range, phase:
plotms(vis='cal.bp.redo', xaxis='freq', yaxis='phase',
spw='0~31', iteraxis='antenna', coloraxis='spw',
plotrange=[-1,-1,-180,180])
# second range, phase:
plotms(vis='cal.bp.redo', xaxis='freq', yaxis='phase',
spw='32~63', iteraxis='antenna', coloraxis='spw',
plotrange=[-1,-1,-180,180])
They look virtually unchanged from the previous solutions with the exception that the amplitude scaling is corrected for the spectrum of the bandpass calibrator. These steps yielded the final version of the delay and bandpass calibration tables, cal.dly.redo and cal.bp.redo, which now would be used for all subsequent calibration steps.
Last checked on CASA Version 6.4.1