Simalma (CASA 5.4) v2

This guide demonstrates how to use simalma, a CASA task that simplifies the process of simulating observations that combine data from the main 12 m array with data from the ALMA Compact Array (ACA). To learn how to create a script of the Python code on this page see Extracting scripts from these tutorials.

ALMA consists of the main array of 12m antennas plus the ACA, which includes an array of 7 m antennas and a separate set of 12 m antennas used for Total Power measurements. CASA enables users to simulate observations using any or all of these components.

Simulating Observations with the Main 12 m Array and the ACA: Manual Combination of the Data

One could simulate observations that use the main array plus the ACA by generating the data for each component separately and then "manually" combining and imaging the data. The approach is to use simobserve to generate simulated uv data sets for each component separately, and then combine and image the resulting Measurement Sets using simanalyze. This technique is general and can be used to simulate observations using multiple 12m array configurations, as well. Total power observations can be simulated either in an independent run of simobserve, or integrated with one of the interferometric simulations. Note that if you simulate total power and interferometric observations simultaneously with simobserve, they must have the same set of pointing centers and the same integration and total time. These are not realistic conditions. For example, to reduce edge effects, the Total Power antennas should observe a larger area on the sky than the main array antennas, by about 1/2 of a primary beam. So, it is generally better to generate the total power data with a separate run of simobserve.

This "manual" method of combining main-array data with ACA data is described in the ACA_Simulation_(CASA_5.4) guide.

The simalma task

The simalma task has been available in CASA since CASA version 4.1. This task takes one set of parameters describing the region of the sky to observe, and makes the appropriate calls to simobserve and simanalyze for ALMA observations. Here we give an example showing how to use simalma.

Set simalma as current task

Reset all parameters to default, then set the project name to m51 and allow simalma to overwrite files

# Set simalma to default parameters
default("simalma")
# Our project name will be "m51", and all simulation products will be placed in a subdirectory "m51/"
project="m51"
overwrite=True

Specify sky model image

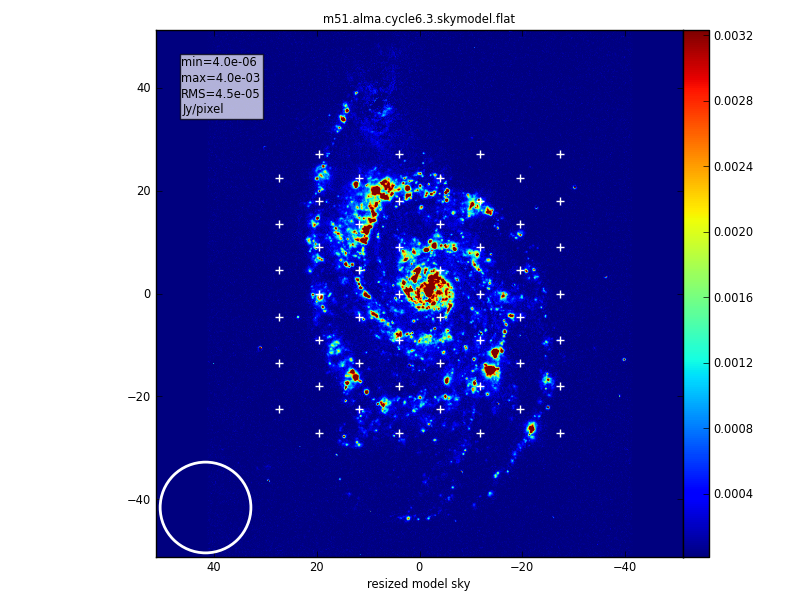
In this example, we'll use an Halpha image of M51 as the model of the sky. The curl command used below will copy a data file with the model image to our local disk and rename it.

# Model sky = Halpha image of M51 
os.system('curl https://casaguides.nrao.edu/images/3/3f/M51ha.fits.txt -f -o M51ha.fits')
skymodel         =  "M51ha.fits"

Note that simalma will not modify your original input image. Rather, it will make a copy m51/m51.skymodel.

To make the M51 Halpha image more suitable to a sub-millimeter ALMA observation, we will modify most of the header parameters from the FITS file. We will:

• place the source in the southern hemisphere with the indirection parameter,
• set the pixel size to 0.1arcsec, to simulate an observation of a galaxy that is smaller in angular size than M51. (M51 itself would require a quite large mosaic, and in any case we'd like the angular scale of pixels in the input model to be significantly smaller than the synthesized beam.)
• set the peak brightness to 0.004 Jy/pixel
• set the center observing frequency to 330GHz, and since it's a 2D image we'll set the single "channel" width to be 50MHz. These parameters are plausible for observing a sub-mm emission line in a galaxy.

# Set model image parameters:
indirection="J2000 23h59m59.96s -34d59m59.50s"
incell="0.1arcsec"
inbright="0.004"
incenter="330.076GHz"
inwidth="50MHz"

---

Set up Observing Parameters, and Run

Hexagonal mosaic overplotted on sky model

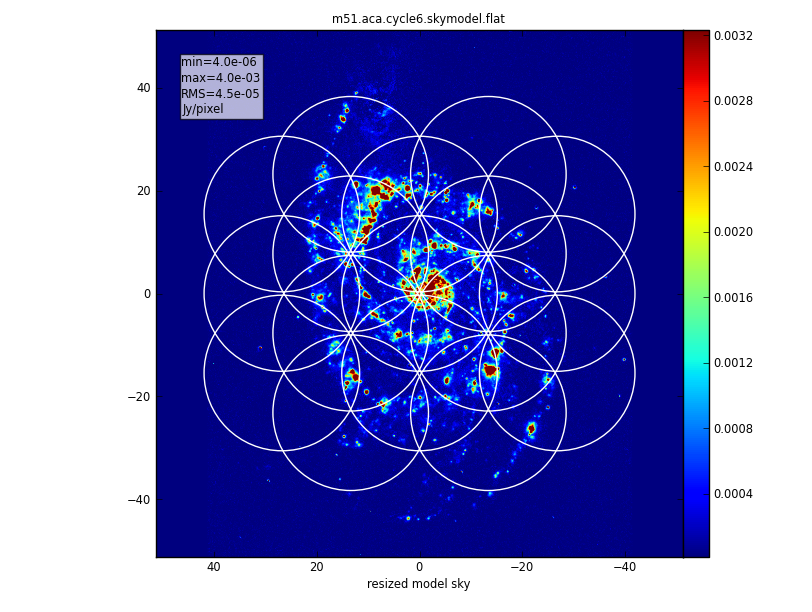
We will simulate observations using the main array in "configuration number 3" from Cycle 6. To that we will add the ACA cycle 6 array. This configuration affords ~0.5 arcsec resolution. Here is a list of configuration files available in CASA 5.4.

antennalist=["alma.cycle6.3.cfg","aca.cycle6.cfg"]

We will set the total 12m array observing time to 30 minutes. In simalma, the 7m array observing time is set by default to be twice the integration time with the 12m array. Therefore, if we leave the inputs at the simalma defaults, the 7m array observations would have a duration of 1 hour. In reality, the time ratios between 12m arrays, 7m arrays, and total power observations vary by array configuration to achieve the correct sensitivity in all arrays/observations. Specific time ratios can be found in Table 7.4 of the ALMA Technical Handbook (see the latest version here). In this case, since we are using the Cycle 6 C43-3 configuration for the 12m observations, Table 7.4 shows that we require a total time for the 7m array observations that is 2.4 times the 12m observation duration. We then set the 12m array observing time (30 min) together with the 7m time (2.4 x 30 min) as a 2-element array in the totaltime parameter:

totaltime=["1800s","4320s"]

For this simulation we will also include "single-dish" total power (TP) observations with three antennas from the 12m Total Power Array. Again, the total time needed for total power observations depends on the ALMA 12m array, and the time ratio between the total power and the ALMA nominal configurations can be found in the Technical Handbook. While the default integration time in simalma for TP observations is 4 times the 12m array time, for this particular simulation the factor should be 4.1. We set this using the tptime parameter.

In CASA 5.4 simulations, the total power observations are simulated in a single track. So the total time of a TP observations should be roughly 8 hours or less, depending on the target declination, to ensure that the target position remains above the horizon. Until this limitation is addressed in a future CASA release, you should limit simulations that include the TP Array to short total integration times.

tpnant = 3
tptime="7380s"

We set the precipitable water vapor to 0.6 mm to represent observations in nominal weather at 330 GHz. The simulation will add noise to the data based on this setting.

pwv=0.6

Because we are simulating a real observation with noise, we will want simalma to also clean the resulting data. By default, simalma will only produce a dirty image unless we set a maximum number of clean iterations with the niter parameter. It is also useful to provide a clean threshold, beyond which no more cleaning is done. For more information on imaging and deconvolution in CASA, please see our First Look Guides. Given the observing parameters in this guide, we set the threshold to 30 mJy, or roughly three times the rms noise in the final image.

niter = 10000
threshold = '30mJy'

To observe the entire galaxy according to our rescaled pixel size, we'll need a 1 arcmin mosaic, and we'll let simalma calculate the pointings for us. We'll also set the final image and cell sizes:

mapsize="1arcmin"
cell = '0.1arcsec'
imsize = [600,600]

Finally you can check the input settings:

dryrun = False
inp

and run the simulation:

go

What does simalma do?

12m observation

Generate visibilities and images for each array

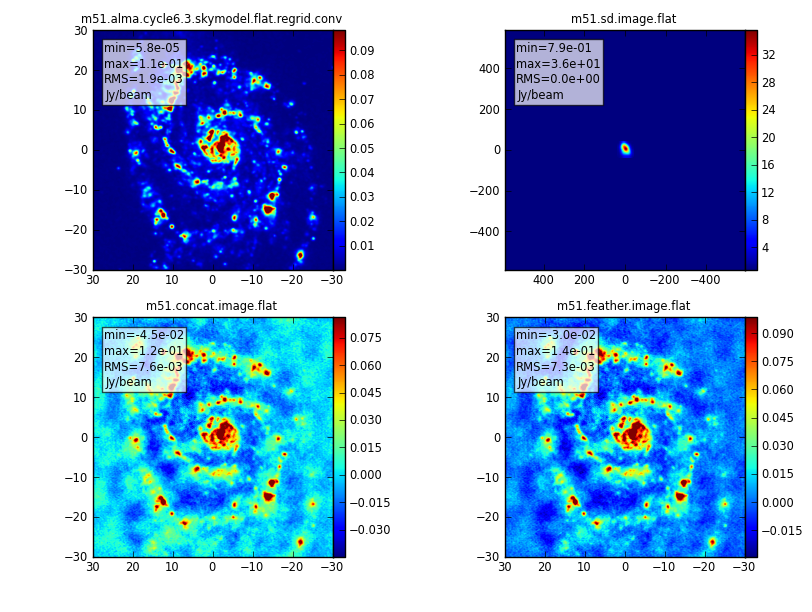
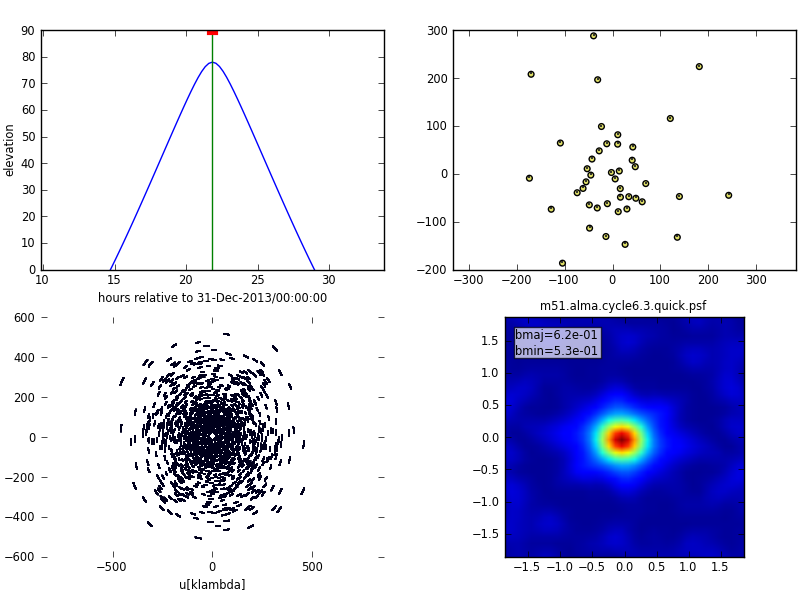
The simalma task first calls simobserve to simulate the visibilities for each of the three array components: the 12 m Main Array, the 7 m Array, and the 12 m Total Power Array. The simobserve task generates a figure showing the elevation of the target, the antenna layout, the uv coverage, and the synthesized dirty beam.

Next simalma generates an image from each of the three array components, separately. This step is not essential to getting the final result from the combined arrays, but it provides a useful diagnostic. The images will be named according to the antennalist parameter above. For example, the ALMA 12m image is called m51.alma.cycle6.3.noisy.image.

ACA hex map

It is useful to know that simalma generates a version of the input sky model convolved to the ACA resolution. In this example it is called m51.aca.tp.skymodel.flat.regrid.conv. That image can be useful to better understand the simulation results.

Note that the total power map covers the same region as the main array mosaic, with an extra pointing position added around the outside edge of the map so that the total power map is larger than the interferometric mosaic. (Total power maps usually have additional noise and artifacts at their edges). Furthermore, a square raster pattern is used instead of the hexagonal pattern of the interferometric array maps.

TP map

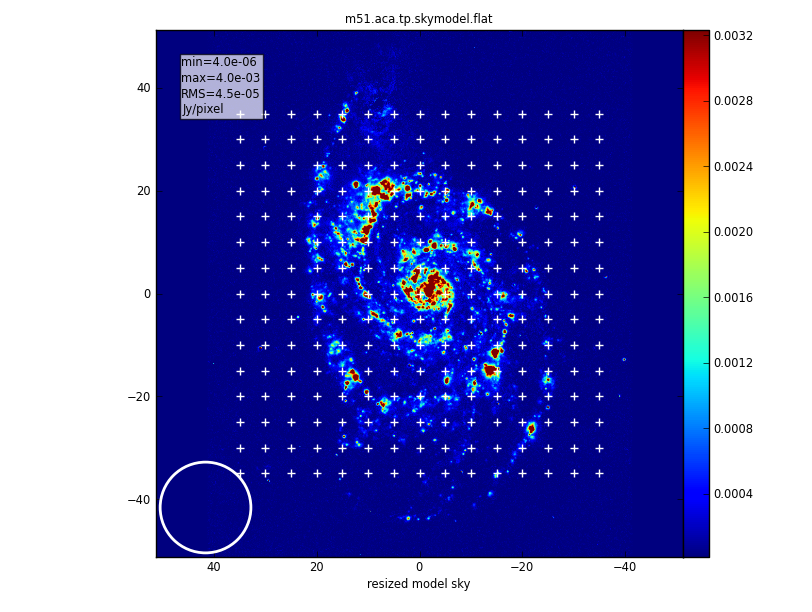
Combine the UV data from the 3 components and make the final image

Next simalma uses simanalyze to combine the three measurement sets and create a single image. It accomplishes this in the following manner.

First, simalma concatenates the two sets of interferometric visibilities, and images them. Diagnostic graphics with "concat" in their names are generated:

Combined interferometric map ACA + 12m

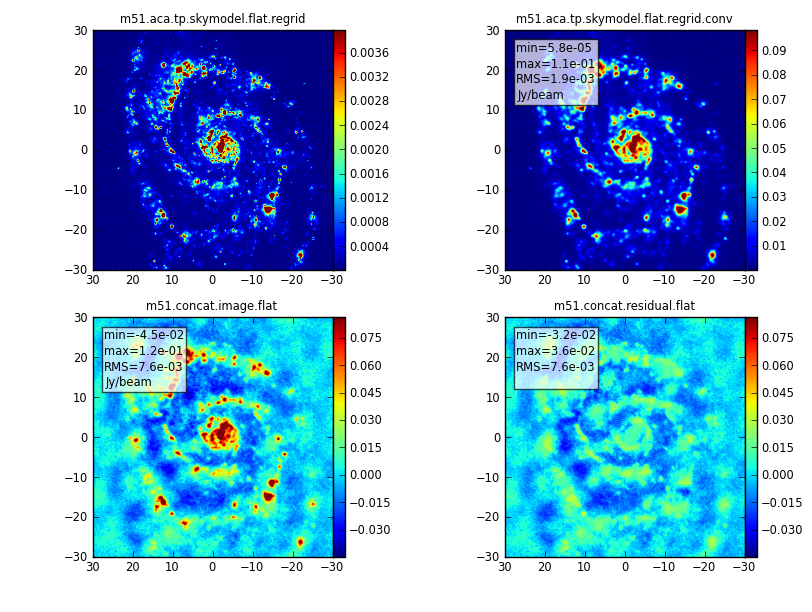
Finally it combines the total power image with the concatenated interferometric image using the CASA task feather.

Note, there are many ways to combine data from separate observations. If you are dealing with real ALMA data, you may wish to discuss options with scientists at your ARC.

Some notes for combining data "manually"

1. When combining interferometric data from different arrays "manually", it is critical to set the relative data weights properly. Simulated data have weights=1, since the thermal noise is generated uniformly per baseline. However, in reality the 7m baselines have lower sensitivity than the 12m baselines, and their weights must be decreased by the sensitivity ratio. simalma uses the visweightscale parameter of concat to apply that lower weight of (7/12)**2 to the 7m visibilities. If you wish to combine data manually, you must do this step yourself.
2. When combining the single dish and interferometric maps in the image plane using the feather task, one must use the interferometric map without the primary beam correction, and first multiply the total power map by the interferometric sensitivity image (".flux") -- this ensures that noise effects are properly handled on the edges of each map. After running feather, the output is masked to 0.2 times the interferometric primary beam, since the total power map was created larger than the interferometric map on purpose, so the edges of the combined image do not contain any interferometric information.:

Combined map