VLA CASA Imaging-CASA4.5.2: Difference between revisions
Created page with "* '''This CASA guide was designed for CASA 4.5.3''' https://casaguides.nrao.edu/index.php?title=VLA-CASA-Flagging-CASA4.5.3 https://casaguides.nrao.edu/index.php?title=VLA-C..." |
m Jott moved page VLA-CASA-Imaging-CASA4.5.3 to VLA-CASA-Imaging-CASA4.5.2 |
(No difference)
| |
Revision as of 03:45, 13 April 2016
- This CASA guide was designed for CASA 4.5.3
https://casaguides.nrao.edu/index.php?title=VLA-CASA-Flagging-CASA4.5.3 https://casaguides.nrao.edu/index.php?title=VLA-CASA-Imaging-CASA4.5.3
Overview
This CASA guide will cover priori data flagging, including online flagging, shadowing, zero clipping, and quacking. It will also cover auto-flagging RFI (Radio Frequency Interference) via TFcrop (Time-Frequency crop) and rflag.
The guide will then move on to imaging the data, and cover topics on the CLEAN algorithm, MS (Multi-Scale) deconvolution, MS-MFS (Multi-Scale, Multi-Frequency Synthesis), outlier fields, spectral indices, image weights and tapering, small scale bias, primary beam correction, image headers, and imaging in widefield mode, which will make use of w-projection.
We will be utilizing data taken with the Karl G. Jansky, Very Large Array, of a supernova remnant G055.7+3.4.. The data were taken on August 23, 2010, in the first D-configuration for which the new wide-band capabilities of the WIDAR (Wideband Interferometric Digital ARchitecture) correlator were available. The 8-hour-long observation includes all available 1 GHz of bandwidth in L-band, from 1-2 GHz in frequency. The observations were made in 8-bit mode, which has the best dynamic range and is thus best suited for rfi excision.
The guide will often reference the CASA cookbook which is available online and as a pdf download.
Obtaining the Data
A copy of the data (5.1GB) can be downloaded from http://casa.nrao.edu/Data/EVLA/SNRG55/SNR_G55_10s.tar.gz These data are already in CASA format and were prepared specifically for this guide.
Once you've downloaded the file, let's untar it:
tar -xzvf SNR_G55_10s.tar.gz
That will create a directory called SNR_G55_10s.ms (6.1GB), which is the MS (Measurement Set).
Starting CASA
Start CASA by typing casa on a terminal command line. If you have not used CASA before, some helpful tips are available on the Getting Started in CASA page.
This guide has been written for CASA version 4.5.2. Please confirm your version before proceeding by checking the message in the command line interface window or the CASA logger after startup.
For this tutorial, we will be running tasks using the task (parameter = value) syntax. When called in this manner, all parameters not explicitly set will use their default values.
Preliminary Data Evaluation
As a first step, use listobs to have a look at the MS:
# In CASA
listobs(vis='SNR_G55_10s.ms', listfile='SNR_G55_10s.listobs')
- listfile: Creates a text document with details for the observation.
#CASA log when listfile is not defined 2016-03-07 16:54:23 INFO listobs ########################################## 2016-03-07 16:54:23 INFO listobs ##### Begin Task: listobs ##### 2016-03-07 16:54:23 INFO listobs listobs(vis="SNR_G55_10s.ms",selectdata=True,spw="",field="",antenna="", 2016-03-07 16:54:23 INFO listobs uvrange="",timerange="",correlation="",scan="",intent="", 2016-03-07 16:54:23 INFO listobs feed="",array="",observation="",verbose=True,listfile="", 2016-03-07 16:54:23 INFO listobs listunfl=False,cachesize=50,overwrite=False) 2016-03-07 16:54:23 INFO listobs ================================================================================ 2016-03-07 16:54:23 INFO listobs MeasurementSet Name: /lustre/aoc/sciops/CASA_Tutorials/SNR_G55_10s.ms MS Version 2 2016-03-07 16:54:23 INFO listobs ================================================================================ 2016-03-07 16:54:23 INFO listobs Observer: Dr. Sanjay Sanjay Bhatnagar Project: uid://evla/pdb/1072564 2016-03-07 16:54:23 INFO listobs Observation: EVLA 2016-03-07 16:54:25 INFO listobs Data records: 3780000 Total elapsed time = 26926 seconds 2016-03-07 16:54:25 INFO listobs Observed from 23-Aug-2010/00:56:36.0 to 23-Aug-2010/08:25:22.0 (UTC) 2016-03-07 16:54:33 INFO listobs 2016-03-07 16:54:33 INFO listobs ObservationID = 0 ArrayID = 0 2016-03-07 16:54:33 INFO listobs Date Timerange (UTC) Scan FldId FieldName nRows SpwIds Average Interval(s) ScanIntent 2016-03-07 16:54:33 INFO listobs 23-Aug-2010/00:56:36.0 - 00:58:06.0 14 0 J1925+2106 12600 [0,1,2,3] [10, 10, 10, 10, 10] [CALIBRATE_PHASE#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 00:58:06.0 - 00:59:36.0 15 0 J1925+2106 12600 [0,1,2,3] [10, 10, 10, 10, 10] [CALIBRATE_PHASE#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 00:59:36.0 - 01:01:05.0 16 0 J1925+2106 12600 [0,1,2,3] [9.89, 9.89, 9.89, 9.89, 9.89] [CALIBRATE_PHASE#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:01:05.0 - 01:02:35.0 17 0 J1925+2106 12600 [0,1,2,3] [10, 10, 10, 10, 10] [CALIBRATE_PHASE#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:02:35.0 - 01:04:05.0 18 0 J1925+2106 12600 [0,1,2,3] [10, 10, 10, 10, 10] [CALIBRATE_PHASE#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:04:05.0 - 01:05:34.0 19 0 J1925+2106 12600 [0,1,2,3] [9.89, 9.89, 9.89, 9.89, 9.89] [CALIBRATE_PHASE#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:05:34.0 - 01:07:04.0 20 0 J1925+2106 12600 [0,1,2,3] [10, 10, 10, 10, 10] [CALIBRATE_PHASE#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:07:04.0 - 01:08:34.0 21 1 G55.7+3.4 12600 [0,1,2,3] [10, 10, 10, 10, 10] [OBSERVE_TARGET#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:08:34.0 - 01:10:04.0 22 1 G55.7+3.4 12600 [0,1,2,3] [10, 10, 10, 10, 10] [OBSERVE_TARGET#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:10:04.0 - 01:11:34.0 23 1 G55.7+3.4 12600 [0,1,2,3] [10, 10, 10, 10, 10] [OBSERVE_TARGET#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:11:34.0 - 01:13:03.0 24 1 G55.7+3.4 12600 [0,1,2,3] [9.89, 9.89, 9.89, 9.89, 9.89] [OBSERVE_TARGET#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:13:03.0 - 01:14:33.0 25 1 G55.7+3.4 12600 [0,1,2,3] [10, 10, 10, 10, 10] [OBSERVE_TARGET#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:14:33.0 - 01:16:03.0 26 1 G55.7+3.4 12600 [0,1,2,3] [10, 10, 10, 10, 10] [OBSERVE_TARGET#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:16:03.0 - 01:17:33.0 27 1 G55.7+3.4 12600 [0,1,2,3] [10, 10, 10, 10, 10] [OBSERVE_TARGET#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:17:33.0 - 01:19:02.0 28 1 G55.7+3.4 12600 [0,1,2,3] [9.89, 9.89, 9.89, 9.89, 9.89] [OBSERVE_TARGET#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:19:02.0 - 01:20:32.0 29 1 G55.7+3.4 12600 [0,1,2,3] [10, 10, 10, 10, 10] [OBSERVE_TARGET#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:20:32.0 - 01:22:02.0 30 1 G55.7+3.4 12600 [0,1,2,3] [10, 10, 10, 10, 10] [OBSERVE_TARGET#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:22:02.0 - 01:23:32.0 31 1 G55.7+3.4 12600 [0,1,2,3] [10, 10, 10, 10, 10] [OBSERVE_TARGET#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:23:32.0 - 01:25:01.0 32 1 G55.7+3.4 12600 [0,1,2,3] [9.89, 9.89, 9.89, 9.89, 9.89] [OBSERVE_TARGET#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:25:01.0 - 01:26:31.0 33 1 G55.7+3.4 12600 [0,1,2,3] [10, 10, 10, 10, 10] [OBSERVE_TARGET#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:26:31.0 - 01:28:01.0 34 1 G55.7+3.4 12600 [0,1,2,3] [10, 10, 10, 10, 10] [OBSERVE_TARGET#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:28:01.0 - 01:29:31.0 35 1 G55.7+3.4 12600 [0,1,2,3] [10, 10, 10, 10, 10] [OBSERVE_TARGET#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:29:31.0 - 01:31:00.0 36 1 G55.7+3.4 12600 [0,1,2,3] [9.89, 9.89, 9.89, 9.89, 9.89] [OBSERVE_TARGET#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:31:00.0 - 01:32:30.0 37 1 G55.7+3.4 12600 [0,1,2,3] [10, 10, 10, 10, 10] [OBSERVE_TARGET#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:32:30.0 - 01:34:00.0 38 1 G55.7+3.4 12600 [0,1,2,3] [10, 10, 10, 10, 10] [OBSERVE_TARGET#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:34:00.0 - 01:35:30.0 39 1 G55.7+3.4 12600 [0,1,2,3] [10, 10, 10, 10, 10] [OBSERVE_TARGET#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:35:30.0 - 01:36:59.0 40 1 G55.7+3.4 12600 [0,1,2,3] [9.89, 9.89, 9.89, 9.89, 9.89] [OBSERVE_TARGET#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:36:59.0 - 01:38:29.0 41 0 J1925+2106 12600 [0,1,2,3] [10, 10, 10, 10, 10] [CALIBRATE_PHASE#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:38:29.0 - 01:39:59.0 42 0 J1925+2106 12600 [0,1,2,3] [10, 10, 10, 10, 10] [CALIBRATE_PHASE#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:39:59.0 - 01:41:29.0 43 0 J1925+2106 12600 [0,1,2,3] [10, 10, 10, 10, 10] [CALIBRATE_PHASE#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 01:41:29.0 - 01:42:58.0 44 1 G55.7+3.4 12600 [0,1,2,3] [9.89, 9.89, 9.89, 9.89, 9.89] [OBSERVE_TARGET#UNSPECIFIED] <snip> 2016-03-07 16:54:33 INFO listobs 08:11:54.0 - 08:13:24.0 305 1 G55.7+3.4 12600 [0,1,2,3] [10, 10, 10, 10, 10] [OBSERVE_TARGET#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 08:13:24.0 - 08:14:54.0 306 1 G55.7+3.4 12600 [0,1,2,3] [10, 10, 10, 10, 10] [OBSERVE_TARGET#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 08:14:54.0 - 08:16:24.0 307 2 0542+498=3C147 12600 [0,1,2,3] [10, 10, 10, 10, 10] [CALIBRATE_AMPLI#UNSPECIFIED,CALIBRATE_BANDPASS#UNSPECIFIED,UNSPECIFIED#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 08:16:24.0 - 08:17:54.0 308 2 0542+498=3C147 12600 [0,1,2,3] [10, 10, 10, 10, 10] [CALIBRATE_AMPLI#UNSPECIFIED,CALIBRATE_BANDPASS#UNSPECIFIED,UNSPECIFIED#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 08:17:54.0 - 08:19:23.0 309 2 0542+498=3C147 12600 [0,1,2,3] [9.89, 9.89, 9.89, 9.89, 9.89] [CALIBRATE_AMPLI#UNSPECIFIED,CALIBRATE_BANDPASS#UNSPECIFIED,UNSPECIFIED#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 08:19:23.0 - 08:20:53.0 310 2 0542+498=3C147 12600 [0,1,2,3] [10, 10, 10, 10, 10] [CALIBRATE_AMPLI#UNSPECIFIED,CALIBRATE_BANDPASS#UNSPECIFIED,UNSPECIFIED#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 08:20:53.0 - 08:22:23.0 311 2 0542+498=3C147 12600 [0,1,2,3] [10, 10, 10, 10, 10] [CALIBRATE_AMPLI#UNSPECIFIED,CALIBRATE_BANDPASS#UNSPECIFIED,UNSPECIFIED#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 08:22:23.0 - 08:23:52.0 312 2 0542+498=3C147 12600 [0,1,2,3] [9.89, 9.89, 9.89, 9.89, 9.89] [CALIBRATE_AMPLI#UNSPECIFIED,CALIBRATE_BANDPASS#UNSPECIFIED,UNSPECIFIED#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs 08:23:52.0 - 08:25:22.0 313 2 0542+498=3C147 12600 [0,1,2,3] [10, 10, 10, 10, 10] [CALIBRATE_AMPLI#UNSPECIFIED,CALIBRATE_BANDPASS#UNSPECIFIED,UNSPECIFIED#UNSPECIFIED] 2016-03-07 16:54:33 INFO listobs (nRows = Total number of rows per scan) 2016-03-07 16:54:33 INFO listobs Fields: 3 2016-03-07 16:54:33 INFO listobs ID Code Name RA Decl Epoch SrcId nRows 2016-03-07 16:54:33 INFO listobs 0 D J1925+2106 19:25:59.605371 +21.06.26.16218 J2000 0 541800 2016-03-07 16:54:33 INFO listobs 1 NONE G55.7+3.4 19:21:40.000000 +21.45.00.00000 J2000 1 3150000 2016-03-07 16:54:33 INFO listobs 2 N 0542+498=3C147 05:42:36.137916 +49.51.07.23356 J2000 2 88200 2016-03-07 16:54:33 INFO listobs Spectral Windows: (5 unique spectral windows and 1 unique polarization setups) 2016-03-07 16:54:33 INFO listobs SpwID Name #Chans Frame Ch0(MHz) ChanWid(kHz) TotBW(kHz) CtrFreq(MHz) BBC Num Corrs 2016-03-07 16:54:33 INFO listobs 0 Subband:0 64 TOPO 1256.000 2000.000 128000.0 1319.0000 4 RR RL LR LL 2016-03-07 16:54:33 INFO listobs 1 Subband:2 64 TOPO 1384.000 2000.000 128000.0 1447.0000 4 RR RL LR LL 2016-03-07 16:54:33 INFO listobs 2 Subband:1 64 TOPO 1648.000 2000.000 128000.0 1711.0000 8 RR RL LR LL 2016-03-07 16:54:33 INFO listobs 3 Subband:0 64 TOPO 1776.000 2000.000 128000.0 1839.0000 8 RR RL LR LL 2016-03-07 16:54:33 INFO listobs Sources: 15 2016-03-07 16:54:33 INFO listobs ID Name SpwId RestFreq(MHz) SysVel(km/s) 2016-03-07 16:54:33 INFO listobs 0 J1925+2106 0 - - 2016-03-07 16:54:33 INFO listobs 0 J1925+2106 1 - - 2016-03-07 16:54:33 INFO listobs 0 J1925+2106 2 - - 2016-03-07 16:54:33 INFO listobs 0 J1925+2106 3 - - 2016-03-07 16:54:33 INFO listobs 1 G55.7+3.4 0 - - 2016-03-07 16:54:33 INFO listobs 1 G55.7+3.4 1 - - 2016-03-07 16:54:33 INFO listobs 1 G55.7+3.4 2 - - 2016-03-07 16:54:33 INFO listobs 1 G55.7+3.4 3 - - 2016-03-07 16:54:33 INFO listobs 2 0542+498=3C147 0 - - 2016-03-07 16:54:33 INFO listobs 2 0542+498=3C147 1 - - 2016-03-07 16:54:33 INFO listobs 2 0542+498=3C147 2 - - 2016-03-07 16:54:33 INFO listobs 2 0542+498=3C147 3 - - 2016-03-07 16:54:34 INFO listobs Antennas: 27: 2016-03-07 16:54:34 INFO listobs ID Name Station Diam. Long. Lat. Offset from array center (m) ITRF Geocentric coordinates (m) 2016-03-07 16:54:34 INFO listobs East North Elevation x y z 2016-03-07 16:54:34 INFO listobs 0 ea01 W09 25.0 m -107.37.25.2 +33.53.51.0 -521.9416 -332.7766 -1.2001 -1601710.017000 -5042006.925200 3554602.355600 2016-03-07 16:54:34 INFO listobs 1 ea02 E02 25.0 m -107.37.04.4 +33.54.01.1 9.8240 -20.4293 -2.7806 -1601150.060300 -5042000.619800 3554860.729400 2016-03-07 16:54:34 INFO listobs 2 ea03 E09 25.0 m -107.36.45.1 +33.53.53.6 506.056 -251.8670 -3.5825 -1600715.950800 -5042273.187000 3554668.184500 2016-03-07 16:54:34 INFO listobs 3 ea04 W01 25.0 m -107.37.05.9 +33.54.00.5 -27.3562 -41.3030 -2.7418 -1601189.030140 -5042000.493300 3554843.425700 2016-03-07 16:54:34 INFO listobs 4 ea05 W08 25.0 m -107.37.21.6 +33.53.53.0 -432.1167 -272.1478 -1.5054 -1601614.091000 -5042001.652900 3554652.509300 2016-03-07 16:54:34 INFO listobs 5 ea06 N06 25.0 m -107.37.06.9 +33.54.10.3 -54.0649 263.8778 -4.2273 -1601162.591000 -5041828.999000 3555095.896400 2016-03-07 16:54:34 INFO listobs 6 ea07 E05 25.0 m -107.36.58.4 +33.53.58.8 164.9788 -92.8032 -2.5268 -1601014.462000 -5042086.252000 3554800.799800 2016-03-07 16:54:34 INFO listobs 7 ea08 N01 25.0 m -107.37.06.0 +33.54.01.8 -30.8810 -1.4664 -2.8597 -1601185.634945 -5041978.156586 3554876.424700 2016-03-07 16:54:34 INFO listobs 8 ea09 E06 25.0 m -107.36.55.6 +33.53.57.7 236.9058 -126.3369 -2.4443 -1600951.588000 -5042125.911000 3554773.012300 2016-03-07 16:54:34 INFO listobs 9 ea10 N03 25.0 m -107.37.06.3 +33.54.04.8 -39.0773 93.0192 -3.3330 -1601177.376760 -5041925.073200 3554954.584100 2016-03-07 16:54:34 INFO listobs 10 ea11 E04 25.0 m -107.37.00.8 +33.53.59.7 102.8054 -63.7682 -2.6414 -1601068.790300 -5042051.910200 3554824.835300 2016-03-07 16:54:34 INFO listobs 11 ea12 E08 25.0 m -107.36.48.9 +33.53.55.1 407.8285 -206.0065 -3.2272 -1600801.926000 -5042219.366500 3554706.448200 2016-03-07 16:54:34 INFO listobs 12 ea13 N07 25.0 m -107.37.07.2 +33.54.12.9 -61.1037 344.2331 -4.6138 -1601155.635800 -5041783.843800 3555162.374100 2016-03-07 16:54:34 INFO listobs 13 ea15 W06 25.0 m -107.37.15.6 +33.53.56.4 -275.8288 -166.7451 -2.0590 -1601447.198000 -5041992.502500 3554739.687600 2016-03-07 16:54:34 INFO listobs 14 ea16 W02 25.0 m -107.37.07.5 +33.54.00.9 -67.9687 -26.5614 -2.7175 -1601225.255200 -5041980.383590 3554855.675000 2016-03-07 16:54:34 INFO listobs 15 ea17 W07 25.0 m -107.37.18.4 +33.53.54.8 -349.9877 -216.7509 -1.7975 -1601526.387300 -5041996.840100 3554698.327400 2016-03-07 16:54:34 INFO listobs 16 ea18 N09 25.0 m -107.37.07.8 +33.54.19.0 -77.4346 530.6273 -5.5859 -1601139.485100 -5041679.036800 3555316.533200 2016-03-07 16:54:34 INFO listobs 17 ea19 W04 25.0 m -107.37.10.8 +33.53.59.1 -152.8599 -83.8054 -2.4614 -1601315.893000 -5041985.320170 3554808.304600 2016-03-07 16:54:34 INFO listobs 18 ea20 N05 25.0 m -107.37.06.7 +33.54.08.0 -47.8454 192.6015 -3.8723 -1601168.786100 -5041869.054000 3555036.936000 2016-03-07 16:54:34 INFO listobs 19 ea21 E01 25.0 m -107.37.05.7 +33.53.59.2 -23.8638 -81.1510 -2.5851 -1601192.467800 -5042022.856800 3554810.438800 2016-03-07 16:54:34 INFO listobs 20 ea22 N04 25.0 m -107.37.06.5 +33.54.06.1 -42.6239 132.8436 -3.5494 -1601173.979400 -5041902.657700 3554987.517500 2016-03-07 16:54:34 INFO listobs 21 ea23 E07 25.0 m -107.36.52.4 +33.53.56.5 318.0509 -164.1850 -2.6957 -1600880.571400 -5042170.388000 3554741.457400 2016-03-07 16:54:34 INFO listobs 22 ea24 W05 25.0 m -107.37.13.0 +33.53.57.8 -210.0959 -122.3887 -2.2577 -1601377.009500 -5041988.665500 3554776.393400 2016-03-07 16:54:34 INFO listobs 23 ea25 N02 25.0 m -107.37.06.2 +33.54.03.5 -35.6245 53.1806 -3.1345 -1601180.861480 -5041947.453400 3554921.628700 2016-03-07 16:54:34 INFO listobs 24 ea26 W03 25.0 m -107.37.08.9 +33.54.00.1 -105.3447 -51.7177 -2.6037 -1601265.153600 -5041982.533050 3554834.858400 2016-03-07 16:54:34 INFO listobs 25 ea27 E03 25.0 m -107.37.02.8 +33.54.00.5 50.6641 -39.4835 -2.7273 -1601114.365500 -5042023.151800 3554844.944000 2016-03-07 16:54:34 INFO listobs 26 ea28 N08 25.0 m -107.37.07.5 +33.54.15.8 -68.9057 433.1889 -5.0602 -1601147.940400 -5041733.837000 3555235.956000 2016-03-07 16:54:34 INFO listobs ##### End Task: listobs ##### 2016-03-07 16:54:34 INFO listobs ##########################################
- J1925+2106, field ID 0: Phase Calibrator;
- G55.7+3.4, field ID 1: The Supernova Remnant;
- 0542+498=3C147, field ID 2: Amplitude/Bandpass Calibrator
We can also see that these sources have associated "scan intents", which indicate their function in the observation. Note that you can select sources based on their intents in certain CASA tasks. The various scan intents in this data set are:
- CALIBRATE_PHASE indicates that this is a scan to be used for gain calibration;
- OBSERVE_TARGET indicates that this is the science target;
- CALIBRATE_AMPLI indicates that this is to be used for flux calibration; and
- CALIBRATE_BANDPASS indicates that these scans are to be used for bandpass calibration.
Note that 3C147 is to be used for both flux and bandpass calibration.
It's important to also note that the antennas have a name and ID associated with them. For example antenna ID 15 is named ea17 ( The "ea" stemming from the Expanded VLA project). When specifying an antenna within a task parameter, we will mainly reference them by name.
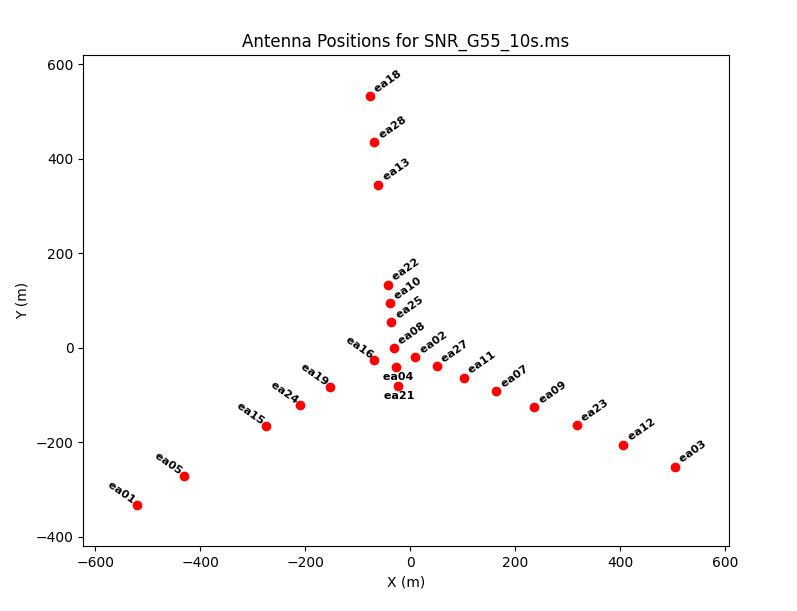
We can see the antenna configuration for this observation by using plotants:
# In CASA
plotants(vis='SNR_G55_10s.ms', figfile='SNR_G55_10s.plotants.png')
This shows that antennas ea01, ea03, and ea18 were on the extreme ends of the west, east, and north arms, respectively. The antenna position diagram is particularly useful as a guide to help determine which antenna to use as the reference antenna later during calibration. Note that antennas on stations 8 of each arm (N08, E08, W08) do not get moved during array reconfigurations, they can therefore at times be good choices as reference antennas. In this case, we'll probably want to choose something closer to the center of the array.
We may also inspect the raw data using plotms. To start with, lets look at a subset of scans on the supernova remnant:
# In CASA
plotms(vis='SNR_G55_10s.ms', scan='30,75,120,165,190,235,303', antenna='ea24', xaxis='freq',
yaxis='amp', coloraxis='spw', iteraxis='scan', correlation='RR,LL')
- coloraxis='spw': Parameter indicates that a different color will be assigned to each spectral window.
- antenna='ea24' : We chose only information for antenna ea24.
- iteraxis='scan': Parameter tells plotms to display a new plot for each scan.
- correlation='RR,LL': We just want to display the right and left circular polarizations, without the cross-hand terms.
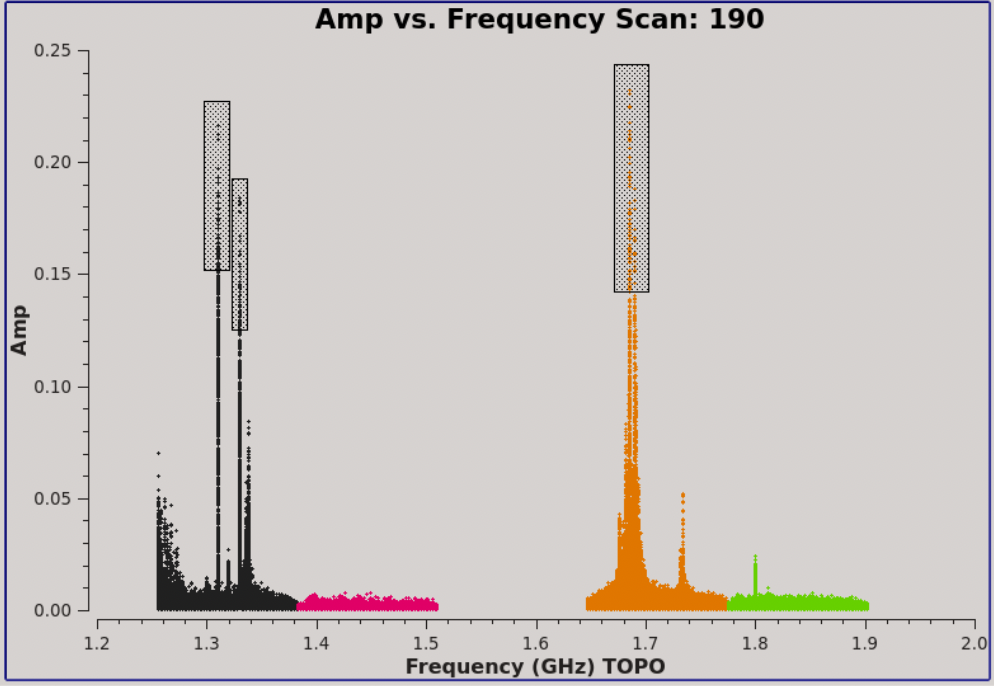
Flipping through to scan 190, we can see that there is significant time and frequency variable RFI present in the observation, as seen by the large spikes in amplitude. In particular, we can see that several spectral windows are quite badly affected. To determine which spectral windows they are, click on the "Mark Regions" tool at the bottom of the plotms GUI (the open box with a green "plus" sign). Use the mouse to select a few of the highest-amplitude points in each of the spectral windows. Click on the "Locate" button (magnifying glass). Information about the selected areas should now display in the logger window:
Frequency in [1.30662 1.31407] or [1.32377 1.33569] or [1.67866 1.69581], Amp in [0.16871 0.217097] or [0.153226 0.186613] or [0.172581 0.235968]: Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:19:58.0 BL=ea16@W02 & ea24@W05[14&22] Spw=0 Chan=27 Freq=1.31 Corr=RR X=1.31 Y=0.17187 (1718/144/1718) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:19:58.0 BL=ea19@W04 & ea24@W05[17&22] Spw=0 Chan=27 Freq=1.31 Corr=LL X=1.31 Y=0.178607 (1975/144/1975) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:19:58.0 BL=ea22@N04 & ea24@W05[20&22] Spw=0 Chan=37 Freq=1.33 Corr=RR X=1.33 Y=0.18105 (2250/144/2250) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:08.0 BL=ea19@W04 & ea24@W05[17&22] Spw=0 Chan=27 Freq=1.31 Corr=LL X=1.31 Y=0.21228 (1975/145/1975) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:08.0 BL=ea21@E01 & ea24@W05[19&22] Spw=0 Chan=27 Freq=1.31 Corr=LL X=1.31 Y=0.181632 (2103/145/2103) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:08.0 BL=ea22@N04 & ea24@W05[20&22] Spw=0 Chan=37 Freq=1.33 Corr=RR X=1.33 Y=0.167068 (2250/145/2250) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:28.0 BL=ea19@W04 & ea24@W05[17&22] Spw=0 Chan=27 Freq=1.31 Corr=LL X=1.31 Y=0.216252 (1818323722/147/1975) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:28.0 BL=ea22@N04 & ea24@W05[20&22] Spw=0 Chan=37 Freq=1.33 Corr=RR X=1.33 Y=0.182341 (1818323997/147/2250) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:38.0 BL=ea07@E05 & ea24@W05[6&22] Spw=0 Chan=27 Freq=1.31 Corr=LL X=1.31 Y=0.175032 (1866691864/148/695) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:38.0 BL=ea09@E06 & ea24@W05[8&22] Spw=0 Chan=27 Freq=1.31 Corr=RR X=1.31 Y=0.176728 (1866692119/148/950) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:38.0 BL=ea16@W02 & ea24@W05[14&22] Spw=0 Chan=27 Freq=1.31 Corr=LL X=1.31 Y=0.170435 (1866692888/148/1719) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:38.0 BL=ea19@W04 & ea24@W05[17&22] Spw=0 Chan=27 Freq=1.31 Corr=LL X=1.31 Y=0.210123 (1866693144/148/1975) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:38.0 BL=ea21@E01 & ea24@W05[19&22] Spw=0 Chan=27 Freq=1.31 Corr=LL X=1.31 Y=0.185065 (1866693272/148/2103) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:38.0 BL=ea22@N04 & ea24@W05[20&22] Spw=0 Chan=37 Freq=1.33 Corr=RR X=1.33 Y=0.158359 (1866693419/148/2250) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:38.0 BL=ea24@W05 & ea27@E03[22&25] Spw=0 Chan=27 Freq=1.31 Corr=RR X=1.31 Y=0.190659 (1866693783/148/2614) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:48.0 BL=ea21@E01 & ea24@W05[19&22] Spw=0 Chan=27 Freq=1.31 Corr=LL X=1.31 Y=0.197052 (1852669347/149/2103) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:48.0 BL=ea22@N04 & ea24@W05[20&22] Spw=0 Chan=37 Freq=1.33 Corr=RR X=1.33 Y=0.183905 (1852669494/149/2250) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:48.0 BL=ea24@W05 & ea27@E03[22&25] Spw=0 Chan=27 Freq=1.31 Corr=RR X=1.31 Y=0.170542 (1852669858/149/2614) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:58.0 BL=ea21@E01 & ea24@W05[19&22] Spw=0 Chan=27 Freq=1.31 Corr=LL X=1.31 Y=0.179017 (1668509051/150/2103) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:58.0 BL=ea22@N04 & ea24@W05[20&22] Spw=0 Chan=37 Freq=1.33 Corr=RR X=1.33 Y=0.177841 (1668509198/150/2250) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:21:08.0 BL=ea21@E01 & ea24@W05[19&22] Spw=0 Chan=27 Freq=1.31 Corr=LL X=1.31 Y=0.193158 (1866681459/151/2103) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:19:58.0 BL=ea19@W04 & ea24@W05[17&22] Spw=2 Chan=19 Freq=1.686 Corr=RR X=1.686 Y=0.209811 (4844192/162/1958) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:19:58.0 BL=ea19@W04 & ea24@W05[17&22] Spw=2 Chan=19 Freq=1.686 Corr=LL X=1.686 Y=0.224424 (4844193/162/1959) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:08.0 BL=ea19@W04 & ea24@W05[17&22] Spw=2 Chan=19 Freq=1.686 Corr=RR X=1.686 Y=0.231918 (1374179750/163/1958) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:08.0 BL=ea19@W04 & ea24@W05[17&22] Spw=2 Chan=19 Freq=1.686 Corr=LL X=1.686 Y=0.209708 (1374179751/163/1959) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:18.0 BL=ea08@N01 & ea24@W05[7&22] Spw=2 Chan=19 Freq=1.686 Corr=RR X=1.686 Y=0.17744 (2898499/164/806) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:18.0 BL=ea10@N03 & ea24@W05[9&22] Spw=2 Chan=19 Freq=1.686 Corr=LL X=1.686 Y=0.177235 (2898756/164/1063) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:18.0 BL=ea19@W04 & ea24@W05[17&22] Spw=2 Chan=19 Freq=1.686 Corr=RR X=1.686 Y=0.230346 (2899651/164/1958) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:18.0 BL=ea19@W04 & ea24@W05[17&22] Spw=2 Chan=19 Freq=1.686 Corr=LL X=1.686 Y=0.199502 (2899652/164/1959) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:28.0 BL=ea08@N01 & ea24@W05[7&22] Spw=2 Chan=19 Freq=1.686 Corr=RR X=1.686 Y=0.177315 (6083110/165/806) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:28.0 BL=ea10@N03 & ea24@W05[9&22] Spw=2 Chan=19 Freq=1.686 Corr=LL X=1.686 Y=0.17881 (6083367/165/1063) Scan=190 Field=G55.7+3.4[1] Time=2010/08/23/05:20:28.0 BL=ea19@W04 & ea24@W05[17&22] Spw=2 Chan=19 Freq=1.686 Corr=RR X=1.686 Y=0.217573 (6084262/165/1958) Found 45 points (45 unflagged) among 101376 in 0s.
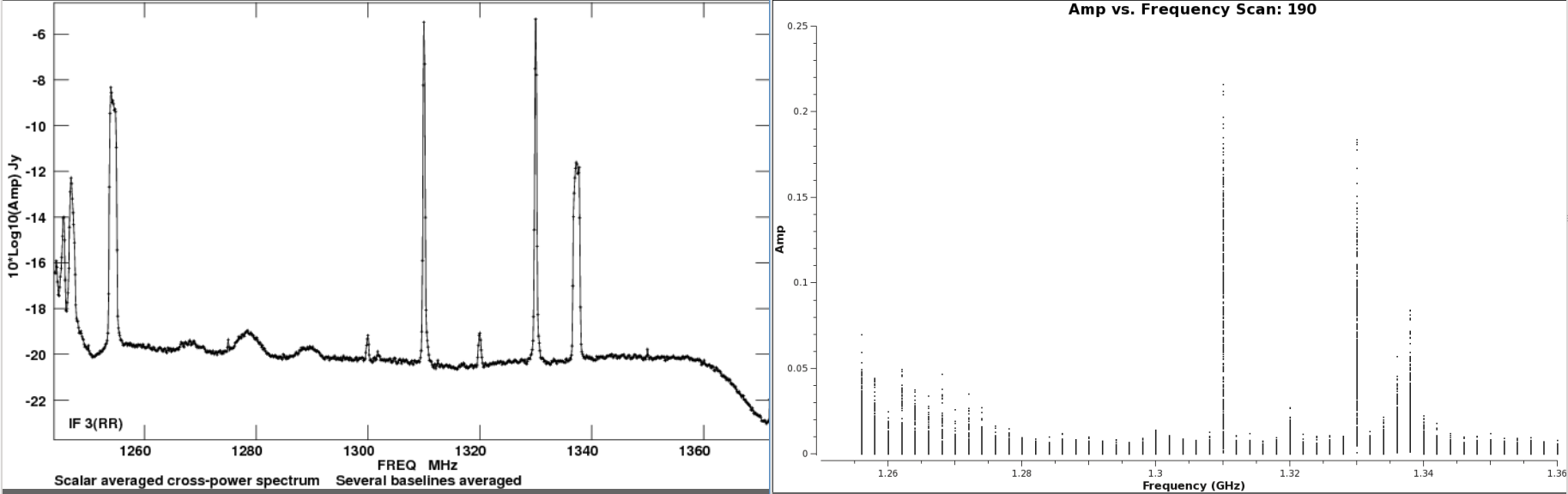
We can see that Spw 0 and 2, are the worst affected by RFI. Also, we get the corresponding frequency where the RFI is present, which looks to be 1.31 and 1.33GHz for spectral window 0, and 1.686GHz for spectral window 2. Visiting the VLA L-Band RFI website, we find that the 1310 and 1330 MHz 'birdies' are due to FAA ASR radars, and the one at 1686MHz is most likely due to a GOES weather satellite. We can compare the plots of the FAA ASR radar from the website, with that of spw 0, and see that the birdies (spikes) are practically identical and fall within the same frequencies.
Priori Calibration and Flagging
Normally, before we proceed with further processing, we should check the operator log for the observation to see if there were any issues noted during the run that need to be addressed. The observing log file for this observation can be found here.
The log has various information, including the start/end times for the observation, frequency bands used, weather, baseline information for recently moved antennas, and any outages or issues that may have been encountered. We can see that antenna ea07 may need position corrections (calibration table SNR_G55_10s.pos will fix this), and several antennas are missing an L-Band receiver, including ea06, ea17, ea20, and ea26. We have already removed these antennas from our MS during the run of split2() and can continue with online flagging.
Online Flags
At the time of importing from the SDM-BDF raw data to a MS, we chose to process the online flags from the Flags.xml file to the FLAG_CMD sub-table within the MS. We also created a txt document which includes a list of online flags.
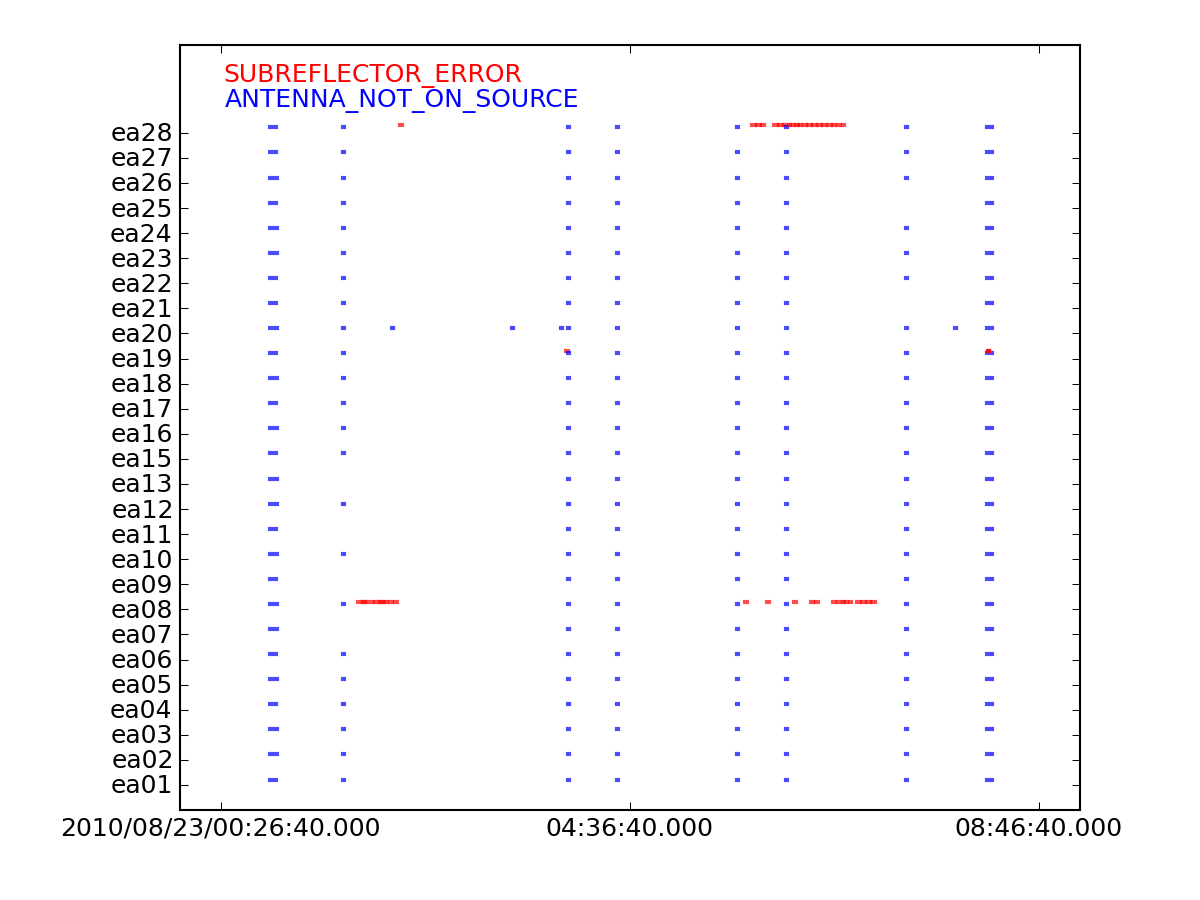
The Flags.xml file holds information of flags created during the observation, such as subreflector issues, and antennas not being on source. We will now want to apply these online flags to the data, but first, let's create a plot of the flags we are about to apply to get an idea of what will be flagged.
We will employ the flagcmd task to apply the online flags.
# In CASA
flagcmd(vis='SNR_G55_10s.ms', inpmode='table', reason='any', action='plot', plotfile='flaggingreason_vs_time.png')
We can see several instances of online flagging in the created image. Most notably, ea28 and ea08 had some subreflector issues througout the observation. Online flags are instances of possible missing data, including:
- ANTENNA_NOT_ON_SOURCE
The JVLA antennas have slewing speeds of 20 degrees per minute in azimuth, and 40 degrees per minute in elevation. Some antennas are slower than others, and may take a few more seconds to reach the next source. The antennas can also take a few seconds to settle down due to small oscillations after having slewed.
- SUBREFLECTOR_ERROR
The FRM (Focus Rotation Mount) located at the apex of the antennas, is responsible for focusing the incoming radio signal to the corresponding receiver. They can at times have issues with their focus and/or rotation axes. Being off target, so much as a few fractions of a degree can result in loss of data, depending on the frequency being observed.
Now that we've plotted the online flags, we will apply them to the MS.
# In CASA
flagcmd(vis='SNR_G55_10s.ms', inpmode='table', reason='any', action='apply', flagbackup=False)
The CASA logger should report the progress as the task applies these flags in chunks. Once it has finished, it will report on the percentage of data that has been flagged.
Shadowed Antennas
Since this is the most compact JVLA configuration, there may be instances where one antenna blocks, or "shadows" another. Therefore, we will run flagdata to remove these data (CASA Cookbook 3.4.2):
# In CASA
flagdata(vis='SNR_G55_10s.ms', mode='shadow', tolerance=0.0, flagbackup=False)
In this particular observation, there does not appear to be much data affected by shadowing, as can be seen in the logger report. One reason why this may be the case, is the antennas were pointed at sources high in elevation.
Zero-Amplitude Data
In addition to shadowing, there may be times during which the correlator writes out pure zero-valued data. In order to remove this bad data, we run flagdata to remove any pure zeroes:
# In CASA
flagdata(vis='SNR_G55_10s.ms', mode='clip', clipzeros=True, flagbackup=False)
Inspecting the logger output which is generated by flagdata shows that there is a small quantity of zero-valued data (4.6%) present in this MS.
Quacking
Now we can utilize the flagdata task one more time in order to run it in quaking mode.
It's common for the array to "settle down" at the start of a scan. Quacking is used to remove data at scan boundaries, and it can apply the same edit to all scans for all baselines.
# In CAS
flagdata(vis='SNR_G55_10s.ms', mode='quack', quackinterval=5.0, quackmode='beg', flagbackup=False)
- quackmode='beg' : Data from the start of each scan will be flagged.
- quackinterval=5.0: Flag the first 5 seconds of every scan.
Backup Data - Flagmanager
Now that we've applied online flags, clipped zero amplitude data, and removed shadowed data, we will create a backup of the MS using flagmanager.
# In CASA
flagmanager(vis='SNR_G55_10s.ms', mode='save', versionname='after_priori_flagging')
From here on forward, if we make a mistake, we can always revert back to this version of the MS by setting mode='restore', and providing the version name we want to restore back to.
Hanning-Smoothing
Strong RFI sources can give rise to the Gibbs phenomenon. To remedy this ringing across the frequency channels, we can employ the Hanning smoothing algorithm via the hanningsmooth task. Note that running this task overwrites the data, and it cannot be reversed. Also, there is a loss in spectral resolution by a factor of two. In addition, the task allows for the creation of a new MS, or to directly operate on the requested column. For this tutorial, we will be directly operating on the data column. Note that hanning-smoothing will remove amplitude spikes, it is therefore not recommended for spectral analysis related science, such as HI. Also note that hanning smoothing cannot be reversed once you apply it to your data.
Let's create before and after images with the plotms task, to see the effects of hanning-smoothing the data.
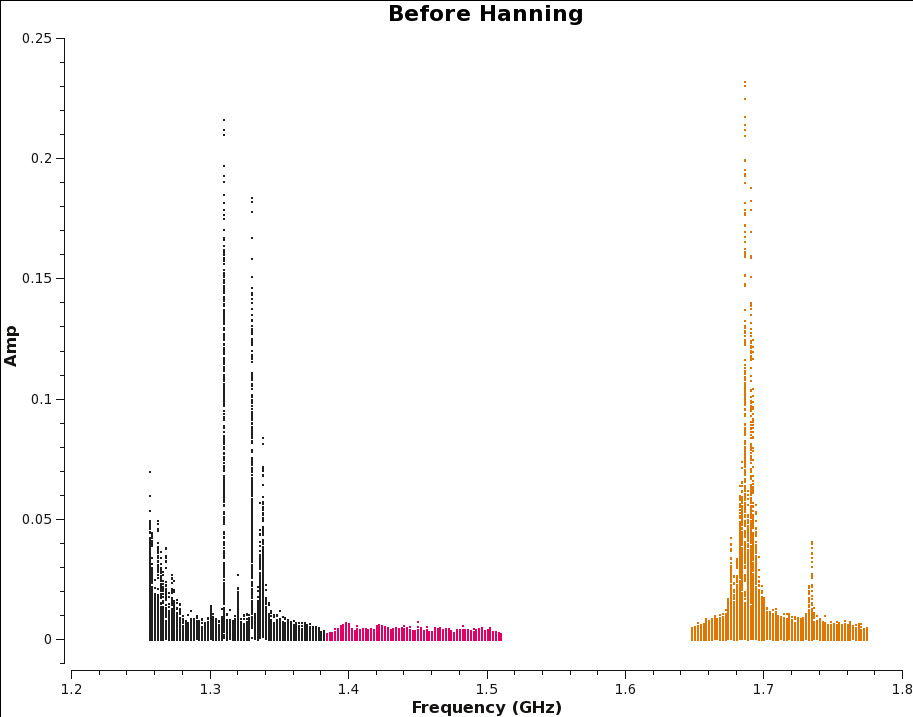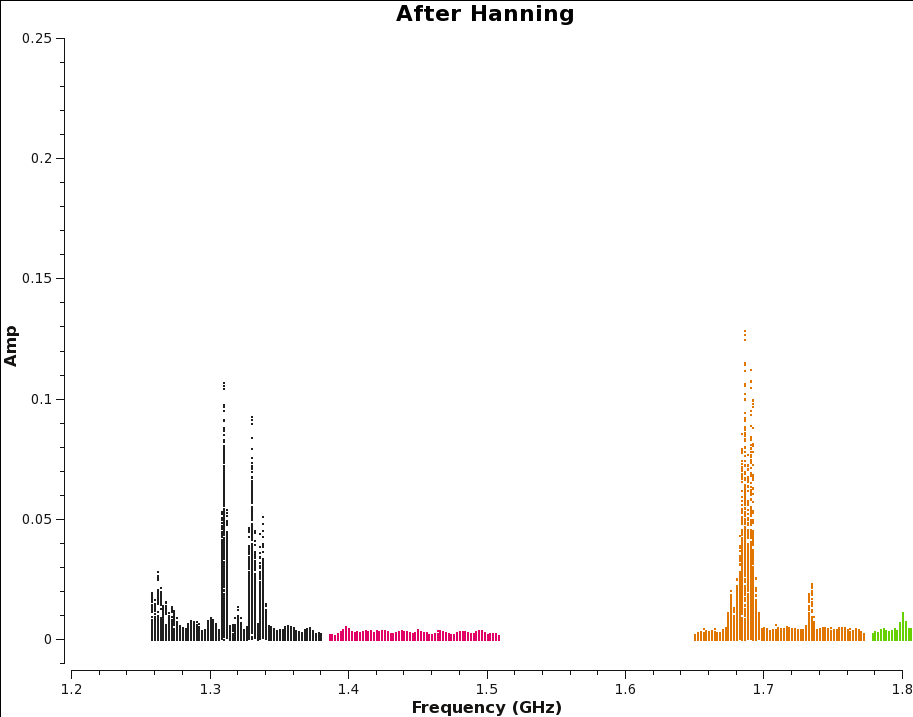
# In CASA
plotms(vis='SNR_G55_10s.ms', scan='190', antenna='ea24', spw='0~2',
xaxis='freq', yaxis='amp', coloraxis='spw', title='Before Hanning',
correlation='RR,LL', plotrange=[1.2,1.8,-0.01,0.25],
plotfile='amp_v_freq.beforeHanning.png')
hanningsmooth(vis='SNR_G55_10s.ms', datacolumn='data')
plotms(vis='SNR_G55_10s.ms', scan='190', antenna='ea24', spw='0~3',
xaxis='freq', yaxis='amp', coloraxis='spw', title='After Hanning',
correlation='RR,LL', plotrange=[1.2,1.8,-0.01,0.25],
plotfile='amp_v_freq.afterHanning.png')
Note that the second call to plotms includes a spectral window outside of the plot range. This is to force plotms to reload the plot. By default, plotms will not redraw a plot if the inputs are unchanged. Within the GUI, checking the "reload" box next to the "Plot" button will do this as well.
We can compare the generated plots and take notice that single channel RFI has spread into three channels, but it has also removed some of the worst RFI. This spreading of RFI to other channels will ultimately result in a little more data being flagged.
Automatic RFI excision
Now that we're done with priori flagging, we can move on to removing some of the RFI present with auto-flagging algorithms used within flagdata. We will employ two CASA tasks, flagdata (tfcrop) and flagdata (rflag). For further details on the two algorithm based tasks we will employ, please see the presentation given at the 5th VLA Data Reduction Workshop by Urvashi Rau.
TFcrop
flagdata (tfcrop) is an algorithm that detects outliers in the 2D time-frequency plane, and can operate on un-calibrated data (non bandpass-corrected). Tfcrop will iterate through chunks of time, and undergo several steps in order to find and excise different types of RFI. (CASA Cookbook 3.4.2.7)
Step 1: Detect short-duration RFI spikes (narrow-band and broad-band).
Step 2: Search for time-persistent RFI.
Step 3: Search for time-persistent, narrow-band RFI.
Step 4: Search for low-level wings of very strong RFI.
More details on the algorithm steps can be found on this webpage
We will apply the auto-flagging tfcrop algorithm for each spectral window. We will walk through the first spw and then include the rest with the same command. Let's first plot the corrected data for scan 190, with all spectral windows, so we can compare the data before and after tfcrop.
# In CASA
plotms(vis='SNR_G55_10s.ms', scan='190', antenna='ea24', xaxis='freq', iteraxis='scan', yaxis='amp',
ydatacolumn='data', plotfile='amp_v_freq_before_tfcrop.png', title='Before TFcrop',
correlation='RR,LL', coloraxis='spw', plotrange=[1.2,2,-0.01,0.25])
Following are a set of flagdata commands which have been found to work reasonably well with these data. Please take some time to play with the parameters and the plotting capabilities. Since these runs set display='both' and action='calculate', the flags are displayed but not actually written to the MS. This allows one to try different sets of parameters before actually applying the flags to the data.
Some representative plots are also displayed. Each column displays an individual polarization product; since we're using all four polarizations, from left to right are RR, RL, LR, and LL. The first row shows the data with current flags applied, and the second includes the flags generated by flagdata. The x-axis is channel number (the spectral window ID is displayed in the top title) and the y-axis of the first two rows is all integrations included in a time "chunk", set by the ntime parameter. These are the data considered by the tfcrop algorithm during its flagging process, and changes in ntime will have some (relatively small) affect on what data are flagged.
Each plot page displays data for a single baseline and time chunk. The buttons at the bottom allow one to step through baseline (backward as well as forward), spw, scan, and field; "Stop Display" will continue the flagging operation without the GUI, and "Quit" aborts the run.
spw 0
# In CASA
flagdata(vis='SNR_G55_10s.ms', mode='tfcrop', spw='0',
datacolumn='data', action='calculate',
display='both', flagbackup=False)
As we iterate through the different scans and baselines, we can see the flagging we can apply, represented by the blue areas. Let's now apply these flags by changing the action parameter.
# In CASA
flagdata(vis='SNR_G55_10s.ms', mode='tfcrop', spw='0',
datacolumn='data', action='apply',
display='', flagbackup=False)
The logger will report the percentage of flagged data in the table selection. We can now apply the tfcrop algorithm to the remaining spectral windows.
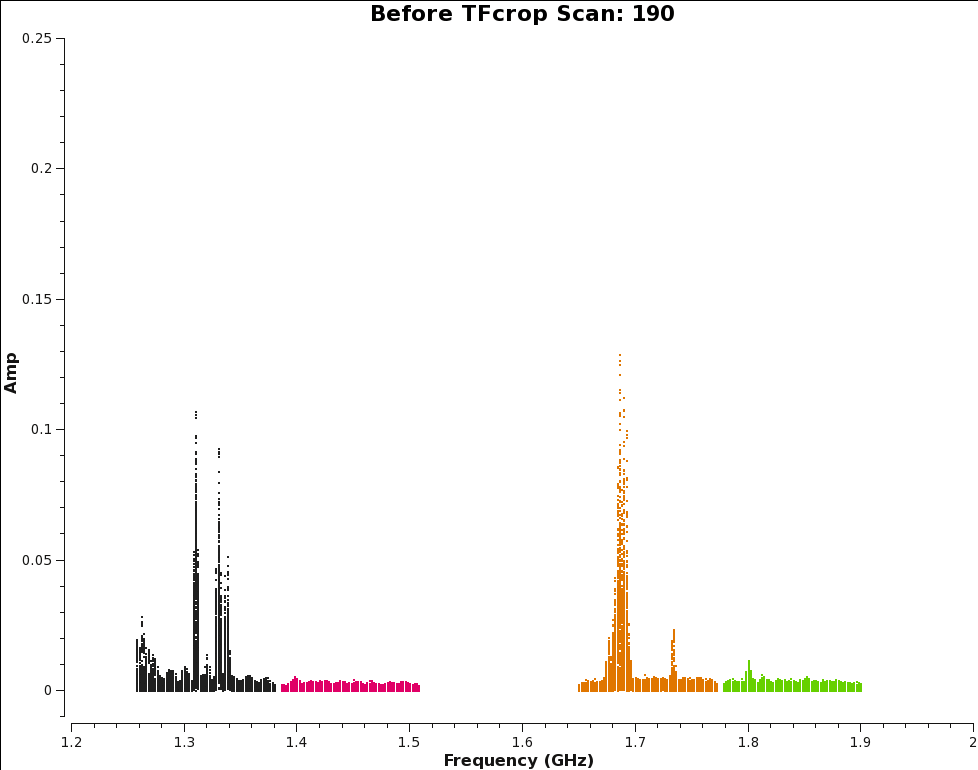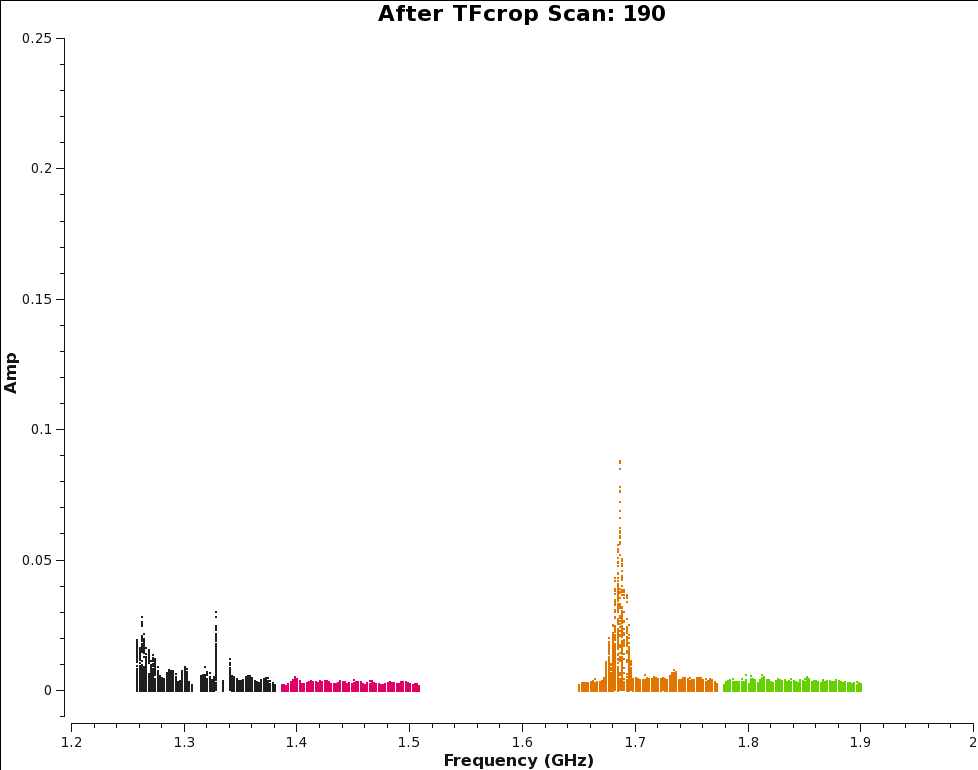
spw 1, 2, 3
# In CASA
flagdata(vis='SNR_G55_10s.ms', mode='tfcrop', spw='1~3',
datacolumn='data', action='apply',
display='both', flagbackup=False)
After tfcrop has gone through and flagged some of the worst RFI, we can inspect the log report and take note of how much has been flagged.
We can also use plotms to review the effects of using tfcrop and compare the image to the one created before applying tfcrop. We can see great improvements, especially for spectral window 0 and 2, which had some of the worst RFI.
# In CASA
plotms(vis='SNR_G55_10s.ms', scan='190', antenna='ea24', xaxis='freq', iteraxis='scan', yaxis='amp',
ydatacolumn='data', plotfile='amp_v_freq_after_tfcrop.png', title='After TFcrop',
correlation='RR,LL', coloraxis='spw', plotrange=[1.2,2,-0.01,0.25])
We now calculate the amount of flagged data so far in our Measurement Set by using the flagdata task with mode='summary', and apply it to a variable.
# In CASA
flagInfo = flagdata(vis='SNR_G55_10s.ms', mode='summary')
print("\n %2.1f%% of G55.7+3.4, %2.1f%% of 3C147, and %2.1f%% of J1925+2106 are flagged. \n" % (100.0 * flagInfo['field']['G55.7+3.4']['flagged'] / flagInfo['field']['G55.7+3.4']['total'], 100.0 * flagInfo['field']['0542+498=3C147']['flagged'] / flagInfo['field']['0542+498=3C147']['total'], 100.0 * flagInfo['field']['J1925+2106']['flagged'] / flagInfo['field']['J1925+2106']['total']))
print("Spectral windows are flagged as follows:")
for spw in range(0,4):
print("SPW %s: %2.1f%%" % (spw, 100.0 * flagInfo['spw'][str(spw)]['flagged'] / flagInfo['spw'][str(spw)]['total']))
The results indicate we have flagged a little over 22% of G55.7+3.4. We can now move on to the other auto-flagging algorithm, rflag.
RFlag
In order to get the best possible result from the automatic RFI excision with flagdata (rflag), we will first apply bandpass calibration to the MS. Since the RFI is time-variable, using the phase calibration source to make an average bandpass over the entire observation will mitigate the amount of RFI present in the calculated bandpass. (For the final calibration, we will use the designated bandpass source 3C147; however, since this object was only observed in the last set of scans, it doesn't sample the time variability and would not provide a good average bandpass.)
Since there are likely to be gain variations over the course of the observation, we will run gaincal to solve for an initial set of antenna-based phases over a narrow range of channels. These will be used to create the bandpass solutions. While amplitude variations will have little effect on the bandpass solutions, it is important to solve for these phase variations with sufficient time resolution to prevent decorrelation when vector averaging the data in computing the bandpass solutions.
In order to choose a narrow range of channels for each spectral window which are relatively RFI-free over the course of the observation, we can look at the data with plotms. Note that it's important to only solve for phase using a narrow channel range, since an antenna-specific delay will cause the phase to vary with respect to frequency over the spectral window, perhaps by a substantial amount.
# In CASA
plotms(vis='SNR_G55_10s.ms', scan='42,65,88,11,134,157', antenna='ea24',
xaxis='channel', yaxis='amp', iteraxis='spw', yselfscale=True, correlation='RR,LL')
- yselfscale=True: sets the y-scaling to be for the currently displayed spectral window, since some spectral windows have much worse RFI and will skew the scale for others.
Looking at these plots, we can choose appropriate channel ranges for each SPW:
SPW 0: 20-24 SPW 1: 49-52 SPW 2: 38-41 SPW 3: 41-44
Using these channel ranges, we run gaincal to calculate phase-only solutions that will be used as input during our initial bandpass calibration. Remember - the calibration tables we are creating now are so that we can use an automatic RFI flagging algorithm. Our final calibration tables will be generated later, after automated flagging. Here are the inputs for our initial pre-bandpass phase calibration:
# In CASA
gaincal(vis='SNR_G55_10s.ms', caltable='SNR_G55_10s.initPh', field='J1925+2106', solint='int',
spw='0:20~24,1:49~52,2:38~41,3:41~44', refant='ea24', minblperant=3,
minsnr=3.0, calmode='p')
- caltable='SNR_G55_10s.initPh': this is the output calibration table that will be written.
- field='J1925+2106': this is the phase calibrator we will use to calibrate the phases.
- solint='int': we request a solution for each 10-second integration.
- pw='0:20~24,1:49~52,2:38~41,3:41~44': note the syntax of this selection: a ":" is used to separate the SPW from channel selection, and "~" is used to indicate an inclusive range.
- refant='ea24': we have chosen ea24 as the reference antenna after inspecting the antenna position diagram (see above). It is relatively close to, but not directly in, the center of the array, which could be important in D-configuration, since you don't want the reference antenna to have a high probability of being shadowed by nearby antennas.
- minblperant=3: the minimum number of baselines which must be present to attempt a phase solution.
- minsnr=3.0: the minimum signal-to-noise a solution must have to be considered acceptable. Note that solutions which fail this test will cause these data to be flagged downstream of this calibration step.
- calmode='p': perform phase-only solutions.
- gaintable='SNR_G55_10s.pos': use the antenna position correction for ea07 that we included in the tar file.
Note that a number of solutions do not pass the requirements of the minimum 3 baselines (generating the terminal message "Insufficient unflagged antennas to proceed with this solve.") or minimum signal-to-noise ratio (outputting "n of x solutions rejected due to SNR being less than 3 ..."). The logger output indicates 324 solutions succeeded, out of 387 attempted.
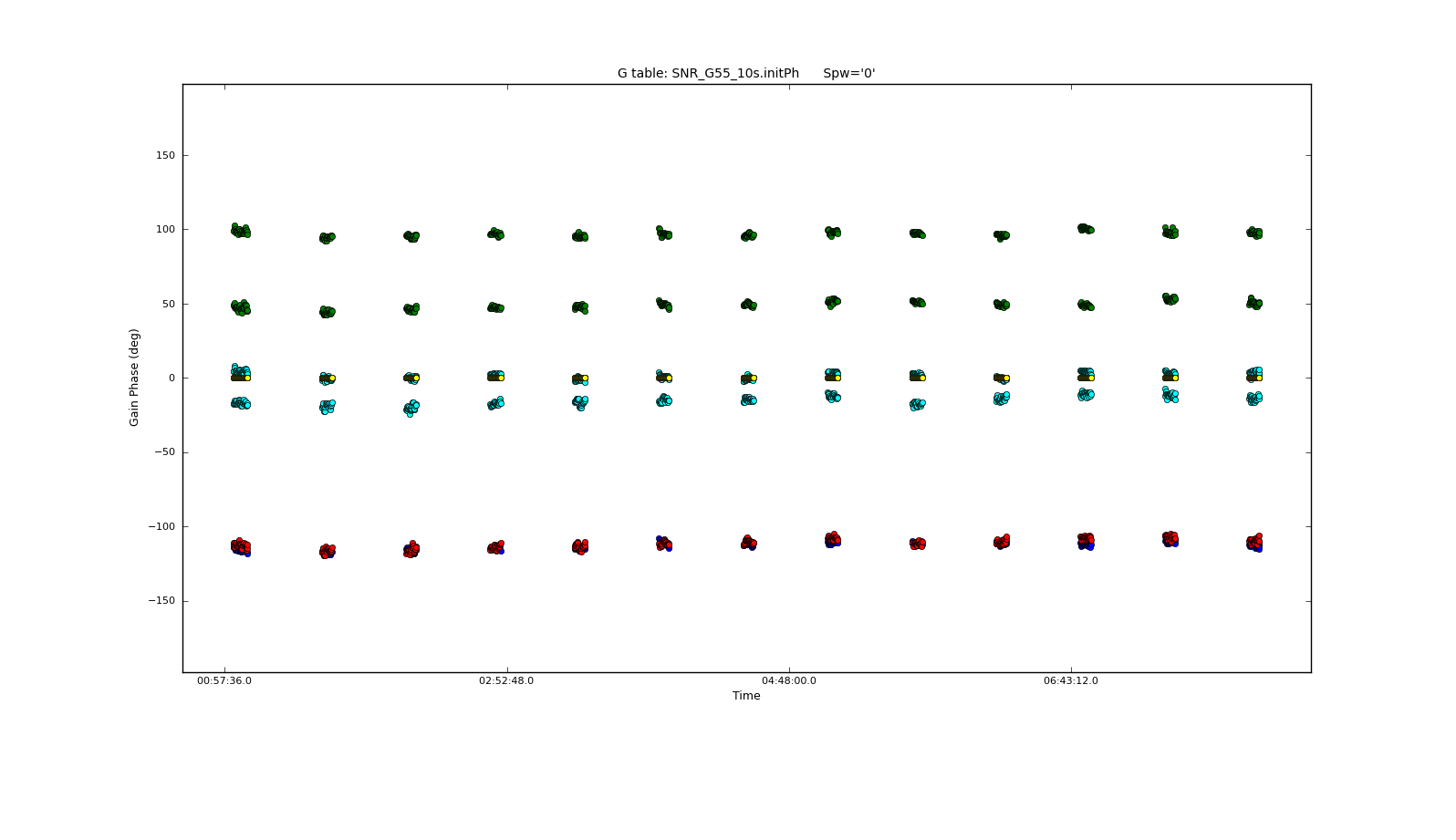
It's always a good idea to inspect the resulting calibration table with plotcal. We will first iterate over antennas for spectral window 0.
# In CASA
plotcal(caltable='SNR_G55_10s.initPh', xaxis='time', yaxis='phase', iteration='antenna',
spw='0', plotrange=[-1,-1,-180,180])
We can see that the phase does not change much over the course of the observation. Let's now inspect the other spectral windows for a few of the antennas.
# In CASA
plotcal(caltable='SNR_G55_10s.initPh', xaxis='time', yaxis='phase', iteration='spw',
antenna='ea01,ea05,ea10,ea24', plotrange=[-1,-1,-180,180])
Now that we've determined our plots look fairly reasonable, we will create a time-averaged bandpass solutions for the phase calibration source using the bandpass task.
# In CASA
bandpass(vis='SNR_G55_10s.ms', caltable='SNR_G55_10s.initBP', field='J1925+2106', solint='inf', combine='scan',
refant='ea24', minblperant=3, minsnr=10.0, gaintable='SNR_G55_10s.initPh',
interp='nearest', solnorm=False)
- solint='inf', combine='scan': the solution interval of 'inf' will automatically break by scans; this requests that the solution intervals be combined over scans, so that we will get one solution per antenna.
- gaintable= 'SNR_G55_10s.initPh': we will pre-apply the initial phase solutions.
- interp='nearest': by default, gaincal will use linear interpolation for pre-applied calibration. However, we want the nearest phase solution to be used for a given time.
Again, we can see that a number of solutions have been rejected by our choice of minsnr.
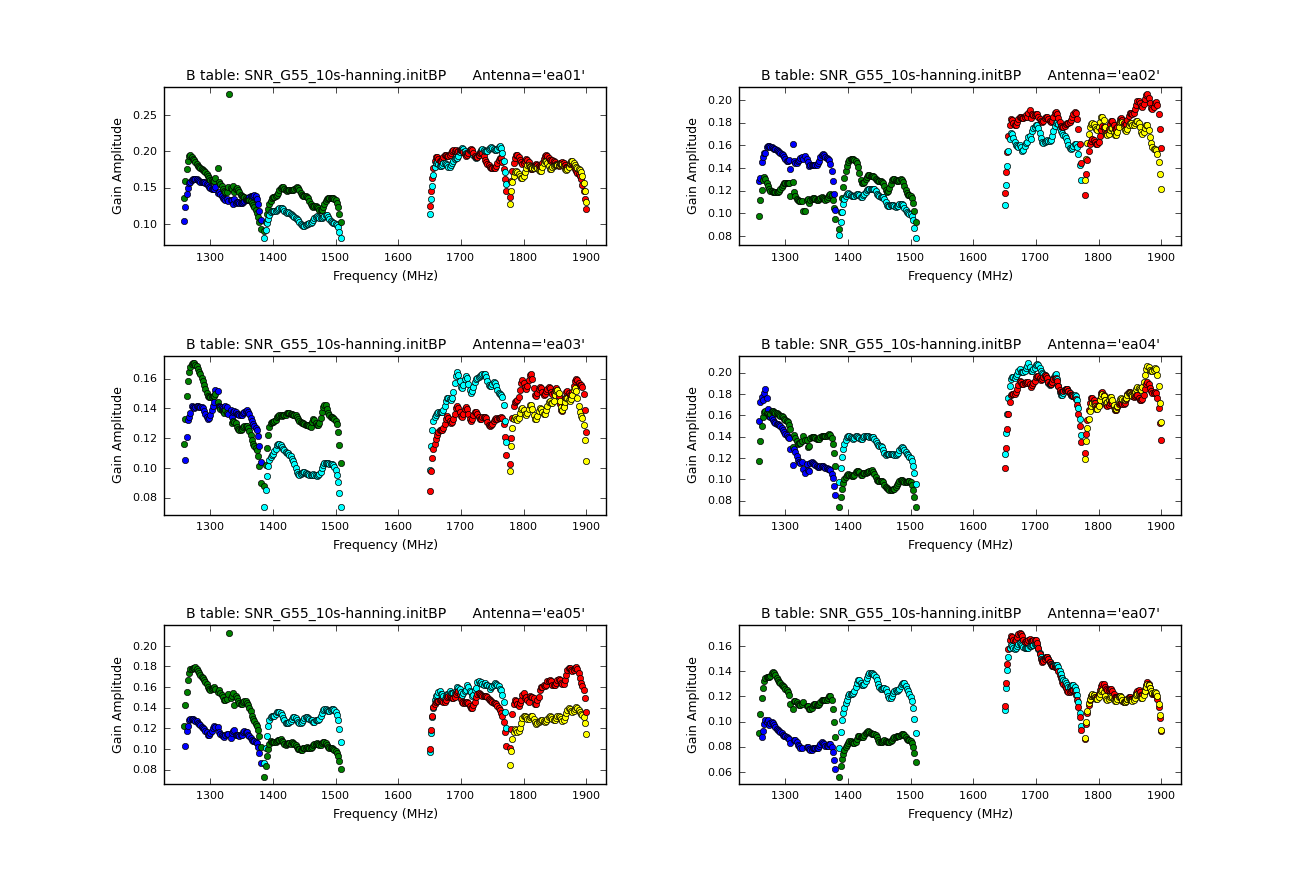
Let us now inspect the resulting bandpass plots with plotcal.
# In CASA
plotcal(caltable='SNR_G55_10s.initBP', xaxis='freq', yaxis='amp',
iteration='antenna', subplot=331)
- subplot=331: displays 3x3 plots per screen
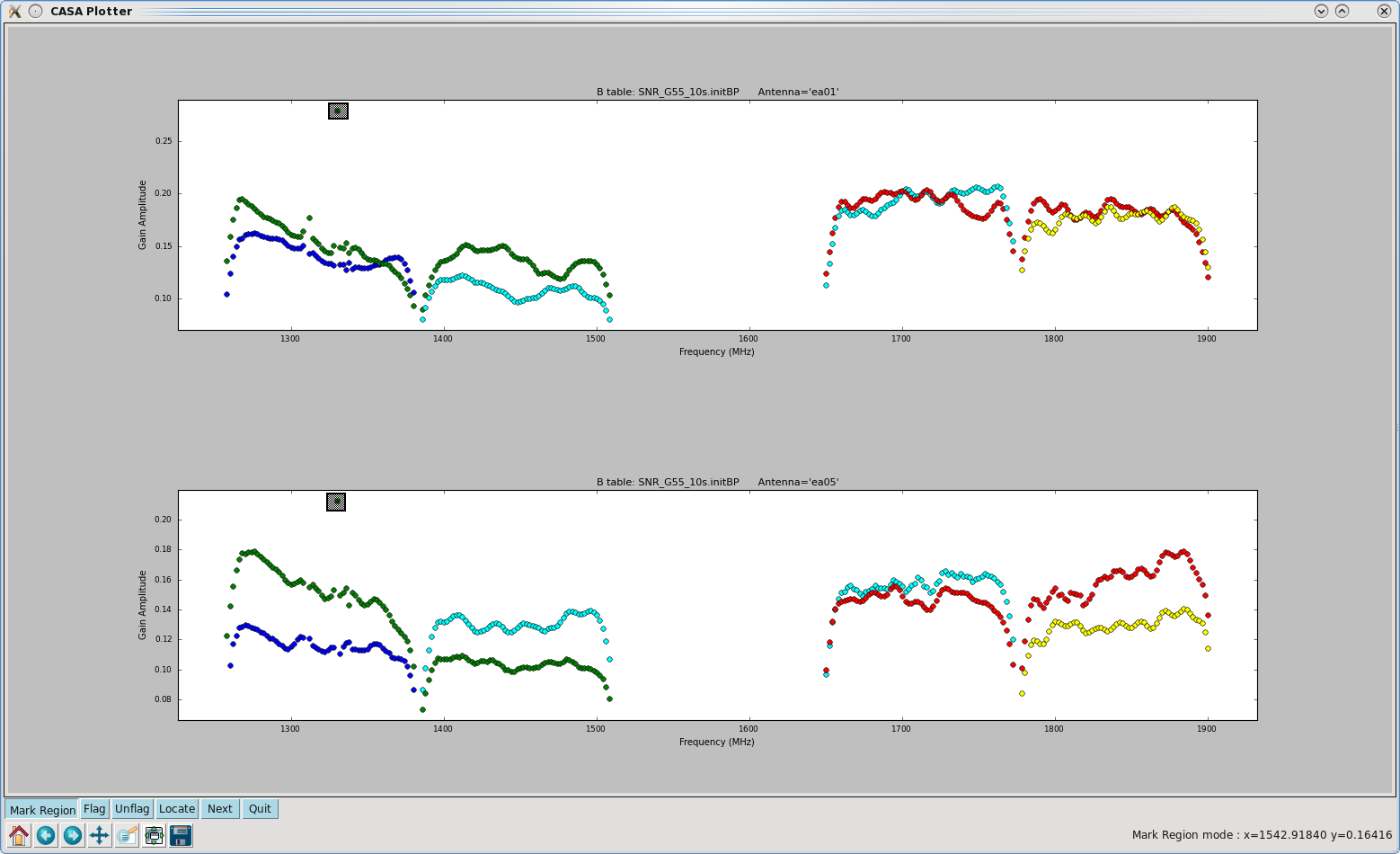
We notice that antenna's ea01 and ea05 have a point that is offset from the rest. Let's plot just these two antennas, locate the point on the plot, and flag it interactively through plotcal. Please note that interactive flagging within plotcal will not create a backup, therefore it may be wise to use flagmanager before doing so.
# In CASA
plotcal(caltable='SNR_G55_10s.initBP', antenna='ea01,ea05', xaxis='freq', yaxis='amp',
iteration='antenna', subplot=211)
We will highlight the points by clicking on the "Mark Region" button, drawing boxes over the points, and clicking on the "Flag" button. Before doing this, one could also get information on the points by clicking on the "Locate" button, which will display details about the highlighted regions. After having flagged the offset points, your plots should update.
We will now apply the bandpass calibration table using applycal.
# In CASA
applycal(vis='SNR_G55_10s.ms', gaintable= 'SNR_G55_10s.initBP', calwt=False)
This operation will flag data that correspond to flagged solutions, so applycal makes a backup version of the flags prior to operating on the data. Note that running applycal might take a little while.
Now that we have bandpass-corrected data with some RFI flagged out, we will run flagdata in flagdata (rflag) mode (CASA Cookbook 3.4.2.8). RFlag, like TFcrop, is an autoflag algorithm which uses a sliding window statistical filter. Data is iterated through in chunks of time, where statistics are accumulated, and thresholds calculated.
Additional information on the algorithm used in rflag, as well as the statistical details that are undertaken can be found on this webpage (sections 2.1.7).
We will use flagdata with mode='rflag', and action='calculate' to first review the amount of data to be flagged. We will also change the datacolumn parameter to 'corrected', since we've applied the bandpass corrections to the MS, and in the process, created the corrected_data column in the MS table.
spw 0
First, let's create a plot of our corrected data before we apply RFlag.
# In CASA
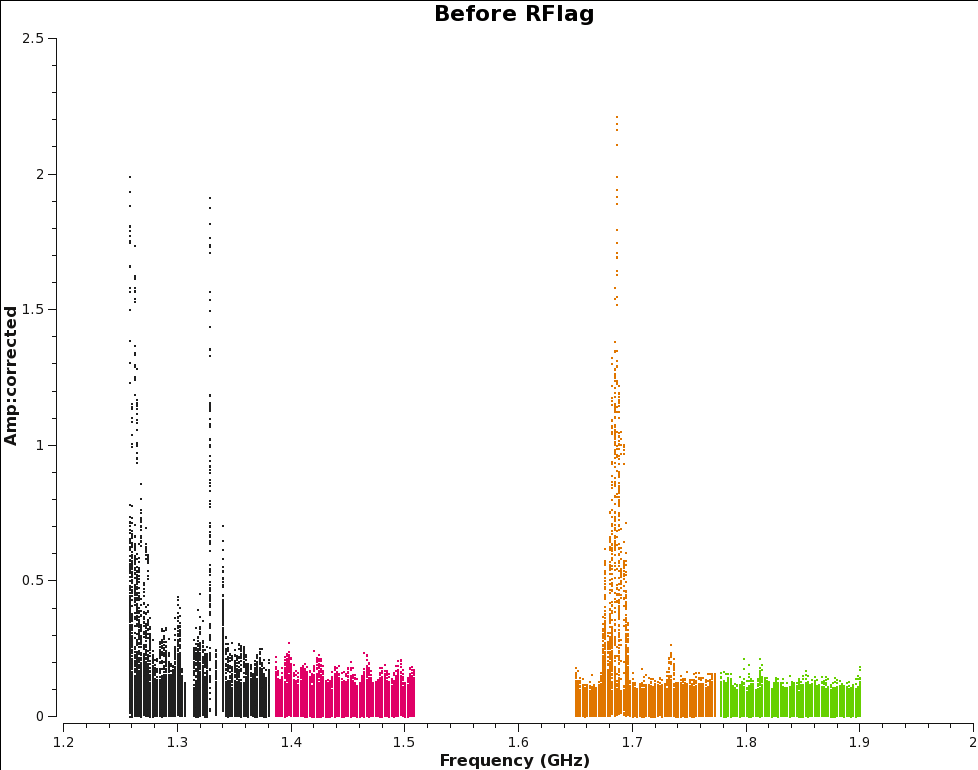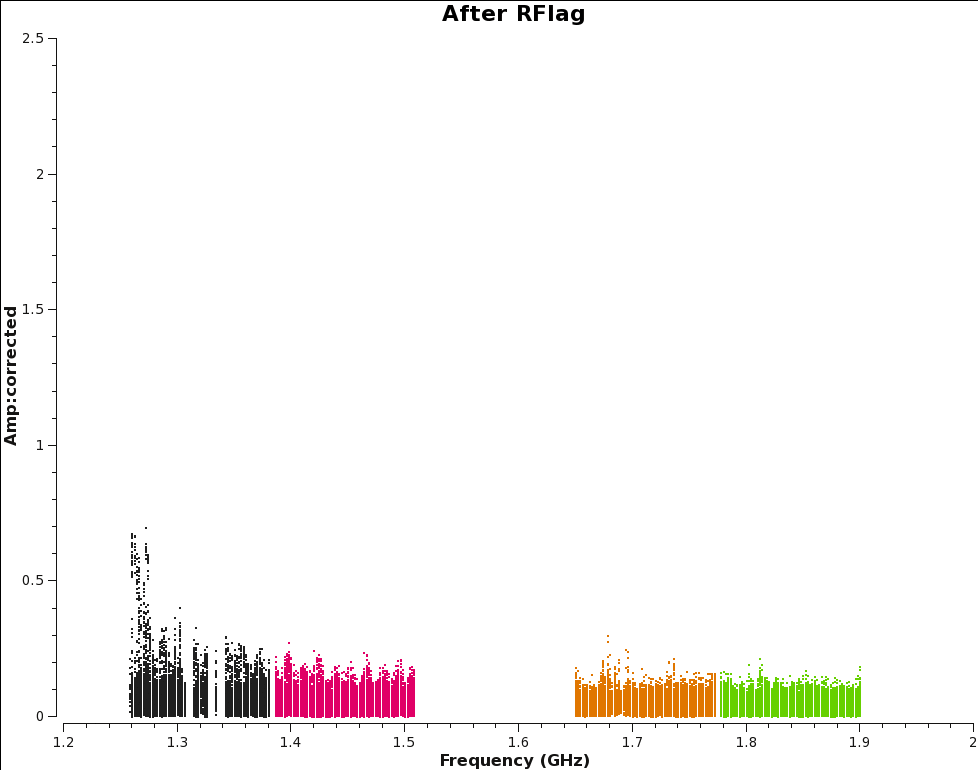
plotms(vis='SNR_G55_10s.ms', scan='190' , antenna='ea24',
xaxis='freq', yaxis='amp', ydatacolumn='corrected', coloraxis='spw', title='Before RFlag',
correlation='RR,LL', plotfile='amp_v_freq.beforeRFlag.png')
flagdata(vis='SNR_G55_10s.ms', mode='rflag', spw='0', datacolumn='corrected',
action='calculate', display='both', flagbackup=False)
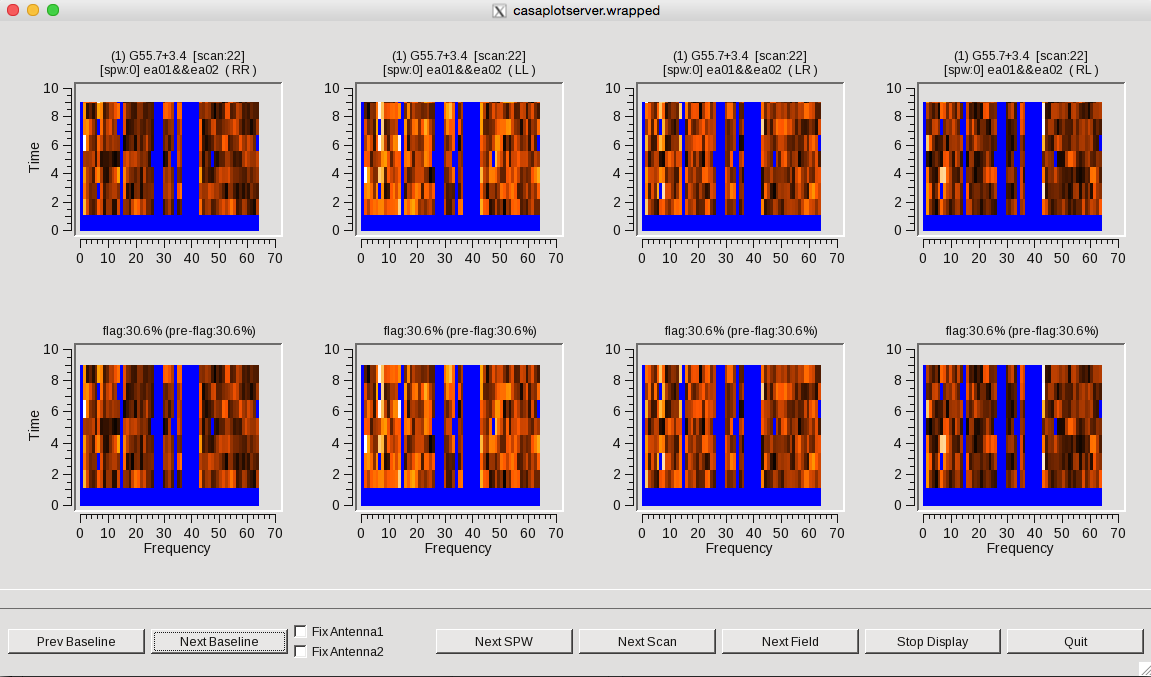
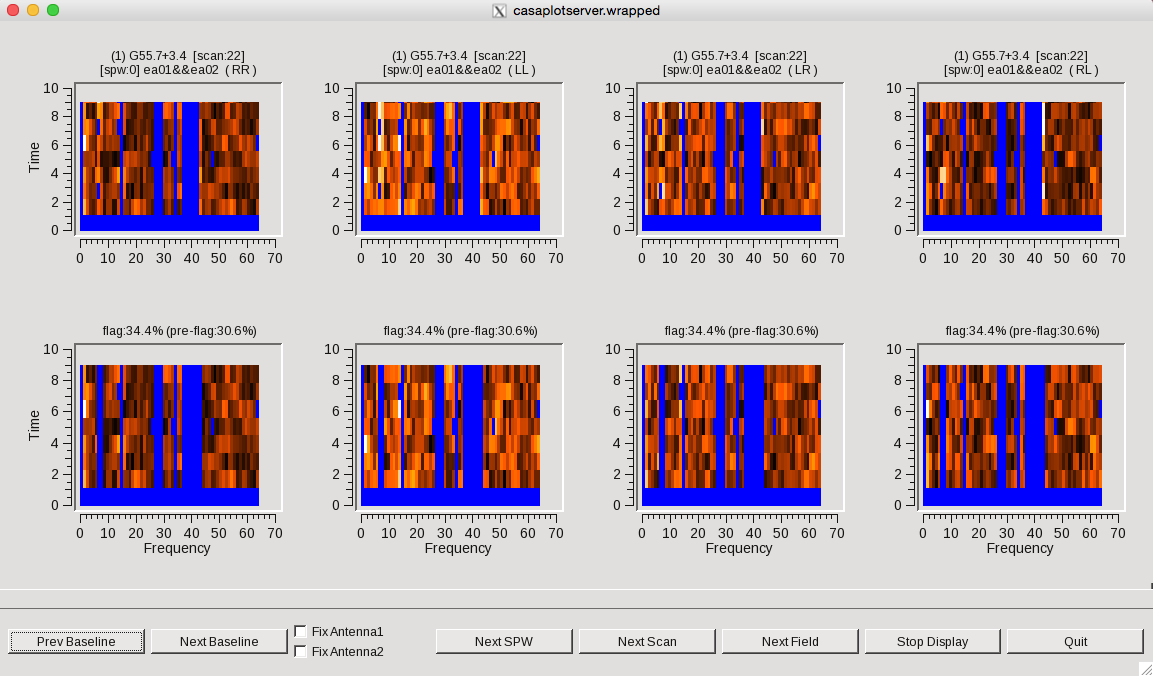
We can see that a lot of RFI is being missed by the default timedevscale and freqdevscale parameters of 5.0. Since we know spw 0 has lots of RFI, we will change the values to 1.5 and apply them. Note that we can always decide that this still isn't good enough and click on "Quit" to change our parameter values.
# In CASA
flagdata(vis='SNR_G55_10s.ms', mode='rflag', spw='0', datacolumn='corrected',
freqdevscale=1.5, timedevscale=1.5, action='apply', display='both', flagbackup=False)
Although RFlag has done a pretty good job of finding the bad data, some still remains. One way to excise the remaining bad data is to use the mode='extend' feature in flagdata, which can extend flags along a chosen axis. First, we will extend the flags across polarization, so if any one polarization is flagged, all data for that time / channel will be flagged:
# In CASA
flagdata(vis='SNR_G55_10s.ms', mode='extend', spw='0', extendpols=True,
action='apply', display='', flagbackup=False)
Now, we will extend the flags in time and frequency, using the "growtime" and "growfreq" parameters. For the data here, the rflag algorithm seems most likely to miss RFI which should be flagged along more of the time axis, so we will try with growtime=50.0, which will flag all data for a given channel if more than 50% of that channel's time is already flagged, and growfreq=90.0, which will flag the entire spectrum for an integration if more than 90% of the channels in that integration are already flagged.
# In CASA
flagdata(vis='SNR_G55_10s.ms', mode='extend', spw='0', growtime=50.0,
growfreq=90.0, action='apply', display='', flagbackup=False)
spw 1, 2, and 3
Now, let's work on SPW's 1,2, and 3. We've chosen display='both', in order to first review the flags, and decide if too much or too litle is being flagged. We can always click on 'Quit', and decide to change the freqdevscale and timedevscale parameters, as we did with spectral window 0. Note that spw 2 has these parameters lower than spw 1/3, as it contains more RFI. To allow the flagging to continue, click on "Stop Display".
# In CASA
flagdata(vis='SNR_G55_10s.ms', mode='rflag', spw='1,3', datacolumn='corrected',
freqdevscale=4.0, timedevscale=4.0, action='apply', display='both', flagbackup=False)
flagdata(vis='SNR_G55_10s.ms', mode='extend', spw='1,3', extendpols=True,
action='apply', display='', flagbackup=False)
flagdata(vis='SNR_G55_10s.ms', mode='extend', spw='1,3', growtime=50.0,
growfreq=90.0, action='apply', display='', flagbackup=False)
flagdata(vis='SNR_G55_10s.ms', mode='rflag', spw='2', datacolumn='corrected',
freqdevscale=2.5, timedevscale=2.5, action='apply', display='both', flagbackup=False)
flagdata(vis='SNR_G55_10s.ms', mode='extend', spw='2', extendpols=True,
action='apply', display='', flagbackup=False)
flagdata(vis='SNR_G55_10s.ms', mode='extend', spw='2', growtime=50.0,
growfreq=90.0, action='apply', display='', flagbackup=False)
Let's create an after RFlag plot to see the improvements.
# In CASA
plotms(vis='SNR_G55_10s.ms', scan='190' , antenna='ea24',
xaxis='freq', yaxis='amp', ydatacolumn='corrected', coloraxis='spw', title='After RFlag',
correlation='RR,LL', plotfile='amp_v_freq.afterRFlag.png', plotrange=[1.2,2,0,2.5])
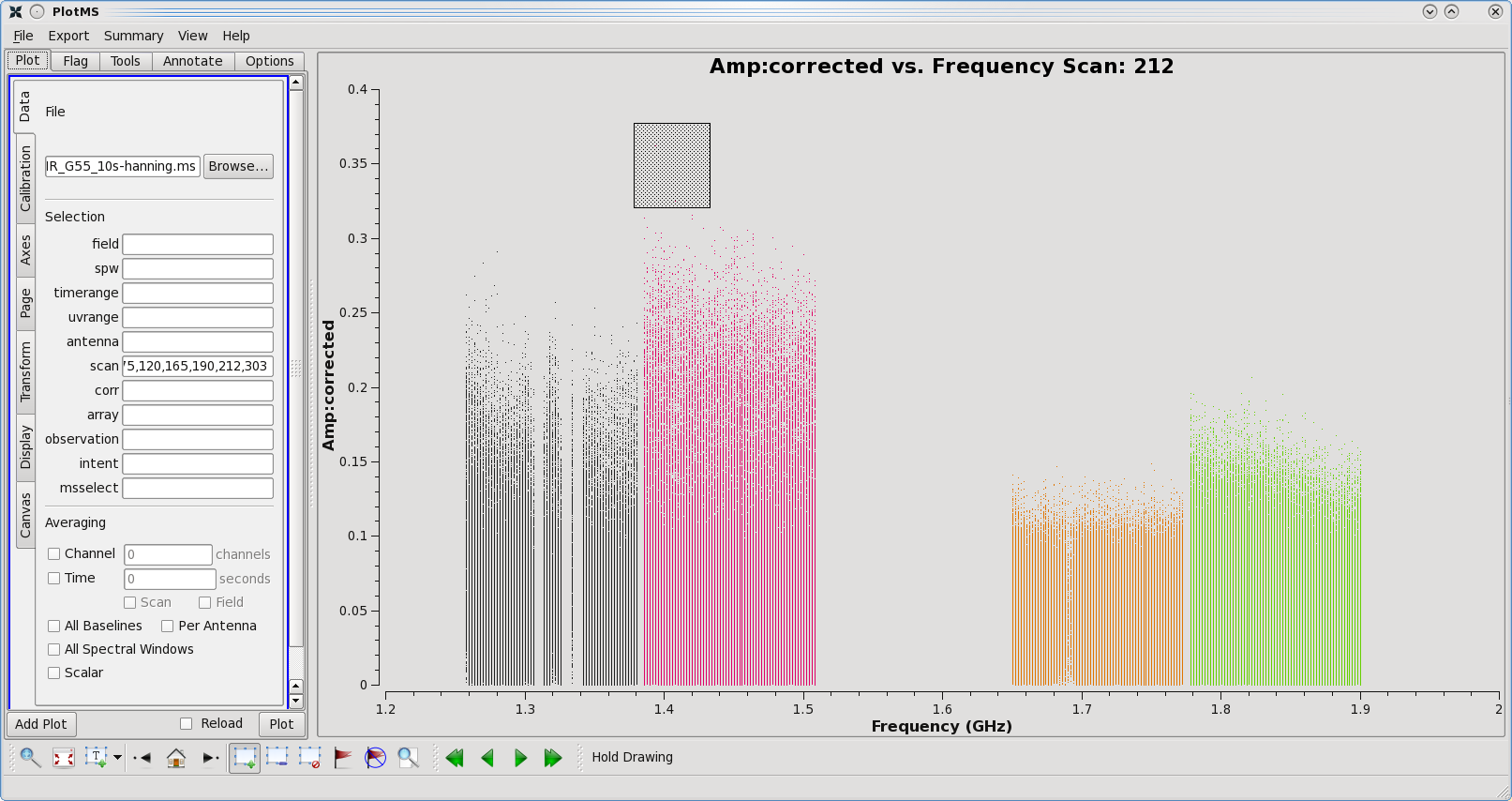
We will now plot amplitude vs. baseline, and look for outliers which we may be able to flag.
# In CASA
plotms(vis='SNR_G55_10s.ms', scan='30,75,120,165,190,235,303', xaxis='baseline', yaxis='amp',
ydatacolumn='corrected', iteraxis='scan', correlation='RR,LL', coloraxis = 'baseline')
It appears that there are a few baselines which have consistently higher-amplitude than the others, indicating that it's probably contaminated by RFI.
Use the plotms tools to identify this baseline, which turns out to be ea04&ea08 and ea04&ea21, and is mostly present for spw 1. Let's flag these baselines.
# In CASA
flagdata(vis='SNR_G55_10s.ms', antenna='ea04&ea08', spw='1', flagbackup=False)
flagdata(vis='SNR_G55_10s.ms', antenna='ea04&ea21', spw='1', flagbackup=False)
We will now run flagdata in summary mode to inspect how much data we have flagged thus far. We can also create a plot of the percentage of flagged data with respect to the frequency. This command will also plot the antennas, with circle size representing the percentage of flagged data per antenna.
# In CASA
flagInfo = flagdata(vis='SNR_G55_10s.ms', mode='summary', action='calculate', display='report', spwchan=T)
print("\n %2.1f%% of G55.7+3.4, %2.1f%% of 3C147, and %2.1f%% of J1925+2106 are flagged. \n" % (100.0 * flagInfo['field']['G55.7+3.4']['flagged'] / flagInfo['field']['G55.7+3.4']['total'], 100.0 * flagInfo['field']['0542+498=3C147']['flagged'] / flagInfo['field']['0542+498=3C147']['total'], 100.0 * flagInfo['field']['J1925+2106']['flagged'] / flagInfo['field']['J1925+2106']['total']))
print("Spectral windows are flagged as follows:")
for spw in range(0,4):
print("SPW %s: %2.1f%%" % (spw, 100.0 * flagInfo['spw'][str(spw)]['flagged'] / flagInfo['spw'][str(spw)]['total']))
So, as a result of the flagging, we have sacrificed almost 28% of the data for G55.7+3.4, and as expected, spectral windows 0 and 2 have the most flagged data.
Interactive Flagging
After plotting our data, it's obvious that there is still some amount of RFI present. We can use plotms to interactively flag points which look bad. A tutorial on flagging data interactively through plotms can be found here. Please note that flagging data through plotms will not create a backup, so it's important to use the flagmanager before deciding to mark your regions for flagging purposes.
# In CASA
flagmanager(vis='SNR_G55_10s.ms', mode='save',
versionname='before_interactive_flagging')
plotms(vis='SNR_G55_10s.ms', scan='30,75,120,165,190,235,303', xaxis='frequency', yaxis='amp',
ydatacolumn='corrected', iteraxis='scan', correlation='RR,LL', coloraxis = 'spw')
Let's iterate through scans and view scan 75. We can see that spectral window 1 has a large amplitude spike. We can use the "mark regions" button (square with green plus sign) to highlight a majority of spike, and the "locate" button (magnifying glass) to give us information on the highlighted region. We will now click on the "flag" button (red flag) and we should see the plot update, having removed the highlighted region.
Imaging
We will now cover topics on imaging with CASA. We will be utilizing the previous data set, which has been calibrated. A copy of the calibrated data (1.2GB) can be downloaded from http://casa.nrao.edu/Data/EVLA/SNRG55/SNR_G55_10s.calib.tar.gz
We will skip the calibration process in this guide, as examples of calibration can be found in several other guides, including the EVLA_Wide-Band_Wide-Field_Imaging guide.
After undergoing the calibration process, we split out the science target, G55.7+3.4, with only the RR,LL correlations, as the cross correlations were not calibrated, nor will be used for our purposes.
The CLEAN Algorithm
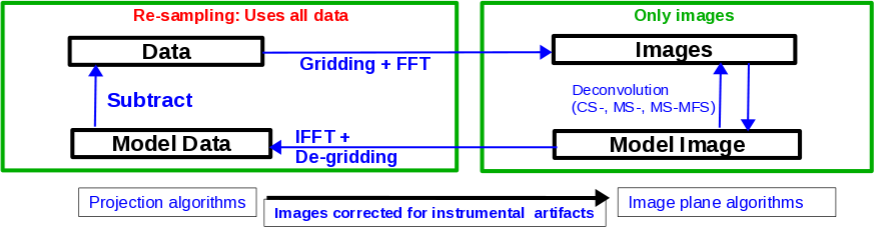
The CLEAN algorithm, developed by J. Högbom (1974) enabled the synthesis of complex objects, even if they have relatively poor Fourier uv-plane coverage. Poor coverage occurs with partial earth rotation synthesis, or with arrays composed of few antennas. The "dirty" image is formed by a simple Fourier inversions of the sampled visibility data, with each point on the sky being represented by a suitably scaled and centered PSF (Point Spread Function, sometimes called the dirty beam). This algorithm attempts to interpolate from the measured (u,v) points across gaps in the (u,v) coverage. It, in short, provides solutions to the convolution equation by representing radio sources by a number of point sources in an empty field.
The brightest points are found by performing a cross-correlation between the dirty image, and the PSF. The brightest parts are subtracted (minor-cycle), and the process is repeated again for the next brighter sources (major-cycle). A large part of the work in CLEAN involves shifting and scaling the dirty beam.
The clean algorithm works well with points sources, as well as most extended objects. Where it can fall short is in speed, as convergence can be slow for extended objects, or for images containing several bright point sources. A solution to deconvolve these images would be the MEM (Maximum Entropy Method) algorithm, which has faster performance, although we can improve the CLEAN algorithm by employing other means, some of which will be mentioned below.
1. Högbom Algorithm
This algorithm will initially find the strength and position of a peak in a dirty image, subtract it from the dirty image, record this position and maginitude, and repeat for further peaks. The remainder of the dirty image is known as the residuals.
The accumulated point sources, now residing in a model, is convolved with an idealized CLEAN beam (usually a Gaussian fitted to the central lobe of the dirty beam), creating a CLEAN image. As the final step, the residuals of the dirty image are then added to the CLEAN image.
2. Clark Algorithm
Clark (1980), developed a FFT-based CLEAN algorithm, which more efficiently shifts and scales the dirty beam by approximating the position and strength of components using a small patch of the dirty beam. This algorithm is the default within the clean task, which involves major and minor cycles.
The algorithm will first select a beam patch, which will include the highest exterior sidelobes. Points are then selected from the dirty image, which are up to a fraction of the image peak, and are greater than the highest exterior sidelobe of the beam. It will then conduct a list-based Högbom CLEAN, creating a model and convolution with an idealized CLEAN beam. This process is the minor cycle.
The major cycle involves transforming the point source model via a FFT (Fast-Fourier Transform), mutiplying this by the weight sampling function (more on this below), and transformed back. This is then subtracted from the dirty image, creating your CLEAN image. The process is then repeated with subsequent minor cycles.
3. Cotton-Schwab Algorithm
This is the default imager mode (csclean), and is a variant of the Clark algorith in which the major cycle involves the subtraction of CLEAN components of ungridded visibility data. This allows the removal of gridding errors, as well as noise. One advantage is its ability to image and clean many seperate fields simultaneously. Fields are cleaned independently in the minor cycle, and components from all fields cleaned together in the major cycles.
This algorithm is faster than the Clark algorithm, except when dealing with a large number of visibility samples, due to the re-gridding process it undergoes. It is most useful in cleaning sensitive high-resolution images at lower frequencies where a number of confusing sources are within the primary beam.
For more details on imaging and deconvolution, you can refer to the Astronomical Society of the Pacific Conference Series book entitled Synthesis Imaging in Radio Astronomy II. The chapter on Deconvolution may prove helpful.
Weights and Tapering
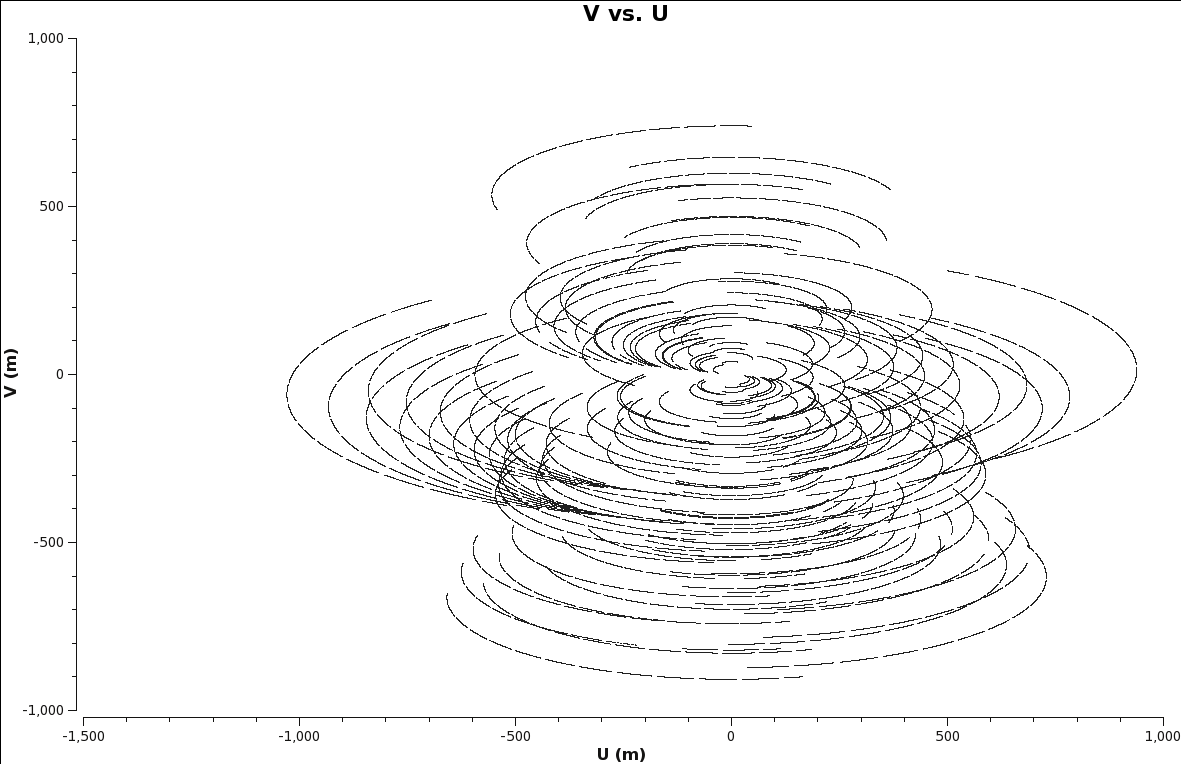
When imaging data, a map is created associating the visibilities with the image. The sampling function, which is a function of the visibilities, is modified by a weight function. [math]\displaystyle{ S(u,v) \to S(u,v)W(u,v) }[/math].
This process can be considered a convolution. The convolution map, is the weights by which each visiblity is multiplied by before gridding is undertaken. Due to the fact that each VLA antenna performs slightly differently, different weights should be applied to each antenna. Therefore, the weight column in the data table reflects how much weight each corrected data sample should receive.
For a brief intro to the different clean algorithms, as well as other deconvolution and imaging information, please see the website kept by Urvashi R.V. here.
The following are a few of the more used forms of weighting, which can be used within the clean task. Each one has their own benefits and drawbacks.
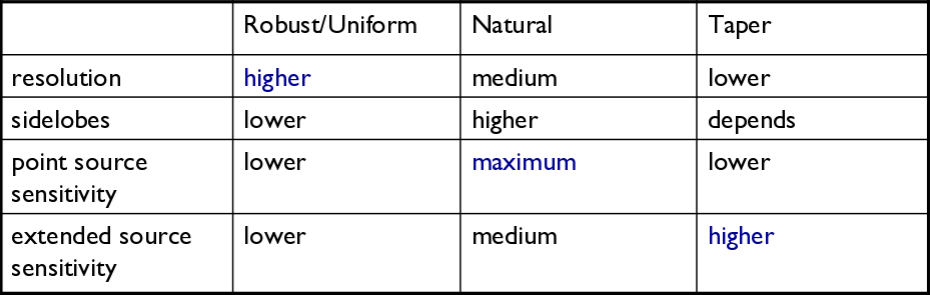
1. Natural: The weight function can be described as [math]\displaystyle{ W(u,v) = 1/ \sigma^2 }[/math], where [math]\displaystyle{ \sigma^2 }[/math] is the noise variance. Natural weighting will maximize point source sensitivity, and provide the lowest rms noise within an image, as well as the highest signal-to-noise. It will also generaly give more weight to short baselines, thus angular resolutions can be degraded. This form of weighting is the default within the clean task.
2. Uniform: The weight function can be described as [math]\displaystyle{ W(u,v) = W(u,v) / W_k }[/math], where [math]\displaystyle{ W_k }[/math] represents the local density of (u,v) points, otherwise known as the gridded weights. This form of weighting will increase the influence of data with lower weight, filling the (u,v) plane more uniformly, thereby reducing sidelobe levels in the field-of-view, but increasing the rms image noise. More weight is given to long baselines, therefore increasing angular resolution. Point source sensitivity is degraded due to the downweighting of some data.
3. Briggs: A flexible weighting scheme, that is a variant of uniform, and avoids giving too much weight to (u,v) points with a low natural weight. Weight function can be described as [math]\displaystyle{ W(u,v) = 1/ \sqrt{1+S_N^2/S_{thresh}^2} }[/math], where [math]\displaystyle{ S_N }[/math] is the natural weight of the cell, [math]\displaystyle{ S_{thresh} }[/math] is a threshold. A high threshold will go to a natural weight, where as a low threshold will go to a uniform weight. This form of weighting also has adjustable parameters. The robust parameter will give variation between resolution and maximum point source sensitivity. It's value can range from -2.0 (close to uniform weight) to 2.0 (close to natural weight). By default, the parameter is set to 0.0, which gives a good trade-off.
I. Tapering: In conjunction with weighting, we can include the uvtaper parameter within clean, which will control the radial weighting of visibilities, in the uv-plane. This in effect, reduces the visibilities, with weights decreasing as a function of uv-radius. The tapering will apodize, or filter/change the shape of the weight function (which is itself a Gaussian), which can be expressed as:
[math]\displaystyle{ W(u,v) = e^{-(u^2+v^2)/t^2} }[/math], where t is the adjustable tapering parameter. This process can smooth the image plane, give more weight to short baselines, but in turn degrade angular resolution. Due to the downweight of some data, point source sensitivity can be degraded. If your observation was sampled by short baselines, tapering may improve sensitivity to extended structures.
Primary and Synthesized Beam
The primary beam of the VLA antennas can be taken to be a Gaussian with FWHM equal to [math]\displaystyle{ 90*\lambda_{cm} }[/math] or [math]\displaystyle{ 45/ \nu_{GHz} }[/math]. Taking our observed frequency to be the middle of the band, 1.5GHz, our primary beam will be around 30 arcmin. Note that if your science goal is to image a source, or field of view that is significantly larger than the FWHM of the VLA primary beam, then creating a mosaic from a number of pointings would be best. For a tutorial on mosaicing, see the 3C391 tutorial.
Since our observation was taken in D-configuration, we can check the Observational Status Summary's section on VLA resolution to find that the synthesized beam will be around 46 arcsec. We want to oversample the synthesized beam by a factor of around five, so we will use a cell size of 8 arcsec.
Since this field contains bright point sources significantly outside the primary beam, we will create images that are 170 arcminutes on a side ([8arcsec * Cell Size]*[1arcmin / 60arsec]), or almost 6x the size of the primary beam. This is ideal for showcasing both the problems inherent in such wide-band, wide-field imaging, as well as some of the solutions currently available in CASA to deal with these issues.
First, it's worth considering why we are even interested in sources which are far outside the primary beam. This is mainly due to the fact that the EVLA, with its wide bandwidth capabilities, is quite sensitive even far from phase center -- for example, at our observing frequencies in L-band, the primary beam gain is as much as 10% around 1 degree away. That means that any imaging errors for these far-away sources will have a significant impact on the image rms at phase center. The error due to a source at distance R can be parametrized as:
[math]\displaystyle{ \Delta(S) = S(R) \times PB(R) \times PSF(R) }[/math]
So, for R = 1 degree, source flux S(R) = 1 Jy, [math]\displaystyle{ \Delta(S) }[/math] = 1 mJy − 100 [math]\displaystyle{ {\mu} }[/math]Jy. Clearly, this will be a source of significant error.
Multi-Scale Clean
Since G55.7+3.4 is an extended source with many spatial scales, the most basic (yet still reasonable) imaging procedure is to use clean with multiple scales. MS-CLEAN is an extension of the classical CLEAN algorithm for handling extended sources. It works by assuming the sky is composed of emission at different spatial scales and works on them simultaneously, thereby creating a linear combination of images at different spatials scales. For a more detailed description of Multi Scale CLEAN, see the paper by J.T. Cornwell entitled Multi-Scale CLEAN deconvolution of radio synthesis images.
It can also be possible to utilize tclean, (t for test) which is a refactored version of clean, with a better interface, and provides more possible combinations of algorithms. It also allows for process computing parallelization of the imaging and deconvolution. Eventually, tclean will replace the current clean task, but for now, we will stick with the original clean, as tclean is merely experimental at the moment.
As is suggested, we will use a set of scales (which are expressed in units of the requested pixel, or cell, size) which are representative of the scales that are present in the data, including a zero-scale for point sources.
Note that interrupting clean by Ctrl+C may corrupt your visibilities -- you may be better off choosing to let clean finish. We are currently implementing a command that will nicely exit to prevent this from happening, but for the moment try to avoid Ctrl+C.
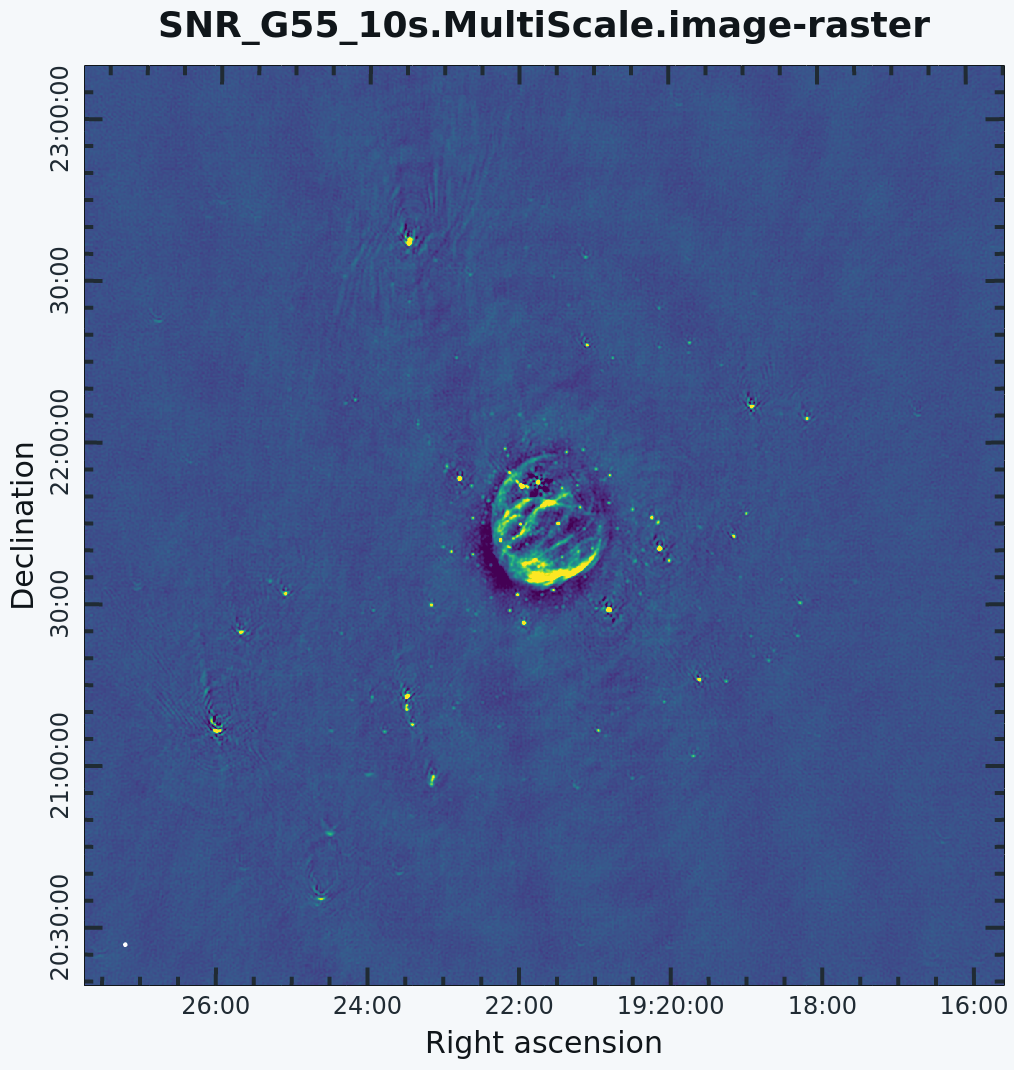

# In CASA
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.MultiScale',
imsize=1280, cell='8arcsec', multiscale=[0,6,10,30,60], smallscale=0.9,
interactive=False, niter=1000, pbcor=True, weighting='briggs', uvtaper='
stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.MultiScale',
imsize=1280, cell='8arcsec', multiscale=[0,6,10,30,60],
interactive=False, niter=1000, weighting='briggs',
stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')
viewer('SN_G55_10s.MultiScale.image')
- imagename='SN_G55_10s.MultiScale': the root filename used for the various clean outputs. These include the final image (<imagename>.image), the relative sky sensitivity over the field (<imagename>.flux), the point-spread function (also known as the dirty beam; <imagename>.psf), the clean components (<imagename>.model), and the residual image (<imagename>.residual).
- imsize=1280: the image size in number of pixels. Note that entering a single value results in a square image with sides of this value.
- cell='8arcsec': the size of one pixel; again, entering a single value will result in a square pixel size.
- multiscale=[0,6,10,30,60]: a set of scales on which to clean. A good rule of thumb when using multiscale is [0, 2xbeam, 5xbeam] (where beam is the synthesized beam) and larger scales up to the maximum scale the interferometer can image. Since these are in units of the pixel size, our chosen values will be multiplied by the requested cell size. Thus, we are requesting scales of 0 (a point source), 48, 80, 240, and 480 arcseconds. Note that 16 arcminutes (960 arcseconds) roughly corresponds to the size of G55.7+3.4.
- smallscale=0.9: This parameter is known as the small scale bias, and helps with faint extended structure, by balancing the weight given to smaller structures which tend to be brighter, but have less flux density. Increasing this value gives more weight to smaller scales. A value of 1.0 weighs the largest scale to zero, and a value of less than 0.2 weighs all scales nearly equally. The default value is 0.6.
- interactive=False: we will let clean use the entire field for placing model components. Alternatively, you could try using interactive=True, and create regions to constrain where components will be placed. However, this is a very complex field, and creating a region for every bit of diffuse emission as well as each point source can quickly become tedious. For a tutorial that covers more of an interactive clean, please see IRC+10216 tutorial.
- niter=1000: this controls the number of iterations clean will do in the minor cycle.
- pbcor=True: We can correct for the relative sky sensitivity while running clean. This will help in creating a near circularly symmetric beam, which may be better able to image extended sources, over long observations. setting this to true, forces the raw image to be rescaled by dividing by the noise and primary beam correction image (<imagename>.flux). Note that this can also be done via the immath task if pbcor=False.
- weighting='briggs': use Briggs weighting with a robustness parameter of 0 (halfway between uniform and natural weighting).
- usescratch=F: do not write the model visibilities to the model data column (only needed for self-calibration)
- imagermode='csclean': use the Cotton-Schwab clean algorithm
- stokes='I': since we have not done any polarization calibration, we only create a total-intensity image.
- threshold='0.1mJy': threshold at which the cleaning process will halt; i.e. no clean components with a flux less than this value will be created. This is meant to avoid cleaning what is actually noise (and creating an image with an artificially low rms). It is advisable to set this equal to the expected rms, which can be estimated using the EVLA exposure calculator. However, in our case, this is a bit difficult to do, since we have lost a hard-to-estimate amount of bandwidth due to flagging, and there is also some residual RFI present. Therefore, we choose 0.1 mJy as a relatively conservative limit.
This is the fastest of the imaging techniques described here, but it's easy to see that there are artifacts in the resulting image. Note that you may have to play with the image color map and brightness/contrast to get a better view of the image details. This can be done by clicking on Data Display Options (wrench icon on top right corner), and choosing "rainbow 3" under basic settings. We can use the viewer to explore the point sources near the edge of the field by zooming in on them. Some have prominent arcs, as well as spots in a six-pointed pattern surrounding them.
Next we will explore some more advanced imaging techniques to mitigate these artifacts.
Multi-Scale, Wide-Field Clean (w-projection)
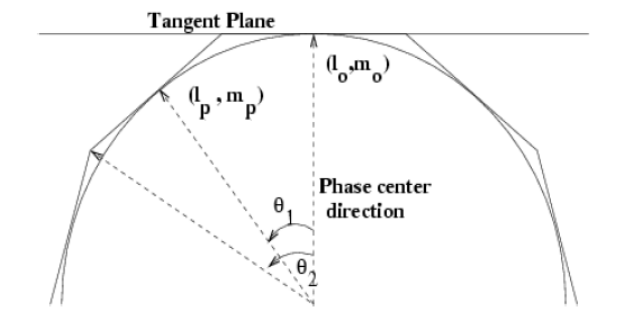
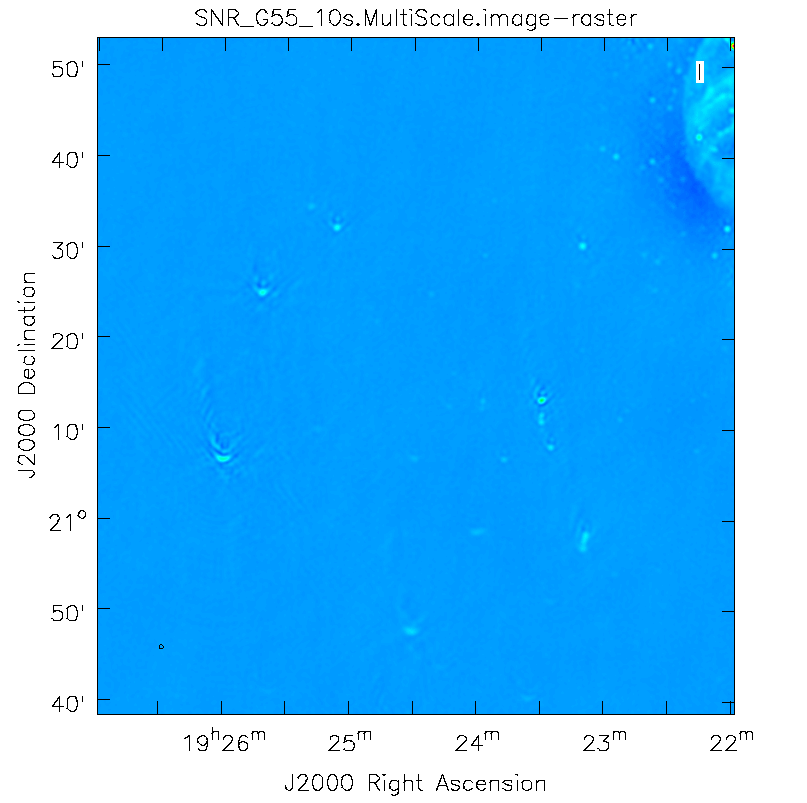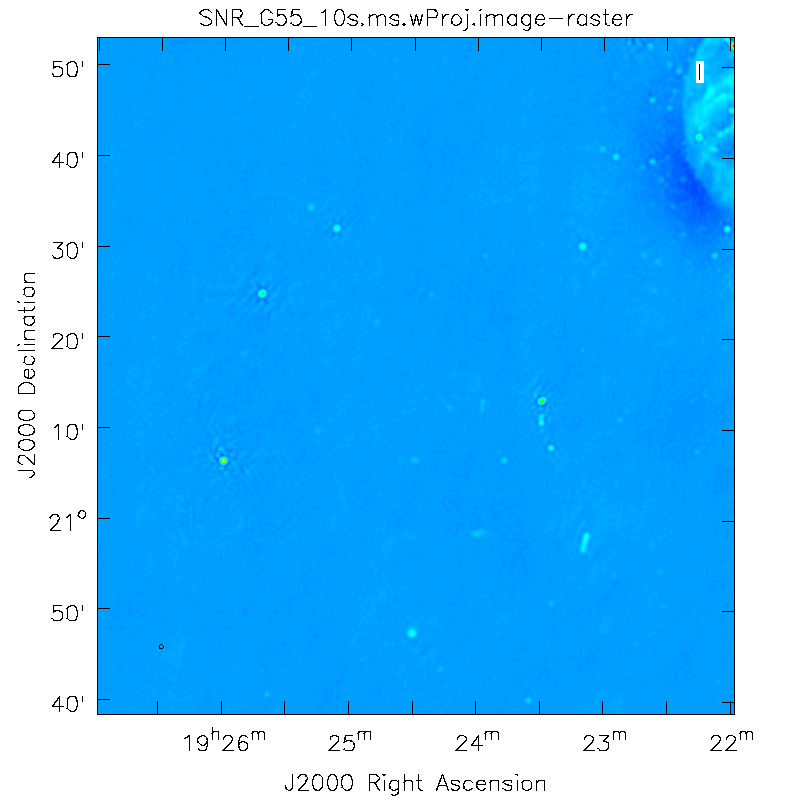
The next clean algorithm we will employ is w-projection, which is a wide-field imaging technique that takes into account the non-coplanarity of the baselines as a function of distance from the phase center. For wide-field imaging, the sky curvature and non-coplanar baselines results in a non-zero w-term. The w-term introduced by the sky and array curvature introduces a phase term that will limit the dynamic range of the resulting image. Applying 2-D imaging to such data will result in artifacts around sources away from the phase center, as we saw in running MS-CLEAN. Note that this affects mostly the lower frequency bands, especially for the more extended configurations, due to the field of view decreasing with higher frequencies.
The w-term can be corrected by faceting (describe the sky curvature by many smaller planes) in either the image or uv-plane, or by employing w-projection. A combination of the two can also be employed within clean by setting the parameter gridmode='widefield'. If w-projection is employed, it will be done for each facet. Note that w-projections is an order of magnitude faster than the faceting algorithm, but will require more memory.
For more details on w-projection, as well as the algorithm itself, see "The Noncoplanar Baselines Effect in Radio Interferometry: The W-Projection Algorithm". Also, the chapter on Imaging with Non-Coplanar Arrays may be helpful.
# In CASA
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.ms.wProj',
gridmode='widefield', imsize=1280, cell='8arcsec',
wprojplanes=128, multiscale=[0,6,10,30,60],
interactive=False, niter=1000, weighting='briggs',
stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')
viewer('SNR_G55_10s.ms.wProj.image')
- gridmode='widefield': Use the w-projection algorithm.
- wprojplanes=128: The number of w-projection planes to use for deconvolution; 128 is the minimum recommended number.
This will take slightly longer than the previous imaging round; however, the resulting image has noticeably fewer artifacts. In particular, compare the same outlier source in the Multi-Scale w-projected image with the Multi-Scale-only image: note that the swept-back arcs have disappeared. There are still some obvious imaging artifacts remaining, though.
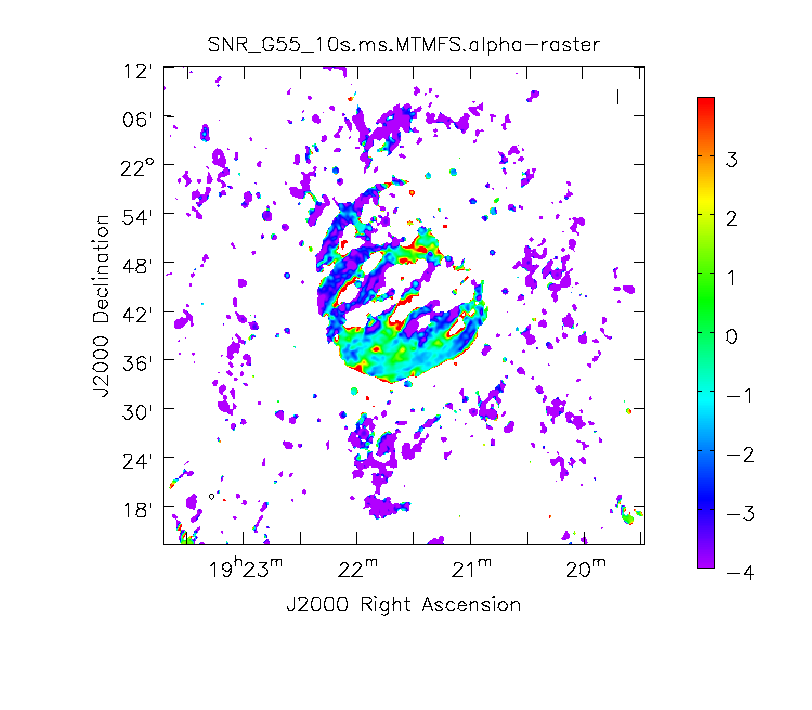
Multi-Scale, Multi-Frequency Synthesis
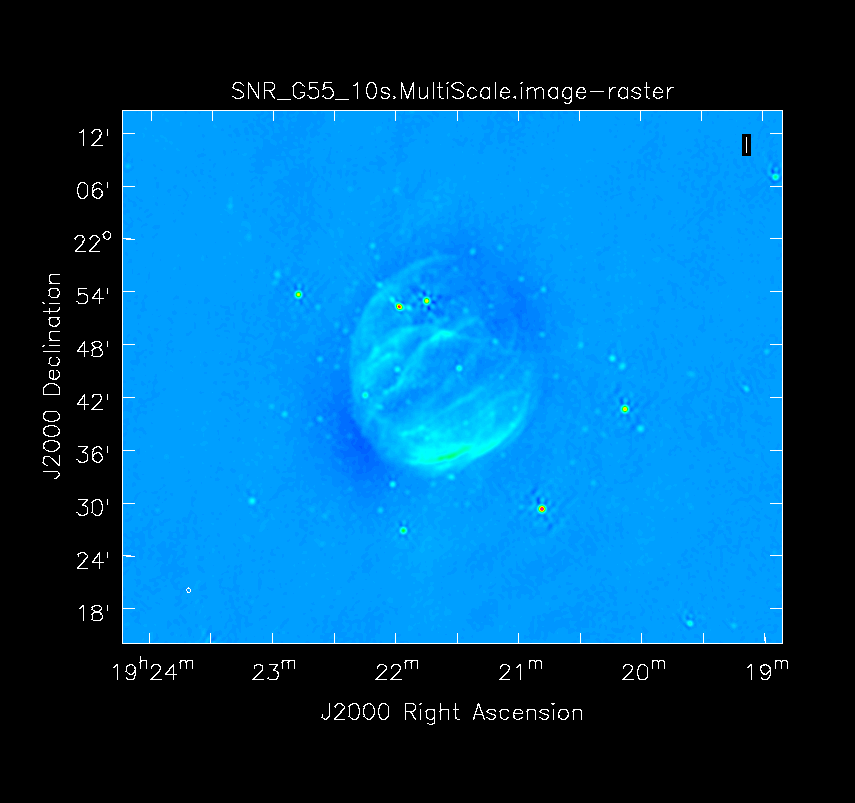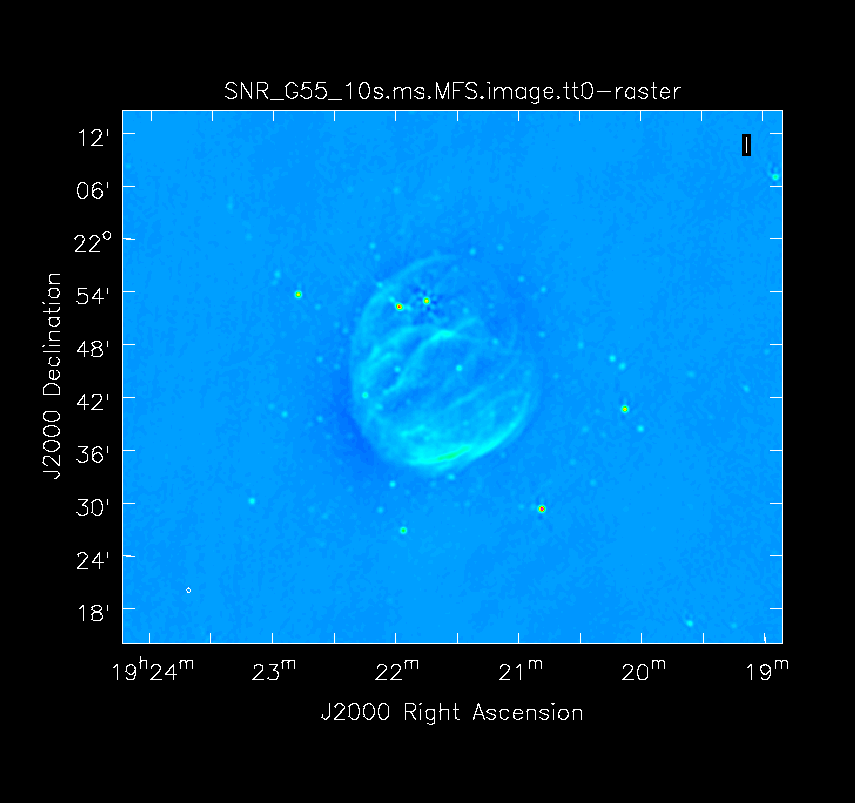
Another consequence of simultaneously imaging the wide fractional bandwidths available with the EVLA is that the primary beam has substantial frequency-dependent variation over the observing band. If this is not accounted for, it will lead to imaging artifacts and compromise the achievable image rms.
If sources which are being imaged have intrinsically flat spectra, this will not be a problem. However, most astronomical objects are not flat-spectrum sources, and without any estimation of the intrinsic spectral properties, the fact that the primary beam is twice as large at 2 than at 1 GHz will have substantial consequences.
Note that the dimentions of the (u,v) plane are measured in wavelengths, and therefore observing at several frequencies, a baseline can sample several ellipses in the (u,v) plane, each with different sizes. We can therefore fill in the gaps in the single frequency (u,v) coverage, hence Multi-Frequency Synthesis (MFS). Also when observing in low-frequencies, it may prove beneficial to observe in small time-chunks, which are spread out in time. This will allow the coverage of more spatial-frequencies, allowing us to employ this algorithm more efficiently.
The Multi-Scale Multi-Frequency-Synthesis (MS-MFS) algorithm provides the ability to simultaneously image and fit for the intrinsic source spectrum. The spectrum is approximated using a polynomial in frequency, with the degree of the polynomial as a user-controlled parameter. A least-squares approach is used, along with the standard clean-type iterations. Using this method of imaging will dramatically improve our (u,v) coverage, hence improving image fidelity.
For a more detailed explanation of the MS-MFS deconvolution algorithm, please see the paper by Urvashi Rau and Tim J. Cornwell entitled A multi-scale multi-frequency deconvolution algorithm for synthesis imaging in radio interferometry
# In CASA
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.ms.MFS',
imsize=1280, cell='8arcsec', mode='mfs', nterms=2,
multiscale=[0,6,10,30,60],
interactive=False, niter=1000, weighting='briggs',
stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')
viewer('SNR_G55_10s.ms.MFS.image.tt0')
viewer('SNR_G55_10s.ms.MFS.image.alpha')
- nterms=2:the number of Taylor terms to be used to model the frequency dependence of the sky emission. Note that the speed of the algorithm will depend on the value used here (more terms will be slower); of course, the image fidelity will improve with a larger number of terms (assuming the sources are sufficiently bright to be modeled more completely).
This will take much longer than the two previous methods, so it would probably be a good time to have coffee or chat about EVLA data reduction with your neighbor at this point.
When clean is done <imagename>.image.tt0 will contain a total intensity image, where tt0 is a suffix to indicate the Taylor term; <imagename>.image.alpha will contain an image of the spectral index in regions where there is sufficient signal-to-noise. Having this spectral index image can help convey information about the emission mechanism involved within the supernova remnant. It can also give information on the optical depth of the source. I've included a color widget on the top of the plot to give an idea of the spectral index variation.
For more information on the multi-frequency synthesis mode and its outputs, see section 5.2.5.1 in the CASA cookbook.
Inspect the brighter point sources in the field near the supernova remnant. You will notice that some of the artifacts which had been symmetric around the sources themselves are now gone; however, since we did not use W-Projection this time, there are still strong features related to the non-coplanar baseline effects still apparent for sources further away.
Multi-Scale, Multi-Frequency, Widefield Clean
Finally, we will combine the W-Projection and MS-MFS algorithms to simultaneously account for both of the effects. Be forewarned -- these imaging runs will take a while, and it's best to start them running and then move on to other things.
First, we will image the autoflagged data. Using the same parameters for the individual-algorithm images above, but combined into a single clean run, we have:
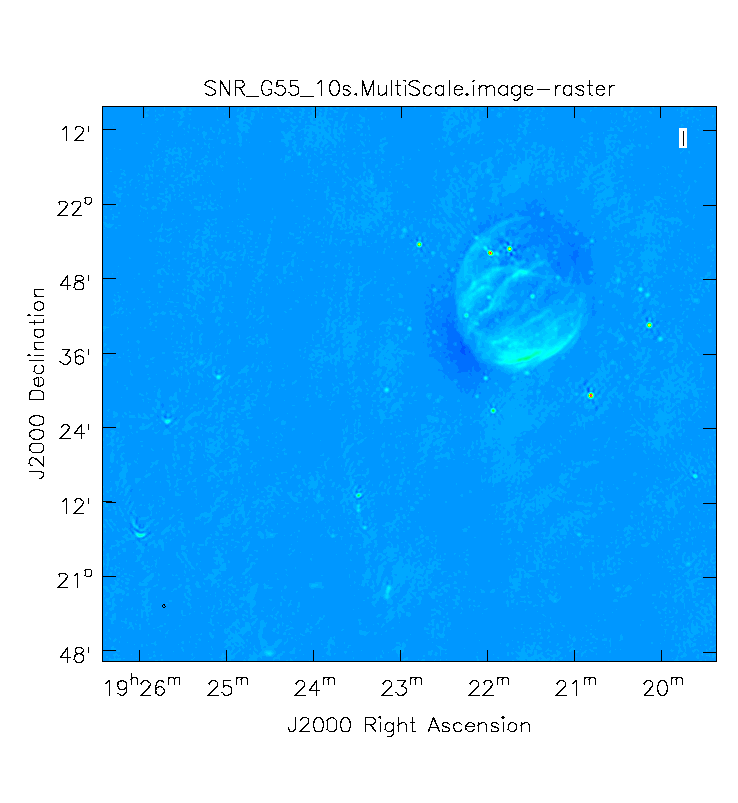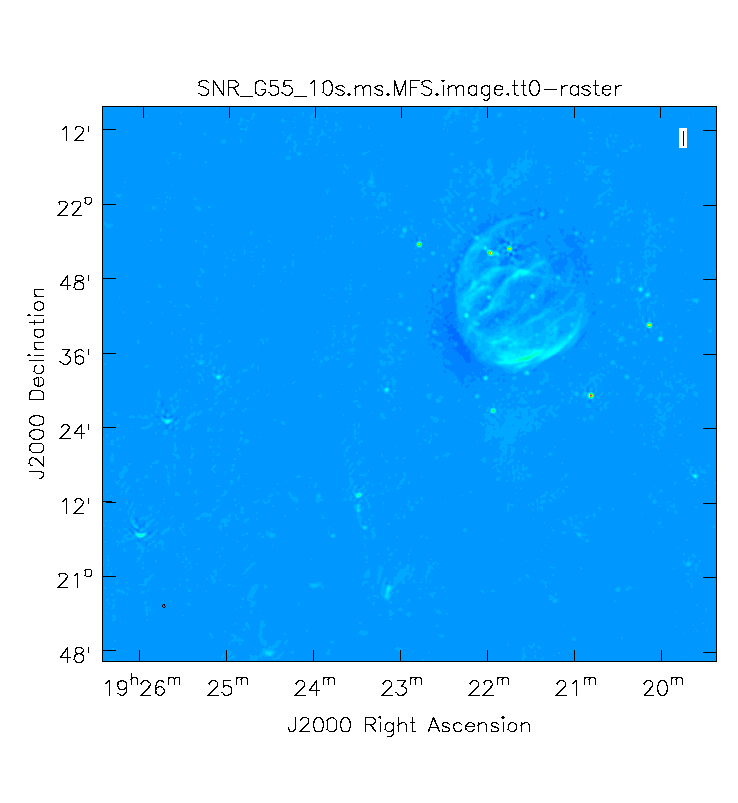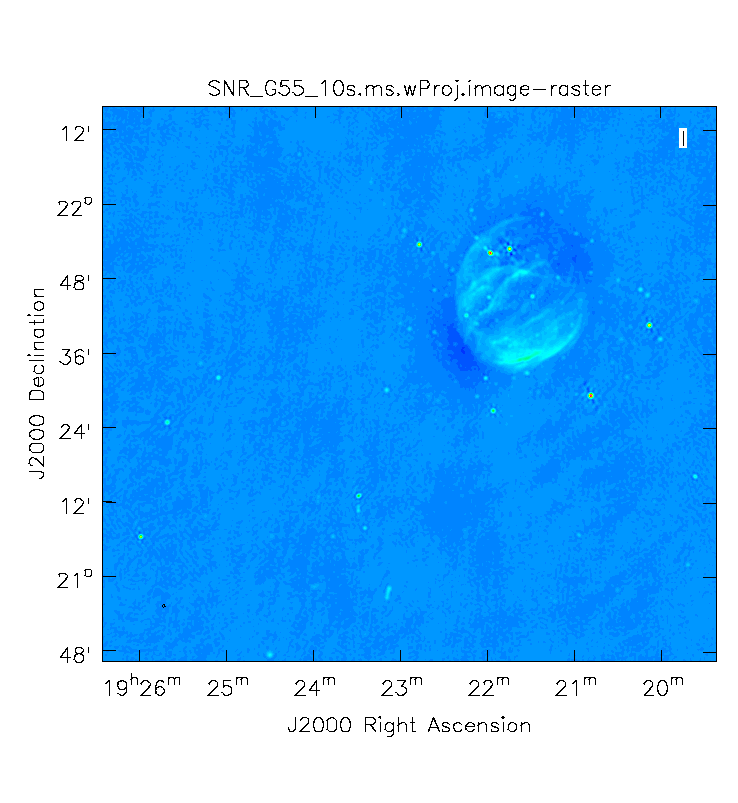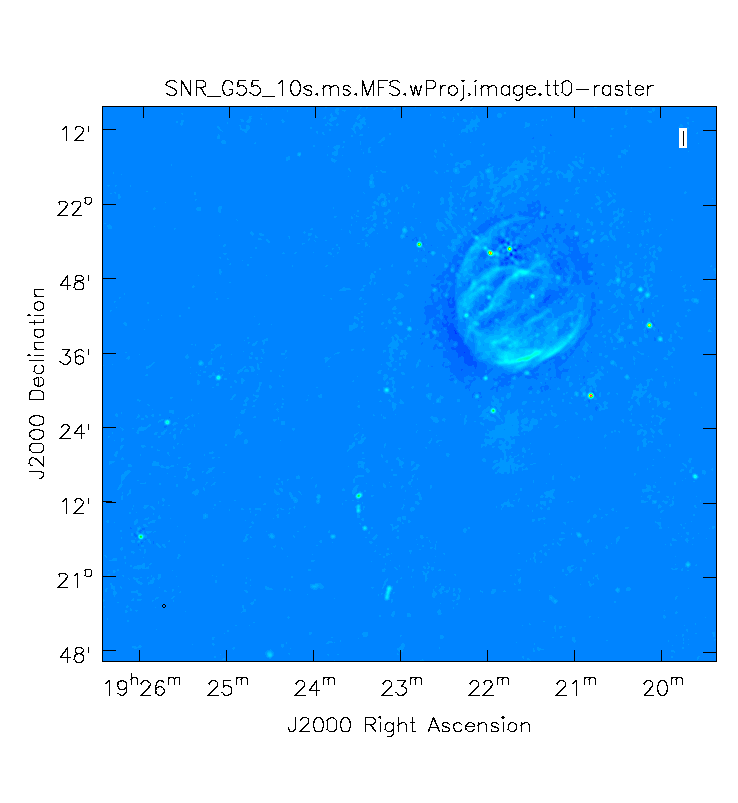
# In CASA
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.ms.MFS.wProj',
gridmode='widefield', imsize=1280, cell='8arcsec', mode='mfs',
nterms=2, wprojplanes=128, multiscale=[0,6,10,30,60],
interactive=False, niter=1000, weighting='briggs',
stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')
viewer('SNR_G55_10s.ms.MFS.wProj.image.tt0')
viewer('SNR_G55_10s.ms.MFS.wProj.image.alpha')
Again, looking at the same outlier source, we can see that the major sources of error have been removed, although there are still some residual artifacts. One possible source of error is the time-dependent variation of the primary beam; another is the fact that we have only used nterms=2, which may not be sufficient to model the spectra of some of the point sources.
Ultimately, it isn't too surprising that there was still some RFI present in our auto-flagged data, since we were able to see this with plotms. It's also possible that the auto-flagging overflagged some portions of the data, also leading to a reduction in the achievable image rms.
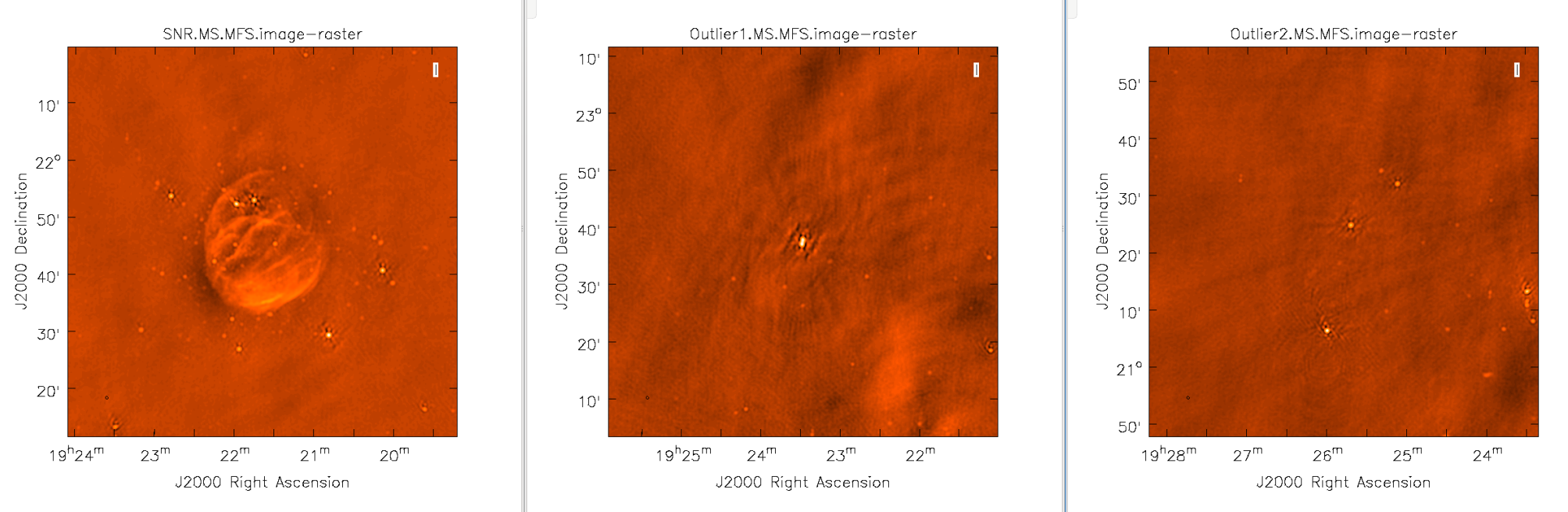
Imaging Outlier Fields
Now we will image the supernova remnant, as well as the bright sources (outliers) towards the edges of the image, creating a 512x512 pixel image for each one. For this, we will be utilizing CLEAN without widefield mode (try it to see the effects) as we will be specifying a phase center, and the images will not be too big, therefore we will not have sources very far from the phase center. We will specify a name for each image, as well as a phase center for each image. This form of imaging is useful for when you have several outlier fields you'd like to image in one go. An outlier file can also be created, if you have a list of sources you'd like to image.
# In CASA
clean(vis='SNR_G55_10s.calib.ms', imagename=['SNR.MS.MFS', 'Outlier1.MS.MFS', 'Outlier2.MS.MFS'],
imsize=[[512,512],[512,512],[512,512]], cell='8arcsec', mode='mfs',
multiscale=[0,6,10,30,60], interactive=False, niter=1000, weighting='briggs',
stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean',
phasecenter=['J2000 19h21m38.271 21d45m48.288', 'J2000 19h23m27.693 22d37m37.180', 'J2000 19h25m46.888 21d22m03.365'])
Primary Beam Correction
In interferomety, the images formed via deconvolution, are representations of the sky, multiplied by the primary beam response of the antenna. The primary beam can be described by a Gaussian with the size depending on the observing frequency. Correcting the primary beam can be done during clean with the pbcor parameter. It can also be done after imaging using the task impbcor for regular data sets, and widebandpbcor for those that use Taylor-term expansion (nterms > 1). The primary beam image is usually the image.flux output image given by CLEAN. The mode parameter may also be changed to divide or multiply.
Image Information
This portions will cover topics on image headers, and frequency reference frames.
Frequency Reference Frame
The velocity within your image is calculated based on your choice of frame, velocity definition, and spectral line rest frequency. The initial frequency reference frame is initially given by the telescope, however, it can be transformed to several other frames, including:
- LSRK - Local Standard of Rest Kinematic. Conventional LSR based on average velocity of stars in the solar neighborhood.
- LSRD - Local Standard of Rest Dynamic. Velocity with respect to a frame in circular motion about the galactic center.
- BARY - Barycentric. Referenced to JPL ephemeris DE403. Slightly different and more accurate than heliocentric.
- GEO - Geocentric. Referenced to the Earth's center. This will just remove the observatory motion.
- TOPO - Topocentric. Fixed observing frequency and constantly changing velocity.
- GALACTO - Galactocentric. Referenced to the dynamical center of the galaxy.
- LGROUP - Local Group. Referenced to the mean motion of Local Group of Galaxies.
- CMB - Cosmic Microwave Background dipole. Based on COBE measurements of dipole anisotropy.
Image Header
The image header holds meta data associated with your CASA image. The task imhead will display this data within the casalog. We will first run imhead with mode='summary':
# In CASA
imhead(imagename='SNR_G55_10s.ms.MFS.wProj.image.tt0', mode='summary')
- mode='summary': gives general information about the image, including the object name, sky coordinates, image units, the telescope the data was taken with, and more.
For further information about the image, let's now run it with mode='list':
# In CASA
imhead(imagename='SNR_G55_10s.ms.MFS.wProj.image.tt0', mode='list')
- mode='list': gives more detailed information, including beam major/minor axes, beam primary angle, and the location of the max/min intensity, and lots more.
We will now want to change our image header units from Jy/beam to Kelvin. To do this, we will run the task with mode='put':
# In CASA
imhead(imagename='SNR_G55_10s.ms.MFS.wProj.image.tt0', mode='put', hdkey='bunit', hdvalue='K')
Let's also change the direction reference frame from J2000 to Galactic:
# In CASA
imhead(imagename='SNR_G55_10s.ms.MFS.wProj.image.tt0', mode='put', hdkey='equinox', hdvalue='GALACTIC')
-- original: Miriam Hutman
--modifications: Lorant Sjouwerman (4.4.0, 2015/07/07)
--modifications: Jose Salcido (4.5.2, 2016/02/24)
Last checked on CASA Version 4.5.3