M100 Band3 Combine 4.3: Difference between revisions
| Line 165: | Line 165: | ||
CASA 4.3.1 initially scales the weights by 2Δν<sub>ch</sub>Δt<sub>ij</sub>, and after the Tsys table applycal step of the calibration process, it further scales the weights by 1/[(Tsys(i) * Tsys(j)] as long as calwt=True. In the subsequent amplitude gain calibration table applycal step of the calibration, the weights are further scaled by a factor of [gain(i)<sup>2</sup> * gain(j)<sup>2</sup>] if calwt=True. This step up-weights data from the best performing antennas from the gain point of view, and importantly for data combination, makes the weights correctly proportional to the antenna size. | CASA 4.3.1 initially scales the weights by 2Δν<sub>ch</sub>Δt<sub>ij</sub>, and after the Tsys table applycal step of the calibration process, it further scales the weights by 1/[(Tsys(i) * Tsys(j)] as long as calwt=True. In the subsequent amplitude gain calibration table applycal step of the calibration, the weights are further scaled by a factor of [gain(i)<sup>2</sup> * gain(j)<sup>2</sup>] if calwt=True. This step up-weights data from the best performing antennas from the gain point of view, and importantly for data combination, makes the weights correctly proportional to the antenna size. | ||
In the calibration scripts for all executions of the 12m and 7m data, found (here), both applycal steps set calwt=True. To verify that the weights come out as expected, we plot the weights of the 7m and 12m data and measure their ratio to be, on average, 7m/12m ~ 0.055/0.3 ~ 0.18. Note that in the plots the points are colored by SPW, so there is only one 12m CO SPW but there are two 7m CO SPWs, and that no averaging can be turned on when plotting the weights. | |||
<source lang="python"> | <source lang="python"> | ||
Revision as of 20:01, 27 July 2015
Overview
This guide describes how to combine the 7m and 12m interferometric data and then how to feather the resulting image with the total power TP image. All of the data for this SV project can be found at https://almascience.nrao.edu/alma-data/science-verification. The guide has been written for data reduced in CASA 4.3.0 and assumes that all calibration tables (Tsys and gain tables) have been applied to the visibility weights using calwt=True. If either of these is not the case for your data, do not follow this guide.
In order to run this guide you will need the following three files:
- 12m array calibrated data: M100_Band3_12m_CalibratedData.ms
- 7m array calibrated data: M100_Band3_7m_CalibratedData.ms
- Total Power image: M100_TP_CO_cube.bl.image
To obtain the fully calibrated 12m data M100_Band3_12m_CalibratedData.ms, either download the file M100_Band3_12m_CalibratedData.tgz or download the uncalibrated 12m data (M100_Band3_12m_UnalibratedData.tgz) and execute the calibration scripts (M100_Band3_12m_CalibrationScripts.tgz). How to obtain the data is described in M100_Band3#Obtaining the Data. An overview of the 12m data and its calibration is located at M100_Band3.
WARNING: Note that the imaging presented in this Guide uses the new calibration (using CASA 4.3) of the same 12-m array data that were released previously (using CASA 3.3). Do not use the previously released CASA 3.3 version of the calibrated 12-m data (either downloaded before 28 July 2015 or identified by the suffix "_CASA3.3" after 28 July 2015) for this tutorial.
To obtain the fully calibrated 7m data M100_Band3_7m_CalibratedData.ms, either download the file M100_Band3_7m_CalibratedData.tgz or download the uncalibrated 7m data (M100_Band3_7m_UnalibratedData.tgz) and execute the calibration scripts (M100_Band3_7m_CalibrationScripts.tgz). How to obtain the data is described in M100_Band3#Obtaining the Data. An overview of the 7m data and its calibration is located at M100_Band3.
To obtain the Total Power image M100_TP_CO_cube.bl.image, either run the M100_Band3_SingleDish_4.3 guide to calibrate and image the Total Power data or download the image file from M100_TP_ReferenceImages.tgz. How to obtain the data is described in M100_Band3#Obtaining the Data. An overview of the Total Power data and its calibration is located at M100_Band3.
Confirm your version of CASA
This guide has been written for CASA release 4.3.0. Please confirm your version before proceeding.
# In CASA
version = casadef.casa_version
print "You are using " + version
if (version < '4.3.0'):
print "YOUR VERSION OF CASA IS TOO OLD FOR THIS GUIDE."
print "PLEASE UPDATE IT BEFORE PROCEEDING."
else:
print "Your version of CASA is appropriate for this guide."
Combine and Image the 7m+12m Interferometric Data
Split off CO spectral windows (SPWs)
# In CASA
os.system('rm -rf m100_*m.ms.listobs')
listobs('M100_Band3_12m_CalibratedData.ms',listfile='M100_12m.ms.listobs')
listobs('M100_Band3_7m_CalibratedData.ms',listfile='M100_7m.ms.listobs')
Running the task "listobs" provides the setups used in the observations at a glance. Below are the first target scans of the 12m and 7m observations and the spectral window tables as generated by listobs; these are excerpts from the complete files obtained in each case. Notice that the six 7m data sets were taken with two slightly different correlator setups (one with four SPWs and the other with two SPWs), so the concatenated data set has six total SPWs.
12m data:
ObservationID = 0 ArrayID = 0 Date Timerange (UTC) Scan FldId FieldName nRows SpwIds Average Interval(s) ScanIntent 10-Aug-2011/19:38:05.8 - 19:50:22.8 11 1 M100 1500 [0,1,2,3] [6.05, 6.05, 6.05, 6.05] [CALIBRATE_WVR#ON_SOURCE,OBSERVE_TARGET#ON_SOURCE] Spectral Windows: (4 unique spectral windows and 1 unique polarization setups) SpwID Name #Chans Frame Ch0(MHz) ChanWid(kHz) TotBW(kHz) CtrFreq(MHz) BBC Num Corrs 0 3840 TOPO 113726.419 488.281 1875000.0 114663.6750 1 XX YY 1 3840 TOPO 111851.419 488.281 1875000.0 112788.6750 2 XX YY 2 3840 TOPO 103663.431 -488.281 1875000.0 102726.1750 3 XX YY 3 3840 TOPO 101850.931 -488.281 1875000.0 100913.6750 4 XX YY
7m data:
ObservationID = 0 ArrayID = 0 Date Timerange (UTC) Scan FldId FieldName nRows SpwIds Average Interval(s) ScanIntent 17-Mar-2013/04:44:04.3 - 04:50:43.7 11 1 M100 261 [0,1,2,3] [10.1, 10.1, 10.1, 10.1] [OBSERVE_TARGET#ON_SOURCE] Spectral Windows: (6 unique spectral windows and 1 unique polarization setups) SpwID Name #Chans Frame Ch0(MHz) ChanWid(kHz) TotBW(kHz) CtrFreq(MHz) BBC Num Corrs 0 ALMA_RB_03#BB_1#SW-01#FULL_RES 4080 TOPO 101945.850 -488.281 1992187.5 100950.0000 1 XX YY 1 ALMA_RB_03#BB_2#SW-01#FULL_RES 4080 TOPO 103761.000 -488.281 1992187.5 102765.1500 2 XX YY 2 ALMA_RB_03#BB_3#SW-01#FULL_RES 4080 TOPO 111811.300 488.281 1992187.5 112807.1500 3 XX YY 3 ALMA_RB_03#BB_4#SW-01#FULL_RES 4080 TOPO 113686.300 488.281 1992187.5 114682.1500 4 XX YY 4 ALMA_RB_03#BB_1#SW-01#FULL_RES 4080 TOPO 111798.250 488.281 1992187.5 112794.1000 1 XX YY 5 ALMA_RB_03#BB_2#SW-01#FULL_RES 4080 TOPO 113673.250 488.281 1992187.5 114669.1000 2 XX YY
<figure id="12m_mosaic.png">
</figure>
<figure id="7m_mosaic.png">
</figure>
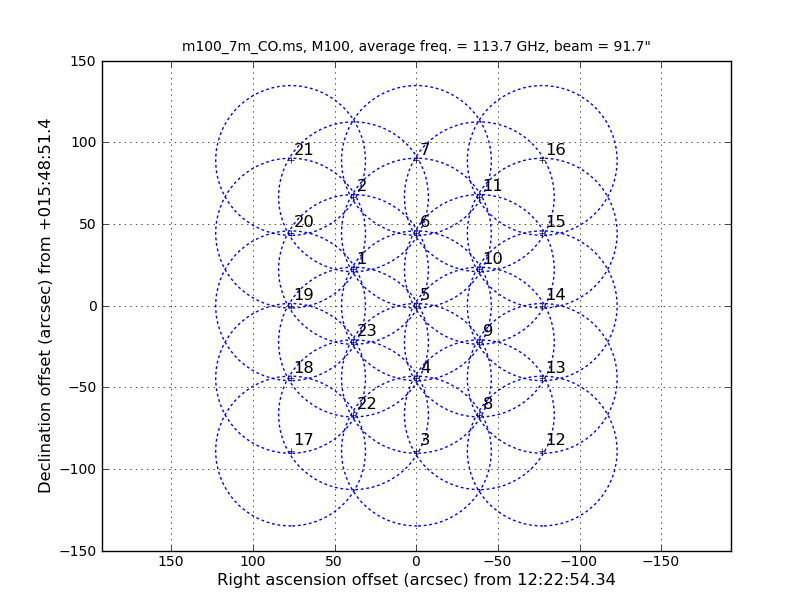
Examination of the listobs files shows that the CO is in SPW='0' for the 12m data and in SPW='3,5' for the 7m data. There are two SPWs containing CO in the 7m data due to the slightly differing correlator setups.
Also note that the integration time per visibility (average interval parameter in listobs) is different: 6.05s for the 12m data and 10.1s for the 7m. This will be important to know later when we check the visibility weights.
Next we split out the CO spectral windows.
# In CASA
os.system('rm -rf M100_12m_CO.ms')
split(vis='M100_Band3_12m_CalibratedData.ms',
outputvis='M100_12m_CO.ms',spw='0',field='M100',
datacolumn='data',keepflags=False)
os.system('rm -rf M100_7m_CO.ms')
split(vis='M100_Band3_7m_CalibratedData.ms',
outputvis='M100_7m_CO.ms',spw='3,5',field='M100',
datacolumn='data',keepflags=False)
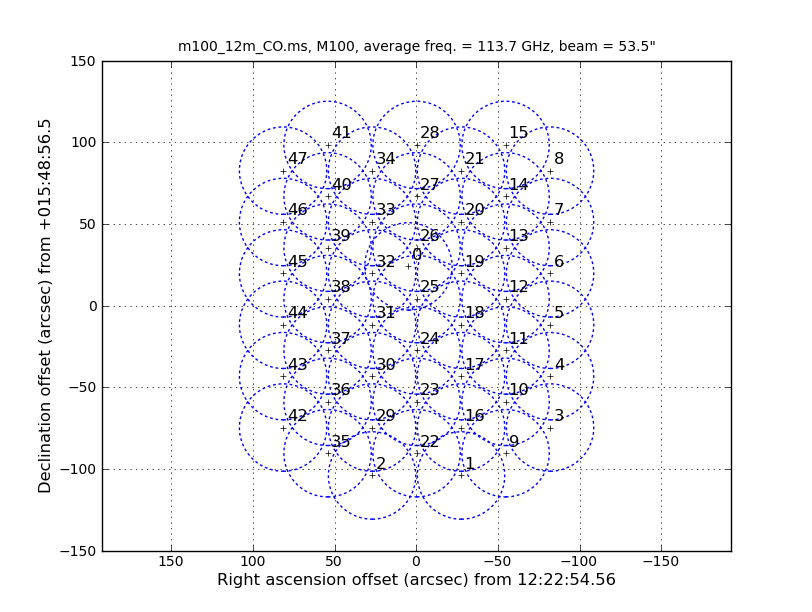
Also of interest is that the 12m data has 47 fields and the 7m has 23 fields (not shown in the excerpts above). The difference in number of pointings is because the 7m antennas have a FWHP (full width half power) primary beam diameter that is 12/7 times larger than the 12m antennas. One easy way to see how the mosaics compare is to install the AnalysisUtils package (see Analysis_Utilities for information on how to download and import AnalysisUtils). Then with AnalysisUtils you can make the following plots (look at the listobs to obtain the sourceid):
# In CASA
os.system('rm -rf *m_mosaic.png')
au.plotmosaic('M100_12m_CO.ms',sourceid='0',figfile='12m_mosaic.png')
au.plotmosaic('M100_7m_CO.ms',sourceid='0',figfile='7m_mosaic.png')
We see that the mosaics cover a common area but that the 7m mosaic is a bit larger. This means that the outer edges of the combined mosaic will be noisier than expected if they overlapped perfectly; this is just something to keep in mind. If you had the case where the mosaic coverages are dramatically different, it would be best to exclude the completely non-overlapping fields from the combination.
NOTE: At this stage one would typically do continuum subtraction (if there is any). However we already know from the individual data reductions that the 3mm continuum emission is quite weak and does not significantly contribute to a 5km/s channel, so we will forgo the the continuum subtraction step. Examples of how to do this if you are so inclined are located in various other ALMA CASAguides.
Checking the weights and concatenating the data
<figure id="7m_WT.png">
</figure>
<figure id="12m_WT.png">
</figure>
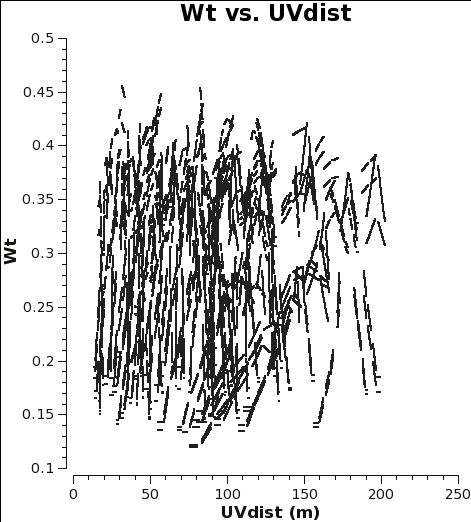
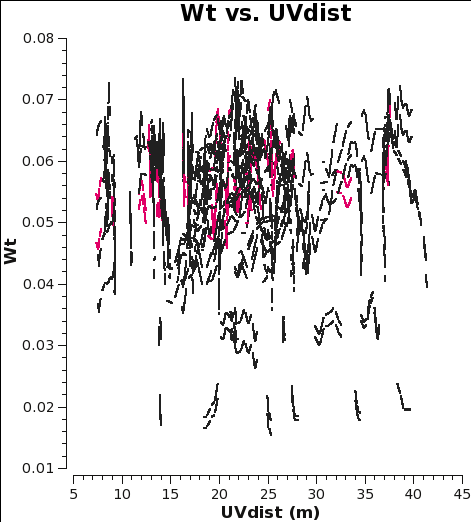
When combining data with disparate properties it is very important that the relative weights of each visibility be in the correct proportion to the other data according to the radiometer equation. Formally, the visibility weights should be proportional to 1/sigma2 where sigma is the variance or rms noise of a given visibility.
The rms noise in a single channel for a single visibility is:
[math]\displaystyle{ \sigma_{ij} (Jy) =\frac{2k}{\eta_{q}\eta_{c}A_{eff}} }[/math] [math]\displaystyle{ \sqrt{\frac{T_{sys,i} T_{sys,j}}{2\Delta\nu_{ch} t_{ij}}} }[/math] [math]\displaystyle{ \times 10^{26}, }[/math]
where:
k is Boltzmann's constant.
Aeff is the effective antenna area which is equal to the aperture efficiency x the geometric area of the antenna. The aperture efficiency depends on the rms antenna surface accuracy.
ηq and ηc are the quantization and correlator efficiencies, respectively. These have values near 1 and will be ignored for the purposes of this casaguide, but see the ALMA Technical Handbook for more information.
Tsys,i is the system temperature for antenna i, and Tsys,j is the system temperature for antenna j
Δνch is the channel frequency width.
tij is the integration time per visibility.
CASA 4.3.1 initially scales the weights by 2ΔνchΔtij, and after the Tsys table applycal step of the calibration process, it further scales the weights by 1/[(Tsys(i) * Tsys(j)] as long as calwt=True. In the subsequent amplitude gain calibration table applycal step of the calibration, the weights are further scaled by a factor of [gain(i)2 * gain(j)2] if calwt=True. This step up-weights data from the best performing antennas from the gain point of view, and importantly for data combination, makes the weights correctly proportional to the antenna size.
In the calibration scripts for all executions of the 12m and 7m data, found (here), both applycal steps set calwt=True. To verify that the weights come out as expected, we plot the weights of the 7m and 12m data and measure their ratio to be, on average, 7m/12m ~ 0.055/0.3 ~ 0.18. Note that in the plots the points are colored by SPW, so there is only one 12m CO SPW but there are two 7m CO SPWs, and that no averaging can be turned on when plotting the weights.
# In CASA
os.system('rm -rf 7m_WT.png 12m_WT.png')
plotms(vis='M100_12m_CO.ms',yaxis='wt',xaxis='uvdist',spw='0:200',
coloraxis='spw',plotfile='12m_WT.png')
#
plotms(vis='M100_7m_CO.ms',yaxis='wt',xaxis='uvdist',spw='0~1:200',
coloraxis='spw',plotfile='7m_WT.png')
<figure id="combine_CO_WT.png">
</figure>
The two key things that are different between the 7m and 12m-array data are that the effective dish areas are different by (7/12)2, and the integration times are different by (10.1/6.05). Since the dish area and the integration time per visibility are in the denominator of the radiometer equation, and assuming the weight of an individual visibility is proportional to 1/sigma2, the ratio of the weights should be (7./12.)4 x (10.1/6.05) = 0.19. This is very close to the value we measure for the ratio of the weights, particularly given that the 7m flux calibration relied on a source which changed substantially over the course of the six 7m-array observations.
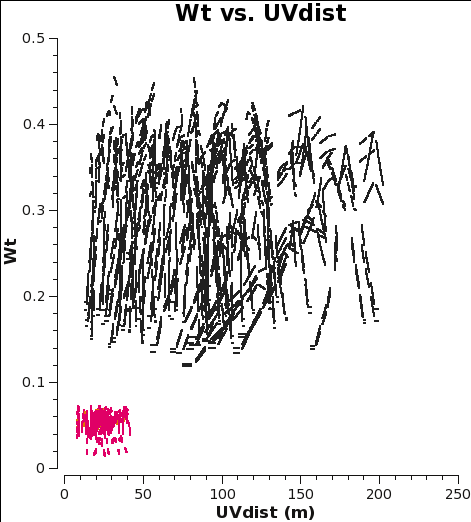
Now concatenate the two data sets and plot the concatenated weights to verify that they are as expected.
# In CASA
# Concat and scale weights
os.system('rm -rf M100_combine_CO.ms')
concat(vis=['M100_12m_CO.ms','M100_7m_CO.ms'],
concatvis='M100_combine_CO.ms')
# In CASA
os.system('rm -rf combine_CO_WT.png')
plotms(vis='M100_combine_CO.ms',yaxis='wt',xaxis='uvdist',spw='0~2:200',
coloraxis='spw',plotfile='combine_CO_WT.png')
Here, we create more instructive plots of the combined data to check that things are in order. (Let each plot finish before cutting and pasting next plot. If plotms gui disappears, exit CASA and restart.)
<figure id="M100_combine_vel.png">
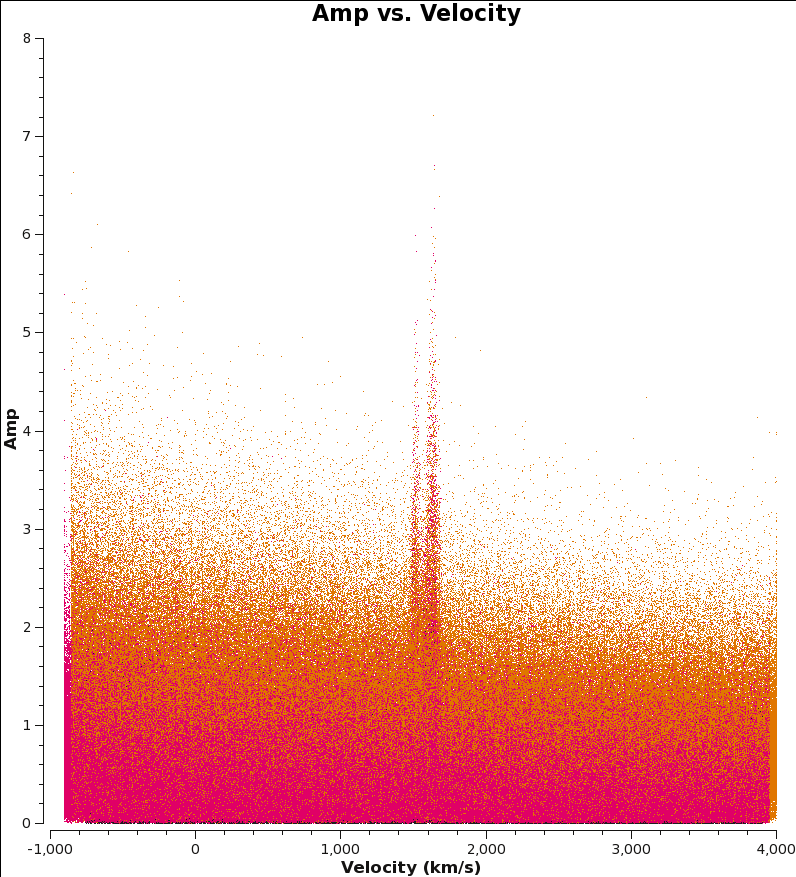
</figure>
One way to assess the relative noise in the combined data is to plot amplitude as a function of uv-distance. Here, it's clear that the 7m data is noisier than the 12m data (note also that this plot is not shown):
# In CASA
os.system('rm -rf M100_combine_uvdist.png')
plotms(vis='M100_combine_CO.ms',yaxis='amp',xaxis='uvdist',spw='', avgscan=True,
avgchannel='5000', coloraxis='spw',plotfile='M100_combine_uvdist.png')
A fairer comparison of these data is achieved by isolating the brightest line channels in individual 12m and 7m data sets (i.e., not the concatenated data sets) and comparing only those channels in amplitude vs. uv-distance. Here the agreement is better, as it is less dominated by the scatter among the several 7m executions.
To plot the CO line as a function of velocity (this plot takes a while):
# In CASA
os.system('rm -rf M100_combine_vel.png')
plotms(vis='M100_combine_CO.ms',yaxis='amp',xaxis='velocity',spw='', avgtime='1e8',avgscan=True,coloraxis='spw',avgchannel='5',
transform=True,freqframe='LSRK',restfreq='115.271201800GHz', plotfile='M100_combine_vel.png')
To see each spectral window independently in plotms, run the command again but remove the call to "plotfile" and add " iteraxis='spw' ".
Image Using An Automasking Technique
The commands in this section perform an iterative automasking procedure down to a user specified threshold=stop*rms where stop is typically 2-3 using the imagemode='mosaic' mode of clean. This mode automatically calculates the correct convolution of the primary beam response of the mosaic when different antenna dish diameters are present. NOTE: even if these data had only been comprised of a single pointing of 7m and 12m-array data, the imagemode='mosaic' mode would be needed to correctly image data with different antenna sizes.
The procedure outlined below takes some care to ensure that the generated masks (i) only have values of 0 or 1; (ii) are themselves masked at the minpb level. It also removes very small masked regions that are consistent with noise bumps using a function in scipy. A typical setting is to remove mask regions that are 1/2 the beam area in pixels. This is one technique under exploration for future pipeline use.
The commands have been split into multiple sections to aid cut and paste. Wait until the current one is done before starting next section. If you stop CASA and restart you will need to cut and paste again from the Define Parameters section on down.
When there is a long series of commands below, it is important to include the beginning cpaste and ending -- in your cut and paste.
Define Parameters
Note that the parameters used here are by design the same as those used to make the stand-alone 7m-array and 12m-array images.
# In CASA
### Initialize
import scipy.ndimage
### Define clean parameters
vis='M100_combine_CO.ms'
prename='M100_combine_CO_cube'
myimage=prename+'.image'
myflux=prename+'.flux'
mymask=prename+'.mask'
myresidual=prename+'.residual'
imsize=800
cell='0.5arcsec'
minpb=0.2
restfreq='115.271201800GHz'
outframe='LSRK'
spw='0~2'
width='5km/s'
start='1400km/s'
nchan=70
robust=0.5
phasecenter='J2000 12h22m54.9 +15d49m15'
scales=[0]
smallscalebias=0.6
### Setup stopping criteria with multiplier for rms.
stop=3.
### Minimum size multiplier for beam area for removing very small mask regions.
pixelmin=0.5
Make Initial Dirty Image and Determine Synthesized Beam area
The dirty image is used to determine the initial peak flux density in the cube and the beam area is used to define the minimum size of masked regions in order to exclude noise bumps from the overall mask.
# In CASA
### Make initial dirty image
os.system('rm -rf '+prename+'.* ' +prename+'_*')
clean(vis=vis,imagename=prename,
imagermode='mosaic',ftmachine='mosaic',minpb=minpb,
imsize=imsize,cell=cell,spw=spw,
weighting='briggs',robust=robust,phasecenter=phasecenter,
mode='velocity',width=width,start=start,nchan=nchan,
restfreq=restfreq,outframe=outframe,veltype='radio',
mask='',
niter=0,interactive=F)
# Determine the beam area in pixels for later removal of very small mask regions
major=imhead(imagename=myimage,mode='get',hdkey='beammajor')['value']
minor=imhead(imagename=myimage,mode='get',hdkey='beamminor')['value']
pixelsize=float(cell.split('arcsec')[0])
beamarea=(major*minor*pi/(4*log(2)))/(pixelsize**2)
print 'beamarea in pixels =', beamarea
Find properties of the dirty image
# In CASA
### Find the peak in the dirty cube.
myimage=prename+'.image'
bigstat=imstat(imagename=myimage)
peak= bigstat['max'][0]
print 'peak (Jy/beam) in cube = '+str(peak)
### Sets threshold of first loop, try 2-4. Subsequent loops are set thresh/2.
thresh = peak / 4.
### If True: find the rms in two line-free channels; If False: Set rms by hand in else statement.
if True:
chanstat=imstat(imagename=myimage,chans='4')
rms1= chanstat['rms'][0]
chanstat=imstat(imagename=myimage,chans='66')
rms2= chanstat['rms'][0]
rms=0.5*(rms1+rms2)
else:
rms=0.011
print 'rms (Jy/beam) in a channel = '+str(rms)
Automasking Loop
On a reasonably fast computer the following will take a couple of hours for this spectral mosaic. For the long series of commands below it is important to include the beginning cpaste and ending -- in your cut and paste.
# In CASA
os.system('rm -rf ' + prename +'_threshmask*')
os.system('rm -rf ' + prename +'_fullmask*')
os.system('rm -rf ' + prename +'.image*')
n=-1
while (thresh >= stop*rms):
n=n+1
print 'clean threshold this loop is', thresh
threshmask = prename+'_threshmask' +str(n)
maskim = prename+'_fullmask' +str(n)
immath(imagename = [myresidual],
outfile = threshmask,
expr = 'iif(IM0 > '+str(thresh) +',1.0,0.0)',
mask=myflux+'>'+str(minpb))
if (n==0):
os.system('cp -r '+threshmask+' '+maskim+'.pb')
print 'This is the first loop'
else:
makemask(mode='copy',inpimage=myimage,
inpmask=[threshmask,mymask],
output=maskim)
imsubimage(imagename=maskim, mask=myflux+'>'+str(minpb),
outfile=maskim+'.pb')
print 'Combined mask ' +maskim+' generated.'
# Remove small masks
os.system('cp -r '+maskim+'.pb ' +maskim+'.pb.min')
maskfile=maskim+'.pb.min'
ia.open(maskfile)
mask=ia.getchunk()
labeled,j=scipy.ndimage.label(mask)
myhistogram = scipy.ndimage.measurements.histogram(labeled,0,j+1,j+1)
object_slices = scipy.ndimage.find_objects(labeled)
threshold=beamarea*pixelmin
for i in range(j):
if myhistogram[i+1]<threshold:
mask[object_slices[i]] = 0
ia.putchunk(mask)
ia.done()
print 'Small masks removed and ' +maskim +'.pb.min generated.'
os.system('rm -rf '+mymask+'')
clean(vis=vis,imagename=prename,
imagermode='mosaic',ftmachine='mosaic',minpb=minpb,
imsize=imsize,cell=cell,spw=spw,
weighting='briggs',robust=robust,phasecenter=phasecenter,
mode='velocity',width=width,start=start,nchan=nchan,
restfreq=restfreq,outframe=outframe,veltype='radio',
mask = maskim+'.pb.min',
multiscale=scales,smallscalebias=smallscalebias,
interactive = F,
niter = 10000,
threshold = str(thresh) +'Jy/beam')
if thresh==stop*rms: break
thresh = thresh/2.
# Run a final time with stop*rms if more than a little above
# stop*rms. Also make a back-up of next to last image
if (thresh < stop*rms and thresh*2.>1.05*stop*rms):
thresh=stop*rms
os.system('cp -r '+myimage+' '+myimage+str(n))
Notes on the Automasking procedure
This script is meant to be a possible stepping stone to optimal automasking -- it is by no means perfect and is certainly slower than optimal but feel free to try it with other datasets. Some notes below:
In addition to the final prename.image (prename.flux etc) this script produces and keeps each iteration of the various mask files which will allow you to explore how the masking proceeded as the threshold for masking and cleaning was lowered. The ones denoted "prename. fullmask*.pb.min" are the ones used in the clean steps themselves. At the end of the process the final "prename. fullmask*.pb.min" will also be stored in the prename.mask. Once you've verified you are happy with the masking, you may want to remove the prename.threshmask* and prename.fullmask* files, as they can be large for large cubes.
Additionally, before running the final loop with thresh=stop*rms the script copies the .image from the preceding clean to prename.image'n' where 'n' equals the loop number of the preceding step. So in this M100 example you will see a M100_combine_cube.image and a M100_combine_cube.image2 where .image is the final image and .image2 is the next to last image. This is done for convenience in the case that thresh=stop*rms is too deep such that clean diverges, you will still be left with the clean image from the preceding loop that you can further investigate to understand why clean diverged. If all goes well with the final loop, the prename.image'n' can also be deleted. Divergence at thresh=stop*rms is often a sign that the image is "dynamic range limited" in other words the rms in channels with bright emission is significantly worse than for a line-free channel.
Image Analysis for the 7m+12m Data
Moment Maps for 7m+12m CO (1-0) Cube
Start by examining the final image cube. Determine the start and stopping channels for the line emission -- this will be used in the "chans" parameter of immoments.
# In CASA
viewer('M100_combine_CO_cube.image')
Next determine the rms noise per channel and use that to exclude pixels from the moment images. All images are shown in the gallery at the end of the following section.
# In CASA
myimage='M100_combine_CO_cube.image'
chanstat=imstat(imagename=myimage,chans='4')
rms1= chanstat['rms'][0]
chanstat=imstat(imagename=myimage,chans='66')
rms2= chanstat['rms'][0]
rms=0.5*(rms1+rms2)
print 'rms in a channel = '+str(rms)
Next make the moment maps. For the integrated intensity: moment 0, a 2 sigma cut often considerably improves the appearance of the image with little effect on the integrated intensity as long as emission free channels are excluded. For higher order moments it is necessary to exclude all low S/N data. Typically 5-6 sigma for the higher moments works well. We also apply further masking based on the .flux image because the edges of the combined mosaic are especially noisy because the 7m mosaic is somewhat larger than the 12m mosaic as described above (see Figures 1 & 2).
# In CASA
os.system('rm -rf M100_combine_CO_cube.image.mom0')
immoments(imagename = 'M100_combine_CO_cube.image',
moments = [0],
axis = 'spectral',chans = '9~61',
mask='M100_combine_CO_cube.flux>0.3',
includepix = [rms*2,100.],
outfile = 'M100_combine_CO_cube.image.mom0')
os.system('rm -rf M100_combine_CO_cube.image.mom1')
immoments(imagename = 'M100_combine_CO_cube.image',
moments = [1],
axis = 'spectral',chans = '9~61',
mask='M100_combine_CO_cube.flux>0.3',
includepix = [rms*5.5,100.],
outfile = 'M100_combine_cube.image.mom1')
Now we can make some figures showing the moment maps:
# In CASA
os.system('rm -rf M100_combine_CO_cube.image.mom*.png')
imview (raster=[{'file': 'M100_combine_CO_cube.image.mom0',
'range': [-0.3,25.],'scaling': -1.3,'colorwedge': T}],
zoom={'blc': [190,150],'trc': [650,610]},
out='M100_combine_CO_cube.image.mom0.png')
imview (raster=[{'file': 'M100_combine_CO_cube.image.mom1',
'range': [1440,1695],'colorwedge': T}],
zoom={'blc': [190,150],'trc': [650,610]},
out='M100_combine_CO_cube.image.mom1.png')
If you plan to use your moment 0 image to make measurements, it needs to be primary beam corrected first. First we need to subimage the .flux cube to extract a single plane that can be used to primary beam correct the moment 0 image.
# In CASA
os.system('rm -rf M100_combine_CO_cube.flux.1ch')
imsubimage(imagename='M100_combine_CO_cube.flux',
outfile='M100_combine_CO_cube.flux.1ch',
chans='35')
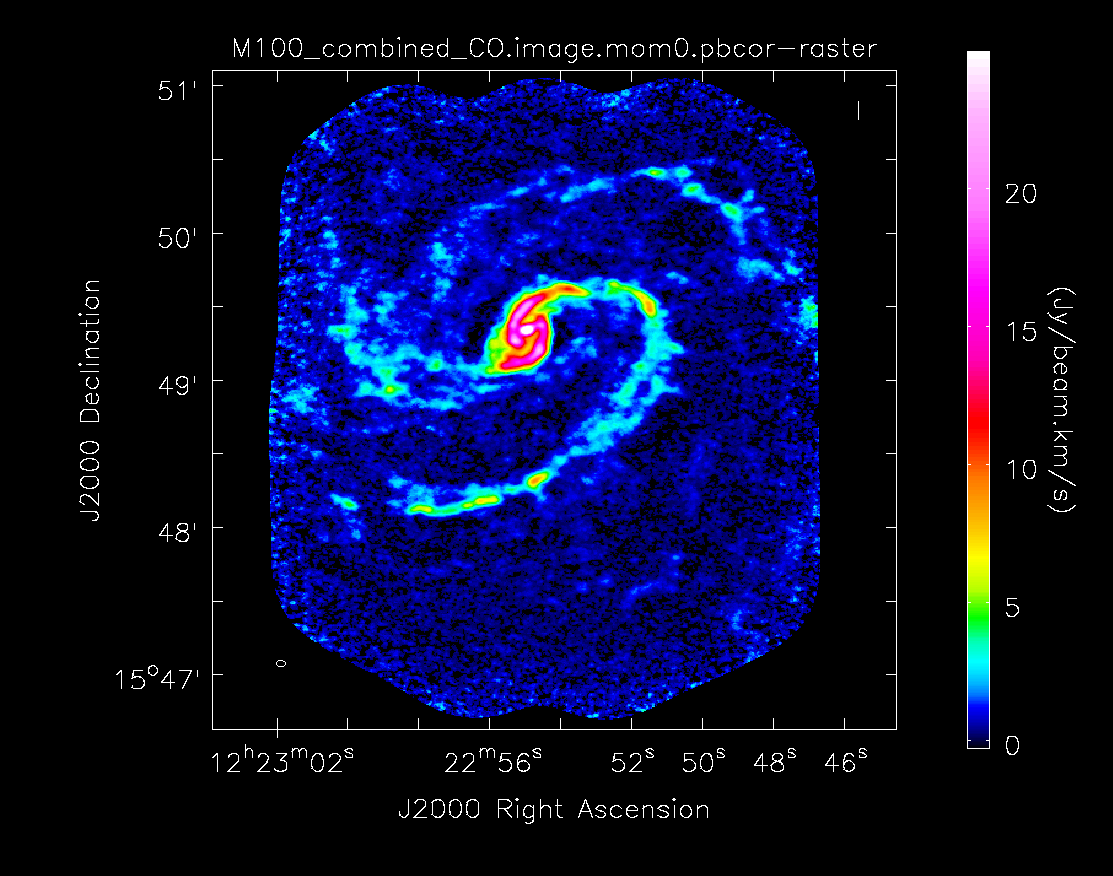
Next, primary beam correct the moment 0 image. This is the version that would be used for measurements, though the uncorrected one can be useful for figures. The difference is clear in the images seen below in the following section.
# In CASA
os.system('rm -rf M100_combine_CO_cube.image.mom0.pbcor')
immath(imagename=['M100_combine_CO_cube.image.mom0', \
'M100_combine_CO_cube.flux.1ch'],
expr='IM0/IM1',
outfile='M100_combine_CO_cube.image.mom0.pbcor')
Have a look at the difference the primary beam correction makes.
# In CASA
imview (raster=[{'file': 'M100_combine_CO_cube.image.mom0',
'range': [-0.3,25.],'scaling': -1.3},
{'file': 'M100_combine_CO_cube.image.mom0.pbcor',
'range': [-0.3,25.],'scaling': -1.3}],
zoom={'blc': [190,150],'trc': [650,610]})
With the viewer open, you can flip back and forth between the images to compare them. Next, make a figure.
# In CASA
os.system('rm -rf M100_combine_CO_cube.image.mom0.pbcor.png')
imview (raster=[{'file': 'M100_combine_CO_cube.image.mom0.pbcor',
'range': [-0.3,25.],'scaling': -1.3,'colorwedge': T}],
zoom={'blc': [190,150],'trc': [650,610]},
out='M100_combine_CO_cube.image.mom0.pbcor.png')
Comparison with 7m, 12m Moment Maps
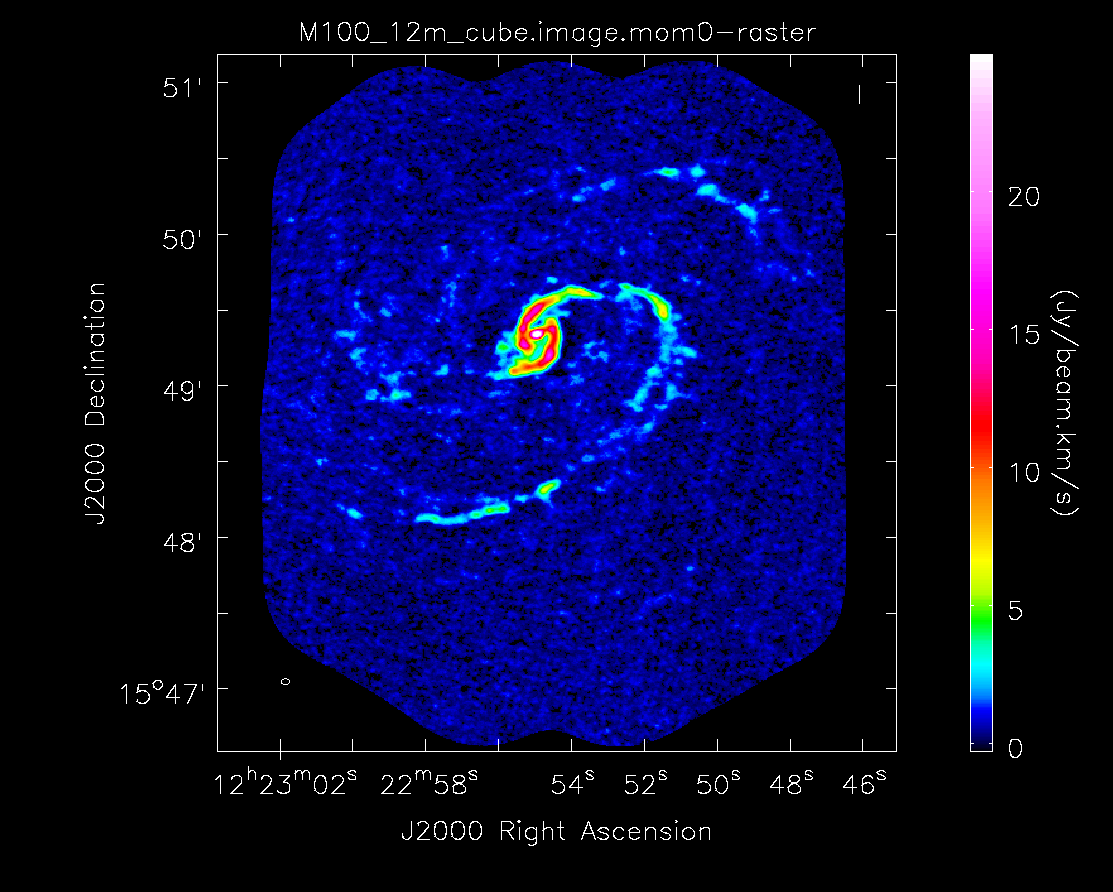
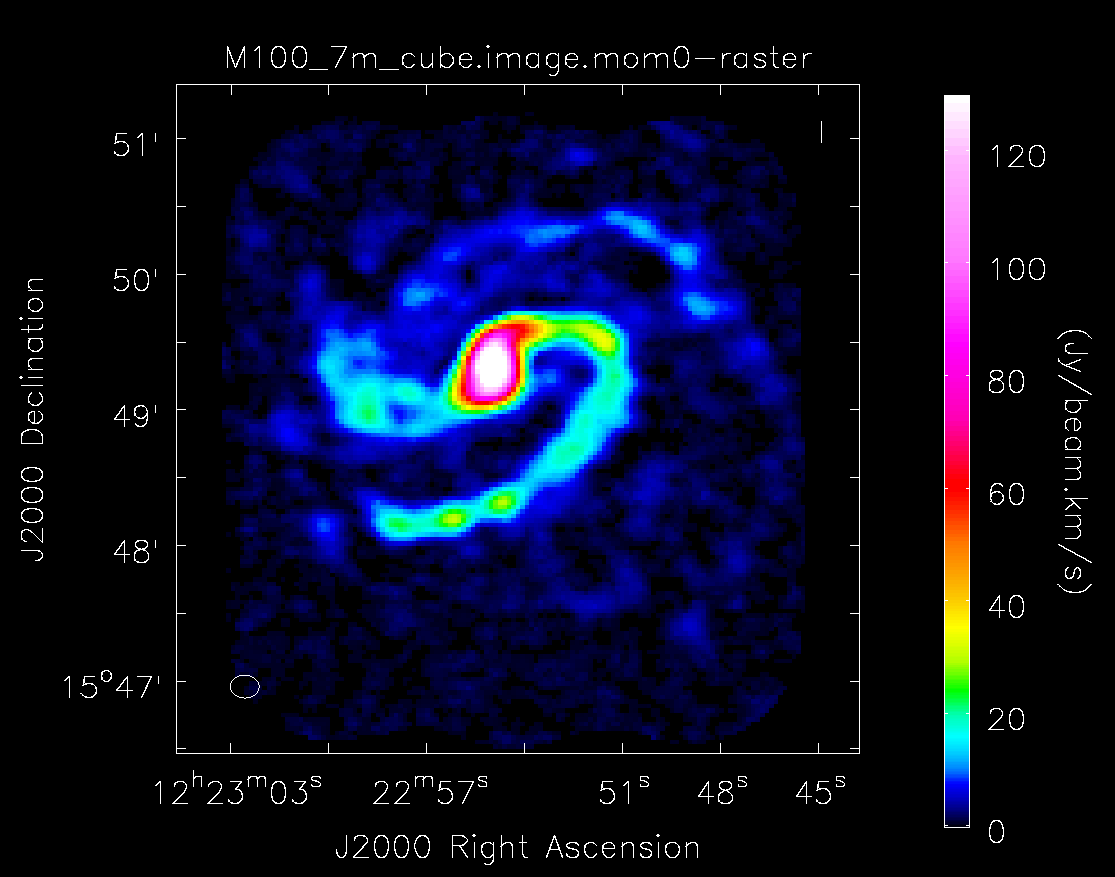
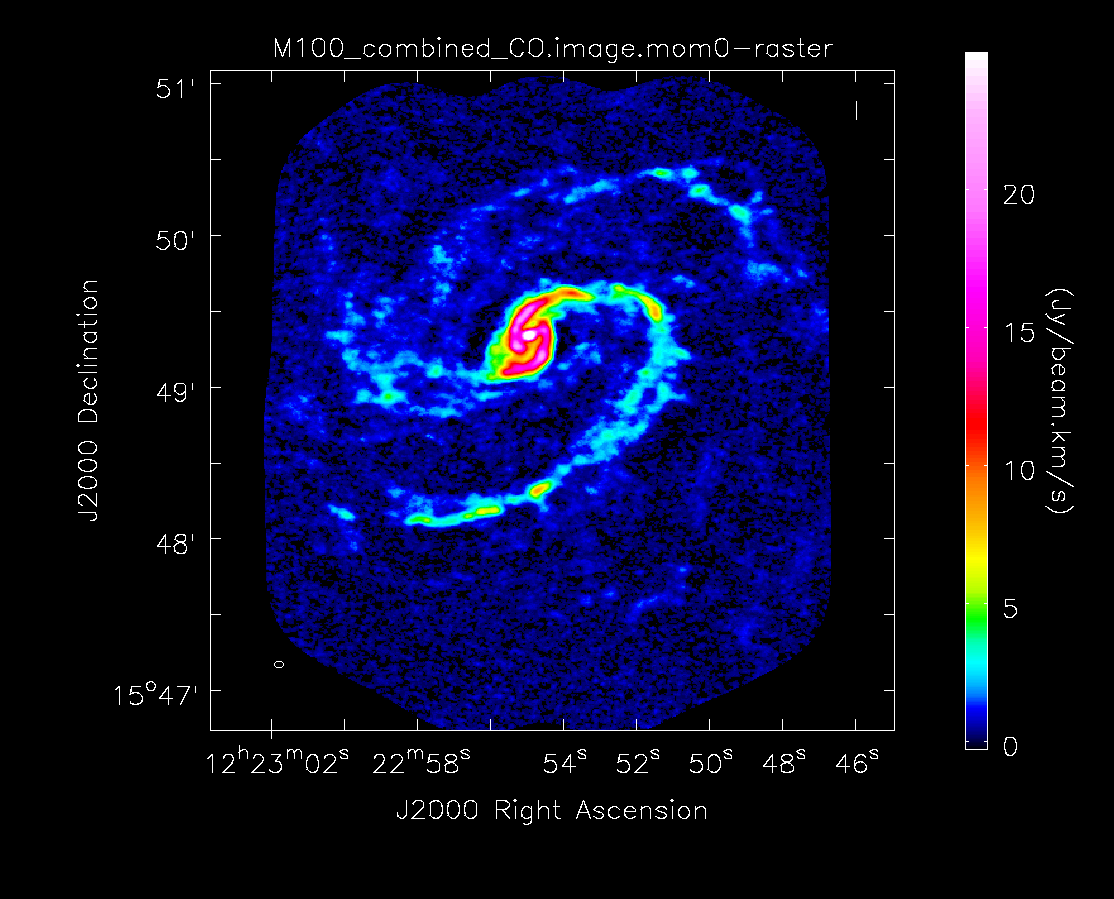
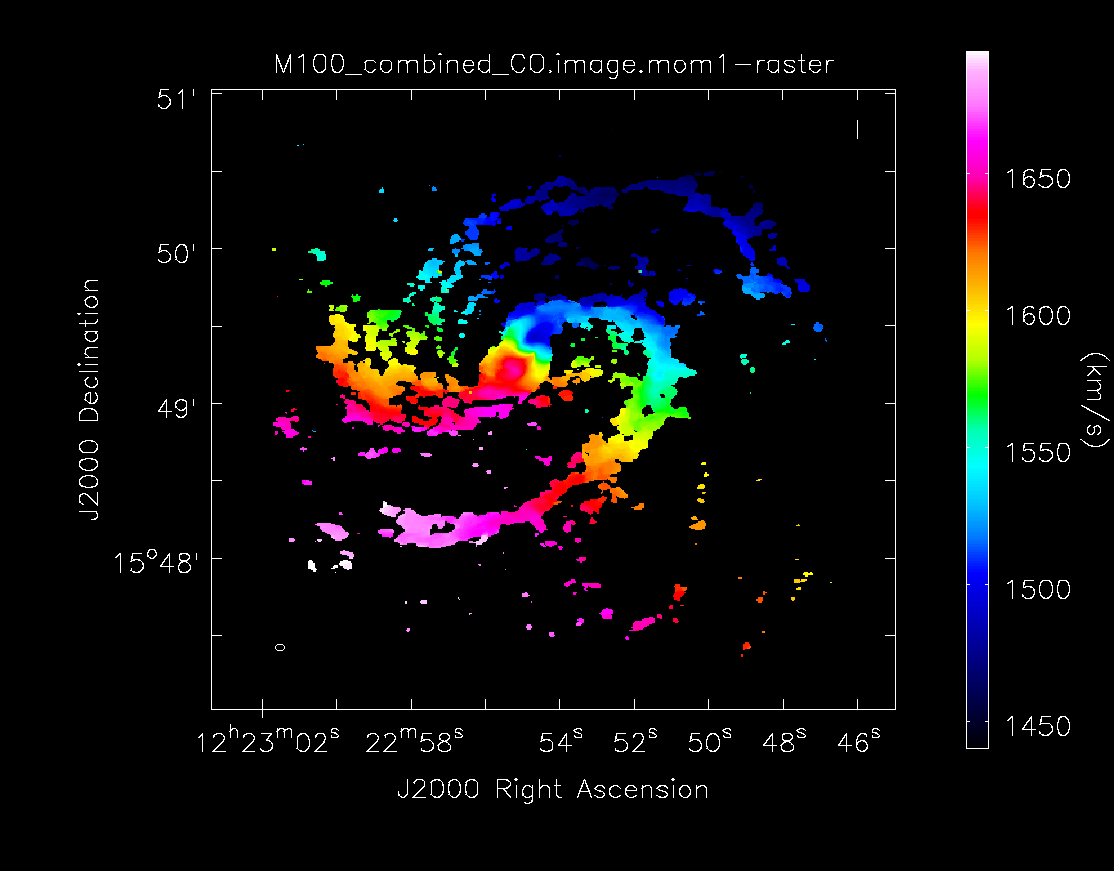
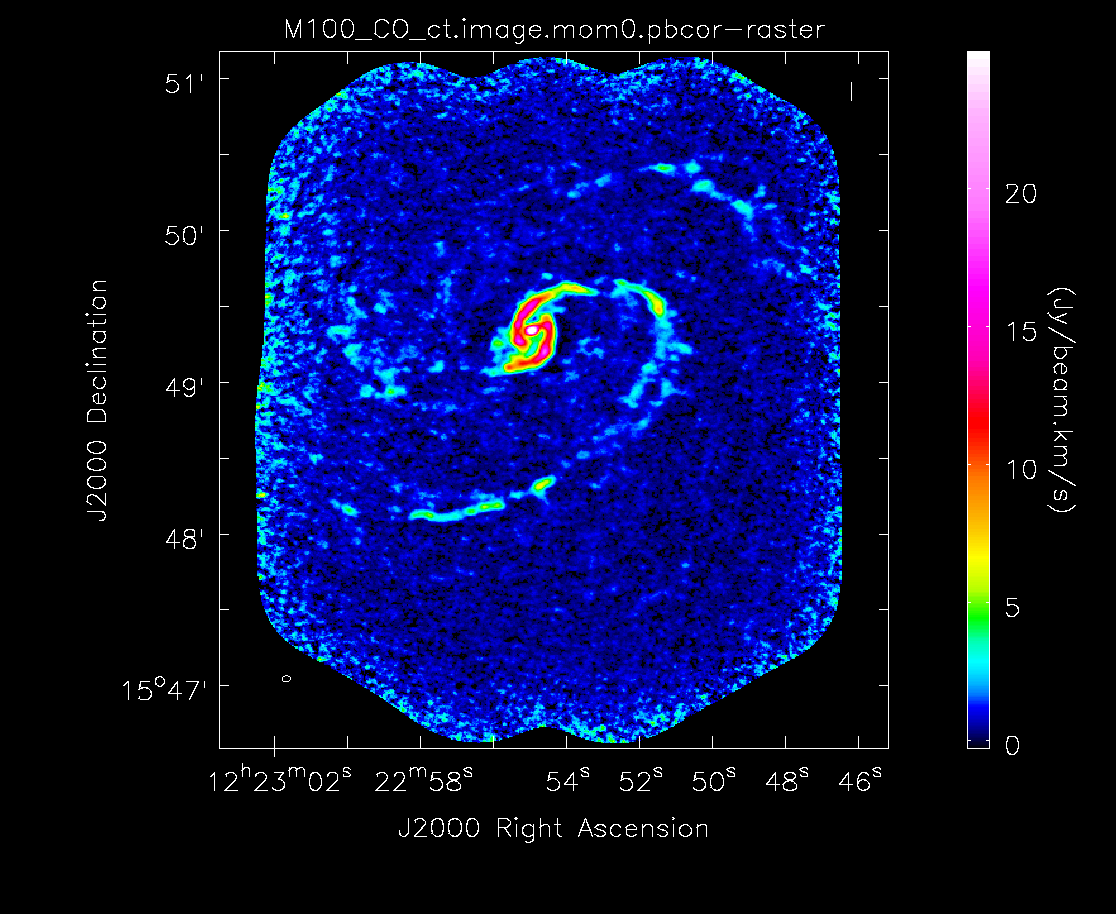
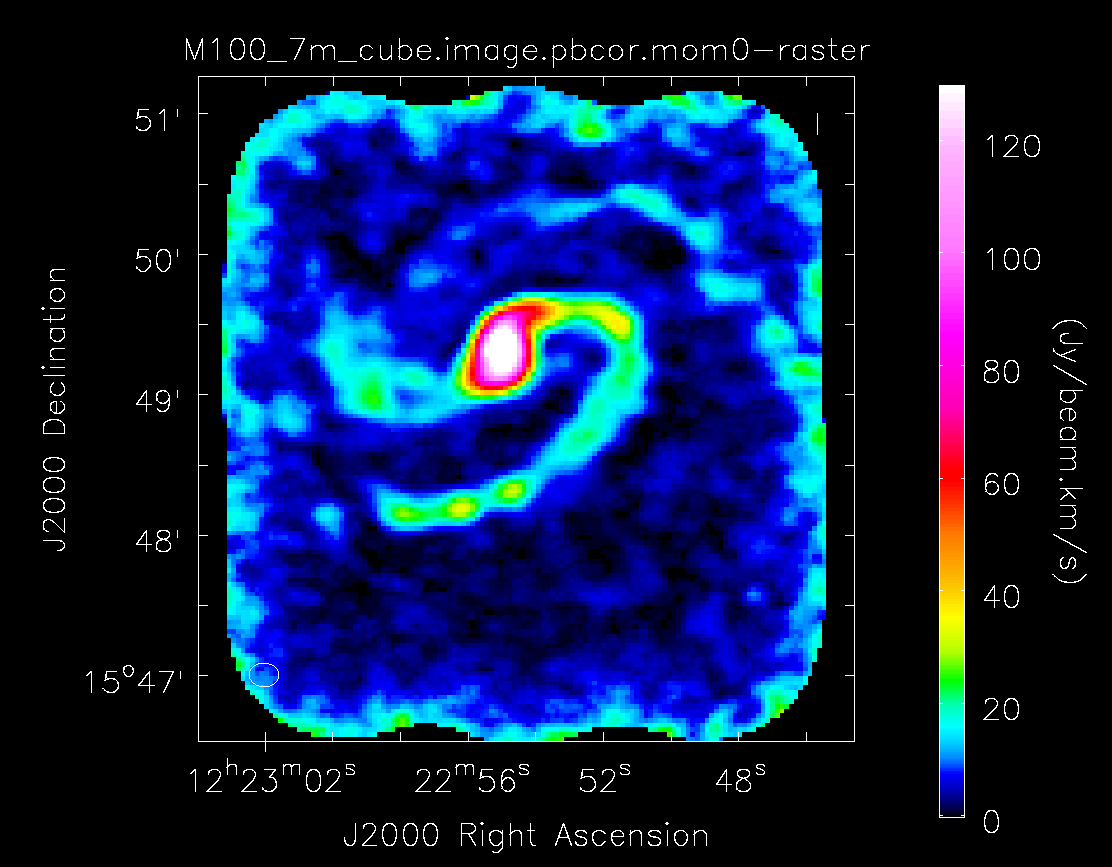
Below the moment maps from the 7m-only and the 12m-only data are shown for comparison. The moment maps were made using clean masks drawn by hand for comparison to the automasking technique; the two appear to be qualitatively similar. Details on the creation of these images (masking, thresholding, and the number of iterations of clean) can be found within the 12m and 7m imaging scripts available with the downloaded package. The range and scaling for the 12m-only figures are the same as that used for the 7m+12m figures for ease of comparison.
As expected, the 7m+12m image shows considerably more extended emission than the 12m-only data and finer detail than the 7m-only data. For comparison, the 7m+12m synthesized beam is 3.80"x2.50", while the 12m-only beam is 3.46"x2.37" and the 7m-only beam is 12.72"x10.12".
-
Moment 0 for 12m data alone (no primary beam correction).
-
Moment 0 for 7m data alone (no primary beam correction).
-
Moment 0 for 12m+7m data (no primary beam correction).
-
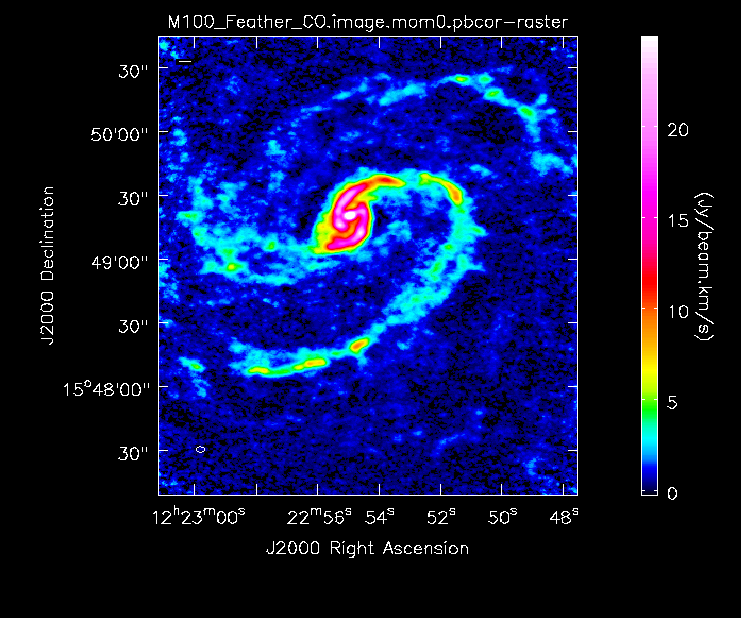
Moment 0 for 12m+7m data with primary beam correction.
-
Moment 1 for 12m data alone.
-
Moment 1 for 7m data alone.
-
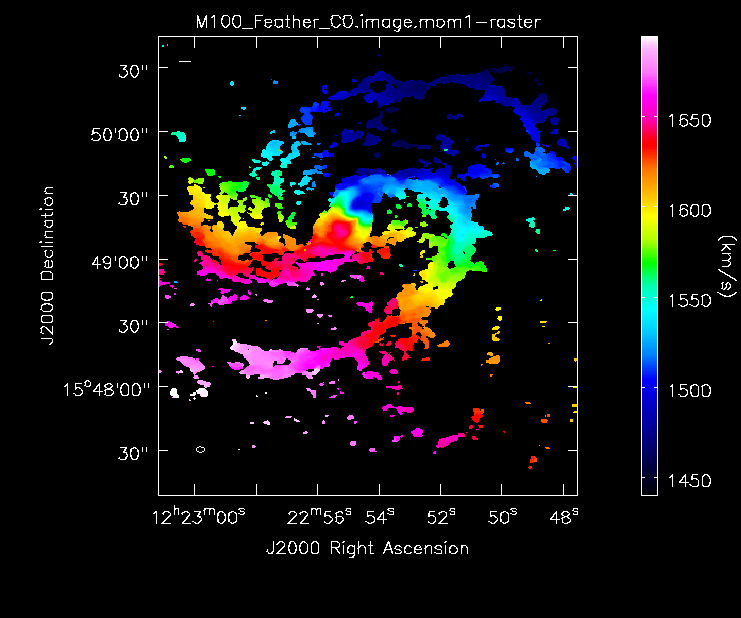
Moment 1 for 12m+7m data.
Convert 7m+12m Images to Fits Format
# In CASA
os.system('rm -rf *.fits')
exportfits(imagename='M100_combine_CO_cube.image',fitsimage='M100_combine_CO_cube.image.fits')
exportfits(imagename='M100_combine_CO_cube.flux',fitsimage='M100_combine_CO_cube.flux.fits')
exportfits(imagename='M100_combine_CO_cube.image.mom0',fitsimage='M100_combine_CO_cube.image.mom0.fits')
exportfits(imagename='M100_combine_CO_cube.image.mom0.pbcor',fitsimage='M100_combine_CO_cube.image.mom0.pbcor.fits')
exportfits(imagename='M100_combine_CO_cube.image.mom1',fitsimage='M100_combine_CO_cube.image.mom1.fits')
Feathering the Total Power and 7m+12m Interferometric Images
In this section the interferometric (7m+12m) image produced above is combined with the Total Power (single dish) image. The "feather" algorithm is employed, in which the two images are combined in the spatial frequency domain, i.e., the low and high spatial frequency components are predominantly taken from the TP and interferometric images, respectively.
Prepare Images for Feathering
Regrid the TP image to match the shape of the 7m+12m image using the task imregrid. The TP image is resampled onto the same grid as that of the "template" 7m+12m image along the first two axes of the cube (i.e., RA and Dec; it is not necessary to regrid the velocity axis, since the axis is already common to the both images).
#In CASA
os.system('rm -rf M100_TP_CO_cube.regrid')
imregrid(imagename='M100_TP_CO_cube.bl.image',
template='M100_combine_CO_cube.image',
axes=[0, 1],
output='M100_TP_CO_cube.regrid')
Now we trim the 7m+12m and (regridded) TP images, in order to exclude the regions masked by the clean task with minpb=0.2 and/or noisy edge regions in the TP image. The viewer task can be used to determine the trimming box. Here we use (x, y) = (219, 148) and (612, 579) [pixels] as the bottom-left and top-right corners, respectively, and set these values to the "box" parameter of the imsubimage task.
#In CASA
os.system('rm -rf M100_TP_CO_cube.regrid.subim')
imsubimage(imagename='M100_TP_CO_cube.regrid',
outfile='M100_TP_CO_cube.regrid.subim',
box='219,148,612,579')
os.system('rm -rf M100_combine_CO_cube.image.subim')
imsubimage(imagename='M100_combine_CO_cube.image',
outfile='M100_combine_CO_cube.image.subim',
box='219,148,612,579')
While the 7m+12m image (before the primary-beam correction) has non-uniform primary beam response (i.e., lower response in the outskirts of the mosaic field), the TP image does not have such non-uniformity. In order to feather the TP and 7m+12m images together, they should have the common response on the sky. Hence we need to multiply the TP image by the 7m+12m primary beam response before proceeding. To do this, create the subimage of the 7m+12m response,
#In CASA
os.system('rm -rf M100_combine_CO_cube.flux.subim')
imsubimage(imagename='M100_combine_CO_cube.flux',
outfile='M100_combine_CO_cube.flux.subim',
box='219,148,612,579')
then multiply it and the TP image using the task immath.
#In CASA
os.system('rm -rf M100_TP_CO_cube.regrid.subim.depb')
immath(imagename=['M100_TP_CO_cube.regrid.subim',
'M100_combine_CO_cube.flux.subim'],
expr='IM0*IM1',
outfile='M100_TP_CO_cube.regrid.subim.depb')
As a result, the feathered image will have the same response as that of the 7m+12m image. The primary-beam correction can be done after the feathering process (see below).
Feather TP Cube with 7m+12m Cube
Now we are ready to execute the feather task to combine the TP and 7m+12m images.
#In CASA
os.system('rm -rf M100_Feather_CO.image')
feather(imagename='M100_Feather_CO.image',
highres='M100_combine_CO_cube.image.subim',
lowres='M100_TP_CO_cube.regrid.subim.depb')
The task produces the combined image in the following way:
- Convert the input images specified by the "highres" and "lowres" parameters onto the spatial frequency plane.
- Combine them on the spatial frequency plane. The weighting is determined by the beam sizes/shapes of the input images.
- Convert it back to the image plane.
Please refer to the online help and documents for the details.
Make Moment Maps of the Feathered Images
We will use the same technique as the 7m+12m image analysis above to make moment maps.
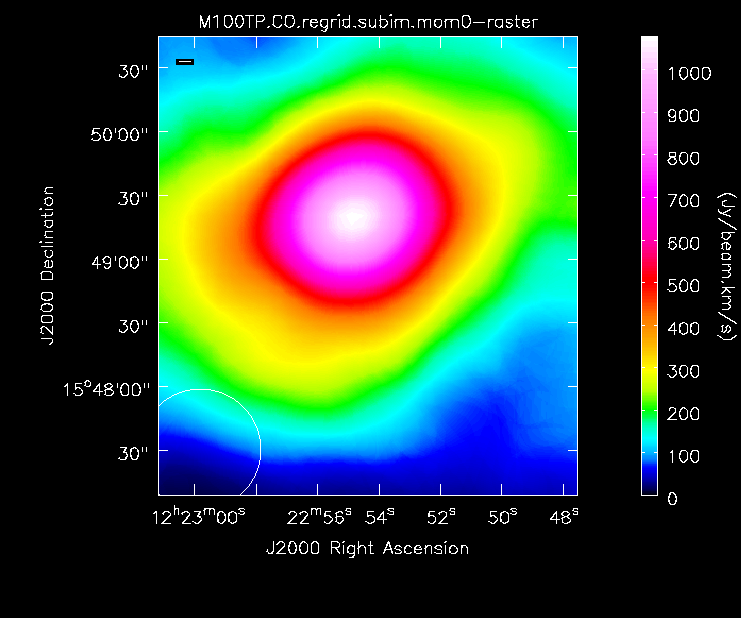
First (but optionally; this is solely for comparison to the feathered images and not needed to create the final feathered images), make moment maps for the (regridded) TP image.
#In CASA
myimage = 'M100_TP_CO_cube.regrid.subim'
chanstat = imstat(imagename=myimage,chans='4')
rms1 = chanstat['rms'][0]
chanstat = imstat(imagename=myimage,chans='66')
rms2 = chanstat['rms'][0]
rms = 0.5*(rms1+rms2)
os.system('rm -rf M100_TP_CO_cube.regrid.subim.mom0')
immoments(imagename='M100_TP_CO_cube.regrid.subim',
moments=[0],
axis='spectral',
chans='10~61',
includepix=[rms*2., 50],
outfile='M100_TP_CO_cube.regrid.subim.mom0')
os.system('rm -rf M100_TP_CO_cube.regrid.subim.mom1')
immoments(imagename='M100_TP_CO_cube.regrid.subim',
moments=[1],
axis='spectral',
chans='10~61',
includepix=[rms*5.5, 50],
outfile='M100_TP_CO_cube.regrid.subim.mom1')
os.system('rm -rf M100_TP_CO_cube.regrid.subim.mom*.png')
imview(raster=[{'file': 'M100_TP_CO_cube.regrid.subim.mom0',
'range': [0., 1080.],
'scaling': -1.3,
'colorwedge': T}],
out='M100_TP_CO_cube.regrid.subim.mom0.png')
imview(raster=[{'file': 'M100_TP_CO_cube.regrid.subim.mom1',
'range': [1440, 1695],
'colorwedge': T}],
out='M100_TP_CO_cube.regrid.subim.mom1.png')
Then make moment maps for the feathered image.
#In CASA
myimage = 'M100_Feather_CO.image'
chanstat = imstat(imagename=myimage,chans='4')
rms1 = chanstat['rms'][0]
chanstat = imstat(imagename=myimage,chans='66')
rms2 = chanstat['rms'][0]
rms = 0.5*(rms1+rms2)
os.system('rm -rf M100_Feather_CO.image.mom0')
immoments(imagename='M100_Feather_CO.image',
moments=[0],
axis='spectral',
chans='10~61',
includepix=[rms*2., 50],
outfile='M100_Feather_CO.image.mom0')
os.system('rm -rf M100_Feather_CO.image.mom1')
immoments(imagename='M100_Feather_CO.image',
moments=[1],
axis='spectral',
chans='10~61',
includepix=[rms*5.5, 50],
outfile='M100_Feather_CO.image.mom1')
os.system('rm -rf M100_Feather_CO.image.mom*.png')
imview(raster=[{'file': 'M100_Feather_CO.image.mom0',
'range': [-0.3, 25.],
'scaling': -1.3,
'colorwedge': T}],
out='M100_Feather_CO.image.mom0.png')
imview(raster=[{'file': 'M100_Feather_CO.image.mom1',
'range': [1440, 1695],
'colorwedge': T}],
out='M100_Feather_CO.image.mom1.png')
Correct the Primary Beam Response
Apply the primary beam response to the feathered image using the task immath,
#In CASA
immath(imagename=['M100_Feather_CO.image',
'M100_combine_CO_cube.flux.subim'],
expr='IM0/IM1',
outfile='M100_Feather_CO.image.pbcor')
and also to the moment 0 image.
#In CASA
os.system('rm -rf M100_combine_CO_cube.flux.1ch.subim')
imsubimage(imagename='M100_combine_CO_cube.flux.subim',
outfile='M100_combine_CO_cube.flux.1ch.subim',
chans='35')
os.system('rm -rf M100_Feather_CO.image.mom0.pbcor')
immath(imagename=['M100_Feather_CO.image.mom0',
'M100_combine_CO_cube.flux.1ch.subim'],
expr='IM0/IM1',
outfile='M100_Feather_CO.image.mom0.pbcor')
Save the primary-beam corrected moment 0 image to a PNG file.
#In CASA
os.system('rm -rf M100_Feather_CO.image.mom0.pbcor.png')
imview(raster=[{'file': 'M100_Feather_CO.image.mom0.pbcor',
'range': [-0.3, 25.],
'scaling': -1.3,
'colorwedge': T}],
out='M100_Feather_CO.image.mom0.pbcor.png')
Compare the Various Images
Now we compare all the images:
-
Primary beam corrected moment 0 for the 12m data.
-
Primary beam corrected moment 0 for the 7m data.
-
Moment 0 for the TP data.
-
Primary beam corrected moment 0 for 7m+12m data.
-
Primary beam corrected moment 0 for TP+7m+12m data.
-
Moment 1 for 12m data.
-
Moment 1 for 7m data.
-
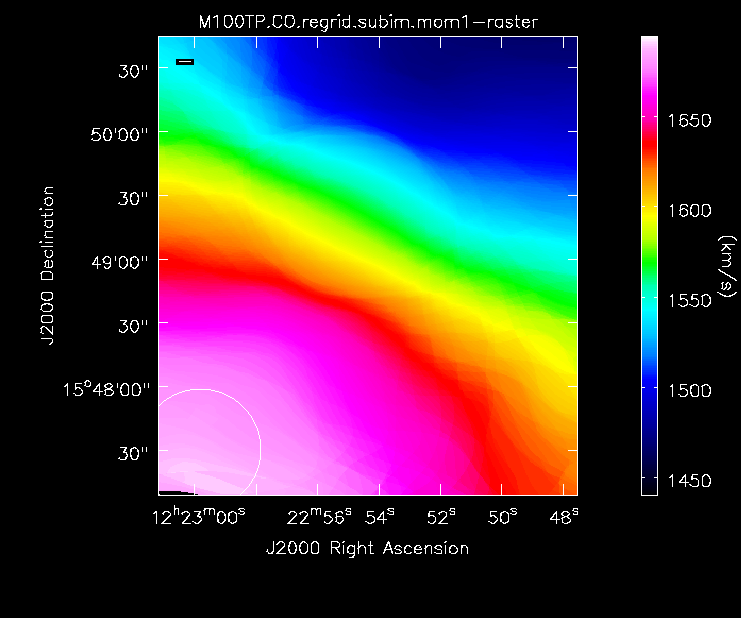
Moment 1 for the TP data.
-
Moment 1 for 7m+12m data.
-
Moment 1 for TP+7m+12m data.
You can see that more extended emission is recovered by adding the TP data to the interferometric data.
For quantitative comparison, we measure the total line fluxes of the various images. The task imstat can be used to do this. For example, for the subimage of the 7m+12m image,
#In CASA
imstat('M100_combine_CO_cube.image.subim')
yields the following:
{'blc': array([0, 0, 0, 0], dtype=int32),
'blcf': '12:23:01.170, +15.47.08.994, I, 1.14733e+11Hz',
'flux': array([ 283.17493916]),
'max': array([ 0.67358762]),
'maxpos': array([172, 253, 0, 49], dtype=int32),
'maxposf': '12:22:55.212, +15.49.15.500, I, 1.14639e+11Hz',
'mean': array([ 0.00105545]),
'medabsdevmed': array([ 0.00845536]),
'median': array([ -2.16333883e-05]),
'min': array([-0.07489366]),
'minpos': array([288, 363, 0, 13], dtype=int32),
'minposf': '12:22:51.193, +15.50.10.498, I, 1.14708e+11Hz',
'npts': array([ 11914560.]),
'quartile': array([ 0.01691275]),
'rms': array([ 0.01795238]),
'sigma': array([ 0.01792133]),
'sum': array([ 12575.23030299]),
'sumsq': array([ 3839.91974015]),
'trc': array([393, 431, 0, 69], dtype=int32),
'trcf': '12:22:47.554, +15.50.44.492, I, 1.146e+11Hz'}
The 'flux' value in the result is the total flux in Jy, but the velocity channels are not taken into account. Since the width of the velocity channels is 5 km/s, the following command gives the integrated line flux in the unit of Jy km/s.
#In CASA
imstat('M100_combine_CO_cube.image.subim')['flux']*5.0
array([ 1415.87469578])
Similarly, the total line fluxes of the TP image (after multiplying the 7m+12m primary beam response), feathered image, and feathered image after the primary-beam correction are
#In CASA
imstat('M100_TP_CO_cube.regrid.subim.depb')['flux']*5.0
imstat('M100_Feather_CO.image')['flux']*5.0
imstat('M100_Feather_CO.image.pbcor')['flux']*5.0
array([ 2776.12281313]) array([ 2776.12277509]) array([ 3055.34553736])
We see the followings from these values:
- The flux recovered by the 7m+12m observations is about a half of the total flux (1416/2776 = 0.510).
- The feathering process preserves the flux of the TP data.
- The flux of the primary-beam corrected feathered image is consistent with the values from the literature (2972 +/- 319 Jy km/s from the BIMA SONG; Helfer et al. 2003).
Last checked on CASA Version 4.3.0.