TWHydraBand7 Simplified: Difference between revisions
| Line 497: | Line 497: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
gaincal(vis='X3c1_wvrtsys.ms',caltable= | gaincal(vis='X3c1_wvrtsys.ms',caltable='X3c1_wvrtsys.scanphase.gcal', | ||
field='0,1,3,4',spw='0~3:4~380',refant='DV06', | field='0,1,3,4',spw='0~3:4~380',refant='DV06', | ||
calmode='p',solint='inf',minsnr=2.0,minblperant=4, | calmode='p',solint='inf',minsnr=2.0,minblperant=4, | ||
Latest revision as of 19:38, 9 May 2012
- A Note on getting the single MS
- An introduction to this data set is available at TWHydraBand7 For CASA 3.4.
- This guide is designed for CASA 3.4.
Preparation
Replace this with information relevant to the setup at the summer school.
Then start CASA.
casapy
This guide requires Python module analysisUtils.
# In CASA
import analysisUtils as au
Confirm your version of CASA
This guide has been written for CASA release 3.4.0. Please confirm your version before proceeding.
# In CASA
version = casalog.version()
print "You are using " + version
if (int(version.split()[4][1:-1]) < 19407):
print "\033[91m YOUR VERSION OF CASA IS TOO OLD FOR THIS GUIDE."
print "\033[91m PLEASE UPDATE IT BEFORE PROCEEDING."
else:
print "Your version of CASA is appropriate for this guide."
Observing Log and Priors
Below is some information that may not be obvious from the data
Like at most telescopes, the ALMA operators and astronomers at the site log any significant issues that were noticed from the online system during the observation. For these Band 7 observations of TW Hya on April 22, 2011, the only issue of note was that antenna DV04 could not observe at Band 7 and will need to be flagged.
First let's examine the basic properties of the data using listobs. Among other information we will be able to deduce what the source ids are and what each source was used for:
3c279 is the bandpass calibrator (field id=0) Titan is the absolute flux calibrator (field id=1) J1147-382 is the secondary phase calibrator (field id=3) J1037-295 is the primary phase calibrator (field id=4)
# In CASA
os.system('rm X3c1.ms.listobs')
listobs('X3c1.ms', verbose=T, listfile='X3c1.ms.listobs')
You can view the listobs output files using command less from the CASA prompt. Below we copy select parts of the listobs output files for reference.
X3c1.ms:
Data records: 278352 Total integration time = 6109.06 seconds
Observed from 22-Apr-2011/00:01:52.9 to 22-Apr-2011/01:43:42.0 (UTC)
Fields: 5
ID Code Name RA Decl Epoch SrcId nRows
0 none 3c279 12:56:11.16657 -05.47.21.5247 J2000 0 23625
1 none Titan 12:49:25.97588 -02.22.41.3024 J2000 1 4842
2 none TW Hya 11:01:51.84498 -34.42.17.1609 J2000 2 175176
3 none J1147-382=QSO 11:47:01.38151 -38.12.11.1179 J2000 3 14832
4 none J1037-295=QSO 10:37:16.08989 -29.34.02.9888 J2000 4 59877
SpwID #Chans Frame Ch1(MHz) ChanWid(kHz) TotBW(kHz) Corrs
0 4 TOPO 184550 1500000 7500000 I
1 128 TOPO 355740.062 15625 2000000 XX YY
2 1 TOPO 356716.625 1796875 1796875 XX YY
3 128 TOPO 356507.813 15625 2000000 XX YY
4 1 TOPO 357484.375 1796875 1796875 XX YY
5 128 TOPO 346792.187 15625 2000000 XX YY
6 1 TOPO 345784.375 1796875 1796875 XX YY
7 128 TOPO 345182.438 15625 2000000 XX YY
8 1 TOPO 344174.625 1796875 1796875 XX YY
9 128 TOPO 344386.763 15625 2000000 XX YY
10 1 TOPO 343378.95 1796875 1796875 XX YY
11 128 TOPO 346324.263 15625 2000000 XX YY
12 1 TOPO 345316.45 1796875 1796875 XX YY
13 128 TOPO 354402.388 15625 2000000 XX YY
14 1 TOPO 355378.95 1796875 1796875 XX YY
15 128 TOPO 356402.388 15625 2000000 XX YY
16 1 TOPO 357378.95 1796875 1796875 XX YY
17 3840 TOPO 356497.936 122.070312 468750 XX YY
18 1 TOPO 356732.189 468750 468750 XX YY
19 3840 TOPO 357734.314 122.070312 468750 XX YY
20 1 TOPO 357499.939 468750 468750 XX YY
21 3840 TOPO 346034.314 122.070312 468750 XX YY
22 1 TOPO 345799.939 468750 468750 XX YY
23 3840 TOPO 343955.936 122.070312 468750 XX YY
24 1 TOPO 344190.189 468750 468750 XX YY
Antennas: 9:
Name Station Diam. Long. Lat.
0 DV04 J505 12.0 m -067.45.18.0 -22.53.22.8
1 DV06 T704 12.0 m -067.45.16.2 -22.53.22.1
2 DV07 J510 12.0 m -067.45.17.8 -22.53.23.5
3 DV08 T703 12.0 m -067.45.16.2 -22.53.23.9
4 DV09 N602 12.0 m -067.45.17.4 -22.53.22.3
5 DV10 N606 12.0 m -067.45.17.1 -22.53.23.6
6 PM01 T702 12.0 m -067.45.18.6 -22.53.24.1
7 PM02 T701 12.0 m -067.45.18.8 -22.53.22.2
8 PM03 J504 12.0 m -067.45.17.0 -22.53.23.0
Things to Notice from above:
- Due to temporary data capture issues in the ALMA system, Titan's position was written to be (0,0). We have pre-corrected this error using fixplanets. Later in the tutorial, we will run fixplanets again to force all three datasets to have the same fixed position for Titan.
- There are a lot of spectral windows! Don't be alarmed. In ALMA data,
- spw=0 is always reserved for the water vapor radiometry data.
- spw=9, 11, 13, 15 are the wideband (TDM) correlator mode with 128 channels per spw default settings for doing pointing and this is all they are used for in these data.
- Currently Tsys data can only be taken in the wide (TDM) correlator mode with 128 channels per spw, these correspond to spws=1, 3, 5, 7 above. The frequencies of these TDM spws were carefully chosen so the the narrowband FDM spws fall within them.
- The 0.5 GHz, high spectral resolution spws that contain all the real source data (science target and calibrators) are 17, 19, 21, and 23
- For quicklook purposes, the ALMA online system produces a channel averaged spw for each channelized spw, these correspond to spw=2,4,6,8,10,12,14,16,18,20,22,24 and shouldn't be used for anything in post-processing as bandpass calibration etc has not been applied.
In the portion of the listobs output that shows the timerange, the final column gives the scan intent. It is important to have a look at this because you can flag and do other operations in CASA using the scan intent as a selection option. Also, these intents will be used in the future for pipeline processing. You will usually want to use them to flag the CALIBRATE_POINTING* and CALIBRATE_ATMOS* (the latter correspond to the hot and cold load measurements used to calculate Tsys) data. This is essential for science or calibration data taken only in TDM (wide bandwidth) mode, i.e. the same mode that the pointing and Tsys data are taken in. For the current data however, that calibration data is recorded in different spws from the useful FDM (narrow bandwidth) data, so we'll be able to separate them by splitting them off at the final step prior to imaging.
<figure id="Ant_pos.png">
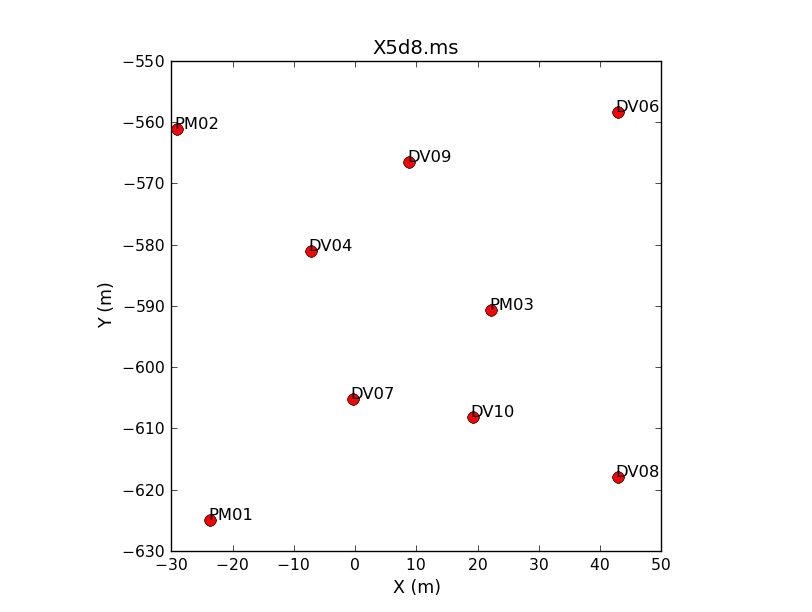
</figure>
Before we move on, its also nice to get an idea where the antennas are with respect to each other. We can use plotants to plot their positions. It is a good idea to check each file since an antenna may have entered or exited the array between observations.
# In CASA
plotants(vis='X3c1.ms',figfile='X3c1.ms.plotants.png')
You can view the output images using any standard image viewer.
Initial Inspection and Flagging
From here we begin to operate on the *wvrtsys.ms files.
Before we begin flagging data, we unflag all data in the measurement sets. If this is your first pass through this section of the guide, no data in the measurement sets will be flagged, and you can skip this step. If you are rerunning the flagging commands below, this will reset your flag columns to their original state. (Warning messages about using task tflagdata can be ignored for now.)
# In CASA
flagdata(vis='X3c1_wvrtsys.ms', mode='manualflag', unflag=T, flagbackup=F)
ALMA data contains both the cross correlation and autocorrelation data. Presently nothing more can be done with the autocorrelation data so we flag it. Additionally, for smaller configurations of the array, and northerly sources one antenna can shadow another, blocking its view. This data also needs to be flagged. Finally, the observing log told us DV04 was not behaving properly at Band 7 and shouldn't be used so we flag that as well.
# In CASA
flagdata(vis='X3c1_wvrtsys.ms',autocorr=True, flagbackup=T)
flagdata(vis='X3c1_wvrtsys.ms',mode='shadow',diameter=12.0, flagbackup=F)
flagdata(vis='X3c1_wvrtsys.ms',antenna='DV04', flagbackup=F)
Next we inspect the data with plotms for additional issues that need flagging, first looking at amplitude vs. time for each of the three datasets. Use the green arrows on the plotms gui to cycle through spws.
<figure id="Tsyswvr_time_spw0_X3x1.png">
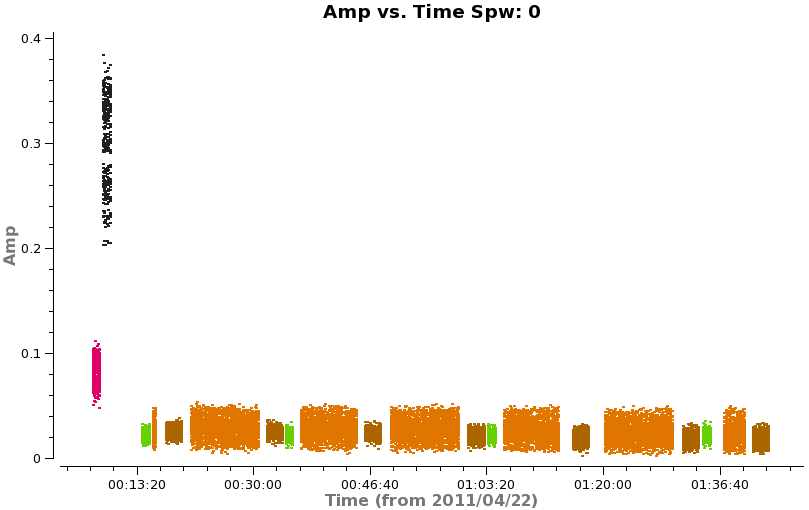
</figure>
Note: when iteraxis is invoked in plotms, unzoom does not always work properly. If you have trouble with this, flip to next page and then back to current one. This usually fixes the problem.
# In CASA
plotms(vis='X3c1_wvrtsys.ms',spw='',xaxis='time',yaxis='amp',field='',avgchannel='1e4',
coloraxis='field',iteraxis='spw')
<figure id="Tsyswvr_time_spw2corr_X3x1.png">
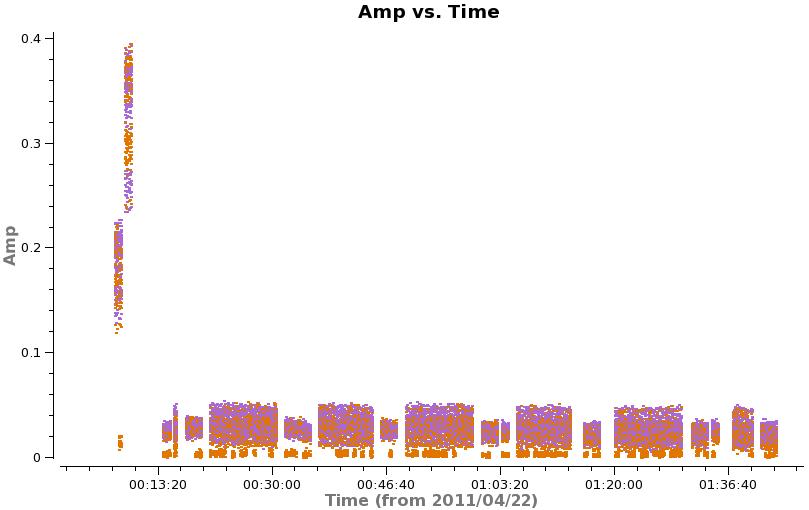
</figure>
Things to Notice:
- In spw=2 there are some low points in all three data files. Use the "Mark Regions" box (left of center on bottom row of icons) to draw small box on low points. Then click the magnifying glass icon to the right of center. The output will be sent to the logger window. Note: keep the marked region small or you can overwhelm the buffer. Locate suggests correlation YY on PM03 is the culprit.
To see this more clearly you can rerun plotms with coloraxis='field' switched to coloraxis='corr'
# In CASA
plotms(vis='X3c1_wvrtsys.ms',spw='2',xaxis='time',yaxis='amp',field='',avgchannel='1e4',
coloraxis='corr')
To further check, you can exclude PM03 from the plot using antenna='!PM03'.
# In CASA
plotms(vis='X3c1_wvrtsys.ms',spw='2',xaxis='time',yaxis='amp',field='',avgchannel='1e4',
coloraxis='corr',antenna='!PM03')
Having confirmed the problem antenna, we flag it below.
# In CASA
flagdata(vis='X3c1_wvrtsys.ms', flagbackup=T,
spw=['2'],
antenna=['PM03'],
correlation=['YY'])
Next we need to inspect the spectral properties of the data to look for issues.
First we look at phase as a function of frequency for a well behaved antenna like DV06. coloraxis='baselines' (note this parameter is called Colorize in the GUI "Display" tab) will show each baseline as a different color. Significant delay errors or baseline errors will show up as phase slopes in these plots. Again you will want to page through the spectral windows.
# In CASA
plotms(vis='X3c1_wvrtsys.ms',spw='',xaxis='frequency',yaxis='phase',field='0',antenna='DV06',
avgtime='1e8',avgscan=T,coloraxis='baseline',iteraxis='spw',xselfscale=T)
Overall these plots look good with no large delays or baseline errors apparent.
<figure id="Birdies_spw2_X3x1.png">
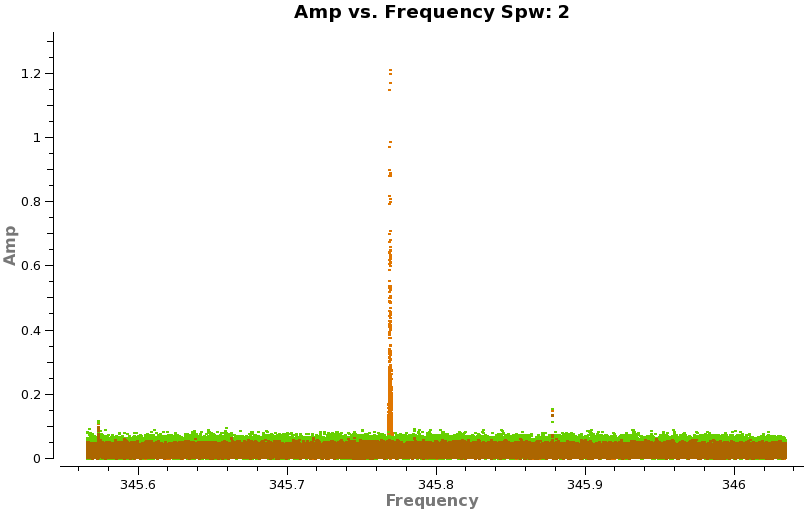
</figure>
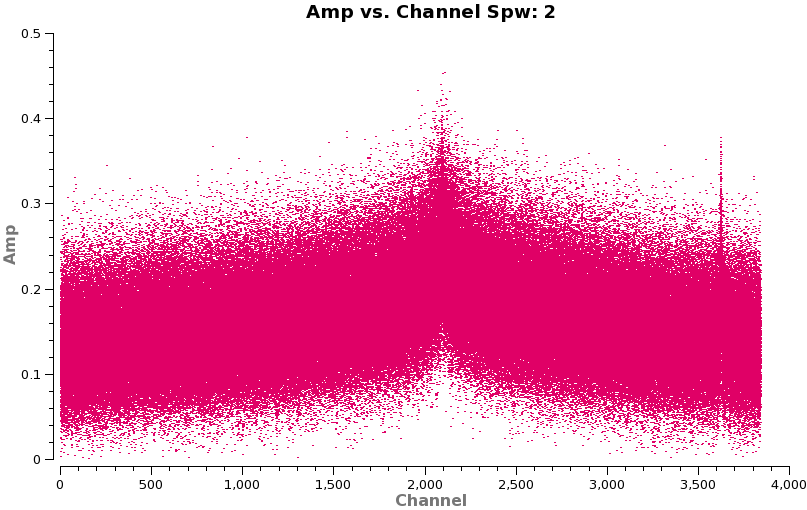
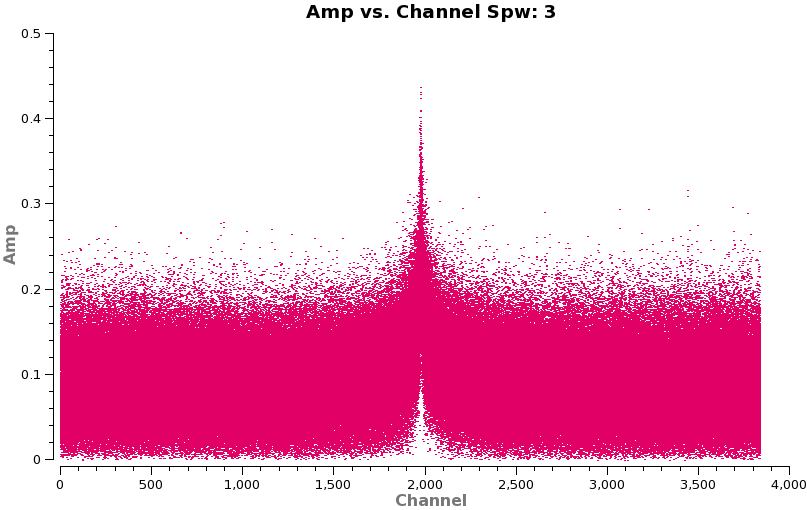
With such high spectral resolution data, one often sees occasional "birdies" in the data. These are typically very narrow weak spectral features that are internally generated in the system. Over time as we track down issues the number of birdies should decrease, but you should always check. This is easiest to do by looking at amplitude vs. frequency for sources observed over a long time range (for sensitivity). It is helpful to look at more than one source to verify the nature of the emission. Below we look at both calibrators (brown and green) and TW Hya (orange). If you have enough sensitivity birdies should be seen on all sources, however, be careful not to mistake real line emission for a birdie even on a calibrator - they can be present as we've seen for Titan.
<figure id="Birdies_spw3_X3x1.png">
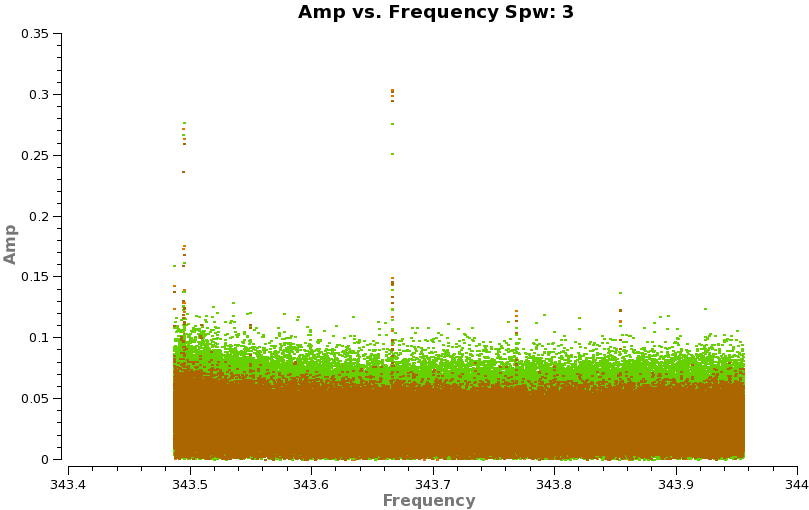
</figure>
# In CASA
plotms(vis='X3c1_wvrtsys.ms',spw='',xaxis='channel',yaxis='amp',field='2,3,4',
avgtime='1e8',avgscan=T,coloraxis='field',iteraxis='spw',xselfscale=T,yselfscale=T)
Now you can zoom in on each region to get channels for flagging, or to save time just go ahead and run the flagging command below where this has been done for you.
# In CASA
flagdata(vis='X3c1_wvrtsys.ms', flagbackup=T,
spw=['0:107;128;237;377~378',
'1:128;237;377~378',
'2:128;377~378',
'3:83;153~154;237;378;384'])
Replot in plotms to check that flagging has been done as anticipated.
Flag Calibrator Spectral Features
In this section, we will flag spectral features in the calibrators so they do not skew the calibration solutions. First make plots of 3C279 and Titan in channel space to get channels for flagging.
<figure id="3C279_Titan_spw1.png">
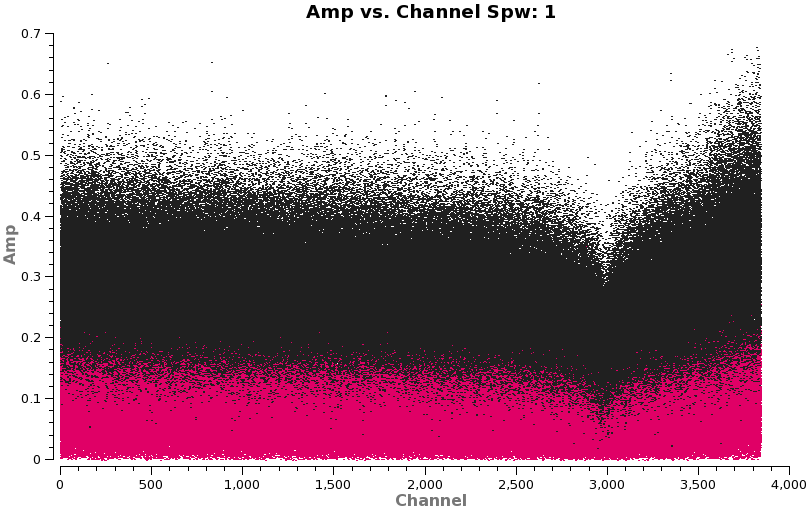
</figure> <figure id="3c279_meso_freq.png">
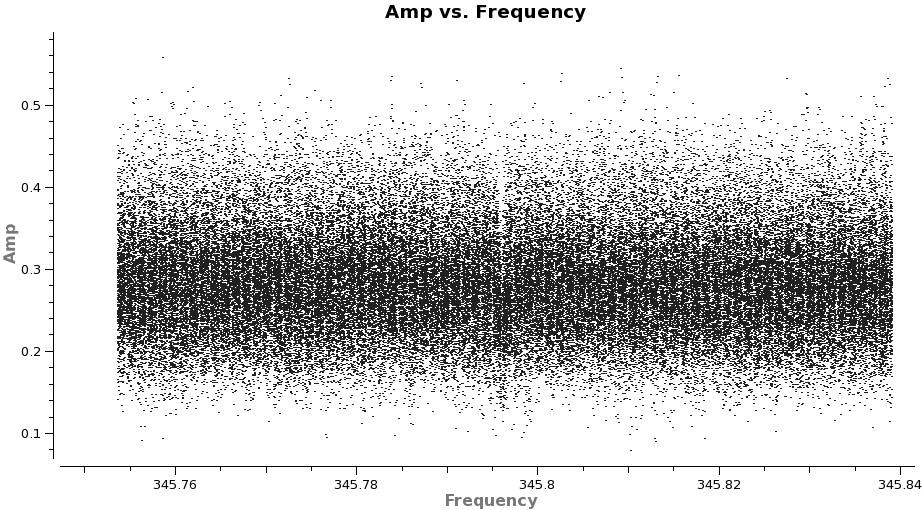
</figure> <figure id="3c279_meso_chann.png">
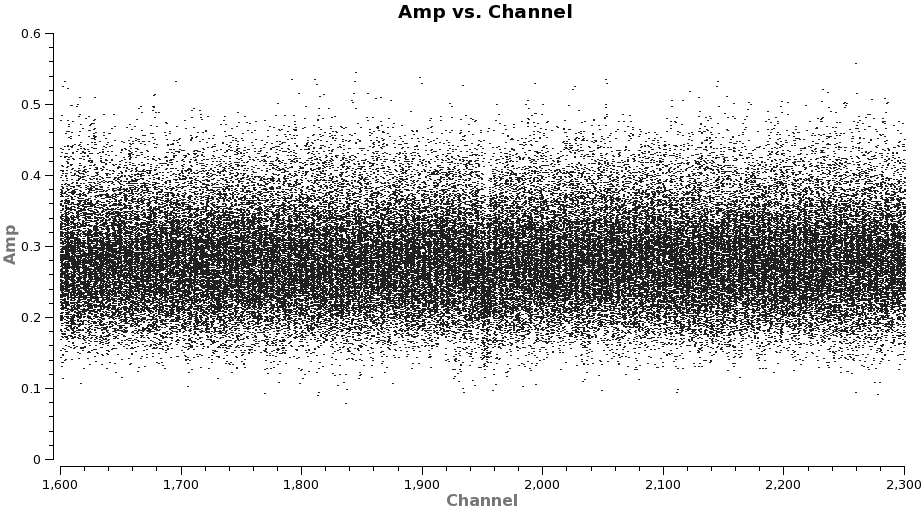
</figure>
# In CASA
plotms(vis='X3c1_wvrtsys.ms',spw='',xaxis='channel',yaxis='amp',field='0,1',
avgtime='1e8',coloraxis='field',iteraxis='spw')
The figure to the right shows a broad absorption line in spw 1 at channel 3000. This is the ozone absorption line at 357.62982 GHz. However, there is another narrow absorption feature in the spectra (spw 2) that is most easily seen on 3C279 (because it is the strongest calibrator). Let's look at it first in frequency space.
# In CASA
plotms(vis='X3c1_wvrtsys.ms',spw='2:160~230',xaxis='frequency',yaxis='amp',
field='0',avgtime='1e8',coloraxis='field')
The absorption feature lies exactly at the rest frequency for CO 3-2 (345.79599 GHz). Because it is so narrow (< 1 MHz), it must originate from a very low pressure region (i.e. high altitude) in the Earth's atmosphere, otherwise it would be more pressure broadened. Indeed, the first detection of CO in the mesosphere was made over 35 years ago (see, e.g. Waters et al. 1976 or Goldsmith et al. 1979). Be aware that the line is stronger as you go up the CO ladder (strength ~ J^3 for low J) because the temperature at that altitude (~50km) is about 250 K. In April 2011, the apparent depth of the feature was about 10% in the 2-1 line and 35% in the 3-2 line. However, the depth of the absorption feature is exaggerated due to the way ALMA normalizes the cross-correlation spectra by the autocorrelation spectra prior to storage. While this technique generally leads to a flat bandpass shape, it will accentuate telluric features because they are emission lines in the single dish spectrum (e.g. JCMT observations of mesospheric CO 3-2 can be found in Preston et al. 1993). Finally, note that large seasonal variations in the line strength have been reported from observations at Onsala.
Now, let's re-plot the line with channel number as the x-axis in order to get the channel range for flagging.
# In CASA
plotms(vis='X3c1_wvrtsys.ms',spw='2:160~230',xaxis='channel',yaxis='amp',
field='0',avgtime='1e8',coloraxis='field')
Now lets look at Titan in more detail.
# In CASA
plotms(vis='X3c1_wvrtsys.ms',spw='',xaxis='channel',yaxis='amp',field='1',
avgtime='1e8',coloraxis='field',iteraxis='spw')
Explicitly back up the flag tables so that flagged regions can be restored later.
# In CASA
flagmanager(vis='X3c1_wvrtsys.ms',mode='save',versionname='X3c1_wvrtsys.before_calspectralflags')
<figure id="Titan_spw2.png">
</figure>
Flag absorption features for all sources.
# In CASA
flagdata(vis='X3c1_wvrtsys.ms', spw=['1:200~384','2:194~196'])
<figure id="Titan_spw3.png">
</figure>
Now we need to flag emission. The very broad CO(3-2) in spw=2 of Titan will prevent us from using it as a calibrator for this spectral window since there are no line-free channels (we will transfer, phase, amplitude, and absolute flux from another Titan spw below). We do want to flag the narrower Titan line in spw=3.
# In CASA
flagmanager(vis='X3c1_wvrtsys.ms',mode='save',versionname='X3c1_wvrtsys.before_emissionflags')
# In CASA
flagdata(vis='X3c1_wvrtsys.ms',
field=['1'],
spw=['3:100~300'])
If you like, check that the right things have been flagged.
# In CASA
plotms(vis='X3c1_wvrtsys.ms',spw='',xaxis='channel',yaxis='amp',field='0,1',
avgtime='1e8',coloraxis='field',iteraxis='spw')
Set Up the Flux Calibrator Model
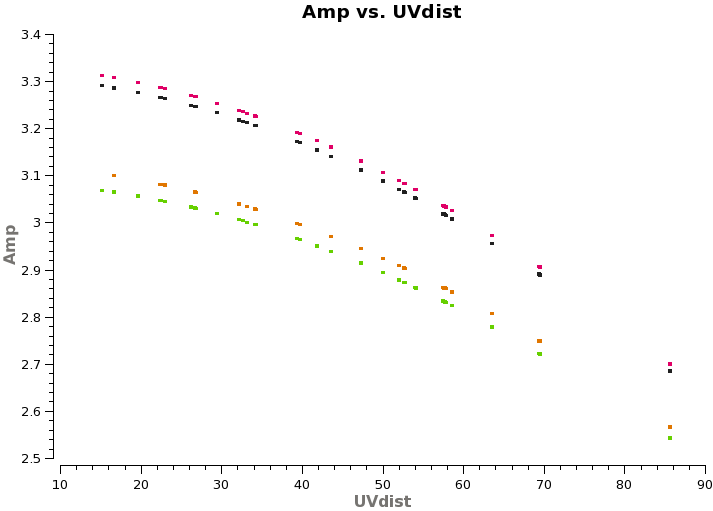
Fill the model data column for Titan with a model for the flux density as a function of baseline. The model is a uniformly illuminated disk with the size obtained from the JPL Horizons ephemeris.
# In CASA
setjy(vis='X3c1_wvrtsys.ms',field='1',
standard='Butler-JPL-Horizons 2010',scalebychan=F)
<figure id="Titan amp vs uvdist.png">
</figure>
After running setjy, it is a good idea to plot the model in order to confirm that it makes sense. In this case, Titan is partially resolved, so we expect the flux density to drop with uv distance, but not so much as to pass through a null. We also expect it to be brighter at higher frequencies since it has a thermal blackbody spectrum.
# In CASA
plotms(vis='X3c1_wvrtsys.ms',field='1',xaxis='uvdist',yaxis='amp',coloraxis='spw',
ydatacolumn='model')
Bandpass Calibration
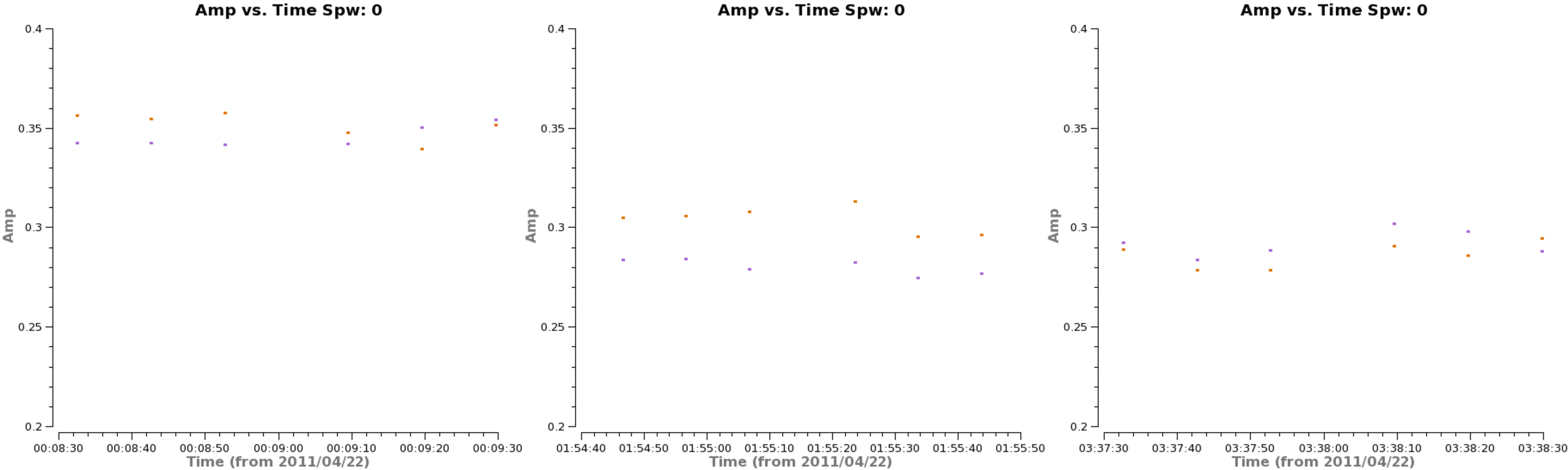
First we need to check how the amplitude and phase of 3C279 behave as a function of time. In order to set a fixed scale on the y-axis, we first make a plot of all the data, excluding antenna DV04. (We must specify ydatacolumn='data' explicitly here because the default value of ydatacolumn equals the value used in the previous execution of plotms. In the previous execution ydatacolumn was set to model. See the online help, help plotms, for details.)
# In CASA
plotms(vis='X3c1_wvrtsys.ms',xaxis='time',yaxis='amp',coloraxis='corr',
field='0',avgchannel='1e4',ydatacolumn='data')
<figure id="ThreeScansAmp.png">
</figure>
We see that the uncalibrated amplitudes range between 0.2-0.4, so let's set this as our scale and examine a representative baseline (DV06-DV07) to see how the amplitude changes with time.
for spw in ['0','1','2','3']:
print "Now showing spw %s " % (spw)
plotms(vis='X3c1_wvrtsys.ms',spw=spw,xaxis='time',yaxis='amp',coloraxis='corr',iteraxis='spw',
field='0',avgchannel='1e4',antenna='DV06&DV07',plotrange=[0,0,0.2,0.4])
user_check=raw_input('press enter to go to the next plot\n')
<figure id="ThreeScansPhase.png">
</figure>
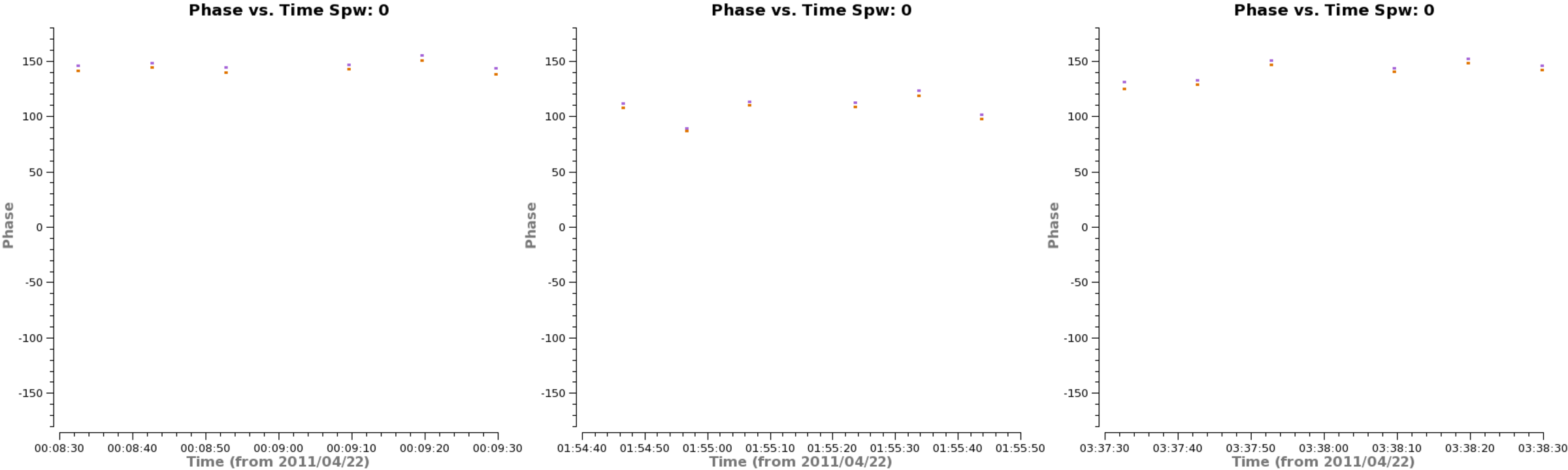
Page through the measurement sets for each spw. This shows significant variations in the amplitude across the three measurement sets. Now do the same with phase.
# In CASA
for spw in ['0','1','2','3']:
plotms(vis='X3c1_wvrtsys.ms',spw=spw,xaxis='time',yaxis='phase',coloraxis='corr',iteraxis='spw',
field='0',avgchannel='1e4',antenna='DV06&DV07',plotrange=[0,0,-180,180])
user_check=raw_input('press enter to go to the next plot\n')
This examination reveals two findings: (1) significant variation in the phase across the three scans, as well as (2) smaller but significant variations within a scan. The first finding suggests that we do not want to combine the scans for bandpass calibration, but instead derive an independent bandpass for each scan. Actually what is more important than a DC offset is if the shape of the amplitude or phase changes from scan to scan. There isn't enough S/N to tell for sure so we will keep them separate. This situation is often the case, which is why we did not concatenate the three datasets prior to calibration. The second finding suggests that we need to correct the phase vs. time behavior of the bandpass calibrator (3C279; field=0) within each scan, before doing the bandpass. We want to chose a relatively narrow range of channels near the center of the spws so that the bandpass phase slopes (to be corrected with the bandpass calibration itself) do not decorrelate the signal. You need to avoid spectral regions that were completely flagged above.
# In CASA
gaincal(vis='X3c1_wvrtsys.ms',caltable='X3c1_wvrtsys.bpphase.gcal',
field='0',spw='0~3:90~110',refant='DV06',
calmode='p',solint='int',minsnr=2.0,minblperant=4)
<figure id="X7ef_wvrtsys.bpphase.X.png">
</figure>
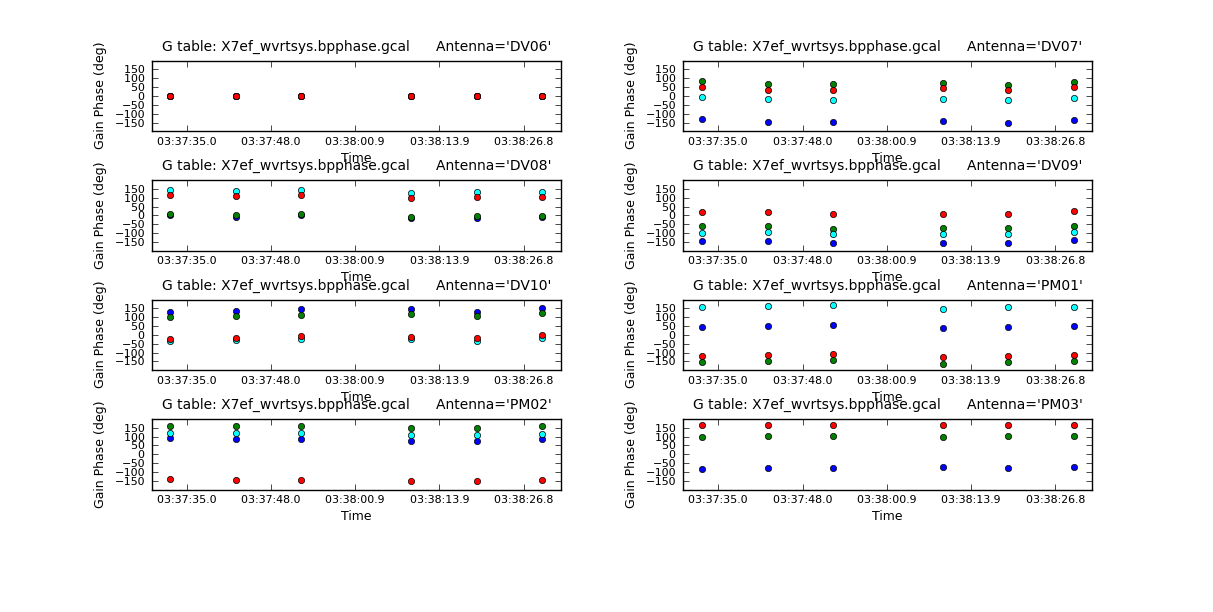
Inspect the phase-only calibration solutions for the bandpass calibrator. Look for any noisy solutions. We do XX and YY separately to reduce confusion in the plot. It will help if you make your plotcal window wide.
# In CASA
plotcal(caltable='X3c1_wvrtsys.bpphase.gcal',xaxis='time',yaxis='phase',spw='',antenna='1~8',
iteration='antenna',subplot=421,plotrange=[0,0,-180,180],
figfile='X3c1_wvrtsys.bpphase.X.png',poln='X')
In the plotcal gui you can use the magnifying glass symbol to zoom in on one of the scans to see the phase variations. The colors are the 4 different spws.
# In CASA
plotcal(caltable='X3c1_wvrtsys.bpphase.gcal',xaxis='time',yaxis='phase',spw='',antenna='1~8',
iteration='antenna',subplot=421,plotrange=[0,0,-180,180],
figfile='X3c1_wvrtsys.bpphase.Y.png',poln='Y')
Next we apply this phase-only correction on the fly while calculating the bandpass solutions.
# In CASA
bandpass(vis='X3c1_wvrtsys.ms',caltable='X3c1_wvrtsys.bandpass.bcal',
field='0',spw='',combine='',refant='DV06',
solint='inf',solnorm=T,minblperant=4,fillgaps=17,
gaintable=['X3c1_wvrtsys.bpphase.gcal'])
You will see some error messages in the terminal, these are just related to the flagged channels. We set fillgaps=17 to interpolate across the smaller regions of flagged channels (mesospheric features and birdies).
<figure id="Bandpass.ampspw0.png">
</figure> <figure id="Bandpass.phasespw0.png">
</figure>
A few words about solint and combine:
In bandpass, the use of solint='inf' (as in "infinite") will derive a bandpass solution for each 3C279 scan, unless combine='scan' (which is the default). Here we set combine=' ' explicitly so that it does not combine the scans into one bandpass. Likewise, field boundaries are only crossed if combine='field', and spw boundaries are only crossed if combine='spw'. In some cases it can be helpful to combine fields if you suffer from lack of S/N, but it is never a good idea to combine spws.
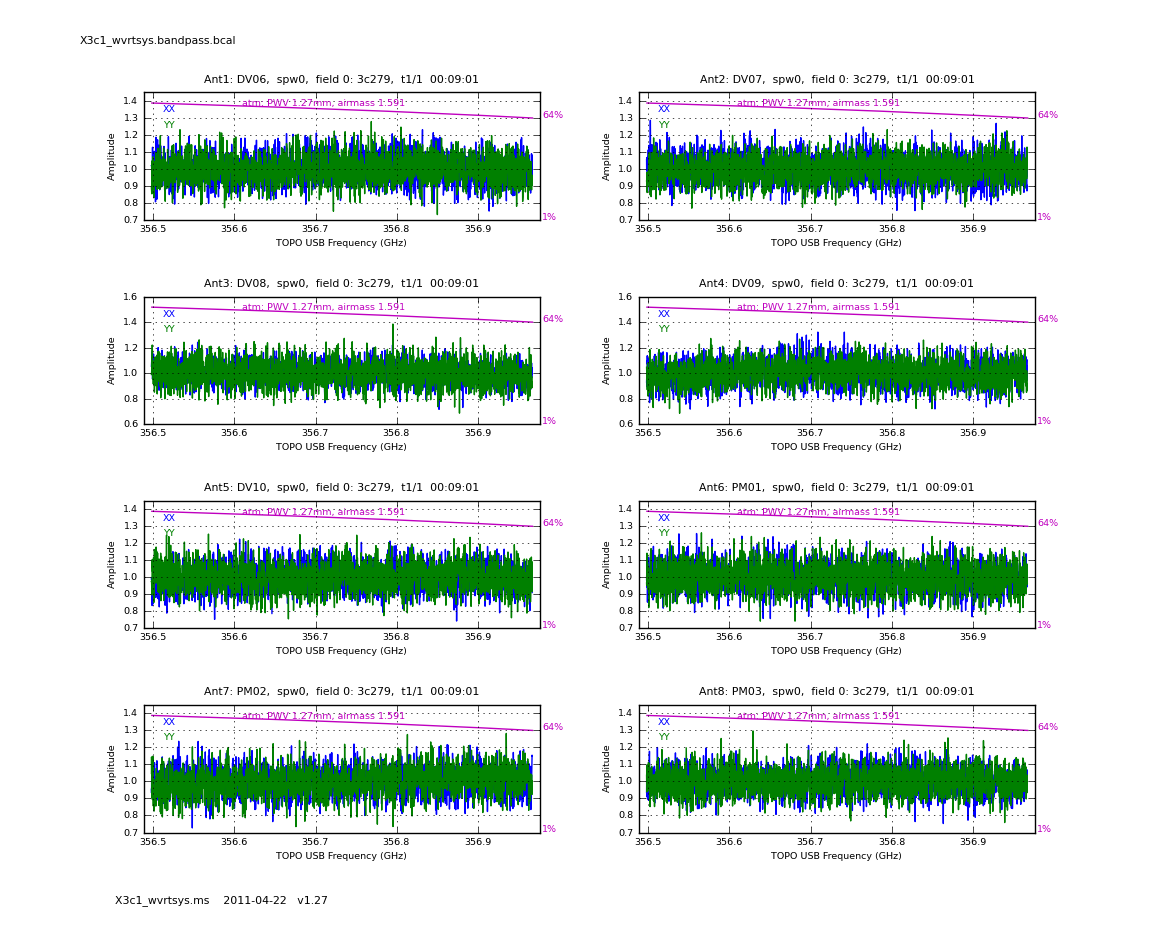
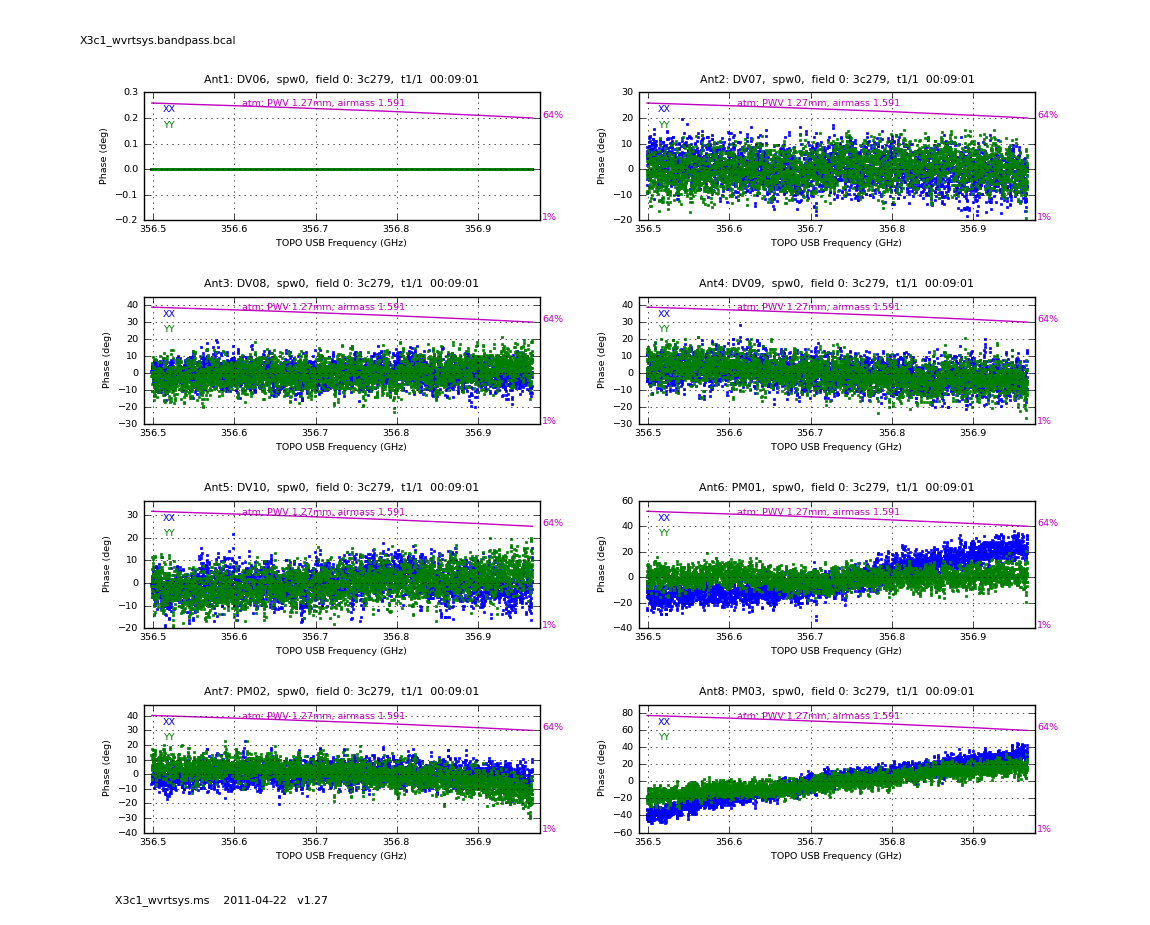
Now inspect the phase and amplitude solutions. You are looking for excursions from smooth fits, or particularly noisy solutions compared to the others.
# In CASA
for spw in [0,1,2,3]:
au.plotbandpass('X3c1_wvrtsys.bandpass.bcal',xaxis='freq',yaxis='amp', spw=spw,
antenna='1~8', subplot=421, figfile='X3c1_wvrtsys.bandpass.amp', showatm=T,
interactive=True)
user_check=raw_input('press enter to go to the next plot\n')
# In CASA
for spw in [0,1,2,3]:
au.plotbandpass('X3c1_wvrtsys.bandpass.bcal',xaxis='freq',yaxis='phase',spw=spw,
antenna='1~8',subplot=421,figfile='X3c1_wvrtsys.bandpass.phs', showatm=T,
interactive=True)
user_check=raw_input('press enter to go to the next plot\n')
The values of phase on DV06 are very close to zero because it was used as the reference antenna.
Gain Calibration
Now that we have a bandpass solution to apply we can solve for the antenna-based phase and amplitude gain calibration. Since the phase changes on a much shorter timescale than the amplitude, we will solve for them separately. In particular, if the phase changes significantly over a scan time, the amplitude would be decorrelated, if the un-corrected phase were averaged over this timescale. Note that we re-solve for the gain solutions of the bandpass calibrator, so we can derive new solutions that are corrected for the bandpass shape. Since the bandpass calibrator will not be used again, this is not strictly necessary, but is useful to check its calibrated flux density for example.
# In CASA
gaincal(vis='X3c1_wvrtsys.ms',caltable='X3c1_wvrtsys.intphase.gcal',
field='0,1,3,4',spw='0~3:4~380',refant='DV06',
calmode='p',solint='int',minsnr=2.0,minblperant=4,
gaintable=['X3c1_wvrtsys.bandpass.bcal'])
Here solint='int' coupled with calmode='p' will derive a single phase solution for each 10 second integration. Note that the bandpass table is applied on-the-fly before solving for the phase solutions, however the bandpass is NOT applied to the data permanently until applycal is run later on.
Although solint='int' (i.e. the integration time of 10 seconds) is the best choice to apply before solving for the amplitude solutions, it is not a good idea to use this to apply to the target. This is because the phase-scatter within a scan can dominate the interpolation between calibrator scans. Instead, we also solve for the phase on the scan time, solint='inf' (but combine=' ' , since we want one solution per scan) for application to the target later on. Unlike the bandpass task, for gaincal, the default of the combine parameter is combine=' ' .
# In CASA
gaincal(vis='X3c1_wvrtsys.ms',caltable='X3c1_wvrtsys.scanphase.gcal',
field='0,1,3,4',spw='0~3:4~380',refant='DV06',
calmode='p',solint='inf',minsnr=2.0,minblperant=4,
gaintable=['X3c1_wvrtsys.bandpass.bcal'])
Alternatively, instead of making a separate phase solution for application to the target, one can also run smoothcal to smooth the solutions derived on the integration time.
Next we apply the bandpass and solint='int' phase-only calibration solutions on-the-fly to derive amplitude solutions. Here the use of solint='inf' , but combine=' ' will result in one solution per scan interval.
# In CASA
gaincal(vis='X3c1_wvrtsys.ms',caltable='X3c1_wvrtsys.amp.gcal',
field='0,1,3,4',spw='0~3:4~380',refant='DV06',
calmode='ap',solint='inf',minsnr=2.0,minblperant=4,
gaintable=['X3c1_wvrtsys.bandpass.bcal','X3c1_wvrtsys.intphase.gcal'])
Now carefully inspect all these solutions looking for discrepant solutions. If you see any, you will need to flag them and rerun the calibration tasks above.
We make plots in X and Y separately for clarity. The colors are showing the spectral windows. <figure id="X3c1_wvrtsys.intphase_X.png">
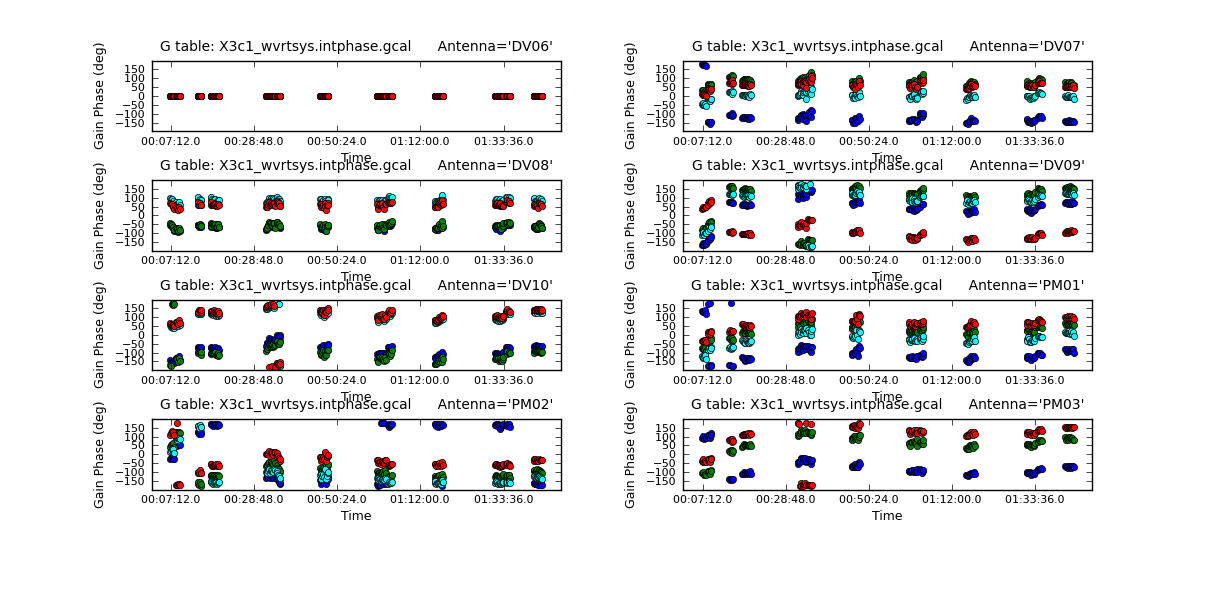
</figure>
# In CASA
plotcal(caltable='X3c1_wvrtsys.intphase.gcal',xaxis='time',yaxis='phase',antenna='1~8',
spw='',field='0,1,3,4',iteration='antenna',subplot=421,
plotrange=[0,0,-180,180],poln='X',figfile='X3c1_wvrtsys.intphase_X.png')
# In CASA
plotcal(caltable='X3c1_wvrtsys.intphase.gcal',xaxis='time',yaxis='phase',antenna='1~8',
spw='',field='0,1,3,4',iteration='antenna',subplot=421,
plotrange=[0,0,-180,180],poln='Y',figfile='X3c1_wvrtsys.intphase_Y.png')
<figure id="X3c1_wvrtsys.scanphase_X.png">
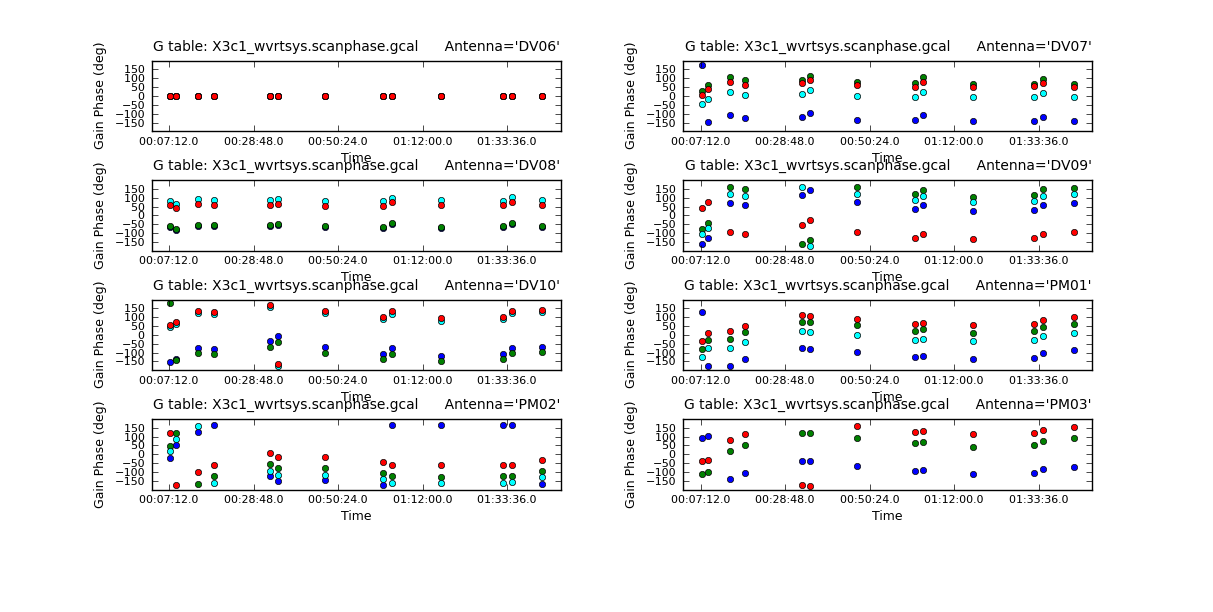
</figure>
# In CASA
plotcal(caltable='X3c1_wvrtsys.scanphase.gcal',xaxis='time',yaxis='phase',antenna='1~8',
spw='',field='0,1,3,4',iteration='antenna',subplot=421,
plotrange=[0,0,-180,180],poln='X',figfile='X3c1_wvrtsys.scanphase_X.png')
# In CASA
plotcal(caltable='X3c1_wvrtsys.scanphase.gcal',xaxis='time',yaxis='phase',antenna='1~8',
spw='',field='0,1,3,4',iteration='antenna',subplot=421,
plotrange=[0,0,-180,180],poln='Y',figfile='X3c1_wvrtsys.scanphase_Y.png')
Since we have taken out the phase as best we can by applying the solint='int' phase-only solution, this plot will give a good idea of the residual phase error. If you see scatter of more than a few degrees here, you should consider going back and looking for more data to flag, particularly bad timeranges etc.
<figure id="X3c1_wvrtsys.amp_phase.png">
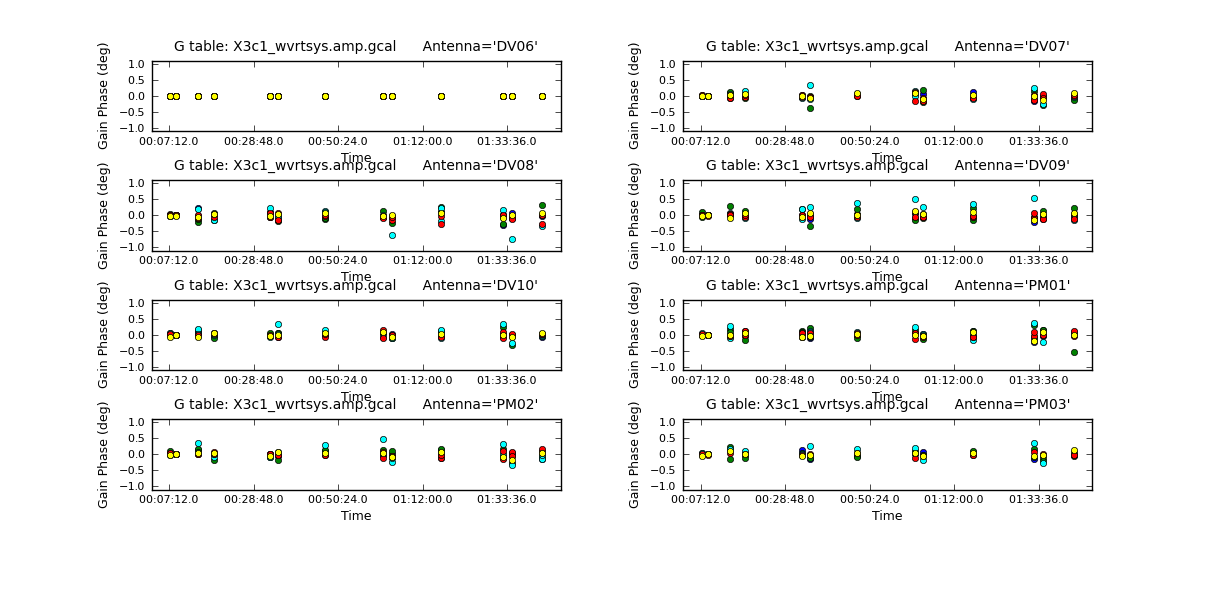
</figure> <figure id="X3c1_wvrtsys.amp_X.png">
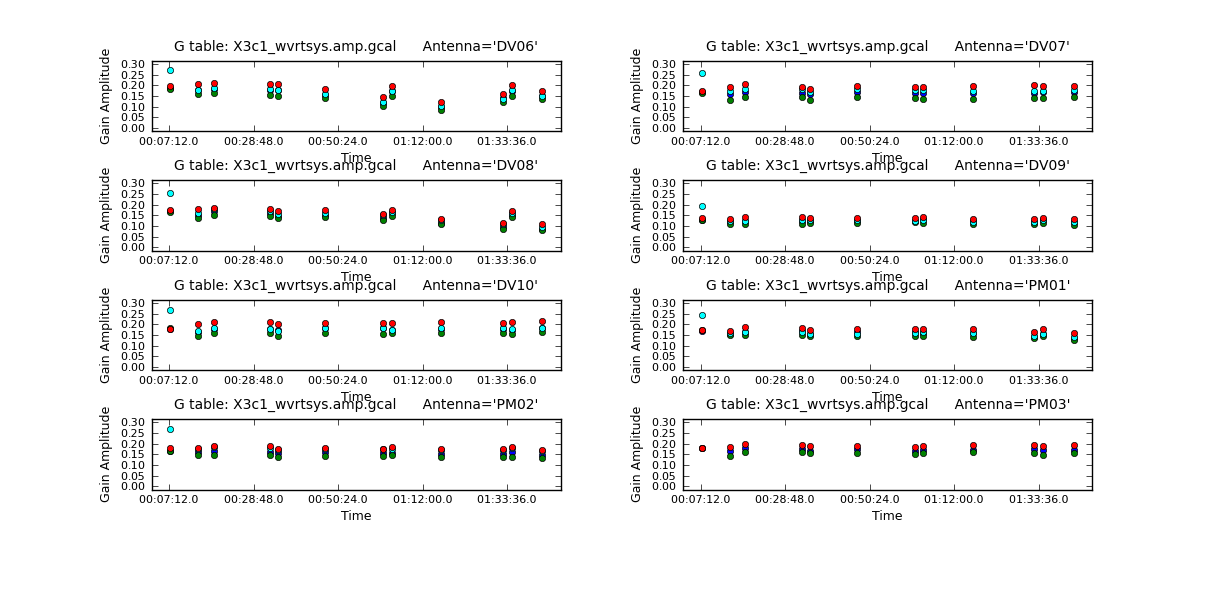
</figure>
# In CASA
plotcal(caltable='X3c1_wvrtsys.amp.gcal',xaxis='time',yaxis='phase',antenna='1~8',
spw='',field='0,1,3,4',plotrange=[0,0,-1,1],
iteration='antenna',subplot=421,figfile='X3c1_wvrtsys.amp_phase.png')
These are very small, as they should be. Now look at the amplitude solutions.
# In CASA
plotcal(caltable='X3c1_wvrtsys.amp.gcal',xaxis='time',yaxis='amp',antenna='1~8',
iteration='antenna',subplot=421,spw='',poln='X',
plotrange=[0,0,0.0,0.3],figfile='X3c1_wvrtsys.amp_X.png')
# In CASA
plotcal(caltable='X3c1_wvrtsys.amp.gcal',xaxis='time',yaxis='amp',antenna='1~8',
iteration='antenna',subplot=421,spw='',poln='Y',
plotrange=[0,0,0.0,0.3],figfile='X3c1_wvrtsys.amp_Y.png')
Flux Calibration
Next we use the flux calibrator (whose flux density was set in setjy above) to derive the flux density of the other calibrators. Note that the flux table REPLACES the amp.gcal in terms of future application of the calibration to the data, i.e. the flux table contains both the amp.gcal and flux scaling. Unlike the gain calibration steps, this is not an incremental table.
# In CASA
fluxscale(vis='X3c1_wvrtsys.ms',caltable='X3c1_wvrtsys.amp.gcal',
fluxtable='X3c1_wvrtsys.flux.cal',reference='1',refspwmap=[0,1,3,3],
listfile='X3c1_wvrtsys.fluxscale.txt')
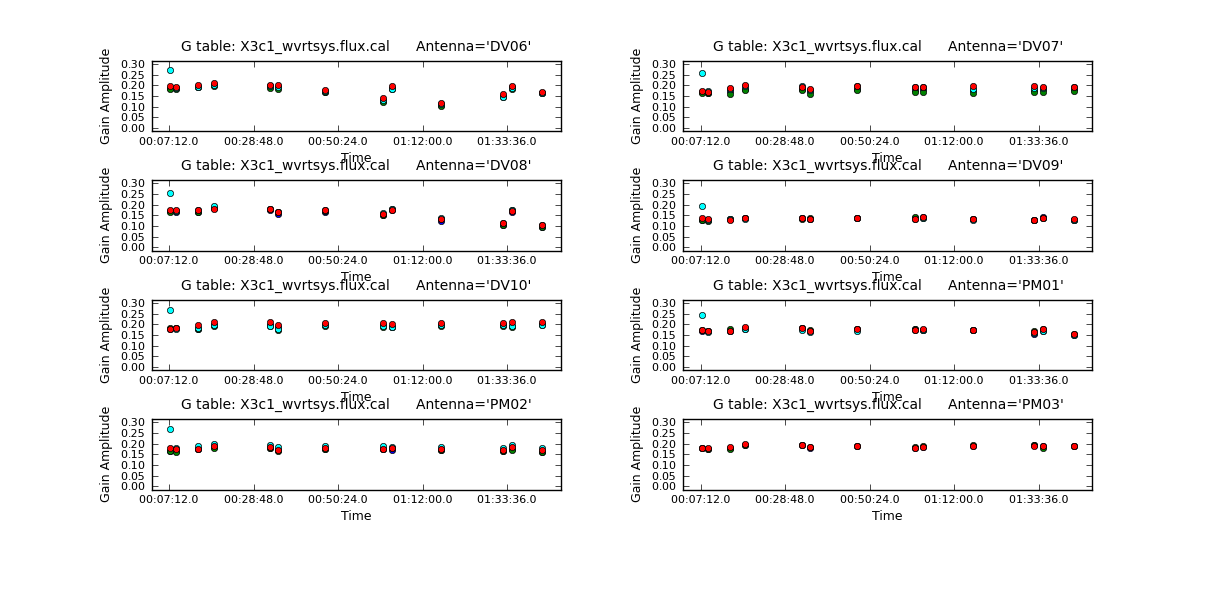
Its a good idea to record the derived fluxscale values using the listfile option. The values can also be viewed in the Log Messages window.
Found reference field(s): Titan Found transfer field(s): 3c279 J1147-382=QSO J1037-295=QSO Spw=2 will be referenced to spw=3 Flux density for 3c279 in SpW=0 is: 10.5734 +/- 0.0190156 (SNR = 556.039, N = 16) Flux density for 3c279 in SpW=1 is: 10.8103 +/- 0.0258999 (SNR = 417.388, N = 16) Flux density for 3c279 in SpW=2 (ref SpW=3) is: 10.4268 +/- 0.0524249 (SNR = 198.891, N = 14) Flux density for 3c279 in SpW=3 is: 10.0122 +/- 0.0216329 (SNR = 462.822, N = 16) Flux density for J1147-382=QSO in SpW=0 is: 1.04139 +/- 0.0167475 (SNR = 62.182, N = 16) Flux density for J1147-382=QSO in SpW=1 is: 0.838983 +/- 0.0191563 (SNR = 43.7968, N = 16) Flux density for J1147-382=QSO in SpW=2 (ref SpW=3) is: 1.02209 +/- 0.025659 (SNR = 39.8337, N = 14) Flux density for J1147-382=QSO in SpW=3 is: 1.299 +/- 0.0199392 (SNR = 65.1484, N = 16) Flux density for J1037-295=QSO in SpW=0 is: 0.967053 +/- 0.00942059 (SNR = 102.653, N = 16) Flux density for J1037-295=QSO in SpW=1 is: 0.758689 +/- 0.0157661 (SNR = 48.1215, N = 16) Flux density for J1037-295=QSO in SpW=2 (ref SpW=3) is: 0.963367 +/- 0.0181981 (SNR = 52.9377, N = 14) Flux density for J1037-295=QSO in SpW=3 is: 1.23762 +/- 0.0150691 (SNR = 82.1297, N = 16)
<figure id="x3c1_wvrtsys.flux_X.png">
</figure>
Now look at the flux solutions.
# In CASA
plotcal(caltable='X3c1_wvrtsys.flux.cal',xaxis='time',yaxis='amp',antenna='1~8',
iteration='antenna',subplot=421,spw='',poln='X',
plotrange=[0,0,0.0,0.3],figfile='X3c1_wvrtsys.flux_X.png')
# In CASA
plotcal(caltable='X3c1_wvrtsys.flux.cal',xaxis='time',yaxis='amp',antenna='1~8',
iteration='antenna',subplot=421,spw='',poln='Y',
plotrange=[0,0,0.0,0.3],figfile='X3c1_wvrtsys.flux_Y.png')
Apply Calibration and Inspect
Now we can use the flagmanager if we want to restore any of the spectral flagging we did prior to bandpass calibration. In this case, we choose to restore the flags of the emission lines on Titan, because we are interested in seeing how strong they are compared to the continuum. However, we leave the strong ozone line and mesospheric CO line flagged on all sources, because we want to get the most accurate continuum flux density for the science target.
# In CASA
flagmanager(vis='X3c1_wvrtsys.ms',mode='restore',versionname='X3c1_wvrtsys.before_emissionflags')
Next we apply the calibration solutions to each source individually, using the gainfield parameter to specify which calibrator's solutions should be applied from each of the gaintable calibration tables.
First, we do 3C279 (the bandpass calibrator), applying all 3 of its solutions to itself (that's why gainfield contains three zeros):
# In CASA
applycal(vis='X3c1_wvrtsys.ms',field='0',
gaintable=['X3c1_wvrtsys.bandpass.bcal','X3c1_wvrtsys.intphase.gcal','X3c1_wvrtsys.flux.cal'],
interp=['nearest','nearest','nearest'],
gainfield=['0','0','0'], flagbackup=T, calwt=F)
Next, we do Titan (the absolute flux calibrator) using the bandpass solution from 3C279:
# In CASA
applycal(vis='X3c1_wvrtsys.ms',field='1',
gaintable=['X3c1_wvrtsys.bandpass.bcal','X3c1_wvrtsys.intphase.gcal','X3c1_wvrtsys.flux.cal'],
interp=['nearest','nearest','nearest'],
gainfield=['0','1','1'], flagbackup=T, calwt=F)
For the secondary phase calibrator, we apply the phase and flux solutions from the primary phase calibrator. This will allow us to check how well the phase transfer to the science target (TW Hya) has worked:
# In CASA
applycal(vis='X3c1_wvrtsys..ms',field='3',
gaintable=['X3c1_wvrtsys..bandpass.bcal','X3c1_wvrtsys..scanphase.gcal','X3c1_wvrtsys..flux.cal'],
interp=['nearest','linear','linear'],
gainfield=['0','4','4'], flagbackup=T, calwt=F)
Next is the Primary phase calibrator:
# In CASA
applycal(vis='X3c1_wvrtsys.ms',field='4',
gaintable=['X3c1_wvrtsys.bandpass.bcal','X3c1_wvrtsys.intphase.gcal','X3c1_wvrtsys.flux.cal'],
interp=['nearest','nearest','nearest'],
gainfield=['0','4','4'], flagbackup=T, calwt=F)
Finally, for the Science Target TW Hya, we apply the phase solutions from both the primary and secondary phase calibrators:
# In CASA
applycal(vis='X3c1_wvrtsys.ms',field='2',
interp=['nearest','linear','linear'],
gaintable=['X3c1_wvrtsys.bandpass.bcal','X3c1_wvrtsys.scanphase.gcal','X3c1_wvrtsys.flux.cal'],
gainfield=['0','3,4','3,4'], flagbackup=T, calwt=F)
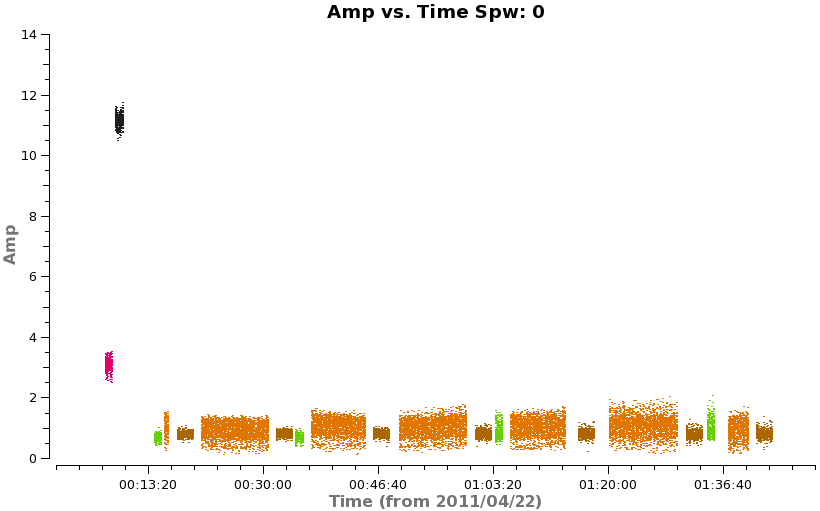
Now we can check the results of applying the calibration solutions.
<figure id="Corrected_vs_time_1.png">
</figure>
# In CASA
plotms(vis='X3c1_wvrtsys.ms',spw='',xaxis='time',yaxis='amp',field='',avgchannel='3840',
coloraxis='field',iteraxis='spw',ydatacolumn='corrected')
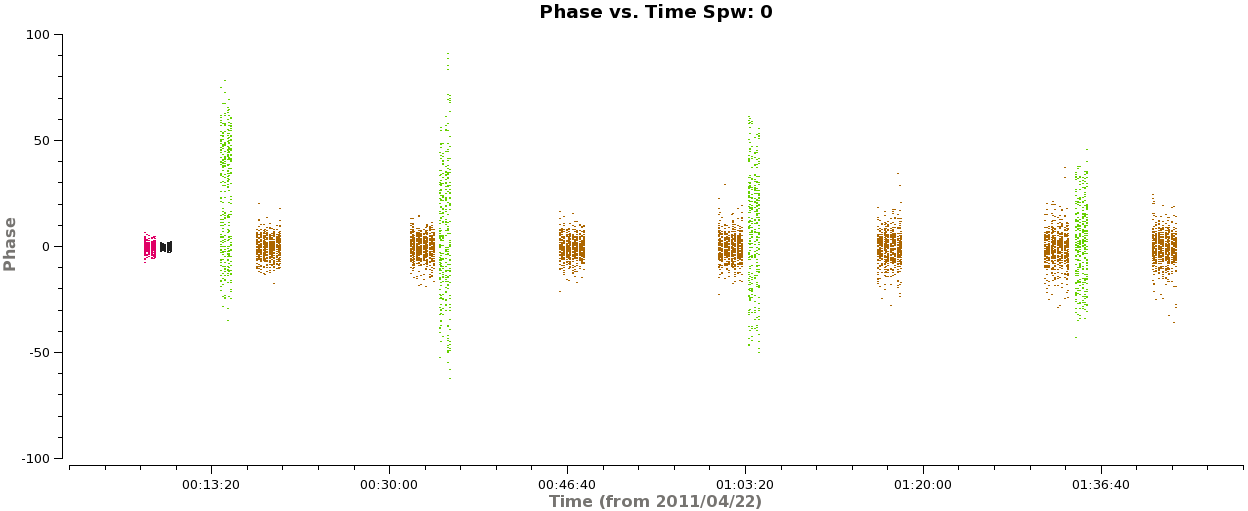
In amplitude, it looks good but there are some noisy points toward the end of the first scheduling block, but it mostly only affects the secondary phase calibrator (green). In phase, we expect all the points to cluster about zero. The large scatter in phase on the secondary phase calibrator is readily apparent:
<figure id="Corrected_phase_vs_time_1.png">
</figure>
# In CASA
plotms(vis='X3c1_wvrtsys.ms',spw='',xaxis='time',yaxis='phase',field='0,1,3,4',avgchannel='3840',
coloraxis='field',iteraxis='spw',ydatacolumn='corrected')
Let's check whether the situation improves when we apply this calibrator's solutions to itself rather than transferring the solutions from the primary phase calibrator (which is 17 degrees away, and observed at a different time).
# In CASA
applycal(vis='X3c1_wvrtsys.ms',field='3',
gaintable=['X3c1_wvrtsys.bandpass.bcal','X3c1_wvrtsys.intphase.gcal','X3c1_wvrtsys.flux.cal'],
interp=['nearest','nearest','nearest'],
gainfield=['0','3','3'],flagbackup=T)
<figure id="Corrected_vs_time_1_field3.png">
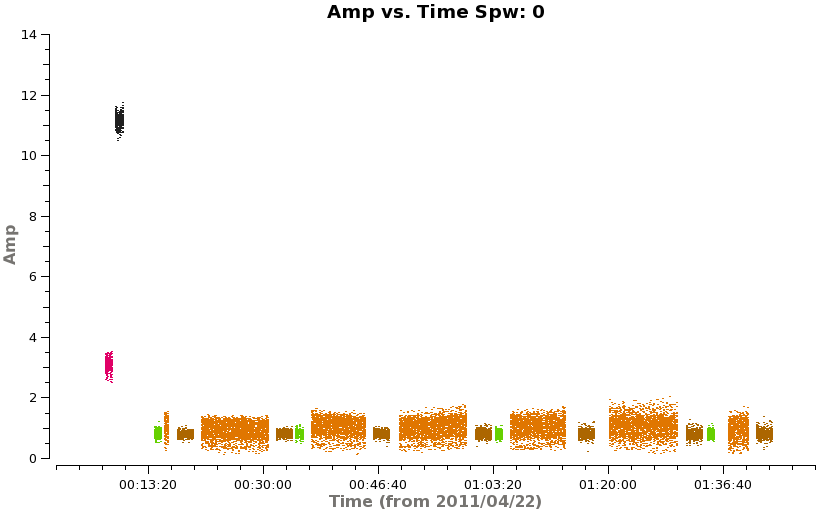
</figure>
# In CASA
plotms(vis='X3c1_wvrtsys.ms',spw='',xaxis='time',yaxis='amp',field='',avgchannel='3840',
coloraxis='field',iteraxis='spw',ydatacolumn='corrected')
<figure id="Corrected_phase_vs_time_1_field3.png">
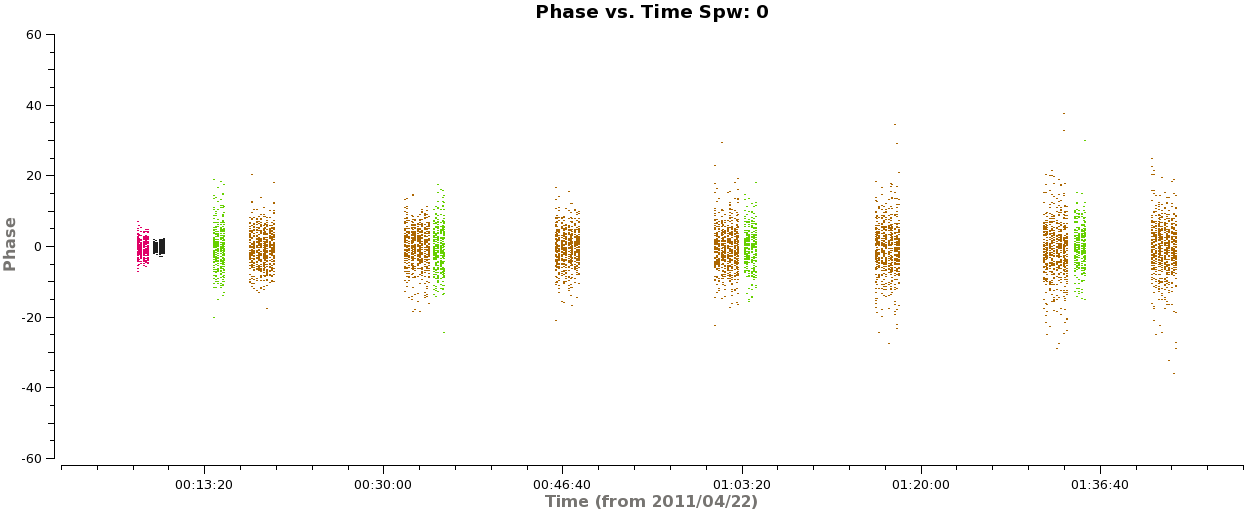
</figure>
# In CASA
plotms(vis='X3c1_wvrtsys.ms',spw='',xaxis='time',yaxis='phase',field='0,1,3,4',
avgchannel='3840', coloraxis='field',iteraxis='spw',
ydatacolumn='corrected')
Indeed, the secondary calibrator looks better now in amplitude and phase. This is an indication that the calibration transfer is not working well in this timerange. Because the effect is not catastrophic and we know we can self-calibrate on TW Hya later, we will let this go for now. Or, if you want you can delve deeper into the data and try to solve the mystery...
In any case, we will re-issue the original applycal so that it is this calibration that our subsequent split will use. This will allow us to check the effect of correcting the secondary phase calibrator with the primary phase calibrator later.
# In CASA
applycal(vis='X3c1_wvrtsys.ms',field='3',
gaintable=['X3c1_wvrtsys.bandpass.bcal', 'X3c1_wvrtsys.scanphase.gcal', 'X3c1_wvrtsys.flux.cal'],
interp=['nearest','linear','linear'],
gainfield=['0','4','4'], flagbackup=T, calwt=F)
Let's check the spectral calibration now. First 3C279 and Titan:
<figure id="X3c1_spw2_corrected_3.4.png">
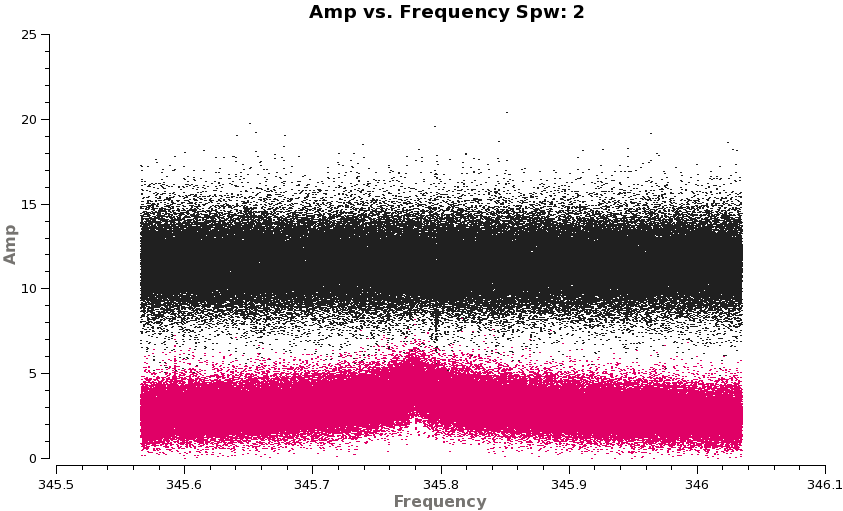
</figure>
# In CASA
plotms(vis='X3c1_wvrtsys.ms',spw='',xaxis='frequency',yaxis='amp',field='0,1',
avgtime='1e8',avgscan=T,coloraxis='field',ydatacolumn='corrected',
iteraxis='spw',xselfscale=T)
Flip through the spws. These look good. Next the two phase calibrators:
# In CASA
plotms(vis='X3c1_wvrtsys.ms',spw='',xaxis='frequency',yaxis='amp',field='3,4',
avgtime='1e8',avgscan=T,coloraxis='field',ydatacolumn='corrected',
iteraxis='spw',xselfscale=T)
Flip through the spws. This also looks good, the secondary phase calibrator is a bit noisier but this is normal. The upswing at the lower frequency end of spw=3 will probably need to be flagged on the science target as well. It corresponds to the edge of an atmospheric feature.
Now for the exciting part, what does the science target look like...
# In CASA
plotms(vis='X3c1_wvrtsys.ms',spw='',xaxis='frequency',yaxis='amp',field='2',
avgtime='1e8',avgscan=T,coloraxis='field',ydatacolumn='corrected',
iteraxis='spw',xselfscale=T)
We see HCO+(4-3) in spw=0 and CO(3-2) in spw=2 as expected. Because the shape of the line profiles varies with baseline, you can already tell that the line emission is resolved.
<figure id="X3c1_CO3_2_uvplot_3.4.png">

</figure> <figure id="X3c1_HCOp4_3_uvplot_3.4.png">
</figure>
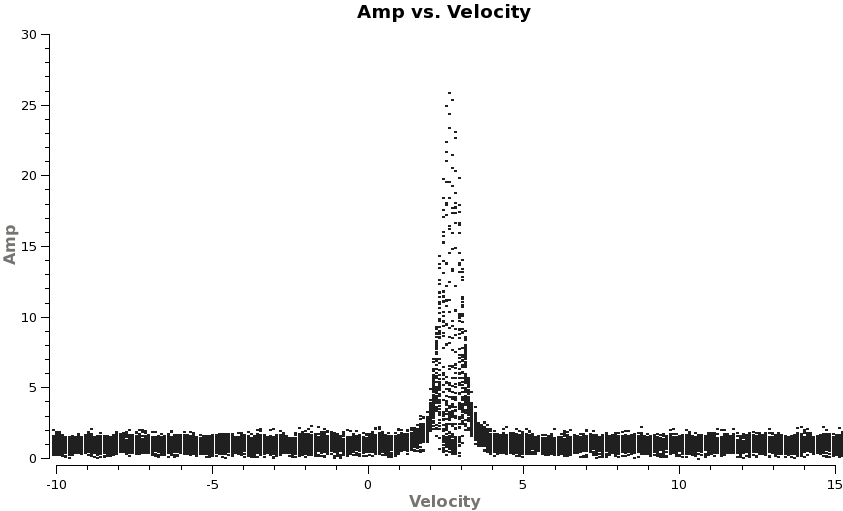
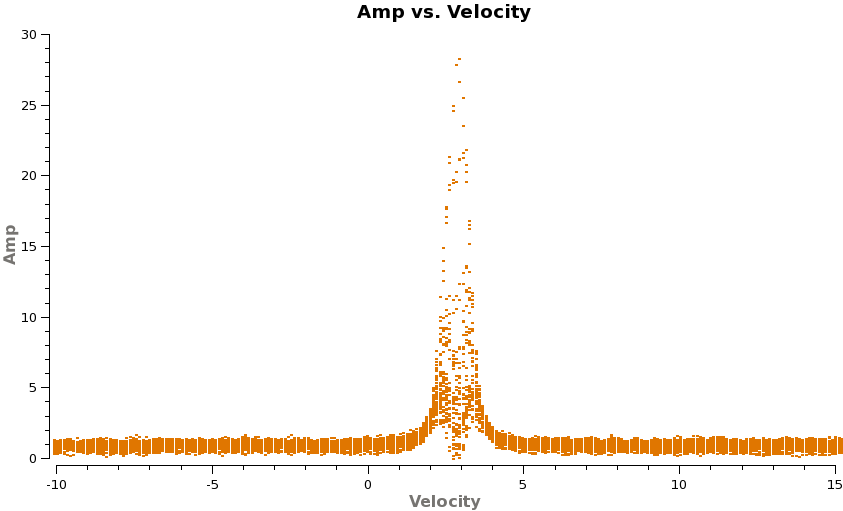
Now check that the velocity of TWHydra is correct in the LSRK frame, it should be around 2.88 km/s.
- CO 3-2 rest freq 345.79599 GHz
- HCO+ 4-3 rest freq 356.7342 GHz
# In CASA
plotms(vis='X3c1_wvrtsys.ms',spw='2',xaxis='velocity',yaxis='amp',field='2',
avgtime='1e8',avgscan=T,transform=T,freqframe='LSRK',
restfreq='345.79599GHz', plotrange=[-10,15,0,0],coloraxis='spw')
# In CASA
plotms(vis='X3c1_wvrtsys.ms',spw='0',xaxis='velocity',yaxis='amp',field='2',
avgtime='1e8',avgscan=T,transform=T,freqframe='LSRK',
restfreq='356.7342GHz',plotrange=[-10,15,0,0],coloraxis='spw')
Both lines show up at the expected velocity.
Concatenate the Data
Here we will concatenate the three datasets prior to imaging.
# In CASA
splitdata=['X3c1_wvrtsys.ms','X5d8_wvrtsys.ms','X7ef_wvrtsys.ms']
os.system('rm -rf Band7multi_april22.ms')
concat(vis=splitdata,concatvis='Band7multi_april22.ms')
If you like you can run listobs on new combined dataset
# In CASA
listobs(vis='Band7multi_april22.ms',verbose=F, listfile='Band7multi_april22.listobs.txt')
<figure id="All_spw2_corrected_3.4.png">
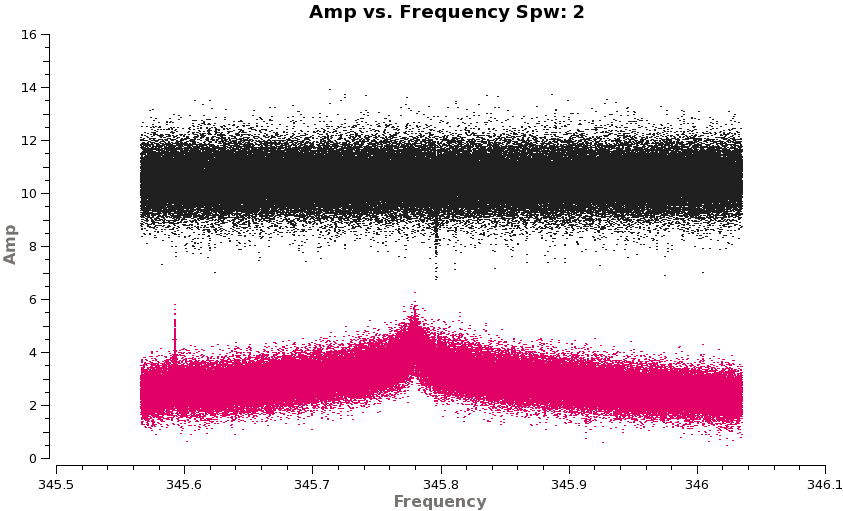
</figure>
You can also examine the spectral uv plots for the combined dataset to see the improvement in S/N:
# In CASA
plotms(vis='Band7multi_april22.ms',spw='',xaxis='frequency',yaxis='amp',field='0,1',
avgtime='1e8',avgscan=T,coloraxis='field',ydatacolumn='corrected',
iteraxis='spw',xselfscale=T)
<figure id="All_CO3_2_uvplot_3.4.png">
</figure>
...and the CO line profile for the combined dataset:
# In CASA
plotms(vis='Band7multi_april22.ms',spw='2',xaxis='velocity',yaxis='amp',field='2',
avgtime='1e8',avgscan=T,transform=T,freqframe='LSRK',restfreq='345.79599GHz',
plotrange=[-10,15,0,0],coloraxis='spw')
Fix Titan's Coordinates
Note that in the near future this step will be unnecessary.
At present, ALMA is writing the J2000 position of ephemeris objects as a fixed position throughout individual scheduling blocks. It is the position of the first observation. In the future, a polynomial describing the position will be filled. Currently, objects like Titan will be at slightly different positions in all three datasets. If we want to image such objects observed across multiple SBs, we need to bring the positions into agreement. Task fixplanets can be used to do this.
# In CASA
fixplanets(vis='Band7multi_april22.ms', field='Titan', fixuvw=True)
Check the header information again to see that the information for Titan has changed. Because concat begins with the final file in the list, the position for Titan will be the one from that ms.
# In CASA
listobs(vis='Band7multi_april22.ms',verbose=F)
ID Code Name RA Decl Epoch SrcId 0 none 3c279 12:56:11.1666 -05.47.21.5247 J2000 0 1 none Titan 12:49:26.5120 -02.22.10.8190 J2000 1 2 none TW Hya 11:01:51.9063 -34.42.17.0212 J2000 2 3 none J1147-382=Q* 11:47:01.3815 -38.12.11.1179 J2000 3 4 none J1037-295=Q* 10:37:16.0899 -29.34.02.9888 J2000 4
Split Calibrated Data
Now we split off the calibrated data for the Science Target as well as the interesting parts of the calibrators for imaging.
# In CASA
os.system('rm -rf TWHydra_corrected.ms')
split(vis='Band7multi_april22.ms',outputvis='TWHydra_corrected.ms',
datacolumn='corrected',spw='',field='2')
# In CASA
os.system('rm -rf J1037_corrected.ms')
split(vis='Band7multi_april22.ms',outputvis='J1037_corrected.ms',
datacolumn='corrected',spw='',field='4')
# In CASA
os.system('rm -rf J1147_corrected.ms')
split(vis='Band7multi_april22.ms',outputvis='J1147_corrected.ms',
datacolumn='corrected',spw='',field='3')
# In CASA
os.system('rm -rf J1147_corrected_with4.ms')
split(vis='Band7multi_april22.ms',outputvis='J1147_corrected_with4.ms',
datacolumn='corrected',spw='',field='3')
# In CASA
os.system('rm -rf Titan_cont.ms')
split(vis='Band7multi_april22.ms',outputvis='Titan_cont.ms',
datacolumn='corrected',spw='0',field='1')
# In CASA
os.system('rm -rf Titan_CO3_2.ms')
split(vis='Band7multi_april22.ms',outputvis='Titan_CO3_2.ms',
datacolumn='corrected',spw='2',field='1')
# In CASA
os.system('rm -rf Titan_unknown.ms')
split(vis='Band7multi_april22.ms',outputvis='Titan_unknown.ms',
datacolumn='corrected',spw='3',field='1')
# In CASA
os.system('rm -rf 3C279_CO3_2.ms')
split(vis='Band7multi_april22.ms',outputvis='3C279_CO3_2.ms',
datacolumn='corrected',spw='2:1900~2000',field='0')
Continue on to Imaging of the Science Target
Now you can continue on to the imaging guide.