VLA Continuum Intro Tutorial: Difference between revisions
| Line 1,142: | Line 1,142: | ||
where <math>G_i</math> is the complex gain for the <math>i^{\mathrm{th}}</math> antenna and <math>V_{ij}</math> is the true visibility. For an array of <math>N</math> antennas, at any given instant, there are <math>N(N-1)/2</math> visibility data, but only <math>N</math> gain factors. For an array with a reasonable number of antennas, <math>N</math> >~ 8, solutions to this set of coupled equations converge quickly. | where <math>G_i</math> is the complex gain for the <math>i^{\mathrm{th}}</math> antenna and <math>V_{ij}</math> is the true visibility. For an array of <math>N</math> antennas, at any given instant, there are <math>N(N-1)/2</math> visibility data, but only <math>N</math> gain factors. For an array with a reasonable number of antennas, <math>N</math> >~ 8, solutions to this set of coupled equations converge quickly. | ||
For a more detailed introduction to self-calibration, see our [https://casaguides.nrao.edu/index.php/Karl_G._Jansky_VLA_Tutorials#Self-calibration_of_VLA_Data VLA Self-calibration Tutorial]. | For a more detailed introduction to self-calibration, see our [https://casaguides.nrao.edu/index.php/Karl_G._Jansky_VLA_Tutorials#Self-calibration_of_VLA_Data VLA Self-calibration Tutorial]. We also have lectures on [https://science.nrao.edu/facilities/alma/naasc-workshops/nrao-cd-stsci/cde_selfcal.pdf Self-calibration] given at NRAO community days. In self-calibrating data, it is useful to keep in mind the structure of a Measurement Set: there are three columns of interest for an MS: the DATA column, the MODEL column, and the CORRECTED_DATA column. In normal usage, as part of the initial split, the CORRECTED_DATA column is set equal to the DATA column. The self-calibration procedure is then: | ||
* Produce an image ([https://casadocs.readthedocs.io/en/v6.5.4/api/tt/casatasks.imaging.tclean.html tclean]) using the CORRECTED_DATA column. | * Produce an image ([https://casadocs.readthedocs.io/en/v6.5.4/api/tt/casatasks.imaging.tclean.html tclean]) using the CORRECTED_DATA column. | ||
| Line 1,248: | Line 1,247: | ||
* In the case of a mosaic, such as here, one should also verify that the solutions are of equal quality for all of the fields. | * In the case of a mosaic, such as here, one should also verify that the solutions are of equal quality for all of the fields. | ||
= On Your Own: 3C391 second frequency and G93.3+6.9 = | = On Your Own: 3C391 second frequency and G93.3+6.9 = | ||
Revision as of 16:33, 23 April 2024
Notes on CASA
This CASA Guide is for Version 6.5.4 of CASA. If you are using a later version of CASA and this is the most recent available guide, then you should be able to use most, if not all, of this tutorial. This guide is meant to be completed using the monolithic CASA and not modular CASA as the GUI may not work correctly otherwise.
There are a number of possible ways to run CASA, described in more detail in Getting Started in CASA. In this tutorial we would like you to use either (or both) of the following methods so that you can familiarize yourself with the CASA software:
- Interactive: examining task inputs. In this mode, one types taskname to load the task, inp to examine the inputs, and go once those inputs have been set to your satisfaction. Allowed inputs are shown in blue and bad inputs are colored red. The input parameters themselves are changed one by one, e.g., selectdata=True. Screenshots of the inputs to various tasks used in the data reduction below are provided, to illustrate which parameters need to be set. More detailed help can be obtained on any task by typing help taskname. Once a task is run, the set of inputs is stored and can be retrieved via tget taskname; subsequent runs will overwrite the previous tget file.
- Pseudo-interactive: task function calls. In this mode, all of the desired inputs to a task are provided at once inn the CASA command line. This tutorial is made up of such calls, which were developed by looking at the inputs for each task and deciding what needed to be changed from default values. For task function calls, only parameters that you want to be different from their defaults need to be set.
This tutorial is largely self-paced. Any time you have a question, or something doesn't look right or you are unsure of, please do summon one of the tutors present in the room.
Data Set
This CASA guide describes the calibration and imaging of a multiple-pointing continuum data set taken with the Karl G. Jansky Very Large Array (VLA) of the supernova remnant 3C 391. The data were taken in early science shared-risk observing mode (before the full operations of the upgraded JVLA started), with 128 MHz of bandwidth in each of two spectral windows, centered at 4.6 and 7.5 GHz. While the observations had a full-polarization correlator setup and included a polarization calibrator, for the purposes of this tutorial we will focus on the total intensity continuum (Stokes I) calibration and imaging only.
You should already have the data set downloaded. If you do not, then it can be downloaded from here http://casa.nrao.edu/Data/EVLA/3C391/3c391_ctm_mosaic_10s_spw0.ms.tgz (but may be difficult to download over conference wi-fi, the data file is 3.1GB).
This data set has been pre-prepared for this tutorial, where several initial processing steps, listed below, have already been conducted. Many of these initial processing steps are often time consuming (> 1 hr), and while necessary in data processing, they go beyond the subject of calibration and imaging of this tutorial. Specifically, the following has been already done:
- The initial raw Science Data Model (SDM) file was converted into a Measurement Set (MS).
- Basic data flagging to account for shadowing of the antennas was applied. These data are from the D configuration, in which antennas are particularly susceptible to being blocked (shadowed) by other antennas in the array, depending upon the elevation of the source.
- The data were averaged from the initial 1-second correlator sample dump to 10-second samples. In the D configuration, the fringe rate is relatively slow and time-average smearing is less of a concern hence we can get away with 10-second averaging.
- Only one spectral window is considered in this step-by-step tutorial, mainly for a concern of disk space on laptops.
Before you can start the tutorial, the data set needs to be unzipped and unpacked (but first place the data set in the directory you will work in):
# In a terminal, inside your working directory: tar xzvf 3c391_ctm_mosaic_10s_spw0.ms.tgz
The Observation
Before starting the calibration process, it is recommended -if not necessary- to get some basic information about the data set. VLA operators that monitor the array when your data are being taken record observing conditions during the observing run, as well as problems with the data caused by the weather or misbehaving array hardware. Such an observing log can be downloaded from the observer log depository for almost all VLA observations.
To get the observing log of our observations, fill in the observing date (in our case 2010-Apr-24) as both the Start and Stop date, and click on the Show Logs button. The relevant log is labeled with the project code, TDEM0001, and can be downloaded as a PDF file.
While inspecting the log, you should find the following:
Information from observing log: There is no C-band receivers on ea13 Antenna ea06 is out of the array Antenna ea15 has some corrupted data Antennas ea10, ea12, ea22 do not have good baseline positions Gusty winds, mixed clouds, API rms up to 11.5.
We will get back to this information in some of later steps.
Now, if you have not yet started CASA, navigate to your working directory where the data set is saved, and start the software.
Once you have CASA up and running, start your data reduction by getting some basic information about the data as the first step: the listobs() task. This task will provide you with a listing of the individual scans (set amounts of time devoted to specific targets) comprising the observation, the frequency setup, source list, and antenna locations. To run the task, type the lines below that do not start with # (this sign marks a comment and is ignored by CASA):
# In CASA
obs_dict = listobs(vis='3c391_ctm_mosaic_10s_spw0.ms')
A Python dictionary containing some of the observation's fundamental information is created in the variable obs_dict and the listobs() output will show up in the CASA logger window.
You should see that there are ten sources observed:
- J1331+3030 = 3C 286, a primary calibrator for the visibility amplitudes, i.e., it is assumed to have a precisely known flux density, and a bandpass calibrator;
- J1822-0938, a calibrator for the visibility phases;
- J0319+4130 = 3C 84, a polarization calibrator (ignored in this tutorial); and
- 3C391 C1--C7, which are 7 fields centered on and surrounding the supernova remnant.
This observation was set up as a 7-pointing mosaic because the supernova remnant is so large that it essentially fills the primary beam.
Excerpt of the listobs() output (cut out lines indicated by [....]):
##########################################
##### Begin Task: listobs #####
listobs(vis="3c391_ctm_mosaic_10s_spw0.ms",selectdata=True,spw="",field="",antenna="",
uvrange="",timerange="",correlation="",scan="",intent="",
feed="",array="",observation="",verbose=True,listfile="",
listunfl=False,cachesize=50,overwrite=False)
================================================================================
MeasurementSet Name: 3c391_ctm_mosaic_10s_spw0.ms MS Version 2
================================================================================
Observer: Dr. James Miller-Jones Project: T.B.D.
Observation: EVLA
Data records: 845379 Total integration time = 28681.5 seconds
Observed from 24-Apr-2010/08:02:10.0 to 24-Apr-2010/16:00:11.5 (UTC)
ObservationID = 0 ArrayID = 0
Date Timerange (UTC) Scan FldId FieldName nRows SpwIds Average Interval(s) ScanIntent
24-Apr-2010/08:02:10.0 - 08:02:30.0 1 0 J1331+3030 650 [0] [10]
08:02:20.0 - 08:09:30.0 2 0 J1331+3030 13975 [0] [10]
08:09:20.0 - 08:16:28.0 3 0 J1331+3030 13975 [0] [10]
08:19:38.0 - 08:24:26.5 4 1 J1822-0938 7035 [0] [10]
08:24:48.0 - 08:29:48.0 5 2 3C391 C1 7590 [0] [10]
08:29:38.0 - 08:34:48.0 6 3 3C391 C2 7821 [0] [10]
08:34:38.0 - 08:39:48.0 7 4 3C391 C3 7821 [0] [10]
08:39:38.0 - 08:44:48.0 8 5 3C391 C4 7821 [0] [10]
08:44:38.0 - 08:49:48.0 9 6 3C391 C5 7843 [0] [10]
08:49:38.0 - 08:54:48.0 10 7 3C391 C6 7843 [0] [10]
08:54:38.0 - 08:59:43.5 11 8 3C391 C7 7843 [0] [10]
09:00:03.0 - 09:01:31.0 12 1 J1822-0938 2925 [0] [10]
09:01:52.0 - 09:06:52.0 13 2 3C391 C1 7941 [0] [10]
09:06:42.0 - 09:11:52.0 14 3 3C391 C2 9801 [0] [10]
09:11:42.0 - 09:16:52.0 15 4 3C391 C3 10075 [0] [10]
09:16:42.0 - 09:21:52.0 16 5 3C391 C4 10050 [0] [10]
09:21:42.0 - 09:26:52.0 17 6 3C391 C5 10075 [0] [10]
09:26:42.0 - 09:31:52.0 18 7 3C391 C6 10075 [0] [10]
09:31:42.0 - 09:36:47.5 19 8 3C391 C7 10075 [0] [10]
09:37:07.0 - 09:38:35.0 20 1 J1822-0938 2900 [0] [10]
[....]
(nRows = Total number of rows per scan)
Fields: 10
ID Code Name RA Decl Epoch SrcId nRows
0 N J1331+3030 13:31:08.287984 +30.30.32.95886 J2000 0 31964
1 J J1822-0938 18:22:28.704200 -09.38.56.83501 J2000 1 39733
2 NONE 3C391 C1 18:49:24.244000 -00.55.40.58001 J2000 2 105580
3 NONE 3C391 C2 18:49:29.149001 -00.57.48.00001 J2000 3 110533
4 NONE 3C391 C3 18:49:19.339000 -00.57.48.00001 J2000 4 110331
5 NONE 3C391 C4 18:49:14.434001 -00.55.40.58001 J2000 5 110862
6 NONE 3C391 C5 18:49:19.339000 -00.53.33.16000 J2000 6 110546
7 NONE 3C391 C6 18:49:29.149001 -00.53.33.16000 J2000 7 109884
8 NONE 3C391 C7 18:49:34.054000 -00.55.40.58001 J2000 8 107178
9 Z J0319+4130 03:19:48.160102 +41.30.42.10305 J2000 9 8768
Spectral Windows: (1 unique spectral windows and 1 unique polarization setups)
SpwID Name #Chans Frame Ch0(MHz) ChanWid(kHz) TotBW(kHz) CtrFreq(MHz) Corrs
0 Subband:0 64 TOPO 4536.000 2000.000 128000.0 4599.0000 RR RL LR LL
Sources: 10
ID Name SpwId RestFreq(MHz) SysVel(km/s)
0 J1331+3030 0 - -
1 J1822-0938 0 - -
2 3C391 C1 0 - -
[....]
##### End Task: listobs #####
##########################################
Notice that in this listobs() output, the first scans are the fields that will be used for calibration - they are observed before the target fields; what do you think: is there a reason to set up observations like that? Is it necessary?
Note the portion listing the spectral windows (in this tutorial there is only one, spw='0'):
Spectral Windows: (1 unique spectral windows and 1 unique polarization setups) SpwID Name #Chans Frame Ch0(MHz) ChanWid(kHz) TotBW(kHz) CtrFreq(MHz) Corrs 0 Subband:0 64 TOPO 4536.000 2000.000 128000.0 4599.0000 RR RL LR LL
In the calibration steps below we will define spw and channel range. Since this C-band instrument configuration uses Full polarization, the spw has 64 channels that are 2.0MHz wide. You can also find what frequency of the first channel is.
Antennas. Note that the antenna IDs (which are numbered sequentially up to the total number of antennas in the array; how many do we have here?) do not correspond to the actual antenna names (ea01 through ea28; these numbers correspond to those painted on the side of the dishes). The antennas can be referenced using either convention; 'that is, 'antenna='22' would correspond to ea23, whereas antenna='ea22' would correspond to ea22. Note that the antenna numbers in the observer log correspond to the actual antenna names, i.e., the 'ea??' numbers given in listobs.
Both to get a sense of the array, as well as identify an antenna for later use in calibration, use the task plotants() (output shown in Figure 1). In general, for calibration purposes, one would like to select an antenna that is close to the center of the array (and that is not listed in the operator's log as having had problems!).
# In CASA
plotants(vis='3c391_ctm_mosaic_10s_spw0.ms',figfile='plotants_3c391_antenna_layout.png')
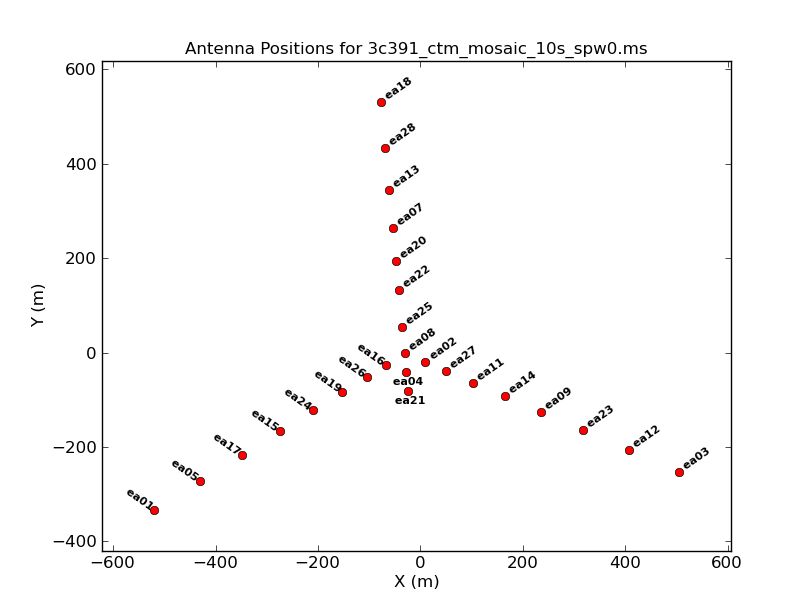
Question:
Please indicate to the tutors that you have arrived to this stage. We will discuss the choice of the reference antenna with the whole group. |
Examining and Editing the Data
It is always a good idea to examine the data before jumping straight into calibration; you do want to remove the most offending RFI before modeling your data. Moreover, from the observer's log, we already know that one antenna will need to be flagged because it does not have a C-band receiver. Start by flagging data known to be bad, after that examine the data visually for any apriori unknown issues, or RFI.
Flagging for known issues
In the VLA scheduling block configuration, it is common to insert a setup scan as the first scan. In the listobs() output above, you might have noticed that the first scan is less than 1 minute long; we can safely flag it since it is a setup scan.
# In CASA
flagdata(vis='3c391_ctm_mosaic_10s_spw0.ms', flagbackup=True, mode='manual', scan='1')
- flagbackup=True : If set to True, flagdata() will save a copy of the existing set of flags before entering any new flags. It is up to you if you want to save every flagging step. For example you could choose to save only major flags, or not save them at all (though think about a situation if you would like to revert an accidental or incorrect flag..). flagbackup=True is the default.
- mode='manual' : Specific data ranges or portions from the set will be selected for editing.
- scan='1' : is chosen to select only the first scan. Note that scan expects an entry in the form of a string (scan=1 would generate an error).
If satisfied with the inputs, run this task. The initial display in the logger should be something like this:
########################################## ##### Begin Task: flagdata ##### . . . . Backup original flags before applying new flags Table type is Measurement Set Creating new backup flag file called flagdata_1 Table type is Measurement Set Manual mode is active Initializing the agents autocorr is 0 There are 1 valid agents in list Running the agentflagger tool ------------------------------------------------------------------------------------ Chunk = 1 [progress: 100%], Observation = 0, Array = 0, Scan = 1, Field = 0 (J1331+3030), Spw = 0, Channels = 64, Corrs = [ RR RL LR LL ], Total Rows = 650 => Data flagged so far 100% ==================================================================================== => Percentage of data flagged in table selection: 100% => Writing flags to the MS . . ##### End Task: flagdata ##### ##########################################
Note that the flags that existed in the data set prior to this run will be saved to another file called flagdata_1. Should you ever need to revert to the data prior to this run, the task flagmanager() can be used. Also note that the values of all the task parameters (explicit or hidden) are given at the start of the task listing.
It is common for the array to require a small amount of time to settle down at the start of a scan. Consequently, it has become standard practice to flag the initial samples from the start of each scan. This is known as 'quack' flagging.
# In CASA
flagdata(vis='3c391_ctm_mosaic_10s_spw0.ms', mode='quack', quackinterval=10.0, quackmode='beg')
- mode='quack' : a flagging mode in which the same edit will be applied to all scans for all baselines.
- quackmode='beg' : In this case, data from the start of each scan will be flagged. Other options include flagging data at the end of the scan.
- quackinterval=10 : In this data set, the sampling time is 10 seconds, hence here the first sample from all scans on all baselines will be flagged.
Now return to the observer's log and find out what antennas have known problems. We will flag these antennas now:
# In CASA
flagdata(vis='3c391_ctm_mosaic_10s_spw0.ms', flagbackup=True, mode='manual', antenna='xxxx')
- antenna='xxxx' : requires a string input. Remember the difference between referring to antenna='ea01' and antenna='01' (discussed a few paragraphs earlier).
Inspecting data and further flagging
Having now done some basic editing of the data, based in part on a priori information, it is time to look at the data to determine if there are any other obvious problems. We will use the plotms() task to examine our data.
# In CASA
clearstat() # This removes any existing table locks generated by flagdata
plotms(vis='3c391_ctm_mosaic_10s_spw0.ms', selectdata=True, correlation='RR,LL', averagedata=True, avgchannel='64', coloraxis='field')
- selectdata=True : We want to plot here only selected subsets of our data.
- correlation='RR,LL' : Plot only the left- and right-handed polarization correlation products. The cross-terms ('RL' and 'LR') will be close to zero for non-polarized sources.
- averagedata=True: We want to average data points before plotting them (often to speed up loading time, but also because it will highlight RFI).
- avgchannel='64' : Here we are plotting fields vs time, so averaging over all 64 channels in the spectral window will make plotting faster.
- coloraxis='field' : Color-code the plotting symbols by field name/number.
The default x- and y-axis parameters are 'time' and 'amp', so the above call to plotms produces an amplitude vs time plot of the data for a selected subset of the data (if desired) and with data averaging (if desired). Many other values have also been left to defaults, but it is possible to select them from within the plotms GUI.
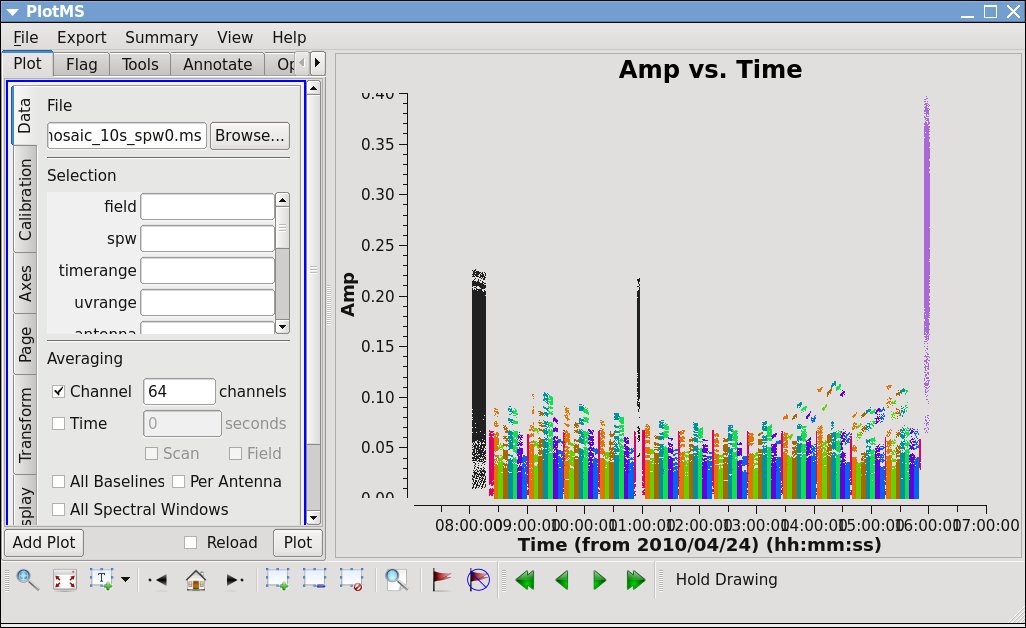 |
You can quickly see that the last source observed (J0319+4130, a polarization calibrator, shown in purple) is the brightest source in this observation. The next brightest is the first source observed (J1331+3030, a.k.a. 3C286, shown in black), which was also observed about a third of the way through the scheduling block. The complex gain calibrator (J1822-0938, shown in magenta) is slightly brighter than the target fields. Even though each of the target scans is on the same source (3C391), the observation is done as a mosaic of 7 fields (see the listobs() output earlier). Each of the 7 3C391 fields is given its own field number/name identification, so each is shown as its own color. The spread of amplitudes in each field is partly due to the difference in gain on each antenna and baseline. Data calibration will take care of much of that scatter.
Across the top of the left panel are a set of tabs labeled Plot, Flag, Tools, Annotate, and Options. In the default view, the Plot tab is visible, and there are a number of tabs running down the side of the left hand panel, including Data, Calibration, Axes, Page, Transform, Display, and Canvas. These allow you to make changes to the plotting selection without having to re-launch plotms. Even if was started with xaxis=' ' (defaulting to 'time'), you can choose a different X-axis by selecting the Axes tab, then using the dropdown menu to switch to (for example) xaxis='Frequency' (although to get something sensible when plotting with frequency, channel averaging must be turned off). You can save the version of the plotms plot as a graphics file by using the menu bar in the plotms GUI to select the Export... option under the Export menu.
You should spend several minutes displaying the data in various ways. Below are three important examples.
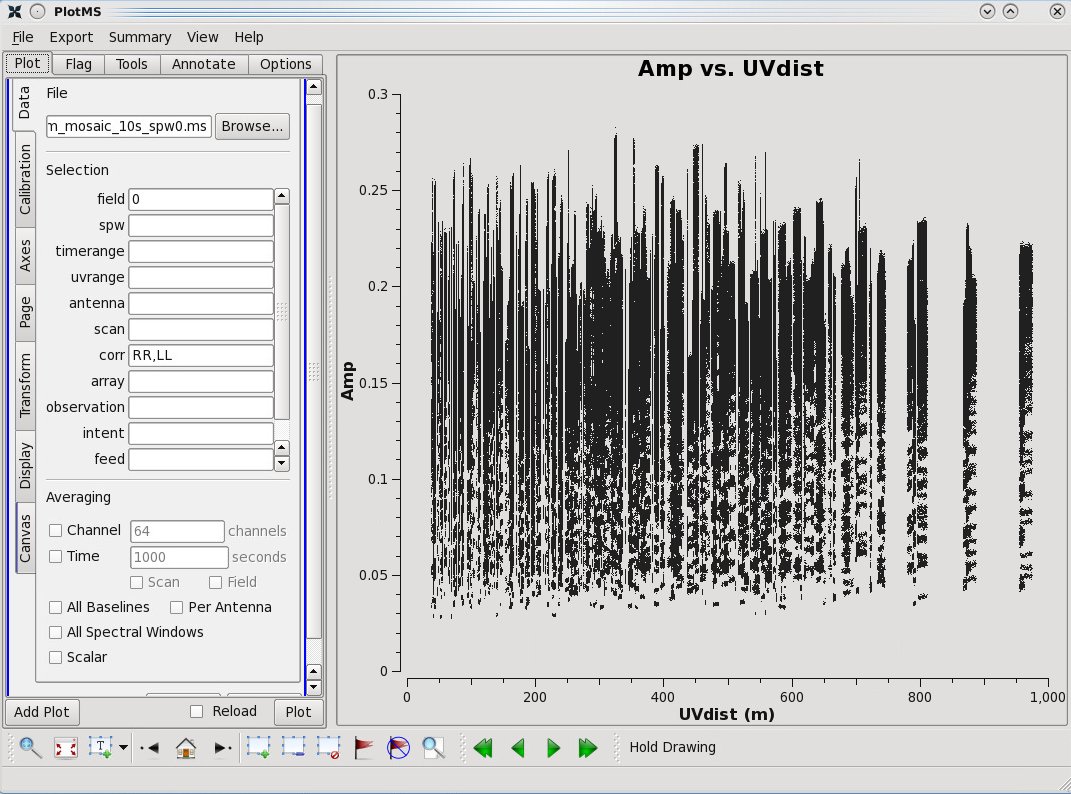
1. Select the Data tab and specify field 0 (source J1331+3030, a.k.a. 3C 286) to display data associated with the amplitude calibrator. Then select the Axes tab and change the X-axis to be UVdist (baseline length in meters). To plot baseline length in wavelengths rather than meters, select UVwave as the X-axis parameter. Remove the channel averaging (Data tab), and plot the data using the Plot button at the bottom of the plotms GUI. The result should be similar to Figure 3A. Again, the scatter is normal at this pre-calibration stage. The important thing is that the amplitude distribution is relatively constant as a function of UV distance or baseline length (i.e., [math]\displaystyle{ \sqrt{u^2+v^2} }[/math] ).
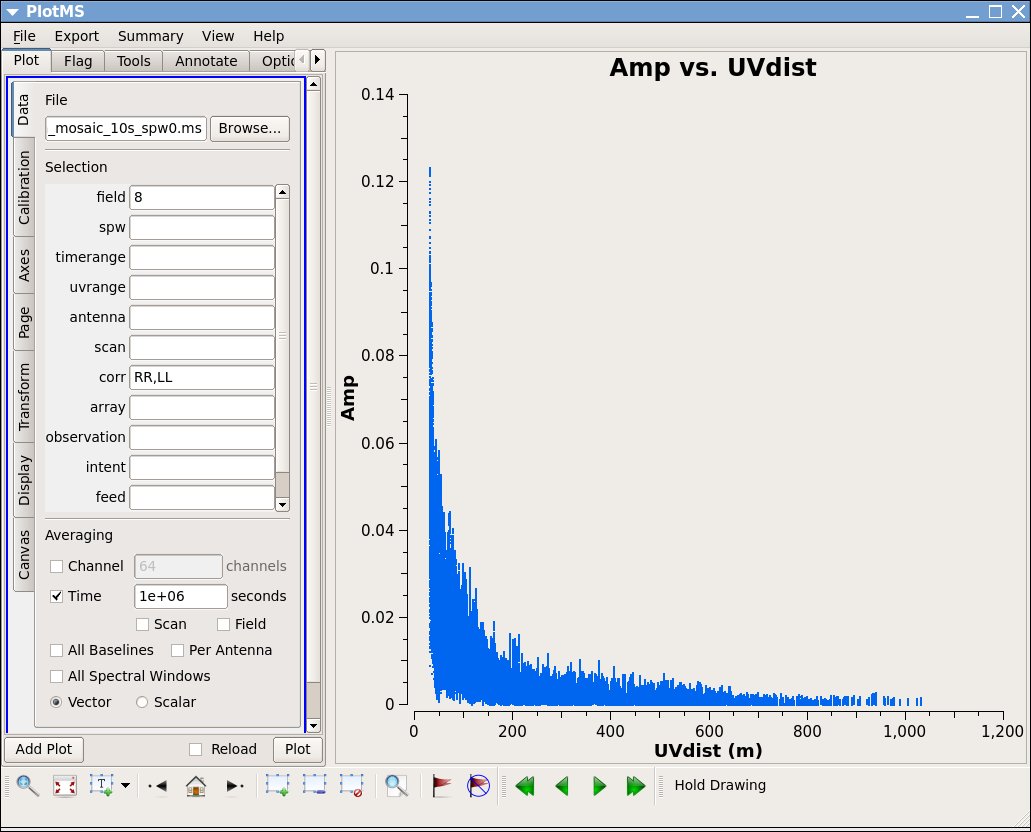
2. By contrast, if you make a similar plot as above but for field 8 (one of the 3C 391 fields), the result is a visibility function that falls rapidly with increasing baseline length. Figure 3B shows this example, including time averaging of '1e6' seconds (any large number that encompasses more than a full scan will do).
 |
 |
Question:
|
3. A final example is shown in Figure 3C. In this example, we have elected to show phase as a function of (frequency) channel for a single baseline (antenna='ea01&ea21' ) on the bandpass calibrator. If you choose to iterate by baseline (e.g., antenna='ea01' and iteraxis='baseline' ), you can see similar phase-frequency variations on all baselines, but with different slopes. These linear variations are 'delays' that need to be calibrated for. We have chosen to colorize by scan; it's clear that the slopes are steady over time. The two different lines for each baseline correspond to the 'RR' and 'LL' polarization correlations.
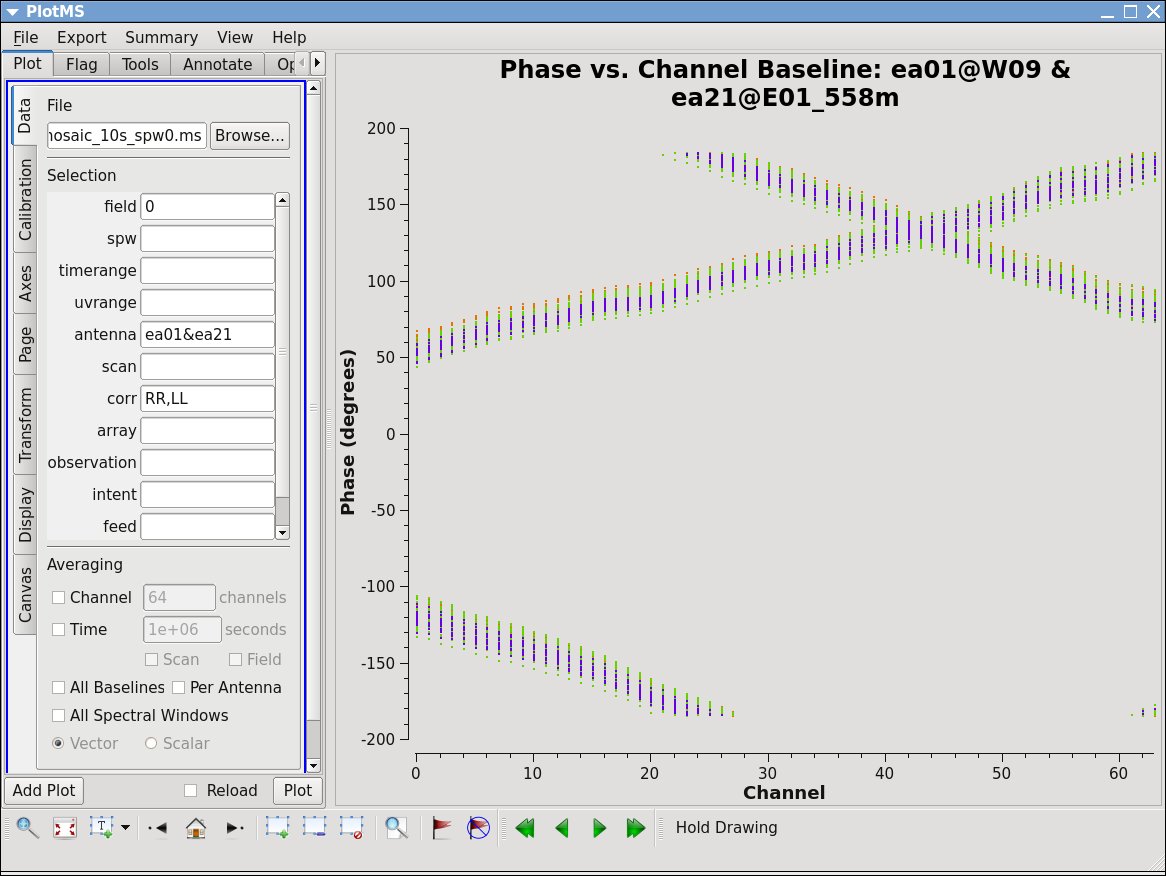 |
At this stage in the data reduction process, you should focus predominantly on the calibrators. The strategy is to determine various corrections from the calibrators, then apply these correction factors to the science target in your observations. The 3C 286 data look relatively clean in that there are no wildly egregious data point (e.g., amplitudes that are 100,000x larger than the rest of the data). You may notice that there are antenna-to-antenna variations (under the Display tab select Colorize by Antenna1). These antenna-to-antenna variations are acceptable, this variation is taken care of by the calibration process.
One final useful plot we will make is a datastream plot of the antenna2 in a baseline for the data versus ea01, using spw 0 and channel 31. This shows when various antennas drop out (assuming that ea01 is in the entire observation).
# In CASA
plotms(vis='3c391_ctm_mosaic_10s_spw0.ms',field='',correlation='RR,LL',
timerange='',antenna='ea01',spw='0:31', xaxis='time',yaxis='antenna2',
plotrange=[-1,-1,0,26],coloraxis='field')
Result is in Figure 4 below. You should immediately see that the flagging we did earlier of antennas 10 and 12 (ea13 and ea15) has taken effect. You may also notice that antennas 1, 6, and 13 (ea02, ea08, and ea16) are missing some blocks toward the beginning and the end of the observing run. Antenna 3 (ea04) is missing the last scan and antenna 23 (ea26) is missing scans near the end. None of these antennas should be chosen as the reference antenna during the calibration process.
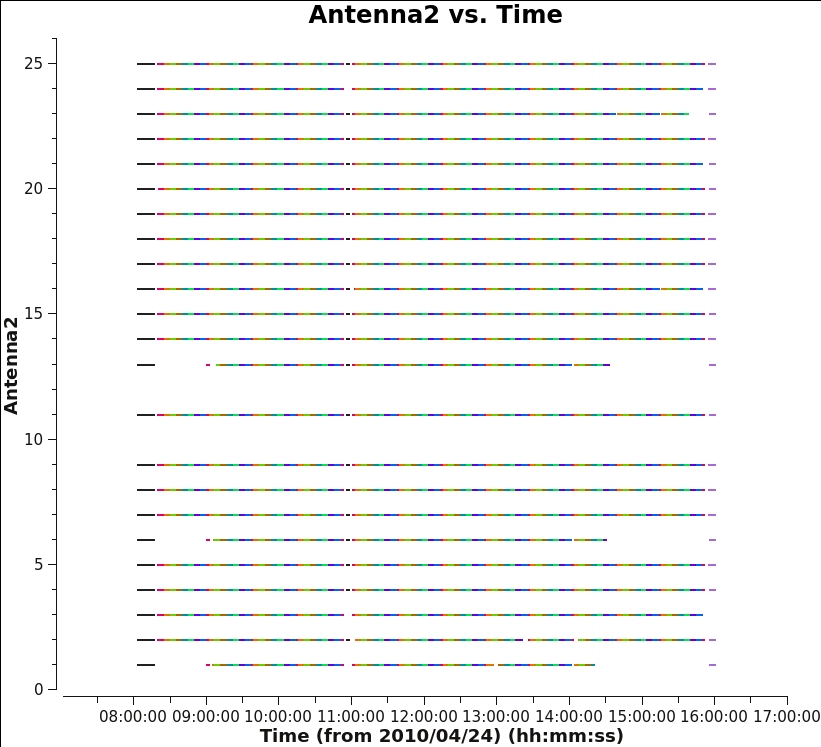 |
Calibrating the Data
We are now ready to begin calibrating the data. The general calibration strategy is to derive a series of scaling factors or corrections from the calibrators, which are then collectively applied to the science data. For more discussion of the philosophy, strategy, and implementation of calibration of synthesis data within CASA, see Synthesis Calibration in the CASA documentation.
Recall that the observed visibility [math]\displaystyle{ V^{\prime} }[/math] between two antennas [math]\displaystyle{ (i,j) }[/math] is related to the true visibility [math]\displaystyle{ V }[/math] by:
[math]\displaystyle{ V^{\prime}_{i,j}(u,v,f) = b_{ij}(t)\,[B_i(f,t) B^{*}_j(f,t)]\,g_i(t) g_j(t)\,V_{i,j}(u,v,f)\,e^{i [\theta_i(t) - \theta_j(t)]} }[/math]
Here we show the visibility as a function of frequency [math]\displaystyle{ f }[/math] and spatial wave numbers [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math]. The other terms are:
- [math]\displaystyle{ g_i }[/math] and [math]\displaystyle{ \theta_i }[/math] are the amplitude and phase portions of what is commonly termed the complex gain. They are shown separately here because they are usually determined separately. For completeness, these are shown as a function of time [math]\displaystyle{ t }[/math] to indicate that they can change with temperature, atmospheric conditions, etc.
- [math]\displaystyle{ B_i }[/math] is the complex bandpass, the instrumental response as a function of frequency [math]\displaystyle{ f }[/math]. As shown here, the bandpass may also vary as a function of time.
- [math]\displaystyle{ b(t) }[/math] is the often-neglected baseline term. It can be important to include for the highest dynamic range images or shortly after a configuration change at the VLA, when antenna positions may not be known well.
Strictly, the equation above is a simplification of a more general measurement equation formalism, but it is a useful simplification in many cases.
Step 1: A priori Antenna Position Corrections
Given the VLA is composed of 27 individual antennas, it is necessary to know their exact positions in order to correctly correlate (match and combine) each signal. Observations are sometimes made before some antenna positions are known exactly, as they can be corrected if the positions are known later. As mentioned in the observing log above, antennas ea10, ea12, and ea22 do not have good baseline positions. Antenna ea10 was not in the array, but, for the other two antennas, any improved baseline positions need to be incorporated. The importance of this step is that the visibility function is a function of [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math]. If the baseline positions are incorrect, then [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math] will be calculated incorrectly and there will be errors in the image. These corrections could also be determined later by a baseline-based calibration incorporating the [math]\displaystyle{ b_{ij} }[/math] term from the equation above, but since they are known a priori it makes sense to incorporate them now.
NRAO monitors the positions of the VLA antennas on a regular basis. The corrections are then placed into an NRAO database. If updated positions were entered into the database AFTER your observation date, the corrections to the newly measured positions can still be applied during your data reduction process in this step. Any updated positions that were entered into the database BEFORE your observations will already be accounted for in your data.
The calculations are inserted via gencal() which allows automated lookup of the corrections. To see how to calculate corrections manually, go to the VLA Baseline Corrections site.
# In CASA
gencal(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic_10s_spw0.antpos',caltype='antpos')
In the logger you can see the corrections reported:
##########################################
##### Begin Task: gencal #####
gencal(vis="3c391_ctm_mosaic_10s_spw0.ms",caltable="3c391_ctm_mosaic_10s_spw0.antpos",caltype="antpos",infile="",spw="",
antenna="",pol="",parameter=[],uniform=True)
Opening MS: 3c391_ctm_mosaic_10s_spw0.ms for calibration.
Initializing nominal selection to the whole MS.
Determine antenna position offests from the baseline correction database
offsets for antenna ea01 : 0.00000 0.00300 0.00000
offsets for antenna ea02 : -0.00080 0.00000 0.00000
offsets for antenna ea03 : -0.00280 0.00000 0.00000
offsets for antenna ea05 : 0.00000 0.00280 0.00000
offsets for antenna ea11 : 0.00090 0.00000 0.00000
offsets for antenna ea12 : -0.01000 0.00450 -0.00170
offsets for antenna ea13 : 0.00000 -0.00080 0.00000
offsets for antenna ea17 : -0.00120 0.00000 0.00000
offsets for antenna ea18 : 0.00040 -0.00080 0.00040
offsets for antenna ea22 : -0.02570 0.00270 -0.01900
offsets for antenna ea23 : -0.00140 0.00000 0.00000
offsets for antenna ea24 : -0.00150 0.00000 0.00000
offsets for antenna ea26 : -0.00190 0.00000 0.00210
offsets for antenna ea27 : 0.00000 0.00190 -0.00160
Beginning specifycal-----------------------
Creating KAntPos Jones table from specified parameters.
Writing solutions to table: 3c391_ctm_mosaic_10s_spw0.antpos
##### End Task: gencal #####
##########################################
This particular set of observations was taken 24 April 2010, so the corrections shown above are for antennas that were moved BEFORE that date, but whose updated positions were not placed into the online database until later. Most likely, the antenna positions were re-measured after 24 April. You can verify this by looking at the online database for the first part of 2010:
; 2010 BASELINE CORRECTIONS IN METERS
;ANT
;MOVED OBSDATE Put_In_ MC(IAT) ANT PAD Bx By Bz
;
JAN27 FEB12 FEB21 01:57 11 E04 0.0000 0.0000 0.0000
JAN27 FEB12 FEB21 01:57 26 W03 -0.0170 0.0204 0.0041
MAR24 MAR25 MAR26 18:28 17 W07 -0.0061 -0.0069 -0.0055
APR21 MAY02 MAY04 23:25 12 E08 -0.0072 0.0045 -0.0017
MAR09 MAY02 MAY04 23:25 22 N04 -0.0220 0.0040 -0.0190
JUN08 JUN20 JUN22 03:00 10 N03 0.0046 -0.0196 0.0090
JUL17 JUL18 21:44 1 W09 0.0000 0.0030 0.0000
JUL17 JUL18 21:44 2 E02 -0.0008 0.0000 0.0000
JUL17 JUL18 21:44 3 E09 -0.0028 0.0000 0.0000
JUL17 JUL18 21:44 5 W08 0.0000 0.0028 0.0000
JUL01 JUL17 JUL18 21:44 6 N06 0.0022 0.0010 0.0059
JUL17 JUL18 21:44 10 N03 0.0008 0.0030 -0.0014
JUL17 JUL18 21:44 11 E04 0.0009 0.0000 0.0000
JUL17 JUL18 21:44 12 E08 -0.0028 0.0000 0.0000
JUL17 JUL18 21:44 13 N07 0.0000 -0.0008 0.0000
JUL17 JUL18 21:44 17 W07 -0.0012 0.0000 0.0000
JUL17 JUL18 21:44 18 N09 0.0004 -0.0008 0.0004
JUL17 JUL18 21:44 22 N04 -0.0037 -0.0013 0.0000
JUL17 JUL18 21:44 23 E07 -0.0014 0.0000 0.0000
JUL17 JUL18 21:44 24 W05 -0.0015 0.0000 0.0000
JUL17 JUL18 21:44 26 W03 -0.0019 0.0000 0.0021
JUL17 JUL18 21:44 27 E03 0.0000 0.0019 -0.0016
Step 2: Initial Flux Density Scaling
The next step is to provide a flux density value for the amplitude calibrator J1331+3030 (a.k.a. 3C 286). Later, for the final step in determining the calibration solutions, we will use the calibrated gains of the two calibrator sources to transfer the flux density scaling to the secondary gain calibrator (J1822-0938).
For the pre-upgrade VLA, the ultimate flux density scale at most frequencies was set long ago by observations of 3C 295. The flux density scaling was then transferred to a small number of primary flux density calibrators, including 3C 286. For the upgraded Karl G. Jansky VLA, the flux density scale at most frequencies is determined from WMAP observations of the planet Mars, which, in turn, was transferred to a small number of primary flux density calibrators. The procedure is to assume that the flux density of a primary calibrator source is known and, by comparison with the observed data for that calibrator, determine the [math]\displaystyle{ g_i }[/math] values (the antenna gains).
To start, let's find the available calibrator models with setjy().
# In CASA
setjy(vis='3c391_ctm_mosaic_10s_spw0.ms', listmodels=True)
This command will show all available calibrator models:
3C123_P.im 3C138_P.im 3C147_A.im 3C147_Q.im 3C286_A.im 3C286_Q.im 3C380_P.im 3C48_P.im README 3C138_A.im 3C138_Q.im 3C147_C.im 3C147_S.im 3C286_C.im 3C286_S.im 3C48_A.im 3C48_Q.im 3C138_C.im 3C138_S.im 3C147_K.im 3C147_U.im 3C286_K.im 3C286_U.im 3C48_C.im 3C48_S.im 3C138_K.im 3C138_U.im 3C147_L.im 3C147_X.im 3C286_L.im 3C286_X.im 3C48_K.im 3C48_U.im 3C138_L.im 3C138_X.im 3C147_P.im 3C196_P.im 3C286_P.im 3C295_P.im 3C48_L.im 3C48_X.im
Since any image could be a potential calibrator model, setjy() will list all *.im and *.mod images in the working directory. In addition, it will list all models that are provided by NRAO with the CASA package, and they will be picked by their names. We will be using the C-band VLA standard model for 3C286 which is aptly named '3C286_C.im':
# In CASA
setjy(vis='3c391_ctm_mosaic_10s_spw0.ms',field='J1331+3030',standard='Perley-Butler 2017',
model='3C286_C.im',usescratch=True,scalebychan=True,spw='')
- field='J1331+3030' : IMPORTANT! If the flux density calibrator is not specified then all sources will be assumed to have the same flux density.
- standard='Perley-Butler 2017' : The flux density scale at the VLA is periodically revised, updated, or expanded. The specified value represents the most recent determination of the flux density scale by R. Perley and B. Butler in 2017, ApJS, 230, 7 (now the default); older scales can also be specified, and might be important if, for example, one was attempting to conduct a careful comparison with a previously published result.
- model='3C286_C.im' : From our Figure 3A, it can be estimated that 3C 286 is roughly a point source at this observation's frequency. Depending upon the frequency and configuration, the source may be slightly resolved. Fiducial model images have been determined from a painstaking set of observations, and, if one is available, it should be used to compensate for slight resolution effects (any deviation of the calibrator from a point source model). In this case, spectral window 0 (at 4.536 GHz) is in the C-band, so we use the C-band model image.
- usescratch=True : Due to current bugs with the virtual model we explicitly write to a model column in the MS by setting usescratch=True.
- scalebychan=True : In order to take account for the intrinsic spectral index of our flux density calibrator 3C286 when we use it as our bandpass calibrator, we let setjy() determine a flux density value per channel rather than one value for the entire spectral window.
- spw=' ' : The original data set contained two spectral windows. However, since we separated spectral window 0 for the data set used in this tutorial, it is not necessary to specify spw. Had the spectral window 0 not been split off from the original data, we might wish to specify the spectral window. The reason for it is that in this observation the spectral windows were sufficiently far away from each other that two different model images for 3C 286 would be appropriate; 3C286_C.im at 4.6 GHz and 3C286_X.im at 7.5 GHz. This would require two separate runs of setjy(), one for each spectral window. If the spectral windows were much closer together, it might be possible to calibrate both using a single, the same model.
Note: In our case here, a model image of a primary flux density calibrator exists (hence we selected model='3C286_C.im' ). However, sometimes (some kinds of polarization calibration or in extreme situations, e.g. there are problems with the scan on the flux density calibrator), it may be necessary to set the flux density of the source explicitly.
The most important output from setjy() should look similar to the following:
Selected 31964 out of 845379 rows. J1331+3030 (fld ind 0) spw 0 [I=7.6686, Q=0, U=0, V=0] Jy @ 4.536e+09Hz, (Perley-Butler 2017) Scaling spw(s) [0]'s model image by channel to I = 7.66964, 7.5989, 7.53174 Jy @(4.535e+09, 4.601e+09, 4.665e+09)Hz ...
The flux density in each Stokes plane (IQUV) for the reference channel 0 is reported (although here set to 0), followed by the I flux density in each of the channels to be used for scaling the data. These values are determined from an analytical formula for the spectrum of the source as a function of frequency so that precise predictions can be estimated for our specific frequencies.
Notes: setjy() will clear any previous calibration model that fits the selection. In this case, no such previous model data was found so all is good. Also, setjy() can return a python dictionary (CASA record) containing the reference flux density used. In our case, you will find the return value in the CASA command line window because we did not assign it to a python variable:
{'0': {'0': {'fluxd': array([ 7.6685524, 0. , 0. , 0. ])},
'fieldName': 'J1331+3030'},
'format': "{field Id: {spw Id: {fluxd: [I,Q,U,V] in Jy}, 'fieldName':field name }}"}
If you would like to store this result in a python dictionary, call the setjy() task by setting it to a variable, e.g. myset = setjy(...).
Setp 3: Initial Phase Calibration
Before solving for the bandpass, we will do an initial phase calibration. The reason for this step is to average over the (typically small) variations of phase with time in the bandpass; depending on frequency and configuration there may occur significant gain variations between different scans especially if the scans are at significantly different elevations - we want to moderate it to help us with bandpass calibration. We will later discard these initial phase solutions. Note, while amplitude variations with time will have little effect on the bandpass solutions, it is important to solve for phase variations with time to prevent de-correlation when vector averaging the data for computing the final bandpass solution (hence our selection of calmode='p' ).
We use the CASA task gaincal to solve for phase versus time for the central channels on our three calibrators:
# In CASA
gaincal(vis='3c391_ctm_mosaic_10s_spw0.ms', caltable='3c391_ctm_mosaic_10s_spw0.G0all',
field='0,1,9', refant='ea21', spw='0:27~36',
gaintype='G',calmode='p', solint='int',
minsnr=5, gaintable=['3c391_ctm_mosaic_10s_spw0.antpos'])
- caltable='3c391_ctm_mosaic_10s_spw0.G0all' : The gain solutions will be stored in this external table.
- field='0,1,9' : Specify the calibrators. Although the bandpass solution will be based only on the bandpass calibrator, We will use this opportunity to inspect solutions for ALL calibrators in order to potentially identify any bad data.
- refant='ea21' : Earlier, by looking at the output from plotants, a reference antenna near the center of the array was noted. Here is the first time that choice is used, as the antenna closest to the center without being shadowed is generally used as the reference antenna. Strictly, all of the gain corrections derived will be relative to this reference antenna.
- spw='0:27~36' : Choose a subset of the channels from which to determine the gain corrections. These should be near the center of the band, and there should be enough channels chosen so that a reasonable signal-to-noise ratio can be obtained; the central 10% of the channels is a good guideline. Particularly at lower frequencies where RFI can manifest itself, one should choose RFI-free frequency channels; the VLA Observing Guide RFI page lists the known RFI frequencies for each band. Also note that, even though these data have only a single spectral window, the syntax requires specifying the spectral window ('0') in order to specify specific channels ('27~36' in this example).
- gaintype='G' : Compute the complex gain solutions, one per antenna per spw per polarization per solution interval. Note that gaintype='G' assumes the V stokes is zero if not told otherwise, so for the case where the calibrator has significant circular polarization, a model incorporating polarization must be used (this can be set with setjy). For the current dataset we know that the calibrator has negligible circular polarization so the V polarization does not need to be set.
- calmode='p' : Solve for only the phase portion of the gain.
- solint='int' : To track the phases, a short solution interval is chosen. (int refers to a single integration time or 10 seconds for this case)
- minsnr=5 : Restrict the solutions to be at relatively high signal-to-noise ratios, although this parameter may need to be varied depending upon the source and frequency.
- gaintable=['3c391_ctm_mosaic_10s_spw0.antpos'] : Having produced antenna position corrections (as we did above with gencal), they should now be applied.
To really see what is going on, we use plotms() to inspect the solutions from gaincal() for a single antenna at a time, iterating through each antenna in sequence by clicking on the Next button (right pointing single green arrow) on the GUI to advance the displayed antenna.
# In CASA
plotms(vis='3c391_ctm_mosaic_10s_spw0.G0all',xaxis='time',yaxis='phase',
coloraxis='corr',iteraxis='antenna',plotrange=[-1,-1,-180,180])
- vis='3c391_ctm_mosaic_10s_spw0.G0all' : the calibration table to examine solutions
- xaxis='time' : plotting phase solutions vs time
- yaxis='phase' : plotting phase solutions vs time
- coloraxis=corr : colorize by polarization (black=R, pink=L; coloring choice is automatic in plotms)
- iteraxis='antenna' : iterating the plot across each antenna
Note: plotms was originally designed to plot visibility data, while the task plotcal (no longer maintained as of CASA version 5.4.0) was used for plotting calibration tables. Plotms has now taken over the functionality of plotcal. However, some of the input parameter names (e.g., "vis" instead of "caltable") still reflect the original design for plotms. Examples of using plotcal to examine calibration tables can be found in the earlier versions of this and other CASA guide tutorials.
Antennas that have been flagged will show a blank plot, as there are no solutions for these antennas. For most antennas, we see a fairly smooth variation with time, so we expect to be able to calibrate the data nicely. However, when you get to ea05, note that there are phase jumps where the phase appears to be oscillating between two states (Figure 5)
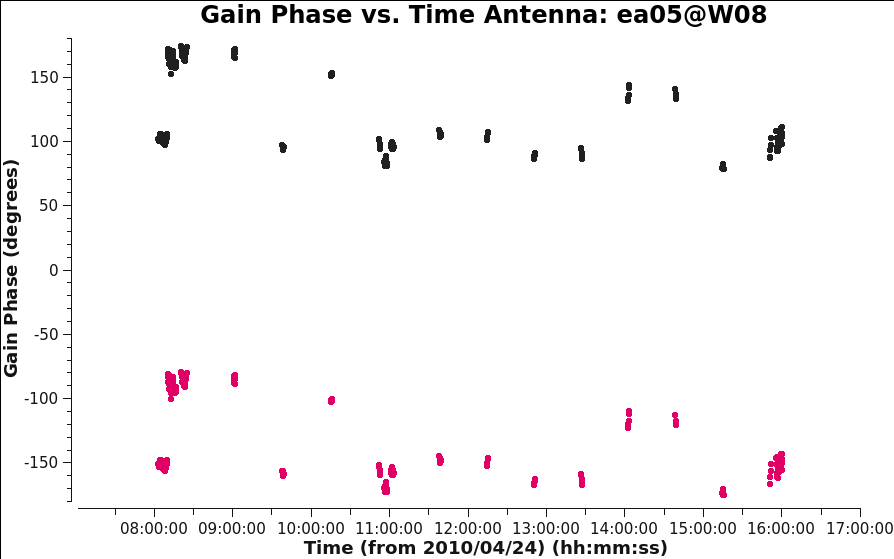 |
Antennas other than ea05 look OK. We will not be able to transfer calibration for antenna ea05 so we flag it from the data:
# In CASA
flagdata(vis='3c391_ctm_mosaic_10s_spw0.ms', flagbackup=True, <set_here_'antenna'_and_'mode'_parameters_to_successfully_flag_ea05>)
The inspection of the initial solutions we have just done, was the only purpose of the .G0all table. We will not use this calibration table any more, and instead we will create a new one, .G0, that will contain initial phase solutions for only the bandpass calibrator. The following call to gaincal() is similar to the one above, but selects only the bandpass calibrator (using the field parameter). It is important that this call is executed after flagging of ea05.
# In CASA
gaincal(vis='3c391_ctm_mosaic_10s_spw0.ms', caltable='3c391_ctm_mosaic_10s_spw0.G0',
field='J1331+3030', refant='ea21', spw='0:27~36', calmode='p', solint='int',
minsnr=5, gaintable=['3c391_ctm_mosaic_10s_spw0.antpos'])
You can inspect these new solutions with plotms() as we did above. For example, plot (with colorization by polarization) for the first block of 3C286 data only:
# In CASA
plotms(vis='3c391_ctm_mosaic_10s_spw0.G0',
xaxis='time',yaxis='phase',coloraxis='corr',field='J1331+3030',iteraxis='antenna',
plotrange=[-1,-1,-180,180],timerange='08:02:00~08:17:00')
Step 4: Delay Calibration
Before we can solve for bandpass, we need to first solve for the antenna-based delays (these delays put a phase ramp versus frequency channel in each spectral window as demonstrated in Figure 3C, we want to remove that slope). The K gain type in gaincal() solves for the relative delays of each antenna relative to the reference antenna (parameter refant), so be sure you pick one that is there for this entire scan and does show any problems. This is not a full global delay, but gives one value per spw per polarization.
# In CASA
gaincal(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic_10s_spw0.K0',
field='J1331+3030',refant='ea21',spw='0:5~58',gaintype='K', solint='inf',combine='scan',minsnr=5,
gaintable=['3c391_ctm_mosaic_10s_spw0.antpos',
'3c391_ctm_mosaic_10s_spw0.G0'])
- field='J1331+3030' : For the bandpass calibrator
- refant='ea21' : Delays will be relative to this antenna, make sure it is there!
- spw='0:5~58' : Widest possible frequency range in the spw, avoiding edge channels because they have lower sensitivity
- gaintype='K' : Compute K (i.e., delay) solutions, one per antenna per spw per polarization per solution interval
- solint='inf ',combine='scan' : Only need one solution averaged over all times and scans. solint='inf ' sets the solution interval to 'infinite' but respects scan boundaries; combine='scan' combines data across scan boundaries
- minsnr=5 : Restrict the solutions to be at relatively high signal-to-noise ratios, although this parameter may need to be varied depending upon the source and frequency.
- gaintable=['3c391_ctm_mosaic_10s_spw0.antpos','3c391_ctm_mosaic_10s_spw0.G0'] : Use the antpos and G0 tables that we just created
Plot these solutions (in nanoseconds) as a function of antenna (Figure 6):
# In CASA
plotms(vis='3c391_ctm_mosaic_10s_spw0.K0',xaxis='antenna1',yaxis='delay',coloraxis='baseline')
You can see that the delays are within around 4 nanoseconds, which is expected for the early science observations with the newly upgraded VLA.
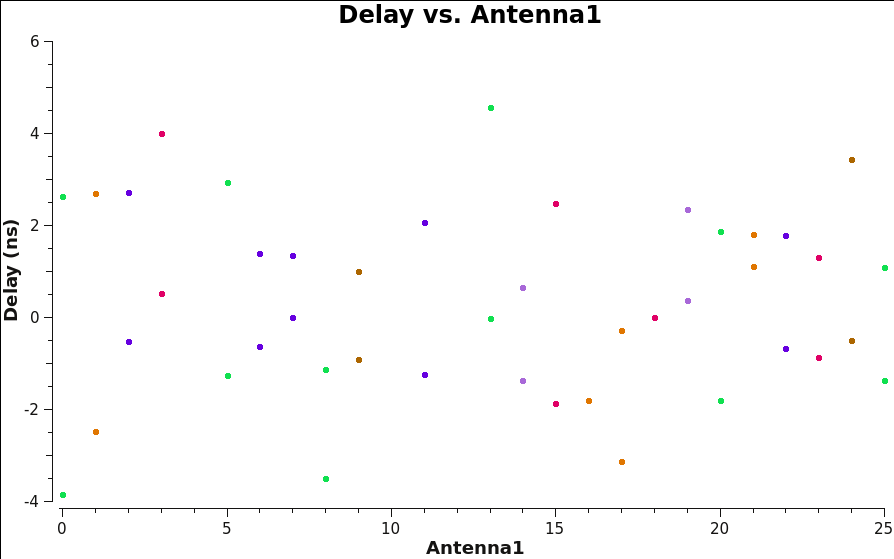 |
Step 5: Bandpass Calibration
This step solves for the complex bandpass, [math]\displaystyle{ B_i }[/math].
All data with the VLA are taken in spectral line mode, even if the science that one is conducting is continuum, and therefore requires a bandpass solution to account for gain variations with frequency. Solving for the bandpass won't hurt continuum data, and in fact it is essential for moderate or high dynamic range imaging. To motivate the need for solving for the bandpass, consider Figure 7. It shows the right circularly polarized data (RR correlation) for the source J1331+3030 that serves as our bandpass calibrator. The data are color coded by Antenna 2. The visibility data are nearly constant with baseline length for this particular calibrator (Figure 3A), and ideally, they would be constant as a function of frequency as well. The variations with frequency are a reflection of the (slightly) different antenna bandpasses.
Exercise: reproduce Figure 7 using plotms().
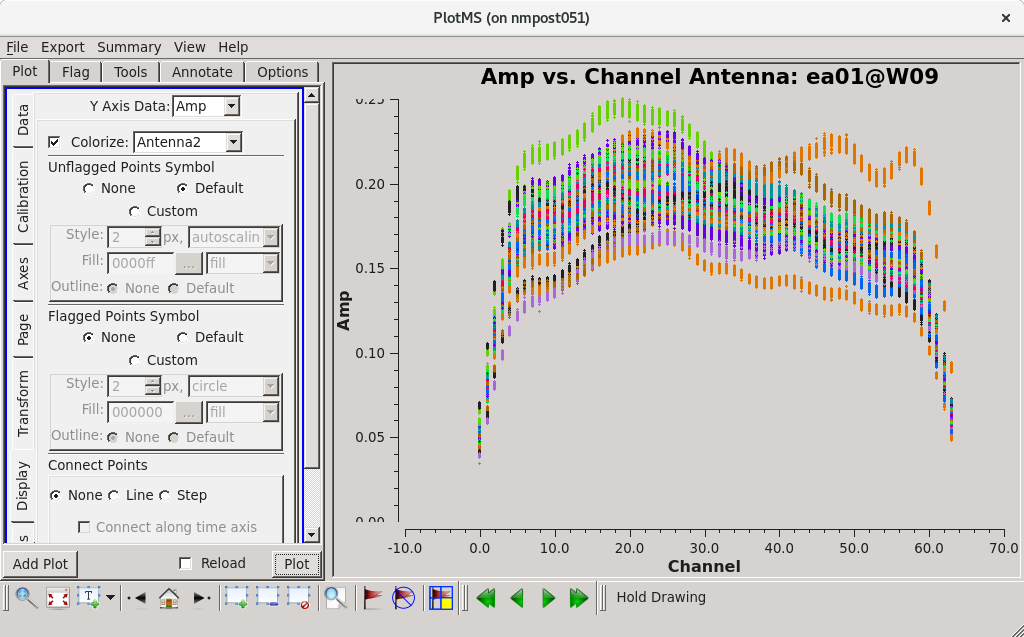 |
We can now solve for the bandpass (i.e. model it), using the phase solutions and delays we just derived in previous steps.
# In CASA
bandpass(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic_10s_spw0.B0',
field='J1331+3030',spw='',refant='ea21',combine='scan',
solint='inf',bandtype='B',
gaintable=['3c391_ctm_mosaic_10s_spw0.antpos',
'3c391_ctm_mosaic_10s_spw0.G0',
'3c391_ctm_mosaic_10s_spw0.K0'])
- caltable='3c391_ctm_mosaic_10s_spw0.B0' : Specify where to store the bandpass corrections.
- solint='inf ', combine='scan' : This observation contains multiple scans on the bandpass calibrator, J1331+3030. Because these are continuum observations, it is probably acceptable to combine all the scans and compute one bandpass correction per antenna, which is achieved by the combination of 'solint='inf ' and combine='scan' . The value inf means infinite, which means to combine solutions for all times, but to respect scan boundaries. combine='scan' additionally averages over all scans. Had combine=' ' then there would have been a bandpass correction derived for each scan (which might be desirable for very high dynamic range spectral line observations).
- bandtype='B' : The bandpass solution will be derived on a channel-by-channel basis. There is an alternate option of parameter bandtype='BPOLY' that will fit an nth order polynomial to the bandpass.
- gaintable=['3c391_ctm_mosaic_10s_spw0.antpos', '3c391_ctm_mosaic_10s_spw0.G0', '3c391_ctm_mosaic_10s_spw0.K0'] : Apply antenna positions, phase solutions, and delays before computing bandpass.
Once again, we can use plotms() to display the bandpass solutions. Note that in the inputs below, the amplitudes are being displayed as a function of frequency channel. The parameters gridrows=2 and gridcols=2 are used to display multiple plots per page (2 plots per page in the y direction and 2 in the x direction). The first command below shows the amplitude solutions (one per polarization; Figure 8A) and the second command below shows the phase solutions (one per each polarization). Parameter iteration='antenna' is used to step through separate plots for each antenna.
# In CASA
plotms(vis='3c391_ctm_mosaic_10s_spw0.B0',field='J1331+3030',
xaxis='chan',yaxis='amp',coloraxis='corr',
iteraxis='antenna',gridrows=2,gridcols=2)
plotms(vis='3c391_ctm_mosaic_10s_spw0.B0',field='J1331+3030',
xaxis='chan',yaxis='phase',coloraxis='corr',plotrange=[-1,-1,-180,180],
iteraxis='antenna',gridrows=2,gridcols=2)
As expected, the bandpass phases are relatively flat (Figure 8B) with the slopes seen in Figure 3C removed by the delay calibration. Residual phase excursions are on the order of a few degrees.
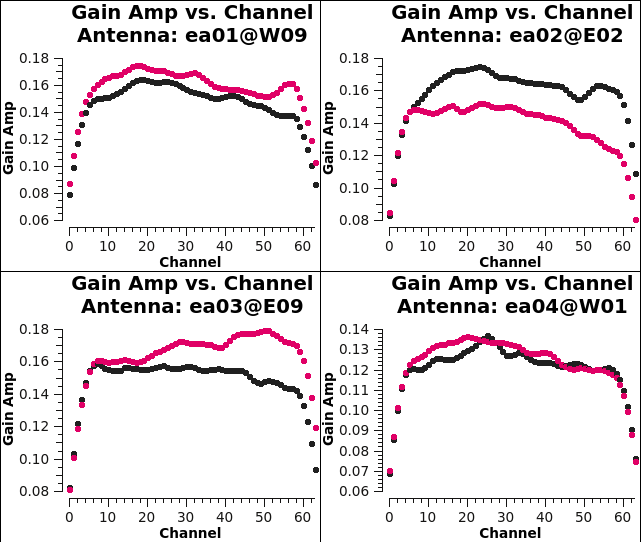 |
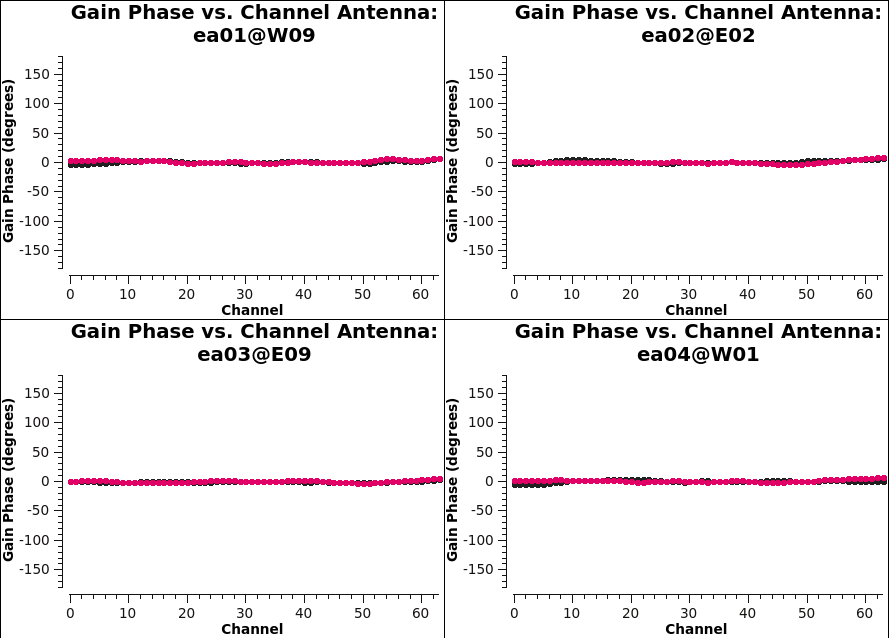 |
Step 6: Gain Calibration
The next step is to derive corrections for the complex antenna gains, [math]\displaystyle{ g_i }[/math] and [math]\displaystyle{ \theta_i }[/math]. As discussed above, the absolute magnitude of the gain amplitudes ([math]\displaystyle{ g_i }[/math]) are determined by reference to a standard flux density calibrator. In order to determine the appropriate complex gains for the target source, and to minimize differences through the atmosphere (neutral and/or ionized) between the lines of sight to the phase calibrator and the target source, you want to observe a so-called phase calibrator that is much closer to the target. If we establish the relative gain amplitudes and phases for different antennas using the phase calibrator, we can later determine the absolute flux density scale by comparing the gain amplitudes, [math]\displaystyle{ g_i }[/math], derived for 3C 286 with those derived for the phase calibrator. This will eventually be done using the task fluxscale. Since there is no such thing as absolute phase, we determine a zero phase by selecting a reference antenna for which the gain phase is defined to be zero.
In principle, one could determine the complex antenna gains for all sources with a single invocation of gaincal; for clarity here, two separate invocations will be used.
In the first step, we derive the appropriate complex gains [math]\displaystyle{ g_i }[/math] and [math]\displaystyle{ \theta_i }[/math] for the flux density calibrator 3C 286.
# In CASA
gaincal(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic_10s_spw0.G1',
field='J1331+3030',spw='0:5~58',
solint='inf',refant='ea21',gaintype='G',calmode='ap',solnorm=False,
gaintable=['3c391_ctm_mosaic_10s_spw0.antpos',
'3c391_ctm_mosaic_10s_spw0.K0',
'3c391_ctm_mosaic_10s_spw0.B0'],
interp=['','','nearest'])
- caltable='3c391_ctm_mosaic_10s_spw0.G1' : Produce a new calibration table containing these gain solutions. In order to make the bookkeeping easier, a '1' is appended to the file name to distinguish it from the earlier set of gain solutions, which are effectively being thrown away.
- spw='0:5~58' : From the inspection of the bandpass, one can determine the range of edge channels that are affected by the bandpass filter rolloff. Because the amplitude is dropping rapidly in these channels, one does not want to include them in the solution.
- field='J1331+3030' : in this first of the two invocations of gaincal, we are finding gain solutions for calibrator source J1331+3030 (3C 286).
- gaintype='G' : with this option, we will determine complex antenna gain solutions separately for each polarization and each spectral window
- calmode='ap', solnorm=False: The objective is to relate the measured data values to the (assumed known) flux density of 3C 286, thus the solution is both amplitude and phase ('ap') and the solutions should not be normalized to unity amplitude.
- solint='inf ' : Produce a solution for each scan. Phase coherence for these observations is good.
- gaintable=['3c391_ctm_mosaic_10s_spw0.antpos', '3c391_ctm_mosaic_10s_spw0.K0', '3c391_ctm_mosaic_10s_spw0.B0'] : Use the antenna position corrections, delays, and bandpass solutions determined earlier before solving for the gain amplitudes.
- interp=[' ',' ','nearest']: the temporal interpolation to use for each gaintable. When there is no attribute included, it will default to 'linear' although it is not recommended to leave all the attributes blank. When there are multiple bandpass solutions, it can be especially important to use 'nearest' for the bandpass table, as linear would allow extrapolation beyond the sampled times. (As there is only one bandpass solution for this Guide, specifying 'nearest' is not strictly necessary as 'linear' and 'nearest' result in the same behavior in the case of a single time solution. We include the specification for demonstration purposes.)
In the second step, the appropriate complex gains for a direction on the sky close to the target source will be determined from the phase calibrator J1822-0938.
# In CASA
gaincal(vis='3c391_ctm_mosaic_10s_spw0.ms',caltable='3c391_ctm_mosaic_10s_spw0.G1',
field='J1822-0938',
spw='0:5~58',solint='inf',refant='ea21',gaintype='G',calmode='ap',
gaintable=['3c391_ctm_mosaic_10s_spw0.antpos',
'3c391_ctm_mosaic_10s_spw0.K0',
'3c391_ctm_mosaic_10s_spw0.B0'],
append=True)
- caltable='3c391_ctm_mosaic_10s_spw0.G1', append=True: In the previous invocation of gaincal(), append was set to False. Here, the gain solutions from the phase calibrator are going to be appended to the existing set from 3C 286 and thus stored in a single table. In following steps, all of these gain solutions will then be used together to derive a set of complex gains that are applied to the science data for the target source.
Questions:
|
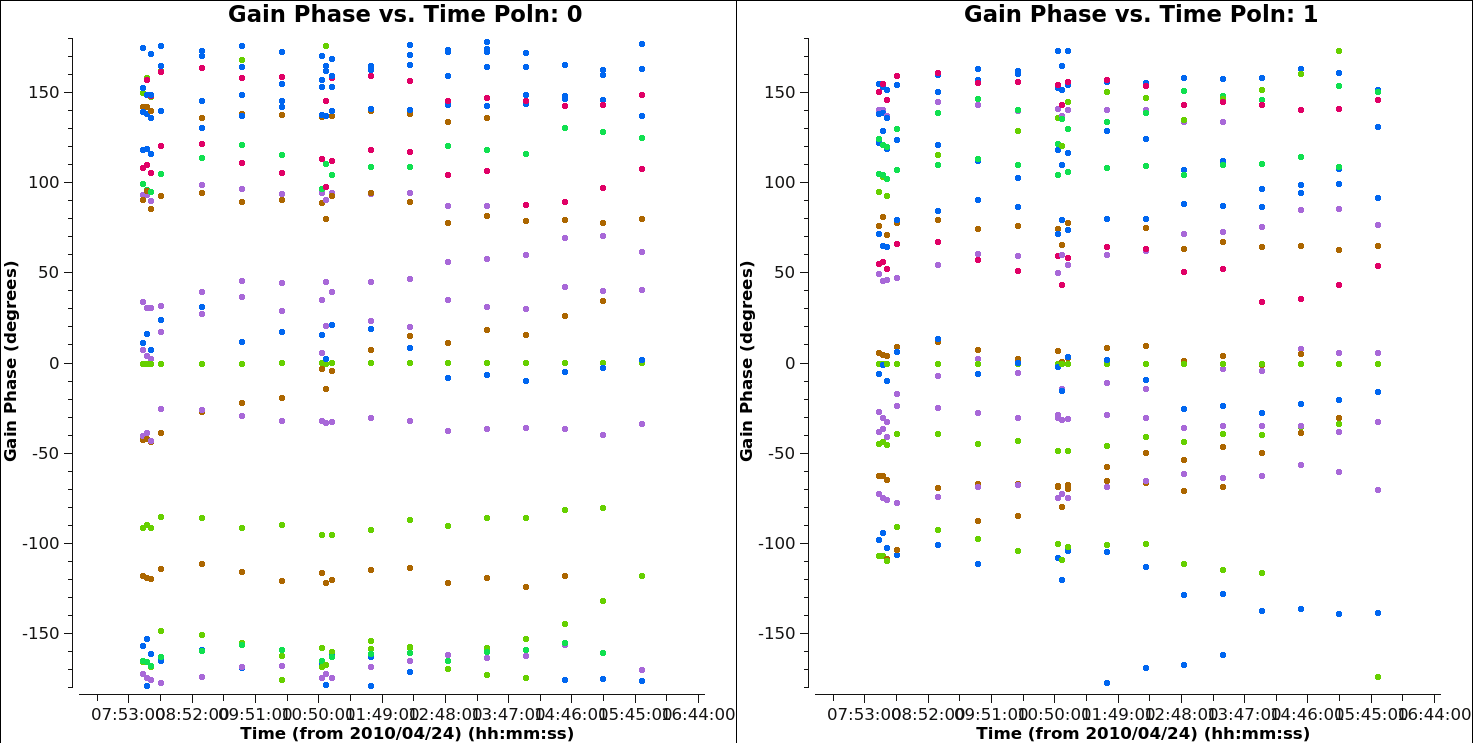
If you check the gain phase solutions using plotms(), you should now see smooth solutions for each antenna as a function of time (see Figures 9A--9B).
# In CASA
plotms(vis='3c391_ctm_mosaic_10s_spw0.G1',xaxis='time',yaxis='phase',
gridrows=1,gridcols=2,iteraxis='corr',coloraxis='baseline',
plotrange=[-1,-1,-180,180],plotfile='plotms_3c391-G1-phase.png')
plotms(vis='3c391_ctm_mosaic_10s_spw0.G1',xaxis='time',yaxis='amp',
gridrows=1,gridcols=2,iteraxis='corr',coloraxis='baseline',
plotfile='plotms_3c391-G1-amp.png')
 |
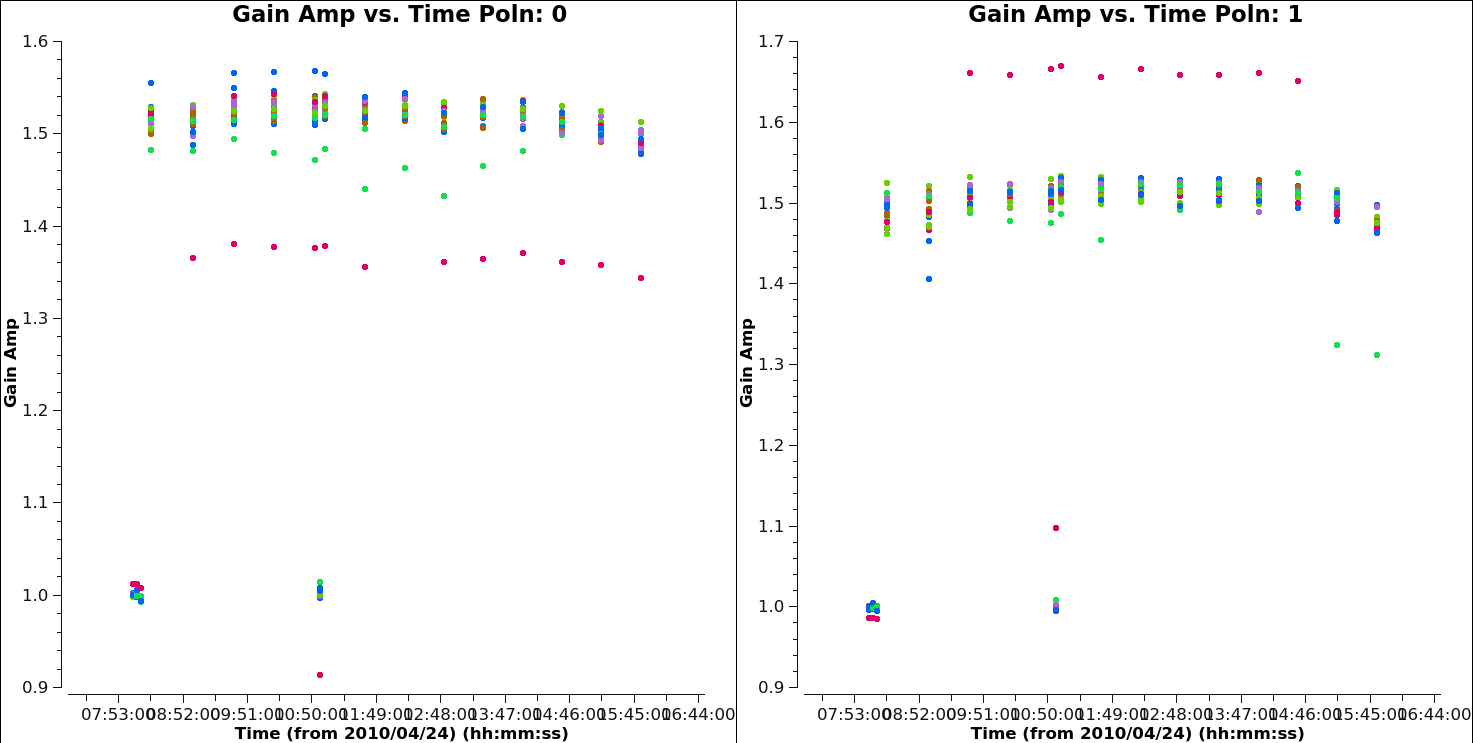 |
The lower gain solution values (near 1.0) correspond to the two scans of 3C 286, while the higher gain solution values (near 1.5) correspond to the scans of the phase calibrator, J1822-0938. At this stage in the calibration, we have not yet solved for the flux density scaling. In order for the amplitude of 3C 286 in the data to match the amplitude of its model (which we set above with setjy), little scaling of the solution is required (value = 1.0). J1822-0938 is fainter than 3C 286, leading to a higher solution value. The ratio of amplitude solutions between the two sources will be used in a later calibration step (fluxscale) to determine the actual flux density of J1822-0938.
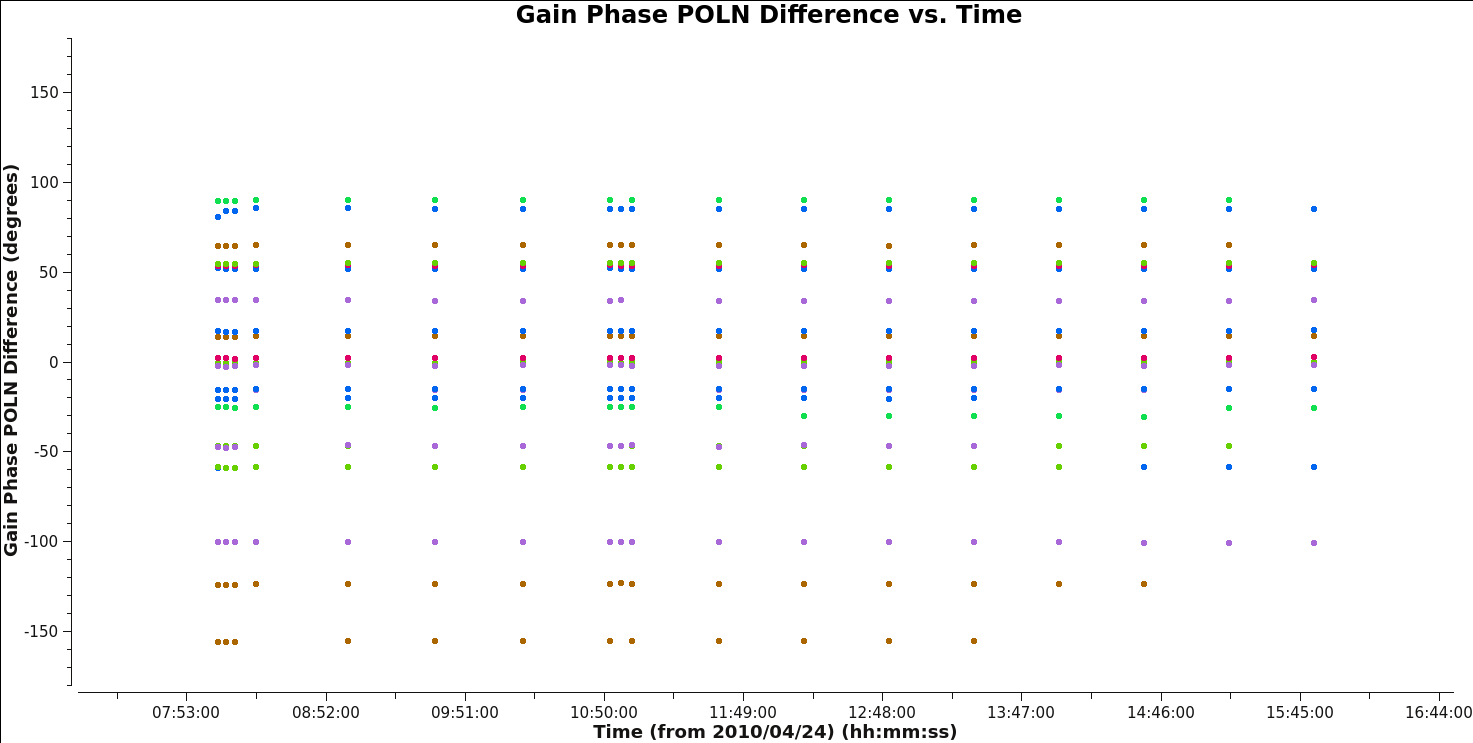
This is also a good time to check that our chosen reference antenna (ea21) has good phase stability (i.e., the phase difference between the right and left polarizations is stable with time). To do this, we plot the complex polarization ratio by selecting correlation=' / ' :
# In CASA
plotms(vis='3c391_ctm_mosaic_10s_spw0.G1', xaxis='time', yaxis='phase',
correlation='/', coloraxis='baseline', plotrange=[-1,-1,-180,180])
As can be seen in Figure 10, there is a bit of drift (a few degrees here and there), but no phase jumps. This means that ea21 is, indeed, a good choice for reference antenna.
 |
Step 7: Scaling the Amplitude Gains
While we know the flux density of our primary calibrator (J1331+3030[math]\displaystyle{ \equiv }[/math]3C 286), the model assumed for the secondary calibrator (J1822-0938) was a point source of 1 Jy located at the phase center. While the secondary calibrator was chosen to be a point source (at least, over some limited range of uv-distance; see the VLA calibrator manual for any u-v restrictions on your calibrator of choice at the observing frequency), its absolute flux density is unknown. Being point-like, secondary calibrators typically vary on timescales of months to years, in some cases by up to 50--100%.
We use the primary (flux) calibrator to determine the system response to a source of known flux density and assume that the mean gain amplitudes for the primary calibrator are the same as those for the secondary calibrator. This allows us to find the true flux density of the secondary calibrator. To do this, we use the task fluxscale, which produces a new calibration table containing properly-scaled amplitude gains for the secondary calibrator.
# In CASA
myscale = fluxscale(vis='3c391_ctm_mosaic_10s_spw0.ms',
caltable='3c391_ctm_mosaic_10s_spw0.G1',
fluxtable='3c391_ctm_mosaic_10s_spw0.fluxscale1',
reference='J1331+3030',
transfer=['J1822-0938'],
incremental=False)
- myscale = fluxscale(...) : fluxscale returns a dictionary of results, which we capture in the variable myscale
- caltable='3c391_ctm_mosaic_10s_spw0.G1' : We provide fluxscale with the calibration table containing the amplitude gain solutions derived earlier.
- fluxtable='3c391_ctm_mosaic_10s_spw0.fluxscale1' : We specify the name of the new output table to be written, which will contain the properly-scaled amplitude gains.
- reference='J1331+3030' : We specify the source with the known flux density.
- transfer=['J1822-0938']: We specify the source whose amplitude gains are to be rescaled; if there were multiple secondary calibrators to be used, this parameter value would need to be a python list.
- incremental=False: Make a new output fluxtable replacing caltable with rescaled transfer gains. If parameter incremental=True then the new table would be used in addition to caltable in subsequent applications.
Task fluxscale will print to the CASA logger the derived flux densities of all calibrator sources specified with the transfer parameter. These are also captured in the return variable from the task. You should examine the output to ensure that it looks sensible. If the data set has more than one spectral window, depending upon where they are spaced and the spectrum of the source, it is possible to find quite different flux densities and spectral indexes for the secondary calibrators. Example output would be
CASA <99>: myscale['1']
Out[99]:
{'0': {'fluxd': array([ 2.29600096, 0. , 0. , 0. ]),
'fluxdErr': array([ 0.00692024, 0. , 0. , 0. ]),
'numSol': array([ 46., 0., 0., 0.])},
'fieldName': 'J1822-0938',
'fitFluxd': 0.0,
'fitFluxdErr': 0.0,
'fitRefFreq': 0.0,
'spidx': array([ 0., 0., 0.]),
'spidxerr': array([ 0., 0., 0.])}
The index '1' above refers to the field number. You can also find the flux density values in the CASA logger:
... Found reference field(s): J1331+3030 Found transfer field(s): J1822-0938 Flux density for J1822-0938 in SpW=0 (freq=4.599e+09 Hz) is: 2.296 +/- 0.00692024 (SNR = 331.781, N = 46) Storing result in 3c391_ctm_mosaic_10s_spw0.fluxscale1 ...
Again, the VLA calibrator manual may be used to check whether the derived flux densities look sensible. Wildly different flux densities or flux densities with very high error bars should be treated with suspicion; in such cases you will have to figure out whether something has gone wrong.
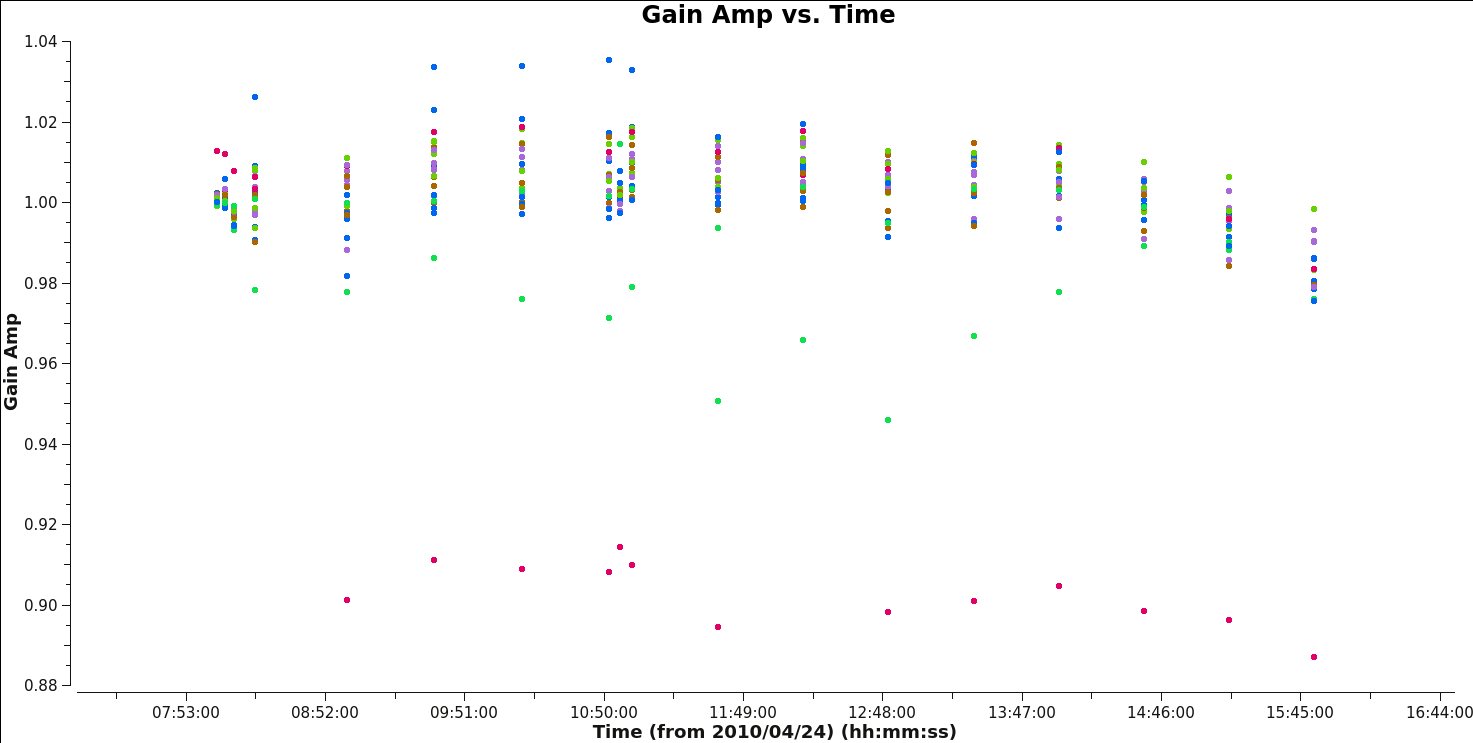
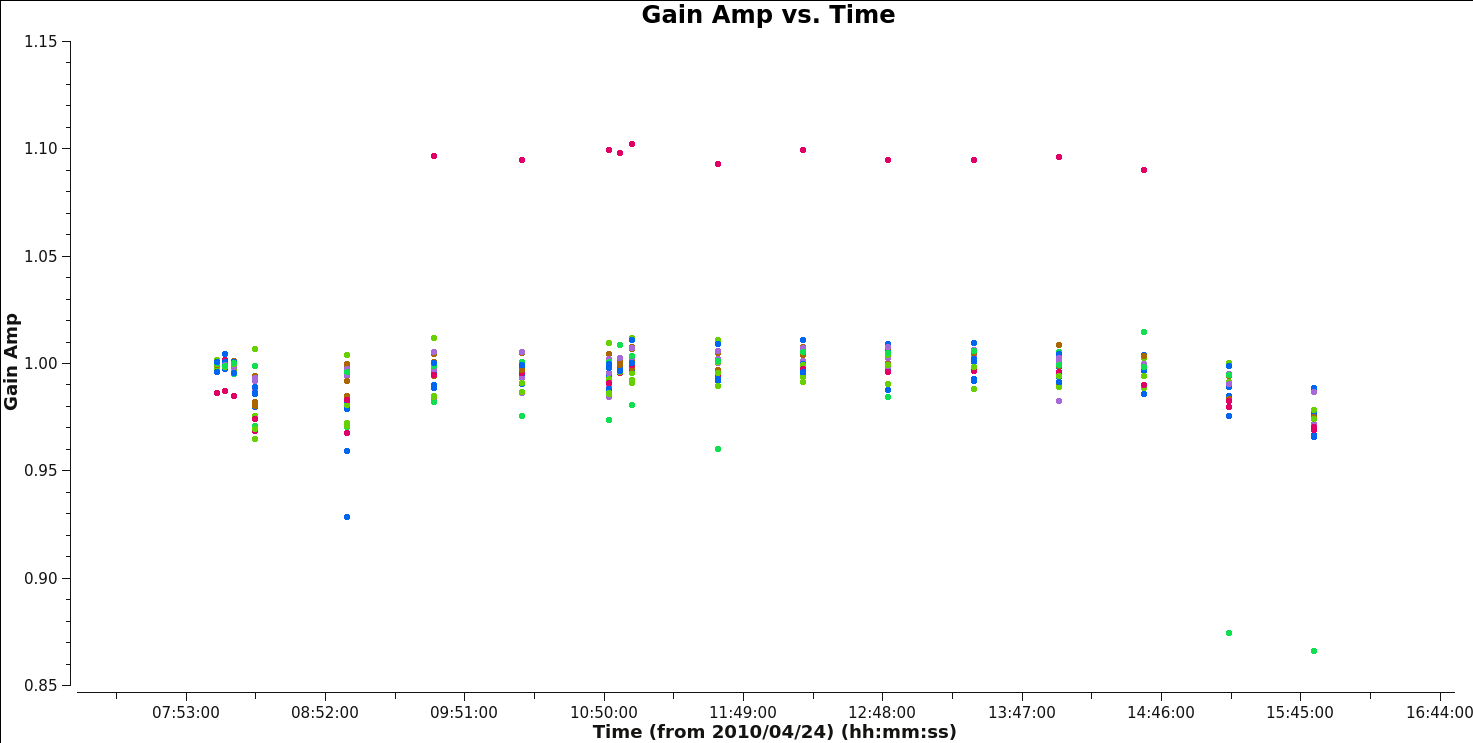
We plot the rescaled amplitudes from this table:
# In CASA
plotms(vis='3c391_ctm_mosaic_10s_spw0.fluxscale1',xaxis='time',yaxis='amp',
correlation='R',coloraxis='baseline')
plotms(vis='3c391_ctm_mosaic_10s_spw0.fluxscale1',xaxis='time',yaxis='amp',
correlation='L',coloraxis='baseline')
You can see in Figures 11A and 11B that the amplitude gain factors are now similar across sources, compared to the raw factors in the G1 table.
 |
 |
Applying the Calibration
Now that we have derived all the calibration solutions, we need to apply them to the actual data, using the task applycal(). The measurement set DATA column contains the original data. To apply the calibration we have derived, we specify the appropriate calibration tables, which are then applied to the DATA column, with the results being written in the CORRECTED_DATA column. If the dataset does not already have a CORRECTED_DATA scratch column, then one will be created in the first applycal() run.
First, we apply the calibration to each individual calibrator, using the gain solutions derived on that calibrator alone to compute the CORRECTED_DATA. To do this, we iterate over the different calibrators, in each case specifying the source to be calibrated (using the field parameter). The relevant function calls are given below.
# In CASA
applycal(vis='3c391_ctm_mosaic_10s_spw0.ms',
field='J1331+3030',
gaintable=['3c391_ctm_mosaic_10s_spw0.antpos',
'3c391_ctm_mosaic_10s_spw0.fluxscale1',
'3c391_ctm_mosaic_10s_spw0.K0',
'3c391_ctm_mosaic_10s_spw0.B0'],
gainfield=['','J1331+3030','',''],
interp=['','nearest','',''],
calwt=False)
applycal(vis='3c391_ctm_mosaic_10s_spw0.ms',
field='J1822-0938',
gaintable=['3c391_ctm_mosaic_10s_spw0.antpos',
'3c391_ctm_mosaic_10s_spw0.fluxscale1',
'3c391_ctm_mosaic_10s_spw0.K0',
'3c391_ctm_mosaic_10s_spw0.B0'],
gainfield=['','J1822-0938','',''],
interp=['','nearest','',''],
calwt=False)
- gaintable : We provide a Python list of the calibration tables to be applied. This list must contain the antenna position corrections (.antpos), the properly-scaled gain calibration for the amplitudes and phases (.fluxscale1) which were just made using fluxscale(), the parallel-hand delays (.K0), and the bandpass solutions (.B0).
- gainfield, interp : To ensure that we use the correct gain amplitudes and phases for a given calibrator (those derived on that same calibrator), we must specify for each calibrator source the particular subset of gain solutions to be applied. This requires use of the gainfield and interp parameters; these are both Python lists, and for the list item corresponding to the calibration table made by fluxscale(), we set gainfield to the field name corresponding to that calibrator, and the desired interpolation type (interp) to nearest.
- calwt=False : Using calwt=True (calibrating the weights) is dependent on having truly representative weights in the data and currently the VLA data does not do this, though ALMA does. For the VLA, we are not yet using system calibration data to compute real (1/Jy2) weights, thus trying to calibrate them during the applycal stage can produce nonsensical results. In particular, experience has shown that calibrating the weights will lead to problems especially in the self-calibration steps. We will instead set the weights before imaging using the statwt() task (further details below).
Finally, we apply the calibration to the target fields in the mosaic, linearly interpolating the gain solutions from the secondary calibrator, J1822-0938. In this case however, we want to apply the amplitude and phase gains derived from the secondary calibrator, J1822-0938, since that is close to the target source on the sky and we assume that the gains applicable to the target source are very similar to those derived in the direction of the secondary calibrator. Of course, this is not strictly true, since the gains on J1822-0938 were derived at a different time and in a different position on the sky from the target. However, assuming that the calibrator was sufficiently close to the target, and the weather was sufficiently well-behaved, then this is a reasonable approximation and should get us a sufficiently good calibration that we can later use self-calibration to correct for the small inaccuracies thus introduced.
The procedure for applying the calibration to the target source is very similar to what we just did for the calibrator sources.
# In CASA
applycal(vis='3c391_ctm_mosaic_10s_spw0.ms',
field='2~8',
gaintable=['3c391_ctm_mosaic_10s_spw0.antpos',
'3c391_ctm_mosaic_10s_spw0.fluxscale1',
'3c391_ctm_mosaic_10s_spw0.K0',
'3c391_ctm_mosaic_10s_spw0.B0'],
gainfield=['','J1822-0938','',''],
interp=['','linear','',''],
calwt=False)
- field : We can calibrate all seven target fields at once by setting field='2~8' .
- gainfield : In this case, we wish to use the gains derived on the secondary calibrator, for the reasons explained in the previous paragraph.
- interp : This time, we linearly interpolate between adjacent calibrator scans, to compute the appropriate gains for the intervening observations of the target.
We should now have fully-calibrated visibilities in the CORRECTED_DATA column of the measurement set, and it is worthwhile pausing to inspect them to ensure that the calibration did what we expected it to. We make some standard plots (see Figures 12A through 12D):
# In CASA
plotms(vis='3c391_ctm_mosaic_10s_spw0.ms',field='0',correlation='RR,LL',
antenna='',avgtime='60',xaxis='channel',yaxis='amp',
ydatacolumn='corrected',coloraxis='corr',
plotfile='plotms_3c391-fld0-corrected-amp.png')
plotms(vis='3c391_ctm_mosaic_10s_spw0.ms',field='0',correlation='RR,LL',
antenna='',avgtime='60',xaxis='channel',yaxis='phase',
ydatacolumn='corrected',coloraxis='corr',
plotrange=[-1,-1,-180,180],
plotfile='plotms_3c391-fld0-corrected-phase.png')
plotms(vis='3c391_ctm_mosaic_10s_spw0.ms',field='1',correlation='RR,LL',
antenna='',avgtime='60',xaxis='channel',yaxis='amp',
ydatacolumn='corrected',coloraxis='corr',
plotfile='plotms_3c391-fld1-corrected-amp.png')
plotms(vis='3c391_ctm_mosaic_10s_spw0.ms',field='1',correlation='RR,LL',
antenna='',avgtime='60',xaxis='channel',yaxis='phase',
ydatacolumn='corrected',coloraxis='corr',
plotrange=[-1,-1,-180,180],
plotfile='plotms_3c391-fld1-corrected-phase.png')
Inspecting the data at this stage may well show up previously-unnoticed bad data. Plotting the corrected amplitude against UV distance or against time is a good way to find such issues. If you find bad data, you can remove them via interactive flagging in plotms() or via manual flagging in flagdata() once you have identified the offending antennas/baselines/channels/times. When you are happy that all data (particularly on your target source) look good, you may proceed. Images 12A through 12D show that there is no sign of bad data remaining.
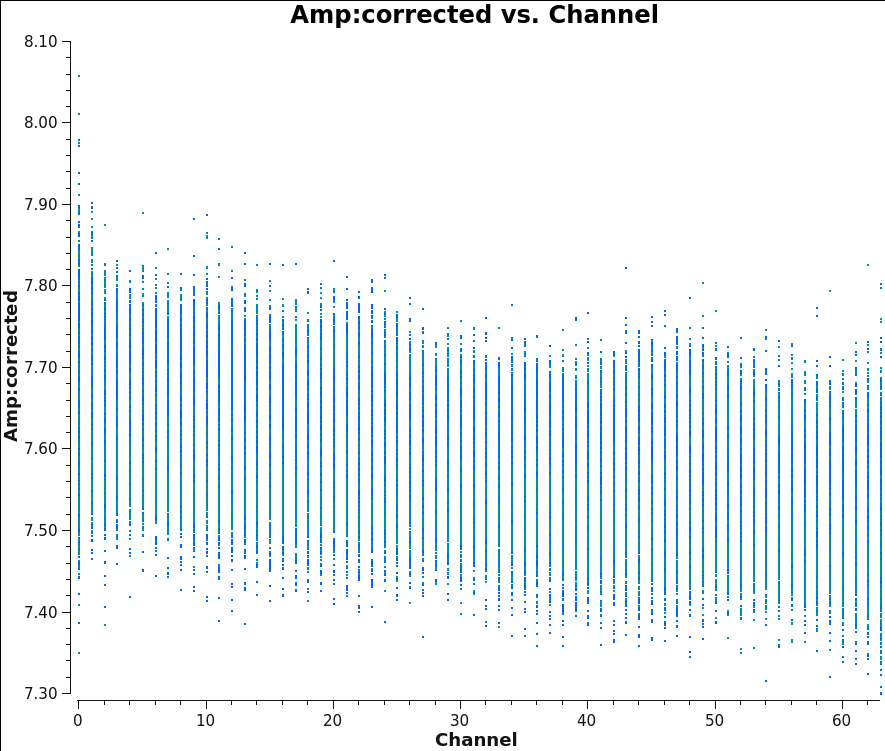 |
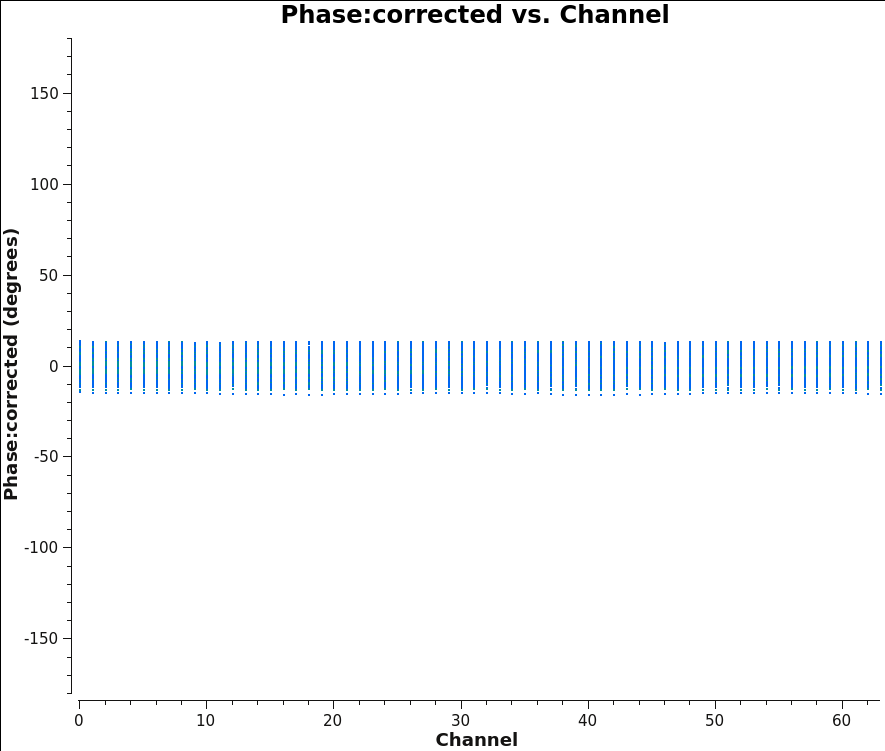 |
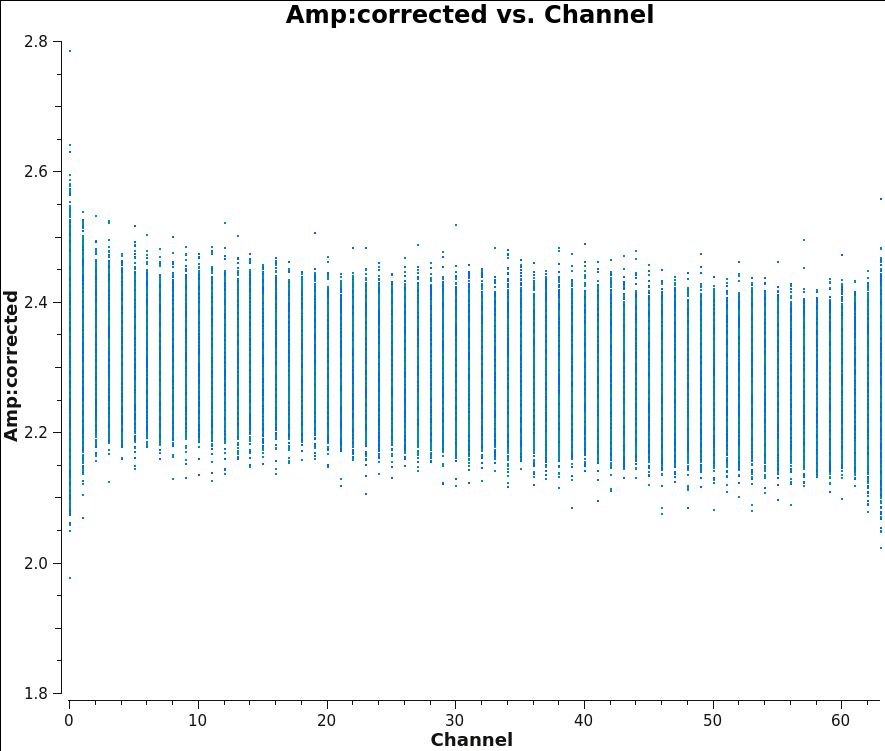 |
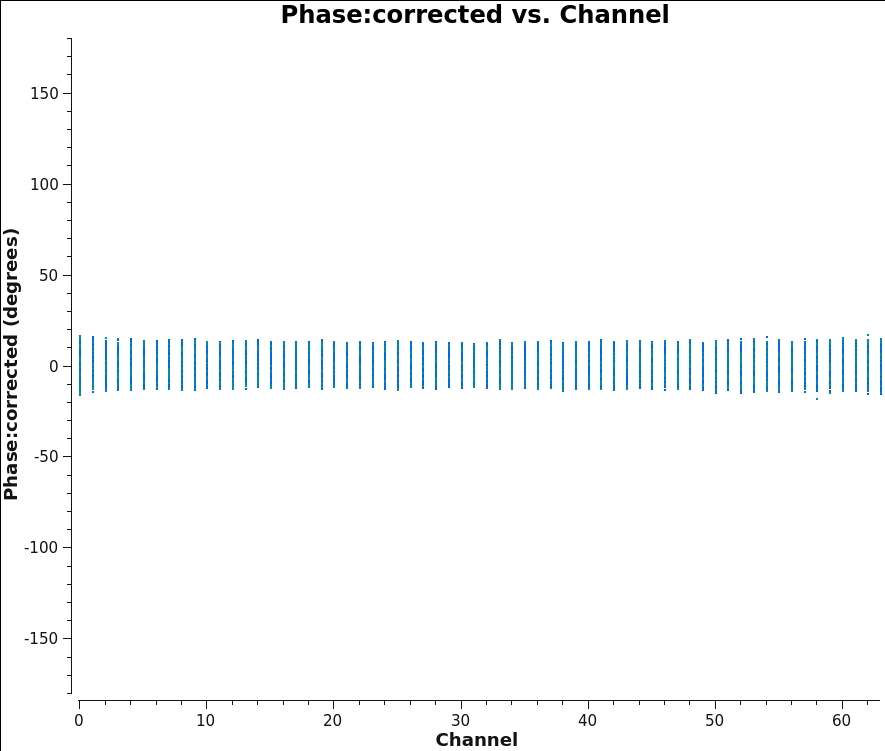 |
Now that the calibration has been applied to the target data we can split off the science targets, creating a new, calibrated measurement set containing all the target fields.
# In CASA
split(vis='3c391_ctm_mosaic_10s_spw0.ms',outputvis='3c391_ctm_mosaic_spw0.ms',
datacolumn='corrected',field='2~8',correlation='RR,LL')
- outputvis : We give the name of the new measurement set to be written, which will contain the calibrated data on the science targets.
- datacolumn : We use the CORRECTED_DATA column, containing the calibrated data which we just wrote using applycal().
- field : We wish to put all the mosaic pointings into a single measurement set, for imaging and joint deconvolution.
- correlation : For the purposes of this tutorial, we have calibrated only the parallel polarization correlations.
Prior to imaging, it is a good idea to run the statwt() task to correct the data weights (weight and sigma columns) in the measurement set. Running statwt() will remove the effects of relative noise scatter that may have been introduced from flagging uneven bits in the visibility data between the channels and times. We will run this task here on the newly calibrated and split-out data set before moving on to imaging.
# In CASA
statwt(vis='3c391_ctm_mosaic_spw0.ms',datacolumn='data')
After running statwt(), if you would like to again inspect the calibrated amplitudes of your data with plotms() , make sure you choose Wt*Amp and corrected data column for your y-axis.
Imaging
Now that we have split off the target data into a separate measurement set with all the calibration applied, it's time to make an image. Recall that the visibility data and the sky brightness distribution (a.k.a. image) are Fourier transform pairs.
[math]\displaystyle{ I(l,m) = \int V(u,v) e^{[2\pi i(ul + vm)]} dudv }[/math]
The [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math] coordinates are the baselines measured in units of the observing wavelength, while the [math]\displaystyle{ l }[/math] and [math]\displaystyle{ m }[/math] coordinates are the direction cosines on the sky. For generality, the sky coordinates are written in terms of direction cosines, but for most VLA (and ALMA) observations they can be related simply to the right ascension ([math]\displaystyle{ l }[/math]) and declination ([math]\displaystyle{ m }[/math]). Also recall that this equation is valid only if the [math]\displaystyle{ w }[/math] coordinate of the baselines can be neglected. This assumption is almost always true at high frequencies and smaller VLA configurations (such as the 4.6 GHz D-configuration observations here). The [math]\displaystyle{ w }[/math] coordinate cannot be neglected at lower frequencies and larger configurations (e.g., 0.33 GHz, A-configuration observations). This expression also neglects other factors, such as the shape of the primary beam. For more information on imaging, see the Synthesis Imaging section of the CASA documentation.
CASA has a task tclean which both Fourier transforms the data and deconvolves the resulting image. For the purposes of this tutorial, we will make a mosaic clean image in Stokes I. We will use a multi-scale cleaning algorithm because the supernova remnant contains both diffuse, extended structure on large spatial scales and finer filamentary structure on smaller scales. This approach will do a better job of modeling the image than the classic clean delta function. For broader examples of many tclean options, please see the Topical Guide for Imaging VLA Data.
Imaging parameters
It is important to have an idea of what values to use for the image pixel (cell) size and the overall size of the image. Setting the appropriate pixel size for imaging depends upon basic optics aspects of interferometry. Use plotms() to look at the newly-calibrated, target-only data set:
# In CASA
plotms(vis='3c391_ctm_mosaic_spw0.ms',xaxis='uvwave',yaxis='amp',
ydatacolumn='data', field='0',avgtime='30',correlation='RR',
plotfile='plotms_3c391-mosaic0-uvwave.png',overwrite=True)
You should obtain a plot similar to Figure 13 with the calibrated visibility amplitude as a function of [math]\displaystyle{ u }[/math]-[math]\displaystyle{ v }[/math] distance. Note that while 'uvdist' and 'uvwave' are in essence the same, they differ in units. The difference is that 'uvdist' is measured in physical units, i.e., meters (as the antenna separation is in meters), whereas 'uvwave' is measured in units of wavelengths at the specific frequency.
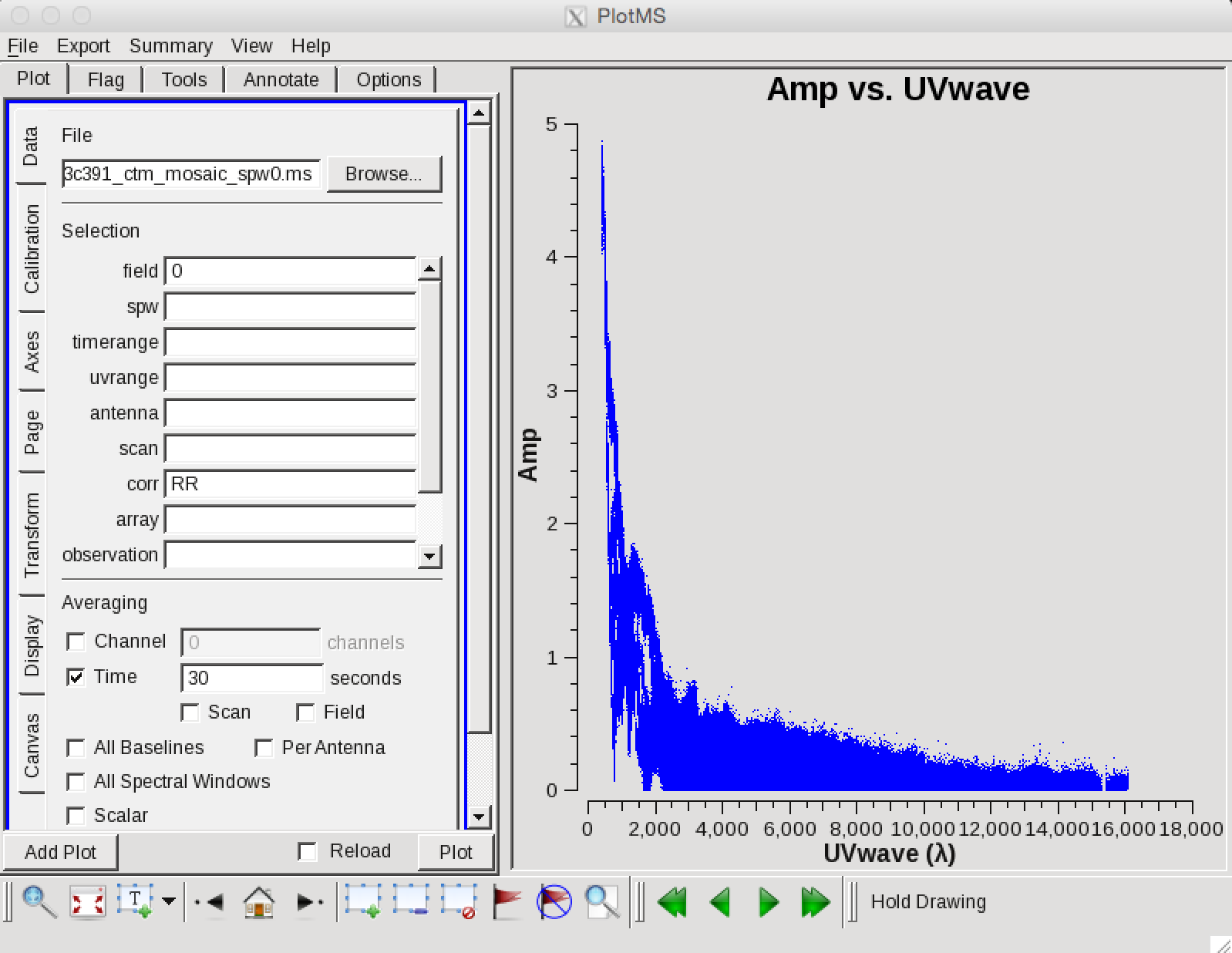 |
The maximum baseline is about 16,000 wavelengths, corresponding to smallest angular scale of 12 arcseconds ([math]\displaystyle{ \lambda/D=1/16000 }[/math]). The most effective cleaning occurs with at least 4-5 pixels across the synthesized beam (the angular resolution). For the angular resolution of 12 arcseconds, a cell size of 2.5 arcseconds will give just under 5 pixels per beam (2.5 arcsec/pixel x 5 pixels/synthesized_beam = 12 arcsec/synthesized_beam).
The supernova remnant itself is known to have a diameter of order 9 arcminutes, corresponding to about 216 pixels for the chosen cell size. The mosaic was set up with 7 fields: one centered on the remnant with 6 flanking fields; the spacing of the fields was chosen based on the size of the antenna primary beam. With the choice of gridder='mosaic' (our main mosaicking algorithm), we will image an area somewhat larger than the size of the supernova remnant in order to have a bit of padding around the outside. Although CASA has the feature that its Fourier transform engine (FFTW) does not require a strict power of 2 for the number of linear pixels in a given image axis, it is somewhat more efficient if the number of pixels on a side is a composite number divisible by any pair of 2 and 3 and/or 5. Because tclean internally applies a padding of 1.2 (= 3 x 2/5), we will use an image size of 480, which is 25 × 3 × 5 (so 480 × 1.2 = 576 = 26 × 32). We therefore set imsize=[480,480] and our mosaic fits comfortably inside the image.
Multi-scale Mosaic Clean
In this tutorial, we will run the cleaning task interactively so that we can set and modify the mask. Task tclean() is powerful with many inputs and a certain amount of experimentation likely is required. Before you execute the task provided below, please read the explanation of the parameters we are setting:
- vis='3c391_ctm_mosaic_spw0.ms' : this split MS contains our 7-pt mosaic fields, now indexed as 0-6. Field 0 is the central field of the mosaic (you can use listobs() to verify this).
- imagename='3c391_ctm_spw0_multiscale' : the output image names will all start with this (e.g., 3c391_ctm_spw0_multiscale.image, 3c391_ctm_spw0_multiscale.rms, etc.)
- specmode='mfs' : Use multi-frequency synthesis imaging. The fractional bandwidth of these data is non-zero (128 MHz at a central frequency of 4.6 GHz). Recall that the [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math] coordinates are defined as the baseline coordinates, measured in wavelengths. Thus, slight changes in the frequency from channel to channel result in slight changes in [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math]. There is an accompanying improvement in [math]\displaystyle{ u }[/math]-[math]\displaystyle{ v }[/math] coverage if the visibility data from the multiple spectral channels are gridded separately onto the [math]\displaystyle{ u }[/math]-[math]\displaystyle{ v }[/math] plane, as opposed to treating all spectral channels as having the same frequency.
- niter=20000,gain=0.1,threshold='1.0mJy' : Recall that the gain is the amount by which a clean component is subtracted during the cleaning process. Parameters niter and threshold are (coupled) means of determining when to stop the cleaning process, with niter specifying to find and subtract that many clean components while threshold specifies a minimum flux density threshold a clean component can have before tclean() stops. See also interactive below. Imaging is an iterative process, and to set the threshold and number of iterations, it is usually wise to clean interactively in the first instance, stopping when spurious emission from sidelobes (arising from gain errors) dominates the residual emission in the field. Here, we have used our experience in interactive mode to set a threshold level based on the rms noise in the resulting image. The number of iterations should then be set high enough to reach this threshold, although this can take many hours if the user does all 20000 iterations.
- gridder='mosaic' : The data consist of a 7-pointing mosaic, since the supernova remnant fills almost the full primary beam at 4.6 GHz. A mosaic combines the data from all of the fields, with imaging and deconvolution being done jointly on all 7 fields. A mosaic both helps compensate for the shape of the primary beam and reduces the amount of large (angular) scale structure that is resolved out by the interferometer.
- interactive=True : Very often, particularly when one is exploring how a source appears for the first time, it can be valuable to interact with the cleaning process. If True, interactive causes a viewer() window to appear. One can then set clean regions, restricting where tclean() searches for clean components, as well as monitor the cleaning process. A standard procedure is to set a large value for niter, and stop the cleaning when it visually appears to be approaching the noise level. This procedure also allows one to change the cleaning region, in cases when low-level intensity becomes visible as the cleaning process proceeds.
- imsize=[480,480],cell=['2.5arcsec'] : See the discussion above regarding the setting of the image size and cell size. If only one number is specified, the same value is used in both x and y directions (square image and/or pixel shape).
- stokes='I' : A single image will be made for total intensity I.
- deconvolver='multiscale', scales=[0, 5, 15, 45], smallscalebias=0.9 : The settings for multiscale are in units of pixels, with 0 pixels equivalent to the traditional delta-function clean. The scales here are chosen to provide delta functions and then three logarithmically scaled sizes to fit to the data. The first scale (5 pixels) is chosen to be comparable to the size of the synthesized beam. The smallscalebias attempts to balance the weight given to larger scales, which often have more flux density, and the smaller scales, which often are brighter. Considerable experimentation is likely to be necessary; one of the authors of this document found that it was useful to clean several rounds with this setting, change to multiscale=[] and remove much of the smaller scale structure, then return to this setting.
- weighting='briggs',robust=0.5 : 3C391 has diffuse, extended emission that is (at least partially) resolved out by the interferometer owing to a lack of short spacings. A naturally-weighted image would show large-scale patchiness in the noise. In order to suppress this effect, Briggs weighting is used (intermediate between natural and uniform weighting), with a default robust factor of 0.5 (which corresponds to something between natural and uniform weighting).
- pbcor=False : by default pbcor=False and a flat-noise image is produced. We can do the primary beam correction later (see below).
- savemodel='modelcolumn' : We recommend here the use of a physical MODEL_DATA scratch column for complicated gridders such as 'mosaic'. This will save some time, as it can be faster in the case of complicated gridding to read data from disk instead of doing all of the computations on-the-fly. However, this has the unfortunate side effect of increasing the size of the ms on disk.
Now, revise the parameters, and run the task:
# In CASA
tclean(vis='3c391_ctm_mosaic_spw0.ms',imagename='3c391_ctm_spw0_multiscale',
field='',spw='',
specmode='mfs',
niter=0,
gain=0.1, threshold='1.0mJy',
gridder='mosaic',
deconvolver='multiscale',
scales=[0, 5, 15, 45], smallscalebias=0.9,
interactive=True,
imsize=[480,480], cell=['2.5arcsec','2.5arcsec'],
stokes='I',
weighting='briggs',robust=0.5,
pbcor=False,
savemodel='modelcolumn')
As mentioned above, we can guide the clean process by allowing it to find clean components only within a user-specified region. When tclean() runs in interactive mode, a viewer() window will pop up as shown in Figure 14. To get a more detailed view of the central regions containing the emission, zoom in by first left clicking on the zoom button (leftmost button in third row) and tracing out a rectangle with the left mouse button and double-clicking inside the zoom box you just made. Play with the color scale to bring out the emission better, by holding down the middle mouse button and moving it around. To create a clean box (a region within which components may be found), hold down the right mouse button and trace out a rectangle around the source, then double-click inside that rectangle to set it as a box. Note that the clean box must turn white for it to be registered; if the box is not white, it has not been set! Alternatively, you can trace out a more custom shape to better enclose the irregular outline of the supernova remnant. To do that, right-click on the closed polygonal icon. Then trace out a shape by right-clicking where you want the corners of that shape. Once you have come full circle, the shape will be traced out in green, with small squares at the corners. Double-click inside this region and the green outline will turn white. You have now set the clean region. If you have made a mistake with your clean box, click on the Erase button, trace out a rectangle around your erroneous region, and double-click inside that rectangle. You can also set multiple clean regions.
 |
At any stage in the cleaning, you can adjust the number of iterations that tclean() will do before returning to the GUI. By default this is set to 100 (see the iterations field in mid-upper left of panel). You probably want to set this to a high number for this mosaic due to the complicated structure, values from 1000 to 5000 later on seem to work. Note that this will override the niter that was set when you started the clean task. tclean() will keep going until it reaches threshold or runs out of cycles (the cycles field to the right of the iterations).
When you are happy with the clean regions, press the green circular arrow button on the far right to continue deconvolution. After completing a cycle, a revised image will come up. As the brightest points are removed from the image (cleaned off), fainter emission may show up. You can adjust the clean boxes each cycle, to enclose all real emission. After many cycles, when only noise is left, you can hit the red-and-white stop-sign icon to stop cleaning. Figure 15 shows the interactive viewer panel later in the process, after cleaning 500 iterations. We have used the polygon tool to add to the clean region, drawing around emission that shows up in the residual image outside of the original clean region. After about 14000 iterations (Figure 16) the residuals are looking good (similar noise level inside and outside the clean region).
 |
 |
Questions:
|
Task tclean() will make several output files, all named with the prefix given as imagename. These include:
- .image: final restored image, with the clean components convolved with a restoring beam and added to the remaining residuals at the end of the imaging process
- .pb: effective response of the telescope (the primary beam)
- .mask: areas where tclean() has been allowed to search for emission
- .model: sum of all the clean components, which also has been stored as the MODEL_DATA column in the measurement set
- .psf: dirty beam, which is being deconvolved from the true sky brightness during the clean process
- .residual: what is left at the end of the deconvolution process; this is useful to diagnose whether or not to clean more deeply
- .weight: image of un-normalized sum of PB-square (for mosaics)
- .sumwt: a single pixel image containing sum of weights per plane
After the imaging and deconvolution process has finished, there are a few ways for you to inspect your image. CASA still has in-built viewer() task, but this task is no longer maintained and will be replaced in future versions of CASA. Therefore, we encourage the user to try using the NRAO replacement visualization tool for images and cubes, CARTA the “Cube Analysis and Rendering Tool for Astronomy”. It is available from the CARTA website. A comparison of the CASAviewer and CARTA, as well as instructions on how to use CARTA at NRAO is provided in the respective section of CASA docs. This tutorial shows Figures generated with CARTA for visualization.
If you would like to use CARTA now, and need some help, please ask one of the tutors to help you out. If you prefer to stick to the simple viewer for the moment, you can start it with the following command:
# In CASA
viewer('3c391_ctm_spw0_multiscale.image')
In viewer, you can adjust the color scale and zoom in to a selected region by assigning mouse buttons to the icons immediately above the image (hover over the icons to get a description of what they do). Also, using the wrench panel to change Display Options will be helpful here. In CARTA these options are available via the Render Configuration widget. Using this widget, one may select the scaling type, the max and min value, adjust the bias/contrast, and choose an appropriate color map to better emphasize the faint emission and compare to the noise (Figure 17).
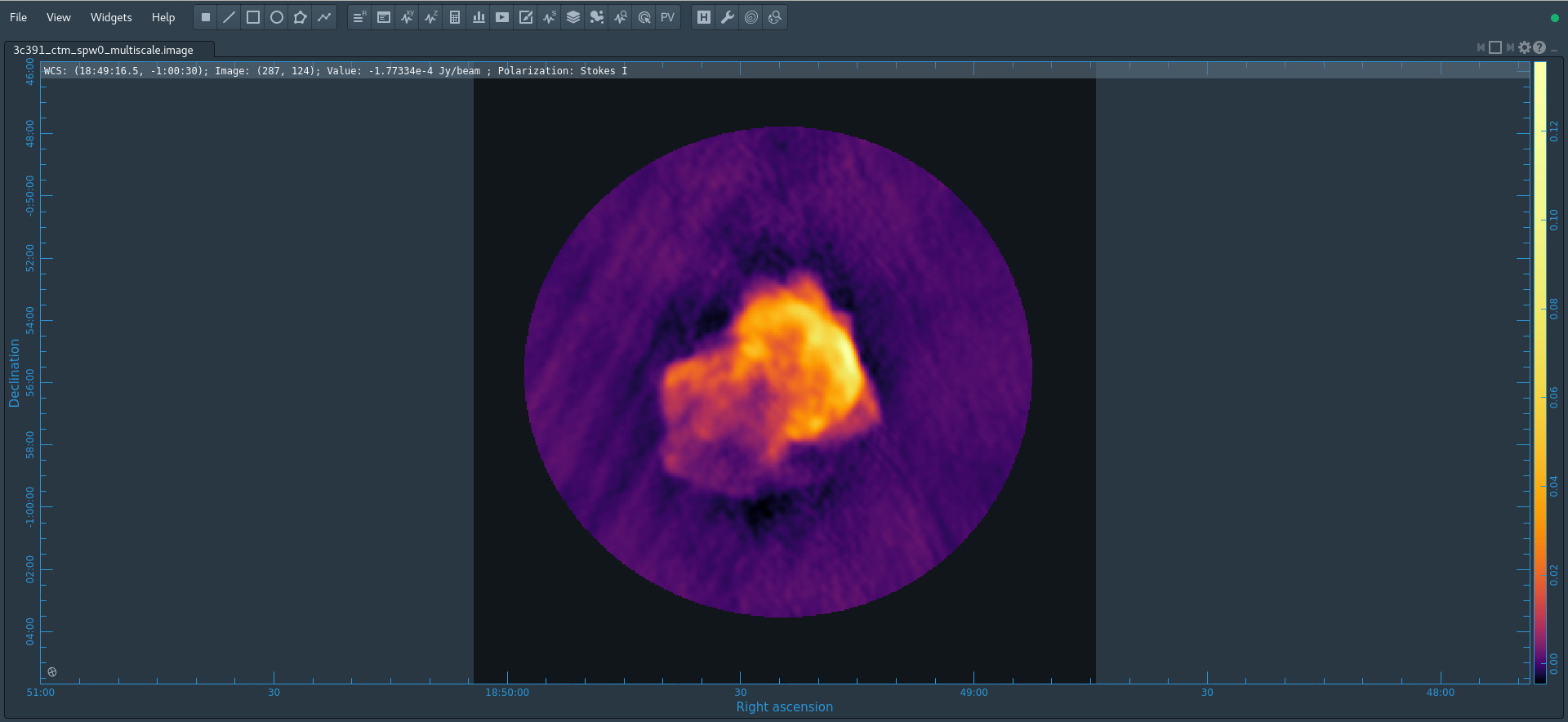 |
The tclean() task naturally operates in a flat noise image, i.e., an image where the effective weighting across the mosaic field of view is set so that the noise is constant. This is so that the clean threshold has a uniform meaning for the stopping criterion and that the image fed into the minor cycles has uniform noise levels. However, this means that the image does not take into account the primary beam fall-off in the edges and interstices of the mosaic. We could have set parameter pbcor=True in tclean(), but it is useful to see the flat-noise image and residuals to evaluate the quality of the clean image. Therefore, we use impbcor() to divide the .image by the .pb image to produce a primary beam corrected restored image:
# In CASA
impbcor(imagename='3c391_ctm_spw0_multiscale.image',pbimage='3c391_ctm_spw0_multiscale.pb',
outfile='3c391_ctm_spw0_multiscale.pbcorimage')
You can open this in the viewer and see that it has indeed raised the noise (and signal) at the edges of the mosaic.
Image Analysis
The three most basic analyses are to determine the peak brightness, the flux density, and the image noise level. These are useful measures of how well the imaging efforts are in approaching the thermal noise limit or in reproducing what is already known about a source. Additional discussion of image analysis and manipulation, including the combination of multiple images, mathematical operations on images, and much more can be found in the Image Analysis section of the CASA documentation.
The most straightforward statistic is the peak brightness, which is determined by imstat.
mystat = imstat(imagename='3c391_ctm_spw0_multiscale.pbcorimage')
This task returns a Python dictionary which we capture in the variable mystat.
The dictionary contains the values which you can extract for further use. For example, for a particular instance of the previous clean, we found:
CASA <4>: mystat
Out[4]:
{'blc': array([0, 0, 0, 0], dtype=int32),
'blcf': '18:50:04.251, -01.05.40.567, I, 4.59835e+09Hz',
'flux': array([ 9.78121725]),
'max': array([ 0.15670438]),
'maxpos': array([288, 256, 0, 0], dtype=int32),
'maxposf': '18:49:16.243, -00.55.00.579, I, 4.59835e+09Hz',
'mean': array([ 0.00387879]),
'medabsdevmed': array([ 0.00120803]),
'median': array([ 0.00038406]),
'min': array([-0.00684072]),
'minpos': array([237, 414, 0, 0], dtype=int32),
'minposf': '18:49:24.744, -00.48.25.580, I, 4.59835e+09Hz',
'npts': array([ 116013.]),
'q1': array([-0.00064426]),
'q3': array([ 0.00203547]),
'quartile': array([ 0.00267972]),
'rms': array([ 0.01261286]),
'sigma': array([ 0.01200169]),
'sum': array([ 449.99001048]),
'sumsq': array([ 18.45584197]),
'trc': array([479, 479, 0, 0], dtype=int32),
'trcf': '18:48:44.407, -00.45.43.065, I, 4.59835e+09Hz'}
CASA <5>: mystat['max'][0]
Out[5]: 0.156704381108284
and so the peak flux density is 0.157 Jy/beam.
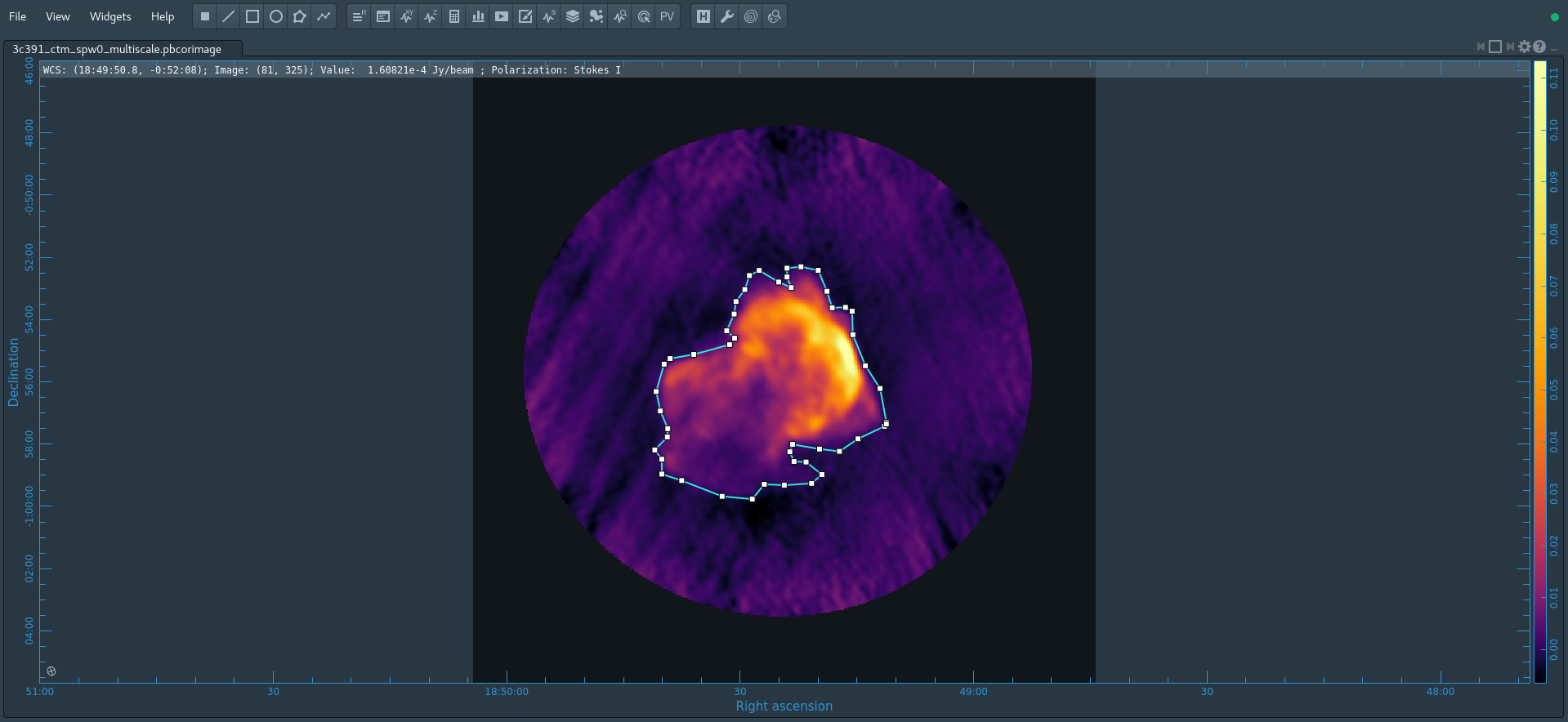 |
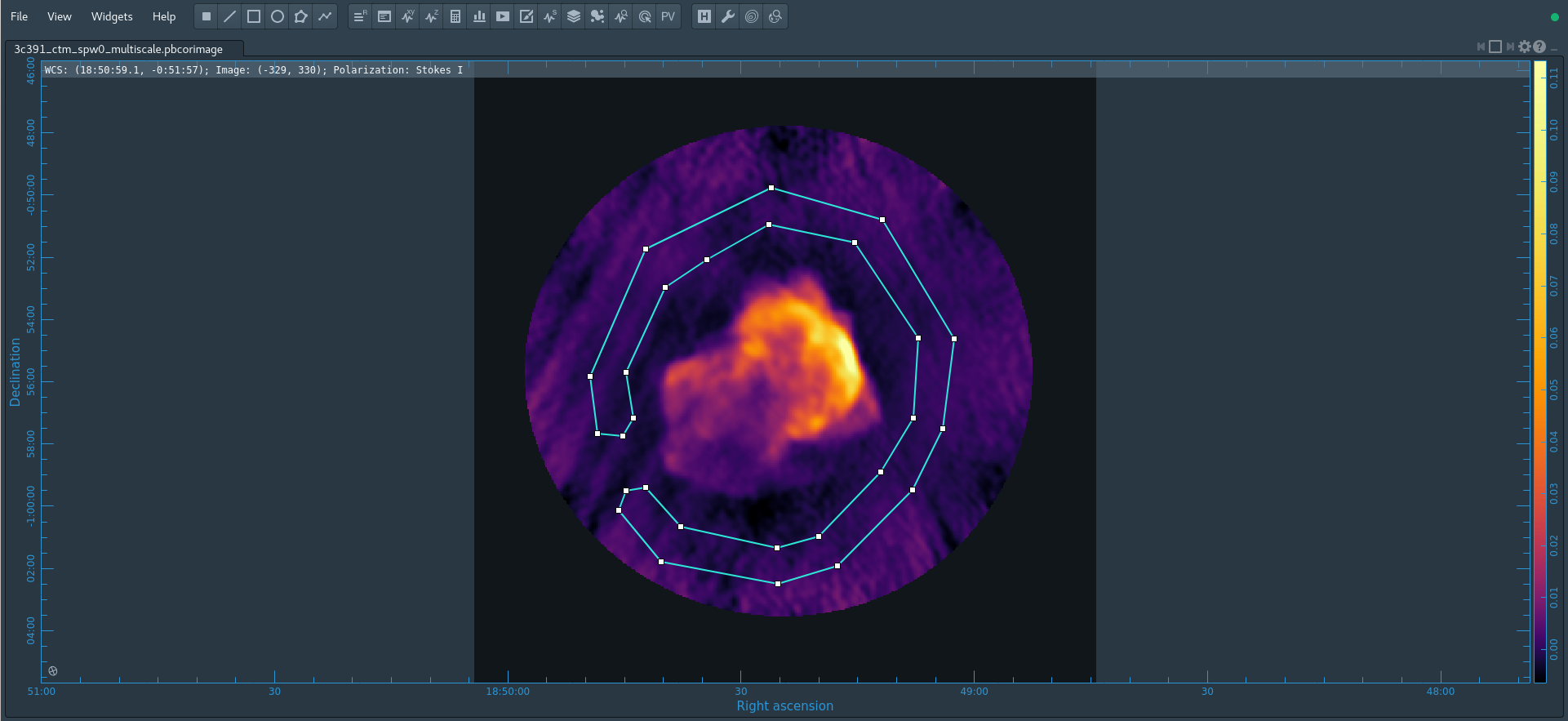 |
The other two statistics require slightly more care. The flux density of a source is determined by integrating its brightness or intensity over some solid angle, i.e.,
[math]\displaystyle{ S = \int d\Omega I }[/math]
where [math]\displaystyle{ I }[/math] is the intensity (measured in units of Jy/beam), [math]\displaystyle{ \Omega }[/math] is the solid angle of the source (e.g., number of synthesized beams), and [math]\displaystyle{ S }[/math] is the flux density (measured in units of Jy). In general, if the noise is well-behaved in the image, when averaged over a reasonable solid angle, the noise contribution should approach 0 Jy. If that is the case, then the flux density of the source is also reported by imstat. However, there are many cases for which a noise contribution of 0 Jy may not be a safe assumption. If the source is in a complicated region (e.g., a star formation region, the Galactic center, near the edge of a galaxy), a better estimate of the source's flux density will be obtained by limiting carefully the solid angle over which the integration is performed.
At this point you may open viewer and use it to display the corrected image or open the image within CARTA (Figure 18). If using viewer then for this analysis, it is better to use the version of the viewer that is run from the OS command line rather than the CASA command line. You can open this from inside CASA using '!':
# In CASA
!casaviewer '3c391_ctm_spw0_multiscale.pbcorimage' &
In viewer, one can choose the function assigned to each mouse button; after zooming into the desired view, assign polygon region to a desired mouse button (e.g., left button) by selecting the polygon tool ![]() to create a polygonal region. If using CARTA one may find a polygonal selection tool to similarly select a polygonal region as shown in Figure 18 with the desired mouse button.
to create a polygonal region. If using CARTA one may find a polygonal selection tool to similarly select a polygonal region as shown in Figure 18 with the desired mouse button.
Using the polygonal selection tool, outline the supernova remnant. Start drawing vertices by clicking on points in the image in succession, when you draw the final vertex then double-click to connect and finalize the region. In CARTA, when you click your mouse inside the region, a bounding box will appear with the vertices shown as draggable solid squares. If you want to adjust the vertices you can do so.
In CARTA, if you find you don't like your region you can dismiss it with the delete key or by double clicking within the region and clicking the "Delete" button, otherwise in the viewer you may select the region and press ESC. Also, in CARTA you can also select under File; Export regions to export regions you have created for later use or likewise in viewer you may save the region using the region panel.
In CARTA, to view statistics one may use the Statistics tool located under the Widgets tab and then select the appropriate region. In viewer, double click inside of that region (using the same mouse button used to make the region), and the statistics will be reported. This will include the flux density value within the region selected.
---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ----
(3c391_ctm_spw0_multiscale.pbcorimage)
Stokes Velocity Frame Doppler Frequency
I 0km/s LSRK RADIO 4.59835e+09
BrightnessUnit BeamArea Npts Sum FluxDensity
Jy/beam 46.0055 18836 4.318515e+02 9.386948e+00
Mean Rms Std dev Minimum Maximum
2.292692e-02 3.106691e-02 2.096504e-02 -1.934644e-03 1.567044e-01
region count
1
---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ----
In our example we find a total Flux density of 9.4 Jy. Note that the numbers you get may be slightly different depending on how deeply you cleaned.
By contrast, for the rms noise level, one can load the original (un-pbcor) image:
# In CASA
!casaviewer '3c391_ctm_spw0_multiscale.image' &
and to exclude the source's emission to the extent possible as shown in Figure 19, as the source's emission will bias the estimated noise level high. Likewise, one should avoid the clean bowl around the source emission. One can repeat the procedure above, defining a polygonal region, then double clicking inside it to determine the statistics. For example, from the region selection shown to the right for off-source statistics:
---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ----
(3c391_ctm_spw0_multiscale.image)
Stokes Velocity Frame Doppler Frequency
I 0km/s LSRK RADIO 4.59835e+09
BrightnessUnit BeamArea Npts Sum FluxDensity
Jy/beam 46.0055 23833 -1.520854e+00 -3.305808e-02
Mean Rms Std dev Minimum Maximum
-6.381295e-05 5.174784e-04 5.135396e-04 -2.055434e-03 1.800399e-03
region count
1
---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ----
Thus the Stokes I rms is 0.5 mJy. It will be useful later on to have the flat-noise and pb-corrected images available separately along with the statistics.
Self-Calibration
Even after the initial calibration using the amplitude calibrator and the phase calibrator, there are likely to be residual phase and/or amplitude errors in the data. Self-calibration is the process of using an existing model, often constructed from imaging the data itself, provided that sufficient visibility data have been obtained. This is essentially always the case with data: the system of equations is wildly over-constrained for the number of unknowns.
More specifically, the observed visibility data on the [math]\displaystyle{ i }[/math]-[math]\displaystyle{ j }[/math] baseline can be modeled as
[math]\displaystyle{ V'_{ij} = G_i G^*_j V_{ij} }[/math]
where [math]\displaystyle{ G_i }[/math] is the complex gain for the [math]\displaystyle{ i^{\mathrm{th}} }[/math] antenna and [math]\displaystyle{ V_{ij} }[/math] is the true visibility. For an array of [math]\displaystyle{ N }[/math] antennas, at any given instant, there are [math]\displaystyle{ N(N-1)/2 }[/math] visibility data, but only [math]\displaystyle{ N }[/math] gain factors. For an array with a reasonable number of antennas, [math]\displaystyle{ N }[/math] >~ 8, solutions to this set of coupled equations converge quickly.
For a more detailed introduction to self-calibration, see our VLA Self-calibration Tutorial. We also have lectures on Self-calibration given at NRAO community days. In self-calibrating data, it is useful to keep in mind the structure of a Measurement Set: there are three columns of interest for an MS: the DATA column, the MODEL column, and the CORRECTED_DATA column. In normal usage, as part of the initial split, the CORRECTED_DATA column is set equal to the DATA column. The self-calibration procedure is then:
- Produce an image (tclean) using the CORRECTED_DATA column.
- Derive a series of gain corrections (gaincal) by comparing the DATA columns and the Fourier transform of the image, which is stored in the MODEL column. These corrections are stored in an external table.
- Apply these corrections (applycal) to the DATA column, to form a new CORRECTED_DATA column, overwriting the previous contents of CORRECTED_DATA.
The following example begins with the standard data set, 3c391_ctm_mosaic_spw0.ms (resulting from the steps above). From this we will make an I-only multiscale image (3c391_ctm_spw0_I.image) -- and in particular the model (3c391_ctm_spw0_I.model) -- to generate a series of gain corrections that will be stored in 3C391_ctm_mosaic_spw0.selfcal1. These gain corrections are then applied to the data to form a set of self-calibrated data, and a new image is then formed (3c391_ctm_spw0_IQUV_selfcal1.image). We first use delmod on the MS to get rid of the previous model.
#In CASA
delmod('3c391_ctm_mosaic_spw0.ms')
tclean(vis='3c391_ctm_mosaic_spw0.ms',imagename='3c391_ctm_spw0_ms_I',
field='',spw='',
specmode='mfs',
niter=500,
gain=0.1,threshold='1mJy',
gridder='mosaic',
deconvolver='multiscale',
scales=[0, 5, 15, 45],smallscalebias=0.9,
interactive=True,
imsize=[480,480],cell=['2.5arcsec','2.5arcsec'],
stokes='I',
weighting='briggs',robust=0.5,
pbcor=False,
savemodel='modelcolumn')
You should not clean very deeply. You want to be sure to capture as much of the source total flux density as possible, but not include low-level questionable features or sub-structure (ripples) that might be due to calibration or clean artifacts.
After you are happy with the image:
#In CASA
gaincal(vis='3c391_ctm_mosaic_spw0.ms',caltable='3c391_ctm_mosaic_spw0.selfcal1',
field='',spw='',selectdata=False,
solint='30s',refant='ea21',minblperant=4,minsnr=3,
gaintype='G',calmode='p')
applycal(vis='3c391_ctm_mosaic_spw0.ms',
field='',spw='',selectdata=False,
gaintable= ['3c391_ctm_mosaic_spw0.selfcal1'],gainfield=[''],interp=['nearest'],
calwt=[False],applymode='calflag')
The CORRECTED_DATA column of the MS now contains the self-calibrated visibilities, they will now be used by tclean. The gaincal step will report a number of solutions with insufficient SNR. By default, with parameter applymode='calflag', data with no good solutions will be flagged by applycal; in this case you will see it report the flagged fraction increasing to about 45%. This may or may not be a good thing. You can control the action of applycal in this regard by changing the value of parameter applymode. The setting applymode='calflagstrict' will be even more stringent about flagging things without valid calibration, while applymode='calonly' will calibrate those with solutions while passing through without changing the data. You can see ahead of time what applycal will do by running with applymode='trial' which will do the reporting but nothing else.
Questions for the Advanced Student:
|
To see what this selfcal has done, do a deep clean:
#In CASA
tclean(vis='3c391_ctm_mosaic_spw0.ms',imagename='3c391_ctm_spw0_multiscale_selfcal1',
field='',spw='',
specmode='mfs',
niter=20000,
gain=0.1,threshold='1mJy',
gridder='mosaic',
deconvolver='multiscale',
scales=[0, 5, 15, 45],smallscalebias=0.9,
interactive=True,
imsize=[480,480],cell=['2.5arcsec','2.5arcsec'],
stokes='I',
weighting='briggs',robust=0.5,
pbcor=False,
savemodel='modelcolumn')
Questions for the Advanced Student:
|
Commonly, this self-cal procedure is applied multiple times. The number of iterations is determined by a combination of the data quality and number of antennas in the array, the structure of the source, the extent to which the original self-calibration assumptions are valid, and the user's patience. With reference to the original self-calibration equation above, if the observed visibility data cannot be modeled well by this equation, no amount of self-calibration will help. A not-uncommon limitation for moderately high dynamic range imaging is that there may be baseline-based factors that modify the true visibility. If the corruptions to the true visibility cannot be modeled as antenna-based, as they are above, self-calibration won't help.
Self-calibration requires experimentation. Do not be afraid to dump an image, or even a set of gain corrections, change something and try again. Having said that, here are several general comments or guidelines:
- Bookkeeping is important! Suppose one conducts 9 iterations of self-calibration. Will it be possible to remember one month later (or maybe even one week later!) which set of gain corrections and images are which? In the example above, the descriptor 'selfcal1' is attached to various files to help keep straight which is what. Successive iterations of self-cal could then be 'selfcal2' , 'selfcal3' , etc.
- Care is required in the setting of imagename. If one has an image that already exists, CASA will continue cleaning it (if it can), which is almost certainly not what one wants during self-calibration. Rather one wants a unique imagename for each pass of self-calibration.
- A common metric for self-calibration is whether the image dynamic range (= max/rms) has improved. An improvement of 10% is quite acceptable.
- Be careful when making images and setting clean regions or masks. Self-calibration assumes that the model is perfect. If one cleans a noise bump, self-calibration will quite happily try to adjust the gains so that the CORRECTED_DATA describe a source at the location of the noise bump. It is far better to exclude some feature of a source or a weak source from initial cleaning and conduct another round of self-calibration than to create an artificial source. If a real source is excluded from initial cleaning, it will continue to be present in subsequent iterations of self-calibration; if it's not a real source, one probably isn't interested in it anyway.
- Start self-calibration with phase-only solutions (parameter calmode='p' in gaincal). As discussed in the High Dynamic Range Imaging lecture, a phase error of 20 deg is as bad as an amplitude error of 10%.
- In initial rounds of self-calibration, consider solution intervals longer than the nominal sampling time (parameter solint in gaincal) and/or lower signal-to-noise ratio thresholds (parameter minsnr in gaincal). Depending upon the frequency and configuration and fidelity of the model image, it can be quite reasonable to start with solint='30s' or solint='60s' and/or minsnr=3 (or even lower). One might also want to consider specifying a uvrange, if, for example, the field has structure on large scales (small [math]\displaystyle{ u }[/math]-[math]\displaystyle{ v }[/math]) that is not well represented by the current image.
- The task applycal will flag data with no good calibration solutions. During the initial self-calibration steps, this flagging may be excessive. If so, one can restore the flags to the state right before running applycal by using the task flagmanager.
- You can track the agreement between the DATA, CORRECTED_DATA, and MODEL in plotms. The options in the Axes tab allows one to select which column is to be plotted. If the MODEL agrees well with the CORRECTED_DATA, one can use shorter solint and/or higher minsnr values.
- You should consider examining the solutions from gaincal by using plotms in order to assure that the corrections are sensible. Smoothly varying phases are good, jumps are usually not. (However, because the phases are plotted ±180 degrees, there can be apparent jumps if the phases are very near +180 deg or −180 deg.)
- In the case of a mosaic, such as here, one should also verify that the solutions are of equal quality for all of the fields.
On Your Own: 3C391 second frequency and G93.3+6.9
Now that you have run through spw 0 of 3C391, you are ready to strike off on your own with other datasets. We have provided two options here, described below. The first option is simplest as it is the same object using a different spectral window; for a more rewarding challenge try the L-band dataset on G93.3+6.9.
You can find the data in the CASA repository. Both datasets -- 3C391 spw 1 (at 7.5 GHz) and Supernova Remnant G93.3+6.9 at L-band -- are contained in this tarball.
1. 3C391 spw 1 (at 7.5 GHz)
This is the second spectral window split off from the 3C391 dataset. You can process this as you did the first time, but beware of RFI in this band. You will have to avoid it through channel ranges and/or edit it out. Once you have processed this data, you can combine the two calibrated MSs in tclean to make a deeper MFS image (this might be tricky).
2. Supernova Remnant G93.3+6.9 at L-band
This is data taken at L-band of an entirely different Supernova Remnant, centered near 1400 MHz. You should be able to process this data in a very similar manner to the C-band data on 3C391. Note that we are not telling you what you will see in the image ahead of time. Here are some data reduction hints to help you along:
- There is strong RFI in this spectral window of the original 2 spw dataset. You will need to find it (e.g., using plotms) and avoid it in imaging. You can also flag those channels using flagdata, but this is not necessary. Note that there is a single baseline that shows very strong interference, see if you can find it. You can flag it using the baseline syntax in flagdata (e.g., parameter antenna='ea0x&ea0y' ).
- We have not edited out bad or dead antennas for you (unlike in 3C391). You will need to find these using plotms and then flagdata them. One helpful plotms trick is to set parameter antenna='ea01' and pick a few channels (like spw='0:30~33' ) and a single scan (e.g., scan='2~3' ) and plot the amp versus Antenna2 on the X-axis. You should see the bad antennas (the low ones). As a check set antenna='ea02' and repeat. Is it the same?
- In spite of RFI, the antenna-based calibration is remarkably resilient to moderate-to-low RFI contamination (which tends to be baseline-based). So rather than flagging channels with RFI, you might try going ahead with calibration and seeing if the solutions make sense. We were able to calibrate this data without flagging channels (only getting the bad baseline noted above).
- There is no observation of a flux calibrator like J1331+3030. You need to use setjy to set the Stokes I flux of the gain calibrator. We use the approximate flux density of 5.8 Jy for J2038+5119.
- The L-band field of view is much larger than at C-band. From the VLA Observational Status Summary (OSS) the resolution should be around 46" in D-config. Use a cellsize of 15" or smaller. What is the primary beam of the VLA at 1.4MHz? How big should you make your image?
- As you clean you will see faint sources all over the field; welcome to L-band imaging. This supernova remnant has lots of structure - try both standard and multi-scale tclean.
Last checked on CASA Version 6.5.4