3C286 Band6Pol Imaging for CASA 5.1

Overview

This guide is designed for CASA 5.1.

This portion of the 3C286_Polarization CASA Guide will cover the imaging of the total power and polarized emission. Details of the ALMA observations are provided at 3C286_Polarization.

This guide picks up where the 3C286_Band6Pol_Calibration_for_CASA_5.1 section left off: right after running the CASA task split to split off the science target from the rest of the measurement set following calibration. If you completed the Calibration section of the guide, then you can continue where you left off, with 3c286_Band6.pol.cal.ms.

If you did not complete the Calibration portion of the guide, then you can instead download the file 3C286_Band6_CalibratedData.tgz (the calibrated uv data) from 3C286_Polarization#Obtaining the Data.

Once the download has finished, unpack the file:

# In a terminal outside CASA
tar -xvzf 3C286_Band6_CalibratedData.tgz

cd 3C286_Band6_CalibratedData

# Start CASA
casa

After that, you should have 3c286_Band6.pol.cal.ms in your working directory.

Full polarization imaging of the target

We will start by making a continuum full Stokes image of 3C286 using tclean. We first define the dataset we will use in all the following steps:

# In CASA
vis='3c286_Band6.pol.cal.ms'

Before starting the cleaning, it makes sense to check if the emission is resolved or not by plotting amplitude as a function of uv-distance. The higher amplitudes at shorter uv-distances suggest that the source is slightly resolved.

# In CASA
plotms(vis, spw='', xaxis='uvwave', yaxis='amp', correlation='XX,YY',
       avgtime='1e8', avgchannel='1000', coloraxis='baseline')

Amplitude vs. uv-distance. The source seems to be slightly resolved.

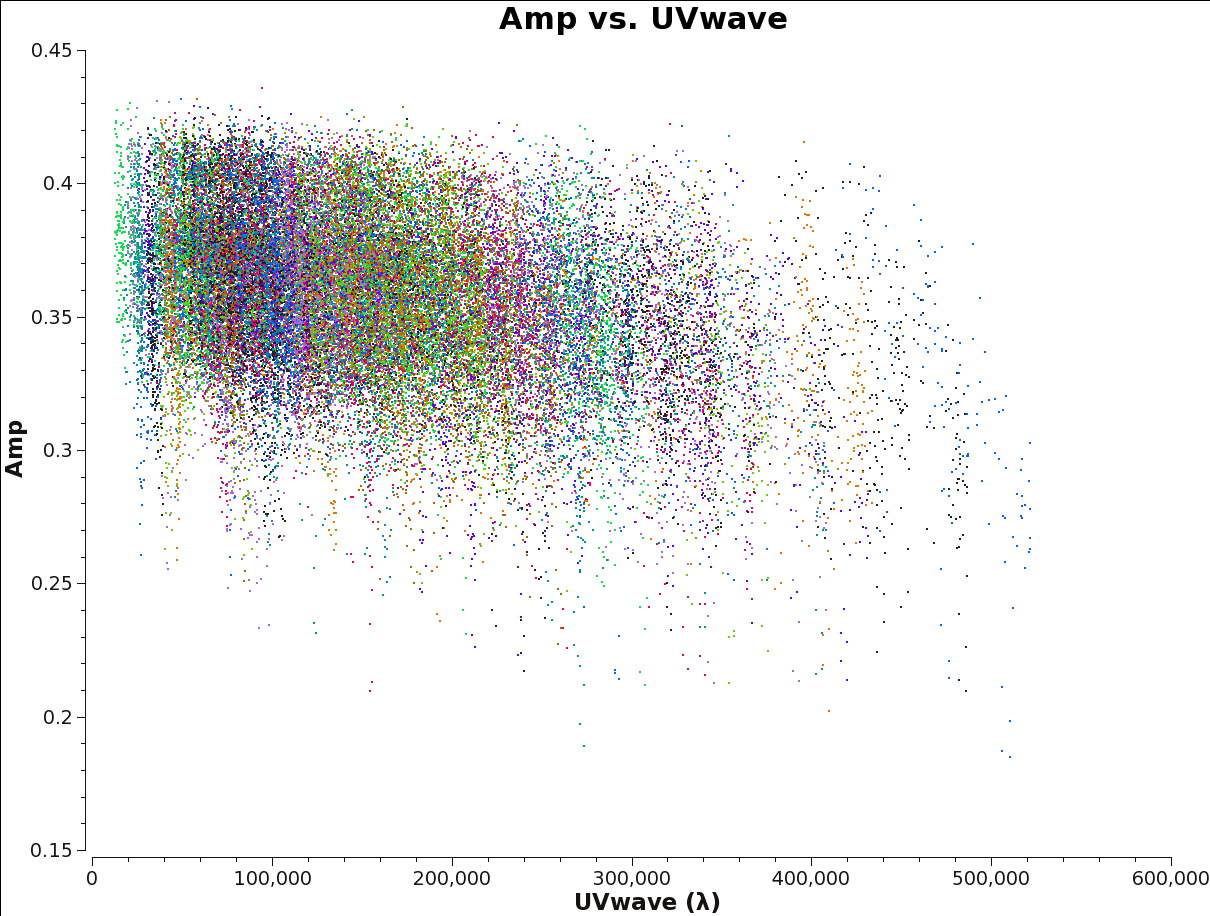
This plot also helps us defining the cellsize needed for the task clean. From the plot we see that the longest baseline is 500 kilo wavelength. This means that the maximum resolution can be approximately 1/500000*206265 arcsec = 0.4 arcsec. We will use a cellsize=0.1, to oversample the beam sufficiently. The FWHM of the primary beam of ALMA in Band 6 is about 25 arcsec, and we want to image out to at least that extent, so we will use imsize=250.

# In CASA

os.system('rm -rf 3c286.cal.StokesIQUV_noselfcal.clean*')
tclean(vis,
      imagename='3c286.cal.StokesIQUV_noselfcal.clean',
      cell=['0.1arcsec'],
      imsize=[250,250],
      deconvolver='clarkstokes',
      stokes='IQUV',
      interactive=True, 
      niter=1000,
      pbcor=True,
      savemodel='modelcolumn')

Specifying interactive=True , the tclean task brings up a viewer to show the residual clean image, clean masks can be defined, and when the residuals are noise-like, the cleaning process can be interrupted, hiting the red X symbol. Please note that the cleaning will not start without any active mask (to activate a mask you need to double click inside the region). See TW Hydra casaguide for further details on the interactive use of clean.

Finally, note that we delete any previous versions of the output images before proceeding with the clean command. This is important, because if images with the supplied root name already exist, CASA will clean those further instead of producing new output images.

After around 300 iterations, using an elliptical clean box around the central source, the residuals are already noise-like, so you can stop the cleaning. You can use the viewer to look at your image.

# In CASA
viewer('3c286.cal.StokesIQUV_noselfcal.clean.image')

Total intensity image of 3C286

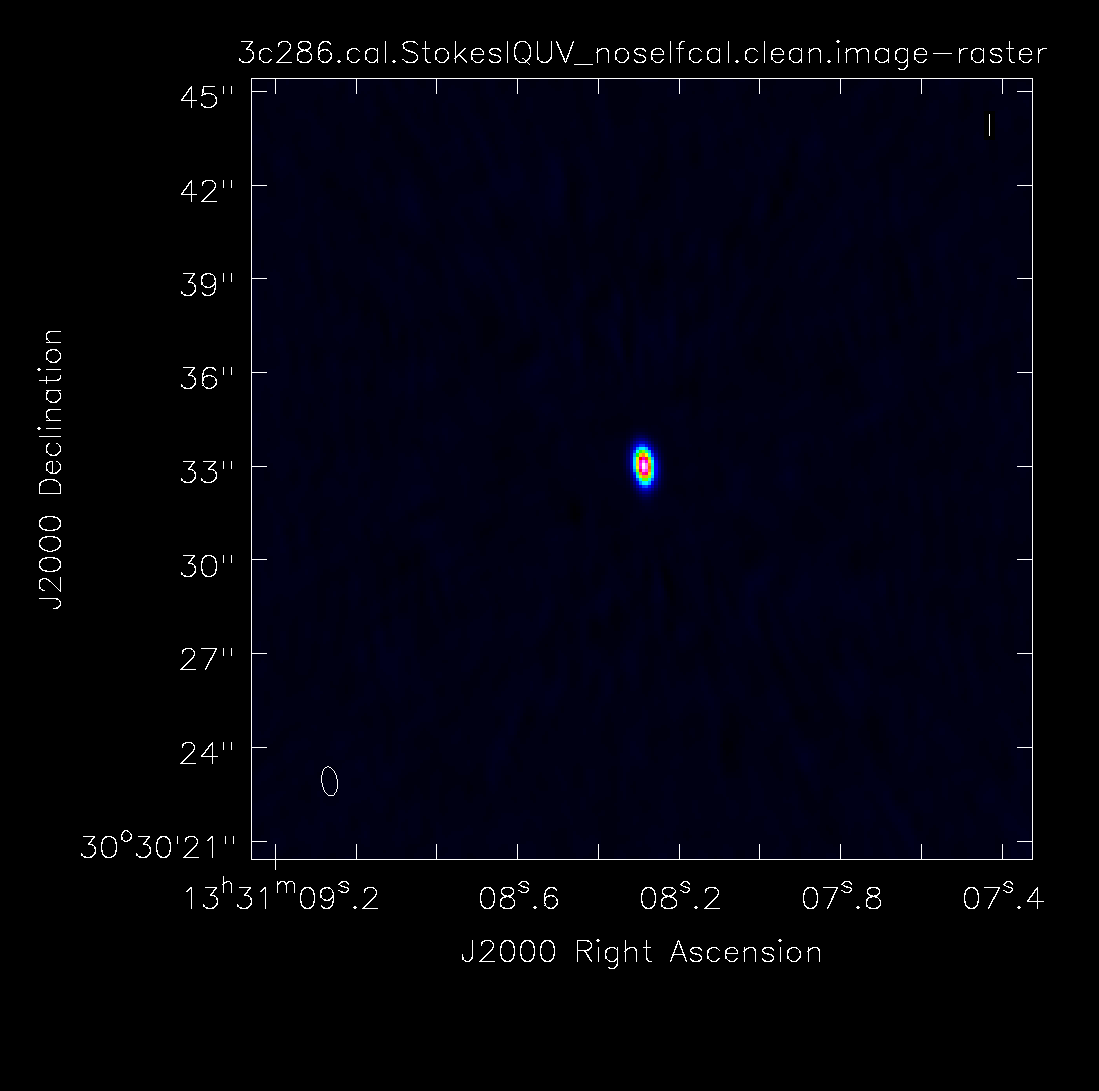
You will notice a warning at the end of the clean command. The model column may not have been saved. Use the following command to make sure the model column is saved.

# In CASA

tclean(vis,
      imagename='3c286.cal.StokesIQUV_noselfcal.clean',
      cell=['0.1arcsec'],
      imsize=[250,250],
      deconvolver='clarkstokes',
      stokes='IQUV',
      interactive=False, 
      niter=0,
      pbcor=True,
      calcres=False,
      calcpsf=False,
      savemodel='modelcolumn')

We will determine some statistics for the image using the task imstat (some details are given below):

# In CASA
calstat=imstat(imagename='3c286.cal.StokesIQUV_noselfcal.clean.image', stokes='I', region='', box='10,10,90,35')
rms=(calstat['rms'][0])
print '>> rms in continuum image: '+str(rms)
calstat=imstat(imagename='3c286.cal.StokesIQUV_noselfcal.clean.image', region='')
peak=(calstat['max'][0])
print '>> Peak in continuum image: '+str(peak)
print '>> Dynamic range in continuum image: '+str(peak/rms)

This tells us that the rms of this image is 0.9 mJy and the peak flux density is ~335.4 mJy. The dynamic range (ratio between peak and rms) is approximately 366.

For future reference, we create a png file of the continuum image:

# In CASA
os.system('rm -rf 3c286.cal.StokesIQUV_noselfcal.clean.png')
imview(raster={'file': '3c286.cal.StokesIQUV_noselfcal.clean.image', 'colorwedge':True,
               'range':[-0.006, 0.4], 'scaling':-0.6, 'colormap':'Rainbow 2'},
                out='3c286.cal.StokesIQUV_noselfcal.clean.png')

The mask you drew for the clean has been saved in your working directory as a file "3c286.cal.StokesIQUV_noselfcal.clean.mask". If you want to use it in the following self-calibration you should rename it. If you downloaded the calibrated data you have already a file mask, named 3c286_StokesIQUV_selfcal.mask.

To rename the file:

# In CASA
os.system('mv 3c286.cal.StokesIQUV_noselfcal.clean.mask 3c286_StokesIQUV_selfcal.mask')

Self-calibration

The quality of the image can be improved by applying the self-calibration to the uv data, see Antennae and TwHydra guides for details on this technique.

The task tclean has automatically saved a model in the header of the measurement set, we use it to self-calibrate through the task gaincal:

# In CASA
os.system('rm -rf 3c286_IQUV.G1p')
gaincal(vis,
        caltable='3c286_IQUV.G1p',
        solint='300s',
        refantmode='strict',
        refant='DV23',minblperant=4,
        calmode='p',minsnr=4)

The critical parameters in this setup are solint and calmode. We will force the reference antenna to remain constant with the reantmode='strict'. We want to calculate phase solutions only so we use calmode=p and we start using solint=300s, which means averaging 30 visibilities in the solution calculation. It is usually best to start with a large solint and then go down to the integration time if the S/N of the data permits.

To check the quality of the solutions we obtained, we plot the gains for each antenna, as function of time:

# In CASA
plotcal(caltable='3c286_IQUV.G1p', xaxis='time', yaxis='phase', iteration='antenna')

Now we apply those solutions to the uv data:

# In CASA

applycal(vis,
         field='',
         gaintable=['3c286_IQUV.G1p'],calwt=False)

and make a new image:

# In CASA

os.system('rm -rf 3c286.cal.StokesIQUV_selfcal1.clean*')
tclean(vis,
      imagename='3c286.cal.StokesIQUV_selfcal1.clean',
      cell=['0.1arcsec'],
      imsize=[250,250],
      deconvolver='clarkstokes',
      stokes='IQUV',
      mask= '3c286_StokesIQUV_selfcal.mask',
      interactive=True,
      pbcor=True,
      niter=1000,
      savemodel='modelcolumn')

calstat=imstat(imagename='3c286.cal.StokesIQUV_selfcal1.clean.image', stokes='I', region='', box='10,10,90,35')
rms=(calstat['rms'][0])
print '>> rms in continuum image: '+str(rms)
calstat=imstat(imagename='3c286.cal.StokesIQUV_selfcal1.clean.image', region='')
peak=(calstat['max'][0])
print '>> Peak in continuum image: '+str(peak)
print '>> Dynamic range in continuum image: '+str(peak/rms)

The rms of this new image is 0.25 mJy/beam, lower than the value measured in the first image (0.9 mJy/beam). We run a second self-calibration, decreasing to 30 sec the solint, apply it to the data, and image it again:

# In CASA
os.system('rm -rf 3c286_IQUV.G2p')
gaincal(vis,
        caltable='3c286_IQUV.G2p',
        solint='30s',
        refant='DV23',minblperant=4,
        calmode='p',minsnr=4)

plotcal(caltable='3c286_IQUV.G2p', xaxis='time', yaxis='phase', iteration='antenna')


applycal(vis,
         field='',
         gaintable=['3c286_IQUV.G2p'],calwt=False)

os.system('rm -rf 3c286.cal.StokesIQUV_selfcal2.clean*')
tclean(vis,
      imagename='3c286.cal.StokesIQUV_selfcal2.clean',
      cell=['0.1arcsec'],
      imsize=[250,250],
      deconvolver='clarkstokes',
      stokes='IQUV',
      mask= '3c286_StokesIQUV_selfcal.mask',
      interactive=True,
      pbcor=True,
      niter=1000,
      savemodel='modelcolumn')

You can notice when the first residual image appears that some residual central emission is evident. Continue the cleaning, by using the green continue button, until the residual image appears as much as possible noise like. In this example we stop the clean after 2 cycles, and we check the image statistics.

# In CASA
calstat=imstat(imagename='3c286.cal.StokesIQUV_selfcal2.clean.image', stokes='I', region='', box='10,10,90,35')
rms=(calstat['rms'][0])
print '>> rms in continuum image: '+str(rms)
calstat=imstat(imagename='3c286.cal.StokesIQUV_selfcal2.clean.image', region='')
peak=(calstat['max'][0])
print '>> Peak in continuum image: '+str(peak)
print '>> Dynamic range in continuum image: '+str(peak/rms)

The rms level in this new image is ~0.2 mJy/beam. This level can be improved by a last run of selfcalibration, this time solving for both amplitude and phase.

# In CASA
os.system('rm -rf 3c286_IQUV.Gap')
gaincal(vis,
        caltable='3c286_IQUV.Gap',
        solint='30s',gaintable=['3c286_IQUV.G2p'],
        refant='DV23',minblperant=4,
        calmode='ap',minsnr=4)

applycal(vis,
         field='',
         gaintable=['3c286_IQUV.G2p','3c286_IQUV.Gap'],calwt=False)

os.system('rm -rf 3c286.cal.StokesIQUV_selfcal_ap.clean*')
tclean(vis,
      imagename='3c286.cal.StokesIQUV_selfcal_ap.clean',
      cell=['0.1arcsec'],
      imsize=[250,250],
      deconvolver='clarkstokes',
      stokes='IQUV',
      mask= '3c286_StokesIQUV_selfcal.mask',
      interactive=True, 
      pbcor=True,
      niter=1000,
      savemodel='modelcolumn')

This time the first residual map shows a new bright extended component which was completely hidden by the noise in the previous images. We add a clean box around it and proceed with the clean. After 10 cycles we stop and check the statistics of the image:

# In CASA
calstat=imstat(imagename='3c286.cal.StokesIQUV_selfcal_ap.clean.image', stokes='I', region='', box='10,10,90,35')
rms=(calstat['rms'][0])
print '>> rms in continuum image: '+str(rms)
calstat=imstat(imagename='3c286.cal.StokesIQUV_selfcal_ap.clean.image', region='')
peak=(calstat['max'][0])
print '>> Peak in continuum image: '+str(peak)
print '>> Dynamic range in continuum image: '+str(peak/rms)

The rms is 0.037 mJy and the peak of the image is 368 mJy, leading to a dynamic range of 9950.

We can consider this result satisfying and stop the self-calibration.

Stokes images

We can extract the Stokes Q, U, and V images from the selfcalibrated image, using the taks immath:

# In CASA
os.system('rm -rf 3c286.cal.StokesI.clean.image*')
immath(imagename='3c286.cal.StokesIQUV_selfcal_ap.clean.image',outfile='3c286.cal.StokesI.clean.image',expr='IM0',stokes='I')
os.system('rm -rf 3c286.cal.StokesQ.clean.image*')
immath(imagename='3c286.cal.StokesIQUV_selfcal_ap.clean.image',outfile='3c286.cal.StokesQ.clean.image',expr='IM0',stokes='Q')
os.system('rm -rf 3c286.cal.StokesU.clean.image*')
immath(imagename='3c286.cal.StokesIQUV_selfcal_ap.clean.image',outfile='3c286.cal.StokesU.clean.image',expr='IM0',stokes='U')
os.system('rm -rf 3c286.cal.StokesV.clean.image*')
immath(imagename='3c286.cal.StokesIQUV_selfcal_ap.clean.image',outfile='3c286.cal.StokesV.clean.image',expr='IM0',stokes='V')

We measure the statistic in each emage, using the task imstat:

# In CASA

I_rms=(imstat(imagename='3c286.cal.StokesI.clean.image', region='', box='10,10,90,35')['rms'][0])
I_peak=(imstat(imagename='3c286.cal.StokesI.clean.image', region='')['max'][0])
Q_rms=(imstat(imagename='3c286.cal.StokesQ.clean.image', region='', box='10,10,90,35')['rms'][0])
Q_peak=(imstat(imagename='3c286.cal.StokesQ.clean.image', region='')['max'][0])
U_rms=(imstat(imagename='3c286.cal.StokesU.clean.image', region='', box='10,10,90,35')['rms'][0])
U_peak=(imstat(imagename='3c286.cal.StokesU.clean.image', region='')['max'][0])

print I_rms, I_peak, Q_rms, Q_peak, U_rms, U_peak

The results of the measurements for the I, Q, and U images are reported in the table below. All flux densities are reported in mJy/beam.

The results obtained from the V image are not reported in the table, since at this time the quality and accuracy of the circular polarization data are still undergoing verification. Results from the V image are therefore not recommended for scientific purposes at this time.

	I	Q	U
rms	0.037	0.026	0.05
Peak	368.3	14.1	59.1
Dyn range	9950	542	1182

Constructing Polarization Intensity and Angle Images

We have now produced the images for all the four Stokes parameters: I, Q, U, and V. Stokes Q and U describe the linear polarization and V describes the circular polarization. Specifically, Q describes the amount of linear polarization aligned with a given axis, and U describes the amount of linear polarization at a 45 deg angle to that axis. The V parameter describes the amount of circular polarization, with the sign (positive or negative) describing the sense of the circular polarization (right- or left-hand circularly polarized).

In general, few celestial sources are expected to show circular polarization, with the notable exception of masers. Terrestrial and satellite sources are often highly circularly polarized. The V image is therefore often worth forming because any V emission could be indicative of unflagged RFI within the data (or problems with the calibration!).

Because the Q and U images both describe the amount of linear polarization, it is more common to work with a linear polarization intensity image, [math]\displaystyle{ P = \sqrt{Q^2 +U^2} }[/math]. We can also calculate the polarization position angle [math]\displaystyle{ \chi = 0.5 arctan U/Q }[/math].

The relevant task is immath; for specific examples of polarization image processing see Polarization Manipulation.

To form the linear polarization image, we combine the Q and U images using the mode='poli' option of immath.

# In CASA
os.system('rm -rf 3c286_Band6.POLI')
immath(outfile='3c286_Band6.POLI',
       mode='poli',
       imagename=['3c286.cal.StokesQ.clean.image','3c286.cal.StokesU.clean.image'],
       sigma='0.0Jy/beam')

# In CASA
calstat=imstat(imagename='3c286_Band6.POLI', region='', box='10,10,90,35')
rms=(calstat['rms'][0])

The measured rms is 0.1 mJy/beam.

To form the polarization position angle image we combine again the Q and U images using the mode='pola' option of immath. The Q and U images can be listed in either order. To avoid displaying the position angle of noise, we can use the polithresh parameter to set a threshold intensity of the linear polarization above which we wish to calculate the polarization angle. An appropriate level here might be the 5σ level of the polarization image, about 0.1 mJy/beam.

# In CASA
os.system('rm -rf 3c286_Band6.POLA')
immath(outfile='3c286_Band6.POLA',
       mode='pola',
       imagename=['3c286.cal.StokesQ.clean.image','3c286.cal.StokesU.clean.image'],
       polithresh='0.5mJy/beam')

If desired, it is also possible to form the fractional linear polarization image, defined as P/I.

# In CASA
os.system('rm -rf 3c286_Band6.RATIO')
immath(outfile='3c286_Band6.RATIO',
       mode='evalexpr',
       imagename=['3c286.cal.StokesI.clean.image','3c286.cal.StokesQ.clean.image','3c286.cal.StokesU.clean.image'],
       expr='sqrt((IM1^2+IM2^2)/IM0[IM0>5e-3]^2)')

Since the total intensity image can (and hopefully does) approach zero in regions free of source emission, dividing by the total intensity can produce very high pixel values in these regions. We therefore wish to restrict our fractional polarization image to regions containing real emission, which we do by setting a threshold in the total intensity image, which in this case corresponds to five times the noise level in the Stokes I image. The computation of the polarized intensity is specified in the previous command by

       expr='sqrt((IM1^2+IM2^2)/IM0[IM0>5e-3]^2)'

with the expression in square brackets setting the threshold in IM0 (the total intensity image). Note that IM0, IM1 and IM2 correspond to the three files listed in the imagename array, in that order. In this case, the order in which the different images are specified is critical.

In order to have a dimensionless value for the ratio image, we now modify the keyword bunit in the header of the file:

# In CASA
imhead('3c286_Band6.RATIO', mode='put', hdkey='bunit', hdvalue='')

Image visualization and analysis

Now we can view these various images using viewer. It is instructive to display the I, P, and [math]\displaystyle{ \chi }[/math] images (total intensity, total linearly polarized intensity, and polarization position angle) together, to show how the polarized emission relates to the total intensity, and how the magnetic field is structured. We can do this using the viewer.

• Begin by loading the linear polarization image in the viewer:

# In CASA
viewer('3c286_Band6.POLI')

• Next, load the total intensity image as a contour image. In the viewer panel, hit the "Open" icon (the leftmost button in the top row of icons in the viewer). This will bring up a 'Load Data' GUI showing all images and MS in the current directory. Select the total intensity image (3c286.cal.StokesI.clean.image) and click the 'Contour Map' button on the right hand side.
• Finally, load the polarization position angle image (3c286_Band6.POLA) as a vector map.

Full-polarization image of 3C286

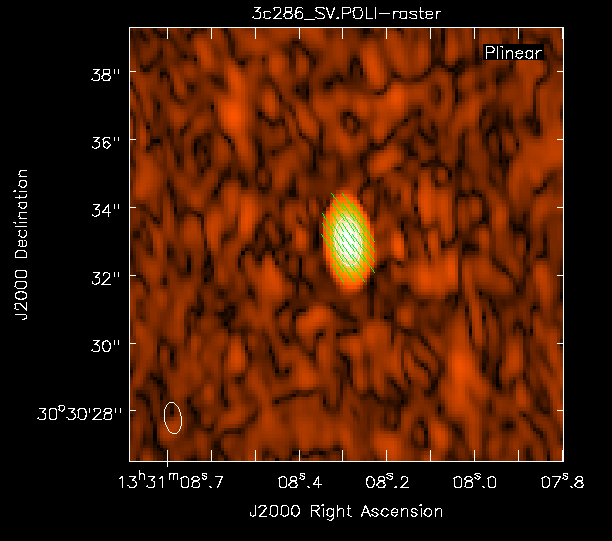
While we set the polithresh parameter when we created the position angle ([math]\displaystyle{ \chi }[/math]) image, a digression here is instructive in the use of LEL Expressions. Had we not set this parameter, the position angle would have been derived for all pixels within the full IQUV image cube. There is only polarized emission from a limited subset of pixels within this image. Therefore, to avoid plotting vectors corresponding to the position angle of pure noise, we now wish to select only the regions where the polarized intensity is brighter than some threshold value. To do this, we use an LEL (Lattice Expression Language) Expression in the 'Load Data' GUI. For our chosen threshold of 0.4 mJy/beam (the 5 sigma level in the P image), we paste the expression

     '3c286_Band6.POLA'['3c286_Band6.POLI'>0.001]

into the LEL Expression box in the GUI, and click the 'Vector Map' button. This would load the vectors only for regions where P>1 mJy/beam.

To optimize the display for ease of interpretation we click the wrench icon to open a 'Data Display Options' GUI. This will have 3 tabs, corresponding to the three images loaded. We can change the image color map and transfer function, the contour levels and color, and the the vector spacing and color.

For the polarization angle vector it is also possible to add a rotation. The polarization position angle as calculated is the electric vector position angle (EVPA). If we are interested in the orientation of the magnetic field, then for an optically thin source the magnetic field orientation is perpendicular to the EVPA, so we must rotate the vectors by 90 degrees. Select the vector image tab in the 'Data Display Options' GUI (labeled as the LEL expression we entered in the Load Data GUI) and enter 90 in the Extra rotation box. If the vectors appear too densely packed on the image, change the spacing of the vectors by setting X-increment and Y-increment to a larger value.

To get quantitative information from the images, we can either use the task imstat (we already used it above) or the task imfit. The task imstat returns the statistics in a Python dictionary, from which we can read what we need in a Python variable. In this example we extract the peak value:

CASA<1> calstat=imstat(imagename='3c286_Band6.POLI', region='')

CASA<2> calstat
  Out[1]: 
{'blc': array([0, 0, 0, 0], dtype=int32),
 'blcf': '13:31:09.255, +30.30.20.460, Plinear, 2.33e+11Hz',
 'flux': array([ 0.12747101]),
 'max': array([ 0.06074611]),
 'maxpos': array([125, 125,   0,   0], dtype=int32),
 'maxposf': '13:31:08.288, +30.30.32.960, Plinear, 2.33e+11Hz',
 'mean': array([ 0.00010715]),
 'medabsdevmed': array([  2.08474630e-05]),
 'median': array([  4.79196569e-05]),
 'min': array([  9.89017863e-08]),
 'minpos': array([ 23, 214,   0,   0], dtype=int32),
 'minposf': '13:31:09.077, +30.30.41.860, Plinear, 2.33e+11Hz',
 'npts': array([ 62500.]),
 'quartile': array([  4.34697722e-05]),
 'rms': array([ 0.00126342]),
 'sigma': array([ 0.00125888]),
 'sum': array([ 6.69700321]),
 'sumsq': array([ 0.09976477]),
 'trc': array([249, 249,   0,   0], dtype=int32),
 'trcf': '13:31:07.329, +30.30.45.360, Plinear, 2.33e+11Hz'}


CASA <2>: calstat['max'][0]                                   
  Out[2]: 0.060746114701032639

The task imfit finds one or more elliptical gaussian components on an image region.

# In CASA
fit_res=imfit(imagename='3c286_Band6.POLI', region='')

CASA <3>: fit_res
  Out[3]: 
{'converged': array([ True], dtype=bool),
 'deconvolved': {'component0': {'beam': {'beamarcsec': {'major': {'unit': 'arcsec',
                                                                  'value': 0.9374216198921204},
                                                        'minor': {'unit': 'arcsec',
                                                                  'value': 0.4946177303791046},
                                                        'positionangle': {'unit': 'deg',
                                                                          'value': 7.5858154296875}},
                                         'beampixels': 52.53745924485295,
                                         'beamster': 1.2348630615213326e-11},
                                'flux': {'error': array([ 0.00011495,  0.        ,  0.        ,  0.        ]),
                                         'polarisation': 'Stokes',
                                         'unit': 'Jy',
                                         'value': array([ 0.06180972,  0.        ,  0.        ,  0.        ])},
                                'ispoint': False,
                                'label': '',
                                'peak': {'error': 0.007763106951837918,
                                         'unit': 'Jy/beam',
                                         'value': 7.694798098602945},
[...]

To extract the flux and its error, we can read them from CASA in Python variables:

# In CASA
fluxPI=fit_res['results']['component0']['flux']['value'][0]
errorPI=fit_res['results']['component0']['flux']['error'][0]

The flux measured in the fitted gaussian is 61.8 mJy with an error of 0.1 mJy.

We now use this method to estimate the fluxes in all the Stokes images:

# In CASA

# First we run imfit 
resI=imfit(imagename = '3c286.cal.StokesI.clean.image', box = '110,110,145,145')
resQ=imfit(imagename = '3c286.cal.StokesQ.clean.image', box = '110,110,145,145')
resU=imfit(imagename = '3c286.cal.StokesU.clean.image', box = '110,110,145,145')
resV=imfit(imagename = '3c286.cal.StokesV.clean.image', box = '110,110,145,145')
 
# and then we extract the flux and error values for each Stokes

fluxI=resI['results']['component0']['flux']['value'][0]
errorI=resI['results']['component0']['flux']['error'][0]

fluxQ=resQ['results']['component0']['flux']['value'][1]
errorQ=resQ['results']['component0']['flux']['error'][1]

fluxU=resU['results']['component0']['flux']['value'][2]
errorU=resU['results']['component0']['flux']['error'][2]
 
fluxV=resV['results']['component0']['flux']['value'][3]
errorV=resV['results']['component0']['flux']['error'][3]

Now we use these values to compute polarization intensity, angle and ratio, and their errors:

# In CASA 
fluxPI  = sqrt( fluxQ**2 + fluxU**2 )
errorPI = sqrt( (fluxQ*errorQ)**2 + (fluxU*errorU)**2 ) / fluxPI

fluxPImjy = 1000*fluxPI
errPImjy  = 1000*errorPI

polRatio = fluxPI / fluxI
errPRat  = polRatio * sqrt( (errorPI/fluxPI)**2 + (errorI/fluxI)**2 )
  
polAngle = 0.5 * degrees( atan2(fluxU,fluxQ) )
errPA    = 0.5 * degrees( sqrt( (fluxQ*errorU)**2 + (fluxU*errorQ)**2 ) / fluxPI**2 )

The results are collected in the following table:

	Flux	err
I (mJy)	375.6	0.35
Q (mJy)	14.4	0.04
U (mJy)	60.1	0.09
Pol int (mJy)	61.8	0.05
P (%)	16.45	0.02
χ (deg)	38.3	0.02

As you can see, the polarization intensity computed from the Q and U fluxes is the same as the one extracted from the polarization image (as it should be!).

Note that the uncertainties quoted above are purely statistical. The systematic errors will be larger, and include (but are not limited to) any net bias in the position angle of the linear feeds in the antennas, the details of different observations (at what parallactic angles, etc.), and other data quality variations (including source structure). We conservatively estimate the position angle uncertainty to be ± 2º.

And now, a quick comparison with previous results from IRAM and CARMA.

Agudo et al. (2012) presented the results of single-dish millimeter measurements of 3C286 with the IRAM 30 m Telescope. Their observations at 1 mm (229 GHz) and 3 mm (86 GHz) produced the following results:

	1 mm	3 mm
P (%)	14.4 ± 1.8	13.5 ± 0.3
χ (deg)	33.1 ± 5.7	37.3 ± 0.8

Hull & Plambeck 2015 (JAI) and CARMA Memo 64 report interferometric polarization data of 3C286 taken with CARMA at 1 mm (225 GHz). Their results are as follows:

	1 mm
χ (deg)	39.2 ± 1.0

Export images in fits format

To get all images in fits format you need to use the task exportfits.

You can add the parameters imagename (the input image) and fitsimage (the name of the output image) one by one or you can run a python cycle over all the images:

# In CASA 
import glob

imagenames=glob.glob("*image") 

for name in imagenames:
    exportfits(imagename=name, fitsimage=name+'.fits')

Last checked on CASA Version 4.3.0.