NGC3256 Band3 - Calibration for CASA 3.3: Difference between revisions
mNo edit summary |
|||
| (148 intermediate revisions by 10 users not shown) | |||
| Line 1: | Line 1: | ||
[[Category:ALMA]][[Category:Calibration]][[Category:Spectral Line]] | |||
==Overview== | ==Overview== | ||
This portion of the [[NGC3256Band3]] CASA Guide will cover the calibration of the raw visibility data. To | This portion of the '''[[NGC3256Band3]]''' CASA Guide will cover the calibration of the raw visibility data. To skip to the imaging portion of the guide, see: '''[[NGC3256 Band3 - Imaging]]'''. | ||
If you haven't already downloaded the raw data, you may do that now by clicking on the region closest to your location and downloading the file named 'NGC3256_Band3_UnCalibratedMSandTablesForReduction.tgz': | |||
[http://almascience.nrao.edu/almadata/sciver/NGC3256 North America] | |||
[http://almascience.eso.org/almadata/sciver/NGC3256 Europe] | |||
[ | [http://almascience.nao.ac.jp/almadata/sciver/NGC3256 East Asia] | ||
Once the download has finished, unpack the file: | Once the download has finished, unpack the file: | ||
<source lang=" | <source lang="bash"> | ||
# In a terminal outside CASA | # In a terminal outside CASA | ||
tar - | tar -xvzf NGC3256_Band3_UnCalibratedMSandTablesForReduction.tgz | ||
cd NGC3256_Band3_UnCalibratedMSandTablesForReduction | |||
# Start CASA | |||
casapy | |||
</source> | </source> | ||
The data have already been | The data have already been converted to CASA Measurement Set (MS) format using the CASA task {{importasdm}}. Accompanying the data are some basic calibration tables you will need for the following reduction, as well as the *.ms.flagversions files that are automatically generated by importasdm. | ||
==Initial Inspection and ''A priori '' Flagging== | ==Initial Inspection and ''A priori '' Flagging== | ||
We will eventually concatenate the six datasets used here into one large dataset. However, we will keep them separate for now, as some of the steps to follow require individual datasets (specifically, the application of the Tsys and WVR tables). We therefore start by defining an array "basename" that includes the names of the six files. This will simplify the following steps by allowing us to loop through the files using a simple for-loop in python. Remember that if you log out of CASA, you will have to re-issue this command. We will remind you of this in the relevant sections by repeating the command at the start. | We will eventually concatenate the six datasets used here into one large dataset. However, we will keep them separate for now, as some of the steps to follow require individual datasets (specifically, the application of the Tsys and WVR tables). We therefore start by defining an array "basename" that includes the names of the six files in chronological order. This will simplify the following steps by allowing us to loop through the files using a simple for-loop in python. Remember that if you log out of CASA, you will have to re-issue this command. We will remind you of this in the relevant sections by repeating the command at the start. | ||
<source lang="python"> | <source lang="python"> | ||
| Line 32: | Line 43: | ||
</source> | </source> | ||
Note that after cutting and pasting a for-loop you often have to press return several times to execute. | |||
The output will be sent to the CASA [http://casa.nrao.edu/docs/userman/UserMansu41.html#UserMansu42.html logger]. You will have to scroll up to see the individual output for each of the six datasets. Here is an example of the most relevant output for the first file in the list. | The output will be sent to the CASA [http://casa.nrao.edu/docs/userman/UserMansu41.html#UserMansu42.html logger]. You will have to scroll up to see the individual output for each of the six datasets. Here is an example of the most relevant output for the first file in the list. | ||
| Line 121: | Line 133: | ||
Another important thing to note is that the position of Titan is listed as 00:00:00.0000 +00.00.00.0000. This is due to the fact that for ephemeris objects, the positions are currently not stored in the asdm. This will be handled correctly in the near future, but at present, we have to fix this offline. We will correct the coordinates below by running the procedure fixplanets, which takes the position from the pointing table. | Another important thing to note is that the position of Titan is listed as 00:00:00.0000 +00.00.00.0000. This is due to the fact that for ephemeris objects, the positions are currently not stored in the asdm. This will be handled correctly in the near future, but at present, we have to fix this offline. We will correct the coordinates below by running the procedure fixplanets, which takes the position from the pointing table. | ||
Seven antennas | The final column of the listobs output in the logger (not shown above) gives the scan intent. This information is used later to flag the pointing scans and the hot and ambient load calibration scans, using scan intent as a selection option. Also these intents will be used in the future for pipeline processing. | ||
Seven antennas were used for the dataset listed above. Note that numbering in python always begins with "0", so the antennas have IDs 0-6. To see what the antenna configuration looked like at the time of the this observation, we will use the task {{plotants}}. | |||
[[File:Uid___A002_X1d54a1_X5_plotants.png|200px|thumb|right|plotants output]] | [[File:Uid___A002_X1d54a1_X5_plotants.png|200px|thumb|right|plotants output]] | ||
| Line 134: | Line 148: | ||
==== Flagging ==== | ==== Flagging ==== | ||
The first editing we will do is some ''a priori'' flagging with {{flagdata}} and {{flagautocorr}}. We will start by flagging the shadowed data and the autocorrelation data. Remember that you first need to redefine the "basename" array if you logged out of CASA prior to starting this section. | The first editing we will do is some ''a priori'' flagging with {{flagdata}} and {{flagautocorr}}. We will start by flagging the shadowed data and the autocorrelation data. ALMA data contains both the cross correlation and autocorrelation data, but here we are only interested in the cross-correlation data. Additionally, for compact configurations of the array, one antenna can shadow another, blocking its view. These data also need to be flagged. | ||
Remember that you first need to redefine the "basename" array if you logged out of CASA prior to starting this section. | |||
<source lang="python"> | <source lang="python"> | ||
| Line 173: | Line 188: | ||
</source> | </source> | ||
==Delay Correction for Antenna DV07== | |||
Due to an issue with antenna DV07 during the commissioning period when these data were taken, it shows large delays in phase for the first three datasets. While the bandpass calibration will attempt to fit and remove small phase delays (i.e., less than one wrap over the bandpass), large delays like those seen here will result in failed solutions. If we want to salvage the data for this antenna, we therefore need to correct the delays by calculating a K-type delay calibration table with {{gencal}}. We emphasize that this is ''not'' usually a part of the typical calibration procedure, but it may be useful to the reader to see how such a correction is made. | |||
Remember that you first need to redefine the "basename" array if you logged out of CASA prior to starting this section. | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
basename=['uid___A002_X1d54a1_X5','uid___A002_X1d54a1_X174','uid___A002_X1d54a1_X2e3', | |||
'uid___A002_X1d5a20_X5','uid___A002_X1d5a20_X174','uid___A002_X1d5a20_X330'] | |||
</source> | </source> | ||
You can see the phase delays by plotting phase versus channel in {{plotms}}, as we do here for a single spw, correlation, and baseline with DV07: | You can see the phase delays by plotting phase versus channel in {{plotms}}, as we do here for a single spw, correlation, and baseline with DV07: | ||
[[File:Cal-DV07delay.png|200px|thumb|right|DV07 Phase vs | [[File:Cal-DV07delay.png|200px|thumb|right|DV07: Phase vs Channel]] | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
plotms(vis=basename[0]+'.ms', xaxis='channel', yaxis='phase', | plotms(vis=basename[0]+'.ms', xaxis='channel', yaxis='phase', | ||
spw=' | spw='3', antenna='PM03&DV07', correlation='XX', avgtime='1e8') | ||
</source> | </source> | ||
The parameters required by | The parameters required by gencal are the delays measured in nanoseconds, first cycling over polarization product, and then over spectral window (thus giving eight numbers in total). We simply estimate these values by eye using the above plot and the corresponding plots for the other spectral windows and polarization products. The purpose here is to get the phases approximately flat as a function of frequency. Any additional phase variations will be corrected for later when we do the bandpass calibration. | ||
Based on the above plot, we estimate that | Based on the above plot, we estimate that the delay for this spw and correlation is approximately -3ns. One full phase wrap over 2GHz corresponds to a delay of 1/(2GHz)=0.5ns. Here we see six wraps and therefore estimate a 3ns delay. The sign convention is such that the delay is positive if the phase is increasing with respect to frequency and negative if it is decreasing, as it is here. Note that the sign convention is reversed between the two basebands, since the channels in the USB run in the ''opposite'' direction to those in the LSB. The wrapping in spectral windows 3,5,7 is therefore all in the same direction with respect to ''frequency''. The value of -3ns that we estimate is for spw 3, correlation XX, and will therefore be the third element in the parameter array. | ||
We then run {{gencal}} for the three datasets in question, supplying the estimated values in the "parameter" array. | We then run {{gencal}} for the three datasets in question, supplying the estimated values in the "parameter" array. As the {{gencal}} task will not overwrite existing tables, the script starts by deleting any existing versions of the calibration tables with the same name. | ||
<source lang="python"> | <source lang="python"> | ||
| Line 207: | Line 222: | ||
gencal(vis=name+'.ms', caltable='cal-'+name+'_del.K', | gencal(vis=name+'.ms', caltable='cal-'+name+'_del.K', | ||
caltype='sbd', antenna='DV07', pol='X,Y', spw='1,3,5,7', | caltype='sbd', antenna='DV07', pol='X,Y', spw='1,3,5,7', | ||
parameter=[ | parameter=[1.00, 1.10, -3.0, -3.0, -3.05, -3.05, -3.05, -3.05]) | ||
</source> | </source> | ||
| Line 234: | Line 249: | ||
applycal(vis=name+'.ms', flagbackup=F, spw='1,3,5,7', | applycal(vis=name+'.ms', flagbackup=F, spw='1,3,5,7', | ||
interp=['nearest','nearest'], gaintable=['cal-'+name+'_del.K', 'cal-'+name+'.W']) | interp=['nearest','nearest'], gaintable=['cal-'+name+'_del.K', 'cal-'+name+'.W']) | ||
</source> | |||
<source lang="python"> | |||
# In CASA | |||
for i in range(3,6): # loop over the last three data sets | for i in range(3,6): # loop over the last three data sets | ||
name=basename[i] | name=basename[i] | ||
| Line 241: | Line 259: | ||
</source> | </source> | ||
Now we split out the | Now you can use plotms to show some of the before-and-after effects of calibration. Just re-run the previous plotms command, repeated below, or if the window is still open, check 'force reload'. This will display the uncorrected phases across the band. To display the corrected phases, you will need to select the CORRECTED data column in the axes tab and replot. | ||
<source lang="python"> | |||
# In CASA | |||
plotms(vis=basename[0]+'.ms', xaxis='channel', yaxis='phase', | |||
spw='1', antenna='', correlation='XX', avgtime='1e8', | |||
coloraxis='baseline', avgscan=T, selectdata=T, field='1037*') | |||
</source> | |||
Now we split out the CORRECTED data column of the datasets with the task {{split}}. We give the resulting datasets the extension "_K_WVR" to indicate that the delay tables and WVR tables have been applied in the DATA column, and we specify spectral windows 0-8 to get rid of the "WVR placeholder" spectral windows. Since split will not overwrite existing files, we start by removing any previous versions of the split ms's before running the split command. | |||
<source lang="python"> | <source lang="python"> | ||
| Line 253: | Line 280: | ||
Next we do the Tsys calibration. Tsys measurements correct for the atmospheric opacity (to first-order) and allow the calibration sources to be measured at elevations that differ from the science target. The Tsys tables for these datasets were provided with the downloadable data. We will start by inspecting them with the task {{plotcal}}: | Next we do the Tsys calibration. Tsys measurements correct for the atmospheric opacity (to first-order) and allow the calibration sources to be measured at elevations that differ from the science target. The Tsys tables for these datasets were provided with the downloadable data. We will start by inspecting them with the task {{plotcal}}: | ||
[[File: | [[File:Cal-tsys_per_spw_7_uid___A002_X1d54a1_X174.png|200px|thumb|right|Example Tsys plot]] | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
for name in basename: | for spw in ['1','3','5','7']: | ||
for name in basename: | |||
spw= | plotcal(caltable='cal-tsys_'+name+'.cal', xaxis='freq', yaxis='amp', | ||
iteration=' | spw=spw, subplot=421, overplot=False, | ||
figfile='cal- | iteration='antenna', plotrange=[0, 0, 40, 180], plotsymbol='.', | ||
figfile='cal-tsys_per_spw_'+spw+'_'+name+'.png') | |||
</source> | </source> | ||
Note that we only plot the spectral windows | Note that we only plot the spectral windows that contain the spectral line data. In addition to plotting on your screen, the above command will also produce a plot file (png) for each of the datasets and spectral windows. An example plot is shown to the right for uid___A002_X1d54a1_X174.ms. | ||
Upon examination of these plots, we see that for uid___A002_X1d54a1_X174.ms, there is a outlying feature in spw=7, antenna DV04. This feature occurs during scans 5 and 9, so we flag those data with the following command: | |||
<source lang="python"> | |||
# In CASA | |||
flagdata(vis='uid___A002_X1d54a1_X174_K_WVR.ms', mode='manualflag', | |||
antenna='DV04', flagbackup = T, scan='5,9', spw='7') | |||
</source> | |||
We will apply the Tsys tables with {{applycal}} | Aside from the large amplitudes in the edge channels (which we will handle below), the plots look acceptable. Note that in the lowest spectral window ID (spw 1), Tsys rises toward higher frequencies. This is due to a spectral line from O2 at 117 GHz. | ||
We will apply the Tsys tables with {{applycal}}. We do this for each field separately so that the appropriate calibration data are applied to the right fields. The "field" parameter specifies the field to which we will apply the calibration, and the "gainfield" parameter specifies the field from which we wish to take the calibration solutions from the gaintable. | |||
<source lang="python"> | <source lang="python"> | ||
| Line 277: | Line 313: | ||
</source> | </source> | ||
We then once again split out the | Without giving the full recipe here, we suggest at this point that you use {{plotms}} to plot channel-averaged amplitudes as a function of time, comparing the DATA and CORRECTED columns after applying the Tsys correction. This way you can check that calibration has done what was expected, which is put the data onto the Kelvin temperature scale. | ||
We then once again split out the CORRECTED data column, this time only retaining spectral windows 1,3,5,7. This will get rid of the extraneous spectral windows, including the channel averaged spectral windows and spw 0, which is the one that contained the WVR data. | |||
<source lang="python"> | <source lang="python"> | ||
| Line 287: | Line 325: | ||
</source> | </source> | ||
The WVR and Tsys tables are now applied in the | The WVR and Tsys tables are now applied in the DATA column of the new measurement sets. These datasets have the extension "_line" to indicate that they only contain the spectral line data and no longer the "channel average" spectral windows. These measurement sets therefore have four spectral windows, with IDs 0-3. | ||
Now that we have applied the Tsys calibration and WVR corrections, we can concatenate the six individual data sets into one big measurement set. We define an array "comvis" that contains the names of the measurement sets we wish to concatenate, and then we run the task {{concat}}. | Now that we have applied the Tsys calibration and WVR corrections, we can concatenate the six individual data sets into one big measurement set. We define an array "comvis" that contains the names of the measurement sets we wish to concatenate, and then we run the task {{concat}}. | ||
| Line 300: | Line 338: | ||
concat(vis=comvis, concatvis='ngc3256_line.ms') | concat(vis=comvis, concatvis='ngc3256_line.ms') | ||
</source> | </source> | ||
We run a {{listobs}} on the resulting concatenated data set to check contains the fields, spectral windows and observing times that we expected: | |||
<source lang="python"> | |||
# In CASA | |||
listobs('ngc3256_line.ms') | |||
</source> | |||
There are now only four spectral windows left: | |||
<pre style="background-color: #fffacd;"> | |||
2011-05-24 07:41:21 INFO listobs 0 128 TOPO 113211.988 15625 2000000 113204.175 XX YY | |||
2011-05-24 07:41:21 INFO listobs 1 128 TOPO 111450.813 15625 2000000 111443 XX YY | |||
2011-05-24 07:41:21 INFO listobs 2 128 TOPO 101506.187 15625 2000000 101514 XX YY | |||
2011-05-24 07:41:21 INFO listobs 3 128 TOPO 103050.863 15625 2000000 103058.675 XX YY | |||
</pre> | |||
and eight antennas have been used in total: | |||
<pre style="background-color: #fffacd;"> | |||
2011-05-24 07:41:21 INFO listobs Antennas: 8: | |||
2011-05-24 07:41:21 INFO listobs ID Name Station Diam. Long. Lat. | |||
2011-05-24 07:41:21 INFO listobs 0 DV04 J505 12.0 m -067.45.18.0 -22.53.22.8 | |||
2011-05-24 07:41:21 INFO listobs 1 DV06 T704 12.0 m -067.45.16.2 -22.53.22.1 | |||
2011-05-24 07:41:21 INFO listobs 2 DV07 J510 12.0 m -067.45.17.8 -22.53.23.5 | |||
2011-05-24 07:41:21 INFO listobs 3 DV08 T703 12.0 m -067.45.16.2 -22.53.23.9 | |||
2011-05-24 07:41:21 INFO listobs 4 DV09 N602 12.0 m -067.45.17.4 -22.53.22.3 | |||
2011-05-24 07:41:21 INFO listobs 5 PM02 T701 12.0 m -067.45.18.8 -22.53.22.2 | |||
2011-05-24 07:41:21 INFO listobs 6 PM03 J504 12.0 m -067.45.17.0 -22.53.23.0 | |||
2011-05-24 07:41:21 INFO listobs 7 DV10 N606 12.0 m -067.45.17.1 -22.53.23.6 | |||
</pre> | |||
==Additional Data Inspection== | ==Additional Data Inspection== | ||
| Line 316: | Line 385: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
flagdata(vis = 'ngc3256_line.ms', flagbackup = | flagdata(vis='ngc3256_line.ms', flagbackup=T, spw=['*:0~16','*:125~127']) | ||
</source> | </source> | ||
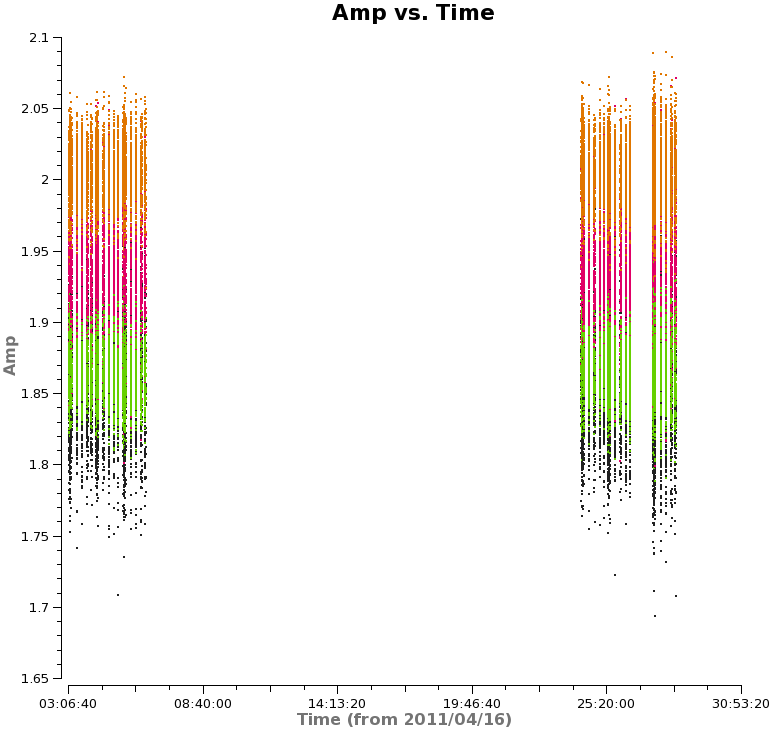
Next, we will look at amplitude versus time, averaging over all channels and colorizing by field. Since the observations take place over two days, you will need to zoom in to examine the data in more detail. In particular, note the difference in Titan's amplitude between the two days and the change in amplitude during the second day. The plot on the right shows a zoom-in on the first day of observations. Scans on Titan are colored red, NGC3256 is orange, and the calibrator 1037-295 is colored black. | Next, we will look at amplitude versus time, averaging over all channels and colorizing by field. Since the observations take place over two days, you will need to zoom in to examine the data in more detail. In particular, note the difference in Titan's amplitude between the two days and the change in amplitude during the second day. The plot on the right shows a zoom-in on the first day of observations, only showing spw 1 in this case. Scans on Titan are colored red, NGC3256 is orange, and the calibrator 1037-295 is colored black. If you select other spws, you can see some outlying points, which will be flagged later on. | ||
[[File:amp_vs_time.png|200px|thumb|right|Amplitude vs. time, averaged over all channels]] | [[File:amp_vs_time.png|200px|thumb|right|Amplitude vs. time for spw 1, averaged over all channels]] | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
plotms(vis='ngc3256_line.ms', xaxis='time', yaxis='amp', | plotms(vis='ngc3256_line.ms', xaxis='time', yaxis='amp', | ||
averagedata=T, avgchannel='128', coloraxis='field') | averagedata=T, avgchannel='128', coloraxis='field', | ||
iteraxis='spw') | |||
</source> | </source> | ||
Titan is our primary flux calibrator. However, for the second day of observations, Titan had moved | Titan is our primary flux calibrator. However, for the second day of observations, Titan had moved too close to Saturn, and Saturn's rings moved into the primary beam. Another way to see this is to plot amplitude versus uv-distance and colorize by scan: | ||
[[File:amp_vs_uvdistTitan_ngc3256_line.png|200px|thumb|right|Amplitude vs. uv-distance for Titan]] | [[File:amp_vs_uvdistTitan_ngc3256_line.png|200px|thumb|right|Amplitude vs. uv-distance for Titan]] | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
plotms(vis='ngc3256_line.ms', xaxis='uvdist', yaxis='amp', field=' | plotms(vis='ngc3256_line.ms', xaxis='uvdist', yaxis='amp', field='Titan', | ||
averagedata=T, avgchannel='128', avgtime='1e8', coloraxis='scan') | averagedata=T, avgchannel='128', avgtime='1e8', coloraxis='scan') | ||
</source> | </source> | ||
| Line 341: | Line 411: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
flagdata(vis = 'ngc3256_line.ms', flagbackup = | flagdata(vis = 'ngc3256_line.ms', flagbackup = T, | ||
timerange='>2011/04/16/12:00:00', field='Titan') | timerange='>2011/04/16/12:00:00', field='Titan') | ||
</source> | </source> | ||
Next, we will fix the position of Titan in the combined dataset. Recall that the position of the Titan field is currently set to 00:00:00.0000 +00.00.00.0000. The following procedure will replace this with the actual position observed by the telescopes and, at the same time, it will recalculate the uvw coordinates: | We also find that during the first day, the Titan observations in spw 2 and 3 are also affected by Saturn. These spectral windows are at lower frequencies and therefore correspond to slightly larger primary beams. This results in Saturn just being picked up in spw 2 and 3, but not in spw 0 and 1. We do not flag these data here, but have to take this effect into account when we do the flux calibration later. | ||
Next, we will fix the position of Titan in the combined dataset. Recall that the position of the Titan field is currently set to 00:00:00.0000 +00.00.00.0000. The following procedure will replace this with the actual mean position observed by the telescopes and, at the same time, it will recalculate the uvw coordinates. | |||
If you are running casa revision r15777 or newer, fixplanets() is already defined as a task. However, if you are using an older revision, then you must first initialize this script with this command: | |||
<code> | |||
execfile(casadef.python_library_directory+'/recipes/fixplanets.py') | |||
</code> | |||
Now fix the position of Titan: | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
fixplanets(vis='ngc3256_line.ms', field='Titan', fixuvw=True) | |||
fixplanets('ngc3256_line.ms', 'Titan', True) | |||
</source> | </source> | ||
The third parameter in fixplanets, set to True, indicates that the uvw-coordinates for Titan are recalculated. Note that for Cycle 0 data, the coordinates of ephemeris objects will be treated correctly in the data. | |||
Now check to see that the coordinates for Titan have been corrected: | |||
<pre style="background-color: #fffacd;"> | |||
2011-05-31 19:19:41 INFO listobs ID Code Name RA Decl Epoch SrcId nVis | |||
2011-05-31 19:19:41 INFO listobs 0 none 1037-295 10:37:16.0790 -29.34.02.8130 J2000 0 61440 | |||
2011-05-31 19:19:41 INFO listobs 1 none Titan 12:51:24.5886 -02.31.59.7035 J2000 1 25344 | |||
2011-05-31 19:19:41 INFO listobs 2 none NGC3256 10:27:51.6000 -43.54.18.0000 J2000 2 239616 | |||
</pre> | |||
Continue to inspect the data with {{plotms}}, plotting different axes and colorizing by the different parameters. Don't forget to average the data if possible to speed the plotting process. You will find the following: | Continue to inspect the data with {{plotms}}, plotting different axes and colorizing by the different parameters. Don't forget to average the data if possible to speed the plotting process. You will find the following: | ||
| Line 361: | Line 447: | ||
*Baselines with PM03 have low amplitudes at 2011/04/17/02:15:00 for spw 0 | *Baselines with PM03 have low amplitudes at 2011/04/17/02:15:00 for spw 0 | ||
*Baselines with PM03 have low amplitudes at 2011/04/16/04:15:15 for spw 2 and 3 | *Baselines with PM03 have low amplitudes at 2011/04/16/04:15:15 for spw 2 and 3 | ||
*For the second day, the baseline DV10-PM03 is corrupted | |||
The times to insert in flagdata can be obtained using plotms Tools Hover/Display. Instead of using the following {{flagdata}} commands, you can also flag by hand in {{plotms}}. To do this, select your bad data by clicking on the 'Mark Regions" button, then on 'Flag". | |||
We flag the bad data with the following commands: | We flag the bad data with the following commands: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
flagdata(vis='ngc3256_line.ms', flagbackup= | flagdata(vis='ngc3256_line.ms', flagbackup=T, spw='3', | ||
correlation='YY', mode='manualflag', selectdata=T, | correlation='YY', mode='manualflag', selectdata=T, | ||
antenna='DV07', timerange='') | antenna='DV07', timerange='') | ||
</source> | |||
<source lang="python"> | |||
# In CASA | |||
flagdata(vis='ngc3256_line.ms', flagbackup=T, spw='3', | |||
correlation='YY', mode='manualflag', selectdata=T, | |||
antenna='DV08', timerange='>2011/04/17/03:00:00') | |||
</source> | |||
flagdata(vis='ngc3256_line.ms', flagbackup= | <source lang="python"> | ||
# In CASA | |||
flagdata(vis='ngc3256_line.ms', flagbackup=T, spw='0', | |||
correlation='', mode='manualflag', selectdata=T, | |||
antenna='PM03', timerange='2011/04/17/02:15:00~02:15:50') | |||
</source> | |||
<source lang="python"> | |||
# In CASA | |||
flagdata(vis='ngc3256_line.ms', flagbackup=T, spw='2,3', | |||
correlation='', mode='manualflag', selectdata=T, | |||
antenna='PM03', timerange='2011/04/16/04:13:50~04:18:00') | |||
</source> | |||
flagdata(vis='ngc3256_line.ms', flagbackup= | <source lang="python"> | ||
# In CASA | |||
flagdata(vis='ngc3256_line.ms', flagbackup=T, spw='', | |||
correlation='', mode='manualflag', selectdata=T, | |||
antenna='PM03&DV10', timerange='>2011/04/16/15:00:00') | |||
</source> | </source> | ||
==Bandpass Calibration== | ==Bandpass Calibration== | ||
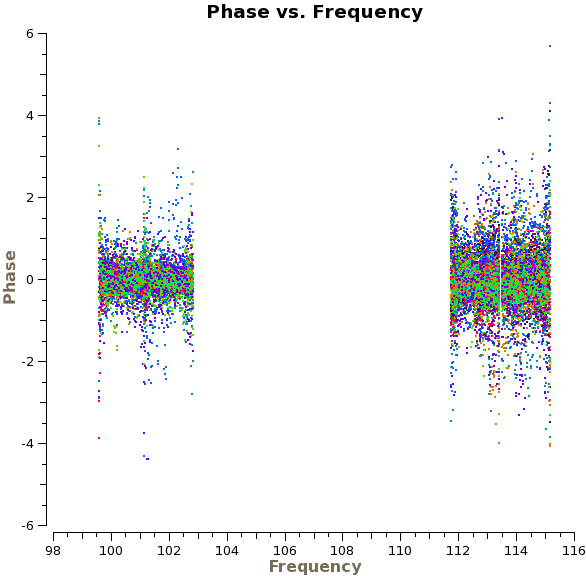
We are now ready to begin the bandpass calibration. First, we will inspect the bandpass calibrator by plotting the phase as a function of frequency and time. For the first plot we use avgscan=T and avgtime='1E6' to average in time over all scans, and we specify coloraxis='baseline' to colorize by baseline. For the second, we use spw='0:30~90' and avgchannel='128' to average over the central 61 channels of the first spectral window. | We are now ready to begin the bandpass calibration. First, we will inspect the bandpass calibrator by plotting the phase as a function of frequency and time. For the first plot we use avgscan=T and avgtime='1E6' to average in time over all scans, and we specify coloraxis='baseline' to colorize by baseline. For the second, we use spw='0:30~90' and avgchannel='128' to average over the central 61 channels of the first spectral window. For both plots we will iterate on antenna, so you will need to use the green arrows at the bottom of the plotms GUI to view different antennas. | ||
[[File:phase_vs_frequency.png|200px|thumb|right|Phase vs. frequency for the phase calibrator, averaged over time]] | [[File:phase_vs_frequency.png|200px|thumb|right|Phase vs. frequency for the phase calibrator, averaged over time]] | ||
| Line 397: | Line 498: | ||
plotms(vis='ngc3256_line.ms', xaxis='freq', yaxis='phase', selectdata=True, | plotms(vis='ngc3256_line.ms', xaxis='freq', yaxis='phase', selectdata=True, | ||
field='1037*', avgtime='1E6', avgscan=T, coloraxis='baseline', iteraxis='antenna') | field='1037*', avgtime='1E6', avgscan=T, coloraxis='baseline', iteraxis='antenna') | ||
</source> | |||
<source lang="python"> | |||
# In CASA | |||
plotms(vis='ngc3256_line.ms', xaxis='time', yaxis='phase', selectdata=True, | plotms(vis='ngc3256_line.ms', xaxis='time', yaxis='phase', selectdata=True, | ||
field='1037*', spw='0:30~90', avgchannel='128', avgscan=T, | field='1037*', spw='0:30~90', avgchannel='128', avgscan=T, | ||
| Line 403: | Line 507: | ||
</source> | </source> | ||
The plot on the right shows the time-averaged phase as a function of frequency for the calibrator 1037-295, | The top plot on the right shows the time-averaged phase as a function of frequency for the calibrator 1037-295, with all baselines shown at once (i.e., without iteraxis='antenna') for presentation purposes. We see that the phase variations across the spectral windows are modest, typically ~30 degrees. The second plot shows how the phase varies as function of time. For clarity, we only show baselines with one antenna and only for the first day of observations. There are clearly phase variations on short time scales that we wish to correct for before calculating the bandpass solutions. | ||
Hence, we run {{gaincal}} on the bandpass calibrator to determine phase-only gain solutions. We will use solint='int' for the solution interval, which means that one gain solution will be determined for every integration time. This will correct for any phase variations in the bandpass calibrator as a function of time, a step which will prevent decorrelation of the vector-averaged bandpass solutions. We will then apply these solutions on-the-fly when we run {{bandpass}}. | Hence, we run {{gaincal}} on the bandpass calibrator to determine phase-only gain solutions. We will use solint='int' for the solution interval, which means that one gain solution will be determined for every integration time. This short integration time is possible because the bandpass calibrator is a very bright point source, so we have very high signal-to-noise and a perfect model. This will correct for any phase variations in the bandpass calibrator as a function of time, a step which will prevent decorrelation of the vector-averaged bandpass solutions. We will then apply these solutions on-the-fly when we run {{bandpass}}. | ||
We will use the average of channels 40 to 80 to increase our signal-to-noise in the determination of the antenna-based phase solutions. Averaging over a subset of channels near the center of the bandpass is acceptable when the phase variation as a function of channel is small, which it is here. For our reference antenna, we choose | We will use the average of channels 40 to 80 to increase our signal-to-noise in the determination of the antenna-based phase solutions. Averaging over a subset of channels near the center of the bandpass is acceptable when the phase variation as a function of channel is small, which it is here. For our reference antenna, we choose DV04. We call the output calibration table "cal-ngc3256.G1". | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
gaincal(vis = 'ngc3256_line.ms', caltable = 'cal-ngc3256.G1', spw = '*:40~80', field = '1037*', | gaincal(vis='ngc3256_line.ms', caltable='cal-ngc3256.G1', spw='*:40~80', field='1037*', | ||
selectdata=T, solint= 'int', refant = ' | selectdata=T, solint='int', refant='DV04', calmode='p') | ||
</source> | </source> | ||
We then check the time variations of the phase solutions with {{plotcal}}. We will plot the XX and YY polarization products separately and make different subplots for each of the spectral windows. This is done by setting the "iteration" parameter to "spw" and specifying subplot=221. By setting the parameter "figfile" to a non-blank value, it will also generate png files of the plots. | We then check the time variations of the phase solutions with {{plotcal}}. We will plot the XX and YY polarization products separately and make different subplots for each of the spectral windows. This is done by setting the "iteration" parameter to "spw" and specifying subplot=221. By setting the parameter "figfile" to a non-blank value, it will also generate png files of the plots. | ||
[[File:cal-phase_vs_time_XX.G1.png|200px|thumb|right|Phase-only gaincal solutions vs. time for correlation XX]] | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
| Line 422: | Line 527: | ||
poln='X', plotsymbol='o', plotrange = [0,0,-180,180], iteration = 'spw', | poln='X', plotsymbol='o', plotrange = [0,0,-180,180], iteration = 'spw', | ||
figfile='cal-phase_vs_time_XX.G1.png', subplot = 221) | figfile='cal-phase_vs_time_XX.G1.png', subplot = 221) | ||
</source> | |||
<source lang="python"> | |||
# In CASA | |||
plotcal(caltable = 'cal-ngc3256.G1', xaxis = 'time', yaxis = 'phase', | plotcal(caltable = 'cal-ngc3256.G1', xaxis = 'time', yaxis = 'phase', | ||
poln='Y', plotsymbol='o', plotrange = [0,0,-180,180], iteration = 'spw', | poln='Y', plotsymbol='o', plotrange = [0,0,-180,180], iteration = 'spw', | ||
| Line 428: | Line 536: | ||
</source> | </source> | ||
Now that we have a first measurement of the phase variations as a function of time, we can determine the bandpass solutions with {{bandpass}}. We will apply the phase calibration table on-the-fly with the parameter "gaintable". | If you examine the solutions closely, you may notice some phase jumps. (For example: Correlation XX, spw 3, antenna DV09). These jumps occur between the individual observing blocks and will thus not affect the science data. Other than that, the solutions look reasonable. | ||
Now that we have a first measurement of the phase variations as a function of time, we can determine the bandpass solutions with {{bandpass}}. We will apply the phase calibration table on-the-fly with the parameter "gaintable". Now that the phases are corrected, the data can be time-averaged over longer intervals to maximise SNR in each individual channel. We determine bandpass solutions for both days separately because we find that for some antennas, the response across the bandwidth has changed slightly in between the two sessions. We first calculate the bandpass solution for the first day. Do not worry about the message "Insufficient unflagged antennas", which relates to the flagged edge channels. | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
bandpass(vis = 'ngc3256_line.ms', caltable = 'cal-ngc3256.B1', gaintable = 'cal-ngc3256.G1', | bandpass(vis = 'ngc3256_line.ms', caltable = 'cal-ngc3256.B1', | ||
field = '1037*', minblperant=3, minsnr=2, solint='inf', | gaintable = 'cal-ngc3256.G1', timerange='<2011/04/16/15:00:00', | ||
bandtype='B', fillgaps=1, refant = ' | field = '1037*', minblperant=3, minsnr=2, solint='inf', combine='scan', | ||
bandtype='B', fillgaps=1, refant = 'DV04', solnorm = T) | |||
</source> | </source> | ||
*caltable = 'cal-ngc3256.B1': Output bandpass calibration table | |||
*caltable = 'cal-ngc3256.B1': | *gaintable = 'cal-ngc3256.G1': Gain calibration table to apply | ||
*gaintable = 'cal-ngc3256.G1': | |||
*minblperant=3: Minimum number of baselines required per antenna for each solve | *minblperant=3: Minimum number of baselines required per antenna for each solve | ||
*minsnr= | *minsnr=2: Minimum SNR for solutions | ||
*solint='inf': This setting, combined with the default combine='scan', sets the solution interval to the entire observation | *solint='inf': This setting, combined with the default combine='scan', sets the solution interval to the entire observation | ||
*combine='scan': The solutions cross scans | |||
*timerange='<2011/04/16/15:00:00': Only determine solutions for the first day | |||
*bandtype='B': The default type of bandpass solution, which does a channel by channel solution for each specified spw | *bandtype='B': The default type of bandpass solution, which does a channel by channel solution for each specified spw | ||
*fillgaps=1: Interpolate channel gaps 1 channel wide | *fillgaps=1: Interpolate channel gaps 1 channel wide | ||
*solnorm=T: Normalize the bandpass amplitudes and phases of the corrections to unity | *solnorm=T: Normalize the bandpass amplitudes and phases of the corrections to unity | ||
And then append the solutions (append=True) for the second day: | |||
<source lang="python"> | |||
# In CASA | |||
bandpass(vis = 'ngc3256_line.ms', caltable = 'cal-ngc3256.B1', | |||
gaintable = 'cal-ngc3256.G1', timerange='>2011/04/16/15:00:00', | |||
field = '1037*', minblperant=3, minsnr=2, solint='inf', combine='scan', | |||
bandtype='B', fillgaps=1, refant = 'DV04', solnorm = T, append=True) | |||
</source> | |||
[[File:Bandpass.B1.png|200px|thumb|right|Bandpass phase and amplitude solutions]] | |||
We then plot the bandpass solutions with the following commands: | We then plot the bandpass solutions with the following commands: | ||
| Line 454: | Line 577: | ||
subplot=212, overplot=False, plotrange = [0,0,-70,70], | subplot=212, overplot=False, plotrange = [0,0,-70,70], | ||
plotsymbol='.', timerange='') | plotsymbol='.', timerange='') | ||
</source> | |||
<source lang="python"> | |||
# In CASA | |||
plotcal(caltable = 'cal-ngc3256.B1', xaxis='freq', yaxis='amp', spw='', | plotcal(caltable = 'cal-ngc3256.B1', xaxis='freq', yaxis='amp', spw='', | ||
subplot=211, overplot=False, | subplot=211, overplot=False, | ||
| Line 460: | Line 586: | ||
</source> | </source> | ||
The solutions seem reasonable, so we will now apply them on-the-fly during gain calibration. | |||
== Gain Calibration == | == Gain Calibration == | ||
| Line 468: | Line 594: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
setjy(vis='ngc3256_line.ms', field='Titan', standard='Butler-JPL-Horizons 2010') | setjy(vis='ngc3256_line.ms', field='Titan', standard='Butler-JPL-Horizons 2010', | ||
spw='0,1,2,3') | |||
</source> | </source> | ||
The flux density of Titan is | The flux density of Titan is 370 mJy at 114 GHz (spw 0) and drops to 288 mJy at 101 GHz (spw 2): | ||
<pre style="background-color: #fffacd;"> | <pre style="background-color: #fffacd;"> | ||
2011-05- | 2011-05-24 08:35:08 INFO setjy Titan spwid= 0 [I=0.37, Q=0, U=0, V=0] Jy, (JPL-Butler Solar System Object) | ||
2011-05-24 08:35:08 INFO setjy Titan spwid= 1 [I=0.3588, Q=0, U=0, V=0] Jy, (JPL-Butler Solar System Object) | |||
2011-05-24 08:35:09 INFO setjy Titan spwid= 2 [I=0.2878, Q=0, U=0, V=0] Jy, (JPL-Butler Solar System Object) | |||
2011-05-24 08:35:10 INFO setjy Titan spwid= 3 [I=0.2966, Q=0, U=0, V=0] Jy, (JPL-Butler Solar System Object) | |||
</pre> | </pre> | ||
| Line 504: | Line 634: | ||
poln='X', plotsymbol='o', plotrange = [0,0,-180,180], iteration= 'spw', | poln='X', plotsymbol='o', plotrange = [0,0,-180,180], iteration= 'spw', | ||
figfile='cal-phase_vs_time_XX.G2.png', subplot = 221) | figfile='cal-phase_vs_time_XX.G2.png', subplot = 221) | ||
</source> | |||
<source lang="python"> | |||
# In CASA | |||
plotcal(caltable = 'cal-ngc3256.G2', xaxis = 'time', yaxis = 'phase', | plotcal(caltable = 'cal-ngc3256.G2', xaxis = 'time', yaxis = 'phase', | ||
poln='Y', plotsymbol='o', plotrange = [0,0,-180,180], iteration= 'spw', | poln='Y', plotsymbol='o', plotrange = [0,0,-180,180], iteration= 'spw', | ||
figfile='cal-phase_vs_time_YY.G2.png', subplot = 221) | figfile='cal-phase_vs_time_YY.G2.png', subplot = 221) | ||
</source> | |||
<source lang="python"> | |||
# In CASA | |||
plotcal(caltable = 'cal-ngc3256.G2', xaxis = 'time', yaxis = 'amp', | plotcal(caltable = 'cal-ngc3256.G2', xaxis = 'time', yaxis = 'amp', | ||
poln='X', plotsymbol='o', plotrange = [], iteration = 'spw', | poln='X', plotsymbol='o', plotrange = [], iteration = 'spw', | ||
figfile='cal-amp_vs_time_XX.G2.png', subplot = 221) | figfile='cal-amp_vs_time_XX.G2.png', subplot = 221) | ||
</source> | |||
<source lang="python"> | |||
# In CASA | |||
plotcal(caltable = 'cal-ngc3256.G2', xaxis = 'time', yaxis = 'amp', | plotcal(caltable = 'cal-ngc3256.G2', xaxis = 'time', yaxis = 'amp', | ||
poln='Y', plotsymbol='o', plotrange = [], iteration = 'spw', | poln='Y', plotsymbol='o', plotrange = [], iteration = 'spw', | ||
| Line 522: | Line 661: | ||
Finally, we will bootstrap the flux density of the secondary calibrator from that of Titan using the task {{fluxscale}}. | Finally, we will bootstrap the flux density of the secondary calibrator from that of Titan using the task {{fluxscale}}. | ||
The new flux table cal-ngc3256.G2.flux replaces the previous cal-ngc3256.G2 table in future application of the calibration to the data, i.e. the new flux table contains both cal-ngc3256.G2 and the newly acquired flux scaling. Unlike the gain calibration steps, this is not an incremental table. | The new flux table cal-ngc3256.G2.flux replaces the previous cal-ngc3256.G2 table in future application of the calibration to the data, i.e. the new flux table contains both cal-ngc3256.G2 and the newly acquired flux scaling. Unlike the gain calibration steps, this is not an incremental table. | ||
<source lang="python"> | <source lang="python"> | ||
| Line 532: | Line 669: | ||
</source> | </source> | ||
Note that we previously flagged the Titan scans from the second day due to contamination from nearby Saturn's rings. We have therefore used the Titan scans from the first day alone to flux calibrate both days' observations. This would not always be an acceptable solution; however, in this case, examination of the measured amplitudes for the phase calibrator over both days indicate that the flux scale is relatively stable. The logger produces the following output: | Note that we previously flagged the Titan scans from the second day due to contamination from nearby Saturn's rings. We have therefore used the Titan scans from the first day alone to flux calibrate both days' observations. This would not always be an acceptable solution; however, in this case, examination of the measured amplitudes for the phase calibrator over both days indicate that the flux scale is relatively stable. | ||
Also note that we have used refspwmap=[0,1,1,1]. This means that the 1037-295 observations in spw 2 and 3 are referenced to Titan observations observed in spw 1. We have to do this here because the Titan data in spw 2 and 3 are contaminated by Saturn, as explained above. | |||
The logger produces the following output: | |||
<pre style="background-color: #fffacd;"> | <pre style="background-color: #fffacd;"> | ||
2011-05- | 2011-05-31 21:32:31 INFO fluxscale Flux density for 1037-295 in SpW=0 is: 1.81638 +/- 0.0179226 (SNR = 101.346, nAnt= 7) | ||
2011-05- | 2011-05-31 21:32:31 INFO fluxscale Flux density for 1037-295 in SpW=1 is: 1.81967 +/- 0.0149109 (SNR = 122.037, nAnt= 7) | ||
2011-05- | 2011-05-31 21:32:31 INFO fluxscale Flux density for 1037-295 in SpW=2 (ref SpW=1) is: 1.90794 +/- 0.0155891 (SNR = 122.389, nAnt= 7) | ||
2011-05- | 2011-05-31 21:32:31 INFO fluxscale Flux density for 1037-295 in SpW=3 (ref SpW=1) is: 1.86595 +/- 0.0153365 (SNR = 121.668, nAnt= 6) | ||
</pre> | </pre> | ||
We find that the flux density of 1037-295 is ~1.8 Jy in | We find that the flux density of 1037-295 is ~1.8 Jy in the higher frequency spectral windows and ~1.9 Jy in the lower frequency spectral windows. This fluxes agree very well with the 3mm measurements from the ATCA and OVRO of a few years ago (see SMA calibrator [http://sma1.sma.hawaii.edu/callist/callist.html?plot=1037-295 list]). | ||
==Applying the calibrations == | ==Applying the calibrations == | ||
| Line 560: | Line 700: | ||
*flagbackup=F: We do not back up the state of the flags before applying calibration | *flagbackup=F: We do not back up the state of the flags before applying calibration | ||
[[File:Amp_vs_freqNGC3256corr.png|200px|thumb|right|Amp vs Freq]] | |||
Let's now use {{plotms}} to examine the corrected amplitude of NGC3256 as a function of frequency: | Let's now use {{plotms}} to examine the corrected amplitude of NGC3256 as a function of frequency: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
| Line 571: | Line 711: | ||
</source> | </source> | ||
Use the "Zoom" tool to zoom in on the different spectral windows. (Note that spw 2-3 are on the left). There are three emission lines in spectral windows 0-1. There is no emission in spw 2 and 3. | Use the "Zoom" tool to zoom in on the different spectral windows. (Note that spw 2-3 are on the left). There are three emission lines in spectral windows 0-1. There is no emission in spw 2 and 3. Also note that there are still some high channels on the edge of spw 2-3. We will exclude these channels for our subsequent imaging. | ||
It also makes sense to plot the corrected amplitudes and phases of 1037-295 as a function of time and frequency, to check that the phases are close to zero and the amplitudes are constant. The result of the amplitude versus time plot is shown to the right. | |||
[[File:amp_vs_time_calibrator.png|200px|thumb|right|Corrected amplitude vs. time for the calibrator]] | |||
<source lang="python"> | |||
# In CASA | |||
plotms(vis='ngc3256_line.ms', xaxis='time', yaxis='amp', | |||
ydatacolumn='corrected', selectdata=True, field='1037*', | |||
averagedata=True, avgchannel='128', avgtime='', | |||
avgscan=False, avgbaseline=F, coloraxis='spw') | |||
</source> | |||
<source lang="python"> | |||
# In CASA | |||
plotms(vis='ngc3256_line.ms', xaxis='freq', yaxis='phase', | |||
ydatacolumn='corrected', selectdata=True, field='1037*', | |||
averagedata=True, avgchannel='', avgtime='1e8', | |||
avgscan=True, avgbaseline=F, coloraxis='baseline') | |||
</source> | |||
Based on the inspection of these plots, we identify some bad data and flag them: | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
flagdata(vis='ngc3256_line.ms', mode='manualflag', | flagdata(vis='ngc3256_line.ms', mode='manualflag', | ||
timerange='2011/04/16/04:13:35~04:13:45', flagbackup = | timerange='2011/04/16/04:13:35~04:13:45', flagbackup = T) | ||
tget(flagdata) | tget(flagdata) | ||
timerange='2011/04/16/05:21:13~05:21:19' | timerange='2011/04/16/05:21:13~05:21:19' | ||
flagdata() | flagdata() | ||
timerange='2011/04/16/04:16:40~04:16:49' | timerange='2011/04/16/04:16:40~04:16:49' | ||
flagdata() | |||
timerange='2011/04/16/04:14:00~04:17:10'; antenna='PM03' | |||
flagdata() | |||
timerange='2011/04/17/00:35:30~01:20:20'; antenna='DV04'; spw='3' | |||
flagdata() | flagdata() | ||
</source> | </source> | ||
| Line 586: | Line 751: | ||
Note that in the above command sequence, we utilize the CASA function [http://casa.nrao.edu/docs/userman/UserMansu36.html#x44-430001.3.5.6 tget]. This function retrieves the last input values for the function specified. | Note that in the above command sequence, we utilize the CASA function [http://casa.nrao.edu/docs/userman/UserMansu36.html#x44-430001.3.5.6 tget]. This function retrieves the last input values for the function specified. | ||
At this point, we will image the secondary calibrator as a check of our calibration. We do this using the task {{clean}}, after first removing any previous versions of the images that may exist in our directory. | Now that we have flagged some of the calibrator data, we should redo the calibration steps above. We start with a {{clearcal}} to reinitialize the calibration columns in ngc3256_line.ms. Specifically, it will set the MODEL data column to unity, and it will set the CORRECTED data column equal to the original DATA column. After the {{clearcal}}, the commands are identical to what has been done above. (The improvements in the calibration are only minor, so in principle, one could carry on with making calibrator images and skip the following eight commands.) | ||
<source lang="python"> | |||
# In CASA | |||
clearcal('ngc3256_line.ms') | |||
</source> | |||
<source lang="python"> | |||
# In CASA | |||
gaincal(vis='ngc3256_line.ms', caltable='cal-ngc3256.G1n', spw='*:40~80', field='1037*', | |||
selectdata=T, solint='int', refant='DV04', calmode='p') | |||
</source> | |||
<source lang="python"> | |||
# In CASA | |||
bandpass(vis = 'ngc3256_line.ms', caltable = 'cal-ngc3256.B1n', | |||
gaintable = 'cal-ngc3256.G1n', timerange='<2011/04/16/15:00:00', | |||
field = '1037*', minblperant=3, minsnr=2, solint='inf', combine='scan', | |||
bandtype='B', fillgaps=1, refant = 'DV04', solnorm = T) | |||
</source> | |||
<source lang="python"> | |||
# In CASA | |||
bandpass(vis = 'ngc3256_line.ms', caltable = 'cal-ngc3256.B1n', | |||
gaintable = 'cal-ngc3256.G1n', timerange='>2011/04/16/15:00:00', | |||
field = '1037*', minblperant=3, minsnr=2, solint='inf', combine='scan', | |||
bandtype='B', fillgaps=1, refant = 'DV04', solnorm = T, append=True) | |||
</source> | |||
<source lang="python"> | |||
# In CASA | |||
setjy(vis='ngc3256_line.ms', field='Titan', standard='Butler-JPL-Horizons 2010', | |||
spw='0,1,2,3') | |||
</source> | |||
<source lang="python"> | |||
# In CASA | |||
gaincal(vis = 'ngc3256_line.ms', caltable = 'cal-ngc3256.G2n', spw = | |||
'*:16~112', field = '1037*,Titan', minsnr=1.0, | |||
solint= 'inf', selectdata=T, solnorm=False, refant = 'DV04', | |||
gaintable = 'cal-ngc3256.B1n', calmode = 'ap') | |||
</source> | |||
<source lang="python"> | |||
# In CASA | |||
fluxscale( vis="ngc3256_line.ms", caltable="cal-ngc3256.G2n", | |||
fluxtable="cal-ngc3256.G2n.flux", reference="Titan", | |||
transfer="1037*", refspwmap=[0,1,1,1]) | |||
</source> | |||
<source lang="python"> | |||
# In CASA | |||
applycal( vis='ngc3256_line.ms', flagbackup=F, field='NGC*,1037*', | |||
interp=['nearest','nearest'], gainfield = ['1037*', '1037*'], | |||
gaintable=['cal-ngc3256.G2n.flux', 'cal-ngc3256.B1n']) | |||
</source> | |||
Having redone the calibration, we will again look at amplitude and phase versus time to check that the amplitudes are stable and the phases are close to zero. | |||
<source lang="python"> | |||
# In CASA | |||
plotms(vis='ngc3256_line.ms', xaxis='time', yaxis='amp', | |||
ydatacolumn='corrected', selectdata=True, field='1037*', | |||
averagedata=True, avgchannel='128', avgtime='', | |||
avgscan=False, avgbaseline=F, coloraxis='spw') | |||
</source> | |||
<source lang="python"> | |||
# In CASA | |||
plotms(vis='ngc3256_line.ms', xaxis='freq', yaxis='phase', | |||
ydatacolumn='corrected', selectdata=True, field='1037*', | |||
averagedata=True, avgchannel='', avgtime='1e8', | |||
avgscan=True, avgbaseline=F, coloraxis='baseline') | |||
</source> | |||
<gallery widths="400px" heights="300px" perrow="2"> | |||
File:amp_vs_time_calibrator2.png|Corrected amplitude vs. time | |||
File:phase_vs_freq_1037.png|Corrected phase vs. frequency | |||
</gallery> | |||
In the first plot we show amplitude vs time, colorized by spectral window. This shows very clearly that the amplitude is constant in time, but varies as a function of frequency, which is intrinsic to the source. The second plot shows that the phases are very flat across all spectral windows. | |||
==Imaging the Calibrators== | |||
At this point, we will image the secondary calibrator as a check of our calibration. We do this using the task {{clean}}, after first removing any previous versions of the images that may exist in our directory. This is an important precaution, since if the image already exists, CASA will clean it further instead of producing a new image. In this {{clean}} run, we choose to use Multi-Frequency Synthesis (mfs) with nterms=2, which implies that the algorithm determines the continuum map and the spectral index map simultaneously. This is required here, because we found with {{fluxscale}} that the flux of 1037-295 increases significantly toward lower frequencies. Therefore, assuming a 'flat' spectral index would not give a good result. Do not be alarmed to see this message: "Multi-term MFS imaging algorithm is new and under active development and testing". The method is working fine and has been tested. | |||
<source lang="python"> | <source lang="python"> | ||
| Line 592: | Line 842: | ||
os.system('rm -rf result-phasecal_cont*') | os.system('rm -rf result-phasecal_cont*') | ||
clean(vis='ngc3256_line.ms', imagename='result-phasecal_cont', field='1037*', | clean(vis='ngc3256_line.ms', imagename='result-phasecal_cont', field='1037*', | ||
spw='*:20~120', selectdata=T, mode='mfs', niter= | spw='*:20~120', selectdata=T, mode='mfs', niter=500, | ||
gain=0.1, threshold='0. | gain=0.1, threshold='0.75mJy', psfmode='hogbom', | ||
interactive=False, mask=[ | interactive=False, mask=[62, 62, 67, 67], imsize=128, | ||
cell='1arcsec', weighting='briggs', robust=0.0) | cell='1arcsec', weighting='briggs', robust=0.0, nterms=2) | ||
</source> | </source> | ||
[[File:phasecal_map.png|200px|thumb|right|Continuum image of phasecal]] | [[File:phasecal_map_lin.png|200px|thumb|right|Continuum image of phasecal]] | ||
[[File:phasecal_map.png|200px|thumb|right|Continuum image of phasecal, with logarithmic color scaling to bring out the weaker features in the map]] | |||
*imagename='result-phasecal_cont': the base name of the output images | *imagename='result-phasecal_cont': the base name of the output images | ||
*spw='*:20~120': We image all spectral windows, ignoring the outermost channels of each | *spw='*:20~120': We image all spectral windows, ignoring the outermost channels of each | ||
*mode='mfs': | *mode='mfs': Mult-Frequency Synthesis: the default mode, which produces one image from all the specified data combined | ||
*niter= | *nterms=2: The number of Taylor terms to be used to model the frequency dependence of the sky emission | ||
*theshold='0. | *niter=500: Maximum number of clean iterations | ||
*psfmode='hogbom': The method used to | *theshold='0.75mJy': Stop cleaning if the maximum residual is below this value. Here we choose a threshold equal to ~1.5 times the rms noise level | ||
*mask=[ | *psfmode='hogbom': The method used to calculate the PSF during minor clean cycles. Hogbom is a good choice for poorly-sampled uv-planes | ||
*imsize= | *mask=[62, 62, 67, 67]: Limits the clean component placement to the region of the source. We know the source is compact so we do not need to worry about boxing interactively | ||
*weighting='briggs', robust=0: a weighting scheme that offers a good compromise between sensitivity and resolution | *imsize=128, cell='1arcsec': Chosen to appropriately sample the resolution element and cover the primary beam | ||
*weighting='briggs', robust=0.0: a weighting scheme that offers a good compromise between sensitivity and resolution | |||
Once the imaging of the secondary calibrator is complete, we will generate some statistics on the image using the task {{imstat}}: | Note that using nterms=2 makes the {{clean}} task considerably slower than before. Once the imaging of the secondary calibrator is complete, we will generate some statistics on the image using the task {{imstat}}. Note that {{clean}} generates several output images when used with nterms=2. The continuum intensity map has suffix .tt0. The spectral index map has suffix .alpha. For more see http://casa.nrao.edu/docs/UserMan/UserMansu227.html . | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
calstat=imstat(imagename='result-phasecal_cont.image', region='', box=' | calstat=imstat(imagename='result-phasecal_cont.image.tt0', region='', box='85,8,120,120') | ||
rms=(calstat['rms'][0]) | rms=(calstat['rms'][0]) | ||
print '>> rms in phase calibrator image: '+str(rms) | print '>> rms in phase calibrator image: '+str(rms) | ||
calstat=imstat(imagename='result-phasecal_cont.image', region='') | calstat=imstat(imagename='result-phasecal_cont.image.tt0', region='') | ||
peak=(calstat['max'][0]) | peak=(calstat['max'][0]) | ||
print '>> Peak in phase calibrator image: '+str(peak) | print '>> Peak in phase calibrator image: '+str(peak) | ||
| Line 622: | Line 874: | ||
</source> | </source> | ||
Here, we have used the "box" parameter in the first call of imstat to find the image rms in a region away from the strong central point source. The image dynamic range in the calibrator image is ~ | Here, we have used the "box" parameter in the first call of {{imstat}} to find the image rms in a region away from the strong central point source. The image dynamic range in the calibrator image is ~3100. We will then look at the image of the secondary calibrator with {{imview}}. | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
imview(raster={'file': 'result-phasecal_cont.image', 'colorwedge':T, | imview(raster={'file': 'result-phasecal_cont.image.tt0', 'colorwedge':T, | ||
'range':[-0.004, 0.250], 'scaling':-2.5, 'colormap':'Rainbow 2'}, | 'range':[-0.004, 0.250], 'scaling':-2.5, 'colormap':'Rainbow 2'}, | ||
out='result-phasecal_map.png', zoom=1) | out='result-phasecal_map.png', zoom=1) | ||
</source> | </source> | ||
This command rasters the image of the phase calibrator to the GUI and outputs the file phasecal_map.png. It uses the Rainbow 2 colomap scheme and includes a colorwedge on the plot. The "range" and "scaling" parameters have been chosen to bring out the weaker features in the map. | This command rasters the image of the phase calibrator to the GUI and outputs the file phasecal_map.png. It uses the Rainbow 2 colomap scheme and includes a colorwedge on the plot. The "range" and "scaling" parameters have been chosen to bring out the weaker features in the map. The calibrator image looks pretty good, from which we conclude that the gain calibration has worked well and we will move on. If the image quality was not acceptable, we would need to flag some more data and redo the calibration to this point. | ||
Now we will apply the calibration to the flux calibrator, Titan, using the solutions we derived for Titan itself. | Now we will apply the calibration to the flux calibrator, Titan, using the time-dependent solutions we derived for Titan itself and the bandpass solutions from 1037*. | ||
<source lang="python"> | <source lang="python"> | ||
| Line 642: | Line 894: | ||
</source> | </source> | ||
Now we will image the flux calibrator (Titan). See the previous call to clean for a description of the various inputs. | Now we will image the flux calibrator (Titan). See the previous call to {{clean}} for a description of the various inputs. This time we will only use spectral windows 0 and 1 because we know that the Titan data in spectral windows 2 and 3 are corrupted by Saturn. | ||
<source lang="python"> | <source lang="python"> | ||
| Line 649: | Line 901: | ||
clean(vis='ngc3256_line.ms', imagename='result-ampcal_cont', | clean(vis='ngc3256_line.ms', imagename='result-ampcal_cont', | ||
field='Titan', spw='0:20~120,1:20~120', mode='mfs', niter=200, | field='Titan', spw='0:20~120,1:20~120', mode='mfs', niter=200, | ||
threshold=' | threshold='5mJy', psfmode='hogbom', mask=[62, 62, 67, 67], imsize=128, | ||
cell='1arcsec', weighting='briggs', robust=0.0) | cell='1arcsec', weighting='briggs', robust=0.0) | ||
</source> | </source> | ||
[[File:ampcal_map.png|200px|thumb|right|Continuum image of Titan]] | [[File:ampcal_map_lin.png|200px|thumb|right|Continuum image of Titan]] | ||
[[File:ampcal_map.png|200px|thumb|right|Continuum image of Titan, with logarithmic color scaling to bring out the weaker features in the map]] | |||
As before, we will generate some statistics on the image: | As before, we will generate some statistics on the image: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
calstat=imstat(imagename="result-ampcal_cont.image",region="",box=" | calstat=imstat(imagename="result-ampcal_cont.image",region="",box="85,8,120,120") | ||
rms=(calstat['rms'][0]) | rms=(calstat['rms'][0]) | ||
print ">> rms in amp calibrator image: "+str(rms) | print ">> rms in amp calibrator image: "+str(rms) | ||
| Line 667: | Line 920: | ||
</source> | </source> | ||
The dynamic range in this image is ~ | The dynamic range in this image is ~74. It's much less than the image of the secondary calibrator because less time was spent observing it (the total on-source time on Titan is only 9 minutes). We will then take a look at the image with {{imview}}, again choosing the data range and scaling parameter to bring out weak features in the map: | ||
<source lang="python"> | <source lang="python"> | ||
| Line 685: | Line 938: | ||
</source> | </source> | ||
This concludes the Calibration section of this CASA Guide. To proceed to the Imaging section, click here: [[NGC3256 Band3 - Imaging]]. To go back to the main NGC3256 page, see: [[NGC3256Band3]]. | This concludes the Calibration section of this CASA Guide. To proceed to the Imaging section, click here: '''[[NGC3256 Band3 - Imaging]]'''. To go back to the main NGC3256 page, see: '''[[NGC3256Band3]]'''. | ||
{{Checked 3.3.0}} | |||
Latest revision as of 15:04, 23 November 2011
Overview
This portion of the NGC3256Band3 CASA Guide will cover the calibration of the raw visibility data. To skip to the imaging portion of the guide, see: NGC3256 Band3 - Imaging.
If you haven't already downloaded the raw data, you may do that now by clicking on the region closest to your location and downloading the file named 'NGC3256_Band3_UnCalibratedMSandTablesForReduction.tgz':
Once the download has finished, unpack the file:
# In a terminal outside CASA
tar -xvzf NGC3256_Band3_UnCalibratedMSandTablesForReduction.tgz
cd NGC3256_Band3_UnCalibratedMSandTablesForReduction
# Start CASA
casapy
The data have already been converted to CASA Measurement Set (MS) format using the CASA task importasdm. Accompanying the data are some basic calibration tables you will need for the following reduction, as well as the *.ms.flagversions files that are automatically generated by importasdm.
Initial Inspection and A priori Flagging
We will eventually concatenate the six datasets used here into one large dataset. However, we will keep them separate for now, as some of the steps to follow require individual datasets (specifically, the application of the Tsys and WVR tables). We therefore start by defining an array "basename" that includes the names of the six files in chronological order. This will simplify the following steps by allowing us to loop through the files using a simple for-loop in python. Remember that if you log out of CASA, you will have to re-issue this command. We will remind you of this in the relevant sections by repeating the command at the start.
# In CASA
basename=['uid___A002_X1d54a1_X5','uid___A002_X1d54a1_X174','uid___A002_X1d54a1_X2e3',
'uid___A002_X1d5a20_X5','uid___A002_X1d5a20_X174','uid___A002_X1d5a20_X330']
The usual first step is then to get some basic information about the data. We do this using the task listobs, which will output a detailed summary of each dataset supplied.
# In CASA
for name in basename:
listobs(vis=name+'.ms')
Note that after cutting and pasting a for-loop you often have to press return several times to execute. The output will be sent to the CASA logger. You will have to scroll up to see the individual output for each of the six datasets. Here is an example of the most relevant output for the first file in the list.
Fields: 3 ID Code Name RA Decl Epoch SrcId nVis 0 none 1037-295 10:37:16.0790 -29.34.02.8130 J2000 0 38759 1 none Titan 00:00:00.0000 +00.00.00.0000 J2000 1 16016 2 none NGC3256 10:27:51.6000 -43.54.18.0000 J2000 2 151249 (nVis = Total number of time/baseline visibilities per field) Spectral Windows: (9 unique spectral windows and 2 unique polarization setups) SpwID #Chans Frame Ch1(MHz) ChanWid(kHz)TotBW(kHz) Ref(MHz) Corrs 0 4 TOPO 184550 1500000 7500000 183300 I 1 128 TOPO 113211.988 15625 2000000 113204.175 XX YY 2 1 TOPO 114188.55 1796875 1796875 113204.175 XX YY 3 128 TOPO 111450.813 15625 2000000 111443 XX YY 4 1 TOPO 112427.375 1796875 1796875 111443 XX YY 5 128 TOPO 101506.187 15625 2000000 101514 XX YY 6 1 TOPO 100498.375 1796875 1796875 101514 XX YY 7 128 TOPO 103050.863 15625 2000000 103058.675 XX YY 8 1 TOPO 102043.05 1796875 1796875 103058.675 XX YY Sources: 48 ID Name SpwId RestFreq(MHz) SysVel(km/s) 0 1037-295 0 - - 0 1037-295 9 - - 0 1037-295 10 - - 0 1037-295 11 - - 0 1037-295 12 - - 0 1037-295 13 - - 0 1037-295 14 - - 0 1037-295 15 - - 0 1037-295 1 - - 0 1037-295 2 - - 0 1037-295 3 - - 0 1037-295 4 - - 0 1037-295 5 - - 0 1037-295 6 - - 0 1037-295 7 - - 0 1037-295 8 - - 1 Titan 0 - - 1 Titan 9 - - 1 Titan 10 - - 1 Titan 11 - - 1 Titan 12 - - 1 Titan 13 - - 1 Titan 14 - - 1 Titan 15 - - 1 Titan 1 - - 1 Titan 2 - - 1 Titan 3 - - 1 Titan 4 - - 1 Titan 5 - - 1 Titan 6 - - 1 Titan 7 - - 1 Titan 8 - - 2 NGC3256 0 - - 2 NGC3256 9 - - 2 NGC3256 10 - - 2 NGC3256 11 - - 2 NGC3256 12 - - 2 NGC3256 13 - - 2 NGC3256 14 - - 2 NGC3256 15 - - 2 NGC3256 1 - - 2 NGC3256 2 - - 2 NGC3256 3 - - 2 NGC3256 4 - - 2 NGC3256 5 - - 2 NGC3256 6 - - 2 NGC3256 7 - - 2 NGC3256 8 - - Antennas: 7: ID Name Station Diam. Long. Lat. 0 DV04 J505 12.0 m -067.45.18.0 -22.53.22.8 1 DV06 T704 12.0 m -067.45.16.2 -22.53.22.1 2 DV07 J510 12.0 m -067.45.17.8 -22.53.23.5 3 DV08 T703 12.0 m -067.45.16.2 -22.53.23.9 4 DV09 N602 12.0 m -067.45.17.4 -22.53.22.3 5 PM02 T701 12.0 m -067.45.18.8 -22.53.22.2 6 PM03 J504 12.0 m -067.45.17.0 -22.53.23.0
This output shows that three fields were observed: 1037-295, Titan, and NGC3256. Field 0 (1037-295) will serve as the gain calibrator and bandpass calibrator; field 1 (Titan) will serve as the flux calibrator; and field 2 (NGC3256) is, of course, the science target.
Note that there are more than four SpwIDs even though the observations were set up to have four spectral windows. The spectral line data themselves are found in spectral windows 1,3,5,7, which have 128 channels each. The first one (spw 1) is centered on the CO(1-0) emission line in the galaxy NGC 3256 and is our highest frequency spectral window. There is one additional spectral window (spw 3) in the Upper Side Band (USB), and there are two spectral windows (spw 5 and 7) in the Lower Side Band (LSB). These additional spectral windows are used to measure the continuum emission in the galaxy, and may contain other emission lines as well.
Spectral windows 2,4,6,8 contain channel averages of the data in spectral windows 1,3,5,7, respectively. These are not useful for the offline data reduction. Spectral window 0 contains the WVR data. You may notice that there are additional SpwIDs listed in the "Sources" section which are not listed in the "Spectral Windows" section. These spectral windows are reserved for the WVRs of each antenna (seven in our case). At the moment, all WVRs point to spw 0, which contains nominal frequencies. The additional spectral windows (spw 9-15) are therefore not used and can be ignored.
Another important thing to note is that the position of Titan is listed as 00:00:00.0000 +00.00.00.0000. This is due to the fact that for ephemeris objects, the positions are currently not stored in the asdm. This will be handled correctly in the near future, but at present, we have to fix this offline. We will correct the coordinates below by running the procedure fixplanets, which takes the position from the pointing table.
The final column of the listobs output in the logger (not shown above) gives the scan intent. This information is used later to flag the pointing scans and the hot and ambient load calibration scans, using scan intent as a selection option. Also these intents will be used in the future for pipeline processing.
Seven antennas were used for the dataset listed above. Note that numbering in python always begins with "0", so the antennas have IDs 0-6. To see what the antenna configuration looked like at the time of the this observation, we will use the task plotants.
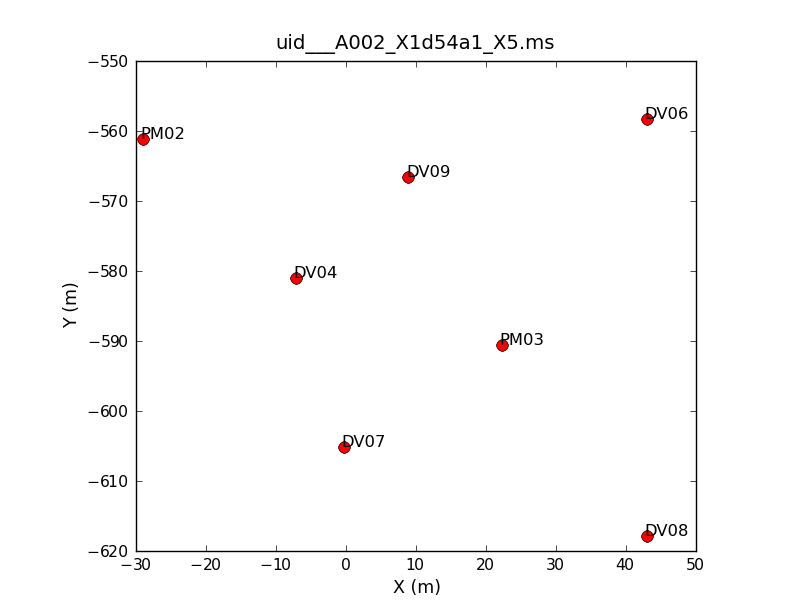
# In CASA
plotants(vis=basename[0]+'.ms', figfile=basename[0]+'_plotants.png')
This will plot the antenna configuration on your screen as well as save it under the specified filename for future reference. This will be important later on when we need to choose a reference antenna, since the reference antenna should be close to the center of the array (as well as stable and present for the entire observation).
If you repeat the plotants command for the other five datasets, you will see that there is an additional antenna (DV10) present on the second day of observations. Other than that, the configuration stays constant during the course of the observations.
Flagging
The first editing we will do is some a priori flagging with flagdata and flagautocorr. We will start by flagging the shadowed data and the autocorrelation data. ALMA data contains both the cross correlation and autocorrelation data, but here we are only interested in the cross-correlation data. Additionally, for compact configurations of the array, one antenna can shadow another, blocking its view. These data also need to be flagged. Remember that you first need to redefine the "basename" array if you logged out of CASA prior to starting this section.
# In CASA
basename=['uid___A002_X1d54a1_X5','uid___A002_X1d54a1_X174','uid___A002_X1d54a1_X2e3',
'uid___A002_X1d5a20_X5','uid___A002_X1d5a20_X174','uid___A002_X1d5a20_X330']
Now we will loop over the datasets, running the two flagging commands:
# In CASA
for name in basename:
flagdata(vis=name+'.ms', flagbackup = F, mode = 'shadow')
flagautocorr(vis=name+'.ms')
There are a number of scans in the data that were used by the online system for pointing calibration. These scans are no longer needed, and we can flag them easily with flagdata by selecting on 'intent':
# In CASA
for name in basename:
flagdata(vis=name+'.ms', mode='manualflag', flagbackup = F, intent='*POINTING*')
Similarly, we can flag the scans corresponding to atmospheric calibration:
# In CASA
for name in basename:
flagdata(vis=name+'.ms', mode='manualflag', flagbackup = F, intent='*ATMOSPHERE*')
We will then store the current flagging state for each dataset using the flagmanager:
# In CASA
for name in basename:
flagmanager(vis = name+'.ms', mode = 'save', versionname = 'Apriori')
Delay Correction for Antenna DV07
Due to an issue with antenna DV07 during the commissioning period when these data were taken, it shows large delays in phase for the first three datasets. While the bandpass calibration will attempt to fit and remove small phase delays (i.e., less than one wrap over the bandpass), large delays like those seen here will result in failed solutions. If we want to salvage the data for this antenna, we therefore need to correct the delays by calculating a K-type delay calibration table with gencal. We emphasize that this is not usually a part of the typical calibration procedure, but it may be useful to the reader to see how such a correction is made.
Remember that you first need to redefine the "basename" array if you logged out of CASA prior to starting this section.
# In CASA
basename=['uid___A002_X1d54a1_X5','uid___A002_X1d54a1_X174','uid___A002_X1d54a1_X2e3',
'uid___A002_X1d5a20_X5','uid___A002_X1d5a20_X174','uid___A002_X1d5a20_X330']
You can see the phase delays by plotting phase versus channel in plotms, as we do here for a single spw, correlation, and baseline with DV07:
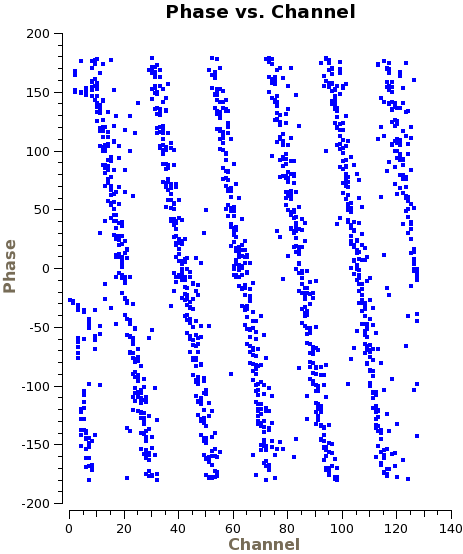
# In CASA
plotms(vis=basename[0]+'.ms', xaxis='channel', yaxis='phase',
spw='3', antenna='PM03&DV07', correlation='XX', avgtime='1e8')
The parameters required by gencal are the delays measured in nanoseconds, first cycling over polarization product, and then over spectral window (thus giving eight numbers in total). We simply estimate these values by eye using the above plot and the corresponding plots for the other spectral windows and polarization products. The purpose here is to get the phases approximately flat as a function of frequency. Any additional phase variations will be corrected for later when we do the bandpass calibration.
Based on the above plot, we estimate that the delay for this spw and correlation is approximately -3ns. One full phase wrap over 2GHz corresponds to a delay of 1/(2GHz)=0.5ns. Here we see six wraps and therefore estimate a 3ns delay. The sign convention is such that the delay is positive if the phase is increasing with respect to frequency and negative if it is decreasing, as it is here. Note that the sign convention is reversed between the two basebands, since the channels in the USB run in the opposite direction to those in the LSB. The wrapping in spectral windows 3,5,7 is therefore all in the same direction with respect to frequency. The value of -3ns that we estimate is for spw 3, correlation XX, and will therefore be the third element in the parameter array.
We then run gencal for the three datasets in question, supplying the estimated values in the "parameter" array. As the gencal task will not overwrite existing tables, the script starts by deleting any existing versions of the calibration tables with the same name.
# In CASA
for i in range(3): # loop over the first three ms's
name=basename[i]
os.system('rm -rf cal-'+name+'_del.K')
gencal(vis=name+'.ms', caltable='cal-'+name+'_del.K',
caltype='sbd', antenna='DV07', pol='X,Y', spw='1,3,5,7',
parameter=[1.00, 1.10, -3.0, -3.0, -3.05, -3.05, -3.05, -3.05])
Note that when you run the gencal command above, CASA may generate the warning "No scr col generation!!!" This just means that there is no field association in the tables generated, so that you can apply them to any of the fields in the observation. This is not important, so you can ignore the warning.
We will apply these K tables to the data in the next section.
WVR Correction and Tsys Calibration
We will now apply the delay correction table and the WVR calibration tables to the data with the task applycal. We do this in two steps. First we will cycle over the three datasets from the first day of observations, because we have to correct the delay error for DV07 for those data. For the last three datasets (i.e. those taken during the second day), we do not need to correct the delays, so we just apply the WVR tables. In the call to applycal, we will specify interpolation="nearest". This is important for the WVR corrections, and it doesn't make a difference for the delay corrections because they have no time dependence.
First, remember to redefine the "basename" array if you've logged out of CASA at any point up until now.
# In CASA
basename=['uid___A002_X1d54a1_X5','uid___A002_X1d54a1_X174','uid___A002_X1d54a1_X2e3',
'uid___A002_X1d5a20_X5','uid___A002_X1d5a20_X174','uid___A002_X1d5a20_X330']
Now loop through the datasets as described above, applying the calibration tables:
# In CASA
for i in range(3): # loop over the first three data sets
name=basename[i]
applycal(vis=name+'.ms', flagbackup=F, spw='1,3,5,7',
interp=['nearest','nearest'], gaintable=['cal-'+name+'_del.K', 'cal-'+name+'.W'])
# In CASA
for i in range(3,6): # loop over the last three data sets
name=basename[i]
applycal(vis=name+'.ms', flagbackup=F, spw='1,3,5,7',
interp='nearest', gaintable='cal-'+name+'.W')
Now you can use plotms to show some of the before-and-after effects of calibration. Just re-run the previous plotms command, repeated below, or if the window is still open, check 'force reload'. This will display the uncorrected phases across the band. To display the corrected phases, you will need to select the CORRECTED data column in the axes tab and replot.
# In CASA
plotms(vis=basename[0]+'.ms', xaxis='channel', yaxis='phase',
spw='1', antenna='', correlation='XX', avgtime='1e8',
coloraxis='baseline', avgscan=T, selectdata=T, field='1037*')
Now we split out the CORRECTED data column of the datasets with the task split. We give the resulting datasets the extension "_K_WVR" to indicate that the delay tables and WVR tables have been applied in the DATA column, and we specify spectral windows 0-8 to get rid of the "WVR placeholder" spectral windows. Since split will not overwrite existing files, we start by removing any previous versions of the split ms's before running the split command.
# In CASA
for name in basename:
os.system('rm -rf '+name+'_K_WVR.ms*')
split(vis=name+'.ms', outputvis=name+'_K_WVR.ms',
datacolumn='corrected', spw='0~8')
Next we do the Tsys calibration. Tsys measurements correct for the atmospheric opacity (to first-order) and allow the calibration sources to be measured at elevations that differ from the science target. The Tsys tables for these datasets were provided with the downloadable data. We will start by inspecting them with the task plotcal:
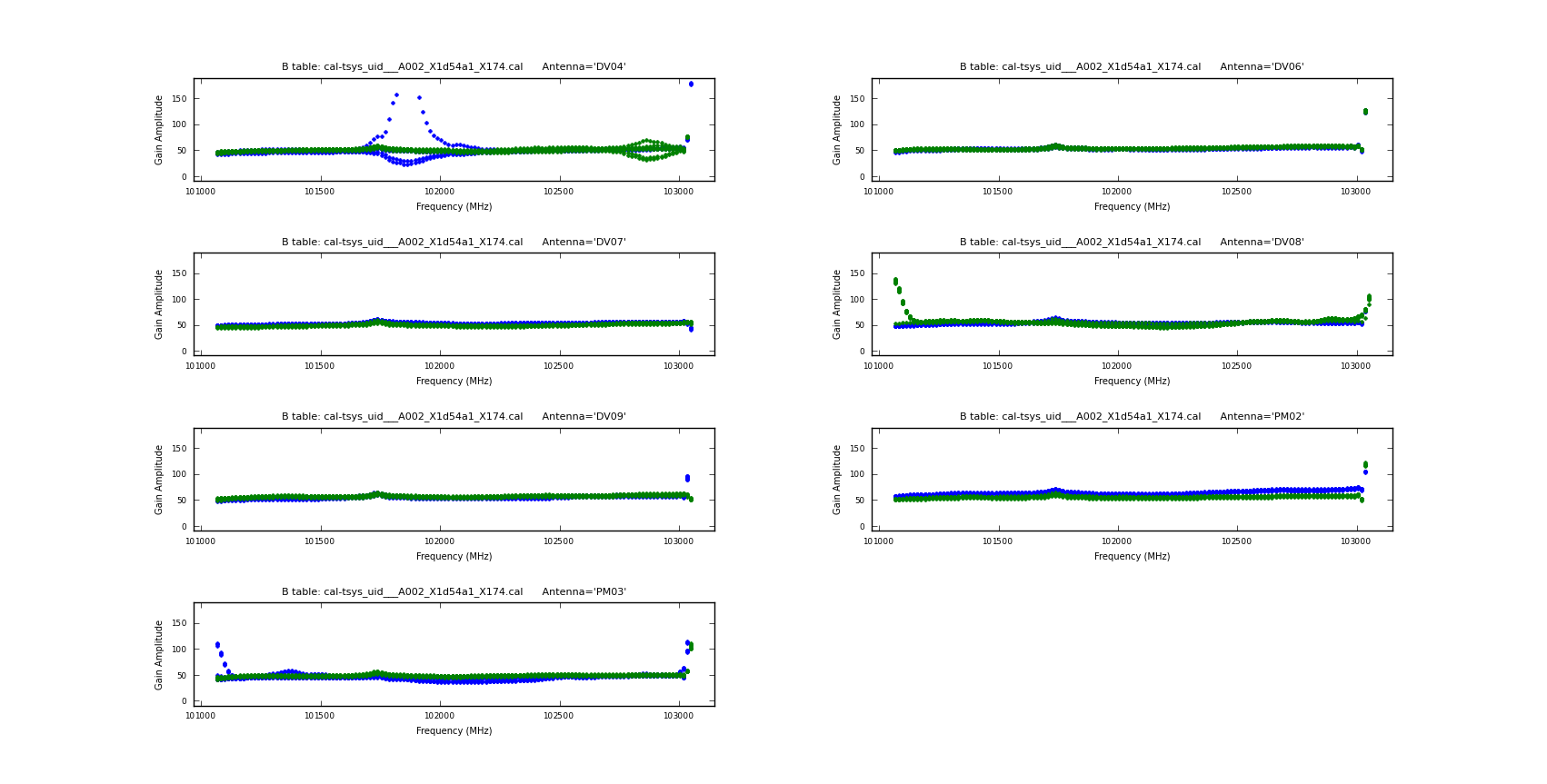
# In CASA
for spw in ['1','3','5','7']:
for name in basename:
plotcal(caltable='cal-tsys_'+name+'.cal', xaxis='freq', yaxis='amp',
spw=spw, subplot=421, overplot=False,
iteration='antenna', plotrange=[0, 0, 40, 180], plotsymbol='.',
figfile='cal-tsys_per_spw_'+spw+'_'+name+'.png')
Note that we only plot the spectral windows that contain the spectral line data. In addition to plotting on your screen, the above command will also produce a plot file (png) for each of the datasets and spectral windows. An example plot is shown to the right for uid___A002_X1d54a1_X174.ms.
Upon examination of these plots, we see that for uid___A002_X1d54a1_X174.ms, there is a outlying feature in spw=7, antenna DV04. This feature occurs during scans 5 and 9, so we flag those data with the following command:
# In CASA
flagdata(vis='uid___A002_X1d54a1_X174_K_WVR.ms', mode='manualflag',
antenna='DV04', flagbackup = T, scan='5,9', spw='7')
Aside from the large amplitudes in the edge channels (which we will handle below), the plots look acceptable. Note that in the lowest spectral window ID (spw 1), Tsys rises toward higher frequencies. This is due to a spectral line from O2 at 117 GHz.
We will apply the Tsys tables with applycal. We do this for each field separately so that the appropriate calibration data are applied to the right fields. The "field" parameter specifies the field to which we will apply the calibration, and the "gainfield" parameter specifies the field from which we wish to take the calibration solutions from the gaintable.
# In CASA
for name in basename:
for field in ['Titan','1037*','NGC*']:
applycal(vis=name+'_K_WVR.ms', spw='1,3,5,7', flagbackup=F, field=field, gainfield=field,
interp='nearest', gaintable=['cal-tsys_'+name+'.cal'])
Without giving the full recipe here, we suggest at this point that you use plotms to plot channel-averaged amplitudes as a function of time, comparing the DATA and CORRECTED columns after applying the Tsys correction. This way you can check that calibration has done what was expected, which is put the data onto the Kelvin temperature scale.
We then once again split out the CORRECTED data column, this time only retaining spectral windows 1,3,5,7. This will get rid of the extraneous spectral windows, including the channel averaged spectral windows and spw 0, which is the one that contained the WVR data.
# In CASA
for name in basename:
os.system('rm -rf '+name+'_line.ms*')
split(vis=name+'_K_WVR.ms', outputvis=name+'_line.ms',
datacolumn='corrected', spw='1,3,5,7')
The WVR and Tsys tables are now applied in the DATA column of the new measurement sets. These datasets have the extension "_line" to indicate that they only contain the spectral line data and no longer the "channel average" spectral windows. These measurement sets therefore have four spectral windows, with IDs 0-3.
Now that we have applied the Tsys calibration and WVR corrections, we can concatenate the six individual data sets into one big measurement set. We define an array "comvis" that contains the names of the measurement sets we wish to concatenate, and then we run the task concat.
# In CASA
comvis=[]
for name in basename:
comvis.append(name+'_line.ms')
os.system('rm -rf ngc3256_line.ms*')
concat(vis=comvis, concatvis='ngc3256_line.ms')
We run a listobs on the resulting concatenated data set to check contains the fields, spectral windows and observing times that we expected:
# In CASA
listobs('ngc3256_line.ms')
There are now only four spectral windows left:
2011-05-24 07:41:21 INFO listobs 0 128 TOPO 113211.988 15625 2000000 113204.175 XX YY 2011-05-24 07:41:21 INFO listobs 1 128 TOPO 111450.813 15625 2000000 111443 XX YY 2011-05-24 07:41:21 INFO listobs 2 128 TOPO 101506.187 15625 2000000 101514 XX YY 2011-05-24 07:41:21 INFO listobs 3 128 TOPO 103050.863 15625 2000000 103058.675 XX YY
and eight antennas have been used in total:
2011-05-24 07:41:21 INFO listobs Antennas: 8: 2011-05-24 07:41:21 INFO listobs ID Name Station Diam. Long. Lat. 2011-05-24 07:41:21 INFO listobs 0 DV04 J505 12.0 m -067.45.18.0 -22.53.22.8 2011-05-24 07:41:21 INFO listobs 1 DV06 T704 12.0 m -067.45.16.2 -22.53.22.1 2011-05-24 07:41:21 INFO listobs 2 DV07 J510 12.0 m -067.45.17.8 -22.53.23.5 2011-05-24 07:41:21 INFO listobs 3 DV08 T703 12.0 m -067.45.16.2 -22.53.23.9 2011-05-24 07:41:21 INFO listobs 4 DV09 N602 12.0 m -067.45.17.4 -22.53.22.3 2011-05-24 07:41:21 INFO listobs 5 PM02 T701 12.0 m -067.45.18.8 -22.53.22.2 2011-05-24 07:41:21 INFO listobs 6 PM03 J504 12.0 m -067.45.17.0 -22.53.23.0 2011-05-24 07:41:21 INFO listobs 7 DV10 N606 12.0 m -067.45.17.1 -22.53.23.6
Additional Data Inspection
Now that the data are concatenated into one dataset, we will do some additional inspection with plotms. First we will plot amplitude versus channel, averaging over time and baselines in order to speed up the plotting process.
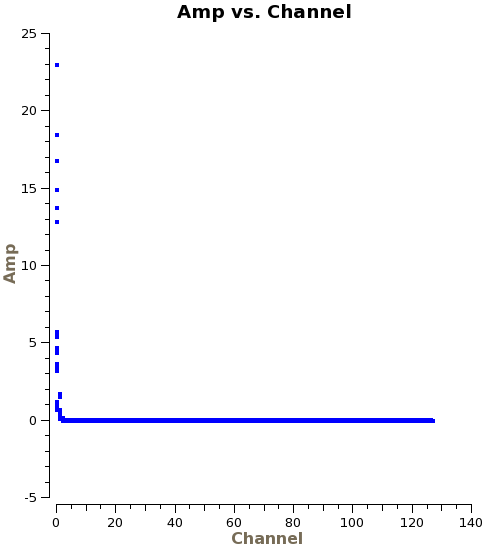
# In CASA
plotms(vis='ngc3256_line.ms', xaxis='channel', yaxis='amp',
averagedata=T, avgbaseline=T, avgtime='1e8', avgscan=T)
From this plot we see that the edge channels have abnormally high amplitudes. We will use flagdata to remove the edge channels from both sides of the bandpass:
# In CASA
flagdata(vis='ngc3256_line.ms', flagbackup=T, spw=['*:0~16','*:125~127'])
Next, we will look at amplitude versus time, averaging over all channels and colorizing by field. Since the observations take place over two days, you will need to zoom in to examine the data in more detail. In particular, note the difference in Titan's amplitude between the two days and the change in amplitude during the second day. The plot on the right shows a zoom-in on the first day of observations, only showing spw 1 in this case. Scans on Titan are colored red, NGC3256 is orange, and the calibrator 1037-295 is colored black. If you select other spws, you can see some outlying points, which will be flagged later on.
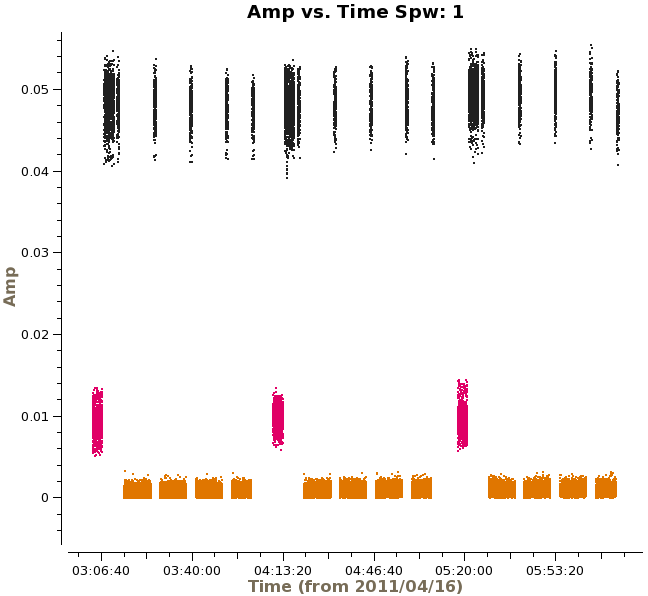
# In CASA
plotms(vis='ngc3256_line.ms', xaxis='time', yaxis='amp',
averagedata=T, avgchannel='128', coloraxis='field',
iteraxis='spw')
Titan is our primary flux calibrator. However, for the second day of observations, Titan had moved too close to Saturn, and Saturn's rings moved into the primary beam. Another way to see this is to plot amplitude versus uv-distance and colorize by scan:
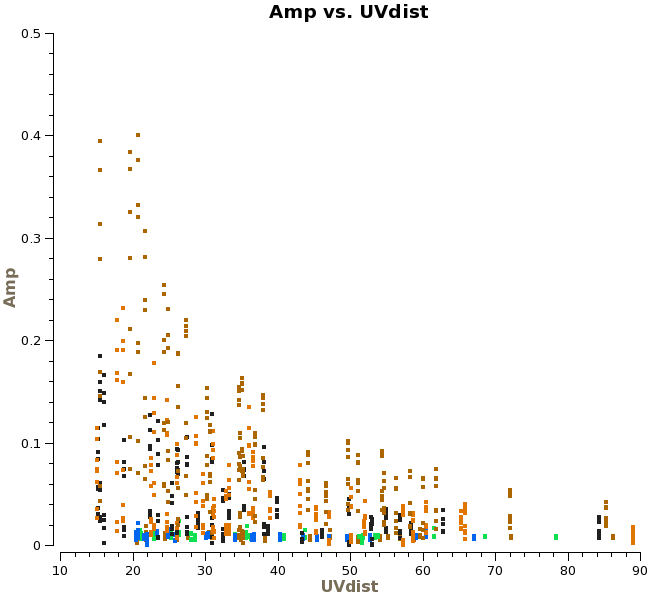
# In CASA
plotms(vis='ngc3256_line.ms', xaxis='uvdist', yaxis='amp', field='Titan',
averagedata=T, avgchannel='128', avgtime='1e8', coloraxis='scan')
If you use the "Mark a region" and "Locate" tools in plotms, you will see the signature of a bright, resolved source during the latter three (last day's) scans. We will therefore need to flag the Titan scans for the second day:
# In CASA
flagdata(vis = 'ngc3256_line.ms', flagbackup = T,
timerange='>2011/04/16/12:00:00', field='Titan')
We also find that during the first day, the Titan observations in spw 2 and 3 are also affected by Saturn. These spectral windows are at lower frequencies and therefore correspond to slightly larger primary beams. This results in Saturn just being picked up in spw 2 and 3, but not in spw 0 and 1. We do not flag these data here, but have to take this effect into account when we do the flux calibration later.
Next, we will fix the position of Titan in the combined dataset. Recall that the position of the Titan field is currently set to 00:00:00.0000 +00.00.00.0000. The following procedure will replace this with the actual mean position observed by the telescopes and, at the same time, it will recalculate the uvw coordinates.
If you are running casa revision r15777 or newer, fixplanets() is already defined as a task. However, if you are using an older revision, then you must first initialize this script with this command:
execfile(casadef.python_library_directory+'/recipes/fixplanets.py')
Now fix the position of Titan:
# In CASA
fixplanets(vis='ngc3256_line.ms', field='Titan', fixuvw=True)
The third parameter in fixplanets, set to True, indicates that the uvw-coordinates for Titan are recalculated. Note that for Cycle 0 data, the coordinates of ephemeris objects will be treated correctly in the data.
Now check to see that the coordinates for Titan have been corrected:
2011-05-31 19:19:41 INFO listobs ID Code Name RA Decl Epoch SrcId nVis 2011-05-31 19:19:41 INFO listobs 0 none 1037-295 10:37:16.0790 -29.34.02.8130 J2000 0 61440 2011-05-31 19:19:41 INFO listobs 1 none Titan 12:51:24.5886 -02.31.59.7035 J2000 1 25344 2011-05-31 19:19:41 INFO listobs 2 none NGC3256 10:27:51.6000 -43.54.18.0000 J2000 2 239616
Continue to inspect the data with plotms, plotting different axes and colorizing by the different parameters. Don't forget to average the data if possible to speed the plotting process. You will find the following:
- Baselines with DV07 have very high amplitudes in spw 3, correlation YY
- Baselines with DV08 have very low amplitudes in spw 3, correlation YY, but only for the last observation
- Baselines with PM03 have low amplitudes at 2011/04/17/02:15:00 for spw 0
- Baselines with PM03 have low amplitudes at 2011/04/16/04:15:15 for spw 2 and 3
- For the second day, the baseline DV10-PM03 is corrupted
The times to insert in flagdata can be obtained using plotms Tools Hover/Display. Instead of using the following flagdata commands, you can also flag by hand in plotms. To do this, select your bad data by clicking on the 'Mark Regions" button, then on 'Flag".
We flag the bad data with the following commands:
# In CASA
flagdata(vis='ngc3256_line.ms', flagbackup=T, spw='3',
correlation='YY', mode='manualflag', selectdata=T,
antenna='DV07', timerange='')
# In CASA
flagdata(vis='ngc3256_line.ms', flagbackup=T, spw='3',
correlation='YY', mode='manualflag', selectdata=T,
antenna='DV08', timerange='>2011/04/17/03:00:00')
# In CASA
flagdata(vis='ngc3256_line.ms', flagbackup=T, spw='0',
correlation='', mode='manualflag', selectdata=T,
antenna='PM03', timerange='2011/04/17/02:15:00~02:15:50')
# In CASA
flagdata(vis='ngc3256_line.ms', flagbackup=T, spw='2,3',
correlation='', mode='manualflag', selectdata=T,
antenna='PM03', timerange='2011/04/16/04:13:50~04:18:00')
# In CASA
flagdata(vis='ngc3256_line.ms', flagbackup=T, spw='',
correlation='', mode='manualflag', selectdata=T,
antenna='PM03&DV10', timerange='>2011/04/16/15:00:00')
Bandpass Calibration
We are now ready to begin the bandpass calibration. First, we will inspect the bandpass calibrator by plotting the phase as a function of frequency and time. For the first plot we use avgscan=T and avgtime='1E6' to average in time over all scans, and we specify coloraxis='baseline' to colorize by baseline. For the second, we use spw='0:30~90' and avgchannel='128' to average over the central 61 channels of the first spectral window. For both plots we will iterate on antenna, so you will need to use the green arrows at the bottom of the plotms GUI to view different antennas.
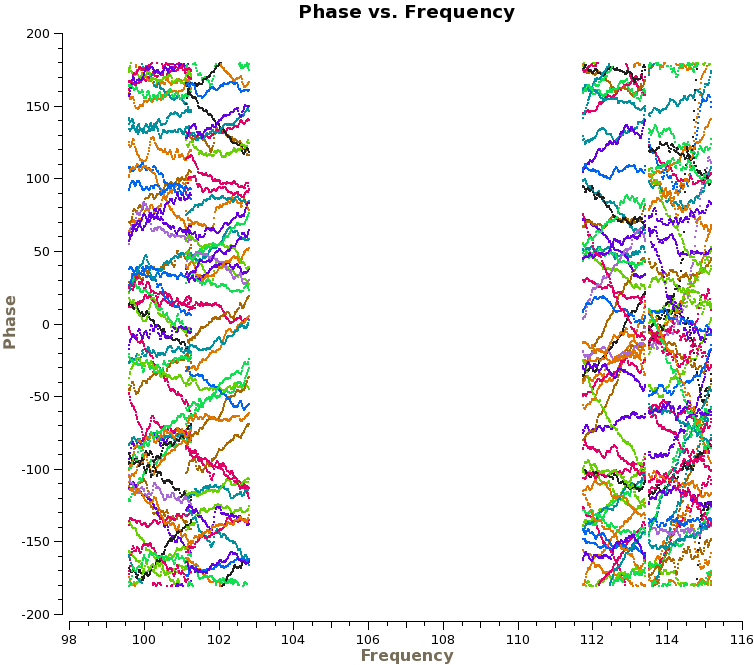
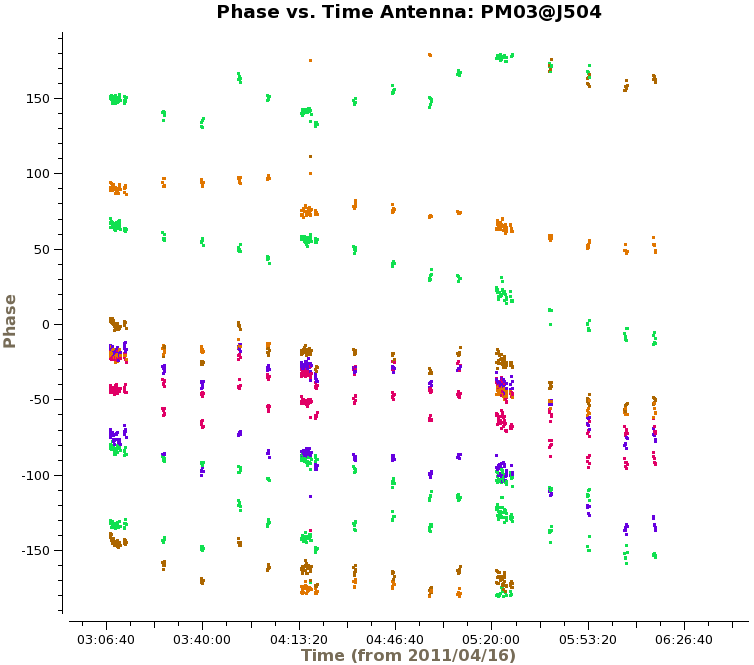
# In CASA
plotms(vis='ngc3256_line.ms', xaxis='freq', yaxis='phase', selectdata=True,
field='1037*', avgtime='1E6', avgscan=T, coloraxis='baseline', iteraxis='antenna')
# In CASA
plotms(vis='ngc3256_line.ms', xaxis='time', yaxis='phase', selectdata=True,
field='1037*', spw='0:30~90', avgchannel='128', avgscan=T,
coloraxis='baseline', iteraxis='antenna')
The top plot on the right shows the time-averaged phase as a function of frequency for the calibrator 1037-295, with all baselines shown at once (i.e., without iteraxis='antenna') for presentation purposes. We see that the phase variations across the spectral windows are modest, typically ~30 degrees. The second plot shows how the phase varies as function of time. For clarity, we only show baselines with one antenna and only for the first day of observations. There are clearly phase variations on short time scales that we wish to correct for before calculating the bandpass solutions.
Hence, we run gaincal on the bandpass calibrator to determine phase-only gain solutions. We will use solint='int' for the solution interval, which means that one gain solution will be determined for every integration time. This short integration time is possible because the bandpass calibrator is a very bright point source, so we have very high signal-to-noise and a perfect model. This will correct for any phase variations in the bandpass calibrator as a function of time, a step which will prevent decorrelation of the vector-averaged bandpass solutions. We will then apply these solutions on-the-fly when we run bandpass.
We will use the average of channels 40 to 80 to increase our signal-to-noise in the determination of the antenna-based phase solutions. Averaging over a subset of channels near the center of the bandpass is acceptable when the phase variation as a function of channel is small, which it is here. For our reference antenna, we choose DV04. We call the output calibration table "cal-ngc3256.G1".
# In CASA
gaincal(vis='ngc3256_line.ms', caltable='cal-ngc3256.G1', spw='*:40~80', field='1037*',
selectdata=T, solint='int', refant='DV04', calmode='p')
We then check the time variations of the phase solutions with plotcal. We will plot the XX and YY polarization products separately and make different subplots for each of the spectral windows. This is done by setting the "iteration" parameter to "spw" and specifying subplot=221. By setting the parameter "figfile" to a non-blank value, it will also generate png files of the plots.
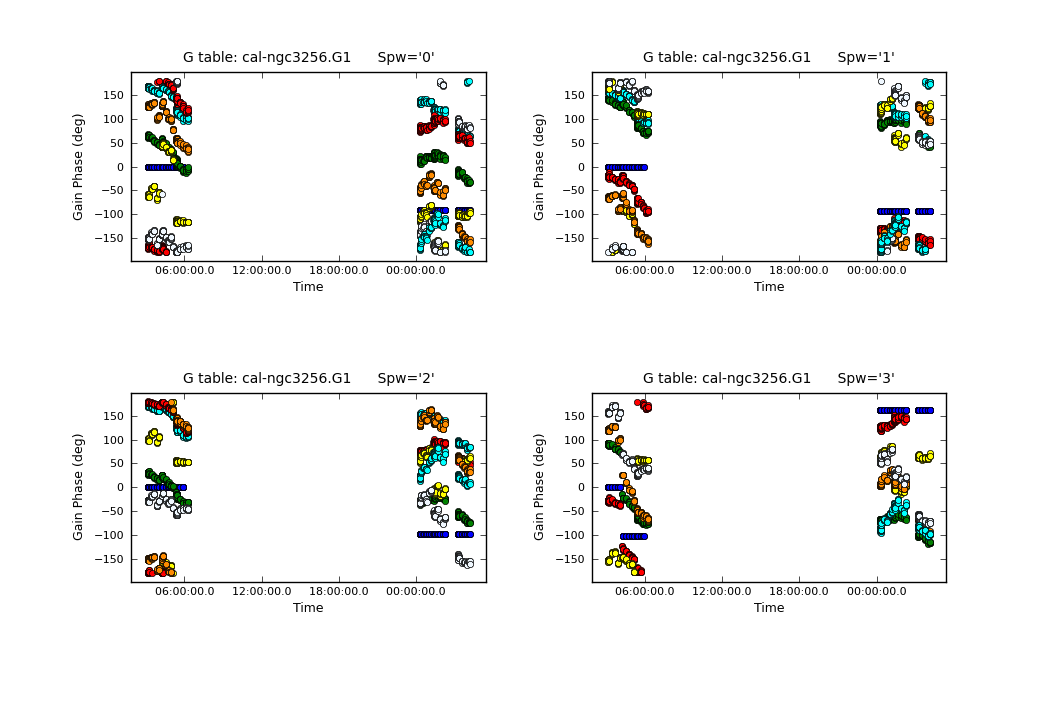
# In CASA
plotcal(caltable = 'cal-ngc3256.G1', xaxis = 'time', yaxis = 'phase',
poln='X', plotsymbol='o', plotrange = [0,0,-180,180], iteration = 'spw',
figfile='cal-phase_vs_time_XX.G1.png', subplot = 221)
# In CASA
plotcal(caltable = 'cal-ngc3256.G1', xaxis = 'time', yaxis = 'phase',
poln='Y', plotsymbol='o', plotrange = [0,0,-180,180], iteration = 'spw',
figfile='cal-phase_vs_time_YY.G1.png', subplot = 221)
If you examine the solutions closely, you may notice some phase jumps. (For example: Correlation XX, spw 3, antenna DV09). These jumps occur between the individual observing blocks and will thus not affect the science data. Other than that, the solutions look reasonable.
Now that we have a first measurement of the phase variations as a function of time, we can determine the bandpass solutions with bandpass. We will apply the phase calibration table on-the-fly with the parameter "gaintable". Now that the phases are corrected, the data can be time-averaged over longer intervals to maximise SNR in each individual channel. We determine bandpass solutions for both days separately because we find that for some antennas, the response across the bandwidth has changed slightly in between the two sessions. We first calculate the bandpass solution for the first day. Do not worry about the message "Insufficient unflagged antennas", which relates to the flagged edge channels.
# In CASA
bandpass(vis = 'ngc3256_line.ms', caltable = 'cal-ngc3256.B1',
gaintable = 'cal-ngc3256.G1', timerange='<2011/04/16/15:00:00',
field = '1037*', minblperant=3, minsnr=2, solint='inf', combine='scan',
bandtype='B', fillgaps=1, refant = 'DV04', solnorm = T)
- caltable = 'cal-ngc3256.B1': Output bandpass calibration table
- gaintable = 'cal-ngc3256.G1': Gain calibration table to apply
- minblperant=3: Minimum number of baselines required per antenna for each solve
- minsnr=2: Minimum SNR for solutions
- solint='inf': This setting, combined with the default combine='scan', sets the solution interval to the entire observation
- combine='scan': The solutions cross scans
- timerange='<2011/04/16/15:00:00': Only determine solutions for the first day
- bandtype='B': The default type of bandpass solution, which does a channel by channel solution for each specified spw
- fillgaps=1: Interpolate channel gaps 1 channel wide
- solnorm=T: Normalize the bandpass amplitudes and phases of the corrections to unity
And then append the solutions (append=True) for the second day:
# In CASA
bandpass(vis = 'ngc3256_line.ms', caltable = 'cal-ngc3256.B1',
gaintable = 'cal-ngc3256.G1', timerange='>2011/04/16/15:00:00',
field = '1037*', minblperant=3, minsnr=2, solint='inf', combine='scan',
bandtype='B', fillgaps=1, refant = 'DV04', solnorm = T, append=True)
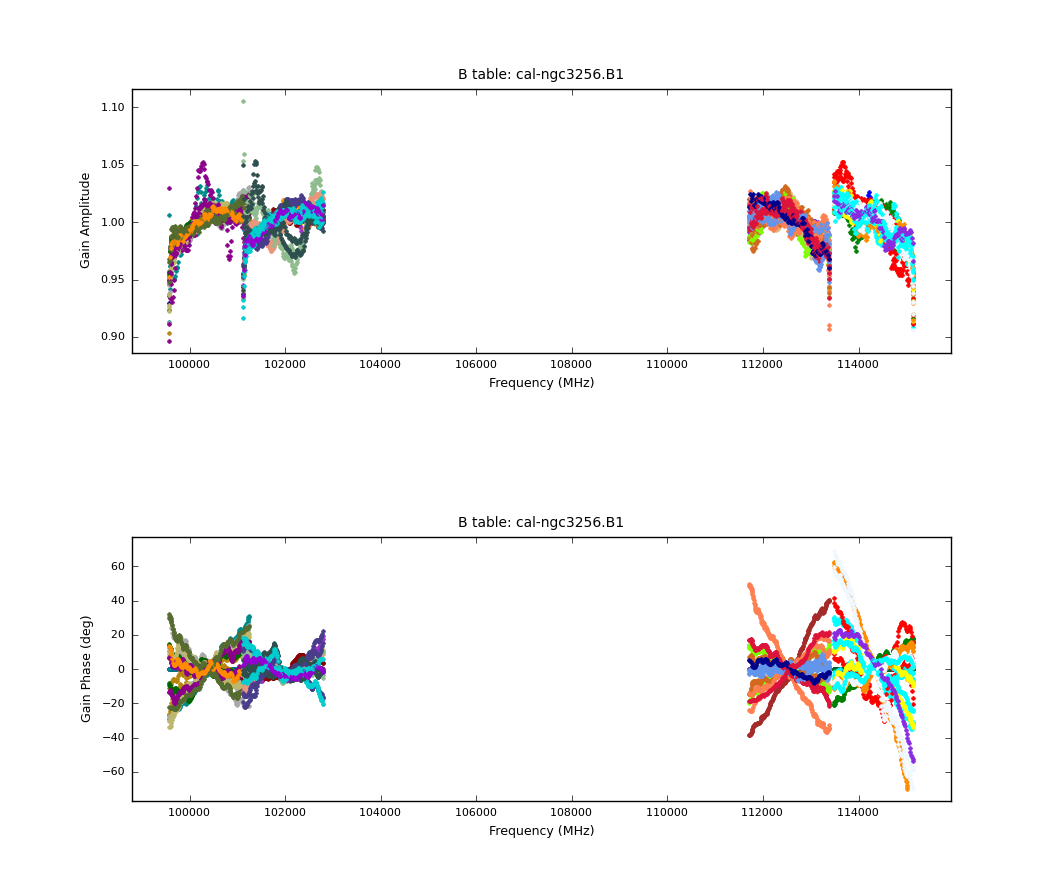
We then plot the bandpass solutions with the following commands:
# In CASA
plotcal(caltable = 'cal-ngc3256.B1', xaxis='freq', yaxis='phase', spw='',
subplot=212, overplot=False, plotrange = [0,0,-70,70],
plotsymbol='.', timerange='')
# In CASA
plotcal(caltable = 'cal-ngc3256.B1', xaxis='freq', yaxis='amp', spw='',
subplot=211, overplot=False,
figfile='bandpass.B1.png', plotsymbol='.', timerange='')
The solutions seem reasonable, so we will now apply them on-the-fly during gain calibration.
Gain Calibration
The first step is to set the flux density for Titan using the task setjy. We will use the Butler-JPL-Horizons 2010 model:
# In CASA
setjy(vis='ngc3256_line.ms', field='Titan', standard='Butler-JPL-Horizons 2010',
spw='0,1,2,3')
The flux density of Titan is 370 mJy at 114 GHz (spw 0) and drops to 288 mJy at 101 GHz (spw 2):
2011-05-24 08:35:08 INFO setjy Titan spwid= 0 [I=0.37, Q=0, U=0, V=0] Jy, (JPL-Butler Solar System Object) 2011-05-24 08:35:08 INFO setjy Titan spwid= 1 [I=0.3588, Q=0, U=0, V=0] Jy, (JPL-Butler Solar System Object) 2011-05-24 08:35:09 INFO setjy Titan spwid= 2 [I=0.2878, Q=0, U=0, V=0] Jy, (JPL-Butler Solar System Object) 2011-05-24 08:35:10 INFO setjy Titan spwid= 3 [I=0.2966, Q=0, U=0, V=0] Jy, (JPL-Butler Solar System Object)
Now we will do a new gain calibration, this time applying the bandpass calibration solutions on-the-fly. We solve for amplitude and phase simultaneously and determine average solutions per scan:
# In CASA
gaincal(vis = 'ngc3256_line.ms', caltable = 'cal-ngc3256.G2', spw =
'*:16~112', field = '1037*,Titan', minsnr=1.0,
solint= 'inf', selectdata=T, solnorm=False, refant = 'DV04',
gaintable = 'cal-ngc3256.B1', calmode = 'ap')
- caltable = 'cal-ngc3256.G2': the output gain calibration table
- minsnr=1.0: To reject solutions with a signal-to-noise less than 1.0
- calmode = 'ap': To solve for amplitude and phase
- spw='*:16~112': to select all spectral windows, but only the inner 75% of the channels of each
- solint='inf': Together with the default for the "combine" parameter, this setting will solve for one solution per scan
- solnorm=F: We do not want to normalize the solutions to unity since we wish to relate the measured amplitudes of the secondary calibrator (1037-295) to the flux calibrator (Titan)
- gaintable = ['cal-ngc3256.B1']: We apply the bandpass calibration on-the-fly
Now we will examine the amplitude and phase solutions as a function of time, iterating on spectral window and plotting the XX and YY correlations separately for clarity. Zoom in on the GUI to examine the plots in more detail. You can also use the "Mark Region" and "Locate" buttons on the toolbar to identify points. Use the field parameter to select which calibrator you want to plot the solutions for.
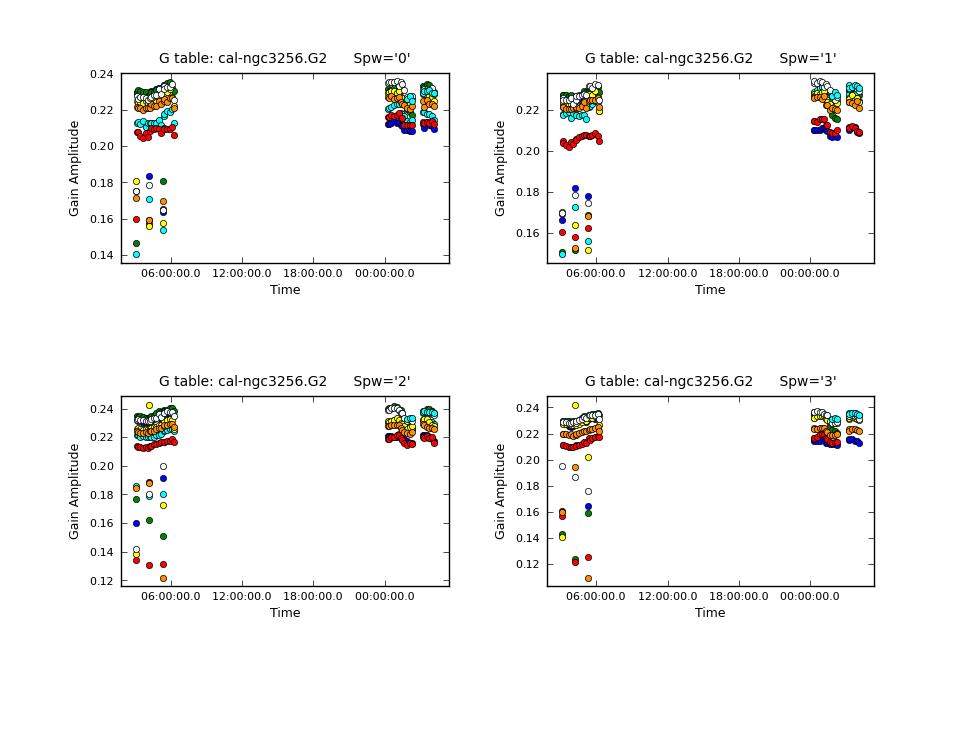
# In CASA
plotcal(caltable = 'cal-ngc3256.G2', xaxis = 'time', yaxis = 'phase',
poln='X', plotsymbol='o', plotrange = [0,0,-180,180], iteration= 'spw',
figfile='cal-phase_vs_time_XX.G2.png', subplot = 221)
# In CASA
plotcal(caltable = 'cal-ngc3256.G2', xaxis = 'time', yaxis = 'phase',
poln='Y', plotsymbol='o', plotrange = [0,0,-180,180], iteration= 'spw',
figfile='cal-phase_vs_time_YY.G2.png', subplot = 221)
# In CASA
plotcal(caltable = 'cal-ngc3256.G2', xaxis = 'time', yaxis = 'amp',
poln='X', plotsymbol='o', plotrange = [], iteration = 'spw',
figfile='cal-amp_vs_time_XX.G2.png', subplot = 221)
# In CASA
plotcal(caltable = 'cal-ngc3256.G2', xaxis = 'time', yaxis = 'amp',
poln='Y', plotsymbol='o', plotrange = [], iteration = 'spw',
figfile='cal-amp_vs_time_YY.G2.png', subplot = 221)
We find very stable amplitude solutions for the phase calibrator. The lower points for the first day are the solutions for Titan.
Finally, we will bootstrap the flux density of the secondary calibrator from that of Titan using the task fluxscale. The new flux table cal-ngc3256.G2.flux replaces the previous cal-ngc3256.G2 table in future application of the calibration to the data, i.e. the new flux table contains both cal-ngc3256.G2 and the newly acquired flux scaling. Unlike the gain calibration steps, this is not an incremental table.
# In CASA
fluxscale( vis="ngc3256_line.ms", caltable="cal-ngc3256.G2",
fluxtable="cal-ngc3256.G2.flux", reference="Titan",
transfer="1037*", refspwmap=[0,1,1,1])
Note that we previously flagged the Titan scans from the second day due to contamination from nearby Saturn's rings. We have therefore used the Titan scans from the first day alone to flux calibrate both days' observations. This would not always be an acceptable solution; however, in this case, examination of the measured amplitudes for the phase calibrator over both days indicate that the flux scale is relatively stable.
Also note that we have used refspwmap=[0,1,1,1]. This means that the 1037-295 observations in spw 2 and 3 are referenced to Titan observations observed in spw 1. We have to do this here because the Titan data in spw 2 and 3 are contaminated by Saturn, as explained above.
The logger produces the following output:
2011-05-31 21:32:31 INFO fluxscale Flux density for 1037-295 in SpW=0 is: 1.81638 +/- 0.0179226 (SNR = 101.346, nAnt= 7) 2011-05-31 21:32:31 INFO fluxscale Flux density for 1037-295 in SpW=1 is: 1.81967 +/- 0.0149109 (SNR = 122.037, nAnt= 7) 2011-05-31 21:32:31 INFO fluxscale Flux density for 1037-295 in SpW=2 (ref SpW=1) is: 1.90794 +/- 0.0155891 (SNR = 122.389, nAnt= 7) 2011-05-31 21:32:31 INFO fluxscale Flux density for 1037-295 in SpW=3 (ref SpW=1) is: 1.86595 +/- 0.0153365 (SNR = 121.668, nAnt= 6)
We find that the flux density of 1037-295 is ~1.8 Jy in the higher frequency spectral windows and ~1.9 Jy in the lower frequency spectral windows. This fluxes agree very well with the 3mm measurements from the ATCA and OVRO of a few years ago (see SMA calibrator list).
Applying the calibrations
Now we will use applycal to apply the bandpass and gaincal tables that we generated in the previous sections. First, we will apply the solutions from the secondary calibrator to the science target and the secondary calibrator itself. We want to use the solutions from the secondary calibrator for the science target because, as the phase calibrator, it was observed throughout the observations. Its flux scale has also now been bootstrapped to that of the flux calibrator, so it can serve as an amplitude and phase calibrator. The application of the solutions to the secondary calibrator itself is a way for us to check the quality of the calibration. Below, we will do the same for the flux calibrator (Titan), applying its amplitude and phase solutions to itself to check the calibration.
# In CASA
applycal( vis='ngc3256_line.ms', flagbackup=F, field='NGC*,1037*',
interp=['nearest','nearest'], gainfield = ['1037*', '1037*'],
gaintable=['cal-ngc3256.G2.flux', 'cal-ngc3256.B1'])
- gaintable=['cal-ngc3256.G2.flux', 'cal-ngc3256.B1']: We apply the gaincal table with the correct flux scaling and the bandpass table
- gainfield = ['1037*', '1037*']: We use the solutions from the secondary calibrator (1037-295) in both tables
- interp='nearest': We opt for interpolation mode "nearest"
- flagbackup=F: We do not back up the state of the flags before applying calibration
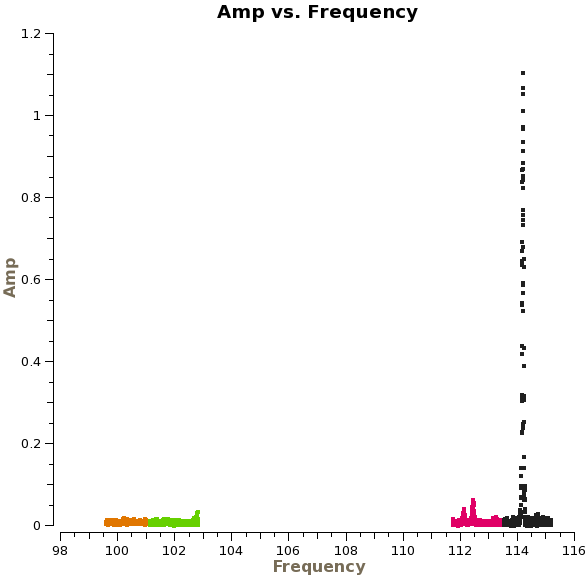
Let's now use plotms to examine the corrected amplitude of NGC3256 as a function of frequency:
# In CASA
plotms(vis='ngc3256_line.ms', xaxis='freq', yaxis='amp',
ydatacolumn='corrected', selectdata=True, field='NGC*',
averagedata=True, avgchannel='', avgtime='10000s',
avgscan=True, avgbaseline=T, coloraxis='spw')
Use the "Zoom" tool to zoom in on the different spectral windows. (Note that spw 2-3 are on the left). There are three emission lines in spectral windows 0-1. There is no emission in spw 2 and 3. Also note that there are still some high channels on the edge of spw 2-3. We will exclude these channels for our subsequent imaging.
It also makes sense to plot the corrected amplitudes and phases of 1037-295 as a function of time and frequency, to check that the phases are close to zero and the amplitudes are constant. The result of the amplitude versus time plot is shown to the right.
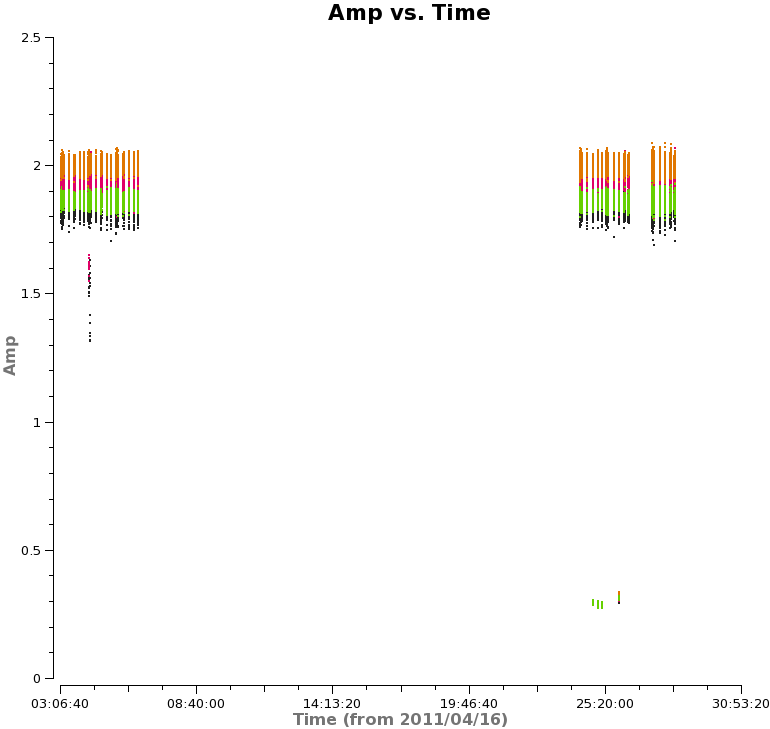
# In CASA
plotms(vis='ngc3256_line.ms', xaxis='time', yaxis='amp',
ydatacolumn='corrected', selectdata=True, field='1037*',
averagedata=True, avgchannel='128', avgtime='',
avgscan=False, avgbaseline=F, coloraxis='spw')
# In CASA
plotms(vis='ngc3256_line.ms', xaxis='freq', yaxis='phase',
ydatacolumn='corrected', selectdata=True, field='1037*',
averagedata=True, avgchannel='', avgtime='1e8',
avgscan=True, avgbaseline=F, coloraxis='baseline')
Based on the inspection of these plots, we identify some bad data and flag them:
# In CASA
flagdata(vis='ngc3256_line.ms', mode='manualflag',
timerange='2011/04/16/04:13:35~04:13:45', flagbackup = T)
tget(flagdata)
timerange='2011/04/16/05:21:13~05:21:19'
flagdata()
timerange='2011/04/16/04:16:40~04:16:49'
flagdata()
timerange='2011/04/16/04:14:00~04:17:10'; antenna='PM03'
flagdata()
timerange='2011/04/17/00:35:30~01:20:20'; antenna='DV04'; spw='3'
flagdata()
Note that in the above command sequence, we utilize the CASA function tget. This function retrieves the last input values for the function specified.
Now that we have flagged some of the calibrator data, we should redo the calibration steps above. We start with a clearcal to reinitialize the calibration columns in ngc3256_line.ms. Specifically, it will set the MODEL data column to unity, and it will set the CORRECTED data column equal to the original DATA column. After the clearcal, the commands are identical to what has been done above. (The improvements in the calibration are only minor, so in principle, one could carry on with making calibrator images and skip the following eight commands.)
# In CASA
clearcal('ngc3256_line.ms')
# In CASA
gaincal(vis='ngc3256_line.ms', caltable='cal-ngc3256.G1n', spw='*:40~80', field='1037*',
selectdata=T, solint='int', refant='DV04', calmode='p')
# In CASA
bandpass(vis = 'ngc3256_line.ms', caltable = 'cal-ngc3256.B1n',
gaintable = 'cal-ngc3256.G1n', timerange='<2011/04/16/15:00:00',
field = '1037*', minblperant=3, minsnr=2, solint='inf', combine='scan',
bandtype='B', fillgaps=1, refant = 'DV04', solnorm = T)
# In CASA
bandpass(vis = 'ngc3256_line.ms', caltable = 'cal-ngc3256.B1n',
gaintable = 'cal-ngc3256.G1n', timerange='>2011/04/16/15:00:00',
field = '1037*', minblperant=3, minsnr=2, solint='inf', combine='scan',
bandtype='B', fillgaps=1, refant = 'DV04', solnorm = T, append=True)
# In CASA
setjy(vis='ngc3256_line.ms', field='Titan', standard='Butler-JPL-Horizons 2010',
spw='0,1,2,3')
# In CASA
gaincal(vis = 'ngc3256_line.ms', caltable = 'cal-ngc3256.G2n', spw =
'*:16~112', field = '1037*,Titan', minsnr=1.0,
solint= 'inf', selectdata=T, solnorm=False, refant = 'DV04',
gaintable = 'cal-ngc3256.B1n', calmode = 'ap')
# In CASA
fluxscale( vis="ngc3256_line.ms", caltable="cal-ngc3256.G2n",
fluxtable="cal-ngc3256.G2n.flux", reference="Titan",
transfer="1037*", refspwmap=[0,1,1,1])
# In CASA
applycal( vis='ngc3256_line.ms', flagbackup=F, field='NGC*,1037*',
interp=['nearest','nearest'], gainfield = ['1037*', '1037*'],
gaintable=['cal-ngc3256.G2n.flux', 'cal-ngc3256.B1n'])
Having redone the calibration, we will again look at amplitude and phase versus time to check that the amplitudes are stable and the phases are close to zero.
# In CASA
plotms(vis='ngc3256_line.ms', xaxis='time', yaxis='amp',
ydatacolumn='corrected', selectdata=True, field='1037*',
averagedata=True, avgchannel='128', avgtime='',
avgscan=False, avgbaseline=F, coloraxis='spw')
# In CASA
plotms(vis='ngc3256_line.ms', xaxis='freq', yaxis='phase',
ydatacolumn='corrected', selectdata=True, field='1037*',
averagedata=True, avgchannel='', avgtime='1e8',
avgscan=True, avgbaseline=F, coloraxis='baseline')
-
Corrected amplitude vs. time
-
Corrected phase vs. frequency
In the first plot we show amplitude vs time, colorized by spectral window. This shows very clearly that the amplitude is constant in time, but varies as a function of frequency, which is intrinsic to the source. The second plot shows that the phases are very flat across all spectral windows.
Imaging the Calibrators
At this point, we will image the secondary calibrator as a check of our calibration. We do this using the task clean, after first removing any previous versions of the images that may exist in our directory. This is an important precaution, since if the image already exists, CASA will clean it further instead of producing a new image. In this clean run, we choose to use Multi-Frequency Synthesis (mfs) with nterms=2, which implies that the algorithm determines the continuum map and the spectral index map simultaneously. This is required here, because we found with fluxscale that the flux of 1037-295 increases significantly toward lower frequencies. Therefore, assuming a 'flat' spectral index would not give a good result. Do not be alarmed to see this message: "Multi-term MFS imaging algorithm is new and under active development and testing". The method is working fine and has been tested.
# In CASA
os.system('rm -rf result-phasecal_cont*')
clean(vis='ngc3256_line.ms', imagename='result-phasecal_cont', field='1037*',
spw='*:20~120', selectdata=T, mode='mfs', niter=500,
gain=0.1, threshold='0.75mJy', psfmode='hogbom',
interactive=False, mask=[62, 62, 67, 67], imsize=128,
cell='1arcsec', weighting='briggs', robust=0.0, nterms=2)
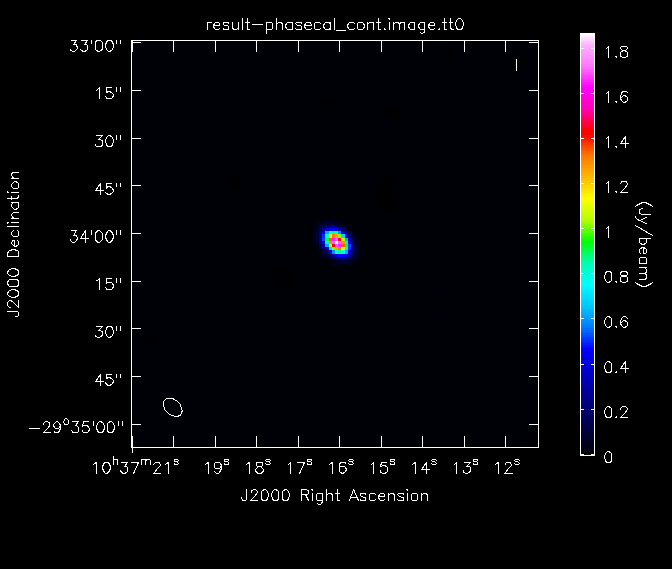
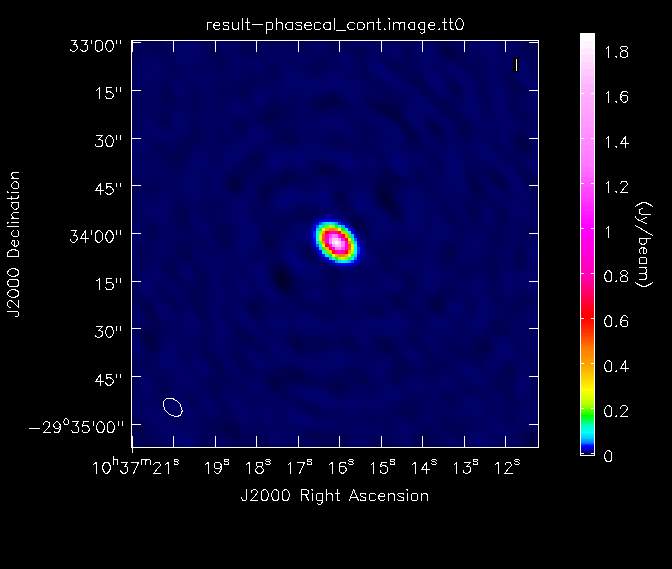
- imagename='result-phasecal_cont': the base name of the output images
- spw='*:20~120': We image all spectral windows, ignoring the outermost channels of each
- mode='mfs': Mult-Frequency Synthesis: the default mode, which produces one image from all the specified data combined
- nterms=2: The number of Taylor terms to be used to model the frequency dependence of the sky emission
- niter=500: Maximum number of clean iterations
- theshold='0.75mJy': Stop cleaning if the maximum residual is below this value. Here we choose a threshold equal to ~1.5 times the rms noise level
- psfmode='hogbom': The method used to calculate the PSF during minor clean cycles. Hogbom is a good choice for poorly-sampled uv-planes
- mask=[62, 62, 67, 67]: Limits the clean component placement to the region of the source. We know the source is compact so we do not need to worry about boxing interactively
- imsize=128, cell='1arcsec': Chosen to appropriately sample the resolution element and cover the primary beam
- weighting='briggs', robust=0.0: a weighting scheme that offers a good compromise between sensitivity and resolution
Note that using nterms=2 makes the clean task considerably slower than before. Once the imaging of the secondary calibrator is complete, we will generate some statistics on the image using the task imstat. Note that clean generates several output images when used with nterms=2. The continuum intensity map has suffix .tt0. The spectral index map has suffix .alpha. For more see http://casa.nrao.edu/docs/UserMan/UserMansu227.html .
# In CASA
calstat=imstat(imagename='result-phasecal_cont.image.tt0', region='', box='85,8,120,120')
rms=(calstat['rms'][0])
print '>> rms in phase calibrator image: '+str(rms)
calstat=imstat(imagename='result-phasecal_cont.image.tt0', region='')
peak=(calstat['max'][0])
print '>> Peak in phase calibrator image: '+str(peak)
print '>> Dynamic range in phase calibrator image: '+str(peak/rms)
Here, we have used the "box" parameter in the first call of imstat to find the image rms in a region away from the strong central point source. The image dynamic range in the calibrator image is ~3100. We will then look at the image of the secondary calibrator with imview.
# In CASA
imview(raster={'file': 'result-phasecal_cont.image.tt0', 'colorwedge':T,
'range':[-0.004, 0.250], 'scaling':-2.5, 'colormap':'Rainbow 2'},
out='result-phasecal_map.png', zoom=1)
This command rasters the image of the phase calibrator to the GUI and outputs the file phasecal_map.png. It uses the Rainbow 2 colomap scheme and includes a colorwedge on the plot. The "range" and "scaling" parameters have been chosen to bring out the weaker features in the map. The calibrator image looks pretty good, from which we conclude that the gain calibration has worked well and we will move on. If the image quality was not acceptable, we would need to flag some more data and redo the calibration to this point.
Now we will apply the calibration to the flux calibrator, Titan, using the time-dependent solutions we derived for Titan itself and the bandpass solutions from 1037*.
# In CASA
applycal(vis='ngc3256_line.ms', flagbackup=F, field='Titan',
interp=['nearest', 'nearest'], gainfield = ['Titan', '1037*'],
gaintable=['cal-ngc3256.G2.flux', 'cal-ngc3256.B1'])
Now we will image the flux calibrator (Titan). See the previous call to clean for a description of the various inputs. This time we will only use spectral windows 0 and 1 because we know that the Titan data in spectral windows 2 and 3 are corrupted by Saturn.
# In CASA
os.system('rm -rf result-ampcal_cont*')
clean(vis='ngc3256_line.ms', imagename='result-ampcal_cont',
field='Titan', spw='0:20~120,1:20~120', mode='mfs', niter=200,
threshold='5mJy', psfmode='hogbom', mask=[62, 62, 67, 67], imsize=128,
cell='1arcsec', weighting='briggs', robust=0.0)
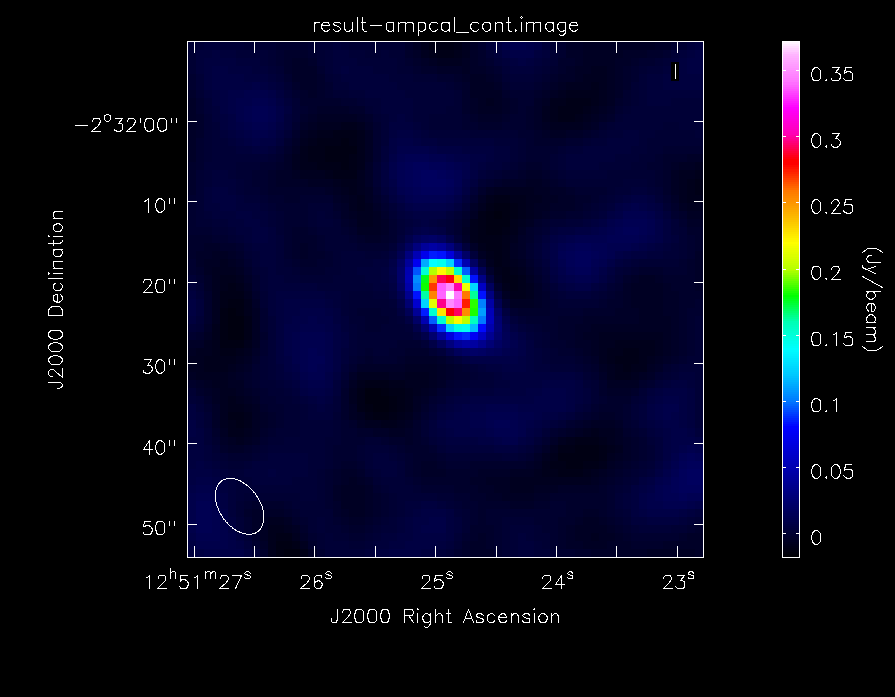
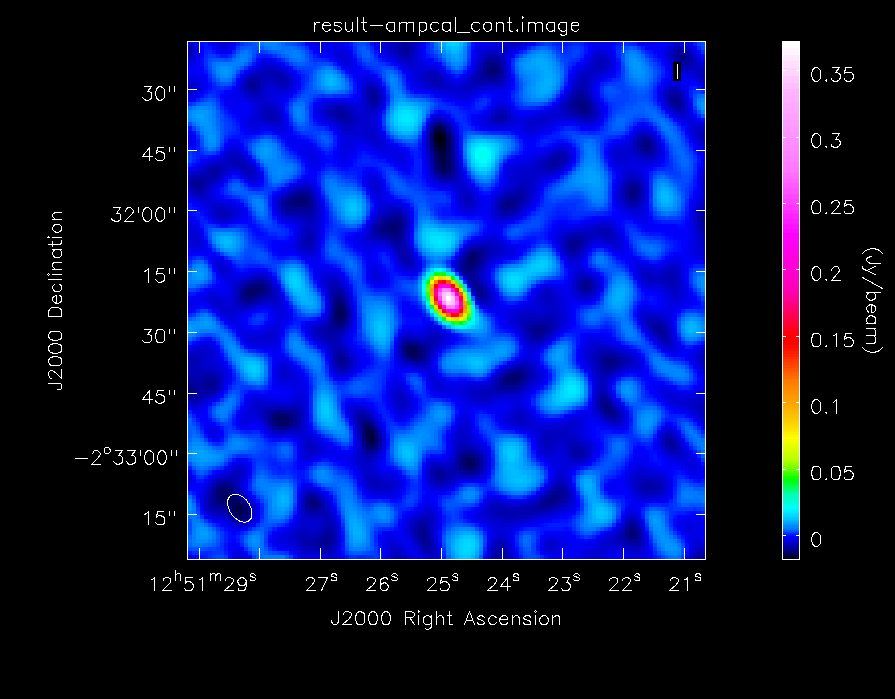
As before, we will generate some statistics on the image:
# In CASA
calstat=imstat(imagename="result-ampcal_cont.image",region="",box="85,8,120,120")
rms=(calstat['rms'][0])
print ">> rms in amp calibrator image: "+str(rms)
calstat=imstat(imagename="result-ampcal_cont.image",region="")
peak=(calstat['max'][0])
print ">> Peak in amp calibrator image: "+str(peak)
print ">> Dynamic range in amp calibrator image: "+str(peak/rms)
The dynamic range in this image is ~74. It's much less than the image of the secondary calibrator because less time was spent observing it (the total on-source time on Titan is only 9 minutes). We will then take a look at the image with imview, again choosing the data range and scaling parameter to bring out weak features in the map:
# In CASA
imview(raster={'file': 'result-ampcal_cont.image', 'colorwedge':T,
'range':[-0.02, 0.250], 'scaling':-1.5, 'colormap':'Rainbow 2'},
out='result-ampcal_map.png', zoom=1)
The image of Titan looks good, which further confirms the quality of the calibration. The last step is to split out the science target, since we no longer need the calibrator data. We run split with field='NGC*' to create ngc3256_line_target.ms:
# In CASA
os.system('rm -rf ngc3256_line_target.ms*')
split(vis='ngc3256_line.ms', outputvis='ngc3256_line_target.ms',
field='NGC*')
This concludes the Calibration section of this CASA Guide. To proceed to the Imaging section, click here: NGC3256 Band3 - Imaging. To go back to the main NGC3256 page, see: NGC3256Band3.
Last checked on CASA Version 3.3.0.