VLA CASA Imaging-CASA6.5.2: Difference between revisions
m Vparekh moved page VLA CASA Imaging-CASA6.4.1 to VLA CASA Imaging-CASA6.5.2 |
|||
| (5 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
<div style="text-align: justify;"> | <div style="text-align: justify;"> | ||
This tutorial provides guidance on imaging procedures in CASA. The tutorial covers basic continuum cleaning and the influence of image weights, as well as wide-band and wide-field imaging techniques, multi-scale clean, an outlier field setup, and primary beam correction. Spectral line imaging procedures are explained but not covered in detail. For a more thorough example of spectral line imaging, refer to the [https://casaguides.nrao.edu/index.php/VLA_high_frequency_Spectral_Line_tutorial_-_IRC%2B10216 VLA high frequency Spectral Line tutorial - IRC+10216]. This imaging tutorial concludes with basic image header calls and the conversion of Jy/beam to K surface brightness units through image arithmetic and header manipulation. In this tutorial, we display all images with the CARTA software. CARTA is the '''C'''ube '''A'''nalysis and '''R'''endering '''T'''ool for '''A'''stronomy, a new tool for image visualization and analysis developed for the VLA, ALMA, and future radio telescopes. CASA is no longer supporting the viewer GUI to display | This tutorial provides guidance on imaging procedures in CASA. The tutorial covers basic continuum cleaning and the influence of image weights, as well as wide-band and wide-field imaging techniques, multi-scale clean, an outlier field setup, and primary beam correction. Spectral line imaging procedures are explained but not covered in detail. For a more thorough example of spectral line imaging, refer to the [https://casaguides.nrao.edu/index.php/VLA_high_frequency_Spectral_Line_tutorial_-_IRC%2B10216 VLA high-frequency Spectral Line tutorial - IRC+10216]. This imaging tutorial concludes with basic image header calls and the conversion of Jy/beam to K surface brightness units through image arithmetic and header manipulation. In this tutorial, we display all images with the CARTA software. CARTA is the '''C'''ube '''A'''nalysis and '''R'''endering '''T'''ool for '''A'''stronomy, a new tool for image visualization and analysis developed for the VLA, ALMA, and future radio telescopes. CASA is no longer supporting the viewer GUI to display images. Hence we encourage users to use the CARTA for image display. For more details about how to use CARTA and open images in it, we refer to the [https://cartavis.org/ CARTA webpage]. | ||
We will be utilizing data taken with the Karl G. Jansky Very Large Array, of a supernova remnant G055.7+3.4. The data were taken on August 23, 2010, in the first D-configuration for which the new wide-band capabilities of the WIDAR (Wideband Interferometric Digital ARchitecture) correlator were available. The 8-hour-long observation includes all available 1 GHz of bandwidth in L-band, from 1 - 2 GHz in frequency. | We will be utilizing data taken with the Karl G. Jansky Very Large Array, of a supernova remnant G055.7+3.4. The data were taken on August 23, 2010, in the first D-configuration for which the new wide-band capabilities of the WIDAR (Wideband Interferometric Digital ARchitecture) correlator were available. The 8-hour-long observation includes all available 1 GHz of bandwidth in the L-band, from 1 - 2 GHz in frequency. | ||
We will skip the calibration process in this guide, as examples of calibration can be found in several other guides, including the | We will skip the calibration process in this guide, as examples of calibration can be found in several other guides, including the | ||
[https://casaguides.nrao.edu/index.php?title=VLA_Continuum_Tutorial_3C391 VLA Continuum Tutorial 3C391] and | [https://casaguides.nrao.edu/index.php?title=VLA_Continuum_Tutorial_3C391 VLA Continuum Tutorial 3C391] and | ||
[https://casaguides.nrao.edu/index.php?title=VLA_high_frequency_Spectral_Line_tutorial_-_IRC%2B10216 VLA high frequency Spectral Line tutorial - IRC+10216] guides. | [https://casaguides.nrao.edu/index.php?title=VLA_high_frequency_Spectral_Line_tutorial_-_IRC%2B10216 VLA high-frequency Spectral Line tutorial - IRC+10216] guides. | ||
A copy of the calibrated data <font color=green>(1.2GB)</font> can be downloaded from [http://casa.nrao.edu/Data/EVLA/SNRG55/SNR_G55_10s.calib.tar.gz http://casa.nrao.edu/Data/EVLA/SNRG55/SNR_G55_10s.calib.tar.gz] | A copy of the calibrated data <font color=green>(1.2GB)</font> can be downloaded from [http://casa.nrao.edu/Data/EVLA/SNRG55/SNR_G55_10s.calib.tar.gz http://casa.nrao.edu/Data/EVLA/SNRG55/SNR_G55_10s.calib.tar.gz] | ||
| Line 39: | Line 39: | ||
<!-- | <!-- | ||
''' 1. Högbom Algorithm '''<br /> | ''' 1. Högbom Algorithm '''<br /> | ||
This algorithm will initially find the strength and position of a peak in a dirty image, subtract it from the dirty image, record this position and | This algorithm will initially find the strength and position of a peak in a dirty image, subtract it from the dirty image, record this position and magnitude, and repeat for further peaks. The remainder of the dirty image is known as the residuals. | ||
The accumulated point sources, now residing in a model, is convolved with an idealized CLEAN beam (usually a Gaussian fitted to the central lobe of the dirty beam), creating a CLEAN image. As the final step, the residuals of the dirty image are then added to the CLEAN image. | The accumulated point sources, now residing in a model, is convolved with an idealized CLEAN beam (usually a Gaussian fitted to the central lobe of the dirty beam), creating a CLEAN image. As the final step, the residuals of the dirty image are then added to the CLEAN image. | ||
''' 2. Clark Algorithm '''<br /> | ''' 2. Clark Algorithm '''<br /> | ||
Clark (1980), developed | Clark (1980), developed an FFT-based CLEAN algorithm, which more efficiently shifts and scales the dirty beam by approximating the position and strength of components using a small patch of the dirty beam. This algorithm is the default within the {{clean}} task, which involves major and minor cycles. | ||
The algorithm will first select a beam patch, which will include the highest exterior sidelobes. Points are then selected from the dirty image, which are up to a fraction of the image peak, and are greater than the highest exterior sidelobe of the beam. It will then conduct a list-based Högbom CLEAN, creating a model and convolution with an idealized CLEAN beam. This process is | The algorithm will first select a beam patch, which will include the highest exterior sidelobes. Points are then selected from the dirty image, which are up to a fraction of the image peak, and are greater than the highest exterior sidelobe of the beam. It will then conduct a list-based Högbom CLEAN, creating a model and convolution with an idealized CLEAN beam. This process is a minor cycle. | ||
The major cycle involves transforming the point source model via | The major cycle involves transforming the point source model via an FFT (Fast-Fourier Transform), multiplying this by the weight sampling function (more on this below), and transforming back. This is then subtracted from the dirty image, creating your CLEAN image. The process is then repeated with subsequent minor cycles. | ||
''' 3. Cotton-Schwab Algorithm '''<br /> | ''' 3. Cotton-Schwab Algorithm '''<br /> | ||
This is the default imager mode (''csclean''), and is a variant of the Clark | This is the default imager mode (''csclean''), and is a variant of the Clark algorithm in which the major cycle involves the subtraction of CLEAN components of ungridded visibility data. This allows the removal of gridding errors, as well as noise. One advantage is its ability to image and clean many separate fields simultaneously. Fields are cleaned independently in the minor cycle, and components from all fields are cleaned together in the major cycles. | ||
This algorithm is faster than the Clark algorithm, except when dealing with a large number of visibility samples, due to the re-gridding process it undergoes. It is most useful in cleaning sensitive high-resolution images at lower frequencies where a number of confusing sources are within the primary beam. | This algorithm is faster than the Clark algorithm, except when dealing with a large number of visibility samples, due to the re-gridding process it undergoes. It is most useful in cleaning sensitive high-resolution images at lower frequencies where a number of confusing sources are within the primary beam. | ||
| Line 66: | Line 66: | ||
[[Image:SNR-G55-uvcoverage-CASA4.5.2.png|400px|thumb|right|'''Figure 2''' <br /> u,v coverage for the 8-hour observation of the supernova remnant G055.7+3.4]] | [[Image:SNR-G55-uvcoverage-CASA4.5.2.png|400px|thumb|right|'''Figure 2''' <br /> u,v coverage for the 8-hour observation of the supernova remnant G055.7+3.4]] | ||
'Weighting' amounts to giving more or less weight to certain visibilities in your data set, based on their location in the uv-plane. Emphasizing long-baseline visibilities improves the resolution of your image, whereas emphasizing shorter baselines improves | 'Weighting' amounts to giving more or less weight to certain visibilities in your data set, based on their location in the uv-plane. Emphasizing long-baseline visibilities improves the resolution of your image, whereas emphasizing shorter baselines improves surface brightness sensitivity. There are three main weighting schemes that are used in interferometry: | ||
1) '''Natural''' weighting: uv cells are weighted based on their rms. Data visibility weights are gridded onto a uv-cell and summed. More visibilities in a cell will thus increase the cell's weight, which will usually emphasize the shorter baselines. Natural weighting therefore results in a better surface brightness sensitivity, but also a larger PSF and therefore degraded resolution. | 1) '''Natural''' weighting: uv cells are weighted based on their rms. Data visibility weights are gridded onto a uv-cell and summed. More visibilities in a cell will thus increase the cell's weight, which will usually emphasize the shorter baselines. Natural weighting, therefore, results in a better surface brightness sensitivity, but also a larger PSF and therefore degraded resolution. | ||
2) '''Uniform''' weighting: The weights are first gridded as in natural weighting but then each cell is corrected such that the weights are independent of the number of visibilities inside. The 'uniform' weighting of the baselines is a better representation of the uv-coverage and sidelobes are more suppressed. Compared to natural weighting, uniform weighting usually emphasizes | 2) '''Uniform''' weighting: The weights are first gridded as in natural weighting but then each cell is corrected such that the weights are independent of the number of visibilities inside. The 'uniform' weighting of the baselines is a better representation of the uv-coverage and sidelobes are more suppressed. Compared to natural weighting, uniform weighting usually emphasizes longer baselines. Consequently, the PSF is smaller, resulting in a better spatial resolution of the image. At the same time, however, the surface brightness sensitivity is reduced compared to natural weighting. | ||
3) '''Briggs''' weighting: This scheme provides a compromise between natural and uniform weighting. The transition can be controlled with the ''robust'' parameter where ''robust=-2'' is close to uniform and ''robust=2'' is close to natural weighting. | 3) '''Briggs''' weighting: This scheme provides a compromise between natural and uniform weighting. The transition can be controlled with the ''robust'' parameter where ''robust=-2'' is close to uniform and ''robust=2'' is close to natural weighting. | ||
Briggs weighting therefore offers a compromise | Briggs weighting, therefore, offers a compromise between spatial resolution and surface brightness sensitivity. Typically, ''robust'' values near zero are used. | ||
Details on the weighting schemes are given in [http://www.aoc.nrao.edu/dissertations/dbriggs/ Daniel Brigg's dissertation (Chapter 3)]. | Details on the weighting schemes are given in [http://www.aoc.nrao.edu/dissertations/dbriggs/ Daniel Brigg's dissertation (Chapter 3)]. | ||
| Line 94: | Line 94: | ||
For uniform weighting, we first grid the inverse variance <math>\omega_i</math> for all selected data onto a grid with uv cell-size given by <math>2/FOV</math> where <math>FOV</math> is the specified field of view (defaults to the image field of view). This forms the gridded weights <math>W_k</math>. The weight of the <math>i</math>-th sample is then:<math>W_i=\omega_i/W_k</math> | For uniform weighting, we first grid the inverse variance <math>\omega_i</math> for all selected data onto a grid with uv cell-size given by <math>2/FOV</math> where <math>FOV</math> is the specified field of view (defaults to the image field of view). This forms the gridded weights <math>W_k</math>. The weight of the <math>i</math>-th sample is then:<math>W_i=\omega_i/W_k</math> | ||
The weight function can be described as <math> W(u,v) = W(u,v) / W_k </math>, where <math> W_k </math> represents the local density of (u,v) points, otherwise known as the gridded weights. This form of weighting will increase the influence of data with lower weight, filling the (u,v) plane more uniformly, thereby reducing sidelobe levels in the field-of-view, but increasing the rms image noise. More weight is given to long baselines, therefore increasing angular resolution. Point source sensitivity is degraded due to the | The weight function can be described as <math> W(u,v) = W(u,v) / W_k </math>, where <math> W_k </math> represents the local density of (u,v) points, otherwise known as the gridded weights. This form of weighting will increase the influence of data with lower weight, filling the (u,v) plane more uniformly, thereby reducing sidelobe levels in the field-of-view, but increasing the rms image noise. More weight is given to long baselines, therefore increasing angular resolution. Point source sensitivity is degraded due to the down weighting of some data. | ||
'''3. Briggs''': A flexible weighting scheme, that is a variant of uniform, and avoids giving too much weight to (u,v) points with a low natural weight. Weight function can be described as | '''3. Briggs''': A flexible weighting scheme, that is a variant of uniform, and avoids giving too much weight to (u,v) points with a low natural weight. Weight function can be described as | ||
<math> W(u,v) = 1/ \sqrt{1+S_N^2/S_{thresh}^2} </math>, where <math> S_N </math> is the natural weight of the cell, <math> S_{thresh} </math> is a | <math> W(u,v) = 1/ \sqrt{1+S_N^2/S_{thresh}^2} </math>, where <math> S_N </math> is the natural weight of the cell, <math> S_{thresh} </math> is a | ||
threshold. | threshold. | ||
A high threshold will go to a natural weight, | A high threshold will go to a natural weight, whereas a low threshold will go to a uniform weight. This form of weighting also has adjustable parameters. The ''robust'' parameter will give variation between resolution and maximum point source sensitivity. Its value can range from -2.0 (close to uniform weight) to 2.0 (close to natural weight). By default, the parameter is set to 0.0, which gives a good trade-off. | ||
<br /> | <br /> | ||
--> | --> | ||
[[Image:Weight_Tapering_table.png|450px|thumb|right|'''Table 1''' <br /> Table summarizing the effects of using weights and tapering.]] | [[Image:Weight_Tapering_table.png|450px|thumb|right|'''Table 1''' <br /> Table summarizing the effects of using weights and tapering.]] | ||
'''Tapering''': In conjunction with the above weighting schemes, one can specify the ''uvtaper'' parameter within [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean], which will control the radial weighting of visibilities in the uv-plane. Figure 2 illustrates the uv-coverage during the observing session used in this guide. The taper in [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] is an elliptical Gaussian function which effectively removes long baselines and degrades the resolution. For extended | '''Tapering''': In conjunction with the above weighting schemes, one can specify the ''uvtaper'' parameter within [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean], which will control the radial weighting of visibilities in the uv-plane. Figure 2 illustrates the uv-coverage during the observing session used in this guide. The taper in [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] is an elliptical Gaussian function which effectively removes long baselines and degrades the resolution. For extended structures, this may be desirable when the long baselines contribute a large fraction of the noise. | ||
<!-- | <!-- | ||
The tapering will apodize, or filter/change the shape of the weight function (which is itself a Gaussian), which can be expressed as: <br /> | The tapering will apodize, or filter/change the shape of the weight function (which is itself a Gaussian), which can be expressed as: <br /> | ||
<math> W(u,v) = e^{-(u^2+v^2)/t^2} </math>, where t is the adjustable tapering parameter. | <math> W(u,v) = e^{-(u^2+v^2)/t^2} </math>, where t is the adjustable tapering parameter. | ||
--> | --> | ||
Tapering can therefore increase the surface brightness sensitivity of the data | Tapering can therefore increase the surface brightness sensitivity of the data but will decrease the point source sensitivity. Too aggressive tapering, however, may also take its toll on the surface brightness sensitivity. | ||
<!-- | <!-- | ||
Due to the | Due to the down weight of some data, point source sensitivity can be degraded, as some antennas and baselines will be suppressed and, in the extreme case, effectively removed from the data averaging. If your observation was sampled by short baselines, tapering may improve sensitivity to extended structures. | ||
--> | --> | ||
| Line 119: | Line 119: | ||
== Primary and Synthesized Beam == | == Primary and Synthesized Beam == | ||
<div style="text-align: justify;"> | <div style="text-align: justify;"> | ||
The primary beam of a single antenna defines the sensitivity across the field of view. For the VLA antennas, the main part of the primary beam can be approximated by a Gaussian with | The primary beam of a single antenna defines the sensitivity across the field of view. For the VLA antennas, the main part of the primary beam can be approximated by a Gaussian with an FWHM equal to <math>42/ \nu_{GHz}</math> arcminutes (for frequencies in the range 1 - 50 GHz). But note that there are sidelobes beyond the Gaussian kernel that are sensitive to bright sources (see below). Taking our observed frequency to be the middle of the L-band, 1.5 GHz, our primary beam (FWHM) will be about 28 arcmin in diameter. | ||
Note: New beam measurements were made recently and are described in [https://library.nrao.edu/public/memos/evla/EVLAM_195.pdf EVLA memo #195]. These newer beam corrections are the default in CASA 5.5.0. | Note: New beam measurements were made recently and are described in [https://library.nrao.edu/public/memos/evla/EVLAM_195.pdf EVLA memo #195]. These newer beam corrections are the default in CASA 5.5.0. | ||
| Line 131: | Line 131: | ||
For the most effective cleaning, we recommend using a pixel size such that there are 3 - 5 pixels across the synthesized beam. Based on the assumed synthesized beam size of 46 arcsec, we will use a cell (pixel) size of 8 arcsec. | For the most effective cleaning, we recommend using a pixel size such that there are 3 - 5 pixels across the synthesized beam. Based on the assumed synthesized beam size of 46 arcsec, we will use a cell (pixel) size of 8 arcsec. | ||
In the [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean] task, the image size is defined by the number of pixels in the RA and dec directions. The execution time of [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean] depends on the image size. Large images generally take more computing time. There are some particular image sizes (by number of pixels) that are computationally inadvisable. For inputs corresponding to such image sizes, the logger will show a recommendation for an appropriate larger, but computationally faster, image size. As a general guideline, we recommend image sizes <math>5*2^n*3^m (n=1,2,... , m=1,2,...)</math> pixel, e.g. 160, 1280 pixels, etc. for improved processing speeds. | In the [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean] task, the image size is defined by the number of pixels in the RA and dec directions. The execution time of [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean] depends on the image size. Large images generally take more computing time. There are some particular image sizes (by a number of pixels) that are computationally inadvisable. For inputs corresponding to such image sizes, the logger will show a recommendation for an appropriate larger, but computationally faster, image size. As a general guideline, we recommend image sizes <math>5*2^n*3^m (n=1,2,... , m=1,2,...)</math> pixel, e.g. 160, 1280 pixels, etc. for improved processing speeds. | ||
Our target field contains bright point sources that are well outside the primary beam. The VLA, in particular when using multi-frequency synthesis (see below), will have significant sensitivity outside the main lobe of the primary beam. Particularly at the lower VLA frequencies, sources that are located outside the primary beam may still be bright enough to be detected in the primary beam sidelobes, causing artifacts that interfere with the targeted field in the main part of the primary beam. Such sources need to be cleaned to remove the dirty beam response of these interfering sources from the entire image. This can be achieved either by creating a very large image that encompasses these interfering sources | Our target field contains bright point sources that are well outside the primary beam. The VLA, in particular when using multi-frequency synthesis (see below), will have significant sensitivity outside the main lobe of the primary beam. Particularly at the lower VLA frequencies, sources that are located outside the primary beam may still be bright enough to be detected in the primary beam sidelobes, causing artifacts that interfere with the targeted field in the main part of the primary beam. Such sources need to be cleaned to remove the dirty beam response of these interfering sources from the entire image. This can be achieved either by creating a very large image that encompasses these interfering sources or by using 'outlier' fields centered on the strongest sources (see the section on outlier fields below). A large image has the added advantage of increasing the field of view for science (albeit at lower sensitivity beyond the primary beam). But other effects will start to become significant, like the non-coplanarity of the sky. Large image sizes will also slow down the deconvolution process. Details are provided in Sanjay Bhatnagar's presentation: [https://science.nrao.edu/science/meetings/2016/vla-data-reduction/copy_of_WF_WB.pdf "Advanced Imaging: Imaging in the Wide-band Wide-field era"] given at the [https://science.nrao.edu/science/meetings/2016/vla-data-reduction/program 2016 VLA data reduction workshop]. | ||
The calls to the [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] task within this guide will create images that are approximately 170 arcminutes on a side, or almost 6x the size of the primary beam, encompassing its first and second sidelobes. This is ideal for showcasing both the problems inherent in wide-band/wide-field imaging, as well as some of the solutions currently available in CASA to deal with these issues. We therefore set the image size to 1280 pixels on each side, for efficient processing speed. (1280 pixels x 8 arcsec/pixel = 170.67 arcmin) | The calls to the [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] task within this guide will create images that are approximately 170 arcminutes on a side, or almost 6x the size of the primary beam, encompassing its first and second sidelobes. This is ideal for showcasing both the problems inherent in wide-band/wide-field imaging, as well as some of the solutions currently available in CASA to deal with these issues. We, therefore, set the image size to 1280 pixels on each side, for efficient processing speed. (1280 pixels x 8 arcsec/pixel = 170.67 arcmin) | ||
</div> | </div> | ||
| Line 175: | Line 175: | ||
* ''imagename='SNR_G55_10s.dirty''': the root filename used for the various [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] outputs. | * ''imagename='SNR_G55_10s.dirty''': the root filename used for the various [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] outputs. | ||
* ''imsize=1280'': the image size in number of pixels. A single value will result in a square image. | * ''imsize=1280'': the image size in a number of pixels. A single value will result in a square image. | ||
* ''cell='8arcsec''': the size of one pixel; again, entering a single value will result in a square pixel size. | * ''cell='8arcsec''': the size of one pixel; again, entering a single value will result in a square pixel size. | ||
| Line 183: | Line 183: | ||
* ''niter=0'': this controls the number of iterations done in the minor cycle. | * ''niter=0'': this controls the number of iterations done in the minor cycle. | ||
* ''interactive=False'': For a tutorial that covers more of an interactive clean, please see the [https://casaguides.nrao.edu/index.php?title=VLA_high_frequency_Spectral_Line_tutorial_-_IRC%2B10216 VLA high frequency Spectral Line tutorial - IRC+10216.] | * ''interactive=False'': For a tutorial that covers more of an interactive clean, please see the [https://casaguides.nrao.edu/index.php?title=VLA_high_frequency_Spectral_Line_tutorial_-_IRC%2B10216 VLA high-frequency Spectral Line tutorial - IRC+10216.] | ||
* ''savemodel='modelcolumn'': controls writing the model visibilities to the model data column. For self-calibration we currently recommend setting savemodel='modelcolumn'. The default value is "none": so, this must be changed for the model to be saved. The use of the virtual model with MTMFS in [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] is still under commissioning, so we recommend currently to set ''savemodel='modelcolumn'.'' | * ''savemodel='modelcolumn'': controls writing the model visibilities to the model data column. For self-calibration, we currently recommend setting savemodel='modelcolumn'. The default value is "none": so, this must be changed for the model to be saved. The use of the virtual model with MTMFS in [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] is still under commissioning, so we recommend currently to set ''savemodel='modelcolumn'.'' | ||
* ''stokes='I''': since we have not done any polarization calibration, we only create a total-intensity image. For using [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] while including various Stoke's parameters, please see the [https://casaguides.nrao.edu/index.php/VLA_Continuum_Tutorial_3C391 3C391 CASA guide.] | * ''stokes='I''': since we have not done any polarization calibration, we only create a total-intensity image. For using [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] while including various Stoke's parameters, please see the [https://casaguides.nrao.edu/index.php/VLA_Continuum_Tutorial_3C391 3C391 CASA guide.] | ||
| Line 204: | Line 204: | ||
|} | |} | ||
The images may be easier to see in more user friendly color scale of viridas. If user wants to change the color scheme in CARTA, click on "Color map" option within the "Render configuration" widget of CARTA. You may also wish to change the Clip Min, Clip Max and Scaling options to your liking. For more information about how to change the brightness and contrast, click the help option (top right) of the Render configuration widget. | The images may be easier to see in a more user-friendly color scale of viridas. If the user wants to change the color scheme in CARTA, click on the "Color map" option within the "Render configuration" widget of CARTA. You may also wish to change the Clip Min, Clip Max, and Scaling options to your liking. For more information about how to change the brightness and contrast, click the help option (top right) of the Render configuration widget. | ||
Note that the clean beam is only defined after some clean iterations. The dirty image has therefore no beam size specified in the header, and the PSF image (Figure 3b) is the representation of the response of the array to a point source. Even though it is empty because we set ''niter=0'', [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] will still produce a model file. Thus we could progress into actual cleaning by simply restarting [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] with the same image root name (and ''niter''>0). | Note that the clean beam is only defined after some clean iterations. The dirty image has therefore no beam size specified in the header, and the PSF image (Figure 3b) is the representation of the response of the array to a point source. Even though it is empty because we set ''niter=0'', [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] will still produce a model file. Thus we could progress into actual cleaning by simply restarting [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] with the same image root name (and ''niter''>0). | ||
| Line 212: | Line 212: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA. Create default clean image. | # In CASA. Create a default clean image. | ||
tclean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.Reg.Clean.niter1K', | tclean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.Reg.Clean.niter1K', | ||
imsize=1280, cell='8arcsec', pblimit=-0.01, niter=1000, savemodel='modelcolumn') | imsize=1280, cell='8arcsec', pblimit=-0.01, niter=1000, savemodel='modelcolumn') | ||
| Line 222: | Line 222: | ||
</source> | </source> | ||
The logger indicates that the image was obtained in two major cycles, and some improvements over the dirty image are visible. But clearly we have not cleaned deep enough yet; the image still has many sidelobes, and an inspection of the residual image shows that it still contains source flux and structure. So let's increase the ''niter'' value to 10,000 and compare the images. | The logger indicates that the image was obtained in two major cycles, and some improvements over the dirty image are visible. But clearly, we have not cleaned deep enough yet; the image still has many sidelobes, and an inspection of the residual image shows that it still contains source flux and structure. So let's increase the ''niter'' value to 10,000 and compare the images. | ||
<source lang="python"> | <source lang="python"> | ||
| Line 228: | Line 228: | ||
tclean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.Reg.Clean.niter10K', | tclean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.Reg.Clean.niter10K', | ||
imsize=1280, cell='8arcsec', pblimit=-0.01, niter=10000, savemodel='modelcolumn') | imsize=1280, cell='8arcsec', pblimit=-0.01, niter=10000, savemodel='modelcolumn') | ||
</source><br /> | |||
Users can also control the execution of the major cycle using the ''nmajor'' parameter. Once [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html#nmajor tclean] reaches the required major cycle executions, then it will stop. | |||
<source lang="python"> | |||
# In CASA. Create default clean image with major cycle 4 | |||
tclean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.Reg.Clean.nmajor4', | |||
imsize=1280, cell='8arcsec', pblimit=-0.01, nmajor=4, niter=10000,savemodel='modelcolumn') | |||
</source><br /> | </source><br /> | ||
| Line 242: | Line 250: | ||
[[Image:SNR_G55_10s_rms_screen2.png|500px|thumb|right|'''Figure 5''' <br /> Attempting to find the lowest rms value within the CLEAN'ed image using niter=1000, in order to calculate our threshold.]] | [[Image:SNR_G55_10s_rms_screen2.png|500px|thumb|right|'''Figure 5''' <br /> Attempting to find the lowest rms value within the CLEAN'ed image using niter=1000, in order to calculate our threshold.]] | ||
As we can see from the resulting images, increasing the niter values (minor cycles) improves our image by reducing prominent sidelobes significantly (Figure 4b). One could now further increase the ''niter'' parameter until the residuals are down to an acceptable level. To determine the number of iterations, one needs to keep in mind that [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] will fail once it starts cleaning too deeply into the noise. At that point, the cleaned flux and the peak residual flux values will start to oscillate as the number of iterations increase. This effect can be monitored on the CASA logger output. To avoid cleaning too deeply, we will set a ''threshold'' parameter that will stop minor cycle clean iterations once a peak residual value is | As we can see from the resulting images, increasing the niter values (minor cycles) improves our image by reducing prominent sidelobes significantly (Figure 4b). One could now further increase the ''niter'' parameter until the residuals are down to an acceptable level. To determine the number of iterations, one needs to keep in mind that [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] will fail once it starts cleaning too deeply into the noise. At that point, the cleaned flux and the peak residual flux values will start to oscillate as the number of iterations increase. This effect can be monitored on the CASA logger output. To avoid cleaning too deeply, we will set a ''threshold'' parameter that will stop minor cycle clean iterations once a peak residual value is reached. | ||
First, we will utilize the ''SNR_G55_10s.Reg.Clean.niter1K.image'' (Figure 4a) image to give us an idea of the rms noise (your sigma value). | First, we will utilize the ''SNR_G55_10s.Reg.Clean.niter1K.image'' (Figure 4a) image to give us an idea of the rms noise (your sigma value). | ||
With the image open within the CARTA, click on the 'Rectangle' button in the region bar at the top of the GUI and draw a square on the image at a position with little source or sidelobe contamination. | With the image open within the CARTA, click on the 'Rectangle' button in the region bar at the top of the GUI and draw a square on the image at a position with little source or sidelobe contamination. Users can also activate the region creation mode, click the ''Show toolbar'' button at the bottom-right corner of the image viewer then click the ''Create region'' button or pressing the ''C'' key. Double-clicking the ''Create region'' icon opens up all available region types (point, line, rectangle, ellipse, polygon, and polyline). Select the polygon and draw a square as mentioned above. After drawing the square in an empty region, click the | ||
Statistic widget from the Widget bar at the top of the GUI. This will open another window of name ''Statistic: Region 1'' (Figure 5) which holds information about the selected region, including the pixel statistics. Take notice of the RMS values. User can draw multiple regions (of any shape which draw over enough amount of pixels) like this at different empty regions to get | Statistic widget from the Widget bar at the top of the GUI. This will open another window of the name ''Statistic: Region 1'' (Figure 5) which holds information about the selected region, including the pixel statistics. Take notice of the RMS values. User can draw multiple regions (of any shape which draw over enough amount of pixels) like this at different empty regions to get a better rms estimation. | ||
The lowest rms value we found was in the order of about <math>5\cdot10^{-5}</math> Jy/beam, which we will use to calculate our threshold. There really is no set standard, but fairly good threshold values can vary anywhere between 3.0 - 5.0*sigma; using clean boxes (see the section on interactive cleaning) allows one to go to lower thresholds. For our purposes, we will choose a threshold of 3*sigma. Doing the math results in a value of <math> 15\cdot10^{-5}</math> or equivalently 0.15mJy/beam. Therefore, for future calls to the [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] task, we will set ''threshold='0.15mJy'''. The clean cycle will be stopped when the residual peak flux density is | The lowest rms value we found was in the order of about <math>5\cdot10^{-5}</math> Jy/beam, which we will use to calculate our threshold. There really is no set standard, but fairly good threshold values can vary anywhere between 3.0 - 5.0*sigma; using clean boxes (see the section on interactive cleaning) allows one to go to lower thresholds. For our purposes, we will choose a threshold of 3*sigma. Doing the math results in a value of <math> 15\cdot10^{-5}</math> or equivalently 0.15mJy/beam. Therefore, for future calls to the [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] task, we will set ''threshold='0.15mJy'''. The clean cycle will be stopped when the residual peak flux density is equal to or less than the ''threshold'' value, or when the maximum number of iterations ''niter'' is reached. To ensure that the stopping criterion is indeed ''threshold'', ''niter'' should be set to a very high number. '''In the following, we nevertheless will use ''niter=1000'' to keep the execution times of [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] on the low end as we focus on explaining different imaging methods.''' | ||
An alternative method to determine the approximate rms of an image is to use the [https://science.nrao.edu/facilities/vla/docs/manuals/propvla/determining VLA Exposure Calculator] and to enter the observing conditions. Make sure that the chosen bandwidth reflects the data after RFI excision. | An alternative method to determine the approximate rms of an image is to use the [https://science.nrao.edu/facilities/vla/docs/manuals/propvla/determining VLA Exposure Calculator] and to enter the observing conditions. Make sure that the chosen bandwidth reflects the data after RFI excision. | ||
| Line 256: | Line 264: | ||
== CLEAN with Weights == | == CLEAN with Weights == | ||
<div style="text-align: justify;"> | <div style="text-align: justify;"> | ||
To see the effects of using different weighting schemes | To see the effects of using different weighting schemes on the image, let's change the ''weighting'' parameter within [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.imaging.tclean.html tclean] and inspect the resulting images. We will be using the ''Natural, Uniform, and Briggs'' weighting algorithms. Here, we have chosen a smaller image size to mainly focus on our science target. | ||
<source lang="python"> | <source lang="python"> | ||
| Line 300: | Line 308: | ||
[[Image:SNR_G55_10s.MultiScale.image2.png|300px|thumb|right|'''Figure 8''' <br /> Artifacts around point sources]] | [[Image:SNR_G55_10s.MultiScale.image2.png|300px|thumb|right|'''Figure 8''' <br /> Artifacts around point sources]] | ||
Since G55.7+3.4 is an extended source with many angular scales, a more advanced form of imaging involves the use of multiple scales. MS-CLEAN is an extension of the classical CLEAN algorithm for handling extended sources. Multi-Scale CLEAN works by assuming the sky is composed of | Since G55.7+3.4 is an extended source with many angular scales, a more advanced form of imaging involves the use of multiple scales. MS-CLEAN is an extension of the classical CLEAN algorithm for handling extended sources. Multi-Scale CLEAN works by assuming the sky is composed of emissions at different angular scales and works on them simultaneously, thereby creating a linear combination of images at different angular scales. For a more detailed description of Multi-Scale CLEAN, see T.J. Cornwell's paper [http://arxiv.org/abs/0806.2228 Multi-Scale CLEAN deconvolution of radio synthesis images]. | ||
If one is interested in measuring the flux density of an extended source as well as the associated uncertainty of that flux density, use the CARTA to first draw a region (using the polygon tool) around the source for which you want to measure the flux density for and it’s associated uncertainty. The lines drawn by the polygon tool will be in editing mode and | If one is interested in measuring the flux density of an extended source as well as the associated uncertainty of that flux density, use the CARTA to first draw a region (using the polygon tool) around the source for which you want to measure the flux density for and it’s associated uncertainty. The lines drawn by the polygon tool will be in editing mode and allow for the vertices to be moved to create whatever shape is desired around the source. Once a satisfactory shape has been created around the source, click on the Statistics Widget. In the opened statistics window, the following quantities should be recorded: BeamArea (the size of the restoring beam in pixels), NumPixels (the number of pixels inside of the region), and FluxDensity (the total flux inside of the region). Once recorded, draw another region several times the size of the restoring beam which only includes noise-like pixels (no sources should be present in this second region). In the statistics window, record the Rms value. Finally - you can compute the error of the total flux like so: | ||
<math> Rms \times \sqrt(\frac{NumPixels}{BeamArea})</math> | <math> Rms \times \sqrt(\frac{NumPixels}{BeamArea})</math> | ||
Note: the value of NumPixels/BeamArea can also be called the number of independent beams and should be >> 1. If it is close to or less than 1, there are other more accurate techniques to use to calculate the error. | Note: the value of NumPixels/BeamArea can also be called the number of independent beams and should be >> 1. If it is close to or less than 1, there are other more accurate techniques to use to calculate the error. | ||
We will use a set of scales (expressed in units of the requested pixel or cell size) | We will use a set of scales (expressed in units of the requested pixel or cell size) that are representative of the scales that are present in the data, including a zero-scale for point sources. | ||
<source lang="python"> | <source lang="python"> | ||
| Line 315: | Line 323: | ||
</source> | </source> | ||
* ''multiscale=[0,6,10,30,60]'': a set of scales on which to clean. A general guideline when using multiscale is 0, 2xbeam, 5xbeam (where beam is the synthesized beam), and larger scales up to about half the minor axis maximum scale of the mapped structure. Since these are in units of | * ''multiscale=[0,6,10,30,60]'': a set of scales on which to clean. A general guideline when using multiscale is 0, 2xbeam, 5xbeam (where beam is the synthesized beam), and larger scales up to about half the minor axis maximum scale of the mapped structure. Since these are in units of pixel size, our chosen values will be multiplied by the requested cell size. Thus, we are requesting scales of 0 (a point source), 48, 80, 240, and 480 arcseconds (8 arcminutes). Note that 16 arcminutes (960 arcseconds) roughly corresponds to the size of G55.7+3.4. | ||
* ''smallscalebias=0.9'': This parameter is known as the '''small scale bias''', and helps with faint extended structure by balancing the weight given to smaller structures, which tend to have higher surface brightness but lower integrated flux density. Increasing this value gives more weight to smaller scales. A value of 1.0 weights the largest scale to zero, and a value of less than 0.2 weights all scales nearly equally. The default value is 0.6. | * ''smallscalebias=0.9'': This parameter is known as the '''small scale bias''', and helps with faint extended structure by balancing the weight given to smaller structures, which tend to have higher surface brightness but lower integrated flux density. Increasing this value gives more weight to smaller scales. A value of 1.0 weights the largest scale to zero, and a value of less than 0.2 weights all scales nearly equally. The default value is 0.6. | ||
| Line 326: | Line 334: | ||
The logger will show how much cleaning is performed on the individual scales. | The logger will show how much cleaning is performed on the individual scales. | ||
This is the fastest of the advanced imaging techniques described here, but it's easy to see that there are artifacts in the resulting image (Figure 7). We can use the {{CARTA}} to explore the point sources near the edge of the field by zooming in on them (Figure 8). In CARTA, one can zoom image by using mouse wheel to scroll up or down. Alternatively, use the zoom buttons from the toolbar at the bottom-right of the image viewer. | This is the fastest of the advanced imaging techniques described here, but it's easy to see that there are artifacts in the resulting image (Figure 7). We can use the {{CARTA}} to explore the point sources near the edge of the field by zooming in on them (Figure 8). In CARTA, one can zoom an image by using the mouse wheel to scroll up or down. Alternatively, use the zoom buttons from the toolbar at the bottom-right of the image viewer. | ||
After zooming in on the area, we can see some radio sources that have prominent arcs, as well as spots with a six-pointed pattern surrounding them. | After zooming in on the area, we can see some radio sources that have prominent arcs, as well as spots with a six-pointed pattern surrounding them. | ||
Next we will further explore advanced imaging techniques to mitigate the artifacts seen toward the edges of the image. | Next, we will further explore advanced imaging techniques to mitigate the artifacts seen toward the edges of the image. | ||
== Multi-Scale, Wide-Field CLEAN (w-projection) == | == Multi-Scale, Wide-Field CLEAN (w-projection) == | ||
| Line 371: | Line 379: | ||
== Multi-Scale, Multi-Term Multi-Frequency Synthesis == | == Multi-Scale, Multi-Term Multi-Frequency Synthesis == | ||
[[Image:MultiFrequency_Synthesis_snapshot.png|350px|thumb|right|'''Figure 11''' <br /> ''Left:'' (u,v) coverage snapshot at a single frequency. ''Right:'' Multi-Frequency Synthesis snapshot of (u,v) coverage. Using this algorithm can greatly improve (u,v) coverage, thereby improving image fidelity.]] | [[Image:MultiFrequency_Synthesis_snapshot.png|350px|thumb|right|'''Figure 11''' <br /> ''Left:'' (u,v) coverage snapshot at a single frequency. ''Right:'' Multi-Frequency Synthesis snapshot of (u,v) coverage. Using this algorithm can greatly improve (u,v) coverage, thereby improving image fidelity.]] | ||
[[Image:SNR_G55_10s.ms.MTMFS.image.tt0-image.png|300px|thumb|right|'''Figure 12''' <br /> Multi-Scale imaged with MT-MFS and nterms=2. Artifacts around point sources close to phase center are reduced while point sources away from the phase center still show artifacts.]] | [[Image:SNR_G55_10s.ms.MTMFS.image.tt0-image.png|300px|thumb|right|'''Figure 12''' <br /> Multi-Scale imaged with MT-MFS and nterms=2. Artifacts around point sources close to the phase center are reduced while point sources away from the phase center still show artifacts.]] | ||
[[Image:SNR_G55_10s.ms.MTMFS.alpha-image2.png|300px|thumb|right|'''Figure 13''' <br /> Spectral Index image]] | [[Image:SNR_G55_10s.ms.MTMFS.alpha-image2.png|300px|thumb|right|'''Figure 13''' <br /> Spectral Index image]] | ||
| Line 378: | Line 386: | ||
The coordinates of the (u,v) plane are measured in wavelengths. Observing at several frequencies results means that a single baseline will sample several ellipses in the (u,v) plane, each with different sizes. We can therefore fill in the gaps in the single frequency (u,v) coverage (Figure 11) to achieve a much better image fidelity. This method is called Multi-Frequency Synthesis (MFS), which is the default cleaning mode in CLEAN. For a more detailed explanation of the MS-MFS deconvolution algorithm, please see the paper [http://arxiv.org/abs/1106.2745 A multi-scale multi-frequency deconvolution algorithm for synthesis imaging in radio interferometry]. | The coordinates of the (u,v) plane are measured in wavelengths. Observing at several frequencies results means that a single baseline will sample several ellipses in the (u,v) plane, each with different sizes. We can therefore fill in the gaps in the single frequency (u,v) coverage (Figure 11) to achieve a much better image fidelity. This method is called Multi-Frequency Synthesis (MFS), which is the default cleaning mode in CLEAN. For a more detailed explanation of the MS-MFS deconvolution algorithm, please see the paper [http://arxiv.org/abs/1106.2745 A multi-scale multi-frequency deconvolution algorithm for synthesis imaging in radio interferometry]. | ||
<!--When observing in low-frequencies, it may prove beneficial to observe in small time-chunks which are spread out in time. This will allow the coverage of more spatial | <!--When observing in low-frequencies, it may prove beneficial to observe in small time-chunks which are spread out in time. This will allow the coverage of more spatial frequencies, allowing us to employ this algorithm more efficiently. | ||
--> | --> | ||
| Line 394: | Line 402: | ||
* ''nterms=2'': the number of Taylor-terms to be used to model the frequency dependence of the sky emission. Note that the speed of the algorithm will depend on the value used here (more terms will be slower). nterms=2 will fit a spectral index, while nterms=3 will fit a spectral index and spectral curvature. | * ''nterms=2'': the number of Taylor-terms to be used to model the frequency dependence of the sky emission. Note that the speed of the algorithm will depend on the value used here (more terms will be slower). nterms=2 will fit a spectral index, while nterms=3 will fit a spectral index and spectral curvature. | ||
For Multi-Term MFS, [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] produces images with extension tt*, where the number in place of the asterisk indicates the Taylor term: <imagename>.image.tt0 is the total intensity image (Figure 12) and <imagename>.image.alpha will contain an image of the spectral index in regions where there is sufficient signal-to-noise (Figure 13). For Figure 12, we have included a colorbar to give an idea of the flux within the image. The spectral index image can help convey information about emission mechanisms as well as optical depth of the source. | For Multi-Term MFS, [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] produces images with extension tt*, where the number in place of the asterisk indicates the Taylor term: <imagename>.image.tt0 is the total intensity image (Figure 12) and <imagename>.image.alpha will contain an image of the spectral index in regions where there is sufficient signal-to-noise (Figure 13). For Figure 12, we have included a colorbar to give an idea of the flux within the image. The spectral index image can help convey information about emission mechanisms as well as the optical depth of the source. | ||
<source lang="python"> | <source lang="python"> | ||
| Line 406: | Line 414: | ||
</source> | </source> | ||
Note: To replicate Figure 13, open the image within the CARTA, click on File -> Preferences -> Render Configuration and change the NaN color to white, and adjust your margins manually to best fit the image in CARTA's viewer window. To adjust the colorbar, click on the settings (on top-right of the image viewer window), click on the "Colorbar" button, and adjust the various parameters to your liking. | Note: To replicate Figure 13, open the image within the CARTA, click on File -> Preferences -> Render Configuration and change the NaN color to white, and adjust your margins manually to best fit the image in CARTA's viewer window. To adjust the colorbar, click on the settings (on the top-right of the image viewer window), click on the "Colorbar" button, and adjust the various parameters to your liking. | ||
For more information on the multi-term, multi-frequency synthesis mode and its outputs, see the [https://casadocs.readthedocs.io/en/v6.5.2/notebooks/synthesis_imaging.html Deconvolution Algorithms section] in the CASA documentation. | For more information on the multi-term, multi-frequency synthesis mode, and its outputs, see the [https://casadocs.readthedocs.io/en/v6.5.2/notebooks/synthesis_imaging.html Deconvolution Algorithms section] in the CASA documentation. | ||
Inspect the brighter point sources in the field near the supernova remnant. You will notice that some of the artifacts, which had been symmetric around the sources, are gone; however, as we did not use w-projection, there are still strong features related to the non-coplanar baseline effects still apparent for sources further away. | Inspect the brighter point sources in the field near the supernova remnant. You will notice that some of the artifacts, which had been symmetric around the sources, are gone; however, as we did not use w-projection, there are still strong features related to the non-coplanar baseline effects still apparent for sources further away. | ||
At this point, [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] takes into account the frequency variation of the synthesized beam but not the frequency variation of the primary beam. For low frequencies and large bandwidths, this can be substantial; e.g., 1 - 2 GHz L-band observations result in a variation of a factor of 2. One effect of imaging with MFS across such a large fractional bandwidth is that primary beam nulls will be blurred; the interferometer is sensitive everywhere in the field of view. However, if there is no correction made to account for the variation in primary beam with frequency, sources away from the phase center appear to have a steeply false spectral slope. A correction for this effect should be made with the task [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.widebandpbcor.html#casatasks.imaging.widebandpbcor widebandpbcor] or set ''pbcor=True'' (see section on Primary Beam Correction below). | At this point, [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] takes into account the frequency variation of the synthesized beam but not the frequency variation of the primary beam. For low frequencies and large bandwidths, this can be substantial; e.g., 1 - 2 GHz L-band observations result in a variation of a factor of 2. One effect of imaging with MFS across such a large fractional bandwidth is that primary beam nulls will be blurred; the interferometer is sensitive everywhere in the field of view. However, if there is no correction made to account for the variation in the primary beam with frequency, sources away from the phase center appear to have a steeply false spectral slope. A correction for this effect should be made with the task [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.widebandpbcor.html#casatasks.imaging.widebandpbcor widebandpbcor] or set ''pbcor=True'' (see the section on Primary Beam Correction below). | ||
== Multi-Scale, Multi-Term Multi-Frequency Synthesis with W-Projection == | == Multi-Scale, Multi-Term Multi-Frequency Synthesis with W-Projection == | ||
| Line 452: | Line 460: | ||
When strong sources are far from the main target but still strong enough to produce sidelobes in the main image, they should be cleaned. Sometimes, however, it is not practical to image very large fields for this purpose. An alternative is to add outlier fields. This mode will allow the user to specify a few locations that are then cleaned along with the main image. The outlier fields should be centered on strong sources that, e.g., are known from sky catalogs or are identified by other means. | When strong sources are far from the main target but still strong enough to produce sidelobes in the main image, they should be cleaned. Sometimes, however, it is not practical to image very large fields for this purpose. An alternative is to add outlier fields. This mode will allow the user to specify a few locations that are then cleaned along with the main image. The outlier fields should be centered on strong sources that, e.g., are known from sky catalogs or are identified by other means. | ||
In order to find outlying sources, it will help to first image a very large field with lower resolution, and to identify bright outliers using the CARTA. By moving the mouse cursor over the sources, we can grab their positions (see WCS coordinates | In order to find outlying sources, it will help to first image a very large field with lower resolution, and to identify bright outliers using the CARTA. By moving the mouse cursor over the sources, we can grab their positions (see WCS coordinates at the top of the image viewer) and use the information within an outlier file. In this example, we've called our file 'outliers.txt'. It contains the names, sizes, and positions of the outliers we want to image (see section [https://casa.nrao.edu/docs/cookbook/casa_cookbook006.html#sec356 5.3.18.1] of the CASA cookbook). | ||
Open your favorite text editor and input the following: | Open your favorite text editor and input the following: | ||
| Line 534: | Line 542: | ||
</source> | </source> | ||
Let us now use the [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.widebandpbcor.html#casatasks.imaging.widebandpbcor widebandpbcor] task for wide-band (''nterms''>1) images. Note that for this task, we will be supplying the image name that is the prefix for the Taylor expansion images, tt0 and tt1, which must be on disk. Such files were created during the last Multi-Scale, Multi-Term, Widefield run of CLEAN. [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.widebandpbcor.html#casatasks.imaging.widebandpbcor widebandpbcor] will generate a set of images with a "pbcor.image.*" extension. | Let us now use the [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.widebandpbcor.html#casatasks.imaging.widebandpbcor widebandpbcor] task for wide-band (''nterms''>1) images. Note that for this task, we will be supplying the image name that is the prefix for the Taylor expansion images, tt0, and tt1, which must be on disk. Such files were created during the last Multi-Scale, Multi-Term, Widefield run of CLEAN. [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.widebandpbcor.html#casatasks.imaging.widebandpbcor widebandpbcor] will generate a set of images with a "pbcor.image.*" extension. | ||
<source lang="python"> | <source lang="python"> | ||
| Line 570: | Line 578: | ||
== Adaptive Scale Pixel (ASP) Clean !!!EXPERIMENTAL!!!== | == Adaptive Scale Pixel (ASP) Clean !!!EXPERIMENTAL!!!== | ||
Recently ASP deconvolution algorithm has been implemented in CASA 6.5.2 [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] version. The ASP decomposition algorithm is designed to reconstruct the sky brightness by adaptively determining the optimal scales. The implementation of ASP algorithm is aimed to improve both image resolution and computation efficiency. The implementation of the ASP algorithm in CASA is still under experiment so user should carefully check their results. For more detail see [https://www.aanda.org/articles/aa/abs/2004/41/aa0354-04/aa0354-04.html Bhatnagar et | Recently ASP deconvolution algorithm has been implemented in CASA 6.5.2 [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] version. The ASP decomposition algorithm is designed to reconstruct the sky brightness by adaptively determining the optimal scales. The implementation of the ASP algorithm is aimed to improve both image resolution and computation efficiency. The implementation of the ASP algorithm in CASA is still under experiment so the user should carefully check their results. For more detail see [https://www.aanda.org/articles/aa/abs/2004/41/aa0354-04/aa0354-04.html Bhatnagar et al. 2004]. | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
| Line 579: | Line 587: | ||
*''deconvolver='asp''': Use the Adaptive Scale Pixel algorithm. | *''deconvolver='asp''': Use the Adaptive Scale Pixel algorithm. | ||
*''fusedthreshold=0.0001'': This parameter switches the deconvolver algorithm asp to hogbom when peak residual is lower than the given threshold. | *''fusedthreshold=0.0001'': This parameter switches the deconvolver algorithm asp to hogbom when the peak residual is lower than the given threshold. | ||
*''largestscale=-1'': This parameter provides | *''largestscale=-1'': This parameter provides the initial guess for the asp algorithm to choose the scales on which to clean (in pixels). Generally, asp uses the default scale sizes [0,w,2w,4w,8w], where w is the width of the point spread function. In this case, we chose largestscale=-1, which suggests users accept these default scales. If this parameter is set, for example, 100, the initial scales would be [0,w,2w,..100]. It is recommended to use default scale values. | ||
<source lang="python"> | <source lang="python"> | ||
| Line 622: | Line 630: | ||
specmode = 'cube' # Spectral definition type (mfs, cube, cubedata, cubesource) | specmode = 'cube' # Spectral definition type (mfs, cube, cubedata, cubesource) | ||
nchan = -1 # Number of channels (planes) in output image; -1 = all data specified by spw, start, and width parameters. | nchan = -1 # Number of channels (planes) in output image; -1 = all data specified by spw, start, and width parameters. | ||
start = '' # Velocity of first channel: e.g '0.0km/s'(''=first channel in first SpW of MS) | start = '' # Velocity of the first channel: e.g '0.0km/s'(''=first channel in first SpW of MS) | ||
width = '' # Channel width e.g '-1.0km/s' (''=width of first channel in first SpW of MS) | width = '' # Channel width e.g '-1.0km/s' (''=width of first channel in first SpW of MS) | ||
outframe = '' # spectral reference frame of output image; '' =input | outframe = '' # spectral reference frame of output image; '' =input | ||
| Line 632: | Line 640: | ||
The spectral dimension of the output cube will be defined by these parameters and [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] will regrid the visibilities to it. Note that invoking [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.manipulation.cvel.html cvel] before imaging is in most cases not necessary, even when two or more measurement sets are being provided at the same time. | The spectral dimension of the output cube will be defined by these parameters and [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] will regrid the visibilities to it. Note that invoking [https://casadocs.readthedocs.io/en/v6.2.0/api/tt/casatasks.manipulation.cvel.html cvel] before imaging is in most cases not necessary, even when two or more measurement sets are being provided at the same time. | ||
The cube is specified by a ''start'' velocity in km/s or MHz, the ''nchan'' number of channels and a channel ''width'' (where the latter can also be negative for decreasing velocity cubes). | The cube is specified by a ''start'' velocity in km/s or MHz, the ''nchan'' number of channels, and a channel ''width'' (where the latter can also be negative for decreasing velocity cubes). | ||
To correct for Doppler effects, [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] also requires a ''outframe'' velocity frame, where the default ''LSRK'' and ''BARY'' are the most popular Local Standard of Rest (kinematic) and sun-earth Barycenter references. ''veltype'' defines whether the data will be gridded via the optical or radio velocity definition. A description of the available options and definitions can be found in the [https://science.nrao.edu/facilities/vla/docs/manuals/obsguide/modes/line VLA observing guide] and the [https://casa.nrao.edu/docs/cookbook/casa_cookbook014.html CASA cookbook]. By default, [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] will produce a cube using the LRSK and radio definitions. | To correct for Doppler effects, [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] also requires a ''outframe'' velocity frame, where the default ''LSRK'' and ''BARY'' are the most popular Local Standard of Rest (kinematic) and sun-earth Barycenter references. ''veltype'' defines whether the data will be gridded via the optical or radio velocity definition. A description of the available options and definitions can be found in the [https://science.nrao.edu/facilities/vla/docs/manuals/obsguide/modes/line VLA observing guide] and the [https://casa.nrao.edu/docs/cookbook/casa_cookbook014.html CASA cookbook]. By default, [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] will produce a cube using the LRSK and radio definitions. | ||
An example of spectral line imaging procedures is provided in the [https://casaguides.nrao.edu/index.php?title=VLA_high_frequency_Spectral_Line_tutorial_-_IRC%2B10216 VLA high frequency Spectral Line tutorial - IRC+10216]. | An example of spectral line imaging procedures is provided in the [https://casaguides.nrao.edu/index.php?title=VLA_high_frequency_Spectral_Line_tutorial_-_IRC%2B10216 VLA high-frequency Spectral Line tutorial - IRC+10216]. | ||
== Beam per Plane == | == Beam per Plane == | ||
| Line 681: | Line 689: | ||
outfile='SNR_G55_10s.ms.MTMFS.wProj.image.tt0-Tb') | outfile='SNR_G55_10s.ms.MTMFS.wProj.image.tt0-Tb') | ||
</source> | </source> | ||
* ''mode='evalexpr' '': [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.analysis.immath.html#casatasks.analysis.immath immath] is used to | * ''mode='evalexpr' '': [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.analysis.immath.html#casatasks.analysis.immath immath] is used to calculate with images | ||
* ''expr'': the mathematical expression to be evaluated. The images are abbreviated as IM0, IM1, ... in the sequence of their appearance in the ''imagename'' parameter. | * ''expr'': the mathematical expression to be evaluated. The images are abbreviated as IM0, IM1, ... in the sequence of their appearance in the ''imagename'' parameter. | ||
| Line 694: | Line 702: | ||
* ''hdkey'': the header keyword that will be changed | * ''hdkey'': the header keyword that will be changed | ||
* ''hdvalue'': the new value for header keyword | * ''hdvalue'': the new value for the header keyword | ||
Launching the CARTA will now show our image in brightness temperature units: | Launching the CARTA will now show our image in brightness temperature units: | ||
| Line 710: | Line 718: | ||
* Parameter ''savemodel'' is used rather than {{clean}}'s ''usescratch'' to indicate whether the model should be saved in a new column in the ms, as a virtual model, or not at all. The default value is "none": so, this must be changed for the image to be saved. The use of the virtual model with MTMFS in [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] is still under commissioning, so we recommend currently to set ''savemodel='modelcolumn'.'' | * Parameter ''savemodel'' is used rather than {{clean}}'s ''usescratch'' to indicate whether the model should be saved in a new column in the ms, as a virtual model, or not at all. The default value is "none": so, this must be changed for the image to be saved. The use of the virtual model with MTMFS in [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] is still under commissioning, so we recommend currently to set ''savemodel='modelcolumn'.'' | ||
* Some parameter default values in [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] are different than the equivalent default values in {{clean}}. | * Some parameter default values in [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] are different than the equivalent default values in {{clean}}. | ||
* The ''auto-multithresh'' automasking algorithm in [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] provides the option to automatically generate clean mask during the deconvolution process by applying flux density thresholds to the residual image. Currently this feature is designed to work for point sources using ''deconvolver=hogbom'' but this feature may be more flexible in future CASA releases. More information about this option is provided in the [https://casadocs.readthedocs.io/en/v6.5.2/notebooks/synthesis_imaging.html#Masks-for-Deconvolution CASA Documentation page on Synthesis Imaging - Masks for Deconvolution]. | * The ''auto-multithresh'' automasking algorithm in [https://casadocs.readthedocs.io/en/v6.5.2/api/tt/casatasks.imaging.tclean.html tclean] provides the option to automatically generate clean mask during the deconvolution process by applying flux density thresholds to the residual image. Currently, this feature is designed to work for point sources using ''deconvolver=hogbom'' but this feature may be more flexible in future CASA releases. More information about this option is provided in the [https://casadocs.readthedocs.io/en/v6.5.2/notebooks/synthesis_imaging.html#Masks-for-Deconvolution CASA Documentation page on Synthesis Imaging - Masks for Deconvolution]. | ||
{{Checked 6.5.2}} | {{Checked 6.5.2}} | ||
Latest revision as of 18:03, 7 February 2023
Imaging
This guide has been prepared for CASA 6.5.2
This tutorial provides guidance on imaging procedures in CASA. The tutorial covers basic continuum cleaning and the influence of image weights, as well as wide-band and wide-field imaging techniques, multi-scale clean, an outlier field setup, and primary beam correction. Spectral line imaging procedures are explained but not covered in detail. For a more thorough example of spectral line imaging, refer to the VLA high-frequency Spectral Line tutorial - IRC+10216. This imaging tutorial concludes with basic image header calls and the conversion of Jy/beam to K surface brightness units through image arithmetic and header manipulation. In this tutorial, we display all images with the CARTA software. CARTA is the Cube Analysis and Rendering Tool for Astronomy, a new tool for image visualization and analysis developed for the VLA, ALMA, and future radio telescopes. CASA is no longer supporting the viewer GUI to display images. Hence we encourage users to use the CARTA for image display. For more details about how to use CARTA and open images in it, we refer to the CARTA webpage.
We will be utilizing data taken with the Karl G. Jansky Very Large Array, of a supernova remnant G055.7+3.4. The data were taken on August 23, 2010, in the first D-configuration for which the new wide-band capabilities of the WIDAR (Wideband Interferometric Digital ARchitecture) correlator were available. The 8-hour-long observation includes all available 1 GHz of bandwidth in the L-band, from 1 - 2 GHz in frequency.
We will skip the calibration process in this guide, as examples of calibration can be found in several other guides, including the VLA Continuum Tutorial 3C391 and VLA high-frequency Spectral Line tutorial - IRC+10216 guides.
A copy of the calibrated data (1.2GB) can be downloaded from http://casa.nrao.edu/Data/EVLA/SNRG55/SNR_G55_10s.calib.tar.gz
Your first step will be to unzip and untar the file in a terminal (before you start CASA):
tar -xzvf SNR_G55_10s.calib.tar.gz
Then start CASA as usual via the casa command, which will bring up the ipython interface and launches the logger.
The CLEAN Algorithm
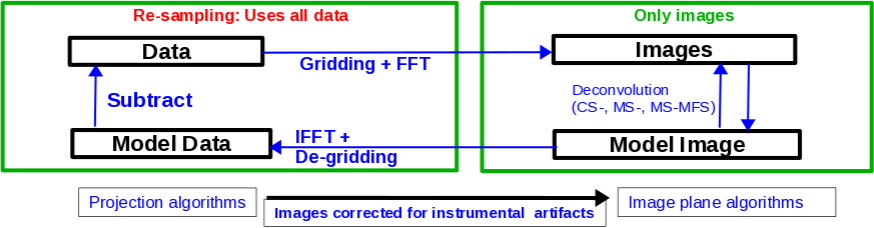
The CLEAN major and minor cycles, indicating the steps undertaken during gridding, projection algorithms, and creation of images.
The CLEAN algorithm, developed by J. Högbom (1974) enabled the synthesis of complex objects, even if they have relatively poor Fourier uv-plane coverage. Poor coverage occurs with partial earth rotation synthesis, or with arrays composed of few antennas. The "dirty" image is formed by a simple Fourier inversion of the sampled visibility data, with each point on the sky being represented by a suitably scaled and centered Point Spread Function (PSF), or dirty beam, which itself is the Fourier inversion of the visibility (u,v) coverage.
The convolution with the dirty beam creates artifacts in the image and limits the dynamic range. The CLEAN algorithm attempts to remove the dirty beam pattern from the image via deconvolution. This implies that it interpolates from the measured (u,v) points across gaps in the (u,v) coverage. In short, CLEAN provides solutions to the convolution equation by representing radio sources by a number of point sources in an empty field. The brightest points are found by performing a cross-correlation between the dirty image, and the PSF. The brightest parts (actually their PSFs) are subtracted, and the process is repeated again for the next brighter sources. Variants of CLEAN, such as multi-scale CLEAN, take into account extended kernels which may be better suited for extended objects.
For single pointings, CASA uses the Hogbom cleaning algorithm by default in the task tclean (deconvolver='hogbom'), which breaks the process into major and minor cycles (see Figure 1). To start with, the visibilities are gridded, weighted, and Fourier transformed to create a (dirty) image. The minor cycles then operate in the image domain to find the clean components that are added to the clean model: repeatedly performing a PSF+image correlation to find the next bright point, then subtracting its PSF from the image. The model image is Fourier transformed back to the visibility domain, degridded, and subtracted from the visibilities. This creates a new residual that is then gridded, weighted, and FFT'ed again to the image domain for the next iteration. The gridding, FFT, degridding, and subtraction processes form a major cycle.
This iterative process is continued until a stopping criterion is reached, such as a maximum number of clean components, or a flux threshold in the residual image.
In CASA tclean, two versions of the PSF can be used: setting deconvolver='hogbom' uses the full-sized PSF for subtraction. This is a thorough but slow method. All other options use a smaller beam patch, which increases the speed. The patch size and length of the minor cycle are internally chosen such that clean converges well without giving up the speed improvement.
In a final step, tclean derives a Gaussian fit to the inner part of the dirty beam, which defines the clean beam. The clean model is then convolved with the clean beam and added to the last residual image to create the final image.
For more details on imaging and deconvolution, we refer to the Astronomical Society of the Pacific Conference Series book entitled Synthesis Imaging in Radio Astronomy II. The chapter on Deconvolution may prove helpful. In addition, imaging presentations are available on the Synthesis Imaging Workshop and VLA Data Reduction Workshop webpages. The CASA Documentation chapter on Synthesis Imaging provides a wealth of information on the CASA implementation of tclean and related tasks.
Finally, we refer users to the VLA Observational Status Summary and the Guide to Observing with the VLA for information on the VLA capabilities and observing strategies.
Weights and Tapering

u,v coverage for the 8-hour observation of the supernova remnant G055.7+3.4
'Weighting' amounts to giving more or less weight to certain visibilities in your data set, based on their location in the uv-plane. Emphasizing long-baseline visibilities improves the resolution of your image, whereas emphasizing shorter baselines improves surface brightness sensitivity. There are three main weighting schemes that are used in interferometry:
1) Natural weighting: uv cells are weighted based on their rms. Data visibility weights are gridded onto a uv-cell and summed. More visibilities in a cell will thus increase the cell's weight, which will usually emphasize the shorter baselines. Natural weighting, therefore, results in a better surface brightness sensitivity, but also a larger PSF and therefore degraded resolution.
2) Uniform weighting: The weights are first gridded as in natural weighting but then each cell is corrected such that the weights are independent of the number of visibilities inside. The 'uniform' weighting of the baselines is a better representation of the uv-coverage and sidelobes are more suppressed. Compared to natural weighting, uniform weighting usually emphasizes longer baselines. Consequently, the PSF is smaller, resulting in a better spatial resolution of the image. At the same time, however, the surface brightness sensitivity is reduced compared to natural weighting.
3) Briggs weighting: This scheme provides a compromise between natural and uniform weighting. The transition can be controlled with the robust parameter where robust=-2 is close to uniform and robust=2 is close to natural weighting. Briggs weighting, therefore, offers a compromise between spatial resolution and surface brightness sensitivity. Typically, robust values near zero are used.
Details on the weighting schemes are given in Daniel Brigg's dissertation (Chapter 3).
For a visual comparison between these three weighting schemes, please see the section on "CLEAN with Weights" in this guide.
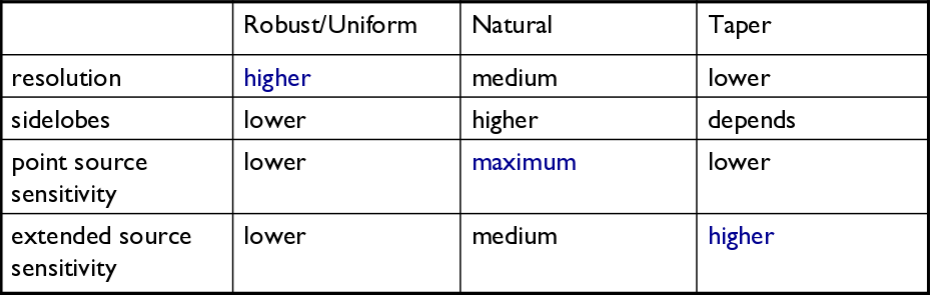
Table summarizing the effects of using weights and tapering.
Tapering: In conjunction with the above weighting schemes, one can specify the uvtaper parameter within tclean, which will control the radial weighting of visibilities in the uv-plane. Figure 2 illustrates the uv-coverage during the observing session used in this guide. The taper in tclean is an elliptical Gaussian function which effectively removes long baselines and degrades the resolution. For extended structures, this may be desirable when the long baselines contribute a large fraction of the noise. Tapering can therefore increase the surface brightness sensitivity of the data but will decrease the point source sensitivity. Too aggressive tapering, however, may also take its toll on the surface brightness sensitivity.
Table 1 summarizes the main effects of the different weighting schemes. We refer to the Synthesis Imaging section of the CASA Documentation for the details of the weighting implementation in CASA's tclean.
Primary and Synthesized Beam
The primary beam of a single antenna defines the sensitivity across the field of view. For the VLA antennas, the main part of the primary beam can be approximated by a Gaussian with an FWHM equal to [math]\displaystyle{ 42/ \nu_{GHz} }[/math] arcminutes (for frequencies in the range 1 - 50 GHz). But note that there are sidelobes beyond the Gaussian kernel that are sensitive to bright sources (see below). Taking our observed frequency to be the middle of the L-band, 1.5 GHz, our primary beam (FWHM) will be about 28 arcmin in diameter.
Note: New beam measurements were made recently and are described in EVLA memo #195. These newer beam corrections are the default in CASA 5.5.0.
If your science goal is to image a source or field of view that is significantly larger than the FWHM of the VLA primary beam, then creating a mosaic from a number of telescope pointings is usually the preferred method. For a tutorial on mosaicking, see the 3C391 tutorial. In this guide, we discuss methods for imaging large areas from single-pointing data.
As these data were taken in the D-configuration, we can check the Observational Status Summary's section on VLA resolution to find that the synthesized beam for uniform weighting will be approximately 46 arcsec. Variations in flagging, weighting scheme, and effective frequency may result in deviations from this value. The synthesized beam is effectively the angular resolution of the image. As we will see later, the synthesized beam of our data hovers around 29 arcsec or, for the extreme of uniform weighting, around 26"x25".
Cell (Pixel) Size and Image Size
For the most effective cleaning, we recommend using a pixel size such that there are 3 - 5 pixels across the synthesized beam. Based on the assumed synthesized beam size of 46 arcsec, we will use a cell (pixel) size of 8 arcsec.
In the tclean task, the image size is defined by the number of pixels in the RA and dec directions. The execution time of tclean depends on the image size. Large images generally take more computing time. There are some particular image sizes (by a number of pixels) that are computationally inadvisable. For inputs corresponding to such image sizes, the logger will show a recommendation for an appropriate larger, but computationally faster, image size. As a general guideline, we recommend image sizes [math]\displaystyle{ 5*2^n*3^m (n=1,2,... , m=1,2,...) }[/math] pixel, e.g. 160, 1280 pixels, etc. for improved processing speeds.
Our target field contains bright point sources that are well outside the primary beam. The VLA, in particular when using multi-frequency synthesis (see below), will have significant sensitivity outside the main lobe of the primary beam. Particularly at the lower VLA frequencies, sources that are located outside the primary beam may still be bright enough to be detected in the primary beam sidelobes, causing artifacts that interfere with the targeted field in the main part of the primary beam. Such sources need to be cleaned to remove the dirty beam response of these interfering sources from the entire image. This can be achieved either by creating a very large image that encompasses these interfering sources or by using 'outlier' fields centered on the strongest sources (see the section on outlier fields below). A large image has the added advantage of increasing the field of view for science (albeit at lower sensitivity beyond the primary beam). But other effects will start to become significant, like the non-coplanarity of the sky. Large image sizes will also slow down the deconvolution process. Details are provided in Sanjay Bhatnagar's presentation: "Advanced Imaging: Imaging in the Wide-band Wide-field era" given at the 2016 VLA data reduction workshop.
The calls to the tclean task within this guide will create images that are approximately 170 arcminutes on a side, or almost 6x the size of the primary beam, encompassing its first and second sidelobes. This is ideal for showcasing both the problems inherent in wide-band/wide-field imaging, as well as some of the solutions currently available in CASA to deal with these issues. We, therefore, set the image size to 1280 pixels on each side, for efficient processing speed. (1280 pixels x 8 arcsec/pixel = 170.67 arcmin)
Clean Output Images
As a result of the CLEAN algorithm, tclean will create a number of output images. For a parameter setting of imagename='<imagename>', these image names will be:
<imagename>.residual: the residual after subtracting the clean model (unit: Jy/beam, where beam refers to the dirty beam)
<imagename>.model: the clean model, not convolved (unit: Jy/pixel)
<imagename>.psf: the point-spread function (dirty beam)
<imagename>.pb: the normalized sensitivity map, which corresponds to the primary beam in the case of a single-pointing image
<imagename>.image: the residual + the model convolved with the clean beam; this is the final image (unit: Jy/beam, where beam refers to the clean beam)
<imagename>.sumwt: a single pixel image containing sum-of-weights (for natural weighting, the sensitivity = 1/sqrt(sumwt).
Additional images will be created for specific algorithms like multi-term frequency synthesis or mosaicking.
Important: If an image file is present in the working directory and the same name is provided in imagename, tclean will use that image (in particular the residual and model image) as a starting point for further cleaning. If you want a fresh run of tclean, first remove all images of that name using 'rmtables()':
Important: By default, tclean sets savemodel to a value of 'none', meaning no model image is saved. Be sure to set this parameter to 'modelcolumn' for any model you wish to save. This is especially important for self-calibration.
# In CASA
rmtables('<imagename>.*')
This method is preferable over 'rm -rf' as it also clears the cache.
Note that interrupting tclean by Ctrl+C may corrupt your visibilities - you may be better off choosing to let tclean finish. We are currently implementing a command that will nicely exit to prevent this from happening, but for the moment try to avoid Ctrl+C.
Dirty Image
First, we will create a dirty image (Figure 3a) to see the improvements as we step through several cleaning algorithms and parameters. The dirty image is the true image on the sky, convolved with the dirty beam, also known as the Point Spread Function (PSF). We create a dirty image by running tclean with niter=0, which will run the task without performing any CLEAN iterations.
# In CASA
tclean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.dirty',
imsize=1280, cell='8arcsec', pblimit=-0.01, niter=0,
stokes='I', savemodel='modelcolumn')
- imagename='SNR_G55_10s.dirty': the root filename used for the various tclean outputs.
- imsize=1280: the image size in a number of pixels. A single value will result in a square image.
- cell='8arcsec': the size of one pixel; again, entering a single value will result in a square pixel size.
- pblimit=-0.01: defines the value of the antenna primary bean gain. A positive value defines a T/F pixel mask that is attached to the output residual and restored images while a negative value does not include this T/F mask.
- niter=0: this controls the number of iterations done in the minor cycle.
- interactive=False: For a tutorial that covers more of an interactive clean, please see the VLA high-frequency Spectral Line tutorial - IRC+10216.
- savemodel='modelcolumn: controls writing the model visibilities to the model data column. For self-calibration, we currently recommend setting savemodel='modelcolumn'. The default value is "none": so, this must be changed for the model to be saved. The use of the virtual model with MTMFS in tclean is still under commissioning, so we recommend currently to set savemodel='modelcolumn'.
- stokes='I': since we have not done any polarization calibration, we only create a total-intensity image. For using tclean while including various Stoke's parameters, please see the 3C391 CASA guide.
# In CARTA
open SNR_G55_10s.dirty.image
# In CARTA
open SNR_G55_10s.dirty.psf
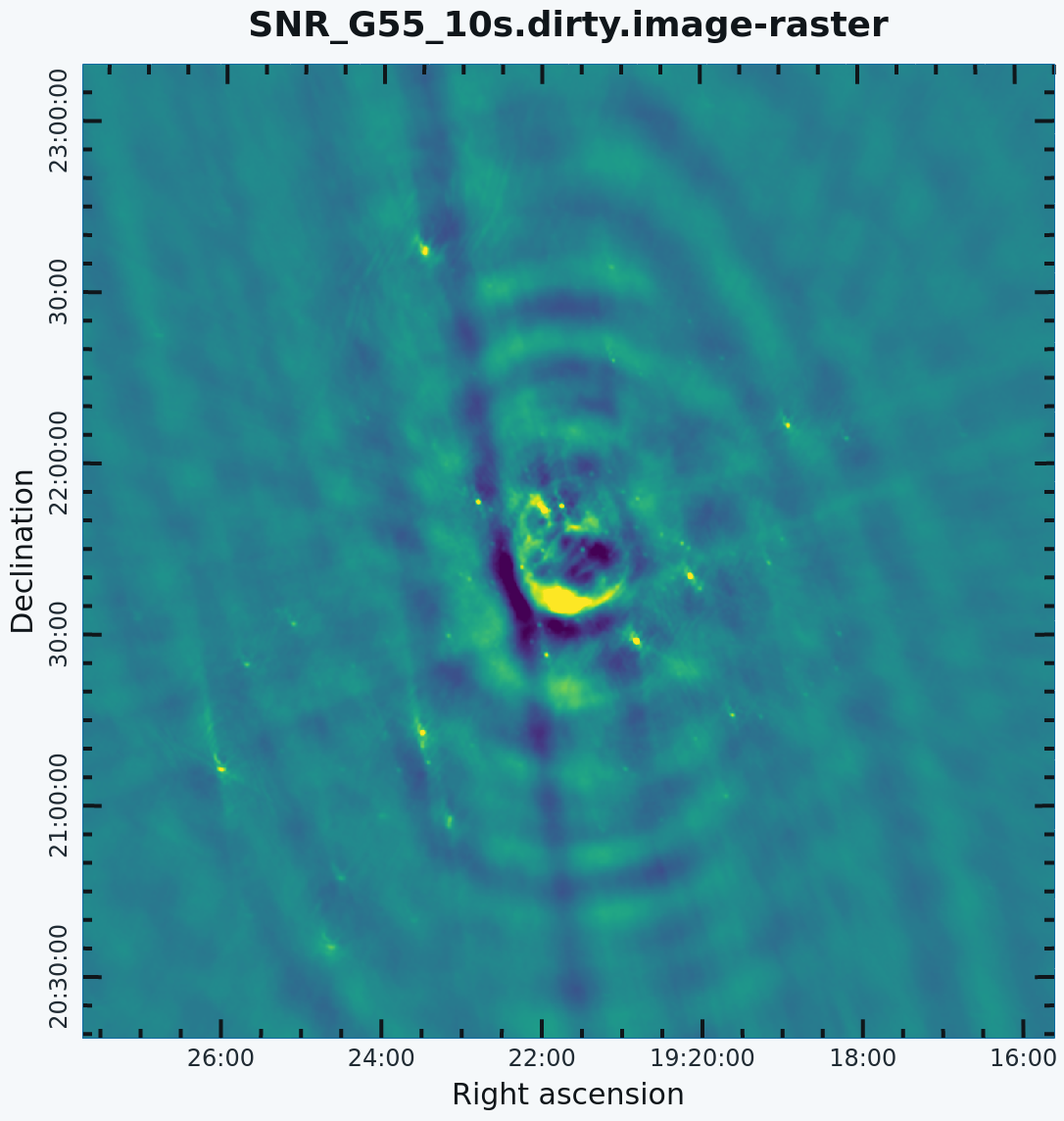 A dirty image of the supernova remnant G55.7+3.4 in viridis scale, with apparent sidelobes. |
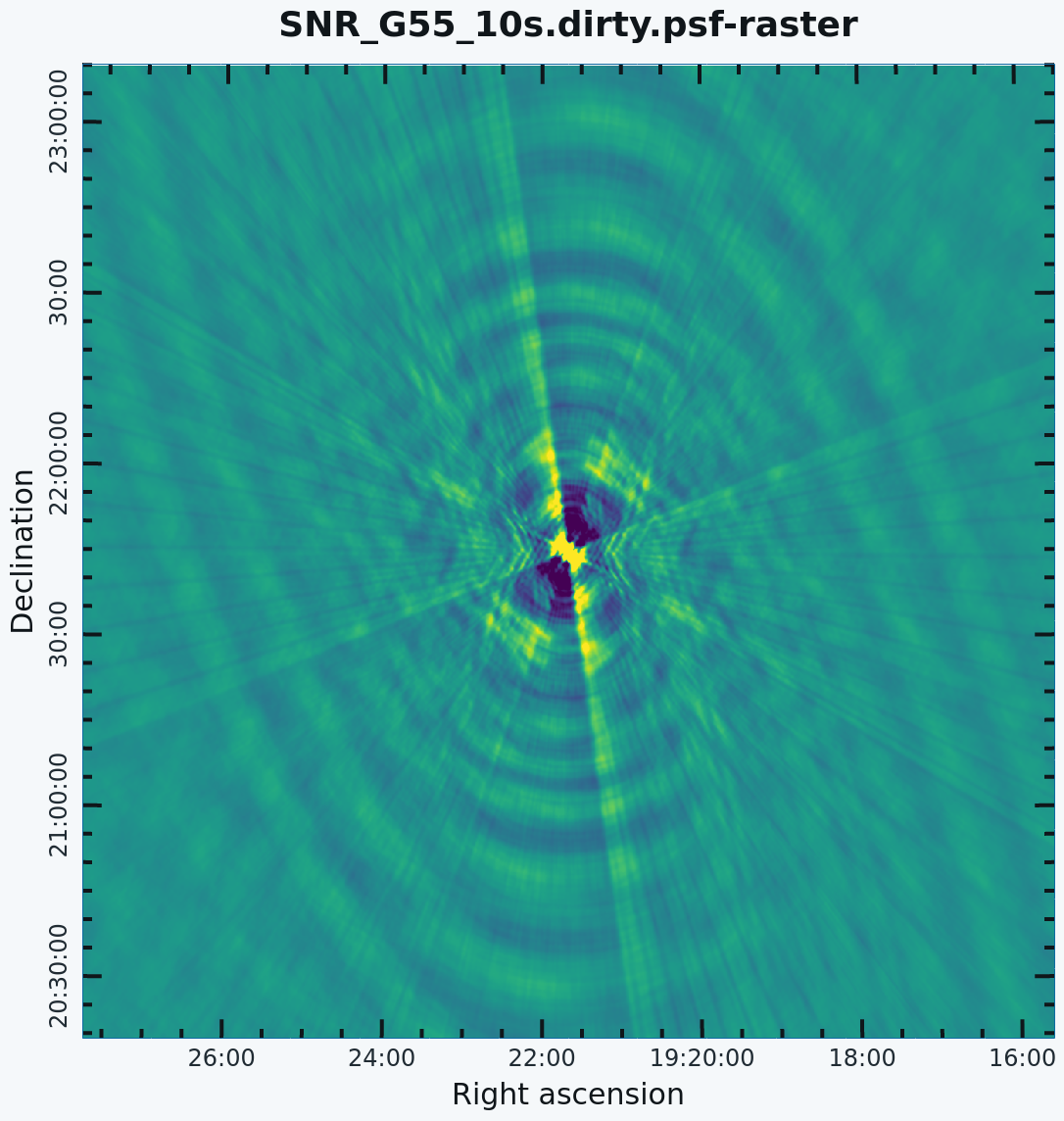 The Point Spread Function (PSF) in viridis scale. This is also known as the dirty beam. |
The images may be easier to see in a more user-friendly color scale of viridas. If the user wants to change the color scheme in CARTA, click on the "Color map" option within the "Render configuration" widget of CARTA. You may also wish to change the Clip Min, Clip Max, and Scaling options to your liking. For more information about how to change the brightness and contrast, click the help option (top right) of the Render configuration widget.
Note that the clean beam is only defined after some clean iterations. The dirty image has therefore no beam size specified in the header, and the PSF image (Figure 3b) is the representation of the response of the array to a point source. Even though it is empty because we set niter=0, tclean will still produce a model file. Thus we could progress into actual cleaning by simply restarting tclean with the same image root name (and niter>0).
Regular CLEAN & RMS Noise
Now, we will create a regular clean image using mostly default values to see how deconvolution improves the image quality. The first run of tclean will use a fixed number of minor cycle iterations of niter=1000 (default is 0); the second will use niter=10000. Note that you may have to play with the image color map and brightness/contrast to get a better view of the image details.
# In CASA. Create a default clean image.
tclean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.Reg.Clean.niter1K',
imsize=1280, cell='8arcsec', pblimit=-0.01, niter=1000, savemodel='modelcolumn')
# In CARTA
open SNR_G55_10s.Reg.Clean.niter1K.image
The logger indicates that the image was obtained in two major cycles, and some improvements over the dirty image are visible. But clearly, we have not cleaned deep enough yet; the image still has many sidelobes, and an inspection of the residual image shows that it still contains source flux and structure. So let's increase the niter value to 10,000 and compare the images.
# In CASA. Create default clean image with niter = 10000
tclean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.Reg.Clean.niter10K',
imsize=1280, cell='8arcsec', pblimit=-0.01, niter=10000, savemodel='modelcolumn')
Users can also control the execution of the major cycle using the nmajor parameter. Once tclean reaches the required major cycle executions, then it will stop.
# In CASA. Create default clean image with major cycle 4
tclean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.Reg.Clean.nmajor4',
imsize=1280, cell='8arcsec', pblimit=-0.01, nmajor=4, niter=10000,savemodel='modelcolumn')
# In CARTA
open SNR_G55_10s.Reg.Clean.niter10K.image
 Regular run of TCLEAN, with niter=1000. |
 Regular run of TCLEAN, with niter=10000. |
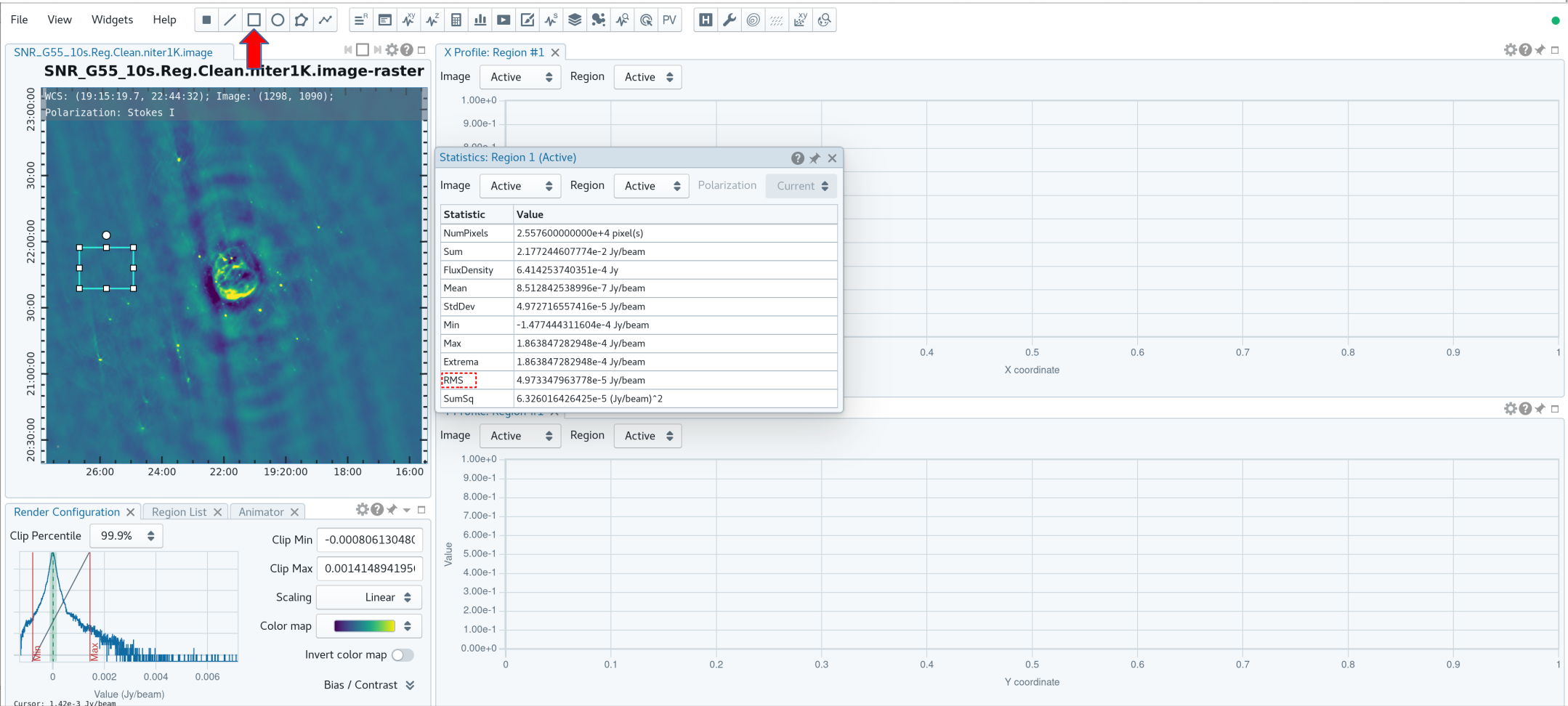
Attempting to find the lowest rms value within the CLEAN'ed image using niter=1000, in order to calculate our threshold.
As we can see from the resulting images, increasing the niter values (minor cycles) improves our image by reducing prominent sidelobes significantly (Figure 4b). One could now further increase the niter parameter until the residuals are down to an acceptable level. To determine the number of iterations, one needs to keep in mind that tclean will fail once it starts cleaning too deeply into the noise. At that point, the cleaned flux and the peak residual flux values will start to oscillate as the number of iterations increase. This effect can be monitored on the CASA logger output. To avoid cleaning too deeply, we will set a threshold parameter that will stop minor cycle clean iterations once a peak residual value is reached.
First, we will utilize the SNR_G55_10s.Reg.Clean.niter1K.image (Figure 4a) image to give us an idea of the rms noise (your sigma value). With the image open within the CARTA, click on the 'Rectangle' button in the region bar at the top of the GUI and draw a square on the image at a position with little source or sidelobe contamination. Users can also activate the region creation mode, click the Show toolbar button at the bottom-right corner of the image viewer then click the Create region button or pressing the C key. Double-clicking the Create region icon opens up all available region types (point, line, rectangle, ellipse, polygon, and polyline). Select the polygon and draw a square as mentioned above. After drawing the square in an empty region, click the Statistic widget from the Widget bar at the top of the GUI. This will open another window of the name Statistic: Region 1 (Figure 5) which holds information about the selected region, including the pixel statistics. Take notice of the RMS values. User can draw multiple regions (of any shape which draw over enough amount of pixels) like this at different empty regions to get a better rms estimation.
The lowest rms value we found was in the order of about [math]\displaystyle{ 5\cdot10^{-5} }[/math] Jy/beam, which we will use to calculate our threshold. There really is no set standard, but fairly good threshold values can vary anywhere between 3.0 - 5.0*sigma; using clean boxes (see the section on interactive cleaning) allows one to go to lower thresholds. For our purposes, we will choose a threshold of 3*sigma. Doing the math results in a value of [math]\displaystyle{ 15\cdot10^{-5} }[/math] or equivalently 0.15mJy/beam. Therefore, for future calls to the tclean task, we will set threshold='0.15mJy'. The clean cycle will be stopped when the residual peak flux density is equal to or less than the threshold value, or when the maximum number of iterations niter is reached. To ensure that the stopping criterion is indeed threshold, niter should be set to a very high number. In the following, we nevertheless will use niter=1000 to keep the execution times of tclean on the low end as we focus on explaining different imaging methods.
An alternative method to determine the approximate rms of an image is to use the VLA Exposure Calculator and to enter the observing conditions. Make sure that the chosen bandwidth reflects the data after RFI excision.
CLEAN with Weights
To see the effects of using different weighting schemes on the image, let's change the weighting parameter within tclean and inspect the resulting images. We will be using the Natural, Uniform, and Briggs weighting algorithms. Here, we have chosen a smaller image size to mainly focus on our science target.
# In CASA. Natural weighting
tclean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.natural', weighting='natural',
imsize=540, cell='8arcsec', pblimit=-0.01, niter=1000, interactive=False, threshold='0.15mJy', savemodel='modelcolumn')
- weighting: specification of the weighting scheme. For Briggs weighting, the robust parameter will be used.
- threshold='0.15mJy': threshold at which the cleaning process will halt.
# In CASA. Uniform weighting
tclean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.uniform',weighting='uniform',
imsize=540, cell='8arcsec', pblimit=-0.01, niter=1000, interactive=False, threshold='0.15mJy', savemodel='modelcolumn')
# In CASA. Briggs weighting, with robust set to 0.0
tclean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.briggs', weighting='briggs', robust=0.0,
imsize=540, cell='8arcsec', pblimit=-0.01, niter=1000, interactive=False, threshold='0.15mJy', savemodel='modelcolumn')
# Open CARTA and select the created images to display.
open SNR_G55_10s.natural.image
open SNR_G55_10s.uniform.image
open SNR_G55_10s.briggs.image
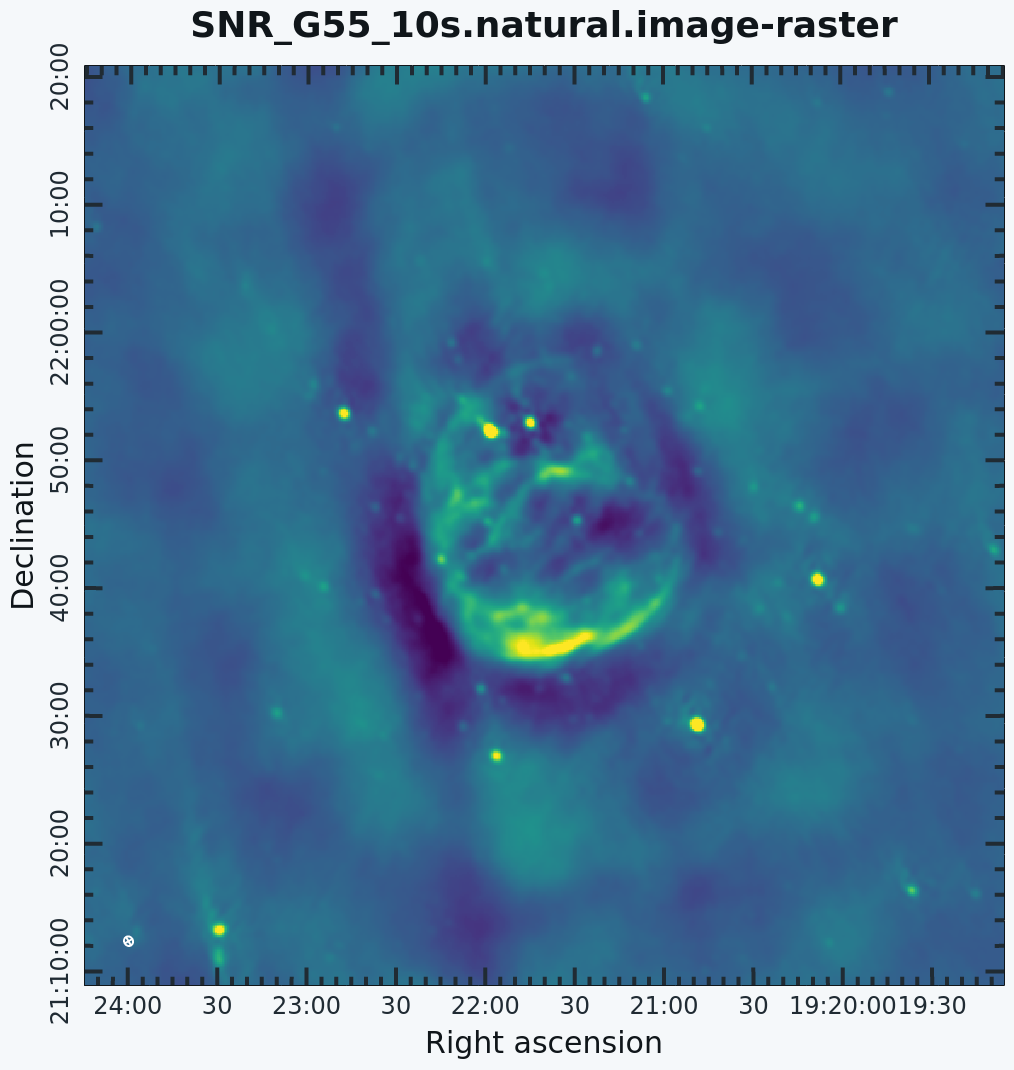 Natural weighting. |
 Uniform weighting. |
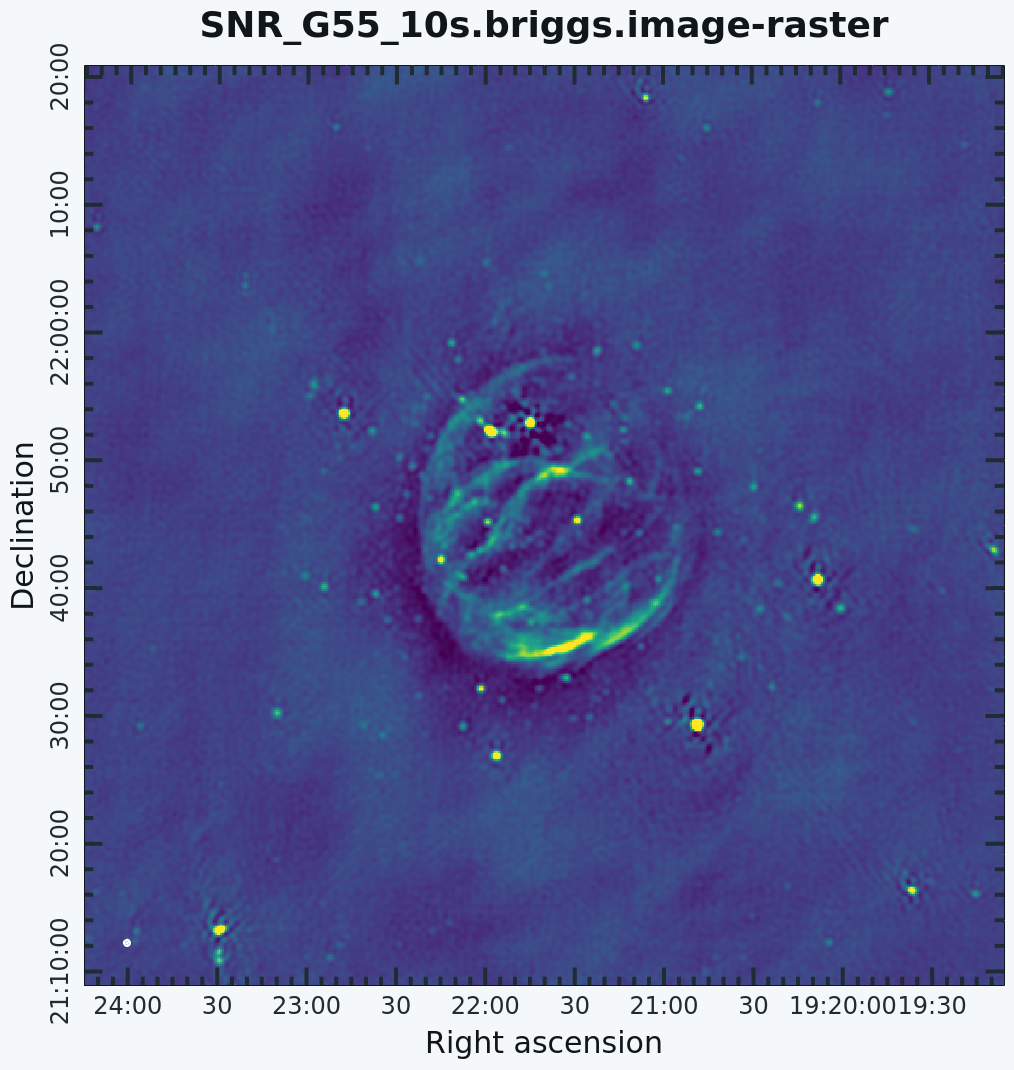 Briggs weighting. |
Figure 6a shows that the natural weighted image is most sensitive to extended emission (beam size of 46"x41"). The negative values around the extended emission (often referred to as a negative 'bowl') are a typical signature of unsampled visibilities near the origin of the uv-plane. That is, the flux density present at shorter baselines (or larger angular scales) than measured in this observation is not represented well. Uniform weighted data (Figure 6b) shows the highest resolution (26"x25") and Briggs (Figure 6c) 'robust=0' (default value is 0.5) is a compromise with a beam of 29"x29". To image more of the extended emission, the 'robust' parameter could be tweaked further toward more positive values.
Multi-Scale CLEAN
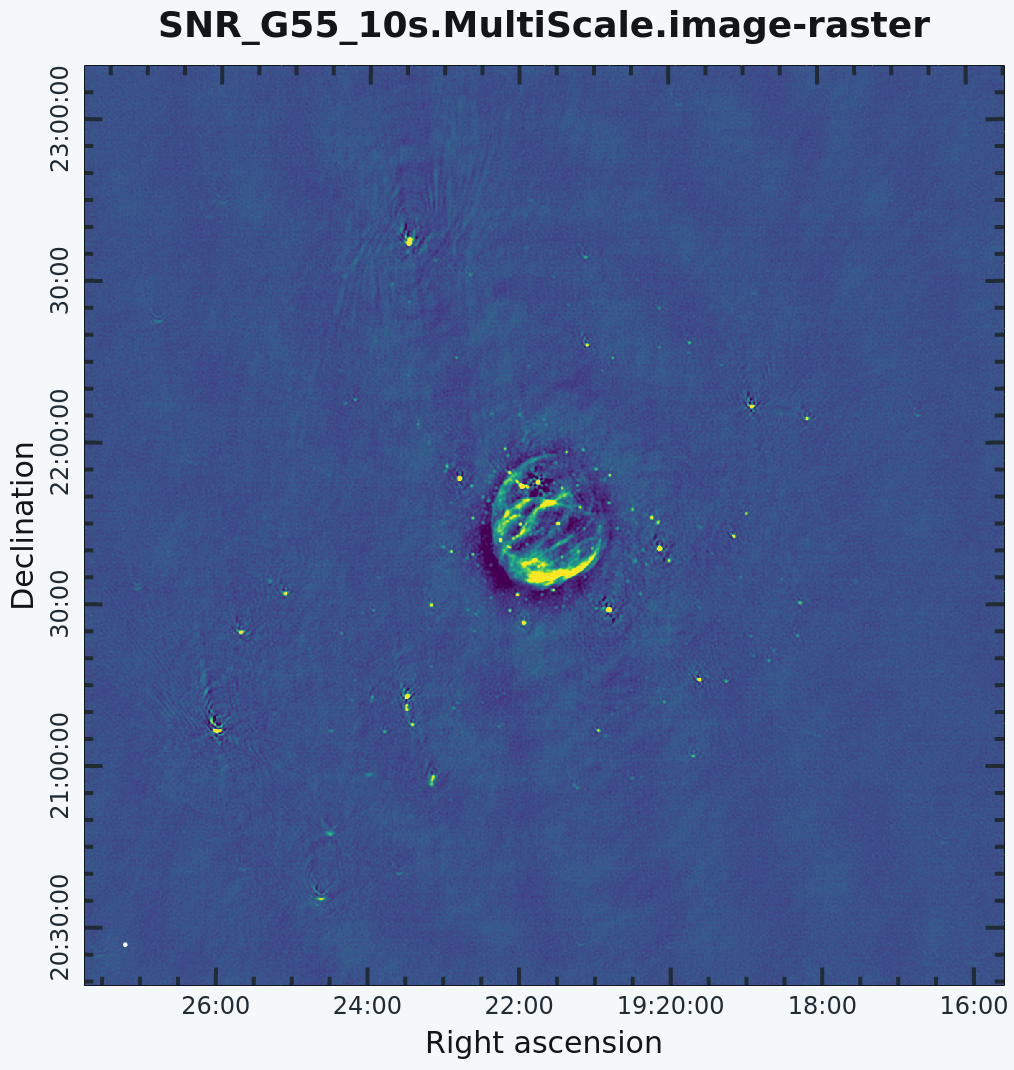
G55.7+3.4 Multi-Scale Clean
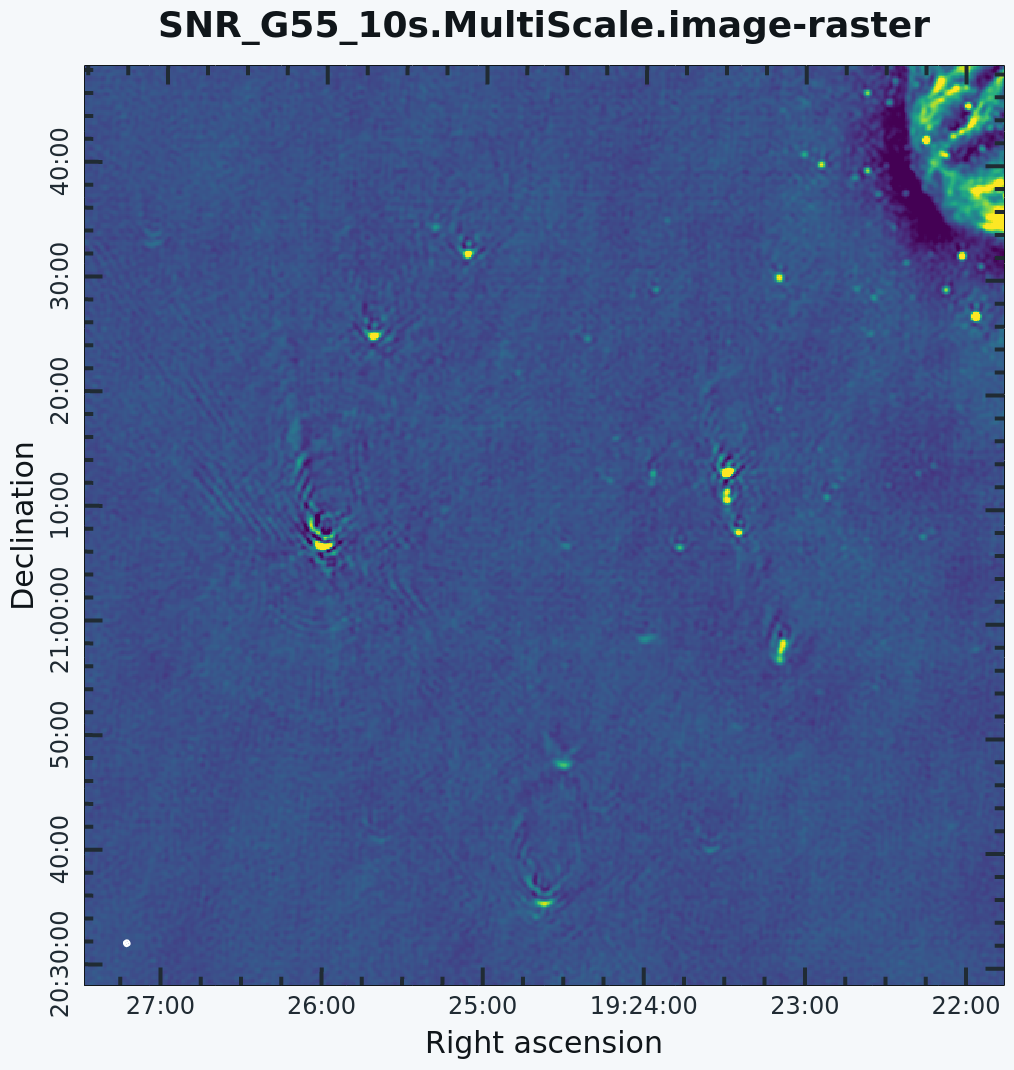
Artifacts around point sources
Since G55.7+3.4 is an extended source with many angular scales, a more advanced form of imaging involves the use of multiple scales. MS-CLEAN is an extension of the classical CLEAN algorithm for handling extended sources. Multi-Scale CLEAN works by assuming the sky is composed of emissions at different angular scales and works on them simultaneously, thereby creating a linear combination of images at different angular scales. For a more detailed description of Multi-Scale CLEAN, see T.J. Cornwell's paper Multi-Scale CLEAN deconvolution of radio synthesis images.
If one is interested in measuring the flux density of an extended source as well as the associated uncertainty of that flux density, use the CARTA to first draw a region (using the polygon tool) around the source for which you want to measure the flux density for and it’s associated uncertainty. The lines drawn by the polygon tool will be in editing mode and allow for the vertices to be moved to create whatever shape is desired around the source. Once a satisfactory shape has been created around the source, click on the Statistics Widget. In the opened statistics window, the following quantities should be recorded: BeamArea (the size of the restoring beam in pixels), NumPixels (the number of pixels inside of the region), and FluxDensity (the total flux inside of the region). Once recorded, draw another region several times the size of the restoring beam which only includes noise-like pixels (no sources should be present in this second region). In the statistics window, record the Rms value. Finally - you can compute the error of the total flux like so: [math]\displaystyle{ Rms \times \sqrt(\frac{NumPixels}{BeamArea}) }[/math] Note: the value of NumPixels/BeamArea can also be called the number of independent beams and should be >> 1. If it is close to or less than 1, there are other more accurate techniques to use to calculate the error.
We will use a set of scales (expressed in units of the requested pixel or cell size) that are representative of the scales that are present in the data, including a zero-scale for point sources.
# In CASA
tclean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.MultiScale', deconvolver='multiscale', scales=[0,6,10,30,60],
smallscalebias=0.9, imsize=1280, cell='8arcsec', pblimit=-0.01, niter=1000,weighting='briggs', stokes='I',
robust=0.0, interactive=False, threshold='0.12mJy', savemodel='modelcolumn')
- multiscale=[0,6,10,30,60]: a set of scales on which to clean. A general guideline when using multiscale is 0, 2xbeam, 5xbeam (where beam is the synthesized beam), and larger scales up to about half the minor axis maximum scale of the mapped structure. Since these are in units of pixel size, our chosen values will be multiplied by the requested cell size. Thus, we are requesting scales of 0 (a point source), 48, 80, 240, and 480 arcseconds (8 arcminutes). Note that 16 arcminutes (960 arcseconds) roughly corresponds to the size of G55.7+3.4.
- smallscalebias=0.9: This parameter is known as the small scale bias, and helps with faint extended structure by balancing the weight given to smaller structures, which tend to have higher surface brightness but lower integrated flux density. Increasing this value gives more weight to smaller scales. A value of 1.0 weights the largest scale to zero, and a value of less than 0.2 weights all scales nearly equally. The default value is 0.6.
# In CARTA
open SNR_G55_10s.MultiScale.image
The logger will show how much cleaning is performed on the individual scales.
This is the fastest of the advanced imaging techniques described here, but it's easy to see that there are artifacts in the resulting image (Figure 7). We can use the Template:CARTA to explore the point sources near the edge of the field by zooming in on them (Figure 8). In CARTA, one can zoom an image by using the mouse wheel to scroll up or down. Alternatively, use the zoom buttons from the toolbar at the bottom-right of the image viewer. After zooming in on the area, we can see some radio sources that have prominent arcs, as well as spots with a six-pointed pattern surrounding them.
Next, we will further explore advanced imaging techniques to mitigate the artifacts seen toward the edges of the image.
Multi-Scale, Wide-Field CLEAN (w-projection)
Faceting when using wide-field gridder, which can be used in conjunction with w-projection.
The next tclean algorithm we will employ is w-projection, which is a wide-field imaging technique that takes into account the non-coplanarity of the baselines as a function of distance from the phase center (Figure 9). For wide-field imaging, the sky curvature and non-coplanar baselines result in a non-zero w-term. The w-term, introduced by the sky and array non-coplanarity, results in a phase term that will limit the dynamic range of the final image. Applying 2-D imaging to such data will result in artifacts around sources away from the phase center, as we saw in running MS-CLEAN. Note that this affects mostly the lower frequency bands where the field of view is large.
The w-term can be corrected by faceting (which projects the sky curvature onto many smaller planes) in either the image or uv-plane. The latter is known as w-projection. A combination of the two can also be employed within tclean by setting the parameters gridder='wproject' and deconvolver='multiscale' . We can estimate whether our image requires W-projection by calculating the recommended number of w-planes using this formula (taken from page 392 of the NRAO 'white book',
[math]\displaystyle{ N_{wprojplanes} = \left ( \frac{I_{FOV}}{\theta_{syn}} \right ) \times \left ( \frac{I_{FOV}}{1\, \mathrm{radian}} \right ) }[/math] where [math]\displaystyle{ N_{wprojplanes} }[/math] is the number of w-projection planes, [math]\displaystyle{ I_{FOV} }[/math] is the image field-of-view and theta_syn is the synthesized beam size. If the recommended number of planes is <=1, then we would not need to turn on the wide-field gridder and can leave it as gridder='standard'. See this link to CASAdocs for a more detailed discussion.
If w-projection is employed, it will be done for each facet. Note that w-projection is an order of magnitude faster than the image-plane based faceting algorithm, but requires more memory.
For more details on w-projection, as well as the algorithm itself, see "The Noncoplanar Baselines Effect in Radio Interferometry: The W-Projection Algorithm". Also, the chapter on Imaging with Non-Coplanar Arrays may be helpful.
# In CASA
tclean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.wProj',
gridder='wproject', wprojplanes=-1, deconvolver='multiscale', scales=[0,6,10,30,60],
smallscalebias=0.9, imsize=1280, cell='8arcsec', pblimit=-0.01, niter=1000, weighting='briggs',
stokes='I', robust=0.0, interactive=False, threshold='0.15mJy', savemodel='modelcolumn')
- gridder='wproject': Use the w-projection algorithm.
- wprojplanes=-1: The number of w-projection planes to use for deconvolution. Setting to -1 allows CLEAN to automatically choose an acceptable number of planes for the given data.
# In CARTA
open SNR_G55_10s.wProj.image
This will take slightly longer than the previous imaging round; however, the resulting image which employs Multi-Scale and w-projection (Figure 10b) has noticeably fewer artifacts than the image which just employed Multi-Scale (Figure 10a). In particular, compare the same outlier source in the Multi-Scale w-projected image with the Multi-Scale-only image: note that the swept-back arcs have disappeared. There are still some obvious imaging artifacts remaining, though.
Multi-Scale, Multi-Term Multi-Frequency Synthesis
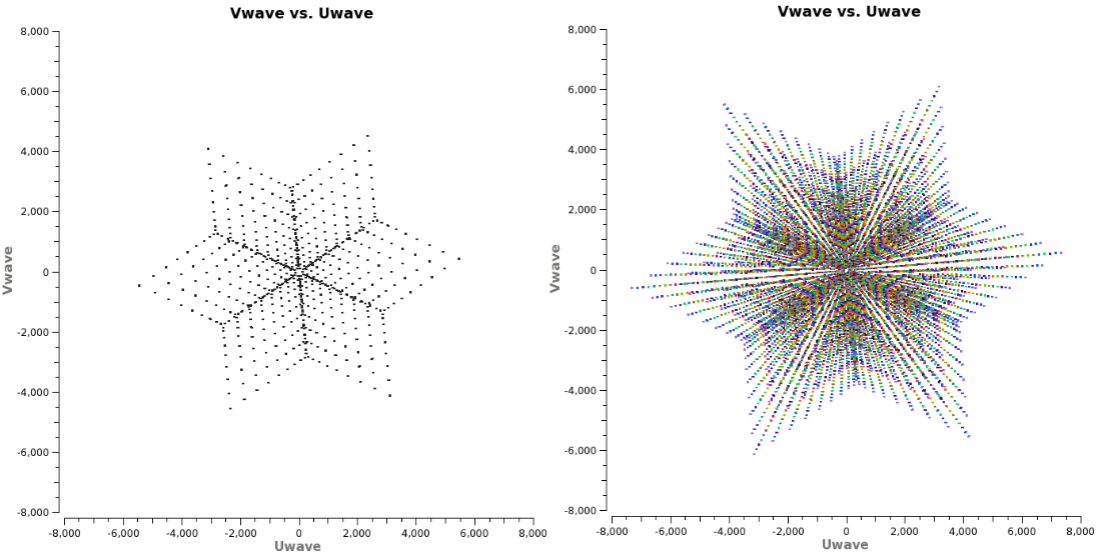
Left: (u,v) coverage snapshot at a single frequency. Right: Multi-Frequency Synthesis snapshot of (u,v) coverage. Using this algorithm can greatly improve (u,v) coverage, thereby improving image fidelity.
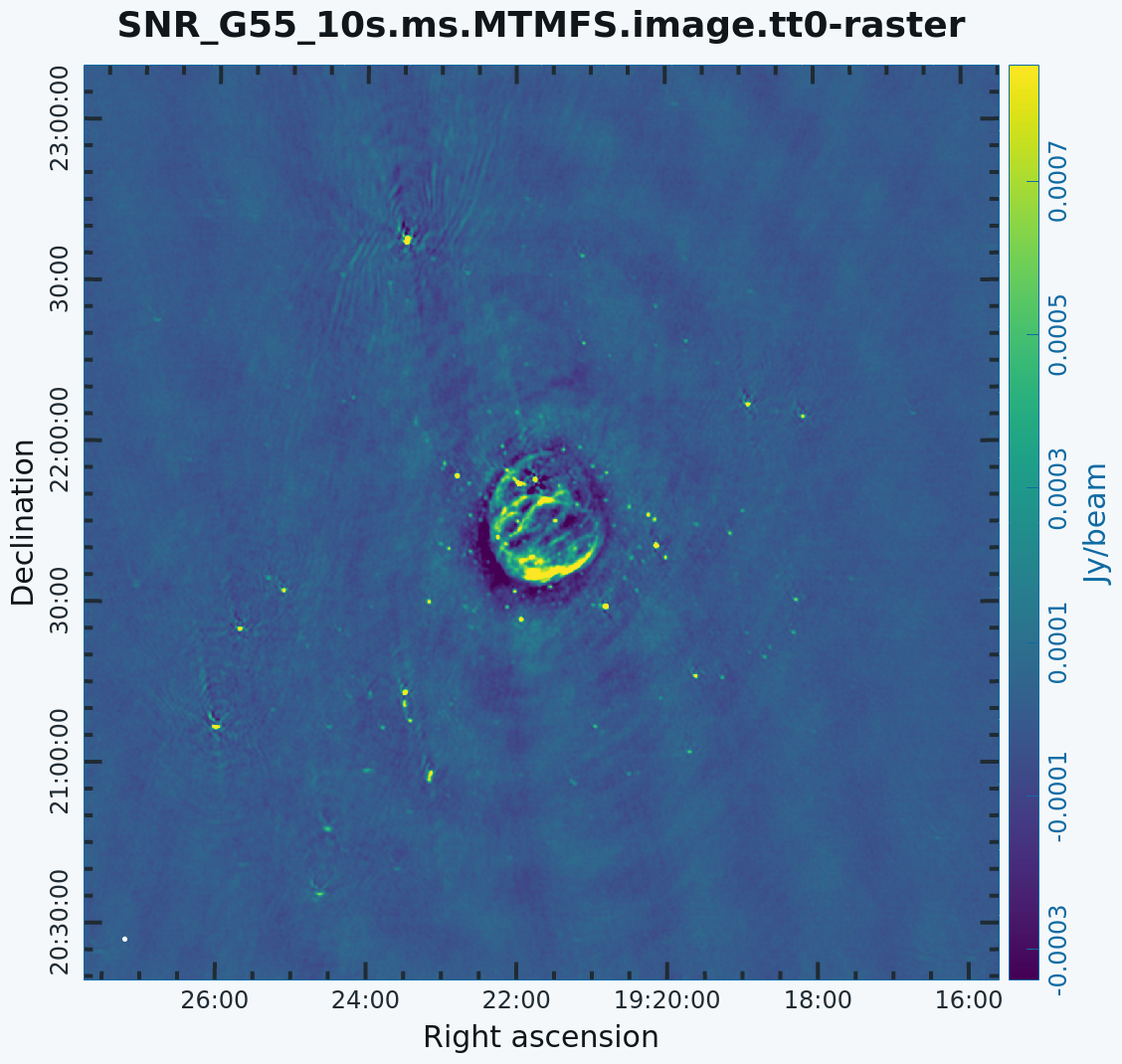
Multi-Scale imaged with MT-MFS and nterms=2. Artifacts around point sources close to the phase center are reduced while point sources away from the phase center still show artifacts.
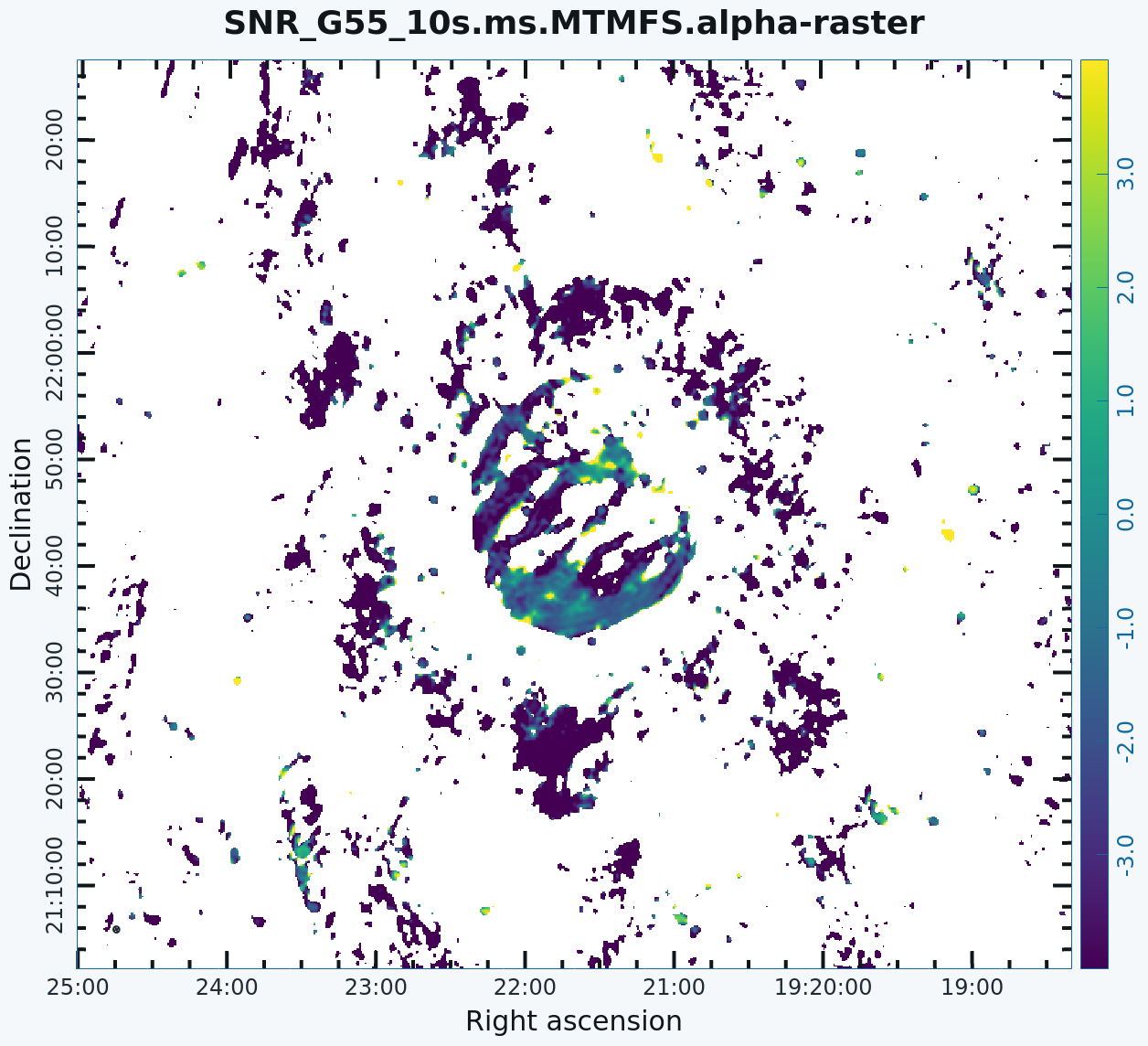
Spectral Index image
A consequence of simultaneously imaging all the frequencies across the wide fractional bandwidth of the VLA is that the primary and synthesized beams have substantial frequency-dependent variation over the observed band. If this variation is not accounted for, it will lead to imaging artifacts and will compromise the achievable image rms.
The coordinates of the (u,v) plane are measured in wavelengths. Observing at several frequencies results means that a single baseline will sample several ellipses in the (u,v) plane, each with different sizes. We can therefore fill in the gaps in the single frequency (u,v) coverage (Figure 11) to achieve a much better image fidelity. This method is called Multi-Frequency Synthesis (MFS), which is the default cleaning mode in CLEAN. For a more detailed explanation of the MS-MFS deconvolution algorithm, please see the paper A multi-scale multi-frequency deconvolution algorithm for synthesis imaging in radio interferometry.
The Multi-Scale, Multi-Term Multi-Frequency Synthesis (MS-MT-MFS) algorithm provides the ability to simultaneously image and fit for the intrinsic source spectrum in each pixel. The spectrum is approximated using a polynomial Taylor-term expansion in frequency, with the degree of the polynomial as a user-controlled parameter. A least-squares approach is used, along with the standard clean-type iterations.
# In CASA
tclean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.ms.MTMFS',
gridder='standard', imsize=1280, cell='8arcsec', specmode='mfs',
deconvolver='mtmfs', nterms=2, scales=[0,6,10,30,60], smallscalebias=0.9,
interactive=False, niter=1000, weighting='briggs', pblimit=-0.01,
stokes='I', threshold='0.15mJy', savemodel='modelcolumn')
- nterms=2: the number of Taylor-terms to be used to model the frequency dependence of the sky emission. Note that the speed of the algorithm will depend on the value used here (more terms will be slower). nterms=2 will fit a spectral index, while nterms=3 will fit a spectral index and spectral curvature.
For Multi-Term MFS, tclean produces images with extension tt*, where the number in place of the asterisk indicates the Taylor term: <imagename>.image.tt0 is the total intensity image (Figure 12) and <imagename>.image.alpha will contain an image of the spectral index in regions where there is sufficient signal-to-noise (Figure 13). For Figure 12, we have included a colorbar to give an idea of the flux within the image. The spectral index image can help convey information about emission mechanisms as well as the optical depth of the source.
# In CARTA
open SNR_G55_10s.ms.MTMFS.image.tt0
# In CARTA
open SNR_G55_10s.ms.MTMFS.alpha
Note: To replicate Figure 13, open the image within the CARTA, click on File -> Preferences -> Render Configuration and change the NaN color to white, and adjust your margins manually to best fit the image in CARTA's viewer window. To adjust the colorbar, click on the settings (on the top-right of the image viewer window), click on the "Colorbar" button, and adjust the various parameters to your liking.
For more information on the multi-term, multi-frequency synthesis mode, and its outputs, see the Deconvolution Algorithms section in the CASA documentation.
Inspect the brighter point sources in the field near the supernova remnant. You will notice that some of the artifacts, which had been symmetric around the sources, are gone; however, as we did not use w-projection, there are still strong features related to the non-coplanar baseline effects still apparent for sources further away.
At this point, tclean takes into account the frequency variation of the synthesized beam but not the frequency variation of the primary beam. For low frequencies and large bandwidths, this can be substantial; e.g., 1 - 2 GHz L-band observations result in a variation of a factor of 2. One effect of imaging with MFS across such a large fractional bandwidth is that primary beam nulls will be blurred; the interferometer is sensitive everywhere in the field of view. However, if there is no correction made to account for the variation in the primary beam with frequency, sources away from the phase center appear to have a steeply false spectral slope. A correction for this effect should be made with the task widebandpbcor or set pbcor=True (see the section on Primary Beam Correction below).
Multi-Scale, Multi-Term Multi-Frequency Synthesis with W-Projection
We will now combine the w-projection and MS-MT-MFS algorithms. Be forewarned -- these imaging runs will take a while, and it's best to start them running and then move on to other things.
Using the same parameters for the individual-algorithm images above, but combined into a single tclean run, we have:
# In CASA
tclean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.ms.MTMFS.wProj',
gridder='wproject',wprojplanes=-1, pblimit=-0.01, imsize=1280, cell='8arcsec', specmode='mfs',
deconvolver='mtmfs', nterms=2, scales=[0,6,10,30,60], smallscalebias=0.9,
interactive=False, niter=1000, weighting='briggs',
stokes='I', threshold='0.15mJy', savemodel='modelcolumn')
# In CARTA
open SNR_G55_10s.ms.MTMFS.wProj.image.tt0
# In CARTA
open SNR_G55_10s.ms.MTMFS.wProj.alpha
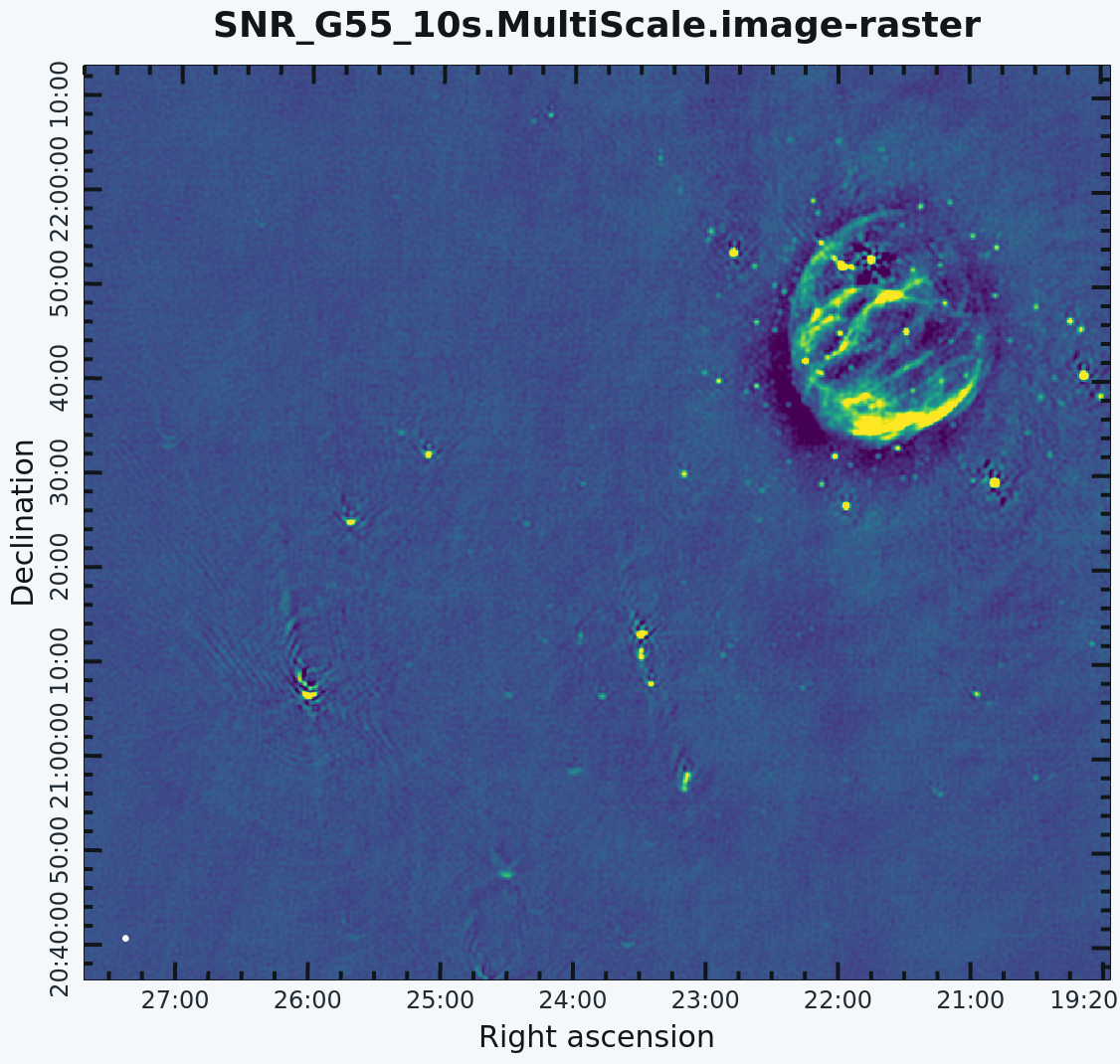 Multi-Scale. |
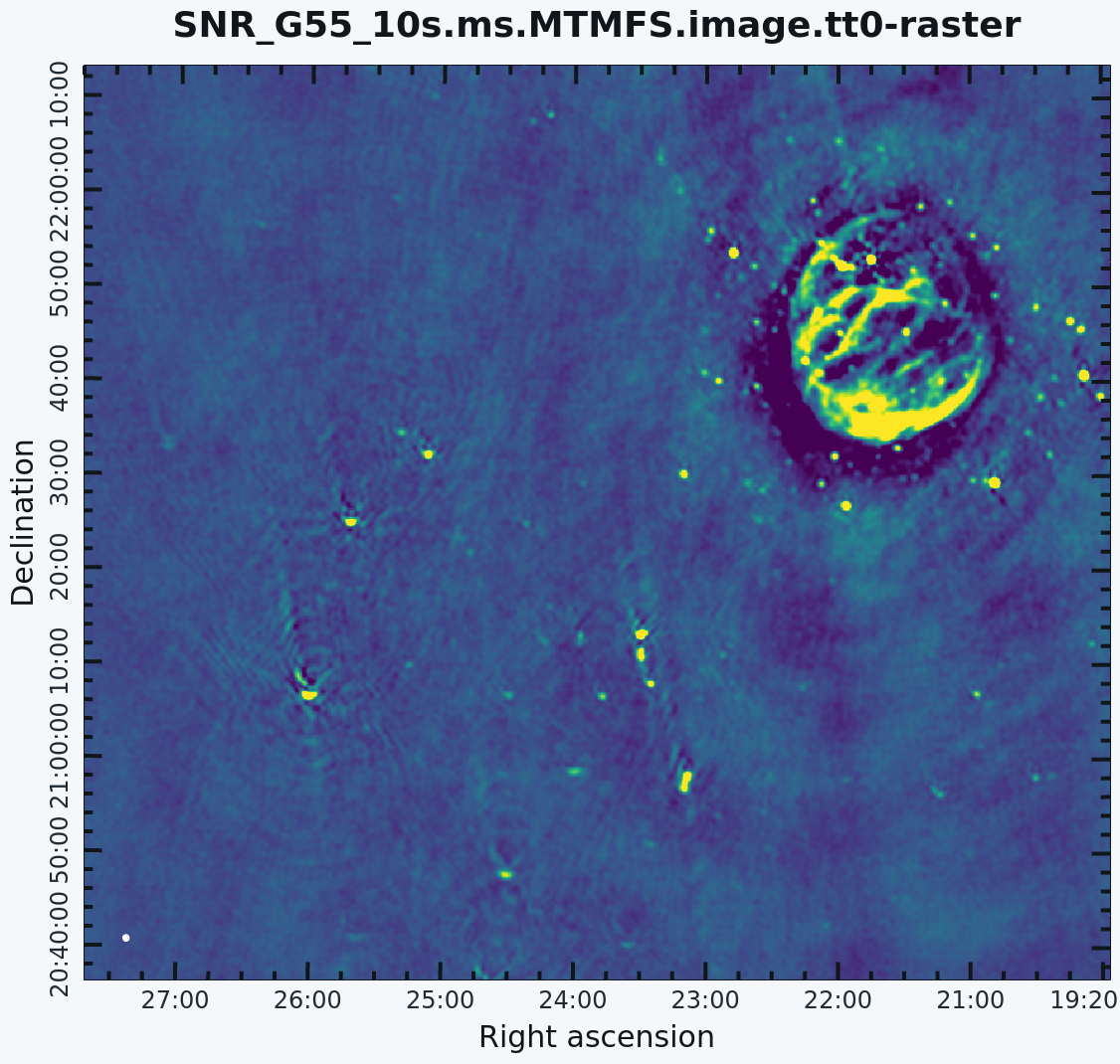 Multi-Scale, MTMFS. |
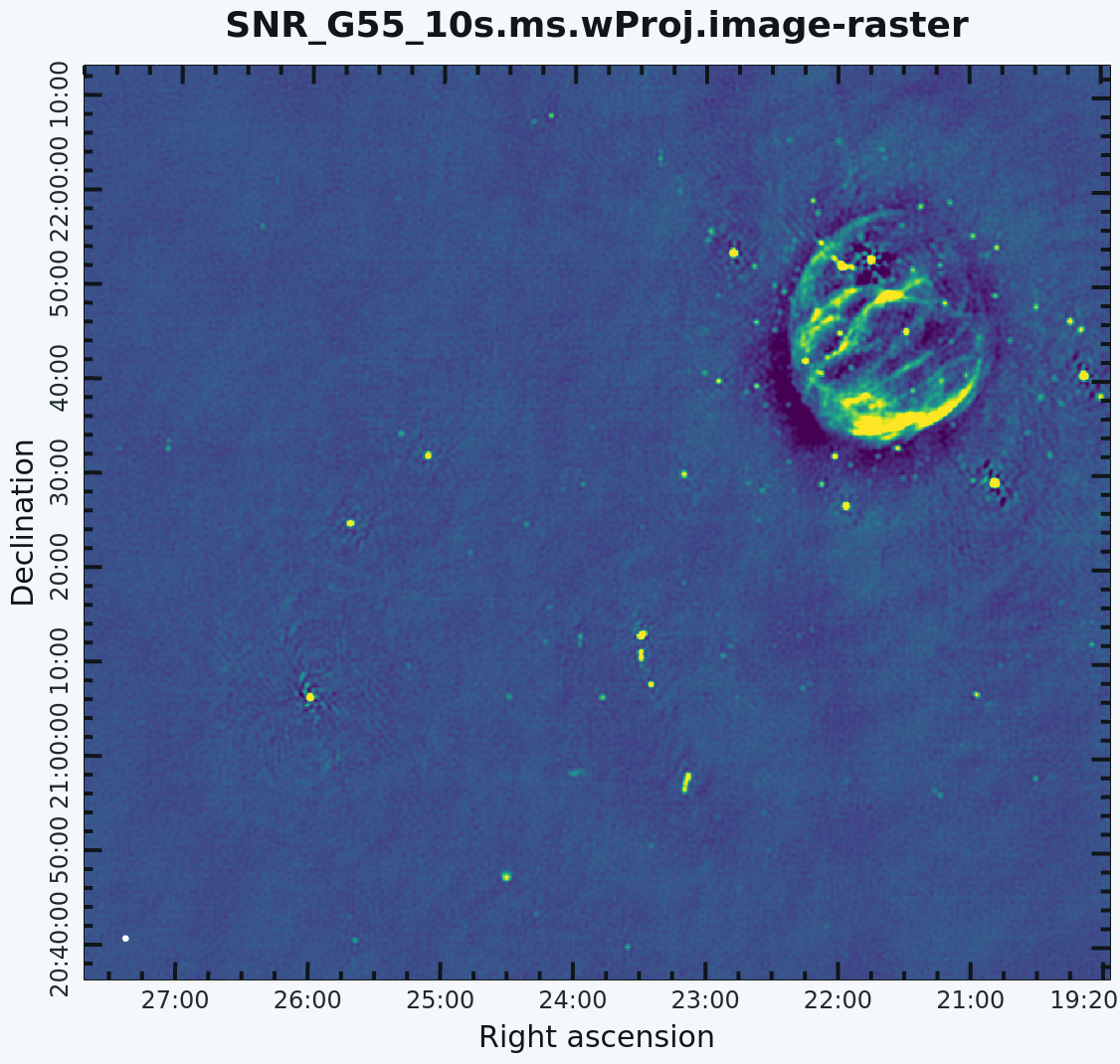 Multi-Scale, w-projection. |
 Multi-Scale, MTMFS, w-projection. |
Again, looking at the same outlier source, we can see that the major sources of error have been removed, although there are still some residual artifacts. One possible source of error is the time-dependent variation of the primary beam; another is the fact that we have only used nterms=2, which may not be sufficient to model the spectra of some of the point sources. Some weak RFI may also show up that may need additional flagging.
Imaging Outlier Fields
When strong sources are far from the main target but still strong enough to produce sidelobes in the main image, they should be cleaned. Sometimes, however, it is not practical to image very large fields for this purpose. An alternative is to add outlier fields. This mode will allow the user to specify a few locations that are then cleaned along with the main image. The outlier fields should be centered on strong sources that, e.g., are known from sky catalogs or are identified by other means.
In order to find outlying sources, it will help to first image a very large field with lower resolution, and to identify bright outliers using the CARTA. By moving the mouse cursor over the sources, we can grab their positions (see WCS coordinates at the top of the image viewer) and use the information within an outlier file. In this example, we've called our file 'outliers.txt'. It contains the names, sizes, and positions of the outliers we want to image (see section 5.3.18.1 of the CASA cookbook).
Open your favorite text editor and input the following:
#content of outliers.txt # #outlier field1 imagename=Outlier1 imsize=[320,320] phasecenter = J2000 19:23:27.693 22.37.37.180 # #outlier field2 imagename=Outlier2 imsize=[320,320] phasecenter = J2000 19:25:46.888 21.22.03.365
tclean will then be executed as follows:
# In CASA
tclean(vis='SNR_G55_10s.calib.ms', imagename='SNR.MS.MFS-Main', outlierfile='outliers.txt',
imsize=[640,640], cell='8arcsec',deconvolver='multiscale', scales=[0,6,10,30,60], smallscalebias=0.9,
interactive=False, niter=1000, weighting='briggs', robust=0, stokes='I', threshold='0.15mJy',
savemodel='modelcolumn',pblimit=-0.01)
- outlierfile='outliers.txt': the name of the outlier file.
We can view the images with CARTA one at a time. Due to the difference in sky coordinates, they cannot be viewed on the same window display.
# In CARTA
open SNR.MS.MFS-Main.image
# In CARTA
open Outlier1.image
# In CARTA
open Outlier2.image
In the resulting images, we have changed the color map to "Hot" in order to show the different colors that can be used within the CARTA. Feel free to play with other color maps that may be better suited for your screen.

|

|
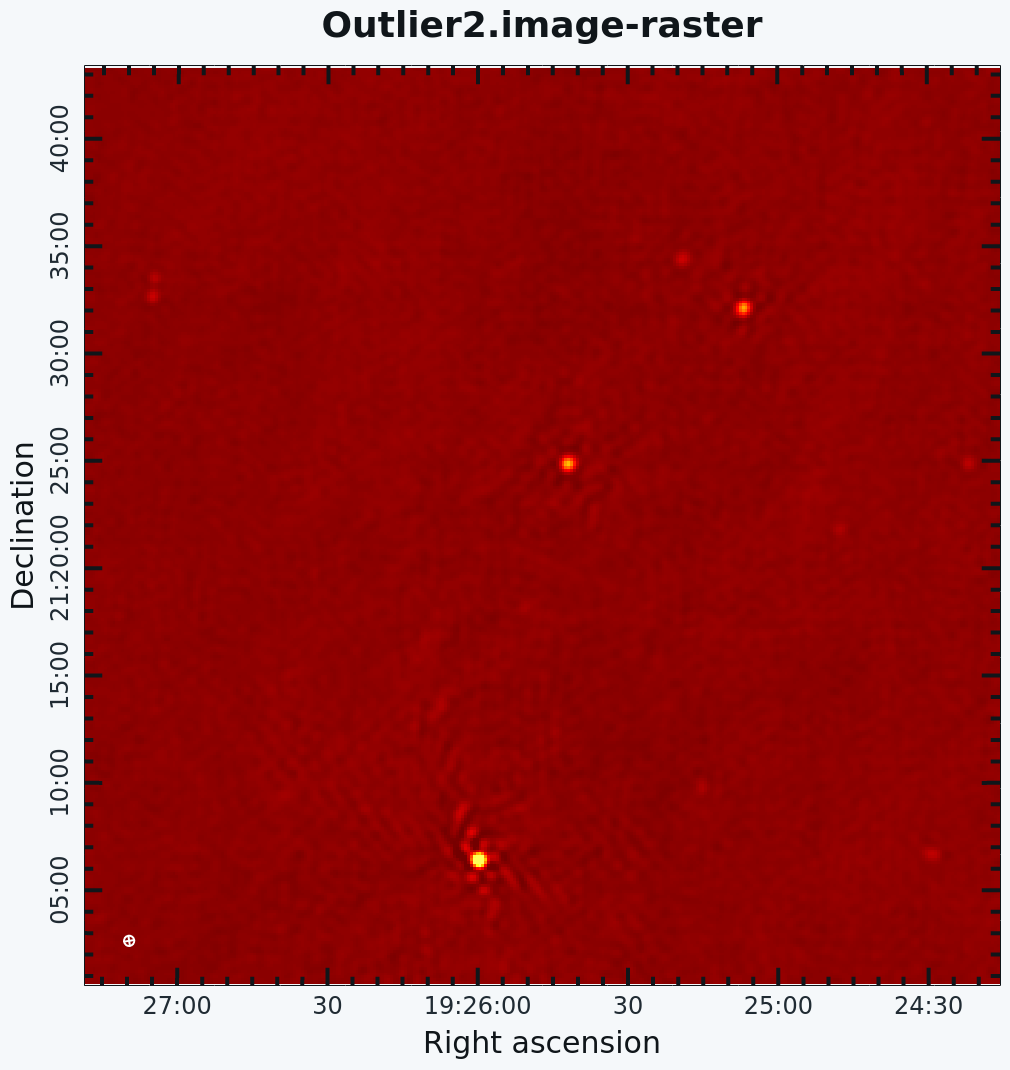
|
Primary Beam Correction
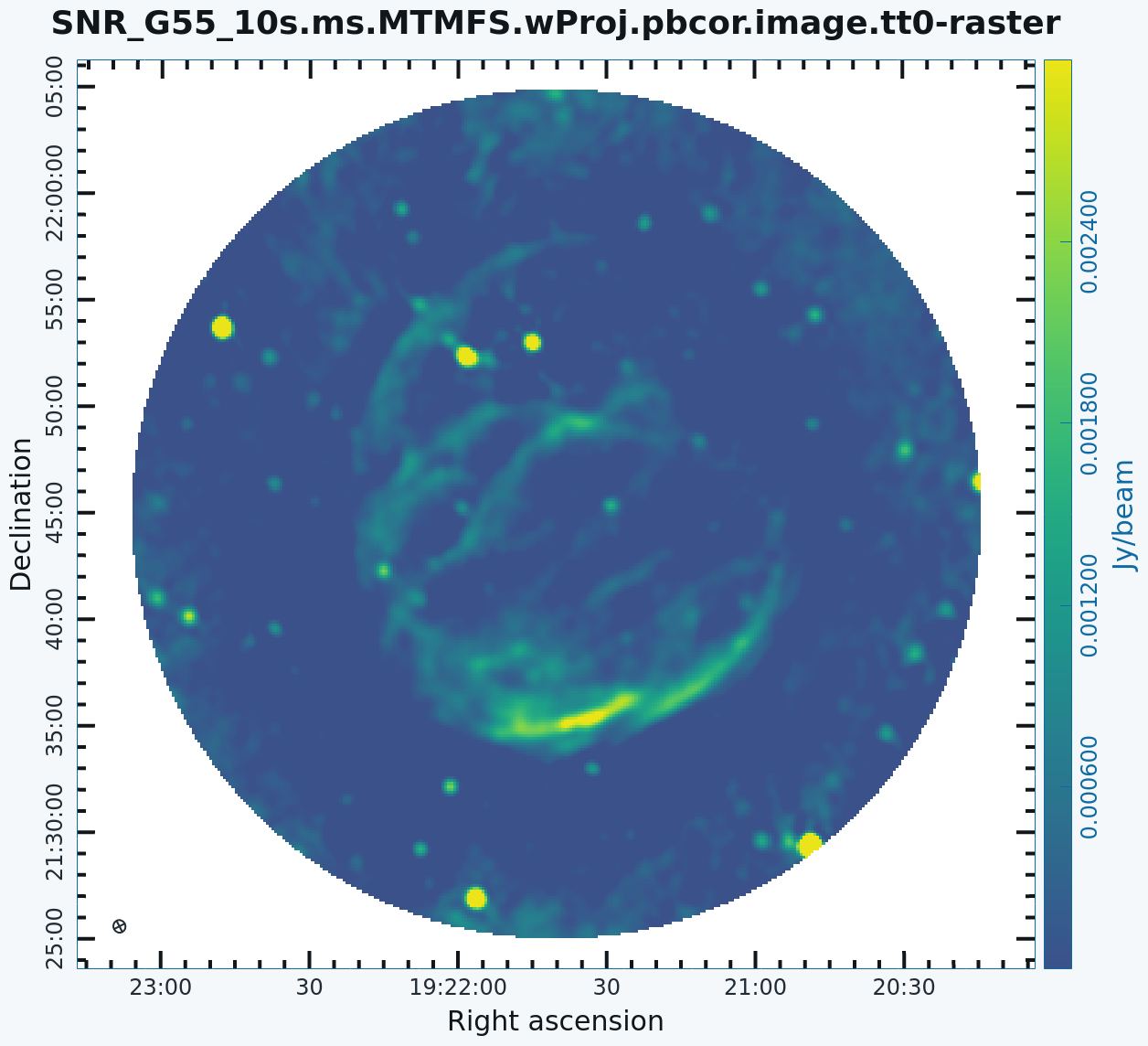
Primary beam corrected image using the widebandpbcor task for the MS.MTMFS.wProj image created during the CLEAN process.
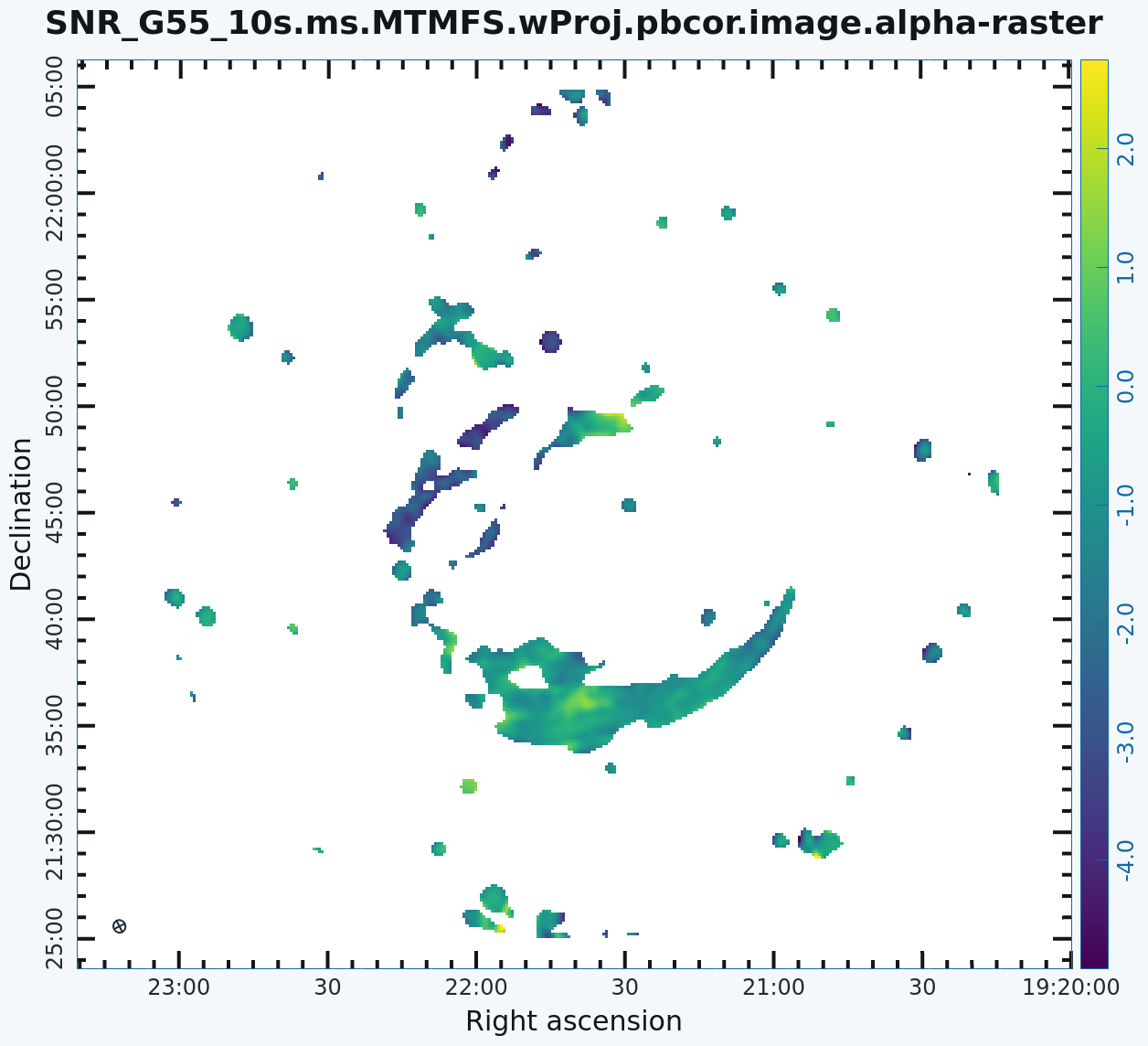
Primary beam corrected spectral index image using the widebandpbcor task.
In interferometry, the images formed via deconvolution are representations of the sky, multiplied by the primary beam response of the antenna. The primary beam can be described as Gaussian with a size depending on the observing frequency. Images produced via tclean are by default not corrected for the primary beam pattern (important for mosaics), and therefore do not have the correct flux density away from the phase center.
Correcting for the primary beam, however, can be done during tclean by using the pbcor parameter. Alternatively, it can be done after imaging using the task impbcor for regular data sets, and widebandpbcor for those that use Taylor-term expansion (nterms > 1). A third alternative is utilizing the task immath to manually divide the <imagename>.image by the <imagename>.flux image (<imagename>.flux.pbcoverage for mosaics).
Flux corrected images usually don't look pretty due to the noise at the edges being increased. Flux densities, however, should only be calculated from primary beam corrected images. Let's run the impbcor task to correct our multiscale image.
# In CASA
impbcor(imagename='SNR_G55_10s.MultiScale.image', pbimage='SNR_G55_10s.MultiScale.pb',
outfile='SNR_G55_10s.MS.pbcorr.image')
- imagename: the image to be corrected
- pbimage: the <imagename>.pb image as a representation of the primary beam
# In CARTA
open SNR_G55_10s.MS.pbcorr.image
Let us now use the widebandpbcor task for wide-band (nterms>1) images. Note that for this task, we will be supplying the image name that is the prefix for the Taylor expansion images, tt0, and tt1, which must be on disk. Such files were created during the last Multi-Scale, Multi-Term, Widefield run of CLEAN. widebandpbcor will generate a set of images with a "pbcor.image.*" extension.
# In CASA
widebandpbcor(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.ms.MTMFS.wProj',
nterms=2, action='pbcor', pbmin=0.2, spwlist=[0,1,2,3],
weightlist=[0.5,1.0,0,1.0], chanlist=[25,25,25,25], threshold='0.6mJy')
- spwlist=[0,1,2,3]: We want to apply this correction to all spectral windows in our calibrated measurement set.
- weightlist=[0.5,1.0,0,1.0]: Since we did not specify reference frequencies during tclean, the widebandpbcor task will pick them from the provided image. Running the task, the logger reports the multiple frequencies used for the primary beam, which are 1.305, 1.479, 1.652, and 1.825 GHz. We selected weights using information external to this guide: The first chosen frequency lies within spectral window 0, which had lots of data flagged due to RFI. The weightlist parameter allows us to give this chosen frequency less weight. The primary beam at 1.6 GHz lies in an area with no data, therefore we give a weight value of zero for this frequency. The remaining frequencies 1.479 and 1.825 GHz lie within spectral windows which contained less RFI, therefore we provide a larger weight percentage. (Exercise for the reader: use an amplitude vs. frequency plot in plotms to verify these claims.)
- pbmin=0.2: Gain level below which not to compute Taylor-coefficients or apply a primary beam correction.
- chanlist=[25,25,25,25]: Make primary beams at frequencies corresponding to channel 25 in each spectral window.
- threshold='0.6mJy': Threshold in the intensity map, below which not to recalculate the spectral index. We adjusted the threshold to get good results, as too high of a threshold resulted in errors and no spectral index image, and too low of a threshold resulted in bogus values for the spectral index image.
Note: CASA may produce a warning stating that Images are not contiguous along the concatenation axis. This is usually an indication of missing channels due to flagging (or unevenly spaced basebands) and is not a cause for worry.
# In CARTA
open SNR_G55_10s.ms.MTMFS.wProj.pbcor.image.tt0
# In CARTA
open SNR_G55_10s.ms.MTMFS.wProj.pbcor.image.alpha
It's important to note that the image will cut off at about 20% of the HPBW, as we are confident of the accuracy within this percentage. Anything outside becomes less accurate, thus there is a mask associated with the creation of the corrected primary beam image (Figure 16). Spectral indices may still be unreliable below approximately 70% of the primary beam HPBW (Figure 17).
It would be a good exercise to use the CARTA to plot both the primary beam corrected image, and the original cleaned image and compare the intensity (Jy/beam) values, which should differ slightly.
Adaptive Scale Pixel (ASP) Clean !!!EXPERIMENTAL!!!
Recently ASP deconvolution algorithm has been implemented in CASA 6.5.2 tclean version. The ASP decomposition algorithm is designed to reconstruct the sky brightness by adaptively determining the optimal scales. The implementation of the ASP algorithm is aimed to improve both image resolution and computation efficiency. The implementation of the ASP algorithm in CASA is still under experiment so the user should carefully check their results. For more detail see Bhatnagar et al. 2004.
# In CASA
tclean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.ASP', deconvolver='asp',
fusedthreshold=0.0001, largestscale=-1, imsize=1280, cell='8arcsec', pblimit=-0.01, niter=1000,weighting='briggs', stokes='I',
robust=0.0, interactive=False, threshold='0.12mJy', savemodel='modelcolumn')
- deconvolver='asp': Use the Adaptive Scale Pixel algorithm.
- fusedthreshold=0.0001: This parameter switches the deconvolver algorithm asp to hogbom when the peak residual is lower than the given threshold.
- largestscale=-1: This parameter provides the initial guess for the asp algorithm to choose the scales on which to clean (in pixels). Generally, asp uses the default scale sizes [0,w,2w,4w,8w], where w is the width of the point spread function. In this case, we chose largestscale=-1, which suggests users accept these default scales. If this parameter is set, for example, 100, the initial scales would be [0,w,2w,..100]. It is recommended to use default scale values.
# In CASA
tclean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.wProj.ASP',
gridder='wproject', wprojplanes=-1, deconvolver='asp',
fusedthreshold=0.0, largestscale=-1, imsize=1280, cell='8arcsec', pblimit=-0.01, niter=1000, weighting='briggs',
stokes='I', robust=0.0, interactive=False, threshold='0.15mJy', savemodel='modelcolumn')
- gridder='wproject': Use the w-projection algorithm.
- wprojplanes=-1: The number of w-projection planes to use for deconvolution. Setting to -1 allows CLEAN to automatically choose an acceptable number of planes for the given data.
# In CARTA
open SNR_G55_10s.ASP.image
# In CARTA
open SNR_G55_10s.wProj.ASP.image
These experimental results are shown in Figure 10a (the image which just employed asp deconvolution) and Figure 10b (the image which employed asp and w-projection).
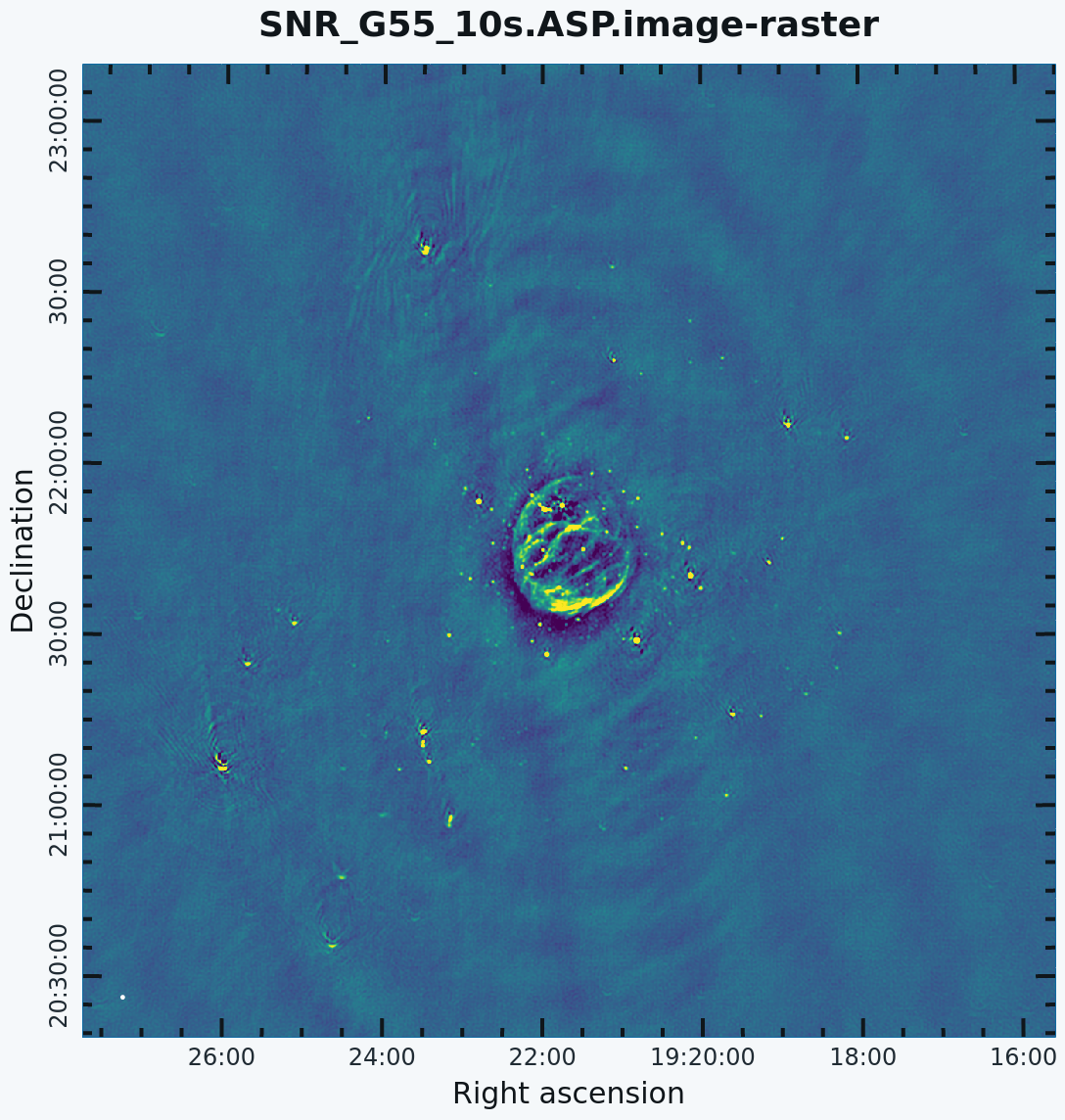 An example of ASP Clean image. |
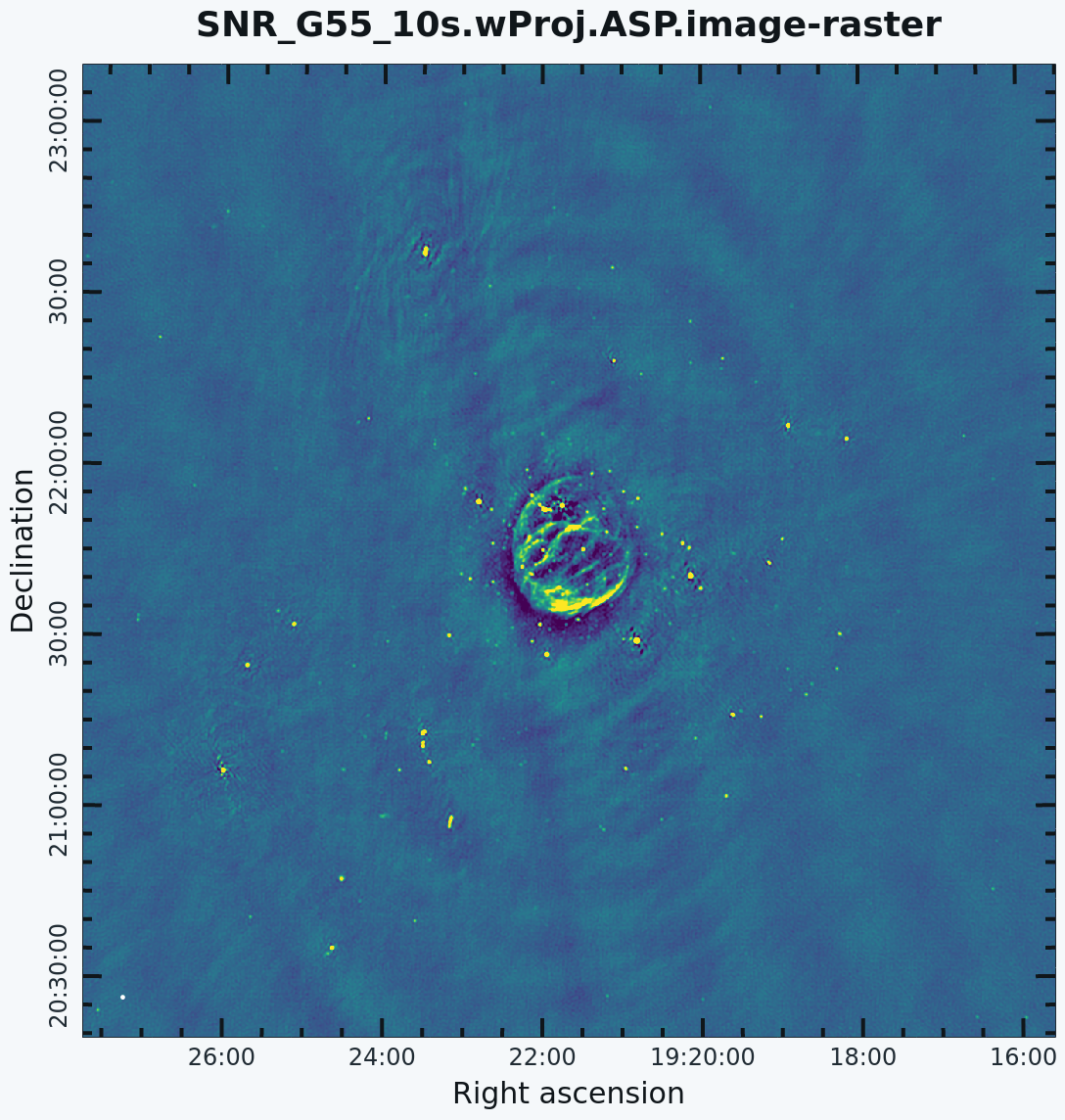 ASP Clean and w-projection image. |
Imaging Spectral Cubes
For spectral line imaging using CASA tclean, set specmode='cube, and the width parameter accepts either frequency or velocity values. Both options will create a spectral axis in frequency, but entering a velocity width will add an additional velocity label.
The following keywords are important for spectral modes (velocity in this example):
# In CASA
specmode = 'cube' # Spectral definition type (mfs, cube, cubedata, cubesource)
nchan = -1 # Number of channels (planes) in output image; -1 = all data specified by spw, start, and width parameters.
start = '' # Velocity of the first channel: e.g '0.0km/s'(''=first channel in first SpW of MS)
width = '' # Channel width e.g '-1.0km/s' (''=width of first channel in first SpW of MS)
outframe = '' # spectral reference frame of output image; '' =input
veltype = 'radio' # Velocity definition of output image
restfreq = '' # Rest frequency to assign to image (see help)
perchanweightdensity = False # Whether to calculate weight density per channel in Briggs style weighting or not
The spectral dimension of the output cube will be defined by these parameters and tclean will regrid the visibilities to it. Note that invoking cvel before imaging is in most cases not necessary, even when two or more measurement sets are being provided at the same time.
The cube is specified by a start velocity in km/s or MHz, the nchan number of channels, and a channel width (where the latter can also be negative for decreasing velocity cubes).
To correct for Doppler effects, tclean also requires a outframe velocity frame, where the default LSRK and BARY are the most popular Local Standard of Rest (kinematic) and sun-earth Barycenter references. veltype defines whether the data will be gridded via the optical or radio velocity definition. A description of the available options and definitions can be found in the VLA observing guide and the CASA cookbook. By default, tclean will produce a cube using the LRSK and radio definitions.
An example of spectral line imaging procedures is provided in the VLA high-frequency Spectral Line tutorial - IRC+10216.
Beam per Plane
For spectral cubes spanning relatively wide ranges in frequency, the synthesized beam can vary substantially across the channels. To account for this, CASA will calculate separate beams for each channel when the difference in beams is more than half a pixel across the cube. All CASA image analysis tasks are capable of handling such cubes.
If it is desired to have a cube with a single synthesized beam, two options are available. It is possible for tclean to do the smoothing, by setting the parameter smonothfactor. The second option is to use the task imsmooth, after cleaning, with kernel='commonbeam'. This task will clean up all header variables such that only a single beam appears in the data. It may be wise to go with this second option, which will allow you to first verify the clean results before smoothing the image.
Image Header
The image header holds meta data associated with your CASA image. The task imhead will display this data within the casalog, and also output the result as a Python dictionary in the CASA terminal. We will first run imhead with mode='summary' :
# In CASA
imhead(imagename='SNR_G55_10s.ms.MTMFS.wProj.image.tt0', mode='summary')
- mode='summary' : gives general information about the image, including the object name, sky coordinates, image units, the telescope the data was taken with, and more.
For further information, run mode='list' . We will assign a variable 'header' to also capture the output dictionary:
# In CASA
header=imhead(imagename='SNR_G55_10s.ms.MTMFS.wProj.image.tt0', mode='list')
- mode='list' : gives more detailed information, including beam major/minor axes, beam primary angle, the location of the max/min intensity, and lots more. Essentially this mode displays the FITS header variables.
Image Conversion
Finally, as an example, we convert our image from intensity to main beam brightness temperature.
We will use the standard equation
[math]\displaystyle{ T=1.222\times 10^{6} \frac{S}{\nu^{2} \theta_{maj} \theta_{min}} }[/math]
where the main beam brightness temperature [math]\displaystyle{ T }[/math] is given in units of Kelvin, the intensity [math]\displaystyle{ S }[/math] in Jy/beam, the reference frequency [math]\displaystyle{ \nu }[/math] in GHz, and the major and minor beam sizes [math]\displaystyle{ \theta }[/math] in arcseconds.
For a beam of 29.30"x29.03" and a reference frequency of 1.579 GHz (as taken from the previous imhead run) we calculate the brightness temperature using immath:
# In CASA
immath(imagename='SNR_G55_10s.ms.MTMFS.wProj.image.tt0', mode='evalexpr',
expr='1.222e6*IM0/1.579^2/(29.30*29.03)',
outfile='SNR_G55_10s.ms.MTMFS.wProj.image.tt0-Tb')
- mode='evalexpr' : immath is used to calculate with images
- expr: the mathematical expression to be evaluated. The images are abbreviated as IM0, IM1, ... in the sequence of their appearance in the imagename parameter.
Since immath only changes the values but not the unit of the image, we will now change the new image header 'bunit' key to 'K'. To do so, we will run imhead with mode='put' :
# In CASA
imhead(imagename='SNR_G55_10s.ms.MTMFS.wProj.image.tt0-Tb', mode='put', hdkey='bunit', hdvalue='K')
- hdkey: the header keyword that will be changed
- hdvalue: the new value for the header keyword
Launching the CARTA will now show our image in brightness temperature units:
# In CARTA
open SNR_G55_10s.ms.MTMFS.wProj.image.tt0-Tb
A few particular issues to look out for:
- The default value of robust is now 0.5; this produces the same behavior as robust=0.0 in AIPS.
- Parameter pblimit is used to ensure that the image is only produced out to a distance from the phasecenter where the sensitivity of the Primary Beam is equal to pblimit. The default value of pblimit is 0.2. For this example, where we are making an image that is much, much larger than the Primary Beam, it is necessary to set pblimit=-0.01 so that no limit is applied.
- Parameter savemodel is used rather than clean's usescratch to indicate whether the model should be saved in a new column in the ms, as a virtual model, or not at all. The default value is "none": so, this must be changed for the image to be saved. The use of the virtual model with MTMFS in tclean is still under commissioning, so we recommend currently to set savemodel='modelcolumn'.
- Some parameter default values in tclean are different than the equivalent default values in clean.
- The auto-multithresh automasking algorithm in tclean provides the option to automatically generate clean mask during the deconvolution process by applying flux density thresholds to the residual image. Currently, this feature is designed to work for point sources using deconvolver=hogbom but this feature may be more flexible in future CASA releases. More information about this option is provided in the CASA Documentation page on Synthesis Imaging - Masks for Deconvolution.
Last checked on CASA Version 6.5.2

