Jupiter: continuum polarization calibration 5.5.0: Difference between revisions

From CASA Guides
Jump to navigationJump to search
← Older edit
Akapinsk (talk | contribs)
689 edits
No edit summary
Fschinze (talk | contribs)
536 edits
 
(59 intermediate revisions by 3 users not shown)
Line 3: Line 3:
| style="background: red; color: white;" | '''DISCLAIMER'''
| style="background: red; color: white;" | '''DISCLAIMER'''
|-
|-
| This is an advanced reference guide to calibration and imaging of pre-upgrade VLA polarimetric data with CASA 5.3.0. If you are a beginning or novice user, please consult relevant [https://casaguides.nrao.edu/index.php/Karl_G._Jansky_VLA_Tutorials CASA guides] first.
| This is an advanced reference guide to calibration and imaging of pre-upgrade VLA polarimetric data with CASA 5.5.0. If you are a beginning or novice user, please consult relevant [https://casaguides.nrao.edu/index.php/Karl_G._Jansky_VLA_Tutorials CASA guides] first.
|}
|}


Line 10: Line 10:
== Data Import ==
== Data Import ==


The data set for this tutorial lives [https://casa.nrao.edu/Data/VLA/Planets6cm/ here] (129MB). This is a VLA 6cm dataset that was observed back in 1999 to set the flux scale for calibration of the VLA. Included in the program were observations of the planets, including Jupiter which we will focus on in this tutorial. These are D-configuration data, with resolution of around 14". <p style="color: #ff0000;"><b> Need more reliable permanent location! </b></p>
The data set for this tutorial lives [https://casa.nrao.edu/Data/VLA/Planets6cm/planets_6cm.fits here: planets_6cm.fits] (129MB). This is a VLA 6cm dataset that was observed back in 1999 to set the flux scale for calibration of the VLA. Included in the program were observations of the planets, including Jupiter which we will focus on in this tutorial. These are D-configuration data, with resolution of around 14".
 


Import the data into CASA. Task <tt>importuvfits()</tt> will read the original AIPS friendly UVFITS format and create a CASA native MS.
Import the data into CASA. Task <tt>importuvfits()</tt> will read the original AIPS friendly UVFITS format and create a CASA native MS.
Line 18: Line 17:
importuvfits(fitsfile='planets_6cm.fits', vis='jupiter6cm.demo.ms', antnamescheme='old')
importuvfits(fitsfile='planets_6cm.fits', vis='jupiter6cm.demo.ms', antnamescheme='old')
</source>
</source>


Check the observation set up and print verbose summary of the observations to the CASA logger
Check the observation set up and print verbose summary of the observations to the CASA logger
Line 25: Line 23:
listobs(vis='jupiter6cm.demo.ms')
listobs(vis='jupiter6cm.demo.ms')
</source>
</source>


The output of this task is fairly long, the abridged version is shown below since we may need some of this information later on during our calibration.
The output of this task is fairly long, the abridged version is shown below since we may need some of this information later on during our calibration.
Line 104: Line 101:
</source>
</source>


 
<p style="color: #ff0000;"> <b>Note</b> (for uvfits sourced directly from archive only): CASA 5.4 and earlier versions will not plot the antennas properly. This is to be resolved in future CASA versions. If this occurs then a reference antenna can be selected using the listobs task and choosing an antenna located on a pad close to the center of the array (Pads numbers increase with distance from the center of the array, ie. "VLA:_N1" and "EVLA:W2" are pads close to the center of the array, where as, "VLA:_N18" is not).</p>


== Data Inspection and Editing ==
== Data Inspection and Editing ==
Line 110: Line 107:
To inspect and interactively flag bad data use task <tt>plotms()</tt>. <b>Note</b>: it is not recommended to use <tt>plotms()</tt> to interactively flag the new post-upgrade VLA data due to their large volume and large bandwidths. However, the old VLA data are much smaller and <tt>plotms()</tt> is capable of managing it interactively.
To inspect and interactively flag bad data use task <tt>plotms()</tt>. <b>Note</b>: it is not recommended to use <tt>plotms()</tt> to interactively flag the new post-upgrade VLA data due to their large volume and large bandwidths. However, the old VLA data are much smaller and <tt>plotms()</tt> is capable of managing it interactively.


First, inspect the primary flux and polarisation angle calibrator, 1331+305 (3C286).
First, inspect the primary flux and polarisation angle calibrator, 1331+305 (3C286). Inspect RR,LL and RL,LR correlations separately due to large amplitude differences between them (when all correlations are plotted together, the RL,LR will seem like bad data due to their much lower amplitudes as compared to RR,LL). Use <tt>Mark Regions</tt> within the <tt>plotms()</tt> GUI to draw boxes around points to flag, and hit <tt>Flag</tt> to flag.  


<source lang="python">
<source lang="python">
plotms(vis='jupiter6cm.demo.ms', selectdata=True, field='1331+305', correlation='RR,LL', xaxis='uvdist', yaxis='amp')
plotms(vis='jupiter6cm.demo.ms', selectdata=True, field='1331+305', correlation='RR,LL', xaxis='uvdist', yaxis='amp')
</source>
</source>
Inspect RR,LL and RL,LR correlations separately due to large amplitude differences between them (when all correlations are plotted together, the RL,LR will seem like bad data due to their much lower amplitudes as compared to RR,LL). Use <tt>Mark Regions</tt> within the <tt>plotms()</tt> GUI to draw boxes around points to flag, and hit <tt>Flag</tt> to flag.


Now, inspect the other two sources we are interested in, the polarisation leakage calibrator (0137+331) and our target source (JUPITER).
Now, inspect the other two sources we are interested in, the polarisation leakage calibrator (0137+331) and our target source (JUPITER).




The flagging can also be done non-interactively as per currently recommended CASA practise. Use task <tt>flagdata()</tt> to do so. For example, from inspecting our data in <tt>plotms()</tt> you should have noticed that Antenna 9 (ID=8) in spw 1 is often bad. The bad data on Antenna 9 for the 0137+331 calibrator and for our target source JUPITER are in the last 4 scans in spw='1', as well as in the last scan for all antennas in both spws on the target source. We can flag these points with the following <tt>flagdata()</tt> task executions.
Flagging can also be done non-interactively as per currently recommended CASA practise. Use task <tt>flagdata()</tt> to do so. For example, from inspecting our data in <tt>plotms()</tt> you should have noticed that Antenna 9 (ID=8) in spw 1 is often bad. The bad data on Antenna 9 are in the last 4 scans in spw='1' for the 0137+331 calibrator and for our target source (JUPITER), as well as in the last scan for all antennas in both spws on the target source. We can flag these points with the following <tt>flagdata()</tt> task executions.


<source lang="python">
<source lang="python">
Line 134: Line 128:


<source lang="python">
<source lang="python">
flagdata(vis='jupiter6cm.demo.ms',mode='clip',field='1331+305',correlation='RR,LL',clipoutside=False,clipminmax=[0,0.75])
flagdata(vis='jupiter6cm.demo.ms',mode='clip',field='1331+305',correlation='ABS_RR,LL',clipoutside=False,clipminmax=[0,0.75])
flagdata(vis='jupiter6cm.demo.ms',mode='clip',field='1331+305',correlation='RL,LR',clipoutside=False,clipminmax=[0,0.04])
flagdata(vis='jupiter6cm.demo.ms',mode='clip',field='1331+305',correlation='ABS_RL,LR',clipoutside=False,clipminmax=[0,0.04])
flagdata(vis='jupiter6cm.demo.ms',mode='clip',field='0137+331',correlation='RR,LL',clipoutside=False,clipminmax=[0,0.56])
flagdata(vis='jupiter6cm.demo.ms',mode='clip',field='0137+331',correlation='ABS_RR,LL',clipoutside=False,clipminmax=[0,0.55])
flagdata(vis='jupiter6cm.demo.ms',mode='clip',field='0137+331',correlation='RL,LR',clipoutside=False,clipminmax=[0,0.01])
flagdata(vis='jupiter6cm.demo.ms',mode='clip',field='0137+331',correlation='ABS_RL,LR',clipoutside=False,clipminmax=[0,0.01])
</source>
</source>
If you are unfamiliar with flagging in CASA, consult detailed topical guide [https://casaguides.nrao.edu/index.php/VLA_CASA_Flagging-CASA5.0.0 Flagging VLA Data].
If you are unfamiliar with flagging in CASA, consult detailed topical guide [https://casaguides.nrao.edu/index.php/VLA_CASA_Flagging-CASA5.0.0 Flagging VLA Data].
Line 145: Line 139:
== Calibration ==
== Calibration ==


=== Set the Flux Density Scale ===
=== Flux Density Scale ===


Set the absolute flux density scale, but only for Stokes I at the moment (total flux density model). Our primary flux calibrator here is 1331+305 (3C286). The default model for CASA 5.3+ is 'Perley-Butler 2017'.  
Set the absolute flux density scale, but only for Stokes I at the moment (total flux density model). Our primary flux calibrator here is 1331+305 (3C286). The default model for CASA 5.5+ is 'Perley-Butler 2017'.  


<source lang="python">
<source lang="python">
Line 158: Line 152:
At this stage the data have an overall flux density scaling determined, but full gain solutions aren't there yet. The relevant task is <tt>gaincal()</tt> (analogous to the AIPS task CALIB). <tt>Gaincal()</tt> will produce a separate table with solutions, and we will use appropriate extensions to keep track of what is what.
At this stage the data have an overall flux density scaling determined, but full gain solutions aren't there yet. The relevant task is <tt>gaincal()</tt> (analogous to the AIPS task CALIB). <tt>Gaincal()</tt> will produce a separate table with solutions, and we will use appropriate extensions to keep track of what is what.


<b>NOTE</b>: Since we have only two single-channel continuum spw, we do not want to do <i>bandpass calibration</i>.  
<b>NOTE</b>: Since we have only two single-channel continuum spw, we do not want to do <i>bandpass calibration</i> nor solve for <i>delays</i> within spws as is currently done with wide bandwidth post-upgrade VLA data.  


Firstly, generate an antenna zenith-angle dependent VLA gain curve calibration table
Firstly, generate an antenna zenith-angle dependent VLA gain curve calibration table
Line 172: Line 166:


# And check the solutions
# And check the solutions
plotcal(caltable='jupiter6cm.demo.G', xaxis='time', yaxis='amp', subplot=333, iteration='antenna')
plotms(vis='jupiter6cm.demo.G', xaxis='time', yaxis='amp', gridrows=3, gridcols=3, iteraxis='antenna')
plotcal(caltable='jupiter6cm.demo.G', xaxis='time', yaxis='phase', plotrange=[-1,-1,-200,200], subplot=333, iteration='antenna')
plotms(vis='jupiter6cm.demo.G', xaxis='time', yaxis='phase', plotrange=[-1,-1,-200,200], gridrows=3, gridcols=3, iteraxis='antenna')
</source>
</source>


If all looks good, bootstrap the flux density scale of the flux calibrator onto the phase calibrators. AIPS called it GETJY, but CASA calls it <tt>fluxscale()</tt>.  
If all looks good, bootstrap the flux density scale of the flux calibrator onto the phase calibrators (CASA's <tt>fluxscale()</tt> task is equivalent to GETJY in AIPS). When executing <tt>fluxscale()</tt>, the calibration table with the extension .G is modified and stored as a new table with the extension .Gflx.


<source lang="python">
<source lang="python">
myFluxscale = fluxscale(vis='jupiter6cm.demo.ms', caltable='jupiter6cm.demo.G', fluxtable='jupiter6cm.demo.Gflx', reference='1331+305', transfer='0137+331', append=False, display=False)
myFluxscale = fluxscale(vis='jupiter6cm.demo.ms', caltable='jupiter6cm.demo.G', fluxtable='jupiter6cm.demo.Gflx', reference='1331+305', transfer='0137+331', incremental=True, append=False, display=False)
</source>
</source>


Line 194: Line 188:
</pre>
</pre>


When executing <tt>fluxscale()</tt>, the calibration table with the extension .G is modified and stored as a new table with the extension .Gflx. So far, solutions have been generated only for the calibrators, and have not yet been transferred to the target source(s).


Before proceeding, inspect the flux density calibration and save results to a file.
Before proceeding, inspect the flux density calibration and save results to a file.


<source lang="python">
<source lang="python">
plotcal(caltable='jupiter6cm.demo.Gflx', xaxis='time', yaxis='amp', showgui=True, figfile='jupiter6cm.demo.Gflx.amp.png')
plotms(vis='jupiter6cm.demo.Gflx', xaxis='time', yaxis='amp', showgui=True, plotfile='jupiter6cm.demo.Gflx.amp.png')


plotcal(caltable='jupiter6cm.demo.Gflx', xaxis='time', yaxis='phase', plotrange=[-1,-1,-200,200], showgui=True, figfile='jupiter6cm.demo.Gflx.phase.png')
plotms(vis='jupiter6cm.demo.Gflx', xaxis='time', yaxis='phase', plotrange=[-1,-1,-200,200], showgui=True, plotfile='jupiter6cm.demo.Gflx.phase.png')
</source>
</source>


Line 208: Line 200:


=== Polarisation calibration ===
=== Polarisation calibration ===
Just as in the step of the initial gain calibration, since our old VLA data have single-channel continuum spws, we do not want to solve for KCROSS delays in our polarisation calibration. Instead, we directly solve for D and X terms.




==== Set the polarisation model ====
==== Set the polarisation model ====


Now, set the polarisation model for the polarised position-angle calibrator (here 1331+305=3C286 which is also our primary flux calibrator). For polarisation properties of your primary polarisation calibrator see [https://science.nrao.edu/facilities/vla/docs/manuals/obsguide/modes/pol#section-4 VLA Polarimetry Guide].
First, set the polarisation model for the polarised position-angle calibrator (here 1331+305=3C286 which is also our primary flux calibrator). For polarisation properties of your primary polarisation calibrator see [https://science.nrao.edu/facilities/vla/docs/manuals/obsguide/modes/pol#section-4 VLA Polarimetry Guide].


<source lang="python">
<source lang="python">
Line 221: Line 215:
d0=33*pi/180 # Polarisation angle 33deg in radians
d0=33*pi/180 # Polarisation angle 33deg in radians


myPolSetjy = setjy(vis='jupiter6cm.demo.ms', field='1331+305', standard='manual', spw='0', fluxdensity=[i0,0,0,0], spix=[alpha,0], reffreq=str(f0)+'GHz', polindex=[c0,0], polangle=[d0,0], scalebychan=True, usescratch=False)
myPolSetjy = setjy(vis='jupiter6cm.demo.ms', field='1331+305', standard='manual', spw='', fluxdensity=[i0,0,0,0], spix=[alpha,0], reffreq=str(f0)+'GHz', polindex=[c0,0], polangle=[d0,0], scalebychan=True, usescratch=False)
</source>
</source>


Line 231: Line 225:
Out[49]:  
Out[49]:  
{'7': {'0': {'fluxd': array([ 7.3109    ,  0.33899165,  0.7613877 ,  0.        ])},
{'7': {'0': {'fluxd': array([ 7.3109    ,  0.33899165,  0.7613877 ,  0.        ])},
  '1': {'fluxd': array([ 7.26237491,  0.33674164,  0.7563341 ,  0.        ])},
   'fieldName': '1331+305'},
   'fieldName': '1331+305'},
  'format': "{field Id: {spw Id: {fluxd: [I,Q,U,V] in Jy}, 'fieldName':field name }}"}
  'format': "{field Id: {spw Id: {fluxd: [I,Q,U,V] in Jy}, 'fieldName':field name }}"}
</pre>
</pre>
==== Solve for the cross-hand delays ====
Solve for the cross-hand delays (RL,LR) delays due to residual delay difference between R and L. For this use the 3C286 calibrator since it had a strong polarised signal in the RL and LR correlations.
<source lang="python">
gaincal(vis='jupiter6cm.demo.ms', caltable='jupiter6cm.demo.K', field='1331+305', spw='', gaintype='KCROSS', solint='inf', combine='scan', refant='11', minsnr=3, gaintable=['jupiter6cm.demo.gc','jupiter6cm.demo.G'], gainfield=['','1331+305'], parang=False)
</source>
Check the results in the CASA logger window
<pre style="background-color: #fffacd;">
For solint = inf, found 2 solution intervals.
Time=1999/04/16/06:38:50.8 Spw=0 Global cross-hand delay=0.102352 nsec
Time=1999/04/16/06:36:31.1 Spw=1 Global cross-hand delay=0.10341 nsec
  Found good Kcross Jones solutions in 2 solution intervals.
Writing solutions to table: jupiter6cm.demo.K
Finished solving.
</pre>
The cross-hand delays in our observations are very small, but if your data were associated with larger delays and you didn't correct for them, the delays would be absorbed into the phases of the D and X solutions we will solve for next. This is particularly important when solving for Q+iU polarisation.




Line 264: Line 236:


<source lang="python">
<source lang="python">
polcal(vis='jupiter6cm.demo.ms', caltable='jupiter6cm.demo.D', field='0137+331', spw='', refant='11', poltype='D+QU', solint='inf', combine='scan',minsnr=3, gaintable=['jupiter6cm.demo.gc', 'jupiter6cm.demo.G', 'jupiter6cm.demo.K'], gainfield=['','0137+331',''])
polcal(vis='jupiter6cm.demo.ms', caltable='jupiter6cm.demo.D', field='0137+331', spw='', refant='11', poltype='D+QU', solint='inf', combine='scan',minsnr=3, gaintable=['jupiter6cm.demo.gc', 'jupiter6cm.demo.G'], gainfield=['','0137+331',''])
</source>
</source>


Line 270: Line 242:


<source lang="python">
<source lang="python">
plotcal(caltable='jupiter6cm.demo.D', xaxis='antenna', yaxis='amp', showgui=True, figfile='jupiter6cm.demo.D.amp.png')
plotms(vis='jupiter6cm.demo.D', xaxis='antenna', yaxis='amp', showgui=True, plotfile='jupiter6cm.demo.D.amp.png')


plotcal(caltable='jupiter6cm.demo.D', xaxis='antenna', yaxis='phase', plotrange=[-1,-1,-200,200], showgui=True, figfile='jupiter6cm.demo.D.phase.png')
plotms(vis='jupiter6cm.demo.D', xaxis='antenna', yaxis='phase', plotrange=[-1,-1,-200,200], showgui=True, plotfile='jupiter6cm.demo.D.phase.png')


plotcal(caltable='jupiter6cm.demo.D', xaxis='antenna', yaxis='snr', showgui=True, figfile='jupiter6cm.demo.D.snr.png')
plotms(vis='jupiter6cm.demo.D', xaxis='antenna', yaxis='snr', showgui=True, plotfile='jupiter6cm.demo.D.snr.png')
</source>
</source>




Line 284: Line 257:


<source lang="python">
<source lang="python">
polcal(vis='jupiter6cm.demo.ms', caltable='jupiter6cm.demo.X', field='1331+305', spw='', refant='11', poltype='Xf', solint='inf', combine='scan',minsnr=3, gaintable=['jupiter6cm.demo.gc', 'jupiter6cm.demo.G', 'jupiter6cm.demo.K','jupiter6cm.demo.D'], gainfield=['','1331+305','',''])
polcal(vis='jupiter6cm.demo.ms', caltable='jupiter6cm.demo.X', field='1331+305', spw='', refant='11', poltype='Xf', solint='inf', combine='scan',minsnr=3, gaintable=['jupiter6cm.demo.gc', 'jupiter6cm.demo.G', 'jupiter6cm.demo.D'], gainfield=['','1331+305','',''])
</source>
</source>


Line 294: Line 267:
For solint = inf, found 2 solution intervals.
For solint = inf, found 2 solution intervals.
Mean position angle offset solution for 1331+305 (spw = 0) = 80.7525 deg.
Mean position angle offset solution for 1331+305 (spw = 0) = 80.7525 deg.
Mean position angle offset solution for 1331+305 (spw = 1) = -12.0478 deg.
Mean position angle offset solution for 1331+305 (spw = 1) = 48.9853 deg.
   Found good Xf Jones solutions in 2 solution intervals.
   Found good Xf Jones solutions in 2 solution intervals.
</pre>
</pre>


<p style="color: #ff0000;"><b> something's broken here, can't run poltype='X' getting SEVERE error then </b></p>
<!--<p style="color: #ff0000;"><b> CASA 5.3 bug (present from CASA 5.0+; reported as JIRA CAS-11762).  </b> For the time being please use CASA <=4.7, split the data set into single SPW (IF) MS files, and calibrate them separately, or just calibrate each spw separately by specifying, in each task, spw='x' where x is whichever spw you want.</p>-->
 


<b>NOTE</b>: If you are using CASA 4.7 or earlier, you may want to use <tt>poltype='X'</tt> in X-term calculations (Mueller matrices). For CASA 5.0 and later this option will not work (the relevant CASA documentation is being updated), and hence you need to use <tt>poltype='Xf'</tt> (Jones matrices). Although 'Xf' should be used predominantly for large bandwidths, which clearly is not the case here, it can also be used for the single channel old VLA data as long as you make sure the <tt>interp</tt> parameter is set to default (which should be <tt>nearest</tt>).


=== Apply the calibration ===
=== Apply the calibration ===
Line 306: Line 279:
Now that we have derived all the calibration solutions and saved them in the tables of multiple extensions, we need to apply them to the actual data. The following tasks will apply the solution tables to the DATA and write a new column CORRECTED_DATA as it is standard for CASA. Important: make sure you set <tt>parang=True</tt>.
Now that we have derived all the calibration solutions and saved them in the tables of multiple extensions, we need to apply them to the actual data. The following tasks will apply the solution tables to the DATA and write a new column CORRECTED_DATA as it is standard for CASA. Important: make sure you set <tt>parang=True</tt>.


<p style="color: #ff0000;"><b> At the moment can't do absolute flux calibration at the same time as applying all other correction, the Amp gets twice as high and phases go all over the place. This is not the case when Gflx applued separately after all the other corrections.. I have no idea why </b></p>


<source lang="python">
applycal(vis='jupiter6cm.demo.ms', field='1331+305', spw='', selectdata=False, gaintable=['jupiter6cm.demo.gc', 'jupiter6cm.demo.G', 'jupiter6cm.demo.D','jupiter6cm.demo.X'], gainfield=['','1331+305'], calwt=[False], parang=True)


<source lang="python">
applycal(vis='jupiter6cm.demo.ms', field='0137+331', spw='', selectdata=False, gaintable=['jupiter6cm.demo.gc', 'jupiter6cm.demo.G', 'jupiter6cm.demo.Gflx','jupiter6cm.demo.D','jupiter6cm.demo.X'], gainfield=['','0137+331','0137+331'], calwt=[False], parang=True)
applycal(vis='jupiter6cm.demo.ms', field='1331+305,0137+331,JUPITER', spw='', selectdata=False, gaintable=['jupiter6cm.demo.gc', 'jupiter6cm.demo.G', 'jupiter6cm.demo.K','jupiter6cm.demo.D','jupiter6cm.demo.X'], calwt=[False], parang=True)


applycal(vis='jupiter6cm.demo.ms', field='0137+331,JUPITER', spw='', selectdata=False, gaintable=['jupiter6cm.demo.Gflx'], calwt=[False], parang=False)
applycal(vis='jupiter6cm.demo.ms', field='JUPITER', spw='', selectdata=False, gaintable=['jupiter6cm.demo.gc', 'jupiter6cm.demo.G', 'jupiter6cm.demo.Gflx','jupiter6cm.demo.D','jupiter6cm.demo.X'], gainfield=['','0137+331','0137+331'], calwt=[False], parang=True)
</source>
</source>


Line 326: Line 299:




== Full Stokes Imaging ==
== Initial imaging (Stokes I) ==
 
We will now image and clean the calibrated Jupiter data. In the next step we will perform self-calibration, so here in the initial imaging we will not clean too deeply and we will also save the model in the MS data (with the use of parameter <tt>savemodel</tt> in <tt>tclean()</tt>).
 
<!--
<b>NOTE</b>: As of CASA 5.3 the recommended task for deconvolution is <tt>tclean()</tt>. However, we found there may be a problem with how <tt>tclean()</tt> handles old, pre-upgrade VLA data. This is currently being investigated, and once resolved, this guide will be updated to demonstrate the <tt>tclean()</tt> use in this data reduction. Meanwhile, please use the standard <tt>clean()</tt> for deconvolution and imaging.
 
Check JIRA Ticket CAS-11971 for details regarding this comment.
 
-->
 
 
Since we set mask="" in our cleaning tasks, the interactive GUI will not allow you to do the deconvolution before you draw the mask on at least one plane. When drawing a mask, make sure to extend it to all channels and all polarisations.
 
<source lang="python">
tclean(vis='jupiter6cm.demo.JUPITER.split.ms', stokes='I', field='', spw='', imagename='jupiter6cm.demo.JUPITER.I.clean1', robust = 0.0, imsize=[288], cell=['3arcsec'], specmode='mfs', deconvolver='hogbom', weighting='briggs', threshold='0.1mJy', mask='', niter=500, interactive=True, cycleniter=100, savemodel='modelcolumn', pblimit=-0.2)
</source>
 
 
Inspect the quality of the cleaned images with <tt>imstat()</tt>.
 
<source lang="python">
imstat(imagename='jupiter6cm.demo.JUPITER.I.clean1.image', stokes='I', box='216,1,287,72')
</source>
 
In this initial imaging the deconvolution will stop with the iteration limit since we set it fairly low. We 'cleaned' approximately 4.3 Jy in this initial imaging step, and reached rms of about 3.52 mJy/bm.
 
<!-- Either of the tasks 'cleaned' approximately 4.3 Jy in this initial imaging step, and we get rms of about 3.52 mJy/bm (using <tt>clean()</tt>).<!-- and 3.9 mJy/bm (using <tt>tclean()</tt>).-->
 
== Self-calibration ==


We will now image and clean the calibrated Jupiter data. The recommended task for deconvolution is <tt>tclean()</tt>.
In the self calibration step we run <tt>gaincal()</tt> that will make use of the newly created MODEL column in our MS file.


<source lang="python">
<source lang="python">
tclean(vis='jupiter6cm.demo.JUPITER.split.ms', stokes='IQUV', field='', spw='', datacolumn='data', imagename='jupiter6cm.demo.JUPITER.IQUV.clean', imsize=[288], cell=['3arcsec'], specmode='mfs', gridder='standard', deconvolver='clarkstokes', weighting='briggs', threshold=5e-05, mask='', niter=10000, interactive=True, cycleniter=100)
gaincal(vis='jupiter6cm.demo.JUPITER.split.ms', caltable='jupiter6cm.demo.JUPITER.split.selfcal1', field='', spw='', gaintype='G', calmode='p', solint='30s', combine='', refant='11', parang=False, append=False, selectdata=False)
</source>
</source>


Inspect the solutions


The <tt>tclean()</tt> task is new for CASA 5.3. However, if you are performing this data reduction in earlier versions of CASA, or just want to use the standard <tt>clean()</tt> here is how you would run it. Note though, that <tt>clean()</tt> will disappear in the future versions of CASA with <tt>tclean()</tt> becoming the only task to perform this step. Both <tt>tclean()</tt> and <tt>clean()</tt> should give you similar results here.
<source lang="python">
plotms(vis='jupiter6cm.demo.JUPITER.split.selfcal1',xaxis='time',yaxis='amp',gridrows=2, gridcols=3, iteraxis='antenna')
plotms(vis='jupiter6cm.demo.JUPITER.split.selfcal1',xaxis='time',yaxis='phase', gridrows=2, gridcols=3 ,iteraxis='antenna',plotrange=[-1,-1,-180,180])
</source>


Note: since we set mask="" in our cleaning tasks, the interactive GUI will not allow you to do the deconvolution before you draw the mask on at least one plane. When drawing a mask, make sure to extend it to all channels and all polarisations.
And apply the calibration to the DATA(creating a CORRECTED column in the MS)


<source lang="python">
<source lang="python">
clean(vis='jupiter6cm.demo.JUPITER.split.ms', stokes='IQUV', field='', spw='', imagename='jupiter6cm.demo.JUPITER.IQUV.oldclean', imsize=[288], cell=['3arcsec'], mode='mfs', psfmode='clarkstokes', imagermode='csclean', weighting='briggs', threshold='0.05mJy', mask='', niter=10000, interactive=True, npercycle=100)
applycal(vis='jupiter6cm.demo.JUPITER.split.ms', field='', spw='', selectdata=False, gaintable=['jupiter6cm.demo.JUPITER.split.selfcal1'], gainfield=[''], interp=['nearest'],calwt=[False], applymode='calflag')
</source>
</source>


Inspect the quality of the cleaned images with <tt>imstat()</tt>, but remember that in this example we did not correct for the primary beam.


Now, image the self-calibrated data


If you are interested in performing self-calibration, consult either the [https://casaguides.nrao.edu/index.php/VLA_5_GHz_continuum_survey_of_Seyfert_galaxies pre-upgrade VLA continuum tutorial] or the [https://casaguides.nrao.edu/index.php/VLA_Continuum_Tutorial_3C391-CASA5.0.0#Self-Calibration JVLA CASA continuum tutorial].
<source lang="python">
tclean(vis='jupiter6cm.demo.JUPITER.split.ms', stokes='I', field='', spw='', imagename='jupiter6cm.demo.JUPITER.I.clean2', robust= 0.0, imsize=[288], cell=['3arcsec'], specmode='mfs', deconvolver='hogbom', weighting='briggs', threshold='0.05mJy', mask='', niter=10000, interactive=True, cycleniter=100, pblimit=-0.2)
</source>




Check the image statistics


== Polarisation Intensity and Angle Images  ==
<source lang="python">
imstat(imagename='jupiter6cm.demo.JUPITER.I.clean2.image', stokes='I', box='216,1,287,72')
</source>


After one cycle of self-calibration with <tt>tclean()</tt> we reached rms=1.10 mJy/bm. But bear in mind that the rms values may differ for you since they will depend on how deeply you cleaned and how good a mask you applied.
== Full Stokes Imaging ==
At this stage we will perform full Stokes imaging to create image of each Stokes parameter that we will later use to create polarised intensity and angle images.
<source lang="python">
tclean(vis='jupiter6cm.demo.JUPITER.split.ms', stokes='IQUV', field='', spw='', imagename='jupiter6cm.demo.JUPITER.IQUV.clean', robust= 0.0, imsize=[288], cell=['3arcsec'], specmode='mfs', deconvolver='clarkstokes', weighting='briggs', threshold='0.05mJy', mask='', niter=10000, interactive=True, cycleniter=100, pblimit=-0.2)
</source>
Inspect the quality of the cleaned images with <tt>imstat()</tt> (do it for each Stokes separately, as otherwise imstat() will return an average of all Stokes). You should be reaching values of about 1.1 mJy/bm (I), 0.62 mJy/bm (Q), 0.90 mJy/bm (U), 0.16 mJy/bm (V).
== Polarisation Intensity and Position Angle Images  ==
[[Image:Jupiter-poli.png|thumb|Polarised intensity (POLI) image of Jupiter with overlaid polarised angle vectors (POLA). ]]
[[Image:Jupiter-oldVLA-stokesI.png|thumb|Total continuum intensity (Stokes I) image of Jupiter with overlaid contours of its polarised intensity (POLI).]]


We now want to save each Stokes plane as separate images. We can use either the <tt>imsubimage()</tt> or <tt>immath()</tt> tasks to do so.  
We now want to save each Stokes plane as separate images. We can use either the <tt>imsubimage()</tt> or <tt>immath()</tt> tasks to do so.  
Line 373: Line 405:




Finally, we want to create the polarization intensity and position angle images.
Finally, we want to create the polarization intensity (POLI) and position angle (POLA) images.  


<source lang="python">
<source lang="python">
immath(imagename=['JUPITER.Q.image','JUPITER.U.image'], mode='poli', outfile='JUPITER.POLI.image')
immath(imagename=['JUPITER.Q.image','JUPITER.U.image'], mode='poli', outfile='JUPITER.POLI.image')
immath(imagename=['JUPITER.Q.image','JUPITER.U.image'], mode='pola', outfile='JUPITER.POLA.image',polithresh='10mJy/beam')
</source>
 
 
We will now use the <tt>polithresh</tt> parameter when creating the polarisation angle image to get rid of the noise. First check the statistic in the POLI image, and then use it as a threshold while creating the POLA image (in the example below equal to 4 sigma).
 
<source lang="python">
imstat(imagename='JUPITER.POLI.image', box='216,1,287,72')
</source>
 
<source lang="python">
immath(imagename=['JUPITER.Q.image','JUPITER.U.image'], mode='pola', outfile='JUPITER.POLA.image',polithresh='4.5mJy/beam')
</source>
</source>


Line 384: Line 426:




And that's it. For the tutorial on how to perform analysis, display and manipulation of the polarisation images now, consult the appropriate [https://casaguides.nrao.edu/index.php/VLA_Continuum_Tutorial_3C391-CASA5.0.0 VLA CASA guides].






And that's it. For the tutorial on how to perform analysis, display and manipulation of the polarisation images now, consult the appropriate [https://casaguides.nrao.edu/index.php/VLA_Continuum_Tutorial_3C391-CASA5.0.0 VLA CASA guides].




{{Checked 5.3.0 }}
{{Checked 5.5.0-149}}


[[Pre-upgrade VLA Tutorials | &#8629; '''Pre-upgrade VLA Tutorials''']]
[[Pre-upgrade VLA Tutorials | &#8629; '''Pre-upgrade VLA Tutorials''']]
<!--Last edited by Trent Seelig, 2019-08-27-->

Latest revision as of 17:00, 13 February 2023

DISCLAIMER
This is an advanced reference guide to calibration and imaging of pre-upgrade VLA polarimetric data with CASA 5.5.0. If you are a beginning or novice user, please consult relevant CASA guides first.


Data Import

The data set for this tutorial lives here: planets_6cm.fits (129MB). This is a VLA 6cm dataset that was observed back in 1999 to set the flux scale for calibration of the VLA. Included in the program were observations of the planets, including Jupiter which we will focus on in this tutorial. These are D-configuration data, with resolution of around 14".

Import the data into CASA. Task importuvfits() will read the original AIPS friendly UVFITS format and create a CASA native MS. 

importuvfits(fitsfile='planets_6cm.fits', vis='jupiter6cm.demo.ms', antnamescheme='old')

Check the observation set up and print verbose summary of the observations to the CASA logger 

listobs(vis='jupiter6cm.demo.ms')

The output of this task is fairly long, the abridged version is shown below since we may need some of this information later on during our calibration. 

##########################################
##### Begin Task: listobs            #####
   Observer: FLUX99     Project:   
Observation: VLA
Computing scan and subscan properties...
Data records: 2021424       Total elapsed time = 85136.5 seconds
   Observed from   15-Apr-1999/23:15:25.0   to   16-Apr-1999/22:54:21.6 (TAI)

[...]

Fields: 13
  ID   Code Name                RA               Decl           Epoch   SrcId      nRows
  0    A    0137+331            01:37:41.299500 +33.09.35.13400 J2000   0          72946
  1    T    0813+482            08:13:36.051800 +48.13.02.26200 J2000   1         227524
  2    A    0542+498            05:42:36.137900 +49.51.07.23400 J2000   2         227058
  3    T    0437+296            04:37:04.174700 +29.40.15.13600 J2000   3         113424
  4         VENUS               04:06:54.109428 +22.30.35.90609 J2000   4         121098
  5    A    0521+166            05:21:09.886000 +16.38.22.05200 J2000   5          81258
  6    T    1411+522            14:11:20.647700 +52.12.09.14100 J2000   6         243608
  7    A    1331+305            13:31:08.288100 +30.30.32.96000 J2000   7         307958
  8         MARS                14:21:41.365747 -12.21.49.45444 J2000   8         118570
  9         NGC7027             21:07:01.593000 +42.14.10.18600 J2000   9         136082
  10        NEPTUNE             20:26:01.136316 -18.54.54.21127 J2000   10        157736
  11        URANUS              21:15:42.828572 -16.35.05.59272 J2000   11         99412
  12        JUPITER             00:55:34.043951 +04.45.44.70633 J2000   12        114750

Spectral Windows:  (2 unique spectral windows and 1 unique polarization setups)
SpwID  Name   #Chans   Frame   Ch0(MHz)  ChanWid(kHz)  TotBW(kHz) CtrFreq(MHz)  Corrs          
  0      none       1   TOPO    4885.100     50000.000     50000.0   4885.1000   RR  RL  LR  LL
  1      none       1   TOPO    4835.100     50000.000     50000.0   4835.1000   RR  RL  LR  LL

Sources: 26
  ID   Name                SpwId RestFreq(MHz)  SysVel(km/s) 
  0    0137+331            0     0              0            
  0    0137+331            1     0              0            
  1    0813+482            0     0              0            
  1    0813+482            1     0              0            
  2    0542+498            0     0              0            
  2    0542+498            1     0              0            
  3    0437+296            0     0              0            
  3    0437+296            1     0              0            
  4    VENUS               0     0              0            
  4    VENUS               1     0              0            
  5    0521+166            0     0              0            
  5    0521+166            1     0              0            
  6    1411+522            0     0              0            
  6    1411+522            1     0              0            
  7    1331+305            0     0              0            
  7    1331+305            1     0              0            
  8    MARS                0     0              0            
  8    MARS                1     0              0            
  9    NGC7027             0     0              0            
  9    NGC7027             1     0              0            
  10   NEPTUNE             0     0              0            
  10   NEPTUNE             1     0              0            
  11   URANUS              0     0              0            
  11   URANUS              1     0              0            
  12   JUPITER             0     0              0            
  12   JUPITER             1     0              0            

Antennas 27
[....]

##### End Task: listobs              #####
##########################################


Check also the array configuration and pick a reference antenna. Here, we will use antenna '11' as a reference since it's located in the middle of the array. 

plotants(vis='jupiter6cm.demo.ms', figfile='jupiter6cm.demo.ant.png')

Note (for uvfits sourced directly from archive only): CASA 5.4 and earlier versions will not plot the antennas properly. This is to be resolved in future CASA versions. If this occurs then a reference antenna can be selected using the listobs task and choosing an antenna located on a pad close to the center of the array (Pads numbers increase with distance from the center of the array, ie. "VLA:_N1" and "EVLA:W2" are pads close to the center of the array, where as, "VLA:_N18" is not).

Data Inspection and Editing

To inspect and interactively flag bad data use task plotms(). Note: it is not recommended to use plotms() to interactively flag the new post-upgrade VLA data due to their large volume and large bandwidths. However, the old VLA data are much smaller and plotms() is capable of managing it interactively.

First, inspect the primary flux and polarisation angle calibrator, 1331+305 (3C286). Inspect RR,LL and RL,LR correlations separately due to large amplitude differences between them (when all correlations are plotted together, the RL,LR will seem like bad data due to their much lower amplitudes as compared to RR,LL). Use Mark Regions within the plotms() GUI to draw boxes around points to flag, and hit Flag to flag. 

plotms(vis='jupiter6cm.demo.ms', selectdata=True, field='1331+305', correlation='RR,LL', xaxis='uvdist', yaxis='amp')

Now, inspect the other two sources we are interested in, the polarisation leakage calibrator (0137+331) and our target source (JUPITER).


Flagging can also be done non-interactively as per currently recommended CASA practise. Use task flagdata() to do so. For example, from inspecting our data in plotms() you should have noticed that Antenna 9 (ID=8) in spw 1 is often bad. The bad data on Antenna 9 are in the last 4 scans in spw='1' for the 0137+331 calibrator and for our target source (JUPITER), as well as in the last scan for all antennas in both spws on the target source. We can flag these points with the following flagdata() task executions. 

flagdata(vis='jupiter6cm.demo.ms', mode='manual', field='0137+331', spw='1', antenna='9', timerange='42:00:00~48:00:00')
flagdata(vis='jupiter6cm.demo.ms', mode='manual', field='JUPITER', spw='1', antenna='9', timerange='16:26:00~22:20:00')
flagdata(vis='jupiter6cm.demo.ms', mode='manual', field='JUPITER', spw='', timerange='21:40:00~22:20:00')


There are more data points to flag -- keep flagging until you are happy with the results. The following commands will get rid of most bad data, but depending on how clean the data you want to proceed with, you may still want to inspect them in plotms() and flag interactively the reminder of bad datapoints. 

flagdata(vis='jupiter6cm.demo.ms',mode='clip',field='1331+305',correlation='ABS_RR,LL',clipoutside=False,clipminmax=[0,0.75])
flagdata(vis='jupiter6cm.demo.ms',mode='clip',field='1331+305',correlation='ABS_RL,LR',clipoutside=False,clipminmax=[0,0.04])
flagdata(vis='jupiter6cm.demo.ms',mode='clip',field='0137+331',correlation='ABS_RR,LL',clipoutside=False,clipminmax=[0,0.55])
flagdata(vis='jupiter6cm.demo.ms',mode='clip',field='0137+331',correlation='ABS_RL,LR',clipoutside=False,clipminmax=[0,0.01])

If you are unfamiliar with flagging in CASA, consult detailed topical guide Flagging VLA Data.


Calibration

Flux Density Scale

Set the absolute flux density scale, but only for Stokes I at the moment (total flux density model). Our primary flux calibrator here is 1331+305 (3C286). The default model for CASA 5.5+ is 'Perley-Butler 2017'. 

setjy(vis='jupiter6cm.demo.ms', field='1331+305', model='3C286_C.im')


Initial gain calibration

At this stage the data have an overall flux density scaling determined, but full gain solutions aren't there yet. The relevant task is gaincal() (analogous to the AIPS task CALIB). Gaincal() will produce a separate table with solutions, and we will use appropriate extensions to keep track of what is what.

NOTE: Since we have only two single-channel continuum spw, we do not want to do bandpass calibration nor solve for delays within spws as is currently done with wide bandwidth post-upgrade VLA data.

Firstly, generate an antenna zenith-angle dependent VLA gain curve calibration table 

gencal(vis='jupiter6cm.demo.ms', caltable='jupiter6cm.demo.gc', caltype='gc')

Now, solve for antenna gains on 1331+305 and 0137+331, using the generated gain curve table (.gc). 

gaincal(vis='jupiter6cm.demo.ms', caltable='jupiter6cm.demo.G', field='1331+305,0137+331', spw='', gaintype='G', calmode='ap', solint='inf', combine='', refant='11', minsnr=3, gaintable=['jupiter6cm.demo.gc'], parang=False)

# And check the solutions
plotms(vis='jupiter6cm.demo.G', xaxis='time', yaxis='amp', gridrows=3, gridcols=3, iteraxis='antenna')
plotms(vis='jupiter6cm.demo.G', xaxis='time', yaxis='phase', plotrange=[-1,-1,-200,200], gridrows=3, gridcols=3, iteraxis='antenna')

If all looks good, bootstrap the flux density scale of the flux calibrator onto the phase calibrators (CASA's fluxscale() task is equivalent to GETJY in AIPS). When executing fluxscale(), the calibration table with the extension .G is modified and stored as a new table with the extension .Gflx. 

myFluxscale = fluxscale(vis='jupiter6cm.demo.ms', caltable='jupiter6cm.demo.G', fluxtable='jupiter6cm.demo.Gflx', reference='1331+305', transfer='0137+331', incremental=True, append=False, display=False)

The output is displayed in the logger as well as stored in the myFluxscale python dictionary. 

 Beginning fluxscale--(MSSelection version)-------
 Found reference field(s): 1331+305
 Found transfer field(s):  0137+331
 Flux density for 0137+331 in SpW=0 (freq=4.8851e+09 Hz) is: 5.29665 +/- 0.00449217 (SNR = 1179.09, N = 54)
 Flux density for 0137+331 in SpW=1 (freq=4.8351e+09 Hz) is: 5.34890 +/- 0.00176819 (SNR = 3025.07, N = 54)
 Fitted spectrum for 0137+331 with fitorder=1: Flux density = 5.32271 +/- 1.70229e-07 (freq=4.86004 GHz) spidx=-0.954124 (degenerate)
 Storing result in jupiter6cm.demo.Gflx
 Writing solutions to table: jupiter6cm.demo.Gflx


Before proceeding, inspect the flux density calibration and save results to a file. 

plotms(vis='jupiter6cm.demo.Gflx', xaxis='time', yaxis='amp', showgui=True, plotfile='jupiter6cm.demo.Gflx.amp.png')

plotms(vis='jupiter6cm.demo.Gflx', xaxis='time', yaxis='phase', plotrange=[-1,-1,-200,200], showgui=True, plotfile='jupiter6cm.demo.Gflx.phase.png')


Polarisation calibration

Just as in the step of the initial gain calibration, since our old VLA data have single-channel continuum spws, we do not want to solve for KCROSS delays in our polarisation calibration. Instead, we directly solve for D and X terms.


Set the polarisation model

First, set the polarisation model for the polarised position-angle calibrator (here 1331+305=3C286 which is also our primary flux calibrator). For polarisation properties of your primary polarisation calibrator see VLA Polarimetry Guide. 

i0=7.3109    # Stokes I value for spw 0 ch 0
f0=4.8851    # Frequency for spw0 ch0 (note that in our data the 'lower' spw is actually higher frequency)
alpha=log(i0/7.35974932)/log(4.8351/f0) # Values from our setjy() run on Stokes I earlier
c0=0.114     # Fractional polarisation 11.4% for 5GHz
d0=33*pi/180 # Polarisation angle 33deg in radians

myPolSetjy = setjy(vis='jupiter6cm.demo.ms', field='1331+305', standard='manual', spw='', fluxdensity=[i0,0,0,0], spix=[alpha,0], reffreq=str(f0)+'GHz', polindex=[c0,0], polangle=[d0,0], scalebychan=True, usescratch=False)

The results are displayed in the CASA logger as well as saved in the myPolSetjy python dictionary 

#In CASA
CASA <49>: myPolSetjy
Out[49]: 
{'7': {'0': {'fluxd': array([ 7.3109    ,  0.33899165,  0.7613877 ,  0.        ])},
  '1': {'fluxd': array([ 7.26237491,  0.33674164,  0.7563341 ,  0.        ])},
  'fieldName': '1331+305'},
 'format': "{field Id: {spw Id: {fluxd: [I,Q,U,V] in Jy}, 'fieldName':field name }}"}


Solve for the leakage terms (D terms)

Solve for polarization leakage on 0137+331. In this step we solve for the instrumental polarization. We will assume here our calibrator has unknown polarisation (poltype='D+QU' if good parallactic coverage, 'D' otherwise, consult polcal() help for more information on options). 

polcal(vis='jupiter6cm.demo.ms', caltable='jupiter6cm.demo.D', field='0137+331', spw='', refant='11', poltype='D+QU', solint='inf', combine='scan',minsnr=3, gaintable=['jupiter6cm.demo.gc', 'jupiter6cm.demo.G'], gainfield=['','0137+331',''])

Check the solutions 

plotms(vis='jupiter6cm.demo.D', xaxis='antenna', yaxis='amp', showgui=True, plotfile='jupiter6cm.demo.D.amp.png')

plotms(vis='jupiter6cm.demo.D', xaxis='antenna', yaxis='phase', plotrange=[-1,-1,-200,200], showgui=True, plotfile='jupiter6cm.demo.D.phase.png')

plotms(vis='jupiter6cm.demo.D', xaxis='antenna', yaxis='snr', showgui=True, plotfile='jupiter6cm.demo.D.snr.png')



Solve for the R-L polarisation angle (X term)

The total polarisation is now correct (since we just calibrated the instrumental polarisation, i.e. D terms), but now the R-L phase needs to be calibrated to obtain an accurate polarisation position angle. 

polcal(vis='jupiter6cm.demo.ms', caltable='jupiter6cm.demo.X', field='1331+305', spw='', refant='11', poltype='Xf', solint='inf', combine='scan',minsnr=3, gaintable=['jupiter6cm.demo.gc', 'jupiter6cm.demo.G', 'jupiter6cm.demo.D'], gainfield=['','1331+305','',''])

Check the solutions in CASA logger window 

The following calibration term is arranged for solve:
.   Xf Jones: table=jupiter6cm.demo.X append=false solint=inf,none refantmode='flex' refant='none' minsnr=3 apmode=AP solnorm=false
For solint = inf, found 2 solution intervals.
Mean position angle offset solution for 1331+305 (spw = 0) = 80.7525 deg.
Mean position angle offset solution for 1331+305 (spw = 1) = 48.9853 deg.
  Found good Xf Jones solutions in 2 solution intervals.


NOTE: If you are using CASA 4.7 or earlier, you may want to use poltype='X' in X-term calculations (Mueller matrices). For CASA 5.0 and later this option will not work (the relevant CASA documentation is being updated), and hence you need to use poltype='Xf' (Jones matrices). Although 'Xf' should be used predominantly for large bandwidths, which clearly is not the case here, it can also be used for the single channel old VLA data as long as you make sure the interp parameter is set to default (which should be nearest).

Apply the calibration

Now that we have derived all the calibration solutions and saved them in the tables of multiple extensions, we need to apply them to the actual data. The following tasks will apply the solution tables to the DATA and write a new column CORRECTED_DATA as it is standard for CASA. Important: make sure you set parang=True. 


applycal(vis='jupiter6cm.demo.ms', field='1331+305', spw='', selectdata=False, gaintable=['jupiter6cm.demo.gc', 'jupiter6cm.demo.G', 'jupiter6cm.demo.D','jupiter6cm.demo.X'], gainfield=['','1331+305'], calwt=[False], parang=True)

applycal(vis='jupiter6cm.demo.ms', field='0137+331', spw='', selectdata=False, gaintable=['jupiter6cm.demo.gc', 'jupiter6cm.demo.G', 'jupiter6cm.demo.Gflx','jupiter6cm.demo.D','jupiter6cm.demo.X'], gainfield=['','0137+331','0137+331'], calwt=[False], parang=True)

applycal(vis='jupiter6cm.demo.ms', field='JUPITER', spw='', selectdata=False, gaintable=['jupiter6cm.demo.gc', 'jupiter6cm.demo.G', 'jupiter6cm.demo.Gflx','jupiter6cm.demo.D','jupiter6cm.demo.X'], gainfield=['','0137+331','0137+331'], calwt=[False], parang=True)


It's a good idea to split the Jupiter target data at this point. We will write the corrected data of our target source to a new single-source MS. 

split(vis='jupiter6cm.demo.ms', outputvis='jupiter6cm.demo.JUPITER.split.ms', field='JUPITER', datacolumn='corrected')

You can use plotms() task to look at the split calibrated data.


Initial imaging (Stokes I)

We will now image and clean the calibrated Jupiter data. In the next step we will perform self-calibration, so here in the initial imaging we will not clean too deeply and we will also save the model in the MS data (with the use of parameter savemodel in tclean()).


Since we set mask="" in our cleaning tasks, the interactive GUI will not allow you to do the deconvolution before you draw the mask on at least one plane. When drawing a mask, make sure to extend it to all channels and all polarisations. 

tclean(vis='jupiter6cm.demo.JUPITER.split.ms', stokes='I', field='', spw='', imagename='jupiter6cm.demo.JUPITER.I.clean1', robust = 0.0, imsize=[288], cell=['3arcsec'], specmode='mfs', deconvolver='hogbom', weighting='briggs', threshold='0.1mJy', mask='', niter=500, interactive=True, cycleniter=100, savemodel='modelcolumn', pblimit=-0.2)


Inspect the quality of the cleaned images with imstat(). 

imstat(imagename='jupiter6cm.demo.JUPITER.I.clean1.image', stokes='I', box='216,1,287,72')

In this initial imaging the deconvolution will stop with the iteration limit since we set it fairly low. We 'cleaned' approximately 4.3 Jy in this initial imaging step, and reached rms of about 3.52 mJy/bm.


Self-calibration

In the self calibration step we run gaincal() that will make use of the newly created MODEL column in our MS file. 

gaincal(vis='jupiter6cm.demo.JUPITER.split.ms', caltable='jupiter6cm.demo.JUPITER.split.selfcal1', field='', spw='', gaintype='G', calmode='p', solint='30s', combine='', refant='11', parang=False, append=False, selectdata=False)

Inspect the solutions 

plotms(vis='jupiter6cm.demo.JUPITER.split.selfcal1',xaxis='time',yaxis='amp',gridrows=2, gridcols=3, iteraxis='antenna')
plotms(vis='jupiter6cm.demo.JUPITER.split.selfcal1',xaxis='time',yaxis='phase', gridrows=2, gridcols=3 ,iteraxis='antenna',plotrange=[-1,-1,-180,180])

And apply the calibration to the DATA(creating a CORRECTED column in the MS) 

applycal(vis='jupiter6cm.demo.JUPITER.split.ms', field='', spw='', selectdata=False, gaintable=['jupiter6cm.demo.JUPITER.split.selfcal1'], gainfield=[''], interp=['nearest'],calwt=[False], applymode='calflag')


Now, image the self-calibrated data 

tclean(vis='jupiter6cm.demo.JUPITER.split.ms', stokes='I', field='', spw='', imagename='jupiter6cm.demo.JUPITER.I.clean2', robust= 0.0, imsize=[288], cell=['3arcsec'], specmode='mfs', deconvolver='hogbom', weighting='briggs', threshold='0.05mJy', mask='', niter=10000, interactive=True, cycleniter=100, pblimit=-0.2)


Check the image statistics 

imstat(imagename='jupiter6cm.demo.JUPITER.I.clean2.image', stokes='I', box='216,1,287,72')


After one cycle of self-calibration with tclean() we reached rms=1.10 mJy/bm. But bear in mind that the rms values may differ for you since they will depend on how deeply you cleaned and how good a mask you applied.


Full Stokes Imaging

At this stage we will perform full Stokes imaging to create image of each Stokes parameter that we will later use to create polarised intensity and angle images. 

tclean(vis='jupiter6cm.demo.JUPITER.split.ms', stokes='IQUV', field='', spw='', imagename='jupiter6cm.demo.JUPITER.IQUV.clean', robust= 0.0, imsize=[288], cell=['3arcsec'], specmode='mfs', deconvolver='clarkstokes', weighting='briggs', threshold='0.05mJy', mask='', niter=10000, interactive=True, cycleniter=100, pblimit=-0.2)

Inspect the quality of the cleaned images with imstat() (do it for each Stokes separately, as otherwise imstat() will return an average of all Stokes). You should be reaching values of about 1.1 mJy/bm (I), 0.62 mJy/bm (Q), 0.90 mJy/bm (U), 0.16 mJy/bm (V).


Polarisation Intensity and Position Angle Images

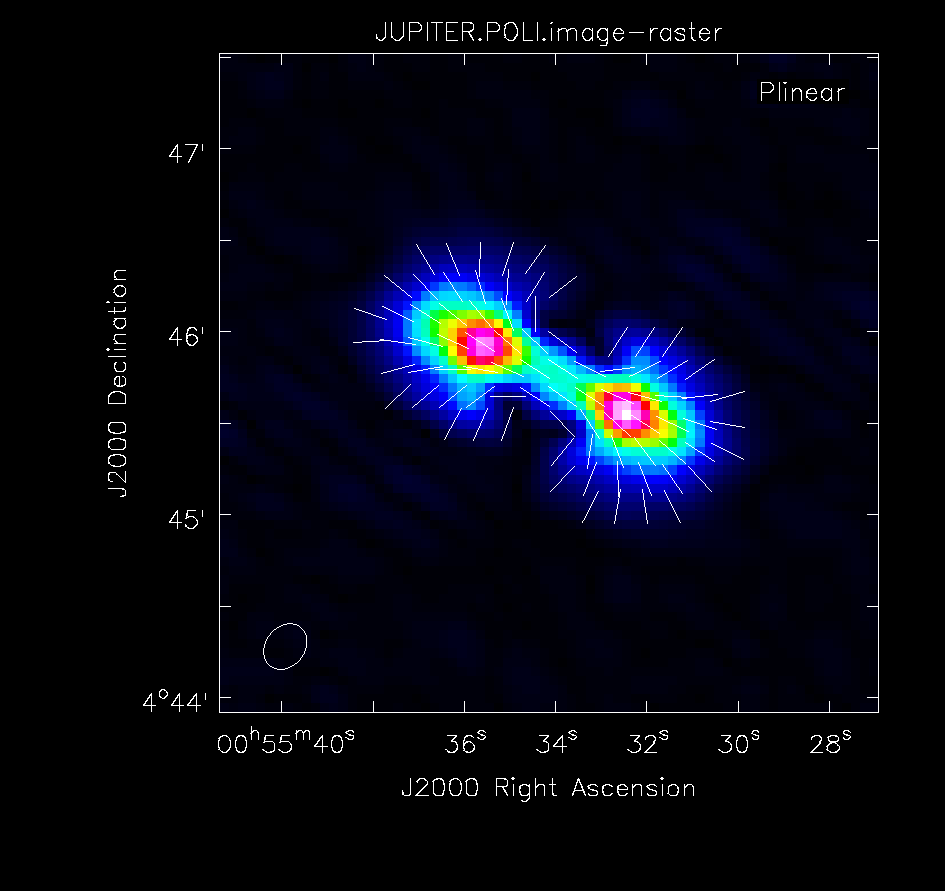
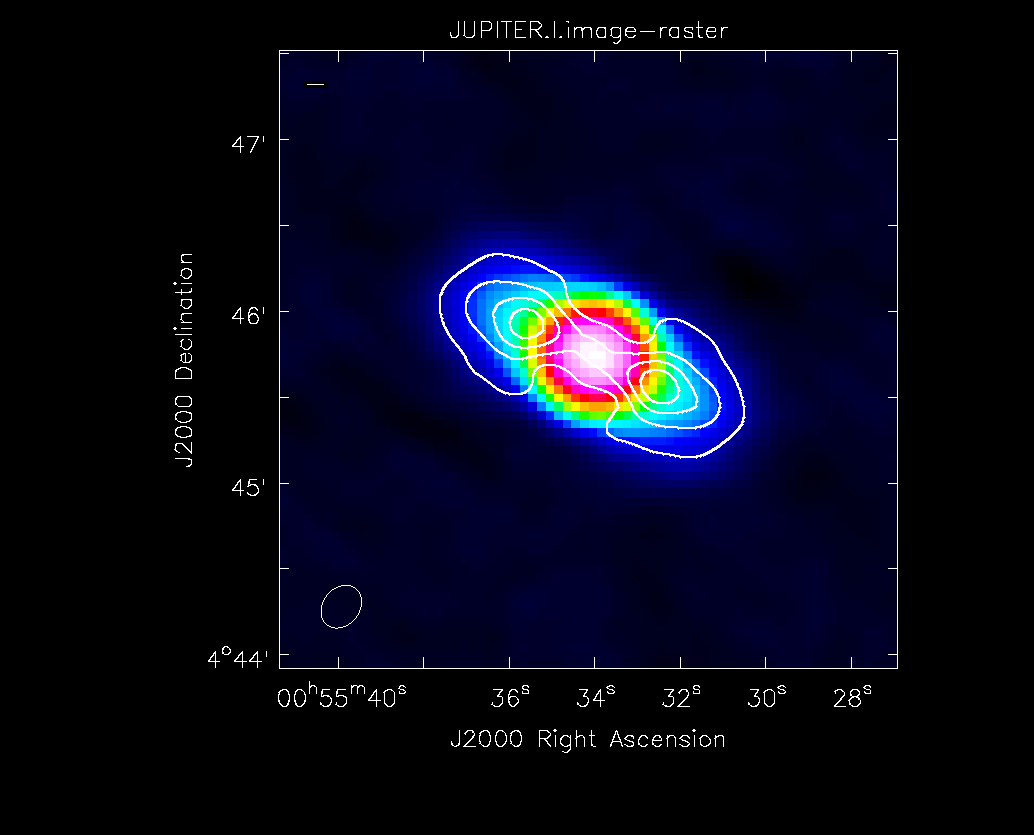
Polarised intensity (POLI) image of Jupiter with overlaid polarised angle vectors (POLA).
Total continuum intensity (Stokes I) image of Jupiter with overlaid contours of its polarised intensity (POLI).

We now want to save each Stokes plane as separate images. We can use either the imsubimage() or immath() tasks to do so.

Run 

imsubimage(imagename='jupiter6cm.demo.JUPITER.IQUV.clean.image',outfile='JUPITER.I.image',stokes='I')
imsubimage(imagename='jupiter6cm.demo.JUPITER.IQUV.clean.image',outfile='JUPITER.Q.image',stokes='Q')
imsubimage(imagename='jupiter6cm.demo.JUPITER.IQUV.clean.image',outfile='JUPITER.U.image',stokes='U')

or 

immath(imagename='jupiter6cm.demo.JUPITER.IQUV.clean.image', mode='evalexpr', stokes='I', expr='IM0', outfile='JUPITER.I.image')
immath(imagename='jupiter6cm.demo.JUPITER.IQUV.clean.image', mode='evalexpr', stokes='Q', expr='IM0', outfile='JUPITER.Q.image')
immath(imagename='jupiter6cm.demo.JUPITER.IQUV.clean.image', mode='evalexpr', stokes='U', expr='IM0', outfile='JUPITER.U.image')


Finally, we want to create the polarization intensity (POLI) and position angle (POLA) images. 

immath(imagename=['JUPITER.Q.image','JUPITER.U.image'], mode='poli', outfile='JUPITER.POLI.image')


We will now use the polithresh parameter when creating the polarisation angle image to get rid of the noise. First check the statistic in the POLI image, and then use it as a threshold while creating the POLA image (in the example below equal to 4 sigma). 

imstat(imagename='JUPITER.POLI.image', box='216,1,287,72')

immath(imagename=['JUPITER.Q.image','JUPITER.U.image'], mode='pola', outfile='JUPITER.POLA.image',polithresh='4.5mJy/beam')

Again, check the statistics of these final images with imstat() and/or viewer().




And that's it. For the tutorial on how to perform analysis, display and manipulation of the polarisation images now, consult the appropriate VLA CASA guides.


Template:Checked 5.5.0-149

↵ Pre-upgrade VLA Tutorials


Retrieved from "https://casaguides.nrao.edu/index.php?title=Jupiter:_continuum_polarization_calibration_5.5.0&oldid=34796"