Protoplanetary Disk Simulation - VLA-CASA5.3.0: Difference between revisions
No edit summary |
No edit summary |
||
| (55 intermediate revisions by the same user not shown) | |||
| Line 98: | Line 98: | ||
The resulting plots of our first simulation are shown in Fig. 4. Since this is a dirty image only (niter=0), the image and residual are the same dirty image. SInce we also did not turn on any thermal noise, the image corruptions are all due to the incomplete uv-coverage of our observations. | The resulting plots of our first simulation are shown in Fig. 4. Since this is a dirty image only (niter=0), the image and residual are the same dirty image. SInce we also did not turn on any thermal noise, the image corruptions are all due to the incomplete uv-coverage of our observations. | ||
{| | {| | ||
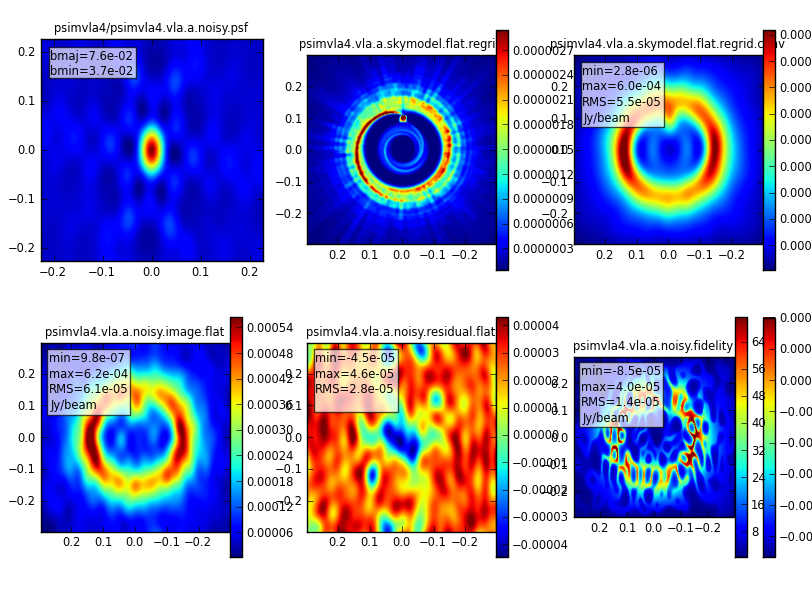
|[[Image:VLAsim-psim1-ana.png|600px|thumb|left|'''Fig. 4:''' Simulated Images for noise-less Q-band observations. | |[[Image:VLAsim-psim1-ana.png|600px|thumb|left|'''Fig. 4:''' Simulated Images for noise-less Q-band observations. '''Upper left:''' the psf of the observations with the clean beam parameters. '''Upper center:''' the Sky model. '''Upper right:''' The sky model convolved with the clean beam. '''Bottom left:''' the simulated image. '''Bottom center:''' the residual image from deconvolution. '''Bottom right:''' the fidelity image (note that a bug in CASAS shows two color wedges for this plot; the inner one is the correct one to use).]] | ||
|} | |} | ||
| Line 112: | Line 112: | ||
</source> | </source> | ||
The only difference to the earlier call of {{simobserve}} is our setting of ''niter=1000, threshold='1e-4Jy' '' which corresponds to a maximum number of 1000 clean iterations and a clean threshold of 0.1mJy. The threshold was chosen based on the previous image to be a few times above the rms of the image. The residual image | The only difference to the earlier call of {{simobserve}} is our setting of ''niter=1000, threshold='1e-4Jy' '' which corresponds to a maximum number of 1000 clean iterations and a clean threshold of 0.1mJy. The threshold was chosen based on the previous image to be a few times above the rms of the image. The residual image is now flatter as expected and the bulk of the sidelobes disappear. | ||
{| | {| | ||
| Line 120: | Line 120: | ||
===Q-band, 128MHz bandwidth, 4mm pwv, 1h integration time, A-configuration=== | ===Q-band, 128MHz bandwidth, 4mm pwv, 1h integration time, A-configuration=== | ||
We now add a precipitable water vapor of 4mm and a ground temperature for spillover of 270K. This can be achieved by the ''user_pwr'' and ''t_ground'' parameters. {{simobserve} only adds thermal noise due to the sky brightness, but not phase noise due to pwv variations across the array. The ''sm.settrop'' tool can be used for the more sophisticated troposhperic models. A description is given in [https://casaguides.nrao.edu/index.php/Corrupting_Simulated_Data_(Simulator_Tool) Corrupting Simulated Data]. | We now add a precipitable water vapor of 4mm and a ground temperature for spillover of 270K. This can be achieved by the ''user_pwr'' and ''t_ground'' parameters. {{simobserve}} only adds thermal noise due to the sky brightness, but not phase noise due to pwv variations across the array. The ''sm.settrop'' tool can be used for the more sophisticated troposhperic models. A description is given in [https://casaguides.nrao.edu/index.php/Corrupting_Simulated_Data_(Simulator_Tool) Corrupting Simulated Data]. | ||
<source lang="python"> | <source lang="python"> | ||
| Line 127: | Line 127: | ||
</source> | </source> | ||
The simobserve output will be identical to Fig. 3 since we do not change any of the displayed parameters. | The simobserve output will be identical to Fig. 2 and 3 since we do not change any of the displayed parameters. Now let's analyze the MS: | ||
<source lang="python"> | <source lang="python"> | ||
| Line 137: | Line 137: | ||
{| | {| | ||
|[[Image:VLAsim-psim3-ana.png|600px|thumb|left|Fig. 6: Output of {{simanalyze}} after injecting noise.]] | |[[Image:VLAsim-psim3-ana.png|600px|thumb|left|'''Fig. 6:''' Output of {{simanalyze}} after injecting noise.]] | ||
|} | |} | ||
| Line 143: | Line 143: | ||
==== Comparison with the VLA Exposure Calculator ==== | ==== Comparison with the VLA Exposure Calculator ==== | ||
We can compare the simulation to the predicted VLA sensitivity via the [http://go.nrao.edu/ect VLA Exposure Calculator Tool ( | We can compare the simulation to the predicted VLA sensitivity via the [http://go.nrao.edu/ect VLA Exposure Calculator Tool (ECT)] ([http://go.nrao.edu/ect Description]). Using winter observing conditions (for good pwv), a medium elevation (cf. Fig. 3), 128MHz bandwidth at a frequency of 44GHz, the ECT predicts a beam size of 0.067" and which is very close to our simulations (cf. Fig. 3 and 6). The ECT output is shown in Fig. 7. | ||
{| | {| | ||
|[[Image:VLAsim-etc.png|400px|thumb|left|Fig. 7: Exposure Calculation for 4mm pwr, 128MHz bandwidth]] | |[[Image:VLAsim-etc.png|400px|thumb|left|'''Fig. 7:''' Exposure Calculation for 4mm pwr, 128MHz bandwidth]] | ||
|} | |} | ||
The rms provided in Fig. 6 is over the entire image and includes the source. It is therefore not representative to the thermal noise. To obtain a better noise figure, we produce an image with the same parameters as simanalyze, but with a larger image size via {{tclean}}. Since the briggs parameter in {{simanalyze}} defaults to robust=0.5, we will use the same value here: | The rms provided in Fig. 6 is over the entire image and includes the source. It is therefore not representative to the thermal noise. To obtain a better noise figure, we produce an image with the same parameters as {{simanalyze}}, but with a larger image size directly via {{tclean}}. Since the briggs parameter in {{simanalyze}} defaults to robust=0.5, we will use the same value here: | ||
<source lang="python"> | <source lang="python"> | ||
| Line 163: | Line 163: | ||
</source> | </source> | ||
and measuring the noise statistics away from the source (Fig. 8), gives a value of about | and measuring the noise statistics away from the source (Fig. 8), gives a value of about 7e-5Jy/beam which is a very good agreement with the predicted noise figure of 6.9e-5 Jy/beam. | ||
{| | {| | ||
|[[Image:VLAsim-tcleanbig.png|600px|thumb|left|Fig. 8: Larger | |[[Image:VLAsim-tcleanbig.png|600px|thumb|left|'''Fig. 8:''' Larger image of the simulation given in Fig. 6, measuring the rms noise in the purple rectangle regions away from the emission. A few low-level sidelobes are still present, however. ]] | ||
|} | |} | ||
===Q-band, 8GHz bandwidth, 4mm pwv, 1h integration time, A-configuration=== | ===Q-band, 8GHz bandwidth, 4mm pwv, 1h integration time, A-configuration=== | ||
To compensate for noise, we will extend our bandwidth from 128MHz to 8GHz. At this time, {{simobserve}} has no chanelization so the simulation will not have the better uv-coverage that is obtained in multi-frequency imaging. Consecutive simulations with different spectral windows, and combined MSs, however, can achieve that. | To compensate for noise, we will extend our bandwidth from 128MHz to 8GHz. At this time, {{simobserve}} has no chanelization so the simulation will not have the better uv-coverage that is obtained in multi-frequency imaging. Consecutive simulations with different spectral windows, and combined MSs, however, can achieve that and we will show how to obtain a multi-channel MS shortly. For large bandwidths, one needs to be careful to not introduce [[https://science.nrao.edu/facilities/vla/docs/manuals/oss2016A/performance/fov/bw-smearing bandwidth smearing]]. Our source is at the center of the image and bandwidth smearing will be minimal. | ||
<source lang="python"> | <source lang="python"> | ||
| Line 185: | Line 185: | ||
</source> | </source> | ||
The image (Fig. 9) is clearly better defined, as expected from a broader | The image (Fig. 9) is clearly better defined, as expected from a broader bandwidth. We also decreased the cleaning threshold to 0.05mJy and added a few more iterations to allow to reach this threshold. | ||
{| | {| | ||
|[[Image:VLAsim-psim4-ana.png|600px|thumb|left|Fig. 9: Imaging with 8GHz bandwidth.]] | |[[Image:VLAsim-psim4-ana.png|600px|thumb|left|'''Fig. 9:''' Imaging with 8GHz bandwidth.]] | ||
|} | |} | ||
<!-- | |||
==== Comparison with the VLA Exposure Calculator ==== | ==== Comparison with the VLA Exposure Calculator ==== | ||
We compare again the simulation to the predicted VLA sensitivity via the [http://go.nrao.edu/ect VLA Exposure Calculator Tool (ETC)] ([http://go.nrao.edu/ect Description]). Using the same conditions and parameters as above, except for 8GHz bandwidth, the | We compare again the simulation to the predicted VLA sensitivity via the [http://go.nrao.edu/ect VLA Exposure Calculator Tool (ETC)] ([http://go.nrao.edu/ect Description]). Using the same conditions and parameters as above, except for 8GHz bandwidth, the ECT predicts a rms of 10.7<math>\mu Jy</math> (Fig. 10): | ||
{| | {| | ||
|[[Image:VLAsim-etc8GHz.png|400px|thumb|left|Fig. | |[[Image:VLAsim-etc8GHz.png|400px|thumb|left|'''Fig. 10''': Exposure time calculation for 4mm pwr, 8GHz bandwidth]] | ||
|} | |} | ||
Note that the VLA exposure calculator switched to 3bit observing to accommodate the large bandwidth. The simulator, however, assumes 8bit | Note that the VLA exposure calculator switched to 3bit observing to accommodate the large bandwidth. The simulator, however, assumes 8bit samplers, which provide about 15% better sensitivity than VLA 3bit correlations (For a discussion, see the [https://science.nrao.edu/facilities/vla/docs/manuals/oss/performance/vla-samplers VLA Samplers] page). | ||
Similar to the case of 128MHz bandwidth, we produce a larger image to be able to measure the image rms in a signal-free region: | Similar to the case of 128MHz bandwidth, we produce a larger image to be able to measure the image rms in a signal-free region: | ||
| Line 216: | Line 218: | ||
</source> | </source> | ||
and measuring the noise statistics away from the source (Fig. | and measuring the noise statistics away from the source (Fig. 11), gives a value of about 1.3e-5Jy/beam which is in reasonable agreement with the exposure calculator prediction. The regions where we measured the noise still contains some residual sidelobe structure and deeper cleaning, especially with a clean mask would improve the noise figure further, bringing it even closer to the predicted value. | ||
{| | {| | ||
|[[Image:VLAsim-tcleanbig8GHz.png|600px|thumb|left|Fig. | |[[Image:VLAsim-tcleanbig8GHz.png|600px|thumb|left|'''Fig. 11:''' Larger Image of the 8GHz simulation in Fig. 9, measuring the rms noise in the purple rectangle regions away from the emission.]] | ||
|} | |} | ||
--> | |||
==== Multi-Term-Multi-Frequency Synthesis Imaging ==== | ==== Multi-Term-Multi-Frequency Synthesis Imaging ==== | ||
In reality | In reality, the 8GHz bandwidth is not confined to a single channel but to many channels. This results in a spread out uv-coverage as it depends on the projected baselines expressed in number of wavelengths. Combining the channels in a multi-frequency synthesis (mfs), therefore does not only increase the sensitivity, but also the image fidelity. This leads to a better defined psf. Channelization and mfs imaging are also reducing bandwidth smearing effects. | ||
As mentioned above, {{simobserve}}, naturally, does not channelize the visibilities when the input image is not chanelized. | |||
In the following, we will channelize the MS and, to show the procedure, we will also apply a spectral index of <math>S\propto\nu^{-1.5}</math> at the same time. | |||
To start with, we need to produce a multi-channel model image. The following script converts our current model image from fits to the CASA image format with {{importfits}}. | |||
We then create 64 planes, apply the spectral index, and fix the headers accordingly to bring them into consecutive frequency order. Each channel is specified to a width of 128MHz (real VLA data would have typical channel widths of 2MHz). Finally, our individual planes are combined into a cube with the '''ia.imageconcat''' tool method. | |||
To start with, we need to produce a multi-channel model image. The following script converts our current model image from | |||
We | |||
<source lang="python"> | <source lang="python"> | ||
| Line 259: | Line 261: | ||
The graphical output of {{simobserve}} and {{simanalyze}} would treat such data as a data cube rather than a multi-channel continuum data set. So we will produce our own graphics and imaging. | The graphical output of {{simobserve}} and {{simanalyze}} would treat such data as a data cube rather than a multi-channel continuum data set. So we will produce our own graphics and imaging. | ||
Let's first have a look at the new uvcoverage, each channel is displayed in a different color in Fig. | Let's first have a look at the new uvcoverage, each channel is displayed in a different color in Fig. 10 (note that the graphical output of {{simobserve}} | ||
<source lang="python"> | <source lang="python"> | ||
| Line 265: | Line 267: | ||
plotms(vis='psimvla4mfs/psimvla4mfs.vla.a.noisy.ms', xaxis='Uwave', yaxis='Vwave',coloraxis='channel') | plotms(vis='psimvla4mfs/psimvla4mfs.vla.a.noisy.ms', xaxis='Uwave', yaxis='Vwave',coloraxis='channel') | ||
</source> | </source> | ||
{| | {| | ||
|[[Image:VLAsim-uvcovermfs.png|400px|thumb|left|Fig. | |[[Image:VLAsim-uvcovermfs.png|400px|thumb|left|'''Fig. 10:''' uv-coverage of chanelized visibilities.]] | ||
|} | |} | ||
{{simanalyze}} would assume that these data are to be imaged as a cube. Our aim, however, is to create a continuum image with the mfs technique, and, to recover the spectral index, we will use the Multi-term Taylor expansion in frequency (mtmfs, see [https://casa.nrao.edu/casadocs/latest/synthesis-imaging/deconvolution-algorithms CASAdocs Deconvolution Algorithms]. We will use nterms=2 | {{simanalyze}} would assume that these data are to be imaged as a cube. Our aim, however, is to create a continuum image with the mfs technique, and, to recover the spectral index, we will use the Multi-term Taylor expansion in frequency (mtmfs, see [https://casa.nrao.edu/casadocs/latest/synthesis-imaging/deconvolution-algorithms CASAdocs Deconvolution Algorithms]). We will use nterms=2 to derive the spectral index. The spectral index map, however, is fairly sensitive to the scales in the image. A regular Hogbom clean based on point sources, typically creates maps with too steep spectral indices when applied to extended emission. To avoid this effect, we therefore use the multi-scale algorithm with a range of scales: | ||
<source lang="python"> | <source lang="python"> | ||
| Line 278: | Line 278: | ||
tclean(vis='psimvla4mfs/psimvla4mfs.vla.a.noisy.ms', imagename='psimvla4mfs/8GHzmfs', imsize=[192, 192], cell='3.11e-3arcsec', specmode='mfs', gridder='standard', deconvolver='mtmfs', nterms=2, scales=[0,2,4,8,13,20,40], niter=1000, threshold='2e-4Jy', weighting='briggs', robust=0.5) | tclean(vis='psimvla4mfs/psimvla4mfs.vla.a.noisy.ms', imagename='psimvla4mfs/8GHzmfs', imsize=[192, 192], cell='3.11e-3arcsec', specmode='mfs', gridder='standard', deconvolver='mtmfs', nterms=2, scales=[0,2,4,8,13,20,40], niter=1000, threshold='2e-4Jy', weighting='briggs', robust=0.5) | ||
</source> | </source> | ||
As before, we are not attempting primary beam corrections as the image is very small compared to the primary beam (cf. Fig. 2). | |||
<!-- | <!-- | ||
| Line 304: | Line 304: | ||
--> | --> | ||
The images can be displayed with the viewer, note that the image itself is now called ''psimvla4mfs/8GHzmfs.image.tt0'' (Fig. 11) and the spectral index map: ''psimvla4mfs/8GHzmfs.alpha'' (Fig. 12). In Fig. 12 we also show the contours of the image on the spectral index map, to check for the signal-to-noise at each position. | |||
The images can be displayed with the viewer, note that the image itself is now called | |||
{| | {| | ||
|[[Image:VLAsim-psim4mfstclean.png|400px|thumb|left|Fig. | |[[Image:VLAsim-psim4mfstclean.png|400px|thumb|left|'''Fig. 11:''' The image of Fig. 9 but using multi-frequency-synthesis (mfs) imaging. ]] | ||
|[[Image:VLAsim-psim4mfstcleanalpha.png|500px|thumb|left|Fig. | |[[Image:VLAsim-psim4mfstcleanalpha.png|500px|thumb|left|'''Fig. 12:''' The spectral index map with image contours overlaid.]] | ||
|} | |} | ||
As seen in Fig. | As seen in Fig. 11, this method should produce a somewhat better fidelity than the non-mfs image shown in Fig. 9, although a direct comparison is difficult given the spectral index that we introduced. The spectral index map itself (Fig. 12), unfortunately, is dominated by noise, even at the brightest regions, due to the pwv that we assumed. This results in a relatively unreliable spectral index map overall, although the values scatter around the spectral index of -1.5 that we inserted earlier. | ||
===Q-band, 8GHz bandwidth, 4mm pwv, 4h integration time, A-configuration=== | ===Q-band, 8GHz bandwidth, 4mm pwv, 4h integration time, A-configuration=== | ||
| Line 347: | Line 322: | ||
</source> | </source> | ||
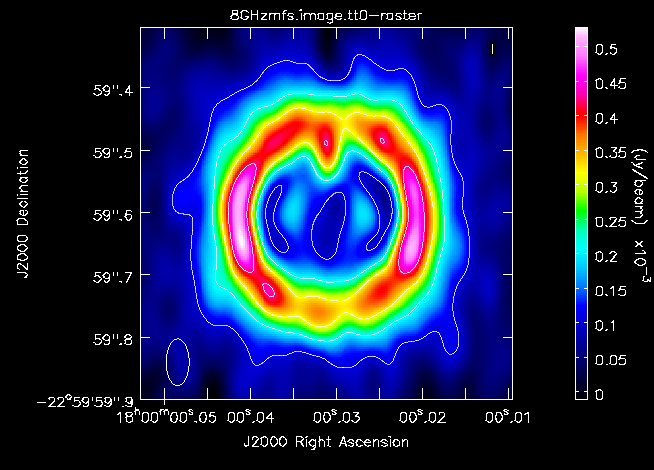
Fig. | Fig. 13 shows a better uv-coverage (lower left image) and the 4h observation is also marked by a wider red bar in the top left image. This also improved the shape of the psf. | ||
{| | {| | ||
|[[Image:VLAsim-psim5-obs.png|600px|thumb|left|Fig. | |[[Image:VLAsim-psim5-obs.png|600px|thumb|left|'''Fig. 13:''' Output of {{simobserve}} with 8GHz bandwidth of 4h of on-source observing time. ]] | ||
|} | |} | ||
| Line 358: | Line 333: | ||
</source> | </source> | ||
Given the expected deeper image we reduced the cleaning threshold to 0. | Given the expected deeper image we reduced the cleaning threshold to 0.02mJy, and the result is shown in Fig. 14. The image now is an almost perfect representation of the true sky model convolved with the clean beam. | ||
{| | {| | ||
|[[Image:VLAsim-psim5-ana.png|600px|thumb|left|Fig. | |[[Image:VLAsim-psim5-ana.png|600px|thumb|left|'''Fig. 14:''' Images after increasing the integration time to 4h.]] | ||
|} | |} | ||
==== Comparison with the VLA Exposure Calculator ==== | |||
We compare again the simulation to the predicted VLA sensitivity via the [http://go.nrao.edu/ect VLA Exposure Calculator Tool (ETC)] ([http://go.nrao.edu/ect Description]). Using 8GHz bandwidth 4h on-source, and a low elevation due to the longer observations, the ECT predicts a rms of 7.1<math>\mu Jy</math> (Fig. 15): | |||
{| | {| | ||
|[[Image:VLAsim- | |[[Image:VLAsim-etc8GHz4h.png|400px|thumb|left|'''Fig. 15''': Exposure time calculation for 4mm pwr, 8GHz bandwidth]] | ||
|} | |} | ||
Note that the VLA exposure calculator switched to 3bit observing to accommodate the large bandwidth. The simulator, however, assumes 8bit samplers, which provide about 15% better sensitivity than VLA 3bit correlations (For a discussion, see the [https://science.nrao.edu/facilities/vla/docs/manuals/oss/performance/vla-samplers VLA Samplers] page). | |||
Similar to the case of 128MHz bandwidth 1h case, we produce a larger image to be able to measure the image rms in a signal-free region: | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
tclean(vis=' | tclean(vis='psimvla5/psimvla5.vla.a.noisy.ms', imagename='psim5-bigimage', imsize=[640, 640], cell='3.11e-3arcsec', specmode='mfs', gridder= 'standard', deconvolver='hogbom', weighting='briggs', robust=0.5, niter=10000, threshold='5e-5Jy') | ||
</source> | </source> | ||
opening the image in the {{viewer}} | |||
<source lang="python"> | |||
# In CASA | |||
viewer('psim5-bigimage.image') | |||
</source> | |||
and measuring the noise statistics away from the source (Fig. 16), gives a value of about 7mJy/beam which is in reasonable agreement with the exposure calculator prediction. | |||
<!-- | |||
The regions where we measured the noise still contains some residual sidelobe structure and deeper cleaning, especially with a clean mask would improve the noise figure further, bringing it even closer to the predicted value. | |||
--> | |||
{| | {| | ||
|[[Image:VLAsim- | |[[Image:VLAsim-tcleanbig8GHz4h.png|600px|thumb|left|'''Fig. 16:''' Larger Image of the 8GHz simulation in Fig. 14, measuring the rms noise in the purple rectangle regions away from the emission.]] | ||
|} | |} | ||
| Line 410: | Line 400: | ||
===Q-band, 8GHz bandwidth, 4mm pwv, 1h integration time, C-configuration=== | ===Q-band, 8GHz bandwidth, 4mm pwv, 1h integration time, C-configuration=== | ||
Our last Q-band simulation will use a precipitable water vapor of 4mm again, but to we will simulate the observations with the VLA C-configuration | Our last Q-band simulation will use a precipitable water vapor of 4mm again, but to we will now simulate the observations with the VLA C-configuration (specified with the ''antennalist'' parameter). | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
simobserve(project=' | simobserve(project='psimvla6', skymodel='ppdisk672_GHz_50pc.fits', inbright='3e-5Jy/pixel', incenter='44GHz', inwidth='8GHz' , setpointings=True, integration='2s', direction='J2000 18h00m00.031s -22d59m59.6s', mapsize= '0.78arcsec', obsmode='int', antennalist='vla.c.cfg', hourangle='transit', totaltime='3600s', thermalnoise='tsys-atm', user_pwv=4, t_ground=270.0, graphics='both', overwrite=True) | ||
</source> | </source> | ||
As expected, the uv-coverage decreases by a factor of about 10 and and the synthesize beam increases by the same factor, as seen in Fig. | As expected, the uv-coverage decreases by a factor of about 10 and and the synthesize beam increases by the same factor, as seen in Fig. 17. | ||
{| | {| | ||
|[[Image:VLAsim- | |[[Image:VLAsim-psim6-obs.png|600px|thumb|left|'''Fig. 17:''' Output of {{simobserve}} using the C-configuration. ]] | ||
|} | |} | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
simanalyze(project=' | simanalyze(project='psimvla6', image=True, vis='psimvla6.vla.c.noisy.ms', imsize=[1728, 1728], interactive=False, niter=1000, threshold='1e-4Jy', weighting='briggs', pbcor=False, stokes='I', analyze=True, showuv=False, showpsf=True, showmodel=True, showconvolved=True, showclean=True, showresidual=True, showdifference=True, showfidelity=True, graphics='both', overwrite=True) | ||
</source> | </source> | ||
Note that the output filenames will now change and reflect C-configuration in their names. The resulting images are displayed in Fig. | Note that the output filenames will now change and reflect C-configuration in their names. The resulting images are displayed in Fig. 18, where the images now look like a point source with the degraded resolution. The surface brightness sensitivity of the observations, however, increase and we can clean to a lower threshold of 0.1mJy. {{simobserve}} automatically detected that the beam is massively oversampled and that a larger image size will provide a better field of view. | ||
{| | {| | ||
|[[Image:VLAsim- | |[[Image:VLAsim-psim6-ana.png|600px|thumb|left|'''Fig. 18:''' C-configuration results.]] | ||
|} | |} | ||
| Line 438: | Line 428: | ||
===X-band, 4GHz bandwidth, 4mm pwv, 1h integration time, A-configuration=== | ===X-band, 4GHz bandwidth, 4mm pwv, 1h integration time, A-configuration=== | ||
Finally, we will go for a X-band (10GHz), A-configuration simulation. Since X-band has a maximum bandwidth of 4GHz, we will reduce it to this value. We will also lower the flux of the model to 0.01mJy given that a the flux of the model will likely be lower, too. | Finally, we will go for a '''X-band (10GHz)''', A-configuration simulation. Since X-band has a maximum bandwidth of 4GHz, we will reduce it to this value. We will also lower the flux of the model to 0.01mJy given that a the flux of the model will likely be lower, too. | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
simobserve(project=' | simobserve(project='psimvla7', skymodel='ppdisk672_GHz_50pc.fits', inbright='1e-5Jy/pixel', incenter='10GHz', inwidth='4GHz' , setpointings=True, integration='2s', direction='J2000 18h00m00.031s -22d59m59.6s', mapsize= '0.78arcsec', obsmode='int', antennalist='vla.a.cfg', hourangle='transit', totaltime='3600s', thermalnoise='tsys-atm', user_pwv=4, t_ground=270.0, graphics='both', overwrite=True) | ||
</source> | </source> | ||
When expressed in wavelengths, the uv-coverage and synthesized beam are somewhere in between that of Q-band A-configuration and C-configuration as expected (Fig. | When expressed in wavelengths, the uv-coverage and synthesized beam are somewhere in between that of Q-band A-configuration and C-configuration as expected (Fig. 19). | ||
{| | {| | ||
|[[Image:VLAsim-psim8-obs.png|600px|thumb|left|Fig. | |[[Image:VLAsim-psim8-obs.png|600px|thumb|left|'''Fig. 19:''' Output of {{simobserve}} for X-band observations. ]] | ||
|} | |} | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
simanalyze(project=' | simanalyze(project='psimvla7', image=True, vis='psimvla7.vla.a.noisy.ms', imsize=[192, 192], interactive=False, niter=1000, threshold='3e-5Jy', weighting='briggs', pbcor=False, stokes='I', analyze=True, showuv=False, showpsf=True, showmodel=True, showconvolved=True, showclean=True, showresidual=True, showdifference=True, showfidelity=True, graphics='both', overwrite=True) | ||
</source> | </source> | ||
The larger primary beam of the X-band data is shown in Fig. | The larger primary beam of the X-band data is shown in Fig. 20, where the model image is barely visible in the center. The simulated images are shown in Fig. 21. The ring shape is still visible in the results although quite blurred. We note that the noise is considerably lower as expected from the lower band noise properties of the receiver and atmosphere. We adjusted the clean threshold accordingly. Again, {{simanalyze}} was overriding the image size as the psf would not have been adequately covered for the lower frequency. | ||
{| | {| | ||
|[[Image:VLAsim-psim8-sky.png|600px|thumb|left|Fig. | |[[Image:VLAsim-psim8-sky.png|600px|thumb|left|'''Fig. 20:''' X-band sky coverage]] | ||
|[[Image:VLAsim-psim8-ana.png|600px|thumb|left|Fig. | |[[Image:VLAsim-psim8-ana.png|600px|thumb|left|'''Fig. 21:''' X-band simulation results.]] | ||
|} | |} | ||
Latest revision as of 20:38, 30 October 2018
The following tutorial shows how to adopt typical parameters for simulating Karl G. Jansky VLA data. We will use the same image as the ALMA tutorial "Protoplanetary Disk Simulation". Follow this link to obtain the protoplanetary disk model image. Model images are in units of Jy/pixel. Other simulation options, e.g. using component lists, or how to use the toolkit are explained in the Simulations in CASA section of the CASAguides.
In Fig. 1 we show the model that we will use for this simulation tutorial.
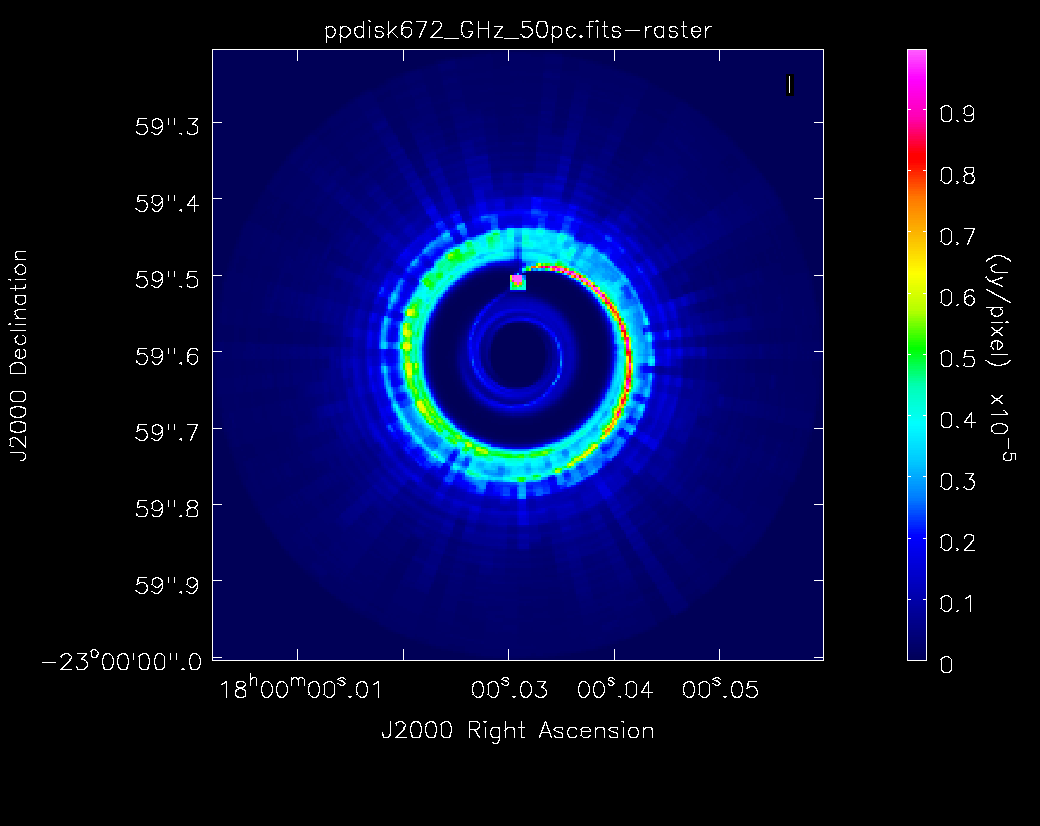 |
The ALMA version of the tutorial shows a way on how to derive the center of the image. We will use their results and specify direction='J2000 18h00m00.031s -22d59m59.6s' for all of our simulations. The image center can also be determined with the CASA viewer. Given that the VLA primary beams at the VLA frequencies are much larger than the image, the precise pointing direction center is less important.
We will use the simobserve and simanalyze tasks similar to the ALMA tutorials (in particular the plotted image sequence). As the model is specified for 672GHz so we will adapt it to work at VLA frequencies.
Note that simobserve has a few limitations. E.g. it cannot simulate different spectral windows. If this is desired, one needs to set up the simulation for each spw separately, and then use concat to merge all MeasurementSets. simobserve also has no option to add pointing errors to the simulated data. All VLA configurations and the VLA receiver temperatures are, however, accessible in simobserve.
Q-band, 128MHz bandwidth, noiseless image, 1h integration time, A-configuration, no deconvolution
Let's start with a simulation at Q-band at 44GHz, with a bandwidth of 128MHz. We will use the VLA A-configuration as it provides the resolution that is needed for the disk to be well resolved. To start with we do not apply any noise to the data:
# In CASA
simobserve(project='psimvla1', skymodel='ppdisk672_GHz_50pc.fits', inbright='3e-5Jy/pixel', incenter='44GHz', inwidth='128MHz' , setpointings=True, integration='2s', direction='J2000 18h00m00.031s -22d59m59.6s', mapsize= '0.78arcsec', obsmode='int', antennalist='vla.a.cfg', hourangle='transit', totaltime='3600s', thermalnoise='', graphics='both', overwrite=True)
project: The name of our project is psimalma1
skymodel: The input model image in Jy/pixel units. We adjust the peak to a lower [math]\displaystyle{ 3\times10^{-5} }[/math]Jy/pixel value with the inbright parameter, as expected at a lower frequency. We also overwrite the fits header to assume that the model is valid for 44GHz with incenter and the bandwidth to 128MHz with inwidth
setpointings: will allow simobserve to derive the pointing positions by its own algorithm. Given that the primary beam at Q-band is about 1arcminutes (see the VLA [observational status summary], and the size of the model is less than an arcsecond, a single pointing will be more than enough.
integration: To avoid time smearing, we follow the guidance for data rates in the OSS and assume 2s per visibility integration.
direction: the center of the map. For a single pointing this is equivalent to the pointing center.
obsmode: int is used for interferometric data such as VLA observations.
antennalist: the VLA configuration antenna position file. The files are available in CASA via 'vla.x.cfg' where 'x' is the name of the array configuration. Here 'vla.a.cfg' is the VLA A configuration (the python command os.getenv("CASAPATH").split()[0]+"/data/alma/simmos/" shows the directory that contains all configurations that are packaged in CASA)
hourangle: is used to simulate observations at a specific hour angle. We use 'transit' for culmination.
totaltime: This is the time on source.
thermalnoise: We leave this parameter empty for this noise-less simulation.
graphics: 'both' will show graphics on the screen and save them as png files in the project directory.
overwrite: True will overwrite previous results: be careful when running multiple setups as the files may have different names and only the files with the same names will be overwritten.
The output of the simulation is shown in Figs. 2 and 3. The first image is the sky coverage which shows clearly that the primary beam exceeds the size of the model image by far. The other ouputs are explained in the caption of Fig. 3.
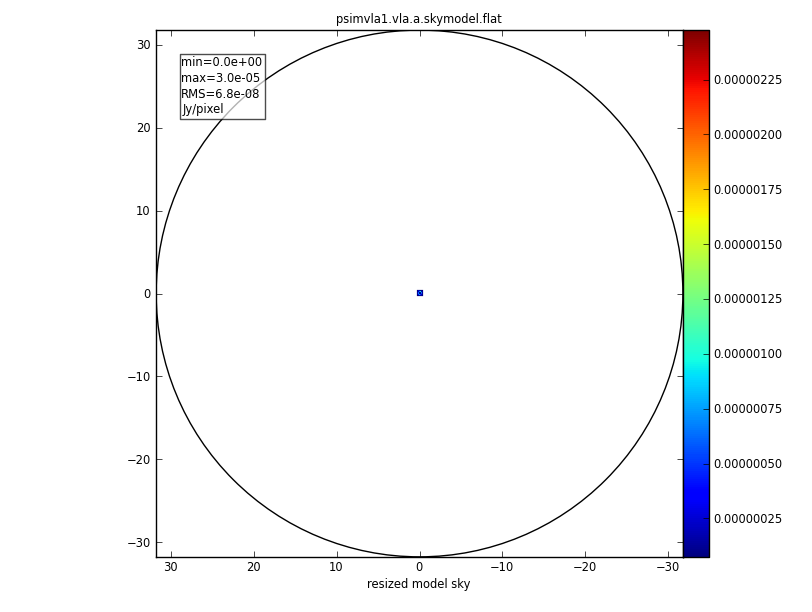 |
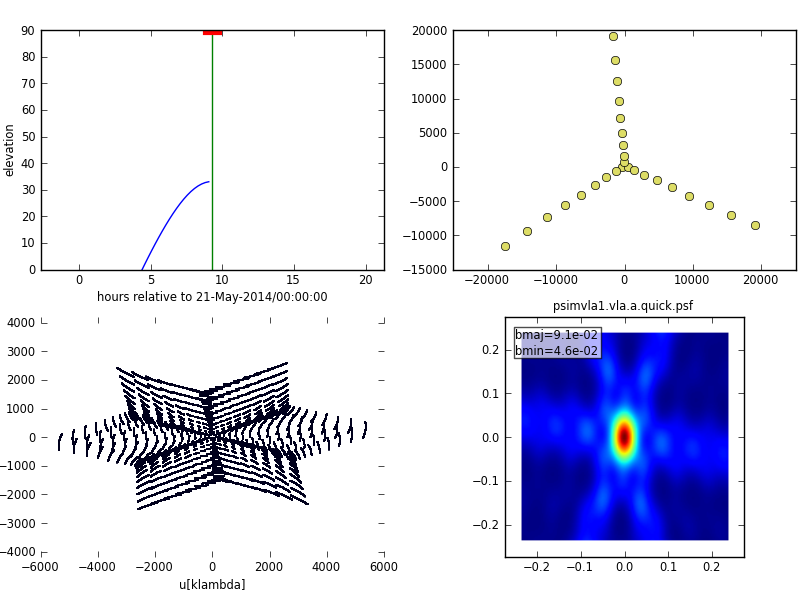 |
The task simanalyze can now process the newly created MeasurementSet and image the data:
# In CASA
simanalyze(project='psimvla1', image=True, vis='psimvla1.vla.a.ms', imsize=[192, 192], interactive=False, niter=0, weighting='briggs', pbcor=False, stokes='I', analyze=True, showuv=False, showpsf=True, showmodel=True, showconvolved=True, showclean=True, showresidual=True, showdifference=True, showfidelity=True, graphics='both', overwrite=True)
project: The project name, same as in our call for simobserve.
image: True will image the visibilities with the following sub-parameters.
vis: The input MeasurementSet. Note that simobserve's notation is to use the project name appended by the antenna configuration file name.
imsize: the number of pixels for the image dimensions. We use 192 for each axis. By default simobserve will use the pixel size of the model image as the cell size for each pixel (3.11 milli-arcseconds in our case).
interactive: If set to True, the cleaning will be interactive to allow the step by step setting of clean boxes and clean depths (see the [VLA imaging topical guide]). We will turn this feature off.
niter: number of clean iterations. We start with a dirty map and set niter=0.
weighting: (cf. Image weighting schemes. We will use briggs which defaults to a robust = 0.5.
pbcor: If set to True the image will be primary beam corrected. In our case of a very large primary beam (see Fig. 1), primary beam correction will introduce very small corrections, so we turn it off.
stokes: The Stokes polarization to be produced, we want Stokes I.
analyze: When set to True simobserve will perform basic analysis of the produced images and produce hard copies of the following displays.
showuv: We set this to False as we already show the uv-coverage in the {simobserve}} output (Fig. 3).
showpsf: Although we already have a plot of that in Fig. 3, we show it here again to have the comparison to the other plots.
showconvolved: produces a plot of the model convolved with the synthesized clean beam.
showclean: shows the deconvolved image (in our case we do not perform deconvolution, but show the plot anyways to be consistent with subsequent runs).
showresidual: a plot of the residual image after deconvolution.
showdifference: displays the difference between output cleaned image and input model sky image convolved with output clean beam, i.e. it shows remaining clean artefacts.
showfidelity: a fidelity image, as defined by [math]\displaystyle{ \frac{I}{|I-T|} }[/math] where [math]\displaystyle{ I }[/math] is the observed image and [math]\displaystyle{ T }[/math] the sky model, see the simanalyze CASAdoc help.
The resulting plots of our first simulation are shown in Fig. 4. Since this is a dirty image only (niter=0), the image and residual are the same dirty image. SInce we also did not turn on any thermal noise, the image corruptions are all due to the incomplete uv-coverage of our observations.
Q-band, 128MHz bandwidth, noiseless image, 1h integration time, A-configuration, cleaned
As a second step we will deconvolve this data set. This could be done with inside the same project, but for a cleaner separation of our use cases, we will create a new MS with simobserve with a modified call of simanalyze:
# In CASA
simobserve(project='psimvla2', skymodel='ppdisk672_GHz_50pc.fits', inbright='3e-5Jy/pixel', incenter='44GHz', inwidth='128MHz' , setpointings=True, integration='2s', direction='J2000 18h00m00.031s -22d59m59.6s', mapsize= '0.78arcsec', obsmode='int', antennalist='vla.a.cfg', hourangle='transit', totaltime='3600s', thermalnoise='', graphics='both', overwrite=True)
simanalyze(project='psimvla2', image=True, vis='psimvla2.vla.a.ms', imsize=[192, 192], interactive=False, niter=1000, threshold='1e-4Jy', weighting='briggs', pbcor=False, stokes='I', analyze=True, showuv=False, showpsf=True, showmodel=True, showconvolved=True, showclean=True, showresidual=True, showdifference=True, showfidelity=True, graphics='both', overwrite=True)
The only difference to the earlier call of simobserve is our setting of niter=1000, threshold='1e-4Jy' which corresponds to a maximum number of 1000 clean iterations and a clean threshold of 0.1mJy. The threshold was chosen based on the previous image to be a few times above the rms of the image. The residual image is now flatter as expected and the bulk of the sidelobes disappear.
 |
Q-band, 128MHz bandwidth, 4mm pwv, 1h integration time, A-configuration
We now add a precipitable water vapor of 4mm and a ground temperature for spillover of 270K. This can be achieved by the user_pwr and t_ground parameters. simobserve only adds thermal noise due to the sky brightness, but not phase noise due to pwv variations across the array. The sm.settrop tool can be used for the more sophisticated troposhperic models. A description is given in Corrupting Simulated Data.
# In CASA
simobserve(project='psimvla3', skymodel='ppdisk672_GHz_50pc.fits', inbright='3e-5Jy/pixel', incenter='44GHz', inwidth='128MHz' , setpointings=True, integration='2s', direction='J2000 18h00m00.031s -22d59m59.6s', mapsize= '0.78arcsec', obsmode='int', antennalist='vla.a.cfg', hourangle='transit', totaltime='3600s', thermalnoise='tsys-atm', user_pwv=4, t_ground=270.0, graphics='both', overwrite=True)
The simobserve output will be identical to Fig. 2 and 3 since we do not change any of the displayed parameters. Now let's analyze the MS:
# In CASA
simanalyze(project='psimvla3', image=True, vis='psimvla3.vla.a.noisy.ms', imsize=[192, 192], interactive=False, niter=1000, threshold='4e-4Jy', weighting='briggs', pbcor=False, stokes='I', analyze=True, showuv=False, showpsf=True, showmodel=True, showconvolved=True, showclean=True, showresidual=True, showdifference=True, showfidelity=True, graphics='both', overwrite=True)
Note that we adjusted the cleaning threshold to account for the higher noise. The results are displayed in Fig. 6. The noise is dominating the image now, which is expected.
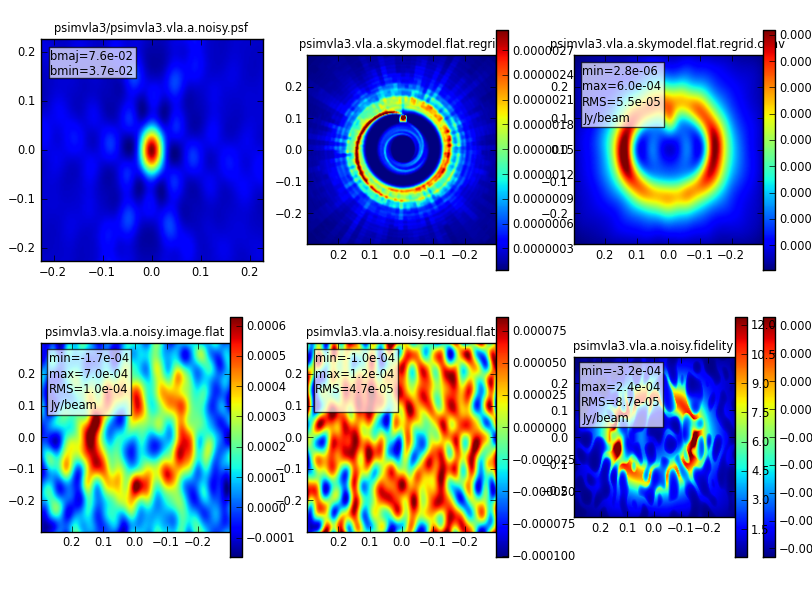 |
Comparison with the VLA Exposure Calculator
We can compare the simulation to the predicted VLA sensitivity via the VLA Exposure Calculator Tool (ECT) (Description). Using winter observing conditions (for good pwv), a medium elevation (cf. Fig. 3), 128MHz bandwidth at a frequency of 44GHz, the ECT predicts a beam size of 0.067" and which is very close to our simulations (cf. Fig. 3 and 6). The ECT output is shown in Fig. 7.
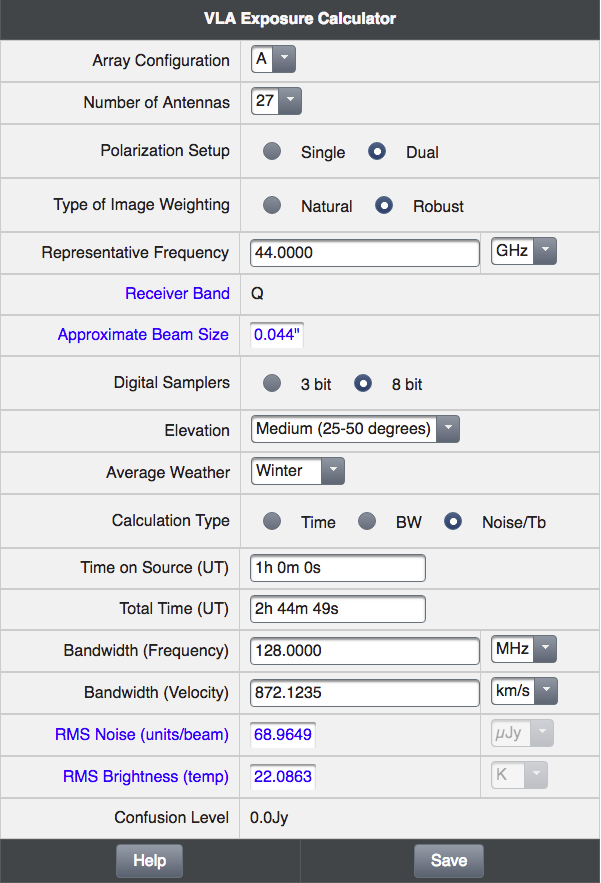 |
The rms provided in Fig. 6 is over the entire image and includes the source. It is therefore not representative to the thermal noise. To obtain a better noise figure, we produce an image with the same parameters as simanalyze, but with a larger image size directly via tclean. Since the briggs parameter in simanalyze defaults to robust=0.5, we will use the same value here:
# In CASA
tclean(vis='psimvla3/psimvla3.vla.a.noisy.ms', imagename='psim3-bigimage', imsize=[640, 640], cell='3.11e-3arcsec', specmode='mfs', gridder= 'standard', deconvolver='hogbom', weighting='briggs', robust=0.5, niter=1000, threshold='4e-4Jy')
opening the image in the viewer
# In CASA
viewer('psim3-bigimage.image')
and measuring the noise statistics away from the source (Fig. 8), gives a value of about 7e-5Jy/beam which is a very good agreement with the predicted noise figure of 6.9e-5 Jy/beam.
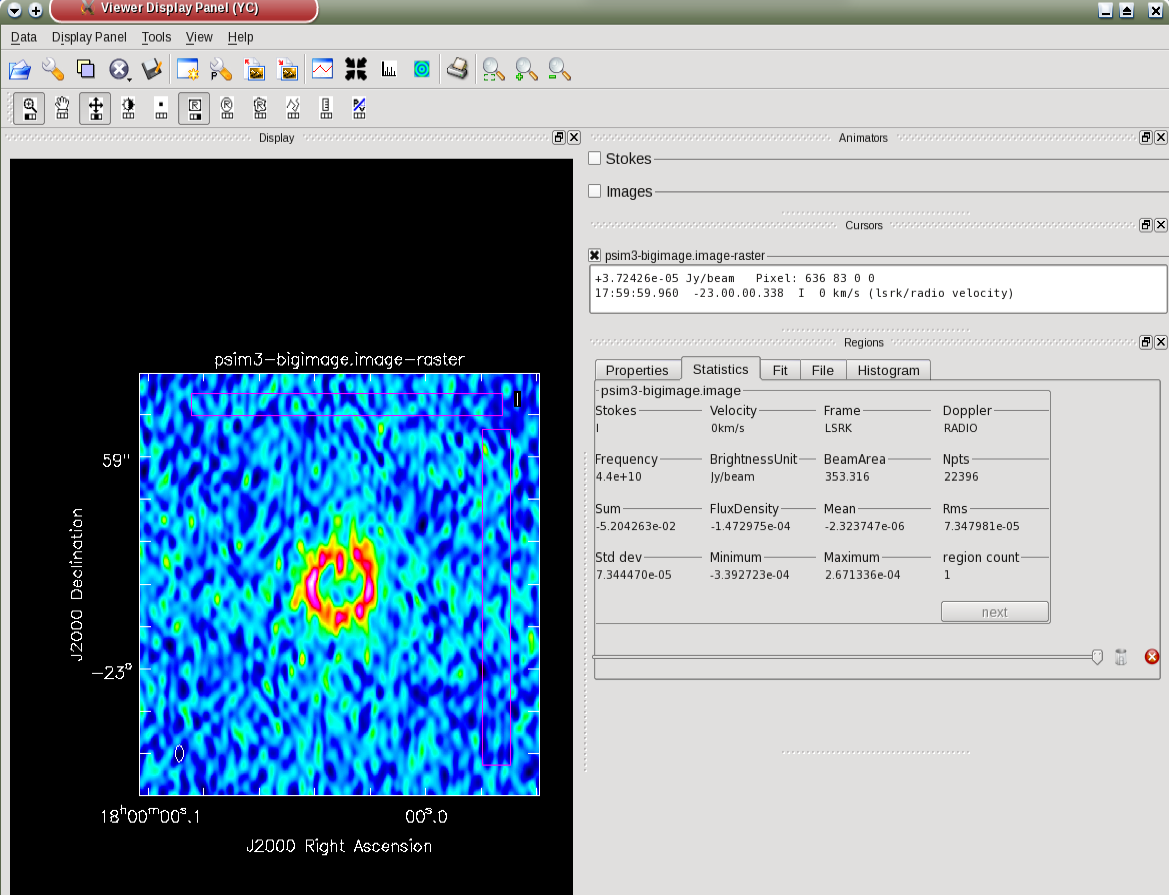 |
Q-band, 8GHz bandwidth, 4mm pwv, 1h integration time, A-configuration
To compensate for noise, we will extend our bandwidth from 128MHz to 8GHz. At this time, simobserve has no chanelization so the simulation will not have the better uv-coverage that is obtained in multi-frequency imaging. Consecutive simulations with different spectral windows, and combined MSs, however, can achieve that and we will show how to obtain a multi-channel MS shortly. For large bandwidths, one needs to be careful to not introduce [bandwidth smearing]. Our source is at the center of the image and bandwidth smearing will be minimal.
# In CASA
simobserve(project='psimvla4', skymodel='ppdisk672_GHz_50pc.fits', inbright='3e-5Jy/pixel', incenter='44GHz', inwidth='8GHz' , setpointings=True, integration='2s', direction='J2000 18h00m00.031s -22d59m59.6s', mapsize= '0.78arcsec', obsmode='int', antennalist='vla.a.cfg', hourangle='transit', totaltime='3600s', thermalnoise='tsys-atm', user_pwv=4, t_ground=270.0, graphics='both', overwrite=True)
The simobserve output again is identical with Fig. 3.
# In CASA
simanalyze(project='psimvla4', image=True, vis='psimvla4.vla.a.noisy.ms', imsize=[192, 192], interactive=False, niter=10000, threshold='5e-5Jy', weighting='briggs', pbcor=False, stokes='I', analyze=True, showuv=False, showpsf=True, showmodel=True, showconvolved=True, showclean=True, showresidual=True, showdifference=True, showfidelity=True, graphics='both', overwrite=True)
The image (Fig. 9) is clearly better defined, as expected from a broader bandwidth. We also decreased the cleaning threshold to 0.05mJy and added a few more iterations to allow to reach this threshold.
 |
Multi-Term-Multi-Frequency Synthesis Imaging
In reality, the 8GHz bandwidth is not confined to a single channel but to many channels. This results in a spread out uv-coverage as it depends on the projected baselines expressed in number of wavelengths. Combining the channels in a multi-frequency synthesis (mfs), therefore does not only increase the sensitivity, but also the image fidelity. This leads to a better defined psf. Channelization and mfs imaging are also reducing bandwidth smearing effects.
As mentioned above, simobserve, naturally, does not channelize the visibilities when the input image is not chanelized.
In the following, we will channelize the MS and, to show the procedure, we will also apply a spectral index of [math]\displaystyle{ S\propto\nu^{-1.5} }[/math] at the same time.
To start with, we need to produce a multi-channel model image. The following script converts our current model image from fits to the CASA image format with importfits. We then create 64 planes, apply the spectral index, and fix the headers accordingly to bring them into consecutive frequency order. Each channel is specified to a width of 128MHz (real VLA data would have typical channel widths of 2MHz). Finally, our individual planes are combined into a cube with the ia.imageconcat tool method.
# In CASA
importfits(fitsimage="ppdisk672_GHz_50pc.fits", imagename="ppdisk_Q_50pc.im")
stats=imstat(imagename='ppdisk_Q_50pc.im')
maximum=stats['max'][0]
ratio=3e-5/maximum
for x in range (0, 64):
y=40+x*0.128
immath(imagename="ppdisk_Q_50pc.im", mode='evalexpr', expr="IM0*"+str(ratio)+"*(("+str(y)+"/40)^-1.5)", outfile="ppdisk_Q_50pc_spx_"+str(x)+".im")
imhead(imagename="ppdisk_Q_50pc_spx_"+str(x)+".im", mode="put", hdkey="crval4", hdvalue=str(y)+"GHz")
imhead(imagename="ppdisk_Q_50pc_spx_"+str(x)+".im", mode="put", hdkey="cdelt4", hdvalue="128MHz")
comb=ia.imageconcat(outfile="ppdisk-combined_spx.im", infiles="ppdisk_Q_50pc_spx*.im", axis=3, relax=True, tempclose=False, reorder=True, overwrite=True)
comb.close()
Using this model cube in simobserve will produce the channelized visibilities:
# In CASA
simobserve(project='psimvla4mfs', skymodel='ppdisk-combined_spx.im', setpointings=True, integration='2s', direction='J2000 18h00m00.031s -22d59m59.6s', mapsize= '0.78arcsec', obsmode='int', antennalist='vla.a.cfg', hourangle='transit', totaltime='3600s', thermalnoise='tsys-atm', user_pwv=4, t_ground=270.0, graphics='none', overwrite=True)
The graphical output of simobserve and simanalyze would treat such data as a data cube rather than a multi-channel continuum data set. So we will produce our own graphics and imaging.
Let's first have a look at the new uvcoverage, each channel is displayed in a different color in Fig. 10 (note that the graphical output of simobserve
# In CASA
plotms(vis='psimvla4mfs/psimvla4mfs.vla.a.noisy.ms', xaxis='Uwave', yaxis='Vwave',coloraxis='channel')
 |
simanalyze would assume that these data are to be imaged as a cube. Our aim, however, is to create a continuum image with the mfs technique, and, to recover the spectral index, we will use the Multi-term Taylor expansion in frequency (mtmfs, see CASAdocs Deconvolution Algorithms). We will use nterms=2 to derive the spectral index. The spectral index map, however, is fairly sensitive to the scales in the image. A regular Hogbom clean based on point sources, typically creates maps with too steep spectral indices when applied to extended emission. To avoid this effect, we therefore use the multi-scale algorithm with a range of scales:
# In CASA
tclean(vis='psimvla4mfs/psimvla4mfs.vla.a.noisy.ms', imagename='psimvla4mfs/8GHzmfs', imsize=[192, 192], cell='3.11e-3arcsec', specmode='mfs', gridder='standard', deconvolver='mtmfs', nterms=2, scales=[0,2,4,8,13,20,40], niter=1000, threshold='2e-4Jy', weighting='briggs', robust=0.5)
As before, we are not attempting primary beam corrections as the image is very small compared to the primary beam (cf. Fig. 2).
The images can be displayed with the viewer, note that the image itself is now called psimvla4mfs/8GHzmfs.image.tt0 (Fig. 11) and the spectral index map: psimvla4mfs/8GHzmfs.alpha (Fig. 12). In Fig. 12 we also show the contours of the image on the spectral index map, to check for the signal-to-noise at each position.
 |
 |
As seen in Fig. 11, this method should produce a somewhat better fidelity than the non-mfs image shown in Fig. 9, although a direct comparison is difficult given the spectral index that we introduced. The spectral index map itself (Fig. 12), unfortunately, is dominated by noise, even at the brightest regions, due to the pwv that we assumed. This results in a relatively unreliable spectral index map overall, although the values scatter around the spectral index of -1.5 that we inserted earlier.
Q-band, 8GHz bandwidth, 4mm pwv, 4h integration time, A-configuration
Let's improve the depth of the observations even further by going to 4h on-source integration, via totaltime='14400s' .
# In CASA
simobserve(project='psimvla5', skymodel='ppdisk672_GHz_50pc.fits', inbright='3e-5Jy/pixel', incenter='44GHz', inwidth='8GHz' , setpointings=True, integration='2s', direction='J2000 18h00m00.031s -22d59m59.6s', mapsize= '0.78arcsec', obsmode='int', antennalist='vla.a.cfg', hourangle='transit', totaltime='14400s', thermalnoise='tsys-atm', user_pwv=4, t_ground=270.0, graphics='both', overwrite=True)
Fig. 13 shows a better uv-coverage (lower left image) and the 4h observation is also marked by a wider red bar in the top left image. This also improved the shape of the psf.
 |
# In CASA
simanalyze(project='psimvla5', image=True, vis='psimvla5.vla.a.noisy.ms', imsize=[192, 192], interactive=False, niter=1000, threshold='2e-5Jy', weighting='briggs', pbcor=False, stokes='I', analyze=True, showuv=False, showpsf=True, showmodel=True, showconvolved=True, showclean=True, showresidual=True, showdifference=True, showfidelity=True, graphics='both', overwrite=True)
Given the expected deeper image we reduced the cleaning threshold to 0.02mJy, and the result is shown in Fig. 14. The image now is an almost perfect representation of the true sky model convolved with the clean beam.
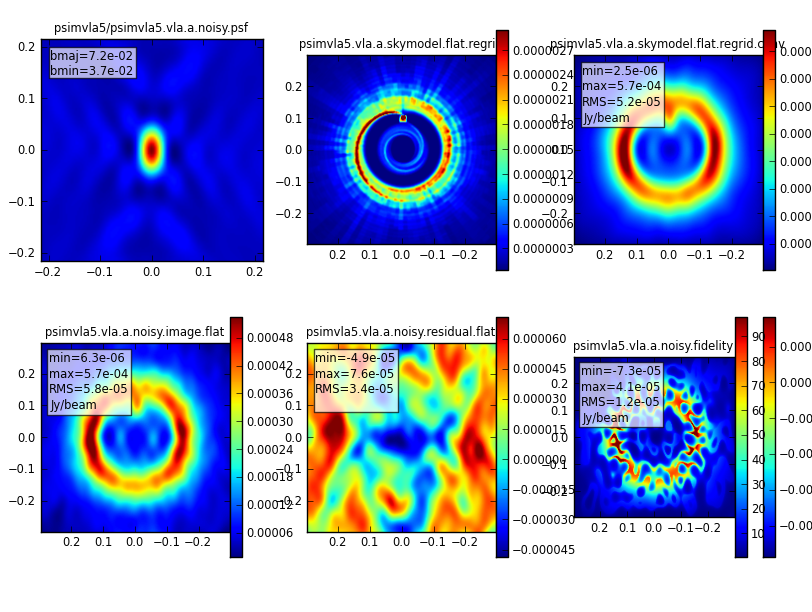 |
Comparison with the VLA Exposure Calculator
We compare again the simulation to the predicted VLA sensitivity via the VLA Exposure Calculator Tool (ETC) (Description). Using 8GHz bandwidth 4h on-source, and a low elevation due to the longer observations, the ECT predicts a rms of 7.1[math]\displaystyle{ \mu Jy }[/math] (Fig. 15):
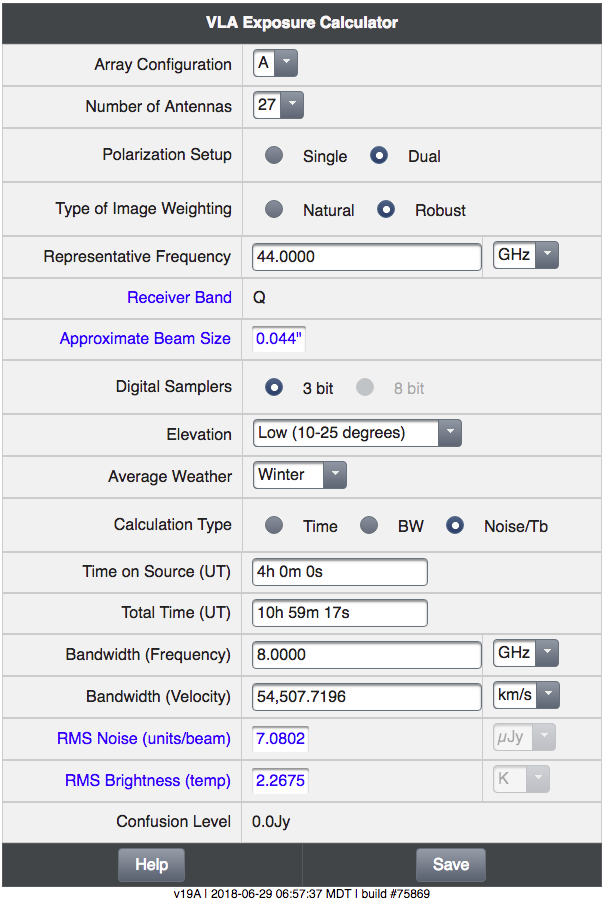 |
Note that the VLA exposure calculator switched to 3bit observing to accommodate the large bandwidth. The simulator, however, assumes 8bit samplers, which provide about 15% better sensitivity than VLA 3bit correlations (For a discussion, see the VLA Samplers page).
Similar to the case of 128MHz bandwidth 1h case, we produce a larger image to be able to measure the image rms in a signal-free region:
# In CASA
tclean(vis='psimvla5/psimvla5.vla.a.noisy.ms', imagename='psim5-bigimage', imsize=[640, 640], cell='3.11e-3arcsec', specmode='mfs', gridder= 'standard', deconvolver='hogbom', weighting='briggs', robust=0.5, niter=10000, threshold='5e-5Jy')
opening the image in the viewer
# In CASA
viewer('psim5-bigimage.image')
and measuring the noise statistics away from the source (Fig. 16), gives a value of about 7mJy/beam which is in reasonable agreement with the exposure calculator prediction.
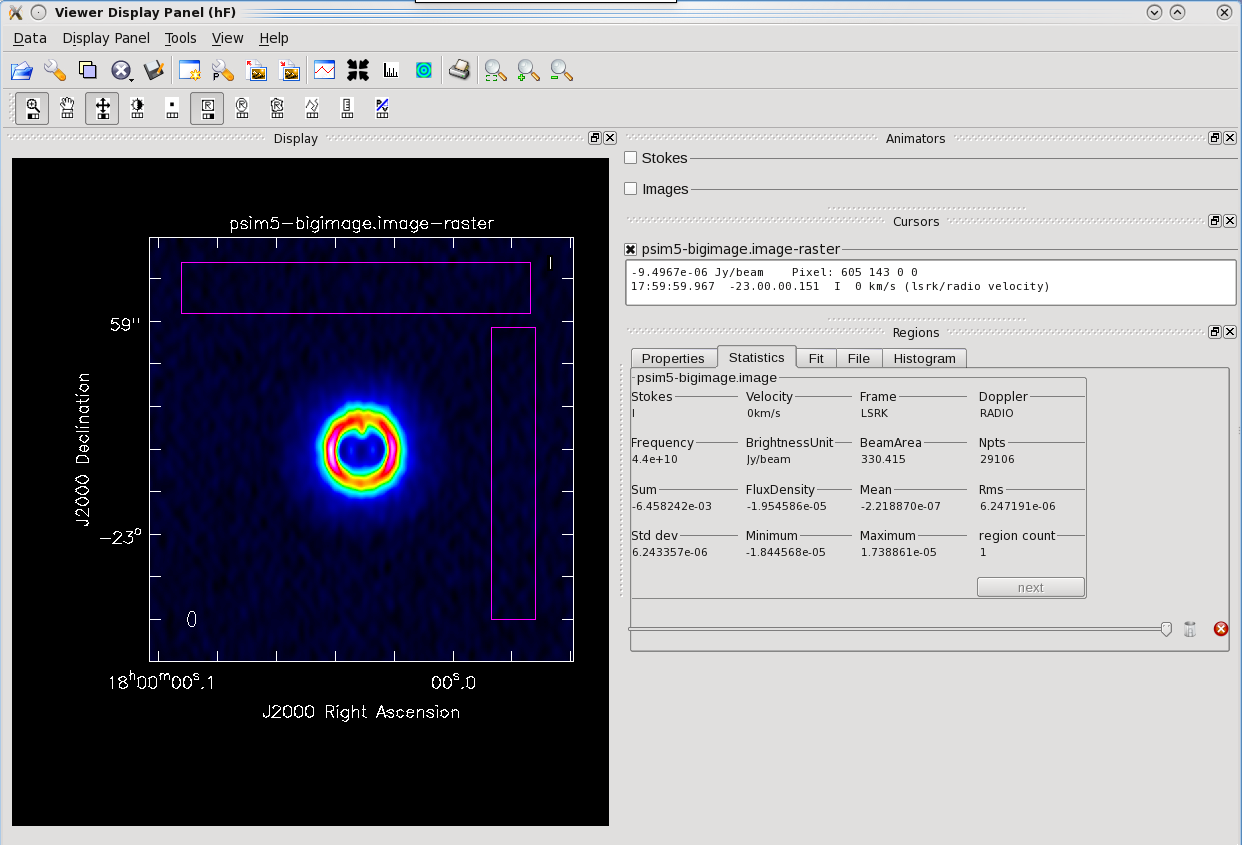 |
Q-band, 8GHz bandwidth, 4mm pwv, 1h integration time, C-configuration
Our last Q-band simulation will use a precipitable water vapor of 4mm again, but to we will now simulate the observations with the VLA C-configuration (specified with the antennalist parameter).
# In CASA
simobserve(project='psimvla6', skymodel='ppdisk672_GHz_50pc.fits', inbright='3e-5Jy/pixel', incenter='44GHz', inwidth='8GHz' , setpointings=True, integration='2s', direction='J2000 18h00m00.031s -22d59m59.6s', mapsize= '0.78arcsec', obsmode='int', antennalist='vla.c.cfg', hourangle='transit', totaltime='3600s', thermalnoise='tsys-atm', user_pwv=4, t_ground=270.0, graphics='both', overwrite=True)
As expected, the uv-coverage decreases by a factor of about 10 and and the synthesize beam increases by the same factor, as seen in Fig. 17.
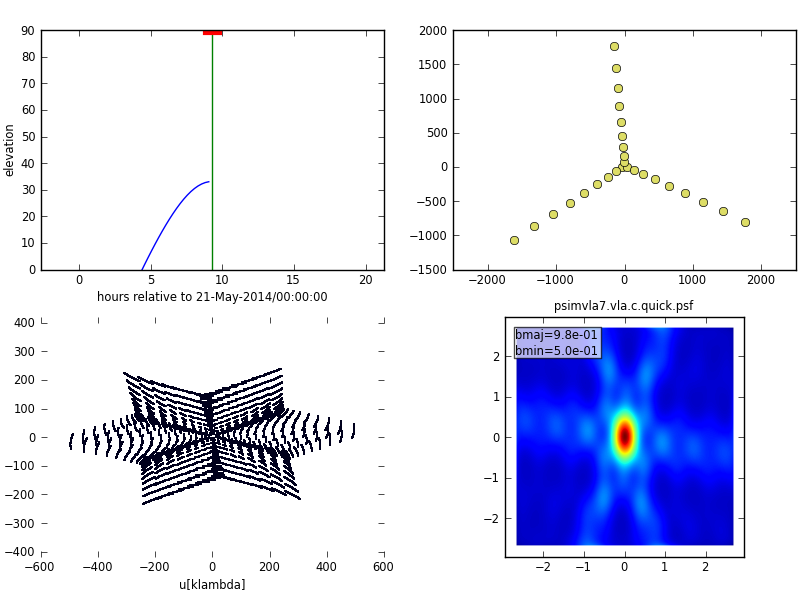 |
# In CASA
simanalyze(project='psimvla6', image=True, vis='psimvla6.vla.c.noisy.ms', imsize=[1728, 1728], interactive=False, niter=1000, threshold='1e-4Jy', weighting='briggs', pbcor=False, stokes='I', analyze=True, showuv=False, showpsf=True, showmodel=True, showconvolved=True, showclean=True, showresidual=True, showdifference=True, showfidelity=True, graphics='both', overwrite=True)
Note that the output filenames will now change and reflect C-configuration in their names. The resulting images are displayed in Fig. 18, where the images now look like a point source with the degraded resolution. The surface brightness sensitivity of the observations, however, increase and we can clean to a lower threshold of 0.1mJy. simobserve automatically detected that the beam is massively oversampled and that a larger image size will provide a better field of view.
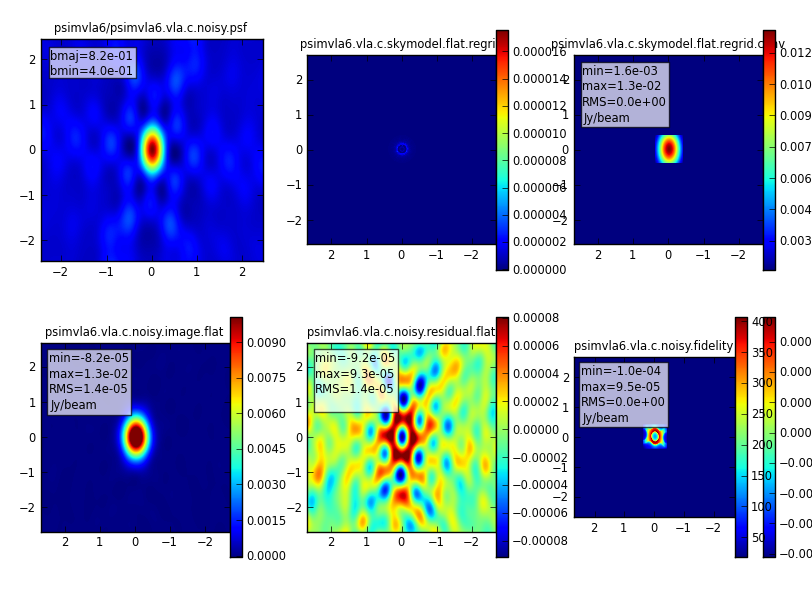 |
To combine data of two different array configurations, we refer to the VLA Data Combination Guide.
X-band, 4GHz bandwidth, 4mm pwv, 1h integration time, A-configuration
Finally, we will go for a X-band (10GHz), A-configuration simulation. Since X-band has a maximum bandwidth of 4GHz, we will reduce it to this value. We will also lower the flux of the model to 0.01mJy given that a the flux of the model will likely be lower, too.
# In CASA
simobserve(project='psimvla7', skymodel='ppdisk672_GHz_50pc.fits', inbright='1e-5Jy/pixel', incenter='10GHz', inwidth='4GHz' , setpointings=True, integration='2s', direction='J2000 18h00m00.031s -22d59m59.6s', mapsize= '0.78arcsec', obsmode='int', antennalist='vla.a.cfg', hourangle='transit', totaltime='3600s', thermalnoise='tsys-atm', user_pwv=4, t_ground=270.0, graphics='both', overwrite=True)
When expressed in wavelengths, the uv-coverage and synthesized beam are somewhere in between that of Q-band A-configuration and C-configuration as expected (Fig. 19).
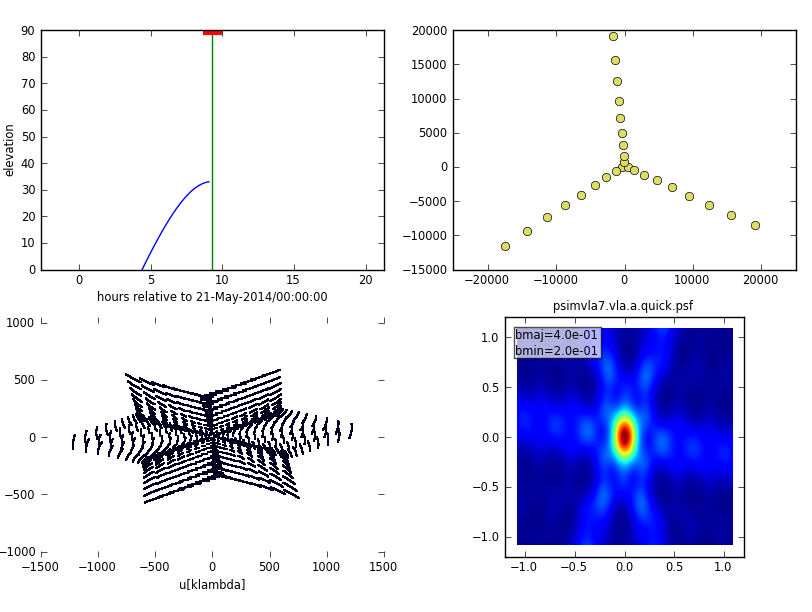 |
# In CASA
simanalyze(project='psimvla7', image=True, vis='psimvla7.vla.a.noisy.ms', imsize=[192, 192], interactive=False, niter=1000, threshold='3e-5Jy', weighting='briggs', pbcor=False, stokes='I', analyze=True, showuv=False, showpsf=True, showmodel=True, showconvolved=True, showclean=True, showresidual=True, showdifference=True, showfidelity=True, graphics='both', overwrite=True)
The larger primary beam of the X-band data is shown in Fig. 20, where the model image is barely visible in the center. The simulated images are shown in Fig. 21. The ring shape is still visible in the results although quite blurred. We note that the noise is considerably lower as expected from the lower band noise properties of the receiver and atmosphere. We adjusted the clean threshold accordingly. Again, simanalyze was overriding the image size as the psf would not have been adequately covered for the lower frequency.
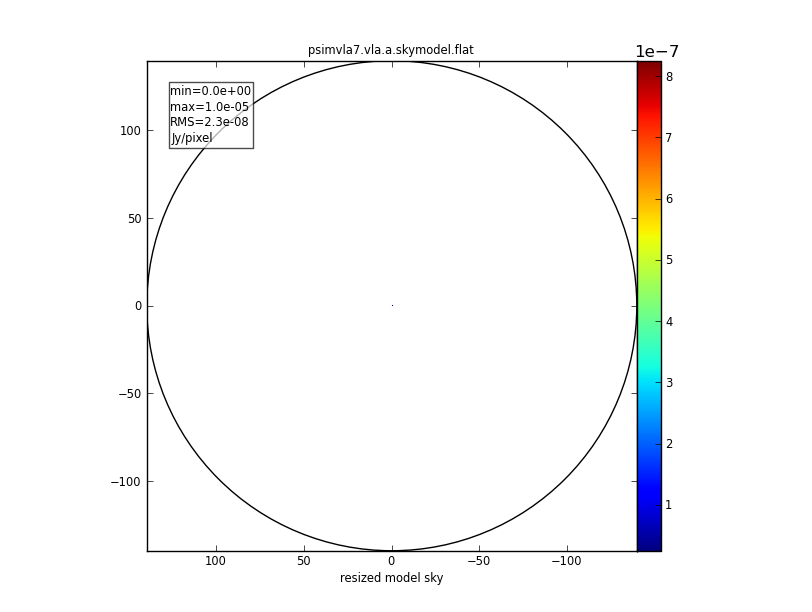 |
 |
