VLA CASA Imaging-CASA4.5.2: Difference between revisions

From CASA Guides
Jump to navigationJump to search
← Older edit
Jott (talk | contribs)
operators
4,947 edits
Jsalcido (talk | contribs)
351 edits
No edit summary
 
(180 intermediate revisions by 5 users not shown)
Line 2: Line 2:
== Imaging ==
== Imaging ==


This tutorial provides guidance on imaging procedures in CASA.  
This tutorial provides guidance on imaging procedures in CASA. The tutorial covers basic continuum cleaning and the influence of image weights, as well as wide-band and wide-field imaging techniques, multi-scale clean, an outlier field setup, and primary beam correction. Spectral line imaging procedures are explained but not covered in detail. For a more thorough example of spectral line imaging, refer to the [https://casaguides.nrao.edu/index.php/VLA_high_frequency_Spectral_Line_tutorial_-_IRC%2B10216 VLA high frequency Spectral Line tutorial - IRC+10216]. This imaging tutorial concludes with basic image header calls and the conversion of Jy/beam to K surface brightness units through image arithmetic and header manipulation.  


We will be utilizing data taken with the Karl G. Jansky Very Large Array, of a supernova remnant G055.7+3.4.. The data were taken on August 23, 2010, in the first D-configuration for which the new wide-band capabilities of the WIDAR (Wideband Interferometric Digital ARchitecture) correlator were available. The 8-hour-long observation includes all available 1 GHz of bandwidth in L-band, from 1-2 GHz in frequency.  
We will be utilizing data, taken with the Karl G. Jansky Very Large Array, of G055.7+3.4, which is a supernova remnant. The data were taken on August 23, 2010, in the first D-configuration for which the wideband capabilities of the WIDAR (Wideband Interferometric Digital ARchitecture) correlator were available. The 8 hour long observation includes all available 1 GHz of bandwidth in L-band, from 1–2 GHz in frequency.  


We will skip the calibration process in this guide, as examples of calibration can be found in several other guides, including the  
We will skip the calibration process as examples of calibration can be found in several other guides, including the  
[https://casaguides.nrao.edu/index.php?title=EVLA_Continuum_Tutorial_3C391 EVLA Continuum Tutorial 3C391] and  
[https://casaguides.nrao.edu/index.php?title=VLA_Continuum_Tutorial_3C391 VLA Continuum Tutorial 3C391] and  
[https://casaguides.nrao.edu/index.php?title=EVLA_high_frequency_Spectral_Line_tutorial_-_IRC%2B10216 EVLA high frequency Spectral Line tutorial - IRC+10216] guides.
[https://casaguides.nrao.edu/index.php?title=VLA_high_frequency_Spectral_Line_tutorial_-_IRC%2B10216 VLA high frequency Spectral Line tutorial - IRC+10216] tutorials.


  A copy of the calibrated data <font color=green>(1.2GB)</font> can be downloaded from [http://casa.nrao.edu/Data/EVLA/SNRG55/SNR_G55_10s.calib.tar.gz http://casa.nrao.edu/Data/EVLA/SNRG55/SNR_G55_10s.calib.tar.gz]  
  A copy of the calibrated data <font color=green>(1.2GB)</font> can be downloaded from [http://casa.nrao.edu/Data/EVLA/SNRG55/SNR_G55_10s.calib.tar.gz http://casa.nrao.edu/Data/EVLA/SNRG55/SNR_G55_10s.calib.tar.gz]  


Your first step will be to unzip and untar the file in a terminal (before you start CASA):
Your first step will be to unzip and untar the file in a terminal window (before you start CASA):


<source lang="bash">
<source lang="bash">
Line 19: Line 19:


Then start casa as usual via the '''casa''' command, which will bring up the ipython interface and launches the logger.
Then start casa as usual via the '''casa''' command, which will bring up the ipython interface and launches the logger.


== The CLEAN Algorithm ==
== The CLEAN Algorithm ==


[[Image:CLEAN_Cycle.png|500px|thumb|right|Fig. 1: The CLEAN major and minor cycles, indicating the steps undertaken during gridding, projection algorithms, and creation of images.]]
[[Image:CLEAN_Cycle.png|500px|thumb|right|'''Figure 1''' <br /> The CLEAN major and minor cycles, indicating the steps undertaken during gridding, projection algorithms, and creation of images.]]


The CLEAN algorithm, developed by J. Högbom (1974) enabled the synthesis of complex objects, even if they have relatively poor Fourier uv-plane coverage. Poor coverage occurs with partial earth rotation synthesis, or with arrays composed of few antennas. The "dirty" image is formed by a simple Fourier inversion of the sampled visibility data, with each point on the sky being represented by a suitably scaled and centered PSF (Point Spread Function, or dirty beam, which is the Fourier inversion of the visibility (u,v) coverage). This algorithm attempts to interpolate from the measured (u,v) points across gaps in the (u,v) coverage. It, in short, provides solutions to the convolution equation by representing radio sources by a number of point sources in an empty field. The brightest points are found by performing a cross-correlation between the dirty image, and the PSF. The brightest parts are subtracted, and the process is repeated again for the next brighter sources. Variants of CLEAN, such as multi-scale CLEAN, take into account extended kernels which may be better suited for extended objects.
The CLEAN algorithm, developed by J. Högbom (1974) enabled the synthesis of complex objects, even if they have relatively poor Fourier uv-plane coverage. Poor coverage occurs with partial earth rotation synthesis or with arrays composed of few antennas. The dirty image is formed by a simple Fourier inversion of the sampled visibility data, with each point on the sky being represented by a suitably scaled and centered PSF (Point Spread Function), or dirty beam, which itself is the Fourier inversion of the visibility (u,v) coverage.  


For single pointings, CASA uses the Cotton-Schwab cleaning algorithm in the task {{clean}} (''imagermode='csclean'''), which breaks the process into major and minor cycles (see Fig. 1). To start with, the visibilities are gridded, weighted, and Fourier transformed to create a (dirty) image. The minor cycle then operates in the image domain to find the clean components that are added to the clean model. The image is Fourier transformed back to the visibility domain, degridded, and the clean model is subtracted. This creates a new residual that is then gridded, weighted, and FFT'ed again to the image domain for the next iteration. The gridding, FFT, degridding, and subtraction processes form the major cycle.  
The convolution with the dirty beam creates artifacts in the image and limits the dynamic range. The CLEAN algorithm attempts to remove the dirty beam pattern from the image via deconvolution. This implies that it interpolates from the measured (u,v) points across gaps in the (u,v) coverage. In short, CLEAN provides solutions to the convolution equation by representing radio sources by a number of point sources in an empty field. The brightest points are found by performing a cross-correlation between the dirty image and the PSF. The brightest parts are then subtracted, and the process is repeated again for the next brighter sources. Variants of CLEAN, such as multi-scale CLEAN, take into account extended kernels which may be better suited for extended objects.


This iterative process is continued until a stopping criterion is reached, such as a maximum number of clean components, or a flux threshold in the residual image.
For single pointings, CASA uses the Cotton-Schwab cleaning algorithm in the task {{clean}} (parameter ''imagermode='csclean'''), which breaks the process into major and minor cycles (see Figure 1). To start with, the visibilities are gridded, weighted, and Fourier transformed to create a dirty image. The minor cycle then operates in the image domain to find the clean components that are added to the clean model. The model image is Fourier transformed back to the visibility domain, degridded, and subtracted from the visibilities. This creates a new residual that is then gridded, weighted, and FFT'ed again to the image domain for the next iteration. The gridding, FFT, degridding, and subtraction processes form the major cycle.  


In CASA {{clean}}, two versions of the PSF can be used (parameter ''psfmode''): ''hogbom'' uses the full sized PSF for subtraction. This is a thorough but slow method. ''psfmode='clark''' uses a smaller beam patch, which increases the speed. The patch size and length of the minor cycle are internally chosen such that clean converges well without giving up the speed improvement. It is thus the default option in {{clean}}.  
This iterative process is continued until a stopping criterion is reached, such as a maximum number of clean components or a flux threshold in the residual image.
 
In CASA {{clean}}, two versions of the PSF can be used: parameter ''psfmode = 'hogbom' ''uses the full-sized PSF for subtraction and is a thorough but slow method. Parameter ''psfmode='clark' ''uses a smaller beam patch, which increases the speed. The patch size and length of the minor cycle are internally chosen such that clean converges well without giving up the speed improvement. Parameter ''psfmode='clark' ''is the default option in {{clean}}.  


<!--
<!--
Line 50: Line 53:
This algorithm is faster than the Clark algorithm, except when dealing with a large number of visibility samples, due to the re-gridding process it undergoes. It is most useful in cleaning sensitive high-resolution images at lower frequencies where a number of confusing sources are within the primary beam.  
This algorithm is faster than the Clark algorithm, except when dealing with a large number of visibility samples, due to the re-gridding process it undergoes. It is most useful in cleaning sensitive high-resolution images at lower frequencies where a number of confusing sources are within the primary beam.  
-->  
-->  
In a final step, {{clean}} derives a Gaussian fit to the inner part of the PSF, which defines the clean beam. The clean model is then convolved with the clean beam and added to the last residual image to create the final image.  
In a final step, {{clean}} derives a Gaussian fit to the inner part of the dirty beam, which defines the clean beam. The clean model is then convolved with the clean beam and added to the last residual image to create the final image.  


Note that the CASA team currently develops a refactored clean task, called  [http://casa.nrao.edu/docs/TaskRef/tclean-task.html tclean]. It has a better interface and provides new algorithms as well as more combinations between imaging algorithms. tclean also includes software to parallelize the computations in a multi-processor environment. Eventually, tclean will replace the current {{clean}} task. For this guide, however, we will stick with the original {{clean}} task, as tclean is still in the development and testing phase. Nevertheless, the reader is encouraged to try tclean and send us feedback through the [https://help.nrao.edu/ NRAO helpdesk].
Note that the CASA team is currently developing a refactored clean task, called  [http://casa.nrao.edu/docs/TaskRef/tclean-task.html tclean]. Task tclean has a better interface, provides new algorithms, and more combinations between imaging algorithms. Task tclean also includes software to parallelize the computations in a multi-processor environment. Eventually, tclean will replace the current {{clean}} task. For this guide, however, we will stick with the original {{clean}} task, as tclean is still in the development and testing phase. Nevertheless, the reader is encouraged to try tclean and send us feedback through the [https://help.nrao.edu/ NRAO helpdesk].


For more details on imaging and deconvolution, we refer to the Astronomical Society of the Pacific Conference Series book entitled [http://www.aspbooks.org/a/volumes/table_of_contents/?book_id=292 Synthesis Imaging in Radio Astronomy II]. The chapter on [http://www.aspbooks.org/a/volumes/article_details/?paper_id=17942 Deconvolution] may prove helpful. In addition, imaging presentations are available on the [https://science.nrao.edu/science/meetings/2014/14th-synthesis-imaging-workshop/lectures Synthesis Imaging Workshop] and [https://science.nrao.edu/science/meetings/2016/vla-data-reduction/program VLA Data Reduction Workshop] webpages. The [https://casa.nrao.edu/docs/cookbook/index.html  CASA cookbook] chapter on [https://casa.nrao.edu/docs/cookbook/casa_cookbook006.html Synthesis Imaging] provides a wealth of information on the CASA implementation of {{clean}} and related tasks.
For more details on imaging and deconvolution, we refer to the Astronomical Society of the Pacific Conference Series book entitled [http://www.aspbooks.org/a/volumes/table_of_contents/?book_id=292 Synthesis Imaging in Radio Astronomy II]; the chapter on [http://www.aspbooks.org/a/volumes/article_details/?paper_id=17942 Deconvolution] may prove helpful. Additionally, imaging presentations are available on the [https://science.nrao.edu/science/meetings/2014/14th-synthesis-imaging-workshop/lectures Synthesis Imaging Workshop] and [https://science.nrao.edu/science/meetings/2016/vla-data-reduction/program VLA Data Reduction Workshop] webpages. The [https://casa.nrao.edu/docs/cookbook/index.html  CASA cookbook] chapter on [https://casa.nrao.edu/docs/cookbook/casa_cookbook006.html Synthesis Imaging] provides a wealth of information on the CASA implementation of {{clean}} and related tasks.
 
Finally, we refer users to the [https://science.nrao.edu/facilities/vla/docs/manuals/oss VLA Observational Status Summary] and the [https://science.nrao.edu/facilities/vla/docs/manuals/obsguide Guide to Observing with the VLA] for information on the VLA capabilities and observing strategies.


Finally, we like to refer to the [https://science.nrao.edu/facilities/vla/docs/manuals/oss VLA Observational Status Summary] and the [https://science.nrao.edu/facilities/vla/docs/manuals/obsguide Guide to Observing with the VLA] for information on the VLA capabilities and observing strategies.


== Weights and Tapering ==
== Weights and Tapering ==


[[Image:SNR-G55-uvcoverage-CASA4.5.2.png|400px|thumb|right|Fig. 2: u,v coverage for the 8-hour observation of the supernova remnant G055.7+3.4]]
[[Image:SNR-G55-uvcoverage-CASA4.5.2.png|400px|thumb|right|'''Figure 2''' <br /> u,v coverage for the 8 hour observation of the supernova remnant G055.7+3.4]]


When imaging data, a map is created associating the visibilities with the image.  
When imaging data, a map is created associating the visibilities with the image.  
The sampling function, which is a function of the visibilities, is modified by a weight function that defines the shape and size of the PSF. Weighting therefore provides some control over the spatial resolution and the surface brightness sensitivity of the map, where either direction can be emphasized.
The sampling function is modified by a weight function that defines the shape and size of the PSF. Weighting therefore provides some control over the spatial resolution and the surface brightness sensitivity of the map, where either direction can be emphasized.
<!-- <math> S(u,v) \to S(u,v)W(u,v) </math>.  
<!-- <math> S(u,v) \to S(u,v)W(u,v) </math>.  
Due to the fact that each VLA antenna performs slightly differently, different weights should be applied to each antenna. Therefore, the weight column in the data table reflects how much weight each corrected data sample should receive.  
Due to the fact that each VLA antenna performs slightly differently, different weights should be applied to each antenna. Therefore, the weight column in the data table reflects how much weight each corrected data sample should receive.  
-->
-->


There are three main weighting schemes (see also Table 1):  
There are three main weighting schemes (see Table 1):  


1) '''Natural''' weighting: The natural weights data based on their rms only. All visibility weights in a cell are being summed. More visibilities in a cell will thus increase the cell's weight, which will emphasize the shorter baselines. Natural weighting therefore results in a larger PSF, better surface brightness sensitivity but also a degraded resolution.  
1) '''Natural''' weighting: This weighs data based on their rms only. Data visibility weights are gridded onto a uv-cell and summed. More visibilities in a cell will thus increase the cell's weight, which will usually emphasize the shorter baselines. Natural weighting therefore results in a larger PSF and better surface brightness sensitivity, but also a degraded resolution.  


2) '''Uniform''' weighting: The weights are first gridded as in natural weighting but then each cell is corrected such that the weights are independent of the number of visibilities inside. Compared to natural weighting, uniform weighting emphasizes the longer baselines. Consequently, the PSF is smaller, which results in a better spatial resolution of the image. At the same time, however, the surface brightness sensitivity is reduced compared to natural weighting. The 'uniform' weighting of the baselines is a better representation of the uv-coverage and sidelobes are more suppressed.  
2) '''Uniform''' weighting: The weights are first gridded as in natural weighting but then each cell is corrected such that the weights are independent of the number of visibilities inside. Compared to natural weighting, uniform weighting usually emphasizes the longer baselines. Consequently the PSF is smaller, which results in a better spatial resolution of the image. At the same time, however, the surface brightness sensitivity is reduced compared to natural weighting. The uniform weighting of the baselines is a better representation of the uv-coverage and sidelobes are more suppressed.  


3) '''Briggs''' weighting: This scheme provides a compromise between natural and uniform weighting. The transition can be controlled with the ''robust'' parameter where ''robust=-2'' is close to uniform and ''robust=2'' close to natural weighting.  
3) '''Briggs''' weighting: This scheme provides a compromise between natural and uniform weighting. The transition can be controlled with the ''robust'' parameter where ''robust=-2'' is close to uniform and ''robust=2'' is close to natural weighting.  
Briggs weighting therefore offers a compromise for between spatial resolution and surface brightness sensitivity, and ''robust'' values near zero are typically being used.
Briggs weighting therefore offers a compromise for between spatial resolution and surface brightness sensitivity, and ''robust'' values near zero are typically used.


Details on the weighting schemes are given in [http://www.aoc.nrao.edu/dissertations/dbriggs/ Daniel Brigg's dissertation (Chapter 3)].
For a visual comparison between these three weighting schemes, please see the section on "CLEAN with Weights" in this guide.
[[Image:Weight_Tapering_table.png|450px|thumb|right|'''Table 1''' <br /> Table summarizing the effects of using weights and tapering.]]
'''Tapering''': In conjunction with the above weighting schemes, one can specify the ''uvtaper'' parameter within {{clean}}, which will control the radial weighting of visibilities in the uv-plane. Figure 2 graphically visualizes the uv-coverage during the observing session. The taper in {{clean}} is an elliptical Gaussian function which effectively removes long baselines and degrades the resolution. This may be desirable for extended structures when long baselines contribute a large fraction of the noise.
Tapering can, therefore, increase the surface brightness sensitivity of the data, but will decrease the point source sensitivity. Too aggressive tapering, however, may also take its toll on the surface brightness sensitivity.
We refer to the [https://casa.nrao.edu/docs/cookbook/casa_cookbook006.html CASA Cookbook Synthesis Imaging] chapter for the details of the weighting implementation in CASA's {{clean}}.
<!--
<!--
For a brief intro to the different clean algorithms, as well as other deconvolution and imaging information, please see the website kept by Urvashi R.V. [http://www.aoc.nrao.edu/~rurvashi/ImagingAlgorithmsInCasa/node2.html#SECTION00223000000000000000 here].
For a brief intro to the different clean algorithms, as well as other deconvolution and imaging information, please see the website kept by Urvashi R.V. [http://www.aoc.nrao.edu/~rurvashi/ImagingAlgorithmsInCasa/node2.html#SECTION00223000000000000000 here].


There are different options for <math> W(u,v) </math> (parameter ''weighting'' in {{clean}}):
There are different options for <math> W(u,v) </math> (parameter ''weighting'' in {{clean}}):
Line 102: Line 114:
-->
-->


[[Image:Weight_Tapering_table.png|450px|thumb|right|Table 1: Table summarizing the effects of using weights and tapering.]]
'''Tapering''': In conjunction with the above weighting schemes, one can specify the ''uvtaper'' parameter within {{clean}}, which will control the radial weighting of visibilities, in the uv-plane. This in effect, reduces the visibilities, with weights decreasing as a function of uv-radius. The taper in {{clean}} is an elliptical Gaussian function.
<!--
<!--
The tapering will apodize, or filter/change the shape of the weight function (which is itself a Gaussian), which can be expressed as: <br />
The tapering will apodize, or filter/change the shape of the weight function (which is itself a Gaussian), which can be expressed as: <br />
<math> W(u,v) = e^{-(u^2+v^2)/t^2} </math>, where t is the adjustable tapering parameter.  
<math> W(u,v) = e^{-(u^2+v^2)/t^2} </math>, where t is the adjustable tapering parameter.  
-->
-->
Tapering can smooth the image plane, give more weight to short baselines, but in turn degrade angular resolution. This process will increase the surface brightness sensitivity of the data. Aggressive tapering, however, can downweight some of the antennas and baselines to a degree where they are essentially not being considered anymore. The point source sensitivity will thus be decreased and in extreme cases the surface brightness sensitivity will suffer, too.
 
<!--
<!--
Due to the downweight of some data, point source sensitivity can be degraded, as some antennas and baselines will suppressed and, in the extreme case, effectively removed from the data averaging. If your observation was sampled by short baselines, tapering may improve sensitivity to extended structures.  
Due to the downweight of some data, point source sensitivity can be degraded, as some antennas and baselines will suppressed and, in the extreme case, effectively removed from the data averaging. If your observation was sampled by short baselines, tapering may improve sensitivity to extended structures.  
-->
-->
We refer to the [https://casa.nrao.edu/docs/cookbook/casa_cookbook006.html CASA Cookbook Synthesis Imaging] chapter for the details of the weighting implementation in CASA's {{clean}}.
== Primary and Synthesized Beam ==
== Primary and Synthesized Beam ==


The primary beam of a single antenna defines the sensitivity across the field of view. For the VLA antennas, the main beam can be approximated by a Gaussian with a FWHM equal to <math>90*\lambda_{cm}</math> or <math>45/ \nu_{GHz}</math>. But note that there are sidelobes beyond the Gaussian kernel that are sensitive to bright sources (see below). Taking our observed frequency to be the middle of the band, 1.5GHz, our primary beam will be around 30 arcmin.  
The primary beam of a single antenna defines the sensitivity across the field of view. For the VLA antennas, the main beam can be approximated by a Gaussian with a FWHM equal to <math>90*\lambda_{cm}</math> arcseconds, or <math>45/ \nu_{GHz}</math> arcminutes. Note that there are sidelobes beyond the Gaussian kernel that are sensitive to bright sources (see below). Taking our observed frequency to be the middle of L-band, 1.5 GHz, our primary beam will be around 30 arcmin.  


If your science goal is to image a source, or field of view that is significantly larger than the FWHM of the VLA primary beam, then creating a mosaic from a number of pointings is usually the preferred method. For a tutorial on mosaicing, see the [https://casaguides.nrao.edu/index.php?title=EVLA_Continuum_Tutorial_3C391 3C391 tutorial]. In the following, however, we will discuss methods to image large maps from single pointing data.  
If your science goal is to image a source or field of view that is significantly larger than the FWHM of the VLA primary beam, then creating a mosaic from a number of pointings is usually the preferred method. For a tutorial on mosaicing, see the [https://casaguides.nrao.edu/index.php?title=VLA_Continuum_Tutorial_3C391 3C391 tutorial]. In the following, however, we will discuss methods to image large areas from single pointing data.  


Since our observation was taken in D-configuration and we can check the [https://science.nrao.edu/facilities/vla/docs/manuals/oss/performance/resolution Observational Status Summary]'s section on VLA resolution to find that the synthesized beam will be around 46 arcsec. We want to oversample the synthesized beam by a factor of around five, so we will use a cell size of 8 arcsec.
Since our data were taken in the D-configuration, we can check the [https://science.nrao.edu/facilities/vla/docs/manuals/oss/performance/resolution Observational Status Summary] section on VLA resolution to find that the synthesized beam will be around 46 arcsec. Flagging, weighting and the exact frequency, however, may result in deviations from this value. As we will see later, the synthesized beam of our data hovers around 29 arcsec and for the extreme of uniform weighting around 26"x25". Oversampling the minor axis by a factor of ~3, we will use a cell (pixel) size of 8 arcsec.


Our field contains bright point sources significantly outside the primary beam. We therefore create images that are 170 arcminutes on a side ([Image Size * Cell Size]*[1arcmin / 60arsec]), or almost 6x the size of the primary beam, catching the first and second sidelobe. This is ideal for showcasing both the problems inherent in such wide-band, wide-field imaging, as well as some of the solutions currently available in CASA to deal with these issues.
Our field contains bright point sources significantly outside the primary beam. The VLA, in particular when using multi-frequency synthesis (see below), will have significant sensitivity outside the main lobe of the primary beam. Particularly at the lower VLA frequencies, sources that are located outside the primary beam may still be bright enough to be detected with sufficient signal-to-noise in the primary beam sidelobes; which can cause artifacts to interfer with the targeted field in the main part of the primary beam. Such sources need to be cleaned to remove the dirty beam response of these interfering sources from the entire image. This can be done by either creating a very large image or by using outlier fields centered on the strongest sources (see section on outlier fields below). A large image has the added advantage of increasing the field of view for science, albeit at lower sensitivity. Other effects will start to become significant, however, like the non-coplanarity of the sky. Large image sizes will also slow down the deconvolution process. Details are provided in Sanjay Bhatnagar's presentation: [https://science.nrao.edu/science/meetings/2016/vla-data-reduction/copy_of_WF_WB.pdf "Advanced Imaging: Imaging in the Wide-band Wide-field era"] given at the [https://science.nrao.edu/science/meetings/2016/vla-data-reduction/program 2016 VLA data reduction workshop].


First, it's worth considering why we are even interested in sources which are far outside the primary beam. This is mainly due to the fact that the VLA, with its wide bandwidth capabilities, is quite sensitive even far from phase center -- for example, at our observing frequencies in L-band, the primary beam gain is as much as 10% around 1 degree away.  That means that any imaging errors for these far-away sources will have a significant impact on the image rms at phase center. The error associated with sidelobes emerging from a source at distance R can be parametrized as:
The calls to CLEAN within this guide will create images that are 170 arcminutes on a side ([Image Size * Cell Size]*[1arcmin / 60arsec]), or almost 6x the size of the primary beam, catching the first and second sidelobes. This is ideal for showcasing both the problems inherent in such wide-band, wide-field imaging, as well as some of the solutions currently available in CASA to deal with these issues.  


<math>
Note that the execution time of {{clean}} depends on the image sizes. Large images generally take more computing time. There are some values, however, that are computationally not advisable. The logger output will then show a recommendation for the next larger but faster image size. As a rule of thumb we recommend image sizes 2<sup>n</sup> * 10 pixels (e.g., 160, 1280 pixels, etc.) for improved processing speeds.
\Delta(S) = S(R) \times PB(R) \times PSF(R)
</math>


So, for R = 1 degree, source flux S(R) = 1 Jy, <math>\Delta(S)</math> = 1 mJy − 100 <math>{\mu}</math>Jy.  Clearly, this will be a source of significant error.
Cleaning far away from the phase center may thus become important in the vicinity of strong sources, in particular at the lower frequency bands where non-thermal emission dominates.


== Clean Output Images ==
== Clean Output Images ==


As a result of the CLEAN algorithm, {{clean}} will create a number of output images. For an ''imagename='<imagename>''', this would be:
As a result of the CLEAN algorithm, {{clean}} will create a number of output images. For an ''imagename='<imagename>''', these outputs are:


'''<imagename>.image''' the residual + the model convolved with the clean beam. This is the final image (unit: Jy/clean beam).  <br>
'''<imagename>.residual''': the residual after subtracting the clean model (unit: Jy/beam, where beam refers to the dirty beam).<br>
'''<imagename>.residual''' the residual after subtracting the clean model (unit: Jy/dirty beam).<br>
'''<imagename>.model''': the clean model, not convolved (unit: Jy/pixel).<br>
'''<imagename>.model''' the clean model, not convolved (unit: Jy/pixel).<br>
'''<imagename>.psf''': the point-spread function (dirty beam)<br>
'''<imagename>.psf''' the point-spread function aka dirty beam<br>
'''<imagename>.flux''': the normalized sensitivity map. For single pointings this corresponds to the primary beam. <br>
'''<imagename>.flux''' the normalized sensitivity map. For single pointings this corresponds to the primary beam. <br>
'''<imagename>.image''': the residual + the model convolved with the clean beam. This is the final image (unit: Jy/beam, where beam refers to the clean beam).  <br>


Additional images will be created for specific algorithms like multi-term frequency synthesis or mosaicking.  
Additional images will be created for specific algorithms like multi-term frequency synthesis or mosaicking.  


Note: If an image file is present in the working directory and the same name is provided in ''imagename'', {{clean}} will use that image (in particular the residual and model image) as a starting point for further cleaning. If you want a fresh run of {{clean}}, first remove all images of that name using 'rmtables()':
<font color=red>'''Important:'''</font> If an image file is present in the working directory '''and''' the same name is provided in ''imagename'', {{clean}} will use that image&#151;in particular the residual and model image&#151;as a starting point for further cleaning. If you want a fresh run of {{clean}}, first remove all images of that name using 'rmtables()':


<source lang="python">
<source lang="python">
Line 154: Line 156:
</source>
</source>


This method is preferable over 'rm -rf' as it also clears the cache.
This method is preferable over ''rm -rf'' as it also clears the cache.
 
<font color=red>'''Note that interrupting {{clean}} by Ctrl+C may corrupt your visibilities&#151;you may be better off choosing to let {{clean}} finish.  We are currently implementing a command that will nicely exit to prevent this from happening but, for the moment, please try to avoid Ctrl+C.'''</font>


'''Note that interrupting {{clean}} by Ctrl+C may corrupt your visibilities - you may be better off choosing to let {{clean}} finish.  We are currently implementing a command that will nicely exit to prevent this from happening, but for the moment try to avoid Ctrl+C.'''


== Dirty Image ==
== Dirty Image ==


[[Image:SN_G55_10s.dirty.image.psf.png|400px|thumb|right|A dirty image of the supernova remnant G55.7+3.4 in greyscale, with apparent sidelobes (left), and the point spread function (PSF), also known as the dirty beam (right).]]
First, we will create a dirty image (Figure 3) to see the improvements as we step through several cleaning algorithms and parameters. The dirty image is the true image on the sky, convolved with the dirty beam (PSF). We will do this by running {{clean}} with parameter ''niter=0'', which will not do any cleaning.
 
First, we will create a dirty image to see the improvements as we step through several cleaning algorithms and parameters. The dirty image is the true image on the sky, convolved with the dirty beam (PSF). We will do this by running {{clean}} with niter=0, which will not perform any minor cycles.  


<source lang="python">
<source lang="python">
Line 168: Line 169:
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.dirty',  
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.dirty',  
       imsize=1280, cell='8arcsec', interactive=False, niter=0,   
       imsize=1280, cell='8arcsec', interactive=False, niter=0,   
       weighting='natural', stokes='I', usescratch=F)
       stokes='I', usescratch=F)
</source>
 
* ''imagename='SNR_G55_10s.dirty''': the root filename used for the various {{clean}} outputs.


* ''imsize=1280'': the image size in number of pixels.  A single value will result in a square image.
* ''cell='8arcsec''': the size of one pixel; again, entering a single value will result in a square pixel size.
* ''niter=0'': this controls the number of iterations done in the minor cycle.
* ''interactive=False'': For a tutorial that covers more of an interactive clean, please see the [https://casaguides.nrao.edu/index.php?title=VLA_high_frequency_Spectral_Line_tutorial_-_IRC%2B10216 VLA high frequency Spectral Line tutorial - IRC+10216.]
* ''usescratch=F'': controls writing the model visibilities to the model data column. For self-calibration we currently recommend setting usescratch=T.
* ''stokes='I''': since we have not done any polarization calibration, we only create a total-intensity image. For using CLEAN while including various Stoke's Parameters, please see the [https://casaguides.nrao.edu/index.php?title=EVLA_Continuum_Tutorial_3C391-CASA4.5 3C391 CASA guide.]
<source lang="python">
# In CASA
viewer('SNR_G55_10s.dirty.image')
viewer('SNR_G55_10s.dirty.image')
</source><br />
<source lang="python">
# In CASA
viewer('SNR_G55_10s.dirty.psf')
</source>
</source>


Note that the clean beam is only defined after some clean iterations. The dirty image has therefore no beam size specified in the header and the PSF image is the representation of the response of the array to a point source.
[[Image:SN_G55_10s.dirty.image.psf.png|400px|thumb|right|'''Figure 3''' <br /> A dirty image of the supernova remnant G55.7+3.4 in greyscale, with apparent sidelobes (left), and the point spread function (PSF), also known as the dirty beam (right).]]
 
The images may be easier to see in grey scale. To do this, click on Data Display Options (wrench icon, upper left corner) within the viewer and change the color map to Greyscale 1. You may also have to change the scaling power options to your liking. To change the brightness and contrast, assign a mouse button to this type of editing by clicking on the Colormap fiddling button (black/white circle icon) and click/drag the mouse over the image to change the brightness (left-right mouse movement) and contrast (up-down mouse movement).
 
Note that the clean beam is only defined after some clean iterations. The dirty image has therefore no beam size specified in the header and the PSF image is the representation of the response of the array to a point source. Even though it is empty with no iterations specified, {{clean}} will still produce the model file. So a continuation into actual cleaning will be possible by just restarting {{clean}} with the same image root name (and parameter ''niter>0'').
 


== Regular CLEAN & RMS Noise ==
== Regular CLEAN & RMS Noise ==
[[Image:SNR_G55_10s.niter.1K_vs_10K.png|400px|thumb|right|Regular run of CLEAN, with niter=1000 (left), compared to niter=10000 (right).]]


We will create a regular clean image which uses mostly default values. The first run of CLEAN will set ''niter=1000'' (default is 500), the second will have ''niter=10000''. Note that you may have to play with the image color map and brightness/contrast to get a better view of the image details. This can be done by clicking on ''Data Display Options'' (wrench icon on top left corner), and choosing "rainbow 3" under ''basic settings'', and adjusting the "Scaling Power Cycles".
We will now create a regular clean image using mostly default values to see how deconvolution improves the image quality. The first run of {{clean}} will use a fixed number of minor cycle iterations of ''niter=1000'' (default is 500), the second will have ''niter=10000''. Note that you may have to play with the image color map and brightness/contrast to get a better view of the image details.  


<source lang="python">
<source lang="python">
Line 184: Line 211:
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.Reg.Clean.niter1K',  
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.Reg.Clean.niter1K',  
       imsize=1280, cell='8arcsec', niter=1000, interactive=False)
       imsize=1280, cell='8arcsec', niter=1000, interactive=False)
</source><br />


viewer('SNR_G55_10s.Reg.Clean.niter1K')
<source lang="python">
# In CASA.
viewer('SNR_G55_10s.Reg.Clean.niter1K.image')
</source>
</source>


Now we will increase the niter value to 10,000 and compare the images.
The logger indicates that the image was obtained in two major cycles and some improvements over the dirty image are visible. But clearly we have not cleaned deep enough yet; the image still has many sidelobes, and an inspection of the residual image shows that it still contains source flux and structure. So let's increase the ''niter'' parameter value to 10,000 and compare the images (Figure 4).


<source lang="python">
<source lang="python">
Line 194: Line 224:
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.Reg.Clean.niter10K',  
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.Reg.Clean.niter10K',  
       imsize=1280, cell='8arcsec', niter=10000, interactive=False)
       imsize=1280, cell='8arcsec', niter=10000, interactive=False)
</source><br />


viewer('SNR_G55_10s.Reg.Clean.niter10K')
<source lang="python">
# In CASA.
viewer('SNR_G55_10s.Reg.Clean.niter10K.image')
</source>
</source>


[[Image:SNR_G55_10s.rms.screen.png|400px|thumb|right|Attempting to find the lowest rms value within the CLEAN'ed image using niter=1000, in order to calculate our threshold.]]
[[Image:SNR_G55_10s.niter.1K_vs_10K.png|400px|thumb|right|'''Figure 4''' <br /> Regular run of CLEAN, with niter=1000 (left), compared to niter=10000 (right).]]
 
As we can see from the resulting images, increasing the niter values (minor cycles) improves our image by reducing prominent sidelobes significantly. One could now further increase the ''niter'' parameter until the residuals are down to an acceptable level. To determine the number of iterations, one needs to keep in mind that {{clean}} will fail once it starts cleaning too deeply into the noise. At that point, the cleaned flux and the peak residual flux values will start to oscillate as the number of iterations increase. This effect can be monitored on the CASA logger output. To avoid cleaning too deeply, we will set a ''threshold'' parameter that will stop minor cycle clean iterations once a peak residual value is being reached.  


As we can see from the resulting images, increasing the niter values (minor cycles) improves our image by eliminiting prominent sidelobes. We will utilize the ''SNR_G55_10s.Reg.Clean.niter1K'' image to give us an idea of the rms noise (your sigma value), which will allow us to calculate the threshold parameter used within CLEAN.
First, we will utilize the ''SNR_G55_10s.Reg.Clean.niter1K.image'' image to give us an idea of the rms noise (your sigma value)(Figure 5).
With this image open within the viewer, click on the Rectangle Drawing button (Rectangle with R) and draw a square on the image at a position with little source or sidelobe contamination. Doing this should open up a Regions dock which holds information about the selected region, including the pixel statistics in the Statistics tab  (double clicking on the box will also bring up this information). Take notice of the rms values as you click/drag the box around empty image locations, or by drawing additional boxes at suitable positions. If the Regions dock is not displayed, click on '''View''' in the menu bar at the top of the viewer and click on the Regions check-box.


With the image open within the viewer, click on the 'Rectangle Drawing' button (Rectangle with R) and draw a square somewhere on the image. Doing this should open up a "Regions" area, which holds information about the area within the drawn box. Choose the "Statistics" tab and take notice of the rms values as you click/drag the box around the image. We are going to attempt to find the lowest rms value somewhere near our science target, without including any radio sources within it (refer to image on the right), and attempting to avoid sidelobes.
[[Image:SNR_G55_10s.rms.screen.png|400px|thumb|right|'''Figure 5''' <br /> Attempting to find the lowest rms value within the CLEAN'ed image using niter=1000, in order to calculate our threshold.]]
 
The lowest rms value we found was in the order of about 4 x 10<sup>-5</sup> Jy/beam, which we will use to calculate our threshold. There really is no set standard, but fairly good threshold values can vary anywhere between 2.0&#150;4.0*sigma; using clean boxes (see the section on interactive cleaning) allows one to go to lower thresholds. For our purposes, we will choose a threshold of 2.5*sigma. Doing the math results in a value of 10 x 10<sup>-5</sup> or, equivalently, 0.10mJy/beam. Therefore, for future calls to the {{clean}} task, we will set parameter ''threshold='0.1mJy'''. The clean cycle will be stopped when the residual peak flux density is either equal to or less than the ''threshold'' value '''or''' when the maximum number of iterations ''niter'' is reached. To ensure that the stopping criterion is indeed the parameter ''threshold'', parameter ''niter'' should be set to a very high number.
 
'''In the following, we nevertheless will use ''niter=1000'' to keep the execution times of {{clean}} on the low end as we focus on explaining different imaging methods.'''
 
An alternative method to determine the approximate rms of an image is to use the [https://science.nrao.edu/facilities/vla/docs/manuals/propvla/determining VLA Exposure Calculator] and to enter the observing conditions. Make sure that the chosen bandwidth reflects the data after RFI excision.


The lowest rms value we found was about 4.965E-5 Jy/beam, which we will use to calculate our threshold. There really is no set standard, but fairly good threshold values can vary anywhere between 2.0-3.0*sigma. For our purposes, we will choose a threshold of 2.5*sigma. Doing the math results in a value of 12.4E-5 or equivalently 0.12mJy/beam. Therefore, for future calls to the CLEAN task, we will set ''threshold=0.1mJy''.


== CLEAN with Weights ==
== CLEAN with Weights ==


To see the effects of using different weight algorithms to your image, let's change the ''weighting'' parameter within clean and inspect the resulting images. We will be using the ''Natural, Uniform, and Briggs'' weighting algorithms. Here, we have chosen a smaller image size to mainly focus on our science target.  
To see the effects of using different weighting schemes to the image, let's change the ''weighting'' parameter within {{clean}} and inspect the resulting images. We will be using the ''Natural, Uniform, and Briggs'' weighting algorithms. Here, we have chosen a smaller image size to mainly focus on our science target.  


<source lang="python">
<source lang="python">
Line 214: Line 255:
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.natural', weighting='natural',
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.natural', weighting='natural',
       imsize=540, cell='8arcsec', niter=1000, interactive=False, threshold='0.1mJy')
       imsize=540, cell='8arcsec', niter=1000, interactive=False, threshold='0.1mJy')
</source>


* ''weighting'': specification of the weighting scheme. For Briggs weighting, the robust parameter will be used.
* ''threshold='0.1mJy''': threshold at which the cleaning process will halt.
<source lang="python">
# In CASA. Uniform weighting
# In CASA. Uniform weighting
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.uniform', weighting='uniform',
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.uniform', weighting='uniform',
       imsize=540, cell='8arcsec', niter=1000, interactive=False, threshold='0.1mJy')
       imsize=540, cell='8arcsec', niter=1000, interactive=False, threshold='0.1mJy')
</source><br />


<source lang="python">
# In CASA. Briggs weighting, with robust set to default of 0.0
# In CASA. Briggs weighting, with robust set to default of 0.0
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.briggs', weighting='briggs',
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.briggs', weighting='briggs',
       imsize=540, cell='8arcsec', niter=1000, interactive=False, threshold='0.1mJy')
       robust=0, imsize=540, cell='8arcsec', niter=1000, interactive=False, threshold='0.1mJy')
</source><br />


<source lang="python">
# In CASA. Open the viewer and select the created images.
viewer()
viewer()
</source>
</source>


[[Image:SNR_G55_11s.nat.uni.briggs.png|1000px|thumb|center| CLEAN images created with different weighting algorithms, including natural (left), uniform (center), and briggs (right).]]
[[Image:SNR_G55_11s.nat.uni.briggs.png|1000px|thumb|center|'''Figure 6''' <br /> CLEAN images created with different weighting algorithms, including natural (left), uniform (center), and briggs (right).]]
 
Figure 6 shows that the natural weighted image is most sensitive to extended emission (beam size of 46"x41"). The negative values around the extended emission, often referred to as a negative bowl, is a typical signature of unsampled visibilities near the origin of the uv-plane. That is, the flux density present at shorter baselines, or larger angular scales than measured in this observation, is not well represented. Uniform weighted data shows the highest resolution (26"x25") and Briggs parameter ''robust=0'' (default value) is a compromise with a beam of 29"x29". To image more of the extended emission, the ''robust'' parameter could be tweaked further toward more positive values.


Now utilizing the viewer and opening each image, we can see that briggs weighting, with robust set to it's default value of 0.0, will result in a combination of natural and uniform weighting.


== Multi-Scale CLEAN ==
== Multi-Scale CLEAN ==


Since G55.7+3.4 is an extended source with many spatial scales, a more advanced form of imaging involves the use of multiple scales. MS-CLEAN is an extension of the classical CLEAN algorithm for handling extended sources. It works by assuming the sky is composed of emission at different spatial scales and works on them simultaneously, thereby creating a linear combination of images at different spatials scales. For a more detailed description of Multi Scale CLEAN, see the paper by J.T. Cornwell entitled  [http://arxiv.org/abs/0806.2228 Multi-Scale CLEAN deconvolution of radio synthesis images].
Since G55.7+3.4 is an extended source with many angular scales, a more advanced form of imaging involves the use of multiple scales. MS-CLEAN is an extension of the classical CLEAN algorithm for handling extended sources. Multi-Scale CLEAN works by assuming the sky is composed of emission at different angular scales and works on them simultaneously, thereby creating a linear combination of images at different angular scales. For a more detailed description of Multi-Scale CLEAN, see T.J. Cornwell's paper [http://arxiv.org/abs/0806.2228 Multi-Scale CLEAN deconvolution of radio synthesis images].
 
As is suggested, we will use a set of scales (which are expressed in units of the requested pixel, or cell, size) which are representative of the scales that are present in the data, including a zero-scale for point sources.  


[[Image:SN_G55.MultiScale.image.png|200px|thumb|right|G55.7+3.4 Multi-Scale Clean]]
We will use a set of scales&#151;expressed in units of the requested pixel or cell size&#151;which are representative of the scales that are present in the data, including a zero-scale for point sources.
[[Image:SN_G55_MultiScale.artifacts.png|200px|thumb|right|Artifacts around point sources]]


<source lang="python">
<source lang="python">
Line 245: Line 295:
       interactive=False, niter=1000,  weighting='briggs', stokes='I',  
       interactive=False, niter=1000,  weighting='briggs', stokes='I',  
       threshold='0.1mJy', usescratch=F, imagermode='csclean')
       threshold='0.1mJy', usescratch=F, imagermode='csclean')
viewer('SN_G55_10s.MultiScale.image')
</source>
</source>


* imagename='SN_G55_10s.MultiScale': the root filename used for the various {{clean}} outputs.  These include the final image (<imagename>.image), the relative sky sensitivity over the field (<imagename>.flux), the point-spread function (also known as the dirty beam; <imagename>.psf), the clean components (<imagename>.model), and the residual image (<imagename>.residual).
* ''multiscale=[0,6,10,30,60]'': a set of scales on which to clean.  A good rule of thumb when using multiscale is 0, 2xbeam, 5xbeam (where beam is the synthesized beam), and larger scales up to about half the minor axis maximum scale of the mapped structure. Since these are in units of the pixel size, our chosen values will be multiplied by the requested cell size. Thus, we are requesting scales of 0 (a point source), 48, 80, 240, and 480 arcseconds (8 arcminutes). Note that 16 arcminutes (960 arcseconds) roughly corresponds to the size of G55.7+3.4.


* imsize=1280: the image size in number of pixels. Note that entering a single value results in a square image with sides of this value. There are imsize values where {{clean}} is not very efficient. The logger should tell you if you hit such a number and suggest a better one. As a rule of thumb, <maths>10*2^n</maths> results ins speedy imsizes.  
* ''smallscalebias=0.9'': This parameter is known as the '''small scale bias''', and helps with faint extended structure, by balancing the weight given to smaller structures, which tend to have higher surface brightness but lower integrated flux density. Increasing this value gives more weight to smaller scales. A value of 1.0 weights the largest scale to zero, and a value of less than 0.2 weighs all scales nearly equally. The default value is 0.6.


* cell='8arcsec': the size of one pixel; again, entering a single value will result in a square pixel size.
<source lang="python">
 
# In CASA
* multiscale=[0,6,10,30,60]: a set of scales on which to clean.  A good rule of thumb when using multiscale is [0, 2xbeam, 5xbeam] (where beam is the synthesized beam) and larger scales up to about half the minor axis maximum scale of the mapped structure. Since these are in units of the pixel size, our chosen values will be multiplied by the requested cell size. Thus, we are requesting scales of 0 (a point source), 48, 80, 240, and 480 arcseconds.  Note that 16 arcminutes (960 arcseconds) roughly corresponds to the size of G55.7+3.4.
viewer('SNR_G55_10s.MultiScale.image')
 
</source>
*smallscalebias=0.9: This parameter is known as the '''small scale bias''', and helps with faint extended structure, by balancing the weight given to smaller structures which tend to be brighter, but have less flux density. Increasing this value gives more weight to smaller scales. A value of 1.0 weighs the largest scale to zero, and a value of less than 0.2 weighs all scales nearly equally. The default value is 0.6.
 
* interactive=False: we will let {{clean}} use the entire field for placing model components. Alternatively, you could try using interactive=True, and create regions to constrain where components will be placed.  However, this is a very complex field, and creating a region for every bit of diffuse emission as well as each point source can quickly become tedious. For a tutorial that covers more of an interactive clean, please see [https://casaguides.nrao.edu/index.php?title=EVLA_high_frequency_Spectral_Line_tutorial_-_IRC%2B10216 IRC+10216 tutorial.]


* niter=1000: this controls the number of iterations {{clean}} will do in the minor cycle.
The logger will show how much cleaning is performed on the individual scales.


* weighting='briggs': use Briggs weighting with a robustness parameter of 0 (halfway between uniform and natural weighting).
This is the fastest of the imaging techniques described here, but it's easy to see that there are artifacts in the resulting image (Figure 7). We can use the {{viewer}} to explore the point sources near the edge of the field by zooming in on them (Figure 8). Click on the Zoom button on the upper left corner and highlight an area by making a square around the portion where you would like to zoom in. Double clicking within the square will zoom in the selected area. The square can be resized by clicking/dragging the corners, or removed by pressing the Esc key. After zooming in, we can see some radio sources have prominent arcs as well as spots with a six-pointed pattern surrounding them.


* stokes='I': since we have not done any polarization calibration, we only create a total-intensity image. For using CLEAN while including various Stoke's Parameters, please see the [https://casaguides.nrao.edu/index.php/EVLA_Continuum_Tutorial_3C391-CASA4.5 3C391 CASA guide.]
{|
| [[Image:SN_G55.MultiScale.image.png|200px|thumb|left|'''Figure 7''' <br /> G55.7+3.4 Multi-Scale Clean]]
| [[Image:SN_G55_MultiScale.artifacts.png|200px|thumb|center|'''Figure 8''' <br /> Artifacts around point sources]]
|}


*threshold='0.1mJy': Flux level at which to stop cleaning.
Next we will explore some more advanced imaging techniques to mitigate the artifacts seen towards the edges of the image.


* usescratch=F: do not write the model visibilities to the model data column (only needed for self-calibration)
* imagermode='csclean': use the Cotton-Schwab clean algorithm
* threshold='0.1mJy': threshold at which the cleaning process will halt; i.e. no clean components with a flux less than this value will be created.  This is meant to avoid cleaning what is actually noise (and creating an image with an artificially low rms).  It is advisable to set this equal to the expected rms, which can be estimated using the [http://go.nrao.edu/ect EVLA exposure calculator].  However, in our case, this is a bit difficult to do, since we have lost a hard-to-estimate amount of bandwidth due to flagging, and there is also some residual RFI present.  Therefore, we choose 0.1 mJy as a relatively conservative limit.
This is the fastest of the imaging techniques described here, but it's easy to see that there are artifacts in the resulting image. We can use the {{viewer}} to explore the point sources near the edge of the field by zooming in on them. Click on the "Zooming" button on the top left corner and highlight an area by making a square around the portion where you would like to zoom-in. Double clicking within the square will zoom-in to the selected area. The square can be resized by clicking/dragging the corners, or removed by pressing the "Esc" key. After zooming in on the area, we can see some radio sources have prominent arcs, as well as spots with a six-pointed pattern surrounding them.
Next we will explore some more advanced imaging techniques to mitigate the artifacts seen towards the edge of the image.


== Multi-Scale, Wide-Field CLEAN (w-projection) ==
== Multi-Scale, Wide-Field CLEAN (w-projection) ==
[[Image:Faceting.png|250px|thumb|right|'''Figure 9''' <br /> Faceting when using wide-field gridmode, which can be used in conjunction with w-projection.]]
[[Image:SNR_G55_MS_vs_MS.wProj.png|500px|thumb|right|'''Figure 10''' <br /> Multi-Scale image of arcs around point sources far from the phase center, versus MS with w-projection (right). We can see the that combining the w-projection algorithm with the multiscale algorithm improves the resulting image by removing prominent artifacts.]]


[[Image:Faceting.png|250px|thumb|right| Faceting when using widefield gridmode, which can be used in conjunction with w-projection. ]]
The next {{clean}} algorithm we will employ is w-projection, which is a wide-field imaging technique that takes into account the non-coplanarity of the baselines as a function of distance from the phase center (Figure 9). For wide-field imaging, the sky curvature and non-coplanar baselines result in a non-zero w-term. The w-term, introduced by the sky and array non-coplanarity, introduces a phase term that will limit the dynamic range of the resulting image. Applying 2-D imaging to such data will result in artifacts around sources away from the phase center, as we saw in running MS-CLEAN. Note that this affects mostly the lower frequency bands where the field of view is large.
[[Image:SNR_G55_MS_vs_MS.wProj.png|500px|thumb|right|Multi-Scale image of arcs around point sources far from the phase center, versus MS with w-projection (right). We can see the that combining the w-projection algorithm with the multiscale algorithm improves the resulting image by removing prominent artifacts.]]


The next {{clean}} algorithm we will employ is w-projection, which is a wide-field imaging technique that takes into account the non-coplanarity of the baselines as a function of distance from the phase center. For wide-field imaging, the sky curvature and non-coplanar baselines results in a non-zero w-term. The w-term introduced by the sky and array curvature introduces a phase term that will limit the dynamic range of the resulting image. Applying 2-D imaging to such data will result in artifacts around sources away from the phase center, as we saw in running MS-CLEAN. Note that this affects mostly the lower frequency bands, especially for the more extended configurations, due to the field of view decreasing with higher frequencies.  
The w-term can be corrected by faceting (which describes the sky curvature by many smaller planes) in either the image or uv-plane. The latter is known as w-projection. A combination of the two can also be employed within {{clean}} by setting the parameter ''gridmode='widefield'''. If w-projection is employed, it will be done for each facet. Note that w-projection is an order of magnitude faster than the image-plane based faceting algorithm, but will require more memory.  


The w-term can be corrected by faceting (describe the sky curvature by many smaller planes) in either the image or uv-plane, or by employing w-projection. A combination of the two can also be employed within {{clean}} by setting the parameter gridmode='widefield'. If w-projection is employed, it will be done for each facet. Note that w-projections is an order of magnitude faster than the faceting algorithm, but will require more memory.
For more details on w-projection, as well as the algorithm itself, see [http://adsabs.harvard.edu/abs/2008ISTSP...2..647C "The Noncoplanar Baselines Effect in Radio Interferometry: The w-projection Algorithm"]. Also, the chapter on [http://www.aspbooks.org/a/volumes/article_details/?paper_id=17953 Imaging with Non-Coplanar Arrays] may be helpful.  
 
For more details on w-projection, as well as the algorithm itself, see [http://adsabs.harvard.edu/abs/2008ISTSP...2..647C "The Noncoplanar Baselines Effect in Radio Interferometry: The W-Projection Algorithm"]. Also, the chapter on [http://www.aspbooks.org/a/volumes/article_details/?paper_id=17953 Imaging with Non-Coplanar Arrays] may be helpful.  


<source lang="python">
<source lang="python">
Line 297: Line 335:
       interactive=False, niter=1000,  weighting='briggs',
       interactive=False, niter=1000,  weighting='briggs',
       stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')
       stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')
</source>
* ''gridmode='widefield''': Use the w-projection algorithm.


* ''wprojplanes=-1'': The number of w-projection planes to use for deconvolution. Setting to -1 forces CLEAN to utilize an acceptable number of planes for the given data.
<source lang="python">
# In CASA
viewer('SNR_G55_10s.ms.wProj.image')
viewer('SNR_G55_10s.ms.wProj.image')
</source>
</source>


* gridmode='widefield': Use the w-projection algorithm.
This will take slightly longer than the previous imaging round; however, the resulting image (Figure 10) has noticeably fewer artifacts.  In particular, compare the same outlier source in the Multi-Scale w-projected image with the Multi-Scale-only image: note that the swept-back arcs have disappeared.  There are still some obvious imaging artifacts remaining, though.


* wprojplanes=-1: The number of w-projection planes to use for deconvolution. Setting to -1 forces CLEAN to recommend and utilize an acceptable number of planes for the given data.


This will take slightly longer than the previous imaging round; however, the resulting image has noticeably fewer artifacts.  In particular, compare the same outlier source in the Multi-Scale w-projected image with the Multi-Scale-only image: note that the swept-back arcs have disappeared. There are still some obvious imaging artifacts remaining, though.
== Multi-Scale Multi-Term Frequency Synthesis ==
[[Image:MultiFrequency_Synthesis_snapshot.png|250px|thumb|right|'''Figure 11''' <br /> Multi-Frequency Synthesis snapshot of (u,v) coverage. We can see from the image on the right, using this algorithm can greatly improve coverage, thereby improving image fidelity.]]
[[Image:SNR_G55_10s.ms.MFS.image.png|200px|thumb|right|'''Figure 12''' <br /> Multi-Scale imaged with MS-MFS and nterms=2. Artifacts around point sources close to phase center are reduced while point sources away from the phase center still show artifacts.]]
[[Image:SN_G55_MS.MFS.alpha.png|200px|thumb|right|'''Figure 13''' <br /> Spectral Index image]]


== Multi-Scale, Multi-Term Frequency Synthesis ==
A consequence of simultaneously imaging the wide fractional bandwidths available with the VLA is that the primary and synthesized beams have substantial frequency-dependent variation over the observing band. If this variation is not accounted for, it will lead to imaging artifacts and compromise the achievable image rms.
[[Image:MultiFrequency_Synthesis_snapshot.png|250px|thumb|right| Multi-Frequency Synthesis snapshot of (u,v) coverage. We can see from the image on the right, using this algorithm can greatly improve coverage, thereby improving image fidelity.]]
[[Image:SNR_G55.ms_to_mfs.gif|200px|thumb|right|Multi-Scale image artifacts versus MS-MFS artifacts near SNR, with nterms=2. We can see artifacts around point sources diminish, improving our image.]]
[[Image:SN_G55_MS.MFS.alpha.png|200px|thumb|right|Spectral Index image]]


Another consequence of simultaneously imaging the wide fractional bandwidths available with the EVLA is that the primary and synthesized beams have substantial frequency-dependent variation over the observing band. If this is not accounted for, it will lead to imaging artifacts and compromise the achievable image rms.
The coordinates of the (u,v) plane are measured in wavelengths. Observing at several frequencies results in a baseline sampling several ellipses of different sizes in the (u,v) plane. By using a method called Multi-Frequency Synthesis (MFS), which is the default cleaning mode in CLEAN, we can fill in the gaps in the single frequency (u,v) coverage to achieve much better image fidelity (Figure 11).  


The dimensions of the (u,v) plane are measured in wavelengths, and therefore observing at several frequencies, a baseline can sample several ellipses in the (u,v) plane, each with different sizes. We can therefore fill in the gaps in the single frequency (u,v) coverage, hence Multi-Frequency Synthesis (MFS). Also when observing in low-frequencies, it may prove beneficial to observe in small time-chunks, which are spread out in time. This will allow the coverage of more spatial-frequencies, allowing us to employ this algorithm more efficiently.  
When observing in low-frequencies, it may prove beneficial to observe in short segments which are spread out in time. This will allow the coverage of more spatial-frequencies, permitting us to employ this algorithm more efficiently.  


The Multi-Scale Multi-Frequency-Synthesis (MS-MFS) algorithm provides the ability to simultaneously image and fit for the intrinsic source spectrum. The spectrum is approximated using a polynomial Taylor Term expansion in frequency, with the degree of the polynomial as a user-controlled parameter. A least-squares approach is used, along with the standard clean-type iterations. Using this method of imaging will dramatically improve our (u,v) coverage, hence improving image fidelity.
The Multi-Scale Multi-Term Frequency Synthesis algorithm provides the ability to simultaneously image and fit for the intrinsic source spectrum in each pixel. The spectrum is approximated using a polynomial Taylor-term expansion in frequency, with the degree of the polynomial as a user-controlled parameter. A least-squares approach is used, along with the standard clean-type iterations.  


For a more detailed explanation of the MS-MFS deconvolution algorithm, please see the paper by Urvashi Rau and Tim J. Cornwell entitled [http://arxiv.org/abs/1106.2745 A multi-scale multi-frequency deconvolution algorithm for synthesis imaging in radio interferometry]
For a more detailed explanation of the MS-MFS deconvolution algorithm, please see the paper [http://arxiv.org/abs/1106.2745 A multi-scale multi-frequency deconvolution algorithm for synthesis imaging in radio interferometry]


<source lang="python">
<source lang="python">
Line 327: Line 371:
       interactive=False, niter=1000,  weighting='briggs',
       interactive=False, niter=1000,  weighting='briggs',
       stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')
       stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')
</source>
* ''nterms=2'': the number of Taylor-terms to be used to model the frequency dependence of the sky emission.  Note that the speed of the algorithm will depend on the value used here (more terms will be slower); nterms=2 will fit a spectral index, and nterms=3 a spectral index and curvature.
When clean is done ''<imagename>.image.tt0'' will contain a total intensity image (Figure 12), where ''tt*'' is a suffix to indicate the Taylor term: ''<imagename>.image.tt0'' is the total intensity image and ''<imagename>.image.alpha'' will contain an image of the spectral index in regions where there is sufficient signal-to-noise (Figure 13). Having this spectral index image can help convey information about the emission mechanism involved within the supernova remnant. This spectral index can also give information on the optical depth of the source.


<source lang="python">
# In CASA
viewer('SNR_G55_10s.ms.MFS.image.tt0')
viewer('SNR_G55_10s.ms.MFS.image.tt0')
</source><br />


<source lang="python">
# In CASA
viewer('SNR_G55_10s.ms.MFS.image.alpha')
viewer('SNR_G55_10s.ms.MFS.image.alpha')
</source>
</source>


* nterms=2:the number of Taylor terms to be used to model the frequency dependence of the sky emission. Note that the speed of the algorithm will depend on the value used here (more terms will be slower); of course, the image fidelity will improve with a larger number of terms (assuming the sources are sufficiently bright to be modeled more completely).
Note: To replicate Figure 13, open the image within the viewer, click on Panel Display Options (wrench with a small P), change background color to white, and adjust your margins under the Margins button. To view the color wedge, click on the Data Display Options (wrench without the P, next to the folder icon), click on the Color Wedge button, click on Yes under display color wedge and adjust the various parameters to your liking.


This will take much longer than the two previous methods, so it would probably be a good time to have coffee or chat about EVLA data reduction with your neighbor at this point.   
For more information on the multi-term, multi-frequency synthesis mode and its outputs, see section [https://casa.nrao.edu/docs/cookbook/casa_cookbook006.html#sec306 5.2.5.1] in the CASA cookbook.   


When clean is done <imagename>.image.tt0 will contain a total intensity image, where tt0 is a suffix to indicate the Taylor term; <imagename>.image.alpha will contain an image of the spectral index in regions where there is sufficient signal-to-noise. Having this spectral index image can help convey information about the emission mechanism involved within the supernova remnant. It can also give information on the optical depth of the source. I've included a color widget on the top of the plot to give an idea of the spectral index variation.  
Inspect the brighter point sources in the field near the supernova remnant. You will notice that some of the artifacts, which had been symmetric around the sources themselves, are now gone. Since we did not use w-projection, however, there are still strong features related to the non-coplanar baseline effects still apparent for sources further away.


For more information on the multi-frequency synthesis mode and its outputs, see section 5.2.5.1 in the [http://casa.nrao.edu/Doc/Cookbook/casa_cookbook.pdf CASA cookbook].
At this point, {{clean}} takes into account the frequency variation of the synthesized beam ''but not'' the frequency variation of the primary beam. For low frequencies and large bandwidths, this can be substantial, e.g., 1&#150;2 GHz L-band observations result in a variation of a factor of 2. One effect of such a large fractional bandwidth is that in multi-frequency synthesis, primary beam nulls will be blurred and the interferometer is sensitive everywhere in the field of view. For spectral slopes, however, a frequency-dependent primary beam causes a steepening as the higher frequencies are less sensitive at a given point away from the phase center. A correction for this effect should be made with the task {{widebandpbcor}} (see section on Primary Beam Correction below).


Inspect the brighter point sources in the field near the supernova remnant.  You will notice that some of the artifacts which had been symmetric around the sources themselves are now gone; however, since we did not use W-Projection this time, there are still strong features related to the non-coplanar baseline effects still apparent for sources further away.


At this point, {{clean}} takes into account the variation of the synthesized beam but not the variation of the primary beam. For low frequencies and large bandwidths, this can be substantial. E.g. 1-2GHz L-band observations result in a variation of a factor of 2. One effect of such a variation is that in multi-frequency synthesis nulls will be blurred and the interferometer is sensitive everywhere in the field of view. For spectral slopes, however, a variation causes a steepening as the higher frequencies are less sensitive at a given point away from the phase center. A correction for this effect should be made with the task {{widebandpbcor}} (see below).
== Multi-Scale Multi-Term Frequency, Widefield CLEAN ==


== Multi-Scale, Multi-Term Frequency, Widefield CLEAN ==
We will now combine the w-projection and MS-MFS algorithms.  Be forewarned&#151;these imaging runs will take a while, and it's best to start them running and then move on to other things.
 
Finally, we will combine the W-Projection and MS-MFS algorithms.  Be forewarned -- these imaging runs will take a while, and it's best to start them running and then move on to other things.


Using the same parameters for the individual-algorithm images above, but combined into a single {{clean}} run, we have:
Using the same parameters for the individual-algorithm images above, but combined into a single {{clean}} run, we have:
Line 358: Line 409:
       interactive=False, niter=1000,  weighting='briggs',
       interactive=False, niter=1000,  weighting='briggs',
       stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')
       stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')
</source><br />


<source lang="python">
# In CASA
viewer('SNR_G55_10s.ms.MFS.wProj.image.tt0')
viewer('SNR_G55_10s.ms.MFS.wProj.image.tt0')
</source><br />


<source lang="python">
# In CASA
viewer('SNR_G55_10s.ms.MFS.wProj.image.alpha')
viewer('SNR_G55_10s.ms.MFS.wProj.image.alpha')
</source>
</source>


[[Image:SNR_G55_MS.MFS.wProj.png|1250px|thumb|center|Here we see the differences as the images progress through the different algorithms used: MS -> MS-MFS -> MS-wProjection -> MS-MFS-wProjection.]]
[[Image:SNR_G55_MS.MFS.wProj.png|1250px|thumb|center|'''Figure 14'''  Here we see the differences as the images progress through the different algorithms used: MS &rarr; MS-MFS &rarr; MS-wProjection &rarr; MS-MFS-wProjection.]]
 
Again, looking at the same outlier source, we can see that the major sources of error have been removed, although there are still some residual artifacts (Figure 14).  One possible source of error is the time-dependent variation of the primary beam; another is the fact that we have only used ''nterms=2'', which may not be sufficient to model the spectra of some of the point sources. Some weak RFI may also show up that may need additional flagging.


Again, looking at the same outlier source, we can see that the major sources of error have been removed, although there are still some residual artifacts.  One possible source of error is the time-dependent variation of the primary beam; another is the fact that we have only used nterms=2, which may not be sufficient to model the spectra of some of the point sources. Some weak RFI may also show up that may need additional flagging.


== Imaging Outlier Fields ==
== Imaging Outlier Fields ==


Now we will image the supernova remnant, as well as the bright sources (outliers) towards the edges of the image, creating a 512x512 pixel image for each one. For this, we will be utilizing CLEAN without widefield mode (try it to see the effects) as we will be specifying a phase center, and the images will not be too big, therefore we will not have sources very far from the phase center. We will specify a name for each image, as well as a phase center for each image. This form of imaging is useful for when you have several outlier fields you'd like to image in one go. An can also be created, if you have a list of sources you'd like to image (see Sect. 5.3.18.1 of the CASA cookbook).
When strong sources are far from the main target, but still strong enough to produce sidelobes in the main image, they should be cleaned. Sometimes, however, it is not practical to image very large fields for this purpose. An alternative is to use outlier fields. This mode will allow the user to specify a few locations that are then cleaned along with the main image. The outlier fields should be centered on strong sources that are known from sky catalogs or are identified by other means.
 
In order to find outlying sources, it will help to image a large field with lower resolution and identify them within the CASA viewer. By moving the mouse cursor over the sources, we can grab their positions and use the information within an outlier file. In this example, we've called our file ''outliers.txt''. It contains the names, sizes, and positions of the outliers we want to image (see section [https://casa.nrao.edu/docs/cookbook/casa_cookbook006.html#sec356 5.3.18.1] of the CASA cookbook).  
 
Open your favorite text editor and input the following:
 
<pre>
#content of outliers.txt
#
#outlier field1
imagename= 'Outlier1.MS.MFS'
imsize=[512,512]
phasecenter = 'J2000 19h23m27.693 22d37m37.180'
#
#outlier field2
imagename='Outlier2.MS.MFS'
imsize=[512,512]
phasecenter = 'J2000 19h25m46.888 21d22m03.365'


</pre>
{{clean}} will then be executed like the following:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
clean(vis='SNR_G55_10s.calib.ms', imagename=['SNR.MS.MFS', 'Outlier1.MS.MFS', 'Outlier2.MS.MFS'],
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR.MS.MFS-Main',
       imsize=[[512,512],[512,512],[512,512]], cell='8arcsec', mode='mfs',
      outlierfile='outliers.txt',
       imsize=[512,512], cell='8arcsec', mode='mfs',
       multiscale=[0,6,10,30,60], interactive=False, niter=1000,  weighting='briggs',
       multiscale=[0,6,10,30,60], interactive=False, niter=1000,  weighting='briggs',
       stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean',
       robust=0, stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')
      phasecenter=['J2000 19h21m38.271 21d45m48.288', 'J2000 19h23m27.693 22d37m37.180', 'J2000 19h25m46.888 21d22m03.365'])
</source>
</source>


[[Image:Outlier_Fields.png|1000px|thumb|center| Images of the supernova remnant and bright outlying sources. ]]
* ''outlierfile='outliers.txt''': the name of the outlier file.
 
We can view the images with {{viewer}} one at a time. Due to the difference in sky coordinates, they cannot be viewed on the same window display.
 
<source lang="python">
# In CASA
viewer('SNR.MS.MFS-Main.image')
</source><br />
 
<source lang="python">
# In CASA
viewer('Outlier1.MS.MFS.image')
</source><br />
 
<source lang="python">
# In CASA
viewer('Outlier2.MS.MFS.image')
</source>
 
We have changed the color map to Hot Metal 2 in order to show the different colors that can be used within the viewer. Feel free to play with other color maps that may be better suited for your screen.
 
[[Image:Outlier_Fields.png|1000px|thumb|center|'''Figure 15''' <br /> Images of the supernova remnant and bright sources far from the phase center (near the edge of, or beyond, the primary beam.) ]]
 


== Primary Beam Correction ==
== Primary Beam Correction ==


In interferomety, the images formed via deconvolution, are representations of the sky, multiplied by the primary beam response of the antenna. The primary beam can be described by a Gaussian with the size depending on the observing frequency. Images produced via {{clean}} are by default not corrected for the primary beam pattern (important for mosaics), and therefore do not have the correct flux.  
In interferometry, the images formed via deconvolution are representations of the sky multiplied by the primary beam response of the antenna. The primary beam can be described as Gaussian with a size depending on the observing frequency. Images produced via {{clean}} are by default not corrected for the primary beam pattern (important for mosaics), and therefore do not have the correct flux density away from the phase center.  


Correcting the primary beam can be done during {{clean}} with the '''pbcor''' parameter. It can also be done after imaging using the task [https://casa.nrao.edu/docs/TaskRef/impbcor-task.html impbcor] for regular data sets, and {{widebandpbcorr}} for those that use Taylor-term expansion (nterms > 1). A third possibility, is utilizing the task {{immath}} to manually divide the ''<imagename>.image'' by the ''<imagename>.flux'' images (''<imagename>.flux.pbcoverage'' for mosaics).  
Correcting for the primary beam, however, can be done during {{clean}} by using the parameter ''pbcor''. Alternatively, it can be done after imaging using the task [https://casa.nrao.edu/docs/TaskRef/impbcor-task.html impbcor] for regular data sets and {{widebandpbcorr}} for those that use Taylor-term expansion (nterms > 1). A third alternative is utilizing the task {{immath}} to manually divide the ''<imagename>.image'' by the ''<imagename>.flux'' image (''<imagename>.flux.pbcoverage'' for mosaics).  


Flux corrected images usually don't look pretty, due to the noise at the edges being increased. Flux densities, however, should only be calculated from primary beam corrected images. Let's run the {{impbcor}} task to correct our multiscale image.
Flux corrected images usually don't look pretty due to the noise at the edges being increased. Flux densities, however, should only be calculated from primary beam corrected images. Let's run the {{impbcor}} task to correct our multiscale image.


<source lang="python">
<source lang="python">
# In CASA
# In CASA
impbcor(imagename='SNR_G55_10s.MultiScale.image', pbimage='SNR_G55_10s.MultiScale.flux', outfile='SNR_G55_10s.MS.pbcorr.image', mode='divide')
impbcor(imagename='SNR_G55_10s.MultiScale.image', pbimage='SNR_G55_10s.MultiScale.flux',  
        outfile='SNR_G55_10s.MS.pbcorr.image')
</source>
</source>


Let us now use the {{widebandpbcor}} task for wideband (nterms>1) images. Note that for this task, we will be supplying the image name that is the prefix for the Taylor expansion images, tt0 and tt1, which must be on disk. Such files were created, e.g., during the last Multi-Scale, Multi-Frequency, Widefield run of CLEAN.
* ''imagename'': the image to be corrected


[[Image:SNR_G55_10s.MS.MFS.wProj.pbcor.image.png|200px|thumb|right| Primary beam corrected image using the MS.MFS.wProj image created during the clean process.]]
* ''pbimage'': the <imagename>.flux image as a representation of the primary beam (<imagename>.flux.pbcoverage for mosaics)
 
<source lang="python">
# In CASA
viewer('SNR_G55_10s.MS.pbcorr.image')
</source>
 
Let us now use the {{widebandpbcor}} task for wide-band (''nterms''>1) images. Note that for this task, we will be supplying the image name that is the prefix for the Taylor expansion images, tt0 and tt1, which must be on disk. Such files were created during the last Multi-Scale, Multi-Frequency, Widefield run of CLEAN. Task {{widebandpbcor}} will generate a set of images with a ''pbcor.image'' extension.
 
[[Image:SNR_G55_10s.MS.MFS.wProj.pbcor.image.png|200px|thumb|right|'''Figure 16''' <br /> Primary beam corrected image using the widebandpbcor task for the MS.MFS.wProj image created during the CLEAN process.]]
[[Image:SNR_G55_10s.MS.MFS.wProj.pbcor.image.alpha.png|200px|thumb|right|'''Figure 17''' <br /> Primary beam corrected spectral index image using the widebandpbcor task.]]


<source lang="python">
<source lang="python">
# In CASA
# In CASA
widebandpbcor(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.ms.MFS.wProj',  
widebandpbcor(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.ms.MFS.wProj',  
               nterms=2, action='pbcor', pbmin=0.2, spwlist=[0,1,2,3],  
               nterms=2, action='pbcor', pbmin=0.2, spwlist=[0,1,2,3],
               weightlist=[0.5,1.0,0,1.0], chanlist=[63,63,63,63], threshold='0.1Jy')
               weightlist=[0.5,1.0,0,1.0], chanlist=[25,25,25,25], threshold='0.6mJy')
</source>
</source>


* spwlist=[0,1,2,3] : We want to apply this correction to all spectral windows in our calibrated measurement set.  
Note that the spectral index image (<imagename>.alpha) will have units in Jy/beam, which is not correct. The software bug has been fixed in CASA 4.6.
* weightlist=[0.5,1.0,0,1.0] : Since we did not specify rest frequencies during CLEAN, the widbandpbcor tasks will pick them from the provided image. Running the task, the logger reports the multiple frequencies used for the primary beam, which are 1.256, 1.429, 1.602, and 1.775 GHz. Having created an amplitude vs. frequency plot of the calibrated measurement set with colorized spectral windows using plotms, we notice that the first chosen frequency lies within spectral window 0, which we know had lots of flagged data due to lots of RFI being present. This weightlist parameter allows us to give this chosen frequency less weight. The primary beam at 1.6GHz lies in an area with no data, therefore we will give a weight value of zero for this frequency. The remaining frequencies 1.429 and 1.775 GHz lie within spectral windows which contained less RFI, therefore we provide a larger weight percentage.
 
* pbmin=0.2 : Gain level below which not to compute Taylor-coefficients or apply a primary beam correction.
* ''spwlist=[0,1,2,3]'': We want to apply this correction to all spectral windows in our calibrated measurement set.  
* chanlist=[63,63,63,63] : Our measurment set contains 64 channels, including zero.
 
* threshold='0.1Jy' : Threshold in the intensity map, below which not to recalculate the spectral index.
* ''weightlist=[0.5,1.0,0,1.0]'': Since we did not specify reference frequencies during {{clean}}, the {{widebandpbcor}} task will pick them from the provided image. Running the task, the logger reports the multiple frequencies used for the primary beam, which are 1.256, 1.429, 1.602, and 1.775 GHz. Having created an amplitude vs. frequency plot of the calibrated measurement set with colorized spectral windows using {{plotms}}, we note that the first chosen frequency lies within spectral window 0, which we know had flagged data due to RFI being present. This parameter ''weightlist'' allows us to give this chosen frequency less weight. The primary beam at 1.6 GHz lies in an area with no data, therefore we will give a weight value of zero for this frequency. The remaining frequencies 1.429 and 1.775 GHz lie within spectral windows which contained less RFI, therefore we provide a larger weight percentage.  


It's important to note that the image will cut off at about 20% of the HPBW, as we are confident of the accuracy within this percentage. Anything outside becomes less accurate, thus there is a mask associated with the creation of the corrected primary beam image.  
* ''pbmin=0.2'': Gain level below which not to compute Taylor-coefficients or apply a primary beam correction.


It would be a good exercise to use {{viewer}} to plot both the primary beam corrected image, and the original cleaned image and compare the intensity (Jy/beam) values, which should differ slightly.
* ''chanlist=[25,25,25,25]'': Make primary beams at frequencies corresponding to channel 25.
 
* ''threshold='0.6mJy''': Threshold in the intensity map, below which not to recalculate the spectral index. We adjusted the threshold to get good results: too high of a threshold resulted in errors and no spectral index image, too low of a threshold resulted in spurious values for the spectral index image.
 
<source lang="python">
# In CASA
viewer('SNR_G55_10s.ms.MFS.wProj.pbcor.image.tt0')
</source><br />
 
<source lang="python">
# In CASA
viewer('SNR_G55_10s.ms.MFS.wProj.pbcor.image.alpha')
</source>
 
It's important to note that the image will cut off at about 20% of the HPBW, as we are confident of the accuracy within this percentage. Anything outside becomes less accurate, thus there is a mask associated with the creation of the corrected primary beam image (Figure 16). Spectral indices may still be unreliable below approximately 70% of the primary beam HPBW (Figure 17).
 
It would be a good exercise to use the {{viewer}} to plot both the primary beam corrected image, and the original cleaned image and compare the intensity (Jy/beam) values, which should differ slightly.


== Image Information ==


== Imaging Spectral Cubes ==
== Imaging Spectral Cubes ==


For spectral line imaging, CASA {{clean}} can be used in either ''mode='frequency''' or ''mode='velocity'''. Both will create a spectral axis in frequency. The velocity mode adds a second velocity label to it.  
For spectral line imaging, CASA {{clean}} can be used in either ''mode='frequency' '' or ''mode='velocity'.'' Both modes will create a spectral axis in frequency, while the velocity mode adds an additional velocity label.  


The following keywords are important for these modes (velocity in this example):
The following keywords are important for spectral modes (velocity in this example):


<source lang="python">
<source lang="python">
Line 439: Line 566:
</source>
</source>


The spectral dimension of the output cube will be defined by these parameters and {{clean}} will regrid the visibilities to it. Note that invoking {{cvel}} before imaging is in most cases not necessary.  
The spectral dimension of the output cube will be defined by these parameters and {{clean}} will regrid the visibilities to the cube. Note that invoking {{cvel}} before imaging is, in most cases, not necessary even when two or more measurement sets are being provided at the same time.  
   
   
The cube is specified by a ''start'' velocity in km/s, the ''nchan'' number of channels and a channel ''width'' (where the latter can also be negative for decreasing velocity cubes).  
The cube is specified by a ''start'' velocity in km/s, the ''nchan'' number of channels, and a channel ''width'' (where the latter can also be negative for decreasing velocity cubes).  


To correct Doppler motions, {{clean}} also requires a velocity frame, where ''LSRK'' and ''BARY'' are the most popular Local Standard of Rest (kinematic) and sun-earth Barycenter references. ''doppler'' defines whether the data will be gridded via the optical or radio velocity definition. A description of the available options and definitions can be found in the [https://science.nrao.edu/facilities/vla/docs/manuals/obsguide/modes/line VLA observing guide]. By default, {{clean}} will produce a cube in LRSK and radio.  
To correct for Doppler effects, {{clean}} also requires a ''outframe'' velocity frame where ''LSRK'' (Local Standard of Rest (kinematic)) and ''BARY'' (Sun-Earth Barycenter) are the most popular references. Parameter ''veltype'' defines whether the data will be gridded via the optical or radio velocity definition. A description of the available options and definitions can be found in the [https://science.nrao.edu/facilities/vla/docs/manuals/obsguide/modes/line VLA observing guide] and the [https://casa.nrao.edu/docs/cookbook/casa_cookbook014.html CASA cookbook]. By default, {{clean}} will produce a cube using the LRSK and radio definitions.  


Note that {{clean}} will always work on the entire cube when searching for the highest residual fluxes in the minor cycle. To perform this per channel, one can set ''chaniter=T''.
Note that {{clean}} will always work on the entire cube when searching for the highest residual fluxes in the minor cycle. To do this per channel, one can set parameter ''chaniter=T''.
 
CASA also offers parameter ''mode='channel'.'' But we do not recommend this mode as the VLA does not observe with Doppler tracking. The fixed frequency observing of the VLA means that spectral features will drift in sky frequency over time. The Doppler correction will then be applied by {{clean}} via parameter ''mode='velocity''' or '' 'frequency' ''. Parameter ''mode='channel' '' will perform the correction only using the first timestamp in the observations. It can also be confusing when imaging some shifted, but overlapping, spectral windows.
 
An example of spectral line imaging procedures is provided in the [https://casaguides.nrao.edu/index.php?title=VLA_high_frequency_Spectral_Line_tutorial_-_IRC%2B10216 VLA high frequency Spectral Line tutorial - IRC+10216].


CASA also offers ''mode='channel' ''. But we do not recommend this mode as the VLA does not Doppler tracking. In other words, the fixed frequency observing of the VLA will let the spectral feature move through frequency space in time. The Doppler correction will be in {{clean}} in ''mode='velocity''' and not on the telescope itself. ''mode='channel' '' can also be confusing when imaging some shifted, but overlapping spectral windows.


== Beam per Plane ==
== Beam per Plane ==
For large spectral cubes, the synthesized beam can vary substantially across the channels. To account for this, CASA will calculate a separate beam for each channel when the difference is more than 5% across the cube. All CASA image analysis tasks are capable to handle such cubes.  
For spectral cubes spanning relatively wide ranges in frequency, the synthesized beam can vary substantially across the channels. To account for this, CASA will calculate separate beams for each channel when the difference is more than half a pixel across the cube. All CASA image analysis tasks are capable of handling such cubes.
 
If it is desired to have a cube with a single synthesized beam, two options are available. Best is to use {{imsmooth}} with parameter ''kernel='commonbeam'.'' This task will smooth each plane to that of the lowest resolution and it will clean up all header variables such that only a single beam appears in the data. The second option is to define parameter ''resmooth=T'' directly in {{clean}}.


If it is desired to have a cube with a single synthesized beam, two options are available. Best is to use {{imsmooth}} with ''kernel='commonbeam' ''. This task will smooth each plane to that of the lowest resolution. It will also clean up all header variables such that only a single beam appears in the data. The second option is to define ''resmooth=T'' directly in {{clean}}.


== Image Header ==
== Image Header ==


The image header holds meta data associated with your CASA image. The task {{imhead}} will display this data within the casalog. We will first run imhead with mode='summary':
The image header holds metadata associated with your CASA image. The task {{imhead}} will display this data within the casalog. We will first run {{imhead}} with parameter ''mode='summary' '':


<source lang="python">
<source lang="python">
Line 463: Line 594:
</source>
</source>


* mode='summary': gives general information about the image, including the object name, sky coordinates, image units, the telescope the data was taken with, and more.
* ''mode='summary' '': gives general information about the image, including the object name, sky coordinates, image units, the telescope the data was taken with, and more.
 
For further information, run parameter ''mode='list' ''. We will assign a variable'' header ''to also capture the output as a Python dictionary:
 
<source lang="python">
# In CASA
header=imhead(imagename='SNR_G55_10s.ms.MFS.wProj.image.tt0', mode='list')
</source>
 
* ''mode='list' '': gives more detailed information, including beam major/minor axes, beam primary angle, and the location of the max/min intensity, and lots more. Essentially this mode displays the FITS header variables.


For further information about the image, let's now run it with mode='list':
 
== Image Conversion ==
 
Finally, as an example, we convert our image from intensity to main beam brightness temperature.
We will use the standard equation
 
<math>T=1.222\times 10^{6} \frac{S}{\nu^{2} \theta_{maj} \theta_{min}} </math>
 
where the main beam brightness temperature <math>T</math> is given in K, the intensity <math>S</math> in Jy/beam, the reference frequency <math>\nu</math> in GHz, and the major and minor beam sizes <math>\theta</math> in arcseconds.
 
For a beam of 29.30"x29.03" and a reference frequency of 1.579 GHz (as taken from the previous {{imhead}} run) we calculate the brightness temperature using {{immath}}:


<source lang="python">
<source lang="python">
# In CASA
# In CASA
imhead(imagename='SNR_G55_10s.ms.MFS.wProj.image.tt0', mode='list')
immath(imagename='SNR_G55_10s.ms.MFS.wProj.image.tt0', mode='evalexpr',
      expr='1.222e6*IM0/1.579^2/(29.30*29.03)',
      outfile='SNR_G55_10s.ms.MFS.wProj.image.tt0-Tb')
</source>
</source>


* mode='list': gives more detailed information, including beam major/minor axes, beam primary angle, and the location of the max/min intensity, and lots more.
* ''mode='evalexpr' '': {{immath}} is used to calcuate with images
 
* ''expr'': the mathematical expression to be evaluated. The images are abbreviated as IM0, IM1, ... in the sequence of their appearance in the ''imagename'' parameter.


We will now want to change our image header units from Jy/beam to Kelvin. To do this, we will run the task with mode='put':
Since {{immath}} only changes the values and not the unit of the image, we will now change the new image header'' 'bunit' ''key to 'K'.
To do so, we will run {{imhead}} with parameter ''mode='put' '':


<source lang="python">
<source lang="python">
# In CASA
# In CASA
imhead(imagename='SNR_G55_10s.ms.MFS.wProj.image.tt0', mode='put', hdkey='bunit', hdvalue='K')
imhead(imagename='SNR_G55_10s.ms.MFS.wProj.image.tt0-Tb', mode='put', hdkey='bunit', hdvalue='K')
</source>
 
* ''hdkey'': the header keyword that will be changed
 
* ''hdvalue'': the new value for header keyword
 
Launching the viewer will now show our image in brightness temperature units:
 
<source lang="python">
# In CASA
viewer('SNR_G55_10s.ms.MFS.wProj.image.tt0-Tb')
</source>
</source>


Line 484: Line 651:
[[Main Page | &#8629; '''CASAguides''']]
[[Main Page | &#8629; '''CASAguides''']]


<!--
-- Original: Miriam Hartman <br />
-- Original: Miriam Hartman <br />
-- Modifications: Lorant Sjouwerman (4.4.0, 2015/07/07) <br />
-- Modifications: Lorant Sjouwerman (4.4.0, 2015/07/07) <br />
-- Modifications: Juergen Ott (4.5.2, 2016/04/14) <br />
-- Modifications: Juergen Ott (4.5.2, 2016/04/14) <br />
-- Topical Guide: Jose Salcido (4.5.2, 2016/04/18) <br />
-- Topical Guide: Jose Salcido (4.5.2, 2016/04/18) <br />
-- Modifications: Juergen Ott (4.5.2, 2016/04/20) <br />
-- Edits: Tony Perreault (4.5.2, 2016/05/20) <br />
-->
{{Checked 4.5.2}}
{{Checked 4.5.2}}

Latest revision as of 19:18, 25 May 2016

Imaging

This tutorial provides guidance on imaging procedures in CASA. The tutorial covers basic continuum cleaning and the influence of image weights, as well as wide-band and wide-field imaging techniques, multi-scale clean, an outlier field setup, and primary beam correction. Spectral line imaging procedures are explained but not covered in detail. For a more thorough example of spectral line imaging, refer to the VLA high frequency Spectral Line tutorial - IRC+10216. This imaging tutorial concludes with basic image header calls and the conversion of Jy/beam to K surface brightness units through image arithmetic and header manipulation.

We will be utilizing data, taken with the Karl G. Jansky Very Large Array, of G055.7+3.4, which is a supernova remnant. The data were taken on August 23, 2010, in the first D-configuration for which the wideband capabilities of the WIDAR (Wideband Interferometric Digital ARchitecture) correlator were available. The 8 hour long observation includes all available 1 GHz of bandwidth in L-band, from 1&#150;2 GHz in frequency.

We will skip the calibration process as examples of calibration can be found in several other guides, including the VLA Continuum Tutorial 3C391 and VLA high frequency Spectral Line tutorial - IRC+10216 tutorials. 

A copy of the calibrated data (1.2GB) can be downloaded from http://casa.nrao.edu/Data/EVLA/SNRG55/SNR_G55_10s.calib.tar.gz

Your first step will be to unzip and untar the file in a terminal window (before you start CASA): 

tar -xzvf  SNR_G55_10s.calib.tar.gz

Then start casa as usual via the casa command, which will bring up the ipython interface and launches the logger.


The CLEAN Algorithm

Figure 1
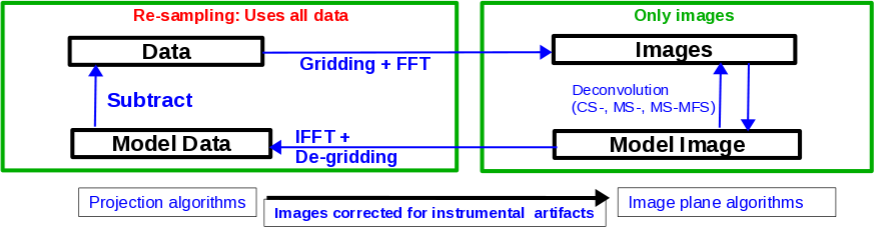
The CLEAN major and minor cycles, indicating the steps undertaken during gridding, projection algorithms, and creation of images.

The CLEAN algorithm, developed by J. Högbom (1974) enabled the synthesis of complex objects, even if they have relatively poor Fourier uv-plane coverage. Poor coverage occurs with partial earth rotation synthesis or with arrays composed of few antennas. The dirty image is formed by a simple Fourier inversion of the sampled visibility data, with each point on the sky being represented by a suitably scaled and centered PSF (Point Spread Function), or dirty beam, which itself is the Fourier inversion of the visibility (u,v) coverage.

The convolution with the dirty beam creates artifacts in the image and limits the dynamic range. The CLEAN algorithm attempts to remove the dirty beam pattern from the image via deconvolution. This implies that it interpolates from the measured (u,v) points across gaps in the (u,v) coverage. In short, CLEAN provides solutions to the convolution equation by representing radio sources by a number of point sources in an empty field. The brightest points are found by performing a cross-correlation between the dirty image and the PSF. The brightest parts are then subtracted, and the process is repeated again for the next brighter sources. Variants of CLEAN, such as multi-scale CLEAN, take into account extended kernels which may be better suited for extended objects.

For single pointings, CASA uses the Cotton-Schwab cleaning algorithm in the task clean (parameter imagermode='csclean'), which breaks the process into major and minor cycles (see Figure 1). To start with, the visibilities are gridded, weighted, and Fourier transformed to create a dirty image. The minor cycle then operates in the image domain to find the clean components that are added to the clean model. The model image is Fourier transformed back to the visibility domain, degridded, and subtracted from the visibilities. This creates a new residual that is then gridded, weighted, and FFT'ed again to the image domain for the next iteration. The gridding, FFT, degridding, and subtraction processes form the major cycle.

This iterative process is continued until a stopping criterion is reached, such as a maximum number of clean components or a flux threshold in the residual image.

In CASA clean, two versions of the PSF can be used: parameter psfmode = 'hogbom' uses the full-sized PSF for subtraction and is a thorough but slow method. Parameter psfmode='clark' uses a smaller beam patch, which increases the speed. The patch size and length of the minor cycle are internally chosen such that clean converges well without giving up the speed improvement. Parameter psfmode='clark' is the default option in clean.

In a final step, clean derives a Gaussian fit to the inner part of the dirty beam, which defines the clean beam. The clean model is then convolved with the clean beam and added to the last residual image to create the final image.

Note that the CASA team is currently developing a refactored clean task, called tclean. Task tclean has a better interface, provides new algorithms, and more combinations between imaging algorithms. Task tclean also includes software to parallelize the computations in a multi-processor environment. Eventually, tclean will replace the current clean task. For this guide, however, we will stick with the original clean task, as tclean is still in the development and testing phase. Nevertheless, the reader is encouraged to try tclean and send us feedback through the NRAO helpdesk.

For more details on imaging and deconvolution, we refer to the Astronomical Society of the Pacific Conference Series book entitled Synthesis Imaging in Radio Astronomy II; the chapter on Deconvolution may prove helpful. Additionally, imaging presentations are available on the Synthesis Imaging Workshop and VLA Data Reduction Workshop webpages. The CASA cookbook chapter on Synthesis Imaging provides a wealth of information on the CASA implementation of clean and related tasks.

Finally, we refer users to the VLA Observational Status Summary and the Guide to Observing with the VLA for information on the VLA capabilities and observing strategies.


Weights and Tapering

Figure 2
u,v coverage for the 8 hour observation of the supernova remnant G055.7+3.4

When imaging data, a map is created associating the visibilities with the image. The sampling function is modified by a weight function that defines the shape and size of the PSF. Weighting therefore provides some control over the spatial resolution and the surface brightness sensitivity of the map, where either direction can be emphasized.

There are three main weighting schemes (see Table 1):

1) Natural weighting: This weighs data based on their rms only. Data visibility weights are gridded onto a uv-cell and summed. More visibilities in a cell will thus increase the cell's weight, which will usually emphasize the shorter baselines. Natural weighting therefore results in a larger PSF and better surface brightness sensitivity, but also a degraded resolution.

2) Uniform weighting: The weights are first gridded as in natural weighting but then each cell is corrected such that the weights are independent of the number of visibilities inside. Compared to natural weighting, uniform weighting usually emphasizes the longer baselines. Consequently the PSF is smaller, which results in a better spatial resolution of the image. At the same time, however, the surface brightness sensitivity is reduced compared to natural weighting. The uniform weighting of the baselines is a better representation of the uv-coverage and sidelobes are more suppressed.

3) Briggs weighting: This scheme provides a compromise between natural and uniform weighting. The transition can be controlled with the robust parameter where robust=-2 is close to uniform and robust=2 is close to natural weighting. Briggs weighting therefore offers a compromise for between spatial resolution and surface brightness sensitivity, and robust values near zero are typically used.

Details on the weighting schemes are given in Daniel Brigg's dissertation (Chapter 3).

For a visual comparison between these three weighting schemes, please see the section on "CLEAN with Weights" in this guide.

Table 1
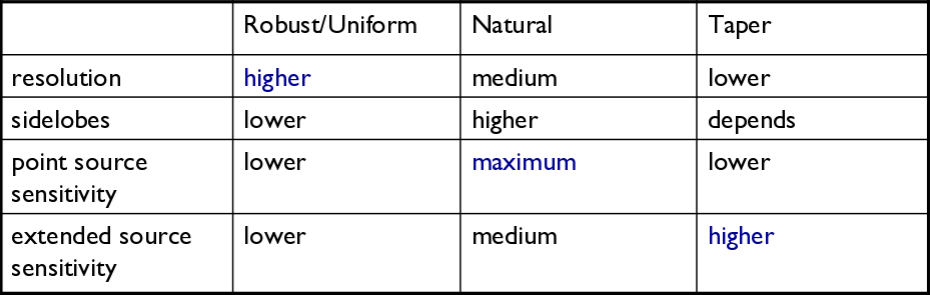
Table summarizing the effects of using weights and tapering.

Tapering: In conjunction with the above weighting schemes, one can specify the uvtaper parameter within clean, which will control the radial weighting of visibilities in the uv-plane. Figure 2 graphically visualizes the uv-coverage during the observing session. The taper in clean is an elliptical Gaussian function which effectively removes long baselines and degrades the resolution. This may be desirable for extended structures when long baselines contribute a large fraction of the noise. Tapering can, therefore, increase the surface brightness sensitivity of the data, but will decrease the point source sensitivity. Too aggressive tapering, however, may also take its toll on the surface brightness sensitivity.

We refer to the CASA Cookbook Synthesis Imaging chapter for the details of the weighting implementation in CASA's clean.


Primary and Synthesized Beam

The primary beam of a single antenna defines the sensitivity across the field of view. For the VLA antennas, the main beam can be approximated by a Gaussian with a FWHM equal to [math]\displaystyle{ 90*\lambda_{cm} }[/math] arcseconds, or [math]\displaystyle{ 45/ \nu_{GHz} }[/math] arcminutes. Note that there are sidelobes beyond the Gaussian kernel that are sensitive to bright sources (see below). Taking our observed frequency to be the middle of L-band, 1.5 GHz, our primary beam will be around 30 arcmin.

If your science goal is to image a source or field of view that is significantly larger than the FWHM of the VLA primary beam, then creating a mosaic from a number of pointings is usually the preferred method. For a tutorial on mosaicing, see the 3C391 tutorial. In the following, however, we will discuss methods to image large areas from single pointing data.

Since our data were taken in the D-configuration, we can check the Observational Status Summary section on VLA resolution to find that the synthesized beam will be around 46 arcsec. Flagging, weighting and the exact frequency, however, may result in deviations from this value. As we will see later, the synthesized beam of our data hovers around 29 arcsec and for the extreme of uniform weighting around 26"x25". Oversampling the minor axis by a factor of ~3, we will use a cell (pixel) size of 8 arcsec.

Our field contains bright point sources significantly outside the primary beam. The VLA, in particular when using multi-frequency synthesis (see below), will have significant sensitivity outside the main lobe of the primary beam. Particularly at the lower VLA frequencies, sources that are located outside the primary beam may still be bright enough to be detected with sufficient signal-to-noise in the primary beam sidelobes; which can cause artifacts to interfer with the targeted field in the main part of the primary beam. Such sources need to be cleaned to remove the dirty beam response of these interfering sources from the entire image. This can be done by either creating a very large image or by using outlier fields centered on the strongest sources (see section on outlier fields below). A large image has the added advantage of increasing the field of view for science, albeit at lower sensitivity. Other effects will start to become significant, however, like the non-coplanarity of the sky. Large image sizes will also slow down the deconvolution process. Details are provided in Sanjay Bhatnagar's presentation: "Advanced Imaging: Imaging in the Wide-band Wide-field era" given at the 2016 VLA data reduction workshop.

The calls to CLEAN within this guide will create images that are 170 arcminutes on a side ([Image Size * Cell Size]*[1arcmin / 60arsec]), or almost 6x the size of the primary beam, catching the first and second sidelobes. This is ideal for showcasing both the problems inherent in such wide-band, wide-field imaging, as well as some of the solutions currently available in CASA to deal with these issues.

Note that the execution time of clean depends on the image sizes. Large images generally take more computing time. There are some values, however, that are computationally not advisable. The logger output will then show a recommendation for the next larger but faster image size. As a rule of thumb we recommend image sizes 2n * 10 pixels (e.g., 160, 1280 pixels, etc.) for improved processing speeds.


Clean Output Images

As a result of the CLEAN algorithm, clean will create a number of output images. For an imagename='<imagename>', these outputs are:

<imagename>.residual: the residual after subtracting the clean model (unit: Jy/beam, where beam refers to the dirty beam).
<imagename>.model: the clean model, not convolved (unit: Jy/pixel).
<imagename>.psf: the point-spread function (dirty beam)
<imagename>.flux: the normalized sensitivity map. For single pointings this corresponds to the primary beam.
<imagename>.image: the residual + the model convolved with the clean beam. This is the final image (unit: Jy/beam, where beam refers to the clean beam).

Additional images will be created for specific algorithms like multi-term frequency synthesis or mosaicking.

Important: If an image file is present in the working directory and the same name is provided in imagename, clean will use that image&#151;in particular the residual and model image&#151;as a starting point for further cleaning. If you want a fresh run of clean, first remove all images of that name using 'rmtables()': 

# In CASA
rmtables('<imagename>.*')

This method is preferable over rm -rf as it also clears the cache.

Note that interrupting clean by Ctrl+C may corrupt your visibilities&#151;you may be better off choosing to let clean finish. We are currently implementing a command that will nicely exit to prevent this from happening but, for the moment, please try to avoid Ctrl+C.


Dirty Image

First, we will create a dirty image (Figure 3) to see the improvements as we step through several cleaning algorithms and parameters. The dirty image is the true image on the sky, convolved with the dirty beam (PSF). We will do this by running clean with parameter niter=0, which will not do any cleaning. 

# In CASA
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.dirty', 
      imsize=1280, cell='8arcsec', interactive=False, niter=0,  
      stokes='I', usescratch=F)
  • imagename='SNR_G55_10s.dirty': the root filename used for the various clean outputs.
  • imsize=1280: the image size in number of pixels. A single value will result in a square image.
  • cell='8arcsec': the size of one pixel; again, entering a single value will result in a square pixel size.
  • niter=0: this controls the number of iterations done in the minor cycle.
  • usescratch=F: controls writing the model visibilities to the model data column. For self-calibration we currently recommend setting usescratch=T.
  • stokes='I': since we have not done any polarization calibration, we only create a total-intensity image. For using CLEAN while including various Stoke's Parameters, please see the 3C391 CASA guide.
# In CASA
viewer('SNR_G55_10s.dirty.image')



# In CASA
viewer('SNR_G55_10s.dirty.psf')
Figure 3
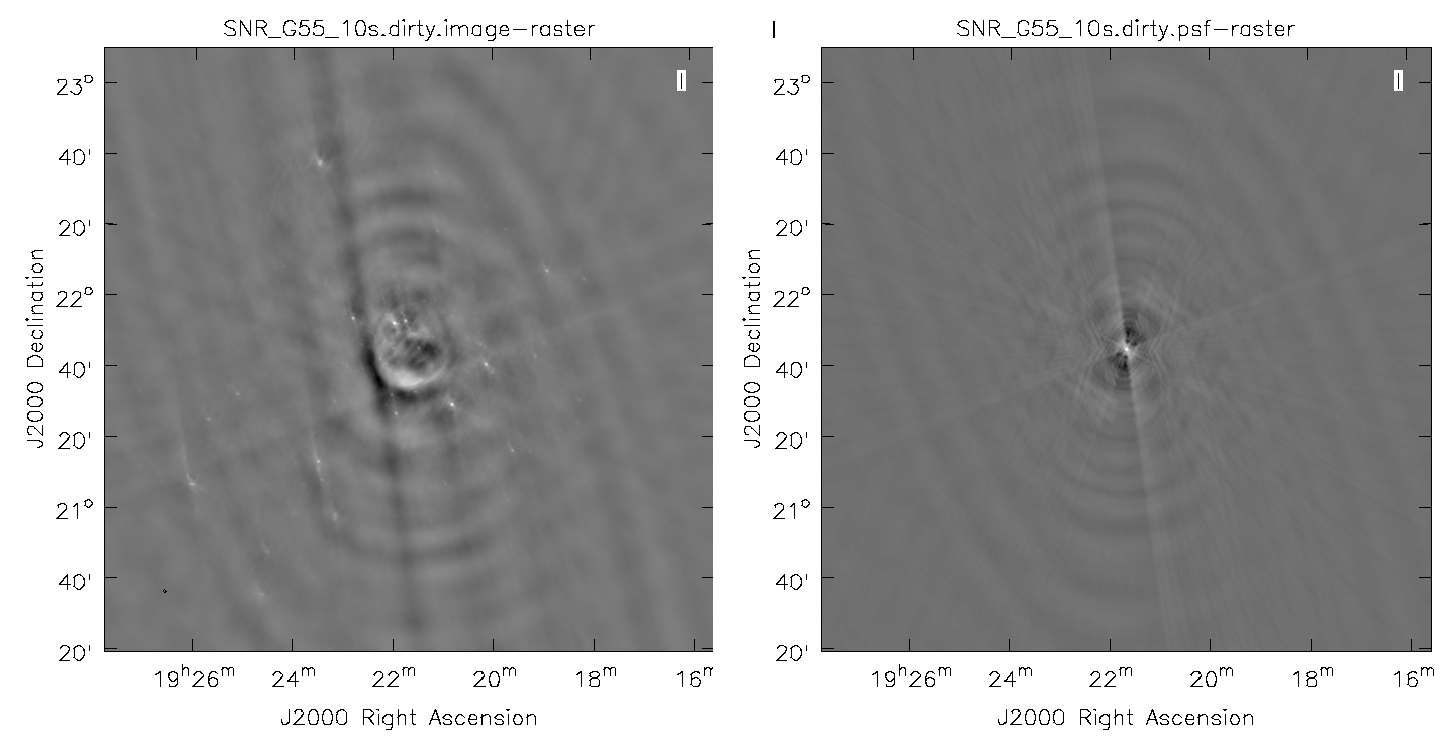
A dirty image of the supernova remnant G55.7+3.4 in greyscale, with apparent sidelobes (left), and the point spread function (PSF), also known as the dirty beam (right).

The images may be easier to see in grey scale. To do this, click on Data Display Options (wrench icon, upper left corner) within the viewer and change the color map to Greyscale 1. You may also have to change the scaling power options to your liking. To change the brightness and contrast, assign a mouse button to this type of editing by clicking on the Colormap fiddling button (black/white circle icon) and click/drag the mouse over the image to change the brightness (left-right mouse movement) and contrast (up-down mouse movement).

Note that the clean beam is only defined after some clean iterations. The dirty image has therefore no beam size specified in the header and the PSF image is the representation of the response of the array to a point source. Even though it is empty with no iterations specified, clean will still produce the model file. So a continuation into actual cleaning will be possible by just restarting clean with the same image root name (and parameter niter>0).


Regular CLEAN & RMS Noise

We will now create a regular clean image using mostly default values to see how deconvolution improves the image quality. The first run of clean will use a fixed number of minor cycle iterations of niter=1000 (default is 500), the second will have niter=10000. Note that you may have to play with the image color map and brightness/contrast to get a better view of the image details. 

# In CASA. Create default clean image.
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.Reg.Clean.niter1K', 
      imsize=1280, cell='8arcsec', niter=1000, interactive=False)



# In CASA.
viewer('SNR_G55_10s.Reg.Clean.niter1K.image')

The logger indicates that the image was obtained in two major cycles and some improvements over the dirty image are visible. But clearly we have not cleaned deep enough yet; the image still has many sidelobes, and an inspection of the residual image shows that it still contains source flux and structure. So let's increase the niter parameter value to 10,000 and compare the images (Figure 4). 

# In CASA. Create default clean image with niter = 10000
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.Reg.Clean.niter10K', 
      imsize=1280, cell='8arcsec', niter=10000, interactive=False)



# In CASA.
viewer('SNR_G55_10s.Reg.Clean.niter10K.image')
Figure 4
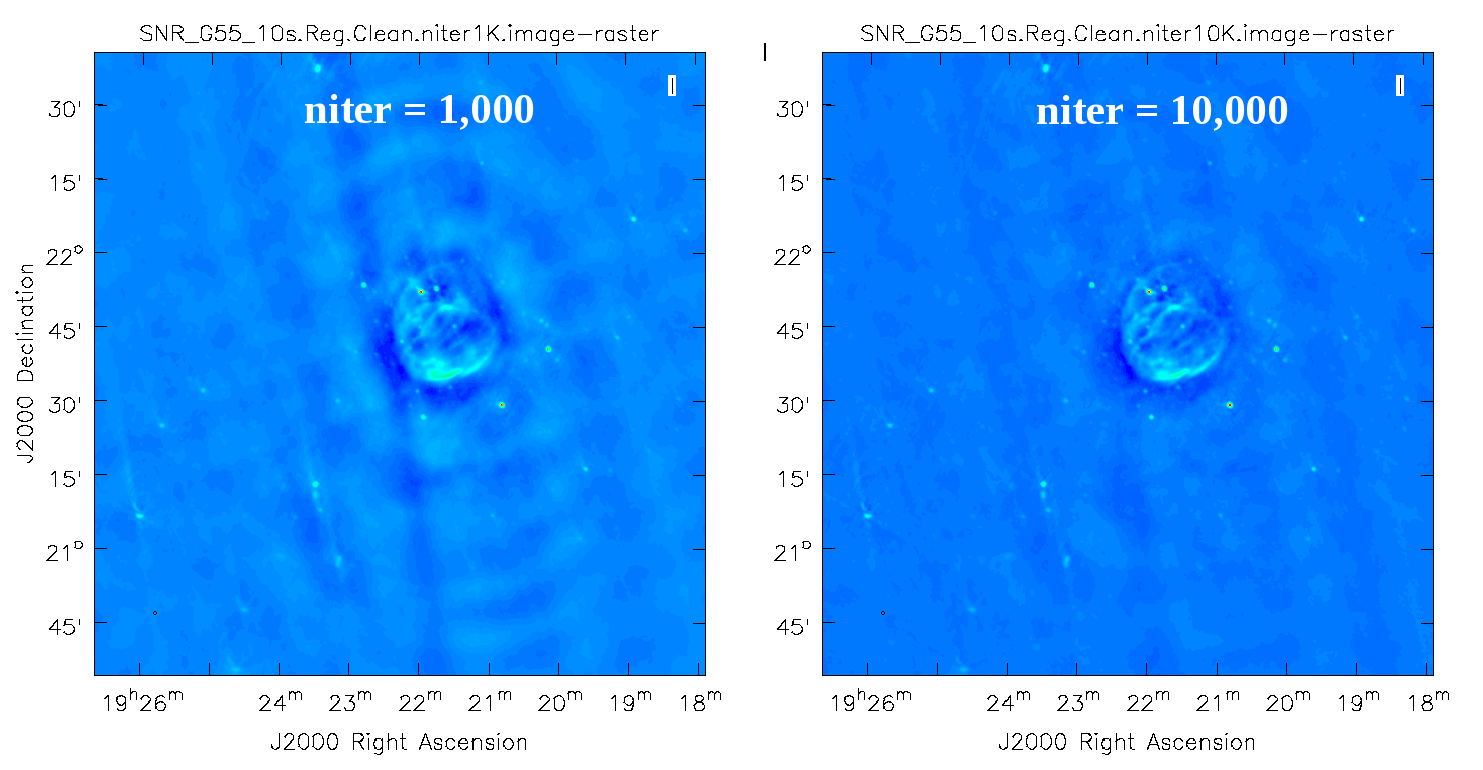
Regular run of CLEAN, with niter=1000 (left), compared to niter=10000 (right).

As we can see from the resulting images, increasing the niter values (minor cycles) improves our image by reducing prominent sidelobes significantly. One could now further increase the niter parameter until the residuals are down to an acceptable level. To determine the number of iterations, one needs to keep in mind that clean will fail once it starts cleaning too deeply into the noise. At that point, the cleaned flux and the peak residual flux values will start to oscillate as the number of iterations increase. This effect can be monitored on the CASA logger output. To avoid cleaning too deeply, we will set a threshold parameter that will stop minor cycle clean iterations once a peak residual value is being reached.

First, we will utilize the SNR_G55_10s.Reg.Clean.niter1K.image image to give us an idea of the rms noise (your sigma value)(Figure 5). With this image open within the viewer, click on the Rectangle Drawing button (Rectangle with R) and draw a square on the image at a position with little source or sidelobe contamination. Doing this should open up a Regions dock which holds information about the selected region, including the pixel statistics in the Statistics tab (double clicking on the box will also bring up this information). Take notice of the rms values as you click/drag the box around empty image locations, or by drawing additional boxes at suitable positions. If the Regions dock is not displayed, click on View in the menu bar at the top of the viewer and click on the Regions check-box.

Figure 5
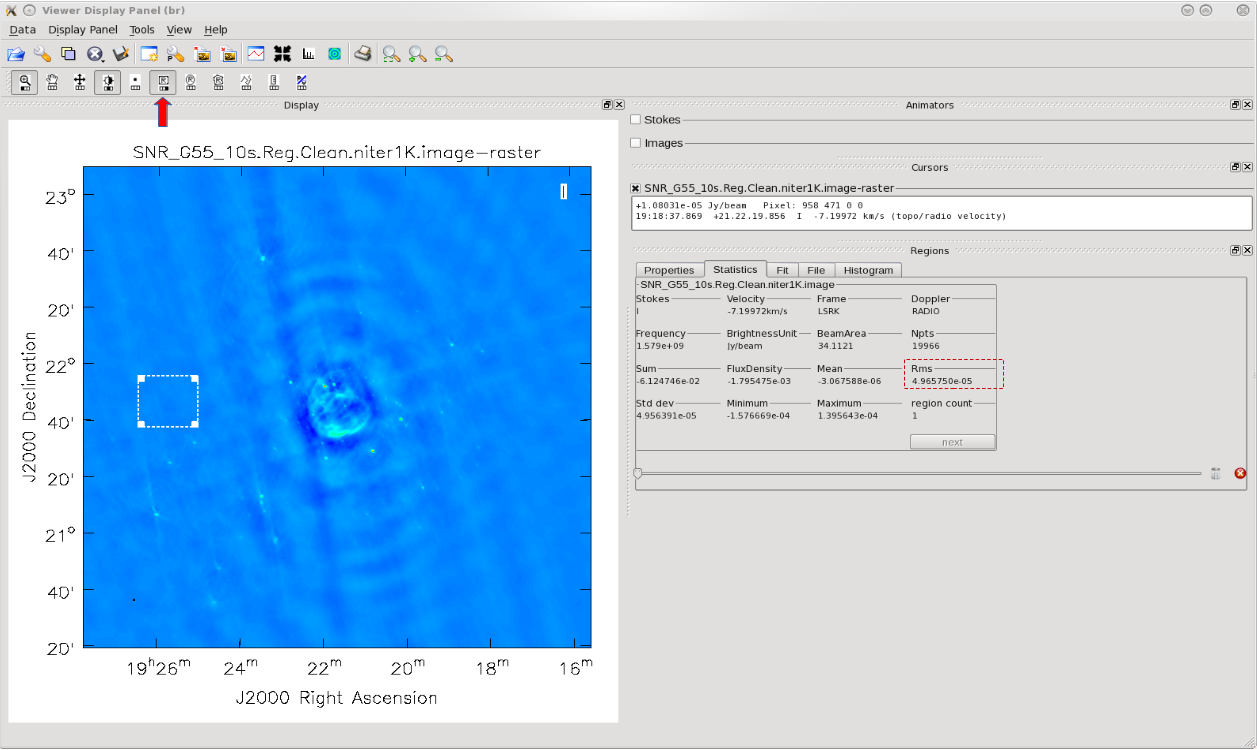
Attempting to find the lowest rms value within the CLEAN'ed image using niter=1000, in order to calculate our threshold.

The lowest rms value we found was in the order of about 4 x 10-5 Jy/beam, which we will use to calculate our threshold. There really is no set standard, but fairly good threshold values can vary anywhere between 2.0&#150;4.0*sigma; using clean boxes (see the section on interactive cleaning) allows one to go to lower thresholds. For our purposes, we will choose a threshold of 2.5*sigma. Doing the math results in a value of 10 x 10-5 or, equivalently, 0.10mJy/beam. Therefore, for future calls to the clean task, we will set parameter threshold='0.1mJy'. The clean cycle will be stopped when the residual peak flux density is either equal to or less than the threshold value or when the maximum number of iterations niter is reached. To ensure that the stopping criterion is indeed the parameter threshold, parameter niter should be set to a very high number.

In the following, we nevertheless will use niter=1000 to keep the execution times of clean on the low end as we focus on explaining different imaging methods.

An alternative method to determine the approximate rms of an image is to use the VLA Exposure Calculator and to enter the observing conditions. Make sure that the chosen bandwidth reflects the data after RFI excision.


CLEAN with Weights

To see the effects of using different weighting schemes to the image, let's change the weighting parameter within clean and inspect the resulting images. We will be using the Natural, Uniform, and Briggs weighting algorithms. Here, we have chosen a smaller image size to mainly focus on our science target. 

# In CASA. Natural weighting
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.natural', weighting='natural',
      imsize=540, cell='8arcsec', niter=1000, interactive=False, threshold='0.1mJy')
  • weighting: specification of the weighting scheme. For Briggs weighting, the robust parameter will be used.
  • threshold='0.1mJy': threshold at which the cleaning process will halt.
# In CASA. Uniform weighting
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.uniform', weighting='uniform',
      imsize=540, cell='8arcsec', niter=1000, interactive=False, threshold='0.1mJy')



# In CASA. Briggs weighting, with robust set to default of 0.0
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.briggs', weighting='briggs',
      robust=0, imsize=540, cell='8arcsec', niter=1000, interactive=False, threshold='0.1mJy')



# In CASA. Open the viewer and select the created images.
viewer()
Figure 6
CLEAN images created with different weighting algorithms, including natural (left), uniform (center), and briggs (right).

Figure 6 shows that the natural weighted image is most sensitive to extended emission (beam size of 46"x41"). The negative values around the extended emission, often referred to as a negative bowl, is a typical signature of unsampled visibilities near the origin of the uv-plane. That is, the flux density present at shorter baselines, or larger angular scales than measured in this observation, is not well represented. Uniform weighted data shows the highest resolution (26"x25") and Briggs parameter robust=0 (default value) is a compromise with a beam of 29"x29". To image more of the extended emission, the robust parameter could be tweaked further toward more positive values.


Multi-Scale CLEAN

Since G55.7+3.4 is an extended source with many angular scales, a more advanced form of imaging involves the use of multiple scales. MS-CLEAN is an extension of the classical CLEAN algorithm for handling extended sources. Multi-Scale CLEAN works by assuming the sky is composed of emission at different angular scales and works on them simultaneously, thereby creating a linear combination of images at different angular scales. For a more detailed description of Multi-Scale CLEAN, see T.J. Cornwell's paper Multi-Scale CLEAN deconvolution of radio synthesis images.

We will use a set of scales&#151;expressed in units of the requested pixel or cell size&#151;which are representative of the scales that are present in the data, including a zero-scale for point sources. 

# In CASA
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.MultiScale', 
      imsize=1280, cell='8arcsec', multiscale=[0,6,10,30,60], smallscalebias=0.9, 
      interactive=False, niter=1000,  weighting='briggs', stokes='I', 
      threshold='0.1mJy', usescratch=F, imagermode='csclean')
  • multiscale=[0,6,10,30,60]: a set of scales on which to clean. A good rule of thumb when using multiscale is 0, 2xbeam, 5xbeam (where beam is the synthesized beam), and larger scales up to about half the minor axis maximum scale of the mapped structure. Since these are in units of the pixel size, our chosen values will be multiplied by the requested cell size. Thus, we are requesting scales of 0 (a point source), 48, 80, 240, and 480 arcseconds (8 arcminutes). Note that 16 arcminutes (960 arcseconds) roughly corresponds to the size of G55.7+3.4.
  • smallscalebias=0.9: This parameter is known as the small scale bias, and helps with faint extended structure, by balancing the weight given to smaller structures, which tend to have higher surface brightness but lower integrated flux density. Increasing this value gives more weight to smaller scales. A value of 1.0 weights the largest scale to zero, and a value of less than 0.2 weighs all scales nearly equally. The default value is 0.6.
# In CASA
viewer('SNR_G55_10s.MultiScale.image')

The logger will show how much cleaning is performed on the individual scales.

This is the fastest of the imaging techniques described here, but it's easy to see that there are artifacts in the resulting image (Figure 7). We can use the viewer to explore the point sources near the edge of the field by zooming in on them (Figure 8). Click on the Zoom button on the upper left corner and highlight an area by making a square around the portion where you would like to zoom in. Double clicking within the square will zoom in the selected area. The square can be resized by clicking/dragging the corners, or removed by pressing the Esc key. After zooming in, we can see some radio sources have prominent arcs as well as spots with a six-pointed pattern surrounding them.

Figure 7
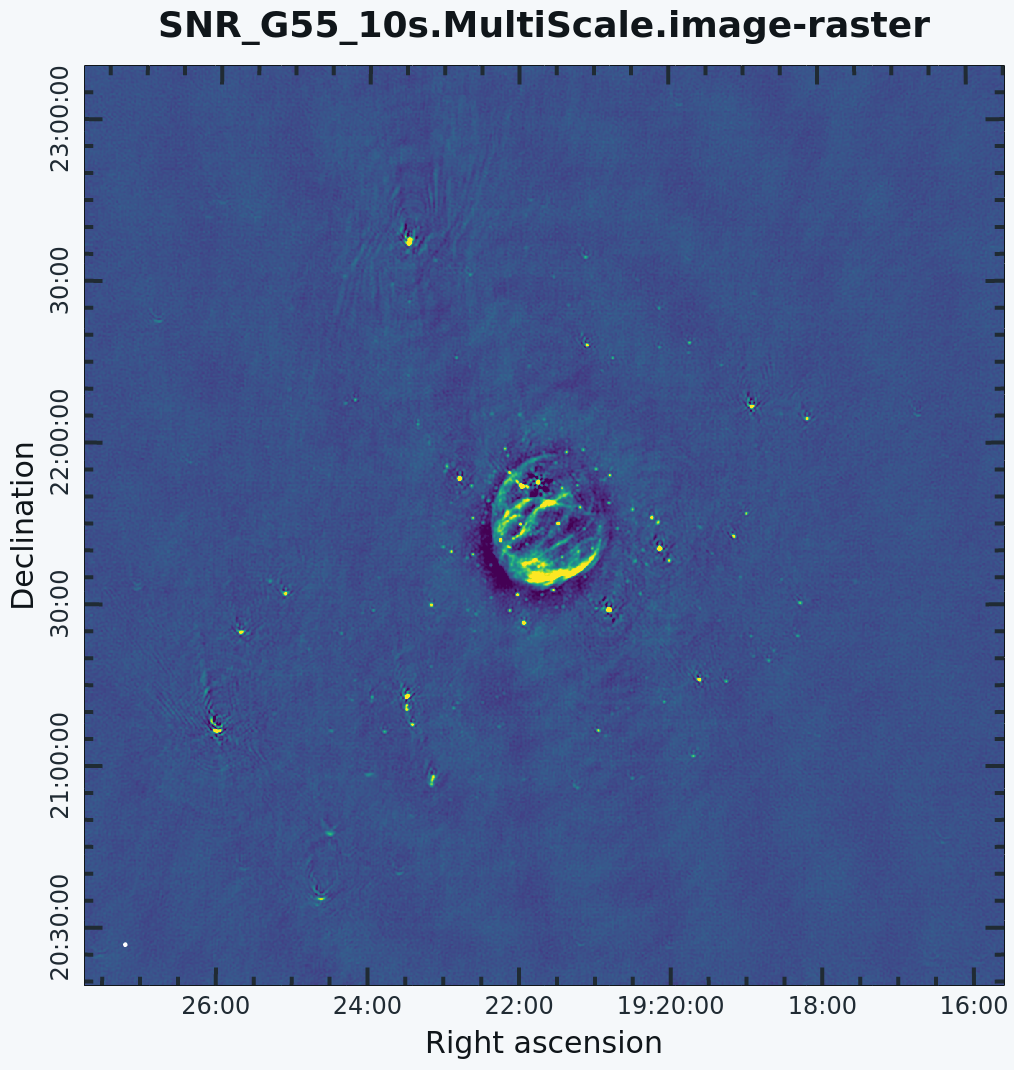G55.7+3.4 Multi-Scale Clean
Figure 8
Artifacts around point sources

Next we will explore some more advanced imaging techniques to mitigate the artifacts seen towards the edges of the image.


Multi-Scale, Wide-Field CLEAN (w-projection)

Figure 9
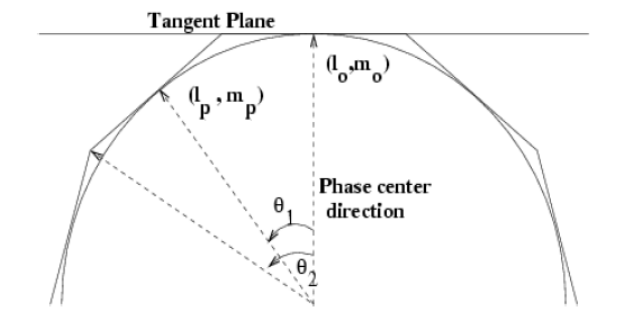
Faceting when using wide-field gridmode, which can be used in conjunction with w-projection.
Figure 10
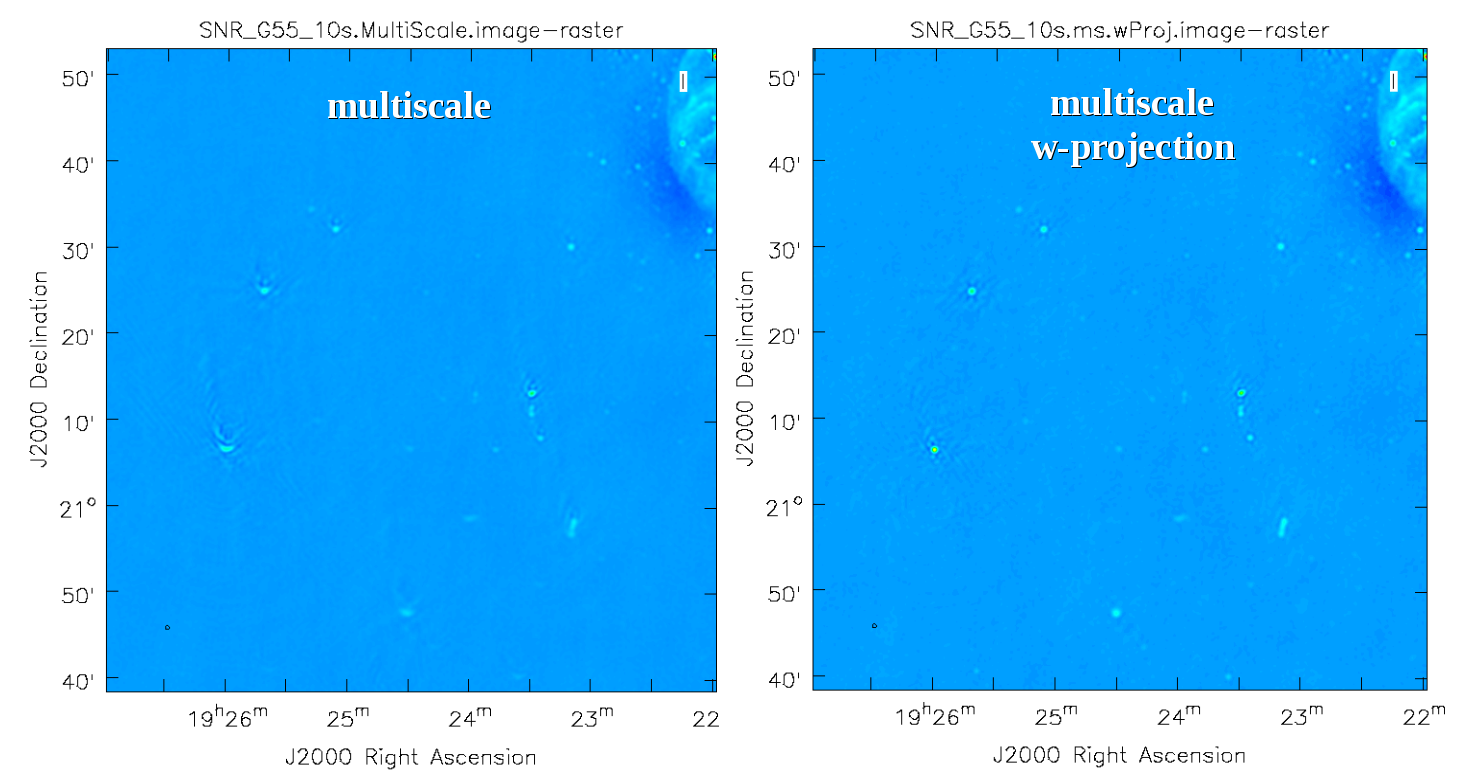
Multi-Scale image of arcs around point sources far from the phase center, versus MS with w-projection (right). We can see the that combining the w-projection algorithm with the multiscale algorithm improves the resulting image by removing prominent artifacts.

The next clean algorithm we will employ is w-projection, which is a wide-field imaging technique that takes into account the non-coplanarity of the baselines as a function of distance from the phase center (Figure 9). For wide-field imaging, the sky curvature and non-coplanar baselines result in a non-zero w-term. The w-term, introduced by the sky and array non-coplanarity, introduces a phase term that will limit the dynamic range of the resulting image. Applying 2-D imaging to such data will result in artifacts around sources away from the phase center, as we saw in running MS-CLEAN. Note that this affects mostly the lower frequency bands where the field of view is large.

The w-term can be corrected by faceting (which describes the sky curvature by many smaller planes) in either the image or uv-plane. The latter is known as w-projection. A combination of the two can also be employed within clean by setting the parameter gridmode='widefield'. If w-projection is employed, it will be done for each facet. Note that w-projection is an order of magnitude faster than the image-plane based faceting algorithm, but will require more memory.

For more details on w-projection, as well as the algorithm itself, see "The Noncoplanar Baselines Effect in Radio Interferometry: The w-projection Algorithm". Also, the chapter on Imaging with Non-Coplanar Arrays may be helpful. 

# In CASA
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.ms.wProj',
      gridmode='widefield', imsize=1280, cell='8arcsec',
      wprojplanes=-1, multiscale=[0,6,10,30,60], 
      interactive=False, niter=1000,  weighting='briggs',
      stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')
  • gridmode='widefield': Use the w-projection algorithm.
  • wprojplanes=-1: The number of w-projection planes to use for deconvolution. Setting to -1 forces CLEAN to utilize an acceptable number of planes for the given data.
# In CASA
viewer('SNR_G55_10s.ms.wProj.image')

This will take slightly longer than the previous imaging round; however, the resulting image (Figure 10) has noticeably fewer artifacts. In particular, compare the same outlier source in the Multi-Scale w-projected image with the Multi-Scale-only image: note that the swept-back arcs have disappeared. There are still some obvious imaging artifacts remaining, though.


Multi-Scale Multi-Term Frequency Synthesis

Figure 11
Multi-Frequency Synthesis snapshot of (u,v) coverage. We can see from the image on the right, using this algorithm can greatly improve coverage, thereby improving image fidelity.
Figure 12
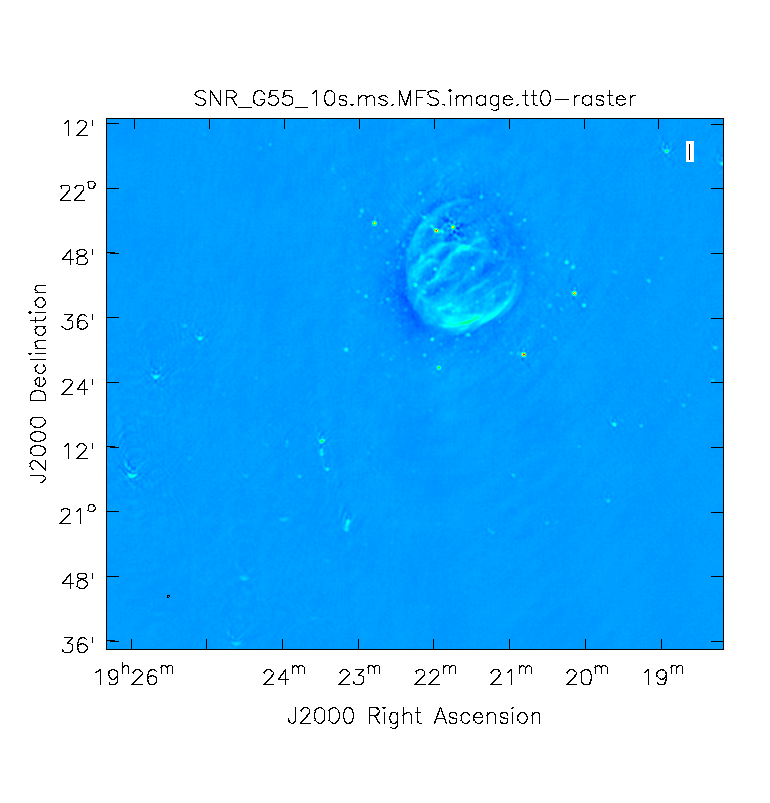
Multi-Scale imaged with MS-MFS and nterms=2. Artifacts around point sources close to phase center are reduced while point sources away from the phase center still show artifacts.
Figure 13
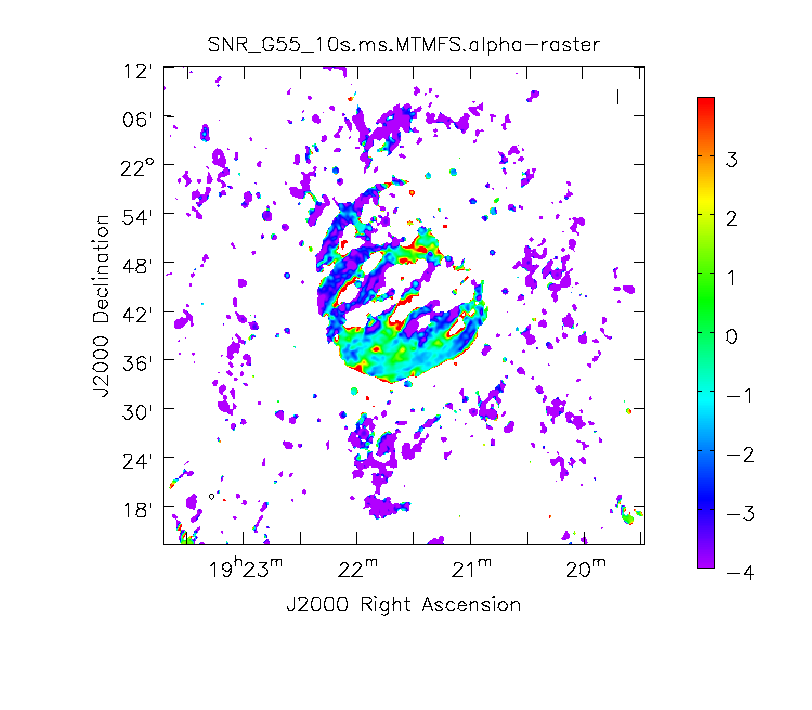
Spectral Index image

A consequence of simultaneously imaging the wide fractional bandwidths available with the VLA is that the primary and synthesized beams have substantial frequency-dependent variation over the observing band. If this variation is not accounted for, it will lead to imaging artifacts and compromise the achievable image rms.

The coordinates of the (u,v) plane are measured in wavelengths. Observing at several frequencies results in a baseline sampling several ellipses of different sizes in the (u,v) plane. By using a method called Multi-Frequency Synthesis (MFS), which is the default cleaning mode in CLEAN, we can fill in the gaps in the single frequency (u,v) coverage to achieve much better image fidelity (Figure 11).

When observing in low-frequencies, it may prove beneficial to observe in short segments which are spread out in time. This will allow the coverage of more spatial-frequencies, permitting us to employ this algorithm more efficiently.

The Multi-Scale Multi-Term Frequency Synthesis algorithm provides the ability to simultaneously image and fit for the intrinsic source spectrum in each pixel. The spectrum is approximated using a polynomial Taylor-term expansion in frequency, with the degree of the polynomial as a user-controlled parameter. A least-squares approach is used, along with the standard clean-type iterations.

For a more detailed explanation of the MS-MFS deconvolution algorithm, please see the paper A multi-scale multi-frequency deconvolution algorithm for synthesis imaging in radio interferometry 

# In CASA
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.ms.MFS',
      imsize=1280, cell='8arcsec', mode='mfs', nterms=2,
      multiscale=[0,6,10,30,60], 
      interactive=False, niter=1000,  weighting='briggs',
      stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')
  • nterms=2: the number of Taylor-terms to be used to model the frequency dependence of the sky emission. Note that the speed of the algorithm will depend on the value used here (more terms will be slower); nterms=2 will fit a spectral index, and nterms=3 a spectral index and curvature.

When clean is done <imagename>.image.tt0 will contain a total intensity image (Figure 12), where tt* is a suffix to indicate the Taylor term: <imagename>.image.tt0 is the total intensity image and <imagename>.image.alpha will contain an image of the spectral index in regions where there is sufficient signal-to-noise (Figure 13). Having this spectral index image can help convey information about the emission mechanism involved within the supernova remnant. This spectral index can also give information on the optical depth of the source. 

# In CASA
viewer('SNR_G55_10s.ms.MFS.image.tt0')



# In CASA
viewer('SNR_G55_10s.ms.MFS.image.alpha')

Note: To replicate Figure 13, open the image within the viewer, click on Panel Display Options (wrench with a small P), change background color to white, and adjust your margins under the Margins button. To view the color wedge, click on the Data Display Options (wrench without the P, next to the folder icon), click on the Color Wedge button, click on Yes under display color wedge and adjust the various parameters to your liking.

For more information on the multi-term, multi-frequency synthesis mode and its outputs, see section 5.2.5.1 in the CASA cookbook.

Inspect the brighter point sources in the field near the supernova remnant. You will notice that some of the artifacts, which had been symmetric around the sources themselves, are now gone. Since we did not use w-projection, however, there are still strong features related to the non-coplanar baseline effects still apparent for sources further away.

At this point, clean takes into account the frequency variation of the synthesized beam but not the frequency variation of the primary beam. For low frequencies and large bandwidths, this can be substantial, e.g., 1&#150;2 GHz L-band observations result in a variation of a factor of 2. One effect of such a large fractional bandwidth is that in multi-frequency synthesis, primary beam nulls will be blurred and the interferometer is sensitive everywhere in the field of view. For spectral slopes, however, a frequency-dependent primary beam causes a steepening as the higher frequencies are less sensitive at a given point away from the phase center. A correction for this effect should be made with the task widebandpbcor (see section on Primary Beam Correction below).


Multi-Scale Multi-Term Frequency, Widefield CLEAN

We will now combine the w-projection and MS-MFS algorithms. Be forewarned&#151;these imaging runs will take a while, and it's best to start them running and then move on to other things.

Using the same parameters for the individual-algorithm images above, but combined into a single clean run, we have: 

# In CASA
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.ms.MFS.wProj',
      gridmode='widefield', imsize=1280, cell='8arcsec', mode='mfs',
      nterms=2, wprojplanes=-1, multiscale=[0,6,10,30,60],  
      interactive=False, niter=1000,  weighting='briggs',
      stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')



# In CASA
viewer('SNR_G55_10s.ms.MFS.wProj.image.tt0')



# In CASA
viewer('SNR_G55_10s.ms.MFS.wProj.image.alpha')
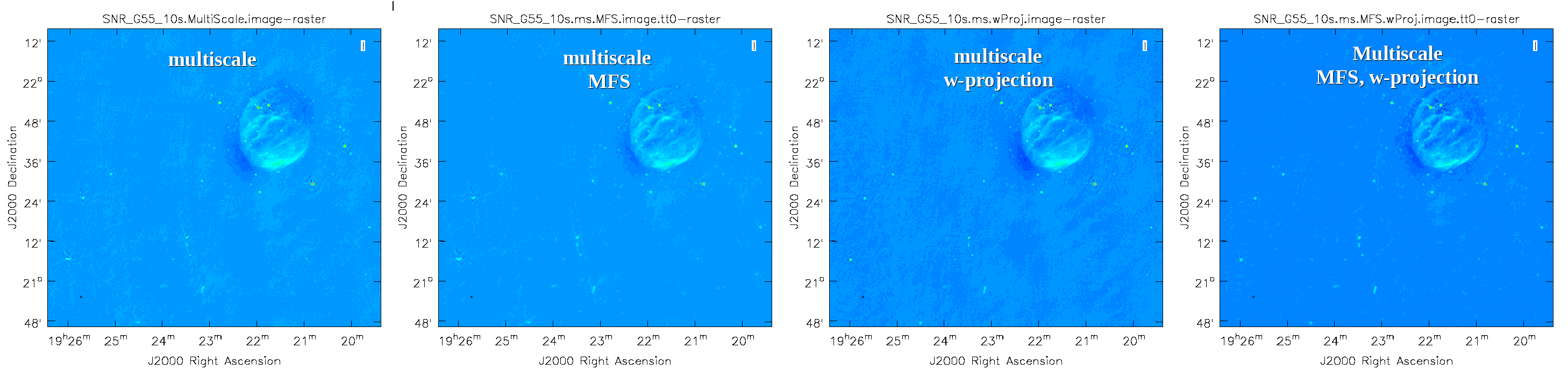
Figure 14 Here we see the differences as the images progress through the different algorithms used: MS → MS-MFS → MS-wProjection → MS-MFS-wProjection.

Again, looking at the same outlier source, we can see that the major sources of error have been removed, although there are still some residual artifacts (Figure 14). One possible source of error is the time-dependent variation of the primary beam; another is the fact that we have only used nterms=2, which may not be sufficient to model the spectra of some of the point sources. Some weak RFI may also show up that may need additional flagging.


Imaging Outlier Fields

When strong sources are far from the main target, but still strong enough to produce sidelobes in the main image, they should be cleaned. Sometimes, however, it is not practical to image very large fields for this purpose. An alternative is to use outlier fields. This mode will allow the user to specify a few locations that are then cleaned along with the main image. The outlier fields should be centered on strong sources that are known from sky catalogs or are identified by other means.

In order to find outlying sources, it will help to image a large field with lower resolution and identify them within the CASA viewer. By moving the mouse cursor over the sources, we can grab their positions and use the information within an outlier file. In this example, we've called our file outliers.txt. It contains the names, sizes, and positions of the outliers we want to image (see section 5.3.18.1 of the CASA cookbook).

Open your favorite text editor and input the following: 

#content of outliers.txt
#
#outlier field1
imagename= 'Outlier1.MS.MFS'
imsize=[512,512]
phasecenter = 'J2000 19h23m27.693 22d37m37.180'
#
#outlier field2
imagename='Outlier2.MS.MFS'
imsize=[512,512]
phasecenter = 'J2000 19h25m46.888 21d22m03.365'

clean will then be executed like the following: 

# In CASA
clean(vis='SNR_G55_10s.calib.ms', imagename='SNR.MS.MFS-Main',
      outlierfile='outliers.txt',
      imsize=[512,512], cell='8arcsec', mode='mfs',
      multiscale=[0,6,10,30,60], interactive=False, niter=1000,  weighting='briggs',
      robust=0, stokes='I', threshold='0.1mJy', usescratch=F, imagermode='csclean')
  • outlierfile='outliers.txt': the name of the outlier file.

We can view the images with viewer one at a time. Due to the difference in sky coordinates, they cannot be viewed on the same window display. 

# In CASA
viewer('SNR.MS.MFS-Main.image')



# In CASA
viewer('Outlier1.MS.MFS.image')



# In CASA
viewer('Outlier2.MS.MFS.image')

We have changed the color map to Hot Metal 2 in order to show the different colors that can be used within the viewer. Feel free to play with other color maps that may be better suited for your screen.

Figure 15
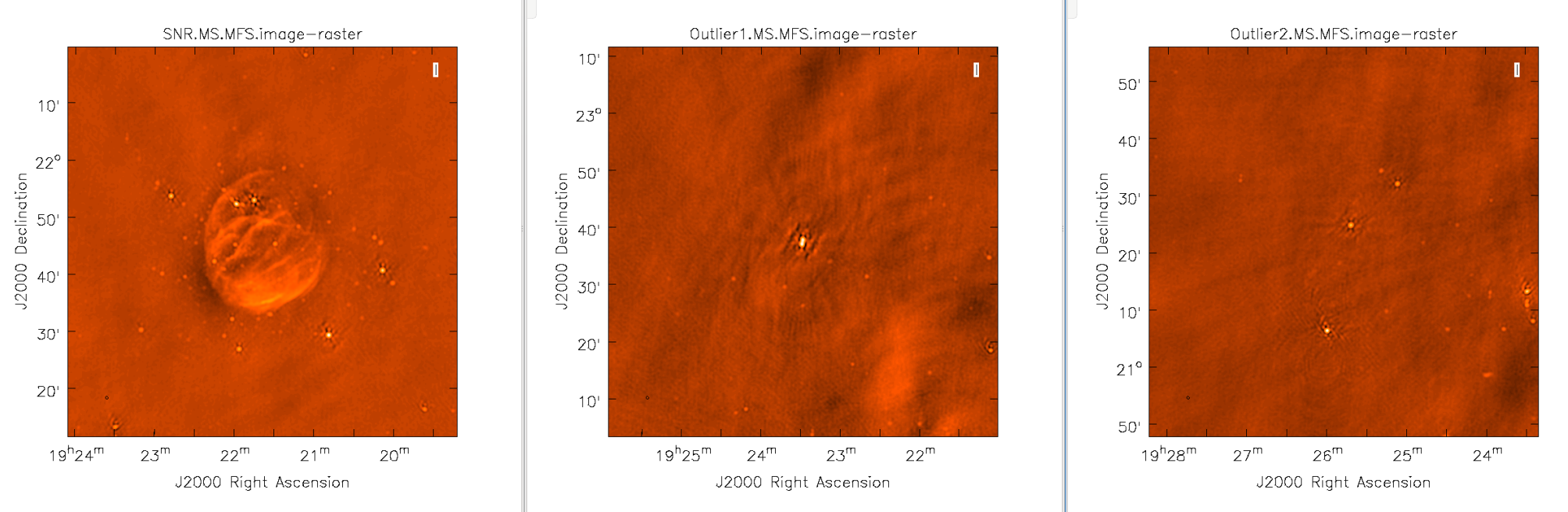
Images of the supernova remnant and bright sources far from the phase center (near the edge of, or beyond, the primary beam.)


Primary Beam Correction

In interferometry, the images formed via deconvolution are representations of the sky multiplied by the primary beam response of the antenna. The primary beam can be described as Gaussian with a size depending on the observing frequency. Images produced via clean are by default not corrected for the primary beam pattern (important for mosaics), and therefore do not have the correct flux density away from the phase center.

Correcting for the primary beam, however, can be done during clean by using the parameter pbcor. Alternatively, it can be done after imaging using the task impbcor for regular data sets and widebandpbcor for those that use Taylor-term expansion (nterms > 1). A third alternative is utilizing the task immath to manually divide the <imagename>.image by the <imagename>.flux image (<imagename>.flux.pbcoverage for mosaics).

Flux corrected images usually don't look pretty due to the noise at the edges being increased. Flux densities, however, should only be calculated from primary beam corrected images. Let's run the impbcor task to correct our multiscale image. 

# In CASA
impbcor(imagename='SNR_G55_10s.MultiScale.image', pbimage='SNR_G55_10s.MultiScale.flux', 
        outfile='SNR_G55_10s.MS.pbcorr.image')
  • imagename: the image to be corrected
  • pbimage: the <imagename>.flux image as a representation of the primary beam (<imagename>.flux.pbcoverage for mosaics)
# In CASA
viewer('SNR_G55_10s.MS.pbcorr.image')

Let us now use the widebandpbcor task for wide-band (nterms>1) images. Note that for this task, we will be supplying the image name that is the prefix for the Taylor expansion images, tt0 and tt1, which must be on disk. Such files were created during the last Multi-Scale, Multi-Frequency, Widefield run of CLEAN. Task widebandpbcor will generate a set of images with a pbcor.image extension.

Figure 16
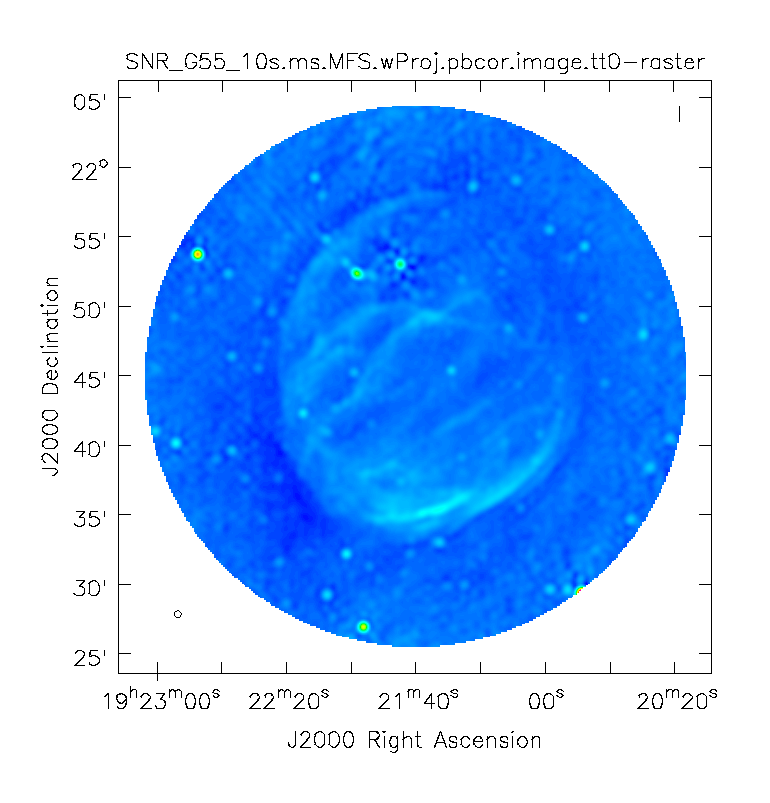
Primary beam corrected image using the widebandpbcor task for the MS.MFS.wProj image created during the CLEAN process.
Figure 17
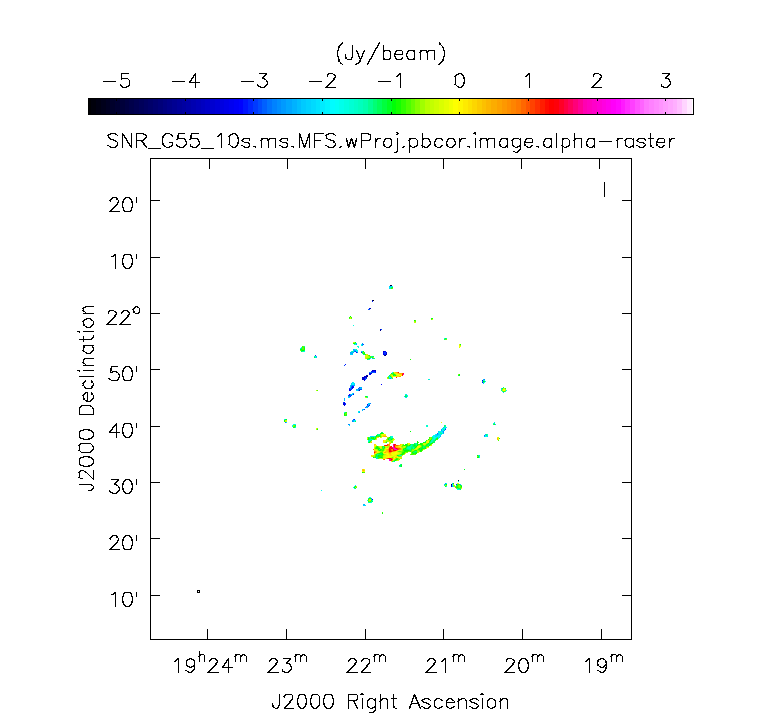
Primary beam corrected spectral index image using the widebandpbcor task.
# In CASA
widebandpbcor(vis='SNR_G55_10s.calib.ms', imagename='SNR_G55_10s.ms.MFS.wProj', 
              nterms=2, action='pbcor', pbmin=0.2, spwlist=[0,1,2,3],
              weightlist=[0.5,1.0,0,1.0], chanlist=[25,25,25,25], threshold='0.6mJy')

Note that the spectral index image (<imagename>.alpha) will have units in Jy/beam, which is not correct. The software bug has been fixed in CASA 4.6.

  • spwlist=[0,1,2,3]: We want to apply this correction to all spectral windows in our calibrated measurement set.
  • weightlist=[0.5,1.0,0,1.0]: Since we did not specify reference frequencies during clean, the widebandpbcor task will pick them from the provided image. Running the task, the logger reports the multiple frequencies used for the primary beam, which are 1.256, 1.429, 1.602, and 1.775 GHz. Having created an amplitude vs. frequency plot of the calibrated measurement set with colorized spectral windows using plotms, we note that the first chosen frequency lies within spectral window 0, which we know had flagged data due to RFI being present. This parameter weightlist allows us to give this chosen frequency less weight. The primary beam at 1.6 GHz lies in an area with no data, therefore we will give a weight value of zero for this frequency. The remaining frequencies 1.429 and 1.775 GHz lie within spectral windows which contained less RFI, therefore we provide a larger weight percentage.
  • pbmin=0.2: Gain level below which not to compute Taylor-coefficients or apply a primary beam correction.
  • chanlist=[25,25,25,25]: Make primary beams at frequencies corresponding to channel 25.
  • threshold='0.6mJy': Threshold in the intensity map, below which not to recalculate the spectral index. We adjusted the threshold to get good results: too high of a threshold resulted in errors and no spectral index image, too low of a threshold resulted in spurious values for the spectral index image.
# In CASA
viewer('SNR_G55_10s.ms.MFS.wProj.pbcor.image.tt0')



# In CASA
viewer('SNR_G55_10s.ms.MFS.wProj.pbcor.image.alpha')

It's important to note that the image will cut off at about 20% of the HPBW, as we are confident of the accuracy within this percentage. Anything outside becomes less accurate, thus there is a mask associated with the creation of the corrected primary beam image (Figure 16). Spectral indices may still be unreliable below approximately 70% of the primary beam HPBW (Figure 17).

It would be a good exercise to use the viewer to plot both the primary beam corrected image, and the original cleaned image and compare the intensity (Jy/beam) values, which should differ slightly.


Imaging Spectral Cubes

For spectral line imaging, CASA clean can be used in either mode='frequency' or mode='velocity'. Both modes will create a spectral axis in frequency, while the velocity mode adds an additional velocity label.

The following keywords are important for spectral modes (velocity in this example): 

# In CASA
mode                = 'velocity'        #  Spectral gridding type (mfs, channel, velocity, frequency)
     nchan          =         -1        #  Number of channels (planes) in output image; -1 = all
     start          =         ''        #  Velocity of first channel: e.g '0.0km/s'(''=first channel in first SpW of MS)
     width          =         ''        #  Channel width e.g '-1.0km/s' (''=width of first channel in first SpW of MS)
<snip>
     outframe       =         ''        #  spectral reference frame of output image; '' =input
     veltype        =    'radio'        #  Velocity definition of output image

<snip>
restfreq            =         ''        #  Rest frequency to assign to image (see help)

The spectral dimension of the output cube will be defined by these parameters and clean will regrid the visibilities to the cube. Note that invoking cvel before imaging is, in most cases, not necessary even when two or more measurement sets are being provided at the same time.

The cube is specified by a start velocity in km/s, the nchan number of channels, and a channel width (where the latter can also be negative for decreasing velocity cubes).

To correct for Doppler effects, clean also requires a outframe velocity frame where LSRK (Local Standard of Rest (kinematic)) and BARY (Sun-Earth Barycenter) are the most popular references. Parameter veltype defines whether the data will be gridded via the optical or radio velocity definition. A description of the available options and definitions can be found in the VLA observing guide and the CASA cookbook. By default, clean will produce a cube using the LRSK and radio definitions.

Note that clean will always work on the entire cube when searching for the highest residual fluxes in the minor cycle. To do this per channel, one can set parameter chaniter=T.

CASA also offers parameter mode='channel'. But we do not recommend this mode as the VLA does not observe with Doppler tracking. The fixed frequency observing of the VLA means that spectral features will drift in sky frequency over time. The Doppler correction will then be applied by clean via parameter mode='velocity' or 'frequency' . Parameter mode='channel' will perform the correction only using the first timestamp in the observations. It can also be confusing when imaging some shifted, but overlapping, spectral windows.

An example of spectral line imaging procedures is provided in the VLA high frequency Spectral Line tutorial - IRC+10216.


Beam per Plane

For spectral cubes spanning relatively wide ranges in frequency, the synthesized beam can vary substantially across the channels. To account for this, CASA will calculate separate beams for each channel when the difference is more than half a pixel across the cube. All CASA image analysis tasks are capable of handling such cubes.

If it is desired to have a cube with a single synthesized beam, two options are available. Best is to use imsmooth with parameter kernel='commonbeam'. This task will smooth each plane to that of the lowest resolution and it will clean up all header variables such that only a single beam appears in the data. The second option is to define parameter resmooth=T directly in clean.


Image Header

The image header holds metadata associated with your CASA image. The task imhead will display this data within the casalog. We will first run imhead with parameter mode='summary' : 

# In CASA
imhead(imagename='SNR_G55_10s.ms.MFS.wProj.image.tt0', mode='summary')
  • mode='summary' : gives general information about the image, including the object name, sky coordinates, image units, the telescope the data was taken with, and more.

For further information, run parameter mode='list' . We will assign a variable header to also capture the output as a Python dictionary: 

# In CASA
header=imhead(imagename='SNR_G55_10s.ms.MFS.wProj.image.tt0', mode='list')
  • mode='list' : gives more detailed information, including beam major/minor axes, beam primary angle, and the location of the max/min intensity, and lots more. Essentially this mode displays the FITS header variables.


Image Conversion

Finally, as an example, we convert our image from intensity to main beam brightness temperature.

We will use the standard equation

[math]\displaystyle{ T=1.222\times 10^{6} \frac{S}{\nu^{2} \theta_{maj} \theta_{min}} }[/math]

where the main beam brightness temperature [math]\displaystyle{ T }[/math] is given in K, the intensity [math]\displaystyle{ S }[/math] in Jy/beam, the reference frequency [math]\displaystyle{ \nu }[/math] in GHz, and the major and minor beam sizes [math]\displaystyle{ \theta }[/math] in arcseconds.

For a beam of 29.30"x29.03" and a reference frequency of 1.579 GHz (as taken from the previous imhead run) we calculate the brightness temperature using immath: 

# In CASA
immath(imagename='SNR_G55_10s.ms.MFS.wProj.image.tt0', mode='evalexpr', 
       expr='1.222e6*IM0/1.579^2/(29.30*29.03)', 
       outfile='SNR_G55_10s.ms.MFS.wProj.image.tt0-Tb')
  • mode='evalexpr' : immath is used to calcuate with images
  • expr: the mathematical expression to be evaluated. The images are abbreviated as IM0, IM1, ... in the sequence of their appearance in the imagename parameter.

Since immath only changes the values and not the unit of the image, we will now change the new image header 'bunit' key to 'K'. To do so, we will run imhead with parameter mode='put' : 

# In CASA
imhead(imagename='SNR_G55_10s.ms.MFS.wProj.image.tt0-Tb', mode='put', hdkey='bunit', hdvalue='K')
  • hdkey: the header keyword that will be changed
  • hdvalue: the new value for header keyword

Launching the viewer will now show our image in brightness temperature units: 

# In CASA
viewer('SNR_G55_10s.ms.MFS.wProj.image.tt0-Tb')


↵ CASAguides

Last checked on CASA Version 4.5.2

Retrieved from "https://casaguides.nrao.edu/index.php?title=VLA_CASA_Imaging-CASA4.5.2&oldid=19807"