ALMA SIS14 apcal: Difference between revisions
| (14 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
This lesson steps through the basic calibration of the phase and amplitude response of each telescope as a function of time. | This lesson steps through the basic calibration of the phase and amplitude response of each telescope as a function of time. In this step we will | ||
== Setup == | == Setup == | ||
To run this tutorial, you need the measurements set " | To run this tutorial, you need the measurements set "sis14_twhya_calonly.ms." This measurement set contains the calibrators from the parent data set. If you are using the pre-provided directory structure then you want to work in the directory (relative to the root for the package): | ||
<pre style="background-color: #fffacd;"> | <pre style="background-color: #fffacd;"> | ||
| Line 13: | Line 13: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
os.system("rm -rf | os.system("rm -rf sis14_twhya_calonly.ms") | ||
os.system("cp -r ../../working_data/ | os.system("cp -r ../../working_data/sis14_twhya_calonly.ms .") | ||
</source> | </source> | ||
| Line 21: | Line 21: | ||
== Overview == | == Overview == | ||
This lesson covers basic calibration. We will use observations of a quasar, which can be assumed to be a point source at the middle of the field. Mainly using the task '''gaincal''', we will derive the time-dependent corrections to the phase and amplitude response of each antenna that cause the observations to best match this model. These corrections are stored in a calibration table by CASA. They can be applied to the data, correcting observations of both the source and the quasar. | This lesson covers basic calibration. We will use observations of a quasar, which can be assumed to be a point source at the middle of the field. Mainly using the task '''gaincal''', we will derive the time-dependent corrections to the phase and amplitude response of each antenna that cause the observations to best match this model. These corrections are stored in a calibration table by CASA. They can be applied to the data, correcting observations of both the source and the quasar. | ||
This whole procedure makes an underlying assumption about the quasar's geometry (we take it to be a point source) and assumes that antenna-dependent terms are calibration issues rather than something astronomical. The latter is a very good assumption that underlies most of the calibration we do. The geometry of the quasar can be checked and modeled in a more sophisticated way if necessary. A future lesson gives an example of this procedure for planets. | This whole procedure makes an underlying assumption about the quasar's geometry (we take it to be a point source) and assumes that antenna-dependent terms are calibration issues rather than something astronomical. The latter is a very good assumption that underlies most of the calibration we do. The geometry of the quasar can be checked and modeled in a more sophisticated way if necessary. A future lesson gives an example of this procedure for planets. | ||
The flow of the lesson is: | The flow of the lesson is: | ||
* We | * We derive phase corrections for each antenna for each scan using '''gaincal'''. | ||
* We | * We inspect these phase corrections using '''plotcal'''. | ||
* We | * We derived shorter timescale phase corrections using '''gaincal''', which we will use to remove decorrelation from the calibrator during amplitude calibration. | ||
* We derive amplitude corrections for each antenna using '''gaincal''' and taking into account | * We derive amplitude corrections for each antenna using '''gaincal''' and taking into account these short-timescale phase corrections. | ||
* We inspect the amplitude corrections using '''plotcal''' | * We inspect the amplitude corrections using '''plotcal'''. | ||
After the main lesson we discuss some additional options and advanced strategies that can be used with '''gaincal.''' | After the main lesson we discuss some additional options and advanced strategies that can be used with '''gaincal.''' | ||
| Line 46: | Line 46: | ||
<pre style="background-color: #fffacd;"> | <pre style="background-color: #fffacd;"> | ||
2014- | 2014-03-06 19:09:04 INFO listobs 19-Nov-2012/07:36:57.0 - 07:39:13.1 4 0 J0522-364 5060 [0] [6.05] [CALIBRATE_BANDPASS#ON_SOURCE, CALIBRATE_PHASE#ON_SOURCE, CALIBRATE_WVR#ON_SOURCE] | ||
2014- | 2014-03-06 19:09:04 INFO listobs 07:44:45.2 - 07:47:01.2 7 1 Ceres 5060 [0] [6.05] [CALIBRATE_AMPLI#ON_SOURCE, CALIBRATE_PHASE#ON_SOURCE, CALIBRATE_WVR#ON_SOURCE] | ||
2014- | 2014-03-06 19:09:04 INFO listobs 07:52:42.0 - 07:53:47.6 10 2 J1037-295 2760 [0] [6.05] [CALIBRATE_PHASE#ON_SOURCE, CALIBRATE_WVR#ON_SOURCE] | ||
2014- | 2014-03-06 19:09:04 INFO listobs 08:04:36.3 - 08:05:41.9 14 2 J1037-295 3000 [0] [6.05] [CALIBRATE_PHASE#ON_SOURCE, CALIBRATE_WVR#ON_SOURCE] | ||
2014- | 2014-03-06 19:09:04 INFO listobs 08:16:20.6 - 08:17:26.2 18 2 J1037-295 3000 [0] [6.05] [CALIBRATE_PHASE#ON_SOURCE, CALIBRATE_WVR#ON_SOURCE] | ||
2014- | 2014-03-06 19:09:04 INFO listobs 08:28:17.1 - 08:29:22.6 22 2 J1037-295 3000 [0] [6.05] [CALIBRATE_PHASE#ON_SOURCE, CALIBRATE_WVR#ON_SOURCE] | ||
2014- | 2014-03-06 19:09:04 INFO listobs 08:40:11.9 - 08:41:17.4 26 2 J1037-295 3000 [0] [6.05] [CALIBRATE_PHASE#ON_SOURCE, CALIBRATE_WVR#ON_SOURCE] | ||
2014- | 2014-03-06 19:09:04 INFO listobs 08:51:57.1 - 08:53:02.6 30 2 J1037-295 3000 [0] [6.05] [CALIBRATE_PHASE#ON_SOURCE, CALIBRATE_WVR#ON_SOURCE] | ||
2014-03-06 19:09:04 INFO listobs 09:01:35.7 - 09:02:41.2 34 2 J1037-295 2530 [0] [6.05] [CALIBRATE_PHASE#ON_SOURCE, CALIBRATE_WVR#ON_SOURCE] | |||
2014-03-06 19:09:04 INFO listobs 09:09:59.1 - 09:11:04.7 38 2 J1037-295 2530 [0] [6.05] [CALIBRATE_PHASE#ON_SOURCE, CALIBRATE_WVR#ON_SOURCE] | |||
</pre> | </pre> | ||
From the output of listobs we can see that this data set contains a single spectral window and | From the output of listobs we can see that this data set contains a single spectral window and observations of three sources: the calibrators J0522-364, Ceres, and J1037-295. The first two are intended to calibrate the flux scale and bandpass; in this lesson we focus on the third calibrator, J1037-295, which we note is '''Field 2''' (you can see this by looking at the intents at the end of the lines for each scan and at the field table). Each visit to the this quasar was about a minute long and in the original data set they bracketed visits to the source. | ||
scan | |||
Following the earlier lesson, we pick out DV22 as a reasonable reference antenna that sits near the center of the array. | Following the earlier lesson, we pick out DV22 as a reasonable reference antenna that sits near the center of the array. | ||
| Line 63: | Line 64: | ||
== Phase Calibration == | == Phase Calibration == | ||
Our first calibration step is to derive a phase correction for each antenna as a function of time. The task '''gaincal''' does this, attempting to match the DATA column (i.e., the measurements) to the MODEL column (the expected visibility). In the absence of any MODEL column (and this is the case here), gaincal tries to match the observed data to a point source of amplitude 1 Jy at the center of the field | === Per Scan Phase Calibration === | ||
Our first calibration step is to derive a phase correction for each antenna as a function of time that will be suitable for correcting the phases of the science data. | |||
The task '''gaincal''' does this, attempting to match the DATA column (i.e., the measurements) to the MODEL column (the expected visibility for the source). In the absence of any MODEL column (and this is the case here), gaincal tries to match the observed data to a point source of amplitude 1 Jy at the center of the field. We'll discuss the correct amplitude scaling in an upcoming lesson, but for now this is perfect - a phase calibrator can usually be taken to be a point source with fixed amplitude at the center of the field, that's the whole idea. | |||
For now, calibrate the phase corrections only using: | For now, calibrate the phase corrections only using: | ||
| Line 69: | Line 74: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
os.system("rm -rf | os.system("rm -rf phase_scan.cal") | ||
gaincal(vis=" | gaincal(vis="sis14_twhya_calonly.ms", | ||
caltable=" | caltable="phase_scan.cal", | ||
field=" | field="2", | ||
solint="inf", | solint="inf", | ||
calmode="p", | calmode="p", | ||
| Line 82: | Line 87: | ||
* First, we delete any previous table using the os.system call. | * First, we delete any previous table using the os.system call. | ||
* Then we tell gaincal to consider the measurement set " | * Then we tell gaincal to consider the measurement set "sis14_twhya_calonly.ms" (via '''vis'''). | ||
* We tell gaincal that we want the output written to the calibration table " | * We tell gaincal that we want the output written to the calibration table "phase_scan.cal" (via '''caltable'''). | ||
* We tell gaincal to consider only the | * We tell gaincal to consider only the phase calibrator, which we know is field number 2 from the listobs ('''field'''=2). | ||
* We ask gaincal to solve only for the phase solutions by saying '''calmode'''="p". | * We ask gaincal to solve only for the phase solutions by saying '''calmode'''="p". | ||
* We specify DV22 as our reference antenna ('''refant'''). This antenna will have phase correction 0 by definition (the other corrections are relative to the refant). | * We specify DV22 as our reference antenna ('''refant'''). This antenna will have phase correction 0 by definition (the other corrections are relative to the refant). | ||
* We ask gaincal to solve for a correction for each "correlation" (i.e., each polarization) by specifying '''gaintype'''="G". | * We ask gaincal to solve for a correction for each "correlation" (i.e., each polarization) by specifying '''gaintype'''="G". | ||
* Finally, we specify that we want to combine data across the longest possible time interval by setting the solution interval to infinity ('''solint'''="inf"), ''but'' because gaincal will not combine across scans (or spws or fields) by default, '''solint'''="inf" can be read "solve for the phase correction for each antenna for each scan." | * Finally, we specify that we want to combine data across the longest possible time interval by setting the solution interval to infinity ('''solint'''="inf"), ''but'' because gaincal will not combine across scans (or spws or fields) by default, '''solint'''="inf" can be read "solve for the phase correction for each antenna for each scan." | ||
''More on solint:'' The timescale over which we calibrated is critical here - our goal with this table is to generate the phase correction to be applied to the source. Therefore, we choose to derive one correction per scan. This means that we get one phase correction for each antenna for each visit to the phase calibrator. In between these corrections we observed the source. This represents an optimum tradeoff of signal to noise vs. precision of the correction. Solving for a finer timescale solution won't be particularly useful (i.e., solving every 6 seconds on the calibrator doesn't help if you then go stare at the source for five minutes) while solving over a longer timescale loses precision in the calibration (e.g., if we averaged over an hour timescale we would blend together many calibrator-source-calibrator cycles). | |||
Run this command the results will be written to a new directory, "phase.cal" that contains the calibration table holding the phase corrections. You may want to briefly inspect the directory using linux/unix commands (e.g., "ls phase.cal") just to understand the directory structure. But this isn't strictly necessary. From CASA's perspective the directory "phase.cal" is now a calibration table suitable for use in other tasks. | Run this command the results will be written to a new directory, "phase.cal" that contains the calibration table holding the phase corrections. You may want to briefly inspect the directory using linux/unix commands (e.g., "ls phase.cal") just to understand the directory structure. But this isn't strictly necessary. From CASA's perspective the directory "phase.cal" is now a calibration table suitable for use in other tasks. | ||
| Line 96: | Line 103: | ||
</pre> | </pre> | ||
== Inspect Your Phase Calibration Table == | === Inspect Your Phase Calibration Table === | ||
Now we plot the results of the calibration. '''plotcal''' is the CASA task for plotting calibration tables. We will plot the phase correction as a function of time for our new table via the command: | Now we plot the results of the calibration. '''plotcal''' is the CASA task for plotting calibration tables. We will plot the phase correction as a function of time for our new table via the command: | ||
| Line 102: | Line 109: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
plotcal(caltable=" | plotcal(caltable="phase_scan.cal", | ||
xaxis="time", | xaxis="time", | ||
yaxis="phase", | yaxis="phase", | ||
subplot=331, | |||
iteration="antenna", | iteration="antenna", | ||
plotrange=[0,0,-180,180], | plotrange=[0,0,-180,180], | ||
markersize=10, | markersize=10, | ||
) | fontsize=10.0, | ||
figfile="sis14_phase_scan.png") | |||
</source> | </source> | ||
This does the following: | This does the following: | ||
* We plot the calibration table " | * We plot the calibration table "phase_scan.cal" | ||
* We choose to plot time on the x-axis. | * We choose to plot time on the x-axis. | ||
* We choose to plot the phase correction to be applied on the y-axis. | * We choose to plot the phase correction to be applied on the y-axis. | ||
| Line 122: | Line 129: | ||
* We set the plot range (via '''plotrange''') to autoscale on the x-axis (0,0) and run from (-180,180) on the y-axis. | * We set the plot range (via '''plotrange''') to autoscale on the x-axis (0,0) and run from (-180,180) on the y-axis. | ||
* We set '''markersize''' and '''fontsize''' to very large values in order to make the plots legible for screen capture. | * We set '''markersize''' and '''fontsize''' to very large values in order to make the plots legible for screen capture. | ||
* (Not important usually, but we also output the plot to a PNG file in order to upload it here). | |||
This produces the plot below. You are able to cycle between successive panels using the buttons at the bottom of the window. For example, because there are more than 9 antennas in these data we will need to do this to see all the plots. Note tat you see two points in each plot because we have a solution for each polarization. | This produces the plot below. You are able to cycle between successive panels using the buttons at the bottom of the window. For example, because there are more than 9 antennas in these data we will need to do this to see all the plots. Note tat you see two points in each plot because we have a solution for each polarization. | ||
| Line 127: | Line 135: | ||
[[Image:plotcal_phase_1.png|center|600px]] | [[Image:plotcal_phase_1.png|center|600px]] | ||
''Phase corrections vs. time for our " | ''Phase corrections vs. time for our "phase_scan.cal" table. Each panel shows one antenna, the two colors show the two correlations. Click next to cycle through all antennas.'' | ||
<pre style="background-color: #E0FFFF;"> | <pre style="background-color: #E0FFFF;"> | ||
| Line 141: | Line 149: | ||
For now, these solutions look good. See how they change only gradually and continuously with time and how the two correlations (green and blue) track one another, though sometimes with an offset. We proceed to amplitude self-calibration. | For now, these solutions look good. See how they change only gradually and continuously with time and how the two correlations (green and blue) track one another, though sometimes with an offset. We proceed to amplitude self-calibration. | ||
== Amplitude Calibration | == Amplitude Calibration == | ||
Now we calibrate the amplitude response of each antenna as a function of time. As with phase, our goal is to reach a correction for each antenna for each scan, suitable for application to the science target. There are a couple of additional complications for the amplitude case. First, remember that the actual flux scale of our data remains unspecified; that will be the topic of a future lesson, in this lesson we solve for the corrections under the default assumption that the amplitude of the calibrator is one Jansky. So these are correct ''relative'' corrections. | |||
The second complication is that decorrelation due to phase errors can confuse the amplitude response of the telescope. That is, if the phase is noisy or corrupted, the amplitude of the calibrator may appear artificially faint. Therefore it is common, though not universal, practice to attempt to correct for phase scatter on the calibrator before deriving amplitude corrections. This step should be viewed as optional but highly recommended; it is a part of the standard ALMA reduction path. Note, however, that unless you can self-calibrate on the science target, these same short timescale phase variations will affect the source. | |||
=== Remove Short-Timescale Phase Variations === | |||
To solve for short timescale variations in phase on the source, we repeat our earlier phase calibration with one key change: we set the solution interval ('''solint''') to "int", meaning one integrations (from the listobs, you can see that this is 6 seconds long). Run the resulting command: | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
os.system("rm -rf | os.system("rm -rf phase_int.cal") | ||
gaincal(vis=" | gaincal(vis="sis14_twhya_calonly.ms", | ||
caltable=" | caltable="phase_int.cal", | ||
field=" | field="2", | ||
solint=" | solint="int", | ||
calmode=" | calmode="p", | ||
refant="DV22", | refant="DV22", | ||
gaintype="G | gaintype="G") | ||
</source> | </source> | ||
and again we can use '''plotcal''' to inspect the results. | |||
# In CASA | # In CASA | ||
plotcal(caltable=" | os.system("rm -rf phase_int.cal") | ||
plotcal(caltable="phase_int.cal", | |||
xaxis="time", | xaxis="time", | ||
yaxis=" | yaxis="phase", | ||
subplot=331, | subplot=331, | ||
iteration="antenna", | iteration="antenna", | ||
plotrange=[0,0,0, | plotrange=[0,0,-180,180], | ||
markersize=5, | |||
fontsize=10.0, | |||
figfile="sis14_phase_int.png") | |||
</source> | </source> | ||
Notice that now we are getting many vary slightly scattered phase corrections for each visit to the phase calibrator, separated by long empty times when the science target was observed. | |||
[[Image:plotcal_phase_int_1.png|center|600px]] | |||
''Phase corrections vs. time solved for our "phase_int.cal" table. Each panel shows one antenna, the two colors show the two correlations. Click next to cycle through all antennas. Notice that we now have many solutions (one per integration) for each visit to the calibrator.'' | |||
=== Per-Scan Amplitude Calibration === | |||
Now we are ready to solve for the amplitude corrections as a function of time. Because this is a table for application to the source, we again solve for one correction for each scan by setting the solution interval to '''inf''' but not allowing gaincal to combine scans. The key difference from before is that we now apply the integration-length phase corrections to the data before | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
os.system("rm -rf | os.system("rm -rf amp_scan.cal") | ||
gaincal(vis=" | gaincal(vis="sis14_twhya_calonly.ms", | ||
caltable=" | caltable="amp_scan.cal", | ||
field=" | field="2", | ||
solint=" | solint="inf", | ||
calmode=" | calmode="a", | ||
refant="DV22", | refant="DV22", | ||
gaintype="G") | gaintype="G", | ||
gaintable="phase_int.cal") | |||
</source> | </source> | ||
Again, this is fairly similar to the earlier phase cal. Key differences are: | |||
* We tell gaincal that we want the output written to a new calibration table "amp_scan.cal" (via '''caltable'''). | |||
* We ask gaincal to solve only for the amplitude solutions by saying '''calmode'''="a". | |||
* We apply a previous calibration table "on the fly", meaning that these corrections are applied before the new ones are derived. We provide the per-integration phase correction table via the '''gaintable''' parameter (="phase_int.cal"). This should remove short-timescale phase variations before | |||
Next we plot the results of this fit, again using '''plotcal''': | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
plotcal(caltable=" | plotcal(caltable="amp_scan.cal", | ||
xaxis="time", | xaxis="time", | ||
yaxis="amp", | yaxis="amp", | ||
subplot=331, | subplot=331, | ||
iteration="antenna", | iteration="antenna", | ||
plotrange=[0,0,0,0]) | plotrange=[0,0,0,0], | ||
markersize=10, | |||
fontsize=10.0, | |||
figfile="sis14_amp_scan.png") | |||
</source> | </source> | ||
== Advanced | * The main difference from the previous plotcal call is that plot "amp" on the y-axis we now auto-scale the y-axis to the range of the data by setting the y part of the '''plotrange''' to 0,0. | ||
[[Image:plotcal_amp_1.png|center|600px]] | |||
''Amplitude (gain) correction vs. time for our scan-length solution. Each antenna is one panel and the two colors (green and blue) show the two polarizations ("correlations").'' | |||
<pre style="background-color: #E0FFFF;"> | |||
What are you looking for in these amplitude? As with phase, a continuous trend is a good sign and sudden discontinuities may be warning | |||
signs. With the gain corrections the actual values of the gain are also potentially of interest. They reflect the actual gain of the | |||
antennas. If one antenna has a very high or - more worrisome - a very low value, this may be a sign of a problem. Perhaps the antenna | |||
was mispointed or otherwise problematic. This may indicate data that eventually need to be flagged. | |||
</pre> | |||
We now have scan averaged phase and amplitude corrections suitable for application to each antenna. In future lessons we will see how to apply these corrections and how to set the amplitude scale to its correct value. We will also see how to solve for frequency-dependent corrections in addition to the time dependent ones derived here. | |||
== Advanced Options == | |||
This lesson described basic calibration flow, but '''gaincal''' is a flexible task with a number of more advanced capabilities that often come up in real calibration flow. Here we briefly discuss several commonly used advanced options. These fall into three broad categories: | |||
* Selecting only part of the data for use in calibration. For example, considering only a single field or set of antennas. | |||
* Averaging together data to increase signal to noise in the solutions. For example, by combining polarizations or spectral windows. | |||
* Layering calibrations on top of one another. For example, deriving an amplitude calibration only after applying a phase or bandpass calibration. | |||
=== Selecting Subsets of Data === | |||
In a number of cases, you will want to calibrate considering only a subset of the data. To do this, gaincal has a number of data selection keywords. We have already the simplest version of this, when we set '''field'''="2" to select only the phase calibrator in the main lesson. Other common applications are: | |||
=== Averaging | * Using '''spw=''' to select only subset of spectral windows or only a few channels, e.g., via spw="0:8~12" selects channels 8 through 12 of spectral window 0. One common reason for this is to select only a narrow range of frequencies when removing short timescale phase variations before a bandpass calibration. | ||
* Using '''uvrange=''' to select only a fixed range of baseline lengths. This can be useful when using calibrators with resolved structure. We will see a concrete example when considering Ceres (a resolved solar system object) in the next section. In that case we select only a short uvrange to solve for the amplitude scale. | |||
* Use '''antenna='''to select only a fixed subset of antennas. This is sometimes done for the same reason as selecting a small uvrange, i.e., to select a subset of antennas for which the calibrator is still useful. | |||
These are only a few examples. There are many reasons you may work with only a subset of the data and gaincal includes a large number of ways to slice the data. | |||
=== Averaging Data === | |||
In cases of a faint calibrator, low signal to noise, or narrow bandwidth it can often be necessary to average data. We have already seen the most common way of doing this, manipulating the solution interval. There are other methods of averaging available: | |||
* By default '''gaincal''' will not average across spectral window, scan, or field boundaries. Setting the '''combine''' field to "scan", "spw", "field" or some combination of these enables averaging across these boundaries. In the case of "scan" and "field", this allows for solutions intervals longer than a scan length (up to the whole length of the data in the case of '''solint'''="inf"). In the case of combine="spw", data at all available frequencies will be combined into a single solution. | |||
* By default '''gaincal''' solves for a solution for each polarization. This is specified by the default '''gaintype'''="G". By switching this to "T" you can tell gaincal to derive an average solution for both polarizations. | |||
=== "Layering" Calibrations === | === "Layering" Calibrations === | ||
Latest revision as of 04:21, 7 March 2014
This lesson steps through the basic calibration of the phase and amplitude response of each telescope as a function of time. In this step we will
Setup
To run this tutorial, you need the measurements set "sis14_twhya_calonly.ms." This measurement set contains the calibrators from the parent data set. If you are using the pre-provided directory structure then you want to work in the directory (relative to the root for the package):
lessons/basic_cal/
and you can copy the data to your working directory using the commands
# In CASA
os.system("rm -rf sis14_twhya_calonly.ms")
os.system("cp -r ../../working_data/sis14_twhya_calonly.ms .")
With this measurement set in place, you can follow the tutorial below inside the "basic_cal/" directory.
Overview
This lesson covers basic calibration. We will use observations of a quasar, which can be assumed to be a point source at the middle of the field. Mainly using the task gaincal, we will derive the time-dependent corrections to the phase and amplitude response of each antenna that cause the observations to best match this model. These corrections are stored in a calibration table by CASA. They can be applied to the data, correcting observations of both the source and the quasar.
This whole procedure makes an underlying assumption about the quasar's geometry (we take it to be a point source) and assumes that antenna-dependent terms are calibration issues rather than something astronomical. The latter is a very good assumption that underlies most of the calibration we do. The geometry of the quasar can be checked and modeled in a more sophisticated way if necessary. A future lesson gives an example of this procedure for planets.
The flow of the lesson is:
- We derive phase corrections for each antenna for each scan using gaincal.
- We inspect these phase corrections using plotcal.
- We derived shorter timescale phase corrections using gaincal, which we will use to remove decorrelation from the calibrator during amplitude calibration.
- We derive amplitude corrections for each antenna using gaincal and taking into account these short-timescale phase corrections.
- We inspect the amplitude corrections using plotcal.
After the main lesson we discuss some additional options and advanced strategies that can be used with gaincal.
Get Oriented
First, as usual we orient ourselves by looking at the output of listobs (and perhaps plotants or a plotms call). See the lesson on getting started for more details.
# In CASA
listobs("sis14_ampandphase.ms")
A snippet of the output is here:
2014-03-06 19:09:04 INFO listobs 19-Nov-2012/07:36:57.0 - 07:39:13.1 4 0 J0522-364 5060 [0] [6.05] [CALIBRATE_BANDPASS#ON_SOURCE, CALIBRATE_PHASE#ON_SOURCE, CALIBRATE_WVR#ON_SOURCE] 2014-03-06 19:09:04 INFO listobs 07:44:45.2 - 07:47:01.2 7 1 Ceres 5060 [0] [6.05] [CALIBRATE_AMPLI#ON_SOURCE, CALIBRATE_PHASE#ON_SOURCE, CALIBRATE_WVR#ON_SOURCE] 2014-03-06 19:09:04 INFO listobs 07:52:42.0 - 07:53:47.6 10 2 J1037-295 2760 [0] [6.05] [CALIBRATE_PHASE#ON_SOURCE, CALIBRATE_WVR#ON_SOURCE] 2014-03-06 19:09:04 INFO listobs 08:04:36.3 - 08:05:41.9 14 2 J1037-295 3000 [0] [6.05] [CALIBRATE_PHASE#ON_SOURCE, CALIBRATE_WVR#ON_SOURCE] 2014-03-06 19:09:04 INFO listobs 08:16:20.6 - 08:17:26.2 18 2 J1037-295 3000 [0] [6.05] [CALIBRATE_PHASE#ON_SOURCE, CALIBRATE_WVR#ON_SOURCE] 2014-03-06 19:09:04 INFO listobs 08:28:17.1 - 08:29:22.6 22 2 J1037-295 3000 [0] [6.05] [CALIBRATE_PHASE#ON_SOURCE, CALIBRATE_WVR#ON_SOURCE] 2014-03-06 19:09:04 INFO listobs 08:40:11.9 - 08:41:17.4 26 2 J1037-295 3000 [0] [6.05] [CALIBRATE_PHASE#ON_SOURCE, CALIBRATE_WVR#ON_SOURCE] 2014-03-06 19:09:04 INFO listobs 08:51:57.1 - 08:53:02.6 30 2 J1037-295 3000 [0] [6.05] [CALIBRATE_PHASE#ON_SOURCE, CALIBRATE_WVR#ON_SOURCE] 2014-03-06 19:09:04 INFO listobs 09:01:35.7 - 09:02:41.2 34 2 J1037-295 2530 [0] [6.05] [CALIBRATE_PHASE#ON_SOURCE, CALIBRATE_WVR#ON_SOURCE] 2014-03-06 19:09:04 INFO listobs 09:09:59.1 - 09:11:04.7 38 2 J1037-295 2530 [0] [6.05] [CALIBRATE_PHASE#ON_SOURCE, CALIBRATE_WVR#ON_SOURCE]
From the output of listobs we can see that this data set contains a single spectral window and observations of three sources: the calibrators J0522-364, Ceres, and J1037-295. The first two are intended to calibrate the flux scale and bandpass; in this lesson we focus on the third calibrator, J1037-295, which we note is Field 2 (you can see this by looking at the intents at the end of the lines for each scan and at the field table). Each visit to the this quasar was about a minute long and in the original data set they bracketed visits to the source.
Following the earlier lesson, we pick out DV22 as a reasonable reference antenna that sits near the center of the array.
Phase Calibration
Per Scan Phase Calibration
Our first calibration step is to derive a phase correction for each antenna as a function of time that will be suitable for correcting the phases of the science data.
The task gaincal does this, attempting to match the DATA column (i.e., the measurements) to the MODEL column (the expected visibility for the source). In the absence of any MODEL column (and this is the case here), gaincal tries to match the observed data to a point source of amplitude 1 Jy at the center of the field. We'll discuss the correct amplitude scaling in an upcoming lesson, but for now this is perfect - a phase calibrator can usually be taken to be a point source with fixed amplitude at the center of the field, that's the whole idea.
For now, calibrate the phase corrections only using:
# In CASA
os.system("rm -rf phase_scan.cal")
gaincal(vis="sis14_twhya_calonly.ms",
caltable="phase_scan.cal",
field="2",
solint="inf",
calmode="p",
refant="DV22",
gaintype="G")
These commands do the following:
- First, we delete any previous table using the os.system call.
- Then we tell gaincal to consider the measurement set "sis14_twhya_calonly.ms" (via vis).
- We tell gaincal that we want the output written to the calibration table "phase_scan.cal" (via caltable).
- We tell gaincal to consider only the phase calibrator, which we know is field number 2 from the listobs (field=2).
- We ask gaincal to solve only for the phase solutions by saying calmode="p".
- We specify DV22 as our reference antenna (refant). This antenna will have phase correction 0 by definition (the other corrections are relative to the refant).
- We ask gaincal to solve for a correction for each "correlation" (i.e., each polarization) by specifying gaintype="G".
- Finally, we specify that we want to combine data across the longest possible time interval by setting the solution interval to infinity (solint="inf"), but because gaincal will not combine across scans (or spws or fields) by default, solint="inf" can be read "solve for the phase correction for each antenna for each scan."
More on solint: The timescale over which we calibrated is critical here - our goal with this table is to generate the phase correction to be applied to the source. Therefore, we choose to derive one correction per scan. This means that we get one phase correction for each antenna for each visit to the phase calibrator. In between these corrections we observed the source. This represents an optimum tradeoff of signal to noise vs. precision of the correction. Solving for a finer timescale solution won't be particularly useful (i.e., solving every 6 seconds on the calibrator doesn't help if you then go stare at the source for five minutes) while solving over a longer timescale loses precision in the calibration (e.g., if we averaged over an hour timescale we would blend together many calibrator-source-calibrator cycles).
Run this command the results will be written to a new directory, "phase.cal" that contains the calibration table holding the phase corrections. You may want to briefly inspect the directory using linux/unix commands (e.g., "ls phase.cal") just to understand the directory structure. But this isn't strictly necessary. From CASA's perspective the directory "phase.cal" is now a calibration table suitable for use in other tasks.
Read more about the choices involved in gaincal at the end of the lesson.
Inspect Your Phase Calibration Table
Now we plot the results of the calibration. plotcal is the CASA task for plotting calibration tables. We will plot the phase correction as a function of time for our new table via the command:
# In CASA
plotcal(caltable="phase_scan.cal",
xaxis="time",
yaxis="phase",
subplot=331,
iteration="antenna",
plotrange=[0,0,-180,180],
markersize=10,
fontsize=10.0,
figfile="sis14_phase_scan.png")
This does the following:
- We plot the calibration table "phase_scan.cal"
- We choose to plot time on the x-axis.
- We choose to plot the phase correction to be applied on the y-axis.
- We want a plot for each antenna and so set iteration to "antenna".
- We want several plots per page, subplot=331 will plot 3x3 panels with one plot per panel.
- We set the plot range (via plotrange) to autoscale on the x-axis (0,0) and run from (-180,180) on the y-axis.
- We set markersize and fontsize to very large values in order to make the plots legible for screen capture.
- (Not important usually, but we also output the plot to a PNG file in order to upload it here).
This produces the plot below. You are able to cycle between successive panels using the buttons at the bottom of the window. For example, because there are more than 9 antennas in these data we will need to do this to see all the plots. Note tat you see two points in each plot because we have a solution for each polarization.

Phase corrections vs. time for our "phase_scan.cal" table. Each panel shows one antenna, the two colors show the two correlations. Click next to cycle through all antennas.
What are you looking for in these tables? A well-behaved calibration table shows continuous trends in phase and often the same pattern in both calibrations - though perhaps with an overall offset. Ideally a stable antenna will change phase only gradually as a function of time. Rapid wrapping may be a sign for alarm. Sudden, large jumps in phases may also be a signal for worry; we often want to be able to interpolate between these corrections and sudden jumps can make this difficult (or impossible). Depending on the application, you may also be interested in the overall amplitude of the solution; e.g., when engaged in iterative self-calibration the amplitude of the phase correction is of interest.
For now, these solutions look good. See how they change only gradually and continuously with time and how the two correlations (green and blue) track one another, though sometimes with an offset. We proceed to amplitude self-calibration.
Amplitude Calibration
Now we calibrate the amplitude response of each antenna as a function of time. As with phase, our goal is to reach a correction for each antenna for each scan, suitable for application to the science target. There are a couple of additional complications for the amplitude case. First, remember that the actual flux scale of our data remains unspecified; that will be the topic of a future lesson, in this lesson we solve for the corrections under the default assumption that the amplitude of the calibrator is one Jansky. So these are correct relative corrections.
The second complication is that decorrelation due to phase errors can confuse the amplitude response of the telescope. That is, if the phase is noisy or corrupted, the amplitude of the calibrator may appear artificially faint. Therefore it is common, though not universal, practice to attempt to correct for phase scatter on the calibrator before deriving amplitude corrections. This step should be viewed as optional but highly recommended; it is a part of the standard ALMA reduction path. Note, however, that unless you can self-calibrate on the science target, these same short timescale phase variations will affect the source.
Remove Short-Timescale Phase Variations
To solve for short timescale variations in phase on the source, we repeat our earlier phase calibration with one key change: we set the solution interval (solint) to "int", meaning one integrations (from the listobs, you can see that this is 6 seconds long). Run the resulting command:
# In CASA
os.system("rm -rf phase_int.cal")
gaincal(vis="sis14_twhya_calonly.ms",
caltable="phase_int.cal",
field="2",
solint="int",
calmode="p",
refant="DV22",
gaintype="G")
and again we can use plotcal to inspect the results.
- In CASA
os.system("rm -rf phase_int.cal") plotcal(caltable="phase_int.cal",
xaxis="time",
yaxis="phase",
subplot=331,
iteration="antenna",
plotrange=[0,0,-180,180],
markersize=5,
fontsize=10.0,
figfile="sis14_phase_int.png")
</source>
Notice that now we are getting many vary slightly scattered phase corrections for each visit to the phase calibrator, separated by long empty times when the science target was observed.

Phase corrections vs. time solved for our "phase_int.cal" table. Each panel shows one antenna, the two colors show the two correlations. Click next to cycle through all antennas. Notice that we now have many solutions (one per integration) for each visit to the calibrator.
Per-Scan Amplitude Calibration
Now we are ready to solve for the amplitude corrections as a function of time. Because this is a table for application to the source, we again solve for one correction for each scan by setting the solution interval to inf but not allowing gaincal to combine scans. The key difference from before is that we now apply the integration-length phase corrections to the data before
# In CASA
os.system("rm -rf amp_scan.cal")
gaincal(vis="sis14_twhya_calonly.ms",
caltable="amp_scan.cal",
field="2",
solint="inf",
calmode="a",
refant="DV22",
gaintype="G",
gaintable="phase_int.cal")
Again, this is fairly similar to the earlier phase cal. Key differences are:
- We tell gaincal that we want the output written to a new calibration table "amp_scan.cal" (via caltable).
- We ask gaincal to solve only for the amplitude solutions by saying calmode="a".
- We apply a previous calibration table "on the fly", meaning that these corrections are applied before the new ones are derived. We provide the per-integration phase correction table via the gaintable parameter (="phase_int.cal"). This should remove short-timescale phase variations before
Next we plot the results of this fit, again using plotcal:
# In CASA
plotcal(caltable="amp_scan.cal",
xaxis="time",
yaxis="amp",
subplot=331,
iteration="antenna",
plotrange=[0,0,0,0],
markersize=10,
fontsize=10.0,
figfile="sis14_amp_scan.png")
- The main difference from the previous plotcal call is that plot "amp" on the y-axis we now auto-scale the y-axis to the range of the data by setting the y part of the plotrange to 0,0.
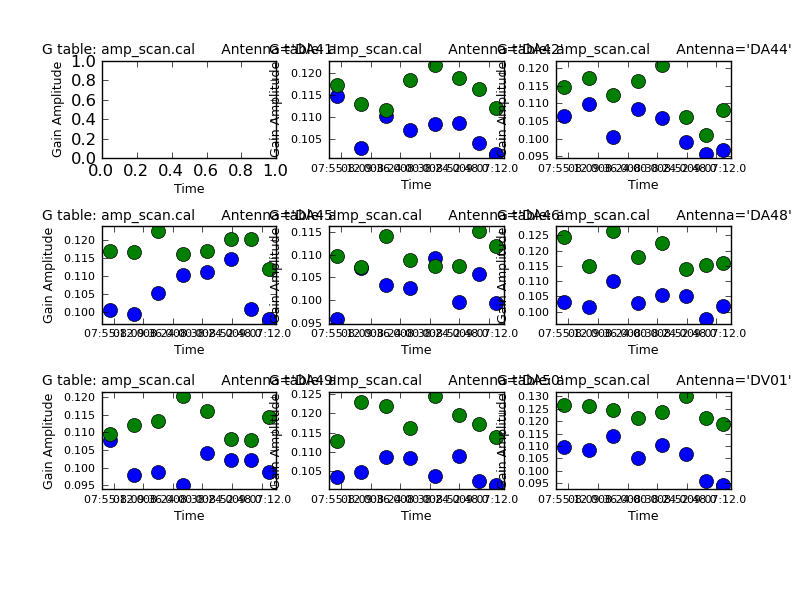
Amplitude (gain) correction vs. time for our scan-length solution. Each antenna is one panel and the two colors (green and blue) show the two polarizations ("correlations").
What are you looking for in these amplitude? As with phase, a continuous trend is a good sign and sudden discontinuities may be warning signs. With the gain corrections the actual values of the gain are also potentially of interest. They reflect the actual gain of the antennas. If one antenna has a very high or - more worrisome - a very low value, this may be a sign of a problem. Perhaps the antenna was mispointed or otherwise problematic. This may indicate data that eventually need to be flagged.
We now have scan averaged phase and amplitude corrections suitable for application to each antenna. In future lessons we will see how to apply these corrections and how to set the amplitude scale to its correct value. We will also see how to solve for frequency-dependent corrections in addition to the time dependent ones derived here.
Advanced Options
This lesson described basic calibration flow, but gaincal is a flexible task with a number of more advanced capabilities that often come up in real calibration flow. Here we briefly discuss several commonly used advanced options. These fall into three broad categories:
- Selecting only part of the data for use in calibration. For example, considering only a single field or set of antennas.
- Averaging together data to increase signal to noise in the solutions. For example, by combining polarizations or spectral windows.
- Layering calibrations on top of one another. For example, deriving an amplitude calibration only after applying a phase or bandpass calibration.
Selecting Subsets of Data
In a number of cases, you will want to calibrate considering only a subset of the data. To do this, gaincal has a number of data selection keywords. We have already the simplest version of this, when we set field="2" to select only the phase calibrator in the main lesson. Other common applications are:
- Using spw= to select only subset of spectral windows or only a few channels, e.g., via spw="0:8~12" selects channels 8 through 12 of spectral window 0. One common reason for this is to select only a narrow range of frequencies when removing short timescale phase variations before a bandpass calibration.
- Using uvrange= to select only a fixed range of baseline lengths. This can be useful when using calibrators with resolved structure. We will see a concrete example when considering Ceres (a resolved solar system object) in the next section. In that case we select only a short uvrange to solve for the amplitude scale.
- Use antenna=to select only a fixed subset of antennas. This is sometimes done for the same reason as selecting a small uvrange, i.e., to select a subset of antennas for which the calibrator is still useful.
These are only a few examples. There are many reasons you may work with only a subset of the data and gaincal includes a large number of ways to slice the data.
Averaging Data
In cases of a faint calibrator, low signal to noise, or narrow bandwidth it can often be necessary to average data. We have already seen the most common way of doing this, manipulating the solution interval. There are other methods of averaging available:
- By default gaincal will not average across spectral window, scan, or field boundaries. Setting the combine field to "scan", "spw", "field" or some combination of these enables averaging across these boundaries. In the case of "scan" and "field", this allows for solutions intervals longer than a scan length (up to the whole length of the data in the case of solint="inf"). In the case of combine="spw", data at all available frequencies will be combined into a single solution.
- By default gaincal solves for a solution for each polarization. This is specified by the default gaintype="G". By switching this to "T" you can tell gaincal to derive an average solution for both polarizations.