M100 Band3 Combine 4.2.2: Difference between revisions
| (96 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
<div style="background-color:#E0FFFF;border:4px solid #FF9966;"> | |||
<div style="font-size:250%; color:red; text-align:center;"> | |||
This page is currently under construction. | |||
</div> | |||
<div style="font-size:200%; color:black; text-align:center"> | |||
DO NOT USE IT. | |||
</div> | |||
<div style="font-size:150%; color:black; text-align:center"> | |||
To navigate the CASAguides pages, visit [http://casaguides.nrao.edu/ | |||
casaguides.nrao.edu | |||
] | |||
</div> | |||
</div> | |||
= Overview = | = Overview = | ||
This guide describes how to combine the 7m and 12m interferometric data and then how to feather the resulting image with the total power TP image. All of the data for this SV project can be found at https://almascience.nrao.edu/alma-data/science-verification. The guide has been written for data reduced in CASA 4.3.0 or later and assumes that all calibration tables (Tsys and gain tables) have been applied to the visibility weights using calwt=True. If either of these is not the case for your data, '''do not follow this guide.''' | |||
In order to run this guide you will need to: | |||
* Either download the fully calibrated 7m data (i.e., M100_Band3_7m_CalibratedData.tgz) or download the uncalibrated 7m data and the relevant, standard calibration scripts available (here) | |||
* Either download the fully calibrated 12m data (i.e. M100_Band3_12m_CalibratedData.tgz) or download the uncalibrated 12m data and the relevant, standard calibration scripts available (here). Note that this is a '''new''' calibration of the same data that were released previously, and so the data reduction path has been updated to current best practices and starts from the raw data files called ASDMs (ALMA Science Data Model). '''Do not use the previously released uncalibrated or calibrated data.''' | |||
* Either run the [[M100_Band3_SingleDish_4.3]] guide to calibrate and image the Total Power data or download the final image (i.e. M100_TP_Image.tgz) | |||
==Confirm your version of CASA== | |||
This guide has been written for CASA release 4.3.0. Please confirm your version before proceeding. | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
os.system('m100_*m.ms.listobs') | version = casadef.casa_version | ||
print "You are using " + version | |||
if (version < '4.3.0'): | |||
print "YOUR VERSION OF CASA IS TOO OLD FOR THIS GUIDE." | |||
print "PLEASE UPDATE IT BEFORE PROCEEDING." | |||
else: | |||
print "Your version of CASA is appropriate for this guide." | |||
</source> | |||
= Combine and Image the 7m+12m Interferometric Data = | |||
== Split off CO spectral windows (SPWs) == | |||
<source lang="python"> | |||
# In CASA | |||
os.system('rm -rf m100_*m.ms.listobs') | |||
listobs('M100_Band3_12m_CalibratedData.ms',listfile='m100_12m.ms.listobs') | listobs('M100_Band3_12m_CalibratedData.ms',listfile='m100_12m.ms.listobs') | ||
listobs('M100_Band3_7m_CalibratedData.ms',listfile='m100_7m.ms.listobs') | listobs('M100_Band3_7m_CalibratedData.ms',listfile='m100_7m.ms.listobs') | ||
</source> | </source> | ||
Below are the | Running the task "listobs" provides the setups used in the observations at a glance. Below are the first target scans of the 12m and 7m observations and the spectral window tables as generated by listobs. The six 7m data sets were taken with two slightly different correlator setups (one with four SPWs and the other with two SPWs), so the concatenated data set has six total SPWs. | ||
<pre style="background-color: #fffacd;"> | <pre style="background-color: #fffacd;"> | ||
| Line 20: | Line 57: | ||
ObservationID = 0 ArrayID = 0 | ObservationID = 0 ArrayID = 0 | ||
Date Timerange (UTC) Scan FldId FieldName nRows SpwIds Average Interval(s) | Date Timerange (UTC) Scan FldId FieldName nRows SpwIds Average Interval(s) ScanIntent | ||
10- | 10-Aug-2011/19:38:05.8 - 19:50:22.8 11 1 M100 1500 [0,1,2,3] [6.05, 6.05, 6.05, 6.05] [CALIBRATE_WVR#ON_SOURCE,OBSERVE_TARGET#ON_SOURCE] | ||
Spectral Windows: (4 unique spectral windows and 1 unique polarization setups) | Spectral Windows: (4 unique spectral windows and 1 unique polarization setups) | ||
SpwID Name #Chans Frame | SpwID Name #Chans Frame Ch0(MHz) ChanWid(kHz) TotBW(kHz) CtrFreq(MHz) BBC Num Corrs | ||
0 3840 TOPO 113726.419 488.281 1875000.0 | 0 3840 TOPO 113726.419 488.281 1875000.0 114663.6750 1 XX YY | ||
1 3840 TOPO 111851.419 488.281 1875000.0 | 1 3840 TOPO 111851.419 488.281 1875000.0 112788.6750 2 XX YY | ||
2 3840 TOPO 103663.431 -488.281 1875000.0 | 2 3840 TOPO 103663.431 -488.281 1875000.0 102726.1750 3 XX YY | ||
3 3840 TOPO 101850.931 -488.281 1875000.0 | 3 3840 TOPO 101850.931 -488.281 1875000.0 100913.6750 4 XX YY | ||
7m data: | 7m data: | ||
ObservationID = 0 ArrayID = 0 | ObservationID = 0 ArrayID = 0 | ||
Date Timerange (UTC) Scan FldId FieldName nRows SpwIds Average Interval(s) | Date Timerange (UTC) Scan FldId FieldName nRows SpwIds Average Interval(s) ScanIntent | ||
17-Mar-2013/04:44:04.3 - 04:50:43.7 11 1 M100 | 17-Mar-2013/04:44:04.3 - 04:50:43.7 11 1 M100 261 [0,1,2,3] [10.1, 10.1, 10.1, 10.1] [OBSERVE_TARGET#ON_SOURCE] | ||
Spectral Windows: ( | Spectral Windows: (6 unique spectral windows and 1 unique polarization setups) | ||
SpwID Name #Chans Frame | SpwID Name #Chans Frame Ch0(MHz) ChanWid(kHz) TotBW(kHz) CtrFreq(MHz) BBC Num Corrs | ||
0 ALMA_RB_03#BB_3#SW-01#FULL_RES 4080 TOPO 111811.300 488.281 1992187.5 | 0 ALMA_RB_03#BB_1#SW-01#FULL_RES 4080 TOPO 101945.850 -488.281 1992187.5 100950.0000 1 XX YY | ||
1 ALMA_RB_03#BB_2#SW-01#FULL_RES 4080 TOPO 103761.000 -488.281 1992187.5 102765.1500 2 XX YY | |||
2 ALMA_RB_03#BB_3#SW-01#FULL_RES 4080 TOPO 111811.300 488.281 1992187.5 112807.1500 3 XX YY | |||
3 ALMA_RB_03#BB_4#SW-01#FULL_RES 4080 TOPO 113686.300 488.281 1992187.5 114682.1500 4 XX YY | |||
4 ALMA_RB_03#BB_1#SW-01#FULL_RES 4080 TOPO 111798.250 488.281 1992187.5 112794.1000 1 XX YY | |||
5 ALMA_RB_03#BB_2#SW-01#FULL_RES 4080 TOPO 113673.250 488.281 1992187.5 114669.1000 2 XX YY | |||
</pre> | </pre> | ||
Examination of the listobs files | <figure id="12m_mosaic.png"> | ||
[[Image:12m_mosaic.png|300px|thumb|right|<caption>FOV of 12m mosaic.</caption>]] | |||
</figure> | |||
<figure id="7m_mosaic.png"> | |||
[[Image:7m_mosaic.png|300px|thumb|right|<caption>FOV of 7m mosaic.</caption>]] | |||
</figure> | |||
Examination of the listobs files shows that the CO is in SPW='0' for the 12m data and in SPW='3,5' for the 7m data. There are two SPWs containing CO in the 7m data due to the slightly differing correlator setups. | |||
Also note that the integration time per visibility (average interval parameter in listobs) is different: | Also note that the integration time per visibility (average interval parameter in listobs) is different: | ||
6.05s for the 12m data and 10.1s for the 7m. This will be important to know later | 6.05s for the 12m data and 10.1s for the 7m. This will be important to know later when we check the visibility weights. | ||
Next we split out the CO spectral windows. | |||
<source lang="python"> | <source lang="python"> | ||
| Line 57: | Line 106: | ||
os.system('rm -rf m100_7m_CO.ms') | os.system('rm -rf m100_7m_CO.ms') | ||
split(vis='M100_Band3_7m_CalibratedData.ms', | split(vis='M100_Band3_7m_CalibratedData.ms', | ||
outputvis='m100_7m_CO.ms',spw=' | outputvis='m100_7m_CO.ms',spw='3,5',field='M100', | ||
datacolumn='data',keepflags=False) | datacolumn='data',keepflags=False) | ||
</source> | </source> | ||
Also of interest is that the 12m data has 47 fields and the 7m has 23 fields (not shown in the excerpts above). The difference in number of pointings is because the 7m antennas have a FWHP (full width half power) primary beam diameter that is 12/7 times larger than the 12m antennas. '''One easy way to see how the mosaics compare is to install the AnalysisUtils package (see [[Analysis_Utilities]])'''. Then with AnalysisUtils you can make the following plots (look at the listobs to obtain the sourceid): | |||
== | <source lang="python"> | ||
# In CASA | |||
os.system('rm -rf *m_mosaic.png') | |||
au.plotmosaic('m100_12m_CO.ms',sourceid='0',figfile='12m_mosaic.png') | |||
au.plotmosaic('m100_7m_CO.ms',sourceid='0',figfile='7m_mosaic.png') | |||
</source> | |||
We see that the mosaics cover a common area but that the 7m mosaic is a bit larger. This means that the outer edges of the combined mosaic will be noisier than expected if they overlapped perfectly; this is just something to keep in mind. If you had the case where the mosaic coverages are dramatically different, it would be best to exclude the completely non-overlapping fields from the combination. | |||
NOTE: At this stage one would typically do continuum subtraction (if there is any). However we already know from the individual data reductions that the 3mm continuum emission is quite weak and does not significantly contribute to a 5km/s channel, so we will forgo the the continuum subtraction step. Examples of how to do this if you are so inclined are located in various other ALMA CASAguides. | |||
== Checking the weights and concatenating the data == | |||
<figure id="7m_WT.png"> | <figure id="7m_WT.png"> | ||
[[File:12m_WT.png|200px|thumb|right|<caption> | [[File:12m_WT.png|200px|thumb|right|<caption> 12m weights.</caption>]] | ||
</figure> | </figure> | ||
<figure id="12m_WT.png"> | <figure id="12m_WT.png"> | ||
[[File:7m_WT.png|200px|thumb|right|<caption> | [[File:7m_WT.png|200px|thumb|right|<caption> 7m weights.</caption>]] | ||
</figure> | </figure> | ||
When combining data with disparate properties it is very important | When combining data with disparate properties it is very important that the relative weights of each visibility be in the correct proportion to the other data according to the radiometer equation. Formally, the | ||
that the relative weights of each visibility be in the correct | visibility weights should be proportional to 1/sigma<sup>2</sup> where sigma is the variance or rms noise of a given visibility. | ||
proportion to the other data according to the radiometer equation. | |||
Formally, the | Assuming that the 7m and 12m antennas have similar apperture and quantization efficiencies (a reasonable assumption since they were designed this way), the rms noise in a single channel for a single visibility is: | ||
visibility weights should be proportional to 1/sigma | |||
is the variance or rms noise of a given visibility. | <math> | ||
\sigma_{ij}=\frac{2k}{A_{eff}} | |||
</math> | |||
<math> | |||
\sqrt{\frac{T_{sys,i} T_{sys,j}}{\Delta\nu_{ch} t_{ij}}}, | |||
</math> | |||
where k is Boltzmann's constant, A<sub>eff</sub> is the effective antenna area, T<sub>sys,i</sub> is the system temperature for antenna i, Δν<sub>ch</sub> is the channel width, and t<sub>ij</sub> is the integration time per visibility. | |||
CASA | CASA initially scales the weights by 2Δν<sub>ch</sub>Δt<sub>ij</sub>, and after the Tsys table applycal step of the calibration process, it further scales the weights by 1/[(Tsys(i) * Tsys(j)] as long as calwt=True. In the subsequent gain calibration table applycal step of the calibration, the weights are further scaled by a factor of [(gain(i))<sup>2</sup> * (gain(j))<sup>2</sup>]. The gains should change very little from antenna to antenna, so this scaling is effectively the average gain<sup>4</sup> (again, as long as calwt=True). In the calibration scripts for all executions of the 12m and 7m data, found (here), both applycal steps set calwt=True. To verify, we plot the weights of the 7m and 12m data and measure their ratio to be, on average, 7m/12m ~ 0.055/0.3 ~ 0.18. Note that in the plots the points are colored by SPW, so there is only one 12m CO SPW but there are two 7m CO SPWs, and that no averaging can be turned on when plotting the weights. | ||
calwt=True for the | |||
weights of the 7m and 12m data. | |||
when plotting the weights. | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
os.system('rm -rf 7m_WT.png 12m_WT.png') | os.system('rm -rf 7m_WT.png 12m_WT.png') | ||
plotms(vis='m100_12m_CO.ms',yaxis='wt',xaxis='uvdist',spw='0 | plotms(vis='m100_12m_CO.ms',yaxis='wt',xaxis='uvdist',spw='0:200', | ||
coloraxis='spw',plotfile='12m_WT.png') | coloraxis='spw',plotfile='12m_WT.png') | ||
# | # | ||
plotms(vis='m100_7m_CO.ms',yaxis='wt',xaxis='uvdist',spw='0~ | plotms(vis='m100_7m_CO.ms',yaxis='wt',xaxis='uvdist',spw='0~1:200', | ||
coloraxis='spw',plotfile='7m_WT.png') | coloraxis='spw',plotfile='7m_WT.png') | ||
</source> | </source> | ||
<figure id="combine_CO_WT.png"> | |||
[[File:combine_CO_WT.png|200px|thumb|right|<caption> 7m and 12m weights after concatenation.</caption>]] | |||
<figure id=" | |||
[[File: | |||
</figure> | </figure> | ||
The two key things that are different between the 7m and 12m-array data are that the effective dish areas are different by (7/12)<sup>2</sup>, and the integration times are different by sqrt(10.1/6.05). Since dish area is in the numerator of the radiometer equation and integration time per visibility is in the denominator, and assuming the weight of an individual visibility is proportional to 1/sigma<sup>2</sup>, the ratio of the weights should be (7./12.)<sup>4</sup> x (10.1/6.05) = 0.19. This is very close to the value we measure for the ratio of the weights, particularly given that the 7m flux calibration relied on a source which changed substantially over the course of the six 7m-array observations. | |||
Now concatenate the two data sets and plot the concatenated weights to verify that they are as expected. | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
# Concat and scale weights | # Concat and scale weights | ||
os.system('rm -rf | os.system('rm -rf M100_combine_CO.ms') | ||
concat(vis=['m100_12m_CO.ms','m100_7m_CO.ms'], | concat(vis=['m100_12m_CO.ms','m100_7m_CO.ms'], | ||
concatvis=' | concatvis='M100_combine_CO.ms') | ||
</source> | </source> | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
os.system('rm -rf | os.system('rm -rf combine_CO_WT.png') | ||
plotms(vis=' | plotms(vis='M100_combine_CO.ms',yaxis='wt',xaxis='uvdist',spw='0~2:200', | ||
coloraxis='spw',plotfile=' | coloraxis='spw',plotfile='combine_CO_WT.png') | ||
</source> | </source> | ||
<figure id=" | Here, we create more instructive plots of the combined data to check that things are in order. (''Let each plot finish before cutting and pasting next plot. If plotms gui disappears, exit CASA and restart.'') | ||
[[File: | |||
<figure id="M100_combine_vel.png"> | |||
[[File:M100_combine_vel.png|200px|thumb|right|<caption> Amplitude as a function of velocity.</caption>]] | |||
</figure> | </figure> | ||
To plot amplitude as a function of uv-distance, noting that the 7m data is noisier than the 12m data: | |||
amplitude as a function of uv-distance | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
os.system('rm -rf | os.system('rm -rf M100_combine_uvdist.png') | ||
plotms(vis=' | plotms(vis='M100_combine_CO.ms',yaxis='amp',xaxis='uvdist',spw='', avgscan=True, | ||
avgchannel='5000', | avgchannel='5000', coloraxis='spw',plotfile='M100_combine_uvdist.png') | ||
</source> | </source> | ||
A fairer comparison of these data is achieved by isolating the brightest line channels in individual 12m and 7m data sets (i.e., not the concatenated data sets) and comparing only those channels in amplitude vs. uv-distance. Here the agreement is better, as it is less dominated by the scatter among the several 7m executions. | |||
To plot the CO line as a function of velocity (this plot takes a while): | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
os.system('rm -rf | os.system('rm -rf M100_combine_vel.png') | ||
plotms(vis=' | plotms(vis='M100_combine_CO.ms',yaxis='amp',xaxis='velocity',spw='', avgtime='1e8',avgscan=True,coloraxis='spw',avgchannel='5', | ||
transform=True,freqframe='LSRK',restfreq='115.271201800GHz', plotfile='M100_combine_vel.png') | |||
transform=True,freqframe='LSRK',restfreq='115.271201800GHz', | |||
</source> | </source> | ||
To see each spectral window independently, run the command again but remove plotfile | To see each spectral window independently in plotms, run the command again but remove the call to "plotfile" and add " iteraxis='spw' ". | ||
== Image Using An Automasking Technique == | |||
The commands in this section perform an iterative automasking procedure down | |||
to a user specified threshold=stop*rms where stop is typically 2-3 using the imagemode='mosaic' mode of clean. This mode automatically calculates the correct convolution of the primary beam response of the mosaic when different antenna dish diameters are present. '''NOTE:''' even if these data had only been comprised of a single pointing of 7m and 12m-array data, the imagemode='mosaic' mode would be needed to correctly image data with different antenna sizes. | |||
The procedure outlined below takes some care to ensure that the generated masks (i) only have values of 0 or 1; (ii) are themselves masked at the minpb level. It also removes very small masked regions that are consistent with noise bumps using a function in scipy. A typical setting is to remove mask regions that are 1/2 the beam area in pixels. This is one technique under exploration for future pipeline use. | |||
The commands | The commands have been split into multiple sections to aid cut and paste. Wait until the current one is done before starting next section. '''If you stop CASA and restart you will need to cut and paste again from the Define Parameters section on down'''. | ||
For the long series of commands below it is important to include the '''beginning cpaste''' and '''ending --''' in your cut and paste. | |||
=== Define Parameters === | === Define Parameters === | ||
Note that the parameters used here are by design the same as those used to make the stand-alone 7m-array and 12m-array images. | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
cpaste | |||
### Initialize | ### Initialize | ||
| Line 196: | Line 233: | ||
### Define clean parameters | ### Define clean parameters | ||
vis=' | vis='M100_combine_CO.ms' | ||
prename=' | prename='M100_combine_cube' | ||
myimage=prename+'.image' | myimage=prename+'.image' | ||
myflux=prename+'.flux' | myflux=prename+'.flux' | ||
| Line 212: | Line 249: | ||
nchan=70 | nchan=70 | ||
robust=0.5 | robust=0.5 | ||
phasecenter='J2000 12h22m54.9 + | phasecenter='J2000 12h22m54.9 +15d49m15' | ||
scales=[0] | scales=[0] | ||
smallscalebias=0.6 | smallscalebias=0.6 | ||
### Setup stopping criteria with multiplier for rms. | ### Setup stopping criteria with multiplier for rms. | ||
stop=3. | stop=3. | ||
### Minimum size multiplier for beam area for removing very small mask regions. | ### Minimum size multiplier for beam area for removing very small mask regions. | ||
pixelmin=0.5 | |||
-- | |||
</source> | </source> | ||
=== Make Initial Dirty Image and | === Make Initial Dirty Image and Determine Synthesized Beam area=== | ||
The dirty image is used to determine the initial peak flux density in the cube and the beam area is used to define the minimum size of masked regions in order to exclude noise bumps from the overall mask. | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
cpaste | |||
### Make initial dirty image | ### Make initial dirty image | ||
os.system('rm -rf '+prename+'.* ' +prename+'_*') | os.system('rm -rf '+prename+'.* ' +prename+'_*') | ||
| Line 239: | Line 279: | ||
mask='', | mask='', | ||
niter=0,interactive=F) | niter=0,interactive=F) | ||
# Determine the beam area in pixels for later removal of very small mask regions | |||
major=imhead(imagename=myimage,mode='get',hdkey='beammajor')['value'] | |||
minor=imhead(imagename=myimage,mode='get',hdkey='beamminor')['value'] | |||
pixelsize=float(cell.split('arcsec')[0]) | |||
beamarea=(major*minor*pi/(4*log(2)))/(pixelsize**2) | |||
print 'beamarea in pixels =', beamarea | |||
-- | |||
</source> | </source> | ||
=== Find properties of the dirty image === | === Find properties of the dirty image === | ||
For the long | For the long series of commands below it is important to include the beginning '''cpaste''' and ending '''--''' in your cut and paste. | ||
<source lang="python"> | <source lang="python"> | ||
| Line 252: | Line 301: | ||
bigstat=imstat(imagename=myimage) | bigstat=imstat(imagename=myimage) | ||
peak= bigstat['max'][0] | peak= bigstat['max'][0] | ||
print 'peak in cube = '+str(peak) | print 'peak (Jy/beam) in cube = '+str(peak) | ||
### Sets threshold of first loop, try 2-4. Subsequent loops are set thresh/2 | ### Sets threshold of first loop, try 2-4. Subsequent loops are set thresh/2. | ||
thresh = peak /4. | thresh = peak / 4. | ||
### If True: find the rms in two line-free channels; If False: Set rms by hand in else statement. | ### If True: find the rms in two line-free channels; If False: Set rms by hand in else statement. | ||
| Line 264: | Line 313: | ||
rms=0.5*(rms1+rms2) | rms=0.5*(rms1+rms2) | ||
else: | else: | ||
rms=0. | rms=0.011 | ||
print 'rms in a channel = '+str(rms) | print 'rms (Jy/beam) in a channel = '+str(rms) | ||
-- | -- | ||
</source> | </source> | ||
=== Automasking Loop === | === Automasking Loop === | ||
On a reasonably fast computer the following will take a couple of hours for this spectral mosaic... | |||
<source lang="python"> | <source lang="python"> | ||
| Line 353: | Line 390: | ||
-- | -- | ||
</source> | </source> | ||
=== Notes on the Automasking procedure === | |||
This script is meant to be a possible stepping stone to optimal automasking -- it is by no means perfect and is certainly slower than optimal but feel free to try it with other datasets. Some notes below: | |||
In addition to the final prename.image (prename.flux etc) this script produces and keeps each iteration of the various mask files which will allow you to explore how the masking proceeded as the threshold for masking and cleaning was lowered. The ones denoted "prename. fullmask*.pb.min" are the ones used in the clean steps themselves. At the end of the process the final "prename. fullmask*.pb.min" will also be stored in the prename.mask. Once you've verified you are happy with the masking, you may want to remove the prename.threshmask* and prename.fullmask* files, as they can be large for large cubes. | |||
Additionally, before running the final loop with thresh=stop*rms the script copies the .image from the preceding clean to prename.image'n' where 'n' equals the loop number of the preceding step. So in this M100 example you will see a M100_combine_cube.image and a M100_combine_cube.image2 where .image is the final image and .image2 is the next to last image. This is done for convenience in the case that thresh=stop*rms is too deep such that clean diverges, you will still be left with the clean image from the preceding loop that you can further investigate to understand why clean diverged. If all goes well with the final loop, the prename.image'n' can also be deleted. Divergence at thresh=stop*rms is often a sign that the image is "dynamic range limited" in other words the rms in channels with bright emission is significantly worse than for a line-free channel. | |||
== Image Analysis for the 7m+12m Data == | |||
=== Moment Maps for 7m+12m CO (1-0) Cube === | |||
Start by examining the final image cube. Determine the start and stopping channels for the line emission -- this will be used in the "chans" parameter of immoments. | |||
<source lang="python"> | |||
# In CASA | |||
viewer('M100_combine_cube.image') | |||
</source> | |||
Next determine the rms noise per channel and use that to exclude pixels from the moment images. All images are shown in the gallery at the end of the following section. | |||
<source lang="python"> | |||
# In CASA | |||
myimage='M100_combine_cube.image' | |||
chanstat=imstat(imagename=myimage,chans='4') | |||
rms1= chanstat['rms'][0] | |||
chanstat=imstat(imagename=myimage,chans='66') | |||
rms2= chanstat['rms'][0] | |||
rms=0.5*(rms1+rms2) | |||
print 'rms in a channel = '+str(rms) | |||
</source> | |||
Next make the moment maps. For the integrated intensity: moment 0, a 2 sigma cut often considerably improves the appearance of the image with little effect on the integrated intensity as long as emission free channels are excluded. For higher order moments it is necessary to exclude all low S/N data. Typically 5-6 sigma for the higher moments works well. We also apply further masking based on the .flux image because the edges of the combined mosaic are especially noisy because the 7m mosaic is somewhat larger than the 12m mosaic as described above (see Figures 1 & 2). | |||
<source lang="python"> | |||
# In CASA | |||
cpaste | |||
os.system('rm -rf M100_combine_cube.image.mom0') | |||
immoments(imagename = 'M100_combine_cube.image', | |||
moments = [0], | |||
axis = 'spectral',chans = '9~61', | |||
mask='M100_combine_cube.flux>0.3',, | |||
includepix = [rms*2,100.], | |||
outfile = 'M100_combine_cube.image.mom0') | |||
os.system('rm -rf M100_combine_cube.image.mom1') | |||
immoments(imagename = 'M100_combine_cube.image', | |||
moments = [1], | |||
axis = 'spectral',chans = '9~61', | |||
mask='M100_combine_cube.flux>0.3', | |||
includepix = [rms*5.5,100.], | |||
outfile = 'M100_combine_cube.image.mom1') | |||
-- | |||
</source> | |||
Now we can make some figures showing the moment maps (*note that this creates different looking files for me than the ones I have included here, which were made in the viewer -- is this true for others?*): | |||
<source lang="python"> | |||
# In CASA | |||
cpaste | |||
os.system('rm -rf M100_combine_cube.image.mom*.png') | |||
imview (raster=[{'file': 'M100_combine_cube.image.mom0', | |||
'range': [-0.3,25.],'scaling': -1.3,'colorwedge': T}], | |||
zoom={'blc': [190,150],'trc': [650,610]}, | |||
out='M100_combine_cube.image.mom0.png') | |||
imview (raster=[{'file': 'M100_combine_cube.image.mom1', | |||
'range': [1440,1695],'colorwedge': T}], | |||
zoom={'blc': [190,150],'trc': [650,610]}, | |||
out='M100_combine_cube.image.mom1.png') | |||
-- | |||
</source> | |||
If you plan to use your moment 0 image to make measurements, it needs to be primary beam corrected first. First we need to subimage the .flux cube to extract a single plane that can be used to primary beam correct the moment 0 image. | |||
<source lang="python"> | |||
# In CASA | |||
os.system('rm -rf M100_combine_cube.flux.1ch') | |||
imsubimage(imagename='M100_combine_cube.flux', | |||
outfile='M100_combine_cube.flux.1ch', | |||
chans='35') | |||
</source> | |||
Then primary beam correct the moment 0 image. This is the version that would be used for measurements, though the uncorrected one can be useful for figures. The difference is clear in the images seen below in the following section. | |||
<source lang="python"> | |||
# In CASA | |||
os.system('rm -rf M100_combine_cube.image.mom0.pbcor') | |||
immath(imagename=['M100_combine_cube.image.mom0', \ | |||
'M100_combine_cube.flux.1ch'], | |||
expr='IM0/IM1', | |||
outfile='M100_combine_cube.image.mom0.pbcor') | |||
</source> | |||
Have a look at the difference the primary beam correction makes. | |||
<source lang="python"> | |||
# In CASA | |||
imview (raster=[{'file': 'M100_combine_cube.image.mom0', | |||
'range': [-0.3,25.],'scaling': -1.3}, | |||
{'file': 'M100_combine_cube.image.mom0.pbcor', | |||
'range': [-0.3,25.],'scaling': -1.3}], | |||
zoom={'blc': [190,150],'trc': [650,610]}) | |||
</source> | |||
With the viewer open, you can flip back and forth between the images to compare them. Next, make a figure. | |||
<source lang="python"> | |||
# In CASA | |||
os.system('rm -rf M100_combine_cube.image.mom0.pbcor.png') | |||
imview (raster=[{'file': 'M100_combine_cube.image.mom0.pbcor', | |||
'range': [-0.3,25.],'scaling': -1.3,'colorwedge': T}], | |||
zoom={'blc': [190,150],'trc': [650,610]}, | |||
out='M100_combine_cube.image.mom0.pbcor.png') | |||
</source> | |||
=== Comparison with 7m, 12m Moment Maps === | |||
Below the moment maps from the 7m-only and the 12m-only data are shown for comparison. The moment maps were made using clean masks drawn by hand for comparison to the automasking technique; the two appear to be qualitatively similar. The range and scaling for the 12m-only figures are the same as that used for the 7m+12m figures for ease of comparison. | |||
As expected, the 7m+12m image shows considerably more extended emission than the 12m-only data and finer detail than the 7m-only data. For comparison, the 7m+12m synthesized beam is 3.80"x2.50", while the 12m-only beam is 3.46"x2.37" and the 7m-only beam is 12.71"x10.09". | |||
<gallery widths=300px heights=300px> | |||
File:12m.png | Moment 0 for 12m data alone (no primary beam correction). | |||
File:7m.png | Moment 0 for 7m data alone (no primary beam correction). | |||
File:combined.png | Moment 0 for 12m+7m data (no primary beam correction). | |||
File:combine_pbcor.png | Moment 0 for 12m+7m data with primary beam correction. | |||
</gallery> | |||
<gallery widths=300px heights=300px> | |||
File:12m_mom1.png | Moment 1 for 12m data alone. | |||
File:7m_mom1.png | Moment 1 for 7m data alone. | |||
File:combine_mom1.png | Moment 1 for 12m+7m data. | |||
</gallery> | |||
=== Convert 7m+12m Images to Fits Format === | |||
<source lang="python"> | |||
# In CASA | |||
cpaste | |||
os.system('rm -rf *.fits') | |||
exportfits(imagename='M100_combine_cube.image',fitsimage='M100_combine_cube.image.fits') | |||
exportfits(imagename='M100_combine_cube.flux',fitsimage='M100_combine_cube.flux.fits') | |||
exportfits(imagename='M100_combine_cube.image.mom0',fitsimage='M100_combine_cube.image.mom0.fits') | |||
exportfits(imagename='M100_combine_cube.image.mom0.pbcor',fitsimage='M100_combine_cube.image.mom0.pbcor.fits') | |||
exportfits(imagename='M100_combine_cube.image.mom1',fitsimage='M100_combine_cube.image.mom1.fits') | |||
-- | |||
</source> | |||
= Feathering the Total Power and 7m+12m Interferometric Images= | |||
== Image the Total Power Data == | |||
Run listobs on the total power data to see what spw contains the CO | |||
<source lang="python"> | |||
In CASA | |||
os.system('rm -rf concat_m100.ms.listobs') | |||
listobs(vis='concat_m100.ms',listfile='concat_m100.ms.listobs') | |||
</source> | |||
Image the TP data | |||
<source lang="python"> | |||
In CASA | |||
os.system('rm -rf TP_CO_cube') | |||
sdimaging(infile='concat_m100.ms', | |||
field=0,spw=15, | |||
specunit='km/s',restfreq='115.271204GHz', | |||
dochannelmap=True, | |||
nchan=70,start=1400,step=5, | |||
gridfunction='gjinc',imsize=[50,50], | |||
cell=['10arcsec','10arcsec'], | |||
outfile='TP_CO_cube') | |||
</source> | |||
=== Determine the TP Restoring Beam and Convert to Jy/beam === | |||
Next we need to determine the restoring beam size. This will depend | |||
on 3 factors | |||
(1) The expected FWHP for the 12m TP dishes which have a -12dB taper | |||
and a Gaussian shape. This is 1.17 lambda / 12m (radians) | |||
(2) Any broadening of the beam due to less than ideal sampling. For | |||
an antenna with -12dB taper, Nyquist = FWHM/2.4. To have less than | |||
1% broadening the sampling should be 2 x Nyquist. | |||
(3) The convolution of the gridding kernel with the combination of | |||
(1) and (2) | |||
<figure id="TP_sampling.png"> | |||
[[File:TP_sampling.png|300px|thumb|right|<caption> TP raster pointings.</caption>]] | |||
</figure> | |||
We have chosen the "gjinc" function in sdimaging because it produces the lease broadening of the effective beam. This is important because any broadening of the effective beam is equivalent to having used a smaller antenna. | |||
For more information on these topics, see Mangum et al. 2007 | |||
(http://adsabs.harvard.edu/abs/2007A%26A...474..679M) | |||
Two functions in the analysis utilities suite can be used to calculate the sampling of the TP data in the X and Y directions and then the final restoring beam, respectively. | |||
<source lang="python"> | |||
In CASA | |||
xSampling,ySampling=au.getTPSampling('concat_m100.ms', | |||
showplot=True,plotfile='TP_sampling.png') | |||
</source> | |||
xSampling = 10.3766 arcsec | |||
ySampling = 15.0002 arcsec | |||
The '''frequency required for au.gjincBeam is the observed sky frequency near the center of the line''' (not the rest | |||
frequency). The pixelsize should be the same as that used for the cell in sdimaging. The sampling parameters were determined by au.getTPSampling | |||
<source lang="python"> | |||
In CASA | |||
RestorBeam=au.gjincBeam(frequency=114.66,pixelsize=10,xSamplingArcsec=xSampling,ySamplingArcsec=ySampling) | |||
</source> | |||
The output to the terminal will be: | |||
Theoretical primary beam FWHP = 52.5822 arcsec | |||
Expected effective restoring beam along scan = 54.4937 arcsec | |||
Expected effective restoring beam between rows = 54.9774 arcsec | |||
Geometric mean = 54.735 arcsec | |||
Next set the restoring beam to the derived value. | |||
<source lang="python"> | |||
In CASA | |||
ia.open('TP_CO_cube') | |||
ia.setrestoringbeam(major=str(RestorBeam)+'arcsec', | |||
minor=str(RestorBeam)+'arcsec', | |||
pa='0deg') | |||
ia.done() | |||
</source> | |||
Convert the image from K to Jy assuming Jy/K = 55.0 | |||
Note currently sdimaging reports that the image it makes is | |||
in Jy/beam. This is a bug. | |||
<source lang="python"> | |||
In CASA | |||
os.system('rm -rf TP_CO_cube_Jy') | |||
immath(imagename='TP_CO_cube', | |||
expr='IM0*55.0', | |||
outfile='TP_CO_cube_Jy') | |||
</source> | |||
== Prepare Images for Feathering == | |||
Regrid TP image to match the shape of the 7m+12m image. | |||
<source lang="python"> | |||
In CASA | |||
os.system('rm -rf TP_CO_cube_Jy.regrid') | |||
imregrid(imagename='TP_CO_cube_Jy', | |||
template='M100_Intcombo_0.193_cube.image', | |||
shape=[800,800,1,70], | |||
axes=[0,1],output='TP_CO_cube_Jy.regrid') | |||
</source> | |||
Subimage both images to a matching size, excluding regions masked by the clean pbmin=0.2 and noisy edge pixels in the TP image. The Viewer can be used to determine a good joint region. | |||
<source lang="python"> | |||
In CASA | |||
os.system('rm -rf M100_Intcombo_0.193_cube.image.subim') | |||
imsubimage(imagename='M100_Intcombo_0.193_cube.image', | |||
outfile='M100_Intcombo_0.193_cube.image.subim', | |||
box='230,184,604,598') | |||
os.system('rm -rf TP_CO_cube_Jy.regrid.subim') | |||
imsubimage(imagename='TP_CO_cube_Jy.regrid', | |||
outfile='TP_CO_cube_Jy.regrid.subim', | |||
box='230,184,604,598') | |||
</source> | |||
Creat subimaged version the mosaic response | |||
<source lang="python"> | |||
In CASA | |||
os.system('rm -rf M100_Intcombo_0.193_cube.flux.subim') | |||
imsubimage(imagename='M100_Intcombo_0.193_cube.flux', | |||
outfile='M100_Intcombo_0.193_cube.flux.subim', | |||
box='230,184,604,598') | |||
</source> | |||
Multiply the TP image by the mosaic beam response of the 7m+12m image | |||
<source lang="python"> | |||
In CASA | |||
os.system('rm -rf TP_CO_cube_Jy.regrid.subim.depb') | |||
immath(imagename=['TP_CO_cube_Jy.regrid.subim', | |||
'M100_Intcombo_0.193_cube.flux.subim'], | |||
expr='IM0*IM1', | |||
outfile='TP_CO_cube_Jy.regrid.subim.depb') | |||
</source> | |||
== Feather TP Cube with 7m+12m Cube == | |||
Feather with default parameters | |||
<source lang="python"> | |||
In CASA | |||
os.system('rm -rf M100_Feather_CO') | |||
feather(imagename='M100_Feather_CO', | |||
highres='M100_Intcombo_0.193_cube.image.subim', | |||
lowres='TP_CO_cube_Jy.regrid.subim.depb') | |||
</source> | |||
== Make Moment Maps of TP and Feathered Images == | |||
We will use the same technique as the 7m+12m image analysis above to make moment maps. | |||
First, make moment maps for the TP image. | |||
<source lang="python"> | |||
In CASA | |||
myimage='TP_CO_cube_Jy.regrid.subim' | |||
chanstat=imstat(imagename=myimage,chans='4') | |||
rms1= chanstat['rms'][0] | |||
chanstat=imstat(imagename=myimage,chans='66') | |||
rms2= chanstat['rms'][0] | |||
rms=0.5*(rms1+rms2) | |||
os.system('rm -rf TP_CO_cube_Jy.regrid.subim.mom0') | |||
immoments(imagename = 'TP_CO_cube_Jy.regrid.subim', | |||
moments = [0], | |||
axis = 'spectral', | |||
chans = '10~61', | |||
includepix = [rms*2.,50], | |||
outfile = 'TP_CO_cube_Jy.regrid.subim.mom0') | |||
os.system('rm -rf TP_CO_cube_Jy.regrid.subim.mom1') | |||
immoments(imagename = 'TP_CO_cube_Jy.regrid.subim', | |||
moments = [1], | |||
axis = 'spectral', | |||
chans = '10~61', | |||
includepix = [rms*5.5,50], | |||
outfile = 'TP_CO_cube_Jy.regrid.subim.mom1') | |||
</source> | |||
<source lang="python"> | |||
In CASA | |||
os.system('rm -rf TP_CO_cube_Jy.regrid.subim .mom*.png') | |||
imview (raster=[{'file': 'TP_CO_cube_Jy.regrid.subim.mom0', | |||
'range': [-0.3,900.],'scaling': -1.0,'colorwedge': T}], | |||
out='TP_CO_cube_Jy.regrid.subim.mom0.png') | |||
imview (raster=[{'file': 'TP_CO_cube_Jy.regrid.subim.mom1', | |||
'range': [1455,1695],'colorwedge': T}], | |||
out='TP_CO_cube_Jy.regrid.subim.mom1.png') | |||
</source> | |||
Make moment maps for the feathered image. | |||
<source lang="python"> | |||
In CASA | |||
myimage='M100_Feather_CO' | |||
chanstat=imstat(imagename=myimage,chans='4') | |||
rms1= chanstat['rms'][0] | |||
chanstat=imstat(imagename=myimage,chans='66') | |||
rms2= chanstat['rms'][0] | |||
rms=0.5*(rms1+rms2) | |||
os.system('rm -rf M100_Feather_CO.mom0') | |||
immoments(imagename = 'M100_Feather_CO', | |||
moments = [0], | |||
axis = 'spectral', | |||
chans = '10~61', | |||
includepix = [rms*2.,50], | |||
outfile = 'M100_Feather_CO.mom0') | |||
os.system('rm -rf M100_Feather_CO.mom1') | |||
immoments(imagename = 'M100_Feather_CO', | |||
moments = [1], | |||
axis = 'spectral', | |||
chans = '10~61', | |||
includepix = [rms*5.5,50], | |||
outfile = 'M100_Feather_CO.mom1') | |||
</source> | |||
<source lang="python"> | |||
In CASA | |||
os.system('rm -rf M100_Feather_CO.mom*.png') | |||
imview (raster=[{'file': 'M100_Feather_CO.mom0', | |||
'range': [-0.3,25.],'scaling': -1.0,'colorwedge': T}], | |||
out='M100_Feather_CO.mom0.png') | |||
imview (raster=[{'file': 'M100_Feather_CO.mom1', | |||
'range': [1455,1695],'colorwedge': T}], | |||
out='M100_Feather_CO.mom1.png') | |||
</source> | |||
=== Primary Beam Correct the Moment 0 Image === | |||
Apply the primary beam response to the feathered image | |||
<source lang="python"> | |||
In CASA | |||
os.system('rm -rf M100_Intcombo_0.193_cube.flux.1ch.subimage') | |||
imsubimage(imagename='M100_Intcombo_0.193_cube.flux', | |||
outfile='M100_Intcombo_0.193_cube.flux.1ch.subimage', | |||
box='230,184,604,598', | |||
chans='35') | |||
</source> | |||
<source lang="python"> | |||
In CASA | |||
os.system('rm -rf M100_Feather_CO.mom0.pbcor') | |||
immath(imagename=['M100_Feather_CO.mom0', \ | |||
'M100_Intcombo_0.193_cube.flux.1ch.subimage'], | |||
expr='IM0/IM1', | |||
outfile='M100_Feather_CO.mom0.pbcor') | |||
</source> | |||
Create a figure of primary beam corrected moment 0. | |||
<source lang="python"> | |||
In CASA | |||
os.system('rm -rf M100_Feather_CO.mom0.pbcor.png') | |||
imview (raster=[{'file': 'M100_Feather_CO.mom0.pbcor', | |||
'range': [-0.3,25.],'scaling': -1.0,'colorwedge': T}], | |||
out='M100_Feather_CO.mom0.pbcor.png') | |||
</source> | |||
=== Compare the Different Images === | |||
Now lets compare all the different images: | |||
<gallery perrow=3 widths=300px heights=300px> | |||
File:12m_pbcor.png | Primary beam corrected moment 0 for the 12m data. | |||
File:7m_pbcor.png | Primary beam corrected moment 0 for the 7m data. | |||
File:TP_CO_cube_Jy.regrid.subim.mom0.png | Moment 0 for the TP data (UPDATE). | |||
File:combine_pbcor.png | Primary beam corrected moment 0 for 7m+12m data. | |||
File:M100_Feather_CO.mom0.pbcor.png | Primary beam corrected moment 0 for TP+7m+12m data (UPDATE). | |||
</gallery> | |||
<gallery perrow=3 widths=300px heights=300px> | |||
File:12m_mom1.png | Moment 1 for 12m data. | |||
File:7m_mom1.png | Moment 1 for 7m data. | |||
File:TP_CO_cube_Jy.regrid.subim.mom1.png | Moment 1 for the TP data (UPDATE). | |||
File:combine_mom1.png | Moment 1 for 7m+12m data. | |||
File:M100_Feather_CO.mom1.png | Moment 1 for TP+7m+12m data (UPDATE). | |||
</gallery> | |||
{{Checked 4.1.0}} | |||
Latest revision as of 23:30, 19 May 2015
This page is currently under construction.
DO NOT USE IT.
To navigate the CASAguides pages, visit [http://casaguides.nrao.edu/ casaguides.nrao.edu ]
Overview
This guide describes how to combine the 7m and 12m interferometric data and then how to feather the resulting image with the total power TP image. All of the data for this SV project can be found at https://almascience.nrao.edu/alma-data/science-verification. The guide has been written for data reduced in CASA 4.3.0 or later and assumes that all calibration tables (Tsys and gain tables) have been applied to the visibility weights using calwt=True. If either of these is not the case for your data, do not follow this guide.
In order to run this guide you will need to:
- Either download the fully calibrated 7m data (i.e., M100_Band3_7m_CalibratedData.tgz) or download the uncalibrated 7m data and the relevant, standard calibration scripts available (here)
- Either download the fully calibrated 12m data (i.e. M100_Band3_12m_CalibratedData.tgz) or download the uncalibrated 12m data and the relevant, standard calibration scripts available (here). Note that this is a new calibration of the same data that were released previously, and so the data reduction path has been updated to current best practices and starts from the raw data files called ASDMs (ALMA Science Data Model). Do not use the previously released uncalibrated or calibrated data.
- Either run the M100_Band3_SingleDish_4.3 guide to calibrate and image the Total Power data or download the final image (i.e. M100_TP_Image.tgz)
Confirm your version of CASA
This guide has been written for CASA release 4.3.0. Please confirm your version before proceeding.
# In CASA
version = casadef.casa_version
print "You are using " + version
if (version < '4.3.0'):
print "YOUR VERSION OF CASA IS TOO OLD FOR THIS GUIDE."
print "PLEASE UPDATE IT BEFORE PROCEEDING."
else:
print "Your version of CASA is appropriate for this guide."
Combine and Image the 7m+12m Interferometric Data
Split off CO spectral windows (SPWs)
# In CASA
os.system('rm -rf m100_*m.ms.listobs')
listobs('M100_Band3_12m_CalibratedData.ms',listfile='m100_12m.ms.listobs')
listobs('M100_Band3_7m_CalibratedData.ms',listfile='m100_7m.ms.listobs')
Running the task "listobs" provides the setups used in the observations at a glance. Below are the first target scans of the 12m and 7m observations and the spectral window tables as generated by listobs. The six 7m data sets were taken with two slightly different correlator setups (one with four SPWs and the other with two SPWs), so the concatenated data set has six total SPWs.
12m data: ObservationID = 0 ArrayID = 0 Date Timerange (UTC) Scan FldId FieldName nRows SpwIds Average Interval(s) ScanIntent 10-Aug-2011/19:38:05.8 - 19:50:22.8 11 1 M100 1500 [0,1,2,3] [6.05, 6.05, 6.05, 6.05] [CALIBRATE_WVR#ON_SOURCE,OBSERVE_TARGET#ON_SOURCE] Spectral Windows: (4 unique spectral windows and 1 unique polarization setups) SpwID Name #Chans Frame Ch0(MHz) ChanWid(kHz) TotBW(kHz) CtrFreq(MHz) BBC Num Corrs 0 3840 TOPO 113726.419 488.281 1875000.0 114663.6750 1 XX YY 1 3840 TOPO 111851.419 488.281 1875000.0 112788.6750 2 XX YY 2 3840 TOPO 103663.431 -488.281 1875000.0 102726.1750 3 XX YY 3 3840 TOPO 101850.931 -488.281 1875000.0 100913.6750 4 XX YY 7m data: ObservationID = 0 ArrayID = 0 Date Timerange (UTC) Scan FldId FieldName nRows SpwIds Average Interval(s) ScanIntent 17-Mar-2013/04:44:04.3 - 04:50:43.7 11 1 M100 261 [0,1,2,3] [10.1, 10.1, 10.1, 10.1] [OBSERVE_TARGET#ON_SOURCE] Spectral Windows: (6 unique spectral windows and 1 unique polarization setups) SpwID Name #Chans Frame Ch0(MHz) ChanWid(kHz) TotBW(kHz) CtrFreq(MHz) BBC Num Corrs 0 ALMA_RB_03#BB_1#SW-01#FULL_RES 4080 TOPO 101945.850 -488.281 1992187.5 100950.0000 1 XX YY 1 ALMA_RB_03#BB_2#SW-01#FULL_RES 4080 TOPO 103761.000 -488.281 1992187.5 102765.1500 2 XX YY 2 ALMA_RB_03#BB_3#SW-01#FULL_RES 4080 TOPO 111811.300 488.281 1992187.5 112807.1500 3 XX YY 3 ALMA_RB_03#BB_4#SW-01#FULL_RES 4080 TOPO 113686.300 488.281 1992187.5 114682.1500 4 XX YY 4 ALMA_RB_03#BB_1#SW-01#FULL_RES 4080 TOPO 111798.250 488.281 1992187.5 112794.1000 1 XX YY 5 ALMA_RB_03#BB_2#SW-01#FULL_RES 4080 TOPO 113673.250 488.281 1992187.5 114669.1000 2 XX YY
<figure id="12m_mosaic.png">
</figure>
<figure id="7m_mosaic.png">
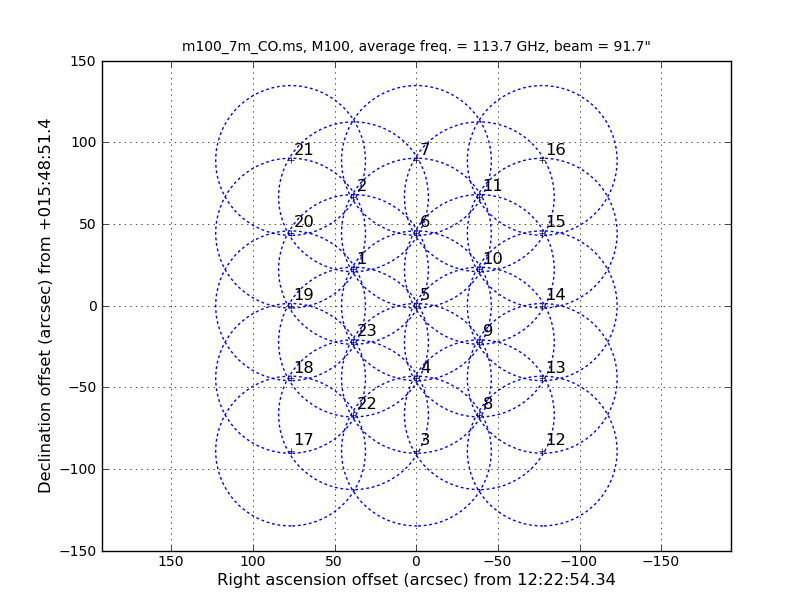
</figure>
Examination of the listobs files shows that the CO is in SPW='0' for the 12m data and in SPW='3,5' for the 7m data. There are two SPWs containing CO in the 7m data due to the slightly differing correlator setups.
Also note that the integration time per visibility (average interval parameter in listobs) is different: 6.05s for the 12m data and 10.1s for the 7m. This will be important to know later when we check the visibility weights.
Next we split out the CO spectral windows.
# In CASA
os.system('rm -rf m100_12m_CO.ms')
split(vis='M100_Band3_12m_CalibratedData.ms',
outputvis='m100_12m_CO.ms',spw='0',field='M100',
datacolumn='data',keepflags=False)
os.system('rm -rf m100_7m_CO.ms')
split(vis='M100_Band3_7m_CalibratedData.ms',
outputvis='m100_7m_CO.ms',spw='3,5',field='M100',
datacolumn='data',keepflags=False)
Also of interest is that the 12m data has 47 fields and the 7m has 23 fields (not shown in the excerpts above). The difference in number of pointings is because the 7m antennas have a FWHP (full width half power) primary beam diameter that is 12/7 times larger than the 12m antennas. One easy way to see how the mosaics compare is to install the AnalysisUtils package (see Analysis_Utilities). Then with AnalysisUtils you can make the following plots (look at the listobs to obtain the sourceid):
# In CASA
os.system('rm -rf *m_mosaic.png')
au.plotmosaic('m100_12m_CO.ms',sourceid='0',figfile='12m_mosaic.png')
au.plotmosaic('m100_7m_CO.ms',sourceid='0',figfile='7m_mosaic.png')
We see that the mosaics cover a common area but that the 7m mosaic is a bit larger. This means that the outer edges of the combined mosaic will be noisier than expected if they overlapped perfectly; this is just something to keep in mind. If you had the case where the mosaic coverages are dramatically different, it would be best to exclude the completely non-overlapping fields from the combination.
NOTE: At this stage one would typically do continuum subtraction (if there is any). However we already know from the individual data reductions that the 3mm continuum emission is quite weak and does not significantly contribute to a 5km/s channel, so we will forgo the the continuum subtraction step. Examples of how to do this if you are so inclined are located in various other ALMA CASAguides.
Checking the weights and concatenating the data
<figure id="7m_WT.png">
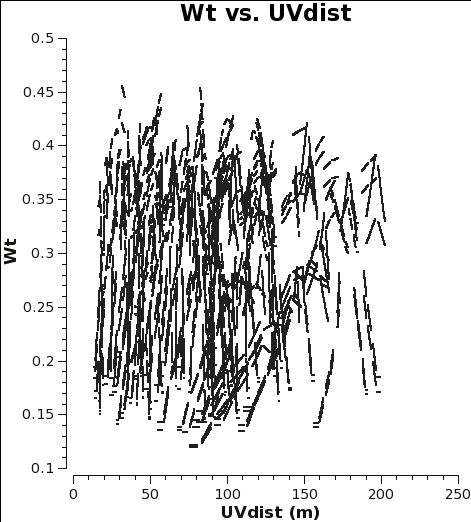
</figure>
<figure id="12m_WT.png">
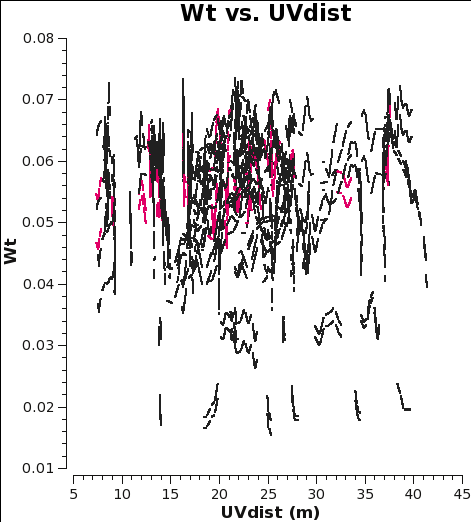
</figure>
When combining data with disparate properties it is very important that the relative weights of each visibility be in the correct proportion to the other data according to the radiometer equation. Formally, the visibility weights should be proportional to 1/sigma2 where sigma is the variance or rms noise of a given visibility.
Assuming that the 7m and 12m antennas have similar apperture and quantization efficiencies (a reasonable assumption since they were designed this way), the rms noise in a single channel for a single visibility is:
[math]\displaystyle{ \sigma_{ij}=\frac{2k}{A_{eff}} }[/math] [math]\displaystyle{ \sqrt{\frac{T_{sys,i} T_{sys,j}}{\Delta\nu_{ch} t_{ij}}}, }[/math]
where k is Boltzmann's constant, Aeff is the effective antenna area, Tsys,i is the system temperature for antenna i, Δνch is the channel width, and tij is the integration time per visibility.
CASA initially scales the weights by 2ΔνchΔtij, and after the Tsys table applycal step of the calibration process, it further scales the weights by 1/[(Tsys(i) * Tsys(j)] as long as calwt=True. In the subsequent gain calibration table applycal step of the calibration, the weights are further scaled by a factor of [(gain(i))2 * (gain(j))2]. The gains should change very little from antenna to antenna, so this scaling is effectively the average gain4 (again, as long as calwt=True). In the calibration scripts for all executions of the 12m and 7m data, found (here), both applycal steps set calwt=True. To verify, we plot the weights of the 7m and 12m data and measure their ratio to be, on average, 7m/12m ~ 0.055/0.3 ~ 0.18. Note that in the plots the points are colored by SPW, so there is only one 12m CO SPW but there are two 7m CO SPWs, and that no averaging can be turned on when plotting the weights.
# In CASA
os.system('rm -rf 7m_WT.png 12m_WT.png')
plotms(vis='m100_12m_CO.ms',yaxis='wt',xaxis='uvdist',spw='0:200',
coloraxis='spw',plotfile='12m_WT.png')
#
plotms(vis='m100_7m_CO.ms',yaxis='wt',xaxis='uvdist',spw='0~1:200',
coloraxis='spw',plotfile='7m_WT.png')
<figure id="combine_CO_WT.png">
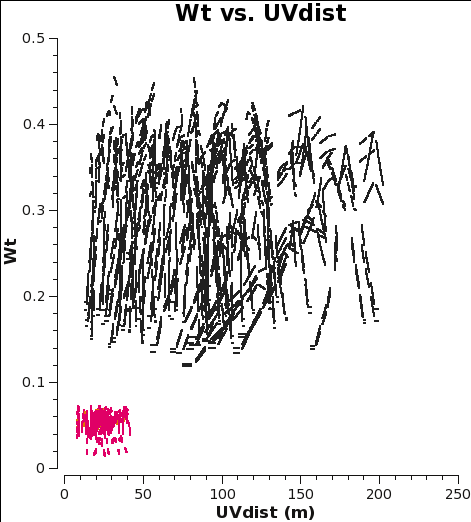
</figure>
The two key things that are different between the 7m and 12m-array data are that the effective dish areas are different by (7/12)2, and the integration times are different by sqrt(10.1/6.05). Since dish area is in the numerator of the radiometer equation and integration time per visibility is in the denominator, and assuming the weight of an individual visibility is proportional to 1/sigma2, the ratio of the weights should be (7./12.)4 x (10.1/6.05) = 0.19. This is very close to the value we measure for the ratio of the weights, particularly given that the 7m flux calibration relied on a source which changed substantially over the course of the six 7m-array observations.
Now concatenate the two data sets and plot the concatenated weights to verify that they are as expected.
# In CASA
# Concat and scale weights
os.system('rm -rf M100_combine_CO.ms')
concat(vis=['m100_12m_CO.ms','m100_7m_CO.ms'],
concatvis='M100_combine_CO.ms')
# In CASA
os.system('rm -rf combine_CO_WT.png')
plotms(vis='M100_combine_CO.ms',yaxis='wt',xaxis='uvdist',spw='0~2:200',
coloraxis='spw',plotfile='combine_CO_WT.png')
Here, we create more instructive plots of the combined data to check that things are in order. (Let each plot finish before cutting and pasting next plot. If plotms gui disappears, exit CASA and restart.)
<figure id="M100_combine_vel.png">
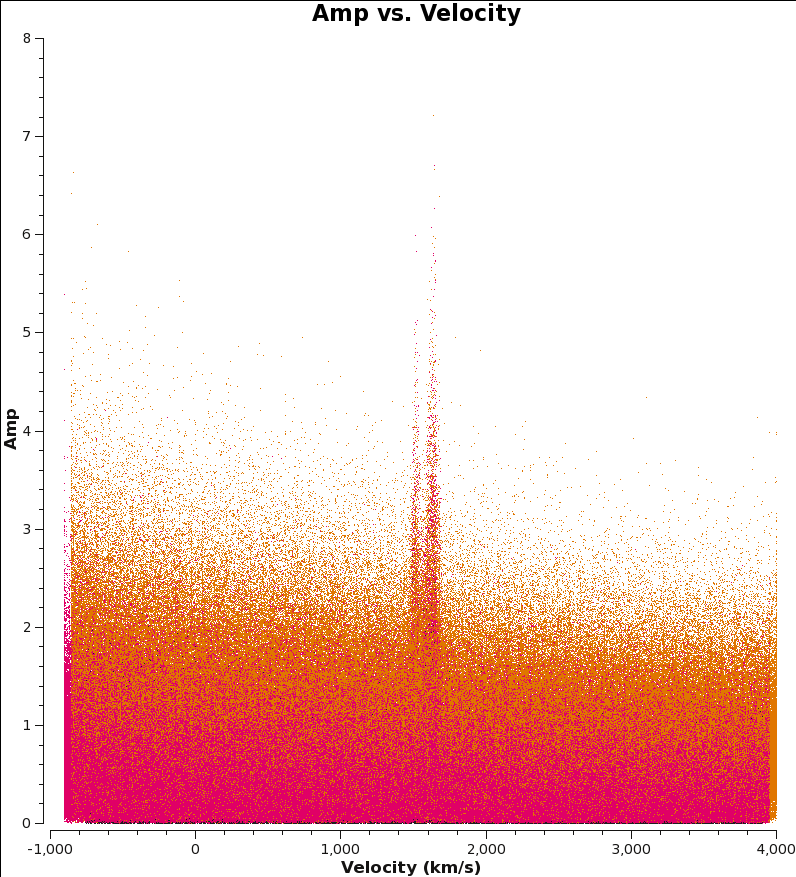
</figure>
To plot amplitude as a function of uv-distance, noting that the 7m data is noisier than the 12m data:
# In CASA
os.system('rm -rf M100_combine_uvdist.png')
plotms(vis='M100_combine_CO.ms',yaxis='amp',xaxis='uvdist',spw='', avgscan=True,
avgchannel='5000', coloraxis='spw',plotfile='M100_combine_uvdist.png')
A fairer comparison of these data is achieved by isolating the brightest line channels in individual 12m and 7m data sets (i.e., not the concatenated data sets) and comparing only those channels in amplitude vs. uv-distance. Here the agreement is better, as it is less dominated by the scatter among the several 7m executions.
To plot the CO line as a function of velocity (this plot takes a while):
# In CASA
os.system('rm -rf M100_combine_vel.png')
plotms(vis='M100_combine_CO.ms',yaxis='amp',xaxis='velocity',spw='', avgtime='1e8',avgscan=True,coloraxis='spw',avgchannel='5',
transform=True,freqframe='LSRK',restfreq='115.271201800GHz', plotfile='M100_combine_vel.png')
To see each spectral window independently in plotms, run the command again but remove the call to "plotfile" and add " iteraxis='spw' ".
Image Using An Automasking Technique
The commands in this section perform an iterative automasking procedure down to a user specified threshold=stop*rms where stop is typically 2-3 using the imagemode='mosaic' mode of clean. This mode automatically calculates the correct convolution of the primary beam response of the mosaic when different antenna dish diameters are present. NOTE: even if these data had only been comprised of a single pointing of 7m and 12m-array data, the imagemode='mosaic' mode would be needed to correctly image data with different antenna sizes.
The procedure outlined below takes some care to ensure that the generated masks (i) only have values of 0 or 1; (ii) are themselves masked at the minpb level. It also removes very small masked regions that are consistent with noise bumps using a function in scipy. A typical setting is to remove mask regions that are 1/2 the beam area in pixels. This is one technique under exploration for future pipeline use.
The commands have been split into multiple sections to aid cut and paste. Wait until the current one is done before starting next section. If you stop CASA and restart you will need to cut and paste again from the Define Parameters section on down.
For the long series of commands below it is important to include the beginning cpaste and ending -- in your cut and paste.
Define Parameters
Note that the parameters used here are by design the same as those used to make the stand-alone 7m-array and 12m-array images.
# In CASA
cpaste
### Initialize
import scipy.ndimage
### Define clean parameters
vis='M100_combine_CO.ms'
prename='M100_combine_cube'
myimage=prename+'.image'
myflux=prename+'.flux'
mymask=prename+'.mask'
myresidual=prename+'.residual'
imsize=800
cell='0.5arcsec'
minpb=0.2
restfreq='115.271201800GHz'
outframe='LSRK'
spw='0~2'
width='5km/s'
start='1400km/s'
nchan=70
robust=0.5
phasecenter='J2000 12h22m54.9 +15d49m15'
scales=[0]
smallscalebias=0.6
### Setup stopping criteria with multiplier for rms.
stop=3.
### Minimum size multiplier for beam area for removing very small mask regions.
pixelmin=0.5
--
Make Initial Dirty Image and Determine Synthesized Beam area
The dirty image is used to determine the initial peak flux density in the cube and the beam area is used to define the minimum size of masked regions in order to exclude noise bumps from the overall mask.
# In CASA
cpaste
### Make initial dirty image
os.system('rm -rf '+prename+'.* ' +prename+'_*')
clean(vis=vis,imagename=prename,
imagermode='mosaic',ftmachine='mosaic',minpb=minpb,
imsize=imsize,cell=cell,spw=spw,
weighting='briggs',robust=robust,phasecenter=phasecenter,
mode='velocity',width=width,start=start,nchan=nchan,
restfreq=restfreq,outframe=outframe,veltype='radio',
mask='',
niter=0,interactive=F)
# Determine the beam area in pixels for later removal of very small mask regions
major=imhead(imagename=myimage,mode='get',hdkey='beammajor')['value']
minor=imhead(imagename=myimage,mode='get',hdkey='beamminor')['value']
pixelsize=float(cell.split('arcsec')[0])
beamarea=(major*minor*pi/(4*log(2)))/(pixelsize**2)
print 'beamarea in pixels =', beamarea
--
Find properties of the dirty image
For the long series of commands below it is important to include the beginning cpaste and ending -- in your cut and paste.
# In CASA
cpaste
### Find the peak in the dirty cube.
myimage=prename+'.image'
bigstat=imstat(imagename=myimage)
peak= bigstat['max'][0]
print 'peak (Jy/beam) in cube = '+str(peak)
### Sets threshold of first loop, try 2-4. Subsequent loops are set thresh/2.
thresh = peak / 4.
### If True: find the rms in two line-free channels; If False: Set rms by hand in else statement.
if True:
chanstat=imstat(imagename=myimage,chans='4')
rms1= chanstat['rms'][0]
chanstat=imstat(imagename=myimage,chans='66')
rms2= chanstat['rms'][0]
rms=0.5*(rms1+rms2)
else:
rms=0.011
print 'rms (Jy/beam) in a channel = '+str(rms)
--
Automasking Loop
On a reasonably fast computer the following will take a couple of hours for this spectral mosaic...
# In CASA
cpaste
n=-1
while (thresh >= stop*rms):
n=n+1
print 'clean threshold this loop is', thresh
threshmask = prename+'_threshmask' +str(n)
maskim = prename+'_fullmask' +str(n)
immath(imagename = [myresidual],
outfile = threshmask,
expr = 'iif(IM0 > '+str(thresh) +',1.0,0.0)',
mask=myflux+'>'+str(minpb))
if (n==0):
os.system('cp -r '+threshmask+' '+maskim+'.pb')
print 'This is the first loop'
else:
makemask(mode='copy',inpimage=myimage,
inpmask=[threshmask,mymask],
output=maskim)
imsubimage(imagename=maskim, mask=myflux+'>'+str(minpb),
outfile=maskim+'.pb')
print 'Combined mask ' +maskim+' generated.'
# Remove small masks
os.system('cp -r '+maskim+'.pb ' +maskim+'.pb.min')
maskfile=maskim+'.pb.min'
ia.open(maskfile)
mask=ia.getchunk()
labeled,j=scipy.ndimage.label(mask)
myhistogram = scipy.ndimage.measurements.histogram(labeled,0,j+1,j+1)
object_slices = scipy.ndimage.find_objects(labeled)
threshold=beamarea*pixelmin
for i in range(j):
if myhistogram[i+1]<threshold:
mask[object_slices[i]] = 0
ia.putchunk(mask)
ia.done()
print 'Small masks removed and ' +maskim +'.pb.min generated.'
os.system('rm -rf '+mymask+'')
clean(vis=vis,imagename=prename,
imagermode='mosaic',ftmachine='mosaic',minpb=minpb,
imsize=imsize,cell=cell,spw=spw,
weighting='briggs',robust=robust,phasecenter=phasecenter,
mode='velocity',width=width,start=start,nchan=nchan,
restfreq=restfreq,outframe=outframe,veltype='radio',
mask = maskim+'.pb.min',
multiscale=scales,smallscalebias=smallscalebias,
interactive = F,
niter = 10000,
threshold = str(thresh) +'Jy/beam')
if thresh==stop*rms: break
thresh = thresh/2.
# Run a final time with stop*rms if more than a little above
# stop*rms. Also make a back-up of next to last image
if (thresh < stop*rms and thresh*2.>1.05*stop*rms):
thresh=stop*rms
os.system('cp -r '+myimage+' '+myimage+str(n))
--
Notes on the Automasking procedure
This script is meant to be a possible stepping stone to optimal automasking -- it is by no means perfect and is certainly slower than optimal but feel free to try it with other datasets. Some notes below:
In addition to the final prename.image (prename.flux etc) this script produces and keeps each iteration of the various mask files which will allow you to explore how the masking proceeded as the threshold for masking and cleaning was lowered. The ones denoted "prename. fullmask*.pb.min" are the ones used in the clean steps themselves. At the end of the process the final "prename. fullmask*.pb.min" will also be stored in the prename.mask. Once you've verified you are happy with the masking, you may want to remove the prename.threshmask* and prename.fullmask* files, as they can be large for large cubes.
Additionally, before running the final loop with thresh=stop*rms the script copies the .image from the preceding clean to prename.image'n' where 'n' equals the loop number of the preceding step. So in this M100 example you will see a M100_combine_cube.image and a M100_combine_cube.image2 where .image is the final image and .image2 is the next to last image. This is done for convenience in the case that thresh=stop*rms is too deep such that clean diverges, you will still be left with the clean image from the preceding loop that you can further investigate to understand why clean diverged. If all goes well with the final loop, the prename.image'n' can also be deleted. Divergence at thresh=stop*rms is often a sign that the image is "dynamic range limited" in other words the rms in channels with bright emission is significantly worse than for a line-free channel.
Image Analysis for the 7m+12m Data
Moment Maps for 7m+12m CO (1-0) Cube
Start by examining the final image cube. Determine the start and stopping channels for the line emission -- this will be used in the "chans" parameter of immoments.
# In CASA
viewer('M100_combine_cube.image')
Next determine the rms noise per channel and use that to exclude pixels from the moment images. All images are shown in the gallery at the end of the following section.
# In CASA
myimage='M100_combine_cube.image'
chanstat=imstat(imagename=myimage,chans='4')
rms1= chanstat['rms'][0]
chanstat=imstat(imagename=myimage,chans='66')
rms2= chanstat['rms'][0]
rms=0.5*(rms1+rms2)
print 'rms in a channel = '+str(rms)
Next make the moment maps. For the integrated intensity: moment 0, a 2 sigma cut often considerably improves the appearance of the image with little effect on the integrated intensity as long as emission free channels are excluded. For higher order moments it is necessary to exclude all low S/N data. Typically 5-6 sigma for the higher moments works well. We also apply further masking based on the .flux image because the edges of the combined mosaic are especially noisy because the 7m mosaic is somewhat larger than the 12m mosaic as described above (see Figures 1 & 2).
# In CASA
cpaste
os.system('rm -rf M100_combine_cube.image.mom0')
immoments(imagename = 'M100_combine_cube.image',
moments = [0],
axis = 'spectral',chans = '9~61',
mask='M100_combine_cube.flux>0.3',,
includepix = [rms*2,100.],
outfile = 'M100_combine_cube.image.mom0')
os.system('rm -rf M100_combine_cube.image.mom1')
immoments(imagename = 'M100_combine_cube.image',
moments = [1],
axis = 'spectral',chans = '9~61',
mask='M100_combine_cube.flux>0.3',
includepix = [rms*5.5,100.],
outfile = 'M100_combine_cube.image.mom1')
--
Now we can make some figures showing the moment maps (*note that this creates different looking files for me than the ones I have included here, which were made in the viewer -- is this true for others?*):
# In CASA
cpaste
os.system('rm -rf M100_combine_cube.image.mom*.png')
imview (raster=[{'file': 'M100_combine_cube.image.mom0',
'range': [-0.3,25.],'scaling': -1.3,'colorwedge': T}],
zoom={'blc': [190,150],'trc': [650,610]},
out='M100_combine_cube.image.mom0.png')
imview (raster=[{'file': 'M100_combine_cube.image.mom1',
'range': [1440,1695],'colorwedge': T}],
zoom={'blc': [190,150],'trc': [650,610]},
out='M100_combine_cube.image.mom1.png')
--
If you plan to use your moment 0 image to make measurements, it needs to be primary beam corrected first. First we need to subimage the .flux cube to extract a single plane that can be used to primary beam correct the moment 0 image.
# In CASA
os.system('rm -rf M100_combine_cube.flux.1ch')
imsubimage(imagename='M100_combine_cube.flux',
outfile='M100_combine_cube.flux.1ch',
chans='35')
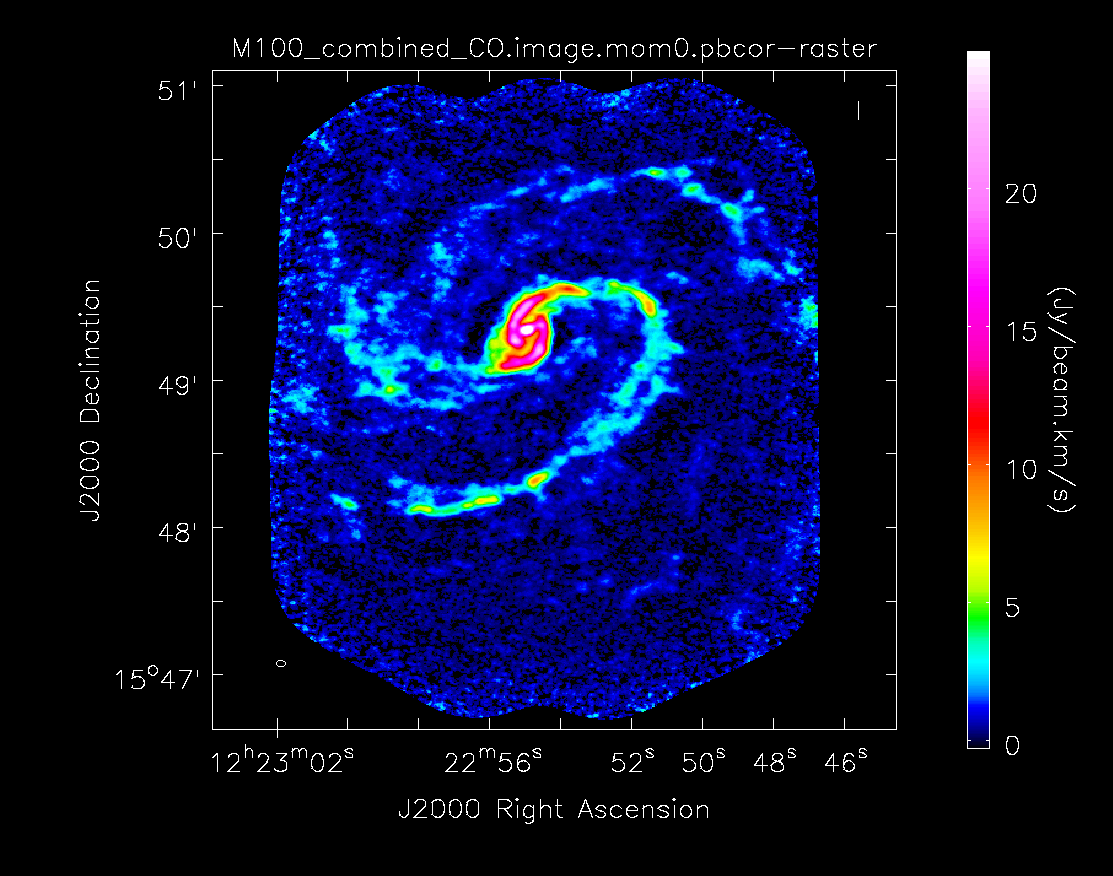
Then primary beam correct the moment 0 image. This is the version that would be used for measurements, though the uncorrected one can be useful for figures. The difference is clear in the images seen below in the following section.
# In CASA
os.system('rm -rf M100_combine_cube.image.mom0.pbcor')
immath(imagename=['M100_combine_cube.image.mom0', \
'M100_combine_cube.flux.1ch'],
expr='IM0/IM1',
outfile='M100_combine_cube.image.mom0.pbcor')
Have a look at the difference the primary beam correction makes.
# In CASA
imview (raster=[{'file': 'M100_combine_cube.image.mom0',
'range': [-0.3,25.],'scaling': -1.3},
{'file': 'M100_combine_cube.image.mom0.pbcor',
'range': [-0.3,25.],'scaling': -1.3}],
zoom={'blc': [190,150],'trc': [650,610]})
With the viewer open, you can flip back and forth between the images to compare them. Next, make a figure.
# In CASA
os.system('rm -rf M100_combine_cube.image.mom0.pbcor.png')
imview (raster=[{'file': 'M100_combine_cube.image.mom0.pbcor',
'range': [-0.3,25.],'scaling': -1.3,'colorwedge': T}],
zoom={'blc': [190,150],'trc': [650,610]},
out='M100_combine_cube.image.mom0.pbcor.png')
Comparison with 7m, 12m Moment Maps
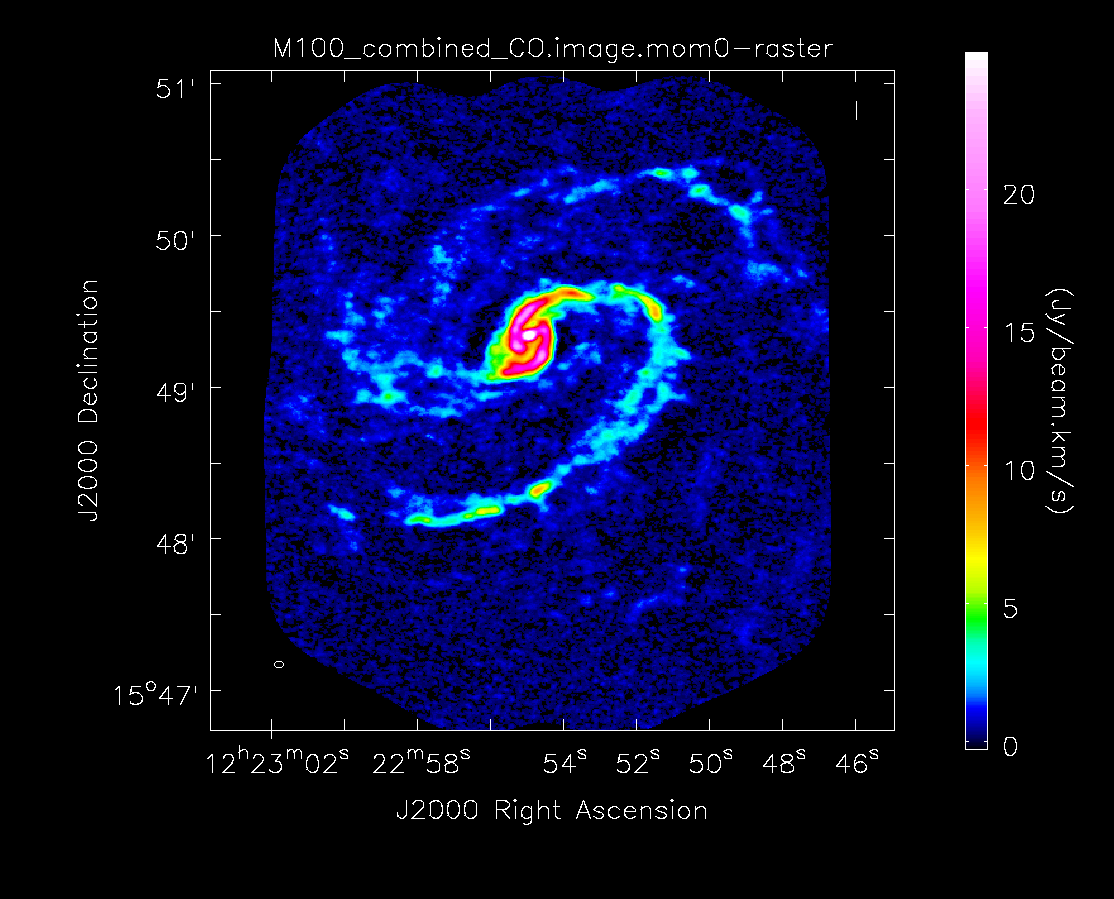
Below the moment maps from the 7m-only and the 12m-only data are shown for comparison. The moment maps were made using clean masks drawn by hand for comparison to the automasking technique; the two appear to be qualitatively similar. The range and scaling for the 12m-only figures are the same as that used for the 7m+12m figures for ease of comparison.
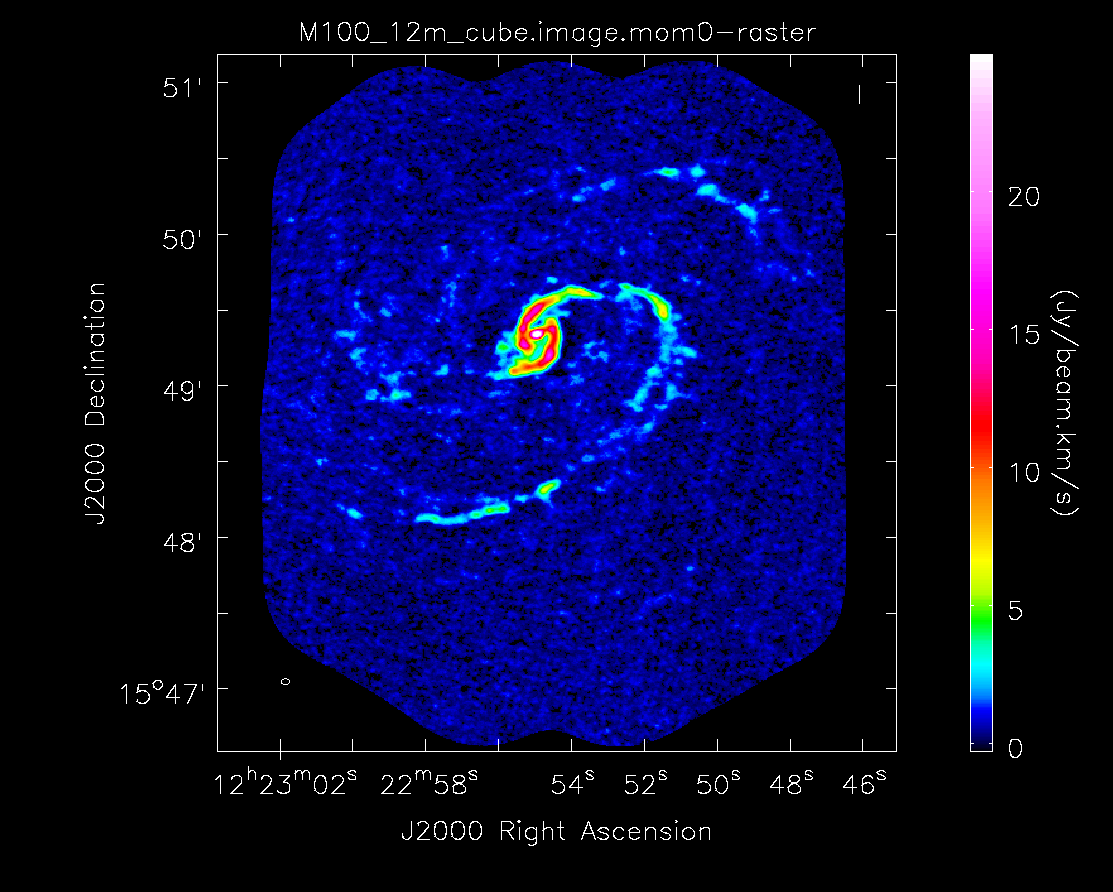
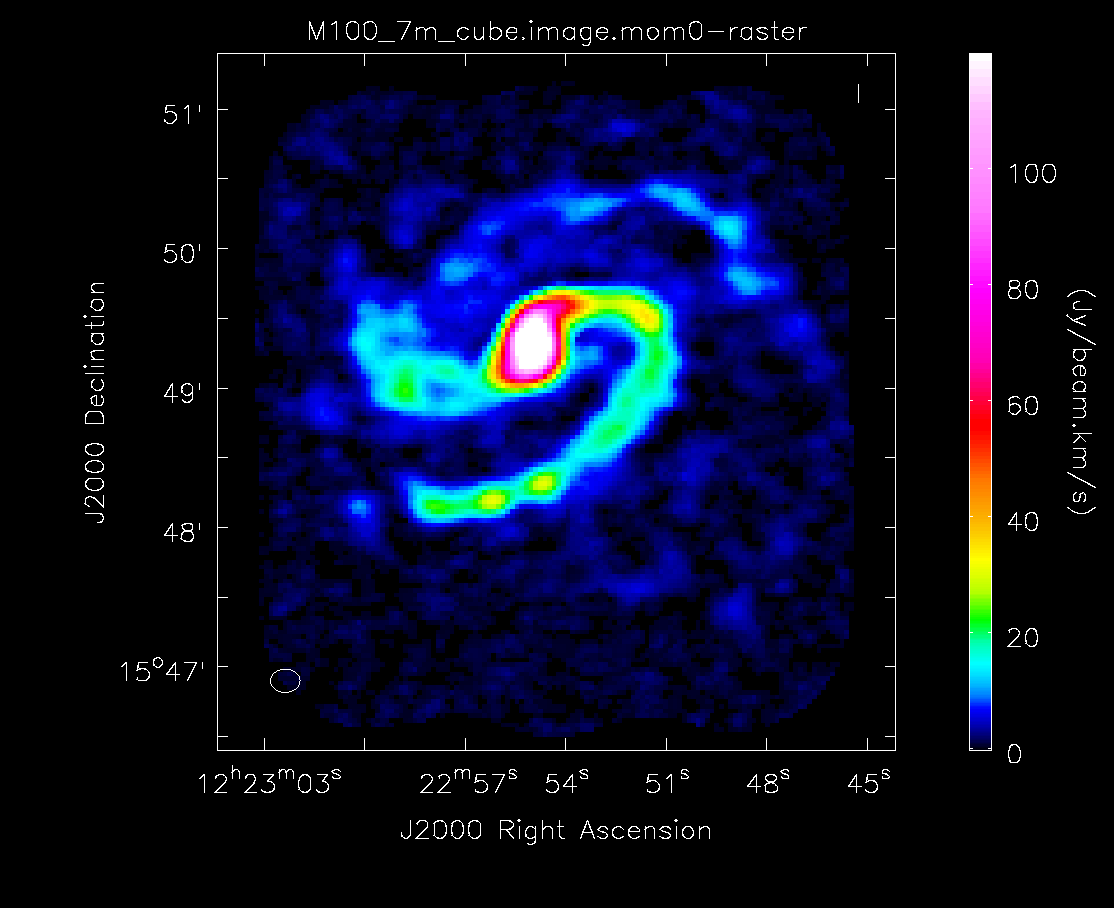
As expected, the 7m+12m image shows considerably more extended emission than the 12m-only data and finer detail than the 7m-only data. For comparison, the 7m+12m synthesized beam is 3.80"x2.50", while the 12m-only beam is 3.46"x2.37" and the 7m-only beam is 12.71"x10.09".
-
Moment 0 for 12m data alone (no primary beam correction).
-
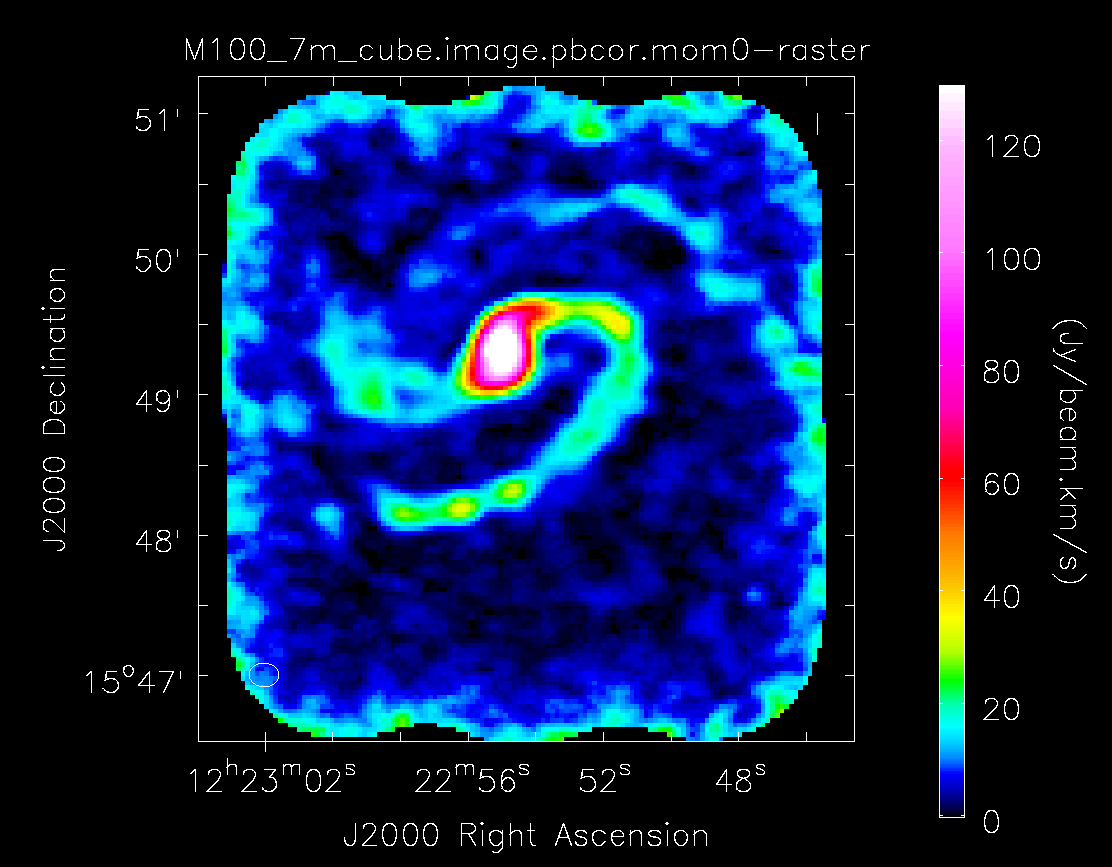
Moment 0 for 7m data alone (no primary beam correction).
-
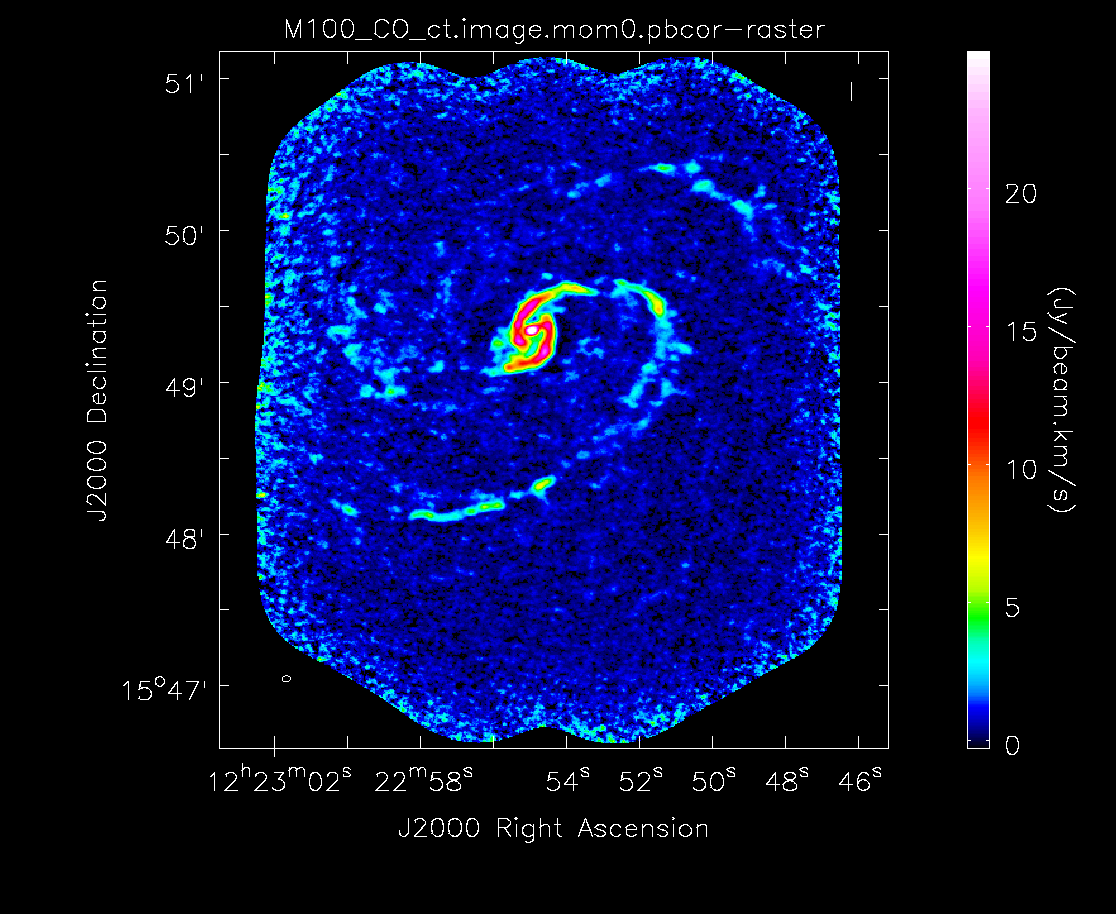
Moment 0 for 12m+7m data (no primary beam correction).
-
Moment 0 for 12m+7m data with primary beam correction.
-
Moment 1 for 12m data alone.
-
Moment 1 for 7m data alone.
-
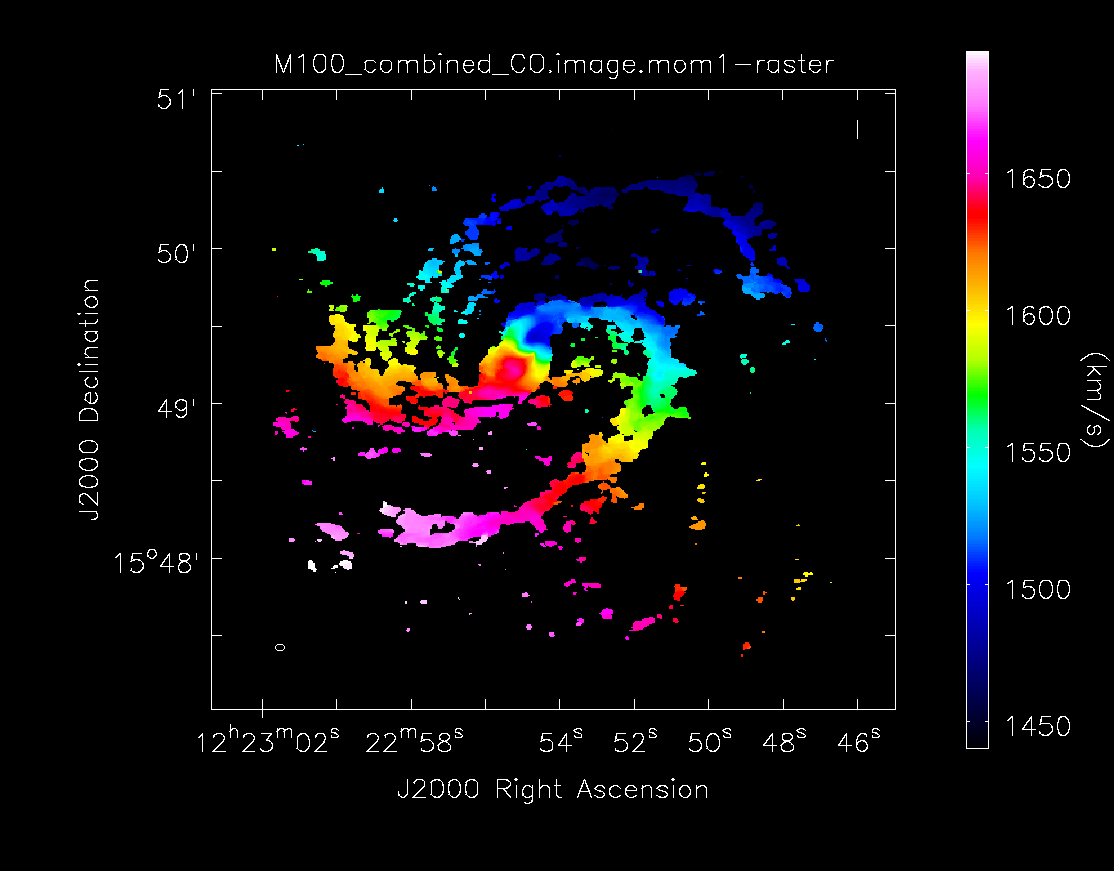
Moment 1 for 12m+7m data.
Convert 7m+12m Images to Fits Format
# In CASA
cpaste
os.system('rm -rf *.fits')
exportfits(imagename='M100_combine_cube.image',fitsimage='M100_combine_cube.image.fits')
exportfits(imagename='M100_combine_cube.flux',fitsimage='M100_combine_cube.flux.fits')
exportfits(imagename='M100_combine_cube.image.mom0',fitsimage='M100_combine_cube.image.mom0.fits')
exportfits(imagename='M100_combine_cube.image.mom0.pbcor',fitsimage='M100_combine_cube.image.mom0.pbcor.fits')
exportfits(imagename='M100_combine_cube.image.mom1',fitsimage='M100_combine_cube.image.mom1.fits')
--
Feathering the Total Power and 7m+12m Interferometric Images
Image the Total Power Data
Run listobs on the total power data to see what spw contains the CO
In CASA
os.system('rm -rf concat_m100.ms.listobs')
listobs(vis='concat_m100.ms',listfile='concat_m100.ms.listobs')
Image the TP data
In CASA
os.system('rm -rf TP_CO_cube')
sdimaging(infile='concat_m100.ms',
field=0,spw=15,
specunit='km/s',restfreq='115.271204GHz',
dochannelmap=True,
nchan=70,start=1400,step=5,
gridfunction='gjinc',imsize=[50,50],
cell=['10arcsec','10arcsec'],
outfile='TP_CO_cube')
Determine the TP Restoring Beam and Convert to Jy/beam
Next we need to determine the restoring beam size. This will depend on 3 factors
(1) The expected FWHP for the 12m TP dishes which have a -12dB taper and a Gaussian shape. This is 1.17 lambda / 12m (radians)
(2) Any broadening of the beam due to less than ideal sampling. For an antenna with -12dB taper, Nyquist = FWHM/2.4. To have less than 1% broadening the sampling should be 2 x Nyquist.
(3) The convolution of the gridding kernel with the combination of (1) and (2)
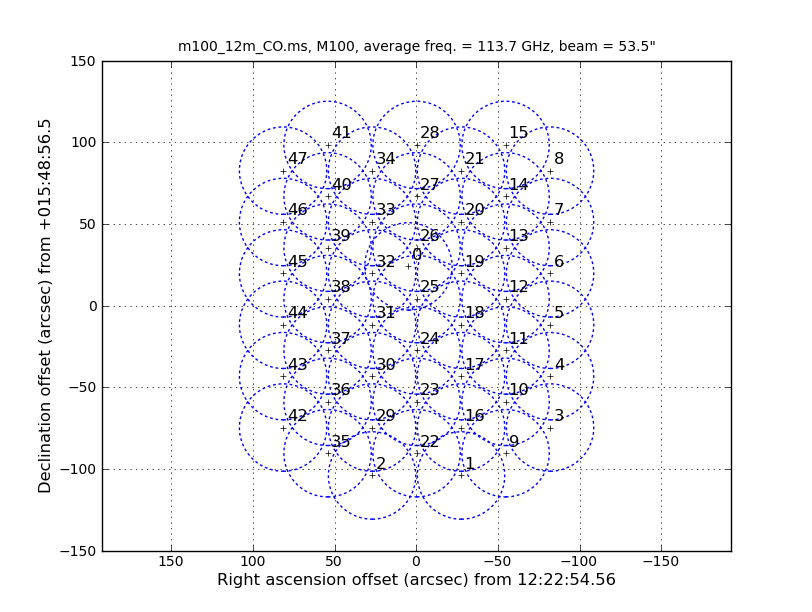
<figure id="TP_sampling.png">
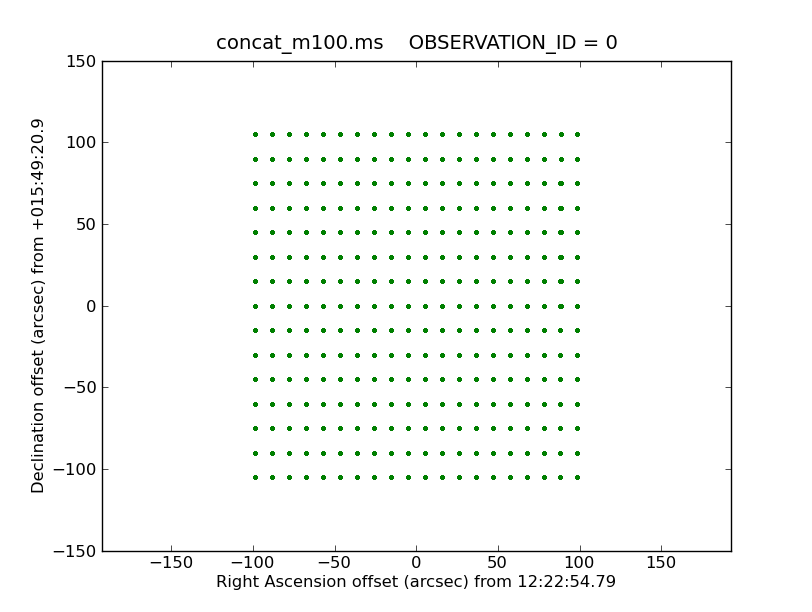
</figure>
We have chosen the "gjinc" function in sdimaging because it produces the lease broadening of the effective beam. This is important because any broadening of the effective beam is equivalent to having used a smaller antenna.
For more information on these topics, see Mangum et al. 2007 (http://adsabs.harvard.edu/abs/2007A%26A...474..679M)
Two functions in the analysis utilities suite can be used to calculate the sampling of the TP data in the X and Y directions and then the final restoring beam, respectively.
In CASA
xSampling,ySampling=au.getTPSampling('concat_m100.ms',
showplot=True,plotfile='TP_sampling.png')
xSampling = 10.3766 arcsec ySampling = 15.0002 arcsec
The frequency required for au.gjincBeam is the observed sky frequency near the center of the line (not the rest frequency). The pixelsize should be the same as that used for the cell in sdimaging. The sampling parameters were determined by au.getTPSampling
In CASA
RestorBeam=au.gjincBeam(frequency=114.66,pixelsize=10,xSamplingArcsec=xSampling,ySamplingArcsec=ySampling)
The output to the terminal will be:
Theoretical primary beam FWHP = 52.5822 arcsec Expected effective restoring beam along scan = 54.4937 arcsec Expected effective restoring beam between rows = 54.9774 arcsec Geometric mean = 54.735 arcsec
Next set the restoring beam to the derived value.
In CASA
ia.open('TP_CO_cube')
ia.setrestoringbeam(major=str(RestorBeam)+'arcsec',
minor=str(RestorBeam)+'arcsec',
pa='0deg')
ia.done()
Convert the image from K to Jy assuming Jy/K = 55.0 Note currently sdimaging reports that the image it makes is in Jy/beam. This is a bug.
In CASA
os.system('rm -rf TP_CO_cube_Jy')
immath(imagename='TP_CO_cube',
expr='IM0*55.0',
outfile='TP_CO_cube_Jy')
Prepare Images for Feathering
Regrid TP image to match the shape of the 7m+12m image.
In CASA
os.system('rm -rf TP_CO_cube_Jy.regrid')
imregrid(imagename='TP_CO_cube_Jy',
template='M100_Intcombo_0.193_cube.image',
shape=[800,800,1,70],
axes=[0,1],output='TP_CO_cube_Jy.regrid')
Subimage both images to a matching size, excluding regions masked by the clean pbmin=0.2 and noisy edge pixels in the TP image. The Viewer can be used to determine a good joint region.
In CASA
os.system('rm -rf M100_Intcombo_0.193_cube.image.subim')
imsubimage(imagename='M100_Intcombo_0.193_cube.image',
outfile='M100_Intcombo_0.193_cube.image.subim',
box='230,184,604,598')
os.system('rm -rf TP_CO_cube_Jy.regrid.subim')
imsubimage(imagename='TP_CO_cube_Jy.regrid',
outfile='TP_CO_cube_Jy.regrid.subim',
box='230,184,604,598')
Creat subimaged version the mosaic response
In CASA
os.system('rm -rf M100_Intcombo_0.193_cube.flux.subim')
imsubimage(imagename='M100_Intcombo_0.193_cube.flux',
outfile='M100_Intcombo_0.193_cube.flux.subim',
box='230,184,604,598')
Multiply the TP image by the mosaic beam response of the 7m+12m image
In CASA
os.system('rm -rf TP_CO_cube_Jy.regrid.subim.depb')
immath(imagename=['TP_CO_cube_Jy.regrid.subim',
'M100_Intcombo_0.193_cube.flux.subim'],
expr='IM0*IM1',
outfile='TP_CO_cube_Jy.regrid.subim.depb')
Feather TP Cube with 7m+12m Cube
Feather with default parameters
In CASA
os.system('rm -rf M100_Feather_CO')
feather(imagename='M100_Feather_CO',
highres='M100_Intcombo_0.193_cube.image.subim',
lowres='TP_CO_cube_Jy.regrid.subim.depb')
Make Moment Maps of TP and Feathered Images
We will use the same technique as the 7m+12m image analysis above to make moment maps.
First, make moment maps for the TP image.
In CASA
myimage='TP_CO_cube_Jy.regrid.subim'
chanstat=imstat(imagename=myimage,chans='4')
rms1= chanstat['rms'][0]
chanstat=imstat(imagename=myimage,chans='66')
rms2= chanstat['rms'][0]
rms=0.5*(rms1+rms2)
os.system('rm -rf TP_CO_cube_Jy.regrid.subim.mom0')
immoments(imagename = 'TP_CO_cube_Jy.regrid.subim',
moments = [0],
axis = 'spectral',
chans = '10~61',
includepix = [rms*2.,50],
outfile = 'TP_CO_cube_Jy.regrid.subim.mom0')
os.system('rm -rf TP_CO_cube_Jy.regrid.subim.mom1')
immoments(imagename = 'TP_CO_cube_Jy.regrid.subim',
moments = [1],
axis = 'spectral',
chans = '10~61',
includepix = [rms*5.5,50],
outfile = 'TP_CO_cube_Jy.regrid.subim.mom1')
In CASA
os.system('rm -rf TP_CO_cube_Jy.regrid.subim .mom*.png')
imview (raster=[{'file': 'TP_CO_cube_Jy.regrid.subim.mom0',
'range': [-0.3,900.],'scaling': -1.0,'colorwedge': T}],
out='TP_CO_cube_Jy.regrid.subim.mom0.png')
imview (raster=[{'file': 'TP_CO_cube_Jy.regrid.subim.mom1',
'range': [1455,1695],'colorwedge': T}],
out='TP_CO_cube_Jy.regrid.subim.mom1.png')
Make moment maps for the feathered image.
In CASA
myimage='M100_Feather_CO'
chanstat=imstat(imagename=myimage,chans='4')
rms1= chanstat['rms'][0]
chanstat=imstat(imagename=myimage,chans='66')
rms2= chanstat['rms'][0]
rms=0.5*(rms1+rms2)
os.system('rm -rf M100_Feather_CO.mom0')
immoments(imagename = 'M100_Feather_CO',
moments = [0],
axis = 'spectral',
chans = '10~61',
includepix = [rms*2.,50],
outfile = 'M100_Feather_CO.mom0')
os.system('rm -rf M100_Feather_CO.mom1')
immoments(imagename = 'M100_Feather_CO',
moments = [1],
axis = 'spectral',
chans = '10~61',
includepix = [rms*5.5,50],
outfile = 'M100_Feather_CO.mom1')
In CASA
os.system('rm -rf M100_Feather_CO.mom*.png')
imview (raster=[{'file': 'M100_Feather_CO.mom0',
'range': [-0.3,25.],'scaling': -1.0,'colorwedge': T}],
out='M100_Feather_CO.mom0.png')
imview (raster=[{'file': 'M100_Feather_CO.mom1',
'range': [1455,1695],'colorwedge': T}],
out='M100_Feather_CO.mom1.png')
Primary Beam Correct the Moment 0 Image
Apply the primary beam response to the feathered image
In CASA
os.system('rm -rf M100_Intcombo_0.193_cube.flux.1ch.subimage')
imsubimage(imagename='M100_Intcombo_0.193_cube.flux',
outfile='M100_Intcombo_0.193_cube.flux.1ch.subimage',
box='230,184,604,598',
chans='35')
In CASA
os.system('rm -rf M100_Feather_CO.mom0.pbcor')
immath(imagename=['M100_Feather_CO.mom0', \
'M100_Intcombo_0.193_cube.flux.1ch.subimage'],
expr='IM0/IM1',
outfile='M100_Feather_CO.mom0.pbcor')
Create a figure of primary beam corrected moment 0.
In CASA
os.system('rm -rf M100_Feather_CO.mom0.pbcor.png')
imview (raster=[{'file': 'M100_Feather_CO.mom0.pbcor',
'range': [-0.3,25.],'scaling': -1.0,'colorwedge': T}],
out='M100_Feather_CO.mom0.pbcor.png')
Compare the Different Images
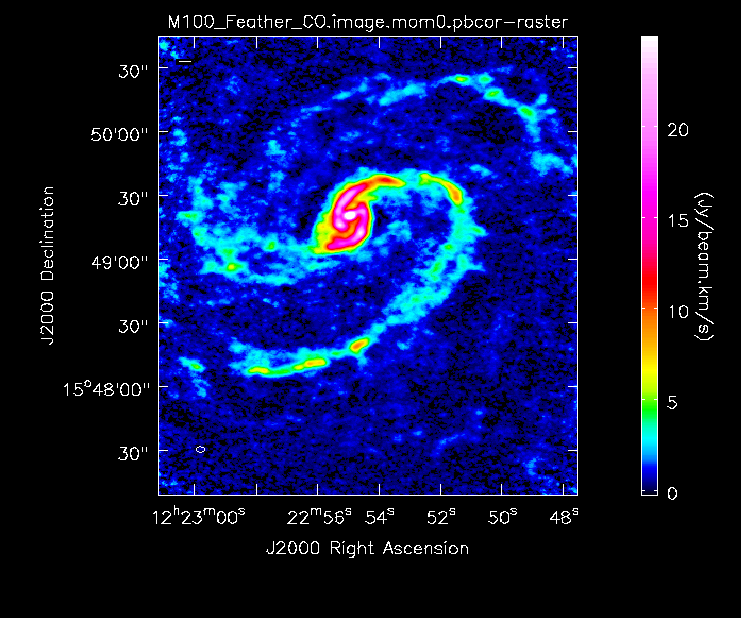
Now lets compare all the different images:
-
Primary beam corrected moment 0 for the 12m data.
-
Primary beam corrected moment 0 for the 7m data.
-
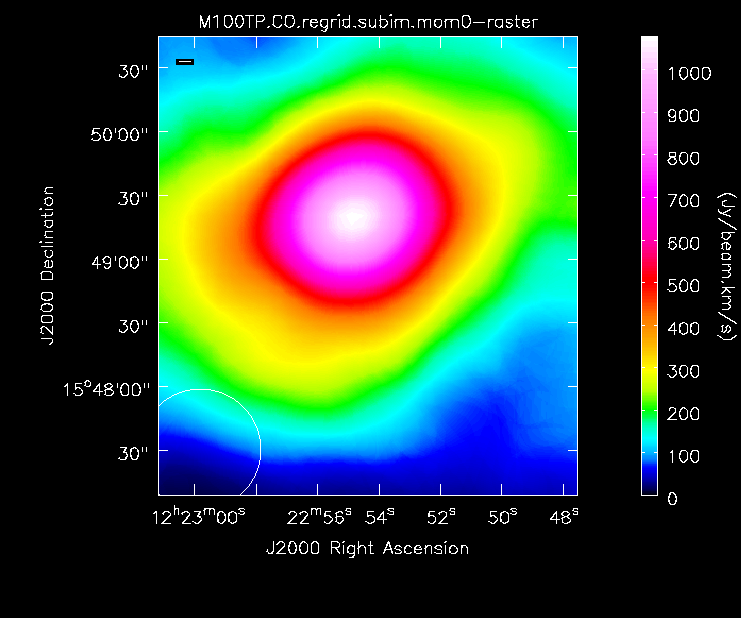
Moment 0 for the TP data (UPDATE).
-
Primary beam corrected moment 0 for 7m+12m data.
-
Primary beam corrected moment 0 for TP+7m+12m data (UPDATE).
-
Moment 1 for 12m data.
-
Moment 1 for 7m data.
-
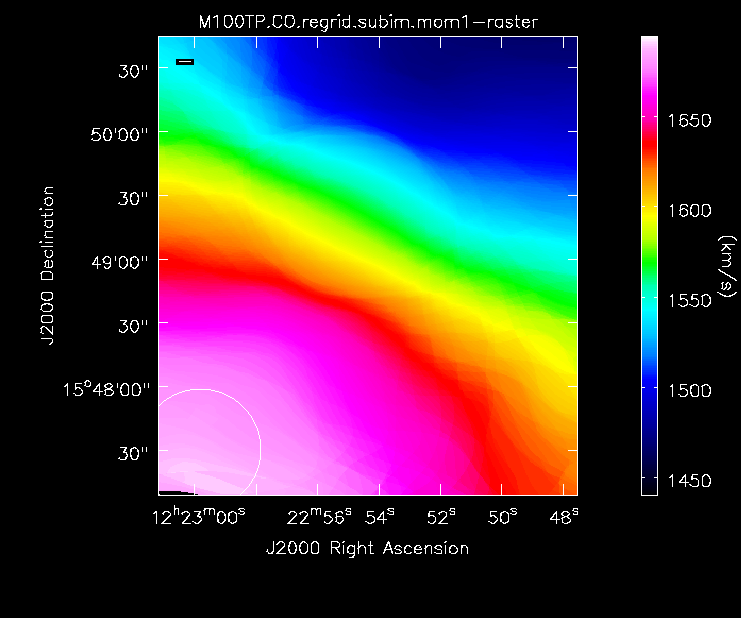
Moment 1 for the TP data (UPDATE).
-
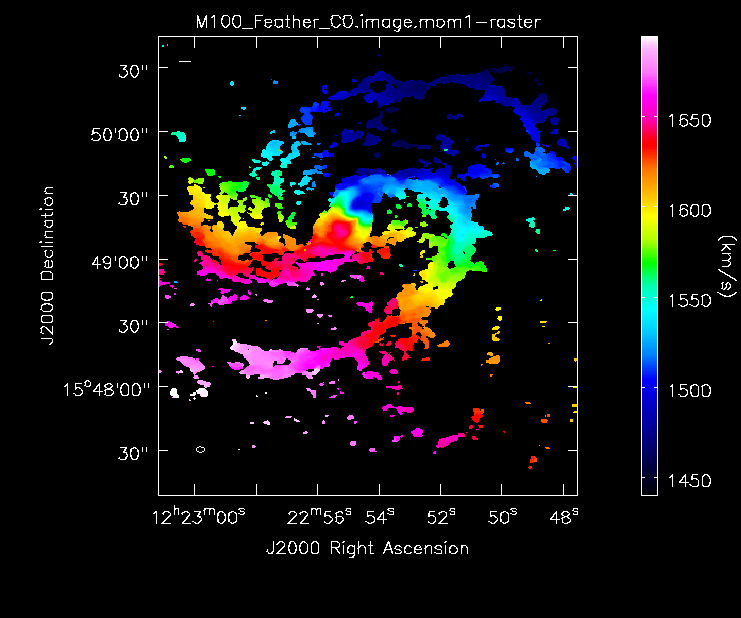
Moment 1 for 7m+12m data.
-
Moment 1 for TP+7m+12m data (UPDATE).
Last checked on CASA Version 4.1.0.