3C286 Band6Pol Calibration for CASA 6.6.1: Difference between revisions
| (60 intermediate revisions by the same user not shown) | |||
| Line 62: | Line 62: | ||
#In CASA | #In CASA | ||
for name in basename: | for name in basename: | ||
importasdm(asdm=name, asis='*') | |||
</source> | </source> | ||
| Line 125: | Line 125: | ||
<pre> | <pre> | ||
Field 0 (J1337-1257) polarization calibrator | Field 0 (J1337-1257) polarization calibrator | ||
Field 1 (J1256-0547 | Field 1 (J1256-0547) [3c279] bandpass calibrator | ||
Field 2 (Ceres) flux calibrator | Field 2 (Ceres) flux calibrator | ||
Field 3 (J1310+3220) complex gain (phase) calibrator | Field 3 (J1310+3220) complex gain (phase) calibrator | ||
| Line 303: | Line 303: | ||
for name in basename: | for name in basename: | ||
gencal(vis = name+'.ms', | gencal(vis = name+'.ms', | ||
caltable = name+'.ms.tsys', | |||
caltype = 'tsys') | |||
</source> | </source> | ||
| Line 314: | Line 314: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
plotms(vis=basename[0]+'.ms.tsys', xaxis='freq', yaxis='tsys', spw='', iteraxis='antenna', coloraxis='scan' | plotms(vis=basename[0]+'.ms.tsys', xaxis='freq', yaxis='tsys', spw='', iteraxis='antenna', coloraxis='scan') | ||
</source> | </source> | ||
| Line 325: | Line 325: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
plotms(vis=basename[0]+'.ms.tsys', xaxis='channel', yaxis='tsys', spw='', iteraxis='antenna', coloraxis='spw' | plotms(vis=basename[0]+'.ms.tsys', xaxis='channel', yaxis='tsys', spw='', iteraxis='antenna', coloraxis='spw') | ||
</source> | </source> | ||
| Line 334: | Line 334: | ||
for name in basename: | for name in basename: | ||
flagdata(vis = name+'.ms.tsys', | flagdata(vis = name+'.ms.tsys', | ||
spw='9:0~3, 11:0~3, 13:0~3, 15:0~3') | spw = '9:0~3, 11:0~3, 13:0~3, 15:0~3') | ||
</source> | </source> | ||
| Line 354: | Line 354: | ||
tie = ['3c286,J1310+3220'], # target, phase cal | tie = ['3c286,J1310+3220'], # target, phase cal | ||
statsource = 'J1256-0547', # BP cal | statsource = 'J1256-0547', # BP cal | ||
wvrflag=['DA54']) | wvrflag = ['DA54']) | ||
# switch back to the original log file | # switch back to the original log file | ||
| Line 385: | Line 385: | ||
tsysmap = tsysspwmap(vis='uid___A002_X85c183_X10a.ms', tsystable='uid___A002_X85c183_X10a.ms.tsys') | tsysmap = tsysspwmap(vis='uid___A002_X85c183_X10a.ms', tsystable='uid___A002_X85c183_X10a.ms.tsys') | ||
tsysmap = tsysmap[:25] # truncate the list to ignore the extra WVR spws not shown in the listobs spw list | tsysmap = tsysmap[:25] # truncate the list to ignore the extra WVR spws not shown in the listobs spw list | ||
tsysmap[21]=13 # fix an error | tsysmap[21] = 13 # fix an error | ||
tsysmap[23]=15 # fix an error | tsysmap[23] = 15 # fix an error | ||
</source> | </source> | ||
| Line 540: | Line 540: | ||
Now that the data are concatenated into one dataset, we will do some additional inspection with {{plotms_6.6.1}}. First we will plot amplitude versus channel for the bandpass calibrator, averaging over time and baselines and choosing XX correlation only in order to speed up the plotting process. | Now that the data are concatenated into one dataset, we will do some additional inspection with {{plotms_6.6.1}}. First we will plot amplitude versus channel for the bandpass calibrator, averaging over time and baselines and choosing XX correlation only in order to speed up the plotting process. | ||
[[File:Amp_time_all_field_6.1.png|300px|thumb|right|| '''Fig 4''' Amplitude vs time for the dataset 3c286_Band6.ms, spw 0, with all channels averaged]][[File: | [[File:Amp_time_all_field_6.1.png|300px|thumb|right|| '''Fig 4''' Amplitude vs time for the dataset 3c286_Band6.ms, spw 0, with all channels averaged]][[File:J1337-1257_timerange_flag_6.6.1.png|300px|thumb|right| '''Fig 5''' Zoom in and locate the problematic time range of the polarization calibrator scan to flag]] | ||
[[File:Amp_uvdist_Ceres_6.1.png|300px|thumb|right| '''Fig 6''' Amplitude vs uv-distance for Ceres]] | [[File:Amp_uvdist_Ceres_6.1.png|300px|thumb|right| '''Fig 6''' Amplitude vs uv-distance for Ceres]] | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
plotms(vis='3c286_Band6.ms', xaxis='channel', yaxis='amp', field='1', correlation='XX', avgbaseline=True, avgtime='1e8', avgscan=True, coloraxis='spw') | plotms(vis='3c286_Band6.ms', xaxis='channel', yaxis='amp', field='1', | ||
correlation='XX', avgbaseline=True, avgtime='1e8', avgscan=True, coloraxis='spw') | |||
</source> | </source> | ||
| Line 584: | Line 585: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
flagdata(vis='3c286_Band6.ms', antenna='DA49') | flagdata(vis='3c286_Band6.ms', antenna='DA49') | ||
flagdata(vis='3c286_Band6.ms', antenna='DA45', field='0,3', spw='1') | flagdata(vis='3c286_Band6.ms', antenna='DA45', field='0,3', spw='1') | ||
flagdata(vis='3c286_Band6.ms', antenna='DA45', scan='48', field='0', spw='2') | flagdata(vis='3c286_Band6.ms', antenna='DA45', scan='48', field='0', spw='2') | ||
flagdata(vis='3c286_Band6.ms', antenna= DV14') | flagdata(vis='3c286_Band6.ms', antenna='DV14') | ||
flagdata(vis='3c286_Band6.ms', antenna='DV04', scan='93',field='0') | flagdata(vis='3c286_Band6.ms', antenna='DV04', scan='93',field='0') | ||
flagdata(vis='3c286_Band6.ms', timerange='2014/07/02/00:25:00~2014/07/02/00:25:10') | flagdata(vis='3c286_Band6.ms', timerange='2014/07/02/00:25:00~2014/07/02/00:25:10') | ||
</source> | </source> | ||
| Line 621: | Line 622: | ||
# In CASA | # In CASA | ||
os.system('rm -rf 3c286_Band6.ms.G0ph') | os.system('rm -rf 3c286_Band6.ms.G0ph') | ||
gaincal(vis='3c286_Band6.ms',caltable='3c286_Band6.ms.G0ph', | gaincal(vis = '3c286_Band6.ms', | ||
field='1', #3c279 | caltable = '3c286_Band6.ms.G0ph', | ||
gaintype='G',solint='int',calmode='p', | field = '1', #3c279 | ||
spw='*:20~45', | gaintype = 'G', | ||
refantmode='strict', | solint = 'int', | ||
refant=refant,smodel=[1,0,0,0]) | calmode = 'p', | ||
spw = '*:20~45', | |||
refantmode = 'strict', | |||
refant = refant, | |||
smodel = [1,0,0,0]) | |||
</source> | </source> | ||
| Line 642: | Line 647: | ||
# In CASA | # In CASA | ||
os.system('rm -rf 3c286_Band6.ms.Bscan') | os.system('rm -rf 3c286_Band6.ms.Bscan') | ||
bandpass(vis='3c286_Band6.ms',caltable='3c286_Band6.ms.Bscan', | bandpass(vis = '3c286_Band6.ms', | ||
field='1', #3c279 | caltable = '3c286_Band6.ms.Bscan', | ||
solint='inf', | field = '1', #3c279 | ||
combine='scan, obs', | solint = 'inf', | ||
refant=refant, | combine = 'scan,obs', | ||
solnorm=True, | refant = refant, | ||
gaintable=['3c286_Band6.ms.G0ph'], | solnorm = True, | ||
interp=['nearest']) | gaintable = ['3c286_Band6.ms.G0ph'], | ||
interp = ['nearest']) | |||
</source> | </source> | ||
* The default type of bandpass solution is bandtype='B' , which does a channel by channel solution for each specified spw | *The default type of bandpass solution is bandtype='B' , which does a channel by channel solution for each specified spw | ||
*caltable = '*.Bscan': Output bandpass calibration table | *caltable = '*.Bscan': Output bandpass calibration table | ||
*gaintable = '.G0ph': gain calibration table to be applied on the fly | *gaintable = '.G0ph': gain calibration table to be applied on the fly | ||
| Line 665: | Line 671: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
plotms(vis='3c286_Band6.ms.Bscan',xaxis='frequency',yaxis='amp' | plotms(vis='3c286_Band6.ms.Bscan', xaxis='frequency', yaxis='amp', | ||
coloraxis='antenna1', iteraxis='spw', gridrows=2, gridcols=2) | |||
</source> | </source> | ||
Figure 7 shows the bandpass solutions table colored by antenna, in each of the four spws. In spw 1 and 3 the presence of atmospheric lines is clearly visible, | Figure 7 shows the bandpass solutions table colored by antenna, in each of the four spws. In spw 1 and 3 the presence of atmospheric lines is clearly visible, | ||
The solutions seem reasonable, so we will apply them on-the-fly during gain calibration | The solutions seem reasonable, so we will apply them on-the-fly during gain calibration moving forward. | ||
=== | === Flux Scaling === | ||
We | We set the flux density for the flux calibrators using {{setjy_6.6.1}}. Ceres has been used as flux calibrator. | ||
The standard catalog Butler-JPL-Horizons 2012 model fits Ceres's resolved visibilities to an emission model appropriate for the distance to Ceres on the observation date. For CASA 5.3 and later, usescratch should be explicitly set to True for any ephemeris calibrator. | The standard catalog Butler-JPL-Horizons 2012 model fits Ceres's resolved visibilities to an emission model appropriate for the distance to Ceres on the observation date. For CASA 5.3 and later, usescratch should be explicitly set to True for any ephemeris calibrator. | ||
| Line 686: | Line 692: | ||
usescratch = True) | usescratch = True) | ||
</source> | </source> | ||
<pre style="background-color: #fffacd;"> | |||
{'2': {'0': {'fluxd': array([1.53510869, 0. , 0. , 0. ])}, | |||
'1': {'fluxd': array([1.56220722, 0. , 0. , 0. ])}, | |||
'2': {'fluxd': array([1.72976518, 0. , 0. , 0. ])}, | |||
'3': {'fluxd': array([1.75838304, 0. , 0. , 0. ])}, | |||
'fieldName': 'Ceres'}, | |||
'format': "{field Id: {spw Id: {fluxd:[I,Q,U,V] in Jy}, 'fieldName':field name}}"} | |||
</pre> | |||
=== Gain Calibration === | |||
Now we determine a gain calibration for the bandpass, flux, and phase calibrators. We will calibrate the polarization calibrator separately. | Now we determine a gain calibration for the bandpass, flux, and phase calibrators. We will calibrate the polarization calibrator separately. | ||
| Line 694: | Line 711: | ||
# Gaincal for 3C279 and Ceres and J1310+3220 | # Gaincal for 3C279 and Ceres and J1310+3220 | ||
os.system('rm -rf 3c286_Band6.ms.G2ph') | os.system('rm -rf 3c286_Band6.ms.G2ph') | ||
gaincal(vis='3c286_Band6.ms', | gaincal(vis = '3c286_Band6.ms', | ||
caltable='3c286_Band6.ms.G2ph', | caltable = '3c286_Band6.ms.G2ph', | ||
gaintype= 'G', | gaintype = 'G', | ||
field='1,2,3', | field = '1,2,3', | ||
solint='int', | solint = 'int', | ||
refant=refant, | refant = refant, | ||
refantmode='strict', | refantmode = 'strict', | ||
calmode = 'p', | calmode = 'p', | ||
gaintable=['3c286_Band6.ms.Bscan'], | gaintable = ['3c286_Band6.ms.Bscan'], | ||
interp=['nearest']) | interp = ['nearest']) | ||
</source> | </source> | ||
| Line 720: | Line 737: | ||
# In CASA | # In CASA | ||
os.system('rm -rf 3c286_Band6.ms.G2amp') | os.system('rm -rf 3c286_Band6.ms.G2amp') | ||
gaincal(vis='3c286_Band6.ms', | gaincal(vis = '3c286_Band6.ms', | ||
caltable = '3c286_Band6.ms.G2amp', | |||
field = '1,2,3', | |||
solint = 'int', | |||
refant = refant, | |||
refantmode = 'strict', | |||
gaintype = 'T', | |||
calmode = 'a', #solve amplitude using G2ph | |||
gaintable = ['3c286_Band6.ms.Bscan','3c286_Band6.ms.G2ph'], | |||
interp = ['nearest','nearest']) | |||
</source> | </source> | ||
| Line 739: | Line 756: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
fluxscale(vis='3c286_Band6.ms', | fluxscale(vis = '3c286_Band6.ms', | ||
caltable='3c286_Band6.ms.G2amp', | caltable = '3c286_Band6.ms.G2amp', | ||
fluxtable = '3c286_Band6.ms.flux', | fluxtable = '3c286_Band6.ms.flux', | ||
reference='2', #Ceres | reference = '2', # Ceres | ||
transfer='1,3') #'J1256-0547', 'J1310+3220' | transfer = '1,3') # 'J1256-0547','J1310+3220' | ||
</source> | </source> | ||
| Line 756: | Line 773: | ||
Found reference field(s): Ceres | Found reference field(s): Ceres | ||
Found transfer field(s): J1256-0547 J1310+3220 | Found transfer field(s): J1256-0547 J1310+3220 | ||
Flux density for J1256-0547 in SpW=0 (freq=2.24e+11 Hz) is: 8. | Flux density for J1256-0547 in SpW=0 (freq=2.24e+11 Hz) is: 8.575 +/- 0.0222941 (SNR = 384.63, N = 28) | ||
Flux density for J1256-0547 in SpW=1 (freq=2.26e+11 Hz) is: 8. | Flux density for J1256-0547 in SpW=1 (freq=2.26e+11 Hz) is: 8.48694 +/- 0.0223375 (SNR = 379.941, N = 28) | ||
Flux density for J1256-0547 in SpW=2 (freq=2.4e+11 Hz) is: 8. | Flux density for J1256-0547 in SpW=2 (freq=2.4e+11 Hz) is: 8.1471 +/- 0.0241656 (SNR = 337.136, N = 28) | ||
Flux density for J1256-0547 in SpW=3 (freq=2.42e+11 Hz) is: 8. | Flux density for J1256-0547 in SpW=3 (freq=2.42e+11 Hz) is: 8.08165 +/- 0.0244227 (SNR = 330.907, N = 28) | ||
Flux density for J1310+3220 in SpW=0 (freq=2.24e+11 Hz) is: 0. | Flux density for J1310+3220 in SpW=0 (freq=2.24e+11 Hz) is: 0.925759 +/- 0.00753979 (SNR = 122.783, N = 27) | ||
Flux density for J1310+3220 in SpW=1 (freq=2.26e+11 Hz) is: 0. | Flux density for J1310+3220 in SpW=1 (freq=2.26e+11 Hz) is: 0.914686 +/- 0.00789673 (SNR = 115.831, N = 26) | ||
Flux density for J1310+3220 in SpW=2 (freq=2.4e+11 Hz) is: 0. | Flux density for J1310+3220 in SpW=2 (freq=2.4e+11 Hz) is: 0.876549 +/- 0.00810848 (SNR = 108.103, N = 27) | ||
Flux density for J1310+3220 in SpW=3 (freq=2.42e+11 Hz) is: 0. | Flux density for J1310+3220 in SpW=3 (freq=2.42e+11 Hz) is: 0.8743 +/- 0.00834474 (SNR = 104.773, N = 27) | ||
Fitted spectrum for J1256-0547 with fitorder=1: Flux density = 8. | Fitted spectrum for J1256-0547 with fitorder=1: Flux density = 8.31993 +/- 0.00938247 (freq=232.86 GHz) spidx: a_1 (spectral index) =-0.73443 +/- 0.0325769 covariance matrix for the fit: covar(0,0)=1.97601e-06 covar(0,1)=1.77371e-05 covar(1,0)=1.77371e-05 covar(1,1)=0.00874273 | ||
Fitted spectrum for J1310+3220 with fitorder=1: Flux density = 0. | Fitted spectrum for J1310+3220 with fitorder=1: Flux density = 0.897572 +/- 0.00151321 (freq=232.86 GHz) spidx: a_1 (spectral index) =-0.732428 +/- 0.0485781 covariance matrix for the fit: covar(0,0)=1.98269e-05 covar(0,1)=0.000155996 covar(1,0)=0.000155996 covar(1,1)=0.087278 | ||
</pre> | </pre> | ||
{{fluxscale_6.6.1}} prints to the CASA logger the derived flux densities of all calibrator sources specified with the ''transfer'' argument. You should examine the output to ensure that the fluxes are reasonable. | {{fluxscale_6.6.1}} prints to the CASA logger the derived flux densities of all calibrator sources specified with the ''transfer'' argument. You should examine the output to ensure that the fluxes are reasonable. | ||
The [http://almascience.org/sc ALMA Calibrator Source Catalogue] can be used to check whether the derived flux densities are reasonable. Wildly different flux densities or flux densities with very high error bars should be treated with suspicion; in such cases you will have to figure out whether something has gone wrong. | The [http://almascience.org/sc ALMA Calibrator Source Catalogue] can be used to check whether the derived flux densities are reasonable. Wildly different flux densities or flux densities with very high error bars should be treated with suspicion; in such cases you will have to figure out whether something has gone wrong. | ||
=== Apply Calibrations for Inspection === | |||
We apply the solutions so far, for inspection purposes only. We will apply all the calibrations at the end: | We apply the solutions so far, for inspection purposes only. We will apply all the calibrations at the end: | ||
| Line 775: | Line 794: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
applycal(vis='3c286_Band6.ms', | applycal(vis = '3c286_Band6.ms', | ||
field='1,2,3', | field = '1,2,3', | ||
calwt=True, | calwt = True, | ||
gaintable=['3c286_Band6.ms.Bscan','3c286_Band6.ms.G2ph','3c286_Band6.ms.flux'], | gaintable = ['3c286_Band6.ms.Bscan','3c286_Band6.ms.G2ph','3c286_Band6.ms.flux'], | ||
interp=['nearest','linear','linear'], | interp = ['nearest','linear','linear'], | ||
parang=False) | parang = False) | ||
</source> | </source> | ||
| Line 789: | Line 808: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
plotms(vis='3c286_Band6.ms', field=' | plotms(vis='3c286_Band6.ms', field='J1256-0547,J1310+3220', spw='0', xaxis='parang', yaxis='amp', correlation='XX,YY', | ||
ydatacolumn='corrected', avgchannel='128', avgbaseline=True, coloraxis='corr', iteraxis='field') | |||
</source> | </source> | ||
| Line 797: | Line 815: | ||
[[Image:amp_parangle_J1310+3220_6.1.png|300px|thumb|center| '''Fig 9''' J1310+3220 amp vs time after bandpass and gain calibration. Spw 0: all baselines have been averaged.]] | [[Image:amp_parangle_J1310+3220_6.1.png|300px|thumb|center| '''Fig 9''' J1310+3220 amp vs time after bandpass and gain calibration. Spw 0: all baselines have been averaged.]] | ||
<br clear=all> | |||
Figure 8 and Figure 9 show the XX and YY data for the bandpass and phase calibrators after the parallel-hand calibration. | Figure 8 and Figure 9 show the XX and YY data for the bandpass and phase calibrators after the parallel-hand calibration. | ||
The effect of source polarization is clearly evident. | The effect of source polarization is clearly evident. | ||
| Line 858: | Line 877: | ||
refant = refant, | refant = refant, | ||
refantmode = 'strict', | refantmode = 'strict', | ||
smodel=[1,0,0,0], | smodel = [1,0,0,0], | ||
gaintable = '3c286_Band6.ms.Bscan', | gaintable = '3c286_Band6.ms.Bscan', | ||
interp='nearest') | interp = 'nearest') | ||
</source> | </source> | ||
We explicitly show some of the default parameters, but they could also be left out -- when a parameter is not specified, its default value is used. | We explicitly show some of the default parameters of {{gaincal_6.6.1}}, but they could also be left out -- when a parameter is not specified, its default value is used. | ||
[[Image: | [[Image:G1_polnratio_scan_6.1.png|thumb| '''Fig 10''' Polarization ratio from the table 3c286_Band6.ms.G1 versus scan number]] | ||
* caltable = '*.G1': the output table. This table will be revised later on, when the source polarization will be estimated. | * caltable = '*.G1': the output table. This table will be revised later on, when the source polarization will be estimated. | ||
| Line 871: | Line 890: | ||
* gaintype='G': this is the default value. We are determining gains for each polarization. | * gaintype='G': this is the default value. We are determining gains for each polarization. | ||
* solint = 'int': one solution per integration. | * solint = 'int': one solution per integration. | ||
* smodel=[1,0,0,0]: we are using an unpolarized model with a Stokes I flux equal to 1. | * smodel=[1,0,0,0]: we are using an unpolarized model with a Stokes I flux equal to 1. | ||
The presence of source polarization in the gains can be seen by plotting the amp vs scan for this table using correlation='/', which forms the complex polarization ratio, shown in Figure 10. The antenna-based complex polarization ratio reveals the sinusoidal variation, which clearly shows the presence of polarization in the source. | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
plotms(vis='3c286_Band6.ms.G1', xaxis='scan', yaxis='GainAmp', coloraxis='antenna1', correlation='/') | |||
</source> | </source> | ||
To inspect the results we generate a partially calibrated dataset, applying this gain table, as well as the bandpass, to the polarization calibrator: | |||
[[Image:Amp_parangle_J1337-1257_6.1.png|300px|thumb|right| '''Fig 11''' J1337-1257 amp vs parang after the application of the bandpass and G1 tables.]] | |||
<source lang="python"> | |||
# In CASA | |||
applycal(vis = '3c286_Band6.ms', | |||
field = '0', | |||
calwt = True, | |||
gaintable = ['3c286_Band6.ms.Bscan','3c286_Band6.ms.G1'], | |||
interp = ['nearest','linear'], | |||
parang=False) | |||
</source> | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
plotms(vis='3c286_Band6.ms | plotms(vis='3c286_Band6.ms', field='0', avgchannel='64', xaxis='parangle', yaxis='amp', ydatacolumn='corrected', correlation='XX,YY', coloraxis='corr') | ||
</source> | </source> | ||
Figure 11 shows the polarization calibrator's amplitude versus parallactic angle after the application of the bandpass and the gain table G1 which we just computed. | |||
The | The source's linear polarization, which rotates with parallactic angle as a function of time, has been absorbed by the gains, since we assumed an unpolarized model for the source. | ||
In order to extract the source polarization information hidden in the gains, we use {{Polfromgain_6.6.1}}. | In order to extract the source polarization information hidden in the gains, we use {{Polfromgain_6.6.1}}. | ||
| Line 903: | Line 926: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
qu=polfromgain(vis='3c286_Band6.ms',tablein='3c286_Band6.ms.G1',caltable='3c286_Band6.ms.G1a') | qu=polfromgain(vis='3c286_Band6.ms', tablein='3c286_Band6.ms.G1', caltable='3c286_Band6.ms.G1a') | ||
print(qu) | print(qu) | ||
</source> | </source> | ||
| Line 913: | Line 936: | ||
<pre style="background-color: #fffacd;"> | <pre style="background-color: #fffacd;"> | ||
{'J1337-1257': { | {'J1337-1257': { | ||
'Spw0': [1.0, 0. | 'Spw0': [1.0, 0.013227418681529856, 0.039849239576474446, 0.0], | ||
'Spw1': [1.0, 0. | 'Spw1': [1.0, 0.013848163127521337, 0.03947996837545822, 0.0], | ||
'Spw2': [1.0, 0. | 'Spw2': [1.0, 0.014538403569321604, 0.0407299275496684, 0.0], | ||
'Spw3': [1.0, 0. | 'Spw3': [1.0, 0.014844803328247997, 0.041510845357872396, 0.0], | ||
'SpwAve': [1.0, 0. | 'SpwAve': [1.0, 0.014114697176655198, 0.04039249521486836, 0.0]}} | ||
</pre> | </pre> | ||
| Line 936: | Line 959: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
plotms(vis='3c286_Band6.ms', | plotms(vis = '3c286_Band6.ms', | ||
ydatacolumn='corrected', | ydatacolumn = 'corrected', | ||
xaxis='freq', yaxis='phase', | xaxis = 'freq', | ||
field='0', | yaxis = 'phase', | ||
avgtime='1e9', | field = '0', | ||
correlation='XY,YX', | avgtime = '1e9', | ||
spw='', antenna='DA48', | correlation = 'XY,YX', | ||
iteraxis='baseline',coloraxis='corr' | spw = '', | ||
antenna = 'DA48', | |||
plotrange=[0,0,-180,180]) | iteraxis = 'baseline', | ||
coloraxis = 'corr', | |||
plotrange = [0,0,-180,180]) | |||
</source> | </source> | ||
This cross-hand delay can be estimated using the gaintype=’KCROSS’ mode of {{gaincal_6.6.1}}. | This cross-hand delay can be estimated using the gaintype=’KCROSS’ mode of {{gaincal_6.6.1}}. | ||
For the cross-hand delay calculation we need to choose a scan where the source's cross-hand contribution is maximum (in absolute value), since this will minimize the mean effect of instrumental polarization. This scan would be the one where the gain ratio is near the mean value in Figure | For the cross-hand delay calculation we need to choose a scan where the source's cross-hand contribution is maximum (in absolute value), since this will minimize the mean effect of instrumental polarization. This scan would be the one where the gain ratio is near the mean value in Figure 10: scan 48. | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
os.system('rm -rf 3c286_Band6.ms.Kcrs') | os.system('rm -rf 3c286_Band6.ms.Kcrs') | ||
gaincal(vis='3c286_Band6.ms', | gaincal(vis = '3c286_Band6.ms', | ||
caltable='3c286_Band6.ms.Kcrs' | caltable = '3c286_Band6.ms.Kcrs', | ||
scan = '48', | |||
scan='48', | gaintype = 'KCROSS', | ||
gaintype='KCROSS', | solint = 'inf', | ||
solint='inf',refant=refant, | refant = refant, | ||
refantmode='strict', | refantmode = 'strict', | ||
smodel=[1,0,1,0], | smodel = [1,0,1,0], | ||
gaintable=['3c286_Band6.ms.Bscan','3c286_Band6.ms.G1'], | gaintable = ['3c286_Band6.ms.Bscan','3c286_Band6.ms.G1'], | ||
interp=['nearest','linear']) | interp = ['nearest','linear']) | ||
</source> | </source> | ||
[[Image:AfterKcr_DA41DA48_6.1.png|300px|thumb|right| ''' | [[Image:AfterKcr_DA41DA48_6.1.png|300px|thumb|right| '''Fig 13''' Baseline DA41&DA48: XY and YX phase vs freq after the cross-hand delay calibration.]] | ||
*caltable='*.Kcrs': the output table. | *caltable='*.Kcrs': the output table. | ||
*scan='48': we select the scan with strong polarization, and we calculate the gain solution using only this scan. | *scan='48': we select the scan with strong polarization, and we calculate the gain solution using only this scan. | ||
*gaintype='KCROSS': solves for a global cross-hand delay. | *gaintype='KCROSS': solves for a global cross-hand delay. | ||
| Line 980: | Line 1,004: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
applycal(vis='3c286_Band6.ms', | applycal(vis = '3c286_Band6.ms', | ||
field='0', | field = '0', | ||
calwt=True, | calwt = True, | ||
gaintable=['3c286_Band6.ms.Bscan','3c286_Band6.ms.G1', '3c286_Band6.ms.Kcrs'], | gaintable = ['3c286_Band6.ms.Bscan','3c286_Band6.ms.G1','3c286_Band6.ms.Kcrs'], | ||
interp=['nearest','linear', 'nearest']) | interp = ['nearest','linear','nearest']) | ||
</source> | </source> | ||
| Line 997: | Line 1,021: | ||
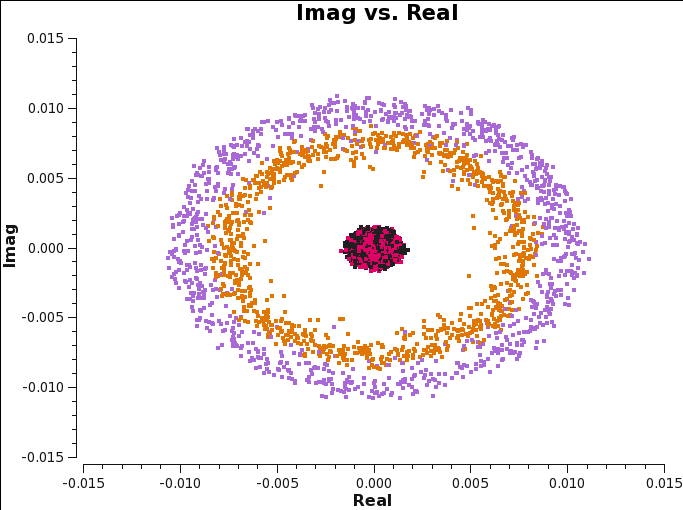
[[File:Imaginary_plane_6.1.png|300px|thumb|right|'''Fig 14''' Imag vs real. Calibration tables applied to the data are B, G1, Kcr.]] | [[File:Imaginary_plane_6.1.png|300px|thumb|right|'''Fig 14''' Imag vs real. Calibration tables applied to the data are B, G1, Kcr.]] | ||
[[File:3c286_Band6.ms.Xfparang.png|300px|thumb|right|'''Fig 15'''. Xfparang cal table for DA41.]] | |||
[[File:AfterXY0_DA41DA48_5.4.png|300px|thumb|right|'''Fig 16''' Baseline DA41&DA48: XY and YX phase vs channels after the Xfparang calibration.]] | |||
[[File:AfterXY0_imagreal_5.4.png|300px|thumb|right|'''Fig 17'''. Imag vs real. Calibration tables applied to the data are B, G1, Kcr, Xfparang.]] | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
plotms(vis='3c286_Band6.ms', | plotms(vis = '3c286_Band6.ms', | ||
ydatacolumn='corrected', | ydatacolumn = 'corrected', | ||
xdatacolumn='corrected', | xdatacolumn = 'corrected', | ||
xaxis='real', yaxis='imag', | xaxis = 'real', | ||
field='0', | yaxis = 'imag', | ||
avgtime='1e9', | field = '0', | ||
avgchannel='128', | avgtime = '1e9', | ||
avgbaseline=True, | avgchannel = '128', | ||
correlation='XY,YX', | avgbaseline = True, | ||
spw='3', | correlation = 'XY,YX', | ||
coloraxis='corr' | spw = '3', | ||
coloraxis = 'corr', | |||
plotrange=[-0.06,0.06,-0.06,0.06]) | plotrange = [-0.06,0.06,-0.06,0.06]) | ||
</source> | </source> | ||
| Line 1,023: | Line 1,050: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
os.system('rm -rf 3c286_Band6.ms.Xfparang') | os.system('rm -rf 3c286_Band6.ms.Xfparang') | ||
S=polcal(vis='3c286_Band6.ms', | S = polcal(vis = '3c286_Band6.ms', | ||
caltable = '3c286_Band6.ms.Xfparang', | |||
field = '0', | |||
poltype = 'Xfparang+QU', | |||
solint = 'inf', | |||
combine = 'scan,obs', | |||
preavg = 300, | |||
smodel = qu['J1337-1257']['SpwAve'], | |||
gaintable = ['3c286_Band6.ms.Bscan','3c286_Band6.ms.G1','3c286_Band6.ms.Kcrs'], | |||
interp = ['nearest','linear','nearest']) | |||
</source> | </source> | ||
| Line 1,045: | Line 1,072: | ||
The output table contains the values of Q, U and the XY-phase. | The output table contains the values of Q, U and the XY-phase. | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
plotms(vis='3c286_Band6.ms.Xfparang',xaxis='frequency',yaxis='phase',iteraxis='antenna',coloraxis='spw' | plotms(vis='3c286_Band6.ms.Xfparang', xaxis='frequency', yaxis='phase', iteraxis='antenna', coloraxis='spw') | ||
</source> | </source> | ||
| Line 1,058: | Line 1,082: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
applycal(vis='3c286_Band6.ms', | applycal(vis = '3c286_Band6.ms', | ||
field='0', | field = '0', | ||
calwt=[True,True,False,False], | calwt = [True,True,False,False], | ||
gaintable=['3c286_Band6.ms.Bscan','3c286_Band6.ms.G1','3c286_Band6.ms.Kcrs', | gaintable = ['3c286_Band6.ms.Bscan','3c286_Band6.ms.G1','3c286_Band6.ms.Kcrs','3c286_Band6.ms.Xfparang'], | ||
interp = ['nearest','linear','nearest','nearest']) | |||
interp=['nearest','linear','nearest','nearest']) | |||
</source> | </source> | ||
Plotting the corrected phase versus frequency (Figure | Plotting the corrected phase versus frequency (Figure 16) and comparing the result with Figure 13, we see that the application of this table does indeed remove spw- and channel-dependent residual phases from the data. The remaining phase offsets (per baseline and correlation) are due to the instrumental polarization effects which will be calibrated below. | ||
<source lang="python"> | |||
# In CASA | |||
plotms(vis = '3c286_Band6.ms', | |||
ydatacolumn = 'corrected', | |||
xaxis = 'freq', | |||
yaxis = 'phase', | |||
field = '0', | |||
avgtime = '1e9', | |||
avgscan = True, | |||
correlation = 'XY,YX', | |||
spw = '', | |||
coloraxis = 'corr', | |||
iteraxis = 'baseline') | |||
</source> | |||
In terms of the real and imaginary parts, the application of the XY-phase | In terms of the real and imaginary parts, the application of the XY-phase calibration removes the slope. What we can see now in the complex plane (Figure 17) is the effect of parallactic angle variation of the source polarization occurring entirely in the real part (over a range between -0.06 and 0.06), with a small complex offset due to the mean instrumental polarization that will be solved for below. | ||
=== Revise gain with good source pol estimate === | === Revise gain with good source pol estimate === | ||
| Line 1,079: | Line 1,117: | ||
# In CASA | # In CASA | ||
os.system('rm -rf 3c286_Band6.ms.G2.polcal') | os.system('rm -rf 3c286_Band6.ms.G2.polcal') | ||
gaincal(vis='3c286_Band6.ms', | gaincal(vis = '3c286_Band6.ms', | ||
caltable='3c286_Band6.ms.G2.polcal', | caltable = '3c286_Band6.ms.G2.polcal', | ||
field='0', | field = '0', | ||
solint='int', | solint = 'int', | ||
refant=refant, | refant = refant, | ||
refantmode='strict', | refantmode = 'strict', | ||
smodel=S['J1337-1257']['SpwAve'], | smodel = S['J1337-1257']['SpwAve'], | ||
gaintable=['3c286_Band6.ms.Bscan'],interp=['nearest'], | gaintable = ['3c286_Band6.ms.Bscan'], | ||
parang=True) | interp = ['nearest'], | ||
parang = True) | |||
</source> | </source> | ||
[[Image:GainsG1_G2polcal_5.4.png| | [[Image:GainsG1_G2polcal_5.4.png|500px|thumb|right|'''Fig 18''' Complex polarization ratio comparison between table G1 and the revised G2.polcal]] | ||
*caltable='*.G2.polcal': the output table. The name reminds us that these are gains for the polarization calibrator. | *caltable='*.G2.polcal': the output table. The name reminds us that these are gains for the polarization calibrator. | ||
| Line 1,096: | Line 1,135: | ||
*parang=True: this time the parallactic angle dependence is corrected for in computing the gains. | *parang=True: this time the parallactic angle dependence is corrected for in computing the gains. | ||
With parang=True the supplied source linear polarization is properly rotated in the parallel-hand visibility model. This new gain solution can be plotted with | With parang=True the supplied source linear polarization is properly rotated in the parallel-hand visibility model. This new gain solution ratio can be plotted with correlation='/' to show that the source polarization is no longer distorting it. | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
plotms(vis='3c286_Band6.ms.G1',xaxis='time',yaxis='amp',field='J1337-1257',correlation='/',coloraxis='antenna1' | plotms(vis='3c286_Band6.ms.G1', xaxis='time', yaxis='amp', field='J1337-1257', correlation='/', coloraxis='antenna1') | ||
plotms(vis='3c286_Band6.ms.G2.polcal',xaxis='time',yaxis='amp',field='J1337-1257',correlation='/',coloraxis='antenna1' | plotms(vis='3c286_Band6.ms.G2.polcal', xaxis='time', yaxis='amp', field='J1337-1257', correlation='/', coloraxis='antenna1') | ||
</source> | </source> | ||
In Figure | In Figure 18 a small distortion can be noticed, in the central scans of table G2.polcal. It is due to antenna DV02 in spw 1, which shows a variation in the ratio slightly different than the average. | ||
Just to check: if qufromgain() is run on this new gain table, the reported source polarization should be statistically indistinguishable from zero. | Just to check: if qufromgain() is run on this new gain table, the reported source polarization should be statistically indistinguishable from zero. | ||
| Line 1,110: | Line 1,149: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
qu2=polfromgain(vis='3c286_Band6.ms',tablein='3c286_Band6.ms.G2.polcal',caltable='3c286_Band6.ms.G2a.polcal') | qu2 = polfromgain(vis='3c286_Band6.ms', tablein='3c286_Band6.ms.G2.polcal', caltable='3c286_Band6.ms.G2a.polcal') | ||
print( | print(qu2) | ||
</source> | </source> | ||
| Line 1,118: | Line 1,157: | ||
<pre style="background-color: #fffacd;"> | <pre style="background-color: #fffacd;"> | ||
'SpwAve': [1.0, 0. | {'J1337-1257': | ||
{'Spw0': [1.0, -0.0003105910631165318, -0.0008989854372679172, 0.0], | |||
'Spw1': [1.0, 0.00030789313801403835, -0.0012251557847778529, 0.0], | |||
'Spw2': [1.0, 0.0010217877488700757, 3.4010732831564205e-05, 0.0], | |||
'Spw3': [1.0, 0.0013222722374015867, 0.0008468052734902653, 0.0], | |||
'SpwAve': [1.0, 0.0005853405152922923, -0.00031083130393098516, 0.0]}} | |||
</pre> | </pre> | ||
| Line 1,132: | Line 1,176: | ||
# In CASA | # In CASA | ||
os.system('rm -rf 3c286_Band6.ms.Df0*') | os.system('rm -rf 3c286_Band6.ms.Df0*') | ||
polcal(vis='3c286_Band6.ms', | polcal(vis = '3c286_Band6.ms', | ||
caltable='3c286_Band6.ms.Df0gen', | caltable = '3c286_Band6.ms.Df0gen', | ||
field='0', #J1337-1257 | field = '0', # J1337-1257 | ||
solint='inf',combine='obs,scan', | solint = 'inf', | ||
preavg=300, | combine = 'obs,scan', | ||
poltype='Dflls', | preavg = 300, | ||
refant='', #solve absolute D-term | poltype = 'Dflls', | ||
smodel=S['J1337-1257']['SpwAve'], | refant = '', # solve absolute D-term | ||
gaintable=['3c286_Band6.ms.Bscan','3c286_Band6.ms.G2.polcal','3c286_Band6.ms.Kcrs', '3c286_Band6.ms.Xfparang'], | smodel = S['J1337-1257']['SpwAve'], | ||
gainfield=['', '', '', ''], | gaintable = ['3c286_Band6.ms.Bscan','3c286_Band6.ms.G2.polcal','3c286_Band6.ms.Kcrs','3c286_Band6.ms.Xfparang'], | ||
interp=['nearest','linear','nearest','nearest']) | gainfield = ['','','',''], | ||
interp = ['nearest','linear','nearest','nearest']) | |||
</source> | </source> | ||
| Line 1,157: | Line 1,202: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
plotms(vis='3c286_Band6.ms.Df0gen',xaxis='frequency',yaxis='amp',spw='0,1',iteraxis='antenna',coloraxis='corr', | plotms(vis='3c286_Band6.ms.Df0gen', xaxis='frequency', yaxis='amp', spw='0,1', iteraxis='antenna', coloraxis='corr', gridrows=3, gridcols=2) | ||
plotms(vis='3c286_Band6.ms.Df0gen',xaxis='frequency',yaxis='amp',spw='2,3',iteraxis='antenna',coloraxis='corr', | plotms(vis='3c286_Band6.ms.Df0gen', xaxis='frequency', yaxis='amp', spw='2,3', iteraxis='antenna', coloraxis='corr', gridrows=3, gridcols=2) | ||
plotms(vis='3c286_Band6.ms.Df0gen',xaxis='frequency',yaxis='real',spw='0,1',iteraxis='antenna',coloraxis='corr', | plotms(vis='3c286_Band6.ms.Df0gen', xaxis='frequency', yaxis='real', spw='0,1', iteraxis='antenna', coloraxis='corr', gridrows=3, gridcols=2) | ||
plotms(vis='3c286_Band6.ms.Df0gen',xaxis='frequency',yaxis='real',spw='2,3',iteraxis='antenna',coloraxis='corr', | plotms(vis='3c286_Band6.ms.Df0gen', xaxis='frequency', yaxis='real', spw='2,3', iteraxis='antenna', coloraxis='corr', gridrows=3, gridcols=2) | ||
plotms(vis='3c286_Band6.ms.Df0gen',xaxis='frequency',yaxis='imag',spw='0,1',iteraxis='antenna',coloraxis='corr', | plotms(vis='3c286_Band6.ms.Df0gen', xaxis='frequency', yaxis='imag', spw='0,1', iteraxis='antenna', coloraxis='corr', gridrows=3, gridcols=2) | ||
plotms(vis='3c286_Band6.ms.Df0gen',xaxis='frequency',yaxis='imag',spw='2,3',iteraxis='antenna',coloraxis='corr', | plotms(vis='3c286_Band6.ms.Df0gen', xaxis='frequency', yaxis='imag', spw='2,3', iteraxis='antenna', coloraxis='corr', gridrows=3, gridcols=2) | ||
</source> | </source> | ||
{| | {| | ||
| [[Image:Df0_amp_5.4.png|300px|thumb| | | [[Image:Df0_amp_5.4.png|300px|thumb|center|''' Fig 19''' Df0 amp vs freq]] | ||
| [[Image:Df0_real_5.4.png|300px|thumb| | | [[Image:Df0_real_5.4.png|300px|thumb|center|'''Fig 20''' Df0 real vs freq]] | ||
| [[Image:Df0_imag_5.4.png|300px|thumb|center|'''Fig | | [[Image:Df0_imag_5.4.png|300px|thumb|center|'''Fig 21''' Df0 imag vs freq]] | ||
|} | |} | ||
| Line 1,177: | Line 1,222: | ||
=== Solving the Global Normalized Gain Amplitudes === | === Solving the Global Normalized Gain Amplitudes === | ||
The final calibration table that needs generated is the X/Y gain amplitude table. When the initial non-polarization calibration, we produced polarization independant gain solutions to preserve the intrinsic linear polarzation of the calibrator. However, this leaves the cross-hand amplitude ratio uncalibrated. We will determine that correction here using the previous calibrations. | The final calibration table that needs generated is the X/Y gain amplitude table. When the initial non-polarization calibration, we produced polarization independant gain solutions to preserve the intrinsic linear polarzation of the calibrator. However, this leaves the cross-hand amplitude ratio uncalibrated. We will determine that correction here using the previous calibrations. | ||
[[File:3c286_Band6.ms.Gxyamp.XY.YX.png|300px|thumb|right|<caption>'''Fig 22''' XY and YX</caption>]] | |||
[[File:3c286_Band6.ms.Gxyamp.polratio.png|300px|thumb|right|<caption>'''Fig 23''' Pol ratio</caption>]] | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
os.system('rm -rf 3c286_Band6.ms.Gxyamp*') | os.system('rm -rf 3c286_Band6.ms.Gxyamp*') | ||
gaincal(vis='3c286_Band6.ms', | gaincal(vis = '3c286_Band6.ms', | ||
caltable = '3c286_Band6.ms.Gxyamp', | |||
field = '0', #J1337-1257 | |||
solint = 'inf', | |||
combine = 'obs,scan', | |||
refant = refant, | |||
refantmode = 'strict', | |||
gaintype = 'G', | |||
calmode = 'a', | |||
smodel = S['J1337-1257']['SpwAve'], | |||
gaintable = ['3c286_Band6.ms.Bscan','3c286_Band6.ms.G2.polcal','3c286_Band6.ms.Kcrs', | |||
'3c286_Band6.ms.Xfparang','3c286_Band6.ms.Df0gen'], | |||
gainfield = ['','','','',''], | |||
interp = ['nearest','linear','nearest','nearest','nearest'], | |||
solnorm = True, | |||
parang = True) | |||
</source> | </source> | ||
| Line 1,202: | Line 1,251: | ||
*gaintype='G': Solve for each polarization separatly. | *gaintype='G': Solve for each polarization separatly. | ||
*smodel=S['J1337-1257']['SpwAve']: we use as model the "S" we calculated above | *smodel=S['J1337-1257']['SpwAve']: we use as model the "S" we calculated above | ||
*gaintable=['*.Bscan','*.G2.polcal','*.Kcrs', '*.Xfparang',' | *gaintable=['*.Bscan','*.G2.polcal','*.Kcrs','*.Xfparang','*.Df0gen']: we apply the bandpass, gain, and cross-hand calibration tables (Kcrs, and Xfparang) | ||
Here we plot the XY amplitudes, and the XY amplitude ratios. We expect these ratios to be near a value of 1. | Here we plot the XY amplitudes, and the XY amplitude ratios. We expect these ratios to be near a value of 1. | ||
| Line 1,208: | Line 1,257: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
plotms(vis='3c286_Band6.ms.Gxyamp',xaxis='antenna1',yaxis='amp',coloraxis=' | # XY and YX | ||
plotms(vis='3c286_Band6.ms.Gxyamp',xaxis='antenna1',yaxis='amp',correlation='/',coloraxis='antenna1',iteraxis='spw', | plotms(vis='3c286_Band6.ms.Gxyamp', xaxis='antenna1', yaxis='amp', coloraxis='corr', iteraxis='spw', gridrows=2, gridcols=2) | ||
# pol ratio | |||
plotms(vis='3c286_Band6.ms.Gxyamp', xaxis='antenna1', yaxis='amp', correlation='/', coloraxis='antenna1', iteraxis='spw', gridrows=2, gridcols=2) | |||
</source> | </source> | ||
| Line 1,220: | Line 1,271: | ||
For verification purposes only we now apply to the polarization calibrator all calibration tables computed in the calibration guide ''except'' the D-terms corrections. | For verification purposes only we now apply to the polarization calibrator all calibration tables computed in the calibration guide ''except'' the D-terms corrections. | ||
In the dir 3C286_Band6_pol_UnCalibrated you should now have all the calibration tables, and you can proceed as follows: | In the dir 3C286_Band6_pol_UnCalibrated you should now have all the calibration tables, and you can proceed as follows: | ||
[[File:Field0.noDterm.Stokes.clean.png|300px|thumb|right|'''Fig 24''' Draw a mask around the point source pol calibrator in the interactive tclean GUI.]] | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
applycal(vis='3c286_Band6.ms', | applycal(vis = '3c286_Band6.ms', | ||
field='0', | field = '0', | ||
calwt=[True,True,False,False], | calwt = [True,True,False,False], | ||
gaintable=['3c286_Band6.ms.Bscan','3c286_Band6.ms.G2.polcal','3c286_Band6.ms.Kcrs', '3c286_Band6.ms.Xfparang'], | gaintable = ['3c286_Band6.ms.Bscan','3c286_Band6.ms.G2.polcal','3c286_Band6.ms.Kcrs','3c286_Band6.ms.Xfparang'], | ||
interp=['nearest','linear', 'nearest','nearest'], | interp = ['nearest','linear','nearest','nearest'], | ||
gainfield=[ | gainfield = ['','','',''], | ||
parang=True) | parang = True) | ||
</source> | </source> | ||
| Line 1,238: | Line 1,291: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
os.system('rm -rf | os.system('rm -rf polcal.StokesIQUV.noDterms*') | ||
tclean(vis='3c286_Band6.ms', | tclean(vis = '3c286_Band6.ms', | ||
field = '0', | |||
imagename = 'polcal.StokesIQUV.noDterms', | |||
cell = ['0.1arcsec'], | |||
imsize = [250,250], | |||
stokes = 'IQUV', | |||
deconvolver = 'clarkstokes', | |||
interactive = True, | |||
weighting = 'briggs', | |||
robust = 0.5, | |||
niter = 500, | |||
cycleniter = 20) | |||
</source> | </source> | ||
<br clear=all> | |||
<div style="float: right; width: 320px;"> | |||
<div style="text-align: center; margin: 5px;"> '''Fig 25.''' Comparison between images of the polarization calibrator with (left panels) and without (right panels) the D-term corrections applied. </div> | |||
[[File:ComparisonI_6.5.4.png|300px|thumb|right|<div style="text-align: center;"> Stokes I </div>]] | |||
[[File:ComparisonQ_6.5.4.png|300px|thumb|right|<div style="text-align: center;"> Stokes Q </div>]] | |||
[[File:ComparisonU_6.5.4.png|300px|thumb|right|<div style="text-align: center;"> Stokes U </div>]] | |||
[[File:ComparisonV_6.5.4.png|300px|thumb|right|<div style="text-align: center;"> Stokes V </div>]] | |||
</div> | |||
The calibrator image should show a point source, so we can clean with a small number of itterations. It is important not to overclean the image. The clean flux is of 1.06 Jy. | The calibrator image should show a point source, so we can clean with a small number of itterations. It is important not to overclean the image. The clean flux is of 1.06 Jy. | ||
Now we apply all the calibration tables, including Df0gen: | Now we apply all the calibration tables with {{applycal_6.6.1}}, including Df0gen and Gxyamp: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
applycal(vis='3c286_Band6.ms', | applycal(vis = '3c286_Band6.ms', | ||
field='0', | field = '0', | ||
calwt=[True,True | calwt = [True,True,False,False,False,False], | ||
gaintable=['3c286_Band6.ms.Bscan','3c286_Band6.ms.G2.polcal','3c286_Band6.ms.Kcrs','3c286_Band6.ms.Xfparang','3c286_Band6.ms.Df0gen','3c286_Band6.ms.Gxyamp'], | gaintable = ['3c286_Band6.ms.Bscan','3c286_Band6.ms.G2.polcal','3c286_Band6.ms.Kcrs', | ||
interp=['nearest','linear', 'linear','nearest', 'nearest','nearest'], | '3c286_Band6.ms.Xfparang','3c286_Band6.ms.Df0gen','3c286_Band6.ms.Gxyamp'], | ||
gainfield=['', '','', '', '',''], | interp = ['nearest','linear','linear','nearest','nearest','nearest'], | ||
parang=True) | gainfield = ['','','','','',''], | ||
parang = True) | |||
</source> | </source> | ||
| Line 1,272: | Line 1,335: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
os.system('rm -rf | os.system('rm -rf polcal.StokesIQUV.withDterms*') | ||
tclean(vis='3c286_Band6.ms', | tclean(vis = '3c286_Band6.ms', | ||
field = '0', | |||
imagename = 'polcal.StokesIQUV.withDterms', | |||
cell = ['0.1arcsec'], | |||
imsize = [250,250], | |||
stokes = 'IQUV', | |||
deconvolver = 'clarkstokes', | |||
weighting = 'briggs', | |||
robust = 0.5, | |||
interactive = True, | |||
niter = 500, | |||
cycleniter = 20) | |||
</source> | </source> | ||
| Line 1,297: | Line 1,360: | ||
Copy the output URL into a browser to view your CARTA session. Select and load:<br> | Copy the output URL into a browser to view your CARTA session. Select and load:<br> | ||
'' | ''polcal.StokesIQUV.noDterms.image''<br> | ||
'' | ''polcal.StokesIQUV.withDterms.image'' | ||
As you can see in Figure 25, the application of D-term calibration clearly improves the images of Stokes Q, U, and V. | |||
<br clear=all> | |||
< | |||
== | == Inspect the corrected pol cal data == | ||
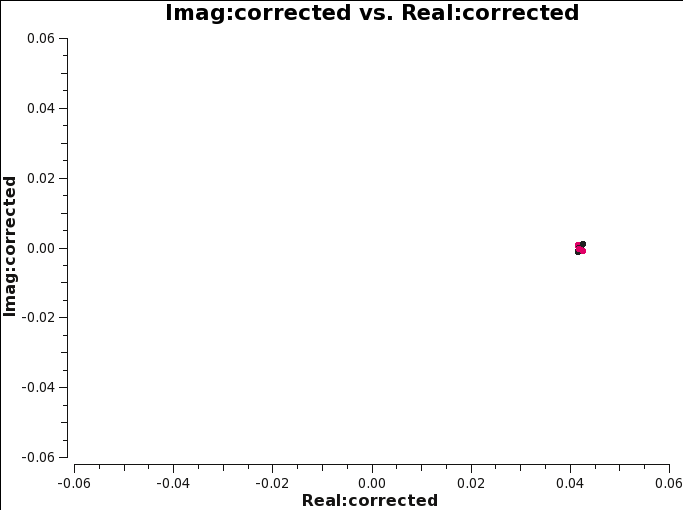
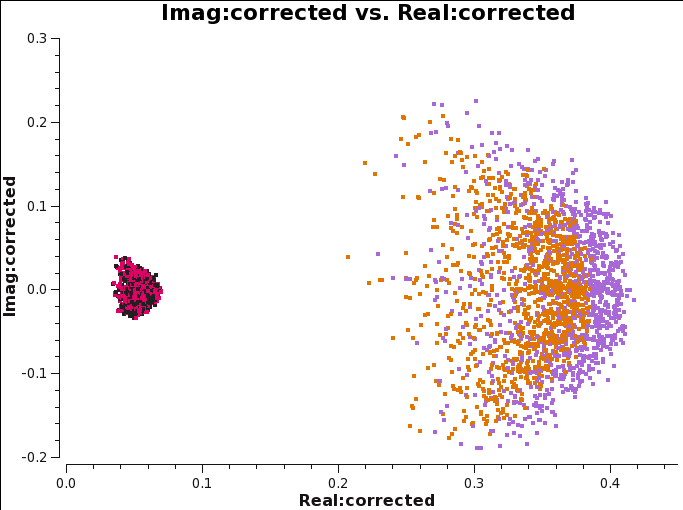
We first plot the complex plane again, and compare the results with Figures 14 and 17. Figure 26 shows clearly that the imaginary part is now zero, while the real part is corrected for the variation shown before; its corrected value is ~0.04. | |||
<div style="float: right; width: 600px;"> | |||
{| | |||
| [[File:AfterAll_imagreal_5.4.png|250px|thumb|'''Fig 26''' Imag vs real. Calibration tables applied to the data are B, G2polcal, Kcr, Xfparang, and D.]] | |||
| [[Image:AfterAll_allants_amp_5.4.png|250px|thumb|'''Fig 27''' XX,YY, XY and YX amp vs channels for all antennas after the whole calibration.]] | |||
|- | |||
| [[Image:AfterAll_allants_phase_5.4.png|250px|thumb|'''Fig 28''' XX,YY, XY and YX amp vs phase for all antennas after the whole calibration.]] | |||
| [[File:AfterAll_1baseline_phase_5.4.png|250px|thumb|'''Fig 29''' Baseline DA41&DA48: XY and YX phase vs frequency after the whole calibration. All scans are averaged.]] | |||
|} | |||
</div> | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
plotms(vis = '3c286_Band6.ms', | |||
ydatacolumn = 'corrected', | |||
xdatacolumn = 'corrected', | |||
xaxis = 'real', | |||
yaxis = 'imag', | |||
field = '0', | |||
avgtime = '1e9', | |||
avgchannel = '128', | |||
avgbaseline = True, | |||
correlation = 'XY,YX', | |||
spw = '3', | |||
coloraxis = 'corr', | |||
plotrange = [-0.06,0.06,-0.06,0.06]) | |||
</source> | </source> | ||
Let's now examine the corrected amplitude and phase of the polarization calibrator. | Let's now examine the corrected amplitude and phase of the polarization calibrator. | ||
| Line 1,336: | Line 1,401: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
plotms(vis='3c286_Band6.ms', xaxis='chan', yaxis='amp', | plotms(vis = '3c286_Band6.ms', | ||
ydatacolumn='corrected', | xaxis = 'chan', | ||
yaxis = 'amp', # or phase | |||
avgtime='1e9' | ydatacolumn = 'corrected', | ||
field = '0', | |||
coloraxis='corr') | avgtime = '1e9', | ||
avgscan = True, | |||
coloraxis = 'corr') | |||
</source> | </source> | ||
<source lang="python"> | |||
# In CASA | |||
plotms(vis = '3c286_Band6.ms', | |||
xaxis = 'freq', | |||
yaxis = 'phase', | |||
ydatacolumn = 'corrected', | |||
field = '0', | |||
avgtime = '1e9', | |||
avgscan = True, | |||
correlation = 'XY,YX', | |||
coloraxis = 'corr', | |||
iteraxis = 'baseline') | |||
</source> | |||
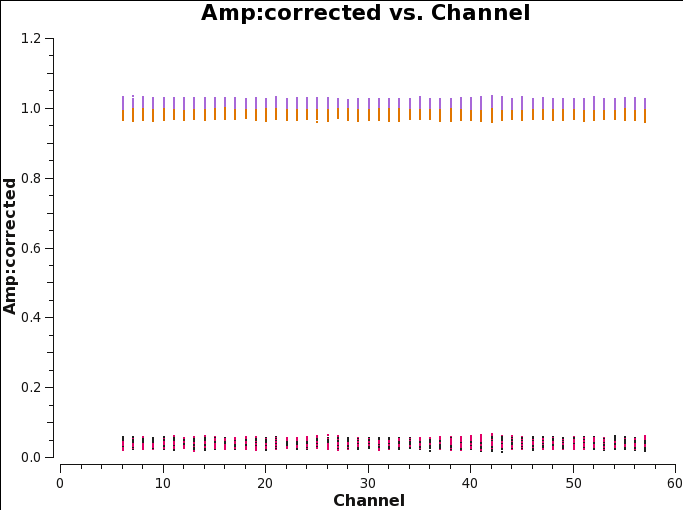
In Figure | In Figure 27 we see that the XX,YY correlations have unitary amplitude, since we didn't scaled the flux. | ||
The XY,YX amplitude value is of the order of 0.04, which means the Stokes U of this source is ~0.04. This value is consistent with what the previous steps revealed. | The XY,YX amplitude value is of the order of 0.04, which means the Stokes U of this source is ~0.04. This value is consistent with what the previous steps revealed. | ||
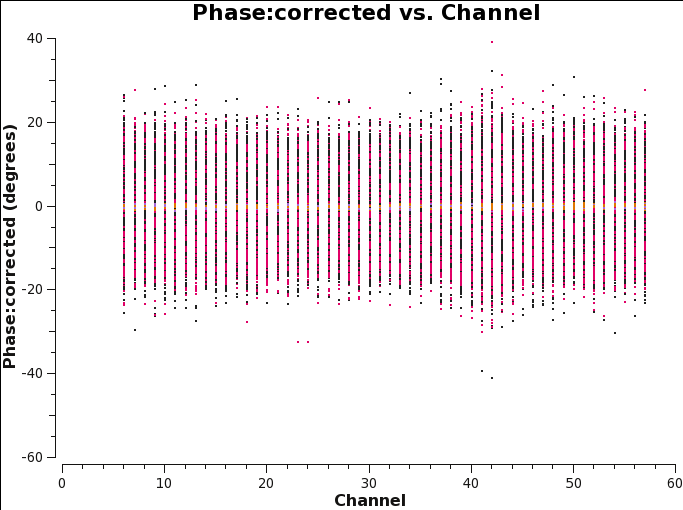
After the calibration all the phases | After the calibration all the phases normalized around zero (Fig 28). | ||
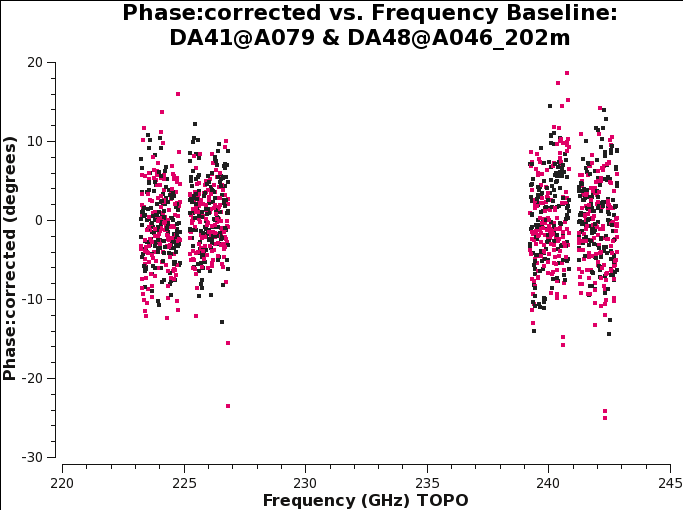
To more clearly show the effect of the D-terms application on the polarization calibrator we also plot the corrected phases of the baseline DA48 | To more clearly show the effect of the D-terms application on the polarization calibrator we also plot the corrected phases of the baseline DA41&DA48 (Fig 29). Comparing this result with Figure 16 we see that the XY and YX phases are now corrected and near zero. | ||
==Applying the calibrations and splitting of the corrected data== | |||
We now apply the solutions from the phase calibrator (field='3') to the science target (field='4'). | We now apply the solutions from the phase calibrator (field='3') to the science target (field='4'). | ||
| Line 1,362: | Line 1,439: | ||
# In CASA | # In CASA | ||
# Apply caltables to fields = 3 & 4 | # Apply caltables to fields = 3 & 4 | ||
applycal(vis='3c286_Band6.ms', | applycal(vis = '3c286_Band6.ms', | ||
field='3,4', | field = '3,4', | ||
calwt=[True,True,False,False,False,False,False], | calwt = [True,True,False,False,False,False,False], | ||
gaintable = ['3c286_Band6.ms.Bscan','3c286_Band6.ms.G2ph','3c286_Band6.ms.flux', | gaintable = ['3c286_Band6.ms.Bscan','3c286_Band6.ms.G2ph','3c286_Band6.ms.flux', | ||
'3c286_Band6.ms.Kcrs','3c286_Band6.ms.Xfparang','3c286_Band6.ms.Df0gen','3c286_Band6.ms.Gxyamp'], | |||
interp=['nearest','linear','linear','nearest','nearest','nearest','nearest'], | interp = ['nearest','linear','linear','nearest','nearest','nearest','nearest'], | ||
gainfield=['', '3', '3','', '', '',''], | gainfield = ['','3','3','','','',''], | ||
parang=True) | parang = True) | ||
</source> | </source> | ||
* gaintable=['*.Bscan', '*.G2ph', '*.flux', '*.Kcrs', '*.Xfparang', '*.Df0gen']: these are all the tables to be applied to the data. | * gaintable=['*.Bscan', '*.G2ph', '*.flux', '*.Kcrs', '*.Xfparang', '*.Df0gen', '*Gxyamp']: these are all the tables to be applied to the data. | ||
* interp=['nearest', 'linear', 'linear', 'nearest', 'nearest', 'nearest']: the corresponding interpolation method | * interp=['nearest', 'linear', 'linear', 'nearest', 'nearest', 'nearest']: the corresponding interpolation method | ||
* gainfield=['', '3', '3','', '', '']: select the field from the corresponding gaintable. Here the phase calibrator gains are applied to both the calibrator itself and the target. | * gainfield=['','3','3','','','','']: select the field from the corresponding gaintable. Here the phase calibrator gains are applied to both the calibrator itself and the target. | ||
* parang=True: apply the parallactic angle correction | * parang=True: apply the parallactic angle correction | ||
| Line 1,381: | Line 1,458: | ||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
plotms(vis='3c286_Band6.ms', field='4', | plotms(vis = '3c286_Band6.ms', | ||
field = '4', | |||
xaxis = 'real', | |||
yaxis = 'imag', | |||
spw = '0', | |||
ydatacolumn = 'data', | |||
xdatacolumn = 'data', | |||
avgchannel = '64', | |||
avgtime = '1e9', | |||
avgscan = True, | |||
coloraxis = 'corr') | |||
</source> | </source> | ||
{| | {| | ||
| [[Image:Field4_beforeall_5.4.png|300px|thumb|center|'''Figure | | [[Image:Field4_beforeall_5.4.png|300px|thumb|center|'''Figure 30''' 3C286: zoom in of the plot of data columns. Imag vs real of parallel- and cross-hand correlations before the calibration. All scans have been averaged.]] | ||
| [[Image:Field4_afterall_5.4.png|300px|thumb|right|''' Figure | | [[Image:Field4_afterall_5.4.png|300px|thumb|right|''' Figure 31''' 3C286: Imag vs real of parallel- and cross-hand correlations after the whole calibration. The corrected amplitude has been flux scaled, so it is in units of Jy.]] | ||
|} | |} | ||
| Line 1,401: | Line 1,483: | ||
# In CASA | # In CASA | ||
os.system('rm -rf 3c286_Band6.pol.cal.ms') | os.system('rm -rf 3c286_Band6.pol.cal.ms') | ||
split(vis='3c286_Band6.ms', | split(vis = '3c286_Band6.ms', | ||
outputvis='3c286_Band6.pol.cal.ms', | outputvis = '3c286_Band6.pol.cal.ms', | ||
field='4', | field = '4', | ||
datacolumn='corrected', | datacolumn = 'corrected', | ||
width=' | width = '4') | ||
</source> | </source> | ||
Using the parameter | Using the parameter ''width'' we average the channels in order to reduce the size of the output file (3c286_Band6.pol.cal.ms will have 16 channels). | ||
In | In TDM observations, averaging more than about 8 channels in dual pol (XX,YY of 128 channels each) or 4 in full Stokes (XX,XY,YX,YY of 64 channels each) would produce significant bandwidth smearing. For details, see the relevant [https://casadocs.readthedocs.io/en/v6.6.1/notebooks/synthesis_imaging.html#Imaging-at-wideband-sensitivity CASA notebook] and [https://safe.nrao.edu/wiki/pub/Main/RadioTutorial/BandwidthSmearing.pdf this document]. | ||
about 8 channels in full Stokes would produce significant bandwidth smearing. | |||
Now you can continue on to [[3C286_Band6Pol_Imaging]]. | Now you can continue on to [[3C286_Band6Pol_Imaging]]. | ||
Latest revision as of 20:55, 8 November 2024
Overview
This portion of the 3C286 Polarization CASA Guide will cover the calibration of the raw visibility data.
To follow this guide you must have downloaded the file 3C286_Band6_UncalibratedData.tgz from 3C286 Polarization#Obtaining the Data.
To skip to the imaging portion of this guide, see 3C286 Band6Pol Imaging.
This guide features CARTA, the “Cube Analysis and Rendering Tool for Astronomy,” which is the new NRAO visualization tool for images and cubes. The CASA viewer (imview) has not been maintained for a few years and will be removed from future versions of CASA. We strongly recommend using CARTA, as it provides a much more efficient, stable, and feature rich user experience. A comparison of the CASA viewer and CARTA, as well as instructions on how to use CARTA at NRAO, is provided in the CARTA section of the CASA docs.
Unpack the Data
Once the file 3C286_Band6_UncalibratedData.tgz has been download, unpack it as follows:
# In a bash terminal outside CASA
tar -xvzf 3C286_Band6_UncalibratedData.tgz
cd 3C286_Band6_UncalibratedData
In the unpacked directory you should see three ASDM files:
- uid___A002_X85c183_X10a
- uid___A002_X85c183_X51a
- uid___A002_X85c183_X822
Confirm your version of CASA
This guide has been written for CASA release 6.6.1. Start CASA, then confirm your version before proceeding.
# In CASA
import casalith
version = '.'.join(map(str,casalith.version()))
print ("You are using {}".format(version))
if (version < '6.6.1'):
print("YOUR VERSION OF CASA IS TOO OLD FOR THIS GUIDE.")
print("PLEASE UPDATE IT BEFORE PROCEEDING.")
else:
print("Your version of CASA is appropriate for this guide.")
Initial Inspection and A priori Calibrations
Import ASDM into CASA MS
We will eventually concatenate the three datasets into one dataset. However, we will keep them separate for now, as some of the steps to follow require individual datasets (specifically, the application of the Tsys and WVR tables). We therefore start by defining an array "basename" that includes the names of the three files in chronological order. This will simplify the following steps by allowing us to loop through the files using a simple for-loop in python. Remember that if you log out of CASA, you will have to re-issue this command.
# In CASA
# Define a python list holding the names of all of our data sets
basename=["uid___A002_X85c183_X10a","uid___A002_X85c183_X51a","uid___A002_X85c183_X822"]
The raw data have been provided to you in the ASDM format. It is the native format of the data produced by the observatory.
Before we can proceed to the calibration, we will need to convert those data to the CASA MS format. This is done simply with the task importasdm.
#In CASA
for name in basename:
importasdm(asdm=name, asis='*')
listobs
The usual first step is then to get some basic information about the data. We do this using the task listobs, which will output a detailed summary of each dataset supplied.
# In CASA
# Loop over each element in the list and create summary file using listobs
for name in basename:
os.system('rm '+name+'.listobs.txt')
listobs(vis=name+'.ms', listfile=name+'.listobs.txt')
Note that after cutting and pasting a for-loop you often have to press return several times to execute. The output will be sent to the CASA logger, or saved in a text file. Here is a snippet from the listobs output for the first file in the list:
Observer: knakanishi Project: uid://A002/X845868/X11
Observation: ALMA
Data records: 10125065 Total elapsed time = 3858.05 seconds
Observed from 01-Jul-2014/21:18:10.9 to 01-Jul-2014/22:22:29.0 (UTC)
ObservationID = 0 ArrayID = 0
Date Timerange (UTC) Scan FldId FieldName nRows SpwIds Average Interval(s) ScanIntent
01-Jul-2014/21:18:10.9 - 21:19:08.3 1 0 J1337-1257 150164 [0,1,2,3,4,5,6,7,8] [1.15, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01] [CALIBRATE_POINTING#ON_SOURCE,CALIBRATE_WVR#ON_SOURCE]
21:20:01.5 - 21:21:04.4 2 0 J1337-1257 501611 [0,9,10,11,12,13,14,15,16] [1.15, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48] [CALIBRATE_SIDEBAND_RATIO#OFF_SOURCE,CALIBRATE_SIDEBAND_RATIO#ON_SOURCE,CALIBRATE_WVR#OFF_SOURCE,CALIBRATE_WVR#ON_SOURCE]
21:21:07.2 - 21:21:22.8 3 0 J1337-1257 95511 [0,9,10,11,12,13,14,15,16] [1.15, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48] [CALIBRATE_ATMOSPHERE#OFF_SOURCE,CALIBRATE_ATMOSPHERE#ON_SOURCE,CALIBRATE_WVR#OFF_SOURCE,CALIBRATE_WVR#ON_SOURCE]
21:21:26.8 - 21:25:39.9 4 0 J1337-1257 720750 [0,17,18,19,20,21,22,23,24] [1.15, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01] [CALIBRATE_POLARIZATION#ON_SOURCE,CALIBRATE_WVR#ON_SOURCE]
21:26:09.0 - 21:26:24.6 5 1 J1256-0547 95511 [0,9,10,11,12,13,14,15,16] [1.15, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48] [CALIBRATE_ATMOSPHERE#OFF_SOURCE,CALIBRATE_ATMOSPHERE#ON_SOURCE,CALIBRATE_WVR#OFF_SOURCE,CALIBRATE_WVR#ON_SOURCE]
21:26:26.3 - 21:29:35.7 6 1 J1256-0547 540547 [0,17,18,19,20,21,22,23,24] [1.15, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01] [CALIBRATE_BANDPASS#ON_SOURCE,CALIBRATE_WVR#ON_SOURCE]
21:29:51.4 - 21:30:07.9 7 2 Ceres 95573 [0,9,10,11,12,13,14,15,16] [1.15, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48] [CALIBRATE_ATMOSPHERE#OFF_SOURCE,CALIBRATE_ATMOSPHERE#ON_SOURCE,CALIBRATE_WVR#OFF_SOURCE,CALIBRATE_WVR#ON_SOURCE]
21:30:09.8 - 21:32:47.3 8 2 Ceres 450461 [0,17,18,19,20,21,22,23,24] [1.15, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01] [CALIBRATE_AMPLI#ON_SOURCE,CALIBRATE_FLUX#ON_SOURCE,CALIBRATE_WVR#ON_SOURCE]
21:33:30.2 - 21:34:27.1 9 3 J1310+3220 150195 [0,1,2,3,4,5,6,7,8] [1.15, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01] [CALIBRATE_POINTING#ON_SOURCE,CALIBRATE_WVR#ON_SOURCE]
21:35:01.2 - 21:35:32.4 10 3 J1310+3220 90117 [0,17,18,19,20,21,22,23,24] [1.15, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01] [CALIBRATE_PHASE#ON_SOURCE,CALIBRATE_WVR#ON_SOURCE]
21:35:46.2 - 21:36:02.3 11 4 3c286 95511 [0,9,10,11,12,13,14,15,16] [1.15, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48] [CALIBRATE_ATMOSPHERE#OFF_SOURCE,CALIBRATE_ATMOSPHERE#ON_SOURCE,CALIBRATE_WVR#OFF_SOURCE,CALIBRATE_WVR#ON_SOURCE]
21:36:03.5 - 21:43:09.2 12 4 3c286 1261328 [0,17,18,19,20,21,22,23,24] [1.15, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01] [OBSERVE_TARGET#ON_SOURCE]
21:43:28.1 - 21:43:59.2 13 3 J1310+3220 90086 [0,17,18,19,20,21,22,23,24] [1.15, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01] [CALIBRATE_PHASE#ON_SOURCE,CALIBRATE_WVR#ON_SOURCE]
21:44:15.4 - 21:51:21.4 14 4 3c286 1261297 [0,17,18,19,20,21,22,23,24] [1.15, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01] [OBSERVE_TARGET#ON_SOURCE]
21:51:43.5 - 21:52:14.2 15 3 J1310+3220 90086 [0,17,18,19,20,21,22,23,24] [1.15, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01] [CALIBRATE_PHASE#ON_SOURCE,CALIBRATE_WVR#ON_SOURCE]
21:52:36.5 - 21:52:53.1 16 4 3c286 95542 [0,9,10,11,12,13,14,15,16] [1.15, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48] [CALIBRATE_ATMOSPHERE#OFF_SOURCE,CALIBRATE_ATMOSPHERE#ON_SOURCE,CALIBRATE_WVR#OFF_SOURCE,CALIBRATE_WVR#ON_SOURCE]
21:52:54.9 - 21:56:26.8 17 4 3c286 630633 [0,17,18,19,20,21,22,23,24] [1.15, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01] [OBSERVE_TARGET#ON_SOURCE]
21:56:46.5 - 21:57:17.0 18 3 J1310+3220 90086 [0,17,18,19,20,21,22,23,24] [1.15, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01] [CALIBRATE_PHASE#ON_SOURCE,CALIBRATE_WVR#ON_SOURCE]
21:58:04.8 - 21:59:02.3 19 0 J1337-1257 150133 [0,1,2,3,4,5,6,7,8] [1.15, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01] [CALIBRATE_POINTING#ON_SOURCE,CALIBRATE_WVR#ON_SOURCE]
21:59:42.7 - 21:59:59.3 20 0 J1337-1257 95542 [0,9,10,11,12,13,14,15,16] [1.15, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48] [CALIBRATE_ATMOSPHERE#OFF_SOURCE,CALIBRATE_ATMOSPHERE#ON_SOURCE,CALIBRATE_WVR#OFF_SOURCE,CALIBRATE_WVR#ON_SOURCE]
22:00:01.2 - 22:04:14.0 21 0 J1337-1257 720750 [0,17,18,19,20,21,22,23,24] [1.15, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01] [CALIBRATE_POLARIZATION#ON_SOURCE,CALIBRATE_WVR#ON_SOURCE]
22:04:58.4 - 22:05:55.5 22 3 J1310+3220 150195 [0,1,2,3,4,5,6,7,8] [1.15, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01] [CALIBRATE_POINTING#ON_SOURCE,CALIBRATE_WVR#ON_SOURCE]
22:06:29.4 - 22:07:00.2 23 3 J1310+3220 90086 [0,17,18,19,20,21,22,23,24] [1.15, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01] [CALIBRATE_PHASE#ON_SOURCE,CALIBRATE_WVR#ON_SOURCE]
22:07:13.2 - 22:07:29.7 24 4 3c286 95573 [0,9,10,11,12,13,14,15,16] [1.15, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48] [CALIBRATE_ATMOSPHERE#OFF_SOURCE,CALIBRATE_ATMOSPHERE#ON_SOURCE,CALIBRATE_WVR#OFF_SOURCE,CALIBRATE_WVR#ON_SOURCE]
22:07:31.6 - 22:14:36.6 25 4 3c286 1261266 [0,17,18,19,20,21,22,23,24] [1.15, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01] [OBSERVE_TARGET#ON_SOURCE]
22:14:56.3 - 22:15:26.5 26 3 J1310+3220 90086 [0,17,18,19,20,21,22,23,24] [1.15, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01] [CALIBRATE_PHASE#ON_SOURCE,CALIBRATE_WVR#ON_SOURCE]
22:16:12.3 - 22:17:08.8 27 0 J1337-1257 150102 [0,1,2,3,4,5,6,7,8] [1.15, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01] [CALIBRATE_POINTING#ON_SOURCE,CALIBRATE_WVR#ON_SOURCE]
22:17:46.8 - 22:18:03.0 28 0 J1337-1257 95573 [0,9,10,11,12,13,14,15,16] [1.15, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48, 0.48] [CALIBRATE_ATMOSPHERE#OFF_SOURCE,CALIBRATE_ATMOSPHERE#ON_SOURCE,CALIBRATE_WVR#OFF_SOURCE,CALIBRATE_WVR#ON_SOURCE]
22:18:15.6 - 22:22:29.0 29 0 J1337-1257 720750 [0,17,18,19,20,21,22,23,24] [1.15, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01, 2.02, 1.01] [CALIBRATE_POLARIZATION#ON_SOURCE,CALIBRATE_WVR#ON_SOURCE]
(nRows = Total number of rows per scan)
This output shows that five fields were observed. The last column of the scan list gives the scan intent. This information is used later to flag the pointing scans and the hot and ambient load calibration scans. These intents are also used for pipeline processing. Examining the intents we can see the purpose of each field:
Field 0 (J1337-1257) polarization calibrator Field 1 (J1256-0547) [3c279] bandpass calibrator Field 2 (Ceres) flux calibrator Field 3 (J1310+3220) complex gain (phase) calibrator Field 4 (3c286) science target
Spectral windows are marked with ID numbers from 0 to 24. You may notice in the Sources lists (not shown here) that there are additional SpwIDs that are not listed in the "Spectral Windows" section; these are related to WVR measurements for each antenna, and you will not need them for calibration.
Examining which spws are used with each scan intent, we determine the following:
spw 0 WVR (used in every scan) spw 1~8 pointing and WVR spw 9~16 Tsys (atmosphere) spw 17~24 bandpass, phase, polarization, and target
Fields: 5
ID Code Name RA Decl Epoch SrcId nRows
0 none J1337-1257 13:37:39.782784 -12.57.24.69312 J2000 0 3400886
1 none J1256-0547 12:56:11.166560 -05.47.21.52458 J2000 1 636058
2 none Ceres 13:29:06.769601 -01.11.10.65438 J2000 2 546034
3 none J1310+3220 13:10:28.663200 +32.20.43.80000 J2000 3 840937
4 none 3c286 13:31:08.288100 +30.30.32.96000 J2000 4 4701150
Spectral Windows: (25 unique spectral windows and 3 unique polarization setups)
SpwID Name #Chans Frame Ch0(MHz) ChanWid(kHz) TotBW(kHz) CtrFreq(MHz) BBC Num Corrs
0 WVR#NOMINAL 4 TOPO 184550.000 1500000.000 7500000.0 187550.0000 0 XX
1 ALMA_RB_06#BB_1#SW-01#FULL_RES 128 TOPO 215242.188 -15625.000 2000000.0 214250.0000 1 XX YY
2 ALMA_RB_06#BB_1#SW-01#CH_AVG 1 TOPO 214234.375 1796875.000 1796875.0 214234.3750 1 XX YY
3 ALMA_RB_06#BB_2#SW-01#FULL_RES 128 TOPO 217242.188 -15625.000 2000000.0 216250.0000 2 XX YY
4 ALMA_RB_06#BB_2#SW-01#CH_AVG 1 TOPO 216234.375 1796875.000 1796875.0 216234.3750 2 XX YY
5 ALMA_RB_06#BB_3#SW-01#FULL_RES 128 TOPO 229257.813 15625.000 2000000.0 230250.0000 3 XX YY
6 ALMA_RB_06#BB_3#SW-01#CH_AVG 1 TOPO 230234.375 1796875.000 1796875.0 230234.3750 3 XX YY
7 ALMA_RB_06#BB_4#SW-01#FULL_RES 128 TOPO 231257.813 15625.000 2000000.0 232250.0000 4 XX YY
8 ALMA_RB_06#BB_4#SW-01#CH_AVG 1 TOPO 232234.375 1796875.000 1796875.0 232234.3750 4 XX YY
9 ALMA_RB_06#BB_1#SW-01#FULL_RES 128 TOPO 224992.188 -15625.000 2000000.0 224000.0000 1 XX YY
10 ALMA_RB_06#BB_1#SW-01#CH_AVG 1 TOPO 223976.562 1781250.000 1781250.0 223976.5625 1 XX YY
11 ALMA_RB_06#BB_2#SW-01#FULL_RES 128 TOPO 226992.188 -15625.000 2000000.0 226000.0000 2 XX YY
12 ALMA_RB_06#BB_2#SW-01#CH_AVG 1 TOPO 225976.562 1781250.000 1781250.0 225976.5625 2 XX YY
13 ALMA_RB_06#BB_3#SW-01#FULL_RES 128 TOPO 239007.813 15625.000 2000000.0 240000.0000 3 XX YY
14 ALMA_RB_06#BB_3#SW-01#CH_AVG 1 TOPO 239976.563 1781250.000 1781250.0 239976.5625 3 XX YY
15 ALMA_RB_06#BB_4#SW-01#FULL_RES 128 TOPO 241007.813 15625.000 2000000.0 242000.0000 4 XX YY
16 ALMA_RB_06#BB_4#SW-01#CH_AVG 1 TOPO 241976.563 1781250.000 1781250.0 241976.5625 4 XX YY
17 ALMA_RB_06#BB_1#SW-01#FULL_RES 64 TOPO 224984.375 -31250.000 2000000.0 224000.0000 1 XX XY YX YY
18 ALMA_RB_06#BB_1#SW-01#CH_AVG 1 TOPO 223968.750 1781250.000 1781250.0 223968.7500 1 XX XY YX YY
19 ALMA_RB_06#BB_2#SW-01#FULL_RES 64 TOPO 226984.375 -31250.000 2000000.0 226000.0000 2 XX XY YX YY
20 ALMA_RB_06#BB_2#SW-01#CH_AVG 1 TOPO 225968.750 1781250.000 1781250.0 225968.7500 2 XX XY YX YY
21 ALMA_RB_06#BB_3#SW-01#FULL_RES 64 TOPO 239015.625 31250.000 2000000.0 240000.0000 3 XX XY YX YY
22 ALMA_RB_06#BB_3#SW-01#CH_AVG 1 TOPO 239968.750 1781250.000 1781250.0 239968.7500 3 XX XY YX YY
23 ALMA_RB_06#BB_4#SW-01#FULL_RES 64 TOPO 241015.625 31250.000 2000000.0 242000.0000 4 XX XY YX YY
24 ALMA_RB_06#BB_4#SW-01#CH_AVG 1 TOPO 241968.750 1781250.000 1781250.0 241968.7500 4 XX XY YX YY
[...]
Antennas: 31:
ID Name Station Diam. Long. Lat. Offset from array center (m) ITRF Geocentric coordinates (m)
East North Elevation x y z
0 DA41 A079 12.0 m -067.45.13.6 -22.53.35.0 116.8369 -920.2897 22.6287 2225122.700426 -5439951.133460 -2481886.481390
1 DA42 A081 12.0 m -067.45.23.9 -22.53.32.5 -174.5620 -842.8378 21.0900 2224863.872997 -5440088.015712 -2481814.531125
2 DA43 A091 12.0 m -067.45.28.7 -22.53.24.2 -312.9125 -584.7726 23.7306 2224774.741865 -5440235.548469 -2481577.816103
3 DA44 A068 12.0 m -067.45.20.6 -22.53.25.7 -82.4244 -631.7829 23.5830 2224981.097391 -5440131.252519 -2481621.067210
4 DA45 A070 12.0 m -067.45.11.9 -22.53.29.3 166.1822 -743.4936 19.8824 2225193.449573 -5439993.765650 -2481722.541223
5 DA46 A058 12.0 m -067.45.17.3 -22.53.32.0 12.7400 -827.0339 21.9689 2225039.860423 -5440023.554679 -2481800.313874
6 DA47 A074 12.0 m -067.45.12.1 -22.53.32.0 161.8144 -828.6212 19.2711 2225176.657096 -5439964.248716 -2481800.726738
7 DA48 A046 12.0 m -067.45.17.0 -22.53.29.3 21.4254 -742.7993 21.6766 2225060.201673 -5440050.345525 -2481722.599573
8 DA49 A029 12.0 m -067.45.18.2 -22.53.25.8 -12.9141 -636.4555 22.1366 2225044.239474 -5440102.024044 -2481624.809292
9 DA51 A082 12.0 m -067.45.08.3 -22.53.29.2 269.0424 -740.9548 16.2831 2225287.766879 -5439952.669219 -2481718.802316
10 DA54 A063 12.0 m -067.45.16.1 -22.53.31.9 46.5810 -823.6376 21.9794 2225071.684905 -5440011.975810 -2481797.189115
11 DA55 A080 12.0 m -067.45.14.7 -22.53.20.2 87.4828 -461.2364 21.1332 2225162.612020 -5440126.242512 -2481462.996898
12 DA56 A064 12.0 m -067.45.14.7 -22.53.31.4 85.6567 -808.0287 21.5198 2225109.988756 -5440002.411268 -2481782.630797
13 DA57 A076 12.0 m -067.45.20.5 -22.53.33.8 -77.9911 -882.7200 24.5713 2224948.593535 -5440040.069448 -2481852.626444
14 DA59 A021 12.0 m -067.45.17.2 -22.53.27.0 14.3185 -672.8117 21.8450 2225063.988913 -5440078.377183 -2481658.189073
15 DA62 A016 12.0 m -067.45.16.4 -22.53.25.1 37.4652 -614.5612 21.7854 2225093.968954 -5440090.535537 -2481604.502426
16 DV01 A072 12.0 m -067.45.12.6 -22.53.24.0 147.1726 -580.5878 18.1840 2225199.253543 -5440058.163697 -2481571.803410
17 DV02 A087 12.0 m -067.45.08.3 -22.53.33.2 269.0953 -864.0700 16.2406 2225269.668853 -5439908.286857 -2481832.204625
[...]
Channel averaged spws are not useful for offline (after observation) data reduction and can be ignored. Therefore, we use the following moving forward:
spw 9,11,13,15: Tsys spw 17,19,21,23: science and calibrations
The science spws are full polarization (XX, XY, YX, YY). They have 64 channels of width 31.250 MHz each, for a bandwidth of 2 GHz per spw. Their center frequencies are:
lower sideband (LSB) spw 17: 224 GHz spw 19: 226 GHz upper sideband (USB) spw 21: 240 GHz spw 23: 242 GHz
Field 3 (phase cal) has no Tsys scans (atmosphere intent, spws 9~16). To increase observation efficiency, Tsys measurements are usually done either on the phase calibrator OR the science target. In the application of Tsys tables, we will apply the closest measurements available to sources missing direct Tsys measurements (see more below).
Choose a Reference Antenna
Thirty-eight antennas were used for the dataset listed above. Note that numbering in python always begins with "0", so the antennas have IDs 0-37. To see what the antenna configuration looked like at the time of this observation, we use the task plotants.
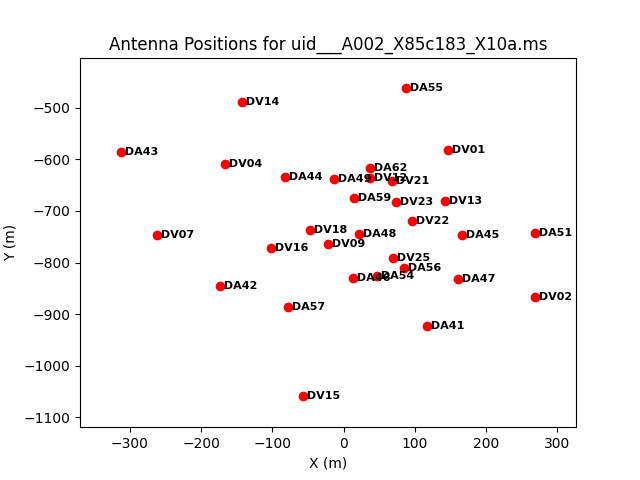
# In CASA
plotants(vis=basename[0]+'.ms', figfile=basename[0]+'_plotants.png')
This will plot the antenna configuration on your screen (see Figure 1) as well as save it under the specified filename for future reference. We need to choose a reference antenna that is close to the center of the array (and is also stable and present for the entire observation). We will use antenna DV23 as reference antenna, and we define a variable to be used in the following tasks:
# In CASA
refant='DV23'
The other two datasets ("uid___A002_X85c183_X51a", "uid___A002_X85c183_X822") have been observed after "uid___A002_X85c183_X10a". From their listobs output we can see that, in both datasets, Ceres was not observed, and the field J1310+3220 does not have Tsys measurements.
A Priori Flagging
The first editing we will do is some a priori flagging with flagdata. ALMA data contain both the cross correlation and autocorrelation data, but here we are only interested in the cross-correlation data.
Now we will loop over the datasets, running these flagging commands:
# In CASA
for name in basename:
flagdata(vis=name+'.ms', mode='manual', autocorr=True, flagbackup=False)
Some scans in the data were used by the online system for pointing and sideband ratio calibration. These scans are no longer needed, and we can flag them easily with flagdata by selecting on 'intent'. Similarly, we can flag the scans corresponding to atmospheric calibration since we no longer need them:
# In CASA
for name in basename:
flagdata(vis=name+'.ms', mode='manual',
intent='*POINTING*,*SIDEBAND_RATIO*,*ATMOSPHERE*', flagbackup=False)
We also flag "shadowed" data where one antenna blocks the line of sight of another.
# In CASA
for name in basename:
flagdata(vis=name+'.ms', mode='shadow', flagbackup=False)
We will then store the current flagging state for each dataset using the flagmanager:
# In CASA
for name in basename:
flagmanager(vis=name+'.ms', mode='save', versionname='Apriori')
See AntennaeBand7_Calibration for details on flagmanager.
Generate Tsys and WVR calibration tables
It turns out that two execution blocks (uid://A002/X85c183/X10a and X51a) out of the three taken on 2014-07-01 were affected by an ASDM SYSCal table issue. As a result, the Tsys values were incorrect and an entire scan is unintentionally flagged after applying the Tsys table. We need to run fixsyscaltimes task on these datasets before making the Tsys table.
# In CASA
from casarecipes.almahelpers import fixsyscaltimes
fixsyscaltimes("uid___A002_X85c183_X10a.ms")
fixsyscaltimes("uid___A002_X85c183_X51a.ms")
fixsyscaltimes("uid___A002_X85c183_X822.ms")
We will loop over the datasets, generating the System Temperature (Tsys) and Water Vapour Radiometer (WVR) calibration tables for each of them.
The Tsys calibration gives a first-order correction for the atmospheric opacity as a function of time and frequency, and associates weights with each visibility that persist through imaging. Each ms file contains Tsys measurements; the task gencal is used to generate calibration tables from these measurements.
# In CASA
for name in basename:
gencal(vis = name+'.ms',
caltable = name+'.ms.tsys',
caltype = 'tsys')
There are different ways to inspect Tsys calibration tables. Here, we use plotms to interactively plot Tsys vs frequency for all antennas.
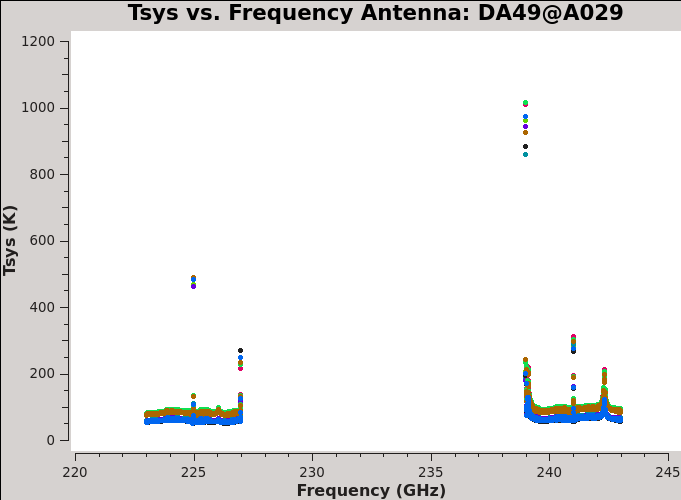
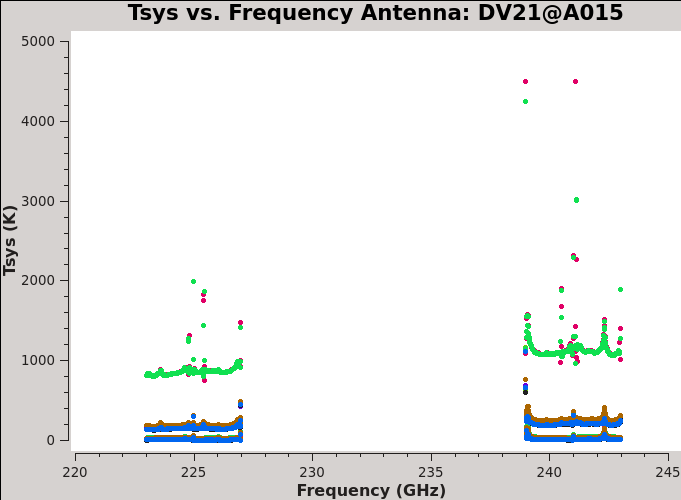
# In CASA
plotms(vis=basename[0]+'.ms.tsys', xaxis='freq', yaxis='tsys', spw='', iteraxis='antenna', coloraxis='scan')
By using the next button it is possible to see the plots for each antenna. You will notice that all antennas have more or less the same behavior as antenna DA49 shown in Figure 2. Antenna DV21 clearly shows higher value of Tsys (see Figure 3); we will flag that antenna later in the combined dataset.
The plots look acceptable, aside from the large amplitudes in the edge channels. To see this more clearly, change the X axis to 'channel', and color by 'spw'.
# In CASA
plotms(vis=basename[0]+'.ms.tsys', xaxis='channel', yaxis='tsys', spw='', iteraxis='antenna', coloraxis='spw')
We flag the first four channels of each spw from the calibration tables.
# In CASA
for name in basename:
flagdata(vis = name+'.ms.tsys',
spw = '9:0~3, 11:0~3, 13:0~3, 15:0~3')
To create the WVR calibration tables we run the task wvrgcal. This task examines the data for each ms as a whole and creates a calibration table containing only phase corrections for each antenna and spw.
# In CASA
for name in basename:
# remember current casa log file name
mylogfile = casalog.logfile()
# sent output to a new log file
casalog.setlogfile(name+'.ms.wvrgcal')
wvrgcal(vis = name+'.ms',
caltable = name+'.ms.wvr',
tie = ['3c286,J1310+3220'], # target, phase cal
statsource = 'J1256-0547', # BP cal
wvrflag = ['DA54'])
# switch back to the original log file
casalog.setlogfile(mylogfile)
- tie: Prioritise tieing the phase of the target and phase cal as well as possible.
- statsource: Compute the statistics (Phase RMS, Disc) on the BP cal only.
- wvrflag: Regard the WVR data for DA54 as bad and replace its data with interpolated values from neighbouring antennas.
Apply Tsys and WVR calibration tables
We will now apply the Tsys and the WVR calibration tables to the data with the task applycal, which reads the specified gain calibration tables, applies them to the (raw) data column, and writes the calibrated results into the corrected column.
- field and gainfield
- It is important to only apply Tsys and WVR corrections obtained close in time to the data being corrected. In addition to looping over data sets, we can define the list of unique source names and loop over these. We set field and gainfield to ensure that the appropriate Tsys and WVR calibrations are applied to each field. field is apply-to. gainfield is apply-from, and the indices match the list in gaintable. For J1337-1257, J1256-0547, and 3c286, this means using calibrations obtained specifically on each of these fields; for J1310+3220, the Tsys from 3c286 is used.
- spwmap
- We need to tell applycal which Tsys spws should be used to correct the science spws. We will only correct the science spws 17,19,21,23, because we will drop the other data in a moment.
Applycal can interpolate and apply calibrations derived from one spectral window to another, even if they do not share the same spectral shape (number of channels and channel width). Our Tsys spws have 128 channels while our science spws have 64, and they are both TDM (full 2 GHz bandwidth). However, this works even for science spws in FDM mode with 3000+ channels each.
- The almahelpers function tsysspwmap can suggest an spwmap. In this case the function produces two errors, which we correct manually.
# In CASA
from casarecipes.almahelpers import tsysspwmap
tsysmap = tsysspwmap(vis='uid___A002_X85c183_X10a.ms', tsystable='uid___A002_X85c183_X10a.ms.tsys')
tsysmap = tsysmap[:25] # truncate the list to ignore the extra WVR spws not shown in the listobs spw list
tsysmap[21] = 13 # fix an error
tsysmap[23] = 15 # fix an error
- The result is shown below with a list of indices underneath to visually see the mapping.
tsysmap = [0,1,2,3,4,5,6,7,8,9, 9,11,11,13,13,15,15, 9, 9,11,11,13,13,15,15] indexlist [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]
- As far as we are concered, everything except for the four values in red are simply placeholders. We just need to ensure:
9 -> 17 11 -> 19 13 -> 21 15 -> 23
Here we cycle over all datasets and fields (except Ceres):
# In CASA
field_names = ['J1337-1257','J1256-0547','3c286']
# loop each MS
for name in basename:
# General calibrators that have their own Tsys
for field_name in field_names:
applycal(vis = name+'.ms',
field = field_name,
spw = '17,19,21,23',
gaintable = [name+'.ms.tsys',name+'.ms.wvr'],
gainfield = [field_name,field_name],
interp = 'linear',
spwmap = [tsysmap,[]],
calwt = True,
flagbackup = False)
# J1310+3220 uses 3c286's Tsys
applycal(vis = name+'.ms',
field = 'J1310+3220',
spw = '17,19,21,23',
gaintable = [name+'.ms.tsys',name+'.ms.wvr'],
gainfield = ['3c286','J1310+3220'],
interp = 'linear',
spwmap = [tsysmap,[]],
calwt = True,
flagbackup = False)
As anticipated in the listobs description, Ceres has been observed only in the first dataset. We correct it separately here:
# In CASA
applycal(vis = basename[0]+'.ms',
field = 'Ceres',
spw = '17,19,21,23',
gaintable = [basename[0]+'.ms.tsys',basename[0]+'.ms.wvr'],
gainfield = ['Ceres','Ceres'],
interp = 'linear',
spwmap = [tsysmap,[]],
calwt = True,
flagbackup = False)
You can use plotms to plot channel-averaged amplitudes as a function of time, comparing the DATA and CORRECTED columns after applying the Tsys correction. This way you can check that calibration has correctly put the data onto the Kelvin temperature scale.
Concatenate and Split
Now we can concatenate the three individual data sets of each day into one big measurement set. We define an array "comvis" that contains the names of the measurement sets we wish to concatenate, and then we run the task concat.
# In CASA
comvis=[]
for name in basename:
comvis.append(name+'.ms')
os.system('rm -rf 3c286_Band6_concat.ms*')
concat(vis=comvis, concatvis='3c286_Band6_concat.ms')
This reports the following error message for each MS.
SEVERE getcell::WEIGHT_SPECTRUM Exception Reported: Table DataManager error: Invalid operation: TSM: no array in row 0 of column WEIGHT_SPECTRUM in <path>/3C286_Band6_UncalibratedData/uid___A002_X85c183_X10a.ms/table.f19 WARN concat::::casa Column WEIGHT_SPECTRUM in table uid___A002_X85c183_X10a.ms has no data. Accessing it will cause errors.
We are ok to proceed. See Combining-Datasets for more information.
Now split out the CORRECTED data column, retaining spectral windows 17,19,21,23. This will get rid of the extraneous spectral windows.
# In CASA
os.system('rm -rf 3c286_Band6.ms')
split(vis='3c286_Band6_concat.ms', outputvis='3c286_Band6.ms',
datacolumn='corrected', spw='17,19,21,23')
The WVR and Tsys tables are now applied in the DATA column of the new measurement set.
Additional Data Inspection
We run a listobs on the resulting concatenated data sets to check that they contain the fields, spectral windows and observing times that we expected:
# In CASA
listobs(vis='3c286_Band6.ms', listfile='3c286_Band6.ms.listobs')
Below is an excerpt from the dataset listobs:
Data records: 7499520 Total elapsed time = 11154.7 seconds Observed from 01-Jul-2014/21:21:27.3 to 02-Jul-2014/00:27:21.9 (UTC) ObservationID = 0 ArrayID = 0 Date Timerange (UTC) Scan FldId FieldName nRows SpwIds Average Interval(s) ScanIntent 01-Jul-2014/21:21:27.3 - 21:25:39.9 4 0 J1337-1257 238080 [0,1,2,3] [2.02, 2.02, 2.02, 2.02] [CALIBRATE_POLARIZATION#ON_SOURCE,CALIBRATE_WVR#ON_SOURCE] [...] ObservationID = 1 ArrayID = 0 Date Timerange (UTC) Scan FldId FieldName nRows SpwIds Average Interval(s) ScanIntent 01-Jul-2014/22:28:02.4 - 22:31:11.6 33 1 J1256-0547 178560 [0,1,2,3] [2.02, 2.02, 2.02, 2.02] [CALIBRATE_BANDPASS#ON_SOURCE,CALIBRATE_WVR#ON_SOURCE] [...] ObservationID = 2 ArrayID = 0 Date Timerange (UTC) Scan FldId FieldName nRows SpwIds Average Interval(s) ScanIntent 01-Jul-2014/23:30:54.6 - 23:34:03.7 65 1 J1256-0547 178560 [0,1,2,3] [2.02, 2.02, 2.02, 2.02] [CALIBRATE_BANDPASS#ON_SOURCE,CALIBRATE_WVR#ON_SOURCE] [...] Fields: 5 ID Code Name RA Decl Epoch SrcId nRows 0 none J1337-1257 13:37:39.782784 -12.57.24.69312 J2000 0 1666560 1 none J1256-0547 12:56:11.166560 -05.47.21.52458 J2000 1 535680 2 none Ceres 13:29:06.769601 -01.11.10.65438 J2000 2 148800 3 none J1310+3220 13:10:28.663200 +32.20.43.80000 J2000 3 773760 4 none 3c286 13:31:08.288100 +30.30.32.96000 J2000 4 4374720 Spectral Windows: (4 unique spectral windows and 1 unique polarization setups) SpwID Name #Chans Frame Ch0(MHz) ChanWid(kHz) TotBW(kHz) CtrFreq(MHz) BBC Num Corrs 0 ALMA_RB_06#BB_1#SW-01#FULL_RES 64 TOPO 224984.375 -31250.000 2000000.0 224000.0000 1 XX XY YX YY 1 ALMA_RB_06#BB_2#SW-01#FULL_RES 64 TOPO 226984.375 -31250.000 2000000.0 226000.0000 2 XX XY YX YY 2 ALMA_RB_06#BB_3#SW-01#FULL_RES 64 TOPO 239015.625 31250.000 2000000.0 240000.0000 3 XX XY YX YY 3 ALMA_RB_06#BB_4#SW-01#FULL_RES 64 TOPO 241015.625 31250.000 2000000.0 242000.0000 4 XX XY YX YY [...]
The scans' original ID numbers have been offset to make scan numbers unique. The three executions are given an ObservationID number; in the next steps, when combining all the scans, we will need to also specify combine='obs' (see below).
Only the four scientific spws with full polarization are included.
Now that the data are concatenated into one dataset, we will do some additional inspection with plotms. First we will plot amplitude versus channel for the bandpass calibrator, averaging over time and baselines and choosing XX correlation only in order to speed up the plotting process.
# In CASA
plotms(vis='3c286_Band6.ms', xaxis='channel', yaxis='amp', field='1',
correlation='XX', avgbaseline=True, avgtime='1e8', avgscan=True, coloraxis='spw')
From these plots we see that the edge channels have high or low amplitudes in the different spws. We will use flagdata to remove four edge channels from both sides of each spw:
# In CASA
flagdata(vis='3c286_Band6.ms', spw='*:0~3,*:60~63')
Next, we flag the antenna with high Tsys, as identified during the Tsys calibration inspection:
# In CASA
flagdata(vis='3c286_Band6.ms', antenna='DV21')
To identify antennas or time ranges that differ from the average values, we carefully inspect the data with plotms, plotting different axes and colorizing by different parameters. Don't forget to average the data if possible to speed the plotting process.
We will look first at amplitude versus time, averaging over all channels and colorizing by field (see Figure 4).
# In CASA
plotms(vis='3c286_Band6.ms', xaxis='time', yaxis='amp', spw='0', correlation='XX,YY', avgchannel='64', coloraxis='field')
Since all three executions are now plotted together, notice we have three scans of the bandpass calibrator. We have only one scan of Ceres, in the first execution as noted before. The last polarization calibrator scan has a noticable dip in amplitude somewhere in time within the scan. Use the magnifying glass to zoom in on this scan and then draw a box to located the problematic time range, as show in Figure 5.
Now plot the amplitude of the flux calibrator, Ceres, as a function of uv-distance.
# In CASA
plotms(vis='3c286_Band6.ms', xaxis='uvdist', yaxis='amp', field='Ceres', correlation='XX,YY', avgchannel='64', avgtime='1e8', coloraxis='antenna1')
Continue to inspect the data with plotms, plotting different axes and colorizing by the different parameters. Don't forget to average the data if possible to speed the plotting process. You will find the following flags are needed:
# In CASA
flagdata(vis='3c286_Band6.ms', antenna='DA49')
flagdata(vis='3c286_Band6.ms', antenna='DA45', field='0,3', spw='1')
flagdata(vis='3c286_Band6.ms', antenna='DA45', scan='48', field='0', spw='2')
flagdata(vis='3c286_Band6.ms', antenna='DV14')
flagdata(vis='3c286_Band6.ms', antenna='DV04', scan='93',field='0')
flagdata(vis='3c286_Band6.ms', timerange='2014/07/02/00:25:00~2014/07/02/00:25:10')
Now that we have completed the above inspection and flagging, we can start the data calibration.
Standard Calibrations
We can now begin calibrating the data. The general data reduction strategy is to derive a series of scaling factors or corrections from the calibrators, which are then collectively applied to the science data. For much more discussion on the philosophy, strategy, and implementation of calibration of synthesis data within CASA, see the Synthesis Calibration notebook in the CASA Docs. The CASA software solves the Hamaker-Bregman-Sault Measurement Equation (ME).
For full polarization calibration there are additional calibration steps, as described in previous casaguides.
We start with the determination of the bandpass and gains. The method is similar to what shown in other casaguides (e.g. the AntennaeBand7_Calibration CASA guide).
We do not actually measure absolute phase values; instead, we fix the phase of a reference antenna to zero for both polarizations, which yields relative phases for all antennas. Difference among antennas in each polarization are preserved, so there is no effect on parallel-hand calibration.
After that we will proceed with the polarization calibration which will correct for the cross-hand influenced terms: [math]\displaystyle{ D^{r} }[/math], [math]\displaystyle{ X^{r} }[/math] and [math]\displaystyle{ P }[/math] (see below for details).
Bandpass
We are now ready to calibrate the bandpass.
We first run gaincal on the bandpass calibrator to determine phase-only gain solutions. We will use solint='int' for the solution interval, which means that one gain solution will be determined for every integration time. This short integration time is possible because the bandpass calibrator is a very bright point source, so we have very high signal-to-noise (SNR) and a perfect model. This will correct for any phase variations in the bandpass calibrator as a function of time, a step which will prevent decorrelation of the vector-averaged bandpass solutions. We will then apply these solutions on-the-fly when we run bandpass.
Note that we use the average of channels 20 to 45 to increase our signal-to-noise in the determination of the antenna-based phase solutions. Averaging over a subset of channels near the center of the bandpass is acceptable when the phase variation as a function of channel is small, which it is here.
We will use refantmode='strict' in all gaincal commands during calibration. This forces the reference antenna to stay constant, which will be important in the polarization calibration.
# In CASA
os.system('rm -rf 3c286_Band6.ms.G0ph')
gaincal(vis = '3c286_Band6.ms',
caltable = '3c286_Band6.ms.G0ph',
field = '1', #3c279
gaintype = 'G',
solint = 'int',
calmode = 'p',
spw = '*:20~45',
refantmode = 'strict',
refant = refant,
smodel = [1,0,0,0])
- caltable='*.G0ph' : the gain solutions will be stored in an external table.
- field=1 : we select the bandpass calibrator 3c279
- gaintype='G': we solve for gains for each polarization
- solint='int': we determine one solution for each integration
- calmode='p': we solve for phase only
- smodel=[1,0,0,0]: we assume an unpolarized model. The values correspond to [I,Q,U,V].
Now that we have a first measurement of the phase variations as a function of time, we can determine the bandpass solutions with bandpass. We will apply the phase calibration table on-the-fly with the parameter "gaintable". Do not worry about the message "Insufficient unflagged antennas", which relates to the flagged edge channels.
# In CASA
os.system('rm -rf 3c286_Band6.ms.Bscan')
bandpass(vis = '3c286_Band6.ms',
caltable = '3c286_Band6.ms.Bscan',
field = '1', #3c279
solint = 'inf',
combine = 'scan,obs',
refant = refant,
solnorm = True,
gaintable = ['3c286_Band6.ms.G0ph'],
interp = ['nearest'])
- The default type of bandpass solution is bandtype='B' , which does a channel by channel solution for each specified spw
- caltable = '*.Bscan': Output bandpass calibration table
- gaintable = '.G0ph': gain calibration table to be applied on the fly
- solint='inf',combine='scan, obs': this setting, sets the solution interval to the entire observation. The G0ph table corrects the phase variations as a function of time so that the per-channel bandpass solution is coherent and high SNR. To the default combine='scan', we need to add also 'obs' since the dataset we are working on is a combination of different observations.
- solnorm=True: Normalize the bandpass amplitudes and phases of the corrections to unity
- interp=['nearest']: apply the nearest solution from the calibration table.
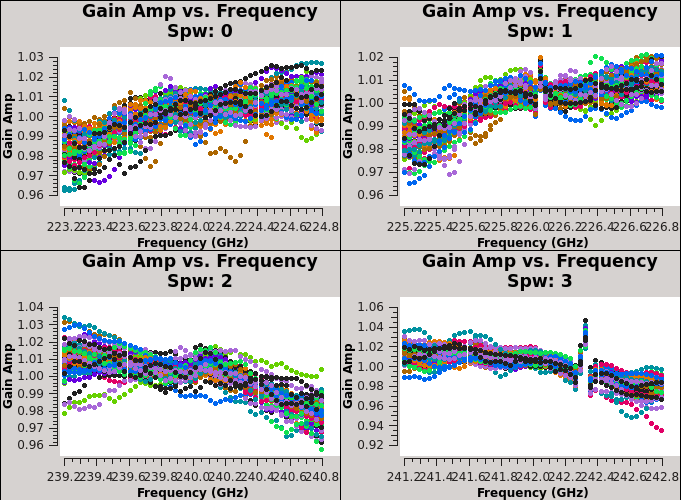
We now plot the bandpass solutions:
# In CASA
plotms(vis='3c286_Band6.ms.Bscan', xaxis='frequency', yaxis='amp',
coloraxis='antenna1', iteraxis='spw', gridrows=2, gridcols=2)
Figure 7 shows the bandpass solutions table colored by antenna, in each of the four spws. In spw 1 and 3 the presence of atmospheric lines is clearly visible, The solutions seem reasonable, so we will apply them on-the-fly during gain calibration moving forward.
Flux Scaling
We set the flux density for the flux calibrators using setjy. Ceres has been used as flux calibrator. The standard catalog Butler-JPL-Horizons 2012 model fits Ceres's resolved visibilities to an emission model appropriate for the distance to Ceres on the observation date. For CASA 5.3 and later, usescratch should be explicitly set to True for any ephemeris calibrator.
# In CASA
# make sure usescratch = True
setjy(vis = '3c286_Band6.ms',
field = '2', # Ceres
spw = '0,1,2,3',
standard = 'Butler-JPL-Horizons 2012',
usescratch = True)
{'2': {'0': {'fluxd': array([1.53510869, 0. , 0. , 0. ])},
'1': {'fluxd': array([1.56220722, 0. , 0. , 0. ])},
'2': {'fluxd': array([1.72976518, 0. , 0. , 0. ])},
'3': {'fluxd': array([1.75838304, 0. , 0. , 0. ])},
'fieldName': 'Ceres'},
'format': "{field Id: {spw Id: {fluxd:[I,Q,U,V] in Jy}, 'fieldName':field name}}"}
Gain Calibration
Now we determine a gain calibration for the bandpass, flux, and phase calibrators. We will calibrate the polarization calibrator separately. We solve first for phase only, applying the bandpass calibration on-the-fly.
# In CASA
# Gaincal for 3C279 and Ceres and J1310+3220
os.system('rm -rf 3c286_Band6.ms.G2ph')
gaincal(vis = '3c286_Band6.ms',
caltable = '3c286_Band6.ms.G2ph',
gaintype = 'G',
field = '1,2,3',
solint = 'int',
refant = refant,
refantmode = 'strict',
calmode = 'p',
gaintable = ['3c286_Band6.ms.Bscan'],
interp = ['nearest'])
- os.system('rm -rf *.G2ph'): removes the table if already existing.
- caltable = '*.G2ph': the output gain calibration table
- gaintype = 'G': is the default type of gain solution , which determine gains for each polarization and spectral window
- field='1,2,3': to specify the bandpass, flux, and phase calibrators.
- calmode = 'p': to solve for phase only.
- solint='int': this setting will solve for one solution per integration
- gaintable = ['*.Bscan']: we apply the bandpass calibration on-the-fly
- interp=['nearest']: as before we use the nearest solution in the table
We solve for the amplitude, applying on-the-fly the bandpass and the phase corrections just computed.
# In CASA
os.system('rm -rf 3c286_Band6.ms.G2amp')
gaincal(vis = '3c286_Band6.ms',
caltable = '3c286_Band6.ms.G2amp',
field = '1,2,3',
solint = 'int',
refant = refant,
refantmode = 'strict',
gaintype = 'T',
calmode = 'a', #solve amplitude using G2ph
gaintable = ['3c286_Band6.ms.Bscan','3c286_Band6.ms.G2ph'],
interp = ['nearest','nearest'])
- gaintype='T': this time we obtain one solution for both polarizations.
We now bootstrap the flux density of the secondary calibrators from that of Ceres using the task fluxscale. The new flux table *.flux, containing the correctly-scaled gains, will replace the previous *.G2amp table when we apply the calibration to the data later.
# In CASA
fluxscale(vis = '3c286_Band6.ms',
caltable = '3c286_Band6.ms.G2amp',
fluxtable = '3c286_Band6.ms.flux',
reference = '2', # Ceres
transfer = '1,3') # 'J1256-0547','J1310+3220'
- caltable='*.G2amp': this is the input table we want to scale
- fluxscale='*.flux': output table, containing scaled gains.
- reference='Ceres': here we specify the source with the known flux density (Ceres or Titan)
- transfer='1,3': these are the sources whose amplitude gains are to be rescaled: 'J1256-0547', and 'J1310+3220'
The logger produces the following output:
Found reference field(s): Ceres Found transfer field(s): J1256-0547 J1310+3220 Flux density for J1256-0547 in SpW=0 (freq=2.24e+11 Hz) is: 8.575 +/- 0.0222941 (SNR = 384.63, N = 28) Flux density for J1256-0547 in SpW=1 (freq=2.26e+11 Hz) is: 8.48694 +/- 0.0223375 (SNR = 379.941, N = 28) Flux density for J1256-0547 in SpW=2 (freq=2.4e+11 Hz) is: 8.1471 +/- 0.0241656 (SNR = 337.136, N = 28) Flux density for J1256-0547 in SpW=3 (freq=2.42e+11 Hz) is: 8.08165 +/- 0.0244227 (SNR = 330.907, N = 28) Flux density for J1310+3220 in SpW=0 (freq=2.24e+11 Hz) is: 0.925759 +/- 0.00753979 (SNR = 122.783, N = 27) Flux density for J1310+3220 in SpW=1 (freq=2.26e+11 Hz) is: 0.914686 +/- 0.00789673 (SNR = 115.831, N = 26) Flux density for J1310+3220 in SpW=2 (freq=2.4e+11 Hz) is: 0.876549 +/- 0.00810848 (SNR = 108.103, N = 27) Flux density for J1310+3220 in SpW=3 (freq=2.42e+11 Hz) is: 0.8743 +/- 0.00834474 (SNR = 104.773, N = 27) Fitted spectrum for J1256-0547 with fitorder=1: Flux density = 8.31993 +/- 0.00938247 (freq=232.86 GHz) spidx: a_1 (spectral index) =-0.73443 +/- 0.0325769 covariance matrix for the fit: covar(0,0)=1.97601e-06 covar(0,1)=1.77371e-05 covar(1,0)=1.77371e-05 covar(1,1)=0.00874273 Fitted spectrum for J1310+3220 with fitorder=1: Flux density = 0.897572 +/- 0.00151321 (freq=232.86 GHz) spidx: a_1 (spectral index) =-0.732428 +/- 0.0485781 covariance matrix for the fit: covar(0,0)=1.98269e-05 covar(0,1)=0.000155996 covar(1,0)=0.000155996 covar(1,1)=0.087278
fluxscale prints to the CASA logger the derived flux densities of all calibrator sources specified with the transfer argument. You should examine the output to ensure that the fluxes are reasonable. The ALMA Calibrator Source Catalogue can be used to check whether the derived flux densities are reasonable. Wildly different flux densities or flux densities with very high error bars should be treated with suspicion; in such cases you will have to figure out whether something has gone wrong.
Apply Calibrations for Inspection
We apply the solutions so far, for inspection purposes only. We will apply all the calibrations at the end:
# In CASA
applycal(vis = '3c286_Band6.ms',
field = '1,2,3',
calwt = True,
gaintable = ['3c286_Band6.ms.Bscan','3c286_Band6.ms.G2ph','3c286_Band6.ms.flux'],
interp = ['nearest','linear','linear'],
parang = False)
- calwt=True: the weight will be calibrated.
- interp=['nearest','linear','linear']: this list indicates the interpolation method to be used when applying the corresponding table. For bandpass table the nearest solution to the source is taken, while for the gain tables a linear interpolation in time is used.
To inspect the results we plot the corrected data for the bandpass and phase calibrators:
# In CASA
plotms(vis='3c286_Band6.ms', field='J1256-0547,J1310+3220', spw='0', xaxis='parang', yaxis='amp', correlation='XX,YY',
ydatacolumn='corrected', avgchannel='128', avgbaseline=True, coloraxis='corr', iteraxis='field')
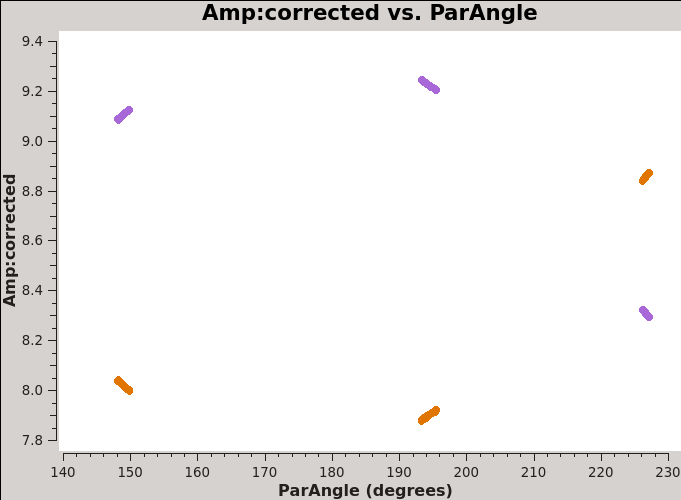
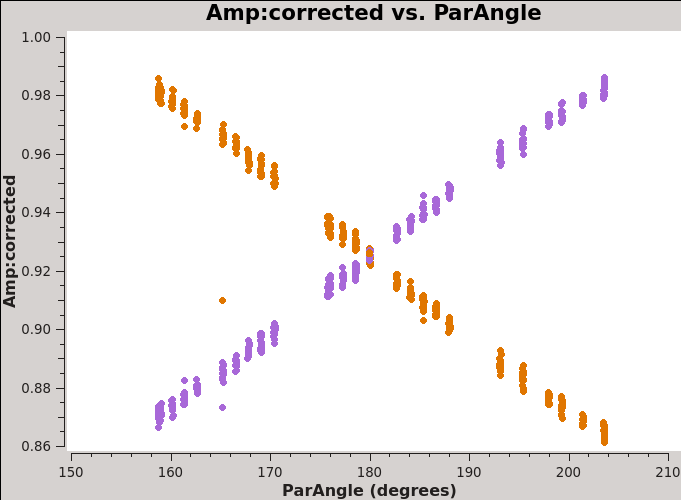
Figure 8 and Figure 9 show the XX and YY data for the bandpass and phase calibrators after the parallel-hand calibration.
The effect of source polarization is clearly evident.
Polarization Calibration
A list of useful references about mathematical and theoretical details of polarization calibration is given in the References section of this guide. Definitely check out the Polarization-Calibration notebook in the CASA Docs. Here we introduce some basic concepts needed to guide you through the calibration steps.
Correlations between circularly polarized feeds are sensitive to total intensity and the source circular polarization, while correlations between linearly polarized feeds are sensitive predominantly to total intensity plus a contribution from the linear polarization. Since the large majority of extragalactic radio sources are quite weakly circularly polarized, the separation of the calibration of the two parallel hand gains from each other and from the instrumental polarization is much easier in interferometers using circularly polarized feeds. For interferometers with linearly polarized feeds the situation is more complex: a contribution from Stokes Q, U, and parallactic angle ψ appears in the real part of all correlations. This complicates the analysis somewhat, but also provides better constraints for estimating and correcting the instrumental polarization.
The polarization response can be described assuming that each feed is perfectly coupled to the polarization state to which it is sensitive, with the addition of a complex factor times the orthogonal polarization; this is called the "leakage" or "D-term" model. The instrumental contribution to the cross-polarized interferometer response (i.e., the effect due to leakage) is independent of parallactic angle, whereas the contribution from the source rotates with parallactic angle for alt-az mount antennas. This makes it possible to uniquely separate the source and instrumental contributions to the polarized response.
In the limit of nearly perfect feeds (any higher order terms involving instrumental polarization can be ignored) and zero circular polarization, the linearized approximation for crossed linearly polarized feeds on one baseline is:
[math]\displaystyle{ \ V_{XX} = (I + Q_{\psi}) + U_{\psi}(d_{Xj}^{*} + d_{Xi}) }[/math]
[math]\displaystyle{ \ V_{XY} = U_{\psi} + I(d_{Yj}^{*} + d_{Xi}) + Q_{\psi} }[/math]
[math]\displaystyle{ \ (d_{Yj}^{*} - d_{Xi}) }[/math]
[math]\displaystyle{ \ V_{YX} = U_{\psi} + I(d_{Yi} + d_{Xj}^{*}) + Q_{\psi} }[/math]
[math]\displaystyle{ \ (d_{Yi} - d_{Xj}^{*}) }[/math]
[math]\displaystyle{ \ V_{YY} = (I - Q_{\psi}) + U_{\psi}(d_{Yi} + d_{Yj}^{*}) }[/math]
Equation 1 Visibilities for one baseline. Linearized approximation for linear feed.
where the functions: [math]\displaystyle{ Q_{\psi}= Q cos2\psi + U sin2\psi }[/math] and [math]\displaystyle{ U_{\psi} = -Q sin2\psi + U cos2\psi }[/math] show the dependence of the source polarization on the parallactic angle (see Figure 8).
In Equation 1 we can recognize a constant complex offset proportional to I in cross-hands visibilities, and a time-dependent contribution of linear polarization from the source, scaled by the D-terms, in all correlations. In order to separate the source and instrumental contributions to the correlations, observations with an array using linear feeds need to include frequent measurements of an unresolved calibrator over a wide range of parallactic angle.
The following steps will allow us to determine all these factors to properly correct the data.
Gains for the polarization calibrator
We start examining the polarization calibrator. Since we are concerned only about its fractional polarization, we do not worry about its absolute total flux density, and just use I=1.0. The first gains we determine will absorb all the polarization contributions, and we will revise them once the source polarization is correctly estimated.
# In CASA
os.system('rm -rf 3c286_Band6.ms.G1')
gaincal(vis = '3c286_Band6.ms',
caltable = '3c286_Band6.ms.G1',
field = '0',
solint = 'int',
refant = refant,
refantmode = 'strict',
smodel = [1,0,0,0],
gaintable = '3c286_Band6.ms.Bscan',
interp = 'nearest')
We explicitly show some of the default parameters of gaincal, but they could also be left out -- when a parameter is not specified, its default value is used.
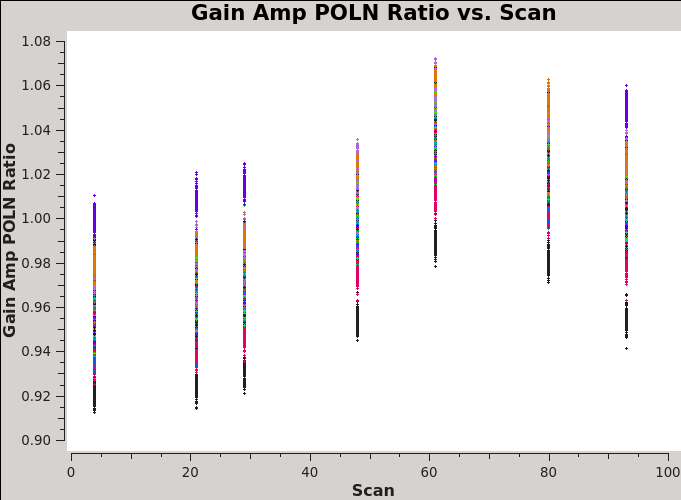
- caltable = '*.G1': the output table. This table will be revised later on, when the source polarization will be estimated.
- calmode = 'ap': this is the default value. We are solving for both amplitude and phase.
- gaintype='G': this is the default value. We are determining gains for each polarization.
- solint = 'int': one solution per integration.
- smodel=[1,0,0,0]: we are using an unpolarized model with a Stokes I flux equal to 1.
The presence of source polarization in the gains can be seen by plotting the amp vs scan for this table using correlation='/', which forms the complex polarization ratio, shown in Figure 10. The antenna-based complex polarization ratio reveals the sinusoidal variation, which clearly shows the presence of polarization in the source.
# In CASA
plotms(vis='3c286_Band6.ms.G1', xaxis='scan', yaxis='GainAmp', coloraxis='antenna1', correlation='/')
To inspect the results we generate a partially calibrated dataset, applying this gain table, as well as the bandpass, to the polarization calibrator:
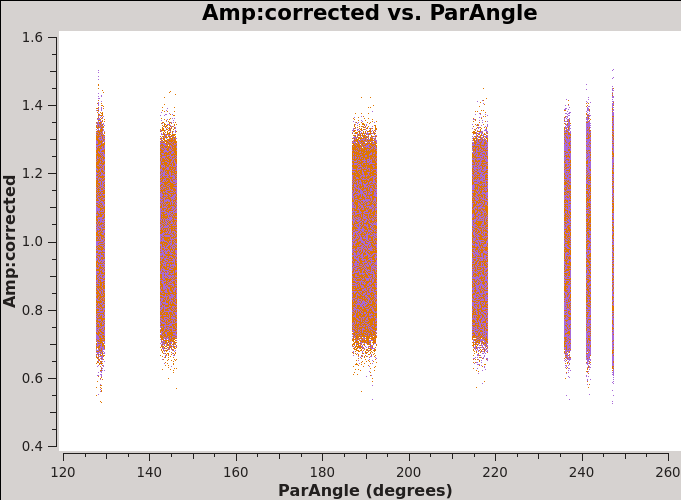
# In CASA
applycal(vis = '3c286_Band6.ms',
field = '0',
calwt = True,
gaintable = ['3c286_Band6.ms.Bscan','3c286_Band6.ms.G1'],
interp = ['nearest','linear'],
parang=False)
# In CASA
plotms(vis='3c286_Band6.ms', field='0', avgchannel='64', xaxis='parangle', yaxis='amp', ydatacolumn='corrected', correlation='XX,YY', coloraxis='corr')
Figure 11 shows the polarization calibrator's amplitude versus parallactic angle after the application of the bandpass and the gain table G1 which we just computed.
The source's linear polarization, which rotates with parallactic angle as a function of time, has been absorbed by the gains, since we assumed an unpolarized model for the source.
In order to extract the source polarization information hidden in the gains, we use polfromgain.
# In CASA
qu=polfromgain(vis='3c286_Band6.ms', tablein='3c286_Band6.ms.G1', caltable='3c286_Band6.ms.G1a')
print(qu)
This script estimates the Q and U amplitudes from the gains, for each spectral window. The results are stored in the python dictionary qu, which will be used later on. For each spectral window, the dictionary contains a list of the results in the order [I,Q,U,V]. The source polarization reported for all spws should be reasonably consistent. This estimate is not as good as can be obtained from the cross-hands, since it relies on the gain amplitude polarization ratio being stable, which may not be precisely true. However, it will be useful later on in removing an ambiguity that occurs in the cross-hand estimates.
The output will be something like this:
{'J1337-1257': {
'Spw0': [1.0, 0.013227418681529856, 0.039849239576474446, 0.0],
'Spw1': [1.0, 0.013848163127521337, 0.03947996837545822, 0.0],
'Spw2': [1.0, 0.014538403569321604, 0.0407299275496684, 0.0],
'Spw3': [1.0, 0.014844803328247997, 0.041510845357872396, 0.0],
'SpwAve': [1.0, 0.014114697176655198, 0.04039249521486836, 0.0]}}
From this output we see that the Q and U values reported for all spws are consistent at ~0.1% level.
Cross-hand delay
When the data have more than one channel per spectral window, it is important to be sure there is no large cross-hand (XY, YX) delay still present in the data. The gain and bandpass calibration will only correct for parallel-hand (XX, YY) delay residuals, since the two polarizations are referenced independently. Plots of cross-hand phases as a function of frequency for a strongly polarized source (i.e., a source whose polarization dominates the instrumental polarization) will show the cross-hand delay as a phase slope with frequency (see Figure 12). This slope will be the same magnitude on all baselines, but with different sign in the two cross-hand correlations (XY, YX).
Note that in this dataset you can produce even higher-SNR plots of the cross-hand delay by using 3C279. However, in this guide we proceed by using the polarization calibrator for all of the polarization calibration steps (cross-hand delay, XY-phase, and leakages).
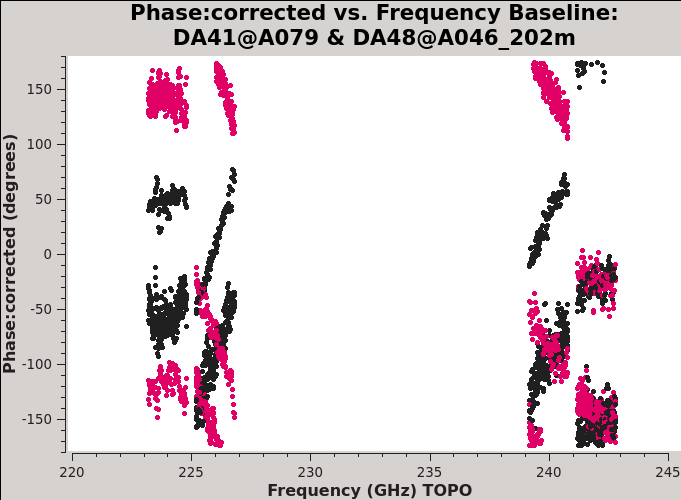
We can plot the corrected column of the dataset (we applied so far the bandpass and the G1 tables) to show this effect on one baseline:
# In CASA
plotms(vis = '3c286_Band6.ms',
ydatacolumn = 'corrected',
xaxis = 'freq',
yaxis = 'phase',
field = '0',
avgtime = '1e9',
correlation = 'XY,YX',
spw = '',
antenna = 'DA48',
iteraxis = 'baseline',
coloraxis = 'corr',
plotrange = [0,0,-180,180])
This cross-hand delay can be estimated using the gaintype=’KCROSS’ mode of gaincal.
For the cross-hand delay calculation we need to choose a scan where the source's cross-hand contribution is maximum (in absolute value), since this will minimize the mean effect of instrumental polarization. This scan would be the one where the gain ratio is near the mean value in Figure 10: scan 48.
# In CASA
os.system('rm -rf 3c286_Band6.ms.Kcrs')
gaincal(vis = '3c286_Band6.ms',
caltable = '3c286_Band6.ms.Kcrs',
scan = '48',
gaintype = 'KCROSS',
solint = 'inf',
refant = refant,
refantmode = 'strict',
smodel = [1,0,1,0],
gaintable = ['3c286_Band6.ms.Bscan','3c286_Band6.ms.G1'],
interp = ['nearest','linear'])
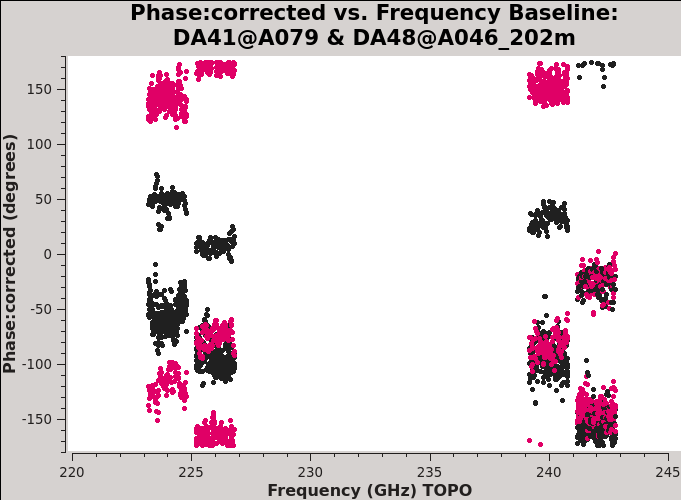
- caltable='*.Kcrs': the output table.
- scan='48': we select the scan with strong polarization, and we calculate the gain solution using only this scan.
- gaintype='KCROSS': solves for a global cross-hand delay.
- smodel=[1,0,1,0]: here we are using a polarized model (a non-zero value for U is assumed). This is just to enforce the assumption of non-zero source polarization signature in the cross-hands in the ratio between data and model. It is not important to specify the polarization Stokes parameters correctly, since here we are only solving for a phase-like quantity.
- gaintable=['*.Bscan','*.G1']: we apply on-the-fly the bandpass and the first gain tables
We apply this new cross-hand delay calibration to the dataset, along with the bandpass and gain tables:
# In CASA
applycal(vis = '3c286_Band6.ms',
field = '0',
calwt = True,
gaintable = ['3c286_Band6.ms.Bscan','3c286_Band6.ms.G1','3c286_Band6.ms.Kcrs'],
interp = ['nearest','linear','nearest'])
Running plotms again we can verify the effect of this calibration (Figure 13). These plots are a nice example of the effect of Kcrs correction on the cross-hand phases: by applying the Kcrs table to the data, the phase slopes vs frequency are corrected. The remaining frequency structure in the cross-hand phase is due to the remaining cross-hand bandpass phase, as well as the instrumental polarization.
XY-phase and QU
We have so far computed the bandpass and gain tables adequate for the parallel hands, and the Kcross table which corrects the cross-hands for a systematic linear phase slope across each spw. In computing bandpass and gains we don't measure absolute phase values; instead, we set the phase of the reference antenna to zero in both polarizations, yielding relative phases for all other antennas. As a result, a single residual phase bandpass relating the phase of the two hands of polarization in the reference antenna remains in the cross-hands of all baselines. The Kcross solution has already accounted for any linear phase slope in this phase bandpass, but we need to solve for any non-linear phase bandpass shape in the XY-phase so that both cross- and parallel-hands can be combined to extract correct Stokes parameters.
To visualize the effect of this XY-phase offset on the data, we can plot the real and imaginary part of the data corrected for bandpass, gains, and cross-hands delay. Figure 14 shows the cross-hands visibilities of the polarization calibrator, averaged per scan and over all baselines, in one spw (averaged in channel). The XY-phase is clearly visible as the slope of cross-hand visibilities in the complex plane. The XY and YX correlations have the same slope with opposite signs because they are complex conjugates of each other. For SNR purposes, this plot is averaged in channel; each channel has its own slope, in fact. The Kcross solution ensures that the channel-average is reasonably coherent.
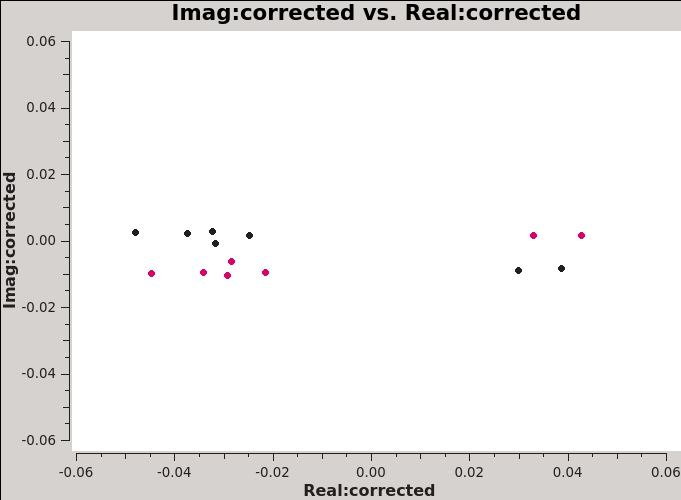
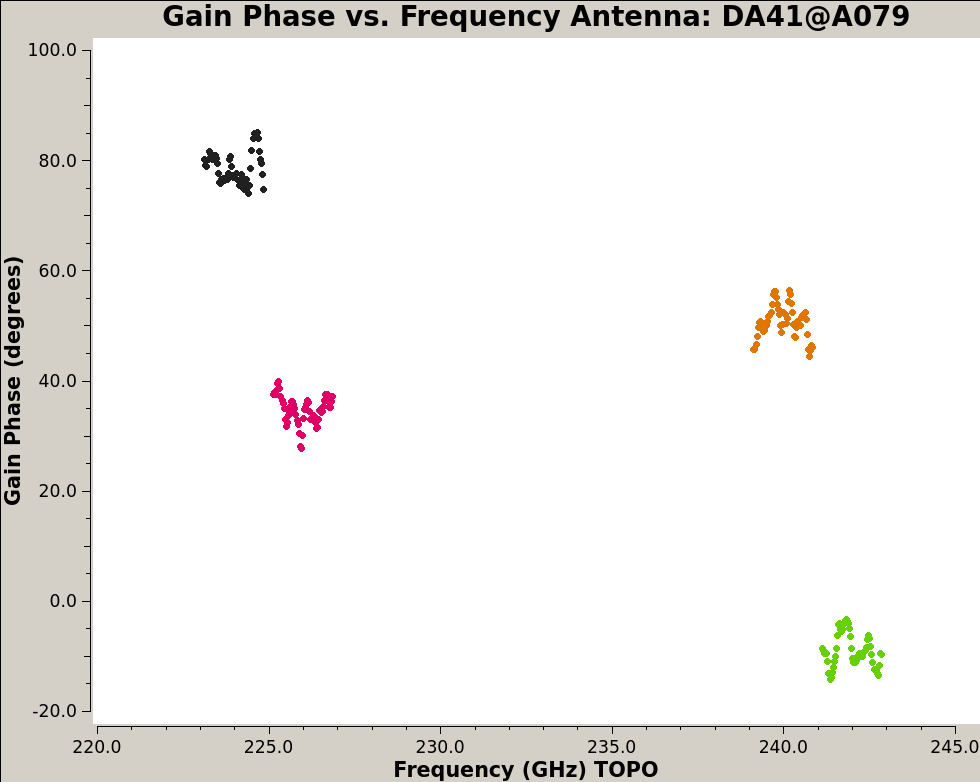
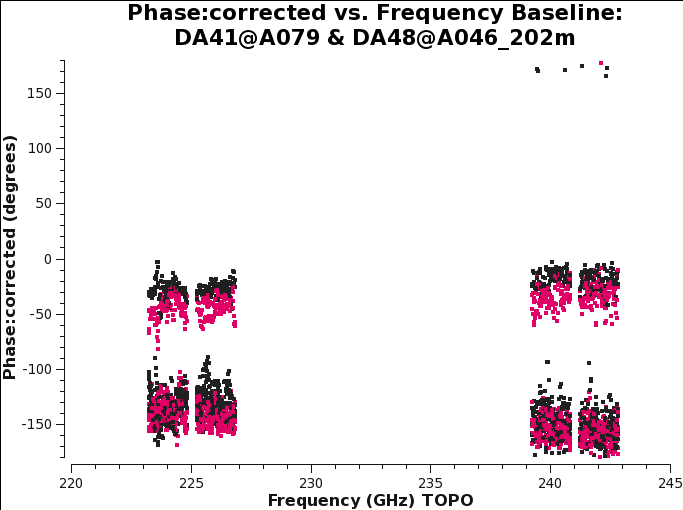
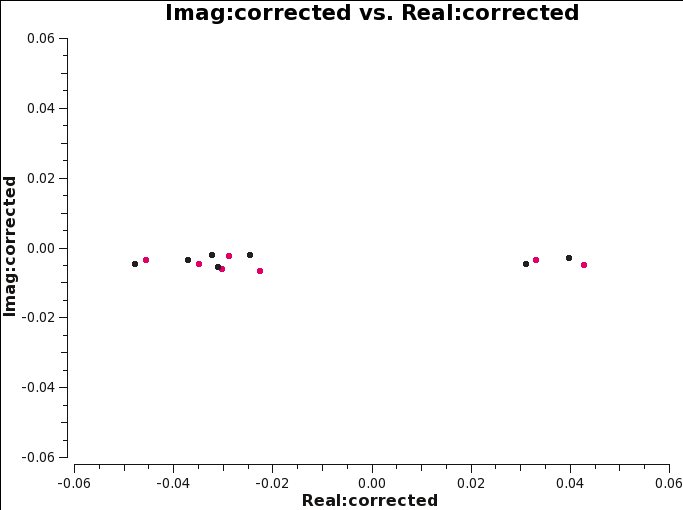
# In CASA
plotms(vis = '3c286_Band6.ms',
ydatacolumn = 'corrected',
xdatacolumn = 'corrected',
xaxis = 'real',
yaxis = 'imag',
field = '0',
avgtime = '1e9',
avgchannel = '128',
avgbaseline = True,
correlation = 'XY,YX',
spw = '3',
coloraxis = 'corr',
plotrange = [-0.06,0.06,-0.06,0.06])
By using the XYf+QU solve in gaincal, we can estimate both the XY-phase offset and the source polarization from the cross-hands. The XYf+QU solve averages all baselines together and first solves for the XY-phase as a function of channel. It then solves for a channel-averaged source polarization (with the channel-dependent XY-phase corrected).
Note that we only require a sufficiently strongly polarized source for this calibration, so that there is an adequate reference signal against which to measure the instrumental effects. It is not necessary to know the precise polarization properties of the calibrator, as long as there is sufficient time for the source polarization contribution to change via parallactic angle rotation. Here we use polcal.
# In CASA
os.system('rm -rf 3c286_Band6.ms.Xfparang')
S = polcal(vis = '3c286_Band6.ms',
caltable = '3c286_Band6.ms.Xfparang',
field = '0',
poltype = 'Xfparang+QU',
solint = 'inf',
combine = 'scan,obs',
preavg = 300,
smodel = qu['J1337-1257']['SpwAve'],
gaintable = ['3c286_Band6.ms.Bscan','3c286_Band6.ms.G1','3c286_Band6.ms.Kcrs'],
interp = ['nearest','linear','nearest'])
- S: A python variable containing the mean source model (Stokes I=1; Q/I; U/I; V=0). This can be used in a revision of the gain calibration and instrumental polarization calibration.
- caltable='*.Xfparang': the output table.
- gaintype='Xfparang+QU': estimate both the XY-phase offset and source polarization from the cross-hands
- solint='inf'; combine='scan,obs': we get one solution for the all dataset. The option "obs" takes into account the different Obs ID which are usually present in different scheduling blocks.
- preavg=300: pre-averaging interval (sec). This limits averaging within the solution interval to within scan boundaries, since the parallactic angle changes from scan to scan are important for the solution.
- smodel=qu['J1337-1257']['SpwAve']: we again are using a polarized model, however this time we are starting with the model determined by polfromgain. This is just to enforce the assumption of non-zero source polarization signature in the cross-hands in the ratio between data and model. It is not important to specify the polarization Stokes parameters correctly, since here we are only solving for a phase-like quantity.
- gaintable=['*.Bscan','*.G1','*.Kcrs']: we apply on-the-fly the bandpass, the gain and the cross-hand delay tables.
The output table contains the values of Q, U and the XY-phase.
# In CASA
plotms(vis='3c286_Band6.ms.Xfparang', xaxis='frequency', yaxis='phase', iteraxis='antenna', coloraxis='spw')
To clarify the effect produced by this calibration on the cross-hand phases, we can apply it to the data:
# In CASA
applycal(vis = '3c286_Band6.ms',
field = '0',
calwt = [True,True,False,False],
gaintable = ['3c286_Band6.ms.Bscan','3c286_Band6.ms.G1','3c286_Band6.ms.Kcrs','3c286_Band6.ms.Xfparang'],
interp = ['nearest','linear','nearest','nearest'])
Plotting the corrected phase versus frequency (Figure 16) and comparing the result with Figure 13, we see that the application of this table does indeed remove spw- and channel-dependent residual phases from the data. The remaining phase offsets (per baseline and correlation) are due to the instrumental polarization effects which will be calibrated below.
# In CASA
plotms(vis = '3c286_Band6.ms',
ydatacolumn = 'corrected',
xaxis = 'freq',
yaxis = 'phase',
field = '0',
avgtime = '1e9',
avgscan = True,
correlation = 'XY,YX',
spw = '',
coloraxis = 'corr',
iteraxis = 'baseline')
In terms of the real and imaginary parts, the application of the XY-phase calibration removes the slope. What we can see now in the complex plane (Figure 17) is the effect of parallactic angle variation of the source polarization occurring entirely in the real part (over a range between -0.06 and 0.06), with a small complex offset due to the mean instrumental polarization that will be solved for below.
Revise gain with good source pol estimate
Now we revise the gain calibration using the full polarization source model we derived above. In this way we will remove from the gains any signature of the source polarization, which is now correctly accounted for in the model "S". Cross-hands are not used here, so cross-hand calibration tables are not needed.
# In CASA
os.system('rm -rf 3c286_Band6.ms.G2.polcal')
gaincal(vis = '3c286_Band6.ms',
caltable = '3c286_Band6.ms.G2.polcal',
field = '0',
solint = 'int',
refant = refant,
refantmode = 'strict',
smodel = S['J1337-1257']['SpwAve'],
gaintable = ['3c286_Band6.ms.Bscan'],
interp = ['nearest'],
parang = True)
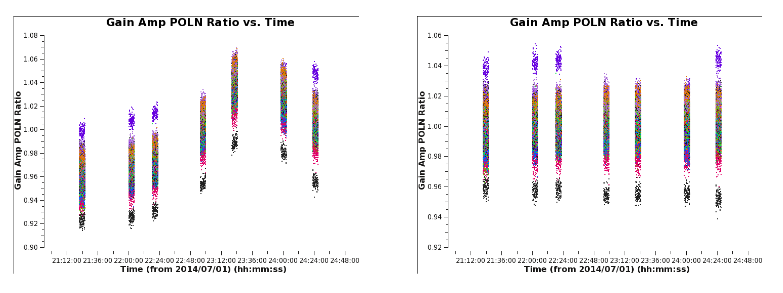
- caltable='*.G2.polcal': the output table. The name reminds us that these are gains for the polarization calibrator.
- smodel=S['J1337-1257']['SpwAve']: here we use as source model the full Stokes model we obtained above.
- parang=True: this time the parallactic angle dependence is corrected for in computing the gains.
With parang=True the supplied source linear polarization is properly rotated in the parallel-hand visibility model. This new gain solution ratio can be plotted with correlation='/' to show that the source polarization is no longer distorting it.
# In CASA
plotms(vis='3c286_Band6.ms.G1', xaxis='time', yaxis='amp', field='J1337-1257', correlation='/', coloraxis='antenna1')
plotms(vis='3c286_Band6.ms.G2.polcal', xaxis='time', yaxis='amp', field='J1337-1257', correlation='/', coloraxis='antenna1')
In Figure 18 a small distortion can be noticed, in the central scans of table G2.polcal. It is due to antenna DV02 in spw 1, which shows a variation in the ratio slightly different than the average.
Just to check: if qufromgain() is run on this new gain table, the reported source polarization should be statistically indistinguishable from zero.
# In CASA
qu2 = polfromgain(vis='3c286_Band6.ms', tablein='3c286_Band6.ms.G2.polcal', caltable='3c286_Band6.ms.G2a.polcal')
print(qu2)
We show here just the average values obtained, which can be compared with the last line of polfromgain() results, reported above. We can see that now the Q (2nd column) and U (3rd column) values are near zero.
{'J1337-1257':
{'Spw0': [1.0, -0.0003105910631165318, -0.0008989854372679172, 0.0],
'Spw1': [1.0, 0.00030789313801403835, -0.0012251557847778529, 0.0],
'Spw2': [1.0, 0.0010217877488700757, 3.4010732831564205e-05, 0.0],
'Spw3': [1.0, 0.0013222722374015867, 0.0008468052734902653, 0.0],
'SpwAve': [1.0, 0.0005853405152922923, -0.00031083130393098516, 0.0]}}
Solving for the Leakage Terms
We can now solve for the instrumental polarization. This solve will produce an absolute instrumental polarization solution that is registered to the assumed source polarization and prior calibrations. To do that we apply all the previous calibrations in order to extract the D-terms from the corrected I, Q and U.
The task used to estimate the D-terms is polcal:
# In CASA
os.system('rm -rf 3c286_Band6.ms.Df0*')
polcal(vis = '3c286_Band6.ms',
caltable = '3c286_Band6.ms.Df0gen',
field = '0', # J1337-1257
solint = 'inf',
combine = 'obs,scan',
preavg = 300,
poltype = 'Dflls',
refant = '', # solve absolute D-term
smodel = S['J1337-1257']['SpwAve'],
gaintable = ['3c286_Band6.ms.Bscan','3c286_Band6.ms.G2.polcal','3c286_Band6.ms.Kcrs','3c286_Band6.ms.Xfparang'],
gainfield = ['','','',''],
interp = ['nearest','linear','nearest','nearest'])
- caltable='*.Df0gen': the output table.
- poltype='Dflls': frequency-dependent LLS solver for instrumental polarization
- refant=: no reference antenna is needed here
- smodel=S['J1337-1257']['SpwAve']: we use as model the "S" we calculated above
- gaintable=['*.Bscan','*.G2.polcal','*.Kcrs', '*.Xfparang']: we apply the bandpass, gain, and cross-hand calibration tables (Kcrs, and Xfparang)
We do not use a reference antenna here because the polarized source provides sufficient constraints to solve for all instrumental polarization parameters on all antennas, relative to the specified source polarization. This is in contrast to the case of an unpolarized calibrator (or the general ciricular basis treatment, even if the calibrator is polarized), where only relative instrumental polarization factors among the antennas may be determined, with one feed on one antenna set to zero instrumental polarization.
Here we plot the amplitude, the real part, and the imaginary part of leakage (D-term) solutions, computed in frame of the telescope.
# In CASA
plotms(vis='3c286_Band6.ms.Df0gen', xaxis='frequency', yaxis='amp', spw='0,1', iteraxis='antenna', coloraxis='corr', gridrows=3, gridcols=2)
plotms(vis='3c286_Band6.ms.Df0gen', xaxis='frequency', yaxis='amp', spw='2,3', iteraxis='antenna', coloraxis='corr', gridrows=3, gridcols=2)
plotms(vis='3c286_Band6.ms.Df0gen', xaxis='frequency', yaxis='real', spw='0,1', iteraxis='antenna', coloraxis='corr', gridrows=3, gridcols=2)
plotms(vis='3c286_Band6.ms.Df0gen', xaxis='frequency', yaxis='real', spw='2,3', iteraxis='antenna', coloraxis='corr', gridrows=3, gridcols=2)
plotms(vis='3c286_Band6.ms.Df0gen', xaxis='frequency', yaxis='imag', spw='0,1', iteraxis='antenna', coloraxis='corr', gridrows=3, gridcols=2)
plotms(vis='3c286_Band6.ms.Df0gen', xaxis='frequency', yaxis='imag', spw='2,3', iteraxis='antenna', coloraxis='corr', gridrows=3, gridcols=2)
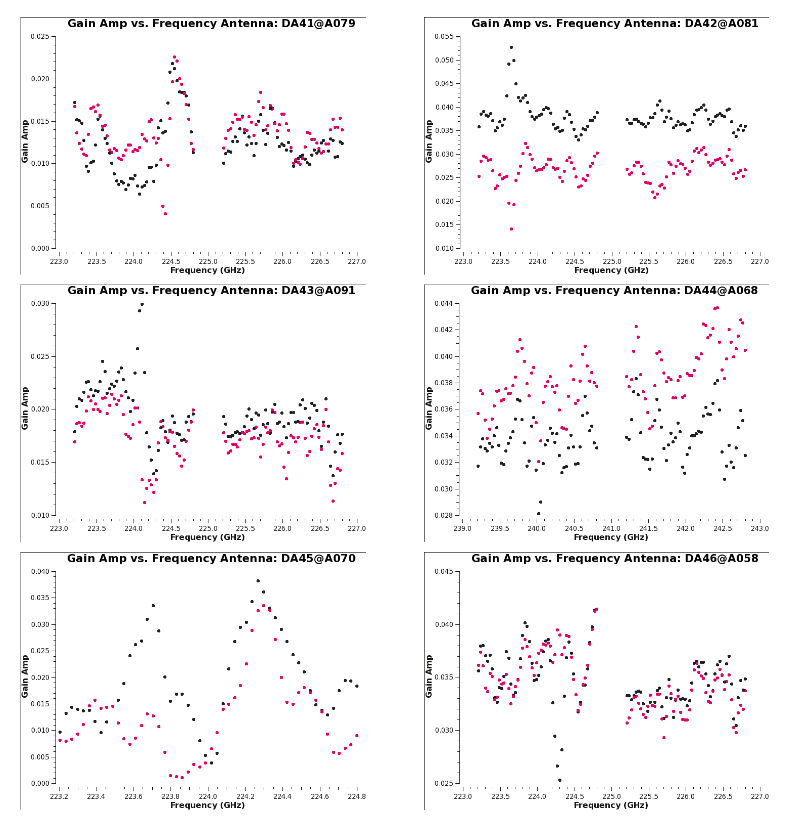 |
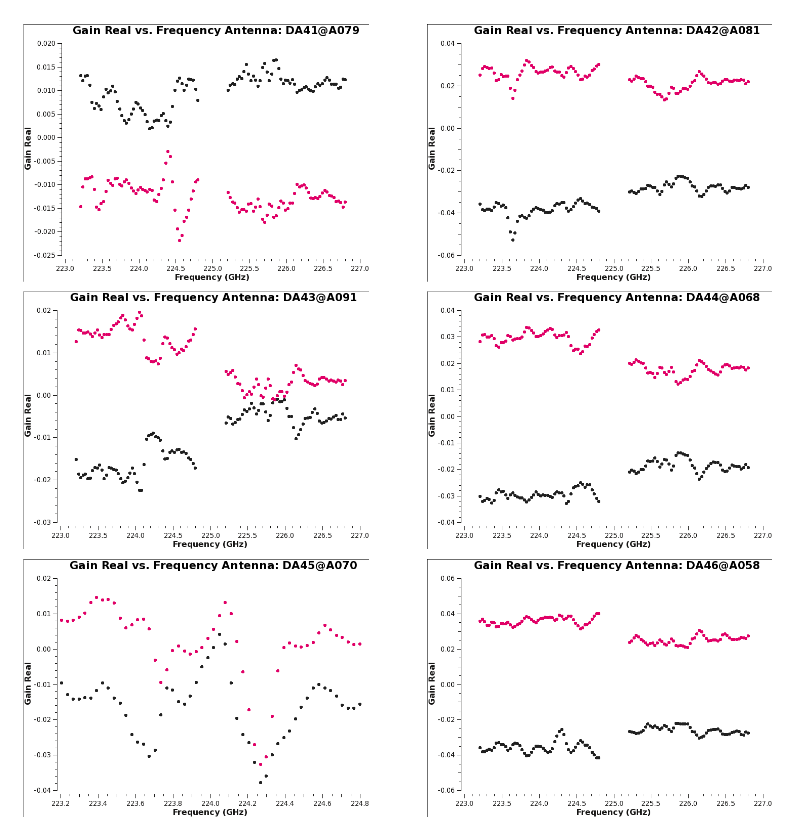 |
 |
The values obtained--a few percent for most of the antennas--are reasonable, and we will apply them to the data.
Solving the Global Normalized Gain Amplitudes
The final calibration table that needs generated is the X/Y gain amplitude table. When the initial non-polarization calibration, we produced polarization independant gain solutions to preserve the intrinsic linear polarzation of the calibrator. However, this leaves the cross-hand amplitude ratio uncalibrated. We will determine that correction here using the previous calibrations.
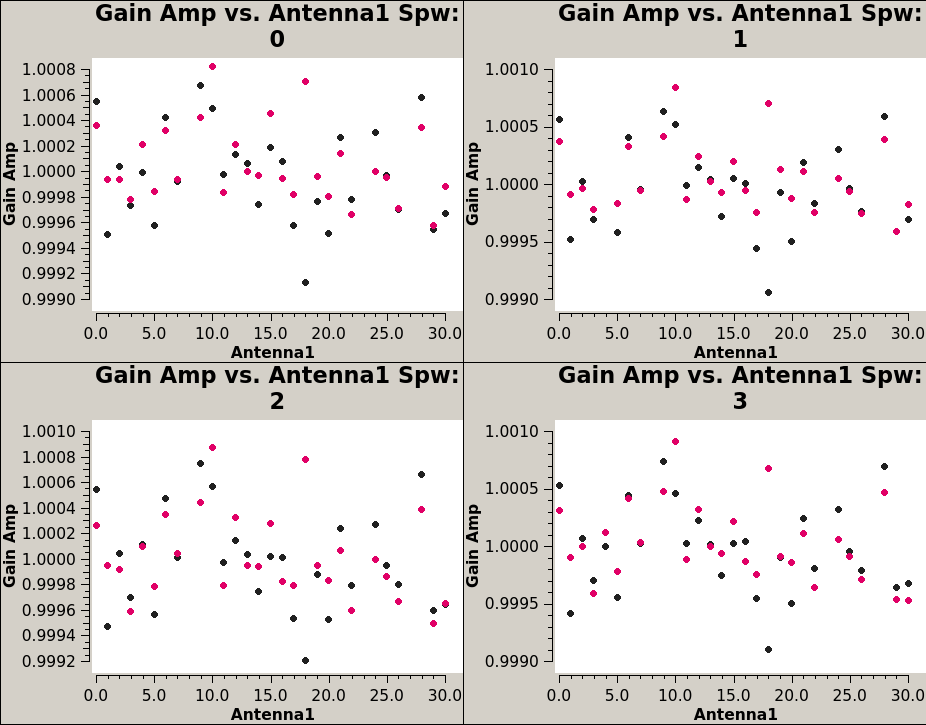
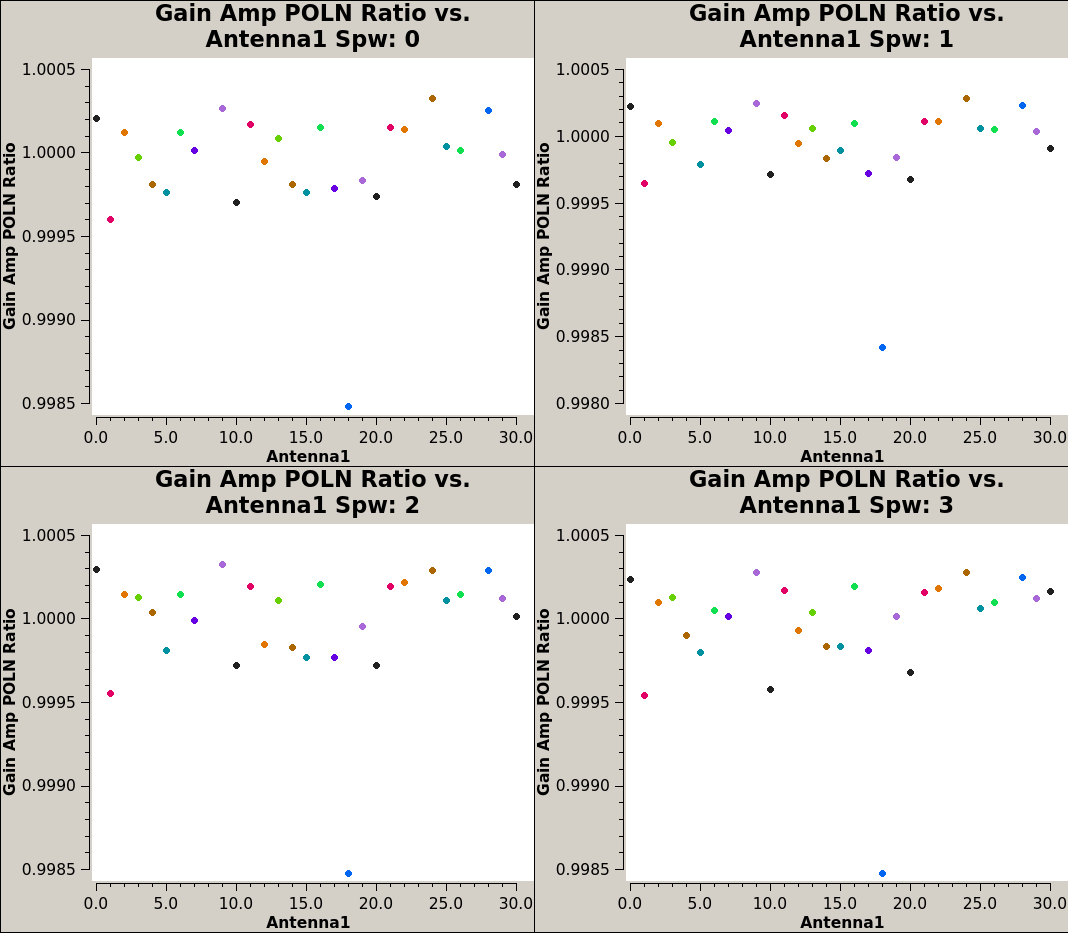
# In CASA
os.system('rm -rf 3c286_Band6.ms.Gxyamp*')
gaincal(vis = '3c286_Band6.ms',
caltable = '3c286_Band6.ms.Gxyamp',
field = '0', #J1337-1257
solint = 'inf',
combine = 'obs,scan',
refant = refant,
refantmode = 'strict',
gaintype = 'G',
calmode = 'a',
smodel = S['J1337-1257']['SpwAve'],
gaintable = ['3c286_Band6.ms.Bscan','3c286_Band6.ms.G2.polcal','3c286_Band6.ms.Kcrs',
'3c286_Band6.ms.Xfparang','3c286_Band6.ms.Df0gen'],
gainfield = ['','','','',''],
interp = ['nearest','linear','nearest','nearest','nearest'],
solnorm = True,
parang = True)
- caltable='*.Gxyamp': the output table.
- gaintype='G': Solve for each polarization separatly.
- smodel=S['J1337-1257']['SpwAve']: we use as model the "S" we calculated above
- gaintable=['*.Bscan','*.G2.polcal','*.Kcrs','*.Xfparang','*.Df0gen']: we apply the bandpass, gain, and cross-hand calibration tables (Kcrs, and Xfparang)
Here we plot the XY amplitudes, and the XY amplitude ratios. We expect these ratios to be near a value of 1.
# In CASA
# XY and YX
plotms(vis='3c286_Band6.ms.Gxyamp', xaxis='antenna1', yaxis='amp', coloraxis='corr', iteraxis='spw', gridrows=2, gridcols=2)
# pol ratio
plotms(vis='3c286_Band6.ms.Gxyamp', xaxis='antenna1', yaxis='amp', correlation='/', coloraxis='antenna1', iteraxis='spw', gridrows=2, gridcols=2)
Before applying all the calibration tables, it is worth verifying the images resulting from a calibration not including the D-terms correction. This test will be done in the following section.
Imaging of the Polarization Calibrator with and without applying D-terms corrections
Before proceeding with the application of all the calibration tables to the data, it makes sense to verify the actual effect of D-terms correction on the images. For verification purposes only we now apply to the polarization calibrator all calibration tables computed in the calibration guide except the D-terms corrections. In the dir 3C286_Band6_pol_UnCalibrated you should now have all the calibration tables, and you can proceed as follows:
# In CASA
applycal(vis = '3c286_Band6.ms',
field = '0',
calwt = [True,True,False,False],
gaintable = ['3c286_Band6.ms.Bscan','3c286_Band6.ms.G2.polcal','3c286_Band6.ms.Kcrs','3c286_Band6.ms.Xfparang'],
interp = ['nearest','linear','nearest','nearest'],
gainfield = ['','','',''],
parang = True)
Now we make a full-polarization image of the polarization calibrator, just for inspection purposes. We use the task tclean interactively, adding a mask around the central source. In the following section you will find a more clear explanation of how to define the cell and imsize parameters.
# In CASA
os.system('rm -rf polcal.StokesIQUV.noDterms*')
tclean(vis = '3c286_Band6.ms',
field = '0',
imagename = 'polcal.StokesIQUV.noDterms',
cell = ['0.1arcsec'],
imsize = [250,250],
stokes = 'IQUV',
deconvolver = 'clarkstokes',
interactive = True,
weighting = 'briggs',
robust = 0.5,
niter = 500,
cycleniter = 20)
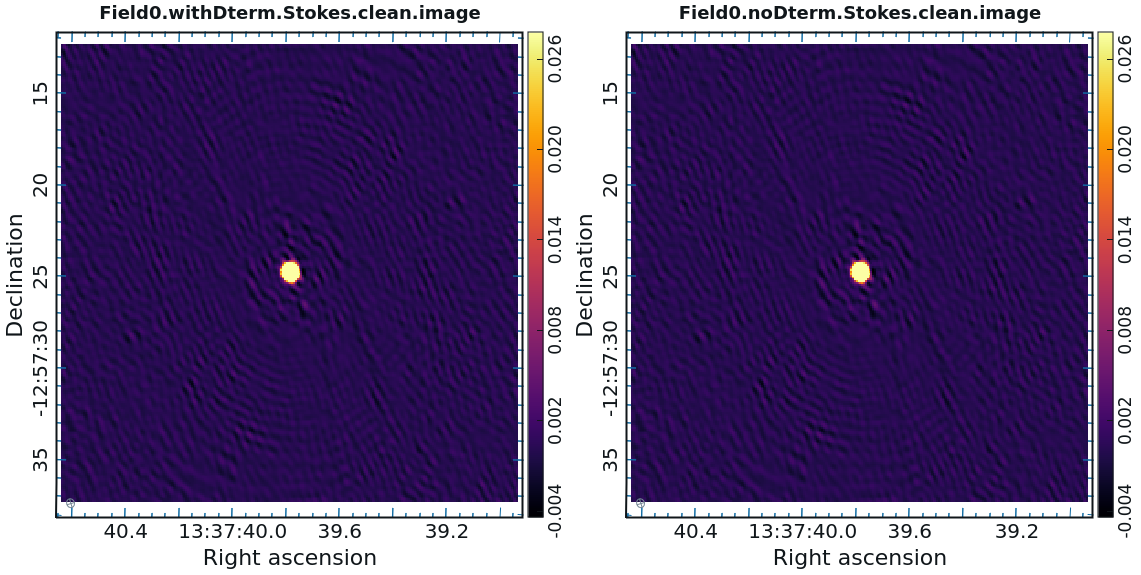
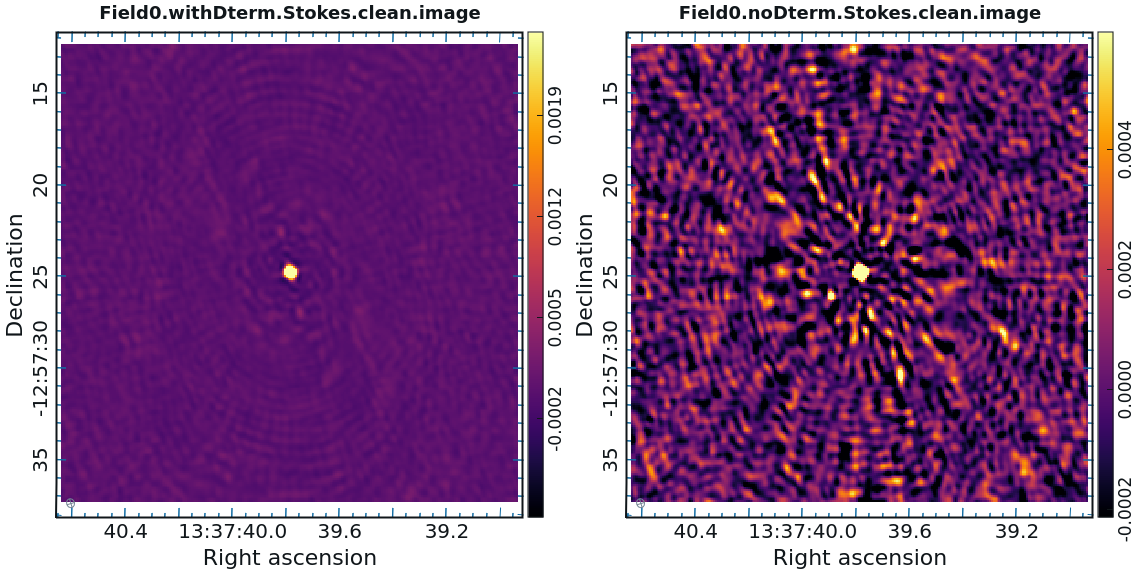
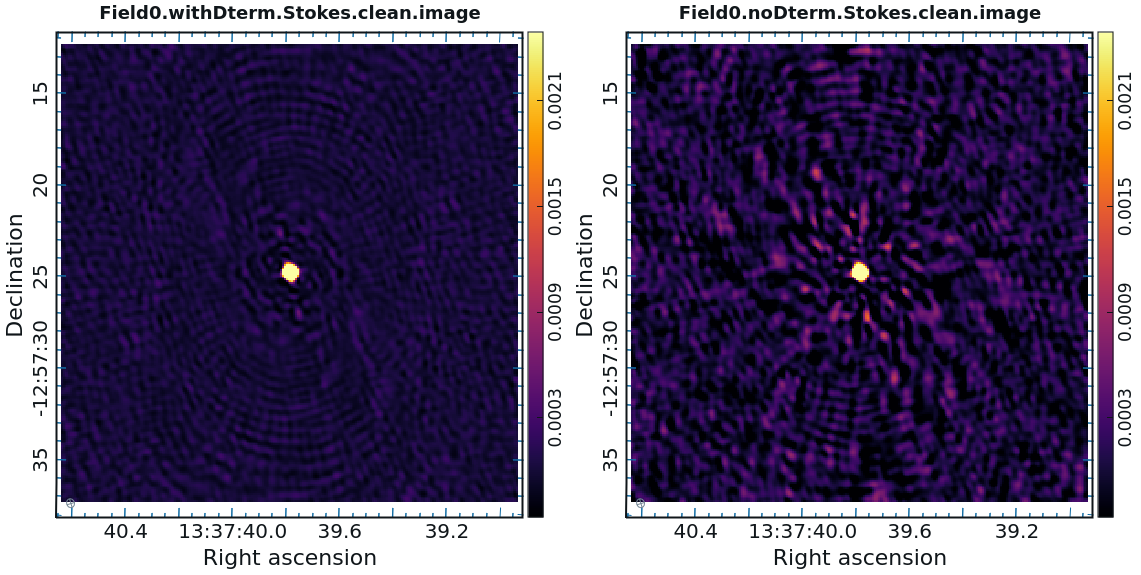
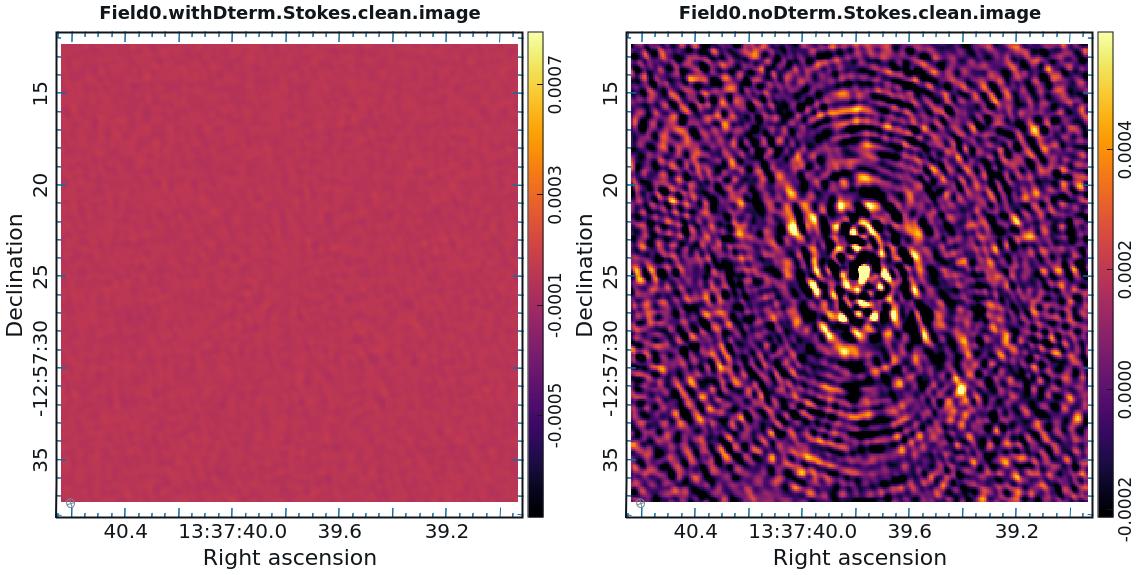
The calibrator image should show a point source, so we can clean with a small number of itterations. It is important not to overclean the image. The clean flux is of 1.06 Jy.
Now we apply all the calibration tables with applycal, including Df0gen and Gxyamp:
# In CASA
applycal(vis = '3c286_Band6.ms',
field = '0',
calwt = [True,True,False,False,False,False],
gaintable = ['3c286_Band6.ms.Bscan','3c286_Band6.ms.G2.polcal','3c286_Band6.ms.Kcrs',
'3c286_Band6.ms.Xfparang','3c286_Band6.ms.Df0gen','3c286_Band6.ms.Gxyamp'],
interp = ['nearest','linear','linear','nearest','nearest','nearest'],
gainfield = ['','','','','',''],
parang = True)
And we clean again:
# In CASA
os.system('rm -rf polcal.StokesIQUV.withDterms*')
tclean(vis = '3c286_Band6.ms',
field = '0',
imagename = 'polcal.StokesIQUV.withDterms',
cell = ['0.1arcsec'],
imsize = [250,250],
stokes = 'IQUV',
deconvolver = 'clarkstokes',
weighting = 'briggs',
robust = 0.5,
interactive = True,
niter = 500,
cycleniter = 20)
The calibration on this data is okay, but we will be improving the calibration using self calibration in 3C286_Band6Pol_Imaging. To reach the same clean flux (~1.06 Jy) more iterations are needed and the residuals level decreases.
After tclean has finished, you should now open the images in CARTA. If using NRAO machines, you can open a new terminal tab, cd to the working directory, then type:
# in terminal
carta --no_browser
Copy the output URL into a browser to view your CARTA session. Select and load:
polcal.StokesIQUV.noDterms.image
polcal.StokesIQUV.withDterms.image
As you can see in Figure 25, the application of D-term calibration clearly improves the images of Stokes Q, U, and V.
Inspect the corrected pol cal data
We first plot the complex plane again, and compare the results with Figures 14 and 17. Figure 26 shows clearly that the imaginary part is now zero, while the real part is corrected for the variation shown before; its corrected value is ~0.04.
# In CASA
plotms(vis = '3c286_Band6.ms',
ydatacolumn = 'corrected',
xdatacolumn = 'corrected',
xaxis = 'real',
yaxis = 'imag',
field = '0',
avgtime = '1e9',
avgchannel = '128',
avgbaseline = True,
correlation = 'XY,YX',
spw = '3',
coloraxis = 'corr',
plotrange = [-0.06,0.06,-0.06,0.06])
Let's now examine the corrected amplitude and phase of the polarization calibrator.
# In CASA
plotms(vis = '3c286_Band6.ms',
xaxis = 'chan',
yaxis = 'amp', # or phase
ydatacolumn = 'corrected',
field = '0',
avgtime = '1e9',
avgscan = True,
coloraxis = 'corr')
# In CASA
plotms(vis = '3c286_Band6.ms',
xaxis = 'freq',
yaxis = 'phase',
ydatacolumn = 'corrected',
field = '0',
avgtime = '1e9',
avgscan = True,
correlation = 'XY,YX',
coloraxis = 'corr',
iteraxis = 'baseline')
In Figure 27 we see that the XX,YY correlations have unitary amplitude, since we didn't scaled the flux. The XY,YX amplitude value is of the order of 0.04, which means the Stokes U of this source is ~0.04. This value is consistent with what the previous steps revealed. After the calibration all the phases normalized around zero (Fig 28). To more clearly show the effect of the D-terms application on the polarization calibrator we also plot the corrected phases of the baseline DA41&DA48 (Fig 29). Comparing this result with Figure 16 we see that the XY and YX phases are now corrected and near zero.
Applying the calibrations and splitting of the corrected data
We now apply the solutions from the phase calibrator (field='3') to the science target (field='4'). Its flux scale has also been bootstrapped to that of the flux calibrator, so it can serve as an amplitude and phase calibrator. We apply to these sources the polarization calibrations (Kcrs, Xfparang, and Df0gen) that we obtained for the polarization calibrator (field='0').
# In CASA
# Apply caltables to fields = 3 & 4
applycal(vis = '3c286_Band6.ms',
field = '3,4',
calwt = [True,True,False,False,False,False,False],
gaintable = ['3c286_Band6.ms.Bscan','3c286_Band6.ms.G2ph','3c286_Band6.ms.flux',
'3c286_Band6.ms.Kcrs','3c286_Band6.ms.Xfparang','3c286_Band6.ms.Df0gen','3c286_Band6.ms.Gxyamp'],
interp = ['nearest','linear','linear','nearest','nearest','nearest','nearest'],
gainfield = ['','3','3','','','',''],
parang = True)
- gaintable=['*.Bscan', '*.G2ph', '*.flux', '*.Kcrs', '*.Xfparang', '*.Df0gen', '*Gxyamp']: these are all the tables to be applied to the data.
- interp=['nearest', 'linear', 'linear', 'nearest', 'nearest', 'nearest']: the corresponding interpolation method
- gainfield=[,'3','3',,,,]: select the field from the corresponding gaintable. Here the phase calibrator gains are applied to both the calibrator itself and the target.
- parang=True: apply the parallactic angle correction
To check the effects of calibration on the scientific target we can compare the plot of imaginary vs real part before the calibration (xdatacolumn & ydatacolumn='data') and after (xdatacolumn & ydatacolumn='corrected'):
# In CASA
plotms(vis = '3c286_Band6.ms',
field = '4',
xaxis = 'real',
yaxis = 'imag',
spw = '0',
ydatacolumn = 'data',
xdatacolumn = 'data',
avgchannel = '64',
avgtime = '1e9',
avgscan = True,
coloraxis = 'corr')
You can see in these plots how the calibration has corrected the real and imaginary parts of the target visibilities. The imaginary parts of both the parallel and the cross-hands are close to zero, while the real parts are ~340 mJy and ~60 mJy, respectively.
We now split the scientific target (field 4) corrected data:
# In CASA
os.system('rm -rf 3c286_Band6.pol.cal.ms')
split(vis = '3c286_Band6.ms',
outputvis = '3c286_Band6.pol.cal.ms',
field = '4',
datacolumn = 'corrected',
width = '4')
Using the parameter width we average the channels in order to reduce the size of the output file (3c286_Band6.pol.cal.ms will have 16 channels). In TDM observations, averaging more than about 8 channels in dual pol (XX,YY of 128 channels each) or 4 in full Stokes (XX,XY,YX,YY of 64 channels each) would produce significant bandwidth smearing. For details, see the relevant CASA notebook and this document.
Now you can continue on to 3C286_Band6Pol_Imaging.
References
- Synthesis Imaging in Radio Astronomy II, 1999, ASP Conference Series, Vol. 180, Editors: Taylor, G. B.; Carilli, C. L.; Perley, R. A.
- Interferometry and Synthesis in Radio Astronomy, 2nd Edition, 2001, Thompson, A.R., Moran, J.M., Swenson, G. W., Ed. Wiley
- AT polarization calibration, 1991, Sault, R. J., Killeen,N.E.B., & Kesteven, M.J., ATNF memo
- Understanding radio polarimetry. I. Mathematical foundations., 1996, Hamaker, J. P.; Bregman, J. D.; Sault, R. J., Astronomy and Astrophysics Supplement, v.117