First Look at Self Calibration CASA 6: Difference between revisions
No edit summary |
No edit summary |
||
| (14 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
''This guide is written for CASA 6. | ''This guide is written for CASA 6.4.1.12 and uses Python 3.'' | ||
This script steps you through continuum imaging and self calibration | This script steps you through continuum imaging and self calibration | ||
| Line 36: | Line 36: | ||
[[File:Imaging-tutorial-selfcal-1_6.1.png|thumb|<caption>Figure 1: Residuals from the first tclean after | [[File:Imaging-tutorial-selfcal-1_6.1.png|thumb|<caption>Figure 1: Residuals from the first tclean after final cycle of cleaning. | ||
Image Statistics: Beam 0.652", 0.504", -65.889°, RMS = 12.9 mJy </caption>]] | |||
| Line 57: | Line 58: | ||
interactive=True, | interactive=True, | ||
savemodel='modelcolumn') | savemodel='modelcolumn') | ||
</source> | </source> | ||
In addition to creating an image, TCLEAN saves the cleaned "model" of the science target with | In addition to creating an image, TCLEAN saves the cleaned "model" of the science target with | ||
| Line 91: | Line 93: | ||
gaintype="G") | gaintype="G") | ||
</source> | </source> | ||
Gaincal does the following: it looks at your ‘data’ column, looks at your ‘model’ column, and figures out what | |||
correction needs to be applied to ‘data’ in order to make it look like ‘model.’ It produces a calibration table (‘*.cal’ | |||
file) with these corrections for each antenna and time, but it does not actually apply these corrections. Applying the | |||
corrections is done with the applycal task (see below). | |||
Figuring out the best averaging parameters is often the key to good self-calibration. You would like the solution | |||
interval to be short enough so that it tracks changes in the atmospheric phase with high accuracy, but long enough | |||
so that you measure phases with good signal-to-noise. Also, ideally you’d like to keep solutions separate for different | |||
spws and polarizations. For faint sources when you need to boost SNR, however, it may be necessary to average over | |||
these parameters to achieve good solutions. | |||
Solint Values: In gaincal, the parameter ’solint’ determines the time interval over which gaincal will derive phase | |||
solutions. Ideally this should be an integer multiple of your integration time (i.e. if your integration time is 3s, your | |||
solint values might be solint=3s, solint=6s, solint=9s, etc.). Solint can range from ‘int’ at minimum (i.e., ‘integration,’ | |||
your integration time for a single integration) to ‘inf’ at maximum (i.e. ‘infinity,’ which is not actually infinity but | |||
rather the maximum time interval allowed.). If you have combine=‘’ set, setting ‘inf’ will be equivalent to combining | |||
all integrations within a single scan, but will not combine across scans (i.e. if your integration time is 3s, and each | |||
scan was 2 minutes long, setting solint=‘inf’ is equivalent to setting solint=‘120s’). If you set combine=‘scan,’ the | |||
effective value of solint=‘inf’ will likewise increase. | |||
Gaintype: ‘gaintype’=‘G’ will cause gaincal to derive solutions for each polarization independently. This becomes | |||
more important if you have a polarized source or a source whose polarization state you do not know. If your source | |||
is unpolarized, it is still a good idea to use ‘gaintype=G’ if you can, as this will yield the most accurate solutions. | |||
However, if you need to increase the S/N of your solutions, ‘calmode’=‘T’ will combine the data across polarizations | |||
and derive a single solution for both. | |||
In the gaincal example above, the first choice of solint is entirely arbitrary. Try it and see what you get. Our goal | |||
is to have no failed solutions at all, and to have good S/N on the solutions we do get. (Always S/N > 3, but ideally | |||
S/N>5 or better.) | |||
Try playing around with different solution intervals or averaging | Try playing around with different solution intervals or averaging | ||
| Line 129: | Line 163: | ||
iteraxis="antenna", | iteraxis="antenna", | ||
plotrange=[0,0,-30,30], | plotrange=[0,0,-30,30], | ||
coloraxis="corr", | |||
titlefont=7, | titlefont=7, | ||
xaxisfont=7, | xaxisfont=7, | ||
| Line 186: | Line 221: | ||
savemodel='modelcolumn') | savemodel='modelcolumn') | ||
</source> | </source> | ||
Image Statistics: Beam 0.639", 0.494", -65.483°, RMS = 5.86 mJy | |||
The residuals do look better this time around. Run the viewer and | The residuals do look better this time around. Run the viewer and | ||
| Line 207: | Line 244: | ||
gaintype="G") | gaintype="G") | ||
</source> | </source> | ||
This time we see a number of failed solutions that gaincal has flagged due to insufficient signal to noise (compared to the threshold set by minSNR). A small number of failed solutions may be expected depending on the solution interval, especially for more extended antennas in the configuration, although ideally you will find a solint that gives you no failed solutions. Failed solutions mean that those data will get flagged (i.e. no longer used) | |||
automatically. It is important to take into account how the resultant flagged baselines affect the beam size and image | |||
fidelity after each gaincal iteration. | |||
Let's plot the calibration table again. At this point, we see much smaller phase scatter | Let's plot the calibration table again. At this point, we see much smaller phase scatter | ||
| Line 225: | Line 266: | ||
iteraxis="antenna", | iteraxis="antenna", | ||
plotrange=[0,0,-30,30], | plotrange=[0,0,-30,30], | ||
coloraxis="corr", | |||
titlefont=7, | titlefont=7, | ||
xaxisfont=7, | xaxisfont=7, | ||
| Line 256: | Line 298: | ||
[[File:Imaging-tutorial-selfcal-3_6.1.png|thumb|<caption>Figure 5: Residuals from the third clean after | [[File:Imaging-tutorial-selfcal-3_6.1.png|thumb|<caption>Figure 5: Residuals from the third clean after 3 main cycles of cleaning. </caption>]] | ||
| Line 278: | Line 320: | ||
savemodel='modelcolumn') | savemodel='modelcolumn') | ||
</source> | </source> | ||
Image Statistics: Beam 0.691", 0.549", -62.883°, RMS = 4.98 mJy | |||
Run a third round of phase-only self calibration using the improved model. | Run a third round of phase-only self calibration using the improved model. | ||
| Line 302: | Line 346: | ||
iteraxis="antenna", | iteraxis="antenna", | ||
plotrange=[0,0,-30,30], | plotrange=[0,0,-30,30], | ||
coloraxis="corr", | |||
titlefont=7, | titlefont=7, | ||
xaxisfont=7, | xaxisfont=7, | ||
| Line 352: | Line 397: | ||
</source> | </source> | ||
[[File:Imaging-tutorial-selfcal-image-4_6.1.png|thumb|<caption>Figure 7: Residuals from the fourth clean after 2 main cycles of cleaning. </caption>]] | [[File:Imaging-tutorial-selfcal-image-4_6.1.png|thumb|<caption>Figure 7: Residuals from the fourth clean after 2 main cycles of cleaning. </caption>]] | ||
Image Statistics: Beam 0.722", 0.565", -58.463°, RMS = 4.88 mJy | |||
The improvement is really marginal at this point. Confident that we have done what we can on the phase, we can experiment with amplitude self calibration. This is potentially dangerous as it has much more potential to change the characteristics of the source than phase self-calibration. We mitigate this somewhat by setting solnorm=True, so that the solutions are normalized. | The improvement is really marginal at this point. Confident that we have done what we can on the phase, we can experiment with amplitude self calibration. This is potentially dangerous as it has much more potential to change the characteristics of the source than phase self-calibration. We mitigate this somewhat by setting solnorm=True, so that the solutions are normalized. | ||
In many cases, it would be perfectly fine to stop self-calibrating once we are satisfied with our phase-only self-calibration | |||
solutions. In this case, we will move on to demonstrating amplitude+phase self-cal. This type of self-cal is potentially | |||
dangerous as it has much more potential to change the characteristics of the source than phase self-calibration. We | |||
mitigate this somewhat by setting solnorm=True, so that the solutions are normalized. | |||
<source lang="python"> | <source lang="python"> | ||
| Line 368: | Line 419: | ||
solnorm=True) | solnorm=True) | ||
</source> | </source> | ||
Note that we have increased our solint back to ’inf.’ This is common for amplitude self-cal: you will want a solint | |||
for the amplitude self-cal that is larger than the solint for your best round of phase-only self-cal. We have also added | |||
the line ’gaintable=...’ This is because we don’t want to let ap self-cal have too many degrees of freedom. Instead, we | |||
force it to use our phase-only solutions first, before it is allowed to calculate amplitude+phase solutions. | |||
Plot the calibration table again: | Plot the calibration table again: | ||
| Line 378: | Line 434: | ||
gridcols=3, | gridcols=3, | ||
iteraxis="antenna", | iteraxis="antenna", | ||
plotrange=[0,0,0,0], | plotrange=[0,0,0,0], | ||
coloraxis="corr", | |||
titlefont=7, | titlefont=7, | ||
xaxisfont=7, | xaxisfont=7, | ||
| Line 387: | Line 444: | ||
</source> | </source> | ||
[[File:Imaging-tutorial-selfcal-plotcal-4_6.1.png|thumb|<caption>Figure 8: Phase solutions after the fourth round of self calibration. </caption>]] | [[File:Imaging-tutorial-selfcal-plotcal-4_6.1.png|thumb|<caption>Figure 8: Phase solutions after the fourth round of self calibration. </caption>]] | ||
| Line 410: | Line 469: | ||
<source lang="python"> | <source lang="python"> | ||
os.system("rm -rf sis14_twhya_selfcal4.ms*") | os.system("rm -rf sis14_twhya_selfcal4.ms*") | ||
split(vis='sis14_twhya_selfcal_3.ms', | |||
outputvis='sis14_twhya_selfcal_4.ms', | outputvis='sis14_twhya_selfcal_4.ms', | ||
datacolumn="corrected") | datacolumn="corrected") | ||
| Line 417: | Line 476: | ||
</source> | </source> | ||
Clean a | Clean a fifth time. | ||
[[File:Imaging-tutorial-selfcal-4_6.1.png|thumb|<caption>Figure 9: Residuals from the fourth tclean after 4 main cycles of cleaning. </caption>]] | [[File:Imaging-tutorial-selfcal-4_6.1.png|thumb|<caption>Figure 9: Residuals from the fourth tclean after 4 main cycles of cleaning. </caption>]] | ||
| Line 439: | Line 498: | ||
savemodel='modelcolumn') | savemodel='modelcolumn') | ||
</source> | </source> | ||
Image Statistics: Beam 1.988", 1.154", -88.964°, RMS = 16.3 mJy, | |||
This time, notice from the residuals that you can clean more deeply. After 4 main cycles, the background residuals look very random on | This time, notice from the residuals that you can clean more deeply. After 4 main cycles, the background residuals look very random on | ||
the scale of the beam size. This is good! | the scale of the beam size. This is good! | ||
Compare the | Compare the fourth and fifth images (you can use an {{imstat}} command or draw a box using the viewer and access the statistics panel). The noise level is dramatically better, while the flux has not changed markedly (this is very | ||
good, it's what we worry about with amplitude self calibration). | good, it's what we worry about with amplitude self calibration). | ||
By assuming that the previous cleans represent good models we have | By assuming that the previous cleans represent good models we have | ||
| Line 449: | Line 510: | ||
order of magnitude. Not bad! | order of magnitude. Not bad! | ||
Whether you are satisfied with the apcal self-calibration in this case or not, it is very important to understand that | |||
amplitude+phase self-cal is not always successful, nor is it always necessary. If you can get good solutions with apcal | |||
self-calibration, you will likely have improved your S/N ratio by an order of magnitude or more over the non-self- | |||
calibrated data. Likewise, if you have had a significant improvement with phase-only self-cal, and you can’t get good | |||
solutions for amplitude+phase, that’s okay - you have still significantly improved your data! | |||
In this case the fourth image is our best continuum image. We can use the data | |||
set (sis14_twhya_selfcal_3.ms) to proceed with later work. In the next lesson we'll do UV | set (sis14_twhya_selfcal_3.ms) to proceed with later work. In the next lesson we'll do UV | ||
continuum subtraction and line imaging. | continuum subtraction and line imaging. | ||
Latest revision as of 16:48, 27 September 2023
This guide is written for CASA 6.4.1.12 and uses Python 3.
This script steps you through continuum imaging and self calibration of the science data for our science target, TW Hydra.
You should have downloaded the data package as part of the previous imaging tutorial. If you haven't done that yet, check the First Look At Imaging Guide for instructions.
In that first tutorial you made a first continuum image in the previous imaging lesson. We start here by repeating that step and then we iteratively self-calibrate the data, focusing on short-timescale phase corrections.
First, copy the calibrated and flagged data from the working directory. Remember that this is our best version of the data.
# In CASA
os.system("rm -rf sis14_twhya_calibrated_flagged.ms")
os.system("tar -xvf ../working/sis14_twhya_calibrated_flagged.ms.tar")
Run a quick listobs to get oriented:
# In CASA
listobs("sis14_twhya_calibrated_flagged.ms")
Now, use tclean to make a continuum image of TW Hydra (field 5). This call is interactive, but the automated approach that we used in the last lesson would also work. See the last lesson for details. Remember that the spectral window that we will image here as continuum also contains a N2H+ emission line. In this case, the N2H+ emission is faint enough that neglecting to flag the line channels before imaging makes no difference to the final continuum image. For this and the other continuum first look tutorials, we have thus ignored the line to focus on the basic steps of imaging and self-calibration. In general, however, you should flag channels containing emission lines in your own data prior to imaging the continuum. To see how to flag line emission prior to imaging the continuum in a spectral window, please see the more advanced tutorial at IRAS16293_Band9_-_Imaging.
Clean until the residuals near TW Hydra are comparable to those in the rest of the image. For example, you might place your clean mask over the central feature, only, and clean with for two main cycles. That is, use the green arrow twice, and then click the red X to finish tclean. Please note that in general, it is good procedure to clean conservatively prior to the initial iterations of self-cal, which is to say: shallowly, erring on the side of missing flux instead of including flux that might be spurious. Tw Hydra, being dominated by bright, compact emission, is relatively forgiving in that respect. For detailed discussion of these points see the TW Hydra Casa Guide and the self-calibration section of the guide to the NA Imaging Template Script.
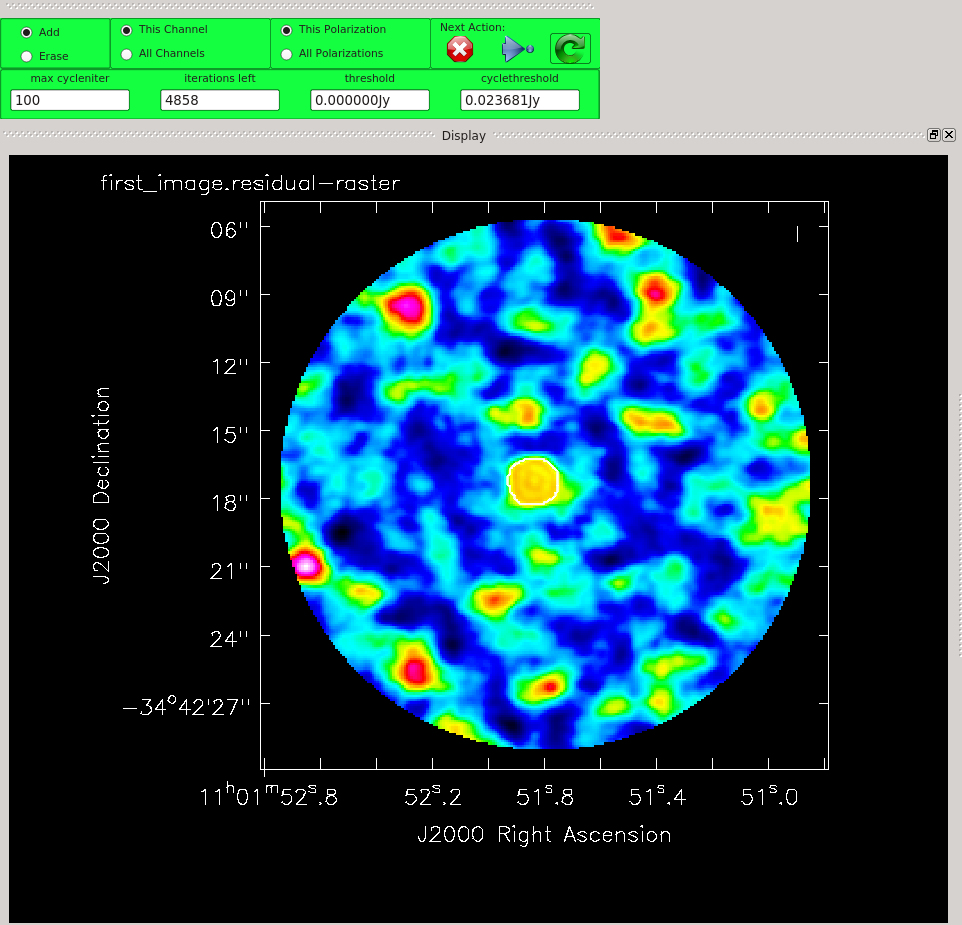
# In CASA
os.system('rm -rf first_image.*')
tclean(vis='sis14_twhya_calibrated_flagged.ms',
imagename='first_image',
field='5',
spw='',
specmode='mfs',
deconvolver='hogbom',
nterms=1,
gridder='standard',
imsize=[250,250],
cell=['0.1arcsec'],
weighting='natural',
threshold='0mJy',
niter=5000,
interactive=True,
savemodel='modelcolumn')
In addition to creating an image, TCLEAN saves the cleaned "model" of the science target with
the measurement set if the parameter savemodel="modelcolumn". This model is required for later self-calibration steps. Note, in the
previous lessons we only had models for the calibrators, not the science target itself. Of
course this model for our science target is not perfect, only as good as the first clean, but it's a
good starting point.
You may see a warning requesting you check in the CASA log that the model was created. Look for the line in the log that says 'Saving model column':
WARN tclean Please check the casa log file for a message confirming that the model was saved after the last major cycle. If it doesn't exist, please re-run tclean with niter=0,calcres=False,calcpsf=False in order to trigger a 'predict model' step that obeys the savemodel parameter.
With a model in place, we are in a position to calibrate the science target directly. We use gaincal, which is the task used both for general gain calibration using an external calibrator, and for self-calibration. We will focus here on phase corrections - generally good practice for self calibration - because amplitude self calibration has a larger potential to change the source characteristics (i.e. introduce artifacts). Figuring out the best averaging parameters is often the key to good self-calibration. You would like the solution interval to be short enough so that it tracks changes in the atmospheric phase with high accuracy, but long enough so that you measure phases with good signal-to-noise. Also, ideally you'd like to keep solutions separate for difference spw's and polarizations, but for faint sources when you need to boost SNR, it may be necessary to average over these parameters to achieve good solutions. Using 30 seconds for the solution interval is a good choice for TW Hydra.
# In CASA
os.system("rm -rf phase.cal")
gaincal(vis="sis14_twhya_calibrated_flagged.ms",
caltable="phase.cal",
field="5",
solint="inf",
calmode="p",
refant="DV22",
gaintype="G")
Gaincal does the following: it looks at your ‘data’ column, looks at your ‘model’ column, and figures out what correction needs to be applied to ‘data’ in order to make it look like ‘model.’ It produces a calibration table (‘*.cal’ file) with these corrections for each antenna and time, but it does not actually apply these corrections. Applying the corrections is done with the applycal task (see below).
Figuring out the best averaging parameters is often the key to good self-calibration. You would like the solution interval to be short enough so that it tracks changes in the atmospheric phase with high accuracy, but long enough so that you measure phases with good signal-to-noise. Also, ideally you’d like to keep solutions separate for different spws and polarizations. For faint sources when you need to boost SNR, however, it may be necessary to average over these parameters to achieve good solutions.
Solint Values: In gaincal, the parameter ’solint’ determines the time interval over which gaincal will derive phase solutions. Ideally this should be an integer multiple of your integration time (i.e. if your integration time is 3s, your solint values might be solint=3s, solint=6s, solint=9s, etc.). Solint can range from ‘int’ at minimum (i.e., ‘integration,’ your integration time for a single integration) to ‘inf’ at maximum (i.e. ‘infinity,’ which is not actually infinity but rather the maximum time interval allowed.). If you have combine=‘’ set, setting ‘inf’ will be equivalent to combining all integrations within a single scan, but will not combine across scans (i.e. if your integration time is 3s, and each scan was 2 minutes long, setting solint=‘inf’ is equivalent to setting solint=‘120s’). If you set combine=‘scan,’ the effective value of solint=‘inf’ will likewise increase.
Gaintype: ‘gaintype’=‘G’ will cause gaincal to derive solutions for each polarization independently. This becomes more important if you have a polarized source or a source whose polarization state you do not know. If your source is unpolarized, it is still a good idea to use ‘gaintype=G’ if you can, as this will yield the most accurate solutions. However, if you need to increase the S/N of your solutions, ‘calmode’=‘T’ will combine the data across polarizations and derive a single solution for both.
In the gaincal example above, the first choice of solint is entirely arbitrary. Try it and see what you get. Our goal is to have no failed solutions at all, and to have good S/N on the solutions we do get. (Always S/N > 3, but ideally S/N>5 or better.)
Try playing around with different solution intervals or averaging options. Bear in mind that you want the shortest possible interval while also retaining separate SPW and polarizations. However, none of this helps you if you don't get good solutions. So you generally will experiment with the following options: (1) combine="scan" or "spw" to allow solutions to cross SPW/scan boundaries, or you can do both using combine="scan,spw"; (2) increase solint to set the solution interval; and (3) toggling gaintype between "G" and "T" (the former generates solutions independently for each polarization, and the latter averages two polarizations before determining the solutions).
It maybe helpful to graph the signal-to-noise ratio (SNR) vs. time or the phase vs. time for different settings using plotms. Note the differences in the SNR for different solint values.
# In CASA
plotms(vis='phase.cal', xaxis='time', yaxis='SNR')
# In CASA
plotms(vis='phase.cal', xaxis='time', yaxis='phase')
Plot the resulting solutions. We are finding nontrivial, though not enormous, solutions (a few 10s of degrees) with the two correlations tracking one another pretty well. If the data were already perfectly calibrated, these values would solve to be zero.
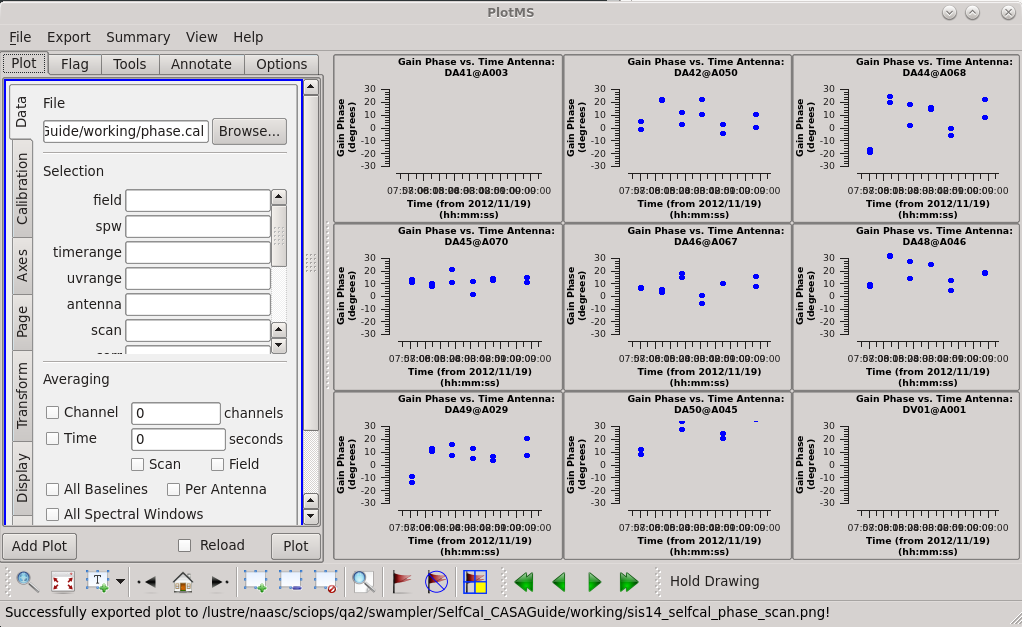
# In CASA
plotms(vis="phase.cal",
xaxis="time",
yaxis="phase",
gridrows=3,
gridcols=3,
iteraxis="antenna",
plotrange=[0,0,-30,30],
coloraxis="corr",
titlefont=7,
xaxisfont=7,
yaxisfont=7,
plotfile="sis14_selfcal_phase_scan.png",
showgui = True)
We are happy with this solution. So let's apply it to the data using applycal. We only care about field 5 (the science target).
# In CASA
applycal(vis="sis14_twhya_calibrated_flagged.ms",
field="5",
gaintable=["phase.cal"],
interp="linear")
At this point the self-calibrated data are stored in the MS in the "corrected data" column. Because we will want to try more rounds of self calibration, it's often useful (though not strictly necessary) at this point to split out the corrected data into a new data set. If you are restarting this tutorial, you need to first delete the output .ms and .flagversions file.
# In CASA
os.system("rm -rf sis14_twhya_selfcal.ms sis14_twhya_selfcal.ms.flagversions")
split(vis="sis14_twhya_calibrated_flagged.ms",
outputvis="sis14_twhya_selfcal.ms",
datacolumn="corrected")
Now clean the self-calibrated data. Again, clean until the residuals on TW Hydra resemble those in the surrounding image.
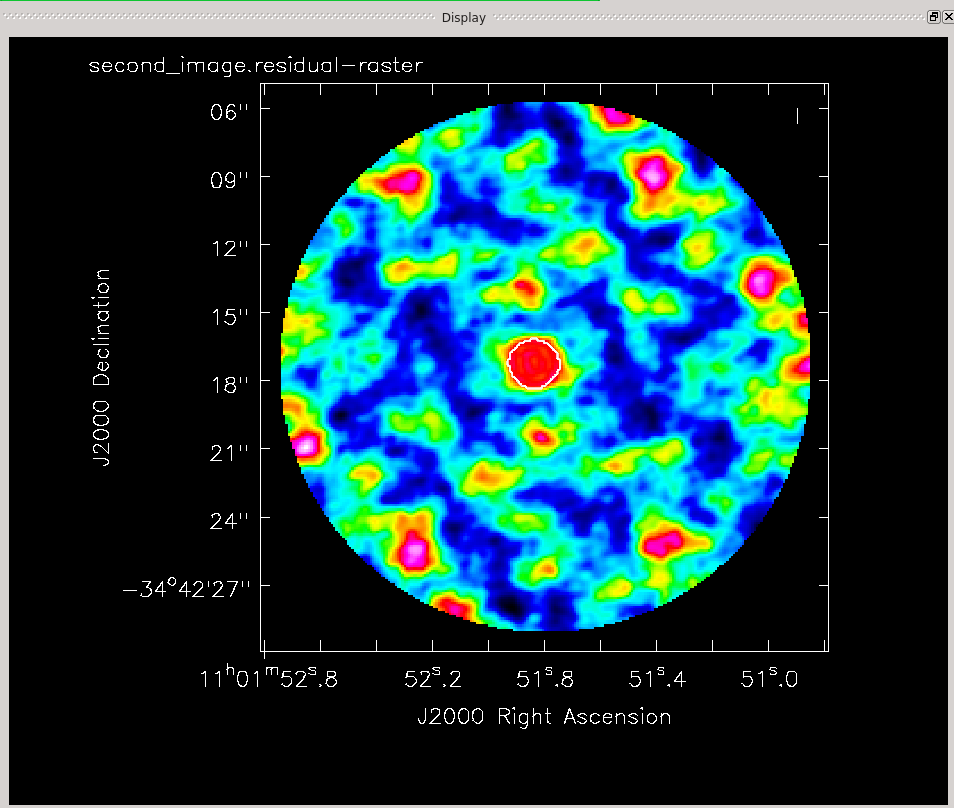
# In CASA
os.system('rm -rf second_image.*')
tclean(vis='sis14_twhya_selfcal.ms',
imagename='second_image',
field='5',
spw='',
specmode='mfs',
deconvolver='hogbom',
nterms=1,
gridder='standard',
imsize=[250,250],
cell=['0.1arcsec'],
weighting='natural',
threshold='0mJy',
interactive=True,
niter=5000,
savemodel='modelcolumn')
Image Statistics: Beam 0.639", 0.494", -65.483°, RMS = 5.86 mJy
The residuals do look better this time around. Run the viewer and compare the first and second images. You should see a noticeable improvement in the noise and some improvement in the signal, so that the overall signal-to-noise (dynamic range) is much improved.
This second clean also produces a model (if the savemodel parameter is set!), hopefully a mildly better one this time.
Now we will run a second round of phase-only self calibration using the improved model.
# In CASA
os.system("rm -rf phase_2.cal")
gaincal(vis="sis14_twhya_selfcal.ms",
caltable="phase_2.cal",
field="5",
solint="170s",
calmode="p",
refant="DV22",
gaintype="G")
This time we see a number of failed solutions that gaincal has flagged due to insufficient signal to noise (compared to the threshold set by minSNR). A small number of failed solutions may be expected depending on the solution interval, especially for more extended antennas in the configuration, although ideally you will find a solint that gives you no failed solutions. Failed solutions mean that those data will get flagged (i.e. no longer used) automatically. It is important to take into account how the resultant flagged baselines affect the beam size and image fidelity after each gaincal iteration.
Let's plot the calibration table again. At this point, we see much smaller phase scatter relative to the model, so we don't expect more phase-only self calibration to do much.
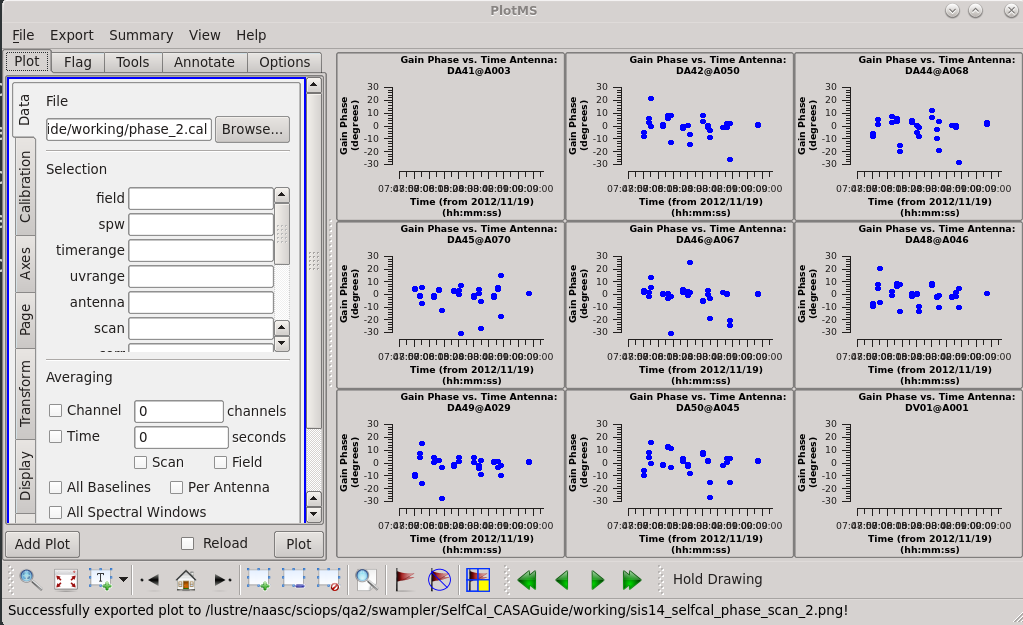
# In CASA
plotms(vis="phase_2.cal",
xaxis="time",
yaxis="phase",
gridrows=3,
gridcols=3,
iteraxis="antenna",
plotrange=[0,0,-30,30],
coloraxis="corr",
titlefont=7,
xaxisfont=7,
yaxisfont=7,
plotfile="sis14_selfcal_phase_scan_2.png",
showgui = True)
Apply the solutions again:
# In CASA
applycal(vis="sis14_twhya_selfcal.ms",
field="5",
gaintable=["phase_2.cal"],
interp="linear")
Split the data off again. Here you can see the work flow for heavily iterative self-calibration. We progressively calibrate, split.
# In CASA
os.system("rm -rf sis14_twhya_selfcal_2.ms sis14_twhya_selfcal_2.ms.flagversions")
split(vis="sis14_twhya_selfcal.ms",
outputvis="sis14_twhya_selfcal_2.ms",
datacolumn="corrected")
Clean a third time.
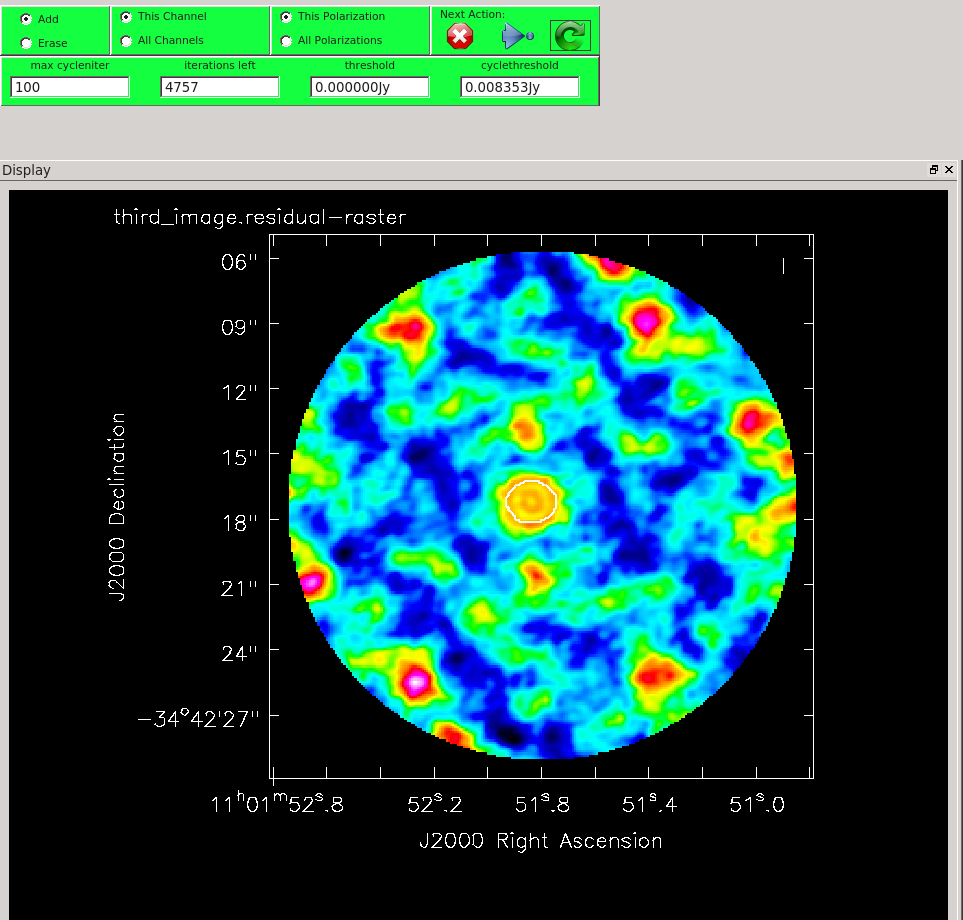
# In CASA
os.system('rm -rf third_image.*')
tclean(vis='sis14_twhya_selfcal_2.ms',
imagename='third_image',
field='5',
spw='',
specmode='mfs',
deconvolver='hogbom',
nterms=1,
gridder='standard',
imsize=[250,250],
cell=['0.1arcsec'],
weighting='natural',
threshold='0mJy',
interactive=True,
niter=5000,
savemodel='modelcolumn')
Image Statistics: Beam 0.691", 0.549", -62.883°, RMS = 4.98 mJy
Run a third round of phase-only self calibration using the improved model.
# In CASA
os.system("rm -rf amp.cal")
gaincal(vis="sis14_twhya_selfcal_2.ms",
caltable="phase_3.cal",
field="5",
solint="30s",
calmode="p",
refant="DV22",
gaintype="T")
# Plot the amplitude solutions.
plotms(vis="phase_3.cal",
xaxis="time",
yaxis="phase",
gridrows=3,
gridcols=3,
iteraxis="antenna",
plotrange=[0,0,-30,30],
coloraxis="corr",
titlefont=7,
xaxisfont=7,
yaxisfont=7,
plotfile="sis14_selfcal_phase_scan_3.png",
showgui = True)
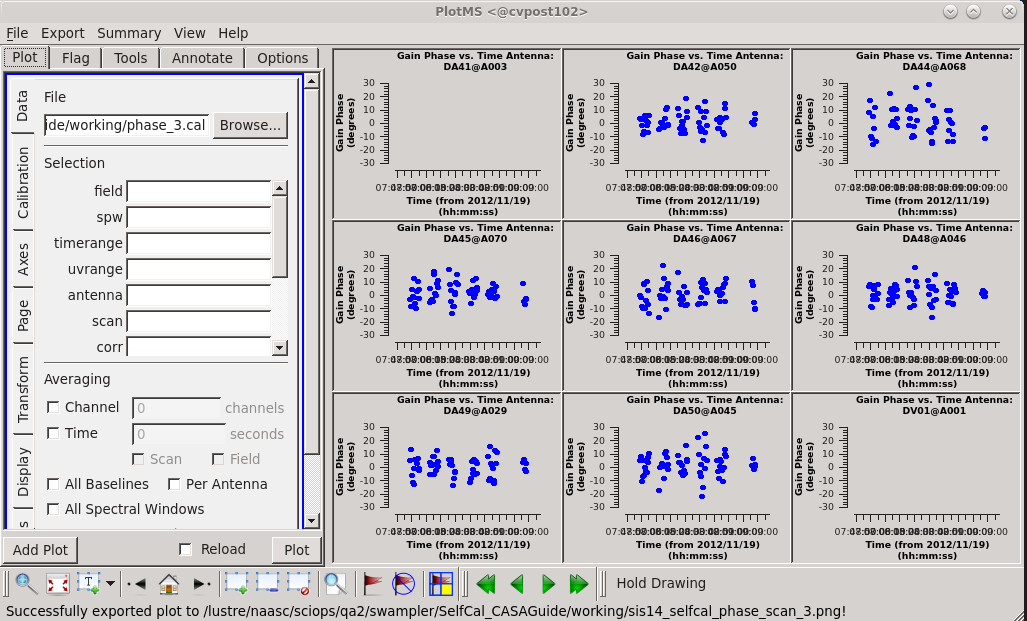
Apply the solutions again:
# In CASA
applycal(vis="sis14_twhya_selfcal_2.ms",
field="5",
gaintable=["phase_3.cal"],
interp="linear")
Split the data off again:
# In CASA
os.system("rm -rf sis14_twhya_selfcal_3.ms sis14_twhya_selfcal_3.ms.flagversions")
split(vis="sis14_twhya_selfcal_2.ms",
outputvis="sis14_twhya_selfcal_3.ms",
datacolumn="corrected")
Clean for a fourth time.
# In CASA
os.system('rm -rf fourth_image.*')
tclean(vis='sis14_twhya_selfcal_3.ms',
imagename='fourth_image',
field='5',
spw='',
specmode='mfs',
deconvolver='hogbom',
nterms=1,
gridder='standard',
imsize=[250,250],
cell=['0.1arcsec'],
weighting='natural',
threshold='0mJy',
interactive=True,
niter=5000)
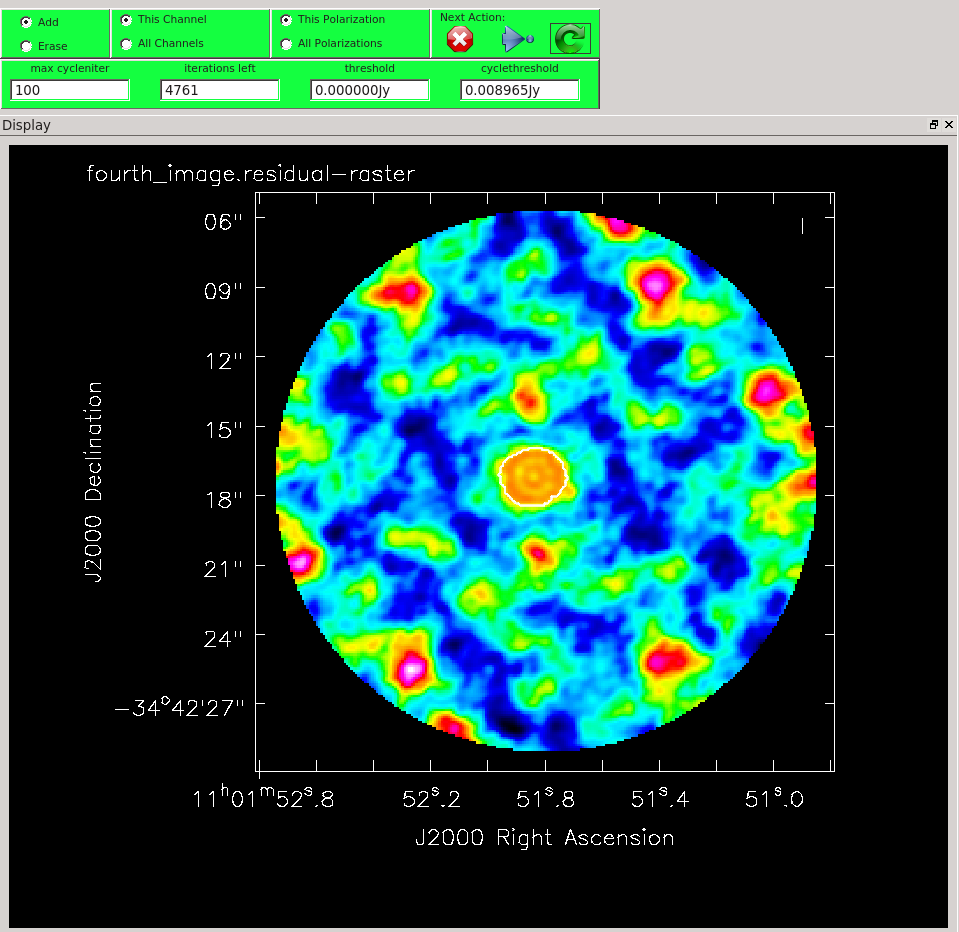
Image Statistics: Beam 0.722", 0.565", -58.463°, RMS = 4.88 mJy
The improvement is really marginal at this point. Confident that we have done what we can on the phase, we can experiment with amplitude self calibration. This is potentially dangerous as it has much more potential to change the characteristics of the source than phase self-calibration. We mitigate this somewhat by setting solnorm=True, so that the solutions are normalized.
In many cases, it would be perfectly fine to stop self-calibrating once we are satisfied with our phase-only self-calibration solutions. In this case, we will move on to demonstrating amplitude+phase self-cal. This type of self-cal is potentially dangerous as it has much more potential to change the characteristics of the source than phase self-calibration. We mitigate this somewhat by setting solnorm=True, so that the solutions are normalized.
os.system("rm -rf amp.cal")
gaincal(vis='sis14_twhya_selfcal_3.ms',
caltable="amp.cal",
field="5",
solint="inf",
calmode="ap",
refant="DV22",
gaintype="G",
solnorm=True)
Note that we have increased our solint back to ’inf.’ This is common for amplitude self-cal: you will want a solint for the amplitude self-cal that is larger than the solint for your best round of phase-only self-cal. We have also added the line ’gaintable=...’ This is because we don’t want to let ap self-cal have too many degrees of freedom. Instead, we force it to use our phase-only solutions first, before it is allowed to calculate amplitude+phase solutions.
Plot the calibration table again:
plotms(vis="amp.cal",
xaxis="time",
yaxis="amp",
gridrows=3,
gridcols=3,
iteraxis="antenna",
plotrange=[0,0,0,0],
coloraxis="corr",
titlefont=7,
xaxisfont=7,
yaxisfont=7,
plotfile="sis14_selfcal_amp_scan.png",
showgui = True)
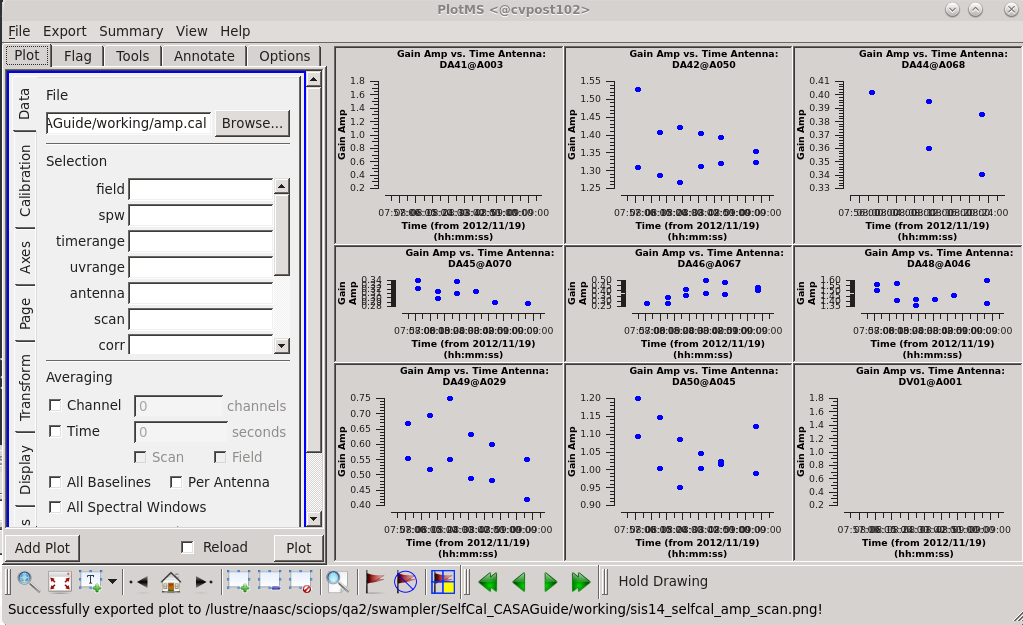
We see a good deal of scatter and some offsets between
correlations. This can be easily visualized within the plotms viewer by selecting the "Display" tab, checking the "colorize" box, and selecting "corr" to colorize the data by correlation. It is at least worth looking at what the effects of applying this will be. So let's apply these solutions on an interim basis.
applycal(vis='sis14_twhya_selfcal_3.ms',
field="5",
gaintable=["amp.cal"],
interp="linear")
At this point the self-calibrated data live in the corrected column. Because we will want to try more rounds of self calibration, it's very useful (though not strictly necessary) at this point to split out the corrected data into a new data set.
os.system("rm -rf sis14_twhya_selfcal4.ms*")
split(vis='sis14_twhya_selfcal_3.ms',
outputvis='sis14_twhya_selfcal_4.ms',
datacolumn="corrected")
Clean a fifth time.
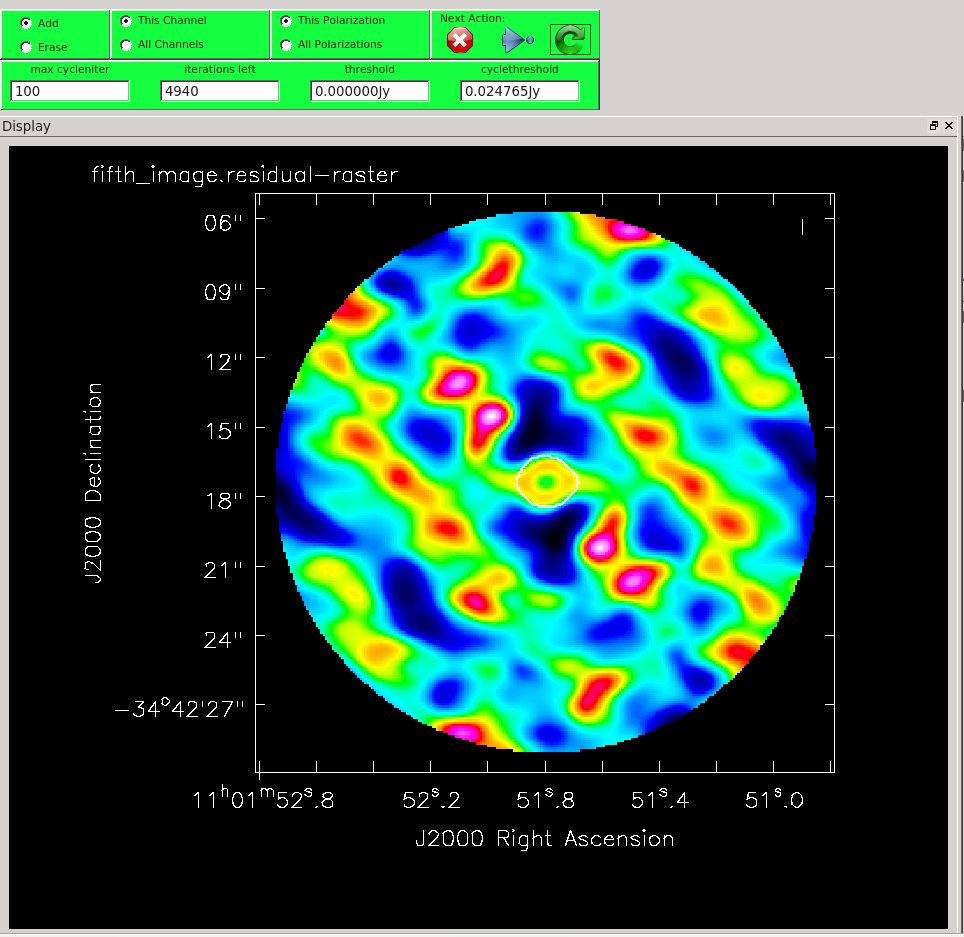
os.system('rm -rf fifth_image.*')
tclean(vis='sis14_twhya_selfcal_4.ms',
imagename='fifth_image',
field='5',
spw='',
specmode='mfs',
deconvolver='hogbom',
nterms=1,
gridder='standard',
imsize=[250,250],
cell=['0.1arcsec'],
weighting='natural',
threshold='0mJy',
interactive=True,
niter=5000,
savemodel='modelcolumn')
Image Statistics: Beam 1.988", 1.154", -88.964°, RMS = 16.3 mJy,
This time, notice from the residuals that you can clean more deeply. After 4 main cycles, the background residuals look very random on the scale of the beam size. This is good!
Compare the fourth and fifth images (you can use an imstat command or draw a box using the viewer and access the statistics panel). The noise level is dramatically better, while the flux has not changed markedly (this is very good, it's what we worry about with amplitude self calibration). By assuming that the previous cleans represent good models we have managed to improve the signal-to-noise on the data by almost an order of magnitude. Not bad!
Whether you are satisfied with the apcal self-calibration in this case or not, it is very important to understand that amplitude+phase self-cal is not always successful, nor is it always necessary. If you can get good solutions with apcal self-calibration, you will likely have improved your S/N ratio by an order of magnitude or more over the non-self- calibrated data. Likewise, if you have had a significant improvement with phase-only self-cal, and you can’t get good solutions for amplitude+phase, that’s okay - you have still significantly improved your data!
In this case the fourth image is our best continuum image. We can use the data set (sis14_twhya_selfcal_3.ms) to proceed with later work. In the next lesson we'll do UV continuum subtraction and line imaging.
(ASIDE: Note that you would need to do the primary beam correction on this data in the same way as you corrected the previous continuum image before making science measurements).