EVLA spectral line IRC10216: Difference between revisions

From CASA Guides
Jump to navigationJump to search
← Older edit
Cbrogan (talk | contribs)
operators
2,345 edits
No edit summary
Cbrogan (talk | contribs)
operators
2,345 edits
 
(157 intermediate revisions by 2 users not shown)
Line 1: Line 1:
[[Category:EVLA]][[Category:Calibration]][[Category:Spectral Line]]
[[Category:EVLA]][[Category:Calibration]][[Category:Spectral Line]]
<pre style="background-color: #FFFF00;">
This tutorial is under construction. There are several things still to be added
in addition to overall polish and further annotation:
* screen captures of task inputs
* more about cleaning in general
* more on image analysis
* multiscale clean maybe
For the time being (until release candidate is built) you want to run this on casapy-test
</pre>


== Overview ==
== Overview ==
Summer school data on IRC+10216. One subband was observed in each of two basebands, the subbands were centered on the HC3N and SiS lines near 36 GHz. Data were loaded with importevla, zero and shadowed data were flagged. Then  
This tutorial describes the data reduction for two spectral lines observed toward the AGB star IRC+10216. This carbon star, which is a few times more massive than our sun, is nearing the end of its life and is thought to be in the process of forming a planetary nebula.
the data were split averaging to 10 seconds and selecting only antennas with a Ka-band receiver, and the spws with Ka-band data.
 
In this EVLA OSRO1 mode observation one subband was observed in each of two basebands, the subbands were centered on the HC3N and SiS lines near 36 GHz. The raw data were loaded into CASA with [[importevla]], where zero and shadowed data were flagged. Then the data were "[[split]]", so we could average from the native 1 second integrations to 10 seconds, select only antennas with Ka-band receivers, and select only spectral windows (called spw in CASA) with Ka-band data. This produces a significantly smaller dataset for processing.
 
The post-split averaged data can be downloaded from http://casa.nrao.edu/Data/EVLA/IRC10216/day2_TDEM0003_10s_norx.tar


<pre style="background-color: #E0FFFF;">
<pre style="background-color: #E0FFFF;">
Line 14: Line 30:
</pre>
</pre>


==Initial Flagging and Inspection==
==Initial Inspection and Flagging==


<source lang="python">
<source lang="python">
Line 20: Line 36:
listobs(vis='day2_TDEM0003_10s_norx')
listobs(vis='day2_TDEM0003_10s_norx')
</source>
</source>
Below we have cut and pasted the most relevant output from the logger.


<pre style="background-color: #fffacd;">
<pre style="background-color: #fffacd;">
Line 79: Line 97:
[[Image:Ant_locations.png|thumb|Antenna locations from running plotants ]]
[[Image:Ant_locations.png|thumb|Antenna locations from running plotants ]]
Look at a graphical plot of the antenna locations and save hardcopy
Look at a graphical plot of the antenna locations and save hardcopy
in case you want it later.
in case you want it later. This will be useful for picking a reference antenna --
typically a good choice is an antenna close to the center of the array. Unless it
shows problems after inspection of the data, we provisionally chose ea02.


[[Image:plotallfields.png|thumb|Result of plotms after selecting colorize by field]]
[[Image:elevationvstime.png|thumb|Elevation as a function of time (after selecting colorize by field).]]
<source lang="python">
<source lang="python">
# In CASA
# In CASA
Line 87: Line 107:
</source>
</source>


Next, let's look at the elevation as a function of time for all sources. It's not the case for these data, but if the elevation is very low (usually at start or end of track) you may want to flag. Also, how near in elevation your flux calibrator is to your target will impact your ultimate absolute flux calibration accuracy. Unfortunately, the target and flux calibrator are not particularly well-matched for this observation, as y ou can show by plotting the elevation for each source:
<source lang="python">
# In CASA
plotms(vis='day2_TDEM0003_10s_norx',
      xaxis='time',yaxis='elevation',correlation='RR,LL',
      avgchannel='64',spw='0:4~60')
</source>
Thus we are strongly dependent on the opacity and gaincurve corrections to get the flux scale right for these data. (This is something to keep in mind when planning observations!)
[[Image:plotallfields.png|thumb|Result of plotms after selecting colorize by field]]
[[Image:Zoom1_mark.png|thumb|Zooming in and marking region (hatched box)]]
[[Image:Zoom1_mark.png|thumb|Zooming in and marking region (hatched box)]]
Next,let's look at all the source amplitudes as a function of time.
<source lang="python">
<source lang="python">
# In CASA
# In CASA
Line 95: Line 131:
</source>
</source>


Select the "Display" tab and colorize by field.  
Select the "Display" tab and colorize by field, and click Plot button.  
 
 
Now zoom in on the region very near zero amplitude for sources J0954+1743 and IRC+10216. To zoom, select the
Zoom tool in lower left corner of  the [[plotms]] GUI, then you can left click to draw a box.
Look for the low values (you may want to zoom a few times to really see the suspect points clearly). Now use the Mark Region and Locate buttons (located along the bottom of the GUI) to see which antenna is causing problems. Since all the "located" baselines include ea12, this is the responsible antenna.
 
<pre style="background-color: #98FB98;">
IMPORTANT NOTES ON PLOTMS:
 
* When using the locate button it is important to have only selected a modest number
of points with the mark region tool (see example of marked region in the thumnail),
otherwise the response will be very slow and possibly hang the tool
(all of the information will be output to your terminal window, not the logger).
 
* Throughout the tutorial, when you are done marking/locate use the Clear Regions
tool to get rid of the marked box before plotting other things.
 
* After flagdata command flagging, you have to force a complete reload of the cache
to look at the same plot again with the new flags applied. To do this change anything
in the plotms GUI (the colorize parameter, antenna, spw, anything) and hit the
plot button.
 
* If the plotms tool does get hung during a plot try clicking the cancel button on the
load progress GUI, and/or if you see a "table locked" message try typing
clearstat on the CASA command line.
 
* Occasionally plotms will get into a strange state that you cannot clear from inside.
We are working on these issues, but for now, when all else fails, exit from casapy and
restart. 


Now zoom in on the region near zero for sources J0954+1743 and IRC+10216
</pre>
Look for the low values. Use the Mark and Locate buttons to see which antenna it is: ea12
 
Now zoom further to see the time range: 03:41:00~04:10:00  
Now click the unmark region button, and then go back to the zoom button to zoom in further to note exactly what the time range is: 03:41:00~04:10:00.


Check the other sideband by changing spw to 1:4~60. You will have to
Check the other sideband by changing spw to 1:4~60. You will have to
rezoom. If you have trouble click on Mark icon and then back to
rezoom. If you have trouble, click on the Mark icon and then back to
zoom.  In spw=1, ea07 is bad from the beginning until after next
zoom.  In spw=1, ea07 is bad from the beginning until after next
pointing run: 03:21:40~04:10:00
pointing run: 03:21:40~04:10:00.  To see this, compare the amplitudes when antenna is set to 'ea07' and when it is set to one of the other antennas, such as 'ea08'.


Now try setting !ea07 in the antenna parameter, this removes ea07
If you set antenna to 'ea12' and zoom in on this intial timerange, you can also see that ea12 is bad during the same time range as for spw 0.  You can also see this by entering '!ea07' for antenna, which removes ea07 from the plot (in CASA selection, ! deselects).
from the plot allowing you to see that ea12 is also bad during the
same time range as for spw 0


We can set up a flagging command to get both bad antennas for the
We can set up a flagging command to get both bad antennas for the
appropriate time/spw
appropriate time and spw:


<source lang="python">
<source lang="python">
Line 122: Line 185:
</source>
</source>


Note because timerange is set, the field parameter is not really
Note that because the chosen timerange is limited to fields 2 and 3,the field parameter is not really
needed here -- the time range is limited to these fields, but
needed; however, flagdata will run fastest if you put as many constraints as possible.
flagdata will run fastest if you put as many constraints as
possible.


Now remove the !ea07 from antenna and replot both spw, zooming in to
Now remove the !ea07 from antenna and replot both spw, zooming in to
be sure that all obviously low points are gone. Also zoom in and
be sure that all obviously low points are gone. Also zoom in and
check 3C286, J1229+0203 is already obvious because it is so bright.  
check 3C286 (J1229+0203 is already obvious because it is so bright!).  


[[Image:IRC10216_uvdist1.png|thumb|Amplitude vs. uv-distance for IRC+10216, both spw (after colorize by spw)]]
[[Image:IRC10216_uvdist1.png|thumb|Amplitude vs. uv-distance for IRC+10216, both spw (after colorize by spw)]]
Lets look more closely at IRC+10216
 
Lets look more closely at IRC+10216:


<source lang="python">
<source lang="python">
Line 141: Line 203:
</source>
</source>


Go to the "display" tab and chose colorize by spw. You can see a
Go to the "display" tab and choose colorize by spw. You can see a
that there are some noisy high points. But now try
that there are some noisy high points. But now try


Line 151: Line 213:
</source>
</source>


Most of the high points on IRC+10216 are due to large scale emission
Most of the high points on IRC+10216 are due to large scale emission on short baselines, but there is still some noisy stuff -- for a target like this with extended emission its best to wait until later to decide what to do about it. We will not be able to get adequate calibration for antennas that are truly bad (even if they don't stand out here) so these will be obvious later.
on short baselines, but there is still some noisy stuff -- do a
locate, to see that antenna ea21 looks suspicious, you can set
antenna=!ea21 to see the effect of removing it.  The rest of the
scatter does not appear associated with a particular antenna or
time. We will wait until later to decide what to do about it. If its
really bad, it we won't be able to get a good calibration for it.


               
==Set the Flux Calibrator==
==Set the Flux Calibrator==
Next, we tell CASA to look up the appropriate fluxes for 3C286:


<source lang="python">
<source lang="python">
# In CASA
# In CASA
setjy(vis='day2_TDEM0003_10s_norx',field='7',spw='0',
setjy(vis='day2_TDEM0003_10s_norx',field='7',spw='0~1',
       modimage='/usr/lib64/casapy/data/nrao/VLA/CalModels/3C286_K.im')
       modimage='/usr/lib64/casapy/data/nrao/VLA/CalModels/3C286_K.im')
</source>
</source>


<source lang="python">
<pre style="background-color: #fffacd;">
# In CASA
The logger output for each spw is:
setjy(vis='day2_TDEM0003_10s_norx',field='7',spw='1',
setjy   J1331+3030  spwid=  0  [I=1.692, Q=0, U=0, V=0] Jy, (Perley-Taylor 99)
      modimage='/usr/lib64/casapy/data/nrao/VLA/CalModels/3C286_K.im')
setjy   J1331+3030  spwid=  1  [I=1.695, Q=0, U=0, V=0] Jy, (Perley-Taylor 99)
</pre>
 
The modimage location is appropriate for running CASA at the AOC. If you are running elsewhere (laptop or Mac), in a terminal type
 
<source lang='bash'>
# in a terminal, outside of CASA:
locate 3C286_K.im  
</source>
</source>


<pre style="background-color: #E0FFFF;">
to find where the models live (the models are always shipped with CASA).
The logger output for spw=0 is:
setjy J1331+3030  spwid=  0  [I=1.692, Q=0, U=0, V=0] Jy, (Perley-Taylor 99)
setjy Using model image /usr/lib64/casapy/data/nrao/VLA/CalModels/3C286_K.im
setjy The model image's reference pixel is 0.00188929 arcsec from J1331+3030's phase center.
setjy Scaling model image to I=1.69182 Jy for visibility prediction.
</pre>


==Bandpass==
==Bandpass==


Before doing the bandpass we need to inspect phase and amplitude
Before determining the bandpass solution, we need to inspect phase and amplitude
variations with time and frequency on the bandpass calibrator to
variations with time and frequency on the bandpass calibrator to
decide how best to proceed. We limit the number of antennas to make
decide how best to proceed. We limit the number of antennas to make
Line 196: Line 254:
       avgtime='1e8',spw='0:4~60',antenna='ea02&ea23')
       avgtime='1e8',spw='0:4~60',antenna='ea02&ea23')
</source>
</source>
 
[[Image:Nobandpass_phase.png|thumb|Phase as a function of channel for ea02 (after colorize by Antenna2, and Custom and upping "Style" to 3.)]]
The phase variation is modest ~10 degrees.  Now expand to all
The phase variation is modest ~10 degrees.  Now expand to all antennas with ea02 and
#antennas with ea02
select colorize by Antenna2, then hit the "Plot" button.


<source lang="python">
<source lang="python">
Line 206: Line 264:
       avgtime='1e8',spw='0:4~60',antenna='ea02')
       avgtime='1e8',spw='0:4~60',antenna='ea02')
</source>
</source>
 
[[Image:Nobandpass_phasetime.png|thumb|Phase as a function of time for ea02 (after colorize by Antenna2, and Custom and upping "Style" to 3.)]]
Go to the "display" tab and chose colorize by antenna2. From this
Go to the "display" tab and chose colorize by antenna2. From this
you can see that the phase variation across the bandpass is
you can see that the phase variation across the bandpass is
Line 242: Line 300:
to noise of the phase vs. time solution. If the phase variation as a
to noise of the phase vs. time solution. If the phase variation as a
function of channel is larger you may need to use only a few
function of channel is larger you may need to use only a few
channels to delay-based closure errors from averaging over
channels to prevent introducing delay-based closure errors as can happen from averaging over
non-bandpass corrected channels.
non-bandpass corrected channels with large phase variations.




Line 249: Line 307:
solution on the integration time of 10 seconds (solint='int').
solution on the integration time of 10 seconds (solint='int').


[[Image:Prebp_phasecal2.png|thumb|Phase only calibration before bandpass. The 4 lines are both polarizations in both spw, unfortunately two of them get the same color green at the moment.]]
<source lang="python">
<source lang="python">
# In CASA
# In CASA
gaincal(vis='day2_TDEM0003_10s_norx',caltable='bpphase.gcal',
gaincal(vis='day2_TDEM0003_10s_norx',caltable='bpphase.gcal',
         field='5',spw='0~1:20~40',
         field='5',spw='0~1:20~40',
         refant='ea02',calmode='p',solint='int',minsnr=2.0)
         refant='ea02',calmode='p',solint='int',minsnr=2.0,
        opacity=0.03,gaincurve=T)
</source>
</source>
Plot the solutions


<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotcal(caltable='bpphase.gcal',xaxis='time',yaxis='phase',
plotcal(caltable='bpphase.gcal',xaxis='time',yaxis='phase',
         iteration='antenna',subplot=331)
         iteration='antenna',subplot=331,plotrange=[0,0,-180,180])
</source>
</source>


After the first set of plots appear, push the "Next" button on the
GUI to see the next set of antennas.


Next we can apply this phase solution on the fly while determining
Next we can apply this phase solution on the fly while determining
the bandpass solutions, solint='inf' will derive a one bandpass
the bandpass solutions on the timescale of the bandpass calibrator scan (solint='inf').
solution for the whole J1229+0203 scan. If there had been two
 
observations of the bandpass calibration for example, this command
[[Image:Bandpass_amp.png|thumb|Amplitude Bandpass solutions]]
would do one bandpass for each scan, if combine='' (combine='scan'
[[Image:Bandpass_phase1.png|thumb|Phase Bandpass solutions]]
is the default).


<source lang="python">
<source lang="python">
Line 274: Line 337:
bandpass(vis='day2_TDEM0003_10s_norx',caltable='bandpass.bcal',field='5',
bandpass(vis='day2_TDEM0003_10s_norx',caltable='bandpass.bcal',field='5',
         refant='ea02',solint='inf',solnorm=T,
         refant='ea02',solint='inf',solnorm=T,
        gaintable=['bpphase.gcal'],spwmap=[[]],
        opacity=0.03,gaincurve=T)
</source>
</source>
'''A few words about solint and combine:'''
The use of  solint='inf' in [[bandpass]] will derive one bandpass
solution for the whole J1229+0203 scan. Note that if there had been two observations of the bandpass calibrator (for example), this command would have combined the data from both scans to form one bandpass solution, because the default of the combine parameter '''for [[bandpass]]''' is combine='scan'. To solve for one bandpass for each bandpass calibrator scan you would also need to include combine='''' '''' in the bandpass call. In all calibration tasks, regardless of solint, scan boundaries are only crossed when combine='scan'. Likewise, field (spw) boundaries are only crossed if combine='field' (combine='spw'), the latter two are not generally good ideas for bandpass solutions. 
Plot the solutions, amplitude and phase:


<source lang="python">
<source lang="python">
# In CASA      
# In CASA
gaintable=['bpphase.gcal'],spwmap=[[]])
plotcal(caltable='bandpass.bcal',xaxis='chan',yaxis='amp',
        iteration='antenna',subplot=331)
</source>
</source>
<source lang="python">
# In CASA
plotcal(caltable='bandpass.bcal',xaxis='chan',yaxis='phase',
        iteration='antenna',subplot=331)
</source>
Note that phases on ea12 look noiser than on other antennas. This
jitter could indicate bad pointing; note that ea12 had just come back in
the array.


This step isn't necessary from a calibration perspective, but if you
This step isn't necessary from a calibration perspective, but if you
Line 286: Line 369:
corrected data on-the-fly without this applycal step. Later applycals
corrected data on-the-fly without this applycal step. Later applycals
will overwrite this one, so no need to worry.
will overwrite this one, so no need to worry.
[[Image:Applybandpass_phase.png|thumb|Phase as a function of channel, plotting the corrected data (after colorize by Antenna2, and Custom and upping "Style" to 3.)]]


<source lang="python">
<source lang="python">
# In CASA
applycal(vis='day2_TDEM0003_10s_norx',field='5',
applycal(vis='day2_TDEM0003_10s_norx',field='5',
         gaintable=['bandpass.bcal'],
         gaintable=['bandpass.bcal'],
         spwmap=[[]],gainfield=['5'])
         spwmap=[[]],gainfield=['5'],
        opacity=0.03,gaincurve=T)
</source>
</source>


<source lang="python">
<source lang="python">
# In CASA
plotms(vis='day2_TDEM0003_10s_norx',field='5',
plotcal(caltable='bandpass.bcal',xaxis='chan',yaxis='amp',
      xaxis='channel',yaxis='phase',ydatacolumn='corrected',
        iteration='antenna',subplot=331)
      correlation='RR',
      avgtime='1e8',spw='0:4~60',antenna='ea02')
</source>
</source>


<source lang="python">
<source lang="python">
# In CASA
plotms(vis='day2_TDEM0003_10s_norx',field='5',
plotcal(caltable='bandpass.bcal',xaxis='chan',yaxis='phase',
      xaxis='channel',yaxis='amp',ydatacolumn='corrected',
        iteration='antenna',subplot=331)
      correlation='RR',
      avgtime='1e8',spw='0:4~60',antenna='ea02')
</source>
</source>


Note that phases on ea12 look noiser than other antennas. This
Note that the phase and amplitude as a function of channel are very flat now.
jitter could indicate bad pointing -- note ea12 had just come back in
the array.


==Gain Calibration==
==Gain Calibration==
Now that we have a bandpass solution to apply we can solve for the antenna-based phase and amplitude gain calibration. Since the phase changes on a much shorter timescale than the amplitude, we will solve for them separately. In particular, if the phase changes significantly over a scan time, the amplitude would be decorrelated, if the un-corrected phase were averaged over this timescale. Note that we re-solve for the gain solutions of the bandpass calibrator, so we can derive new solutions that are corrected for the bandpass shape. Since the bandpass calibrator will not be used again, this is not strictly necessary, but is useful to check its calibrated flux density for example.


<source lang="python">
<source lang="python">
Line 317: Line 404:
         field='2,5,7',spw='0~1:4~60',
         field='2,5,7',spw='0~1:4~60',
         refant='ea02',calmode='p',solint='int',minsnr=2.0,
         refant='ea02',calmode='p',solint='int',minsnr=2.0,
         gaintable=['bandpass.bcal'],spwmap=[[]])
         gaintable=['bandpass.bcal'],spwmap=[[]],
        opacity=0.03,gaincurve=T)
</source>
</source>
[[Image:allcal_phaseint2.png|thumb|Plot of phase solutions on an integration time.]]
Here solint='int' coupled with calmode='p' will derive a single phase solution for each 10 second integration. Note that the bandpass table is applied on-the-fly before solving for the phase solutions, however the bandpass is NOT applied to the data permanently until applycal is run later on.
Now look at the phase solution, and note the obvious scatter within a scan time.


<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotcal(caltable='intphase.gcal',xaxis='time',yaxis='phase',
plotcal(caltable='intphase.gcal',xaxis='time',yaxis='phase',
         iteration='antenna',subplot=331)
         iteration='antenna',subplot=331,plotrange=[0,0,-180,180])
</source>
</source>


Although solint='int' (i.e. the integration time of 10 seconds) is the best choice to apply before for solving for the amplitude solutions, it is not a good idea to use this to apply to the target. This is because the phase-scatter within a scan can dominate the interpolation between calibrator scans. Instead, we also solve for the phase on the scan time, solint='inf' (but combine='''' '''', since we want one solution per scan) for application to the target later on. '''Unlike the bandpass task,''' for gaincal, the default of the combine parameter is combine='''' ''''.
[[Image:allcal_phaseinf2.png|thumb|Plot of phase solutions on a scan time.]]
<source lang="python">
<source lang="python">
# In CASA
# In CASA
Line 331: Line 426:
         field='2,5,7',spw='0~1:4~60',
         field='2,5,7',spw='0~1:4~60',
         refant='ea02',calmode='p',solint='inf',minsnr=2.0,
         refant='ea02',calmode='p',solint='inf',minsnr=2.0,
         gaintable=['bandpass.bcal'],spwmap=[[]])
         gaintable=['bandpass.bcal'],spwmap=[[]],
        opacity=0.03,gaincurve=T)
</source>
</source>


Line 337: Line 433:
# In CASA
# In CASA
plotcal(caltable='scanphase.gcal',xaxis='time',yaxis='phase',
plotcal(caltable='scanphase.gcal',xaxis='time',yaxis='phase',
         iteration='antenna',subplot=331)
         iteration='antenna',subplot=331,plotrange=[0,0,-180,180])
</source>
</source>
Alternatively, one can also run [[smoothcal]] to smooth the solutions derived on the integration time.
Next we apply the bandpass and solint='int' phase-only calibration solutions on-the-fly to derive amplitude solutions.
Here the use of solint='inf', but combine='''' '''' will result in one solution per scan interval.


<source lang="python">
<source lang="python">
Line 345: Line 446:
         field='2,5,7',spw='0~1:4~60',
         field='2,5,7',spw='0~1:4~60',
         refant='ea02',calmode='ap',solint='inf',minsnr=2.0,
         refant='ea02',calmode='ap',solint='inf',minsnr=2.0,
         gaintable=['bandpass.bcal','intphase.gcal'],spwmap=[[],[]])
         gaintable=['bandpass.bcal','intphase.gcal'],spwmap=[[],[]],
        opacity=0.03,gaincurve=T)
</source>
</source>
[[Image:allcal_ampphase.png|thumb|Plot of residual phase solutions on a scan time]]
Now let's look at the resulting phase solutions.  Since we have taken out the phase as best we can by applying the solint='int' phase-only solution, this plot will give a good idea of the residual phase error. If you see scatter of more than a few degrees here, you should consider going back and looking for more data to flag, particularly bad timeranges etc.


<source lang="python">
<source lang="python">
Line 354: Line 459:
</source>
</source>


Indeed, both antenna ea12 (all times) and ea23 (first 1/3 of observation) show particularly large residual phase noise.
[[Image:allcal_amp.png|thumb|Plot of amplitude solutions on a scan time]]
<source lang="python">
<source lang="python">
# In CASA
# In CASA
Line 359: Line 466:
         iteration='antenna',subplot=331)
         iteration='antenna',subplot=331)
</source>
</source>
Note that the amplitude solutions for ea12 are very low; this is another indication that this antenna is dubious.
Next we use the flux calibrator (whose flux density was set in [[setjy]] above) to derive the flux of the other calibrators. Note that the flux table REPLACES the amp.gcal in terms of future application of the calibration to the data, i.e. the flux table contains both the amp.gcal and flux scaling. Unlike the gain calibration steps, this is not an incremental table.


<source lang="python">
<source lang="python">
Line 366: Line 477:
</source>
</source>


 
[[Image:allcal_flux.png|thumb|Plot of flux corrected amplitude solutions.]]
<source lang="python">
It is a good idea to note down for your records the derived flux densities:
# In CASA
plotcal(caltable='flux.cal',xaxis='time',yaxis='amp',
        iteration='antenna',subplot=331)
</source>


<pre style="background-color: #fffacd;">
<pre style="background-color: #fffacd;">
fluxscale Flux density for J0954+1743 in SpW=0 is: 0.274144 +/- #0.00108416 (SNR = 252.862, nAnt= 18)
Flux density for J0954+1743 in SpW=0# is: 0.267699 +/- 0.00103786
fluxscale Flux density for J0954+1743 in SpW=1 is: 0.280975 +/- #0.00107734 (SNR = 260.805, nAnt= 18)
  (SNR = 257.934, nAnt= 19)
fluxscale Flux density for J1229+0203 in SpW=0 is: 30.4866 +/- 0(SNR = inf, nAnt= 18)
Flux density for J0954+1743 in SpW=1# is: 0.279468 +/- 0.000735923
fluxscale Flux density for J1229+0203 in SpW=1 is: 30.1742 +/- 0(SNR = inf, nAnt= 18)
  (SNR = 379.752, nAnt= 19)
Flux density for J1229+0203 in SpW=0# is: 30.5454 +/- 0  
  (SNR = inf, nAnt= 19)
Flux density for J1229+0203 in SpW=1# is: 30.2306 +/- 0  
  (SNR = inf, nAnt= 19)
</pre>
</pre>
Obviously, the signal-to-noise for J1229+0203 can't be infinity! This is just an indication that their is only one scan for this source, and we derived a scan based amplitude solution, so there is no variation to calculate.
Next, check that the flux.cal table looks as expected.


<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotms(vis='day2_TDEM0003_10s_norx',field='5',ydatacolumn='corrected',
plotcal(caltable='flux.cal',xaxis='time',yaxis='amp',
      xaxis='time',yaxis='amp',correlation='RR,LL',
        iteration='antenna',subplot=331)
      avgchannel='64',spw='0:4~60',antenna='')
</source>
</source>


==Applycal and Inspect==
==Applycal and Inspect==
Now we apply the calibration to each source, according to which tables are appropriate, and which source should be used to do that particular calibration. For the calibrators, all bandpass solutions come from the bandpass calibrator (id=5), and the phase and amplitude calibration comes from their own solutions.


<source lang="python">
<source lang="python">
Line 393: Line 509:
applycal(vis='day2_TDEM0003_10s_norx',field='2',
applycal(vis='day2_TDEM0003_10s_norx',field='2',
         gaintable=['bandpass.bcal','intphase.gcal','flux.cal'],
         gaintable=['bandpass.bcal','intphase.gcal','flux.cal'],
         spwmap=[[],[],[]],gainfield=['5','2','2'])
         spwmap=[[],[],[]],gainfield=['5','2','2'],
        opacity=0.03,gaincurve=T)
</source>
</source>


Line 400: Line 517:
applycal(vis='day2_TDEM0003_10s_norx',field='5',
applycal(vis='day2_TDEM0003_10s_norx',field='5',
         gaintable=['bandpass.bcal','intphase.gcal','flux.cal'],
         gaintable=['bandpass.bcal','intphase.gcal','flux.cal'],
         spwmap=[[],[],[]],gainfield=['5','5','5'])
         spwmap=[[],[],[]],gainfield=['5','5','5'],
        opacity=0.03,gaincurve=T)
</source>
</source>


Line 407: Line 525:
applycal(vis='day2_TDEM0003_10s_norx',field='7',
applycal(vis='day2_TDEM0003_10s_norx',field='7',
         gaintable=['bandpass.bcal','intphase.gcal','flux.cal'],
         gaintable=['bandpass.bcal','intphase.gcal','flux.cal'],
         spwmap=[[],[],[]],gainfield=['5','7','7'])
         spwmap=[[],[],[]],gainfield=['5','7','7'],
        opacity=0.03,gaincurve=T)
</source>
</source>
For the target we apply the bandpass from id=5, and the calibration from the gain calibrator (id=2):


<source lang="python">
<source lang="python">
Line 414: Line 535:
applycal(vis='day2_TDEM0003_10s_norx',field='3',
applycal(vis='day2_TDEM0003_10s_norx',field='3',
         gaintable=['bandpass.bcal','scanphase.gcal','flux.cal'],
         gaintable=['bandpass.bcal','scanphase.gcal','flux.cal'],
         spwmap=[[],[],[]],gainfield=['5','2','2'])
         spwmap=[[],[],[]],gainfield=['5','2','2'],
        opacity=0.03,gaincurve=T)
</source>
</source>


Now inspect the corrected data
Now inspect the corrected data:
 
[[Image:applycal_inspect.png|thumb|Plot of calibrated amplitudes over time.]]
<source lang="python">
<source lang="python">
# In CASA
# In CASA
Line 426: Line 548:
</source>
</source>


This source looks good
This plot shows some data deviating from the average amplitudes. Use methods described above to
mark a region for a small number of deviant data points, and click "Locate". You will find that ea12 is responsible.


<source lang="python">
<source lang="python">
Line 435: Line 558:
</source>
</source>


Here we see some problems, with high points. Do some mark regions
Here we see some problems, with high points. Mark some regions
and locate to find out which antennas, which spws. Pay special
and locate in [[plotms]] to find out which antennas and in which spws. Pay special
attention to antennas that shows some dubious behavior from the
attention to antennas that have been called out already as showing some dubious behavior.
start.


What you find is that ea07 which we flagged spw=1 above, is also bad
What you find is that ea07 which we flagged spw=1 above, is also bad for the same timerange in spw=0. This was not obvious in the raw data, because spw=0 was adjusted in the on-line system by a gain attenuator, while spw=1 wasn't. So a lack of power on this antenna can look like very low (and obvious) amplitudes in spw=1 but not for spw=0. Looking carefully you'll see that ea07 is actually pretty noisy throughout.
for the same timerange in spw=0. This was not obvious in the raw
[[Image:ea12.png|thumb|Plot of antenna ea12 by itself]]
data, because spw=0 was adjusted by a gain attenuator, while spw=1
[[Image:ea23.png|thumb|Plot of antenna ea23 by itself]]
wasn't. So a lack of power in spw=1 will look like very low
amplitudes -- not so after the adjustment made to spw=0.


ea12 needs to be flagged completely its just a bit noisy all around.
From the locate we also find that ea12 and ea23 show some high points; to see this, replot baselines using each of them alone:


ea23 is pretty noisy during the first scans between intial and
<source lang="python">
second pointing.
plotms(vis='day2_TDEM0003_10s_norx',field='2',ydatacolumn='corrected',
      xaxis='time',yaxis='amp',correlation='RR,LL',
      avgchannel='64',spw='0:4~60',antenna='ea12')
</source>


Because the target has resolved structure, its best to look at it as
<source lang="python">
a function of uvdistance.
plotms(vis='day2_TDEM0003_10s_norx',field='2',ydatacolumn='corrected',
      xaxis='time',yaxis='amp',correlation='RR,LL',
      avgchannel='64',spw='0:4~60',antenna='ea23')
</source>
 
ea12 needs to be flagged completely its just a bit noisy all around and ea23 is pretty noisy during the first scans between initial and second pointing. Recall that these are antennas we became suspicious of while inspecting the calibration solutions.
 
[[Image:target_uvdist.png|thumb|IRC+12216 as a function of uv-distance (after colorize by Antenna2).]]
Now lets see how the target looks. Because the target has resolved structure, its best to look at it as
a function of uvdistance. We'll go ahead and exclude the three antennas we already know have problems.


<source lang="python">
<source lang="python">
Line 458: Line 590:
plotms(vis='day2_TDEM0003_10s_norx',field='3',ydatacolumn='corrected',
plotms(vis='day2_TDEM0003_10s_norx',field='3',ydatacolumn='corrected',
       xaxis='uvdist',yaxis='amp',correlation='RR,LL',
       xaxis='uvdist',yaxis='amp',correlation='RR,LL',
       avgchannel='64',spw='0:4~60',antenna='')
       avgchannel='64',spw='0:4~60',antenna='!ea07;!ea12;!ea23')
</source>
</source>


in "display" tab chose colorize by antenna2, here you will see that the spikes
in "display" tab choose colorize by antenna2; then you can see that the spikes
are caused by a single antenna. Use, zoom, mark, and locate to see which one.
are caused by a single antenna. Use, zoom, mark, and locate to see which one.
Also look at spw=1.
Also look at spw=1.


Turns out to be ea28, to confirm, replot with antenna=!ea28, and
Turns out to be ea28; to confirm, replot with antenna=!ea28, and


<source lang="python">
<source lang="python">
Line 471: Line 603:
plotms(vis='day2_TDEM0003_10s_norx',field='3',ydatacolumn='corrected',
plotms(vis='day2_TDEM0003_10s_norx',field='3',ydatacolumn='corrected',
       xaxis='uvdist',yaxis='amp',correlation='RR,LL',
       xaxis='uvdist',yaxis='amp',correlation='RR,LL',
      avgchannel='64',spw='0:4~60',antenna='!ea07;!ea12;!ea23;!ea28')
</source>
To see if it's restricted to a certain time
<source lang="python">
# In CASA
plotms(vis='day2_TDEM0003_10s_norx',field='3',ydatacolumn='corrected',
      xaxis='time',yaxis='amp',correlation='RR,LL',
       avgchannel='64',spw='0:4~60',antenna='ea28')
       avgchannel='64',spw='0:4~60',antenna='ea28')
</source>
</source>


Its got issues until 2/3 through. Plot another distant antenna to compare.
 
We will go ahead and flag it all, since its hanging far out on the north
Baselines with ea28 clearly show issues until about two-thirds of the way through the observation.  
Plot another distant antenna to compare. We will go ahead and flag it all, since its hanging far out on the north
arm by itself.
arm by itself.


These data need to be flagged and then all the calibration steps run
The additional data we've identified as bad need to be flagged, and then all the calibration steps will need to be run
again.
again.


Line 486: Line 628:
         field=['',''],
         field=['',''],
         spw=['',''],
         spw=['',''],
         antenna=['ea12,ea28','ea07,ea23'],
         antenna=['ea07,ea12,ea28','ea07,ea23'],
         timerange=['','03:21:40~04:10:00'])
         timerange=['','03:21:40~04:10:00'])
</source>
</source>


==Redo Calibration after more Flagging==
==Redo Calibration after more Flagging==
After flagging, you'll need to repeat the calibration steps above.  Here, we append  _redo to the table names to distinguish them from the first round, in case we want to compare with previous versions.


<source lang="python">
<source lang="python">
Line 496: Line 640:
gaincal(vis='day2_TDEM0003_10s_norx',caltable='bpphase_redo.gcal',
gaincal(vis='day2_TDEM0003_10s_norx',caltable='bpphase_redo.gcal',
         field='5',spw='0~1:20~40',
         field='5',spw='0~1:20~40',
         refant='ea02',calmode='p',solint='int',minsnr=2.0)
         refant='ea02',calmode='p',solint='int',minsnr=2.0,
        opacity=0.03,gaincurve=T)
</source>
</source>


Line 504: Line 649:
         field='5',
         field='5',
         refant='ea02',solint='inf',solnorm=T,
         refant='ea02',solint='inf',solnorm=T,
         gaintable=['bpphase_redo.gcal'],spwmap=[[]])
         gaintable=['bpphase_redo.gcal'],spwmap=[[]],
        opacity=0.03,gaincurve=T)
</source>
</source>


Line 512: Line 658:
         field='2,5,7',spw='0~1:4~60',
         field='2,5,7',spw='0~1:4~60',
         refant='ea02',calmode='p',solint='int',minsnr=2.0,
         refant='ea02',calmode='p',solint='int',minsnr=2.0,
         gaintable=['bandpass_redo.bcal'],spwmap=[[]])
         gaintable=['bandpass_redo.bcal'],spwmap=[[]],
        opacity=0.03,gaincurve=T)
</source>
</source>


Line 520: Line 667:
         field='2,5,7',spw='0~1:4~60',
         field='2,5,7',spw='0~1:4~60',
         refant='ea02',calmode='p',solint='inf',minsnr=2.0,
         refant='ea02',calmode='p',solint='inf',minsnr=2.0,
         gaintable=['bandpass_redo.bcal'],spwmap=[[]])
         gaintable=['bandpass_redo.bcal'],spwmap=[[]],
        opacity=0.03,gaincurve=T)
</source>
</source>


Line 529: Line 677:
         refant='ea02',calmode='ap',solint='inf',minsnr=2.0,
         refant='ea02',calmode='ap',solint='inf',minsnr=2.0,
         gaintable=['bandpass_redo.bcal','intphase_redo.gcal'],
         gaintable=['bandpass_redo.bcal','intphase_redo.gcal'],
         spwmap=[[],[]])
         spwmap=[[],[]],
        opacity=0.03,gaincurve=T)
</source>
</source>
   
   
Line 539: Line 688:


<pre style="background-color: #fffacd;">
<pre style="background-color: #fffacd;">
fluxscale Flux density for J0954+1743 in SpW=0 is: 0.274097 +/- 0.00110645 (SNR = 247.726, nAnt= 18)
Flux density for J0954+1743 in SpW=0 is: 0.279304 +/- 0.00114727 (SNR = 243.452, nAnt= 16)
fluxscale Flux density for J0954+1743 in SpW=1 is: 0.281065 +/- 0.00107598 (SNR = 261.217, nAnt= 18)
Flux density for J0954+1743 in SpW=1 is: 0.287039 +/- 0.00107576 (SNR = 266.824, nAnt= 16)
fluxscale Flux density for J1229+0203 in SpW=0 is: 30.488 +/- 0 (SNR = inf, nAnt= 18)
Flux density for J1229+0203 in SpW=0 is: 30.5932 +/- 0 (SNR = inf, nAnt= 16)
fluxscale Flux density for J1229+0203 in SpW=1 is: 30.1777 +/- 0 (SNR = inf, nAnt= 18)
Flux density for J1229+0203 in SpW=1 is: 30.2475 +/- 0 (SNR = inf, nAnt= 16)
</pre>
</pre>
Feel free to pause here and remake the calibration solution plots from above, just be sure to put in the revised table names.
==Redo Applycal and Inspect==
Now, apply all the new calibrations, which will overwrite the old ones.  These commands are identical to those above, with the exception of the _redo part of each calibration filename.


<source lang="python">
<source lang="python">
Line 549: Line 704:
applycal(vis='day2_TDEM0003_10s_norx',field='2',
applycal(vis='day2_TDEM0003_10s_norx',field='2',
         gaintable=['bandpass_redo.bcal','intphase_redo.gcal','flux_redo.cal'],
         gaintable=['bandpass_redo.bcal','intphase_redo.gcal','flux_redo.cal'],
         spwmap=[[],[],[]],gainfield=['5','2','2'])
         spwmap=[[],[],[]],gainfield=['5','2','2'],
        opacity=0.03,gaincurve=T)
</source>
</source>


Line 556: Line 712:
applycal(vis='day2_TDEM0003_10s_norx',field='5',
applycal(vis='day2_TDEM0003_10s_norx',field='5',
         gaintable=['bandpass_redo.bcal','intphase_redo.gcal','flux_redo.cal'],
         gaintable=['bandpass_redo.bcal','intphase_redo.gcal','flux_redo.cal'],
         spwmap=[[],[],[]],gainfield=['5','5','5'])
         spwmap=[[],[],[]],gainfield=['5','5','5'],
        opacity=0.03,gaincurve=T)
</source>
</source>
 
[[Image:gaincal_corrflag.png|thumb|Gain calibrator after further flagging and recalibration]]
[[Image:target_corrflag.png|thumb|IRC+10216 after further flagging and recalibration (after selecting colorize by spw).]]
<source lang="python">
<source lang="python">
# In CASA
# In CASA
applycal(vis='day2_TDEM0003_10s_norx',field='7',
applycal(vis='day2_TDEM0003_10s_norx',field='7',
         gaintable=['bandpass_redo.bcal','intphase_redo.gcal','flux_redo.cal'],
         gaintable=['bandpass_redo.bcal','intphase_redo.gcal','flux_redo.cal'],
         spwmap=[[],[],[]],gainfield=['5','7','7'])
         spwmap=[[],[],[]],gainfield=['5','7','7'],
        opacity=0.03,gaincurve=T)
</source>
</source>


Line 570: Line 729:
applycal(vis='day2_TDEM0003_10s_norx',field='3',
applycal(vis='day2_TDEM0003_10s_norx',field='3',
         gaintable=['bandpass_redo.bcal','scanphase_redo.gcal','flux_redo.cal'],
         gaintable=['bandpass_redo.bcal','scanphase_redo.gcal','flux_redo.cal'],
         spwmap=[[],[],[]],gainfield=['5','2','2'])
         spwmap=[[],[],[]],gainfield=['5','2','2'],
        opacity=0.03,gaincurve=T)
</source>
</source>
Now you can inspect the calibrated data again. Except for random scatter things look pretty good.


<source lang="python">
<source lang="python">
Line 580: Line 742:
</source>
</source>


Lets check the target again, looking at both spws, and selecting "Display" colorize by spw. You can use the Mark and Locate buttons to assess that the remaining scatter seems random, i.e. no particular antenna or time range appears to be responsible.


<source lang="python">
<source lang="python">
# In CASA
# In CASA
plotms(vis='day2_TDEM0003_10s_norx',field='3',ydatacolumn='corrected',
plotms(vis='day2_TDEM0003_10s_norx',field='3',ydatacolumn='corrected',
       xaxis='time',yaxis='amp',correlation='RR,LL',
       xaxis='uvdist',yaxis='amp',correlation='RR,LL',
       avgchannel='64',spw='0:4~60',antenna='')
       avgchannel='64',spw='0~1:4~60',antenna='')
</source>
</source>


==Split==
==Split==
Now we split the data into individual files. This is not strictly necessary, as you can select the appropriate fields in later clean stages, but it is safer in case for example you get confused with later processing and want to fall back to this point (this is especially a good idea if you plan to do continuum subtraction or self calibration later on). It also makes smaller individual files in case you want to copy to another machine or colleague.
Here, we split off the data for the phase calibrator and the target:


<source lang="python">
<source lang="python">
# In CASA
# In CASA
split(vis='day2_TDEM0003_10s_norx',outputvis='day2_J0954',
split(vis='day2_TDEM0003_10s_norx',outputvis='J0954',
       field='2')
       field='2')
</source>
</source>
Line 598: Line 765:
<source lang="python">
<source lang="python">
# In CASA
# In CASA
split(vis='day2_TDEM0003_10s_norx',outputvis='day2_IRC10216',
split(vis='day2_TDEM0003_10s_norx',outputvis='IRC10216',
       field='3')
       field='3')
</source>
</source>
To reinitialize the scratch columns for use by later tasks, we need to run clearcal for both new datasets


<source lang="python">
<source lang="python">
# In CASA
# In CASA
split(vis='day2_TDEM0003_10s_norx',outputvis='day2_3C286',
clearcal(vis='J0954')
      field='7')
</source>
</source>
<source lang="python">
# In CASA
clearcal(vis='IRC10216')
</source>
== UV Continuum Subtraction ==
[[Image:irc10216_uvspec.png|thumb|UV-plot of the spectral line signal in both spw for IRC+10216.]]
Now we can make a vector averaged uv-plot of the calibrated target spectral line data. It is important to
note that you will only see signal in such a plot if (1) the data are well calibrated, (2) there is significant signal near the phase center of the observations. If this isn't true for your data, you
will need to make an initial line+continuum cube to determine the line-free channels.
<source lang="python">
plotms(vis='IRC10216',field='',ydatacolumn='corrected',
      xaxis='channel',yaxis='amp',correlation='RR',
      avgtime='1e8',avgscan=T,spw='0~1:4~60',antenna='')
</source>
in the Display tab, choose colorize by spw and change the Unflagged points symbol to custom and Style of 3.
You should see the "horned profile" typical of a rotation shell. From this plot, you can guess that strong
line emission is restricted to channels 18 to 47 (zoom in if necessary to see exactly what the channel numbers are).
In the Data tab you can also click on "all baselines" to average all baselines, but this is a little harder to see.
Now we want to use the line free channels to create a model of the continuum emission that can be subtracted to form a line-only dataset. We want to refrain from going to close to the edges of the band -- these channels are typically noisy, and we don't want to get too close to the line channels because we could only see strong line emission in the vector averaged uv-plot.
<source lang="python">
uvcontsub2(vis='IRC10216',fitspw='0~1:4~13;52~60',
      want_cont=T)
</source>
The "want_cont=T" will produce new two new datasets, IRC10216.contsub is the continuum subtracted line data, and IRC10216.cont is the continuum estimate (note however, that it is still a multi-channel cube).
==Image the Spectral Line Data==
Here we make images from the continuum-subtracted, calibrated spectral line data. Because the spectral line emission from IRC+10216 has significant extended emission, it is very important to run clean interactively, and make a clean mask.
[[Image:viewer_interactive.png|thumb|Channel 28 shown for the HC3N cube shown in the interactive viewer with the white contour showing the mask contour drawn with the polygon tool.]]




==Clean==


<source lang="python">
<source lang="python">
# In CASA
# In CASA
clean(vis='day2_IRC10216',imagename='day2_IRC10216_spw1.cube_r0.5',
clean(vis='IRC10216.contsub',imagename='IRC10216_HC3N.cube_r0.5',
       imagermode='csclean',
       imagermode='csclean',
       imsize=300,cell=['0.4arcsec'],spw='1:5~58',
       imsize=300,cell=['0.4arcsec'],spw='0:5~58',
       mode='velocity',interpolation='linear',
       mode='velocity',interpolation='linear',
       restfreq='36.30963GHz',outframe='LSRK',
       restfreq='36.39232GHz',outframe='LSRK',
       weighting='briggs',robust=0.5,
       weighting='briggs',robust=0.5,
       mask='HC3N_r0.5.mask',          
       interactive=T,
       interactive=F,threshold='3.0mJy',niter=100000)
       threshold='3.0mJy',niter=100000)
</source>
</source>


   
It will take a little while to grid the data, but [[viewer]] will open when it's ready to start an interactive clean. Use the "tape deck" at the bottom of the Viewer display GUI to step through to the channel with the most extended (in angular size) emission, select "all channels" for the clean mask, select the polygon tool (second in from the right) and make a single mask that applies to all channels (see example in thumbnail). Once you make the polygon region, you need to double click inside it to save the mask region -- if you see the polygon turn white you will know you succeeded. Note, that if you had the time and patience you could make a clean mask for each channel, and this would create a slightly better result.
 
[[Image:SiS_interactive.png|thumb|Channel 16 shown for the SiS cube in the interactive viewer with the white contour showing the mask contour drawn with the polygon tool.]]
 
After making the mask you should check that the emission in all the other channels fits within the mask you made using the "tape deck" to move back and forth. If you need to include more area in the mask, you can chose the "erase" toggle at the top, and then encircle your existing mask with a polygon and double click inside. Then go back to "add" toggle at top and make a new mask. Alternatively, you can erase a part of the mask, or you can add to the existing mask by drawing new polygons. Feel free to experiment with this a bit.
 
To continue with [[clean]] use the "Next action" buttons in the green area on the Viewer Display GUI: The red X will stop [[clean]] where you are, the blue arrow will stop the interactive part of [[clean]], but continue to clean non-interactively until reaching the stopping niter or threshold (whichever comes first), and the green arrow will clean until it reaches the "iterations" parameter on the left side of the green area.
 
Keep cleaning, by using the green Next Action arrow until the residual displayed in the viewer looks "noise like". To speed things up, you might change the iteration parameter in the viewer to something like 300. This parameter can also be set in the task command. You will notice that in this particular case, there are residuals that cannot be cleaned -- these are due to the extended resolved out structure on size scales larger than the array is sensitive to (the "Largest Angular Scale" or LAS that the array is sensitive to can be calculated from the shortest baseline length).
 
Repeat the process for the SiS line using the call below, note that the emission for this line is less extended than the HC3N -- this has to do with the different excitation requirements of the two different lines. The SiS is excited closer to the central star than the HC3N.


<source lang="python">
<source lang="python">
# In CASA
# In CASA
clean(vis='day2_IRC10216',imagename='day2_IRC10216_spw0.cube_r0.5',
clean(vis='IRC10216.contsub',imagename='IRC10216_SiS.cube_r0.5',
       imagermode='csclean',
       imagermode='csclean',
       imsize=300,cell=['0.4arcsec'],spw='0:5~58',
       imsize=300,cell=['0.4arcsec'],spw='1:5~58',
       mode='velocity',interpolation='linear',
       mode='velocity',interpolation='linear',
       restfreq='36.39232GHz',outframe='LSRK',
       restfreq='36.30963GHz',outframe='LSRK',
       weighting='briggs',robust=0.5,
       weighting='briggs',robust=0.5,
       mask='HC3N_r0.5.mask',    
       interactive=T,
       interactive=F,threshold='3.0mJy',niter=100000)
       threshold='3.0mJy',niter=100000)
</source>
</source>
==Image the Continuum data==
Below the use of mode='mfs' will make a single multi-frequency synthesis image out of the specified spw. Again you should make an interactive clean mask. Since no threshold is set, you will need to stop cleaning when the residual looks noise like using the red x "Next Action" button (it will be done when the viewer comes back the second time).


<source lang="python">
<source lang="python">
# In CASA
# In CASA
clean(vis='day2_IRC10216',imagename='day2_IRC10216_spw0.cube_r0.5_mulit',
clean(vis='IRC10216.cont',imagename='IRC10216.36GHzcont',
       imagermode='',
       mode='mfs',imagermode='csclean',
       imsize=300,cell=['0.4arcsec'],spw='0:5~58',
       imsize=300,cell=['0.4arcsec'],spw='0~1:5~59',
      mode='velocity',interpolation='linear',
      restfreq='36.39232GHz',outframe='LSRK',
       weighting='briggs',robust=0.5,
       weighting='briggs',robust=0.5,
      mask='HC3N_r0.5.mask',
       interactive=T)
      multiscale = [0,25,50,75],
       interactive=F,threshold='3.0mJy',niter=10000)
</source>
</source>
Now look at the result in the viewer if you like
<source lang="python">
# In CASA
Viewer
</source>
==Image Analysis and Viewing==
Next make integrated intensity maps (moment 0) and integrated velocity maps (moment 1). To do this, we'll want to know what channels the line emission starts and ends on, and also the rms noise in a single channel. So first lets open the viewer:
<source lang="python">
# In CASA
viewer
</source>
Then use the Viewer tape deck to see which channels have significant line emission. For HC3N, the line channel range in the cube is 11 to 40, and it is the same for SiS.
Then use the tape deck to go to a line free channel, select the box region tool and make a box. When you double click in the box, the image statistics for the whole cube will print to the terminal and for the channel you are one, it will print to a pop up window. Move the box around a bit to see what the variation is. You should get something like 2 mJy. Note that the rms is much worse in channels with strong emission because of the low dynamic range of these data. If you want the box tool to go away, hit the escape key.
Now lets make the moment 0 and moment 1 maps. For moment zero, its best to limit the calculation to image channels with significant signal in them, but not to apply a flux cutoff, as this will bias the derived integrated intensities upward.
[[Image:irc10216.jpg|thumb|HC3N moment 0 map with white continuum contours superposed.]]
[[Image:irc10216_sismom0.jpg|thumb|SiS moment 0 map with white continuum contours superposed.]]
<source lang="python">
# In CASA
immoments(imagename='IRC10216_HC3N.cube_r0.5.image',moments=[0],
          axis='spectral',
          chans='11~40',
          outfile='IRC10216_HC3N.cube_r0.5.image.mom0')
</source>
<source lang="python">
# In CASA
immoments(imagename='IRC10216_SiS.cube_r0.5.image',moments=[0],
          axis='spectral',
          chans='11~40',
          outfile='IRC10216_SiS.cube_r0.5.image.mom0')
</source>
For moment 1, it is essential to apply a conservative flux cutoff to limit the calculation to high signal-to-noise areas. Here we use about 5sigma.
<source lang="python">
# In CASA
immoments(imagename='IRC10216_HC3N.cube_r0.5.image/',moments=[1],
          axis='spectral',
          chans='11~40',excludepix=[-100,0.01],
          outfile='IRC10216_HC3N.cube_r0.5.image.mom1')
</source>
<source lang="python">
# In CASA
immoments(imagename='IRC10216_SiS.cube_r0.5.image/',moments=[1],
          axis='spectral',
          chans='11~40',excludepix=[-100,0.01],
          outfile='IRC10216_SiS.cube_r0.5.image.mom1')
</source>
Now user the viewer to further explore the images you've made.
[[Main Page | &#8629; '''CASAguides''']]
--[[User:Cbrogan|Crystal Brogan]]

Latest revision as of 16:19, 19 May 2010


This tutorial is under construction. There are several things still to be added 
in addition to overall polish and further annotation:
* screen captures of task inputs
* more about cleaning in general
* more on image analysis
* multiscale clean maybe

For the time being (until release candidate is built) you want to run this on casapy-test

Overview

This tutorial describes the data reduction for two spectral lines observed toward the AGB star IRC+10216. This carbon star, which is a few times more massive than our sun, is nearing the end of its life and is thought to be in the process of forming a planetary nebula.

In this EVLA OSRO1 mode observation one subband was observed in each of two basebands, the subbands were centered on the HC3N and SiS lines near 36 GHz. The raw data were loaded into CASA with importevla, where zero and shadowed data were flagged. Then the data were "split", so we could average from the native 1 second integrations to 10 seconds, select only antennas with Ka-band receivers, and select only spectral windows (called spw in CASA) with Ka-band data. This produces a significantly smaller dataset for processing.

The post-split averaged data can be downloaded from http://casa.nrao.edu/Data/EVLA/IRC10216/day2_TDEM0003_10s_norx.tar 

Information from observing log:
There are no Ka-band receivers on ea11, ea13, ea14, ea16, ea17, ea18, ea26  
Antennas ea10, ea06 are out of the array
Antenna ea12 is newly back
The pointing is often bad on ea15
Antennas ea10, ea12, ea22 do not have good baseline positions

Initial Inspection and Flagging

# In CASA
listobs(vis='day2_TDEM0003_10s_norx')

Below we have cut and pasted the most relevant output from the logger. 

Fields: 4
  ID   Code Name         RA            Decl           Epoch   SrcId nVis   
  2    D    J0954+1743   09:54:56.8236 +17.43.31.2224 J2000   2     65326  
  3    NONE IRC+10216    09:47:57.3820 +13.16.40.6600 J2000   3     208242 
  5    F    J1229+0203   12:29:06.6997 +02.03.08.5982 J2000   5     10836  
  7    E    J1331+3030   13:31:08.2880 +30.30.32.9589 J2000   7     5814   
   (nVis = Total number of time/baseline visibilities per field) 
Spectral Windows:  (2 unique spectral windows and 1 unique polarization setups)
  SpwID  #Chans Frame Ch1(MHz)    ChanWid(kHz)TotBW(kHz)  Ref(MHz)    Corrs           
  0          64 TOPO  36387.2295  125         8000        36387.2295  RR  RL  LR  LL  
  1          64 TOPO  36304.542   125         8000        36304.542   RR  RL  LR  LL  
Sources: 10
  ID   Name         SpwId RestFreq(MHz)  SysVel(km/s) 
  0    J1008+0730   0     0.03639232     -0.026       
  0    J1008+0730   1     0.03639232     -0.026       
  2    J0954+1743   0     0.03639232     -0.026       
  2    J0954+1743   1     0.03639232     -0.026       
  3    IRC+10216    0     0.03639232     -0.026       
  3    IRC+10216    1     0.03639232     -0.026       
  5    J1229+0203   0     0.03639232     -0.026       
  5    J1229+0203   1     0.03639232     -0.026       
  7    J1331+3030   0     0.03639232     -0.026       
  7    J1331+3030   1     0.03639232     -0.026       
Antennas: 19:
  ID   Name  Station   Diam.    Long.         Lat.         
  0    ea01  W09       25.0 m   -107.37.25.2  +33.53.51.0  
  1    ea02  E02       25.0 m   -107.37.04.4  +33.54.01.1  
  2    ea03  E09       25.0 m   -107.36.45.1  +33.53.53.6  
  3    ea04  W01       25.0 m   -107.37.05.9  +33.54.00.5  
  4    ea05  W08       25.0 m   -107.37.21.6  +33.53.53.0  
  5    ea07  N06       25.0 m   -107.37.06.9  +33.54.10.3  
  6    ea08  N01       25.0 m   -107.37.06.0  +33.54.01.8  
  7    ea09  E06       25.0 m   -107.36.55.6  +33.53.57.7  
  8    ea12  E08       25.0 m   -107.36.48.9  +33.53.55.1  
  9    ea15  W06       25.0 m   -107.37.15.6  +33.53.56.4  
  10   ea19  W04       25.0 m   -107.37.10.8  +33.53.59.1  
  11   ea20  N05       25.0 m   -107.37.06.7  +33.54.08.0  
  12   ea21  E01       25.0 m   -107.37.05.7  +33.53.59.2  
  13   ea22  N04       25.0 m   -107.37.06.5  +33.54.06.1  
  14   ea23  E07       25.0 m   -107.36.52.4  +33.53.56.5  
  15   ea24  W05       25.0 m   -107.37.13.0  +33.53.57.8  
  16   ea25  N02       25.0 m   -107.37.06.2  +33.54.03.5  
  17   ea27  E03       25.0 m   -107.37.02.8  +33.54.00.5  
  18   ea28  N08       25.0 m   -107.37.07.5  +33.54.15.8  

Summary of Observing Strategy
Gain Calibrator: J0954+1743 field id=2
Bandpass Calibrator: J1229+0203   field id=5
Flux Calibrator: J1331+3030 (3C286) field id=7
Target: IRC+10216  field id=3
Ka-band spws = 0,1
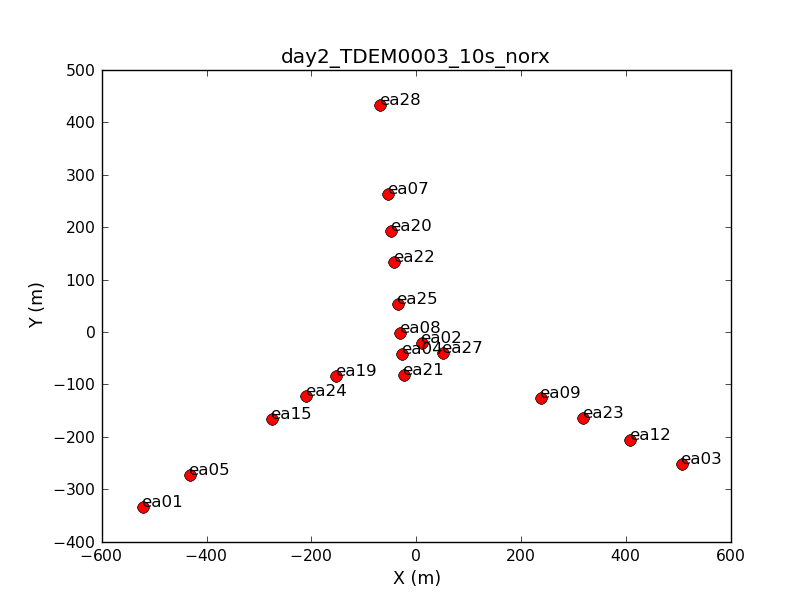
Antenna locations from running plotants

Look at a graphical plot of the antenna locations and save hardcopy in case you want it later. This will be useful for picking a reference antenna -- typically a good choice is an antenna close to the center of the array. Unless it shows problems after inspection of the data, we provisionally chose ea02.

Elevation as a function of time (after selecting colorize by field).
# In CASA
plotants(vis='day2_TDEM0003_10s_norx',figfile='ant_locations.png')

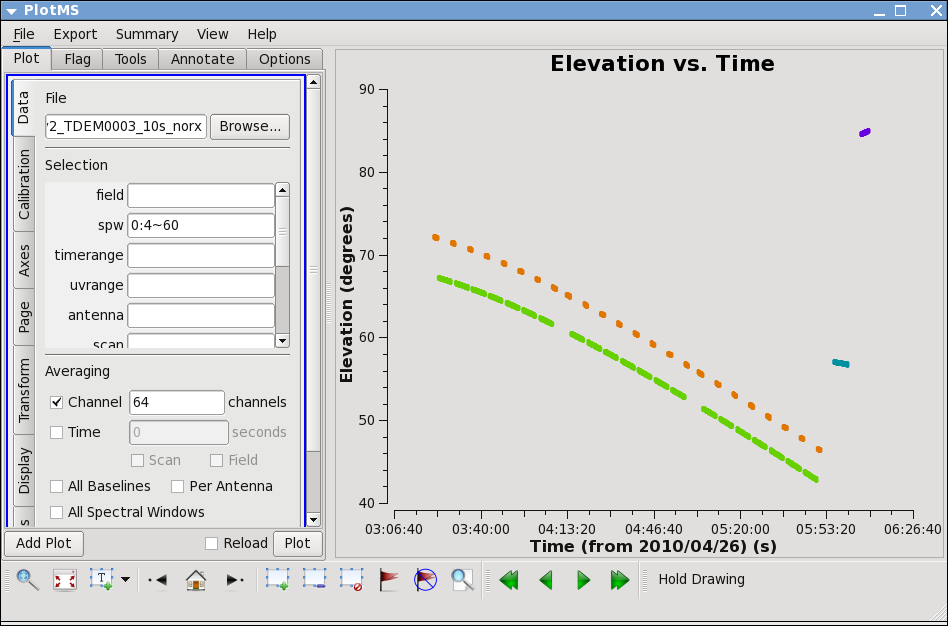
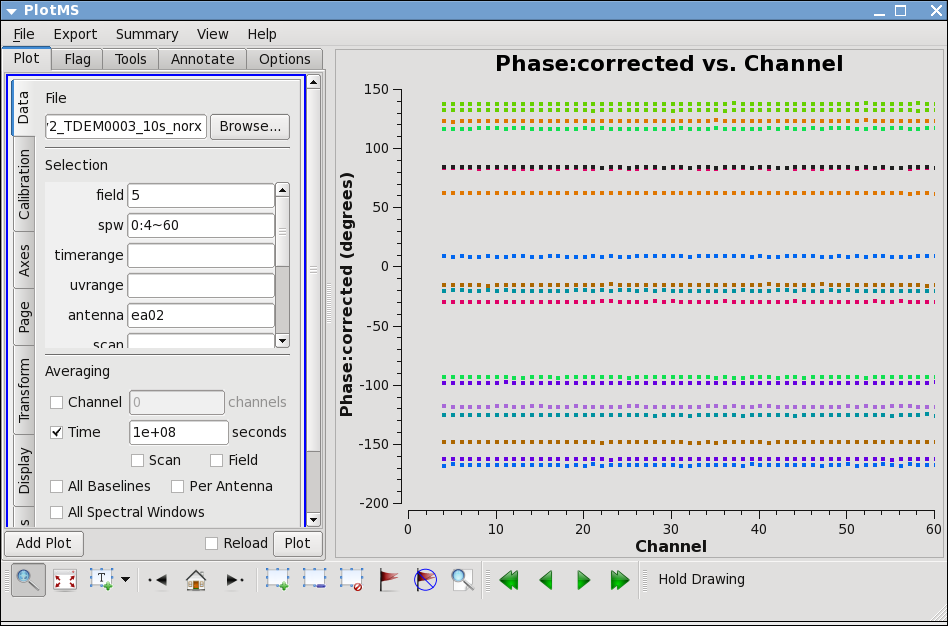
Next, let's look at the elevation as a function of time for all sources. It's not the case for these data, but if the elevation is very low (usually at start or end of track) you may want to flag. Also, how near in elevation your flux calibrator is to your target will impact your ultimate absolute flux calibration accuracy. Unfortunately, the target and flux calibrator are not particularly well-matched for this observation, as y ou can show by plotting the elevation for each source: 


# In CASA
plotms(vis='day2_TDEM0003_10s_norx',
       xaxis='time',yaxis='elevation',correlation='RR,LL',
       avgchannel='64',spw='0:4~60')

Thus we are strongly dependent on the opacity and gaincurve corrections to get the flux scale right for these data. (This is something to keep in mind when planning observations!)

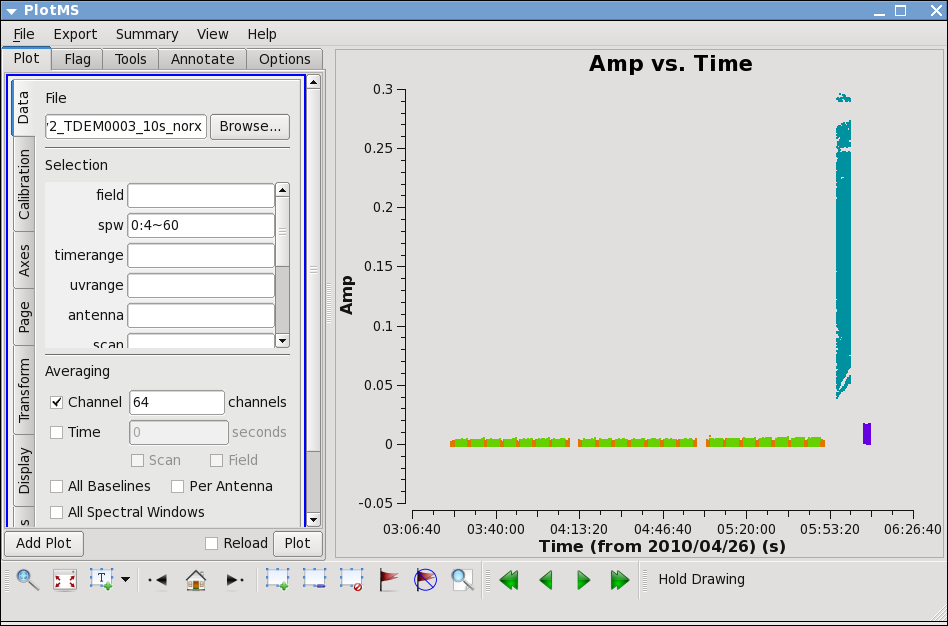
Result of plotms after selecting colorize by field
Zooming in and marking region (hatched box)

Next,let's look at all the source amplitudes as a function of time. 

# In CASA
plotms(vis='day2_TDEM0003_10s_norx',
       xaxis='time',yaxis='amp',correlation='RR,LL',
       avgchannel='64',spw='0:4~60')

Select the "Display" tab and colorize by field, and click Plot button.


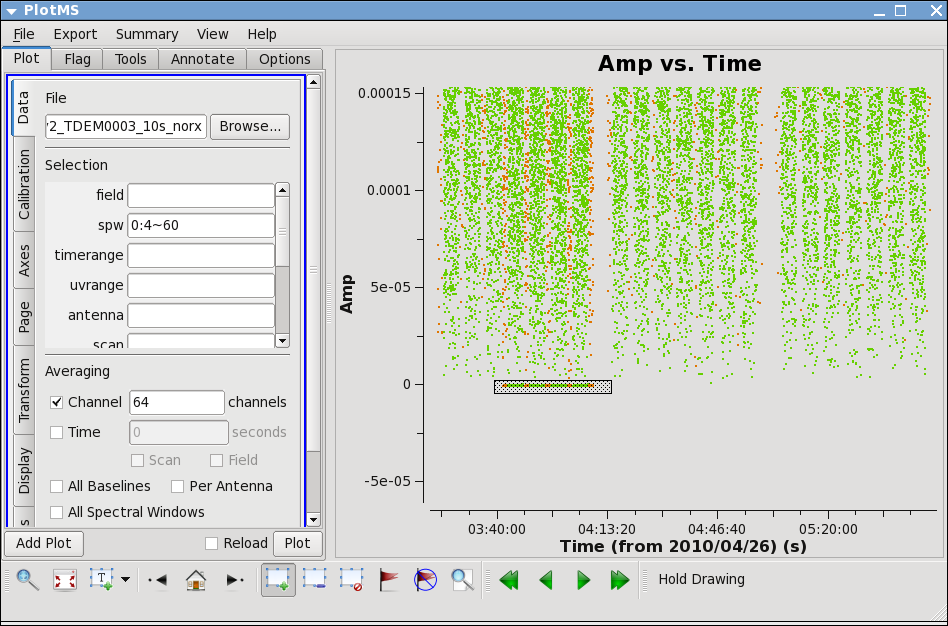
Now zoom in on the region very near zero amplitude for sources J0954+1743 and IRC+10216. To zoom, select the Zoom tool in lower left corner of the plotms GUI, then you can left click to draw a box. Look for the low values (you may want to zoom a few times to really see the suspect points clearly). Now use the Mark Region and Locate buttons (located along the bottom of the GUI) to see which antenna is causing problems. Since all the "located" baselines include ea12, this is the responsible antenna. 

IMPORTANT NOTES ON PLOTMS:

* When using the locate button it is important to have only selected a modest number 
of points with the mark region tool (see example of marked region in the thumnail), 
otherwise the response will be very slow and possibly hang the tool 
(all of the information will be output to your terminal window, not the logger). 

* Throughout the tutorial, when you are done marking/locate use the Clear Regions 
tool to get rid of the marked box before plotting other things. 

* After flagdata command flagging, you have to force a complete reload of the cache 
to look at the same plot again with the new flags applied. To do this change anything 
in the plotms GUI (the colorize parameter, antenna, spw, anything) and hit the 
plot button.

* If the plotms tool does get hung during a plot try clicking the cancel button on the 
load progress GUI, and/or if you see a "table locked" message try typing 
clearstat on the CASA command line.

* Occasionally plotms will get into a strange state that you cannot clear from inside. 
We are working on these issues, but for now, when all else fails, exit from casapy and 
restart.

Now click the unmark region button, and then go back to the zoom button to zoom in further to note exactly what the time range is: 03:41:00~04:10:00.

Check the other sideband by changing spw to 1:4~60. You will have to rezoom. If you have trouble, click on the Mark icon and then back to zoom. In spw=1, ea07 is bad from the beginning until after next pointing run: 03:21:40~04:10:00. To see this, compare the amplitudes when antenna is set to 'ea07' and when it is set to one of the other antennas, such as 'ea08'.

If you set antenna to 'ea12' and zoom in on this intial timerange, you can also see that ea12 is bad during the same time range as for spw 0. You can also see this by entering '!ea07' for antenna, which removes ea07 from the plot (in CASA selection, ! deselects).

We can set up a flagging command to get both bad antennas for the appropriate time and spw: 

# In CASA
flagdata(vis='day2_TDEM0003_10s_norx',
         field=['2,3','2,3'],
         spw=['','1'],
         antenna=['ea12','ea07'],
         timerange=['03:41:00~04:10:00','03:21:40~04:10:00'])

Note that because the chosen timerange is limited to fields 2 and 3,the field parameter is not really needed; however, flagdata will run fastest if you put as many constraints as possible.

Now remove the !ea07 from antenna and replot both spw, zooming in to be sure that all obviously low points are gone. Also zoom in and check 3C286 (J1229+0203 is already obvious because it is so bright!).

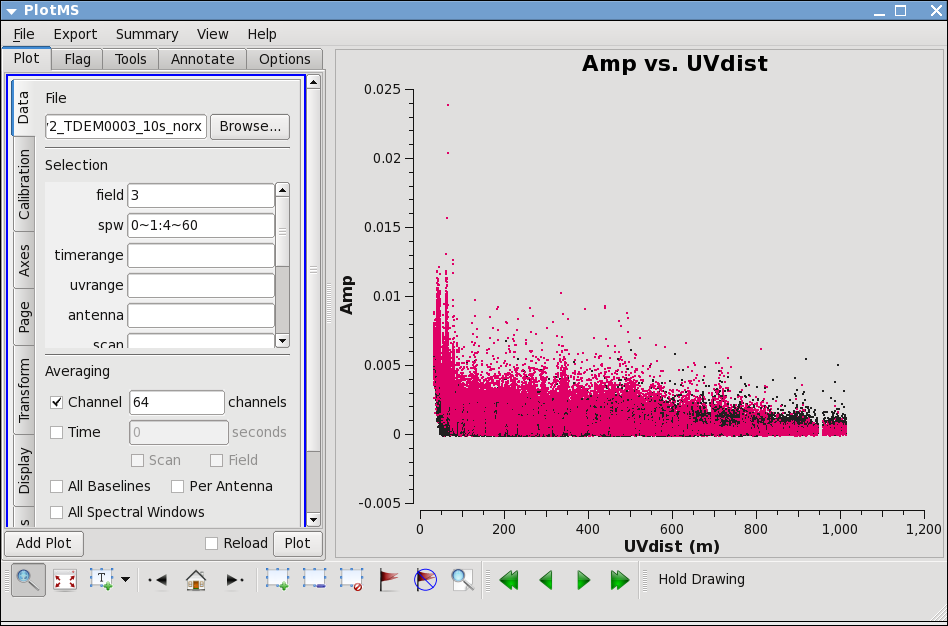
Amplitude vs. uv-distance for IRC+10216, both spw (after colorize by spw)

Lets look more closely at IRC+10216: 

# In CASA
plotms(vis='day2_TDEM0003_10s_norx',field='3',
       xaxis='time',yaxis='amp',correlation='RR,LL',
       avgchannel='64',spw='0~1:4~60')

Go to the "display" tab and choose colorize by spw. You can see a that there are some noisy high points. But now try 

# In CASA
plotms(vis='day2_TDEM0003_10s_norx',field='3',
       xaxis='uvdist',yaxis='amp',correlation='RR,LL',
       avgchannel='64',spw='0~1:4~60')

Most of the high points on IRC+10216 are due to large scale emission on short baselines, but there is still some noisy stuff -- for a target like this with extended emission its best to wait until later to decide what to do about it. We will not be able to get adequate calibration for antennas that are truly bad (even if they don't stand out here) so these will be obvious later.

Set the Flux Calibrator

Next, we tell CASA to look up the appropriate fluxes for 3C286: 

# In CASA
setjy(vis='day2_TDEM0003_10s_norx',field='7',spw='0~1',
      modimage='/usr/lib64/casapy/data/nrao/VLA/CalModels/3C286_K.im')

The logger output for each spw is:
setjy	  J1331+3030  spwid=  0  [I=1.692, Q=0, U=0, V=0] Jy, (Perley-Taylor 99)
setjy	  J1331+3030  spwid=  1  [I=1.695, Q=0, U=0, V=0] Jy, (Perley-Taylor 99)

The modimage location is appropriate for running CASA at the AOC. If you are running elsewhere (laptop or Mac), in a terminal type 

# in a terminal, outside of CASA:
locate 3C286_K.im

to find where the models live (the models are always shipped with CASA).

Bandpass

Before determining the bandpass solution, we need to inspect phase and amplitude variations with time and frequency on the bandpass calibrator to decide how best to proceed. We limit the number of antennas to make the plot easier to see. We chose ea02 as it seems like a good candidate for the reference antenna. 

# In CASA
plotms(vis='day2_TDEM0003_10s_norx',field='5',
       xaxis='channel',yaxis='phase',correlation='RR',
       avgtime='1e8',spw='0:4~60',antenna='ea02&ea23')
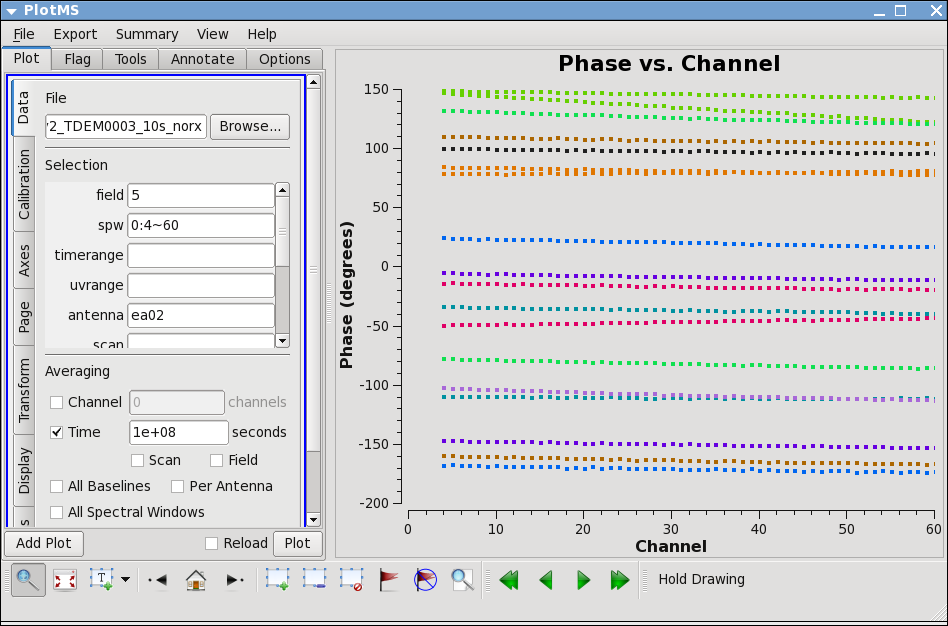
Phase as a function of channel for ea02 (after colorize by Antenna2, and Custom and upping "Style" to 3.)

The phase variation is modest ~10 degrees. Now expand to all antennas with ea02 and select colorize by Antenna2, then hit the "Plot" button. 

# In CASA
plotms(vis='day2_TDEM0003_10s_norx',field='5',
       xaxis='channel',yaxis='phase',correlation='RR',
       avgtime='1e8',spw='0:4~60',antenna='ea02')
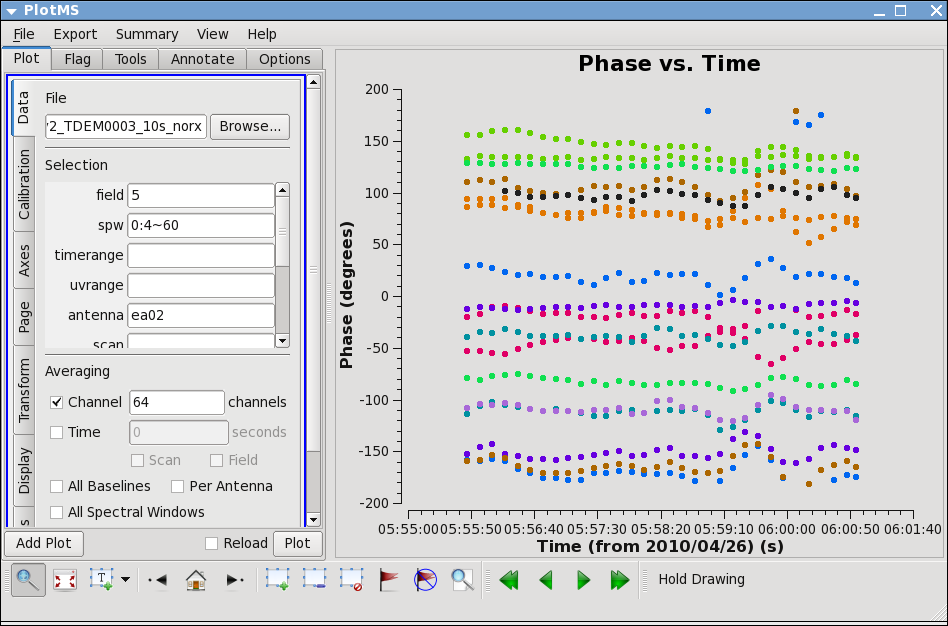
Phase as a function of time for ea02 (after colorize by Antenna2, and Custom and upping "Style" to 3.)

Go to the "display" tab and chose colorize by antenna2. From this you can see that the phase variation across the bandpass is modest. Next check LL, and spw=1, both correlations. Also check other antennas if you like.

Now look at the phase as a function of time. 

# In CASA
plotms(vis='day2_TDEM0003_10s_norx',field='5',
       xaxis='time',yaxis='phase',correlation='RR',
       avgchannel='64',spw='0:4~60',antenna='ea02&ea23')


Expand to all antennas with ea02 

# In CASA
plotms(vis='day2_TDEM0003_10s_norx',field='5',
       xaxis='time',yaxis='phase',correlation='RR',
       avgchannel='64',spw='0:4~60',antenna='ea02')

You can see that the phase variations are smooth, but do vary significantly over the 5 minutes of observation -- in most cases by a few 10s of degrees. Zoom in to see this better if you want.

The conclusion from this investigation is that you need to correct the phase variations with time before solving for the bandpass to prevent decorrelation of the vector averaged bandpass solution. Since the phase variation as a function of channel is modest, you can average over several channels to increase the signal to noise of the phase vs. time solution. If the phase variation as a function of channel is larger you may need to use only a few channels to prevent introducing delay-based closure errors as can happen from averaging over non-bandpass corrected channels with large phase variations.


Since the bandpass calibrator is quite strong we do the phase-only solution on the integration time of 10 seconds (solint='int').

Phase only calibration before bandpass. The 4 lines are both polarizations in both spw, unfortunately two of them get the same color green at the moment.
# In CASA
gaincal(vis='day2_TDEM0003_10s_norx',caltable='bpphase.gcal',
        field='5',spw='0~1:20~40',
        refant='ea02',calmode='p',solint='int',minsnr=2.0,
        opacity=0.03,gaincurve=T)

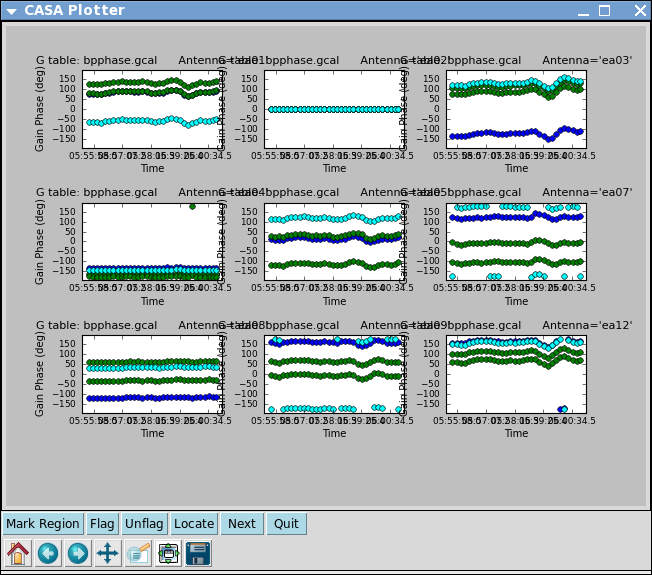
Plot the solutions 

# In CASA
plotcal(caltable='bpphase.gcal',xaxis='time',yaxis='phase',
        iteration='antenna',subplot=331,plotrange=[0,0,-180,180])

After the first set of plots appear, push the "Next" button on the GUI to see the next set of antennas.

Next we can apply this phase solution on the fly while determining the bandpass solutions on the timescale of the bandpass calibrator scan (solint='inf').

Amplitude Bandpass solutions
Phase Bandpass solutions
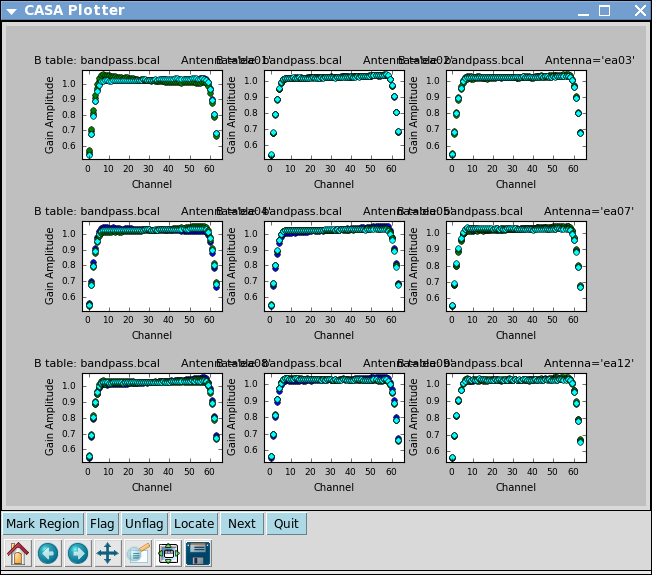
# In CASA
bandpass(vis='day2_TDEM0003_10s_norx',caltable='bandpass.bcal',field='5',
        refant='ea02',solint='inf',solnorm=T,
        gaintable=['bpphase.gcal'],spwmap=[[]],
        opacity=0.03,gaincurve=T)

A few words about solint and combine:

The use of solint='inf' in bandpass will derive one bandpass solution for the whole J1229+0203 scan. Note that if there had been two observations of the bandpass calibrator (for example), this command would have combined the data from both scans to form one bandpass solution, because the default of the combine parameter for bandpass is combine='scan'. To solve for one bandpass for each bandpass calibrator scan you would also need to include combine=' ' in the bandpass call. In all calibration tasks, regardless of solint, scan boundaries are only crossed when combine='scan'. Likewise, field (spw) boundaries are only crossed if combine='field' (combine='spw'), the latter two are not generally good ideas for bandpass solutions.

Plot the solutions, amplitude and phase: 

# In CASA
plotcal(caltable='bandpass.bcal',xaxis='chan',yaxis='amp',
        iteration='antenna',subplot=331)

# In CASA
plotcal(caltable='bandpass.bcal',xaxis='chan',yaxis='phase',
        iteration='antenna',subplot=331)

Note that phases on ea12 look noiser than on other antennas. This jitter could indicate bad pointing; note that ea12 had just come back in the array.

This step isn't necessary from a calibration perspective, but if you want to go ahead and check the bandpass calibration on the bandpass calibrator you can run applycal here. In future we hope to plot corrected data on-the-fly without this applycal step. Later applycals will overwrite this one, so no need to worry.

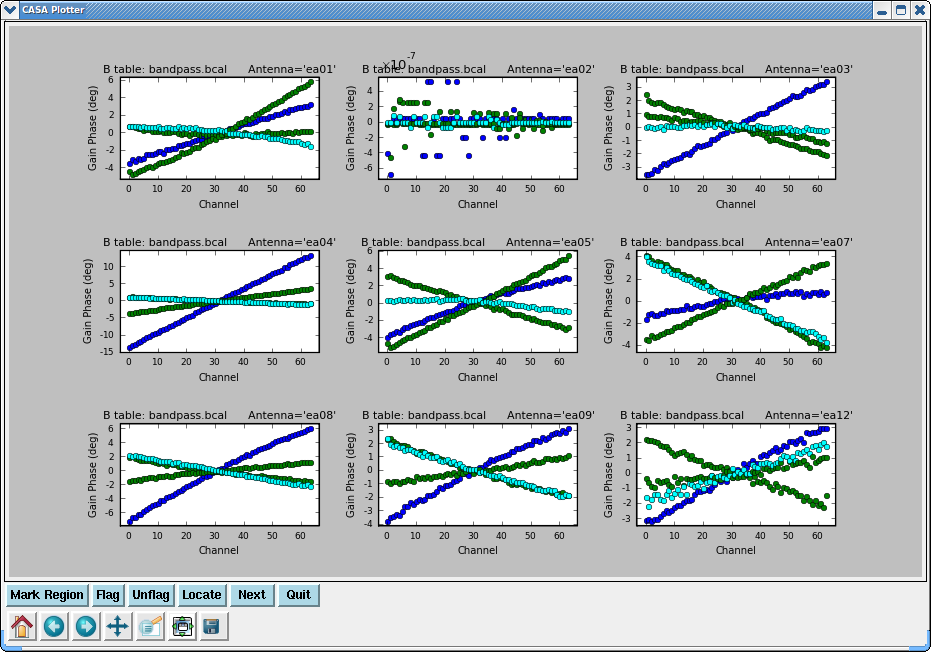
Phase as a function of channel, plotting the corrected data (after colorize by Antenna2, and Custom and upping "Style" to 3.)
applycal(vis='day2_TDEM0003_10s_norx',field='5',
        gaintable=['bandpass.bcal'],
        spwmap=[[]],gainfield=['5'],
        opacity=0.03,gaincurve=T)

plotms(vis='day2_TDEM0003_10s_norx',field='5',
       xaxis='channel',yaxis='phase',ydatacolumn='corrected',
       correlation='RR',
       avgtime='1e8',spw='0:4~60',antenna='ea02')

plotms(vis='day2_TDEM0003_10s_norx',field='5',
       xaxis='channel',yaxis='amp',ydatacolumn='corrected',
       correlation='RR',
       avgtime='1e8',spw='0:4~60',antenna='ea02')

Note that the phase and amplitude as a function of channel are very flat now.

Gain Calibration

Now that we have a bandpass solution to apply we can solve for the antenna-based phase and amplitude gain calibration. Since the phase changes on a much shorter timescale than the amplitude, we will solve for them separately. In particular, if the phase changes significantly over a scan time, the amplitude would be decorrelated, if the un-corrected phase were averaged over this timescale. Note that we re-solve for the gain solutions of the bandpass calibrator, so we can derive new solutions that are corrected for the bandpass shape. Since the bandpass calibrator will not be used again, this is not strictly necessary, but is useful to check its calibrated flux density for example. 

# In CASA
gaincal(vis='day2_TDEM0003_10s_norx',caltable='intphase.gcal',
        field='2,5,7',spw='0~1:4~60',
        refant='ea02',calmode='p',solint='int',minsnr=2.0,
        gaintable=['bandpass.bcal'],spwmap=[[]],
        opacity=0.03,gaincurve=T)
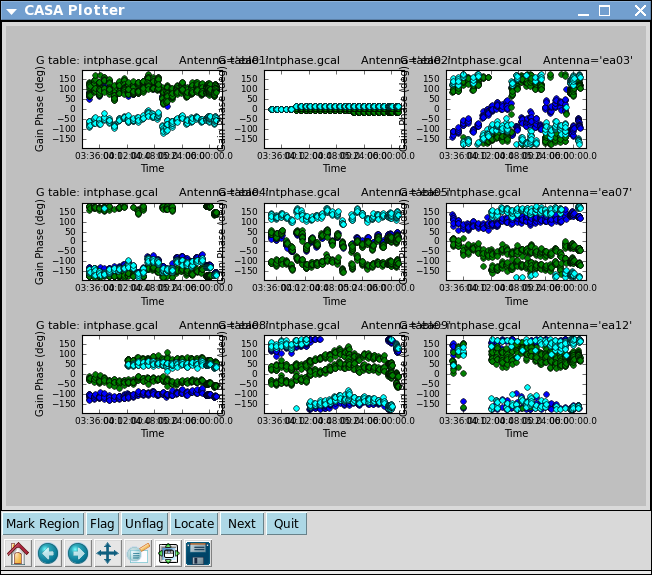
Plot of phase solutions on an integration time.

Here solint='int' coupled with calmode='p' will derive a single phase solution for each 10 second integration. Note that the bandpass table is applied on-the-fly before solving for the phase solutions, however the bandpass is NOT applied to the data permanently until applycal is run later on.

Now look at the phase solution, and note the obvious scatter within a scan time. 

# In CASA
plotcal(caltable='intphase.gcal',xaxis='time',yaxis='phase',
        iteration='antenna',subplot=331,plotrange=[0,0,-180,180])

Although solint='int' (i.e. the integration time of 10 seconds) is the best choice to apply before for solving for the amplitude solutions, it is not a good idea to use this to apply to the target. This is because the phase-scatter within a scan can dominate the interpolation between calibrator scans. Instead, we also solve for the phase on the scan time, solint='inf' (but combine=' ', since we want one solution per scan) for application to the target later on. Unlike the bandpass task, for gaincal, the default of the combine parameter is combine=' '.

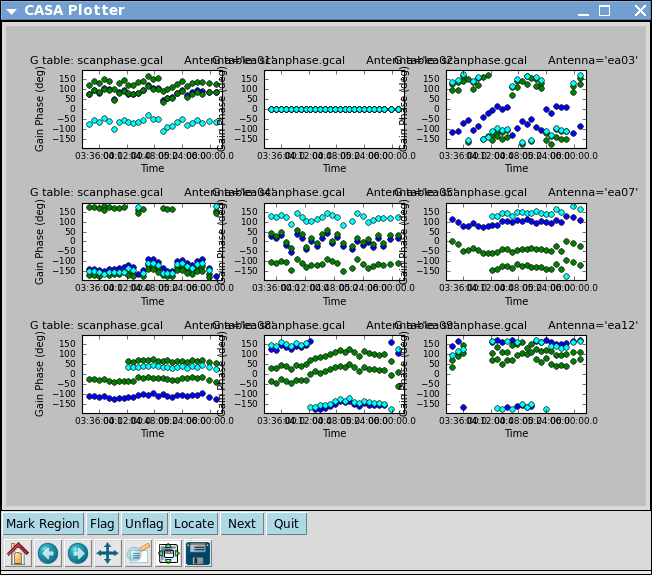
Plot of phase solutions on a scan time.
# In CASA
gaincal(vis='day2_TDEM0003_10s_norx',caltable='scanphase.gcal',
        field='2,5,7',spw='0~1:4~60',
        refant='ea02',calmode='p',solint='inf',minsnr=2.0,
        gaintable=['bandpass.bcal'],spwmap=[[]],
        opacity=0.03,gaincurve=T)

# In CASA
plotcal(caltable='scanphase.gcal',xaxis='time',yaxis='phase',
        iteration='antenna',subplot=331,plotrange=[0,0,-180,180])

Alternatively, one can also run smoothcal to smooth the solutions derived on the integration time.

Next we apply the bandpass and solint='int' phase-only calibration solutions on-the-fly to derive amplitude solutions. Here the use of solint='inf', but combine=' ' will result in one solution per scan interval. 

# In CASA
gaincal(vis='day2_TDEM0003_10s_norx',caltable='amp.gcal',
        field='2,5,7',spw='0~1:4~60',
        refant='ea02',calmode='ap',solint='inf',minsnr=2.0,
        gaintable=['bandpass.bcal','intphase.gcal'],spwmap=[[],[]],
        opacity=0.03,gaincurve=T)
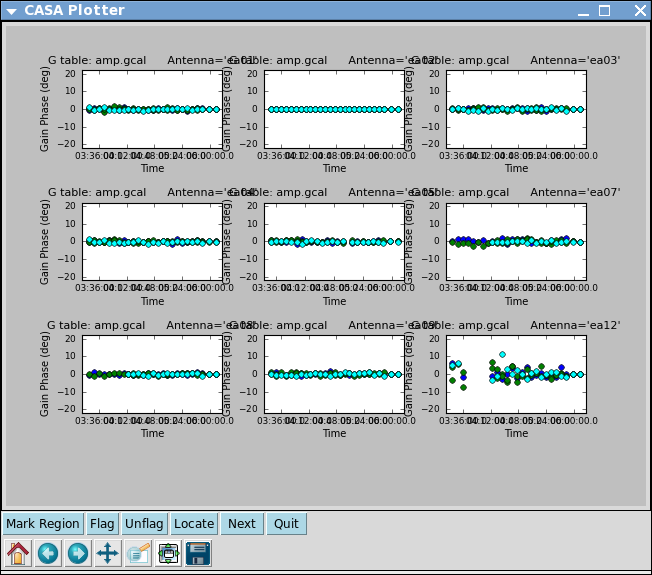
Plot of residual phase solutions on a scan time

Now let's look at the resulting phase solutions. Since we have taken out the phase as best we can by applying the solint='int' phase-only solution, this plot will give a good idea of the residual phase error. If you see scatter of more than a few degrees here, you should consider going back and looking for more data to flag, particularly bad timeranges etc. 

# In CASA       
plotcal(caltable='amp.gcal',xaxis='time',yaxis='phase',
        iteration='antenna',subplot=331)

Indeed, both antenna ea12 (all times) and ea23 (first 1/3 of observation) show particularly large residual phase noise.

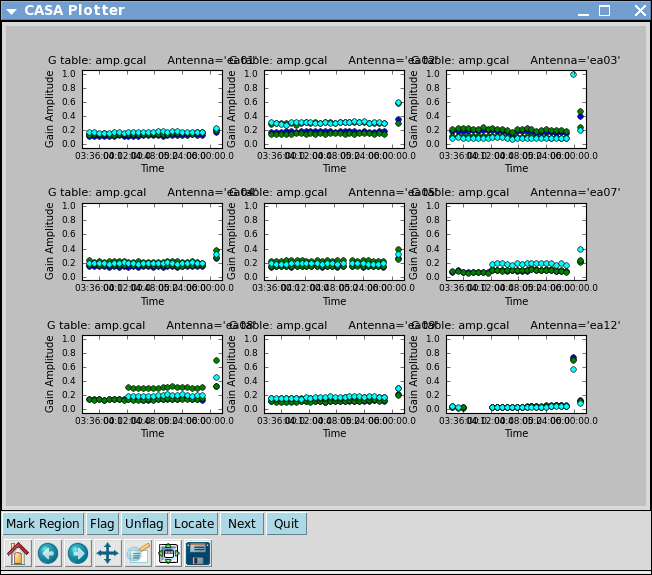
Plot of amplitude solutions on a scan time
# In CASA
plotcal(caltable='amp.gcal',xaxis='time',yaxis='amp',
        iteration='antenna',subplot=331)

Note that the amplitude solutions for ea12 are very low; this is another indication that this antenna is dubious.

Next we use the flux calibrator (whose flux density was set in setjy above) to derive the flux of the other calibrators. Note that the flux table REPLACES the amp.gcal in terms of future application of the calibration to the data, i.e. the flux table contains both the amp.gcal and flux scaling. Unlike the gain calibration steps, this is not an incremental table. 

# In CASA
fluxscale(vis='day2_TDEM0003_10s_norx',caltable='amp.gcal',
          fluxtable='flux.cal',reference='7')
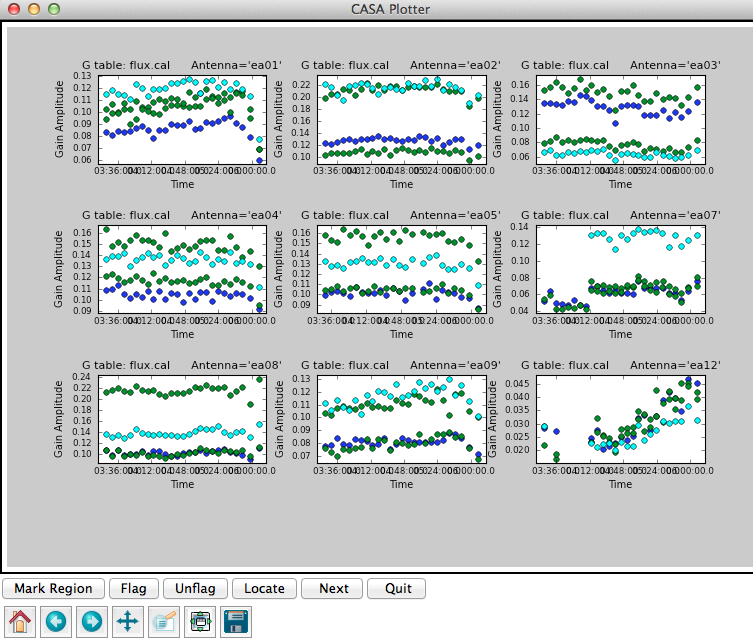
Plot of flux corrected amplitude solutions.

It is a good idea to note down for your records the derived flux densities: 

Flux density for J0954+1743 in SpW=0# is: 0.267699 +/- 0.00103786 
   (SNR = 257.934, nAnt= 19)
Flux density for J0954+1743 in SpW=1# is: 0.279468 +/- 0.000735923 
   (SNR = 379.752, nAnt= 19)
Flux density for J1229+0203 in SpW=0# is: 30.5454 +/- 0 
   (SNR = inf, nAnt= 19)
Flux density for J1229+0203 in SpW=1# is: 30.2306 +/- 0 
   (SNR = inf, nAnt= 19)

Obviously, the signal-to-noise for J1229+0203 can't be infinity! This is just an indication that their is only one scan for this source, and we derived a scan based amplitude solution, so there is no variation to calculate.

Next, check that the flux.cal table looks as expected. 

# In CASA
plotcal(caltable='flux.cal',xaxis='time',yaxis='amp',
        iteration='antenna',subplot=331)

Applycal and Inspect

Now we apply the calibration to each source, according to which tables are appropriate, and which source should be used to do that particular calibration. For the calibrators, all bandpass solutions come from the bandpass calibrator (id=5), and the phase and amplitude calibration comes from their own solutions. 

# In CASA
applycal(vis='day2_TDEM0003_10s_norx',field='2',
        gaintable=['bandpass.bcal','intphase.gcal','flux.cal'],
        spwmap=[[],[],[]],gainfield=['5','2','2'],
        opacity=0.03,gaincurve=T)

# In CASA
applycal(vis='day2_TDEM0003_10s_norx',field='5',
        gaintable=['bandpass.bcal','intphase.gcal','flux.cal'],
        spwmap=[[],[],[]],gainfield=['5','5','5'],
        opacity=0.03,gaincurve=T)

# In CASA
applycal(vis='day2_TDEM0003_10s_norx',field='7',
        gaintable=['bandpass.bcal','intphase.gcal','flux.cal'],
        spwmap=[[],[],[]],gainfield=['5','7','7'],
        opacity=0.03,gaincurve=T)

For the target we apply the bandpass from id=5, and the calibration from the gain calibrator (id=2): 

# In CASA
applycal(vis='day2_TDEM0003_10s_norx',field='3',
        gaintable=['bandpass.bcal','scanphase.gcal','flux.cal'],
        spwmap=[[],[],[]],gainfield=['5','2','2'],
        opacity=0.03,gaincurve=T)

Now inspect the corrected data:

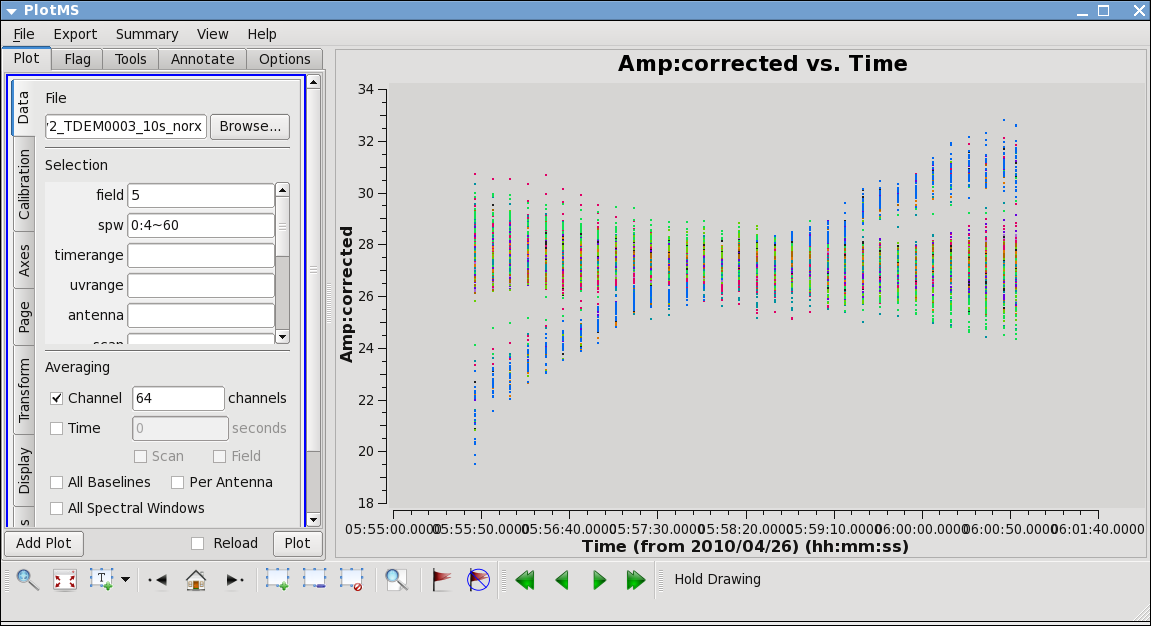
Plot of calibrated amplitudes over time.
# In CASA
plotms(vis='day2_TDEM0003_10s_norx',field='5',ydatacolumn='corrected',
       xaxis='time',yaxis='amp',correlation='RR,LL',
       avgchannel='64',spw='0:4~60',antenna='')

This plot shows some data deviating from the average amplitudes. Use methods described above to mark a region for a small number of deviant data points, and click "Locate". You will find that ea12 is responsible. 

# In CASA
plotms(vis='day2_TDEM0003_10s_norx',field='2',ydatacolumn='corrected',
       xaxis='time',yaxis='amp',correlation='RR,LL',
       avgchannel='64',spw='0:4~60',antenna='')

Here we see some problems, with high points. Mark some regions and locate in plotms to find out which antennas and in which spws. Pay special attention to antennas that have been called out already as showing some dubious behavior.

What you find is that ea07 which we flagged spw=1 above, is also bad for the same timerange in spw=0. This was not obvious in the raw data, because spw=0 was adjusted in the on-line system by a gain attenuator, while spw=1 wasn't. So a lack of power on this antenna can look like very low (and obvious) amplitudes in spw=1 but not for spw=0. Looking carefully you'll see that ea07 is actually pretty noisy throughout.

Plot of antenna ea12 by itself
Plot of antenna ea23 by itself

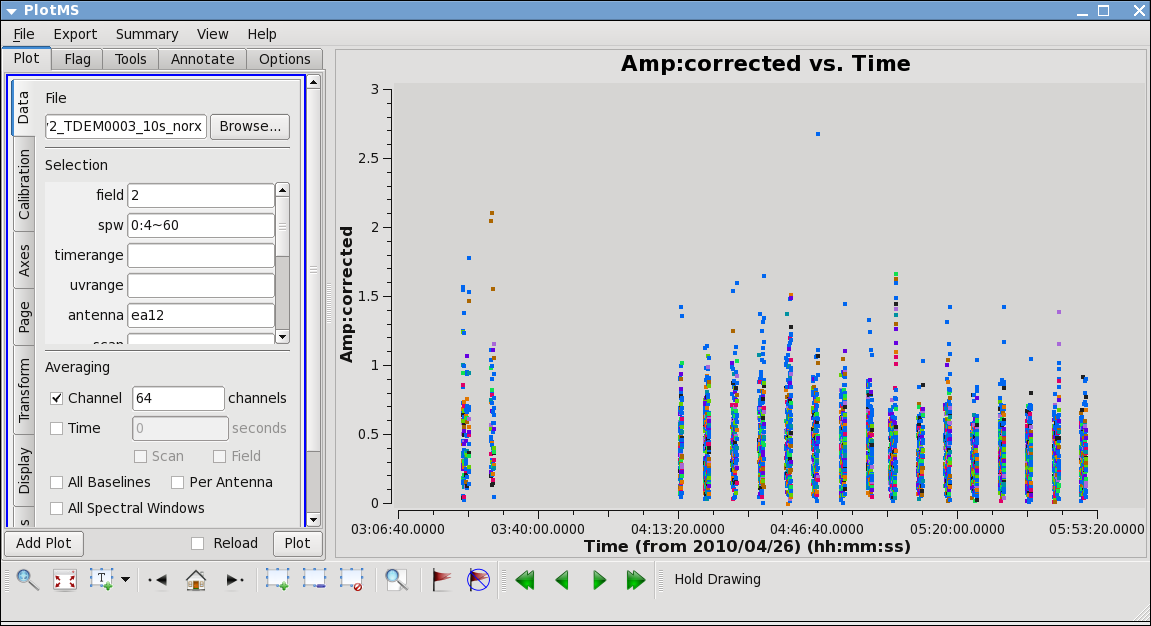
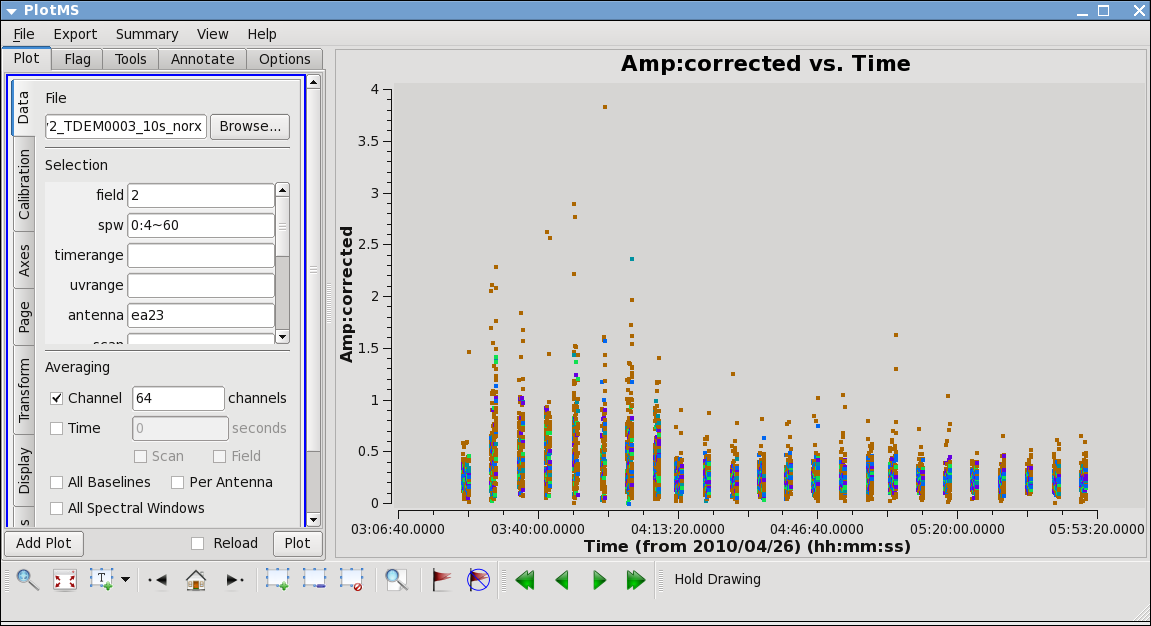
From the locate we also find that ea12 and ea23 show some high points; to see this, replot baselines using each of them alone: 

plotms(vis='day2_TDEM0003_10s_norx',field='2',ydatacolumn='corrected',
       xaxis='time',yaxis='amp',correlation='RR,LL',
       avgchannel='64',spw='0:4~60',antenna='ea12')

plotms(vis='day2_TDEM0003_10s_norx',field='2',ydatacolumn='corrected',
       xaxis='time',yaxis='amp',correlation='RR,LL',
       avgchannel='64',spw='0:4~60',antenna='ea23')

ea12 needs to be flagged completely its just a bit noisy all around and ea23 is pretty noisy during the first scans between initial and second pointing. Recall that these are antennas we became suspicious of while inspecting the calibration solutions.

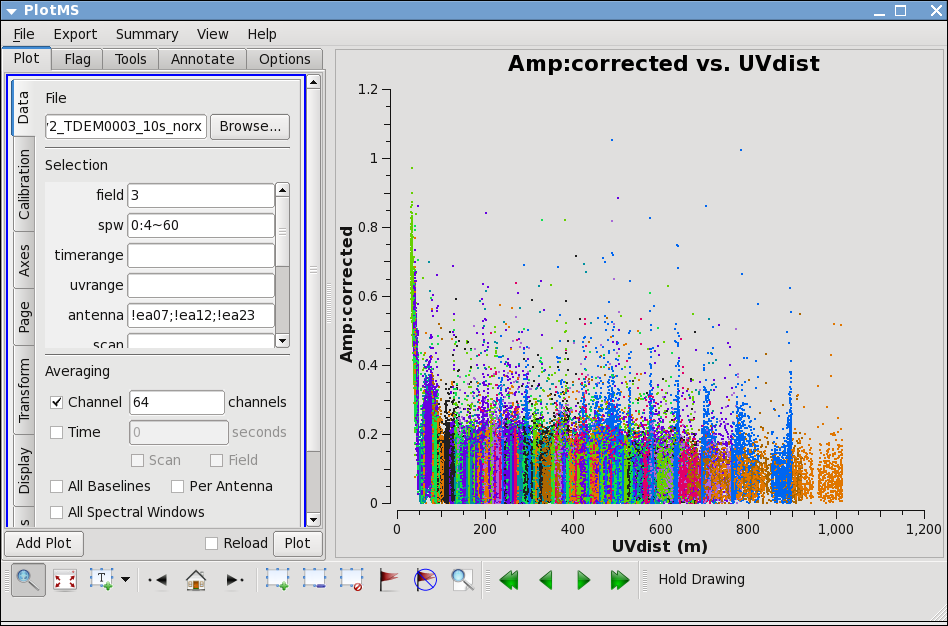
IRC+12216 as a function of uv-distance (after colorize by Antenna2).

Now lets see how the target looks. Because the target has resolved structure, its best to look at it as a function of uvdistance. We'll go ahead and exclude the three antennas we already know have problems. 

# In CASA
plotms(vis='day2_TDEM0003_10s_norx',field='3',ydatacolumn='corrected',
       xaxis='uvdist',yaxis='amp',correlation='RR,LL',
       avgchannel='64',spw='0:4~60',antenna='!ea07;!ea12;!ea23')

in "display" tab choose colorize by antenna2; then you can see that the spikes are caused by a single antenna. Use, zoom, mark, and locate to see which one. Also look at spw=1.

Turns out to be ea28; to confirm, replot with antenna=!ea28, and 

# In CASA
plotms(vis='day2_TDEM0003_10s_norx',field='3',ydatacolumn='corrected',
       xaxis='uvdist',yaxis='amp',correlation='RR,LL',
       avgchannel='64',spw='0:4~60',antenna='!ea07;!ea12;!ea23;!ea28')

To see if it's restricted to a certain time 

# In CASA
plotms(vis='day2_TDEM0003_10s_norx',field='3',ydatacolumn='corrected',
       xaxis='time',yaxis='amp',correlation='RR,LL',
       avgchannel='64',spw='0:4~60',antenna='ea28')


Baselines with ea28 clearly show issues until about two-thirds of the way through the observation. Plot another distant antenna to compare. We will go ahead and flag it all, since its hanging far out on the north arm by itself.

The additional data we've identified as bad need to be flagged, and then all the calibration steps will need to be run again. 

# In CASA
flagdata(vis='day2_TDEM0003_10s_norx',
         field=['',''],
         spw=['',''],
         antenna=['ea07,ea12,ea28','ea07,ea23'],
         timerange=['','03:21:40~04:10:00'])

Redo Calibration after more Flagging

After flagging, you'll need to repeat the calibration steps above. Here, we append _redo to the table names to distinguish them from the first round, in case we want to compare with previous versions. 

# In CASA
gaincal(vis='day2_TDEM0003_10s_norx',caltable='bpphase_redo.gcal',
        field='5',spw='0~1:20~40',
        refant='ea02',calmode='p',solint='int',minsnr=2.0,
        opacity=0.03,gaincurve=T)

# In CASA
bandpass(vis='day2_TDEM0003_10s_norx',caltable='bandpass_redo.bcal',
        field='5',
        refant='ea02',solint='inf',solnorm=T,
        gaintable=['bpphase_redo.gcal'],spwmap=[[]],
        opacity=0.03,gaincurve=T)

# In CASA
gaincal(vis='day2_TDEM0003_10s_norx',caltable='intphase_redo.gcal',
        field='2,5,7',spw='0~1:4~60',
        refant='ea02',calmode='p',solint='int',minsnr=2.0,
        gaintable=['bandpass_redo.bcal'],spwmap=[[]],
        opacity=0.03,gaincurve=T)

# In CASA
gaincal(vis='day2_TDEM0003_10s_norx',caltable='scanphase_redo.gcal',
        field='2,5,7',spw='0~1:4~60',
        refant='ea02',calmode='p',solint='inf',minsnr=2.0,
        gaintable=['bandpass_redo.bcal'],spwmap=[[]],
        opacity=0.03,gaincurve=T)

# In CASA
gaincal(vis='day2_TDEM0003_10s_norx',caltable='amp_redo.gcal',
        field='2,5,7',spw='0~1:4~60',
        refant='ea02',calmode='ap',solint='inf',minsnr=2.0,
        gaintable=['bandpass_redo.bcal','intphase_redo.gcal'],
        spwmap=[[],[]],
        opacity=0.03,gaincurve=T)

# In CASA      
fluxscale(vis='day2_TDEM0003_10s_norx',caltable='amp_redo.gcal',
          fluxtable='flux_redo.cal',reference='7')

Flux density for J0954+1743 in SpW=0 is: 0.279304 +/- 0.00114727 (SNR = 243.452, nAnt= 16)
Flux density for J0954+1743 in SpW=1 is: 0.287039 +/- 0.00107576 (SNR = 266.824, nAnt= 16)
Flux density for J1229+0203 in SpW=0 is: 30.5932 +/- 0 (SNR = inf, nAnt= 16)
Flux density for J1229+0203 in SpW=1 is: 30.2475 +/- 0 (SNR = inf, nAnt= 16)

Feel free to pause here and remake the calibration solution plots from above, just be sure to put in the revised table names.

Redo Applycal and Inspect

Now, apply all the new calibrations, which will overwrite the old ones. These commands are identical to those above, with the exception of the _redo part of each calibration filename. 

# In CASA
applycal(vis='day2_TDEM0003_10s_norx',field='2',
        gaintable=['bandpass_redo.bcal','intphase_redo.gcal','flux_redo.cal'],
        spwmap=[[],[],[]],gainfield=['5','2','2'],
        opacity=0.03,gaincurve=T)

# In CASA
applycal(vis='day2_TDEM0003_10s_norx',field='5',
        gaintable=['bandpass_redo.bcal','intphase_redo.gcal','flux_redo.cal'],
        spwmap=[[],[],[]],gainfield=['5','5','5'],
        opacity=0.03,gaincurve=T)
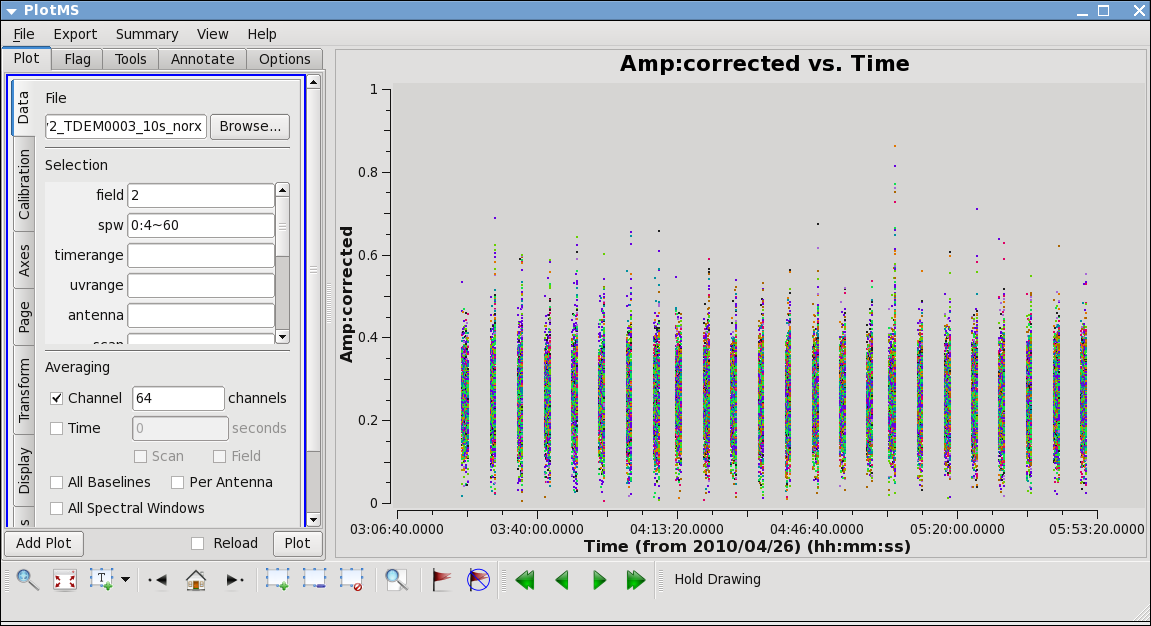
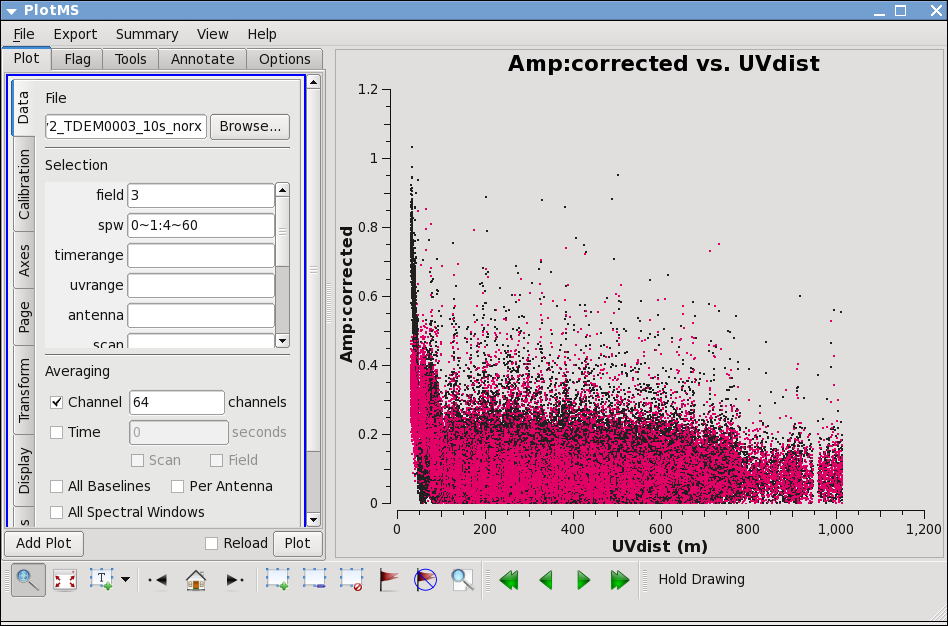
Gain calibrator after further flagging and recalibration
IRC+10216 after further flagging and recalibration (after selecting colorize by spw).
# In CASA
applycal(vis='day2_TDEM0003_10s_norx',field='7',
        gaintable=['bandpass_redo.bcal','intphase_redo.gcal','flux_redo.cal'],
        spwmap=[[],[],[]],gainfield=['5','7','7'],
        opacity=0.03,gaincurve=T)

# In CASA
applycal(vis='day2_TDEM0003_10s_norx',field='3',
        gaintable=['bandpass_redo.bcal','scanphase_redo.gcal','flux_redo.cal'],
        spwmap=[[],[],[]],gainfield=['5','2','2'],
        opacity=0.03,gaincurve=T)

Now you can inspect the calibrated data again. Except for random scatter things look pretty good. 

# In CASA
plotms(vis='day2_TDEM0003_10s_norx',field='2',ydatacolumn='corrected',
       xaxis='time',yaxis='amp',correlation='RR,LL',
       avgchannel='64',spw='0:4~60',antenna='')

Lets check the target again, looking at both spws, and selecting "Display" colorize by spw. You can use the Mark and Locate buttons to assess that the remaining scatter seems random, i.e. no particular antenna or time range appears to be responsible. 

# In CASA
plotms(vis='day2_TDEM0003_10s_norx',field='3',ydatacolumn='corrected',
       xaxis='uvdist',yaxis='amp',correlation='RR,LL',
       avgchannel='64',spw='0~1:4~60',antenna='')

Split

Now we split the data into individual files. This is not strictly necessary, as you can select the appropriate fields in later clean stages, but it is safer in case for example you get confused with later processing and want to fall back to this point (this is especially a good idea if you plan to do continuum subtraction or self calibration later on). It also makes smaller individual files in case you want to copy to another machine or colleague.

Here, we split off the data for the phase calibrator and the target: 

# In CASA
split(vis='day2_TDEM0003_10s_norx',outputvis='J0954',
      field='2')

# In CASA
split(vis='day2_TDEM0003_10s_norx',outputvis='IRC10216',
      field='3')

To reinitialize the scratch columns for use by later tasks, we need to run clearcal for both new datasets 

# In CASA
clearcal(vis='J0954')

# In CASA
clearcal(vis='IRC10216')

UV Continuum Subtraction

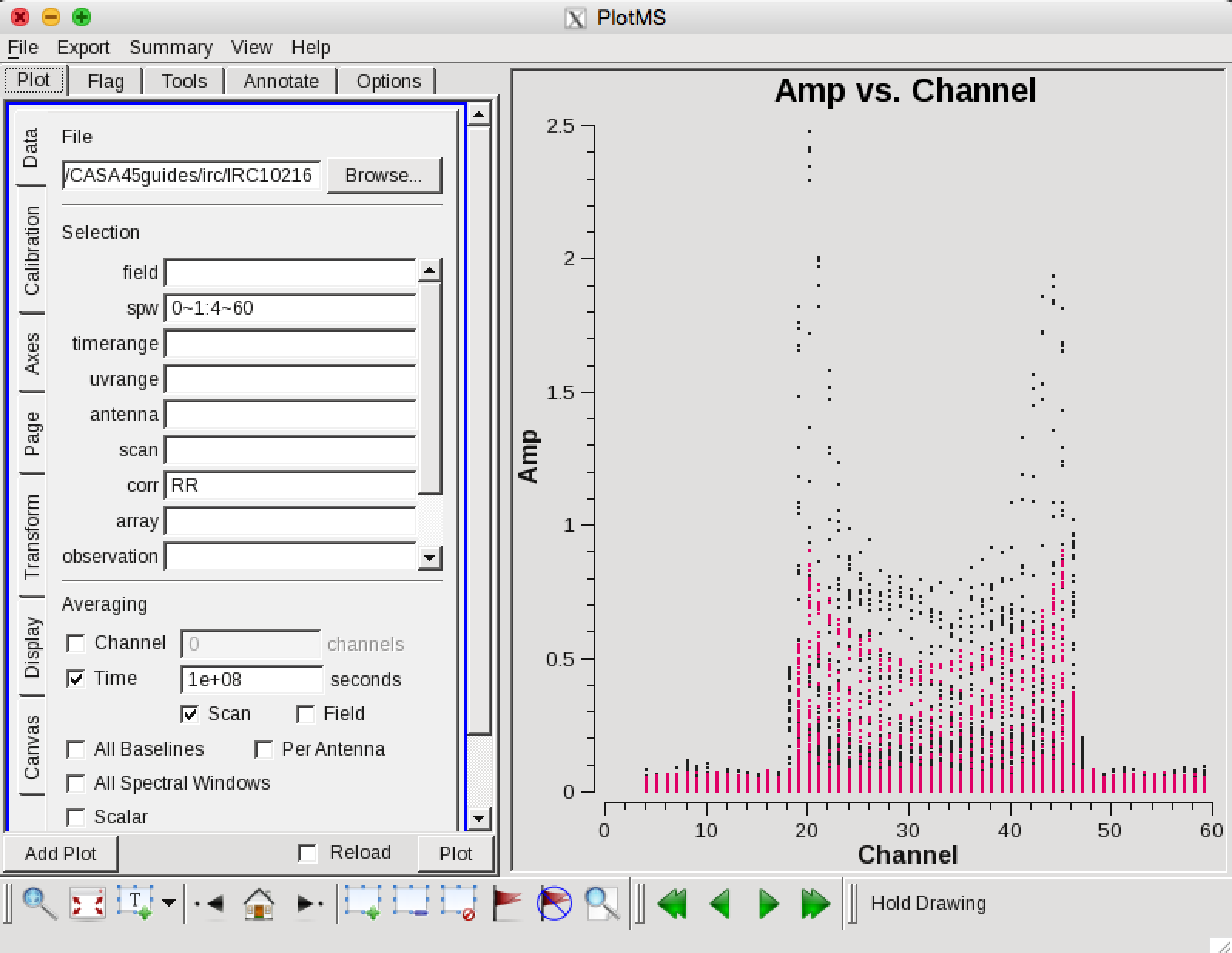
UV-plot of the spectral line signal in both spw for IRC+10216.

Now we can make a vector averaged uv-plot of the calibrated target spectral line data. It is important to note that you will only see signal in such a plot if (1) the data are well calibrated, (2) there is significant signal near the phase center of the observations. If this isn't true for your data, you will need to make an initial line+continuum cube to determine the line-free channels. 

plotms(vis='IRC10216',field='',ydatacolumn='corrected',
       xaxis='channel',yaxis='amp',correlation='RR',
       avgtime='1e8',avgscan=T,spw='0~1:4~60',antenna='')

in the Display tab, choose colorize by spw and change the Unflagged points symbol to custom and Style of 3.

You should see the "horned profile" typical of a rotation shell. From this plot, you can guess that strong line emission is restricted to channels 18 to 47 (zoom in if necessary to see exactly what the channel numbers are).

In the Data tab you can also click on "all baselines" to average all baselines, but this is a little harder to see.

Now we want to use the line free channels to create a model of the continuum emission that can be subtracted to form a line-only dataset. We want to refrain from going to close to the edges of the band -- these channels are typically noisy, and we don't want to get too close to the line channels because we could only see strong line emission in the vector averaged uv-plot. 

uvcontsub2(vis='IRC10216',fitspw='0~1:4~13;52~60',
       want_cont=T)

The "want_cont=T" will produce new two new datasets, IRC10216.contsub is the continuum subtracted line data, and IRC10216.cont is the continuum estimate (note however, that it is still a multi-channel cube).

Image the Spectral Line Data

Here we make images from the continuum-subtracted, calibrated spectral line data. Because the spectral line emission from IRC+10216 has significant extended emission, it is very important to run clean interactively, and make a clean mask.

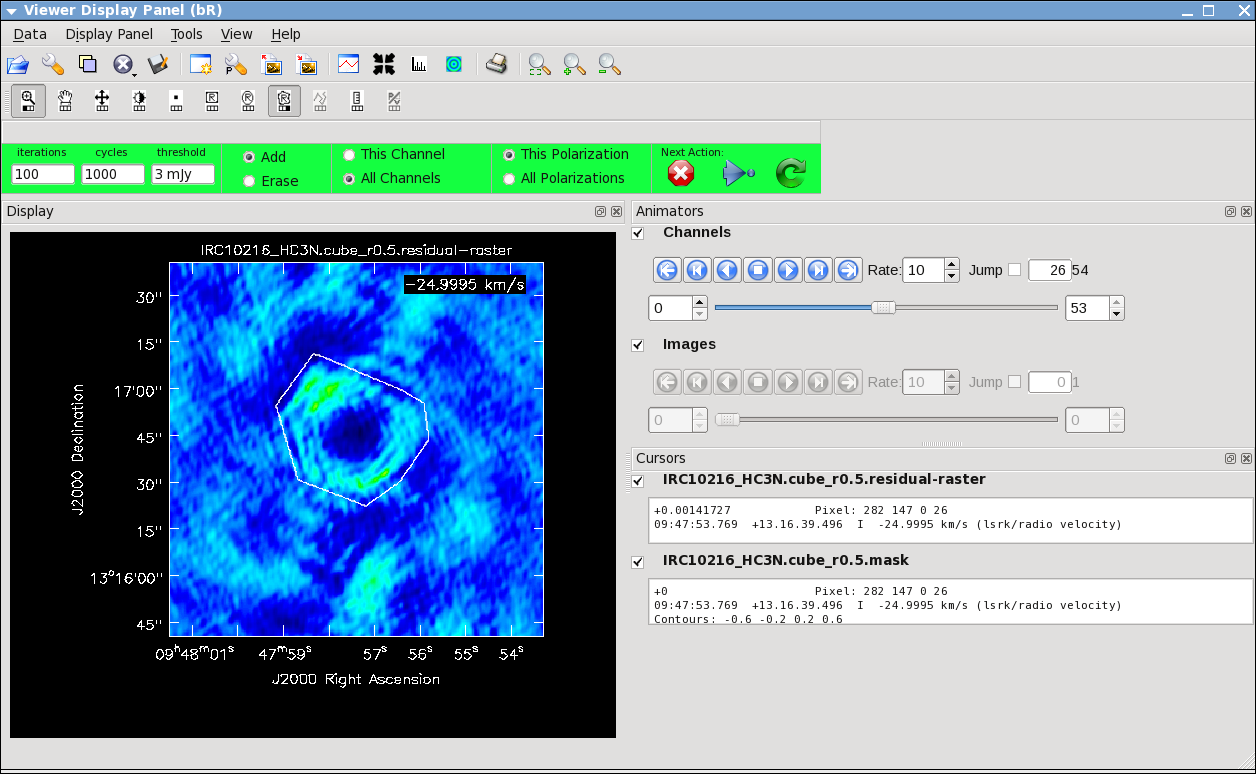
Channel 28 shown for the HC3N cube shown in the interactive viewer with the white contour showing the mask contour drawn with the polygon tool.


# In CASA
clean(vis='IRC10216.contsub',imagename='IRC10216_HC3N.cube_r0.5',
      imagermode='csclean',
      imsize=300,cell=['0.4arcsec'],spw='0:5~58',
      mode='velocity',interpolation='linear',
      restfreq='36.39232GHz',outframe='LSRK',
      weighting='briggs',robust=0.5,
      interactive=T,
      threshold='3.0mJy',niter=100000)

It will take a little while to grid the data, but viewer will open when it's ready to start an interactive clean. Use the "tape deck" at the bottom of the Viewer display GUI to step through to the channel with the most extended (in angular size) emission, select "all channels" for the clean mask, select the polygon tool (second in from the right) and make a single mask that applies to all channels (see example in thumbnail). Once you make the polygon region, you need to double click inside it to save the mask region -- if you see the polygon turn white you will know you succeeded. Note, that if you had the time and patience you could make a clean mask for each channel, and this would create a slightly better result.

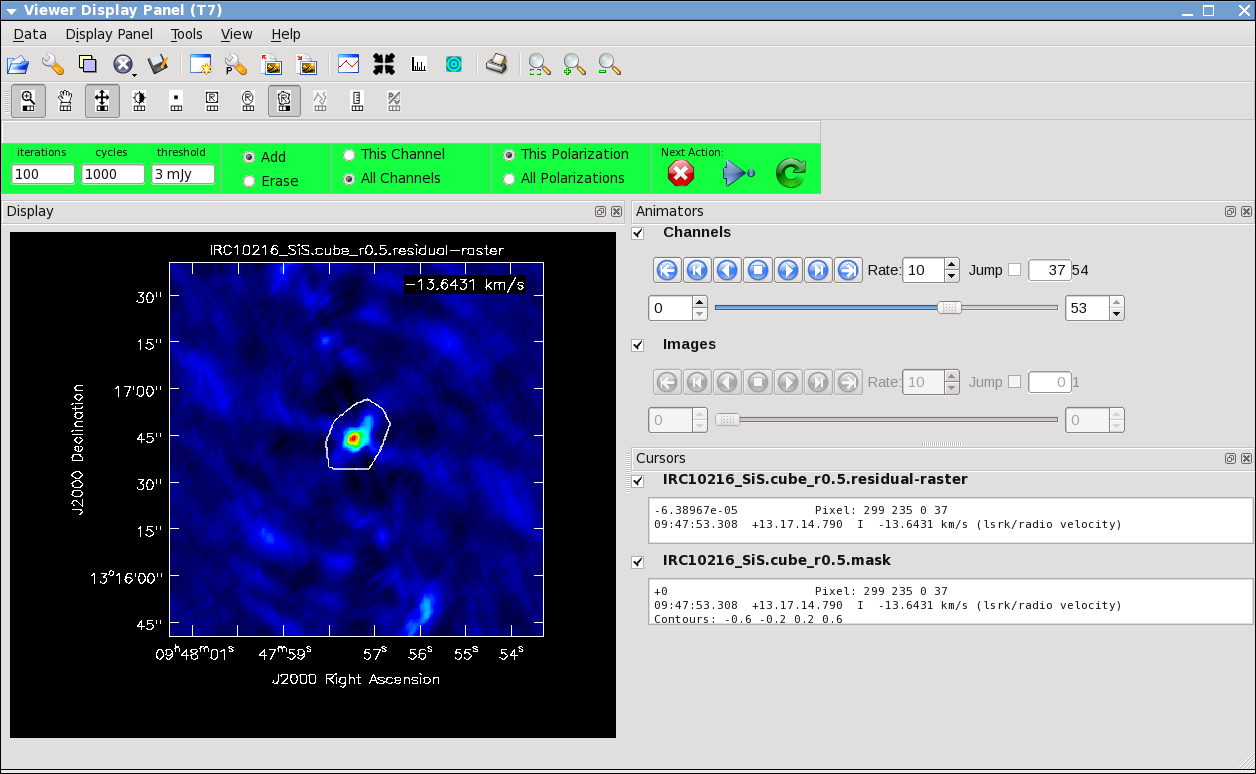
Channel 16 shown for the SiS cube in the interactive viewer with the white contour showing the mask contour drawn with the polygon tool.

After making the mask you should check that the emission in all the other channels fits within the mask you made using the "tape deck" to move back and forth. If you need to include more area in the mask, you can chose the "erase" toggle at the top, and then encircle your existing mask with a polygon and double click inside. Then go back to "add" toggle at top and make a new mask. Alternatively, you can erase a part of the mask, or you can add to the existing mask by drawing new polygons. Feel free to experiment with this a bit.

To continue with clean use the "Next action" buttons in the green area on the Viewer Display GUI: The red X will stop clean where you are, the blue arrow will stop the interactive part of clean, but continue to clean non-interactively until reaching the stopping niter or threshold (whichever comes first), and the green arrow will clean until it reaches the "iterations" parameter on the left side of the green area.

Keep cleaning, by using the green Next Action arrow until the residual displayed in the viewer looks "noise like". To speed things up, you might change the iteration parameter in the viewer to something like 300. This parameter can also be set in the task command. You will notice that in this particular case, there are residuals that cannot be cleaned -- these are due to the extended resolved out structure on size scales larger than the array is sensitive to (the "Largest Angular Scale" or LAS that the array is sensitive to can be calculated from the shortest baseline length).

Repeat the process for the SiS line using the call below, note that the emission for this line is less extended than the HC3N -- this has to do with the different excitation requirements of the two different lines. The SiS is excited closer to the central star than the HC3N. 

# In CASA
clean(vis='IRC10216.contsub',imagename='IRC10216_SiS.cube_r0.5',
      imagermode='csclean',
      imsize=300,cell=['0.4arcsec'],spw='1:5~58',
      mode='velocity',interpolation='linear',
      restfreq='36.30963GHz',outframe='LSRK',
      weighting='briggs',robust=0.5,
      interactive=T,
      threshold='3.0mJy',niter=100000)

Image the Continuum data

Below the use of mode='mfs' will make a single multi-frequency synthesis image out of the specified spw. Again you should make an interactive clean mask. Since no threshold is set, you will need to stop cleaning when the residual looks noise like using the red x "Next Action" button (it will be done when the viewer comes back the second time). 

# In CASA
clean(vis='IRC10216.cont',imagename='IRC10216.36GHzcont',
      mode='mfs',imagermode='csclean',
      imsize=300,cell=['0.4arcsec'],spw='0~1:5~59',
      weighting='briggs',robust=0.5,
      interactive=T)

Now look at the result in the viewer if you like 

# In CASA
Viewer

Image Analysis and Viewing

Next make integrated intensity maps (moment 0) and integrated velocity maps (moment 1). To do this, we'll want to know what channels the line emission starts and ends on, and also the rms noise in a single channel. So first lets open the viewer: 

# In CASA 
viewer

Then use the Viewer tape deck to see which channels have significant line emission. For HC3N, the line channel range in the cube is 11 to 40, and it is the same for SiS.

Then use the tape deck to go to a line free channel, select the box region tool and make a box. When you double click in the box, the image statistics for the whole cube will print to the terminal and for the channel you are one, it will print to a pop up window. Move the box around a bit to see what the variation is. You should get something like 2 mJy. Note that the rms is much worse in channels with strong emission because of the low dynamic range of these data. If you want the box tool to go away, hit the escape key.

Now lets make the moment 0 and moment 1 maps. For moment zero, its best to limit the calculation to image channels with significant signal in them, but not to apply a flux cutoff, as this will bias the derived integrated intensities upward.

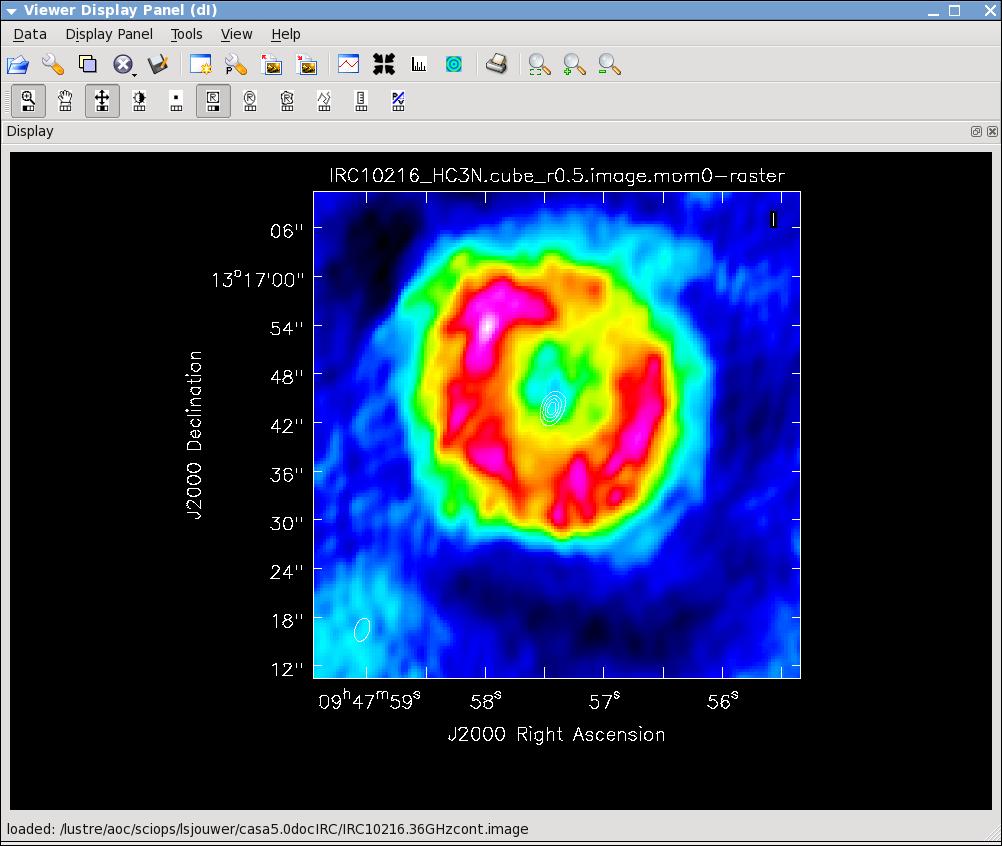
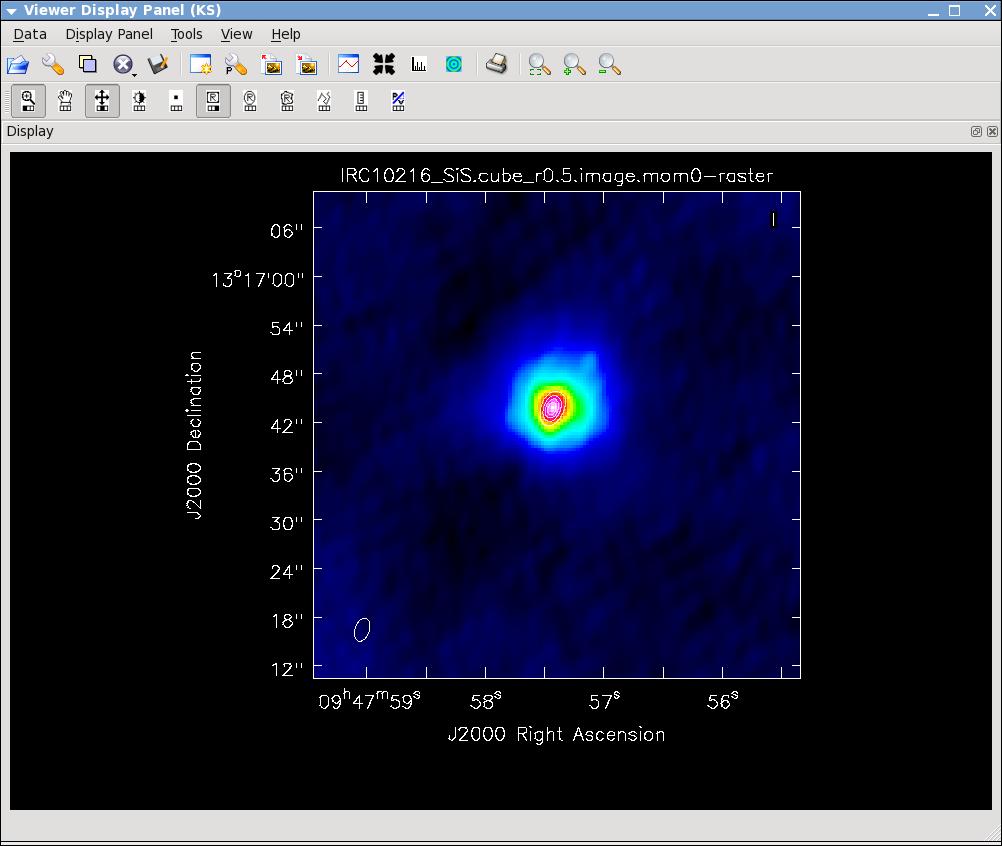
HC3N moment 0 map with white continuum contours superposed.
SiS moment 0 map with white continuum contours superposed.
# In CASA
immoments(imagename='IRC10216_HC3N.cube_r0.5.image',moments=[0],
          axis='spectral',
          chans='11~40',
          outfile='IRC10216_HC3N.cube_r0.5.image.mom0')

# In CASA
immoments(imagename='IRC10216_SiS.cube_r0.5.image',moments=[0],
          axis='spectral',
          chans='11~40',
          outfile='IRC10216_SiS.cube_r0.5.image.mom0')

For moment 1, it is essential to apply a conservative flux cutoff to limit the calculation to high signal-to-noise areas. Here we use about 5sigma. 

# In CASA
immoments(imagename='IRC10216_HC3N.cube_r0.5.image/',moments=[1],
          axis='spectral',
          chans='11~40',excludepix=[-100,0.01],
          outfile='IRC10216_HC3N.cube_r0.5.image.mom1')

# In CASA
immoments(imagename='IRC10216_SiS.cube_r0.5.image/',moments=[1],
          axis='spectral',
          chans='11~40',excludepix=[-100,0.01],
          outfile='IRC10216_SiS.cube_r0.5.image.mom1')

Now user the viewer to further explore the images you've made.


↵ CASAguides

--Crystal Brogan

Retrieved from "https://casaguides.nrao.edu/index.php?title=EVLA_spectral_line_IRC10216&oldid=3262"