Simulating ngVLA Data-CASA5.4.1: Difference between revisions
No edit summary |
No edit summary |
||
| (135 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
=== Introduction === | |||
The following tutorial shows how to create simulated data for the next generation Very Large Array (ngVLA). The ngVLA is composed of different subarrays that make up the current reference design. The configuration files for the different subarrays can be used for simulations and calculations that investigate the scientific capabilities of the ngVLA. Each configuration (.cfg) file contains the name of the observatory, the antenna positions, the coordinate system of the antenna positions and the diameter and pad name of each antenna. For these configuration files, the coordinate system is 'global', which signifies that the positions x, y, z are in meters relative to the Earth center following the FITS WCS convention. | |||
[[Image:Model_93GHz_new_v2.png|400px|thumb|'''Figure 1:''' Model image]] | |||
CASA provides two ways to create a simulation: the {{simobserve}} task and the [https://casa.nrao.edu/casadocs-devel/stable/global-tool-list/tool_simulator ''<tt>sm</tt> toolkit'']. With these methods we can generate measurement sets (MSs), add thermal noise, and predict model visibilities, from which we can explore the ngVLA’s imaging capabilities. The {{simobserve}} task is very user friendly but it is important to be aware that it has several limitations and it has been designed primarily for ALMA and the VLA. For this reason, we also demonstrate the use of the <tt>sm</tt> toolkit, which provides much more flexibility in setting the observational parameters and is more compatible with observatories that are not recognized by CASA. | |||
In this tutorial we present three example simulations: (i) {{simobserve}} using a model image, (ii) {{simobserve}} using a component list, and (iii) a <tt>sm</tt> toolkit simulation. For more information about component lists, refer to the | |||
[https://casaguides.nrao.edu/index.php/Simulation_Guide_Component_Lists_(CASA_5.1) Simulation Guide Component Lists] and the [https://casaguides.nrao.edu/index.php/Create_a_Component_List_for_Selfcal Simulation Guide Component List for Selfcal]. The model image used in portions of this guide, a 93 GHz model of a protoplanetary disk, is shown in Figure 1. The next section will explain how to obtain the model image. We will also show how to create and use a component list instead of a model image for the simulations. | |||
We will create example continuum simulations at 93 GHz, consisting of a single channel observed for a total of 4 hours with a 60 second correlator integration time'''†''' . We will then add to these simulations an amount of thermal noise that is representative of the ngVLA's continuum sensitivity. The array configuration used in this guide is the Main ngVLA subarray, which is composed of 214 18 m antennas and extends over a maximum baseline of 1005.4 km. The configuration file we will use throughout this tutorial is called ngvla-main-revC.cfg. The next section will explain how to obtain this file. | |||
'''†''' We choose this integration time in order to keep the MS files small. Time smearing is not an issue for simulated observations, but this value would need to be reconsidered before scheduling actual observations, e.g., on the order of 0.2 second correlator integration time. | |||
=== Obtaining the Necessary Files for this Guide === | |||
Before creating the first simulation we need to obtain the configuration file and model image. Configuration files for each ngVLA subarray can be downloaded from the [http://ngvla.nrao.edu/page/tools ngVLA Configuration Tools] portion of the ngVLA website. The configuration file we will use throughout this tutorial is called [http://ngvla.nrao.edu/system/media_files/binaries/121/original/ngvla-main-revC.cfg?1543949616 ngvla-main-revC.cfg], which can be directly downloaded. | |||
Alternatively, these configuration files are included as part of CASA distributions 5.5 and greater. They can also be added to older versions of CASA by running the following command inside CASA to update CASA's data repository: | |||
<source lang="python"> | |||
# In CASA | |||
!update-data | |||
</source> | |||
The configuration files are stored inside CASA in a folder along with configuration files for other observatories. Since the path to this folder may depend on your operating system and CASA version, a convenient way to find the path to the configuration files is to run the following command inside CASA: | |||
<source lang="python"> | |||
# In CASA | |||
configdir = casa.values()[0]['data']+'/alma/simmos/' | |||
</source> | |||
We will use this path later in this guide as part of the simulation with the <tt>sm</tt> toolkit. For simulations with the {{simobserve}} task, only the configuration file name needs to be given since the task will automatically try to find the file in this folder. | |||
We | We also need to obtain the model image before we start the simulations. The model image used in portions of this guide, [https://casa.nrao.edu/Data/ngVLA/ppmodel_image_93GHz.fits.gz ppmodel_image_93GHz.fits.gz], can be directly downloaded and will then need to be unzipped using gunzip, before using it in the simulations. | ||
=== Estimating the Scaling Parameter for Adding Thermal Noise === | |||
This section describes the procedure we will use to add noise to our simulations and the relevant calculations that we need to prepare for this. | |||
Simobserve's parameter to corrupt the simulated data is called '''thermalnoise''' and for interferometric data the allowed values are ''"tsys-atm"'', ''"tsys-manual"'' or " " (refer to the [https://casaguides.nrao.edu/index.php/Corrupting_Simulated_Data_(Simulator_Tool) Corrupting Simulated Data guide] for more details). The option " " will not add any noise to the data, and the option ''"tsys-atm"'' is only applicable to ALMA since it uses site parameters which are specific to that observatory. For the option ''"tsys-manual"'', it is necessary to supply several additional parameters which are required to construct an atmospheric model. In order to achieve the desired sensitivity without atmospheric modeling, we have chosen to corrupt the simulated data using the [https://casa.nrao.edu/docs/CasaRef/simulator.setnoise.html#x822-8350002.4.1 "<tt>sm.setnoise</tt>"] function of the <tt>sm</tt> toolkit. In addition to the modes ''"tsys-atm"'' and ''"tsys-manual"'', this function also allows the option of ''"simplenoise"''. As the name indicates, ''"simplenoise"'' adds random Gaussian noise to the visibilities based on a simple scaling factor. We will use this same technique for all three example simulations, i.e., those made with the {{simobserve}} task and those made with the <tt>sm</tt> toolkit. | |||
In order to estimate the scaling factor for the ''"simplenoise"'' parameter in <tt>sm.setnoise</tt> we use the following procedure: | |||
The RMS noise (<math>\sigma_{NA}</math>) in an untapered, naturally-weighted Stokes I image will be approximately (see [https://casa.nrao.edu/casadocs/casa-5.4.0/global-tool-list/tool_simulator/methods "<tt>setnoise</tt> function"]) | |||
<math>\sigma_{NA} \sim \frac{\sigma_{simple}}{ \sqrt{n_{ch}\,n_{pol}\,n_{baselines}\,n_{integrations} }}</math> (1) | |||
where <math>\sigma_{simple}</math> is the simplenoise parameter in <tt>sm.setnoise</tt> and corresponds to the noise per visibility, <math>n_{ch}</math> is the total number of channels across all spectral windows, <math>n_{pol}</math> is the number of polarizations used for Stokes I (typically 2) and <math>n_{integrations}</math> is the number of correlator integration times in the MS (i.e., total on-source time / integration time). For the example simulations in this guide, the track time is 4 hrs and the integration time is 60 sec, thus <math>n_{integrations}=240</math>. Additionally, for these examples the total number of channels is 1 and the number of polarizations is 2. The number of baselines <math>n_{baselines}</math> is | |||
<math>N(N-1)/2</math> where N is the number of antennas in the array. For the array configuration used in this guide (ngvla-main-revC.cfg), N=214 and therefore <math>n_{baselines}= 22791</math>. | |||
If you already know the expected image noise (<math>\sigma_{NA}</math>) for your untapered, naturally-weighted image, you can solve for the scaling parameter <math>\sigma_{simple}</math> in the above equation (1) and pass <math>\sigma_{simple}</math> to the simplenoise parameter in <tt>sm.setnoise</tt>. | |||
'''If instead you want to calculate the expected sensitivity for an ngVLA image, we suggest the following procedure:''' | |||
'''(i)''' Calculate the expected untapered, naturally weighted point source sensitivity (<math>\sigma_{NA}</math>) using one of the ngVLA performance tables. In Appendix D of [http://library.nrao.edu/public/memos/ngvla/NGVLA_55.pdf ngVLA memo #55] there are key performance metrics for 6 subarrays which are tabulated as a function of frequency and resolution. For our example, we find in Table 10 of ngVLA memo #55 that the untapered, naturally weighted point source sensitivity of the Main interferometric array at 93 GHz is 0.83 uJy/beam for a 1 hour observation. | |||
'''(ii)''' Scale that number to the desired observation length, in this case <math>t_{track}=4\,h</math>. Therefore, <math>\sigma_{NA} = 0.83/\sqrt{(t_{track}/1\,hour)} = 0.415\,\text{uJy/beam}</math>. | |||
'''(iii)''' Use the expected image noise (<math>\sigma_{NA}</math>) in the above equation (1) to solve for the scaling factor <math>\sigma_{simple}</math>. In this case, <math>\sigma_{simple}=0.415*\sqrt{1*2*22791*240} = 1.4\,\text{mJy}</math>. | |||
Once you have derived the scaling factor <math>\sigma_{simple}</math>, run <tt>sm.setnoise</tt> and corrupt the visibilities of the noise-free MS. Your resulting untapered, naturally-weighted image will then have an RMS approximately equal to your desired image noise. Since it is not easy to undo this step, it is a good idea to make a copy of the noise-free MS before adding noise. The following mock example outlines this procedure: | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
os.system('cp -r noise_free.ms noisy.ms) | ## Create a copy of the noise-free MS: | ||
os.system('cp -r noise_free.ms noisy.ms') | |||
## Open the MS we want to add noise to with the sm tool: | |||
sm.openfromms('noisy.ms') | sm.openfromms('noisy.ms') | ||
sm.setnoise(mode = | |||
## Set the noise level using the simplenoise parameter estimated earlier in this section: | |||
sm.setnoise(mode = 'simplenoise', simplenoise = sigma_simple) | |||
## Add noise to the 'DATA' column (and the 'CORRECTED_DATA' column if present): | |||
sm.corrupt() | sm.corrupt() | ||
## Close the sm tool: | |||
sm.done() | sm.done() | ||
</source> | </source> | ||
Note that this example will not execute without a MS named ''"noise_free.ms"'' and a defined variable <tt>sigma_simple</tt>. See below for working examples of this procedure used in conjunction with the creation of simulated MSs and the prediction of model visibilities. | |||
===Example Simulation using Simobserve with a Model Image=== | |||
We will use the {{simobserve}} task to create our first noise-free measurement set (MS), using the configuration file and model image described in the Introduction. | |||
===Simobserve | |||
We | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
simobserve(project = | simobserve(project = 'ngVLA_214_ant_60s_noise_free', | ||
skymodel = | skymodel = 'ppmodel_image_93GHz.fits', | ||
setpointings = True, | setpointings = True, | ||
integration = '60s', | integration = '60s', | ||
obsmode = 'int', | obsmode = 'int', | ||
antennalist = | antennalist = 'ngvla-main-revC.cfg', | ||
hourangle = 'transit', | hourangle = 'transit', | ||
totaltime = '14400s', | totaltime = '14400s', | ||
thermalnoise = '', | thermalnoise = '', | ||
graphics = 'none' | graphics = 'none') | ||
</source> | </source> | ||
'''project:''' Simobserve will | '''project:''' Simobserve will create a folder with the project name in your current working directory, and this folder will contain all the resulting files including the noise-free MS. | ||
''' | '''skymodel:''' The input model image in Jy/pixel units, can be a single image or a spectral cube. The simulated MS will inherit the number of channels, central frequency, source direction, and peak flux of this input model. These can be adjusted using the optional parameters '''inbright''', '''indirection''', '''incell''', '''incenter''', and '''inwidth'''. In this example, we do not modify these optional parameters. | ||
''' | '''setpointings:''' We choose the value of True, which allows {{simobserve}} to derive the pointing positions using its own algorithm and properties of the input model image. Since the size of the model is much smaller than the primary beam, a single pointing will be generated (instead of a mosaic). We also set the expanded parameter '''integration''' to '60s' (our chosen correlator integration time) and leave other expanded parameters set to their default values. | ||
'''totaltime | '''obsmode:''' We set this parameter to 'int' to simulate interferometric data. We also set values for several expandable parameters. For '''antennalist''', we give the name of the configuration file for the ngVLA Main interferometric array. {{simobserve}} will read this file from a directory inside the CASA distribution (see the section on Obtaining the Necessary Files for this Guide). We set '''totaltime''' to the total on-source observation time, use the '''hourangle''' parameter to center our observation time on transit, and leave other expanded parameters as default. | ||
'''thermalnoise:''' We leave this parameter empty | '''thermalnoise:''' We leave this parameter empty to create a noise-free simulation. We will add the noise later in a separate step. | ||
'''graphics:''' | '''graphics:''' This will show graphics on the screen and/or save them as png files in the project directory. However, at the moment this is not working properly for baselines larger than a few hundred km. For this reason, we use 'none' in this example. | ||
'''Now, to add thermal noise, we do the following:''' | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
## Create a copy of the noise-free MS: | |||
os.system('cp -r ngVLA_214_ant_60s_noise_free/ngVLA_214_ant_60s_noise_free.ngvla-main-revC.ms ngVLA_214_ant_60s_noisy.ms') | os.system('cp -r ngVLA_214_ant_60s_noise_free/ngVLA_214_ant_60s_noise_free.ngvla-main-revC.ms ngVLA_214_ant_60s_noisy.ms') | ||
## Open the MS we want to add noise to with the sm tool: | |||
sm.openfromms('ngVLA_214_ant_60s_noisy.ms') | sm.openfromms('ngVLA_214_ant_60s_noisy.ms') | ||
sm.setnoise(mode = 'simplenoise', simplenoise = | |||
## | ## Set the noise level using the simplenoise parameter estimated in the section on Estimating the Scaling Parameter for Adding Thermal Noise: | ||
sigma_simple = '1.4mJy' | |||
sm.setnoise(mode = 'simplenoise', simplenoise = sigma_simple) | |||
## Add noise to the 'DATA' column (and the 'CORRECTED_DATA' column if present): | |||
sm.corrupt() | sm.corrupt() | ||
## Close the sm tool: | |||
sm.done() | sm.done() | ||
</source> | </source> | ||
===Example Simulation using Simobserve with a Component List=== | |||
Instead of using a model image we can use a component list for the simulation. '''Warning:''' At the moment, this method may take several times longer than using a model image due to internal issues with {{simobserve}}. Below is a simple example of how to make a component list consisting of a single point source. | |||
Instead of using a model image we can | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
## | ## Position of the source that we want to observe: | ||
direction = 'J2000 00:00:00.0 +24.00.00.0' | |||
## | ## Use the component list (cl) tool to make a model centered at the direction given above, and with a source flux of 10 uJy: | ||
cl.addcomponent(dir = direction, flux = 10e-6, freq = '93GHz') | |||
## Name of the component list model: | |||
cl.rename(filename = 'my_component.cl') | cl.rename(filename = 'my_component.cl') | ||
## | ## Close the component list: | ||
cl.done() | cl.done() | ||
</source> | </source> | ||
Now, we can use {{simobserve}} using the generated component list: | |||
Now, we can | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
simobserve(project | simobserve(project = 'ngVLA_214_ant_60s_noise_free', | ||
complist = 'my_component.cl' , | complist = 'my_component.cl' , | ||
compwidth = ' | compwidth = '10GHz', | ||
setpointings = True, | setpointings = True, | ||
integration = '60s', | integration = '60s', | ||
obsmode = 'int', | obsmode = 'int', | ||
antennalist = | antennalist = 'ngvla-main-revC.cfg', | ||
hourangle = 'transit', | hourangle = 'transit', | ||
totaltime = ' | totaltime = '14400s', | ||
thermalnoise = '', | thermalnoise = '', | ||
graphics = 'none' | graphics = 'none') | ||
</source> | </source> | ||
Most of the parameters are the same as the previous example. The parameters which are specific to using a component list are: | |||
'''complist:''' Here we provide the component list created above. The expandable parameter '''compwidth''' indicates the bandwidth of the component, which will be used to set the bandwidth of the MS and resulting images. | |||
===<tt>sm</tt> toolkit | Then we can add the thermal noise in the same way as in the section, Example Simulation using Simobserve with a Model Image. | ||
===Example Simulation using <tt>sm</tt> toolkit with either a Model Image or a Component List=== | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
## | |||
## Set the name of the configuration file for the ngVLA Main subarray: | |||
conf_file = 'ngvla-main-revC.cfg' | conf_file = 'ngvla-main-revC.cfg' | ||
## | ## Set the path to the configuration file within the CASA distribution. | ||
## configdir = casa.values()[0]['data']+'/alma/simmos/' | ## If using CASA version older than 5.5, see the section on Obtaining the Necessary Files for this Guide: | ||
configdir = casa.values()[0]['data']+'/alma/simmos/' | |||
## Use simutil to read the .cfg file: | |||
## Use simutil to read the .cfg file | |||
from simutil import simutil | from simutil import simutil | ||
u = simutil() | u = simutil() | ||
xx,yy,zz,diam,padnames,telescope,posobs = u.readantenna(configdir+conf_file) | |||
############################################################## | ######################################################################## | ||
## Setting the observation framework | ## Setting the observation framework, i.e., defining the sources, ## | ||
## similar to what we would do in the OPT when setting up | ## resources, and scans similar to what we would do in the ## | ||
## | ## Observation Preparation Tool (OPT) when setting up an observation. ## | ||
############################################################## | ######################################################################## | ||
## Simulate measurement set using the simulation utilities sm tool | ## Simulate measurement set using the simulation utilities sm tool: | ||
ms_name = 'ngVLA_214_ant_60s_noise_free.ms' ## Name of your measurement set | ms_name = 'ngVLA_214_ant_60s_noise_free.ms' ## Name of your measurement set | ||
sm.open( ms_name ) | sm.open( ms_name ) | ||
## Get the position of the ngVLA using the measures utilities (me) | ## Get the position of the ngVLA using the measures utilities (me): | ||
pos_ngVLA = me.observatory('ngvla') | pos_ngVLA = me.observatory('ngvla') | ||
## | ## Set the antenna configuration using the sm tool using the positions, | ||
## diameter and names of the antennas as read from the configuration file | ## diameter, and names of the antennas as read from the configuration file: | ||
sm.setconfig(telescopename = telescope, x = xx, y = yy, z = zz, | sm.setconfig(telescopename = telescope, x = xx, y = yy, z = zz, | ||
dishdiameter = diam.tolist(), mount = 'alt-az', | dishdiameter = diam.tolist(), mount = 'alt-az', | ||
antname = padnames, | antname = padnames, padname = padnames, | ||
coordsystem = 'global', referencelocation = pos_ngVLA) | coordsystem = 'global', referencelocation = pos_ngVLA) | ||
## Set the spectral windows, in this case, as a single channel. | |||
## Simulation with a channel resolution of 10 GHz: | |||
sm.setspwindow(spwname = 'Band6', freq = '93GHz', deltafreq = '10GHz', | |||
freqresolution = '10GHz', nchannels = 1, stokes = 'RR RL LR LL') | |||
## | ## Set feed parameters for the antennas: | ||
sm.setfeed('perfect R L') | sm.setfeed('perfect R L') | ||
## | ## Set the field of observation that we are going to simulate | ||
## (where the telescope is pointing), in this example we are using | ## (where the telescope is pointing), in this example we are using | ||
## a Dec of +24deg | ## a Dec of +24deg. | ||
sm.setfield(sourcename = 'My source', | sm.setfield(sourcename = 'My source', | ||
sourcedirection = ['J2000','00h0m0.0','+24.0.0.000']) | sourcedirection = ['J2000','00h0m0.0','+24.0.0.000']) | ||
## | ## Set the limit of the observation for the antennas: | ||
sm.setlimits(shadowlimit = 0.001, elevationlimit = '8.0deg') | sm.setlimits(shadowlimit = 0.001, elevationlimit = '8.0deg') | ||
## | ## Weight to assign autocorrelation: | ||
sm.setauto(autocorrwt = 0.0) | sm.setauto(autocorrwt = 0.0) | ||
## | ## Integration time or how often the array writes one visibility | ||
## referencetime is the start date (today's date) and epoch measure ('utc'): | |||
integrationtime = '60s' | integrationtime = '60s' | ||
sm.settimes(integrationtime = integrationtime, usehourangle = True, | sm.settimes(integrationtime = integrationtime, usehourangle = True, | ||
referencetime = me.epoch('utc', 'today')) | referencetime = me.epoch('utc', 'today')) | ||
## | ## Setting the observation duration, which for our example is 4 hrs | ||
## because usehourangle=True above, these times are relative to HA=0: | |||
starttime = '-2h' | starttime = '-2h' | ||
stoptime = '2h' | stoptime = '2h' | ||
sm.observe('My source', 'Band6', starttime = starttime, stoptime = stoptime) | sm.observe('My source', 'Band6', starttime = starttime, stoptime = stoptime) | ||
## < steps for predicting model visibilities and adding noise can optionally appear here in this order > | |||
## sm.predict... | |||
## sm.setnoise... | |||
## sm.corrupt... | |||
## Close the simulator tool: | |||
sm.close() | |||
</source> | </source> | ||
The above example will create a noise-free and source-free MS, which may be useful for certain studies (e.g., properties of the PSF). If desired, the steps to add sources and/or noise could be added to the above script after <tt>sm.observe</tt> or they can be run separately as in the examples below. | |||
If we want sources in the field we can predict the visibilities using <tt>sm.predict</tt> function by providing either a CASA image or a component list. | |||
Note the default behavior of <tt>sm.predict</tt> shown here will not include any attenuation by the antenna's primary beam. This may be fine for simulations of a compact source near the beam center, but not for wide-field simulations and mosaics. For more control over the predict step, see <tt>sm.setoptions</tt> or consider doing the visibility prediction using <tt>im.ft</tt> or {{tclean}}. | |||
'''If using a component list, follow the steps below:''' | |||
<source lang="python"> | <source lang="python"> | ||
## Using the same component list that we generated in section | ## Using the same component list that we generated in the section on Example Simulation using Simobserve with a Component List | ||
## predicts the visibility of the source | ## predicts the visibility of the source | ||
sm.predict( complist = 'my_component.cl') | sm.openfromms('ngVLA_214_ant_60s_noise_free.ms') | ||
sm.predict( complist = 'my_component.cl') | |||
sm.close() | sm.close() | ||
</source> | </source> | ||
'''However, if instead you want to use a model image, follow the steps below:''' | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
## To | |||
## To import the fits file as a CASA image: | |||
model_file = 'ppmodel_image_93GHz' | model_file = 'ppmodel_image_93GHz' | ||
importfits( fitsimage = model_file+'.fits', imagename = model_file+'.image') | importfits( fitsimage = model_file+'.fits', imagename = model_file+'.image') | ||
## Note: | ## Note: A warning is produced in CASA when running importfits about the image not having a beam or angular resolution. This is expected since the model is in units of Jy/pixel and it can be safely ignored. | ||
## To predict the model visibilities | ## To predict the model visibilities: | ||
sm.openfromms('ngVLA_214_ant_60s_noise_free.ms') | |||
sm.predict( imagename = model_file+'.image') | sm.predict( imagename = model_file+'.image') | ||
| Line 266: | Line 294: | ||
</source> | </source> | ||
Note | Note the model image should have units of Jy/pixel and not Jy/beam. | ||
Finally, in order to add thermal noise we do the following: | |||
'''Finally, in order to add thermal noise, we do the following:''' | |||
<source lang="python"> | <source lang="python"> | ||
# In CASA | # In CASA | ||
## Adding noise | |||
## Adding noise using the 'simplenoise' parameter estimated in the section on Estimating the Scaling Parameter for Adding Thermal Noise: | |||
sigma_simple = '1.4mJy' | |||
os.system('cp -r ngVLA_214_ant_60s_noise_free.ms ngVLA_214_ant_60s_noisy.ms') | os.system('cp -r ngVLA_214_ant_60s_noise_free.ms ngVLA_214_ant_60s_noisy.ms') | ||
sm.openfromms('ngVLA_214_ant_60s_noisy.ms') | sm.openfromms('ngVLA_214_ant_60s_noisy.ms') | ||
sm.setnoise(mode = 'simplenoise', simplenoise = | sm.setnoise(mode = 'simplenoise', simplenoise = sigma_simple) | ||
sm.corrupt() | sm.corrupt() | ||
sm.done() | sm.done() | ||
</source> | |||
===Comparison of the Results with the Expected Image Noise=== | |||
Here we will create an image to confirm that the noise we added is as expected, using the simulated MS created in the section, Example Simulation using Simobserve with a Model Image. | |||
In order to determine an appropriate cell size we use <tt>im.advise</tt>, a helper function which suggests recommended values of certain imaging parameters. The third value returned by <tt>im.advise</tt> is the maximum cell size that will allow the longest baselines to be gridded. We want to avoid using a value larger than this maximum size to ensure that all the data is used during imaging. | |||
<source lang="python"> | |||
# In CASA | |||
im.open('ngVLA_214_ant_60s_noisy.ms') | |||
print( im.advise() ) | |||
im.close() | |||
</source> | |||
For this MS, <tt>im.advise</tt> gives a value of 0.0003331 arcseconds which we round down to 0.3 mas. We then choose an image size of 3000 pixels in order to have a field of view comparable to our original model image. | |||
Since it will be difficult to accurately measure the image noise with the source present, we can arrange for {{tclean}} to subtract the model and image only the residual visibilities. We will do this by setting the {{tclean}} ''startmodel'' parameter to that of our model image. | |||
<source lang="python"> | |||
# In CASA | |||
tclean(vis = 'ngVLA_214_ant_60s_noisy.ms', datacolumn = 'data', imagename = 'sm_clean_noisy', imsize = 3000, cell = '0.3mas', startmodel = 'ppmodel_image_93GHz.image', specmode = 'mfs', gridder = 'standard', deconvolver = 'hogbom', weighting = 'natural', niter = 0) | |||
</source> | |||
We can then open the residual image using the {{viewer}}: | |||
<source lang="python"> | |||
# In CASA | |||
viewer('sm_clean_noisy.residual') | |||
</source> | </source> | ||
Figure 2 shows our residual image. The noise pattern in your image may look different since each execution of <tt>sm.corrupt</tt> will generate different random numbers, but the RMS should be very similar. Since we have subtracted the same model that we used to predict the source visibilities, the residual image will contain only on the noise we added with ''"simplenoise"''. This residual image is essentially equivalent to the image you would get for a simulation without any sources in the field. Using the statistics tab, we can see that the image RMS and standard deviation are in good agreement with the expected image RMS of 0.415 uJy/beam from the section on Estimating the Scaling Parameter for Adding Thermal Noise. | |||
{| | |||
|[[Image:Residual_93GHz.png|500px|thumb|left|'''Figure 2:''' Residual image]] | |||
|} | |||
We can also take a look at the restored image created with the above call to {{tclean}}. '''Be aware, this image is not a realistic representation of what you should expect from deconvolution.''' Because we have set the ''startmodel'' parameter, this restored image is simply the input model convolved by the clean beam and added to the residual image. If we had tried to create and clean a dirty image instead of using the ''startmodel'' parameter, {{tclean}} would not have converged precisely to the original model and the residuals would have also contained contributions from the source. A complete discussion of deconvolution is outside the scope of this guide, but the general reasons for this include UV-coverage, signal-to-noise ratio, quality of the PSF, and choice of cleaning parameters. This can usually be improved by adjusting certain parameters (e.g., Briggs weighting, outer UV-taper) at the expense of decreased image sensitivity, which will be explored further in a ngVLA imaging fidelity guide that is currently in preparation. | |||
We can open the restored image using the {{viewer}}: | |||
<source lang="python"> | |||
# In CASA | |||
viewer('sm_clean_noisy.image') | |||
</source> | |||
Figure 3 shows the restored image. Again, the noise pattern in your image will look different but the signal-to-noise ratio should be similar. | |||
{| | |||
|[[Image:Clean_93GHz.png|500px|thumb|left|'''Figure 3:''' Restored image]] | |||
|} | |||
=== Next Generation Very Large Array Model Repository === | |||
This repository holds a set of standard models that have been used for science verification and array configuration testing for the Next Generation Very Large Array (ngVLA). The models are in FITS format. The surface brightness scales are in Jy/pixel -- appropriate as input to the CASA simulator to obtain visibility units in Jy. | |||
Following are a few notes on usage of these models, short summaries of the models, and links to references that have more detail in each case. | |||
'''(i)''' The ngVLA configurations can be found in: | |||
https://ngvla.nrao.edu/page/tools | |||
Alternatively, these configuration files are included as part of CASA distributions 5.5 and greater. They can also be added to older versions of CASA by running the following command inside CASA to update CASA's data repository: | |||
<source lang="python"> | |||
# In CASA | |||
!update-data | |||
</source> | |||
The configuration files are stored inside CASA in a folder along with configuration files for other observatories. Since the path to this folder may depend on your operating system and CASA version, a convenient way to find the path to the configuration files is to run the following command inside CASA: | |||
<source lang="python"> | |||
# In CASA | |||
configdir = casa.values()[0]['data']+'/alma/simmos/' | |||
</source> | |||
'''(ii)''' Models vary significantly in source size and pixel scale. Make sure to use the appropriate configuration for the imaging test of interest. | |||
'''(iii)''' The models are noiseless. Noise should be added to the visibilities as specified in the CASA guide. | |||
If you need assistance in using these models, or if you would like advice on generating your own model, please consult the [https://casaguides.nrao.edu/index.php/Simulating_ngVLA_Data-CASA5.4.1 CASA guide], or contact the [https://help.nrao.edu/ CASA help desk]. | |||
-------- | |||
=== Models in the Repository === | |||
'''1. CO velocity cube models for high redshift galaxies''' | |||
A model to test imaging of CO emission using the PLAINS array. | |||
Models for the velocity field of CO emission from a typical spiral galaxy, placed at various redshifts. The intrinsic model is based on the velocity field of the CO 1-0 emission from M51 presented in Helfer et al. (2003, ApJS, 145, 259), scaled in line luminosity, velocity width, and galaxy size to match the galaxy types given below. | |||
[https://casa.nrao.edu/Data/ngVLA/M51.Z0.5.FITS.gz M51.Z0.5.FITS]: CO 1-0 at z = 0.5, Mgas = 0.8e10 (alpha/3.4) Mo | |||
[https://casa.nrao.edu/Data/ngVLA/M51.Z2.FITS.gz M51.Z2.FITS]: CO 2-1 at z = 2.0, Mgas = 2.0e10 Mo | |||
[https://casa.nrao.edu/Data/ngVLA/M51.Z4.2.FITS.gz M51.Z4.2.FITS]: CO 2-1 at z = 2.0, Mgas = 6.9e10 Mo | |||
Reference: Imaging Molecular Gas at High Redshift, Carilli & Shao 2018, in ASP Vol 517: Science with the ngVLA, p. 535 | |||
http://aspbooks.org/a/volumes/article_details/?paper_id=38715 | |||
'''2. Imaging of CO Emission''' | |||
[https://casa.nrao.edu/Data/ngVLA/SPIDERWEB.FITS.gz SPIDERWEB.FITS]: A model to test imaging of CO emission using the PLAINS array. | |||
Velocity integrated CO 1-0 emission of an extreme starburst galaxy with very extended CO emission at z = 2.2. The model is based on a high resolution cosmological simulation of an extreme starburst (Narayanan D., et al., 2015, Nature, 525, 496), scaled in size and luminosity to match the CO emission seen in the Spiderweb radio galaxy at z = 2.1, with a molecular gas mass of 2e11 (alpha/3.4) M_o (Emonts B. et al., 2016, Science, 354, 1128) | |||
Reference: The Molecular High-z Universe on Large Scales: Low-Surface-Brightness CO and the Strength of the ngVLA Core 2018, Emonts et al. in ASP Vol 517: Science with the ngVLA, p. 587 | |||
http://aspbooks.org/a/volumes/article_details/?paper_id=38748 | |||
'''3. Stellar Photospheres''' | |||
A set of models of stellar radio photospheres used to test imaging of the FULL array. | |||
The 38 GHz models of the red supergiant, Betelgeuse, is based on parameters derived from high resolution imaging with the VLA (Lim et al. 1998, Nature, 392, 575; O?Gorman et al. 2017, A & A, 602, L10). The models for the hot main sequence stars at 85 GHz, Sirius and Theta Leonis, are based on optical properities in the Hipparcos catalog (Perryman et al. 1997, A & A, 323, L49). For Betelgeuse and Sirius, both a uniform disk model, and a model with 10% surface brightness structures, on different scales ('spots'), is available. | |||
[https://casa.nrao.edu/Data/ngVLA/BETEL38-UNIFORM.FITS.gz BETEL38-UNIFORM.FITS]: alpha Orionis (Betelgeuse), M1 Ia star at 222 pc at 38 GHz, uniform disk | |||
[https://casa.nrao.edu/Data/ngVLA/BETEL-SPOTS38.FITS.gz BETEL-SPOTS38.FITS]: alpha Orionis (Betelgeuse), M1 Ia star at 222 pc at 38 GHz, uniform disk | |||
[https://casa.nrao.edu/Data/ngVLA/SIRIUS85.FITS.gz SIRIUS85.FITS]: alpha Canis Majoris (Sirius), A0 star at 2.6 pc, 85 GHz, uniform disk | |||
[https://casa.nrao.edu/Data/ngVLA/SIRIUS85-SPOTS.FITS.gz SIRIUS85-SPOTS.FITS]: Same, but with +/- 10% brightness fluctuations. | |||
[https://casa.nrao.edu/Data/ngVLA/THETLEO.FITS.gz THETLEO.FITS]: Theta Leonis, A2 V star at 51 pc, 85 GHz | |||
Reference: Imaging Stellar Radio Photospheres with the Next Generation Very Large Array, Carilli et al. in ASP Vol 517: Science with the ngVLA, p. 369 | |||
http://aspbooks.org/a/volumes/article_details/?paper_id=38696 | |||
'''4. High Fidelity Imaging''' | |||
[https://casa.nrao.edu/Data/ngVLA/CYGXMOD2.FITS.gz CYGXMOD2.FITS]: A model developed to test high fidelity imaging for the MAIN array. | |||
The model is based on the best 8 GHz VLA image, scaled to a smaller size, and clipped and blanked to remove off-source noise. The core was also removed and replaced with point source. | |||
Reference: High Dynamic Range Imaging, Carilli 2019, ngVLA Memo 64 | |||
http://library.nrao.edu/public/memos/ngvla/NGVLA_64.pdf | |||
'''5. Deep Field Imaging''' | |||
[https://casa.nrao.edu/Data/ngVLA/EGSPS8.4.FITS.gz EGSPS8.4.FITS]: A model to test deep field imaging using the MAIN array. | |||
The model is comprised of 6000 point sources over a 6arcmin field, derived using S-cubed radio sky simulator (Wilman et al. 2008 , MNRAS, 388, 1335), in a power law distribution, ranging from 100 nJy to 4 mJy (note: the brightest source was increased from 1 mJy to 4 mJy for more stringent dynamic range tests for ngVLA reference configuration tests). | |||
Reference: Deep Fields at 8 GHz, Carilli et al. 2018, ngVLA memo 35 | |||
http://library.nrao.edu/public/memos/ngvla/NGVLA_35.pdf | |||
'''6. Deep Imaging of Free-Free Emission ''' | |||
[https://casa.nrao.edu/Data/ngVLA/NGC5713.FFB.JY.PIX.FITS.gz NGC5713.FFB.JY.PIX.FITS]: A model to explore deep imaging of Free-Free emission from nearby galaxies using the CORE array. | |||
The 30 GHz free-free model was derive from the H-alpha image of the star forming galaxy, NGC 5713, at a distance of 27 Mpc, with a native resolution of 2". | |||
Reference: Project Overview, Carilli et al. 2015, ngVLA memo 5 | |||
http://library.nrao.edu/public/memos/ngvla/NGVLA_05.pdf | |||
'''7. Proto-planetary Disks''' | |||
[https://casa.nrao.edu/Data/ngVLA/pp_model_3mm.fits.gz pp_model_3mm.fits]: A model to explore imaging of planetary systems. The model is at 3 mm and the disk is at +24 Declination. | |||
Reference: Ricci, L., Isella, A., Liu, S., & Li, H. 2018, in Astronomical Society of the Pacific Conference Series, Vol. 517, Science with a Next Generation Very Large Array, ed. E. Murphy, 147. | |||
http://aspbooks.org/a/volumes/article_details/?paper_id=38671 | |||
{{Checked 5.4.1}} | {{Checked 5.4.1}} | ||
Latest revision as of 03:47, 9 February 2021
Introduction
The following tutorial shows how to create simulated data for the next generation Very Large Array (ngVLA). The ngVLA is composed of different subarrays that make up the current reference design. The configuration files for the different subarrays can be used for simulations and calculations that investigate the scientific capabilities of the ngVLA. Each configuration (.cfg) file contains the name of the observatory, the antenna positions, the coordinate system of the antenna positions and the diameter and pad name of each antenna. For these configuration files, the coordinate system is 'global', which signifies that the positions x, y, z are in meters relative to the Earth center following the FITS WCS convention.
CASA provides two ways to create a simulation: the simobserve task and the sm toolkit. With these methods we can generate measurement sets (MSs), add thermal noise, and predict model visibilities, from which we can explore the ngVLA’s imaging capabilities. The simobserve task is very user friendly but it is important to be aware that it has several limitations and it has been designed primarily for ALMA and the VLA. For this reason, we also demonstrate the use of the sm toolkit, which provides much more flexibility in setting the observational parameters and is more compatible with observatories that are not recognized by CASA.
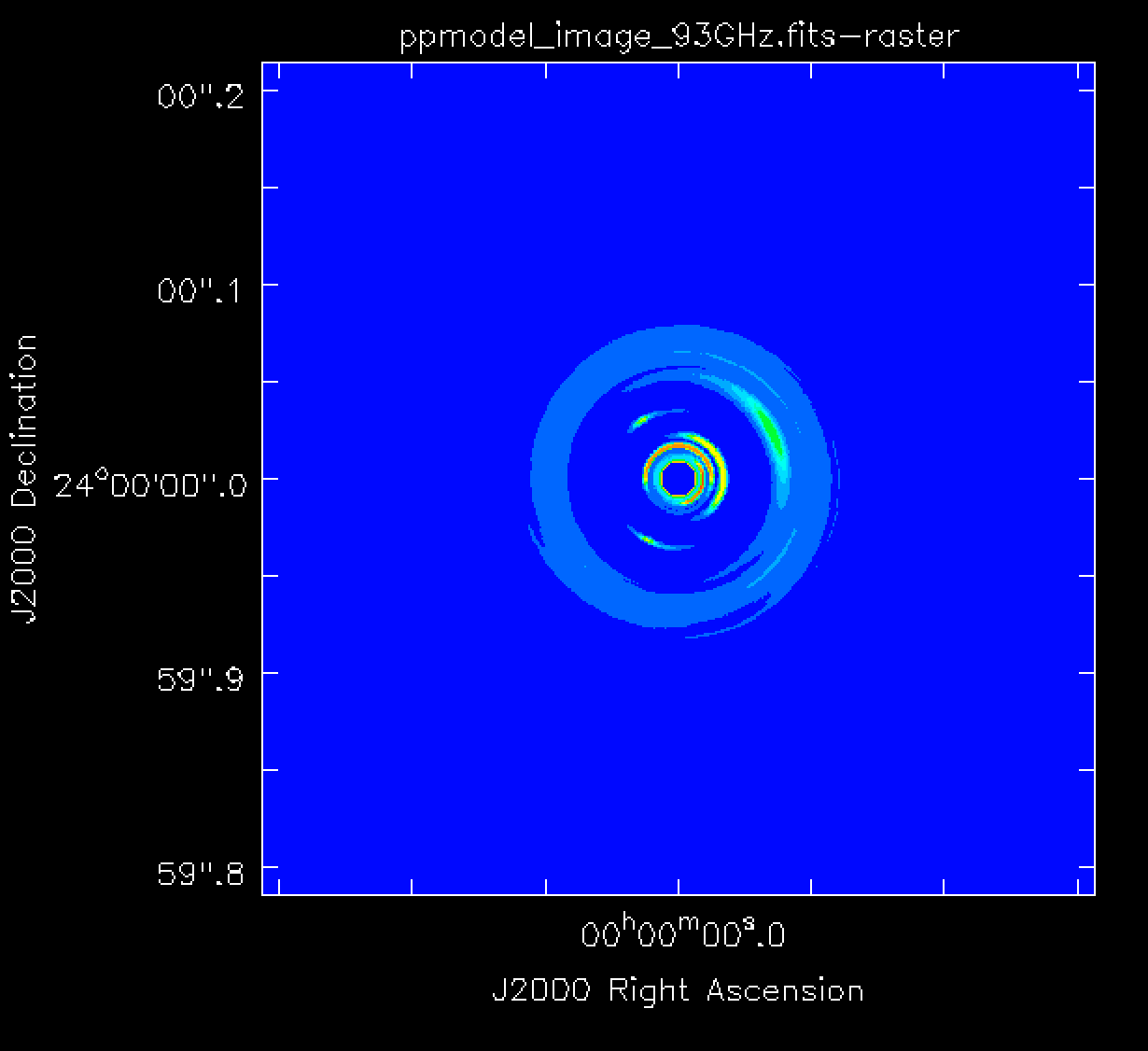
In this tutorial we present three example simulations: (i) simobserve using a model image, (ii) simobserve using a component list, and (iii) a sm toolkit simulation. For more information about component lists, refer to the Simulation Guide Component Lists and the Simulation Guide Component List for Selfcal. The model image used in portions of this guide, a 93 GHz model of a protoplanetary disk, is shown in Figure 1. The next section will explain how to obtain the model image. We will also show how to create and use a component list instead of a model image for the simulations.
We will create example continuum simulations at 93 GHz, consisting of a single channel observed for a total of 4 hours with a 60 second correlator integration time† . We will then add to these simulations an amount of thermal noise that is representative of the ngVLA's continuum sensitivity. The array configuration used in this guide is the Main ngVLA subarray, which is composed of 214 18 m antennas and extends over a maximum baseline of 1005.4 km. The configuration file we will use throughout this tutorial is called ngvla-main-revC.cfg. The next section will explain how to obtain this file.
† We choose this integration time in order to keep the MS files small. Time smearing is not an issue for simulated observations, but this value would need to be reconsidered before scheduling actual observations, e.g., on the order of 0.2 second correlator integration time.
Obtaining the Necessary Files for this Guide
Before creating the first simulation we need to obtain the configuration file and model image. Configuration files for each ngVLA subarray can be downloaded from the ngVLA Configuration Tools portion of the ngVLA website. The configuration file we will use throughout this tutorial is called ngvla-main-revC.cfg, which can be directly downloaded.
Alternatively, these configuration files are included as part of CASA distributions 5.5 and greater. They can also be added to older versions of CASA by running the following command inside CASA to update CASA's data repository:
# In CASA
!update-data
The configuration files are stored inside CASA in a folder along with configuration files for other observatories. Since the path to this folder may depend on your operating system and CASA version, a convenient way to find the path to the configuration files is to run the following command inside CASA:
# In CASA
configdir = casa.values()[0]['data']+'/alma/simmos/'
We will use this path later in this guide as part of the simulation with the sm toolkit. For simulations with the simobserve task, only the configuration file name needs to be given since the task will automatically try to find the file in this folder.
We also need to obtain the model image before we start the simulations. The model image used in portions of this guide, ppmodel_image_93GHz.fits.gz, can be directly downloaded and will then need to be unzipped using gunzip, before using it in the simulations.
Estimating the Scaling Parameter for Adding Thermal Noise
This section describes the procedure we will use to add noise to our simulations and the relevant calculations that we need to prepare for this. Simobserve's parameter to corrupt the simulated data is called thermalnoise and for interferometric data the allowed values are "tsys-atm", "tsys-manual" or " " (refer to the Corrupting Simulated Data guide for more details). The option " " will not add any noise to the data, and the option "tsys-atm" is only applicable to ALMA since it uses site parameters which are specific to that observatory. For the option "tsys-manual", it is necessary to supply several additional parameters which are required to construct an atmospheric model. In order to achieve the desired sensitivity without atmospheric modeling, we have chosen to corrupt the simulated data using the "sm.setnoise" function of the sm toolkit. In addition to the modes "tsys-atm" and "tsys-manual", this function also allows the option of "simplenoise". As the name indicates, "simplenoise" adds random Gaussian noise to the visibilities based on a simple scaling factor. We will use this same technique for all three example simulations, i.e., those made with the simobserve task and those made with the sm toolkit.
In order to estimate the scaling factor for the "simplenoise" parameter in sm.setnoise we use the following procedure:
The RMS noise ([math]\displaystyle{ \sigma_{NA} }[/math]) in an untapered, naturally-weighted Stokes I image will be approximately (see "setnoise function") [math]\displaystyle{ \sigma_{NA} \sim \frac{\sigma_{simple}}{ \sqrt{n_{ch}\,n_{pol}\,n_{baselines}\,n_{integrations} }} }[/math] (1)
where [math]\displaystyle{ \sigma_{simple} }[/math] is the simplenoise parameter in sm.setnoise and corresponds to the noise per visibility, [math]\displaystyle{ n_{ch} }[/math] is the total number of channels across all spectral windows, [math]\displaystyle{ n_{pol} }[/math] is the number of polarizations used for Stokes I (typically 2) and [math]\displaystyle{ n_{integrations} }[/math] is the number of correlator integration times in the MS (i.e., total on-source time / integration time). For the example simulations in this guide, the track time is 4 hrs and the integration time is 60 sec, thus [math]\displaystyle{ n_{integrations}=240 }[/math]. Additionally, for these examples the total number of channels is 1 and the number of polarizations is 2. The number of baselines [math]\displaystyle{ n_{baselines} }[/math] is [math]\displaystyle{ N(N-1)/2 }[/math] where N is the number of antennas in the array. For the array configuration used in this guide (ngvla-main-revC.cfg), N=214 and therefore [math]\displaystyle{ n_{baselines}= 22791 }[/math].
If you already know the expected image noise ([math]\displaystyle{ \sigma_{NA} }[/math]) for your untapered, naturally-weighted image, you can solve for the scaling parameter [math]\displaystyle{ \sigma_{simple} }[/math] in the above equation (1) and pass [math]\displaystyle{ \sigma_{simple} }[/math] to the simplenoise parameter in sm.setnoise.
If instead you want to calculate the expected sensitivity for an ngVLA image, we suggest the following procedure:
(i) Calculate the expected untapered, naturally weighted point source sensitivity ([math]\displaystyle{ \sigma_{NA} }[/math]) using one of the ngVLA performance tables. In Appendix D of ngVLA memo #55 there are key performance metrics for 6 subarrays which are tabulated as a function of frequency and resolution. For our example, we find in Table 10 of ngVLA memo #55 that the untapered, naturally weighted point source sensitivity of the Main interferometric array at 93 GHz is 0.83 uJy/beam for a 1 hour observation.
(ii) Scale that number to the desired observation length, in this case [math]\displaystyle{ t_{track}=4\,h }[/math]. Therefore, [math]\displaystyle{ \sigma_{NA} = 0.83/\sqrt{(t_{track}/1\,hour)} = 0.415\,\text{uJy/beam} }[/math].
(iii) Use the expected image noise ([math]\displaystyle{ \sigma_{NA} }[/math]) in the above equation (1) to solve for the scaling factor [math]\displaystyle{ \sigma_{simple} }[/math]. In this case, [math]\displaystyle{ \sigma_{simple}=0.415*\sqrt{1*2*22791*240} = 1.4\,\text{mJy} }[/math].
Once you have derived the scaling factor [math]\displaystyle{ \sigma_{simple} }[/math], run sm.setnoise and corrupt the visibilities of the noise-free MS. Your resulting untapered, naturally-weighted image will then have an RMS approximately equal to your desired image noise. Since it is not easy to undo this step, it is a good idea to make a copy of the noise-free MS before adding noise. The following mock example outlines this procedure:
# In CASA
## Create a copy of the noise-free MS:
os.system('cp -r noise_free.ms noisy.ms')
## Open the MS we want to add noise to with the sm tool:
sm.openfromms('noisy.ms')
## Set the noise level using the simplenoise parameter estimated earlier in this section:
sm.setnoise(mode = 'simplenoise', simplenoise = sigma_simple)
## Add noise to the 'DATA' column (and the 'CORRECTED_DATA' column if present):
sm.corrupt()
## Close the sm tool:
sm.done()
Note that this example will not execute without a MS named "noise_free.ms" and a defined variable sigma_simple. See below for working examples of this procedure used in conjunction with the creation of simulated MSs and the prediction of model visibilities.
Example Simulation using Simobserve with a Model Image
We will use the simobserve task to create our first noise-free measurement set (MS), using the configuration file and model image described in the Introduction.
# In CASA
simobserve(project = 'ngVLA_214_ant_60s_noise_free',
skymodel = 'ppmodel_image_93GHz.fits',
setpointings = True,
integration = '60s',
obsmode = 'int',
antennalist = 'ngvla-main-revC.cfg',
hourangle = 'transit',
totaltime = '14400s',
thermalnoise = '',
graphics = 'none')
project: Simobserve will create a folder with the project name in your current working directory, and this folder will contain all the resulting files including the noise-free MS.
skymodel: The input model image in Jy/pixel units, can be a single image or a spectral cube. The simulated MS will inherit the number of channels, central frequency, source direction, and peak flux of this input model. These can be adjusted using the optional parameters inbright, indirection, incell, incenter, and inwidth. In this example, we do not modify these optional parameters.
setpointings: We choose the value of True, which allows simobserve to derive the pointing positions using its own algorithm and properties of the input model image. Since the size of the model is much smaller than the primary beam, a single pointing will be generated (instead of a mosaic). We also set the expanded parameter integration to '60s' (our chosen correlator integration time) and leave other expanded parameters set to their default values.
obsmode: We set this parameter to 'int' to simulate interferometric data. We also set values for several expandable parameters. For antennalist, we give the name of the configuration file for the ngVLA Main interferometric array. simobserve will read this file from a directory inside the CASA distribution (see the section on Obtaining the Necessary Files for this Guide). We set totaltime to the total on-source observation time, use the hourangle parameter to center our observation time on transit, and leave other expanded parameters as default.
thermalnoise: We leave this parameter empty to create a noise-free simulation. We will add the noise later in a separate step.
graphics: This will show graphics on the screen and/or save them as png files in the project directory. However, at the moment this is not working properly for baselines larger than a few hundred km. For this reason, we use 'none' in this example.
Now, to add thermal noise, we do the following:
# In CASA
## Create a copy of the noise-free MS:
os.system('cp -r ngVLA_214_ant_60s_noise_free/ngVLA_214_ant_60s_noise_free.ngvla-main-revC.ms ngVLA_214_ant_60s_noisy.ms')
## Open the MS we want to add noise to with the sm tool:
sm.openfromms('ngVLA_214_ant_60s_noisy.ms')
## Set the noise level using the simplenoise parameter estimated in the section on Estimating the Scaling Parameter for Adding Thermal Noise:
sigma_simple = '1.4mJy'
sm.setnoise(mode = 'simplenoise', simplenoise = sigma_simple)
## Add noise to the 'DATA' column (and the 'CORRECTED_DATA' column if present):
sm.corrupt()
## Close the sm tool:
sm.done()
Example Simulation using Simobserve with a Component List
Instead of using a model image we can use a component list for the simulation. Warning: At the moment, this method may take several times longer than using a model image due to internal issues with simobserve. Below is a simple example of how to make a component list consisting of a single point source.
# In CASA
## Position of the source that we want to observe:
direction = 'J2000 00:00:00.0 +24.00.00.0'
## Use the component list (cl) tool to make a model centered at the direction given above, and with a source flux of 10 uJy:
cl.addcomponent(dir = direction, flux = 10e-6, freq = '93GHz')
## Name of the component list model:
cl.rename(filename = 'my_component.cl')
## Close the component list:
cl.done()
Now, we can use simobserve using the generated component list:
# In CASA
simobserve(project = 'ngVLA_214_ant_60s_noise_free',
complist = 'my_component.cl' ,
compwidth = '10GHz',
setpointings = True,
integration = '60s',
obsmode = 'int',
antennalist = 'ngvla-main-revC.cfg',
hourangle = 'transit',
totaltime = '14400s',
thermalnoise = '',
graphics = 'none')
Most of the parameters are the same as the previous example. The parameters which are specific to using a component list are:
complist: Here we provide the component list created above. The expandable parameter compwidth indicates the bandwidth of the component, which will be used to set the bandwidth of the MS and resulting images.
Then we can add the thermal noise in the same way as in the section, Example Simulation using Simobserve with a Model Image.
Example Simulation using sm toolkit with either a Model Image or a Component List
# In CASA
## Set the name of the configuration file for the ngVLA Main subarray:
conf_file = 'ngvla-main-revC.cfg'
## Set the path to the configuration file within the CASA distribution.
## If using CASA version older than 5.5, see the section on Obtaining the Necessary Files for this Guide:
configdir = casa.values()[0]['data']+'/alma/simmos/'
## Use simutil to read the .cfg file:
from simutil import simutil
u = simutil()
xx,yy,zz,diam,padnames,telescope,posobs = u.readantenna(configdir+conf_file)
########################################################################
## Setting the observation framework, i.e., defining the sources, ##
## resources, and scans similar to what we would do in the ##
## Observation Preparation Tool (OPT) when setting up an observation. ##
########################################################################
## Simulate measurement set using the simulation utilities sm tool:
ms_name = 'ngVLA_214_ant_60s_noise_free.ms' ## Name of your measurement set
sm.open( ms_name )
## Get the position of the ngVLA using the measures utilities (me):
pos_ngVLA = me.observatory('ngvla')
## Set the antenna configuration using the sm tool using the positions,
## diameter, and names of the antennas as read from the configuration file:
sm.setconfig(telescopename = telescope, x = xx, y = yy, z = zz,
dishdiameter = diam.tolist(), mount = 'alt-az',
antname = padnames, padname = padnames,
coordsystem = 'global', referencelocation = pos_ngVLA)
## Set the spectral windows, in this case, as a single channel.
## Simulation with a channel resolution of 10 GHz:
sm.setspwindow(spwname = 'Band6', freq = '93GHz', deltafreq = '10GHz',
freqresolution = '10GHz', nchannels = 1, stokes = 'RR RL LR LL')
## Set feed parameters for the antennas:
sm.setfeed('perfect R L')
## Set the field of observation that we are going to simulate
## (where the telescope is pointing), in this example we are using
## a Dec of +24deg.
sm.setfield(sourcename = 'My source',
sourcedirection = ['J2000','00h0m0.0','+24.0.0.000'])
## Set the limit of the observation for the antennas:
sm.setlimits(shadowlimit = 0.001, elevationlimit = '8.0deg')
## Weight to assign autocorrelation:
sm.setauto(autocorrwt = 0.0)
## Integration time or how often the array writes one visibility
## referencetime is the start date (today's date) and epoch measure ('utc'):
integrationtime = '60s'
sm.settimes(integrationtime = integrationtime, usehourangle = True,
referencetime = me.epoch('utc', 'today'))
## Setting the observation duration, which for our example is 4 hrs
## because usehourangle=True above, these times are relative to HA=0:
starttime = '-2h'
stoptime = '2h'
sm.observe('My source', 'Band6', starttime = starttime, stoptime = stoptime)
## < steps for predicting model visibilities and adding noise can optionally appear here in this order >
## sm.predict...
## sm.setnoise...
## sm.corrupt...
## Close the simulator tool:
sm.close()
The above example will create a noise-free and source-free MS, which may be useful for certain studies (e.g., properties of the PSF). If desired, the steps to add sources and/or noise could be added to the above script after sm.observe or they can be run separately as in the examples below.
If we want sources in the field we can predict the visibilities using sm.predict function by providing either a CASA image or a component list.
Note the default behavior of sm.predict shown here will not include any attenuation by the antenna's primary beam. This may be fine for simulations of a compact source near the beam center, but not for wide-field simulations and mosaics. For more control over the predict step, see sm.setoptions or consider doing the visibility prediction using im.ft or tclean.
If using a component list, follow the steps below:
## Using the same component list that we generated in the section on Example Simulation using Simobserve with a Component List
## predicts the visibility of the source
sm.openfromms('ngVLA_214_ant_60s_noise_free.ms')
sm.predict( complist = 'my_component.cl')
sm.close()
However, if instead you want to use a model image, follow the steps below:
# In CASA
## To import the fits file as a CASA image:
model_file = 'ppmodel_image_93GHz'
importfits( fitsimage = model_file+'.fits', imagename = model_file+'.image')
## Note: A warning is produced in CASA when running importfits about the image not having a beam or angular resolution. This is expected since the model is in units of Jy/pixel and it can be safely ignored.
## To predict the model visibilities:
sm.openfromms('ngVLA_214_ant_60s_noise_free.ms')
sm.predict( imagename = model_file+'.image')
sm.close()
Note the model image should have units of Jy/pixel and not Jy/beam.
Finally, in order to add thermal noise, we do the following:
# In CASA
## Adding noise using the 'simplenoise' parameter estimated in the section on Estimating the Scaling Parameter for Adding Thermal Noise:
sigma_simple = '1.4mJy'
os.system('cp -r ngVLA_214_ant_60s_noise_free.ms ngVLA_214_ant_60s_noisy.ms')
sm.openfromms('ngVLA_214_ant_60s_noisy.ms')
sm.setnoise(mode = 'simplenoise', simplenoise = sigma_simple)
sm.corrupt()
sm.done()
Comparison of the Results with the Expected Image Noise
Here we will create an image to confirm that the noise we added is as expected, using the simulated MS created in the section, Example Simulation using Simobserve with a Model Image.
In order to determine an appropriate cell size we use im.advise, a helper function which suggests recommended values of certain imaging parameters. The third value returned by im.advise is the maximum cell size that will allow the longest baselines to be gridded. We want to avoid using a value larger than this maximum size to ensure that all the data is used during imaging.
# In CASA
im.open('ngVLA_214_ant_60s_noisy.ms')
print( im.advise() )
im.close()
For this MS, im.advise gives a value of 0.0003331 arcseconds which we round down to 0.3 mas. We then choose an image size of 3000 pixels in order to have a field of view comparable to our original model image.
Since it will be difficult to accurately measure the image noise with the source present, we can arrange for tclean to subtract the model and image only the residual visibilities. We will do this by setting the tclean startmodel parameter to that of our model image.
# In CASA
tclean(vis = 'ngVLA_214_ant_60s_noisy.ms', datacolumn = 'data', imagename = 'sm_clean_noisy', imsize = 3000, cell = '0.3mas', startmodel = 'ppmodel_image_93GHz.image', specmode = 'mfs', gridder = 'standard', deconvolver = 'hogbom', weighting = 'natural', niter = 0)
We can then open the residual image using the viewer:
# In CASA
viewer('sm_clean_noisy.residual')
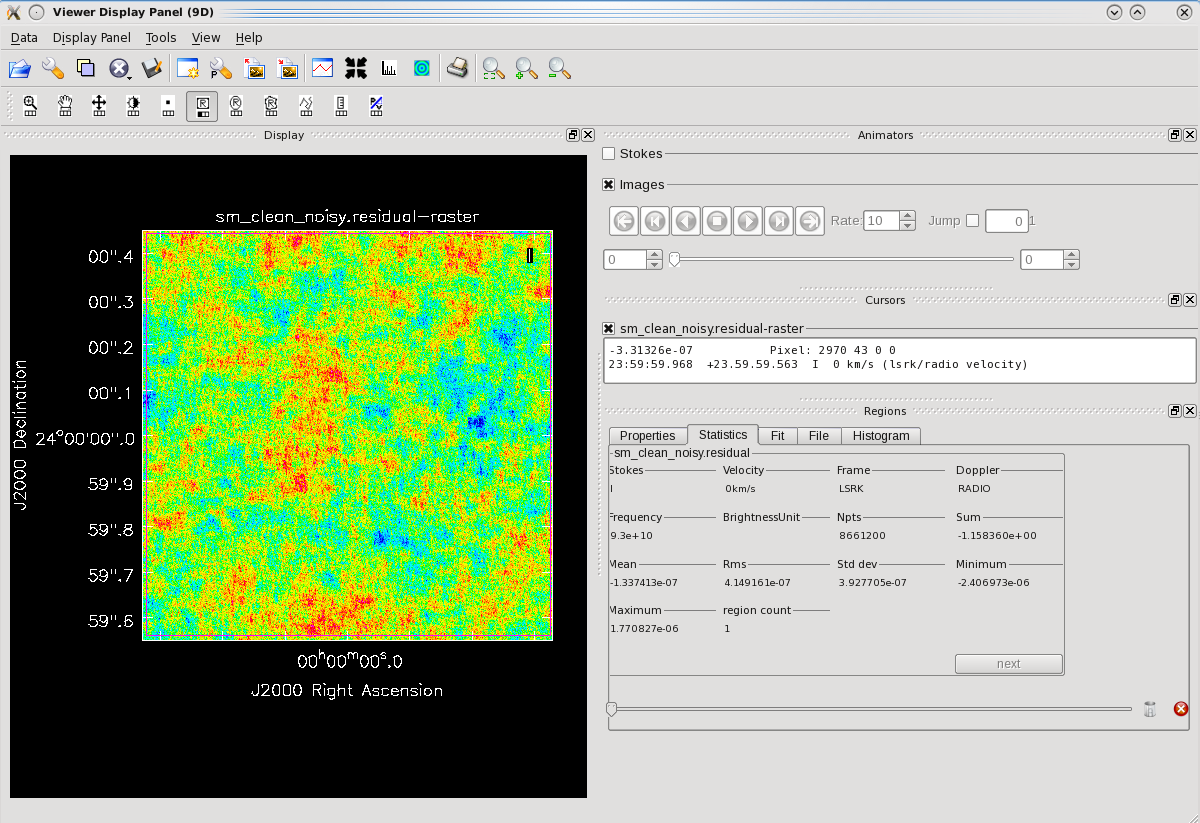
Figure 2 shows our residual image. The noise pattern in your image may look different since each execution of sm.corrupt will generate different random numbers, but the RMS should be very similar. Since we have subtracted the same model that we used to predict the source visibilities, the residual image will contain only on the noise we added with "simplenoise". This residual image is essentially equivalent to the image you would get for a simulation without any sources in the field. Using the statistics tab, we can see that the image RMS and standard deviation are in good agreement with the expected image RMS of 0.415 uJy/beam from the section on Estimating the Scaling Parameter for Adding Thermal Noise.
 |
We can also take a look at the restored image created with the above call to tclean. Be aware, this image is not a realistic representation of what you should expect from deconvolution. Because we have set the startmodel parameter, this restored image is simply the input model convolved by the clean beam and added to the residual image. If we had tried to create and clean a dirty image instead of using the startmodel parameter, tclean would not have converged precisely to the original model and the residuals would have also contained contributions from the source. A complete discussion of deconvolution is outside the scope of this guide, but the general reasons for this include UV-coverage, signal-to-noise ratio, quality of the PSF, and choice of cleaning parameters. This can usually be improved by adjusting certain parameters (e.g., Briggs weighting, outer UV-taper) at the expense of decreased image sensitivity, which will be explored further in a ngVLA imaging fidelity guide that is currently in preparation.
We can open the restored image using the viewer:
# In CASA
viewer('sm_clean_noisy.image')
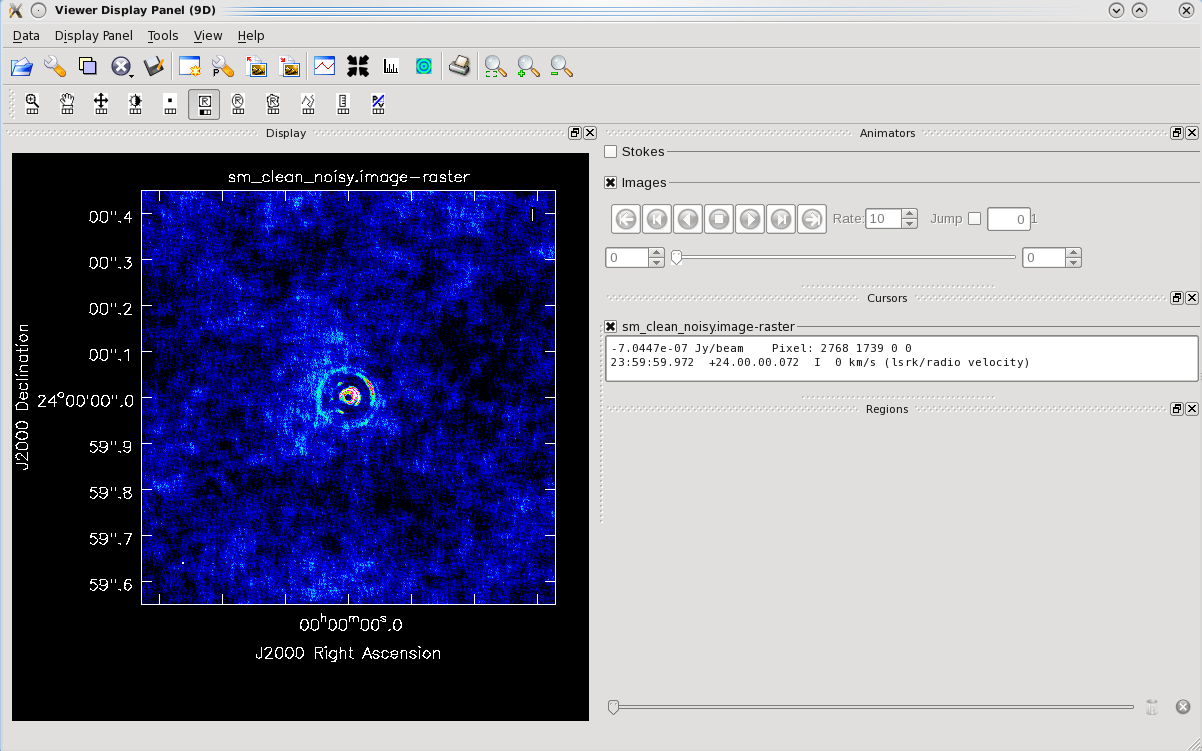
Figure 3 shows the restored image. Again, the noise pattern in your image will look different but the signal-to-noise ratio should be similar.
 |
Next Generation Very Large Array Model Repository
This repository holds a set of standard models that have been used for science verification and array configuration testing for the Next Generation Very Large Array (ngVLA). The models are in FITS format. The surface brightness scales are in Jy/pixel -- appropriate as input to the CASA simulator to obtain visibility units in Jy.
Following are a few notes on usage of these models, short summaries of the models, and links to references that have more detail in each case.
(i) The ngVLA configurations can be found in:
https://ngvla.nrao.edu/page/tools
Alternatively, these configuration files are included as part of CASA distributions 5.5 and greater. They can also be added to older versions of CASA by running the following command inside CASA to update CASA's data repository:
# In CASA
!update-data
The configuration files are stored inside CASA in a folder along with configuration files for other observatories. Since the path to this folder may depend on your operating system and CASA version, a convenient way to find the path to the configuration files is to run the following command inside CASA:
# In CASA
configdir = casa.values()[0]['data']+'/alma/simmos/'
(ii) Models vary significantly in source size and pixel scale. Make sure to use the appropriate configuration for the imaging test of interest.
(iii) The models are noiseless. Noise should be added to the visibilities as specified in the CASA guide.
If you need assistance in using these models, or if you would like advice on generating your own model, please consult the CASA guide, or contact the CASA help desk.
Models in the Repository
1. CO velocity cube models for high redshift galaxies
A model to test imaging of CO emission using the PLAINS array.
Models for the velocity field of CO emission from a typical spiral galaxy, placed at various redshifts. The intrinsic model is based on the velocity field of the CO 1-0 emission from M51 presented in Helfer et al. (2003, ApJS, 145, 259), scaled in line luminosity, velocity width, and galaxy size to match the galaxy types given below.
M51.Z0.5.FITS: CO 1-0 at z = 0.5, Mgas = 0.8e10 (alpha/3.4) Mo
M51.Z2.FITS: CO 2-1 at z = 2.0, Mgas = 2.0e10 Mo
M51.Z4.2.FITS: CO 2-1 at z = 2.0, Mgas = 6.9e10 Mo
Reference: Imaging Molecular Gas at High Redshift, Carilli & Shao 2018, in ASP Vol 517: Science with the ngVLA, p. 535
http://aspbooks.org/a/volumes/article_details/?paper_id=38715
2. Imaging of CO Emission
SPIDERWEB.FITS: A model to test imaging of CO emission using the PLAINS array.
Velocity integrated CO 1-0 emission of an extreme starburst galaxy with very extended CO emission at z = 2.2. The model is based on a high resolution cosmological simulation of an extreme starburst (Narayanan D., et al., 2015, Nature, 525, 496), scaled in size and luminosity to match the CO emission seen in the Spiderweb radio galaxy at z = 2.1, with a molecular gas mass of 2e11 (alpha/3.4) M_o (Emonts B. et al., 2016, Science, 354, 1128)
Reference: The Molecular High-z Universe on Large Scales: Low-Surface-Brightness CO and the Strength of the ngVLA Core 2018, Emonts et al. in ASP Vol 517: Science with the ngVLA, p. 587
http://aspbooks.org/a/volumes/article_details/?paper_id=38748
3. Stellar Photospheres
A set of models of stellar radio photospheres used to test imaging of the FULL array.
The 38 GHz models of the red supergiant, Betelgeuse, is based on parameters derived from high resolution imaging with the VLA (Lim et al. 1998, Nature, 392, 575; O?Gorman et al. 2017, A & A, 602, L10). The models for the hot main sequence stars at 85 GHz, Sirius and Theta Leonis, are based on optical properities in the Hipparcos catalog (Perryman et al. 1997, A & A, 323, L49). For Betelgeuse and Sirius, both a uniform disk model, and a model with 10% surface brightness structures, on different scales ('spots'), is available.
BETEL38-UNIFORM.FITS: alpha Orionis (Betelgeuse), M1 Ia star at 222 pc at 38 GHz, uniform disk
BETEL-SPOTS38.FITS: alpha Orionis (Betelgeuse), M1 Ia star at 222 pc at 38 GHz, uniform disk
SIRIUS85.FITS: alpha Canis Majoris (Sirius), A0 star at 2.6 pc, 85 GHz, uniform disk
SIRIUS85-SPOTS.FITS: Same, but with +/- 10% brightness fluctuations.
THETLEO.FITS: Theta Leonis, A2 V star at 51 pc, 85 GHz
Reference: Imaging Stellar Radio Photospheres with the Next Generation Very Large Array, Carilli et al. in ASP Vol 517: Science with the ngVLA, p. 369
http://aspbooks.org/a/volumes/article_details/?paper_id=38696
4. High Fidelity Imaging
CYGXMOD2.FITS: A model developed to test high fidelity imaging for the MAIN array.
The model is based on the best 8 GHz VLA image, scaled to a smaller size, and clipped and blanked to remove off-source noise. The core was also removed and replaced with point source.
Reference: High Dynamic Range Imaging, Carilli 2019, ngVLA Memo 64
http://library.nrao.edu/public/memos/ngvla/NGVLA_64.pdf
5. Deep Field Imaging
EGSPS8.4.FITS: A model to test deep field imaging using the MAIN array.
The model is comprised of 6000 point sources over a 6arcmin field, derived using S-cubed radio sky simulator (Wilman et al. 2008 , MNRAS, 388, 1335), in a power law distribution, ranging from 100 nJy to 4 mJy (note: the brightest source was increased from 1 mJy to 4 mJy for more stringent dynamic range tests for ngVLA reference configuration tests).
Reference: Deep Fields at 8 GHz, Carilli et al. 2018, ngVLA memo 35
http://library.nrao.edu/public/memos/ngvla/NGVLA_35.pdf
6. Deep Imaging of Free-Free Emission
NGC5713.FFB.JY.PIX.FITS: A model to explore deep imaging of Free-Free emission from nearby galaxies using the CORE array.
The 30 GHz free-free model was derive from the H-alpha image of the star forming galaxy, NGC 5713, at a distance of 27 Mpc, with a native resolution of 2".
Reference: Project Overview, Carilli et al. 2015, ngVLA memo 5
http://library.nrao.edu/public/memos/ngvla/NGVLA_05.pdf
7. Proto-planetary Disks
pp_model_3mm.fits: A model to explore imaging of planetary systems. The model is at 3 mm and the disk is at +24 Declination.
Reference: Ricci, L., Isella, A., Liu, S., & Li, H. 2018, in Astronomical Society of the Pacific Conference Series, Vol. 517, Science with a Next Generation Very Large Array, ed. E. Murphy, 147.
http://aspbooks.org/a/volumes/article_details/?paper_id=38671
Last checked on CASA Version 5.4.1.