CASA Guides:P-band casa guide 5.0: Difference between revisions
No edit summary |
|||
| (6 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
<!--By [http://www.aoc.nrao.edu/~pjaganna/Site/Home.html Preshanth Jagannathan] & [https://safe.nrao.edu/wiki/bin/view/Main/HuibIntemaWebHome Huib Intema] & Frank Schinzel--> | <!--By [http://www.aoc.nrao.edu/~pjaganna/Site/Home.html Preshanth Jagannathan] & [https://safe.nrao.edu/wiki/bin/view/Main/HuibIntemaWebHome Huib Intema] & Frank Schinzel--> | ||
<b>This CASA Guide is for Version | <b>This CASA Guide is for Version 5.0 of CASA.</b> If you are using a later version of CASA and this is the most recent available guide, then you should be able to use most, if not all, of this casaguide, as we try to limit script breaking changes in CASA development. | ||
== Overview == | == Overview == | ||
| Line 242: | Line 242: | ||
<source lang='python'> | <source lang='python'> | ||
# In CASA | # In CASA | ||
%cpaste | |||
# Press Enter or Return, then copy/paste the following: | |||
axis = 'scan' | axis = 'scan' | ||
for id, stats in summary_1[ axis ].iteritems(): | for id, stats in summary_1[ axis ].iteritems(): | ||
print '%s %s: %5.1f percent flagged' % ( axis, id, 100. * stats[ 'flagged' ] / stats[ 'total' ] ) | print '%s %s: %5.1f percent flagged' % ( axis, id, 100. * stats[ 'flagged' ] / stats[ 'total' ] ) | ||
-- | |||
</source> | </source> | ||
| Line 269: | Line 273: | ||
summary_2 = flagdata(vis='3C129_pband.ms' , mode='summary') | summary_2 = flagdata(vis='3C129_pband.ms' , mode='summary') | ||
# | # | ||
%cpaste | |||
# Press Enter or Return, then copy/paste the following: | |||
axis = 'scan' | axis = 'scan' | ||
for value, stats in summary_2[ axis ].iteritems(): | for value, stats in summary_2[ axis ].iteritems(): | ||
old_stats = summary_1[ axis ][ value ] | old_stats = summary_1[ axis ][ value ] | ||
print '%s %s: %5.1f percent flagged additionally' % ( axis, value, 100. * ( stats[ 'flagged' ] - old_stats[ 'flagged' ] ) / stats[ 'total' ] ) | print '%s %s: %5.1f percent flagged additionally' % ( axis, value, 100. * ( stats[ 'flagged' ] - old_stats[ 'flagged' ] ) / stats[ 'total' ] ) | ||
-- | |||
# | # | ||
plotms(vis='3C129_pband.ms',xaxis='freq',yaxis='amp',antenna='ea01',correlation='XX,YY', | plotms(vis='3C129_pband.ms',xaxis='freq',yaxis='amp',antenna='ea01',correlation='XX,YY', | ||
| Line 297: | Line 305: | ||
</source> | </source> | ||
On the command line you should see a notification stating: "FJones (iononsphere) apply now provisionally includes disp. delay." which indicates that both Faraday rotation as well as dispersive delay corrections for the ionosphere are applied. | |||
[[File:3c147_postbandpass_rflag.png|200px|thumb|right|Figure 4d: <i>plotms</i> output after RFI flagging with <i>mode='rflag'</i>]] | [[File:3c147_postbandpass_rflag.png|200px|thumb|right|Figure 4d: <i>plotms</i> output after RFI flagging with <i>mode='rflag'</i>]] | ||
| Line 311: | Line 321: | ||
summary_3 = flagdata(vis='3C129_pband.ms' , mode='summary') | summary_3 = flagdata(vis='3C129_pband.ms' , mode='summary') | ||
# | # | ||
%cpaste | |||
# Press Enter or Return, then copy/paste the following: | |||
axis = 'scan' | axis = 'scan' | ||
for value, stats in summary_3[ axis ].iteritems(): | for value, stats in summary_3[ axis ].iteritems(): | ||
old_stats = summary_2[ axis ][ value ] | old_stats = summary_2[ axis ][ value ] | ||
print '%s %s: %5.1f percent flagged additionally' % ( axis, value, 100. * ( stats[ 'flagged' ] - old_stats[ 'flagged' ] ) / stats[ 'total' ] ) | print '%s %s: %5.1f percent flagged additionally' % ( axis, value, 100. * ( stats[ 'flagged' ] - old_stats[ 'flagged' ] ) / stats[ 'total' ] ) | ||
-- | |||
# | # | ||
plotms(vis='3C129_pband.ms',xaxis='freq',yaxis='amp',antenna='ea01',correlation='XX,YY', | plotms(vis='3C129_pband.ms',xaxis='freq',yaxis='amp',antenna='ea01',correlation='XX,YY', | ||
| Line 415: | Line 429: | ||
The VLA at P-band measures the incoming radio waves using dual-dipole feeds mounted near the primary focus of the dishes. While much effort is put into mechanically making these dual-dipoles orthogonal, and to strongly suppress any cross-talk between the electronic signal paths of both dipoles, there is some (frequency-dependent) polarization leakage between them. Furthermore, the P-band feeds are mounted and aligned on each antenna by hand, allowing for 5-10 degrees difference in the orientation of the dipoles between antennas. For both intensity and polarization imaging, it is important to calibrate the polarization products in our data to optimize the (i) orthogonality between X and Y for each antenna, and (ii) the alignment between Xs and Ys of different antennas. Note that this does not (yet) include calibration of the absolute polarization angle; for which we need a linearly polarized source with known polarization angle. | The VLA at P-band measures the incoming radio waves using dual-dipole feeds mounted near the primary focus of the dishes. While much effort is put into mechanically making these dual-dipoles orthogonal, and to strongly suppress any cross-talk between the electronic signal paths of both dipoles, there is some (frequency-dependent) polarization leakage between them. Furthermore, the P-band feeds are mounted and aligned on each antenna by hand, allowing for 5-10 degrees difference in the orientation of the dipoles between antennas. For both intensity and polarization imaging, it is important to calibrate the polarization products in our data to optimize the (i) orthogonality between X and Y for each antenna, and (ii) the alignment between Xs and Ys of different antennas. Note that this does not (yet) include calibration of the absolute polarization angle; for which we need a linearly polarized source with known polarization angle. | ||
First, we calibrate the cross delay, which is the difference in delay between the two polarizations of the reference antenna; in our case ea09. Remember that the regular delay calibration arbitrarily set the delays for both polarizations of the reference antenna to zero. In reality there will be a small, but noticeable, physical path length difference between these two polarizations, for which we try to correct. This calibration uses the same scan on 3C147, assuming that 3C147 is unpolarized at P-band (which is a good approximation). | First, we calibrate the cross delay, which is the difference in delay between the two polarizations of the reference antenna; in our case ea09. Remember that the regular delay calibration arbitrarily set the delays for both polarizations of the reference antenna to zero. In reality there will be a small, but noticeable, physical path length difference between these two polarizations, for which we try to correct. This calibration uses the same scan on 3C147, assuming that 3C147 is unpolarized at P-band (which is a good approximation). Although 3C147 has very low intrinsic polarization at P-band, it is strong enough that gaincal can solve for the cross-delays from the leakage signals which are of the order 5-10%. If all P-band dipoles were perfectly aligned, this would result in virtually zero leakage between the polarizations and thus we would have to use a polarized source to solve for the cross delay. | ||
<source lang='python'> | <source lang='python'> | ||
# In CASA | # In CASA | ||
gaincal(vis='3C129_pband.ms', caltable='3C129_pband.Kc1', field='3C147', solint='inf', refant='ea09', minsnr=3.0, gaintype='KCROSS', parang=True, | gaincal(vis='3C129_pband.ms', caltable='3C129_pband.Kc1', field='3C147', solint='inf', refant='ea09', minsnr=3.0, gaintype='KCROSS', parang=True, | ||
gaintable=[ '3C129_pband.antpos','3C129_pband.rq','3C129_pband.tecim','3C129_pband.K1', '3C129_pband.B1','3C129_pband.Gs1'], | scan='3', gaintable=[ '3C129_pband.antpos','3C129_pband.rq','3C129_pband.tecim','3C129_pband.K1', '3C129_pband.B1','3C129_pband.Gs1'], | ||
interp=['','','','nearest,nearestflag', 'nearest,nearestflag', 'nearest,nearestflag'] ) | interp=['','','','nearest,nearestflag', 'nearest,nearestflag', 'nearest,nearestflag'] ) | ||
| Line 426: | Line 440: | ||
</source> | </source> | ||
This plot shows a small, ~2 nanosec, delay between X and Y. Note that the table is generated in such a way this correction is exactly equal for all antennas, since in fact gaincal solves for only a single, antenna-independent, delay between X and Y. There are four spectral windows with larger delays up to -37 nsec, namely 8, 12, 16, and 17. You can use the Locate feature of <i>plotcal</i> to identify which is which. Note that the table is generated in such a way that this correction gets applied to all antennas. | |||
Next we determine the leakage of the X signal into Y, and Y into X. For a well-behaved instrument, the magnitude of the leakage (D-terms) should be much less than one. Since the leakage is frequency dependent, we solve for leakage for each frequency channel, somewhat similar to bandpass calibration. The way to do this in CASA is through the <i>polcal()</i> task with the option <i>poltype = 'Df'</i>. Again, we can inspect (and edit) the leakage calibration table with <i>plotcal()</i> | Next we determine the leakage of the X signal into Y, and Y into X. For a well-behaved instrument, the magnitude of the leakage (D-terms) should be much less than one. Since the leakage is frequency dependent, we solve for leakage for each frequency channel, somewhat similar to bandpass calibration. The way to do this in CASA is through the <i>polcal()</i> task with the option <i>poltype = 'Df'</i>. Again, we can inspect (and edit) the leakage calibration table with <i>plotcal()</i> | ||
| Line 497: | Line 511: | ||
</source> | </source> | ||
Now we split off the calibrated target field data, meaning that the visibilities of source | Now we split off the calibrated target field data, meaning that the visibilities of source 3C129 get copied from the <i>CORRECTED_DATA</i> column to the <i>DATA</i> column of a new measurement set. This is convenient for further processing. | ||
<source lang='python'> | <source lang='python'> | ||
| Line 611: | Line 625: | ||
{{Checked | {{Checked 5.0.0}} | ||
Latest revision as of 23:20, 29 August 2017
This CASA Guide is for Version 5.0 of CASA. If you are using a later version of CASA and this is the most recent available guide, then you should be able to use most, if not all, of this casaguide, as we try to limit script breaking changes in CASA development.
Overview
This webpage provides a basic description on how to use CASA to reduce data from the upper part of the new VLA low-band system, also known as P-band, covering roughly 220-480 MHz. The goal is to make a wide-field continuum stokes I image of a typical blank field using the full effective bandwidth. The dataset that will be downloaded in this guide has a size of 26.46 GB and will require a total of ~140 GB of disk space if all generated files are kept.
Note: Starting with CASA 5.0 IPython 5.1.0 is used which for interactive CASA sessions. This does not allow to readily paste and execute multiple lines of code like in previous versions of the interpreter. If this is needed at any point in this tutorial, we use "%cpaste" to allow the copy/paste of loops, conditions, etc.. Press "Enter" (or "Return") after "--" at the end, this stops (or exits) the copy/paste prompt and will return you to the CASA prompt.
Obtaining the raw data
For this guide, we'll use some test data that was taken in B-configuration. To get a copy of the raw data, download P_band_3C129.tgz onto your computer running CASA and untar it (i.e. tar -xvfz <filename>).
Alternatively, the raw data can also be obtained from the NRAO archive, go to the NRAO advance archive query page, and enter the following search parameter in the field Archive File ID (leave the rest on default):
imag-test-copy.57080.956837025464
The search should return a single row for Archive File: imag-test-copy.57080.956837025464, taken on Feb. 27, 2015 (or "15-Feb-27 22:57:52"). Check the box next to it. Next, fill in your email and select the "SDM-BDF dataset (all files)" option. Note, you may find it easier to download a tar file, in which case, you'll want to check the box for Create MS or SDM tar file. Click "Get My Data" and follow the on-screen prompts to reach the next page, where you should click "Retrieve over internet". The next page should report that the data staging is in progress. Wait until you receive an e-mail reporting that your archive data is copied, which should take a few minutes. Download the data onto your computer running CASA and untar it (i.e. tar -xvfz <filename>).
Starting CASA
Start CASA by typing
casa
on the (linux) command line. This should start a CASA interactive python (iPython) session, and open a separate log window. The CASA version is reported at startup, both in the python session and the log window.
Importing the raw data into CASA
We will begin by importing our data into the measurement set format (CASA standard) from the binary format (SDM-BDF) as downloaded from the archive. We do this by means of the importevla task.
# In CASA
importevla(asdm='imag-test-copy.57080.956837025464', vis ='3C129.ms', savecmds=True, outfile='importflags.txt')
This task calls the external tool asdm2MS to perform the conversion. Together with the visibility data, also the flag commands from the VLA online system are imported. These flags are not directly applied, but stored in the importflags.txt file and applied later.
Preliminary data inspection
# In CASA
listobs(vis='3C129.ms', verbose = True, listfile = '3C129.listobs')
Alternatively, you can also output to the logger by running the command without the listfile argument. The sample listobs output shown has flag verbose=False for the sake of brevity.
# In CASA
listobs(vis='3C129.ms',verbose=False)
================================================================================
MeasurementSet Name: /lustre/aoc/sciops/fschinze/P_band_tutorial/3C129.ms MS Version 2
================================================================================
Observer: Project: uid://evla/sdm/X2
Observation: EVLA(27 antennas)
Data records: 4714983 Total elapsed time = 1422 seconds
Observed from 27-Feb-2015/22:57:54.0 to 27-Feb-2015/23:21:36.0 (UTC)
Fields: 2
ID Code Name RA Decl Epoch SrcId nRows
0 NONE 3C147 05:42:36.127300 +49.51.07.17800 J2000 0 1307124
1 NONE 3C129 04:48:58.200000 +45.02.01.00000 J2000 1 3407859
Spectral Windows: (19 unique spectral windows and 1 unique polarization setups)
SpwID Name #Chans Frame Ch0(MHz) ChanWid(kHz) TotBW(kHz) CtrFreq(MHz) BBC Num Corrs
0 EVLA_P#A0C0#0 128 TOPO 224.000 125.000 16000.0 231.9375 12 XX XY YX YY
1 EVLA_P#A0C0#1 128 TOPO 240.000 125.000 16000.0 247.9375 12 XX XY YX YY
2 EVLA_P#A0C0#2 128 TOPO 256.000 125.000 16000.0 263.9375 12 XX XY YX YY
3 EVLA_P#A0C0#3 128 TOPO 272.000 125.000 16000.0 279.9375 12 XX XY YX YY
4 EVLA_P#A0C0#4 128 TOPO 288.000 125.000 16000.0 295.9375 12 XX XY YX YY
5 EVLA_P#A0C0#5 128 TOPO 304.000 125.000 16000.0 311.9375 12 XX XY YX YY
6 EVLA_P#A0C0#6 128 TOPO 320.000 125.000 16000.0 327.9375 12 XX XY YX YY
7 EVLA_P#A0C0#7 128 TOPO 336.000 125.000 16000.0 343.9375 12 XX XY YX YY
8 EVLA_P#A0C0#8 128 TOPO 352.000 125.000 16000.0 359.9375 12 XX XY YX YY
9 EVLA_P#A0C0#9 128 TOPO 368.000 125.000 16000.0 375.9375 12 XX XY YX YY
10 EVLA_P#A0C0#10 128 TOPO 384.000 125.000 16000.0 391.9375 12 XX XY YX YY
11 EVLA_P#A0C0#11 128 TOPO 400.000 125.000 16000.0 407.9375 12 XX XY YX YY
12 EVLA_P#A0C0#12 128 TOPO 416.000 125.000 16000.0 423.9375 12 XX XY YX YY
13 EVLA_P#A0C0#13 128 TOPO 432.000 125.000 16000.0 439.9375 12 XX XY YX YY
14 EVLA_P#A0C0#14 128 TOPO 448.000 125.000 16000.0 455.9375 12 XX XY YX YY
15 EVLA_P#A0C0#15 128 TOPO 464.000 125.000 16000.0 471.9375 12 XX XY YX YY
16 EVLA_P#B0D0#16 64 TOPO 310.000 500.000 32000.0 325.7500 15 XX XY YX YY
17 EVLA_P#B0D0#17 1024 TOPO 310.000 62.500 64000.0 341.9688 15 XX XY YX YY
18 EVLA_P#B0D0#18 64 TOPO 342.000 500.000 32000.0 357.7500 15 XX XY YX YY
Antennas: 27 'name'='station'
ID= 0-3: 'ea01'='N12', 'ea02'='N16', 'ea03'='W28', 'ea05'='E20',
ID= 4-7: 'ea06'='N20', 'ea07'='N32', 'ea08'='E28', 'ea09'='W08',
ID= 8-11: 'ea10'='E36', 'ea11'='W12', 'ea12'='N36', 'ea13'='W04',
ID= 12-15: 'ea14'='E08', 'ea15'='E24', 'ea16'='W24', 'ea17'='E04',
ID= 16-19: 'ea18'='W36', 'ea19'='MAS', 'ea20'='N04', 'ea21'='E32',
ID= 20-23: 'ea22'='N24', 'ea23'='E16', 'ea24'='W32', 'ea25'='W20',
ID= 24-26: 'ea26'='E12', 'ea27'='N08', 'ea28'='N28'
You can inspect the output text file 3C129.listobs in your favorite text editor (e.g., gedit). When taking some time to familiarize yourself with the output format, you will see that:
- The observation consists of 5 scans, namely:
- 3C147 (hardware setup)
- 3C147 (setting requantizers)
- 3C147 (primary calibrator)
- 3C129 (target)
- 3C129 (target)
- The frequency coverage is 222 - 478 MHz, divided into 16 x 16 MHz spectral windows, each having 128 x 0.125 MHz channels. There are also two spectral windows with 64x0.5 MHz and one spectral window with 1024x0.0625 MHz.
- Visibilities are recorded every 2 seconds in full polarization (4 polarization products labelled XX,XY,YX,YY).
- Of the 28 VLA antennas labelled ea01 - ea028, antenna ea04 is not participating in this observation.
- Source, antenna and spectral window IDs start at zero, but scan IDs start at one.
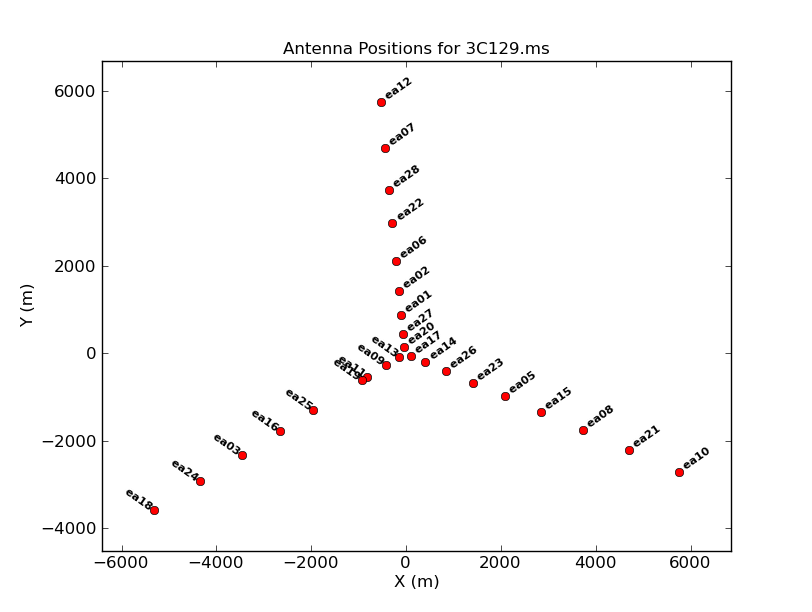
The array configuration can be inspected using:
# In CASA
plotants(vis='3C129.ms', figfile='3C129_pband_plotants.png')
Initial processing steps - Antenna Position, Requantizer Gain, Ionospheric Correction
When importing the data, we saved the flags from the online system to an ASCII text file. This gives us the opportunity to review the flag commands before applying them. For our data set, the flag file is called importflags.txt. Please load this file into your favorite text editor. The bulk of the flag commands refer to times when the VLA is slewing (ANTENNA_NOT_ON_SOURCE) or when the movable secondary reflector of the VLA's Cassegrain system is not in place (SUBREFLECTOR_ERROR). The latter can cause antenna gain variations (amplitude and phase), so it is safest to apply all the flags. The final two rows in the flag file will remove visibilities that are pure zero, and flag antennas that are partly blocked by other antennas (shadowing) which occurs mostly in compact configurations when observing along a VLA arm).
# In CASA
flagdata(vis='3C129.ms', mode='list', inpfile='importflags.txt', action='apply', reason='any', flagbackup=True)
This call, before applying the new flags to the data, created a new flagbackup file called flagdata_1 which can be used by the task flagmanager to restore the state of the measurement set prior applying the flags from importflags.txt.
Antenna Position Corrections
Now that we have applied the import flags, we will correct for the antenna position offsets. Antenna positional errors translates to an error in the measured visibilities and need to be accounted for before we proceed with any of the other calibration steps.
# In CASA
gencal(vis='3C129.ms',caltable='3C129_pband.antpos',caltype='antpos')
The logger output shows that there are 13 antennas with positional offsets:
2016-11-28 22:51:37 INFO gencal offsets for antenna ea03 : 0.00290 0.00000 0.00000 2016-11-28 22:51:37 INFO gencal offsets for antenna ea08 : 0.00000 0.00390 0.00000 2016-11-28 22:51:37 INFO gencal offsets for antenna ea10 : -0.00170 0.00000 0.00400 2016-11-28 22:51:37 INFO gencal offsets for antenna ea11 : 0.00000 0.00160 -0.00170 2016-11-28 22:51:37 INFO gencal offsets for antenna ea13 : 0.00000 0.00050 0.00000 2016-11-28 22:51:37 INFO gencal offsets for antenna ea16 : -0.00180 0.00680 0.00230 2016-11-28 22:51:37 INFO gencal offsets for antenna ea18 : 0.00470 0.00350 0.00000 2016-11-28 22:51:37 INFO gencal offsets for antenna ea21 : -0.00160 0.00000 0.00210 2016-11-28 22:51:37 INFO gencal offsets for antenna ea23 : 0.00140 0.00200 -0.00150 2016-11-28 22:51:37 INFO gencal offsets for antenna ea24 : 0.00380 0.00000 -0.00340 2016-11-28 22:51:37 INFO gencal offsets for antenna ea25 : 0.00330 0.00000 -0.00110 2016-11-28 22:51:37 INFO gencal offsets for antenna ea26 : 0.00000 0.00190 0.00000 2016-11-28 22:51:37 INFO gencal offsets for antenna ea27 : -0.00120 0.00070 0.00000
Ionospheric TEC Corrections
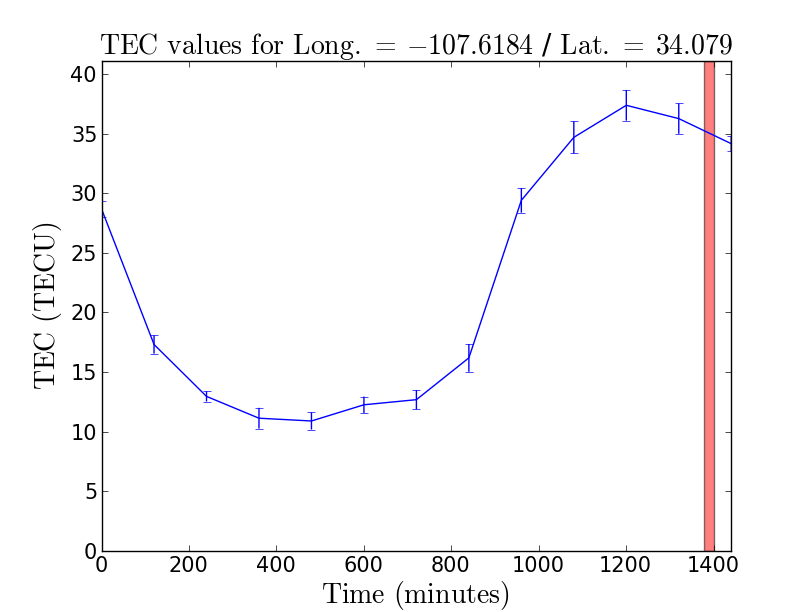
Low frequency observations are affected by the ionosphere. A delay in the signal path is introduced between the two polarization of light that varies both as a function of time and line of sight (direction dependent). The delay is proportional to the Total Electron Content (TEC) along the line of sight and is inversely proportional to the square of the frequency. GPS measurements at two different frequencies provides us with an estimate of the TEC per square meter. This correction has been implemented in CASA which we shall apply as a calibration table by means of the gencal task. The task requires a TEC map that we will generate utilizing CASA recipes. For more information, see the section on ionospheric corrections in the CASA documentation archives. For some versions of CASA, the first plot to the right (Figure 2) may not be generated if you have already run plotants: to generate this plot, you will need to quit CASA and start it again. If the IONEX data file was not downloaded you might be missing the curl package in the environment you are running CASA in. In this case you can provide the required file manually by downloading: ftp://cddis.gsfc.nasa.gov/gnss/products/ionex/2015/058/igsg0580.15i.Z, unziping it, and placing it in the directory from which you started CASA. The current implementation in CASA is in the development stage, however since the CASA 5.0 release both the Faraday rotation correction and dispersive delay corrections for the ionosphere are enabled. In previous releases only Faraday rotation corrections are enabled. In this example we will generate the calibration table and apply it throughout calibration.
# In CASA
from recipes import tec_maps
#
tec_image, tec_rms_image = tec_maps.create(vis='3C129.ms',doplot=True)
#
gencal(vis='3C129.ms',caltable='3C129_pband.tecim',caltype='tecim',infile=tec_image)
# Spatial plots like shown in Figure 3 can be looked at using the CASA viewer for the TEC values
viewer('3C129.ms.IGS_TEC.im')
# and for TEC rms
viewer('3C129.ms.IGS_RMS_TEC.im')

A word of caution regarding the TEC map generation. The IGS website updates measurements only two weeks after the date of observation.
Requantizer Gains
The next step will correct the visibility amplitudes for the signal leveling (requantizer gains) that occurs at the inputs of the WIDAR correlator. These levels (per antenna, per polarization, per spectral window) are stored with the measurement set (in the SYSPOWER sub-table). This step is currently not essential, since the levels get set only once at the start of an observation and bandpass calibration will correct for this. But it will make your bandpass plots look better if you have multiple spectral windows. And, more importantly, in general it is possible to trigger the setting of requantizers throughout an observation. This is the case for new observations, when a P-band scan is preceded by a P-band setup scan, which itself is preceded by a scan with a different telescope configuration.
The correction is done by means of the gencal task, where information in the SYSPOWER sub-table gets translated into a gain table.
# In CASA
gencal(vis='3C129.ms',caltype='rq',caltable='3C129_pband.rq')
Dead antennas
Now it is time to have a first visual look at the uncalibrated visibility data. It is important to identify dead antennas / polarizations early on, so we can exclude them from further data processing (which is the most efficient data reduction). A convenient way of doing this is through the plotms task on bright calibrator(s) (see the listobs() output), in our case 3C147 (see Fig. 4a).
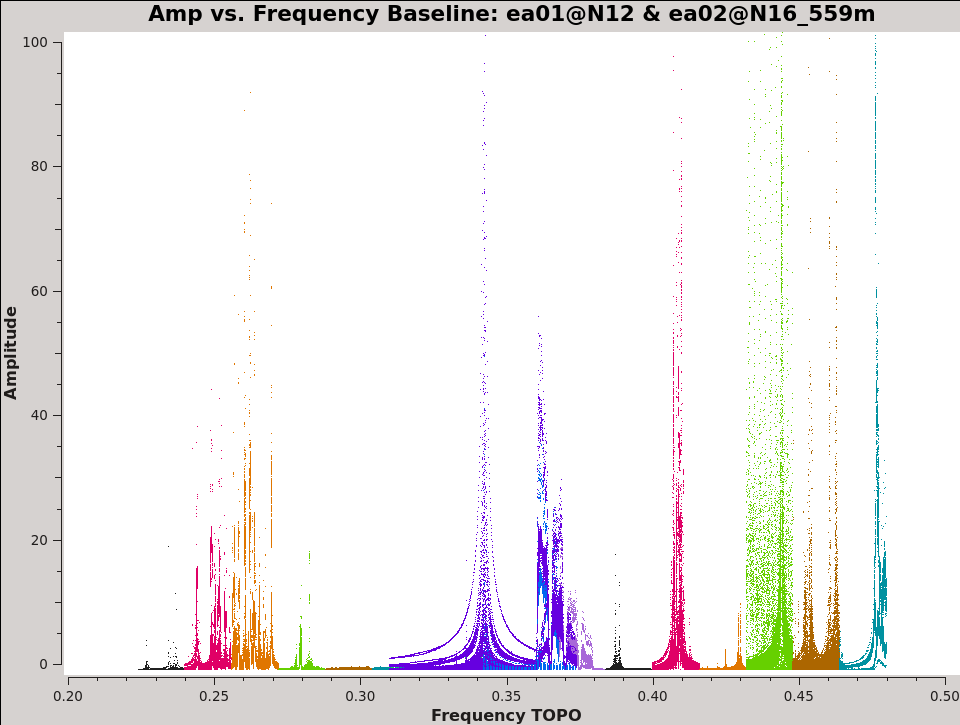
# In CASA
plotms(vis='3C129.ms',xaxis='freq',yaxis='amp',antenna='ea01',correlation='XX,YY', field='3C147',
plotrange=[0.2,0.5,0.0,100.0], coloraxis='spw',xlabel='Frequency',ylabel='Amplitude',iteraxis='baseline',
plotfile='3C129_pband_3C147_prebp.png')
This will load the plotms window that has queued up all the baselines of antenna ea01 and is currently displaying the first amplitude vs frequency plot with the colors representing the different spectral windows. Note that we are only plotting the XX and YY correlation of the antennas. This is because we expect most of the power in the linear cross correlation products to be in these two correlations. Notice that some spectral windows in particular are badly affected due to radio frequency interference (RFI). This is the issue that we will deal with after identifying dead antennas. If you scroll through the baselines using the green forward button in the plotms viewer, you will notice that the amplitude is particularly low when you encounter ea19. If we make a quick plot of the baselines made by ea19 (put ea19 in the antenna field) we can see that there is no power in any of the polarizations indicating this antenna was dead and can be flagged out. It is also good to check for high power levels in cross-hand correlations in comparison to the parallel-hand correlations, which would uncover swapped polarization labels and severely mis-aligned dipoles. At the end of this tutorial some hints on solving for swapped or mislabeled dipole polarizations are given. In addition to the dead antenna, we also make sure that the first two scans are flagged, which were not labelled as setup scans but were used to set the attenuators and requantizers.
# In CASA
flagdata(vis='3C129.ms',mode='manual',antenna='ea19')
#
flagdata(vis='3C129.ms',mode='manual',scan='1~2')
We also noticed sharp RFI peaks during our data examination. To prevent Gibbs ringing, it is best to hanning smooth the data at this juncture before we proceed further with automatic flagging. Now is a good time to get a cup of coffee while hanning smoothing the data.

# In CASA
hanningsmooth(vis='3C129.ms',outputvis='3C129_pband.ms',datacolumn='data')
We should replot the primary calibrator to see the effect of hanning smoothing on the data and the RFI (Fig. 4b).
# In CASA
plotms(vis='3C129_pband.ms',xaxis='freq',yaxis='amp',antenna='ea01',correlation='XX,YY',
field='3C147', plotrange=[0.2,0.5,0.0,100.0], coloraxis='spw',xlabel='Frequency',ylabel='Amplitude',
iteraxis='baseline', plotfile='3C129_pband_3C147_prebp_hanning.png')
Automatic flagging
Before throwing away bad spectral windows by hand, we'll let the automated flaggers in CASA have a go at it. The main task for this is flagdata(). While working on your data, flagdata() produces an abundance of output, not all of which is easy to understand. To help with this, we can get the flag status of our data before and after auto-flagging by running flagdata() in the summary mode. This first call provides the flag statistics of the flagging up to now, before any auto-flagging:
summary_1 = flagdata(vis='3C129_pband.ms', mode='summary')
This returns a python dictionary with flagged versus total visibilities along various axes (antenna, scan, spw, field, correlation, etc.). For example, if we want to know the percentage flagged per scan, run the following (note that the scans may not appear in sorted order):
# In CASA
%cpaste
# Press Enter or Return, then copy/paste the following:
axis = 'scan'
for id, stats in summary_1[ axis ].iteritems():
print '%s %s: %5.1f percent flagged' % ( axis, id, 100. * stats[ 'flagged' ] / stats[ 'total' ] )
--
For this example, you will notice that scans 1 and 2 (the dummy scans on 3C147) are 100 percent flagged, which is what we did during the initial flagging.
We will run flagdata() in the tfcrop mode, which will (per scan, per baseline, per spectral window, per polarization) look for visibility amplitude outliers. It uses a 5-piece polynomial in an attempt to remove any intrinsic bandpass (amplitude) structure (we did not calibrate for bandpass yet). We run the task twice to allow for slightly deeper flagging and separate treatment of the parallel and cross-hand correlations. For the first run, we tell CASA to make a backup of our visibility flag status up to here, giving us an option to restore them if we choose over-aggresive flagging parameters and consequently over-flag our data. The flag backup file name is reported in the log window, and can be found in the 3C129_pband.ms.flagversions directory.
# In CASA
flagdata(vis='3C129_pband.ms', field='*', mode='tfcrop', datacolumn='data', timecutoff=4., freqcutoff=3., maxnpieces=5,
action='apply', display='report', flagbackup=True, combinescans=True, ntime='3600s', correlation='ABS_XY,ABS_YX')
#
flagdata(vis='3C129_pband.ms', field='*', mode='tfcrop', datacolumn='data', timecutoff=3., freqcutoff=3., maxnpieces=2,
action='apply', display='report', flagbackup=False, combinescans=True, ntime='3600s', correlation='ABS_XX,ABS_YY')
#
flagdata(vis='3C129_pband.ms', mode='extend')
As a note of caution: When executing flagdata with mode='extend', all flags that were ever applied to the dataset will get extended. Repeat execution of this command will incrementally flag more and more around already flagged data.
Let's get another flag summary to see how much extra data was flagged:
# In CASA
summary_2 = flagdata(vis='3C129_pband.ms' , mode='summary')
#
%cpaste
# Press Enter or Return, then copy/paste the following:
axis = 'scan'
for value, stats in summary_2[ axis ].iteritems():
old_stats = summary_1[ axis ][ value ]
print '%s %s: %5.1f percent flagged additionally' % ( axis, value, 100. * ( stats[ 'flagged' ] - old_stats[ 'flagged' ] ) / stats[ 'total' ] )
--
#
plotms(vis='3C129_pband.ms',xaxis='freq',yaxis='amp',antenna='ea01',correlation='XX,YY',
field='3C147', plotrange=[0.2,0.5,0.0,100.0], coloraxis='spw',xlabel='Frequency',ylabel='Amplitude',
iteraxis='baseline', plotfile='3C129_pband_3C147_prebp_hanning_automatic.png')
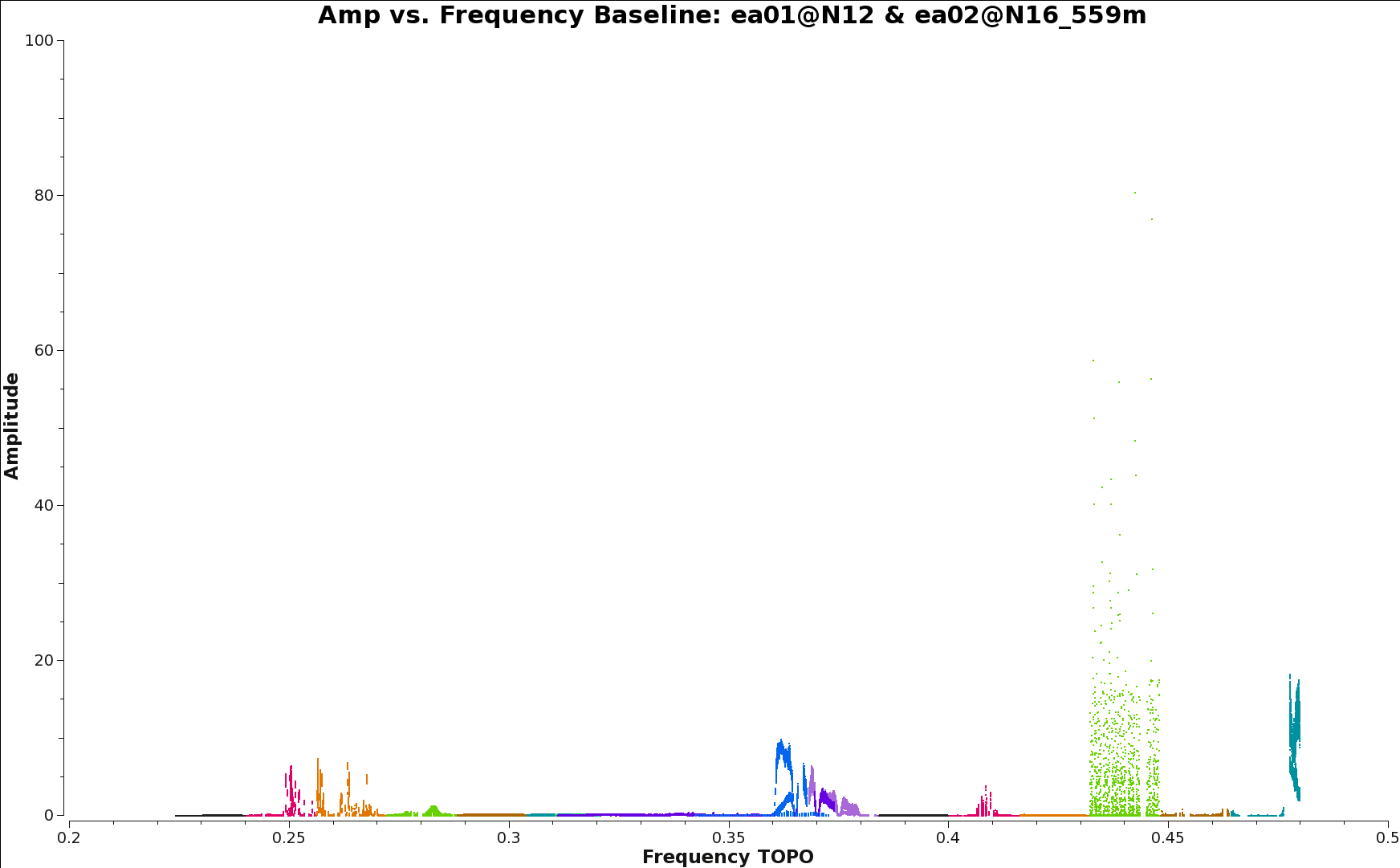
There is quite a bit of RFI that gets missed in RFI-rich spectral windows as can be seen in Fig. 4c. The solution to this is to provide the flagging routines with more contrast between healthy and affected data. For this, we will perform a preliminary bandpass calibration to take out the bandpass shape. We will do some coarse preliminary calibration and apply it to the calibrator before flagging for RFI once more.
# In CASA
gaincal(vis='3C129_pband.ms', caltable='3C129_pband.G0', gaintype='G', calmode='p', solint='int', field='3C147',refant='ea09',
gaintable=['3C129_pband.antpos','3C129_pband.rq','3C129_pband.tecim'])
#
gaincal(vis='3C129_pband.ms', caltable='3C129_pband.K0', gaintype='K', solint='inf', field='3C147',refant='ea09',
gaintable=['3C129_pband.antpos','3C129_pband.rq','3C129_pband.tecim','3C129_pband.G0'])
#
bandpass(vis='3C129_pband.ms', caltable='3C129_pband.B0', solint='inf', field='3C147',refant='ea09', minsnr=2.0,
gaintable=['3C129_pband.antpos','3C129_pband.rq','3C129_pband.tecim','3C129_pband.G0','3C129_pband.K0'])
#
applycal(vis='3C129_pband.ms', field='3C147', applymode='calflagstrict',
gaintable=['3C129_pband.antpos','3C129_pband.rq','3C129_pband.tecim','3C129_pband.G0','3C129_pband.K0','3C129_pband.B0'] )
On the command line you should see a notification stating: "FJones (iononsphere) apply now provisionally includes disp. delay." which indicates that both Faraday rotation as well as dispersive delay corrections for the ionosphere are applied.
We will now flag the corrected data column that contains the coarsely calibrated visibilities which provide better contrast to the flagging algorithms to remove the RFI present. We will begin by running the RFLAG algorithm in the task flagdata. We will again use summary mode to see how much more of the observed data was flagged.
# In CASA
flagdata(vis='3C129_pband.ms', field='3C147', mode='rflag', datacolumn='corrected', timedevscale=4., freqdevscale=3.,
action='apply', flagbackup=True, combinescans=True, ntime='3600s', maxnpieces=5)
#
flagdata(vis='3C129_pband.ms', field='3C147', mode='rflag', datacolumn='corrected', timedevscale=4., freqdevscale=3.,
action='apply', flagbackup=True, combinescans=True, ntime='3600s', maxnpieces=5)
#
summary_3 = flagdata(vis='3C129_pband.ms' , mode='summary')
#
%cpaste
# Press Enter or Return, then copy/paste the following:
axis = 'scan'
for value, stats in summary_3[ axis ].iteritems():
old_stats = summary_2[ axis ][ value ]
print '%s %s: %5.1f percent flagged additionally' % ( axis, value, 100. * ( stats[ 'flagged' ] - old_stats[ 'flagged' ] ) / stats[ 'total' ] )
--
#
plotms(vis='3C129_pband.ms',xaxis='freq',yaxis='amp',antenna='ea01',correlation='XX,YY',
field='3C147', plotrange=[0.2,0.5,0.0,100.0], coloraxis='spw',xlabel='Frequency',ylabel='Amplitude',
iteraxis='baseline', plotfile='3C147_postbandpass_rflag.png', ydatacolumn='corrected')
Taking another visual look at the data using plotms, we examine the effect of the automated flagging on the calibrator (Fig. 4d). We find that most spectral windows are RFI free and that about 60% of the data was flagged. We typically expect between 40-60% of flagging due to interference in a significant fraction of the band. In this example, a more careful RFI flagging approach is likely to recover more usable spectrum.
Flux Density Calibration
The initial flagging has cleaned up most of the stray RFI across the band. This allows us to proceed with the actual calibration of the data. Before we get to the calibration tables, it's essential to do the flux density calibration of our calibrator 3C147. This is done by the setjy task. Before we run the task we first clear the preliminary calibration that was carried out to enable better flagging. We do that by running the clearcal task.
# In CASA
clearcal(vis='3C129_pband.ms')
#
setjy(vis='3C129_pband.ms', standard='Scaife-Heald 2012', field='3C147')
Delay and bandpass calibration
First, we use the full bandwidth on a single scan on the primary calibrator to determine a single delay per antenna, per polarization. This will determine a single (approximate) phase slope across frequency, mainly caused by propagation effects in the (time-variable) ionosphere, cable length differences, and electronics in the signal paths from antenna feeds to correlator. Note that for a single short (5-10 minutes) scan on the calibrator, we can get away with solving for a time-invariant delay per antenna, per polarization. We will use scan 3 on 3C147.

# In CASA
gaincal(vis='3C129_pband.ms', caltable='3C129_pband.K1', field='3C147', solint='inf', refant='ea09', gaintype='K',
gaintable=['3C129_pband.antpos','3C129_pband.tecim','3C129_pband.rq'],parang=True)
#
plotcal(caltable='3C129_pband.K1', xaxis='antenna', yaxis='delay', markersize=2.0,
plotrange=[0,30,-50.,50.],figfile='3C147_delay.png')
Since we picked ea09 as our reference antenna, the delays for this antenna ID (=0) are arbitrarily set to zero. All other delays should be within 30 nanosec or so (which they should be for this data set). Larger values should be treated with suspicion, possibly indicating a problem with the antenna or polarization. We will use the bandpass calibration to verify this in the next step.
To determine the bandpass calibration, we use the same source and scan and apply the delay calibration before solving for the bandpass. Note that we request a minimum SNR of 3, which will make the solve fail for the worst, but not all, channels.
# In CASA
bandpass( vis='3C129_pband.ms', caltable='3C129_pband.B1', field='3C147', solint='inf', refant='ea09', minsnr=3.0,
parang = True, gaintable=['3C129_pband.antpos','3C129_pband.tecim','3C129_pband.rq','3C129_pband.K1'],
interp=['','','','nearest,nearestflag'])
After solving, we inspect the bandpass calibration amplitudes and phase, and flag any obvious residual outliers. Outliers may be found above or below the average bandpass curves, and tend to arise in the same channel (frequency) ranges for all antennas. Don't spend more than 1 minute per antenna for this tutorial and don't worry about missing some bad points; these bad channels will likely get flagged in a later stage anyway. Note that the bandpass amplitudes (Fig. 6) and phases may differ between polarizations of the same antenna. Also note that the bandpass phases across frequency should not have an overall gradient (this should be removed by the delay calibration). Also note that bandpass phases may wrap around from +/-180 to -/+180 degrees. If that is problematic, re-run the phase plotcal() with plotrange = [ 200.,500.,0.,360. ]. Also note that there are no bandpass solutions for antennas ea19 and ea28, and only a few solutions for ea14.
# In CASA
plotcal(caltable='3C129_pband.B1', xaxis='freq', yaxis='amp', iteration='antenna', markersize=2.0)
#
plotcal(caltable='3C129_pband.B1', xaxis='freq', yaxis='phase', iteration='antenna', plotrange=[ 200.,500.,-180.,180. ], markersize = 2.0)
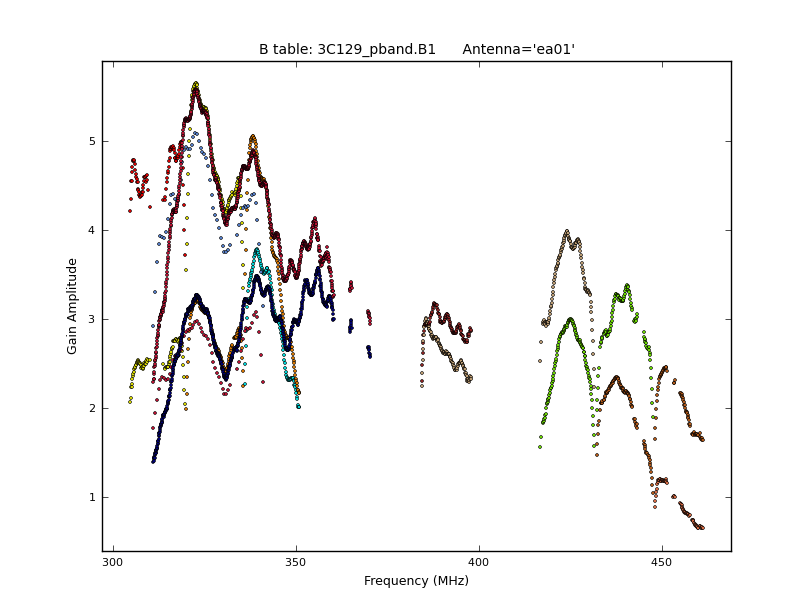 |
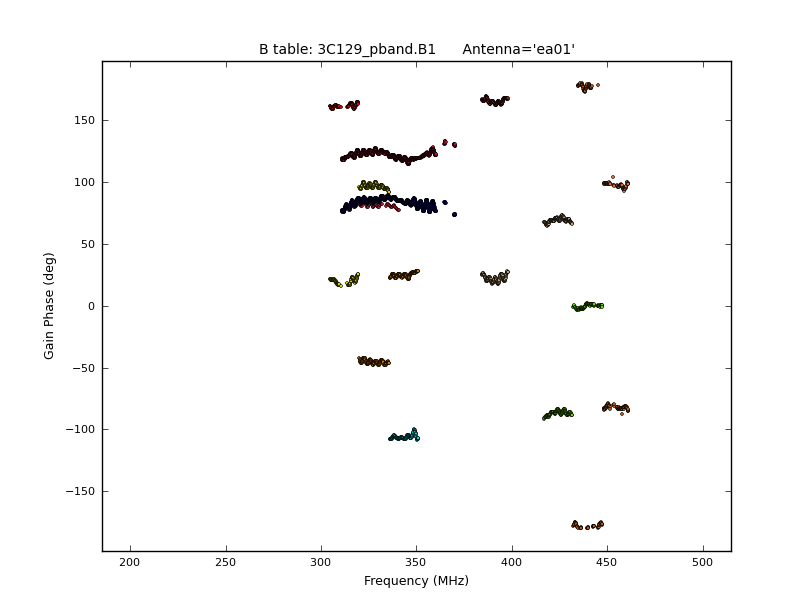 |
Flagging is made easier by maximizing the plotcal() window. We don't set the scale for plotting the bandpass amplitudes, which is convenient when flagging outliers as it will auto-rescale. While plotting the bandpass phases we do fix the scale, as it provides a better feeling for the relevant magnitude of phase outliers. Flagging of outliers is done using the Mark Region and Flag buttons. For more information on interactive flagging, see the topical guide Flagging VLA Data in CASA. We are using this mechanism to efficiently flag data manually, since it is done per antenna rather than per baseline. These 'flags' will not be permanent until we call applycal() later on, but are effective while applying the calibration on the fly, as we will do in subsequent calibration steps.
Gain calibration
With the delay and bandpass calibration in place, we will now look more closely at the time-variable behaviour of the VLA. We use the same scan on our primary calibrator, 3C147, over the full effective bandwidth to determine gain calibrations: one complex value per antenna, per polarization, per integration time. The delay and bandpass tables are applied on the fly.
# In CASA
gaincal( vis='3C129_pband.ms', caltable='3C129_pband.G1', field='3C147', solint = 'int',
refant = 'ea09', minsnr = 3.0, gaintype = 'G', calmode = 'ap',
gaintable = ['3C129_pband.antpos','3C129_pband.rq','3C129_pband.tecim', '3C129_pband.K1', '3C129_pband.B1' ],
interp = ['','','','nearest,nearestflag', 'nearest,nearestflag' ], parang = True )
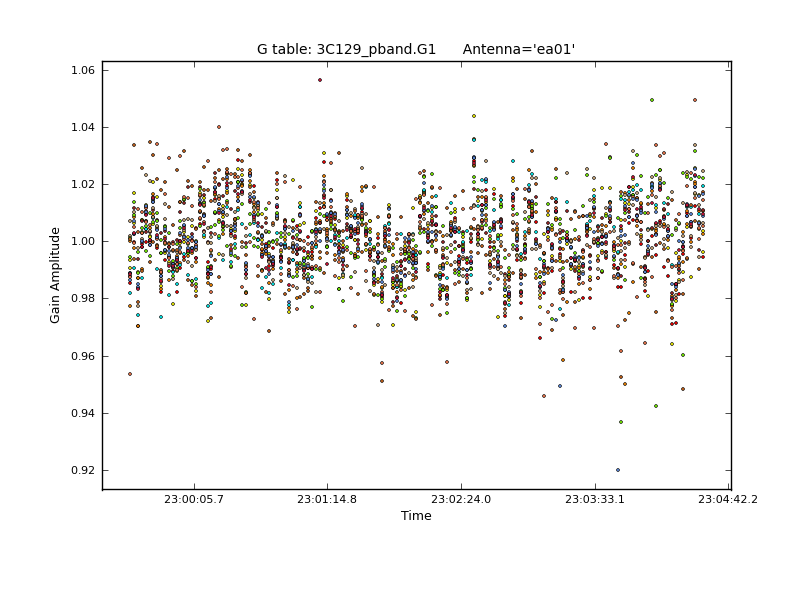 |
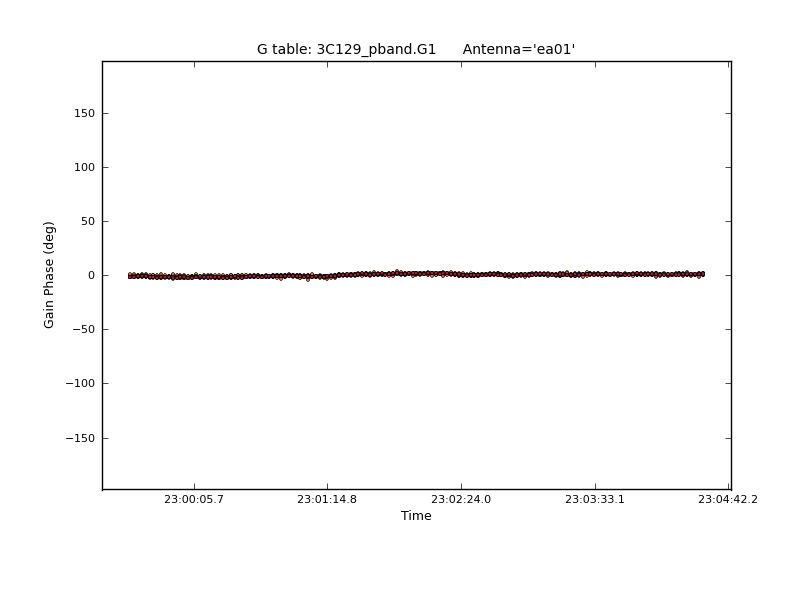 |
Similar to the bandpass flagging, we will flag outlier gain solutions in both amplitude and phase. For the amplitudes, the final scatter around an average close to one should be a few percent (see Fig. 7). Note antennas ea08, ea09 have particularly noisy solutions. Remember that the gain solutions for both polarizations can be flagged together, as we will lose the equivalent data of the surviving polarization anyway.
# In CASA
plotcal(caltable='3C129_pband.G1', xaxis='time', yaxis='amp', iteration='antenna', markersize=2.0 )
#
plotcal(caltable='3C129_pband.G1', xaxis='time', yaxis='phase', iteration='antenna',
plotrange=[ None,None,-180.,180.], markersize=2.0)
Note that when plotting gains against time, it is convenient to use auto-scaling of the time axis by putting None in the first two fields of plotrange.
Next, we will prepare a smoothed and interpolated version of the gain calibration table, which will be applied later to the target field data. This prevents flagging of target field data when one of the edges of a calibrator scan is flagged for one or more antennas. The result can be inspected with plotcal.
# In CASA
smoothcal(vis='3C129_pband.ms', tablein='3C129_pband.G1', caltable='3C129_pband.Gs1', smoothtype='median', smoothtime = 60.*60.)
#
plotcal(caltable='3C129_pband.Gs1', xaxis='time', yaxis='amp', iteration='antenna', plotrange=[ None,None,0.8,1.2 ], markersize=2.0)
#
plotcal(caltable='3C129_pband.Gs1', xaxis='time', yaxis='phase', iteration='antenna', plotrange=[ None,None,-10.,10. ], markersize=2.0)
Instrumental polarization calibration
The VLA at P-band measures the incoming radio waves using dual-dipole feeds mounted near the primary focus of the dishes. While much effort is put into mechanically making these dual-dipoles orthogonal, and to strongly suppress any cross-talk between the electronic signal paths of both dipoles, there is some (frequency-dependent) polarization leakage between them. Furthermore, the P-band feeds are mounted and aligned on each antenna by hand, allowing for 5-10 degrees difference in the orientation of the dipoles between antennas. For both intensity and polarization imaging, it is important to calibrate the polarization products in our data to optimize the (i) orthogonality between X and Y for each antenna, and (ii) the alignment between Xs and Ys of different antennas. Note that this does not (yet) include calibration of the absolute polarization angle; for which we need a linearly polarized source with known polarization angle.
First, we calibrate the cross delay, which is the difference in delay between the two polarizations of the reference antenna; in our case ea09. Remember that the regular delay calibration arbitrarily set the delays for both polarizations of the reference antenna to zero. In reality there will be a small, but noticeable, physical path length difference between these two polarizations, for which we try to correct. This calibration uses the same scan on 3C147, assuming that 3C147 is unpolarized at P-band (which is a good approximation). Although 3C147 has very low intrinsic polarization at P-band, it is strong enough that gaincal can solve for the cross-delays from the leakage signals which are of the order 5-10%. If all P-band dipoles were perfectly aligned, this would result in virtually zero leakage between the polarizations and thus we would have to use a polarized source to solve for the cross delay.
# In CASA
gaincal(vis='3C129_pband.ms', caltable='3C129_pband.Kc1', field='3C147', solint='inf', refant='ea09', minsnr=3.0, gaintype='KCROSS', parang=True,
scan='3', gaintable=[ '3C129_pband.antpos','3C129_pband.rq','3C129_pband.tecim','3C129_pband.K1', '3C129_pband.B1','3C129_pband.Gs1'],
interp=['','','','nearest,nearestflag', 'nearest,nearestflag', 'nearest,nearestflag'] )
plotcal(caltable='3C129_pband.Kc1', xaxis='antenna', yaxis='delay', markersize=2.0)
This plot shows a small, ~2 nanosec, delay between X and Y. Note that the table is generated in such a way this correction is exactly equal for all antennas, since in fact gaincal solves for only a single, antenna-independent, delay between X and Y. There are four spectral windows with larger delays up to -37 nsec, namely 8, 12, 16, and 17. You can use the Locate feature of plotcal to identify which is which. Note that the table is generated in such a way that this correction gets applied to all antennas.
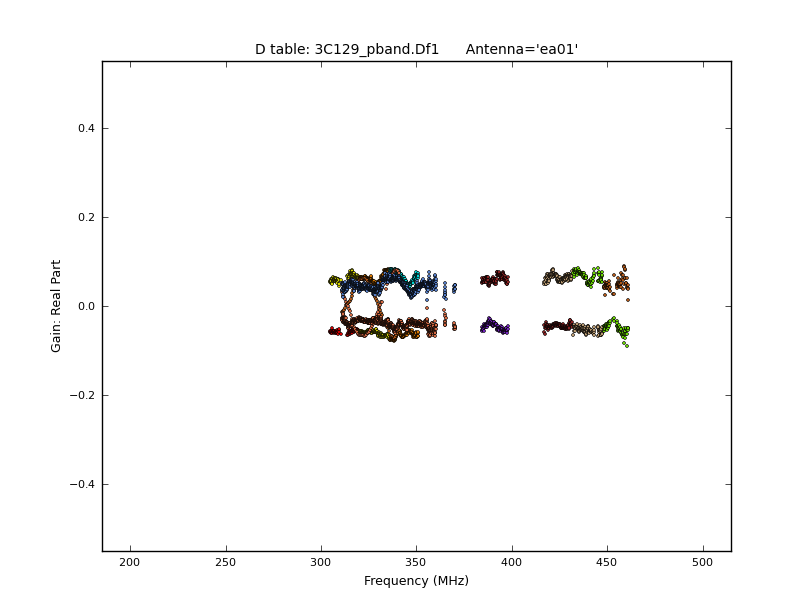
Next we determine the leakage of the X signal into Y, and Y into X. For a well-behaved instrument, the magnitude of the leakage (D-terms) should be much less than one. Since the leakage is frequency dependent, we solve for leakage for each frequency channel, somewhat similar to bandpass calibration. The way to do this in CASA is through the polcal() task with the option poltype = 'Df'. Again, we can inspect (and edit) the leakage calibration table with plotcal()
# In CASA
polcal(vis='3C129_pband.ms', caltable='3C129_pband.Df1', field='3C147', solint='inf', refant='ea09', minsnr=3.0, poltype = 'Df',
gaintable=[ '3C129_pband.antpos','3C129_pband.rq','3C129_pband.tecim','3C129_pband.K1', '3C129_pband.B1',
'3C129_pband.Gs1','3C129_pband.Kc1'],
interp=['','','','nearest,nearestflag', 'nearest,nearestflag', 'nearest,nearestflag', 'nearest,nearestflag' ] )
#
plotcal(caltable='3C129_pband.Df1', xaxis='freq', yaxis='amp', iteration='antenna', plotrange=[ 200.,500.,0.,1. ], markersize=2.0)

Before starting any flagging, it is best to first cycle past all antennas to get a feel for the magnitude of the leakage terms. For most antennas, both leakage terms are roughly equal in amplitude across the band, with values between 0 and 0.15. Few have higher leakages (up to 0.3). The most likely explanation is a larger misalignment of the P-band feed of these antennas relative to the others. Examples are ea05, ea11, and ea24. These antennas do not need to be flagged, but are merely expected to benefit most from this polarization calibration. Some examples of suspicious data that is probably best to flag: antenna ea03 has a peculiar bump in one of the leakage terms, ea12 has an upturn at the low-frequency end of the band, ea14 has a peak near the low-frequency end of the band. These can all be flagged interactively using plotcal.
It is better not to flag based on phases, because the closer the amplitude of the leakage terms get to zero, the more erratic the phase behaviour will be. An alternative is to flag based on the real and imaginary parts, which you may or may not want to do.
# In CASA
plotcal(caltable='3C129_pband.Df1', xaxis='freq', yaxis='amp', iteration='antenna', plotrange=[ 200.,500.,0.,1. ], markersize=2.0)
#
plotcal(caltable='3C129_pband.Df1', xaxis='freq', yaxis='real', iteration='antenna', plotrange=[ 200.,500.,-0.5,0.5 ], markersize=2.0)
#
plotcal(caltable='3C129_pband.Df1', xaxis='freq', yaxis='imag', iteration='antenna', plotrange=[ 200.,500.,-0.5,0.5 ], markersize=2.0)
Re-iterate bandpass and leakage calibration
The largest instrumental effects on our data are now captured in several relevant calibration tables. But since we have used uncalibrated / partially calibrated data to determine these calibration tables, there are improvements to be obtained when re-determining some calibration tables. In this section we re-calibrate the bandpass and polarization leakage since these are expected to have changed most. Our re-calibrations will be relative to the existing bandpass and leakage calibrations, so that we can more easily see deviations from the ideal case.
First, we update the bandpass calibration by determining a new, relative bandpass table while applying all previous calibrations. In the ideal case that our data and previous calibrations were perfect, the new bandpass table would contain gain amplitudes and phases of one and zero, respectively, for all (unflagged) antennas, polarizations and channels.
# In CASA
bandpass(vis='3C129_pband.ms', caltable='3C129_pband.B2', field='3C147', solint='inf', refant='ea09', minsnr=3.0, parang = True,
gaintable=[ '3C129_pband.antpos','3C129_pband.rq','3C129_pband.tecim','3C129_pband.K1', '3C129_pband.B1',
'3C129_pband.Gs1','3C129_pband.Kc1','3C129_pband.Df1'],
interp=['','','','nearest,nearestflag','nearest,nearestflag','nearest,nearestflag','nearest,nearestflag','nearest,nearestflag'])
#
plotcal(caltable='3C129_pband.B2' , xaxis='freq', yaxis='amp', iteration='antenna', plotrange=[ 200.,500.,0.,2. ], markersize=2.0)
#
plotcal(caltable='3C129_pband.B2', xaxis='freq', yaxis='phase', iteration='antenna', plotrange=[ 200.,500.,-180.,180. ], markersize=2.0)
In the plotcal() calls above, the vertical axis scales have been chosen to indicate the relevance of the ideal case of unity amplitudes and zero phases. For most antennas, the bandpass solutions are close to ideal. Some antennas show some noticeable structure across frequency. A general guideline for flagging (or not) is that we expect the relative bandpass to be close to one in amplitude and vary smoothly in frequency.
# In CASA
polcal(vis='3C129_pband.ms', caltable='3C129_pband.Df2', field='3C147', solint='inf', refant='ea09', minsnr=3.0, poltype = 'Df',
gaintable=[ '3C129_pband.antpos','3C129_pband.rq','3C129_pband.tecim','3C129_pband.K1',
'3C129_pband.B1','3C129_pband.Gs1','3C129_pband.Kc1','3C129_pband.B2'],
interp=['','','','nearest,nearestflag', 'nearest,nearestflag', 'nearest,nearestflag', 'nearest,nearestflag', 'nearest,nearestflag' ] )
#
plotcal(caltable='3C129_pband.Df2', xaxis='freq', yaxis='amp', iteration='antenna', plotrange=[ 200.,500.,None,None ], markersize=2.0)
Transfer of calibrations to the target field
So far we have used one scan on the primary calibrator 3C147 to derive various calibration tables. These calibrations will now be applied to all scans of all sources in our measurement set, which includes 3C147 itself and our target field 3C129. As described above, the task applycal() creates a CORRECTED_DATA column in which the calibrated visibilities get stored. This may take a while.
# In CASA
applycal(vis='3C129_pband.ms', parang=True, applymode='calflagstrict', flagbackup=True, gaintable=['3C129_pband.antpos','3C129_pband.rq',
'3C129_pband.tecim','3C129_pband.K1','3C129_pband.B1','3C129_pband.Gs1','3C129_pband.Kc1','3C129_pband.B2','3C129_pband.Df2'],
interp = ['','','','nearest,nearestflag', 'nearest,nearestflag', 'nearest,nearestflag', 'nearest,nearestflag','nearest,nearestflag',
'nearest,nearestflag'])
Now we split off the calibrated target field data, meaning that the visibilities of source 3C129 get copied from the CORRECTED_DATA column to the DATA column of a new measurement set. This is convenient for further processing.
# In CASA
split(vis='3C129_pband.ms', outputvis='3C129_pband_target.ms', datacolumn='corrected', field='3C129')
Imaging
At this point, we're ready to make a first image of our target field. Imaging in CASA is done by means of the CLEAN task. The task implements algorithms for wide field imaging, such as W-Projection (Cornwell et al. 2008 http://arxiv.org/abs/0807.4161) and Multi Term Multi Frequency Synthesis ( Rau et al. 2011 http://arxiv.org/abs/1106.2745) both of which we will utilize to make our initial image. Even though our source of concern, the radio galaxy, lies in the centre of our field. The observations were carried out in B configuration resulting in an effective maximum resolution of approximately 5x5 arcsecs. To effectively model the source spectral index in the sky, we will utilize the MTMFS algorithm and use the W-Projection algorithm to make a wide field image (The full beam at P Band is about 3 degrees in diameter). So, going by these requirements, we can now compute the required cell and image size. To Nyquist sample the beam we need at least 3 pixels across the synthesized beam width, along the major and minor axes of the point spread function. Consulting the resolution guide of NRAO science page, we can see that the expected HPBW for B - Configuration, P -Band Observation is 18.5 arcsec. So, we can sample it well by using a 5 arcsec cellsize. Having done that, if we decide to make a wide field image to account for all the point sources we will set the image size parameter to 4096 pixels. To enable the wide-field algorithm, we set the gridmode='widefield': this invokes the W-Projection algorithm, upon which we set the number of W-Projection planes to be 128. We set the imager mode as Multi Frequency Synthesis using the mode='mfs' parameter along with the number of Taylor terms to be considered during imaging to be 2. This allows for the source spectral variation to be modeled by a second order polynomial. We launch the interactive clean process, but only for spw='3~8' due to RFI issues. Note, running the first clean call will take at least ~10 min to process.
# In CASA
clean(vis='3C129_pband_target.ms', imagename='3C129_initial_clean', cell=['5.0arcsec','5.0arcsec'], imsize=[4860,4860], mode='mfs',
nterms=2, gridmode='widefield', wprojplanes=128, stokes='I', niter=10000, spw='3~8', interactive=True,
minpb=0.1, usescratch=True, weighting='briggs', robust=0.0)
 |
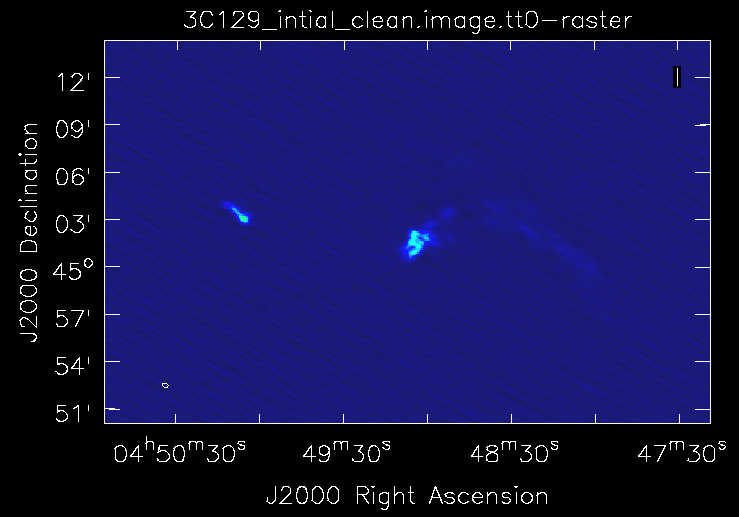 |
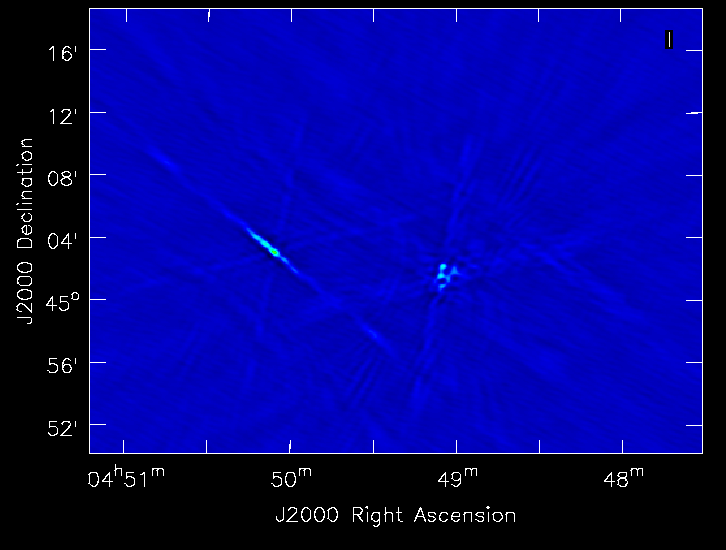
The CLEAN command launches an interactive session after a 100 iterations of clean and produces a wide field map with two sources at the center and a lot of bright sources far out in the field. As it is a snapshot image, the bright sources have significant side lobes and so tight clean boxing can help. This can done in the interactive viewer interface that pops up. This topic has been covered extensively in the 3C391 imaging tutorial, which can be found here (https://casaguides.nrao.edu/index.php?title=EVLA_Continuum_Tutorial_3C391#Initial_Imaging). If we proceed with interactive clean with subsequent steps to keep boxing out the strong sources that pop up in the image, we finally see the extended emission from the target radio galaxy begin to emerge. Continue boxing and cleaning to ensure that the residuals of the boxed cleaning look noise like (~10000 clean iterations). We now stop the interactive task and look at the final image it produced.
# In CASA
viewer('3C129_initial_clean.image.tt0')
The recovered structure at the center of the map should resemble what is shown in Fig. 10b. If the image looks worse then boxing of bright features in the map needs to be done more carefully. Note the image has some sources still showing strong side lobes and imaging artifacts around them. We expected this as we have carried out phase calibration only on our flux calibrator and have just transferred the solutions over to our target field. Since we used the usescratch=True, the MODEL_DATA column in the measurement set now contains the initial image model, which we will self calibrate against to produce a better image. Also in clean, do notice that the spw's utilized are the cleanest spectral windows that are totally RFI free.
Self Calibration
We now proceed to compute gain phase solutions for our target field using the gaincal task as the first step in self-calibration.
# In CASA
gaincal(vis='3C129_pband_target.ms', caltable='3C129_pband_target.ScG0', field='3C129', solint='inf', refant='ea09',
spw='3~8',minsnr=3.0, gaintype='G', parang=True, calmode='p')
#
applycal(vis='3C129_pband_target.ms', gaintable=['3C129_pband_target.ScG0'], applymode='calflagstrict')
Having applied these gain solutions, we will once again image the target measurement set which we now expect to have better gain solutions and consequently a better image. We do this by invoking the CLEAN command.
# In CASA
clean(vis='3C129_pband_target.ms', imagename='3C129_clean_sc0', cell=['5.0arcsec','5.0arcsec'], imsize=[4860,4860], mode='mfs',
nterms=2, gridmode='widefield', wprojplanes=128, stokes='I', niter=10000, spw='3~8', interactive=True,
minpb=0.1, usescratch=True, weighting='briggs', robust=0.0)
viewer('3C129_clean_sc0.image.tt0')
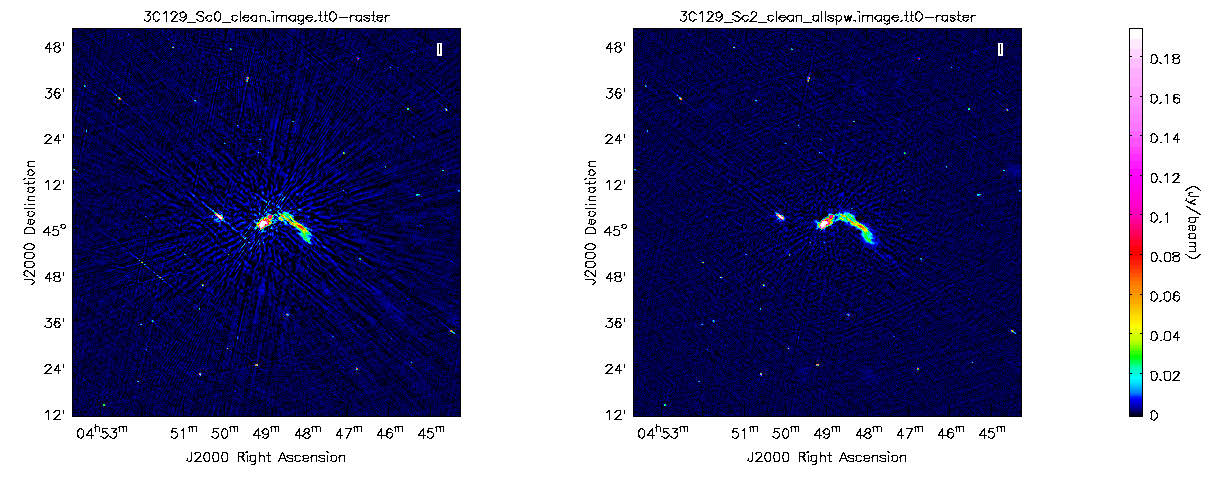
On boxing and cleaning, we already notice that the imaging artifacts have reduced significantly. We also see that the target source appears to contain more structure and a greater amount of flux. Further self calibration iterations involving an amplitude & phase gain calibration, or even an on target bandpass and leakage calibration, are all possible steps that can be introduced into the self-cal imaging loop. These steps, and introducing Multi Scale Clean for the extended source, are possible improvements on the current strategy implemented.
Appendix: Some P-band data issues you may want to know about
Unfortunately, there are a few known issues with JVLA P-band observing. Most problems were discovered during the P-band commissioning period and have been fixed for newer data sets, but the archive keeps part of this history alive. Here we will go over some of those issues, and (if possible) provide ways of fixing them.
Polarization labeling
For a long period, P-band feeds have been labelled as being circular (R and L), while they are linear (X and Y). It is still possible to generate data with incorrect polarization labeling, however for standard observations this should not be the case anymore. A contributed task fixlowband() is available to recognize and fix this problem. This may seem mostly harmless, but does make a difference for polarization calibration. The following (non-standard) task will check and fix this (and another related problem of swapped polarizations):
Download this tarball in your CASA working directory, open a shell there, and type the following commands:
tar -xzvf casa_vla_lowband.tar.gz
buildmytasks
Now go back to your CASA session and type:
# In CASA
execfile('mytasks.py')
#
fixlowband(vis='TSUB0001_pband_prehs.ms')
Re-run the listobs() task to check if the fix was correctly applied.
Swapped polarizations
Throughout the whole history of the new VLA low-band system, even up to this day, there have been mistakes in the cabling of the full signal chain. This results in that some antennas have the X-polarization signal come in as Y and vice versa. The way to notice this in visibility data is that for baselines with one swapped antenna most power will be in the cross-hand correlations (XY and YX) rather than the parallel-hand correlations (XX and YY). Once antennas with this feature are manually identified, a contributed task swappol() is available to fix this problem (see under polarization labelling).
Double data descriptor entries
The data description table is part of the measurement set, and provides a link between the recorded visibilities, the spectral window information and the polarization information. For some data sets, the data description table contains two entries for each P-band spectral window, one pointing towards a circular (RL) polarization definition, and one pointing towards a linear (XY) polarization definition. A contributed task fixlowband() is available to recognize and fix this problem.
Continuous Radio Frequency Interference (RFI)
The wide bandwidth of the low-band receiver is (unfortunately) guaranteed to contain significant amounts of RFI. There are a few RFI sources that are active all the time, and are visible in all array configurations. The default P-band observing setup of 16 x 16 MHz tries to capture as much of the continuous RFI in as few spectral windows as possible, allowing for a simple RFI mitigation strategy in which these spectral windows (spws 1,2 and 9,10, but possibly more) can be immediately flagged.
Two spectral window setup
In the early commissioning period, the default setup for P-band observing was to use 2 spectral windows of 1024 channels each to cover 256 MHz of bandwidth from 230 - 486 MHz. However, it was noticed that strong, narrow-band RFI events were causing data to be lost for the whole spectral window in which they occured. To make the system more robust against data loss from these events, the frequency range was divided into 16 x 16 MHz, and shifted downwards by 6 MHz to capture ever-present RFI into as few spectral windows as possible. If your data has only two P-band spectral windows, please be aware that a higher data loss due to RFI is possible. There is no way to repair this.
Bandpass ripples
Due to signal reflections in cables and within the VLA dish, sinusoidal amplitude and phase modulations are always present in P-band data. This is most easily seen in bandpass calibration plots of amplitude versus frequency. In some cases, mostly due to cable & connector problems, these modulations can be very strong (~up to 50 percent of the average amplitude level). These modulations tend not to vary over the duration of an observation and can therefore be removed through bandpass and polarization calibration. If they are found to be variable (e.g., by inspecting bandpass solutions for separate calibrator scans), the offending antenna / polarization should be flagged.
High cross-polarization
On each antenna, the P-band feed (dipole) is visually aligned with respect to the primary focus support legs. This is normally done within 5-10 degrees accuracy. On rare occasions the dipole on one antenna has accidentally rotated to much larger angles because the locking bolt on the back of the feed was not completely tightened. The result is a high cross-polarization in the baseline visibilities that include this antenna. If this is the case, it is safest to flag this data, since there is a possibility that the dipole has rotated during the observations.
Useful links
Last checked on CASA Version 5.0.0