VLA CASA Bandpass Slope-CASA6.4.1
This CASA Guide is for CASA version 6.5.4
If new to CASA, or to VLA data reduction in CASA, it is strongly recommended to start with the Getting Started in CASA guide, the IRC+10216 spectral line tutorial, or the VLA 3C391 Continuum Tutorial before proceeding with this tutorial.
Also note that this guide is meant to be used with monolithic CASA and not pip-wheel, because the GUIs have not been validated.
This tutorial uses the default calibrator model distributed with this version. A different CASA version or CASA update may provide a different model than used here, in particular in Ka-band (a.k.a. A-band, i.e., in the 28-40 GHz range), so be aware when using CASA installed on the NRAO machines that are current. The plots and results will be different than in this guide in those cases.
For the purpose of this tutorial it is also safe to ignore any annoying messages about the "leap second table" being "out of date"..
Purpose Background and Method Overview
For the standard VLA flux density calibrators 3C138, 3C147, 3C286 and 3C48, the CASA distribution includes angular and spectral models that are referenced during calibration (see the note in bright lime green at the top of this tutorial). The models account for the observational source characteristics for these standard calibrators, resulting in improved calibration solutions that therefore more accurately represent the instrumental and atmospheric corrections. These VLA standard calibrators, however, exhibit a negative spectral index (i.e., flux density decreasing with increasing frequency) and become relatively weak at high frequencies.
Although the standard VLA flux density calibrators are usually still sufficiently bright enough for absolute flux density calibration even at the higher frequency bands, a good delay and bandpass determination — which could be important for spectral line observations or measuring the spectral index of continuum sources — may require higher signal-to-noise ratio bandpass solutions derived from either a long integration time or a very bright source (refer to the Spectral Line (Bandpass Setup) section within the Guide to Observing with the VLA). Generally, instead of a long integration on a fainter source, additional observations of non-standard, but bright bandpass calibrator alternatives are used. Unfortunately, the spectral characteristics of these sources will be undetermined, and no a-priori flux density model is available. If not accounted for, using undetermined spectral behavior will introduce bias in the delay and bandpass calibration.
Whereas there are different ways of doing this depending on the trade-offs one chooses to make, here, instead of using a bandpass determined from the standard flux density calibrator that might be noisier and transferring this noise to the target source, a less noisy bandpass from a different source is applied. To avoid bias to an undesired and initially unknown spectral index of that source, one needs to determine and model its spectral behavior so that it can be taken out during the determination of the bandpass using this brighter (higher signal-to noise) source.
This tutorial describes how to determine the spectral characteristics for a point-like source and how to correct the delay and bandpass solutions for such an effect using alternative bandpass calibrator sources. This is accomplished by following the four general steps (below) to obtain a delay and bandpass calibration as determined from a non-standard bandpass calibrator source, and avoid including the (higher) noise of the flux density calibrator in the bandpass:
Steps to perform: A) After a phase-only self-calibration iteration, determine a good delay and bandpass calibration using the alternative bandpass calibrator. B) Use this first-step delay and bandpass solution to calibrate the standard flux densty calibrator using the the non-standard bandpass calibrator source. This will bias the standard flux density calibrator observations with the spectral features of the bandpass calibrator, the contamination of which will be removed in the next step. C) Compare the newly self-calibrated and initial bandpass-corrected non-standard bandpass calibrator fluxes (as function of frequency) with the self-calibrated and initial bandpass-corrected standard flux density calibrator. Fitting these fluxes will yield the spectral characteristics, including the spectral index, of the bandpass calibrator. D) With this flux density and spectral index model, determine a new, second-step delay and bandpass calibration using the non-standard bandpass calibrator source. This method therefore does not use the flux density calibrator for bandpass calibration; the flux density calibrator is only used for obtaining the model spectral behavior of the alternative bandpass calibrator, which then can be used as if it were a standard.
These resulting delay and bandpass solution tables then can be applied to the rest of the (target) data.
Obtaining the (Tutorial-Modified) Data and Starting CASA
The data used in this guide are taken for a target field in Ka-band with four 2-GHz basebands paired to two chunks of 4 GHz contiguous frequency coverage centered at 29 and 36.5 GHz for a total of 8 GHz frequency coverage. That is, each baseband consists of a series of 16 consecutive 128-MHz subbands "attached" to another baseband for a total of 64 individual spectral windows.
As this tutorial only concerns bandpass calibration, all scans on fields other than the flux density and bandpass calibrator fields were removed from the measurement set (MS). All pre-calibration steps including flagging, antenna position offsets, requantizer gains, opacity corrections, and gain-elevation curves were applied. The original data (TVER0004.sb14459364.eb14492359.56295.26287841435) can be obtained through the NRAO archive and has a raw size of 57.04 GB.
The trimmed measurement set used here, G192-BP.ms, can be downloaded directly from http://casa.nrao.edu/Data/EVLA/G192/G192-BP.ms.tar.gz either by clicking on the link or by using operating system tools like wget (dataset size: 3.4 GB).
The first steps will be to obtain, uncompress and untar the file in a terminal (before starting CASA):
# in a terminal, outside of CASA, prepare the measurement set: cd <download/working directory> (this tutorial uses up to 10GB in these directories) wget http://casa.nrao.edu/Data/EVLA/G192/G192-BP.ms.tar.gz tar -xzf G192-BP.ms.tar.gz
Then move to the working directory (if not the same as the location of the raw data) and optionally move/copy or link the data to a preferred shortcut name; the my-vis shortcut name used below is just an example name and can be changed to anything more descriptive and less cryptic. This is particularly useful if the original observation name has it's full extent like TVER0004.sb14459364.eb14492359.56295.26287841435, for example:
# OPTIONAL ! # in a terminal, outside of CASA, rename (shorten) the MS to a symbolic link (Linux / Unix): ln -s <path-to-data>/G192-BP.ms my-vis.ms
To start CASA, type:
# If using NRAO computing resources, in a terminal and outside of CASA, start the default package: casa-pipe
or better, to make sure to be running the CASA version for which this tutorial was designed (the exact name of the installed versions to choose from can be obtained by typing casa -ls):
# in a terminal outside of CASA, start the specific package: casa -r 6.5.4-9-pipeline-2023.1.0.124
If you are not using NRAO computing resources, you will need to download and install this specific CASA version. You can obtain the most current version of CASA from the CASA Download Page.
This will initialize CASA, set the necessary paths appropriately and start up a logger window on the desktop. Starting CASA will also create a file casa-<date-time>.log which will contain all the messages that are printed to the CASA logger window. It is recommended to keep log files intact as a reminder of the steps completed in the data reduction. The most recent (i.e., current) log file may also be helpful when submitting a helpdesk ticket.
For convenience, the logger window can be rescaled and the font size can be changed as desired; see the options under the View menu. More easily, remove clutter columns by moving the mouse to the logger window and press "Ctrl-N", "Ctrl-Y","Ctrl-E", (New Years Eve is one way to remember).
Examining the Measurement Set (MS) and Pre-Defining Variables
In order to proceed, it is important to know the details of the observation as captured in the data set. Typical pieces of information to look for are 1) the calibrator sources with their intents, and 2) finding a reference antenna, next to the overall structure of the frequency setup and sequence of observing scans (fields). Furthermore, at this stage it is also useful to 3) set the flux model for the standard flux density calibrator, although that can be done at later stages too; it is done here to finish up the preparations before doing the actual bandpass calibration procedure.
From here on in this tutorial, the actual G192-BP.ms name string of the MS directory will be replaced by the variable value stored in id_ms (identify-the-MS). This makes the instructions below less dependent on the actual name of the data root so that if another measurement set name is used, only the definition here needs to be edited to the other file name. In order to do that first define these parameters as variables inside of CASA:
# In CASA, define the data root and MS:
visbase = 'G192-BP' # Comment: (or whatever base name the data set or link to be used has, like "my-vis" above - without the ".ms" !)
id_ms = visbase + '.ms' # Comment: (this should match and find the measurement set created earlier)
Frequency setup, calibrator intents, scan listing, etc
Use listobs to summarize the MS (the summary mode of vishead does not reveal calibrator intents by default):
# In CASA, dump the MS listing into a file in the working directory:
listobs(vis=id_ms, listfile=visbase+'_list.txt');
In this version of CASA, some commands such as listobs, gaincal, and bandpass will return a Python dictionary to the terminal. If you want to suppress this action, you can either:
- Assign the command to direct the output to a variable, e.g., my_listobs=listobs(...), or;
- Add a semicolon (i.e., ;) after the closing parentheses as seen in the command above. This will prevent the return dictionary to be printed in the terminal.
This will write the listobs output of the input MS (stored as the variable id_ms) to a file called <visbase>_list.txt, which can be examined using various operating system tools in a terminal, or within CASA by using an explanation mark (!) before the command, such as cat, less, or more. You may prefer to use an editor and keep it on the desktop for frequent consultation with e.g. emacs, vi, or gedit, etc.:
# OPTIONAL: In CASA, view the file with the MS listing, e.g.:
!emacs <visbase>_list.txt
================================================================================
MeasurementSet Name: <path-to-data>/<visbase>.ms MS Version 2
================================================================================
Observer: Dr. Observer Project: uid://evla/pdb/7303457
Observation: EVLA
Data records: 1769355 Total elapsed time = 4563 seconds
Observed from 03-Jan-2013/06:31:48.0 to 03-Jan-2013/07:47:51.0 (UTC)
ObservationID = 0 ArrayID = 0
Date Timerange (UTC) Scan FldId FieldName nRows SpwIds Average Interval(s) ScanIntent
03-Jan-2013/06:31:48.0 - 06:36:42.0 6 0 3C147 704865 [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63] [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 5.94, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [CALIBRATE_FLUX#UNSPECIFIED,OBSERVE_TARGET#UNSPECIFIED]
07:40:27.0 - 07:47:51.0 64 1 3c84-J0319+413 1064490 [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63] [6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6] [CALIBRATE_BANDPASS#UNSPECIFIED,OBSERVE_TARGET#UNSPECIFIED]
(nRows = Total number of rows per scan)
Fields: 2
ID Code Name RA Decl Epoch SrcId nRows
0 E 3C147 05:42:36.137916 +49.51.07.23356 J2000 0 704865
1 F 3c84-J0319+413 03:19:48.160102 +41.30.42.10305 J2000 1 1064490
Spectral Windows: (64 unique spectral windows and 1 unique polarization setups)
SpwID Name #Chans Frame Ch0(MHz) ChanWid(kHz) TotBW(kHz) CtrFreq(MHz) BBC Num Corrs
0 EVLA_KA#A1C1#2 128 TOPO 34476.000 1000.000 128000.0 34539.5000 10 RR LL
1 EVLA_KA#A1C1#3 128 TOPO 34604.000 1000.000 128000.0 34667.5000 10 RR LL
2 EVLA_KA#A1C1#4 128 TOPO 34732.000 1000.000 128000.0 34795.5000 10 RR LL
3 EVLA_KA#A1C1#5 128 TOPO 34860.000 1000.000 128000.0 34923.5000 10 RR LL
<snip>
13 EVLA_KA#A1C1#15 128 TOPO 36140.000 1000.000 128000.0 36203.5000 10 RR LL
14 EVLA_KA#A1C1#16 128 TOPO 36268.000 1000.000 128000.0 36331.5000 10 RR LL
15 EVLA_KA#A1C1#17 128 TOPO 36396.000 1000.000 128000.0 36459.5000 10 RR LL
16 EVLA_KA#A2C2#18 128 TOPO 36476.000 1000.000 128000.0 36539.5000 11 RR LL
17 EVLA_KA#A2C2#19 128 TOPO 36604.000 1000.000 128000.0 36667.5000 11 RR LL
18 EVLA_KA#A2C2#20 128 TOPO 36732.000 1000.000 128000.0 36795.5000 11 RR LL
<snip>
29 EVLA_KA#A2C2#31 128 TOPO 38140.000 1000.000 128000.0 38203.5000 11 RR LL
30 EVLA_KA#A2C2#32 128 TOPO 38268.000 1000.000 128000.0 38331.5000 11 RR LL
31 EVLA_KA#A2C2#33 128 TOPO 38396.000 1000.000 128000.0 38459.5000 11 RR LL
32 EVLA_KA#B1D1#34 128 TOPO 26976.000 1000.000 128000.0 27039.5000 13 RR LL
33 EVLA_KA#B1D1#35 128 TOPO 27104.000 1000.000 128000.0 27167.5000 13 RR LL
34 EVLA_KA#B1D1#36 128 TOPO 27232.000 1000.000 128000.0 27295.5000 13 RR LL
<snip>
45 EVLA_KA#B1D1#47 128 TOPO 28640.000 1000.000 128000.0 28703.5000 13 RR LL
46 EVLA_KA#B1D1#48 128 TOPO 28768.000 1000.000 128000.0 28831.5000 13 RR LL
47 EVLA_KA#B1D1#49 128 TOPO 28896.000 1000.000 128000.0 28959.5000 13 RR LL
48 EVLA_KA#B2D2#50 128 TOPO 28976.000 1000.000 128000.0 29039.5000 14 RR LL
49 EVLA_KA#B2D2#51 128 TOPO 29104.000 1000.000 128000.0 29167.5000 14 RR LL
50 EVLA_KA#B2D2#52 128 TOPO 29232.000 1000.000 128000.0 29295.5000 14 RR LL
<snip>
61 EVLA_KA#B2D2#63 128 TOPO 30640.000 1000.000 128000.0 30703.5000 14 RR LL
62 EVLA_KA#B2D2#64 128 TOPO 30768.000 1000.000 128000.0 30831.5000 14 RR LL
63 EVLA_KA#B2D2#65 128 TOPO 30896.000 1000.000 128000.0 30959.5000 14 RR LL
Sources: 128
ID Name SpwId RestFreq(MHz) SysVel(km/s)
0 3C147 0 - -
0 3C147 1 - -
0 3C147 2 - -
<snip>
0 3C147 61 - -
0 3C147 62 - -
0 3C147 63 - -
1 3c84-J0319+413 0 - -
1 3c84-J0319+413 1 - -
1 3c84-J0319+413 2 - -
<snip>
1 3c84-J0319+413 61 - -
1 3c84-J0319+413 62 - -
1 3c84-J0319+413 63 - -
<snip>
Antennas: 22:
ID Name Station Diam. Long. Lat. Offset from array center (m) ITRF Geocentric coordinates (m)
East North Elevation x y z
1 ea02 N56 25.0 m -107.37.47.9 +34.00.38.4 -1105.2071 12254.3069 -34.2426 -1600128.383400 -5035104.146500 3565024.672100
2 ea03 N16 25.0 m -107.37.10.9 +33.54.48.0 -155.8511 1426.6436 -9.3827 -1601061.956000 -5041175.880700 3556058.037600
3 ea05 W08 25.0 m -107.37.21.6 +33.53.53.0 -432.1184 -272.1472 -1.5070 -1601614.092200 -5042001.650900 3554652.508900
<snip>
This redacted MS contains only scans on the flux density calibrator 3C147 (field 0) and the bandpass calibrator 3c84-J0319+413 (field 1, a.k.a. 3C84). Both fields have 64 spectral windows (spws); each spw consists of 128 dual (RR, LL) polarization 1 MHz wide channels, for a total bandwidth of 128 MHz per spw.
The intents for these fields are clearly included in the scan listing (CALIBRATE_FLUX and CALIBRATE_BANDPASS). For convenience, variables will be used to recall the general use of these intents without having to remember their details like field ID numbers or name strings — variable names aren't strings so therefore using them also avoids typing the quotes when filling in task parameters (as will be seen in most of the below):
# In CASA, define field identifiers using standard variable names:
id_flx = '3C147' #Comment: (or '0' for using the field name or field ID respectively)
id_bp = '3c84-J0319+413' #Comment: (or '1')
Selecting a reference antenna form the array configuration
As a first step, a reference antenna for all phase calibrations needs to be specified. Since observations were performed with the VLA in the most extended A-configuration, it is desirable to use an antenna that is near the center of the array (for the most compact D-configuration select an antenna that is unlikely to get shadowed, i.e., in the outskirts of the array). Futhermore, it needs to have valid calibrator data on all baselines with the least amount of data flagged. The array can be mapped with plotants:
# In CASA, plot antenna locations:
plotants(vis=id_ms, antindex=True, logpos=True, figfile=id_ms+'_plotants.pdf')
- antindex=True also labels the antennas with their ID number (in parenteses).
- logpos=True shows a logarithmic plot to emphasize the center distribution, useful for picking a reference antenna in extended configurations - use the default (False) for compact configurations to emphasize the outlyer stations.
- figfile=filename.ext output file for the image generated; here using the PDF format extension - other format extensions can be .ps (PostScript) or .png (Portable Network Graphics)
 |
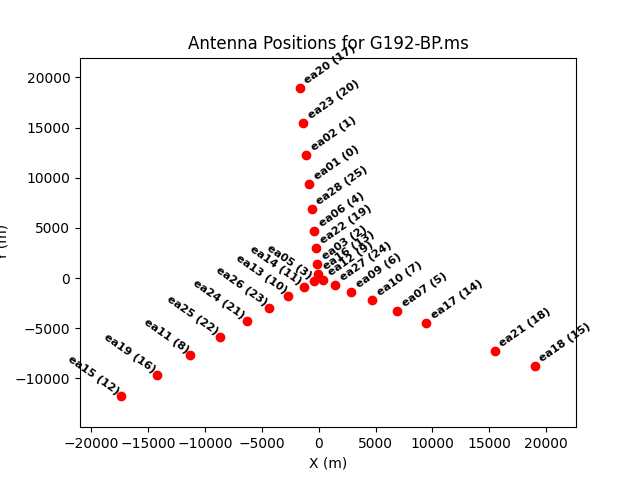 |
You can view the image produced by calling a variety of viewers from within CASA, again using the ! command to call an external application such as evince or ghostview when dealing with PDF files on Linux, or xv when dealing with png files. If you're running CASA on a Mac, the Preview app will handle both PDF and png files.
As can be seen with either with the logarithmic-scale (Figure 1a) or possibly after zooming in on the linear-scale (Figure 1b), note that antenna ea05 (with ID 3) is located close to the center. Using the flagdata task with mode='summary' it can be seen that ea05 has a low percentage of flags. Therefore, this antenna can be used with some confidence as the reference antenna; for convenience, introduce a standard descriptive variable name for it:
# In CASA, define the reference antenna identifier using a standard name:
id_ref = 'ea05' #Comment: (or '3' or 'W08' which are the antenna ID number or pad name for ea05)
Setting the Model of the Flux Density Calibrator
To start preparing for a flux comparison later (in step C), insert the spectral and angular models for the flux density calibrator, here 3C147 (field 0), with the
setjy task in the model column in MS. Use the 'Perley-Butler 2017' standard and 3C147_A.im for Ka-band (which can be written as id_flx+'_A.im because here fortunately id_flx and the model name agree):
# In CASA, insert the the flux density calibrator model in the MS model column:
setjy(vis=id_ms, field=id_flx, scalebychan=True,
standard='Perley-Butler 2017', model=id_flx+'_A.im', usescratch=True);
- scalebychan=True: If scalebychan=False setjy would use a single value per spectral window.
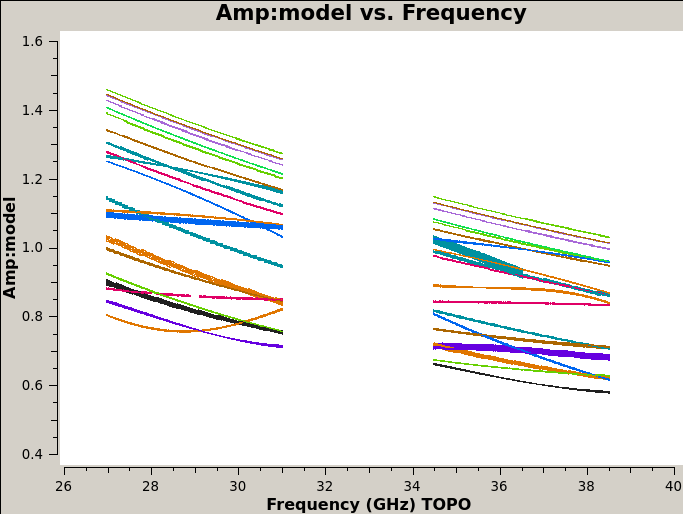
Inspecting the logger report shows that the flux density calibrator (3C147 here) has amplitudes ranging from about 1.0 to about 1.5 Jy across the spws. (Note the output sorting in increasing spw number, not in frequency.)
The model data can be plotted, e.g. for antenna ea03, by using plotms (Figure 2):
# In CASA, plot the model amplitude as function of frequency
# for baselines to antenna ea03:
plotms(vis=id_ms, xaxis='freq', field=id_flx, coloraxis='ant2',
yaxis='amp', ydatacolumn='model', antenna='ea03')
This plot shows baselines to antenna ea03. Since both a spectral and an angular model for this well resolved calibrator was provided, each baseline has a somewhat different amplitude and phase behavior as function of frequency for baselines to this antenna. Selecting another antenna for the plot will slightly change the curves. Also, a different CASA version or other update (or picking the wrong sourceName_frequencyBand model) would show a different behavior.
A) Calibrating Initial Delays and Bandpass Solutions
Start this entire bandpass calibration procedure with a phase-only, time-dependent (self-)calibration solution for the bandpass calibrator using the parameter gaintype='G' option in gaincal, which should be easy for these supposedly bright sources. Note that the calibration solutions are written to a calibration table, cal.ign, where 'ign' after the standardized calibration table prefix name (cal)stands for per-integration gain. This table is not a variable but a file/directory name in the working directory so it needs to be quoted in the input parameter. Solutions for each integration will remove most of the (phase) decorrelation of the signal allowing for the delay/bandpass calibration to succeed. For best results, the phase variations will be derived from a narrow range of channels near the centers of each spw (say 60~68 here, out of the 128 available per spw), narrow enough to not be affected by uncorrected delay (i.e., reduce possible decorrelation by excluding any large phase differences due to a phase slope over the frequency range of the spw):
# In CASA, do a phase-only self-calibration on the bandpass calibrator
# (self-calibrating amplitudes is premature before determining a
# preliminary bandpass calibration and will be done in a later step):
gaincal(vis=id_ms, caltable='cal.ign', refant=id_ref, minsnr=3,
field=id_bp, gaintype='G',
spw='*:60~68', solint='int', calmode='p')
- refant=id_ref : Use the variable identifying the reference antenna (ea05 here) as the reference antenna.
- solint='int' : Do a per-integration solve (every 6 seconds, which is the time-averaging applied to the data for this tutorial).
- minsnr=3 : Apply a minimum signal-to-noise cutoff of three. Solutions with less signal-to-noise than this value will be flagged.
- gaintable is not set here as earlier calibrations (to prepare for this tutorial have already been applied.)
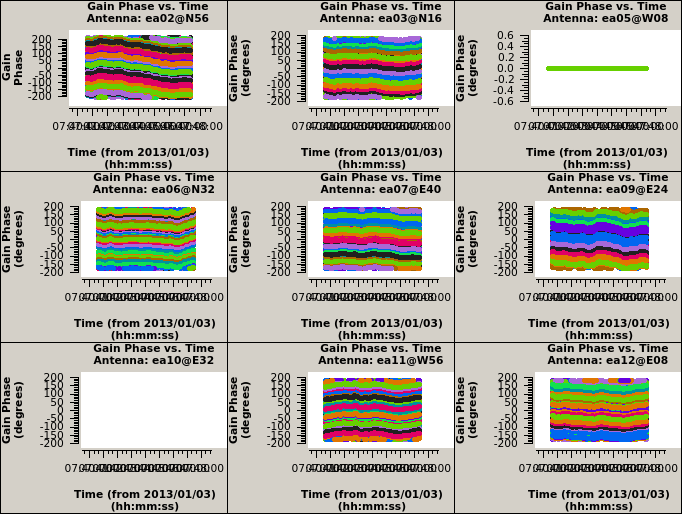
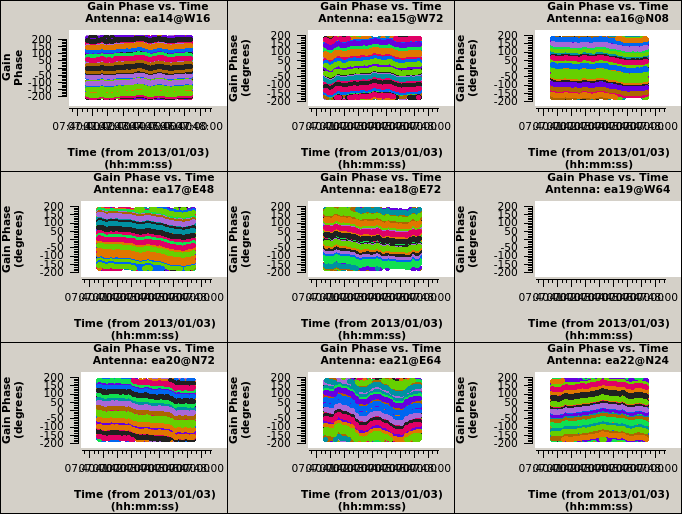
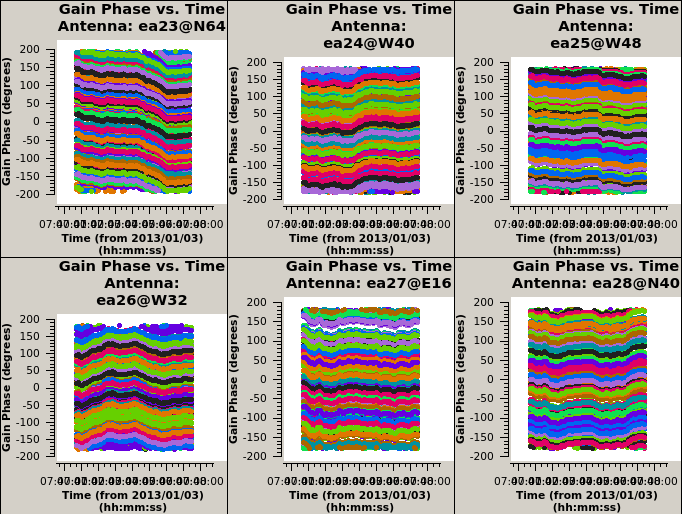
Check that the phase solutions, colored by spw, are smoothly varying, supposedly reflecting the changing phases due to atmospheric effects (i.e., for these high frequencies due to the troposphere):
# In CASA, plot phase solutions as function of time, displaying one-for-one
# a plot for baselines to each antena:
plotms(vis='cal.ign', xaxis='time', coloraxis='spw', iteraxis='antenna', yaxis='phase')
Note that the first plot showing the results for antenna ea01 is empty as ea01 previously was fully flagged, and so were ea10, ea13 and ea19 (ea04 was not part of the array configuration). Click on the green right arrow to pass through the plots for the other antennas. Also note that the reference antenna (ea05 here) has all phases equal to zero degrees, which they should be by definition for the reference antenna.
Multipanel plots of the phase solutions can be written to output files as well as to the screen display (Figures 3a, 3b, & 3c). The output files that are generated are in the format of their extention in the plotfile parameter, in this case PNG files, and if the parameter is set to create output in the working directory, can be viewed at any occasion using CASA by executing an external viewer program, e.g., !xv <visbase>_cal.ign_p1*.png; or by running an image viewing application such as xv, Preview, Gimp, Photoshop, etc., external to CASA at the operating system level. Note that the hardcopy only shows the first page, requiring three plotms instances of 3x3 plots to cover all antennas in the MS.
# In CASA, dump images of multi-panel plots for different antenna-ID ranges
# (antenna-ID 1 to 10, not 1-9 as the antenna with index 7 is not present
# as can be noticed in the MS summary <visbase>_list.txt.
# Unlike anything else in CASA-python indexing, antenna IDs start at one
# instead of zero):
plotms(vis='cal.ign', xaxis='time', yaxis='phase',
antenna='1~10', gridrows=3, gridcols=3, iteraxis='antenna',
coloraxis='spw', plotfile=visbase+'_cal.ign_p1.png')
Note that recently the name of the output file gets appended with the selection of the iteraxis (e.g., G192-BP_cal.ign_p1_Antennaea02@N56,ea03@N16,ea05@W08,ea06@N32,ea07@E40,ea09@E24,ea10@E32,ea11@W56,ea12@E08.png and there unfortunately seems to be no possibility to switch that off; to get the file name as specified in the plotfile-parameter one would edit the file name using the operating system tools.
# second page batch (next nine antennas)
plotms(vis='cal.ign', xaxis='time', yaxis='phase',
antenna='11~19', gridrows=3, gridcols=3, iteraxis='antenna',
coloraxis='spw', plotfile=visbase+'_cal.ign_p2.png')
# third page batch (remaining six antennas)
plotms(vis='cal.ign', xaxis='time', yaxis='phase',
antenna='20~26', gridrows=2, gridcols=3, iteraxis='antenna',
coloraxis='spw', plotfile=visbase+'_cal.ign_p3.png')
The next step is to solve for the residual delays using the parameter gaintype='K' option in gaincal and store the solutions in the cal.dly table (dly for delay). Note that this currently does not do a global fringe-fitting solution for delays. Instead, it determines a baseline-based delay solution per spw for all baselines to the reference antenna, treating these as antenna-based delays. In most cases, with high enough S/N to get baseline-based delay solutions, this will suffice. Avoid the edge channels of each spectral window by de-selecting them (say, select channels 5~122 here, from the 128 available per spw):
# In CASA, determine residual delays from the bandpass calibrator scans:
gaincal(vis=id_ms, caltable='cal.dly', refant=id_ref, minsnr=3,
gaintable=['cal.ign'], field=id_bp,
gaintype='K', spw='*:5~122', solint='inf')
Note that this applies the initial phase table cal.ign to reduce decorrelation due to short-term phase fluctuations (as they will be corrected by the solutions in cal.ign).
Alternatively, one can derive a delay across all spws of a baseband. If this is desired, use parameter combine='spw' in gaincal and run the task for each baseband separately (here, in four groups of 16 spw). The solutions from the second and following runs can be appended to the same calibration table via parameter append=True.
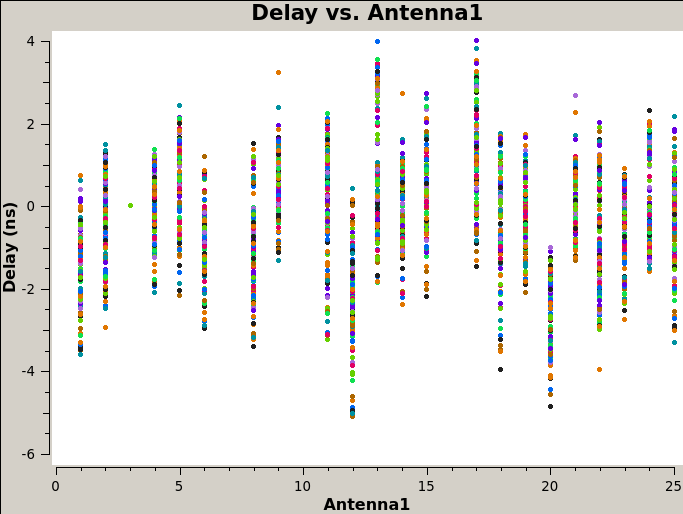
Now plot the delays as a function of antenna index (using one colored dot for each spw and polarization):
# In CASA, display the delay solutions for each spw as function of antenna-ID:
plotms(vis='cal.dly', xaxis='ant1', yaxis='delay', coloraxis='spw')
The delays range from around -5 to 4 nanoseconds (Figure 4).
Now solve for the antenna bandpasses using the previously generated tables cal.ign and cal.dly correcting for possible decorrelation due to phase and delay inaccuracies, and store the solutions in cal.bp (bp for bandpass):
# In CASA, determine the bandpass from the bandpass calibrator scans:
bandpass(vis=id_ms, caltable='cal.bp', refant=id_ref,
gaintable=['cal.ign', 'cal.dly'], field=id_bp,
solnorm=False, bandtype='B', solint='inf')
WARNING: Set solnorm=False here; otherwise there will be some offsets seen later between spws due to the way the amplitude scaling adjusts weights internally during solving.
Expect to see solutions failing due to "Insufficient unflagged antennas" — these are for bad channels that have been pre-flagged.
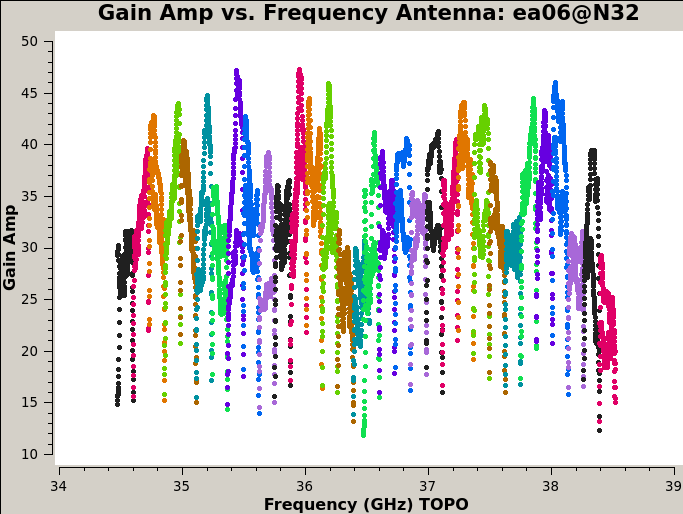
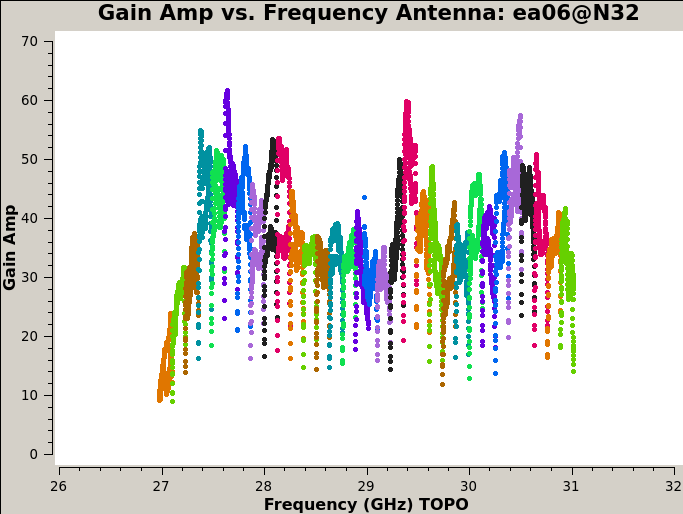
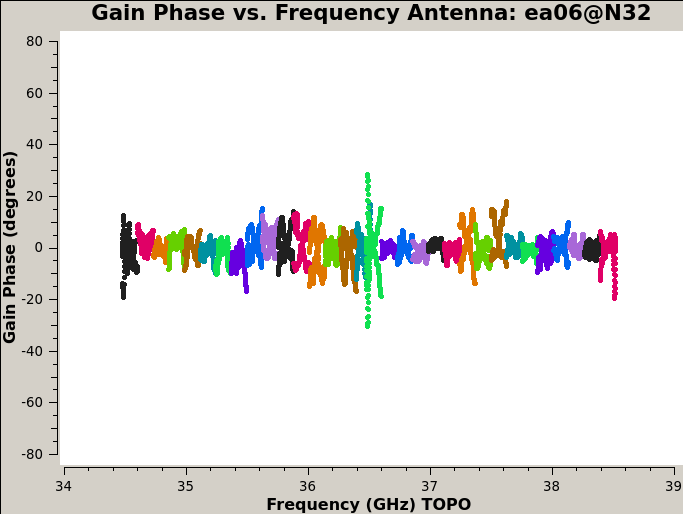
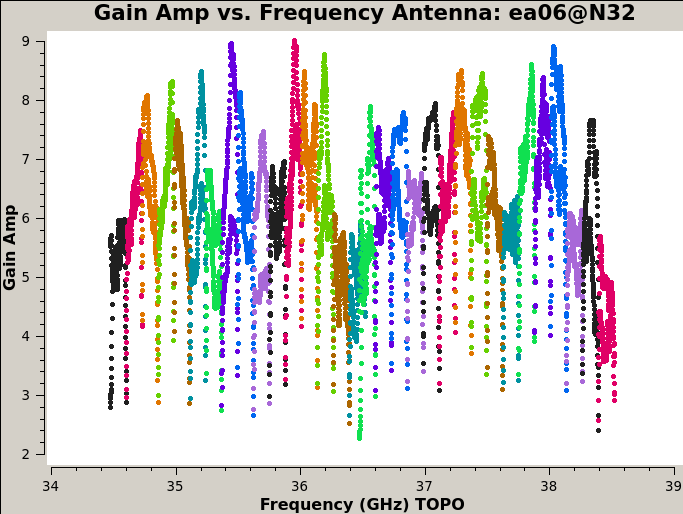
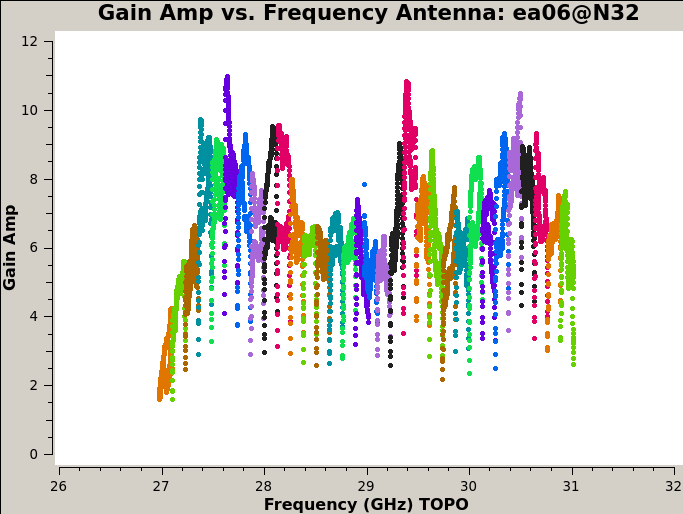
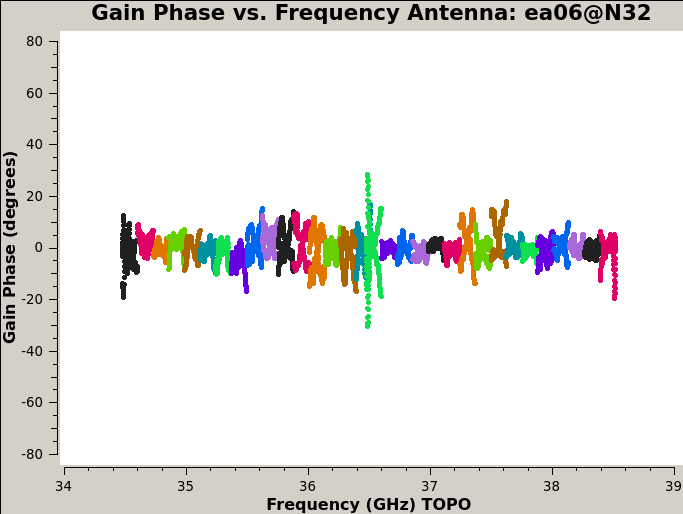
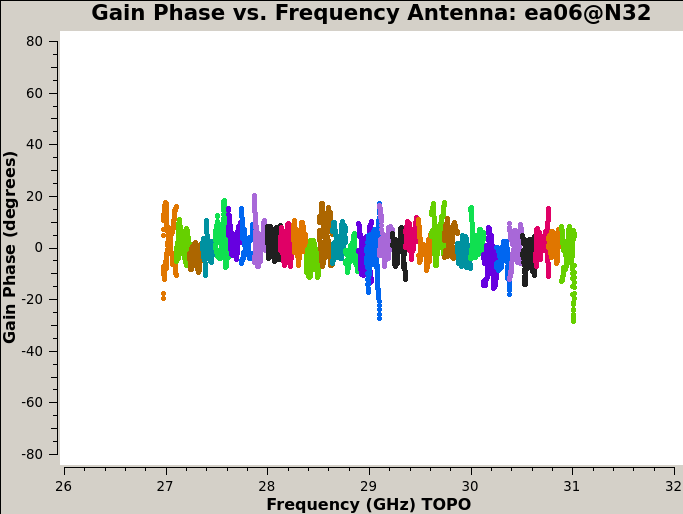
Plot the amplitude and phase soutions of this new bandpass. Note that the first panel with ea01 is empty as it is completely flagged. Proceed to ea06 to see the plots as shown in Figures 5a, 5b, 6a, and 6b:
# In CASA, display the bandpass solutions for amplitude and phase for
# the different (2x 4GHz) spw ranges; first range, amplitude:
plotms(vis='cal.bp', xaxis='freq', coloraxis='spw', iteraxis='antenna',
yaxis='amp', spw='0~31')
# second range, amplitude:
plotms(vis='cal.bp', xaxis='freq', coloraxis='spw', iteraxis='antenna',
yaxis='amp', spw='32~63')
# first range, phase:
plotms(vis='cal.bp', xaxis='freq', coloraxis='spw', iteraxis='antenna',
yaxis='phase', spw='0~31', plotrange=[-1,-1,-80,80])
# second range, phase:
plotms(vis='cal.bp', xaxis='freq', coloraxis='spw', iteraxis='antenna',
yaxis='phase', spw='32~63', plotrange=[-1,-1,-80,80])
B) Applying the Initial Bandpass Solutions to the Flux Density Calibrator
Since there is no a priori spectral information for the chosen bandpass calibrator (here 3c84-J0319+413), bootstrapping it is needed to determine its spectral behavior. This information is then used to re-determine the bandpass in order to avoid folding the intrinsic spectral shape of the bandpass calibrator into the bandpass calibration.
First, repeat the phase-only self-calibration solution with the preliminary determined delay and bandpass calibration in step A, this time for both the bandpass and the flux density calibrator (which need to be separated by a comma) and store the solutions in cal.ign2pha (use the 2pha to distinguish it as the second stage for phase-only). This will correct for short-term phase decorrelation of the signals. Similarly to avoid decorrelation due to a wide frequency range, use the narrow center channel range (which was channel 60~68):
# In CASA, phase-only self-calibrate the flux density and bandpass calibrators
# the same way by using the obtained first-step bandpass calibration above:
gaincal(vis=id_ms, caltable='cal.ign2pha', refant=id_ref, minsnr=3,
gaintable=['cal.dly', 'cal.bp'], field=id_flx+','+id_bp,
gaintype='G', solint='int', calmode='p')
This again allows to calibrate both phase and gain for each scan, now corrected (biased) with the delay and bandpass of the bandpass calibrator. Store the solutions in cal.ign2 (use the 2 to distinguish it as the second pass gain calibration):
# In CASA, now self-calibrate the phase-corrected amplitudes as well:
gaincal(vis=id_ms, caltable='cal.ign2', refant=id_ref, minsnr=3,
gaintable=['cal.dly', 'cal.bp','cal.ign2pha'], field=id_flx+','+id_bp,
gaintype='G', solint='inf', calmode='ap')
C) Bootstrapping the Bandpass Calibrator Field Spectrum
With full, phase and amplitude gain solutions for both the flux density and bandpass calibrators, now use fluxscale to scale the gain amplitudes of the bandpass calibrator using those of the flux density calibrator. Store the solutions in cal.bpflx and the flux density results for the bandpass calibrator in <visbase>+'_'+id_bp+'_fluxinfo.txt':
# In CASA, determine the bandpass calibrator fluxes as function of frequency by
# using the fluxes set for the flux density calibrator with setjy earlier and
# store the output dictionary with these values in the variable flux_bp:
flux_bp = fluxscale(vis=id_ms, caltable='cal.ign2',
fluxtable='cal.bpflx', reference=id_flx, transfer=id_bp,
listfile=visbase+'_'+id_bp+'_fluxinfo.txt', fitorder=1)
- flux_bp = fluxscale(...): the python dictionary returned by the fluxscale task will be stored in the flux_bp variable. Inspect the dictionary flux_bp by typing "print flux_bp" at the CASA command line. Alternatively, when not interested in the dictionary type fluxscale(...); with a semicolon after the parentheses and not assigning it to a variable. This will prevent the dictionary to be printed in the terminal. Here however the dictionary is captured in flux_bp as it is going to be used below.
- fluxtable='cal.bpflx': this is the output scaled gain table containing the flux density of the bandpass calibrator as function of frequency. Since this is only used to find the spectral index of the bandpass calibrator source field, this table is not used further.
- listfile=visbase+'_'+id_bp+'_fluxinfo.txt': an output file that contains the derived flux values and fit information.
- fitorder=1: only find a (linear) spectral index, ignoring curvature in the spectrum.
- reference=id_flx: the reference field from which the flux scaling is transferred (here: the flux density calibrator 3C147, field 0, assigned by id_flx)
- transfer=id_bp: the target field to which the flux scaling is transferred (here: the bandpass calibrator 3c84-J0319+413, field 1, assigned by id_bp)
The last line in the file (and displayed in the logger) shows, using the default model supplied with this CASA version:
Fitted spectrum for 3c84-J0319+413 with fitorder=1: Flux density = 27.1659 +/- 0.0318191 (freq=32.5128 GHz) spidx: a_1 (spectral index) =-0.625709 +/- 0.00965836
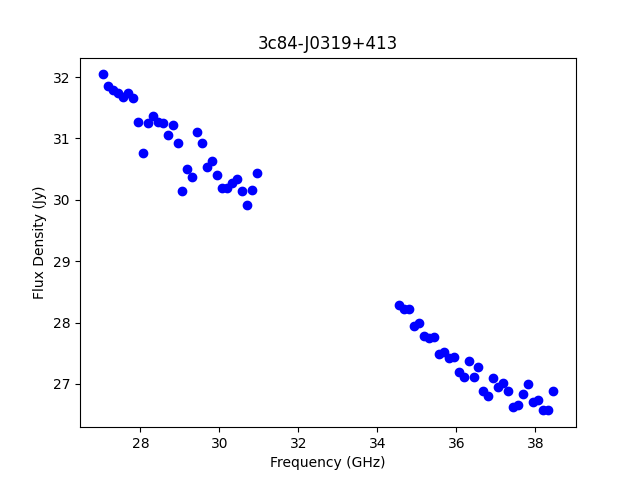
Exercise of using Python within CASA to generate a plot using matpoltlib
As an exercise in using Python within CASA, the following section shows how to use Python and matplotlib in order to generate a plot using the information in the returned flux_bp dictionary (Figure 7). Note that is is an optional exercise and is not required in order to continue processing the data and can be skipped. The Python script will iterate over two loops to fill the parameter variables used in the plotting.
Note that the use of ipython in the command line requires the use of "%cpaste" to allow copy/pasting of loops, conditions, etc.. Press Enter (or Return) after "--" at the end. This exits the copy/paste prompt and will return the CASA command line prompt.
# In CASA, use python code to plot the model spectrum of the bandpass calibrator:
import matplotlib.pyplot as pl
%cpaste
# Press Enter or Return, then copy/paste the following:
freq = flux_bp['freq'] / 1e9
spw_list = range(0,64)
spw_str = []
for i in spw_list:
thisspw = str(i)
spw_str.append(thisspw)
bootstrapped_fluxes = []
for j in spw_str:
thisflux = flux_bp['1'][j]['fluxd'][0]
if thisflux == None:
continue
else:
bootstrapped_fluxes.append(thisflux)
pl.clf()
pl.plot(freq, bootstrapped_fluxes, 'bo')
pl.xlabel('Frequency (GHz)')
pl.ylabel('Flux Density (Jy)')
pl.title(id_bp)
pl.savefig('bandpass.png')
--
End of Python exercise.
The model from fluxscale
is used to fill the MODEL column with the bandpass
source's spectral information using
setjy.
With standard='fluxscale' , we can directly use the
flux_bp python dictionary as input via fluxdict:
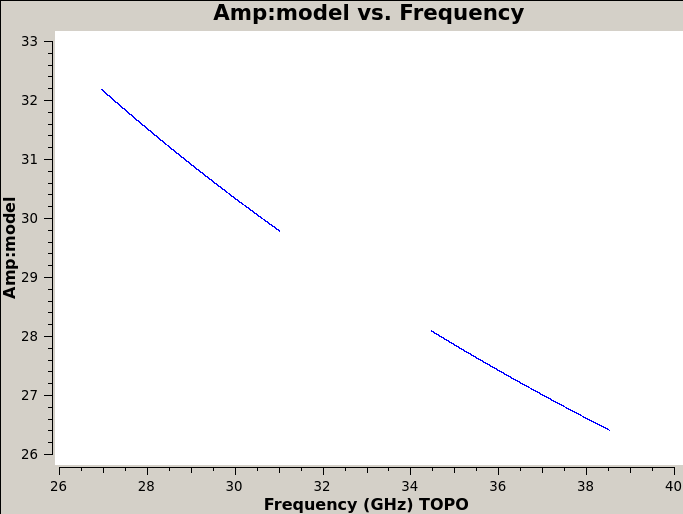
# In CASA, insert the spectral information for the bandpass calibrator field:
setjy(vis=id_ms, field=id_bp, scalebychan=True,
standard = 'fluxscale', fluxdict=flux_bp, usescratch=True);
Check with plotms that the data have been appropriately filled (Figure 8):
# In CASA, display the spectral model of the bandpass calibrator field, in this
# case for a specific baseline (which should be identical for all baselines
# for a point-like source, otherwise it will depend on baseline length):
plotms(vis=id_ms, field=id_bp, antenna='ea05&ea02',
xaxis='freq', yaxis='amp', ydatacolumn='model')
D) Creating a New Bandpass using the Bandpass Calibrator Spectral Model
Next, redo the previous calibration using this new model information as if it were a standard flux density calibrator. Although the commands are the same as issued earlier, keep in mind that the model values for the bandpass calibrator have changed and, therefore, the results of these calibration calculations accordingly will differ if the specral index differs significanlty from the spectral index of the flux density calibrator:
# In CASA, redo a phase-only self-calibration on the bandpass calibrator:
gaincal(vis=id_ms, caltable='cal.ign.redo', refant=id_ref, minsnr=3,
field=id_bp, gaintype='G',
spw='*:60~68', solint='int', calmode='p')
# In CASA, re-determine residual delays from the bandpass calibrator scans:
gaincal(vis=id_ms, caltable='cal.dly.redo', refant=id_ref, minsnr=3,
gaintable=['cal.ign.redo'], field=id_bp,
gaintype='K', spw='*:5~122', solint='inf')
# In CASA, re-determine the bandpass from the bandpass calibrator scans:
bandpass(vis=id_ms, caltable='cal.bp.redo', refant=id_ref,
gaintable=['cal.ign.redo', 'cal.dly.redo'], field=id_bp,
solnorm=False, bandtype='B', solint='inf')
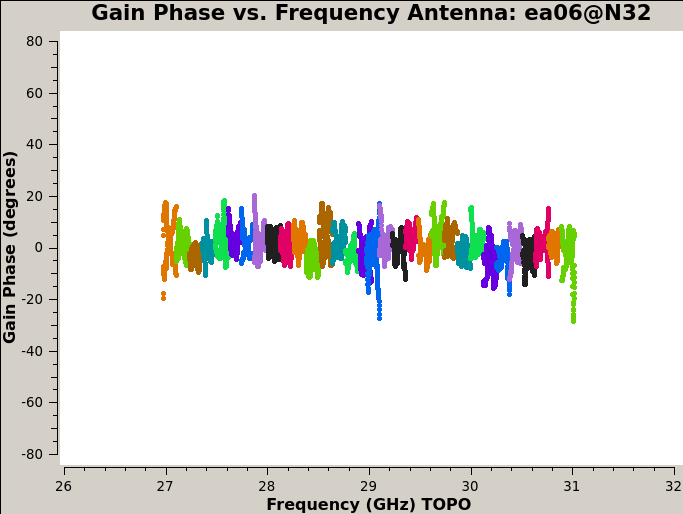
Finally, inspect these solutions (Figures 9a, 9b, 10a, and 10b; again note that antenna ea01 is fully flagged):
# In CASA, display and check the bandpass solutions; first range, amplitude:
plotms(vis='cal.bp.redo', xaxis='freq', coloraxis='spw', iteraxis='antenna',
yaxis='amp', spw='0~31')
# second range, amplitude:
plotms(vis='cal.bp.redo', xaxis='freq', coloraxis='spw', iteraxis='antenna',
yaxis='amp', spw='32~63')
# first range, phase:
plotms(vis='cal.bp.redo', xaxis='freq', coloraxis='spw', iteraxis='antenna',
yaxis='phase', spw='0~31', plotrange=[-1,-1,-80,80])
# second range, phase:
plotms(vis='cal.bp.redo', xaxis='freq', coloraxis='spw', iteraxis='antenna',
yaxis='phase', spw='32~63', plotrange=[-1,-1,-80,80])
As in this particualr observation the spectral indices for the flux density calibrator (3C147: -0.696, standard) and the bandpass calibrator (3c84-J0319+413: -0.626, derived here) are very similar, the solutions look virtually unchanged from the previous solutions with the exception that the amplitude scaling is corrected for the spectrum of the bandpass calibrator. These steps yielded the final version of the delay and bandpass calibration tables, cal.dly.redo and cal.bp.redo, which now would be used for all subsequent calibration steps.
Last checked on CASA Version 6.5.4
Cheat Sheet - All Commands Summarized
In the tutorial above, these commands were used. Apart from the %cpaste section (that requires typing the double dash -- to end the section), all commands are intended to be single-line commands and the space-indented line commands are informational (mostly plots) rather than essential. Obviously, lines starting or include with a hash-tag, the octothorp #, are comment lines and need not be issued.
Note that the automatic formatting by the browser may introduce some weirdness in displaying the pre-formatted text and single line commands; be aware when copy/pasting that the line is complete, i.e., the task commands must be ending with the closing parenthesis and/or semicolon.
# in a terminal, outside of CASA
wget http://casa.nrao.edu/Data/EVLA/G192/G192-BP.ms.tar.gz
tar -xzf G192-BP.ms.tar.gz
casa -r 6.5.4-9-pipeline-2023.1.0.124
# inside CASA, on command line
visbase='G192-BP'
id_ms=visbase+'.ms'
listobs(vis=id_ms,listfile=visbase+'_list.txt');
id_flx='3C147'
id_bp='3c84-J0319+413'
plotants(vis=id_ms,antindex=True,logpos=True, figfile=id_ms+'_plotants.pdf')
id_ref='ea05'
setjy(vis=id_ms,field=id_flx,scalebychan=True,standard='Perley-Butler 2017',model=id_flx+'_A.im',usescratch=True);
plotms(vis=id_ms,field=id_flx,antenna='ea03',xaxis='freq',yaxis='amp',ydatacolumn='model',coloraxis='ant2')
# *** Step A) ***
gaincal(vis=id_ms,caltable='cal.ign',field=id_bp,spw='*:60~68',gaintype='G',refant=id_ref,calmode='p',solint='int',minsnr=3)
plotms(vis='cal.ign',xaxis='time',yaxis='phase',iteraxis='antenna',coloraxis='spw')
plotms(vis='cal.ign',xaxis='time',yaxis='phase',antenna='1~11',gridrows=3,gridcols=3,iteraxis='antenna',coloraxis='spw',plotfile=visbase+'_cal.ign_p1.png')
plotms(vis='cal.ign',xaxis='time',yaxis='phase',antenna='12~20',gridrows=3,gridcols=3,iteraxis='antenna',coloraxis='spw',plotfile=visbase+'_cal.ign_p2.png')
plotms(vis='cal.ign',xaxis='time',yaxis='phase',antenna='21~26',gridrows=2,gridcols=3,iteraxis='antenna',coloraxis='spw',plotfile=visbase+'_cal.ign_p3.png')
gaincal(vis=id_ms,caltable='cal.dly',field=id_bp,spw='*:5~122',gaintype='K',gaintable=['cal.ign'],refant=id_ref,solint='inf',minsnr=3)
plotms(vis='cal.dly',xaxis='ant1',yaxis='delay',coloraxis='spw')
bandpass(vis=id_ms,caltable='cal.bp',gaintable=['cal.ign','cal.dly'],field=id_bp,refant=id_ref,solnorm=False,bandtype='B',solint='inf')
plotms(vis='cal.bp',xaxis='freq',yaxis='amp',spw='0~31',iteraxis='antenna',coloraxis='spw',plotrange=[-1,-1,0,80])
plotms(vis='cal.bp',xaxis='freq',yaxis='amp',spw='32~63',iteraxis='antenna',coloraxis='spw',plotrange=[-1,-1,0,80])
plotms(vis='cal.bp',xaxis='freq',yaxis='phase',spw='0~31',iteraxis='antenna',coloraxis='spw',plotrange=[-1,-1,-80,80])
plotms(vis='cal.bp',xaxis='freq',yaxis='phase',spw='32~63',iteraxis='antenna',coloraxis='spw',plotrange=[-1,-1,-80,80])
# *** Step B) ***
gaincal(vis=id_ms,caltable='cal.ign2pha',field=id_flx+','+id_bp,gaintable=['cal.dly','cal.bp'],gaintype='G',refant=id_ref,calmode='p',solint='int',minsnr=3)
gaincal(vis=id_ms,caltable='cal.ign2',field=id_flx+','+id_bp,gaintable=['cal.dly','cal.bp','cal.ign2pha'],gaintype='G',refant=id_ref,calmode='ap',solint='inf',minsnr=3)
# *** Step C) ***
flux_bp=fluxscale(vis=id_ms,caltable='cal.ign2',fluxtable='cal.bpflx',reference=id_flx,transfer=id_bp,listfile=visbase+'_'+id_bp+'_fluxinfo.txt',fitorder=1)
import matplotlib.pyplot as pl
%cpaste
freq = flux_bp['freq'] / 1e9
spw_list = range(0,64)
spw_str = []
for i in spw_list:
thisspw = str(i)
spw_str.append(thisspw)
bootstrapped_fluxes = []
for j in spw_str:
thisflux = flux_bp['1'][j]['fluxd'][0]
if thisflux ==None:
continue
else:
bootstrapped_fluxes.append(thisflux)
pl.clf()
pl.plot(freq,bootstrapped_fluxes,'bo')
pl.xlabel('Frequency (GHz)')
pl.ylabel('Flux Density (Jy)')
pl.title(id_bp)
pl.savefig('bandpass.png')
--
setjy(vis=id_ms,field=id_bp,scalebychan=True,standard='fluxscale',fluxdict=flux_bp,usescratch=True);
plotms(vis=id_ms,field=id_bp,antenna='ea05&ea02',xaxis='freq',yaxis='amp',ydatacolumn='model')
# *** Step D) ***
gaincal(vis=id_ms,caltable='cal.ign.redo',field=id_bp,spw='*:60~68',gaintype='G',refant=id_ref,calmode='p',solint='int',minsnr=3)
gaincal(vis=id_ms,caltable='cal.dly.redo',gaintable=['cal.ign.redo'],field=id_bp,spw='*:5~122',gaintype='K',refant=id_ref,solint='inf',minsnr=3)
bandpass(vis=id_ms,caltable='cal.bp.redo',gaintable=['cal.ign.redo','cal.dly.redo'],field=id_bp,refant=id_ref,solnorm=False,bandtype='B',solint='inf')
plotms(vis='cal.bp.redo',xaxis='freq',yaxis='amp',spw='0~31',iteraxis='antenna',coloraxis='spw',plotrange=[-1,-1,0,15])
plotms(vis='cal.bp.redo',xaxis='freq',yaxis='amp',spw='32~63',iteraxis='antenna',coloraxis='spw',plotrange=[-1,-1,0,15])
plotms(vis='cal.bp.redo',xaxis='freq',yaxis='phase',spw='0~31',iteraxis='antenna',coloraxis='spw',plotrange=[-1,-1,-80,80])
plotms(vis='cal.bp.redo',xaxis='freq',yaxis='phase',spw='32~63',iteraxis='antenna',coloraxis='spw',plotrange=[-1,-1,-80,80])
###